Decorrelation Sensitivity of Auditory Nerve and Anteroventral Cochlear Nucleus Fibers to Broadband and Narrowband Noise

Abstract

Binaural neurons show remarkable sensitivity to temporal differences in the waveforms at the two ears. This ability obviously requires temporal coding of sound waveforms in the monaural afferents that converge on such binaural neurons. We introduce a new analysis to investigate how well responses of single monaural neurons support discrimination of decorrelations in waveforms. Spike trains from auditory nerve (AN) and anteroventral cochlear nucleus (AVCN) neurons of cats to many repetitions of a set of broadband and narrowband noise tokens were obtained. The normalized correlation between the noise tokens ranged from 0.99 to –1. A coincidence and signal detection analysis was used to perform a correlation discrimination task using the monaural spike trains. The correlation discrimination thresholds derived from AVCN neurons were lower than those derived from AN fibers and sometimes as low as human psychophysical just noticeable differences. Importantly, low detection thresholds required comparisons of spike trains at small internal delays. Bandwidth dependence of neural decorrelation thresholds agreed with psychophysical data when large internal delays contributed to the detection. We conclude that, in the context of correlation discrimination, coding by AVCN fibers is superior to that by AN fibers and that these discriminations require a distribution of internal or best delays in binaural processing that differs from the predictions from studies of discrimination in interaural time delays.

Introduction

Sensitivity to interaural sound differences helps human spatial perception. The vast majority of binaural physiological studies has addressed the remarkable sensitivity to interaural time differences (ITDs). However, humans also show an exquisite sensitivity to other forms of binaural differences. This ability has been extensively studied psychophysically (for review, see Durlach and Colburn, 1978) and puts different constraints on the binaural system than the processing of ITDs. Early psychophysical work (Licklider, 1948; Sayers and Cherry, 1957) revealed that the interaural correlation of the waveforms to the two ears is a core concept to understand human performance on a variety of binaural tasks. Therefore, understanding of binaural processing will benefit from physiological study of sensitivity to interaural correlation.

In psychoacoustic studies, sensitivity to interaural correlation has been measured extensively and systematically by mixing independent noise sources (Pollack and Trittipoe, 1959a; Gabriel and Colburn, 1981; Koehnke et al., 1986; Bernstein and Trahiotis, 1996; Culling et al., 2001; Boehnke et al., 2002). Single-neuron sensitivity to such stimuli, in which the normalized correlation is the primary parameter varied, has received little attention. Yin et al. (1987) in the cat and Albeck and Konishi (1995) in the barn owl found that binaural cells are sensitive to interaural correlation in a manner that agrees with a cross-correlation model. Recent studies analyzed such responses with a signal detection theoretic approach (Coffey et al., 2004; Shackleton et al., 2005). Remarkably, the interaural correlation thresholds of binaural cells in the inferior colliculus (IC) of the guinea pig were high compared with human psychophysical just noticeable differences (jnds) (Shackleton et al., 2005), whereas the same cells discriminate ITDs as well as humans do (Shackleton et al., 2003).

Sensitivity to temporal interaural differences obviously requires temporal information in the monaural afferents projecting to the sites of binaural integration. This temporal coding has been well studied but not in the framework of binaural performance. In the present paper, we study how well monaural input pathways, auditory nerve (AN) and trapezoid body (TB), support the discrimination of interaural changes in correlation. Recently, we proposed the correlogram as a tool for quantification of neural responses to arbitrary stimuli (Joris, 2003; Louage et al., 2004, 2005). These correlograms, in fact, describe the output of an array of coincidence detectors. Coincidence detection is used by the binaural neurons of the medial superior olive (Goldberg and Brown, 1969; Moushegian et al., 1975; Yin and Chan, 1990). Here, we extend the use of correlograms within the framework of detection theory (Green and Swets, 1966). Based on monaural responses, we determine the performance of an “ideal observer” in a correlation discrimination task and compare this performance with human psychophysical jnds. We reported previously that responses of TB fibers to broadband noise show enhanced temporal properties when compared with those of AN fibers (Louage et al., 2005), and here we report that decorrelation discrimination based on responses of single TB fibers is better than those based on AN fibers and sometimes as good as human psychophysical performance.

Materials and Methods

Animal preparation. We recorded from the AN and the TB in separate experiments. Cats with normal eardrums and middle ears were anesthetized with a mixture of acepromazine (0.2 mg/kg) and ketamine (20 mg/kg). A venous cannula allowed infusion of Ringer's solution and sodium pentobarbital at doses sufficient to maintain an areflexic state. A tracheostoma was made, the pinnae were removed, and the bullae were exposed and vented with a 30-cm-long polyethylene tube (inner diameter of 0.9 mm). The animal was placed in a double-walled soundproof room (Industrial Acoustics Company, Niederkrüchten, Germany). In AN experiments, the nerve trunk was exposed via a posterior fossa craniotomy. In TB experiments, a laryngopharyngectomy was performed and the basioccipital bone was exposed after resection of the prevertebral muscles. The TB was exposed by drilling a longitudinal slit as close as possible to the medial wall of the bulla and ∼3–5 mm rostral to the jugular foramen. A micromanipulator was used to support a hydraulic microdrive (Trent Wells, Coulterville, CA). Glass micropipettes, filled with 3 m NaCl or KCl, were positioned in the TB under visual control, just lateral or medial to the rootlets of the abducens nerve. The angle of penetration ranged from 0 to 30° mediolaterally relative to the midsagittal plane. After placing the electrode in the TB, the basioccipital bone was covered with warm 3% agar.

Instrumentation. Dynamic phones (supertweeter; Radio Shack, Fort Worth, TX) were connected to hollow Teflon earpieces, which fit tightly in the transversely cut ear canals. Custom software, run within Matlab (MathWorks, Natick, MA) on a personal computer, was used to synthesize the stimuli and control the digital hardware (Tucker-Davis Technologies, Alachua, FL). The transfer function of the closed acoustic assembly was obtained via a probe whose tip was placed within 2 mm of the ear drum and that was coupled to a ½ inch (12.7 mm) condenser microphone and conditioning amplifier (Brüel and Kjær, Nærum, Denmark). All stimuli were compensated for this transfer function, and the stimuli were specified in sound pressure level (SPL) (decibels relative to 20 μPa). The neural signal was amplified and filtered (300 Hz to 3 kHz) (DAM 80; World Precision Instruments, Sarasota, FL), and spikes were converted to standard transistor–transistor logic pulses with a custom-built peak detection circuit. These pulses were timestamped to an accuracy of 1 μs (ET-1; Tucker-Davis Technologies).

Stimuli and data collection. The search stimulus was a noise burst (duration of 300 ms, repeated every 500 ms, 70 dB SPL, bandwidth of 40 kHz). When recording from the TB, the search stimulus was delivered to both ears. When the activity of a single fiber was isolated, the excitatory ear was determined. Binaural neurons were occasionally encountered but are not considered in this report. Spontaneous rate (SR), minimum rate threshold, and characteristic frequency (CF) of single fibers were measured using an automated threshold-tracking program. Short tone bursts at CF (duration of 25 ms, repeated every 100 ms, 200 repetitions, rise–fall time of 2.5 ms, starting in sine phase) were then presented at increasing SPL in 10 dB steps. Various response metrics were displayed on-line.

Next, a rate-level function was obtained to a broadband Gaussian noise (1000 ms, repeated every 1200 ms, 5–10 repetitions). The bandwidth of the broadband noise was set from 50 to 8000 Hz or from 100 to 35000 Hz, depending on CF. The broadband noise was presented from 10 to 90 dB SPL in 5 or 10 dB steps. A rate-level function was also obtained to a narrowband Gaussian noise (bandwidth of the narrowband noise was 100 Hz and centered on the CF of the fiber).

After the basic physiological parameters and rate-level functions of a fiber were collected, we started testing its decorrelation sensitivity with broadband noise by recording responses to eight broadband tokens. These noise tokens N_α(t) were calculated by mixing (Fig. 1 A) two independent tokens of Gaussian broadband (50–8000 or 100–35000 Hz) noise, A(t) and B(t), according to the equation

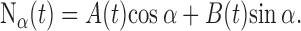(1)

A straightforward calculation (van der Heijden and Trahiotis, 1997) shows that the normalized correlation ρ_αβ between two of such mixtures, N_α(t) and N_β(t), equals

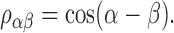(2)

By using a set of equally spaced mixing angles, α = 0, Δ, 2Δ..., adjacent pairs of noise tokens have the same mutual correlation cosΔ. Noise tokens with spacing 2Δ have correlation cos2Δ, etc. Equal spacing thus results in multiple pairs of tokens having the same correlation. Using a spacing Δ of 0.1415 radians, our set of mixing angles was α = 0, Δ, 2Δ, 3Δ, 4Δ, 5Δ, π /2, π (Fig. 1 A). Figure 1 B shows the correlation values between the noise tokens corresponding to α = 0, Δ, 2Δ (horizontal dimension) and α = 0, Δ, 2Δ, 3Δ, 4Δ, 5Δ, π /2, π (vertical dimension). The six largest values of ρ thus obtained are 1, 0.99, 0.96, 0.91, 0.84, and 0.76. Our choice of spacing results in many pairs representing small decorrelations from ρ = 1, thus improving the sampling in the region of the expected discrimination threshold. All possible pairs of noise tokens yielded 18 different correlation values. In general, actual correlation values vary around the expected ρ with a variance that increases with shorter duration, narrower bandwidth, and expected correlation. Because of the long duration (1000 ms) and the large bandwidth of the noise samples, the actual value of ρ between our tokens differed <1% from the expected value of ρ. The number of repetitions, usually 25–65, was chosen to collect ∼3000 spikes per token. Noise tokens were presented in a fixed order, and the next token was delivered after all repetitions of the previous token were presented; we refer to all repetitions of the eight noise tokens as a sequence. Sequences were presented at SPLs chosen on the basis of the rate-level function for broadband noise. The first level tested was in the middle of the dynamic range, the second at saturation level, and the third at ∼10 dB above the rate threshold.

Figure 1.

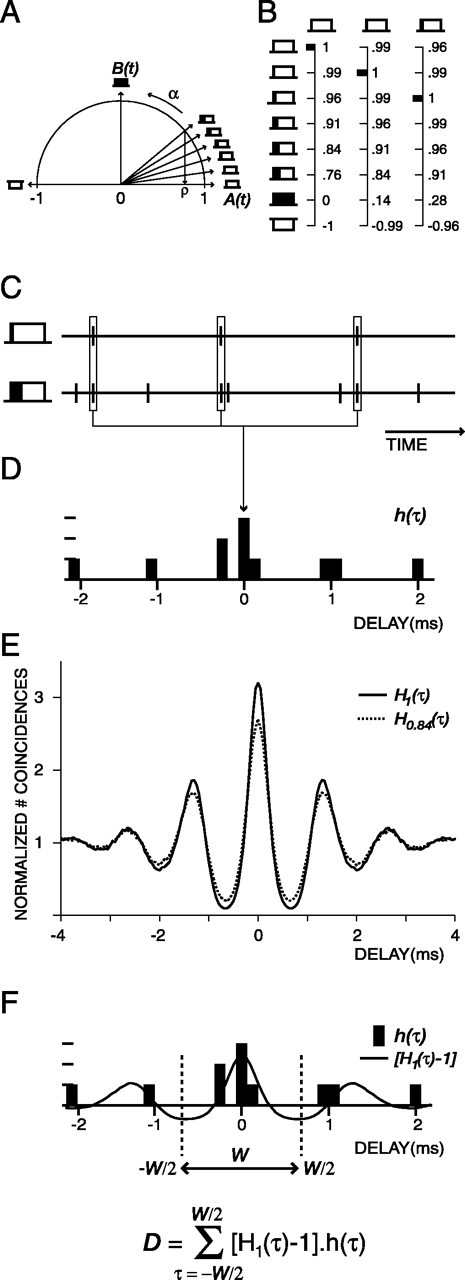
Construction of the stimuli and the decision variable. A, The unit circle represents the eight mixing angles, α, and the rectangles symbolically represent the corresponding noise tokens. B, Mutual correlations between the noise tokens. Columns represent the mutual correlation between the first, second, and third token with the other tokens. Large correlations occur many times. C, Two spike trains obtained from two noise tokens. D, The correlogram h(τ) is obtained from the responses shown under C. E, The average correlograms H_ρ(τ) obtained from responses to perfectly correlated waveforms (ρ = 1; solid line) and partially decorrelated waveforms (ρ = 0.84; dashed line). F, Weighting the correlogram h(τ) with the weighting function [H₁(τ) – 1] and integrating over a certain range of delays W yields the decision variable D.

After presenting sequences with broadband tokens at three SPLs, we switched to sequences with narrowband tokens at three SPLs. These tokens were obtained by mixing two independent samples of narrowband (CF –50 to CF +50 Hz) Gaussian noise according to Equation 1. The set of expected normalized correlations was the same as for the broadband noise. The actual normalized correlation differed from the expected values by <10%. The SPLs at which sequences were presented were chosen on the basis of the rate-level function for narrowband noise in a similar way as with the broadband noise. If time allowed, responses to broadband and narrowband sequences were collected at additional SPLs.

Synchronization to tones. From the short pure tone responses, vector strength (R) was determined; R is the Fourier component of the peristimulus time histogram (PSTH) at the stimulus frequency, normalized by the total number of spikes (Goldberg and Brown, 1969), and was calculated over an analysis window of 10–25 ms relative to the stimulus onset to eliminate the onset response, which was not always in phase with the sustained response. Significance (p < 0.001) of phase locking was evaluated with the Rayleigh test (Mardia and Jupp, 2000).

PSTH classification. Fibers of the TB were classified into different categories based on the shape of their PSTH (bin width, 0.1 ms) to short pure tone bursts at CF, presented at multiple SPLs, including at least 60, 70, and 80 dB SPL. “Primary-like” (PL) PSTHs resemble those of AN fibers, with an initial peak followed by a monotonic decline in rate to a steady-state response (Pfeiffer, 1966). “Primary-like-with-notch” (PL_N) fibers have PSTHs with a brief notch after the initial peak. This notch is difficult to detect for fibers that phase lock and have a CF lower than 1200 Hz (Pfeiffer, 1966; Smith et al., 1993), and such fibers were therefore classified as “phase-lockers” (PHLs). PSTHs with regularly spaced peaks of discharge whose period was unrelated to the stimulus waveform were classified as “chopper” (CHOP). We sometimes obtained PSTHs whose initial peak had an unusually long latency (>11 ms): these PSTHs were classified as “unusual.” Fibers for which no responses to short tone bursts were available were classified as “no PSTH.”

Discriminability of decorrelated noise tokens. We used signal detection theory (Green and Swets, 1966) to determine the discriminability of changes in correlation by an ideal observer that has available the relative spike times to different waveforms. As in the bulk of psychophysical studies, we chose a base or reference condition of either ρ = 1 or ρ = 0. Thus, we determine the neural threshold at which a decrease in correlation of perfectly correlated waveforms (ρ = 1) becomes detectable and the neural threshold at which an increase in correlation of uncorrelated waveforms (ρ = 0) becomes detectable.

Figure 1 shows how the spike times of two spike trains were converted into a decision variable D. The spike trains were binned with Δτ wide (50 μs) bins, and the time intervals between all spikes of the two spike trains were measured (Fig. 1C). These intervals were tallied in a histogram h(τ) (Fig. 1 D) whose bin values were divided by the normalization factor r_A r_B Δτ T, where r_A and r_B are the average spike rates of the two spike trains, and T is the duration of the spike trains. For a detailed discussion of this factor, see Louage et al. (2004). When averaging the histograms of Figure 1 D over all possible waveform pairs having a given stimulus correlation ρ, the grand histogram or correlogram is obtained (Fig. 1 E: solid line, ρ = 1; dotted line, ρ = 0.84). Each correlogram provides an exhaustive description of the relative timing characteristics of the responses to the two waveforms and, at ρ = 1, is identical to the shuffled autocorrelogram (SAC) that we described in previous publications (Louage et al., 2004).

Now the ideal observer has to decide whether the time intervals obtained from a single pair of responses (Fig. 1 D) are evoked by either identical waveforms or slightly decorrelated waveforms. In terms of the histograms in Figure 1, the question is whether the single histogram h(τ) (Fig. 1 D) is a realization of either the ρ = 1 correlogram H₁(τ) (Fig. 1 E, solid line) or of, say, a ρ = 0.84 correlogram H_0.84(τ) representing slightly decorrelated waveform pairs (Fig. 1 E, dashed line). It is obvious that not all bins of h(τ) are equally useful for this decision: the two correlograms H₁(τ) and H_0.84(τ) differ predominantly at their central and secondary peaks, whereas their flanks are nearly identical. What is needed is a set of weighting factors to convert the differences between the curves into a single decision variable while taking into account the sizes and signs of the local differences (Cramér, 1946). In our case, the varied stimulus parameter is ρ. To arrive at a decision variable that is optimized for detecting variations of ρ, one must take the weighting factors w(τ) proportional to the local changes of H_ρ(τ) induced by changes in ρ from unity. For instance, if we are interested in the change of H(τ) induced by a small decrease of ρ from a value of 1, a practical choice for the weighting factors would be w(τ) = H₁(τ) – H_0.9(τ). Figure 2, first row, shows the effect of changes in ρ for two AN fibers. The curves in the panels of the first row are grand correlograms of spike trains corresponding to waveforms with ρ values as indicated in the legend. For the low-CF fiber (Fig. 2 A), the correlograms scale down to a flat line at unity when ρ changes from 1 to 0 and next resume an oscillatory shape, in anti-phase compared with ρ = 1 when ρ changes from 0 to –1. Figure 2 B shows correlograms obtained from responses of a high-CF fiber. When ρ changes from 1 to 0, the correlograms scale down to a flat line at unity value and resume their original shape at ρ =–1. The correlograms corresponding to ρ =±1 are virtually identical.

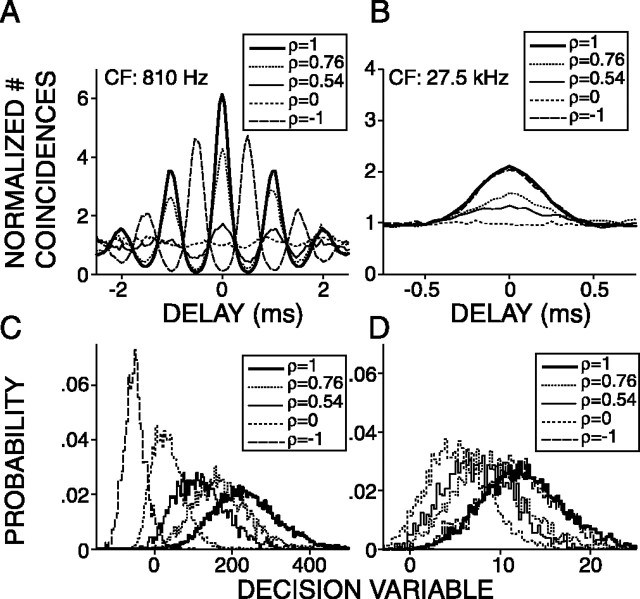
Figure 2.

Top row, Average correlograms of responses to broadband noise tokens (bandwidth, 100–30000 Hz; duration, 1000 ms) for different values of correlation ρ as indicated in the legend. The left column shows data from a low-CF(810Hz) AN fiber. The right column shows data from a high-CF (27,500 Hz) AN fiber. Bottom row, Distributions of the decision variable for each value of ρ indicated in the top row.

Observing that decorrelations from unity generally result in scaling down H(τ) uniformly toward the horizontal line at unity, we further simplify to w(τ) = H₁(τ) – 1. This weighting function is illustrated in Figure 1 F. The final expression for the decision variable D becomes

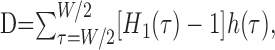(3)

where W is the range of delays considered. Our default value for W is 10 ms, but the effect of varying W is studied below in Results (see Figs. 10, 14).

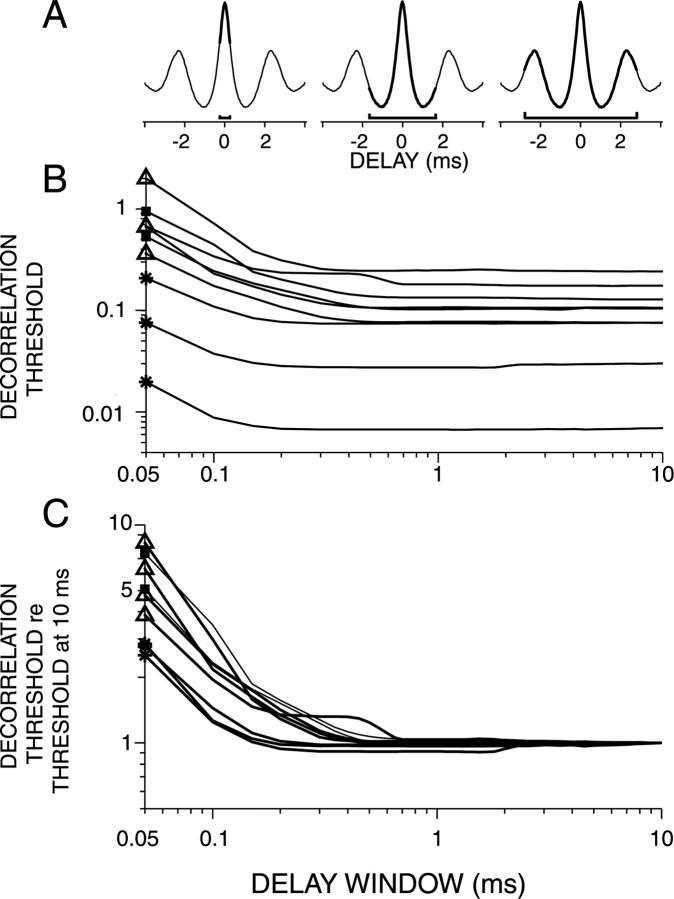
Figure 10.

A, Schematic illustrations of increases in the delay window W. B, Decorrelation thresholds obtained from broadband noise responses plotted versus W. Each line represents a single fiber. C, Same fibers as in B. The decorrelation thresholds are normalized to the thresholds at W = 10 ms. Symbols on ordinate indicate fiber type (same symbols as in Fig. 6).

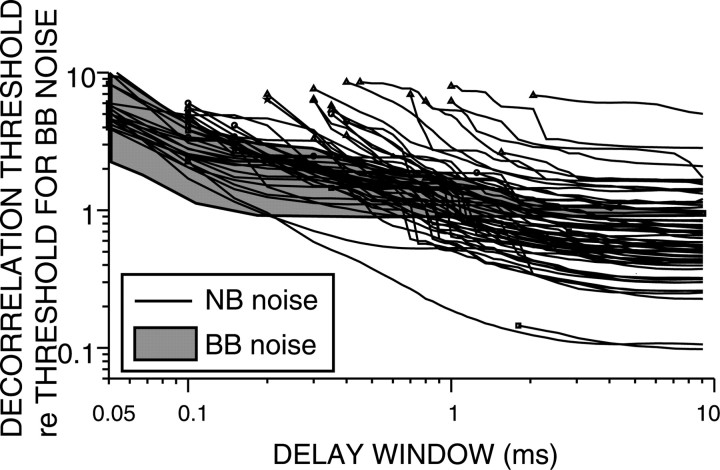
Figure 14.

Decorrelation thresholds obtained from narrowband (NB) and broadband (BB) noise responses plotted versus the delay window W. The shaded area represents all decorrelation thresholds obtained with broadband noise responses (Fig. 10C). Each line represents the narrow band noise decorrelation thresholds of a single fiber. All thresholds are normalized to the broadband noise decorrelation threshold at W = 10 ms. Same symbols as in Figure 6.

All possible pairs that can be constructed from the individual trials of spike trains were listed and arranged into groups according to the normalized correlation between their respective waveforms. Each pair yields a single estimate of D, and, for each value of correlation, the distribution of D was determined. Figure 2, second row, shows examples of probability density functions (PDFs) of D corresponding to waveform correlations indicated in the legends of the first row. Next, the distance or “detection index” d′ between a distribution corresponding to ρ and the reference distribution was calculated according to (Green and Swets, 1966)

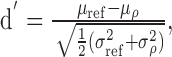(4)

where μ and σ denote mean and SD of D and the subscript “ref” refers to the reference condition, i.e., either ρ = 1 or ρ = 0 (Fig. 2 A, B). By convention, the threshold of decorrelation detection was defined as the decorrelation value at which d′= 1.

Results

We report results for 134 TB fibers obtained from seven cats and for 53 AN fibers obtained from four cats. First we show data for individual AN and TB fibers, and next we report population data. When calculating the decorrelation threshold, we had to chose an analysis window, a delay window W (Fig. 1F), and a base correlation. When not stated otherwise, the analysis window extended from 50 to 1000 ms, W extended from a delay of –5 to +5 ms, and the base correlation was ρ = 1. The implications of these choices will be discussed below.

Examples for individual AN fibers

Figure 3 shows steps (each column) in the analysis to determine the decorrelation thresholds for three AN fibers, arranged from low (top) to high (bottom) CF. The three curves in each panel of the first column show the grand correlograms, H(τ), of spike train pairs corresponding to correlated (ρ = 1), uncorrelated (ρ = 0), and anti-correlated (ρ =–1) noise tokens. The correlograms corresponding to ρ = 1 and ρ =–1 oscillate in anti-phase for the low and mid-CF fibers (Fig. 3A,D) and are identical for the high-CF fiber (Fig. 3C). The correlograms corresponding to ρ = 0 are flat (Fig. 3A,D,G), with unity value attributable to normalization. The shape of the correlograms for ρ = 1 and ρ = –1 is consistent with the expected cross-correlation function of the “effective” stimulus to the fiber as determined by the mechanical and transduction events that precede spike initiation at the cochlear site that excites the fiber. For a detailed description of the shape of correlograms, see Louage et al. (2004).

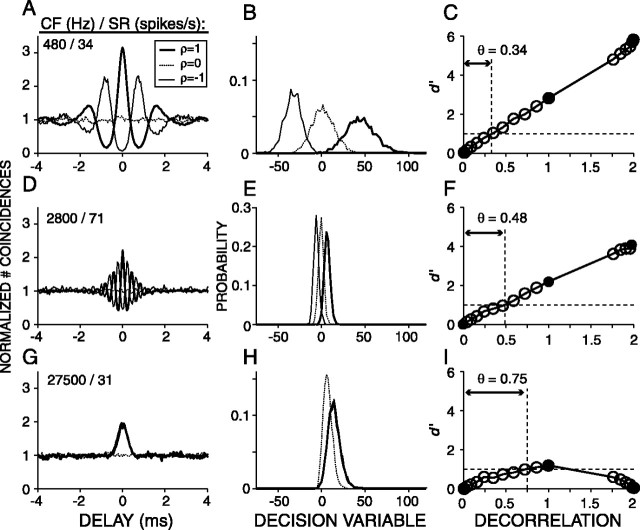
Figure 3.

Examples of correlograms (left column), distributions of the decision variable (middle column), and correlation sensitivity curves (right column) for three AN fibers arranged from low to high CF. CF and SR are indicated in the left corner of each panel in the first column. The stimuli were eight frozen broadband (0.1–30 kHz) noise tokens with 18 values of mutual normalized correlation (ρ). Filled circles in the right column are d′ values for ρ = 1, 0, and –1 and correspond to the curves shown in the left and middle columns. Open circles show d′ for intermediate values of ρ. The horizontal dashed lines in the panels of the right column indicate d′= 1, and the vertical dashed lines indicate the decorrelation threshold θ.

Figure 3, second column, illustrates PDFs of the decision variable D corresponding to waveform correlations 1, 0, and –1. A typical sequence, in which the eight waveforms were presented 35 times, yielded 78,100 D values, which were arranged into 18 PDFs corresponding to the 18 values of ρ (see Materials and Methods). The PDFs have an approximately Gaussian shape (Figs. 2C,D, 3B,E,H); the median kurtosis and skewness of all the distributions of all sequences (n = 5671) was 3.11 and 0.21, respectively (3 and 0 for a Gaussian distribution), justifying the use of Gaussian expression for d′ (Eq. 4). For the low-CF fibers, the PDFs of D shift to more negative values with increasing decorrelation (Fig. 3B,E), but for the high-CF fiber, the mean of the PDF is always >0 and changes nonmonotonically with ρ (Fig. 3H), and the PDFs corresponding to ρ = 1 and ρ =–1 are virtually identical. This is expected from the similarity of their correlograms (Fig. 3G), which is attributable to envelope coding (Joris, 2003). For all fibers, the separation between the distributions with changing ρ follows the same trend as the central peaks of the average correlograms with changing ρ (Fig. 3, first and second columns), i.e., a monotonic increase in separation with increasing decorrelation for the low-CF fibers and a nonmonotonical trend for the high-CF fiber. The variances of the PDFs, however, reflect properties of the responses that are not shown by the average correlograms but that are important to the discrimination performance of an ideal observer.

Figure 3, right column, illustrates the detection index, d′, which takes into account both the mean and variance of the distributions (Eq. 4). We will refer to d′ versus decorrelation as a correlation sensitivity curve (CSC). The abscissa shows the degree of decorrelation relative to the reference condition. Thus, decorrelations of 0, 1, 2 for reference condition ρ = 1 correspond to waveform correlations of 1, 0, –1, respectively. For the fiber with the lowest CF (Fig. 3C), the CSC has a linear shape over the full range of ρ. The decorrelation threshold was expressed as the amount of decorrelation needed to reach d′= 1 and was determined by linear interpolation. For the high-CF fiber (Fig. 3I), the CSC has a nonmonotonic shape: d′ increases with increasing decorrelation, reaches its maximum value at a decorrelation of 1, and decreases with additional decorrelation. The dome shape of the CSC of Figure 3I reflects the synchronization of the fiber to the envelope of the effective stimulus: the waveforms corresponding to +ρ and –ρ have inverted fine structure but the same envelope.

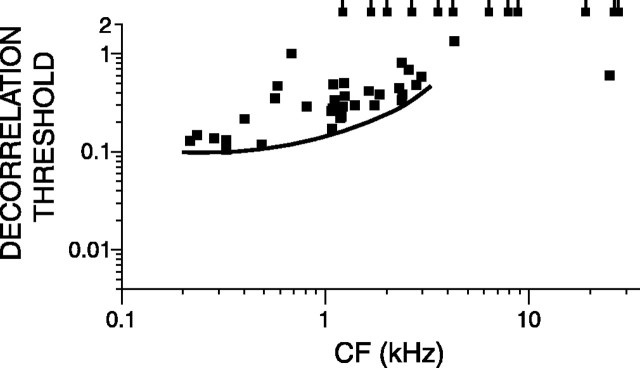
Figure 4 plots the decorrelation thresholds versus CF using broadband noise tokens for a group of 45 AN fibers for which responses obtained at 70 dB SPL were available. The lowest thresholds are at decorrelations of ∼0.1 and occur with low-CF fibers. The solid line marks a lower bound for the lowest thresholds. The lowest thresholds slightly increase with CF, and, above 1 kHz, a significant number of fibers, indicated by a tailed symbol at the top of the figure, do not reach d′= 1. The thresholds obtained with auditory nerve fibers are higher than human behavioral thresholds but show similar trends as will be discussed below.

Figure 4.

Decorrelation threshold plotted versus CF for a population of AN fibers for broadband noise presented at 70 dB SPL. Each data point represents a single fiber. The stimuli were a set of eight 1 s frozen broadband tokens delivered at 70 dB SPL. When the decorrelation threshold of a fiber was not reached, it is represented by a tailed square at a threshold value of 2. The solid line traces the minimum thresholds.

Correlograms, distributions, and CSCs of TB fibers

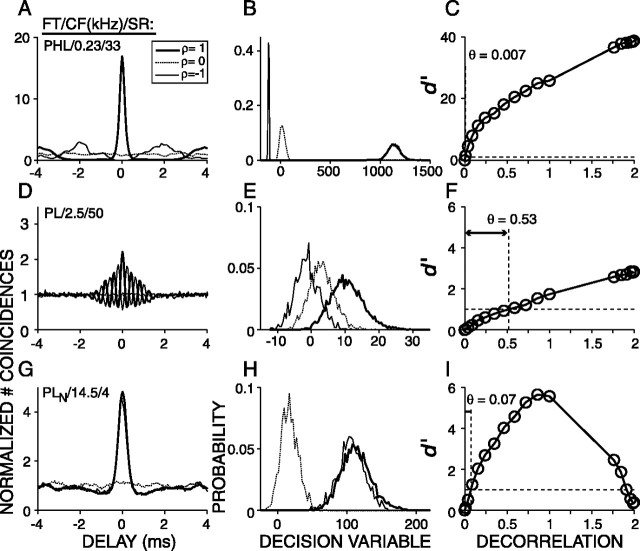
Figure 5 shows data for three TB fibers, arranged from low (top) to high (bottom) CF and has the same layout as Figure 3. Compared with the low-CF AN fiber (Fig. 3A), the correlogram for ρ = 1 of the PHL fiber (Fig. 5A) has a much higher and narrower central peak, the variances of its PDFs are much lower (Fig. 5B), its CSC has a pronounced curvilinear shape, and the decorrelation threshold is much lower. With noise, this PHL fiber had a high spike rate (170 spikes/s), and, with pure tones at CF, its responses were highly entrained and “high-sync” (R > 0.9) (Joris et al., 1994). The response properties of this PHL fiber are thus clearly different from those of low-CF AN fibers and are superior regarding decorrelation detection.

Figure 5.

Same as Figure 3 but now for three TB fibers. Fiber type (FT), CF, and SR are indicated in the left corner of each panel in the first column.

The second row of Figure 5 shows data for a mid-CF PL fiber. Compared with the mid-CF AN fiber (Fig. 3D–F), the correlograms, PDFs, and the CSC are very similar. At these CFs, firing properties of PL fibers (Joris et al., 1994; Rhode and Greenberg, 1994; Louage et al., 2005) are indeed known to be similar to those of AN fibers.

The third row of Figure 5 shows data for a high-CF PL_N fiber. Compared with the high-CF AN fiber (Fig. 3), the correlograms corresponding to ρ =±1 have a higher central peak (panel G), the PDFs corresponding to ρ = 1 and ρ = 0 are more separated (panel H), and the decorrelation threshold is lower (panel I). Thus, also for this high-CF TB fiber, response properties seem such as to improve decorrelation sensitivity.

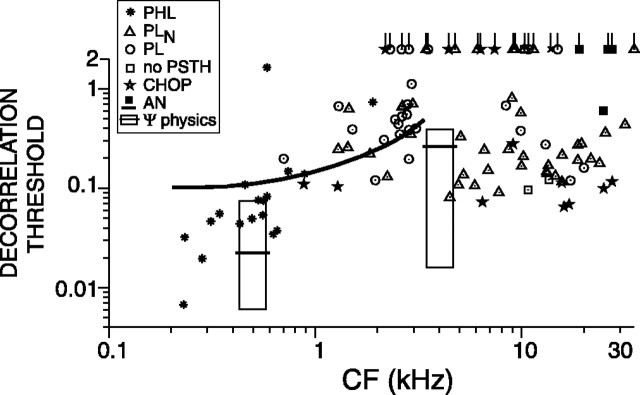
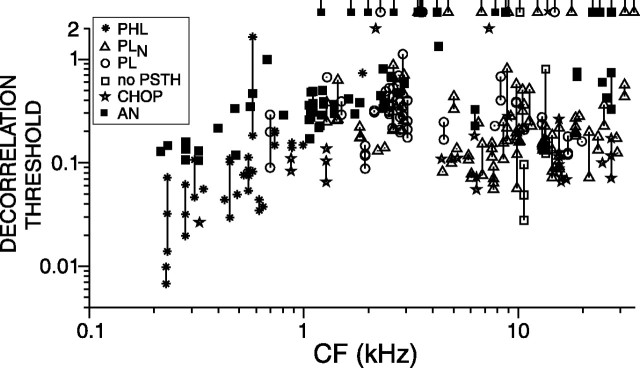
Figure 6 shows the decorrelation thresholds for a population of TB and AN fibers for which responses obtained at 70 dB SPL were available. The solid line is the lower envelope to the lowest AN thresholds in Figure 4. Most TB fibers (68 of 106) yield lower thresholds than AN fibers. The two boxes show the range of reported human decorrelation jnds from base correlation 1 for narrowband noise at 500 Hz (Pollack and Trittipoe, 1959a; Gabriel and Colburn, 1981; Koehnke et al., 1986) and 4 kHz (Koehnke et al., 1986). The black horizontal lines in the rectangles show the medians of reported thresholds. In psychophysical experiments, the stimulus duration is found to affect thresholds; a value <1 s is typically used. Thus, comparison of the neural thresholds with psychophysical data must take stimulus duration into consideration, as will be done in Figure 9.

Figure 6.

Decorrelation threshold versus CF for a population of AN and TB fibers for broadband noise delivered at 70 dB SPL. Each data point represents a single fiber. The stimuli were 1-s-long broadband noise tokens delivered at 70 dB SPL. When the decorrelation threshold of a fiber was not reached, it is represented by a tailed symbol (asterisk, PHL; circle, PL; triangle, PL_N; star, CHOP) at a threshold value of 2.1. The boxes represent the range of human psychophysical decorrelation jnds for narrowband noise at 500 Hz and 4 kHz. The black horizontal lines in these rectangles show the median of reported thresholds. The thick black line is the lower bound of AN thresholds (Fig. 4).

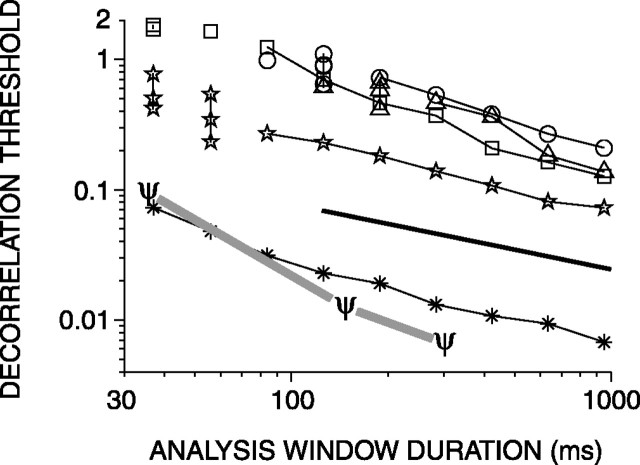
Figure 9.

Decorrelation thresholds obtained from broadband noise responses plotted versus analysis window duration. Each line represents a single fiber. The trend line (thick solid line) indicates a decrease by a factor of 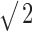per doubling of the duration. The ψ symbols indicate human decorrelation thresholds from reference correlation one. Other symbols indicate response classes as in Figure 6.

Effect of SPL on correlation sensitivity

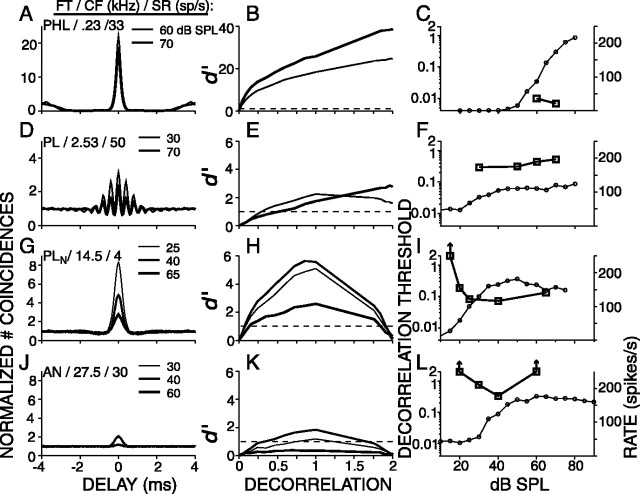
The data shown so far were all obtained at 70 dB SPL but, for many fibers, sequences were presented at additional levels. Figure 7 shows data for four fibers, arranged from low (top) to high (bottom) CF. The first column shows superimposed correlograms for ρ = 1 and representing different SPLs as indicated in the right top corner of each panel. The second column shows the CSCs that correspond to the SPLs in the first column. The third column shows panels with two ordinates: the right ordinate indicates the average firing rate (open circles), and the left ordinate indicates the decorrelation threshold (open squares). The first row of Figure 7 shows a low-CF (230 Hz) PHL fiber. At 60 and 70 dB SPL, the correlograms have very narrow and high central peaks (Fig. 7A). The CSCs of this fiber have a curvilinear shape. This shape differs from the linear CSC of low-CF AN fibers (Fig. 3A) and resembles the shape of psychophysical d′(ρ) functions (Bernstein and Trahiotis, 1996; Culling et al., 2001). The decorrelation sensitivity of this fiber is the best of our entire TB population and is nearly two orders of magnitude lower than the low-CF AN fiber (Fig. 3A). It is comparable with the lowest human psychophysical decorrelation jnds reported. The decorrelation thresholds at the two levels tested, 60 and 70 dB SPL, are comparable (0.009 and 0.007) (Fig. 7C).

Figure 7.

Examples of SPL dependence for four fibers. Left, Correlograms at different SPLs, indicated in the right top corner of each panel. Also indicated are the fiber type (FT), CF, and SR. Middle, CSCs of the same data. The dashed horizontal lines are at d′= 1. Right, Each panel has two ordinates: the right ordinate indicates rate (circles, linear scale), and the left ordinate indicates decorrelation thresholds (squares, logarithmic scale). Note that the fiber of the first row is the same as in Figure 5.

The second row of Figure 7 shows a mid-CF (2530 Hz) PL fiber. The left panel shows two correlograms obtained at 30 and 70 dB SPL. Both correlograms have the shape of a damped oscillation superimposed on a broad peak, but the relative size of these two components differs at the two SPLs (Fig. 7D). This shape difference with level reflects a shift in balance between phase locking to the envelope and fine structure. As a consequence, the CSC at 70 dB SPL is monotonic, whereas the CSC at 30 dB SPL is nonmonotonic (Fig. 7E). The decorrelation threshold is lowest, 0.3, at 30 dB SPL and increases to 0.53 at 70 dB SPL.

The bottom two rows of Figure 7 show two high-CF fibers: a PL_N (third row) and an AN (fourth row) fiber. Their correlograms have the shape of a single central peak (Fig. 7G,J), and their CSCs are nonmonotonic (Fig. 7H,K). The decorrelation threshold versus SPL curves (Fig. 7I,L) are U shaped. At the lowest SPLs, below rate threshold, the decorrelation threshold is undefined. With increasing SPL, the threshold decreases and shows a minimum at SPLs in the upper end of the dynamic range of the rate-level curve. Additional increase in SPL causes again an increase in threshold. For the PL_N fiber, this increase is small, whereas for the AN fiber, the increase is marked and the threshold is undefined at 60 dB SPL. The nonmonotonic shape of the decorrelation threshold versus level curves of high-CF fibers probably reflects two counterbalancing mechanisms. On the one hand, with decreasing SPL, too few spikes are available to result in an accurate estimate; on the other hand, with increasing SPL, envelope coding declines.

Figure 8 shows all measured decorrelation thresholds derived from responses of TB and AN fibers. Multiple points connected by a vertical line represent those fibers from which we obtained thresholds at more than one SPL. When only one SPL was tested, a single data point represents a single fiber. Undefined thresholds are not illustrated except when all thresholds were undefined; in those cases, a tailed data point is plotted at the arbitrary value of 2.1. Different symbols represent the different fiber types. The stimuli were presented at levels ranging from 15 to 100 dB, with a median of 70 dB SPL. In general, differences between different CFs (Fig. 4) and between AN and TB fibers (Fig. 6) persist when stimuli are delivered at SPLs other than 70 dB: thresholds are lower at low CFs, and TB fibers are more sensitive (t test, p < 0.00001) to decorrelation. When selecting, for each fiber, the SPL that results in the lowest threshold, and excluding fibers for which no threshold could be defined, the overall averages of the thresholds of AN and TB fibers are 0.37 and 0.17, respectively. Among TB fibers, the PSTH classes are not equally sensitive to decorrelation: the averages of the minimum thresholds of PHL fibers, chopper fibers, PL_N fibers, and PL fibers are 0.1, 0.12, 0.17, and 0.3, respectively.

Figure 8.

Decorrelation thresholds versus CF for a population of 134 TB fibers and 53 AN fibers pooled from 11 cats. Each vertical line connecting two or more data points represents data from a single fiber obtained at multiple SPLs. Same symbols as in Figure 6.

Effect of the analysis parameters

In psychophysical experiments, decorrelation thresholds increase with decreasing stimulus duration (Pollack and Trittipoe, 1959b; Bernstein and Trahiotis, 1997). In the previous sections, we calculated neural decorrelation thresholds by using the entire response to the stimulus. The analysis, however, offers the possibility to use shorter parts of the response, as if the stimulus had been shortened. Figure 9 shows, for five fibers, the decorrelation thresholds corresponding to nonoverlapping windows of different durations. Both the ordinate and the abscissa are scaled logarithmically. The thresholds shown are averages calculated for nonoverlapping windows. The number of windows increased with shorter window duration but did not exceed five. For example, the threshold at 950 ms represents only one measurement, whereas the threshold at 283 ms represents the mean of three measurements. Shortening of the analysis window increases the uncertainty in the effective correlation and increases the scatter in the thresholds: by averaging thresholds from several windows, this scatter is reduced. At short windows, some measurements yielded undefined thresholds: in those cases, only the defined thresholds of individual measurements are shown and connected by a vertical line. Overall, thresholds decreased as durations increased up to the longest value tested (950 ms). For durations longer than ∼150 ms, thresholds decrease as predicted mathematically (Green and Swets, 1966, their Chap. 9), i.e., by a factor of 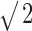for each doubling of the duration (indicated by the trend line in Fig. 9). For durations shorter than 100 ms, thresholds decrease at a higher rate, are not always defined, and are more variable over different intervals. The reduced correlation sensitivity with short durations is probably attributable to the small number of spikes on which threshold estimation is based. Figure 9 also shows the duration dependency (ψ symbols) of human decorrelation thresholds, as published by Bernstein and Trahiotis (1997). Human and neural thresholds follow the same trend, but the decrease in human thresholds is steeper.

Another parameter that requires a choice in the analysis for decorrelation threshold is the delay window W (Fig. 1F). When W = 50 μs, which is also the bin width used to construct the correlograms, thresholds are solely based on the statistics of the coincidence counts in one bin at delay zero. With larger W, coincidence counts of adjacent bins add and contribute to the decision of the ideal observer. In fact, increasing W simulates the recruitment of coincidence detectors with best delays that differ from zero (see Discussion).

Figure 10B shows the effect of the width of W on the decorrelation threshold for a set of representative fibers, and Figure 10C shows, for the same fibers, thresholds relative to the threshold obtained at W = 10 ms. Thresholds always decrease with increasing W. For low-CF AN fibers, this decrease is slower than for high-sync TB fibers or high-CF fibers (data not shown). Thus, for low-CF AN fibers, a larger value of W is needed to reach optimal decorrelation sensitivity. For all CFs, most of the decrease occurs at widths shorter than 200 μs. These data suggest that bins around the maximum in the correlogram are most useful for discriminating decorrelated broadband waveforms; this is as expected, knowing that correlograms of broadband noise responses are damped.

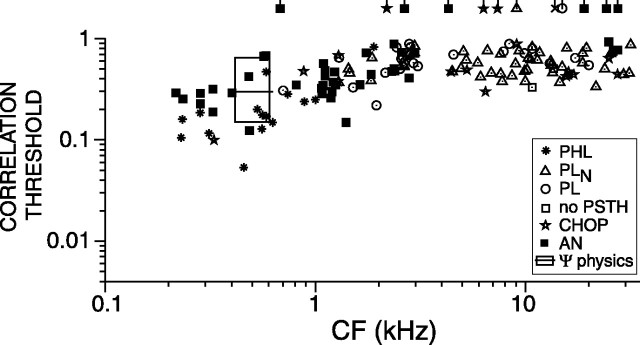
Psychophysical studies consistently show that human jnds for change in correlation (Δρ jnds) are higher when the reference condition is ρ = 0 than for ρ = 1. So far, we showed neural Δρ thresholds for a reference correlation of 1, but, using the same data, we can obtain thresholds for any other reference condition by selecting another reference distribution in Equation 4. Figure 11 shows Δρ thresholds toward correlation 1, from base correlation ρ = 0. The box shows the range of reported human correlation jnds from base correlation 0 (Gabriel and Colburn, 1981; Boehnke et al., 2002); the black horizontal line shows the median of the reported thresholds. When compared with thresholds from base 1, thresholds from base 0 show a similar CF dependence, are generally higher, and exhibit smaller differences between AN and TB fibers. The latter fact is consistent with the shape of the CSCs: at a decorrelation of 1 (i.e., approximately ρ = 0), the CSCs of low-CF AN and TB fibers are linear and have comparable slopes (Figs. 3, 5, right column). Interestingly, discrimination thresholds of AN and TB fibers are similar to human thresholds.

Figure 11.

Correlation discrimination thresholds from base correlation of zero, plotted versus CF. Each data point represents a single fiber. Same symbols as in Figure 6. The box represents human correlation jnds from the literature.

Correlograms and correlation sensitivity curves with narrowband noise

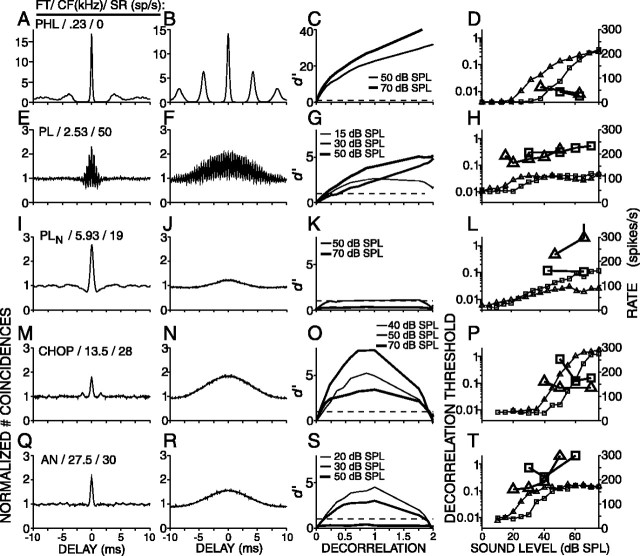
A surprising finding in psychophysical studies (Gabriel and Colburn, 1981) is that decorrelation jnds improve by narrowing the noise bandwidth (see Discussion). We evaluated decorrelation thresholds for 100-Hz-wide narrowband noise tokens that were centered at the CF of the fibers. When compared with broadband noise, the effective stimulus for narrowband noise is less affected by peripheral filtering and has slower envelope fluctuations. Figure 12 shows correlograms obtained from responses to broadband (first column) and narrowband (second column) noise, CSCs obtained from responses to narrowband noise (third column), rate versus level curves of responses to broadband and narrowband noise (fourth column), and decorrelation threshold versus level (fourth column), for five fibers arranged from low (top) to high (bottom) CF. For fibers with CFs below the limit of phase locking (Fig. 12, rows 1, 2), the responses to CF-centered narrowband noise (Fig. 12B,F) yield correlograms that have the shape of a damped oscillation with an oscillation frequency corresponding to CF and with less damping than seen in correlograms of responses to broadband noise (Fig. 12, B,F vs A,E). Above the limit of phase locking, fibers synchronize to the envelope of the effective stimulus, and their responses to narrowband noise yield correlograms that have the shape of a single peak that is broader than that to broadband noise. These findings nicely agree with the mathematical fact that noise bandwidth is proportional to the average frequency of envelope fluctuations (Rice, 1954).

Figure 12.

Decorrelation sensitivity for narrow and broadband noise for 5 fibers. Left column, Correlograms obtained from responses to broadband noise. Second column, Correlograms obtained from responses to narrowband (100 Hz) noise centered on the CF of the fiber. Third column, CSCs obtained from responses to narrowband noise tokens at different SPLs. Right column, Combined rate-level and correlation threshold curves as in Figure 7. Small symbols represent the average firing rates, and large symbols represent the decorrelation thresholds. Triangles indicate narrowband noise results, and squares indicate broadband noise results. FT, Fiber type.

The third column of Figure 12 shows CSCs derived from responses to the narrowband noise tokens at different SPLs. These CSCs are similar to those derived from responses to broadband noise tokens (Figs. 2, 3, 5): their shape is linear or curvilinear for CFs below the phase-locking limit and nonmonotonic for CFs exceeding the limit of phase locking.

The right column of Figure 12 shows rate versus overall SPL (small symbols) and decorrelation thresholds versus overall SPL (large symbols) for both narrowband (triangles) and broadband (squares) noise. As expected, the rate versus level curves for narrowband noise are shifted to lower sound levels than those to broadband noise because much of the energy of the broadband noise falls outside the peripheral filter. Moreover, in PL_N fibers, the maximum firing rate to the narrowband noise was typically lower than to the broadband noise (Fig. 12L).

For the low-CF fiber (Fig. 12D), the decorrelation thresholds decrease with increasing SPL and are very similar for the broadband and narrowband noise tokens. For the fibers with higher CFs (Fig. 12H,L,P,T), the threshold versus level curves have a minimum at sound levels that approximately correspond to the upper end of the dynamic range of the rate-level curves. When compared with the minimum thresholds for broadband noise (squares), those for narrowband noise (triangles) are lower (except for the PL_N fiber) and occur at somewhat lower sound levels.

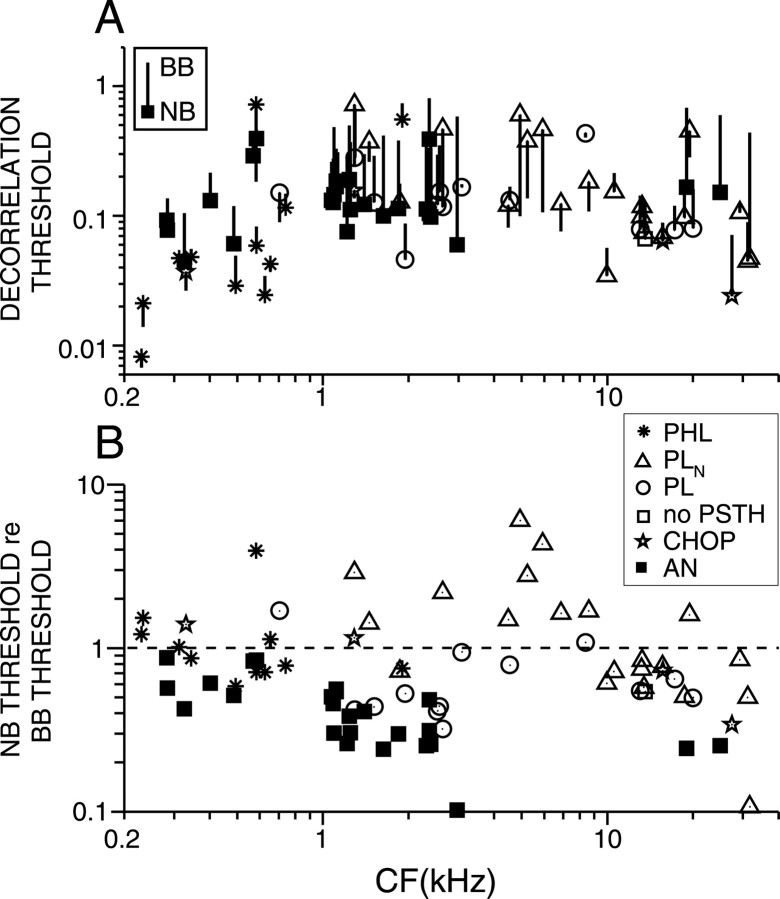
Figure 13A plots decorrelation thresholds for narrow and broadband noise versus CF. Only data for which thresholds were obtained at multiple SPLs are shown. Each line represents a single fiber; the lines ending with a symbol represent the minimum threshold obtained from responses to narrowband noise, and the lines ending without a symbol represent the minimum threshold obtained from responses to broadband noise. The direction of the line thus indicates whether thresholds are lower or higher in the broadband condition. The decorrelation thresholds derived from AN fiber responses to narrowband noise are ∼0.1 and are more or less invariant with CF. Decorrelation thresholds derived from TB responses to narrowband noise cover a range from 0.008 to 0.8; PHL fibers yield the lowest thresholds, and PL_N fibers with CFs between 1 and 10 kHz tend to yield the highest thresholds.

Figure 13.

A, Decorrelation thresholds for narrowband and broadband noise. Only fibers that were tested at different SPLs are shown. Each line represents a single fiber. The symbol represents the minimum decorrelation threshold derived from narrowband (NB) noise responses, and the other end of each line represents the minimum decorrelation threshold derived from broadband (BB) noise responses. B, Thresholds from narrowband responses expressed relative to the minimum thresholds derived from broadband noise responses. Same symbols as in Figure 6.

Figure 13B shows the ratio of the minimum decorrelation threshold obtained from responses to narrowband noise to the minimum threshold obtained from responses to broadband noise. Each symbol represents a fiber; data points above the dashed line (ratio of 1) thus represent fibers for which the narrowband decorrelation threshold was higher than the broadband decorrelation threshold. Strikingly, the narrowband thresholds are smaller than the broadband thresholds for all AN fibers. The ratio is ∼0.8 at low CFs and decreases to values of ∼0.2 at 20 kHz.

For TB fibers, the ratio of narrowband to broadband thresholds is on average higher than with AN fibers, and this is especially the case for PL_N fibers with CFs between 1 and 10 kHz. These fibers exhibited a firing behavior that clearly differed from AN fibers: their maximum firing rate with narrowband noise was lower than that with broadband noise (Fig. 12L), and the minimum decorrelation threshold for broadband noise was obtained at relatively high SPLs. At these high SPLs, responses of PL_N fibers to broadband noise yield average correlograms with higher central peaks than those of AN fibers (Louage et al., 2005). Thus, the monaural spatiotemporal integration of AN inputs by globular bushy cells favors discrimination of broadband over narrowband noise.

Figure 14 shows the effect of increasing W on the decorrelation thresholds derived from narrowband (individual lines) and broadband (shaded area) noise responses of AN and TB fibers. Thresholds are relative to those obtained with broadband noise at W = 10 ms (Fig. 10B). All thresholds decrease with increasing W. At small W, decorrelation thresholds derived from narrowband responses are higher compared with those derived from broadband responses. At W longer than 1.5 ms, most decorrelation thresholds derived from narrowband responses are smaller than those derived from broadband noise responses. This phenomenon is consistent with the slower damping of correlograms of narrowband responses and suggests a possible mechanism for the psychophysical paradox mentioned above. With narrowband noise, coincidence detectors with characteristic delays corresponding to the secondary peaks of the correlograms can significantly contribute to the detection of change in correlation because the secondary peaks are large. In contrast, with broadband noise, coincidence detectors at these secondary peaks contribute less because the secondary peaks are small.

Neural code and decorrelation sensitivity

Which features of the response are most important for the performance of the ideal observer? Figure 15A shows the decorrelation threshold derived from broadband noise responses versus the average rate of the monaural response. Each data point represents data obtained from a single sequence, and a single fiber may contribute several data points, for multiple sequences. On average, thresholds tend to decrease with increasing firing rate, but the trend is weak (r = –0.29) and much smaller than the effect of the type of fiber from which the responses are derived.

Figure 15.

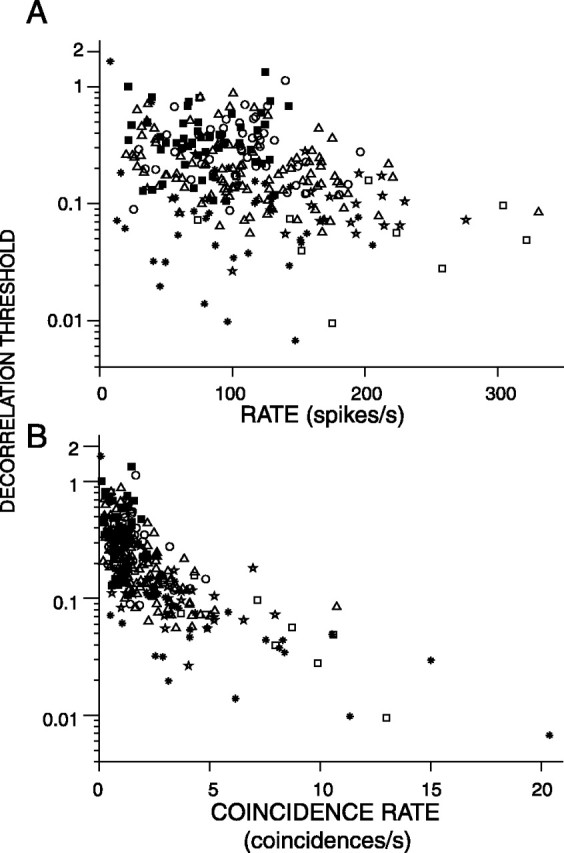
A, Decorrelation thresholds obtained from broadband noise responses plotted versus the average rate of the responses. B, Decorrelation thresholds obtained from broadband noise responses plotted versus the coincidence rate of the responses. Fibers studied at multiple SPLs contribute multiple data points. Same symbols as in Figure 6.

Figure 15B shows the decorrelation threshold versus the maximum coincidence rate of the response, obtained from the maximum of the correlogram for ρ = 1. The coincidence rate is high when the average firing rate is high and/or the temporal precision of firing is high (Louage et al., 2005). The performance of the ideal observer is best when a lot of coincidence counts are available (Fig. 15B). Thus, what is needed for high decorrelation sensitivity are responses containing many precisely timed spikes. This occurs mostly in responses of the PHL type (Louage et al., 2005).

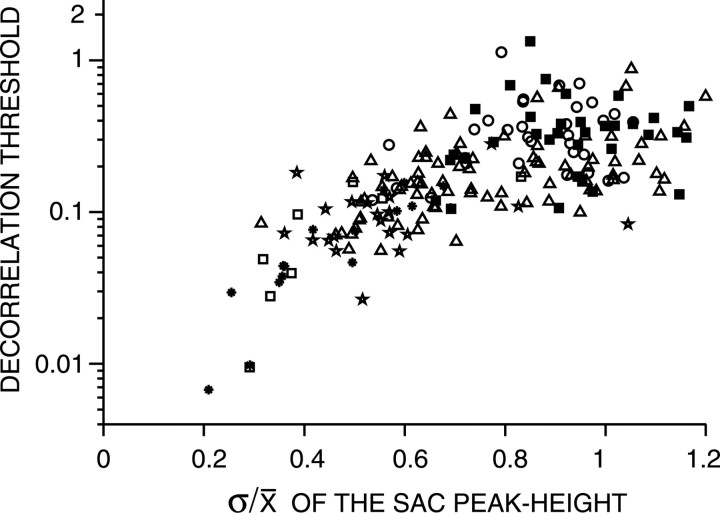
Figure 16 plots the decorrelation thresholds derived from broadband noise responses versus the ratio of the SD to the mean of the coincidence counts at delay 0 for ρ = 1. This σ/μ ratio, which is in fact the coefficient of variation of the coincidence counts of the SAC at delay 0, quantifies the reproducibility of the output rate of the coincidence detector during repeated stimulation with the same stimulus. Note that the σ/μ ratio is based on a correlation analysis of multiple responses to a single noise token. Figure 16 shows a clear relationship between decorrelation thresholds and the σ/μ ratio: the fibers with the best performance (lowest decorrelation thresholds) also have the lowest σ/μ ratios. From Figure 16, it is clear that all PHL fibers, most chopper fibers, half of the PL_N fibers, and a few PL fibers have lower σ/μ ratios than AN fibers. These data confirm that the response properties of most TB fibers differ from their AN inputs in a way that is favorable for correlation discrimination.

Figure 16.

Decorrelation thresholds obtained from broadband noise plotted versus the ratio of the SD to the mean of the coincidence counts of the correlogram for ρ = 1, at delay τ = 0. The thresholds were obtained with W = 5 ms. Fibers studied at multiple SPLs contribute multiple data points. Same symbols as in Figure 6.

Discussion

We applied a coincidence analysis to responses from AN and TB fibers to a set of frozen noise tokens with mutual correlation ranging from 0.99 to –1. The resulting coincidence counts were processed by an ideal observer who judged whether the responses corresponded to identical stimuli or not. The decorrelation sensitivity of the ideal observer was much higher with TB fiber responses than with AN fiber responses and sometimes as good as human decorrelation jnds.

Enhanced temporal coding in the anteroventral cochlear nucleus

Joris et al. (1994) found that TB responses to low-frequency tones yield higher vector strengths (> 0.9, high-sync) than AN responses and hypothesized that this temporal enhancement serves to improve binaural sensitivity as realized in the superior olivary complex (SOC). In two recent studies (Louage et al., 2004, 2005), we developed metrics that quantify temporal properties of neural responses to arbitrary stimuli, and we found that TB responses to broadband noise are also enhanced compared with the AN. In the present study, we test the hypothesis of improved binaural sensitivity in the specific context of correlation detection. We separately used TB and AN responses as inputs to an optimal binaural processor and found that TB responses yielded better correlation discrimination than AN responses. This supports the view that monaural processing in the anteroventral cochlear nucleus (AVCN) is a crucial step in arriving at a high level of accuracy in binaural processing. This monaural preprocessing can be described as a reduction of “internal noise.”

Improved thresholds were not restricted to low-frequency stimulus components but also occur for high frequencies, in which temporal coding is restricted to the envelope. Moreover, the superiority of TB responses occurred in all cell types encountered. In particular, most choppers, likely to be stellate cells, also show improved thresholds, and these are based on envelope timing rather than on fine structure. Stellate cells do not project to the binaural nuclei in the SOC involved in fine time comparisons (Cant and Benson, 2003). The temporal enhancement in AVCN may thus reflect a general strategy for reducing internal noise rather than an optimization for a particular binaural task such as ITD discrimination at low frequencies.

Albeck and Konishi (1995) found that the rate versus correlation curves of binaural neurons of low-level nuclei in the barn owl have linear or parabolic shapes. We do not explicitly show coincidence counts versus correlation values in this study. However, the data as plotted in Figure 2A show that the relationship between coincidence count and correlation (at zero delay) is also parabolic (expansive) for our monaural data.

Relationship between neural decorrelation jnds and human psychophysics

Before comparing our data with psychophysics, we emphasize that our use of a perfect coincidence detector is not meant to imply similar perfection in binaural physiology. Ideal observers are artificial devices providing upper limits on performance based on the information at a certain processing stage. In the absence of detailed knowledge on the neural conversion of monaural temporal information to binaural sensitivity, this approach is the only way to arrive at quantitative conclusions concerning binaural processing based on monaural responses.

As in humans (Bernstein and Trahiotis, 1996), decorrelation thresholds of AN and TB fibers are lower at low than at high frequencies (Figs. 4, 6, 8). Moreover, the lowest thresholds from TB fibers match human decorrelation jnds (Fig. 6). Also, psychophysical jnds from base 0 are much higher than those from base 1 (Gabriel and Colburn, 1981), as is the case for AN and TB fibers (Figs. 6, 11). To the extent that single neuron activity in the two AVCNs is linked to the perception of interaural correlation, these findings are consistent with the lower envelope hypothesis, which states that the limits of psychophysical performance are set by the most sensitive neurons (Parker and Newsome, 1998).

Nevertheless, the decorrelation thresholds from single fiber responses also differ in some respects from human decorrelation jnds. Human jnds are small over a wide range of SPLs (Pollack and Trittipoe, 1959b; Gabriel and Colburn, 1981; van de Par et al., 2001). As is true for many other psychophysical tasks, the behavioral range appears to be wider than the range covered by single neurons (Fig. 7I,L) and indicates that some degree of pooling across fibers is needed. Another difference between neural and psychophysical jnds is the effect of stimulus duration. Human thresholds decrease up to durations of ∼300 ms and stabilize with additional increase of duration (Pollack and Trittipoe, 1959b). Neural thresholds, however, steadily decrease up to the largest durations tested (1 s) (Fig. 9).

A methodological difference between the present study and human psychophysical studies is our use of a single, “frozen,” noise token, whereas the behavioral data were obtained with running noise. Our use of a single noise waveform eliminates all stimulus variability, so we cannot evaluate the relative contributions of stimulus variability and response variability (internal noise). Gabriel and Colburn's (1981) analyses, however, suggest that stimulus variability plays only a minor role, if any, in interaural correlation discrimination.

Our AVCN decorrelation thresholds are much lower than thresholds found in the guinea pig IC (Shackleton et al., 2005). It is unclear whether this discrepancy indicates suboptimal binaural comparison of the temporal information from monaural afferents. Species, anatomical level, and methodological differences might contribute to the discrepancy. In particular, our stimuli were 1 s in duration, whereas Shackleton and Palmer (2005) used short (50 ms) noise bursts; both physiological thresholds (Fig. 9) and human jnds (Bernstein and Trahiotis, 1997) increase with shortening of stimulus duration.

Role of internal delays in decorrelation sensitivity

In our analysis, we calculated coincidences at different values of τ between monaural spike trains. Different values of τ can be realized by so-called internal delays, i.e., differential delays between the inputs from the two ears to a binaural cell. For a coincidence detector, the physiological manifestation of internal delay is a maximum or “best delay” in its noise-delay function (i.e., a graph of average response rate as a function of ITD). Our analysis implicitly assumes the availability of a population of coincidence detectors covering a range W of internal or best delays. Correlogram values at each τ then represent the output rate of individual coincidence detectors with an internal delay equal to τ.

An important insight from our analysis is that different discrimination tasks require different distributions of internal delays. Recent studies of ITD sensitivity in the guinea pig have emphasized the need for neurons with best delays outside the physiological range, so that it is sampled by the steepest slope of noise-delay functions (McAlpine et al., 2001; Harper and McAlpine, 2004). However, for a correlation detection task, the requirements are orthogonal to those for an ITD detection task: maximal changes in rate are obtained at the peak rather than at the slopes of noise-delay functions (Fig. 10) (Yin et al., 1987), and therefore neurons with best delays within the physiological range are most useful for decorrelation detection.

In fact, within the context of decorrelation discrimination, small internal delays contribute most to the performance. Figure 10 shows that the decorrelation thresholds for broadband noise are based on delays below 400 μs; larger internal delays do not further improve performance. Practically speaking, the range of delays that corresponds to only the central peak of the correlogram is sufficient to arrive at the performance of the ideal observer. This is exactly the range of best delays observed in binaural neurons in the IC (McAlpine et al., 2001; Hancock and Delgutte, 2004; Joris et al., 2005). In that respect, our computed thresholds for broadband noise are physiologically plausible.

A seemingly paradoxical psychophysical phenomenon is that decorrelation detection is better for a low-frequency, narrowband noise than for broadband noise (Gabriel and Colburn, 1981). This trend is contrary to what would be expected from statistical arguments concerning the effects of sample size on detectability (Green and Swets, 1966; Gabriel and Colburn, 1981; van der Heijden and Trahiotis, 1998). Our analysis suggests an interesting possibility to understand this paradox. Indeed, for AN, PHL, and PL fibers, we observed that decorrelation thresholds were often lower for the narrowband than for the broadband condition (Figs. 12, 13). The explanation for this surprising finding is found in Figure 14. As expected, the correlograms obtained with 100-Hz-wide noise are much less damped than those obtained with broadband noise (Fig. 12). Consequently, the useful range of internal delays is larger in the narrowband case, in many cases extending to 3 ms (Fig. 14). Thus, decorrelations in narrowband noise would be detected at lower thresholds than broadband noise if large internal delays are present. Such large internal delays (>2 ms) were reported in a psychophysical study by van der Heijden and Trahiotis (1999); the existence of large internal delays is also well documented physiologically (Yin and Kuwada, 1983; Fitzpatrick et al., 2000; McAlpine et al., 2001; Hancock and Delgutte, 2004; Joris et al., 2005). Note that lowering of discrimination thresholds with narrowing of bandwidth was not observed in PL_N fibers (Fig. 13B), probably because narrowing of bandwidth caused a decrease in average firing rate in these neurons (Fig. 12, row 3).

In summary, our results show that the small decorrelation detection thresholds observed in humans are consistent with a coincidence analysis of single fibers and that this analysis requires small internal delays. Conversely, long delays may also be required to explain psychophysically observed effects of bandwidth.