Right–Left Asymmetries in the Whisking Behavior of Rats Anticipate Head Movements

Abstract

Rats use rhythmic movements of their vibrissae (whiskers) to tactually explore their environment. This “whisking” behavior has generally been reported to be strictly synchronous and symmetric about the snout, and it is thought to be controlled by a brainstem central pattern generator. Because the vibrissae can move independently of the head, however, maintaining a stable perception of the world would seem to require that rats adjust the bilateral symmetry of whisker movements in response to head movements. The present study used high-speed videography to reveal dramatic bilateral asymmetries and asynchronies in free-air whisking during head rotations. Kinematic analysis suggested that these asymmetric movements did not serve to maintain any fixed temporal relationship between right and left arrays, but rather to redirect the whiskers to a different region of space. More specifically, spatial asymmetry was found to be strongly correlated with rotational head velocity, ensuring a “look-ahead” distance of almost exactly one whisk. In contrast, bilateral asynchrony and velocity asymmetry were only weakly dependent on head velocity. Bilateral phase difference was found to be independent of the whisking frequency, suggesting the presence of two distinct left and right central pattern generators, connected as coupled oscillators. We suggest that the spatial asymmetries are analogous to the saccade that occurs during the initial portion of a combined head–eye gaze shift, and we begin to develop the rat vibrissal system as a new model for studying vestibular and proprioceptive contributions to the acquisition of sensory data.

Introduction

As an animal explores a novel environment, it must ensure that it not only moves to search previously unexplored regions of the space, but also that it maintains a stable perception of the world. This means that the animal must either mechanically or neurally compensate for its own movements (for review, see Cullen, 2004). An example of mechanical compensation for self-movement occurs during visual exploration: during a combined head–eye gaze shift, the eyes lead the head in making an initial saccade to a new spatial location. Subsequent head motion is then canceled out through the vestibulo-ocular reflex (VOR), which moves the eye with a velocity equal and opposite to that of the head (Guitton et al., 2003; Land, 2004).

Rat whisking movements resemble eye movements in that the whiskers can rotate independently of the head. Several recent studies have indicated that, similar to right–left eye movements, movements of the right and left vibrissal arrays are yoked. Specifically, during free-air whisking behavior, the right and left vibrissae are reported to protract and retract synchronously and to preserve spatial symmetry about the snout (Carvell and Simons, 1990; Fee et al., 1997; Gao et al., 2001; Harvey et al., 2001; Berg and Kleinfeld, 2003; Hattox et al., 2003; Sachdev et al., 2003). These studies have interpreted the bilateral symmetry of whisking to suggest that it is under the control of a precise brainstem central pattern generator (CPG), as suggested initially by Semba and Komisaruk (1984). Several recent studies have indicated that whiskers move symmetrically during free-air whisking, although asymmetric whisking has been reported to occur during object contact (Wineski, 1983; Sachdev et al., 2003).

Notably, most of these recent studies used behavioral tasks that minimized head movements, and none quantified the consequences of simultaneous head and whisker rotations for perceptual stability. If both the head and vibrissae rotate simultaneously, the rat must somehow compensate for the head movements to interpret incoming data from the vibrissae. The present study used high-speed video to examine the extent to which bilateral free-air whisking movements were influenced by head rotations in the horizontal plane. The results showed a high degree of whisking asymmetry that seems to be less related to perceptual stability and more related to the anticipation of future head movements.

Materials and Methods

Behavioral training.

Three adult female (4–7 months old) Long–Evans rats were water restricted during 1 month of training and videography. The behavioral setup is shown in Figure 1A. On each day of training (5 d/week), rats were placed in a square cage with a tunnel exiting the front. A door blocked the end of the tunnel. The cage and tunnel were elevated 5 inches above the table surface, and experimenters always stood 2 feet away from the cage. Before each trial began, a pipette filled with 1 ml of water was placed 10 inches radially away from the tunnel and 7 inches above the tabletop, level with the middle of the tunnel. The pipette was placed at a random angular location along a centrally located grid that spanned a 90° arc in front of the cage (Fig. 1A). The pipette could be slid radially through the grid so that it maintained the same angular position as it moved closer to the end of the tunnel.

Figure 1.

Experimental setup and image tracking. A, Top view of the behavioral setup. Two cameras were orthogonally positioned so as to obtain a bird’s-eye view and a side view of the search space. The shaded arc represents the possible reward locations, beginning 5 inches from the center of the tunnel and spanning three inches radially outward. B, Representative video frame illustrating the manual tracking procedure. Small black dots are points tracked on the initial linear portions of the rostral- and caudal-most whiskers. Large white dots are points tracked to quantify the head angle. Image has been black–white reversed for visual clarity. C, Coordinate systems used to quantify whisker angles. World coordinates are simply standard Cartesian coordinates. Snout coordinates are fixed to the head of the rat. Asterisks indicate the tracked angles in both coordinate frames. Thick black lines labeled “m” represent the mid-array angle calculated by averaging the positions of the rostral- and caudal-most whiskers. D, A schematic of a typical whisk representing the morphological whisk parameters listed in Table 1. Pro, Protraction; Ret, retraction.

A trial began when the experimenter opened the door at end of the tunnel. Rats traveled down the tunnel and poked their heads out through the door in search of the water reward. As the rat performed this initial exploration, the experimenter used a single swift sliding motion to push the pipette closer to the rat, 5–8 inches away from the tunnel end. When the rat found the pipette, it received ∼0.5 ml of water. This immediate reward encouraged the rats to actively search the space instead of investigating and chewing on the doorway. After the initial reward, the pipette was completely removed from the search space and placed 1–1.5 feet away from the tunnel door. This meant that the rat was exploring completely empty space and had no possible tactile contact with anything in the environment. The rats were then videotaped as they searched the open, empty space for 8–20 s. The pipette was then replaced into a second random position in the grid, and the trial ended when the rat found the second reward, consisting of the remaining 0.5 ml of water in the pipette. After the second reward, rats retracted their heads into the tunnel and the door was closed. Another trial began 3–5 min later. Rats occasionally traveled back down the tunnel to return to the square cage at some point during this intertrial interval, but this was not a requirement for the next trial to begin. All procedures were approved in advance by the Northwestern University Animal Care and Use Committee.

High-speed videography.

Two high-speed video cameras (Fastcam PCI; Photron, San Diego, CA) were used to film the rats from two orthogonal angles at 250 frames per second. One camera captured a “bird’s-eye view” of the search space. The second camera captured a side view of the rat to monitor head tilt out of the horizontal plane. We restricted analysis to those video clips in which the head and the macrovibrissae were visible. These clips corresponded to instances in which the head was sufficiently horizontal to be captured in the depth of field of the first camera. Two infrared (IR) flood lights (wavelength, 940 nm), two IR light-emitting diode arrays, and two IR ring emitters positioned on each camera (wavelength, 880 nm for both) illuminated the search space of the rat. A wave- length of 880 nm ensured that no visual cues were available for the rats because it is outside of their visible range (Birch and Jacobs, 1975; Deegan and Jacobs, 1993).

Controlling for olfactory, auditory, and visual cues.

To ensure that the rats were required to search for the reward solely with their whiskers, olfactory, auditory, and visual cues were minimized. In addition to working in the IR, care was taken to ensure that the auditory environment was identical for all trials. An ultrasound detector (D230; Pettersson Elektronik AB, Uppsala, Sweden) was used to ensure that no high-frequency auditory cues were associated with the position of the reward.

Olfactory cues from the water reward were minimized in the following ways. First, the water reward was placed 1.5 feet from the cage door during filming. The pipette was always in the same orientation, and its open end was always facing the same direction. Second, a beaker of water (to refill the pipette with) was always located at the right side of the search space 20 inches from the tunnel opening of the cage. We found no side biases either in the whisking patterns on either side of the search space or in the amount of time the rats spent searching either side of the search space. Occasionally, a portion of the water reward would fall onto the tabletop below the search space instead of being consumed by the rat. These drops were randomly located and had no correlation with the location of future rewards. Rats were not observed to spend any extra time over the locations of these drops. Thus, it is unlikely that olfactory cues had an effect on the rats’ searching patterns.

Video analysis.

Each frame of video data was saved as a tiff file and imported into Matlab 7.0 (Mathworks, Nattick, MA). Within Matlab, the horizontal angular position of the head was found by manually locating the tip of the nose and the junction of the ears with the head (Fig. 1B, white points). The head angle was then defined to be the angle of the line that connected the tip of the nose with the average of the two ear points. The error in tracking the head angle was evaluated by tracking a 1 s trial (250 frames) four times and comparing the tracked head angle in each frame. The average error in tracking the head position was 0.06 ± 0.56°, with a maximum error of 3.38°. Vertical head movements were tracked by manually locating the tip of the nose and the eye in the side view camera.

The two most rostral and two most caudal whiskers were manually tracked on both the right and left sides along the initial (approximately linear) portion of the whisker (Fig. 1B, black points). The average tracking error for the rostral whiskers was 6 ± 4.5°, with a maximum error of 8°. The caudal whiskers had an average error of 1.5 ± 4.5° and a maximum error of 2°. This tracking analysis provided us with the angular positions of the most rostral and caudal whiskers on the right and left sides. In the present study, we wanted to describe “gross” movements of the whisker arrays, so the rostral and caudal whisker positions were averaged on each side. This average angle is a good indicator of the position of the entire array at any time. Thus, for each side, we analyzed the rostral-most, the caudal-most, and the average whisker positions. The present study was not designed to examine detailed rostral–caudal differences within the array.

The quality of the video was high enough to provide an accurate estimate of the arc position of the whisker in the array during portions of each trial. We identified the arc position of each whisker tracked in this study. The rostral-most whisker tracked in any trial belonged to the sixth arc, ensuring that all whiskers tracked in this study were actuated by sling muscles (Dörfl, 1982).

After computing the head and whisker angles in each video frame, the sequence of head and whisker angles that composed a trial were low-pass filtered to smooth tracking noise. All whisker angles were filtered at 20 Hz. Both vertical and horizontal head angles were filtered at 10 Hz. Filtering the head angles at 20 Hz instead of at 10 Hz did not change any of the results.

Coordinate systems for quantifying whisker trajectories.

We analyzed whisker movements in both “world-based” and “snout-based” coordinates (Fig. 1C). “World” coordinates were equivalent to standard Cartesian coordinates and did not move with the rat. In “snout” coordinates, the 0–180° axis was defined along the caudal–rostral midline of the rat to pass through the snout. This meant that protractions on both the right and left sides were represented as increasing angular values and that symmetric whisking movements would be reflected as identical angles on the two sides. Whisker trajectories were quantified using the variables described in Table 1. Note that protraction time is defined as the time of peak protraction, that is, the time when protraction ended and retraction began. Retraction time is defined as the time of peak retraction, that is, the time when retraction ended and protraction began. Both protraction and retraction times have units of time. In contrast, the protraction set point is defined as the angle at which protraction ended and retraction began; retraction set point is the angle at which retraction ended and protraction began. Protraction and retraction setpoints have units of degrees. Figure 1D illustrates the calculation of these variables for a schematic of a typical whisk.

Table 1.

Methods of calculating whisking parameters

Variable name	Method of calculation
Continuous variables
Position	Angular position of the whiskers was calculated in both snout and world coordinates (see Fig. 1B). The angular position of the head was only meaningful in world coordinates.
Velocity	Angular velocity of the whiskers (head) was calculated as the time derivative of the angular position of the whiskers (head).
Angle of symmetry	The angle of symmetry was defined as the angle about which the whisker arrays were symmetric in world coordinates.
Array extent	Array extent for the right (left) side was calculated as the difference in the angular positions of the rostral and caudal whisker for the right (left) side.
Discrete variables
Protraction set point	Protraction set point was defined as the angle at which the protraction ended and retraction began. (The rat protracted its whiskers to the protraction set point.)
Retraction set point	Retraction set point was defined as the angle at which the retraction ended and the next whisk began. (The rat retracted its whiskers to the retraction set point.)
Protraction amplitude	Protraction amplitude was defined as the difference between the retraction set point of the previous whisk and the protraction set point of the current whisk.
Retraction amplitude	Retraction amplitude was defined as the absolute value of the difference between the protraction and retraction set points of that whisk.
Protraction time	Protraction time was defined as the time of peak protraction, that is, the time when protraction ended and retraction began. If the protraction set point was maintained for more than one frame, the average time of peak protraction was taken.
Retraction time	Retraction time was defined as the time of peak retraction, that is, the time when retraction ended and the next whisk began. If the retraction set point was maintained for more than one frame, the average time of peak retraction was taken.
Protraction and retraction durations	Protraction and retraction durations were defined as the length of time it took the rat to perform the protraction or retraction, respectively.
Protraction and retraction velocities	Protraction and retraction velocities were defined as the average velocity over a protraction or retraction, respectively. Velocities were calculated by dividing the amplitudes by the durations.
Protraction and retraction time differences	The protraction (retraction) time difference between the right and left whisker arrays was defined as the difference between the times of peak protraction (retraction) on right and left sides.

See Figure 1D for a schematic of these parameters.

Results

The results presented below were derived from 15,863 frames (63.452 s) of videographic data recorded over 90 distinct trials of free whisking behavior of three rats (see movies, available at www.jneurosci.org as supplemental material). This amounted to 373 whisks, defined from retraction to retraction. Data were pooled across the three rats, because the animals showed no significant differences in searching behaviors or whisking patterns.

We first demonstrate the presence of asymmetric and asynchronous whisking in freely whisking rats and then examine three possible explanations for the generation of the asymmetric and asynchronous movement. First, whisking behavior is stereotyped, so that one or more whisking parameters must maintain bilateral symmetry with respect to the world. In the presence of head rotations, enforced symmetry of one parameter could lead to an overall asymmetric motion. Second, the bilateral whisking movements compensate for head movements in analogy to the VOR, moving with an equal magnitude but opposite direction to the head. Third, the whisking movements allow the rat to more comprehensively cover the search space, ensuring that it whisks over previously unexplored regions of the environment.

Whisking during head rotations in the horizontal plane is asymmetric and asynchronous

Two dominant patterns of whisking

Two distinct bilateral whisking patterns occurred during the exploratory whisking behavior of the three rats. “Synchronous” (SYN) whisking was defined to occur when the right and left whisker arrays moved in synchrony. The right–left time difference for peak protractions and retractions was required to be no >12 ms (10% of the average cycle time). In SYN whisking, right and left whisker arrays maintained roughly equal velocities, amplitudes, durations, set points, and frequencies at all times, thus conserving spatial symmetry about the snout. A representative example of SYN whisking is shown in Figure 2A.

Figure 2.

Examples of bilateral whisking patterns. In each example, the black trace represents the mid-array angular position of the left whisker array with respect to the snout. The gray trace represents the mid-array angular position of the right whisker array with respect to the snout. A, SYN whisking. B, ASYN whisking. Note that the time scale is shorter than the other examples. C, DF whisking. The shaded region highlights the portion of this trial that was considered DF whisking. D, SS whisking. The shaded region highlights the portion of this trial that was considered SS whisking. deg, Degree.

The other whisking pattern involved whisker movements that were distinctly left–right asynchronous and asymmetric about the snout. In this pattern, termed “asynchronous” (ASYN) whisking (Fig. 2B), the two sides moved at approximately the same frequency but reached peak protraction and retraction with time differences of >12 ms.

Two whisking anomalies were observed that underscore the independence of the left and right whisker arrays. “Different frequency” (DF) whisking, exemplified in Figure 2C, was defined to occur if the difference in frequency between the two sides was ≥1.5 Hz. Although the traces of Figure 2C show an example in which one array is moving at nearly twice the frequency of the other, there were examples in which one side moved at noninteger multiples of the other. In other words, we did not find that the two sides necessarily had to move in harmonic ratios. The second anomaly, “single-sided” (SS) whisking, consisted of instances in which one side stayed protracted and stationary while the other side continued to whisk for at least one cycle (Fig. 2D). Although DF and SS probably do not represent distinct patterns of whisking, they are important illustrations of the degree of bilateral independence.

In theory, SS whisking might be considered a special case of DF whisking; however, we chose to distinguish it for two reasons. First, during SS whisking, one array remains completely stationary, resulting in a unique “zero-velocity” condition. Second, the amplitudes of SS whisking were similar between the two sides of the face (Fig. 2D). In DF whisking, the amplitudes were clearly not the same between the two sides (Fig. 2C). These two anomalous whisking behaviors indicate a high degree of bilateral independence.

Table 2 indicates the percentage of time the rats spent performing each pattern of whisking. Notably, asynchronous patterns of whisking accounted for ∼84% of all whisking. Only ∼16% of trials involved SYN whisking. To ensure that the asynchronous whisking patterns were not merely an artifact of having averaged the rostral and caudal whisker angles to obtain the midarray angles (Fig. 1C), we also analyzed the proportions of all different patterns of whisking for the rostral-most and caudal-most whiskers before averaging. As shown in Table 2, averaging had only a very small effect on the classification of whisking patterns. If anything, averaging the positions of rostral and caudal whiskers tended to increase the apparent symmetry of the motion.

Table 2.

Percentages of time that rats performed each of the different whisking patterns, as quantified for rostral-most, caudal-most, and mid-array whisker positions

	SYN	ASYN			Total OP
		Pure ASYN	DF	SS
Rostral	13.60	68.62	15.80	1.98	86.40
Caudal	12.37	74.52	10.41	2.70	87.63
Mid-array	16.14	67.68	12.44	3.74	83.86

Note that mid-array percentages are not the average of rostral and caudal values. This is because the mid-array trajectories were deliberately calculated by averaging rostral and caudal whisker angles in each video frame. This ′blurred′ the details of individual rostral and caudal trajectories and thus provided a conservative estimate of the amount of ASYN whisking. Accordingly, the fraction of SYN whisking appears higher for the mid-array trajectories. See Materials and Methods and Figure 1C for details.

Quantifying whisking asynchrony and asymmetry

By definition, OP whisking requires that right and left arrays start and end the whisk with time differences of >12 ms. SYN whisking requires that the two arrays start and end the whisk with time differences ≤12 ms. An initial analysis indicated that separating SYN from ASYN whisking would require breaking each episode of whisking into trials that lasted, on average, only two or three whisks. This resulted in an unacceptable reduction in the amount of continuous data available for analysis. Therefore, to quantify the asynchronies and asymmetries, analysis was performed grouping the data across both whisking patterns (SYN and ASYN). Figure 3A quantifies the temporal asynchrony across both patterns and demonstrates that the right–left time differences vary over a considerable range. Consistent with the data presented previously, Figure 3A shows that 84% of our data has a left–right phase difference of >10% (0.1) of the whisking cycle.

Figure 3.

Asynchrony and asymmetry of whisking. A, Histogram of the time differences between left and right peak protractions and retractions as a fraction of the average duration of a whisk cycle (121 ms). B, Histogram of the set point differences between left and right arrays as a fraction of the average whisk amplitude (40°). Values >1 indicate spatial asymmetries greater than the amplitude of the average whisk. L, Left; R, right; Avg., average.

If the whiskers move asynchronously (as is defined for ASYN whisking), it is clear that they cannot possibly maintain continuous positional symmetry about the snout. However, they might be transiently symmetric, for example, at either the protraction or retraction set points of the whisk. Figure 3B quantifies the difference between left and right set points of protraction and retraction and demonstrates that the majority of our data are bilaterally asymmetric. Combined with the examples of Figure 2, these results clearly indicate that positional symmetry is not consistently maintained about the snout, either continuously or at the set points of a whisk.

Whisking symmetry and synchrony are minimally affected by vertical head movements

The placement of the reward pipette at a single horizontal level (7 inches above the tabletop) encouraged the rats to whisk in a single horizontal plane. Nevertheless, rats were frequently observed to make large head movements in the vertical plane, as assessed from the side-view video camera. These movements were quantified, and relationships between whisker asymmetry and these head movements were examined.

Specifically, we investigated the relationship between the peak protraction/retraction times and the angular head position and velocity in the vertical plane. We also investigated the relationship between left–right differences in whisker position as well as the angular head position and velocity in the vertical plane. Because horizontal and vertical head movements were often observed to occur together, we calculated partial correlations between vertical head movements and whisker asymmetry and asynchrony. Whisker asynchrony was found to be independent of both vertical head position and velocity (p > 0.01). The highest partial correlation coefficient between vertical head position and whisker asymmetry was r = 0.03. Similarly, the maximum partial correlation between vertical head velocity and the whisker asymmetry was r = 0.04. This strongly suggests that head movements in the vertical plane minimally affect whisker asynchrony and asymmetry. Additional detailed analysis of this data is outside the scope of the present study.

Explanations for the asymmetric and asynchronous whisking behavior

Having demonstrated that significant asymmetric and asynchronous whisking exists in the freely behaving animal, we next set out to determine the origin of the asymmetries.

The asynchronies and asymmetries do not result from fixed spatial or temporal relationships between right–left arrays

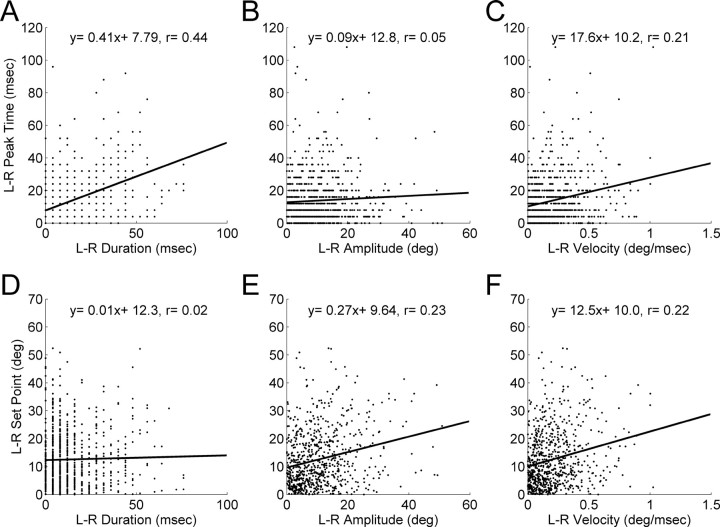
One possible explanation for the asynchronous and asymmetric nature of OP whisking is that it results from a fixed right–left relationship between whisking parameters in world-centered coordinates. For example, if protraction amplitudes were fixed in world coordinates, then a head rotation to the left would cause the left whiskers to reach a more rostral position with respect to the snout than the right whiskers. To test this possibility, we examined whether the bilateral symmetry of any of the three fundamental whisking parameters (velocity, amplitude, and duration) (Table 1) was related to the asynchrony and asymmetry of whisking.

Figure 4A–C plots whisking asynchrony (left–right times of peak protractions and left–right times of peak retractions) versus left–right differences in whisk duration, amplitude, and average whisk velocity. If the asynchrony resulted from duration, amplitude, or velocity being held fixed in world coordinates, the graphs should exhibit a negative slope. Instead, all graphs clearly illustrate either zero (Fig. 4B) (p = 0.33) or positive (Fig. 4A,C) correlation.

Figure 4.

Asynchronies and asymmetries do not result from bilaterally fixed relationships between whisker arrays in world coordinates. A–C, The synchrony of each whisk (left–right time difference of peak protractions/retractions) is plotted as a function of duration (A), amplitude (B), and velocity (C) in world coordinates. Linear regressions showed no significant correlation for B (p > 0.10). A positive correlation was found for A and C (slope and correlation coefficient as shown). D–F, The symmetry of each whisk (left–right protraction and retraction set points) is plotted as a function of duration (D), amplitude (E), and velocity (F) in world coordinates. The correlation between symmetry and left–right durations (D) is not significant (p = 0.70). The left–right amplitudes (E) and left–right velocities (F) show weak but positively sloping relationships. L, Left; R, right.

Figure 4D–F plots whisking asymmetry (left–right protraction set points and left–right retraction set points) versus left–right differences in whisk duration, amplitude, and average whisk velocity. Again, all graphs clearly illustrate either zero (Fig. 4D) (p = 0.70) or positive (Fig. 4E,F) correlation. In no case was a negative correlation observed. Thus, neither the observed asynchronies nor the asymmetries in snout coordinates result from any single whisk parameter being held fixed in world coordinates.

The right–left asymmetry does not exactly compensate for the rotational head velocity

The results above have demonstrated that bilateral preservation of whisking parameters in world coordinates cannot explain the asymmetric and asynchronous whisking. A second possible explanation is that head movements directly affect whisker motion, so that the whiskers move “equal and opposite” to the head. In the visual system, the VOR ensures that the eyes compensate for head rotations in three dimensions, thus stabilizing the image on the retina (Guitton et al., 2003; Land, 2004). Because the whiskers exhibit very little vertical motion (Bermejo et al., 2002), we would not expect them to compensate for vertical head movements. However, they might compensate for horizontal head rotations so as to maintain a constant velocity about the snout, in analogy to the horizontal component of the VOR. For example, during a head rotation to the left, the left whiskers would have to slow down in world coordinates by an amount exactly equal to the head velocity, whereas the right whiskers would have to speed up by the same amount.

This means that in world coordinates, the sum of the right and left whisking velocities should exactly equal twice the head velocity. Figure 5 illustrates that this relationship is present in the data but that the correlation is relatively weak (r = 0.28). This suggests that the rat may be partially accommodating for the head velocity in its whisking movements but that the compensation is far from ideal.

Figure 5.

Velocity asymmetry does not depend on head velocity. In world coordinates, the sum of whisking velocities correlates weakly with head velocity with a slope of 2.06. This slope is statistically indistinguishable from the slope of 2.00 that would occur if one side sped up by the head velocity, while the other side slowed down by the head velocity (p = 0.30). Vel, Velocity; deg, degree.

Whisking asymmetries serve to more comprehensively cover the search space

The spatial asymmetry in whisking anticipates head movements.

The analysis above has shown that asymmetric whisking does not result from the rat trying to keep its whisking velocities symmetric either in snout or world coordinates. However, inspection of the video data revealed that spatially, the whiskers seemed to be “looking ahead” of the rat’s head. We therefore quantified the difference in angular positions of the whiskers as a function of head velocity, as shown in Figure 6A. The negative slope means that the right whiskers are more caudal than the left whiskers when the rat is turning to the right, whereas the left whiskers are more caudal than the right whiskers when the rat is turning to the left. Importantly, the slope of the relationship (115 ms) is almost exactly equal to the average duration of one whisk (121 ms). This means that the bilateral difference in whisker position at any point during the current whisk is almost exactly the angular distance that the head will move over the course of a whisk. In effect, the whiskers are predicting the head movement by centering themselves about the head position one whisk in the future.

Figure 6.

Spatial asymmetry depends on head velocity. For all graphs, head velocities are, by definition, represented in world coordinates. This means that a negative velocity indicates that the rat is turning to the right. A, Instantaneous left–right whisker position difference versus instantaneous head velocity plotted continuously over all whisks. The slope of the best linear fit is 115 ms, which approximately equals the average duration of a single whisk (121 ms). B, Instantaneous left–right whisker position difference versus instantaneous head velocity during protractions only. C, Instantaneous left–right position difference versus instantaneous head velocity during retractions only. deg, Degree.

Importantly, this relationship exists at every point in time, not just at the start of the whisk. When a linear best fit was performed on a subset of the data that included only the set points, the relationship between head velocity and left–right whisker asymmetry was found to have a correlation coefficient (r = −0.58) and slope (−100°/s) that did not statistically differ from the data set as a whole (p = 0.76 and p = 0.08, respectively). This suggests that the whisker positions are being controlled in real-time, not only at the beginning or end of a whisking cycle.

To examine whether the relationship between whisker spatial asymmetry and head velocity was more prominent for protraction or retraction, the right–left differences in whisker positions were plotted during protraction only (Fig. 6B) and during retraction only (Fig. 6C) as a function of head velocity. It is clear that the relationship for retraction is stronger (r = −0.69) than that for protraction (r = −0.49). In other words, the symmetry of retractions depends more strongly on head velocity than does the symmetry of protractions (p < 0.001, two-tailed t test). The slopes of the relationships are also different: −99.2 ms for protraction and −138 ms for retraction (p < 0.001). Both of these slopes are different from the 121 ms mean duration of a whisk but fall within the observed range for whisk duration, namely from 95 to 166 ms. These relationships were also observed for each of the three rats individually. For each rat, the slopes and correlation coefficients were in the same ranges as those described above.

We next tested whether the whiskers were predicting future head movement or responding to actual head movement. Whisker asymmetry was plotted as a function of actual head movement during a 116 ms interval and as a function of predicted head movement (based on the instantaneous velocity of the head) during that same 116 ms interval. A duration of 116 ms was chosen because it was the value closest to the 115 ms slope shown in Figure 6A, while still being an integer multiple of our video sampling period (4 ms per video frame). Figure 7A shows that whisker asymmetry is directly related to the actual distance the head has moved in 116 ms (r = 0.47). The slope of the best linear fit is exactly 1.0, suggesting that, on average, the difference in whisker position is exactly equal to the angular distance the head will actually move in a whisk.

Figure 7.

The whiskers are anticipating, not reacting to, head movements. A, Left–right whisker position difference at the present time (t = 0) plotted versus the actual head movement that occurred in the subsequent 116 ms. B, Left–right whisker position difference at the present time (t = 0) plotted versus the predicted head movement. Predicted head movement was found by taking the instantaneous velocity at t = 0 and multiplying that velocity by 116 ms. The slopes in both A and B are statistically indistinguishable from 1.0, but the correlation coefficient is significantly higher in B than in A (p < 0.001). deg, Degree.

Figure 7B shows the relationship between whisker asymmetry and predicted head movement. To generate this graph, we found the instantaneous head velocity at each point during the whisk. The predicted head movement was then calculated by assuming that the rat kept its head velocity constant over a 116 ms duration. The slope of Figure 7B is 0.99 and does not differ significantly from the slope of 1.0 shown in Figure 7A (p = 0.35). However, the correlation between whisker asymmetry and predicted head movement is higher than the correlation between whisker asymmetry and actual head position (0.58 vs 0.47; p < 0.001). This suggests that the whisker asymmetry is predicting future head movement instead of responding to actual head movement. Note that differences between actual and predicted movements are very small, as expected, because large changes in head velocity are unlikely to take place within a 116 ms interval.

Finally, it is important to point out that in a number of cases we observed asynchronous whisking while the head was stationary (6 whisks of 21 head stationary whisks) and, conversely, SYN whisking when the head was turning (52 whisks of 393 whisks during head rotation).

Temporal asymmetry in whisking is weakly correlated with head movements.

Figures 6 and 7 indicate that the rat scans different regions of space in a way that depends directly on head velocity. In theory, the whiskers could also potentially scan those different spatial regions at different times. To test whether left–right protraction/retraction time differences were correlated with the head velocity, we needed to average the head velocity over some time window around the peaks. We chose time windows that varied from 4 to 100 ms (in increments of 4 ms) before and after the protraction/retraction. The time delay between right and left whiskers (asynchrony) was then correlated with the head velocity averaged over each of these windows. The results of this analysis showed that the correlation between asynchrony and head velocity was greatest when the head velocity was averaged over the 52 ms preceding the protraction. Figure 8A illustrates the relationship between the left–right time differences and head velocity averaged over this 52 ms time window. The negative slope means that during a head turn to the right, the right whiskers will reach peak protraction before the left whiskers, and the reverse will hold for a head turn to the left. Even at this best window, the temporal correlation is much weaker than the spatial correlation [0.34 compared with 0.59 (Fig. 6); p < 0.001].

Figure 8.

Bilateral time and phase differences. For all graphs, negative head velocities indicate that the rat’s head is turning to the right. Negative time and phase differences indicate that the left whisker array peaks before (leads) the right. A, The largest correlation (r = 0.34) between left–right whisker time differences and head velocity was found for protractions, with the head velocity averaged over 52 ms following the protraction. A duration of 52 ms was chosen because a brute-force windowing analysis showed that it yielded the largest correlation with protraction time differences (see Results). Data for retractions are not shown because they yielded an even weaker correlation than that found for protraction. B, The phase difference between the whisker arrays (time lag as a fraction of the whisking cycle) was not well correlated with the head velocity. C, The phase difference between the two arrays does not depend on whisking frequency (p = 0.47, slope not significantly different from zero). deg, Degree.

To further examine the temporal relationships between the two sides, we computed the left–right phase difference (fraction of the whisk cycle) at the peak protraction. This result is shown in Figure 8B and shows a similarly weak correlation with head velocity. Thus, neither the time nor the phase difference between the arrays correlates with the head velocity. Finally, as shown in Figure 8C, the phase difference between the arrays was found to be independent of whisking frequency (p = 0.47), suggesting a coupled oscillator network between the two sides of the face.

Air currents and elasticity of the skin and musculature are unlikely to play a major role in asymmetries

In the absence of active control, the whiskers would be subject to the force of air as the head turned, causing the whiskers on the ipsilateral side to the head rotation to become more rostral and the contralateral whiskers to lag behind in an angular position. Figure 6A indicates exactly the opposite positioning of the whiskers during a head turn. This provides evidence that the asymmetries present in whisking motion are actively induced by the rat and not caused passively by air currents.

Like all skin and tissue, the skin and musculature of the rat’s mystacial pad has some intrinsic elasticity. When the whiskers are protracted from their resting position, the elasticity of the skin is likely to be partly responsible for the ensuing retraction (Dörfl, 1982; Berg and Kleinfeld, 2003). When the head is turned to the right, for example, the skin on the left side of the face is pulled tauter than the skin on the right side. This disparity could potentially cause asymmetric movement of the whiskers during head rotations.

If the asymmetric whisking motions were related to the elasticity of the skin, however, we would expect a correlation to exist between the absolute head angle and the whisker asymmetries and/or asynchronies. Specifically, we would expect the asymmetry and asynchrony of the whiskers to be greatest at large and small head angles. However, we found no correlation between the whisker asynchronies and the absolute head position (p = 0.08) and only a weak correlation between left–right whisker asymmetry and head position (r = 0.13). Although we cannot completely rule out the possibility of elasticity effects, we can conclude that it is unlikely to be a major effect on the whisking asymmetries.

Discussion

Asymmetric and asynchronous whisking

This study is the first to quantify asymmetric and asynchronous movements in the free-air whisking behavior of rats and to reveal a direct influence of head movements on whisking behavior. In contrast to numerous studies reporting mostly synchronous and symmetric whisking in the absence of object contact (Carvell and Simons, 1990; Fee et al., 1997; Gao et al., 2001; Harvey et al., 2001; Berg and Kleinfeld, 2003; Hattox et al., 2003; Sachdev et al., 2003), this study found that the vast majority (∼84%) of whisking is both asynchronous and asymmetric. A likely explanation for this apparent discrepancy is that the present study deliberately required head rotations, resulting in an over-representation of ASYN whisking. Importantly, ASYN whisking patterns sometimes occurred when the head was stationary, suggesting that head rotation is not necessary for asynchronous whisking, but is “almost” sufficient. The qualifier almost is added because in a few exceptional cases SYN whisking occurred during slow head rotations. Intriguingly, although ASYN whisking dominated during head rotations and SYN whisking when the head was stationary, DF and SS whisking occurred equally regardless of head rotation. This further singles out these whisking patterns as anomalies.

Implications of spatial and temporal asymmetry during head rotation

Figure 7 indicates that the whiskers are not reacting to current head movement, but rather predicting the movement of the head in one whisk’s time. In other words, the whiskers are looking ahead of the current position of the head to anticipate head movements. This makes good sense behaviorally. When exploring an environment where there may be obstacles, there is strong motivation to search previously unexplored space. During head rotations, that unsearched space is the region ipsilateral to the direction of head motion and caudal to a symmetric whisk. This is precisely the space that we show rats to explore during head turns. The rat thus appears to use its whiskers to search in advance of the head, presumably to avoid running into unexpected obstacles. This also suggests that the time required for the rat to “brake” its head rotation should be less than or equal to the whisk duration (∼120 ms).

One surprising result of this study is the weak relationship between head velocity and right–left time differences of peak protraction and retraction. Although temporal asynchrony is large (up to 108 ms), it is not nearly as well correlated with head velocity as is spatial asymmetry. Temporal asynchronies could, theoretically, be used to differentially search particular regions of space during head rotations. For example, the rat could choose to stop protraction on right and left sides at different points in time, thus selecting whisk amplitudes and the particular (spatial) regions swept out by each side. Our results, however, do not support this hypothesis. Figure 8 illustrates that temporal asynchronies are not used to selectively search particular regions of space.

We therefore propose that temporal asynchronies are not constrained by head motion. This leaves the temporal component of whisking free to be under more cognitive control, used perhaps to determine when a particular region of space (or part of an object) is sampled. If the rat is encoding spatial characteristics of the environment through the timing of whisker input (Ahissar et al., 2000; Ahissar and Arieli, 2001), we would expect temporal asynchronies to become particularly relevant during object exploration and feature extraction. Alternatively, the rat may use efference copies of whisking movements (Fee et al., 1997) to maintain perceptual stability.

A second surprising result was the absence of bilateral whisking symmetry in either velocity or phase. These results would seem to conflict with studies that demonstrate the importance of these variables in neural coding (Ahissar et al., 2000; Pinto et al., 2000; Shoykhet et al., 2000; Jones et al., 2004; Moore, 2004; Arabzadeh et al., 2005) and in texture perception (Hartmann et al., 2003; Neimark et al., 2003; Andermann et al., 2004). We suggest the following explanation: the behavioral task used in this study required the rat to find a small object (pipette) in a large search space. The rat was more likely concerned with searching novel space than with the exact timing of whisker motion. In the presence of objects, the asymmetries of the rat’s whisking movements may more closely reflect the importance of velocity and/or phase. Thus, we predict that the rat can differentially use position or velocity control, depending on task requirements.

Implications for central pattern generation

Substantial evidence exists for the presence of a distributed whisking CPG located in the rat brainstem. In addition to anatomical and pharmacological research (Hattox et al., 2002, 2003), studies have shown that whisking rhythmicity and synchrony are preserved without sensory feedback from the vibrissae (Welker, 1964; Gao et al., 2001; Berg and Kleinfeld, 2003). To date, coupling between proposed CPG networks has only been explored unilaterally, for muscles that control protraction (intrinsic muscles) and retraction (extrinsic muscles) (Dörfl, 1982; Berg and Kleinfeld, 2003). Our results support the existence of two distinct left- and right-side CPGs. Because bilateral phase difference is independent of whisking frequency (Fig. 8C), it is probable that the two CPGs are connected as coupled oscillators. The present results cannot address whether bilateral coupling occurs between the intrinsic or extrinsic muscles, or both.

Our results show that spatial and temporal differences in the output of the two putative CPGs depend directly on rotational head velocity. Head velocity information presumably arises from the vestibular system and/or proprioceptors in neck muscles. Anatomical studies have demonstrated connections from the vestibular system to the facial motor nucleus in both cats (Shaw and Baker, 1983) and rats (Hattox et al., 2002). Because the data show asymmetries during both protraction and retraction, head velocity information is likely to contribute to the activity of both intrinsic and extrinsic muscle groups.

Comparisons to the VOR and vestibulo-collic reflex

This main result of this study is that vibrissae continuously predict the movement of the head during the next 115 ms (approximately one whisk). This prediction occurs throughout both protraction and retraction, although with slightly different time constants (Fig. 6). In the visual system, a similar anticipatory movement occurs during combined head–eye gaze shifts. During this type of visual exploration, the eyes reach a new fixation point before the head moves to that point (Guitton et al., 2003; Land, 2004). Once the eyes have reached the target, they begin to compensate for head movement through the VOR. In the free-whisking task of the present study, the future position of the head seems to serve as an analog to the fixation point.

It is similarly informative to compare our findings to the vestibulo-collic reflex (VCR). The VCR stabilizes the head in space through activation of neck muscles, but the reflex is modulated depending on whether head movement is active or passive (Cullen, 2004; Roy and Cullen, 2004). When the goal of head movement is perceptual stabilization, the VCR exactly accommodates for head movements. When the goal of movement is to change the region of space actively being searched, the reflex is suppressed. Neurophysiological recordings have shown that a cancellation signal is present only when the activation of neck proprioceptors matches the motor-generated expectation during active head movements (Cullen and Roy, 2004; Roy and Cullen, 2004).

We suggest that the following analogies may apply when comparing vibrissal and visual systems. When the rat’s goal is to move its head to a new region of space, the whiskers are used to look in advance of the head. This corresponds directly to the initial saccade phase of a combined head–eye gaze shift and is consistent with suppression of the VCR during active head movements. A different situation arises when the rat’s goal is perceptual stabilization, as might occur during object exploration. In this case, we predict that whisker movements should compensate for head rotations like the VOR during a head–eye gaze shift, or like the VCR during passively imposed head movements. Notably, our data lend some support to this idea. Figure 5B demonstrates that right–left whisker velocities are changing such that they partially compensate for head rotation. The compensation has the correct magnitude (slope has a magnitude of 2) and the correct sign (slope is positive). We predict that this type of compensation should be accentuated during behaviors that require perceptual stabilization.

An increasing number of studies have found that relationships between eye, head, and trunk movements during naturalistic behaviors are complex and vary between individuals. For example, the amplitude of head movements during a gaze shift depends strongly on the initial alignment of the eyes (Volle and Guitton, 1993), but can also depend on task difficulty and on the individual (Stern et al., 2005). In addition, the extent of VOR suppression is also highly individualistic (Cullen and Roy, 2004). The present study suggests that the relationship between body, head, and whisker movements in rats may be developed as a new model system, complementary to the primate model, for studying vestibular and proprioceptive contributions to sensory acquisition and cancellation of reafferent signals.