Deciphering the Spike Train of a Sensory Neuron: Counts and Temporal Patterns in the Rat Whisker Pathway

Abstract

Rats achieve remarkable texture discriminations by sweeping their facial whiskers along surfaces. This work explores how neurons at two levels of the sensory pathway, trigeminal ganglion and barrel cortex, carry information about such stimuli. We identified two biologically plausible coding mechanisms, spike counts and patterns, and used “mutual information” to quantify how reliably neurons in anesthetized rats reported texture when “decoded” according to these candidate mechanisms. For discriminations between surfaces of different coarseness, spike counts could be decoded reliably and rapidly (within 30 ms after stimulus onset in cortex). Information increased as responses were considered as spike patterns with progressively finer temporal precision. At highest temporal resolution (spike sequences across six bins of 4 ms), the quantity of “information” in patterns rose 150% for ganglion neurons and 110% for cortical neurons above that in spike counts. In some cases, patterns permitted discriminations not supported by spike counts alone.

Introduction

Rats have a well developed texture discrimination capacity (Carvell and Simons, 1990), and the aim of the present work is to explore potential neuronal coding mechanisms underlying this capacity. In rats, as in humans (Gamzu and Ahissar, 2001), tactile object exploration derives from active palpation; rats sweep their whiskers across surfaces in a rhythmic forward–backward cycle to create neuronal representations of the contacted objects (Kleinfeld et al., 2006). The signals from each whisker are transduced by specialized receptors (Ebara et al., 2002); first-order neurons with cell body in the trigeminal ganglion innervate these receptors. From the trigeminal ganglion, signals travel to the brainstem. Axons of the second-order neurons cross the midline and travel to the thalamic somatosensory nuclei; thalamic neurons project to the layer IV “barrels” of primary somatosensory cortex (Woolsey and Van der Loos, 1970). Here, we analyze the responses of neurons in the trigeminal ganglion and barrel cortex.

The stimuli consisted of controlled movements of a mechanical device, in which the motion reproduced the vibrations recorded earlier when a whisker swept across various surfaces: a smooth surface and a set of sandpapers, each with a characteristic grain size. Recently, we showed that the whisker vibrations associated with different textures evoked ganglion and cortical responses that, averaged across trials, differed according to texture (Arabzadeh et al., 2005). The differences were apparent in both the spike count and the temporal profile of spikes. To quantify the neuronal coding of texture, we now analyze the same dataset with the goal of determining the features and parameters of neuronal activity that vary systematically from one texture to another. Our approach is to apply measures of “mutual information” (Shannon, 1948; Cover and Thomas, 1991), hereafter referred to as “information.” Using this framework, we can determine the maximum amount of knowledge (the upper bound of information) available to an observer who “reads off” the spike train signals (Rieke et al., 1997; Borst and Theunissen, 1999). The strategy is to identify biologically plausible coding mechanisms and then to quantify how reliably neurons transmit texture information when their responses are “decoded” according to each of the candidate mechanisms.

Principal questions include the following. How much information is carried by the number of spikes, and how does such spike count information build up during a single trial? How much additional information, beyond that available in spike count, is conveyed by the temporal pattern of spikes? We draw particular attention to the dependence of information transmission on the “internal clock” (the register of temporal structure within a spike pattern) and the “external clock” (knowledge of when the spike pattern occurred within the course of a single trial). To what extent does the quantity of decodable information depend on the precision of these clocks?

Materials and Methods

Measurement of neuronal responses.

Methods have been described in detail previously by Arabzadeh et al. (2005): an abbreviated version is given here. Experiments were conducted in accordance with National Institutes of Health and institutional standards for the care and use of animals in research. Subjects were adult male Wistar rats. In one set of anesthetized rats (urethane, 1.5 g/kg), “electrical whisking” (Brown and Waite, 1974; Szwed et al., 2003) was generated by stimulating the right facial nerve for 60 ms to produce whisker protraction, followed by a passive 65 ms whisker retraction. For a selected whisker, horizontal and vertical movements at the base were registered by a two-channel optical sensor. The two voltage signals were digitized at 7634 samples per second. Whisker movement was studied for 10 min under each of six conditions: free whisk (no object contact) and contact with five surfaces. From the vibration signal recorded as the whisker swept through the air or along a texture, a 50 s continuous record was extracted and sliced into 100 unique trials of 500 ms (consecutively numbered trials 1–100), each trial composed of two-dimensional position signals across four 125 ms whisks. For the present analysis, we selected trial number 50 and measured neuronal responses to 100 identical repetitions. This approach allows us to focus on neuronal firing reliability because it eliminates stimulus variability (the trial-to-trial differences in the detailed whisker vibration that were normally caused by the slightly varying trajectory on each of 100 unique trials).

We measure neuronal responses to the first of the four whisks, except for analyses of external clock precision. The stimulus set was constructed by splicing trials together at the point of maximum retraction. A free-whisk trial always separated two successive texture trials. A block was composed of five different texture trials (t₁–t₅) with free whisk trials (fw) interspersed, e.g., fw–t₃–fw–t₅–fw–t₁–fw–t₂–fw–t₄. Before stimulus delivery, signals were low-pass filtered at 500 Hz. The stimulus set used in the physiology experiments originated from a C3 whisker recording.

The noise stimulus was constructed by selecting values of horizontal velocity and vertical velocity independently from a Gaussian distribution 7634 times per second. The stimulus was then low-pass filtered (Chebyshev type II) at 500 Hz. The noise stimulus was presented for 10 min after conclusion of the texture stimuli.

In urethane-anesthetized rats, neuronal recordings were made simultaneously from two sites. Ganglion neurons were recorded by advancing a single electrode (Frederick Haer Company, Bowdoinham, ME) to a position determined by stereotaxic coordinates. Cortical recordings were obtained by inserting a 100 microelectrode array (Cyberkinetcs, Foxborough, MA) to a depth of 700–1000 μm in left barrel cortex (Rousche et al., 1999). Ganglion recordings were always single units, whereas cortical recordings consisted of a multiunit cluster at each channel.

The receptive field centers in the ganglion-only recordings were C3, E1, D6, E6, and γ (twice). The receptive field centers in the cortex-only recordings were A1, B4, E5, and E3 (twice). Receptive field centers in the paired ganglion–cortex recordings were δ (twice), E3 (twice), C2 (twice), and E4.

Texture stimuli were delivered to a single whisker using a motor constructed from two orthogonal pairs of parallel piezoelectric wafers driven independently by horizontal and vertical signals. The whisker was inserted into a metal tube 1 mm from the skin. The second set of rats thus received whisker vibrations identical to those recorded previously during active whisking in the first set of rats.

Information theoretic analysis of spike trains.

The information that the neuronal response conveys about the stimulus can be quantified by Shannon’s mutual information formula (Cover and Thomas, 1991), abbreviated hereafter as information:

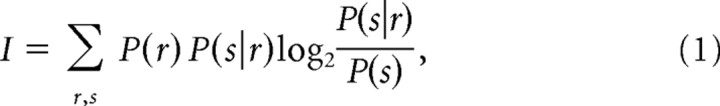where P(s) is the probability of presentation of texture stimulus s, P(s|r) is the posterior probability of s given observation of response r, and P(r) is the probability of response r unconditional on the stimulus. Information determines the maximum amount of knowledge (the upper bound of information) available to an observer who knows the posterior probabilities P(s|r) and uses them to read off the signals available in a single observation of a spike train (Rieke et al., 1997).

The amount of information transmitted by a neuron depends on assumptions about how the activity is read off. We distinguished between activity decoded according to cumulative spike count and spike pattern (Panzeri et al., 2001; Petersen et al., 2001). Information in the cumulative spike count was obtained by counting the spikes from stimulus onset (t = 0) until some time t = T. When T was set to the end of the stimulus presentation (125 ms), the cumulative spike count was referred to as whole-whisk spike count.

To compare the relative rise time of information in ganglion and cortex, we defined “information flow” as the derivative of the cumulative information. The cross-correlogram between ganglion and cortical information flows was then measured using the following equation:

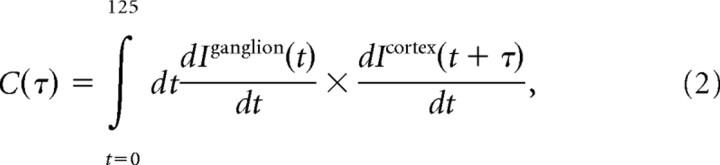where I^ganglion(t) and I^cortex(t) denote the cumulative information in ganglion and cortex at time t.

Information in the spike pattern was obtained by subdividing a window of 24 ms length into time bins and then shifting the window along the spike train in steps of 1 ms. Activity within the 24 ms window then became a “word” made up of a sequence of “letters,” each letter signifying the presence or absence of a spike in that bin, 1 or 0 (Strong et al., 1998). The maximum precision allowed because of finite sampling of posterior probabilities (see bias correction below) was six bins of 4 ms.

Optimal pattern decoding assumes the observer’s capacity to maintain two clocks: an internal clock to register the local temporal structure of the spikes within a window, and an external clock to register the time of the sliding window throughout the stimulus. We measured information while progressively degrading the two clocks. Degrading the internal clock corresponded to increasing the bin size, ΔT_internal. To increase ΔT_internal from 4 to 8 ms, we randomly shuffled spike occurrences between adjoining pairs of 4 ms time bins. To further increase ΔT_internal from 8 to 12 ms, we randomly shuffled spike occurrences between adjoining triplets of 4 ms time bins. Finally, to degrade the “pattern” until it was equivalent to the spike count in the 24 ms window, we increased ΔT_internal from 12 to 24 ms.

Spike pattern information at time t, i.e., when the sliding window spans t-24 to t ms, results from comparing the spike pattern present in this window with the posterior probabilities P(s|r) constructed at that exact window position. Hence, optimal decoding would require the observer to have a perfect external clock, i.e., to know the current window position and thus obtain the correct posterior probabilities given in Equation 1. To degrade the external clock, we added uncertainty, ΔT_external, to this alignment. The decoder then would base its interpretation of the current response r not on the correct posterior distribution P(s|r) but on an approximated posterior distribution Q(s|r) obtained by pooling the frequency distribution of spike pattern r across all sliding windows between (t-24) − (ΔT_external/2) and t + (ΔT_external/2):

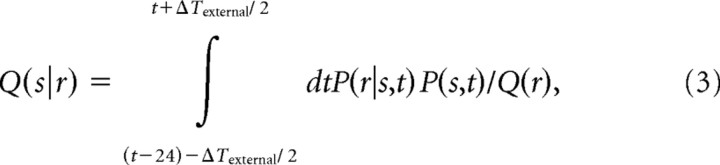where P(s,t) = P(s)/ΔT_external, and, in this particular equation, we made it explicit that P(r|s) P(r|s,t) depends on the time t at which the sliding window begins.

There is in general no closed-form analytical expression for this information lost by a decoder that uses an approximated posterior distribution (Merhav et al., 1994). However, Latham and Nirenberg (2005) derived a closed-form upper bound to the information lost by a mismatched decoder. Generalizing their work to the case of external clock imprecision, we derived an upper bound to the information lost when using Q(s|r) rather than P(s|r), indicated as ΔI_external and expressed as follows:

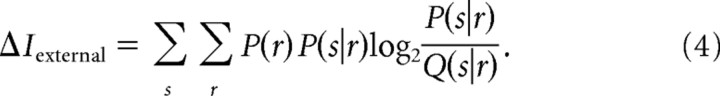It is useful to note that ΔI_external is guaranteed not to diverge to infinity. In fact, Q(s|r) = 0 implies that either P(s) = 0 [which in turn implies that P(s|r) = 0] or that Q(r|s) = 0. In the latter case, P(r|s) must be 0 at all times t entering the integration in Equation 4. Taking into account that 0log(0) converges to 0, this is enough to ensure the nondivergence of ΔI_external.

The quantity

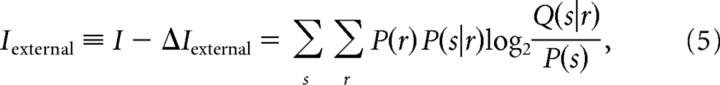is a lower bound to the information that can be extracted by a decoder that works with the imprecise probability, Q(s|r). In the following, we use I_external in Equation 5 as a single equation to compute how the information available to the decoder depends on both the external and internal clocks. All quantities reported in Results are computed through Equation 5. I_external depends on the internal clock through the response r (which is shuffled to provide the specified internal clock precision) and depends on the external clock through Q(s|r). When ΔT_external = 0, then Q(s|r) = P(s r), so that I_external becomes equal to the full pattern information I in Equation 1. In particular, when ΔT_external = 0 and ΔT_internal = 24 ms, Equation 5 is equal to the spike count information in the sliding window. When instead ΔT_external is greater than 0, then I_external does not necessarily equal the information in Equation 1 and is a lower bound to the information that can be extracted by a decoder that works with clock imprecisions ΔT_external and ΔT_internal, respectively.

Bias correction.

The probabilities in Equation 1 were estimated from a limited number of experimental trials per stimulus, N = 100, potentially leading to an upward bias in information (Panzeri and Treves, 1996). We used a number of bias-correction procedures (Panzeri and Treves, 1996; Strong et al., 1998; Nemenman et al., 2004). Because they all gave almost identical results, we present only results based on the “quadratic extrapolation” correction procedure of Strong et al. (1998). The bias problem was much more prominent for spike patterns than for spike counts because computing spike pattern probabilities involves sampling a higher-dimensional response space. To rule out the possibility that spike pattern information was artificially inflated upward by failure to eliminate all of the bias, we recomputed spike pattern information using a data-robust lower bound that is virtually unbiased and tight in most cases, as follows (for details, see Pola et al., 2005). First, we “binarized” the spike pattern word by setting the letter to 1 in the rare occasions in which there was more than one spike per bin; this reduced the bias and could not increase information. Second, instead of computing the spike pattern information through Equation 1, we computed it through a simplified formula (Pola et al., 2005, their Eq. 5.12), which is an unbiased lower bound to the spike pattern information. We then verified that the values of the lower bound approximation were not statistically different from I in Equation 1 (t test, p > 0.9). This suggests that our robust lower bound was a tight approximation to the true spike pattern information in Equation 1.

Data manipulation both for experimental and analytical work was in Matlab (MathWorks, Natick, MA).

Results

Features of neuronal responses to texture stimuli

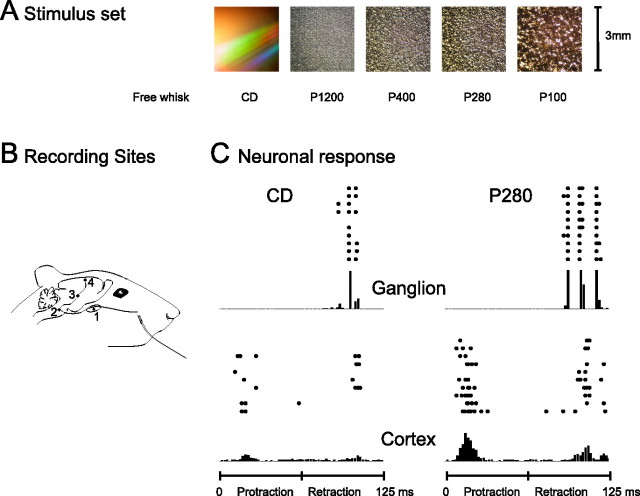
In anesthetized rats, we stimulated the facial nerve to produce forward–backward whisking (Brown and Waite, 1974; Szwed et al., 2003) across textures and measured the accompanying vibrations of the whisker shaft. There were six experimental conditions (Fig. 1A). In free whisk, the whisker moved forward and backward through the air, at the rate of eight whisking cycles per second, without contacting any object; in the five other conditions, the whisker moved at eight cycles per second, in contact with the following surfaces: a smooth compact disk (CD) and four different sandpapers (P1200, P400, P280, and P100, ordered by increasing grain size). We later used the vibrations as a stimulus set for a second group of rats, “playing back” the vibrations in a randomized sequence while recording neuronal activity at two stages of the sensory pathway: the trigeminal ganglion cells (first-order neurons that innervate the sensory receptors) and the barrel cortex neurons, which are the first site of cortical integration (Fig. 1B). Recordings in the ganglion were single units, whereas cortical recordings consisted of a small cluster of neurons at each electrode.

Figure 1.

Texture stimuli and neuronal responses. A, Stimuli consisted of whisker trajectories previously recorded during free whisking and contact with five different surfaces. B, Simplified scheme of the sensory pathway. The primary afferent neuron has a cell body in the ganglion (1) and projects into the brainstem trigeminal nuclei (2). The second-order neuron projects to the contralateral thalamus (3). The thalamic neuron projects to barrel cortex (4). The data consist of ganglion and cortical activity. C, Spike trains recorded from ganglion (top row) and cortex (bottom row) in response to 10 randomly selected whisker sweeps along the CD surface (left column) and P280 sandpaper (right column). PSTHs below the raster plots represent summated activity across all 100 trials. The timescale corresponds to the two phases, protraction and retraction, of a 125 ms whisk cycle. Note that the cortical cluster responded during both phases of whisker movement and the ganglion cell only during retraction.

Figure 1C illustrates neuronal activity recorded simultaneously at two levels of the pathway in response to CD (left column) and P280 (right column). Stimulus site was whisker E4. Several potential texture coding mechanisms are evident. Both the ganglion neuron (top row) and the cortical cluster (bottom row) responded with a greater number of spikes on each trial to P280: clearly, an observer could read off spike count per whisk to distinguish the stimuli. Beyond firing rate, it is clear that the temporal sequence of spikes differed according to the texture. For example, for the ganglion cell, CD contact gave rise to one peak in the peristimulus time histogram (PSTH), followed at a short temporal interval by a smaller peak; P280 resulted in three separate PSTH peaks with slightly longer intervals between them. For the cortical cluster, the different textures appear to have evoked responses with differing spike sequences, yet the impact of spike timing in representing textures cannot be evaluated solely by visual inspection.

Although the spike counts and temporal patterns are most visible in the PSTH from summated trials, sensory judgments usually are made from single contacts or small numbers of contacts (Carvell and Simons, 1990) (M. von Heimendahl, personal communication). Both the ganglion and cortex neurons exhibited trial-to-trial variations, which pose limits to how well the stimulus could be identified on a single trial. Thus, the key question in coding is not whether the average neuronal responses differed according to the stimulus; rather, what was the scale of this difference compared with the trial-by-trial response variability? We now investigate how reliably stimuli were encoded in a single whisk and which features of the neuronal response contributed to stimulus discriminability.

In this report, we present a detailed analysis of the cortical neuronal cluster and the ganglion neuron illustrated above. We then show the generality of their principal results to the full set of recorded neurons.

Spike counts

Behavioral experiments indicate that rats require only a few whisks over a texture to perform a roughness discrimination task. We analyzed the spikes recorded during single whisking cycles whose time course is given at the top of Figure 2A. Each whisk lasted 125 ms and consisted of protraction (0–60 ms) and retraction (60–125 ms). Aligned below the whisk cycle time course are the spike trains of the cortical cell cluster for trial numbers 51–55 on two texture stimuli, CD (black traces) and P280 (gray traces).

Figure 2.

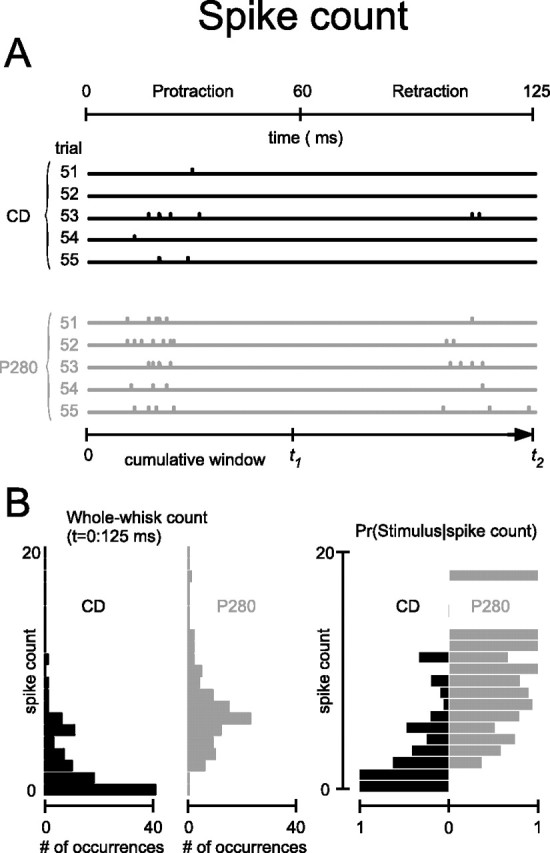
Texture-specific spike counts. A, Cortical activity during five successive trials on two textures, CD (black) and P280 (gray). The scale under the bottom panel indicates the time from stimulus onset until T over which cumulative spike counts can be computed. B, Left, Distribution of whole-whisk spike counts measured from 100 presentations of CD (black) and P280 (gray). Right, Conditional probabilities of the two stimuli of interest given an observed value of spike count.

How would the stimulus discrimination proficiency of a spike count observer develop along the time course of stimulus presentation? We evaluated this by measuring the cumulative spike count: the buildup of spikes from stimulus onset until some time T, at which point the discrimination would be made. The mechanism is illustrated schematically along the time axis at the bottom of Figure 2A. A cumulative spike count code can be evaluated over any accumulation time (Fig. 2A, bottom, t₁). One important time point to consider is for T equal to the end of the stimulus presentation (t₂ along the time axis); in this case, the cumulative spike count is equivalent to the whole-stimulus spike count. This is the most commonly used activity measure in the study of stimulus discrimination and behavior (Britten et al., 1992; Gold and Shadlen, 2001; Luna et al., 2005) and we consider it first.

Frequencies of spike counts accumulated across the entire whisk (0–125 ms), from 100 trials on textures CD (black) and P280 (gray), are given in the left panel of Figure 2B. For P280, the spike count distribution was shifted to higher values compared with the distribution for CD. From this, we can derive the conditional probability distributions: the probabilities that either of the two stimuli was presented given that a particular spike count occurred (Fig. 2B, right). Observing from zero to two spikes on a single trial would lead an observer to assign the stimulus with higher probability to CD, whereas observing three or more spikes would lead to assignment of P280.

The elements of the conditional probability distributions provide an intuitive account for how spike counts can support stimulus discrimination and appear in the calculation of the mutual information (Eq. 1).

Information carried by spike counts

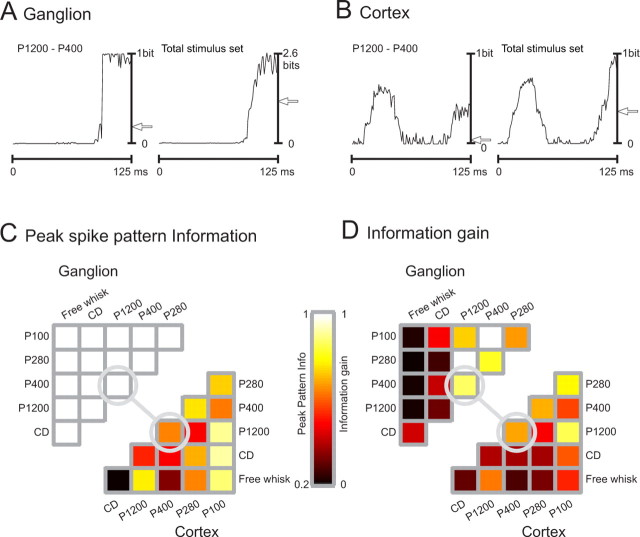
We now apply information analyses to quantify how the cumulative spike count distributions could support texture discriminations and how information varied dynamically across the response period. Information carried by the cortical cluster about the pairwise discrimination CD–P280 (the same stimulus pair shown in Fig. 2) is given in the left panel of Figure 3A. Stimulus entropy was 1 bit. Information showed a rapid rise beginning at 7 ms and reached a peak of nearly 0.6 bits during whisker protraction, ∼23 ms into the whisk cycle. As the whisker rested in the forward position, cumulative information decreased slightly before rebounding at 100–125 ms as a result of stimulus-evoked responses during retraction.

Figure 3.

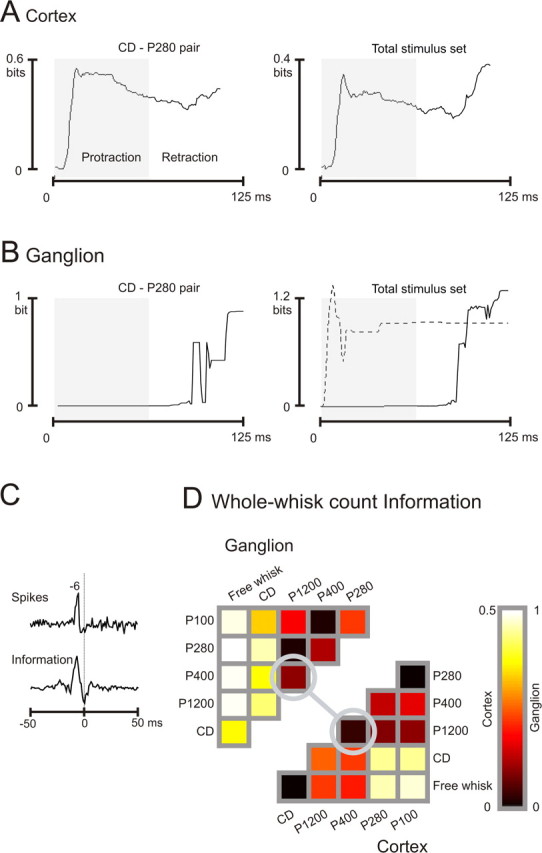
Spike count information. A, Cumulative information carried by the cortical cluster during presentation of stimulus pair CD–P280 (left) and the total stimulus set (right). To highlight information accumulation in relation to the whisk cycle, the protraction phase is shaded. In this and all figures, time steps were 1 ms. B, Cumulative information carried by the ganglion cell during presentation of stimulus pair CD–P280 (left) and the total stimulus set (right, solid line). During the protraction phase (shaded), the cell carried no information. A second ganglion cell carried information only during whisker protraction (right, dashed line). C, Correlation between ganglion and cortex spike times (top trace), and correlation between the rate of ganglion and cortex information flow (bottom trace). D, Matrix of all pairwise information values for ganglion (top left) and cortex (bottom right). Circles indicate the stimulus pair P400–P1200. Note the different information scales for the two plots.

Information carried about the total stimulus set (six different stimuli) is given in the right panel of Figure 3A. Stimulus entropy was 2.58 bits. Similar to the pairwise case, information rose rapidly and reached a peak at 16 ms. A second wave of information was transmitted during whisker retraction.

We can better understand the time course of information present in cortical spike trains by examining subcortical inputs. For the ganglion cell recorded simultaneously with the cortical cluster, spike count information about CD versus P280 is given in the left panel of Figure 3B. Because the neuron was sensitive only to whisker retraction, information was at baseline until 90 ms, when it rose sharply as the whisker moved backward. At the end of the response period, the cumulative information was ∼0.9 bits. Information carried about the total stimulus set is given in the right panel (solid line). Absence of information during whisker protraction resulted from the complete silence of the neuron during this phase of the whisking cycle.

Whereas the cortical cluster carried information during both whisking phases, the ganglion cell was directionally selective (retraction only) for both the stimulus pair CD–P280 and the total stimulus set. The dataset included a comparable number of ganglion cells with opposing phase preference. For one such cell, cumulative information about the total stimulus set is illustrated by the dashed line in Figure 3B, right panel. Information rose sharply within a few milliseconds of whisker protraction onset. The constant value of cumulative information from 40 ms onward reflects the fact that this “protraction cell” added no additional spikes during whisker retraction. Although the protraction cell was not recorded simultaneously, it is nevertheless clear that the time course of information seen in cortex could result from the integration of cells with time courses of information like those of the two ganglion cells.

Because one of the two illustrated ganglion cells (Fig. 3B, solid lines) was recorded simultaneously with the cortical cluster, it was possible to directly tap into signal transmission along the ascending sensory pathway. We measured (1) the correlation between ganglion and cortical spike times and (2) the correlation between the rate of ganglion and cortical information flow. Rate of information flow was computed as the derivative in 1 ms steps of the cumulative information (see Materials and Methods). Spike correlations are best examined during white-noise stimulation because the random stimulus variation over time prevents the appearance of cross-correlation peaks attributable solely to stimulus structure. The top plot of Figure 3C shows the spike time cross-correlogram between ganglion and cortex (the reference signal) constructed from a 10 min period of velocity white noise (see Materials and Methods). Ganglion cell spikes preceded cortical cell spikes by 5–7 ms, consistent with the known transmission time between the two centers. The bottom plot of Figure 3C shows the information flow cross-correlogram between ganglion and cortex, drawn from the total texture stimulus set (Fig. 3A,B, right columns), and its peak is exactly aligned with the ganglion–cortex spike correlogram. The numbers of spikes in cortex, in quantities specific to certain stimuli, thus appear to be the result of rapid integration of ascending signals, such that the informative message emerges in cortex after a delay equivalent to the pathway transmission time. The cortical representation of texture, at least as measured by this spike count of the cluster, does not emerge from prolonged intracortical reverberations.

Coding efficiency is the ratio between measured information and stimulus set entropy (Arabzadeh et al., 2004). For the ganglion cell, pairwise information between CD and P280, based on whole-whisk spike counts, had an efficiency of 90% (0.9 bits compared with stimulus entropy of 1 bit). Ganglion cell efficiency for the total stimulus set was 48% (1.24 bits; stimulus entropy, 2.58 bits). For the cortical cluster, coding efficiency was 44% for the selected stimulus pair and 14% for the total stimulus set. The markedly higher efficiency for the CD–P280 stimulus pair suggests that the spike counts evoked by other stimuli within the set might have been poorly discriminable. To visualize the heterogeneity of coding efficiency, we plotted the whole-whisk (0–125 ms) cumulative spike count information for all 15 stimulus pairs. Figure 3D illustrates pairwise stimulus discriminability for the ganglion cell (top left) and the cortical cluster (bottom right). Rows and columns are labeled by a stimulus, and colored entries give the information available between the two corresponding stimuli. For the ganglion cell, free whisk could be perfectly discriminated from all sandpaper textures (P100, P280, P400, and P1200); information values were above 0.96 bits. Free whisk versus CD could be discriminated slightly less reliably (0.72 bits). CD showed highly reliable discriminability against the remaining textures (0.65–0.9 bits). In contrast, all pairwise comparisons between P100, P280, P400, and P1200 resulted in much lower discriminability.

To understand the distribution of pairwise information values for the cortical cluster, we can posit three classes of stimuli along a gradient: (1) free whisk and CD, (2) P1200 and P400, and (3) P280 and P100 (the coarsest sandpapers) (Fig. 1A). For any discrimination between classes 1 and 3, the neuronal response carried a relatively high amount of information. For any discrimination between class 2 and either class 1 or 3, the neuronal response carried an intermediate amount of information. For any discrimination between textures within a class, the neuronal response carried essentially no information. One such within-class stimulus pair, P400–P1200, is highlighted by the circles in Figure 3D. We will now test whether stimulus pairs such as this, indiscriminable by spike count alone, may become discriminable by spike patterns.

Spike patterns

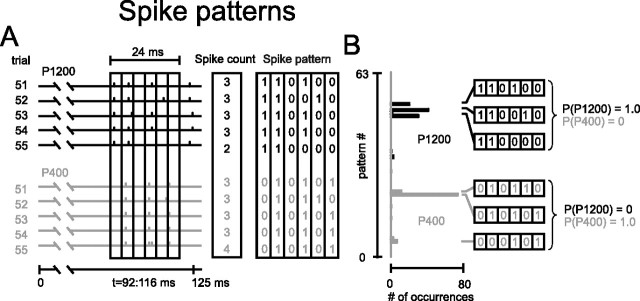
The preceding section described the amount of information available to a decoder that discriminated between stimuli based purely on the number of spikes accumulated over a period lasting some tens or hundreds of milliseconds. In contrast, a decoder may be sensitive to “spike patterns:” the specific temporal sequences of spikes across the response. If so, then such patterns might convey additional information beyond that present in the spike count (MacKay and McCulloch, 1952). To illustrate how spike patterns can be texture specific when spike counts are not, Figure 4 illustrates both ways of characterizing spike trains. The data are from the ganglion cell discussed previously. In A, responses to textures P1200 and P400 (the two stimuli circled in Fig. 3D) are given for trials 51–55. A temporal window of 24 ms length was shifted along the spike train in steps of 1 ms; the window is shown at a position of 92–116 ms. To the right of the spike train, spike counts in this window are given for five trials. Because the numbers of spikes in this window did not differ according to texture, spike counts could not support reliable discrimination. To consider a potential spike pattern code, the window was subdivided into six bins of 4 ms, and the occurrence or absence of a spike in each bin was registered as 1 or 0 (see Materials and Methods). Now the response in the window of interest is a spike sequence on each trial (Fig. 4A, right).

Figure 4.

Texture-specific spike patterns. A, Left, Ganglion activity during five successive trials on two textures, P1200 (black) and P400 (gray). The box outlines a 24 ms sliding window spanning 92 to 116 ms along the whisk cycle (see time axis below spike trains). The window is in turn subdivided into six bins of 4 ms. Middle, Spike counts during the indicated window did not distinguish between the stimuli. Right, Spike patterns during the same window, in which binary values indicate the presence or absence of a spike in each bin, discriminated between the stimuli. B, Distribution of observed spike patterns from 100 presentations of P1200 (black) and P400 (gray). “pattern #” refers to binary value of the 64 possible spike patterns. For each stimulus, the three patterns with the highest number of occurrences are illustrated with their corresponding conditional probabilities.

The firing patterns are informative, of course, only if they occur reliably and in a stimulus-specific manner across a large number of trials. In an analogous procedure to spike counts, the reliability of patterns can be assessed by determining how frequently each possible pattern occurred across 100 trials. A pattern was designated by the decimal value of the base 2 word; for example, 0 1 0 1 0 1 was called pattern number 21. With six digits, there are 64 patterns with decimal values going from 0 (0 0 0 0 0 0) to 63 (1 1 1 1 1 1). In Figure 4B, the vertical axis gives pattern number and the horizontal axis the number of occurrences across 100 trials for the window position of interest, 92–116 ms. It is evident that P1200 and P400 each induced distinctive spike patterns. The three most frequent patterns for each stimulus are shown on the right side of Figure 4B (these same patterns were present in the two sets of trials given in A). From the relative frequencies of each spike pattern, we can derive the conditional probability distributions: the probabilities that either of the two stimuli was presented given that a particular spike pattern occurred within the window of interest. Observing pattern numbers 48, 50, or 52 on a single trial would lead an observer to assign the stimulus with certainty to P1200, whereas observing pattern numbers 5, 21, or 22 would lead an observer to assign the stimulus to P400.

Information carried by spike patterns

Having seen the mechanism through which a temporal sequence of spikes can improve texture discriminations, we now present the spike pattern information carried by the same ganglion and cortical neurons examined previously. We applied a 24 ms sliding window, subdivided into six bins of 4 ms, and the occurrence or absence of a spike in each bin was registered as 1 or 0 (see Materials and Methods). Figure 5A plots the time course of pattern information for the ganglion cell about the stimulus pair P1200–P400. At ∼95 ms, pattern information reached 1 bit (thus able to support perfect discriminability) and remained there. The whole-whisk spike count information about this stimulus pair is indicated by the arrow (Fig. 3D, circled value), and it is evident that the spike pattern yielded substantially more information than did the spike count alone.

Figure 5.

Spike pattern information. A, Time course of spike pattern information about stimulus pair P1200–P400 (left) and the total stimulus set (right) for the ganglion cell. Each point reports information in the 24 ms window (6 bins of 4 ms) preceding the point. The horizontal arrow indicates the whole-whisk spike count information. B, Time course of spike pattern information about the stimulus pair P1200–P400 (left) and the total stimulus set (right) for the cortical cell cluster. Conventions as in A. C, For each stimulus pair, peak spike pattern information is indicated for the ganglion cell (top left) and the cortical cluster (bottom right). Stimulus pair P1200–P400, illustrated in A and B, is indicated by the circles. The ganglion cell carried errorless information about this and all stimulus pairs. The cortical cluster carried ∼0.7 bits. D, The gain in information available from the spike pattern compared with the whole-whisk spike count, for the ganglion cell (top left) and the cortical cluster (bottom right). These values result from the subtraction of the values in Figure 3D from those in C.

The right panel in Figure 5A plots the information of ganglion cell about the total stimulus set. Peak spike pattern information reached the entropy of the stimulus set (2.58 bits). In contrast, the whole-whisk spike count information was ∼1.2 bits (arrow).

Figure 5B presents the same analysis for the simultaneously recorded cortical cell cluster. For the stimulus pair P1200–P400 (left panel), pattern information approached 0.7 bits during whisker protraction and ∼0.45 bits during whisker retraction. The two phases of the whisk cycle are now readily apparent as two discrete epochs of high information flow. These values can be contrasted with the absence of whole-whisk spike count information (see arrow near 0). For the total stimulus set, the pattern information of the cortical cluster reached a peak value of ∼0.75 bits during protraction and 1 bit during retraction (right panel). Whole-whisk spike count information was ∼0.4 bits (arrow). In summary, as was found for the ganglion cell, the ongoing spike pattern carried much more information than did the number of spikes across the entire stimulus.

To assess the heterogeneity across the whole-stimulus set, Figure 5C illustrates the peak spike pattern information about each stimulus pair. For the ganglion cell (top left), peak information values for all pairwise discriminations were 1 bit (errorless). For the cortical cluster (bottom right), peak pattern information values ranged from 0.4 to 1 bit, with the exception of CD–free whisk, which remained poorly discriminable (0.2 bits) even when patterns were considered. A direct comparison between pairwise pattern and count information can be made by computing the information gain I_gain supported by spike pattern: I_gain = I_pattern − I_count (Fig. 5D). For the ganglion cell, some stimulus pairs for which whole-whisk spike count information was near 0 became perfectly discriminable when patterns were considered (P400–P100 and P1200–P280). The stimulus pair P1200–P400 that was chosen for illustration in Figure 4 is another example of a pair whose discriminability was near 0 by spike count for both ganglion and cortex (Fig. 3D) yet became highly discriminable when spike patterns were considered. As a general rule, stimulus pairs that showed high discriminabilities by spike counts (e.g., free whisk or CD vs P100 or P280) show little additional gain by spike patterns. In contrast, stimulus pairs that showed low discriminabilities by spike counts gave high values of information gain (0.4–1 bit).

Dependence of spike pattern information on the internal clock and the external clock

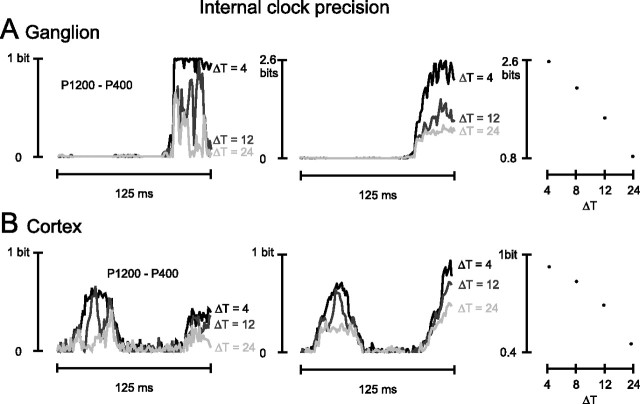
In the spike pattern analysis up to this point, the information carried by any observed pattern was computed according to the stimulus–response conditional probabilities within a single temporal window. This is illustrated concretely in Figure 4, in which the pattern detection window was set at 92–116 ms. Optimal pattern decoding thus assumes the observer’s capacity to maintain two clocks: (1) the internal clock would register the local temporal structure of the spike pattern (e.g., 0 1 0 1 0 1), and (2) the external clock would register the time of the sliding window along the stimulus course (e.g., 92–116 ms). The decoder would use both clocks to solve the following problem: what is the probability of each stimulus given that pattern (0 1 0 1 0 1) has occurred during the window 92–116 ms?

It is important to consider how well a spike pattern decoder could discriminate between stimuli if it could apply only suboptimal temporal precision. Suppose a target neuron could accurately register the position of the ongoing response window with respect to the whisking cycle, yet its long membrane time constants for integrating inputs (or some other physiological property) would not permit it to distinguish incoming temporal patterns; this would correspond to a precise external clock coupled with an imprecise internal clock (Victor and Purpura, 1996; Strong et al., 1998; Panzeri et al., 2001). To mimic this situation, we measured information when the external clock was left intact but the precision of the spike times within the ongoing window was made progressively coarser. Precision of spike times is determined by bin size, referred to as ΔT_internal. To widen ΔT_internal from 4 ms (the most precise internal clock evaluated) to 8 ms, we randomly shuffled spike occurrences between adjoining pairs of 4 ms time bins. In practice, this created a 24 ms window comprising three 8 ms bins, each time bin containing the same number of spikes as previously. To further widen ΔT_internal from 8 to 12 ms, we randomly shuffled spike occurrences between adjoining triplets of 4 ms time bins; this created a 24 ms window with the same number of spikes but with their timing registered with 12 ms precision. Finally, we widened ΔT_internal to 24 ms. In this condition, all information in spike timing within the sliding window was lost, whereas spike count information was unchanged.

Results are given for the ganglion cell and the cortical cell cluster in Figure 6, A and B, respectively. The information about stimulus pair P1200–P400 is shown in the left panels and for the total stimulus set in the middle panel. For clarity, the plots for ΔT_internal = 8 ms are not illustrated. The degree of dependence of information on internal clock precision was not dramatically different for ganglion and cortex, as summarized in the right panels of Figure 6, A and B. Refining ΔT_internal from 8 to 4 ms caused a 23 and 11% increase in information for ganglion and cortex, respectively. This suggests that cortical spike trains conserved the spiking sequence as relayed to them by subcortical inputs at least up to the 4 ms resolution tested here and that the precise temporal structure of spikes carried stimulus information.

Figure 6.

Effect of internal clock precision on available information. A, Time course of the ganglion cell pattern information about stimulus pair P1200–P400 (left) and the total stimulus set (middle). Each plot refers to a different degree of internal clock precision; ΔT_internal is indicated simply as ΔT. Right, Peak spike pattern information about the total stimulus set as a function of internal clock precision (ΔT). B, Time course of the cortical cell cluster pattern information about the stimulus pair P1200–P400 (left) and the total stimulus set (middle). Conventions are the same as in A. Right, Peak spike pattern information about the total stimulus set as a function of internal clock precision (ΔT).

Suppose an observer receiving the spike trains had imperfect signals regarding the time course of the whisking cycle (the so-called “reference signal”) (Fee et al., 1997). We refer to the whisking signal by a general term, the external clock. In this case, the observer must decode the stimulus by registering the internal temporal structure of the spike pattern, while assigning the time label to the current position of the sliding window with some uncertainty. The problem to be solved is as follows (again referring to the example in Fig. 4): what is the probability of each stimulus given that a pattern (e.g., 0 1 0 1 0 1) has occurred at some poorly defined temporal position within the stimulus cycle?

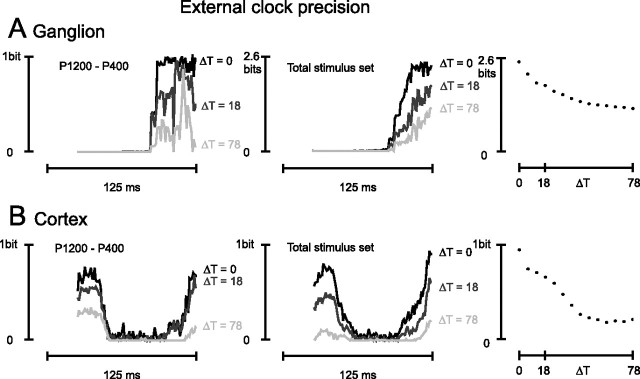
To see the effect of external clock imprecision, we measured information (I_external in Materials and Methods; Eq. 4) when the internal temporal structure of the spike pattern was left intact but the time label assigned to the current position of the sliding window was made uncertain. In practice, this is equivalent to measuring the stimulus specificity of a given pattern after the pattern probability distributions have been pooled across a window position widened by the amount ΔT_external, referred to as the external clock uncertainty (see Materials and Methods). The expanded time window spanned both sides of the ongoing sliding window, with ΔT_external/2 on each side. In Figure 7A, left panel, the ganglion cell responses are examined for the stimulus pair P1200–P400. The black line gives the ongoing spike pattern information when the external clock was errorless (ΔT_external = 0 ms). The dark gray and light gray lines give the ongoing spike pattern Information when ΔT_external = 18 and 78 ms, respectively. Information diminished as external clock uncertainty increased. A similar result holds for the information about the total stimulus set (Fig. 7A, middle). Still, it is important to note that peak ongoing spike pattern information was >1 bit, even for ΔT_external = 78. The right panel of Figure 7A reports this peak information value for each value of external clock precision, revealing a gradual decrease as ΔT_external increased. This signifies that spike patterns could be decoded, although not optimally, even without the presence of an external clock.

Figure 7.

Effect of external clock precision on available information. A, Time course of the ganglion cell pattern information about stimulus pair P1200–P400 (left) and the total stimulus set (middle). Each plot refers to a different degree of external clock precision; ΔT_external is indicated simply as ΔT. Right, Peak spike pattern information about the total stimulus set as a function of external clock precision (ΔT). B, Time course of the cortical cell cluster pattern information about stimulus pair P1200–P400 (left) and the total stimulus set (middle). Conventions are the same as in A. Right, Peak spike pattern information about the total stimulus set as a function of external clock precision (ΔT). To prevent the expanded time window (widened by the amount ΔT_external) from including spike patterns corresponding to the preceding stimulus, the analysis of the external clock precision was performed on the second whisk responses (see Materials and Methods). Information values corresponding to the first 24 ms of the whisk cycle are also excluded because they partially correspond to the late retraction phase of the preceding whisk cycle and are not specific to the second whisk. Slight differences with Figure 5, A and B, and the black traces of Figure 6 result from the fact that different whisks are analyzed.

Figure 7B illustrates the effects of external clock uncertainty on the cortical cell cluster for the stimulus pair P1200–P400 (left panel) and for the total stimulus set (middle panel). A striking difference from the ganglion cell is that the capacity to extract information from the cortical spike patterns became negligible when ΔT_external increased beyond ∼40 ms. The plot in the right panel indicates a steep decline in information even for small values of ΔT_external. This could occur if, for example, a given spike pattern were characteristic of one texture if it occurred in a certain time window, but were characteristic of another texture if it occurred in a different time window.

Generalization of the principal results to the entire neuronal population

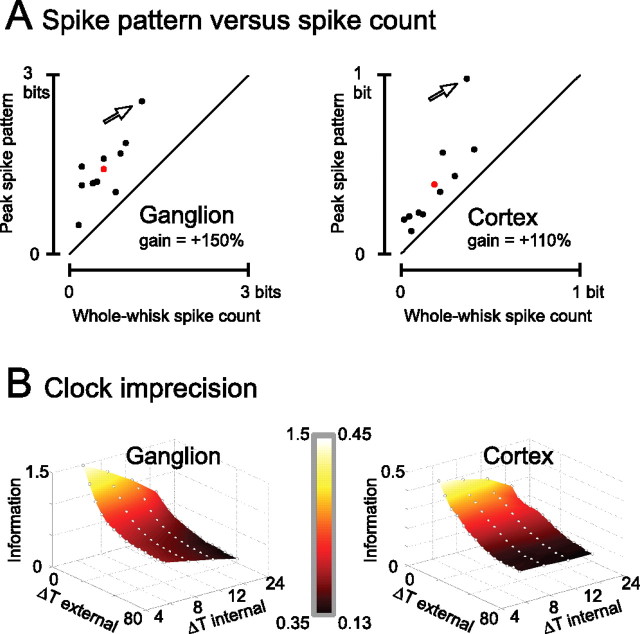
To extend the main findings from the simultaneously recorded ganglion cell and cortical cluster described previously, we now consider the full set of recorded neurons. Two issues are of interest: how much information could be extracted from spike counts, and how much additional information could be extracted from spike patterns compared with spike count? To what degree does spike pattern information depend on the precision of the observer’s internal and external clocks? For the total stimulus set, the peak information carried by the ongoing spike pattern versus that carried by the whole-whisk spike count is given in Figure 8A for the 10 ganglion cells (left panel) and 10 cortical clusters (right panel). Mean values for the scatter plots are given by the red points; on average, the spike pattern gain was 150% for the ganglion and 110% for the cortex. At both stages of the pathway, every recording showed some information gain when decoded by pattern. For the ganglion cell examined in the preceding sections, pattern information reached the entropy of the stimulus set such that the spike train of this cell alone could supply the decoder with perfect knowledge concerning which of six possible stimuli was presented on a single trial (arrow).

Figure 8.

Count and pattern information for the full set of recorded neurons. A, Scatter plot of the whole-whisk spike count information versus peak spike pattern information about the full stimulus set for 10 ganglion single units (left) and 10 cortical clusters (right). The neurons analyzed in the preceding sections are indicated by arrows. Although they carried more information than average (red points), their ratio of pattern to count information was comparable with the rest of the dataset. B, Effect of both external clock precision (ΔT_external) and internal clock precision (ΔT_internal) on spike pattern information, averaged for the full set of ganglion (left) and cortical (right) neurons. From the surface plots, the interaction between the two clocks can be discerned.

With what temporal precision must a target population read off the spike train to obtain all of the available information in the patterns? Figure 8B illustrates the available texture information as a function of the clock precision with which the observer decodes the spikes within the sliding 24 ms window. The surfaces represent values averaged across the full dataset, the same neurons as A. The points corresponding to maximum internal and external clock precision (ΔT_external = 0 ms and ΔT_internal = 4 ms) are equivalent to the average peak pattern information values (red points in A).

For both ganglion and cortical neurons, the precise sequence of spikes within the window carried supplementary information provided that the time of occurrence within the whisk cycle was known. This is given by the strong dependence of information on ΔT_internal when ΔT_external = 0 ms. In particular, when ΔT_internal = 4 ms, the ganglion and cortical population carried on average 1.5 and 0.45 bits of information, respectively. Increasing ΔT_internal to 24 ms (i.e., considering only spike counts within the sliding window) caused a drop in information to 0.8 and 0.28 bits for ganglion and cortex, respectively. In general, then, spike counts carried much less information than did patterns, whether the count was made over a 24 ms sliding window or over the full whisking cycle, as reported previously.

We consider next the dependence of information on the external clock imprecision. For the ganglion cells, the structure of spike patterns carried information even if the observer had poor knowledge of the time of pattern occurrence within the whisk cycle. For ΔT_external = 78 ms, such that the time of occurrence of the spike pattern would not even be specified as whisker protraction or retraction, the decoder could still obtain more information than it could from spike count. In contrast, for cortex, there was little dependence of information on internal clock precision when external clock uncertainty was greater than ∼18 ms: lack of dependence on ΔT_internal implies that pure spike count in the ongoing window (ΔT_internal = 24 ms) was equally informative as spike pattern (ΔT_internal = 4 ms). In other words, the spike patterns of cortical neurons carried significant amounts of additional Information only when the observer had access to a precise external clock.

In conclusion, substantially different signals about texture can be extracted from spike trains of ganglion and cortical depending on the temporal precision available to the decoder. Information increased as responses were considered as spike patterns with progressively finer temporal precision. Moreover, the neurons receiving input from the ganglion cells and the cortical cell clusters could decode the patterns optimally if there were an independent signal reporting when, in the course of the whisk cycle, the spike patterns occurred; dependence on external clock was particularly strong for cortical spike trains. In Discussion, we will argue that such pattern information could indeed be read off because independent signals about whisking cycle are present in barrel cortex.

Discussion

How much information is carried by spike count, and what is its temporal profile?

Each trial [a 125 ms forward–backward movement of the whisker (a whisk)] consisted of a texture-specific vibration (Hipp et al., 2006). Response magnitudes in both ganglion and cortex are correlated with the integral of the velocity spectrogram across the whisk [a quantity known as “equivalent noise level” (ENL) (Arabzadeh et al., 2005)]. Thus, some pairs of texture vibrations with widely separated ENL values evoked significantly different numbers of spikes. For the most discriminable pairs of stimuli, cumulative spike counts over the whole whisk carried up to 1 bit of information for the selected ganglion cell and 0.5 bits for the cortical cluster (Fig. 3D).

What would be the optimal spike count decoding mechanism? A common simplifying assumption is that sensory information is conveyed by the number of spikes fired across the whole response period (Britten et al., 1992; Gold and Shadlen, 2001), a quantity captured by our whole-whisk spike count. However, recent studies suggest that cortical cell spike counts during the initial response period better covary with the animal’s judgment of the stimulus (Luna et al., 2005). Consistent with this idea, the cortical spike trains illustrated here could support stimulus discrimination as well by the spike count from 0–30 ms (Fig. 3A) as they could by the whole-stimulus spike count. This rapid time course is consistent with the buildup of spike count information in rat somatosensory cortex during simpler decoding problems, such as the location of a stimulus site on the whisker pad (Petersen and Diamond, 2000; Panzeri et al., 2001; Petersen et al., 2001, 2002) and the forepaw (Foffani et al., 2004), or the velocity of a sinusoidal vibration (Arabzadeh et al., 2003, 2004); it also agrees with investigations in other sensory modalities in which the earliest cortical responses carry large quantities of stimulus information (Tovee et al., 1993; Buracas et al., 1998; Rolls et al., 1999; Furukawa and Middlebrooks, 2002).

How much additional information is conveyed by the temporal pattern of spikes?

Spike timing codes were first conjectured on the basis that they could constitute an additional information channel beyond that available in the spike count, thus increasing the channel capacity of the nervous system (MacKay and McCulloch, 1952). Solid evidence for spike pattern information in mammalian cortex has been difficult to obtain, and it was thus suggested that the precise pattern of spikes across the stimulus presentation reflects random processes, unrelated to the stimuli (Shadlen and Newsome, 1994). Subsequently, experiments using simplified, stereotyped stimuli were able to reveal the presence of spike timing information in mammalian cortex in limited quantities [i.e., <50% above that in spike count alone (Victor and Purpura, 1996; Panzeri et al., 2001, Foffani et al., 2004)]. In our dataset, the motivation to test the potential information in spike patterns was particularly compelling given that an observer using only spike counts would completely fail in some texture judgments (Fig. 3D). The result was that spike patterns could allow some stimulus discriminations to be performed reliably, even when those discriminations were “noisy” by spike count alone.

In the present study, spike patterns conveyed much more extra information (beyond counts) than was found using simplified, stereotyped stimuli; it is tempting to conjecture that, as stimulus complexity increases, the nervous system resorts increasingly to the extra timing channel to increase its information capacity.

Although the spike times carried informative signals about the texture, it should be noted that the spike timing patterns were not generated ex novo in the brain but rather emerged in the stimulus itself. Rather than converting a spatial stimulus into a temporal code (Panzeri et al., 2001; Petersen et al., 2001; Foffani et al., 2004; Johansson and Birznieks, 2004), the whisker system conserves the velocity profile of the vibration itself (Arabzadeh et al., 2005; Hipp et al., 2006) in the temporal pattern of spikes.

What is the dependence of spike pattern information on clock precision?

Studies of information transmission normally consider “ideal observers” that are able to extract all available signals in the spike train. Following this convention, we first evaluated spike pattern information by considering an observer with maximal internal clock and external clock precision; in other words, the observer could register spike times with precision corresponding to six time bins of 4 ms each and also had knowledge of when the spike pattern occurred within the course of a single trial (Fig. 5). Spike pattern information was >100% greater than spike count information. Still, it is notable that cortical information was less sensitive to errors in internal timing than was that of the trigeminal ganglion (Fig. 8). Although the functional significance is a matter of speculation, one possibility is suggested by the fact that, when a whisker contacts a textured surface multiple times under controlled artificial whisking (Arabzadeh et al., 2005) and presumably under natural behavioral conditions, there are minute differences in the precise vibration profile on each contact. Cortical neurons, by their reduced sensitivity to such minute differences, might carry a message that is more informative about stimulus identity (stable temporal features common to the multiple trials) while avoiding information loss attributable to trial-to-trial temporal variation.

We then evaluated the information that would be available to an observer with nonmaximal internal clock precision. Internal clock degradation, generated by increasing ΔT_internal from 4 to 8, 12, and 24 ms, caused a reduction in information content. This means that a decoder could gain full pattern information only if it could register a sequence of incoming spikes with at least 4 ms precision. The fact that there were still significant information gains for both ganglion and cortex when ΔT_internal was reduced from 8 to 4 ms (Fig. 6, right column) suggests that the true precision of the spike train may exceed 4 ms.

We then evaluated the information that would be available to an observer with nonmaximal external clock precision: the observer might register the local structure of the spike pattern but not the time of the pattern within the whisk cycle. External clock degradation, generated by adding ΔT_external to the time window across which the spike pattern probability distribution was compiled, caused a reduction in information content. Given its dependence on the external clock, could spike pattern information be fully exploited? Recently, evidence has been accumulating for a “whisking signal” in barrel cortex with good temporal precision (Fee et al., 1997; O’Connor et al., 2002; Ganguly and Kleinfeld, 2004). The external clock signal appears to arise by both motor copy (Ahrens and Kleinfeld, 2004) and sensory signals from the whisker follicle (Szwed et al., 2003). Full spike pattern information could be recovered by integration of the whisking signal together with the spike pattern. Targets of barrel cortex include motor cortex, basal ganglia, pons, and cerebellum. Only those populations possessing knowledge of the external clock would be able to optimally extract texture information from spike patterns.

Connection to behavior

The current experiments were run under conditions in which the sensory input was precisely controlled and yet resembled as closely as possible what occurs during natural tactile behavior. It is difficult at this point to relate the information available in spike trains to the rats’ tactile capacities. For our stimuli, the mean size of the sandpaper grains was 15, 35, 52, or 162 μm. Rats can discriminate between sandpapers with grain sizes of 400 and 2000 μm with over 85% performance (Guic-Robles et al., 1989); mice can reliably discriminate between sandpapers with grain sizes 50 and 190 μm (Cybulska-Klosowicz and Kossut, 2001). However, the selected stimulus pairs were presented to the animals at the outset of training, and the experimental design did not include a ladder protocol for estimating threshold. It is safe to assume that rats could learn to make much finer discriminations than those cited above and could likely be trained to discriminate between most stimulus pairs in the present work.

Likewise, it is not possible to state how many whisking cycles, and what kinetics, rats would use to perform such discriminations during behavioral testing. There is evidence for changes in whisking motor strategy according to the discrimination task. In general, rats whisk a greater number of times, and with higher speed, when the task is difficult (Carvell and Simons, 1995). In our experience, rats perform an easy texture discrimination task by directing approximately two to four whisks along the surface of interest (M. von Heimendahl, unpublished observations). We believe, therefore, that the number of whisk cycles examined in the present analysis approximates the behaviorally relevant quantity.

Still, the ultimate measure of sensory coding mechanisms requires investigations of behaving animals. In particular, one must look for the connection between neuronal spike trains and sensory discriminations. If, for example, a rat could be trained to discriminate between two textures that evoke equivalent firing rates but distinctive firing patterns and the spike pattern present in single trials could predict behavior, this would constitute strong evidence that spike patterns encode texture.