Ambiguous Encoding of Stimuli by Primary Sensory Afferents Causes a Lack of Independence in the Perception of Multiple Stimulus Attributes

Abstract

Accurate sensory perception often depends on the independent encoding and subsequent integration of multiple stimulus attributes. In the weakly electric fish Eigenmannia, P- and T-type primary afferent fibers are specialized for encoding the amplitude and phase, respectively, of electrosensory stimuli. We used a stimulus estimation technique to quantify the ability of P- and T-units to encode random modulations in amplitude and phase. As expected, P-units exhibited a clear preference for encoding amplitude modulations, whereas T-units exhibited a clear preference for encoding phase modulations. Surprisingly, both types of afferents also encoded their nonpreferred stimulus attribute when it was presented in isolation or when the preferred stimulus attribute was sufficiently weak. Because afferent activity can be affected by modulations in either amplitude or phase, it is not possible to unambiguously distinguish between these two stimulus attributes by observing the activity of a single afferent fiber. Simple model neurons with a preference for encoding either amplitude or phase also encoded their nonpreferred stimulus attribute when it was presented in isolation, suggesting that such ambiguity is unavoidable. Using the well known jamming avoidance response as a probe of electrosensory perception, we show that the ambiguity at the single-neuron level gives rise to a systematic misrepresentation of stimuli at the population level and a resulting misperception of the amplitude and phase of electrosensory stimuli.

Introduction

The electric fish Eigenmannia generates a quasi-sinusoidal electric organ discharge (EOD) at frequencies ranging from 200 to 600 Hz. Nearby objects subject the EOD feedback signal to amplitude modulation (AM) and phase modulation (PM), providing information that the fish use to actively sense their environment through active electrolocation (von der Emde, 1999). The independent processing of AM and PM is important in distinguishing the resistive and capacitive components of complex impedances, which allows them to discriminate living from nonliving objects (von der Emde, 1998). The EOD is also subjected to AM and PM because of interference from conspecific EODs, which plays an important role in electric communication (Carlson, 2006) and in executing the jamming avoidance response (JAR), in which two fish with similar EOD frequencies shift their frequencies away from each other to avoid interference (Heiligenberg, 1991).

There are two distinct types of primary afferents devoted to encoding AM and PM, referred to as P- and T-units, respectively (Scheich et al., 1973; Zakon, 1986). T-units are tightly phase locked to the EOD and fire one spike per EOD cycle, providing a precise marker of the timing of positive transitions in the EOD (Zakon, 1986). Information about PM is ultimately extracted by midbrain neurons that compare the precise spike times of different T-units (Heiligenberg and Rose, 1985; Carr et al., 1986a,b). Although P-units loosely phase lock to the EOD, they do not fire a spike during each cycle; instead, their probability of firing is proportional to EOD amplitude (Scheich et al., 1973; Zakon, 1986). Hindbrain neurons that receive afferent input from P-units detect upstrokes and downstrokes in EOD amplitude through increases and decreases in the firing rates of P-units (Gabbiani et al., 1996; Metzner et al., 1998).

Several recent studies have applied information-theoretic techniques to quantify the encoding of amplitude modulations by P-units and their postsynaptic targets in Eigenmannia and related species (Gabbiani et al., 1996; Wessel et al., 1996; Metzner et al., 1998; Kreiman et al., 2000; Bastian et al., 2002; Krahe et al., 2002; Oswald et al., 2004; Chacron et al., 2005). Despite the importance of differential phase information for electrosensory processing, no study has applied similar methods to quantify the encoding of phase modulations by the T-unit pathway or the degree to which information about amplitude and phase is independently encoded by the two separate pathways. We used a stimulus estimation technique to quantify the ability of P- and T-units to encode random modulations in amplitude and phase. Although P-units showed a clear preference for AM and T-units for PM, both types of units were also able to encode their nonpreferred stimulus feature, revealing that individual primary afferents provide an ambiguous representation of these two stimulus attributes. We also found that model neurons with a preference for encoding either AM or PM exhibited similar ambiguities. Using the JAR as a probe of electrosensory perception, we show that this ambiguity gives rise to a systematic misperception of the amplitude and phase of electrosensory stimuli.

Materials and Methods

Animals.

We used a total of 30 adult Eigenmannia (12–17 cm in total length) obtained from tropical fish dealers under the commercial name “glass knife fish.” Environmental conditions in the holding tanks were identical to those described previously (Kawasaki, 1994). Fish were immobilized, and their EODs were silenced by intramuscular injection of Flaxedil (gallamine triethiodide, 3–5 μl of a 3.0 mg/ml solution; Sigma, St. Louis, MO). Ventilation was provided by a stream of aerated water fed into the fish’s mouth. All procedures were in accordance with guidelines established by the National Institutes of Health and were approved by the University of Virginia Institutional Animal Care and Use Committee.

Electrophysiology.

Fish were placed in a sponge-lined clamp that gently held them on their side such that their ventral edge was angled slightly downward. We exposed the posterior branch of the anterior lateral line nerve, which is located just beneath the skin surface and just rostral to the operculum. We made intracellular recordings from individual primary afferent fibers using 3 m KCl-filled glass microelectrodes that were pulled using a Flaming/Brown micropipette puller (model P-97; Sutter Instruments, Novato, CA) to yield resistances of 30–50 MΩ. Activity was amplified 10× on an AxoClamp 2B amplifier (Molecular Devices, Palo Alto, CA) with an indifferent chlorided silver electrode placed next to the recording electrode. The resulting signal was sent to an analog-to-digital converter with a sampling rate of 20 kHz (model AD1; Tucker-Davis Technologies, Gainesville, FL). Electric stimuli were digital-to-analog converted at a sampling rate of 20 kHz (model DA3-4; Tucker-Davis Technologies), attenuated to the desired carrier amplitude using a programmable attenuator (model PA4; Tucker-Davis Technologies), and delivered to the fish through an anodal electrode placed in the mouth and a pair of cathodal electrodes placed on either side of the fish using homemade isolators with field effect transistors. Stimulus modulation waveforms and intracellular potentials were saved using custom-made software for Matlab 7.0.1 (MathWorks, Natick, MA).

Stimulus generation.

Stimuli were numerically generated using custom-made software for Matlab 7.0.1, according to the following equation:

where V(t) is the stimulus voltage at time t, A_c is the carrier amplitude, f_c is the carrier frequency, and s_AM(t) and s_PM(t) are time-varying modulations in amplitude and phase, respectively. The carrier frequency (f_c) was set to within 5 Hz of the fish’s EOD frequency as measured before the experiment. The carrier amplitude (A_c) was adjusted to 1–3 mV/cm near the gill cover. The AM [s_AM(t)] and PM [s_PM(t)] waveforms were generated independently and could therefore be presented completely in isolation [i.e., stimuli with only AM, for which s_PM(t) = 0 for all values of t, or stimuli with only PM, for which s_AM(t) = 0 for all values of t], or both amplitude and phase could be modulated simultaneously with independent variation in s_AM(t) and s_PM(t).

Three types of random stimulus modulations were used, including simultaneous random AM and random PM [s_AM(t) and s_PM(t) were both randomly modulated independently], separate random AM [s_AM(t) was randomly modulated, whereas s_PM(t) = 0 for all values of t], and separate random PM [s_PM(t) was randomly modulated, whereas s_AM(t) = 0]. Each random modulation waveform consisted of low-pass-filtered (cutoff frequency, 20 Hz) Gaussian distributions with specified SDs (σ_AM and σ_PM, which represent the average depth of the random modulations). For most experiments, σ_AM varied from 10 to 25% of the carrier amplitude and σ_PM varied from 10 to 30° of the carrier phase, although smaller values were used in some experiments. We choose a cutoff frequency of 20 Hz because preliminary results using higher cutoff frequencies revealed maximal information rates at frequencies below 10–20 Hz. Other cutoff frequencies yielded qualitatively similar results, although the coding fractions for all stimuli decreased as the cutoff frequency increased (Wessel et al., 1996). Four types of sinusoidal stimulus modulations were used, including AM presented alone [s_AM(t) was sinusoidally modulated, whereas s_PM(t) = 0 for all values of t], PM presented alone [s_PM(t) was sinusoidally modulated, whereas s_AM(t) = 0 for all values of t], and two stimuli that simulated the modulations caused by combining the fish’s own EOD (frequency = f₁) with a neighbor’s EOD (frequency = f₂), where the difference in frequency (Df = f₂ − f₁) was either positive [Df > 0, for which both s_AM(t) and s_PM(t) were sinusoidally modulated and the PM start angle was advanced by 90° relative to AM] or negative [Df < 0, for which both s_AM(t) and s_PM(t) were sinusoidally modulated and the PM start angle was delayed by 90° relative to AM]. For all four stimuli, the modulation rate was set at 2 Hz, AM depths were equal to 25%, and PM depths were equal to 15°.

Stimulus estimation.

Spike trains from primary sensory afferents and model neurons were represented as follows:

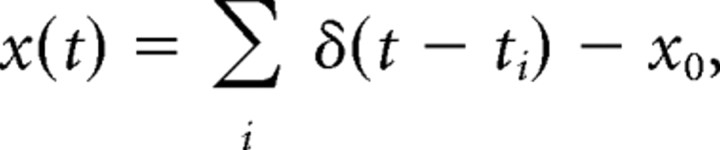where t_i are the spike occurrence times, and x₀ is the mean spike rate. Linear estimates of random modulation waveforms were generated by convolving spike trains with a filter, h(t), as follows:

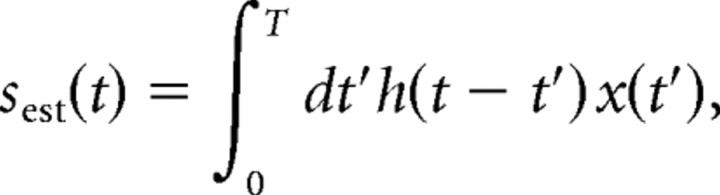chosen so as to minimize the mean square error between the stimulus and the estimate (Wessel et al., 1996; Gabbiani and Koch, 1998; Gabbiani and Metzner, 1999). We quantified the ability of spike trains to encode information about random AM and random PM using the coding fraction (γ_AM and γ_PM), which ranges from 0 when estimation is at chance level to 1 when the stimulus is perfectly estimated, or 0–100% when expressed as a percentage of the stimulus encoded (Gabbiani and Koch, 1998; Gabbiani and Metzner, 1999). Because phase is encoded in an absolute sense in the periphery, we converted random PM waveforms to frequency (derivative of phase) before stimulus estimation. After stimulus estimation, we converted the actual and estimated stimuli and optimal filters back to phase (integral of frequency) for clarity of presentation.

Spike train analysis.

Both P- and T-units phase lock to the carrier signal, but T-units fire during each cycle whereas P-units repeatedly skip cycles (Scheich et al., 1973; Zakon, 1986). We therefore designated each primary afferent as a T-unit if it fired during each cycle of the carrier signal and a P-unit if it did not. It is possible to induce P-units to fire during each carrier cycle and to induce T-units to skip cycles, but this requires unnaturally intense and weak carrier amplitudes, respectively, well outside the range of natural EOD intensities (Scheich et al., 1973; Feng and Bullock, 1977). In addition, P-units rapidly adapt to changes in stimulus intensity, whereas T-units do not (Scheich et al., 1973). Based on these characteristics, we further verified the distinction between P- and T-units by manipulating the carrier amplitude: P-units could be induced to fire during each cycle by increasing the carrier amplitude to values >3 mV/cm, but because of adaptation, this effect was always transient and P-units began skipping cycles a few seconds after increasing the intensity; T-units could be induced to skip cycles but only at very low stimulus intensities (<0.5 mV/cm).

We estimated the spike rates of P-units using a low-pass filter with a cutoff frequency equal to 2.5 times the cutoff frequency for random modulations or 2.5 times the modulation rate for sinusoidal modulations. Spike rates were then expressed as a percentage of the mean value. To analyze changes in the spike times of T-units, we computed spike times relative to an arbitrary, constant phase of the unmodulated stimulus carrier cycle (Heiligenberg and Partridge, 1981). To examine the neural representations of sinusoidal stimulus modulations in two dimensions (AM vs PM), we plotted the mean relative spike rate of P-units against the mean relative spike time of T-units (Heiligenberg and Partridge, 1981). Because the sampling rate of T-unit spike times was dependent on the stimulus carrier frequency, which varied from fish to fish and differed from the sampling rate of P-unit spike rates (20 kHz), the spike time values were low-pass filtered to yield a universal sampling rate of 20 kHz. This allowed us to plot P-unit relative spike rate against T-unit relative spike time.

Modeling.

We generated leaky integrate-and-fire model neurons (Gabbiani and Koch, 1998) as follows:

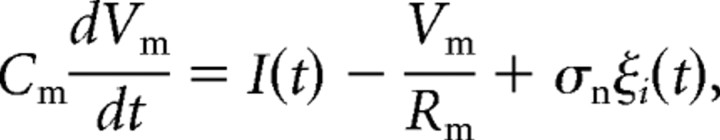where V_m is the membrane potential, I is the input current, C_m is the membrane capacitance (0.1 nF), R_m is the membrane resistance (10 MΩ), and σ_nξ_i represents a noise term drawn from a normal distribution (ξ_i) with mean 0 and SD σ_n. Whenever V_m reached threshold (V_th), a spike was generated, and V_m was reset to 0 for a refractory period of 1 ms. All parameters except σ_n and V_th were held constant. The stimulus current (I) was a sine wave with a carrier frequency of 400 Hz and a peak-to-peak amplitude of 1.0 nA that was subjected to random AM and random PM, presented both separately and simultaneously (cutoff frequency, 20 Hz; σ_AM = 20%; σ_PM = 15°).

We generated separate populations of model amplitude and time coders based on the AM and PM coding fractions, respectively, observed during simultaneous presentation of random AM and random PM. We set a threshold equal to 25% of the maximum AM or PM coding fraction and then randomly drew from the distribution above this threshold by making the probability of drawing a particular combination of σ_n and V_th proportional to the mean coding fraction obtained for that combination.

Behavior.

Although phase information is represented in an absolute sense in the periphery, information about PM is extracted centrally by comparing differential phase between different portions of the body surface (Heiligenberg et al., 1978; Heiligenberg and Rose, 1985; Carr et al., 1986a,b; Heiligenberg, 1991). Analyzing the effects of ambiguities on central physiology and behavior therefore requires the use of a phase chamber, which divides the fish into electrically isolated head and trunk compartments, allowing one to independently modulate amplitude and differential phase (Heiligenberg and Bastian, 1980; Rose and Heiligenberg, 1985; Takizawa et al., 1999; Carlson and Kawasaki, 2004). Sinusoidal electric stimuli were delivered to the head through an anodal electrode placed in the mouth and cathodal electrodes placed on either side of the head, whereas stimuli were delivered to the trunk through an anodal pin electrode placed in the dorsal musculature and cathodal electrodes placed on either side of the body. The carrier frequency was set to within 5 Hz of the fish’s EOD frequency as measured before the experiment. The amplitude was adjusted to 1–3 mV/cm near the skin surface. In each case, the trunk compartment was presented with an unmodulated signal, whereas the head compartment was presented with a sinusoidally modulated stimulus (AM, PM, Df > 0, or Df < 0) with a modulation rate of 2 Hz, AM depths of 25%, and PM depths of 15°. Although the fish’s electric organ is silenced by Flaxedil, the EOD command signal can still be recorded through a tail electrode that picks up the activity of the electromotor neurons that normally drive the electric organ. We thereby recorded the fish’s EOD frequency shifts in response to sinusoidal modulations presented three times for 30 s, each from a baseline of no modulation (Takizawa et al., 1999). Responses were expressed as the mean frequency shift per unit time (hertz per minute).

Data analysis.

Stimulus estimation, modeling, spike train analysis, and behavioral response analysis were done using custom-made software for Matlab 7.0.1. All statistical analyses were done using Statistica 6.1 (StatSoft, Tulsa, OK) with a two-tailed α = 0.05. Unless otherwise noted, all reported values are the mean ± SEM.

Results

Individual primary afferents preferentially encode either AM or PM but also encode their nonpreferred stimulus attribute

We recorded responses to random AM and random PM, presented both separately and simultaneously, from a total of 21 T-units and 45 P-units. If AM and PM are encoded independently by two distinct populations of primary afferent fibers, then P-units should primarily encode AM whereas T-units should primarily encode PM. This was indeed the case when random AM and random PM were presented simultaneously. When they were presented separately, however, P- and T-units each encoded both stimulus waveforms. For example, the P-unit shown in Figure 1A encoded 71.82% of the random AM stimulus waveform (σ_AM = 25%) but only 4.809% of the random PM stimulus waveform (σ_PM = 15°) when they were presented together (Fig. 1A1). When random AM and random PM were presented separately (Fig. 1A2), the encoding of random AM did not change appreciably (70.64%), but the encoding of random PM increased dramatically (48.90%). Similarly, the T-unit shown in Figure 1B encoded 75.89% of the random PM stimulus waveform (σ_PM = 15°) but only 2.657% of the random AM stimulus waveform (σ_AM = 25%) when they were presented together (Fig. 1B1). When presented separately (Fig. 1B2), the encoding of random PM did not change appreciably (78.55%), but the encoding of random AM increased to 32.80%.

Figure 1.

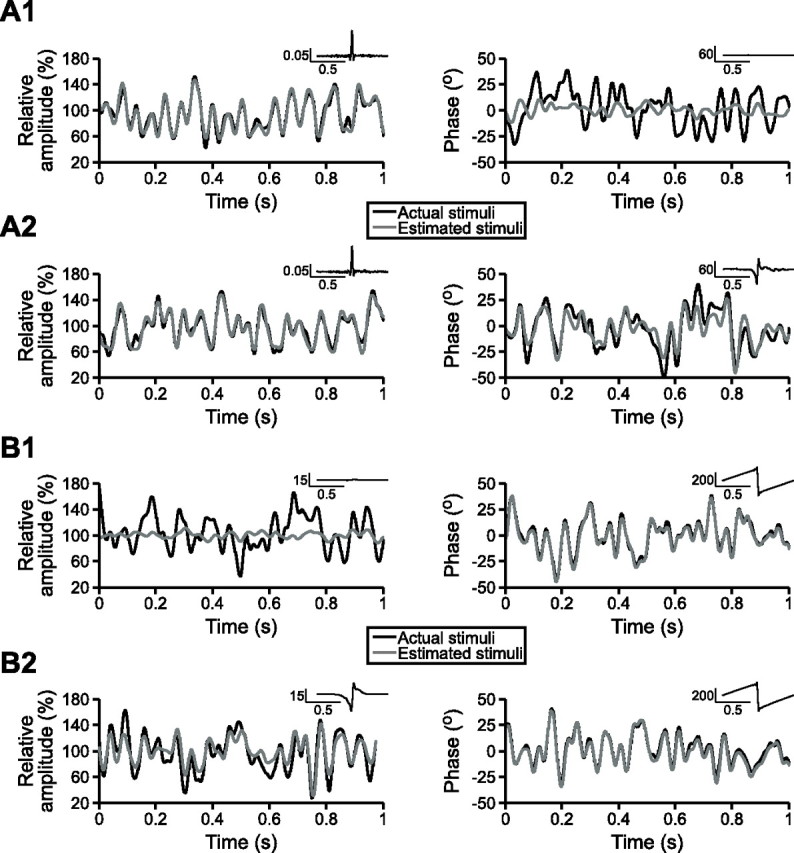
Primary afferents encode random modulations of their preferred and nonpreferred stimulus attributes. One-second segments of actual and estimated random AM (left column) and random PM (right column). In each case, σ_AM is equal to 25% and σ_PM is equal to 15°. Insets in the top right corner show the optimal filters used to generate the estimated stimuli. A, Stimulus estimation results from a single P-unit when random AM and random PM were presented simultaneously (A1) and separately (A2). B, Stimulus estimation results from a single T-unit when random AM and random PM were presented simultaneously (B1) and separately (B2).

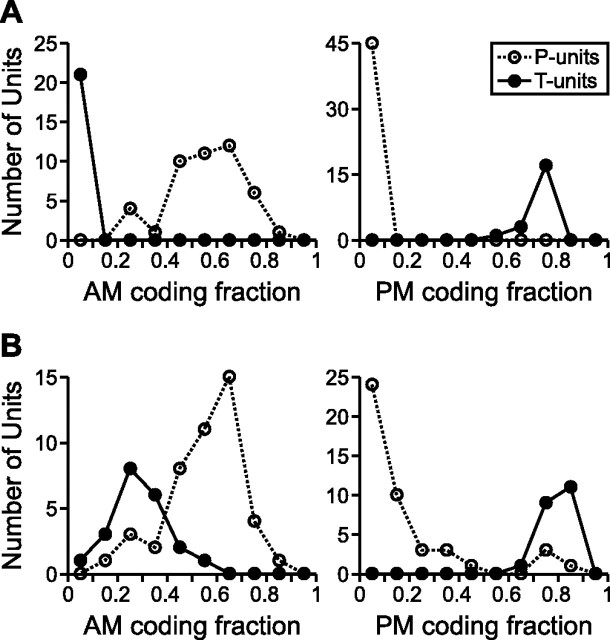
Across the population of primary afferents, with σ_AM varying from 10 to 25% and σ_PM varying from 10 to 30°, the mean coding fractions for each unit resulting from the simultaneous presentation of random AM and random PM revealed two distinct, non-overlapping populations that agreed with our a priori classification, with P-units exhibiting a preference for AM and T-units exhibiting a preference for PM (Fig. 2A). Therefore, during simultaneous presentation of random AM and random PM, the AM coding fraction of P-units was significantly greater than that of T-units (0.5560 ± 0.0214 vs 0.0249 ± 0.0018, respectively; t₍₆₄₎ = 16.88; p < 0.000001), whereas the PM coding fraction of T-units was significantly greater than that of P-units (0.7379 ± 0.0140 vs 0.0583 ± 0.0014, respectively; t₍₆₄₎ = 70.21; p < 0.000001). When random AM and random PM were presented separately, there was still a significant difference between both the AM coding fractions of P- and T-units (0.5556 ± 0.0220 vs 0.2928 ± 0.0255, respectively; t₍₆₄₎ = 7.172; p < 0.000001) and the PM coding fractions of P- and T-units (0.1780 ± 0.0312 vs 0.7967 ± 0.0104, respectively; t₍₆₄₎ = 13.35; p < 0.000001), but, in both cases, the distributions of the two types of units showed extensive overlap (Fig. 2B), unlike the complete separation of distributions that resulted from simultaneous random AM and random PM (Fig. 2A). The AM coding fractions of T-units were significantly smaller during simultaneous random AM and random PM than during separate random AM (t₍₂₀₎ = 11.14; p < 0.000001). Similarly, the PM coding fractions of P-units were significantly smaller during simultaneous random AM and random PM than during separate random PM (t₍₄₄₎ = 3.860; p < 0.001). Thus, the encoding of the nonpreferred stimulus attribute varied depending on the presence or absence of the preferred stimulus attribute. In addition, the PM coding fractions of T-units were significantly smaller during simultaneous random AM and random PM than during separate random PM (t₍₂₀₎ = 6.100; p < 0.00001), indicating that AM serves as a source of noise for the encoding of PM by T-units. There was, however, no significant difference between the separate and simultaneous AM coding fractions of P-units (t₍₄₄₎ = 0.0925; p = 0.9267).

Figure 2.

Distributions of the mean AM and PM coding fractions for all P- and T-units, when random AM and random PM were presented simultaneously (A) and separately (B), with σ_AM ranging from 10 to 25% and σ_PM ranging from 10 to 30° (bin size of 0.1).

For each unit, we quantified the degree of selectivity for a particular stimulus attribute using a selectivity index, defined as SI = (γ_AM − γ_PM)/(γ_AM + γ_PM), which ranges from −1 (maximum PM selectivity) to 0 (no selectivity) to 1 (maximum AM selectivity). As an example, the selectivity index of the P-unit shown in Figure 1A was 0.8745 when random AM and random PM were presented simultaneously but only 0.1819 when random AM and random PM were presented separately, and the selectivity index of the T-unit shown in Figure 1B was −0.9323 when random AM and random PM were presented simultaneously but only −0.4109 when random AM and random PM were presented separately. Across the population of primary afferents, P-units exhibited significantly greater selectivity for AM when random AM and random PM were presented simultaneously (SI of 0.7927 ± 0.0129) than when they were presented separately (SI of 0.5867 ± 0.0476; t₍₄₄₎ = 4.414; p < 0.0001), and T-units similarly exhibited significantly greater selectivity for PM when random AM and random PM were presented simultaneously (SI of −0.9324 ± 0.0059) than when they were presented separately (SI of −0.4791 ± 0.0381; t₍₂₀₎ = 13.35; p < 0.000001).

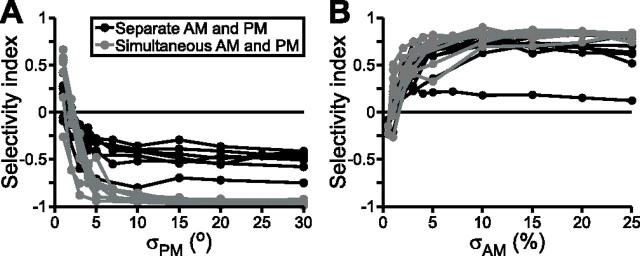
For several units, we varied σ_AM or σ_PM to quantify the dependence of stimulus selectivity on relative stimulus strength. For seven T-units, we varied σ_PM from 1 to 30° while keeping σ_AM constant at 20%. These units maintained strong PM selectivity when σ_PM was greater than ∼5°, but, below this value, selectivity for PM dropped sharply, often resulting in selectivity for AM when σ_PM dropped below 1–2° (Fig. 3A). Thus, decreases in σ_PM resulted in a significant reduction in PM selectivity (repeated-measures ANOVA; F_(9,18) = 37.14; p < 0.000001). Independent of this effect, PM selectivity was significantly greater when random AM and random PM were presented simultaneously than when they were presented separately (F_(1,2) = 461.11; p < 0.01). For nine P-units, we varied σ_AM from 0.5 to 25% while keeping σ_PM constant at 10°. The P-units exhibited strong AM selectivity when σ_AM was greater than ∼3%. Below this value, however, selectivity for AM dropped sharply, often resulting in selectivity for PM when σ_AM dropped below 0.5–1% (Fig. 3B). Similar to the PM selectivity of T-units, decreases in σ_AM resulted in a significant reduction in AM selectivity (repeated-measures ANOVA; F_(8,16) = 7.555; p < 0.001). Unlike the T-units, however, there was no significant difference in selectivity between simultaneous and separate presentation of random AM and random PM (F_(1,2) = 2.999; p = 0.22). However, this lack of significance was likely attributable to the relatively low number of units tested with various levels of σ_AM (n = 9), because the entire P-unit population (n = 45) did show a significantly greater degree of AM selectivity when random AM and random PM were presented simultaneously than when they were presented separately, as described above. Thus, the selectivity of primary afferents for a particular stimulus attribute is dependent on the statistics of both AM and PM.

Figure 3.

Selectivity for AM or PM varies with the relative average depths of modulation. The selectivity index varies from −1 (maximum PM selectivity) to 0 (no selectivity) to 1 (maximum AM selectivity). A, Selectivity of seven T-units as a function of σ_PM, with σ_AM held constant at 20%. B, Selectivity of nine P-units as a function of σ_AM, with σ_PM held constant at 10°.

Encoding of the preferred and nonpreferred stimulus attributes result from changes in the same spike train variables

Because organisms have no previous knowledge of stimuli independent of the information provided by their primary sensory afferents (Bialek et al., 1991; Rieke et al., 1997) and variation in the activity of a given P- or T-unit could result from either AM or PM, these findings indicate that information about AM and PM is ambiguously represented by individual afferents. However, the actual degree of ambiguity in the information available to the organism partly depends on how afferent activity is processed. It has been suggested that postsynaptic neurons may decode afferent activity by implementing filters that are similar to the optimal reconstruction filters obtained using the stimulus estimation technique (Bialek et al., 1991; Rieke et al., 1997). Although these filters are optimal and therefore vary depending on stimulus statistics (Wessel et al., 1996), there were consistent differences in the shapes of the optimal filters used to estimate AM and PM for both P- and T-units. For example, although the optimal AM filters obtained for the P-unit shown in Figure 1A are nearly identical regardless of whether random AM was presented alone or together with random PM, their shape was dramatically different from the optimal PM filter obtained in response to random PM presented alone. Similarly, the shapes of the optimal PM filters for the T-unit shown in Figure 1B are quite different from the shape of the optimal AM filter obtained in response to random AM presented alone. If the postsynaptic neurons filter presynaptic afferent activity by implementing the optimal reconstruction filter for their preferred stimulus attribute, then the resulting readout of the afferent spike trains may actually provide unambiguous information about that attribute. If this is the case, then the encoding of random PM by P-units and random AM by T-units would simply be an artifact of the stimulus estimation method that does not reflect any ambiguity in the actual information made available to postsynaptic neurons.

To address this problem, we made the assumption that the postsynaptic targets of both types of afferents implement the optimal reconstruction filter for estimating the preferred stimulus attribute of their primary afferent. We therefore applied the PM filters of T-units to their spike trains obtained in response to random AM presented alone and asked whether reliable information about PM is obtained; in this case, reliable information corresponds to an estimate that approaches the baseline (no PM). However, these estimates deviated substantially from baseline (Fig. 4A). Applying the PM filters of T-units obtained in response to random PM presented alone (σ_PM = 15°) to the spike trains in response to random AM presented alone (σ_AM = 25%) yielded an average estimate of σ_PM = 2.54 ± 0.25° (n = 10 units), two orders of magnitude higher than the behavioral threshold of 0.029° (Rose and Heiligenberg, 1985). We similarly applied the AM filters of P-units to their spike trains in response to random PM presented alone, and these also yielded spurious estimates of AM (Fig. 4B). Applying the AM filters of P-units obtained in response to random AM presented alone (σ_AM = 25%) to the spike trains in response to random PM presented alone (σ_PM = 15°) yielded an average estimate of σ_AM = 6.83 ± 0.68% (n = 43 units), also two orders of magnitude higher than the behavioral threshold of 0.05% (Rose and Heiligenberg, 1985). Therefore, if the postsynaptic targets of the primary afferents implement the optimal reconstruction filter for estimating their preferred stimulus attribute, the nonpreferred stimulus attribute will give rise to spurious information when it occurs in isolation.

Figure 4.

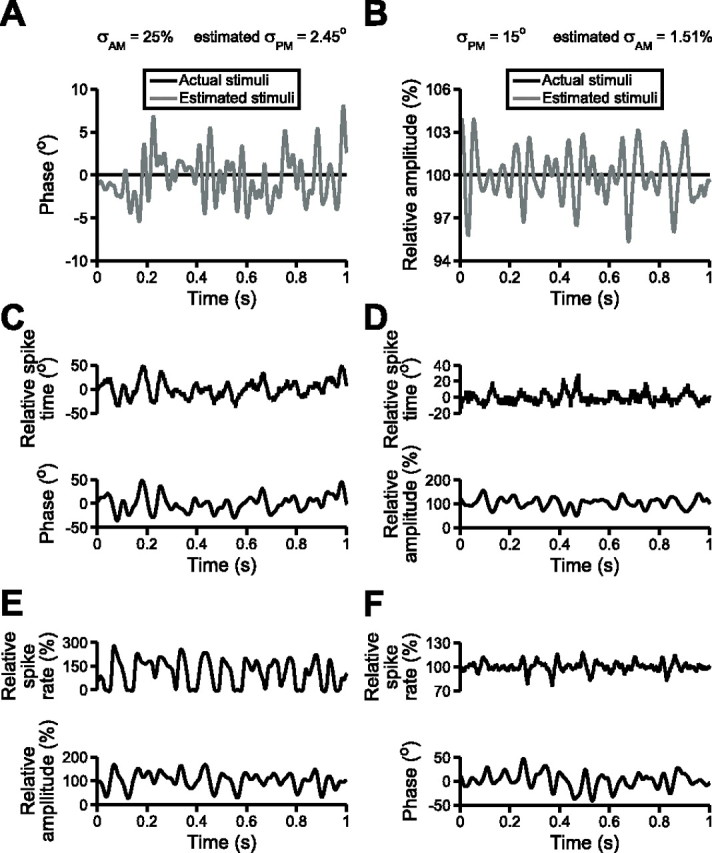
The nonpreferred stimulus feature elicits spurious estimates of the preferred stimulus feature. A, Applying the optimal filter obtained from the response of a T-unit to random PM presented alone (σ_PM = 15°) to the spike train in response to random AM presented alone (σ_AM = 25%) generates a spurious estimate of PM. B, Applying the optimal filter obtained from the response of a P-unit to random AM presented alone (σ_AM = 25%) to the spike train in response to random PM presented alone (σ_PM = 15°) generates a spurious estimate of AM. C, Changes in the relative spike times of a T-unit during random PM presented alone (σ_PM = 15°). D, Changes in the relative spike times of the same T-unit during random AM presented alone (σ_AM = 25%). E, Changes in the relative spike rate of a P-unit during random AM presented alone (σ_AM = 25%). F, Changes in the relative spike rate of the same P-unit during random PM presented alone (σ_PM = 15°).

Unfortunately, without obtaining simultaneous recordings from primary afferents and their postsynaptic targets, it is impossible to strictly determine how the postsynaptic neurons actually filter afferent activity. Thus, another approach toward quantifying the ambiguity of the information provided by primary afferents is to use our extensive knowledge of the response properties of neurons in the central electrosensory pathways and apply a biophysically plausible readout onto the spike trains of P- and T-units to determine whether AM and PM both induce changes in the relevant spike train variables. For the T-unit pathway, spike timing is the relevant variable for encoding PM (Heiligenberg and Rose, 1985; Carr et al., 1986a,b; Heiligenberg, 1991). Relative spike times closely followed random PM stimuli (Fig. 4C), and spike times showed a clear negative relationship with stimulus amplitude (Fig. 4D). In response to random PM presented alone, with σ_PM = 15°, the average SD of relative T-unit spike times was 15.38 ± 0.10° (n = 21). In response to random AM presented alone, the average SD of T-unit spike times was 3.88 ± 0.27° when σ_AM was equal to 20% (n = 11) and 5.70 ± 0.92° when σ_AM was equal to 25% (n = 11).

During low-frequency AM occurring over a large portion of the body surface, the postsynaptic targets of P-units extract information about upstrokes and downstrokes in EOD amplitude through increases and decreases in P-unit spike rate (Gabbiani et al., 1996; Metzner et al., 1998). We therefore applied a low-pass filter to P-unit spike trains and analyzed the variation in spike rate during random AM and random PM. Spike rates closely followed stimulus amplitude (Fig. 4E) and also covaried with random PM stimuli (Fig. 4F). In response to random AM presented alone, with σ_AM = 25%, the average SD of P-unit spike rates was 81.54 ± 4.74% (n = 45). The average SD of P-unit spike rates during random PM presented alone was 41.68 ± 8.22% when σ_PM was equal to 10° (n = 23) and 46.46 ± 6.82% when σ_PM was equal to 15° (n = 43). For both P- and T-units, then, encoding of the nonpreferred stimulus attribute resulted from changes in the same spike train variables that encode the preferred stimulus attribute.

Model neurons that preferentially encode either AM or PM also encode their nonpreferred stimulus attribute

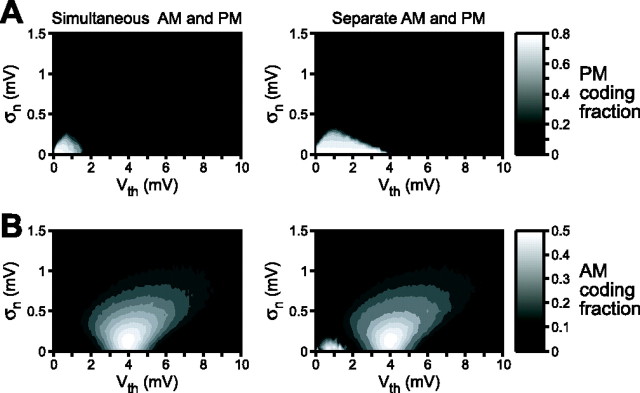
Is the lack of independence between AM and PM encoding a necessary feature of a sensory system designed to encode the amplitude and phase of periodic signals? To address this question, we constructed standard leaky integrate-and-fire neuron models (Gabbiani and Koch, 1998). We varied two parameters: (1) the threshold voltage for action potential generation (V_th) and (2) a noise term that added Gaussian-distributed noise of a given SD (σ_n) to the membrane voltage. Model neuron responses to simultaneous presentation of random AM and random PM revealed the existence of two distinct populations: neurons with low thresholds and low noise exhibited a preference for PM (Fig. 5A), whereas neurons with high thresholds and greater noise exhibited a preference for AM (Fig. 5B). This finding agrees with previous descriptions of threshold differences between P- and T-units (Scheich et al., 1973). Similar to the actual primary afferents, however, there was extensive overlap between the AM and PM coding fractions when random AM and random PM were presented separately (Fig. 5), demonstrating that model neurons with a preference for PM were also able to encode AM and vice versa.

Figure 5.

Contour plots of mean PM (A) and AM (B) coding fractions as a function of action potential threshold (V_th) and neuronal noise (σ_n) obtained from 10 model simulations. The bars to the right show the scaling of the contour plots. The values of V_th are in relation to the resting membrane potential, which is arbitrarily set at 0. The left column shows the coding fractions obtained from simultaneous presentation of random AM and random PM, and the right column shows the coding fractions obtained from separate presentation of random AM and random PM.

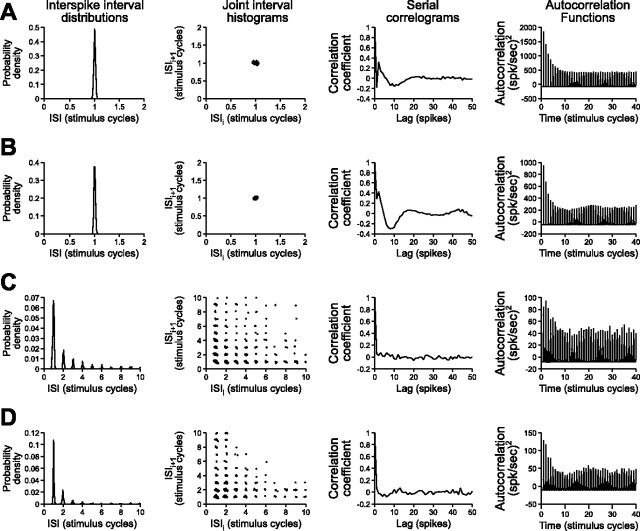
Based on the coding fractions obtained during simultaneous random AM and random PM stimulation, we generated separate populations of amplitude- and time-coding model neurons (n = 50 each). To compare the patterns of activity in these model neurons with the actual primary afferents, we analyzed several spike train variables, including interspike interval distributions, joint interval histograms, serial correlograms, and autocorrelation functions (Gabbiani and Koch, 1998). The activity patterns of model time-coding neurons (Fig. 6A) were very similar to those of T-units (Fig. 6B), whereas the activity patterns of model amplitude-coding neurons (Fig. 6C) were very similar to those of P-units (Fig. 6D). To assess the degree of ambiguity in the encoding of AM and PM by the model neuron populations, we calculated the same SI as for the primary afferents. The model amplitude-coding neurons were significantly more selective for AM when random AM and random PM were presented simultaneously (SI of 0.9168 ± 0.0066) than when they were presented separately (SI of 0.7432 ± 0.0621; t₍₄₉₎ = 2.767; p < 0.01). Similarly, the model time-coding neurons were significantly more selective for PM when random AM and random PM were presented simultaneously (SI of −0.9207 ± 0.0105) than when they were presented separately (SI of −0.5319 ± 0.0346; t₍₄₉₎ = 10.10; p < 0.000001). Therefore, like the actual primary afferents, the selectivity of both model populations was greater when random AM and random PM were presented simultaneously than when they were presented separately, suggesting the possibility that ambiguity at the level of individual primary afferents may be unavoidable.

Figure 6.

Patterns of activity in model neurons and primary sensory afferents during random modulations of their preferred stimulus feature, including interspike interval (ISI) distributions, joint interval histograms (plots of interspike interval against the preceding interspike interval), serial correlograms (correlations between the interspike intervals of spikes separated by various delays, or lags), and autocorrelation functions (probabilities of spike occurrence as a function of time after a spike at time = 0). The time bases and intervals are normalized to the duration of the stimulus carrier cycle for comparison. A, Model time-coding neuron with a low threshold (V_th = 0.7 mV) and low noise term (σ_n = 0.05 mV) during random PM stimulation (σ_PM = 15°). B, T-unit during random PM stimulation (σ_PM = 15°). C, Model amplitude-coding neuron with a high threshold (V_th = 4.6 mV) and large noise term (σ_n = 0.25 mV) during random AM stimulation (σ_AM = 20%). D, P-unit during random AM stimulation (σ_AM = 20%).

Ambiguous encoding of AM and PM gives rise to a misperception of the actual amplitude and phase of electrosensory stimuli

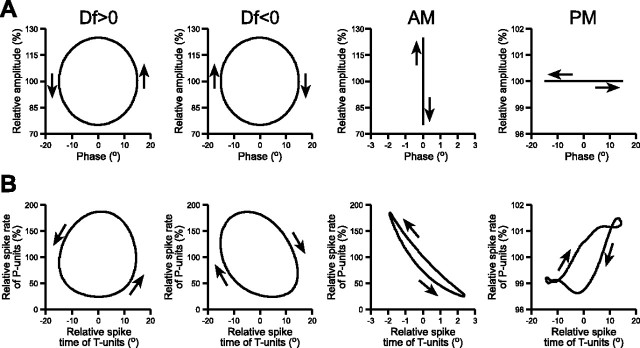
Although AM and PM are encoded with a certain amount of ambiguity by individual afferents, it is possible that the organism obtains unambiguous information about AM and PM by pooling the information made available from all afferents and performing stimulus estimation at the population level. To address this question, we took advantage of the JAR, a robust, easily quantified behavior that has been extensively studied at both the neural and behavioral levels (Heiligenberg, 1991). To properly execute the JAR, a fish determines whether it has a higher or lower EOD frequency than its neighbor (Df < 0 or Df > 0, respectively) by analyzing the temporal relation between sinusoidal AM and PM that results from the summation of their EODs (Heiligenberg and Bastian, 1980; Heiligenberg and Partridge, 1981; Heiligenberg, 1991; Takizawa et al., 1999). By plotting AM against PM in a Lissajous graph that evolves over time, one obtains a circle that rotates clockwise for Df < 0 and counterclockwise for Df > 0 (Fig. 7A).

Figure 7.

Neural representations of sinusoidal stimulus modulations. A, Sinusoidal stimulus modulations, plotted as Lissajous graphs of relative voltage versus phase. Df > 0 consists of sinusoidal AM and sinusoidal PM, with the PM start angle advanced by 90° relative to AM, whereas Df < 0 consists of sinusoidal AM and sinusoidal PM, with the PM start angle delayed by 90° relative to AM. B, Neural representations of the stimuli in A, plotted as Lissajous graphs of the mean relative spike rate of P-units (n = 33) versus the mean relative spike time of T-units (n = 16).

We recorded from individual afferent fibers during stimulation with Df > 0, Df < 0, sinusoidal AM, and sinusoidal PM and compared the stimulus modulations with their neural representations, in terms of P-unit spike rates and T-unit spike times (Heiligenberg and Partridge, 1981), the same variables that we used in our analysis of responses to random AM and random PM (Fig. 4C–F). As shown previously, the neural representations of Df > 0 and Df < 0 exhibit the same sense of rotation as the actual stimuli (Heiligenberg and Partridge, 1981; Heiligenberg, 1991) (Fig. 7B). Neither sinusoidal AM nor sinusoidal PM exhibit any sense of rotation in a Lissajous graph (Fig. 7A). However, the responses of the primary afferents to their nonpreferred stimulus attribute resulted in a neural representation of sinusoidal AM with a counterclockwise rotation and a neural representation of sinusoidal PM with a clockwise rotation (Fig. 7B). We therefore hypothesized that sinusoidal AM is perceived as Df > 0, whereas sinusoidal PM is perceived as Df < 0.

To test this hypothesis, we measured EOD frequency shifts in response to these four stimuli using a phase chamber (Fig. 8A). If the JAR results from an accurate perception of the stimulus sense of rotation, then Df > 0 should elicit a frequency decrease and Df < 0 should elicit a frequency increase, but neither sinusoidal AM nor sinusoidal PM should elicit any frequency shift. If, however, the fish’s perception is distorted by the neural representation provided by P- and T-units, then sinusoidal AM should elicit frequency decreases and sinusoidal PM should elicit frequency increases. Figure 8B shows representative responses from a single individual, confirming that Df > 0 elicits frequency decreases and Df < 0 elicits frequency increases, further revealing that sinusoidal AM elicits frequency decreases and sinusoidal PM elicits frequency increases. We measured the mean shifts in EOD frequency in response to these four stimuli in 22 individuals (Fig. 9A). All 22 individuals responded to Df > 0 with frequency decreases, Df < 0 with frequency increases, and sinusoidal AM with frequency decreases (sign test, p < 0.000001). All but one individual responded to sinusoidal PM with frequency increases (p < 0.0001).

Figure 8.

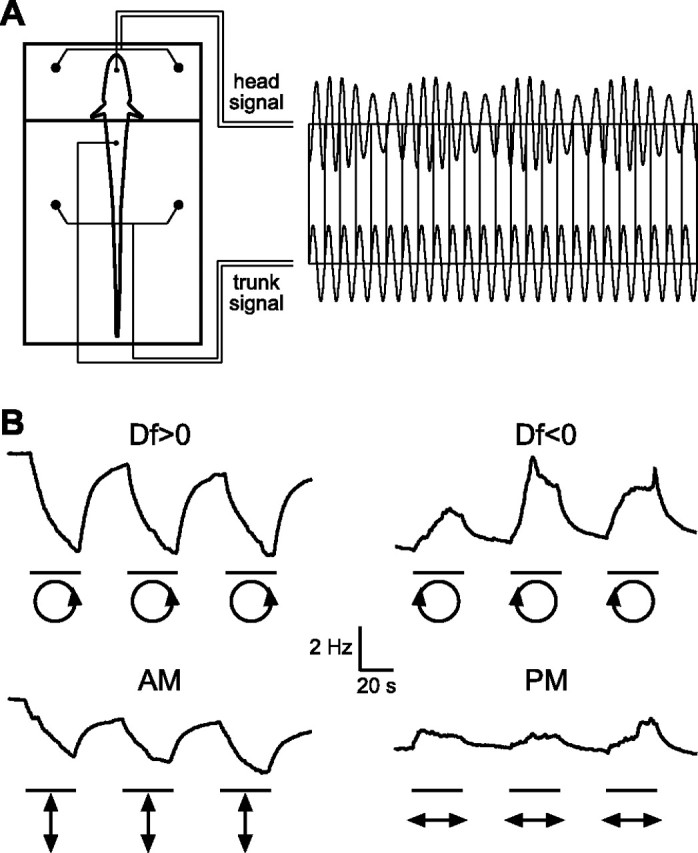
Measuring EOD frequency shifts in response to sinusoidal modulations using the phase chamber. A, The phase chamber electrically divides the fish into separate head and trunk compartments, allowing one to independently modulate AM and differential PM. The trunk compartment is presented with an unmodulated signal, whereas the head compartment is presented with a modulated stimulus. EOD frequency is recorded from an electrode placed next to the tail. B, EOD frequency shifts from a single individual in response to Df > 0, Df < 0, sinusoidal AM, and sinusoidal PM. The bars beneath each trace delimit the periods of stimulus modulation, and the icons below each bar show Lissajous plots of the stimulus modulations (AM plotted against PM, after Fig. 7A).

Figure 9.

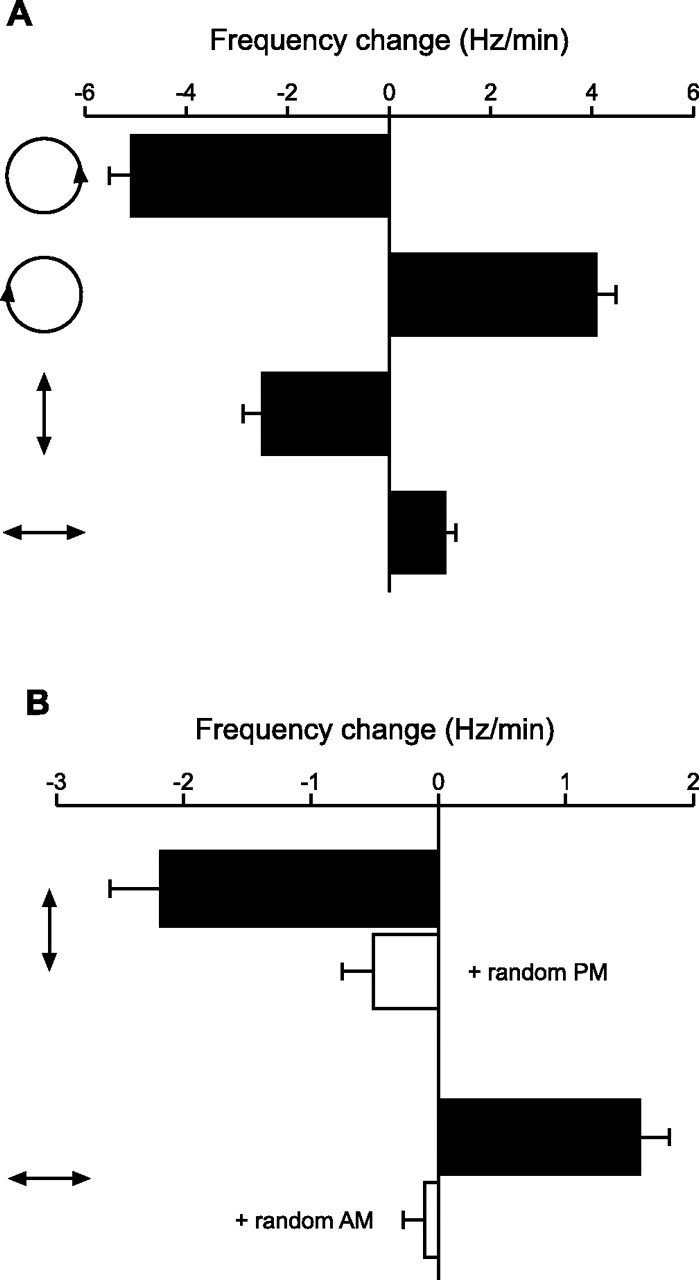
Shifts in EOD frequency in response to sinusoidal stimulus modulations. A, Changes in EOD frequency in response to Df > 0, Df < 0, sinusoidal AM, and sinusoidal PM (mean ± SEM; n = 22). Icons to the left show Lissajous plots of the stimulus modulations (AM plotted against PM, after Fig. 7A). B, Changes in EOD frequency in response to sinusoidal AM, with and without random PM, and sinusoidal PM, with and without random AM (mean ± SEM; n = 8). Icons to the left show Lissajous plots of the sinusoidal stimulus modulations. Note the difference in scaling between A and B, which is attributable to the relatively stronger responses to Df > 0 and Df < 0 compared with the responses to AM and PM.

We also wondered whether the ambiguous encoding of AM and PM by primary sensory afferents influences behavioral responses to natural jamming stimuli (Df > 0 and Df < 0). If the nonpreferred stimulus attribute had no effect on primary afferent responses to natural jamming stimuli, then the shape and size of the neural representation Lissajous graphs of Df > 0 and Df < 0 would be identical; only the sense of rotation would differ. However, the effect of the nonpreferred stimulus attribute on the responses of primary afferents to Df > 0 and Df < 0 led to a difference in the shape and size of the Df > 0 and Df < 0 neural representations (Fig. 7B). We quantified this difference by calculating the area enclosed within the Lissajous graphs using numerical integration (in which relative amplitude is expressed as a dimensionless fraction and time is expressed in degrees of relative phase). The areas enclosed within the Lissajous graphs of the Df > 0 and Df < 0 stimuli were both equal to 11.78°. However, the area enclosed within the Lissajous graph of the Df > 0 neural representation (37.92°) was slightly greater than the area enclosed within the Lissajous graph of the Df < 0 neural representation (36.22°). Therefore, if the intensity of natural jamming stimuli is accurately perceived, then one would predict no difference in the strength of frequency shifts in response to Df > 0 and Df < 0. If the perceived strength of the jamming stimuli is distorted by the ambiguous neural representation, however, then one would predict stronger frequency shifts in response to Df > 0 than Df < 0, which was indeed the case (Figs. 8B, 9A) (magnitude of Df > 0 response, 5.104 ± 0.4092; magnitude of Df < 0 response, 4.100 ± 0.3716; t₍₂₁₎ = 2.107; p < 0.05). Along these same lines, the areas enclosed by the Lissajous graphs of sinusoidal AM and sinusoidal PM stimuli are both 0°, because the graphs are completely closed. The Lissajous graphs of the neural representations, however, have areas of 0.8825° for AM and 0.2180° for PM. Thus, differences in the relative magnitude of frequency shifts in response to Df > 0, Df < 0, sinusoidal AM, and sinusoidal PM (Figs. 8B, 9A) are in agreement with relative differences in the areas of the neural representation Lissajous graphs (Df > 0 > Df < 0 > AM > PM) but not the areas of the stimulus Lissajous graphs (Df > 0 = Df < 0 > AM = PM).

Although these findings are consistent with our hypothesis, it is possible that AM and PM are accurately perceived but elicit frequency shifts as behaviors distinct from the JAR (Takizawa et al., 1999). That is, sinusoidal modulation of P-unit firing rates alone may drive EOD frequency decreases, whereas sinusoidal modulation of T-unit spike times alone may drive EOD frequency increases. We therefore conducted two control experiments designed to disrupt the responses of primary afferents to sinusoidal modulations of their nonpreferred stimulus attribute. If frequency decreases in response to AM rely solely on the encoding of AM by P-units and not on the AM responses of T-units, then selectively eliminating the AM responses of T-units while preserving the AM responses of P-units should not have any effect on the behavior. We achieved such a manipulation by adding random PM to sinusoidal AM. When the fish are stimulated with both AM and PM, their P-units selectively respond to AM whereas their T-units selectively respond to PM (Figs. 1, 2). In this case, because the PM is random, this causes the relative spike times of T-units to vary randomly with respect to the sinusoidal modulations in spike rate of the P-units. This treatment strongly reduced the magnitude of frequency shifts in response to sinusoidal AM (t₍₇₎ = 5.873; p < 0.001) (Fig. 9B). We conducted a similar control experiment to determine whether behavioral responses to sinusoidal PM relied on the PM responses of P-units by adding random AM to sinusoidal PM. Again, this treatment strongly reduced the magnitude of frequency shifts (t₍₇₎ = 5.674; p < 0.001) (Fig. 9B). These results support our hypothesis that the behavioral responses to sinusoidal AM and sinusoidal PM result from the ambiguous representation of stimuli by primary afferents.

Discussion

Although the electrosensory system of Eigenmannia is specialized for processing AM and PM using separate populations of primary afferents, the encoding of these attributes is not independent. Some researchers have challenged the existence of two categories of afferents (Viancour, 1979), but more recent work has clearly shown that P- and T-units give rise to functionally and anatomically distinct central pathways (Maler et al., 1981; Carr and Maler, 1986; Mathieson et al., 1987; Heiligenberg, 1991; Kawasaki, 2005). Indeed, our results reveal separate populations of amplitude- and time-coding afferents that agree with our a priori classification of P- and T-units, respectively (Fig. 2A). However, both types of units also respond to their nonpreferred stimulus feature when the preferred feature is absent or sufficiently weak relative to the nonpreferred feature.

T-units encode PM because their spikes are tightly phase locked to the carrier, causing their relative spike times to vary with changes in phase (Fig. 4C) (Scheich et al., 1973). However, they also encode AM because of an amplitude-dependent latency shift (Fig. 4D). This effect is relatively weak compared with the shift induced by all but the smallest phase modulations, so that, during simultaneous AM and PM, the encoding of PM predominates. Nevertheless, the amplitude-dependent latency shift still affects spike timing and thereby serves as a source of noise that reduces PM encoding. In contrast, P-units encode AM because their probability of firing during each cycle, and therefore firing rate, varies with amplitude (Fig. 4E) (Scheich et al., 1973). When amplitude remains constant and there is a fixed probability of firing, P-units also encode PM because of their relatively sporadic phase locking: when phase is modulated, this leads to small changes in interspike interval, and therefore spike rate (Fig. 4F). When amplitude and phase are both modulated independently, variation in the probability of firing over time exerts a much greater effect on spike rate than these small shifts in interspike interval, and the encoding of AM predominates.

Because both types of afferents are affected by both attributes, it is impossible to obtain unambiguous information about AM and PM solely by analyzing the activity of individual afferents. Nevertheless, there are possible mechanisms by which this ambiguity could be resolved. For instance, the synaptic transfer function between a primary afferent and its postsynaptic target in the hindbrain could act as a filter that prevents the postsynaptic neuron from responding to the nonpreferred attribute. For both types of afferents, however, the preferred and nonpreferred attributes elicited changes in the same variables that are important for the central processing of AM and PM (Heiligenberg, 1991), namely the spike rates of P-units and the spike times of T-units, respectively (Fig. 4C–F). Furthermore, spurious estimates of the preferred attribute were obtained when the optimal filter for estimating that attribute was applied to responses to the nonpreferred attribute (Fig. 4A,B). It therefore seems unlikely that a synaptic filter could resolve this ambiguity. These results also reveal that precise spike-timing information is not necessary for P-units to encode PM, because such information is lost when applying a low-pass filter to estimate spike rate or when applying the optimal filter for estimating AM.

Although individual afferents represent AM and PM ambiguously, it is possible that unambiguous information is obtained through a population code. We did not directly address this by stimulating multiple afferents with identical random modulations to obtain a population-level stimulus estimate. At least in the context of the JAR, however, our behavioral results indicate that these ambiguities are not resolved but give rise to systematic errors in perception: behavioral responses to sinusoidal modulations were consistent with the average representations of those modulations by primary afferents but not the actual stimuli. EOD frequency decreases in response to sinusoidal AM have been described previously but were interpreted as a behavior distinct from the JAR that did not depend on T-unit responses (Takizawa et al., 1999). We directly addressed this by adding random PM to sinusoidal AM to selectively disrupt T-unit responses to AM and found that this greatly reduced the magnitude of frequency decreases. Our findings therefore suggest that this behavior results from a misperception of sinusoidal AM as a Df > 0 stimulus attributable to the responses of both P- and T-units. Similarly, our results suggest that sinusoidal PM is incorrectly perceived as a Df < 0 stimulus.

An important question is whether ambiguity has any effect on electrosensory perception in a natural setting. During natural jamming, P- and T-units always provide an accurate representation of the temporal relationship between AM and PM because there is a fixed ratio between AM and PM depth (Heiligenberg, 1991), as seen in the shared sense of rotation of the Lissajous graphs of jamming stimuli (Fig. 7A) and their neural representations (Fig. 7B). However, the effects of the nonpreferred attribute caused differences in the shape and size of these representations (Fig. 7B). Thus, although these ambiguities do not affect the direction of frequency shifts in response to jamming, they may be responsible for the different magnitude of behavioral responses to Df > 0 and Df < 0 (Figs. 8B, 9A) and likewise may influence the perceived intensity of communication stimuli, which involve Df > 0 and Df < 0 at larger modulation rates than those that elicit the JAR. Furthermore, JARs can be elicited by nonsinusoidal modulations (Heiligenberg, 1991) at latencies less than the duration of a single modulation cycle (Bullock et al., 1972): the key factor is the relative timing between changes in amplitude and differences in phase. Therefore, it is likely that large objects that induce AM and/or PM over large areas of the body surface could be mistakenly perceived as jamming stimuli and thereby elicit frequency shifts (Rose and Heiligenberg, 1986).

It remains unknown whether ambiguity affects active electrolocation, for which the relationship between amplitude and phase varies depending on the electrical properties of objects (von der Emde, 1999). Many neurons in the hindbrain and midbrain process information relevant to both the JAR and active electrolocation (Bell and Maler, 2005; Kawasaki, 2005). In fact, jamming of electrolocation occurs in the presence of a neighbor with a similar EOD frequency because the resulting interference induces AM and PM within the same frequency range that is relevant for detecting objects passing through the electric field (Heiligenberg, 1973). Furthermore, neurons that respond selectively to the temporal relationship between AM and PM are found in the midbrain of Sternopygus, a related species that does not perform a JAR (Rose et al., 1987), suggesting that the neural circuitry for the JAR is evolutionarily derived from active electrolocation circuitry. Previous work describing the electrical images of objects and their neural representations have focused on stimulus amplitude and neural activity in the P-unit pathway (Assad et al., 1999; Nelson and MacIver, 1999; Nelson, 2005) and not on capacitance-induced phase shifts in the EOD or T-unit responses (but see Rose and Heiligenberg, 1986; von der Emde, 1998). Although Eigenmannia can discriminate between purely resistive objects and objects with capacitance (von der Emde, 1998), the ability to resolve small differences may be limited by encoding ambiguity. However, it may not be important in a natural situation to distinguish the resistive and capacitive components of objects but simply to associate specific objects with particular patterns of activity across the afferent population. Conversely, the neural pathways devoted to the JAR and active electrolocation begin to diverge in the midbrain (Bell and Maler, 2005), indicating that ambiguity could be resolved during active electrolocation despite its effects on the JAR.

Perceptual illusions are widespread in humans and other animals (Nieder, 2002; Wade, 2004). Many illusions result from artificial manipulation of sensory cues that are generally reliable in a natural setting. Studies based on such illusions provide insight into the mechanisms used by the nervous system to extract information (Spillman and Dresp, 1995; Eagleman, 2001). The current study is unique because it reveals that illusions can also result from uncertainty in the information provided by peripheral sensory neurons, a factor that could distort perception in a natural setting. Our modeling results raise the possibility that ambiguity may be unavoidable in neurons designed to encode the amplitude and phase of periodic signals. This claim is supported by our observation that primary afferents in the mormyriform electric fish Gymnarchus encode AM and PM with similar ambiguity (our unpublished observations), despite the fact that Gymnarchus is only distantly related to Eigenmannia and shares no common electrogenic or electroreceptive ancestors (Bullock et al., 1983). Primary auditory afferents encode phase/frequency and amplitude using mechanisms similar to those used by the electrosensory system (Ruggero, 1992), and phase-locked spikes are affected by an amplitude-dependent latency shift (Anderson et al., 1971; Dallos, 1986). In this respect, it is interesting that human pitch perception, primarily considered a function of frequency, is also influenced by amplitude (Hartmann, 1978; Rossing and Houtsma, 1986; Neuhoff and McBeath, 1996). Similarly, motion perception by the human visual system varies with contrast (Anstis, 2003, 2004). Although the underlying mechanisms for these effects remain to be seen, ambiguity in the encoding of multiple stimulus attributes may play a role.