Abstract
The distinctive branching patterns of dendritic arbors are essential for neuronal information processing. The final shape of an arbor is the result of intrinsic and extrinsic factors. However, the cellular mechanisms that underlie branch patterning are unknown. In many biological systems, locally acting factors are intrinsically organized into spacing patterns that guide patterned morphogenesis. Here, we show that neurons contain two types of periodic and regular elements (PADREN1s and PADREN2s) that are arranged into a spacing pattern. The wavelength of the pattern is ∼20 μm. Dendritic branches occur preferentially within PADREN1s, and specific PADREN lengths correspond to specific arbor types. The lengths of the PADRENs also change over time and can be modified by activity. However, PADRENs are intrinsically organized, possibly by a reaction-diffusion process. PADRENs reveal a previously unrecognized level of neuronal organization that may provide insight into how the distinct branching patterns of the dendrites are intrinsically organized.
Keywords: dendrite, arbor, branching, morphology, pattern, branch spacing
Introduction
The distinctive branching patterns of dendritic arbors represent a remarkable level of cellular organization and contribute to neuronal information processing (Mainen and Sejnowski, 1996; Agmon-Snir et al., 1998; Single and Borst, 1998; Schaefer et al., 2003; Polsky et al., 2004). These attributes make it of interest to understand how dendrites are organized. Evidence shows that locally and globally acting factors contribute to arbor morphology. For example, transcription factors (Grueber et al., 2003; Aizawa et al., 2004; Gaudilliere et al., 2004; Li et al., 2004), endocrine signals (Niblock et al., 2000; Danzer et al., 2001), and target-derived factors (Blaser et al., 1990) can modify the entire arbor. Conversely, regulators of cytoskeletal assembly (Threadgill et al., 1997; Nakayama et al., 2000; Akum et al., 2004), vesicle trafficking (Shi et al., 2003; Rosso et al., 2005), membrane insertion (Murthy et al., 2003), and protein synthesis (Lu et al., 2004; Pan et al., 2004) can modify subdendritic regions (Greenough and Chang, 1988; Horch and Katz, 2002; Lohmann et al., 2002). Extrinsic signals such as synaptic activity (Kossel et al., 1995; Morrison and Mason, 1998; Maletic-Savatic et al., 1999; Sin et al., 2002; Vaillant et al., 2002) and other cell–cell interactions (Kossel et al., 1997; Redmond et al., 2000) can activate both locally and globally acting factors.
Arbor structure is, in part, a function of the spacing of branches along dendritic shafts. Cell-type-specific branching patterns, such as those corresponding to pyramidal and multipolar neurons, can be elaborated autonomously (Bartlett and Banker, 1984a). How this intrinsic organization occurs may be conceptually analogous to events observed during embryogenesis, in which locally acting factors are intrinsically organized into periodically recurring elements termed “spacing patterns” that guide the formation of patterned morphologies (Malacinski, 1984). Here, we show that dendrites contain two types of intrinsically organized elements that are arranged into a spacing pattern. We term these elements PADREN1s and PADREN2s (for periodic and regular elements). PADRENs may be organized by a reaction-diffusion process, a likely mode of organization during ontogeny. PADREN1s preferentially contain branch points, and PADREN dimensions correspond to specific arbor morphologies. We suggest that PADRENs are an intrinsic, intermediate level of neuronal organization that contribute to dendritic branch patterning.
Materials and Methods
Neuron cultures.
Primary neuronal cultures were prepared as described previously (Brewer et al., 1993) in accordance with the Brown University Animal Care and Use Committee. Briefly, the pertinent brain region was removed from embryonic day 18 rat embryos, trypsinized (0.25%), and triturated. Cells were plated in 10% FBS in DMEM (Invitrogen, Carlsbad, CA) at 37°C onto poly-l-lysine-coated (0.1 mg/ml) glass coverslips (Carolina Biological, Burlington, NC). Plating densities were 45 cells/mm2 for hippocampal or neocortical neurons and 100 cells/mm2 for cerebellar neurons. Three hours after plating, the DMEM/FBS was removed and replaced with Neurobasal media [Neurobasal, B27, 1×; penicillin–streptomycin, 1×, and glutamax, 0.5× (Invitrogen)] at 37°C. One-half of the existing media was removed and replaced with new media every 4 d until use.
Fixation and immunocytochemistry.
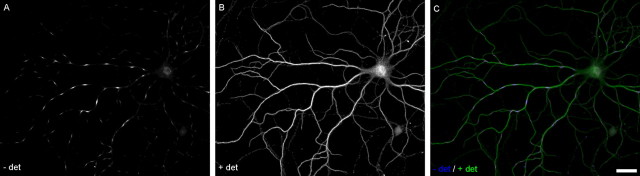
Cultures were handled as gently as possible before and after fixation. Cells were fixed for 5 min in 6% paraformaldehyde/4% sucrose in PBS at 37°C. Fix was removed and replaced with PBS at room temperature for 15 min, which was removed and replaced with block (20% FBS/0.02% NaN3 in PBS) for 1 h at 4°C. Block was removed, and primary antibodies were added for 12 h at 4°C. Coverslips were washed in PBS, and appropriate secondary antibody was added in block for 2 h, rinsed three times for 15 min, and mounted on glass slides in PermaFluor mounting media (Thermo Electron Corporation, Waltham, MA). After this procedure (which did not include detergent), we observed patterned regions of plasma membrane permeable to antibodies directed against intracellular epitopes (PADREN1s) that alternated with impermeable regions (PADREN2s) (see Fig. 1, Fig. 2) (for additional information, see supplemental data, available at www.jneurosci.org material).
Figure 1.
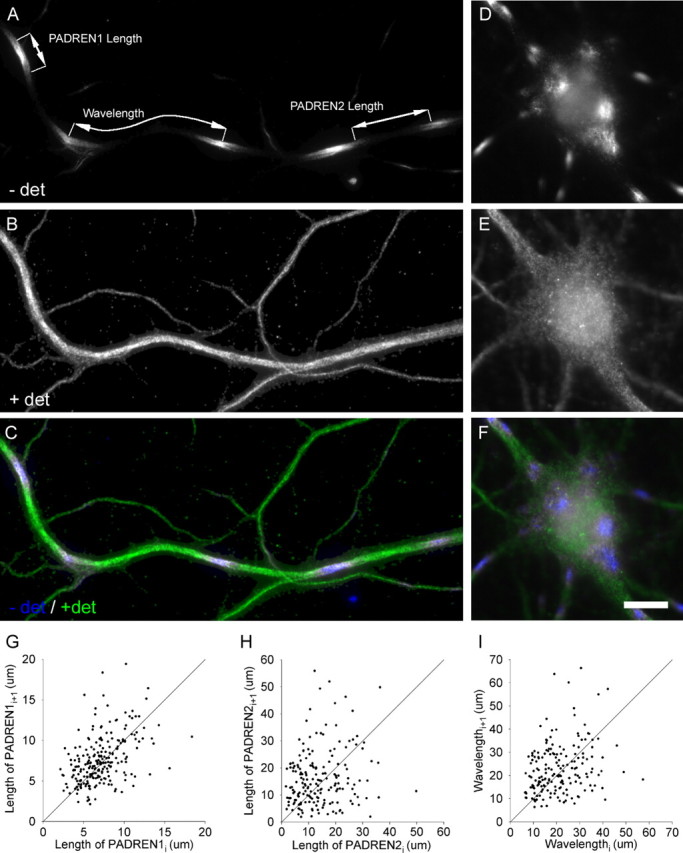
PADRENs form a spacing pattern. PADREN stripes (A) in the dendrite and spots (D) in the soma of a 17 DIV hippocampal neuron. Signal represents immunostaining before application of detergent (− det) using the mouse 5F9 anti-MAP2 antibody. Leaders in A demarcate a PADREN1 length, PADREN2 length, and a wavelength. B, E, Signal represents immunostaining after application of detergent (+ det) using rabbit polyclonal anti-MAP2 antibodies. C, F, Merged signals. Scale bar, 10 μm. G–I, Scatter plots of adjacent (ith + 1 vs ith) PADREN1 lengths (G), PADREN2 lengths (H), and wavelengths (I) in 17 DIV cells show that adjacent lengths are similar. The line Lengthi + 1 = Lengthi is illustrated for comparison.
Figure 2.
PADRENs form a spacing pattern. PADRENs in a 17 DIV hippocampal neuron. A, Immunostaining before application of detergent (− det) using the mouse 5F9 anti-MAP2 antibody. B, Immunostaining after application of detergent (+ det) using rabbit polyclonal anti-MAP2 antibodies. C, Merge. Scale bar, 30 μm.
To observe the distribution of intracellular proteins without the confound of variable permeability, cultures were treated exactly as described above (without mounting) and then incubated in 0.1% Triton X-100 (1 h at 4°C) to completely permeabilize the membrane. The permeabilized cells were then incubated in a different set of primary and secondary antibodies. This extended procedure (completed in 24 h) was used in all cultures quantified to produce data presented here.
Antibodies.
The staining for all results shown here was performed using mouse anti-microtubule-associated protein (MAP2), clone 5F9 (1:1000; Upstate Biotechnology, Waltham, MA) after the first, detergent-free incubations (to visualize PADREN1s) and rabbit anti-MAP2 (1:1000; Chemicon, Temecula, CA) after detergent permeabilization to visualize dendritic morphology and to verify uniform distribution of the MAP2 protein. Results were confirmed using other antibodies during both the detergent-free and post-detergent incubations. These antibodies include mouse anti-pan neurofilament (1:500; Zymed, Carlsbad, CA), anti-MAP2, clone HM-2 (1:1000; Sigma, St. Louis, MO), anti-tubulin, clone 2G10 (1:1000; Upstate Biotechnology), and rabbit anti-neurofilament (1:500; Chemicon). Secondary antibodies were conjugated to Alexa Fluor 488 (1:1000) or cyanine 3 (1:500) (Invitrogen).
EGTA buffered zero-calcium media treatment.
Existing media were removed and replaced with 1 mm EGTA buffered zero-calcium DMEM (Invitrogen) for 2 min, which was in turn removed and replaced with more buffered DMEM for an additional 15 min. The buffered DMEM media were equilibrated with the incubator atmosphere at 37°C before addition to the cultures. Care was taken not to contact the culture monolayer with a pipette during media exchanges. We calculated the concentration of external calcium to be <1 nm during the second round of buffered zero-calcium DMEM [assuming KA EGTA = 2.4 × 107 m−1 (Rockwell and Storey, 1999)].
Pharmacological treatments.
Cultures were gently removed from the incubator and placed on Styrofoam to limit cooling. Drugs were added in a DMSO (Sigma) or water vehicle to the existing media and mixed by gently pipetting approximately three-fourths of the media up and down one time. Four coverslips were treated per condition. At most, 16 wells on a plate were treated to limit total handling time to <3 min. Cultures were then returned to the incubator for the remainder of the experiment. Drugs were of highest available grade and obtained from Sigma unless noted. Stock solutions were prepared under sterile conditions and stored at −20°C. Dilutions to working concentrations were as follows: 1:250 KCl, 1:250 NaCl, 1:133 nocodazole, 1:400 taxol, 1:167 d, l-APV (Tocris Cookson, Ellisville, MO), 1:100 CNQX (Tocris Cookson), 1:1000 glutamate (Tocris Cookson), and 1:500 tetrodotoxin.
Sampling.
All results were repeated to the same qualitative degree in at least three independent experiments. Across-condition comparisons were between wells on the same (24-well) plate to ensure equivalent handling. Data shown are from single representative experiments. For selection of cells to compute the fraction of cells containing a certain number of PADREN1s in at least one dendrite, coverslips were systematically sampled according to a square grid that covered the extent of the coverslip (sample fields 1.8 mm apart; 1.1 mm2 in area; 31 sample fields per coverslip). Each sample comprised all cells whose somas fell within the sample field. The number of cells in each sample field was divided by the area of the field to compute cell density. For PADREN length distributions, cells were also systematically sampled (same field spacing and area as above; 16 sampling fields per coverslip). All cells in each sample field having at least five PADREN1s in at least one dendrite were photographed. The soma was positioned in approximately the center of each photograph. When this procedure yielded >30 photos per condition, the excess were discarded blindly.
Image acquisition.
Fluorescence images were acquired with IP-Lab Spectrum software (Scanalytics, Fairfax, VA) on a Nikon (Melville, NY) E800 microscope using 20×/0.75 numerical aperture (NA), 40×/1.0 NA, or 60×/1.4 NA objectives and a SenSys cooled CCD camera (Roper Scientific, Tucson, AZ). All images were acquired as grayscale (eight-bit) images and were not post-processed.
Analysis.
Image analysis was preformed on raw grayscale (eight-bit) or corresponding pseudocolor (24-bit) images in NIH Image J. Color images in the figures are a merge of the intensities of corresponding pixels in the grayscale images (G1xy and G2xy). Each color pixel was computed according to [[R = (if G1xy > G2xy, then G2xy; else G1xy)], [G = G2xy], [B = G1xy]]. Image resolutions were determined empirically from fluorescent beads (Invitrogen) and are as follows: 20×, 0.32 μm/pixel; 40×, 0.156 μm/pixel; 60×, 0.102 μm/pixel. All measured objects were >10 pixels along the measured dimension to ensure that digitization error was on average ≤5%. Only PADRENs along primary dendritic shafts were measured. Data was compiled in Microsoft (Seattle, WA) Excel, and statistical tests were preformed using SPSS version 11.5 (SPSS, Chicago, IL). To test statistical significance, unless noted, a Mann–Whitney U test was used to compare two samples, and a Kruskal–Wallis test was used to compare samples across multiple conditions. Measurements within each sample were approximately independent. A custom test is described below. Averages are reported as mean ± SEM.
Definition of dendritic PADREN1 length, PADREN2 length, and wavelength.
The edge of a PADREN1 region was defined as the position in which the average pixel intensity was equal to the maximal average pixel intensity in a 3 × 3 window in the PADREN1 minus the minimum average pixel intensity in PADREN2s divided by two (e.g., position of half-maximal intensity). Because PADREN1s and PADREN2s partition the dendrite, PADREN1 edges are also PADREN2 edges. The length of a PADREN1 or a PADREN2 region is the distance along the longitudinal axis of the dendrite between its edges. The pattern “wavelength” is the distance from the midpoint of one PADREN1 to the midpoint of an adjacent (i.e., separate by exactly one PADREN2) PADREN1, again along the longitudinal axis of the dendrite (see Fig. 1A).
Computation of “significant association” with PADRENs.
A branch point can either originate from a PADREN1 or not originate from a PADREN1. In each cell i, we modeled the number of branches originating from PADREN1s by chance as a binomial experiment, where Xi is a binomial random variable that assigns a probability to a given number of branches originating from a PADREN1. Particularly, we assumed that the probability pi of a branch in cell i originating from a PADREN1 by chance is equivalent to the fraction of shaft length occupied by PADREN1s in cell i. This allowed us to compute the expected number of branches, E(Xi), originating from PADREN1s according to ni × pi, where ni is the total number of branch points in cell i. The variance, V(Xi), is computed according to ni × pi × qi (where qi is the fraction of shaft length occupied by PADREN2s) (for implications of this model, see supplemental data, available at www.jneurosci.org as supplemental material). We next defined another random variable T, which assigns a probability to a total number of branch points originating from PADREN1s by chance in N total cells (i.e., T = X1 + Xi +… + XN). Then E(T) is the sum of the expected values for each Xi, and V(T) is the sum of the variances for each Xi [reasonably assuming that Cov(Xi, Xj) = 0]. When pi ≈ 0.5, the distribution of T is approximately normal with E(T) ≈ μ and V(T) ≈ σ2. Therefore, we consider branch points to be “significantly associated” with one of the PADREN types if the observed value of T is greater or less than zα = 0.05 SDs from E(T), i.e., if |T − E(T)|/∘V(T) > Zα = 0.05.
Results
Observation of PADRENs
When applying antibodies against intracellular epitopes to aldehyde-fixed neurons in the absence of detergent, we observed regularly spaced regions of immunostaining that were arranged into a pattern of “stripes” in the neurites (Fig. 1A, Fig. 2) and “spots” in the cell body (Fig. 1D) (see supplemental material, available at www.jneurosci.org; only dendritic stripes are considered further here). We suspected that these regions could reflect dendritic areas possessing unique functional properties, so we called the immunostained regions PADREN1s and the unstained regions PADREN2s. We observed PADRENs in hippocampal, neocortical, and cerebellar neurons (supplemental material, available at www.jneurosci.org) from both rats and mice (data not shown) under a wide variety of fixation and immunostaining procedures (supplemental material, available at www.jneurosci.org). However, PADRENs were not observed when the same antibodies were used in unfixed cells. We thus conclude that a pattern of PADRENs is a common and readily observed feature of aldehyde-fixed neurons.
Dendritic PADRENs are arranged into a spacing pattern
To quantitatively confirm that PADRENs are arranged into a pattern, we tested whether the arrangement of PADREN1s forms a spacing pattern. “Spacing pattern” denotes an arrangement of elements in which the distribution of distances between adjacent elements of a type is not exponential. This definition is commonly used to demonstrate the presence of patterns in nature (Malacinski, 1984). To show that the distribution of distances between the centers of adjacent PADREN1s (i.e., wavelength) (Fig. 1A) was not exponential, we used a Kolmogorov–Smirnov test to compare the distribution of distances with an exponential distribution of the same mean. This analysis showed that the distribution of wavelengths was significantly nonexponential (p < 1 × 10−10) (for a graphical comparison, see supplemental material, available at www.jneurosci.org) but was nearly normal (p = 0.02, Kolmogorov–Smirnov test; data versus a normal distribution with the same mean and SD). The distribution of PADREN1 lengths and PADREN2 lengths was also nonexponential (p < 0.005 in both cases). Thus, PADRENs are arranged into a spacing pattern.
Adjacent PADRENs of a type and adjacent wavelengths within individual dendrites are also very similar. To show this similarity, we systematically sampled cells and plotted the lengths of adjacent PADRENs of a type or wavelengths as ordered pairs (Fig. 1G–I). Showing that adjacent PADREN lengths and wavelengths tend to be similar, points cluster near the line Lengthi+1 = Lengthi. The average wavelength was 22.64 ± 0.75 μm.
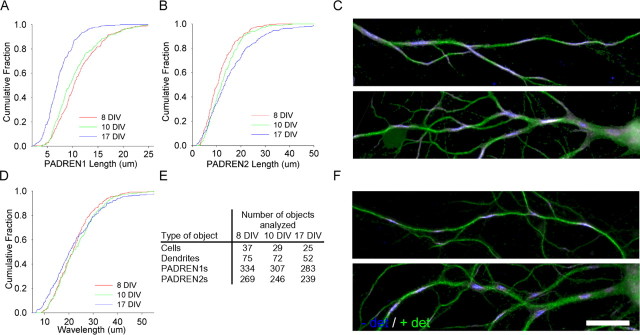
PADREN lengths change during development
Many neuronal properties, such as the extent of arborization (Bartlett and Banker, 1984b) and synapse composition (Lee and Sheng, 2000), develop over the first 2 weeks in culture. We wondered whether PADREN lengths also change during development. We examined PADREN lengths in 8, 10, and 17 d in vitro (DIV) cultures (Fig. 3A, B). Average PADREN1 lengths decreased ∼35% from 8 to 17 DIV, whereas average PADREN2 lengths increased ∼33%. Remarkably, the distribution of wavelengths was the same at each time point, suggesting that the distance between adjacent PADREN1s is conserved (Fig. 3D).
Figure 3.
PADREN lengths change during development. PADREN lengths change with cell age from 8 to 17 DIV (PADREN1 lengths, p < 1 × 10−10; PADREN2 lengths, p = 2.5 × 10−5; Kruskal–Wallis test). Cumulative distributions showing PADREN1 lengths decrease across development (A), whereas PADREN2 lengths increase (B) (PADREN1 lengths, 8 vs 10 DIV, p = 0.14; 10 vs 17 DIV, p = 5 × 10−9; PADREN2 lengths, 8 vs 10 DIV, p = 0.057; 10 vs 17 DIV, p = 0.001; Tukey’s honestly significant difference post hoc multiple comparisons test). D, Remarkably, wavelength is conserved (p = 0.24, Kruskal–Wallis test). E, The table shows the type (left column) and number (right columns) of objects analyzed at each time point to produce the data in A, B, and D. Cell density decreased 20% during this time interval (data not shown). Examples of PADRENs in 10 DIV (C) and 17 DIV (F) hippocampal neurons. Scale bar, 20 μm.
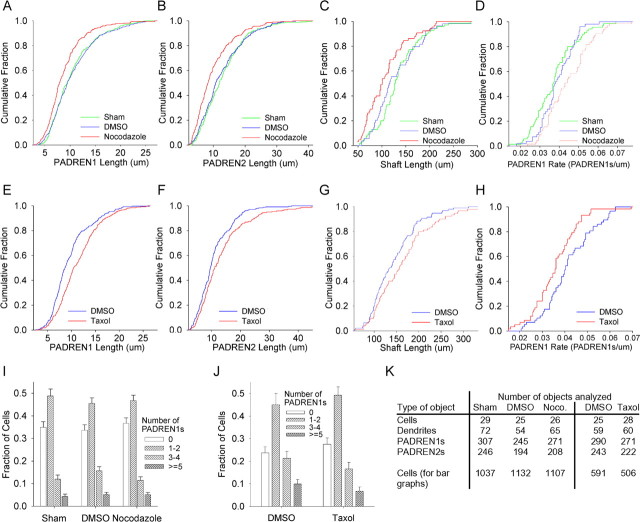
PADRENs scale with dendritic lengths
The experiments presented above suggest that PADRENs are an integral component of dendrites. To further test this idea, we treated cultures with drugs that acutely scale dendritic shaft lengths, and we then asked whether PADREN lengths scaled correspondingly. If shaft lengths and PADREN lengths scale correspondingly, the sum of the scaling factors for the PADREN length distributions, weighted by the fraction of dendrite each PADREN type occupies, should yield the scaling factor for the shaft length distribution. To decrease dendritic lengths, we applied the microtubule polymerization inhibitor nocodazole (15 μg/ml; 2 h) (De Brabander et al., 1976) (Fig. 4A–D). This treatment caused dendritic shaft lengths to scale down: multiplying each shaft length in the control condition by a constant scaling factor (factor of 0.80) resulted in a distribution that recapitulated the distribution of shaft lengths in the nocodazole-treated condition. To quantify the degree of recapitulation, we used a Mann–Whitney U test to compute the probability that the scaled-control shaft lengths and nocodazole-treated shaft lengths were samples from the same population and found that this probability was high (p = 0.73). Nocodazole also caused PADREN lengths to scale down (PADREN1 lengths, factor of 0.83, degree of recapitulation, p = 0.78; PADREN2 lengths, factor of 0.77, degree of recapitulation, p = 0.96). Finally, we asked whether the scaling of the PADRENs corresponded to the scaling of the dendrites. The sum of the scaling factors for the PADREN length distributions, weighted by the fraction of dendrite each PADREN type occupied, yielded the scaling factor for the shaft length distribution (e.g., 0.83 × 0.5 + 0.77 × 0.5 ≈ 0.80; each PADREN type occupied ∼50% of the dendrite). Thus, PADREN lengths and shaft lengths scaled correspondingly.
Figure 4.
PADRENs scale with dendritic lengths. Shaft lengths and PADREN lengths scale correspondingly in 10 DIV hippocampal neurons. Cumulative distributions showing that nocodazole (15 μg/ml, 2 h) causes PADREN1 lengths (A), PADREN2 lengths (B), and dendritic shaft lengths (C) to significantly scale down (nocodazole vs DMSO, PADREN1 lengths, p = 2.9 × 10−6; PADREN2 lengths, p = 1.4 × 10−5; shaft lengths, p = 0.012). There is no evidence that the number of PADRENs per branch changed, because the PADREN1 rate (number of PADREN1s per length of shaft) increased (p = 0.011), as expected if shafts became shorter but contained the same number of PADRENs (D). Conversely, in the presence of taxol (500 nm, 4 h), PADREN1 lengths (E), PADREN2 lengths (F), and dendritic shaft lengths (G) significantly scale up [taxol vs DMSO, PADREN1 lengths, p = 5.6 × 10−7; PADREN2 lengths, p = 0.002; shaft lengths, p = 0.037 (an additional 35 DMSO-treated shaft lengths and 30 taxol-treated shaft lengths from a separate experiment were added to achieve a p < 0.05 increase in shaft length)]. Again, there is no evidence that the number of PADRENs changed, because the PADREN1 rate decreased significantly (p = 0.006), as expected if the number of PADRENs remained constant as the lengths of the shafts increased (H). I, J, Neither treatment changed the fraction of cells with at least one dendrite containing different numbers of PADREN1s or changed cell density (data not shown). Graph bars represent average fraction of cells per 40× field in each “Number of PADREN1s” category; error bars represent SEM. K, A table showing the type (left column) and number of objects analyzed (right columns) under each condition to produce the data shown in A–J.
In the converse experiment, we lengthened dendritic shafts by applying the microtubule depolymerization inhibitor taxol (500 nm, 4 h). Under these conditions, we observed scaling in the opposite direction (Fig. 4E–H). Dendritic lengths scaled up (factor of 1.14; degree of recapitulation, p = 0.78), as did PADREN lengths (PADREN1 lengths, factor of 1.19, degree of recapitulation, p = 0.89; PADREN2 lengths, factor of 1.16, degree of recapitulation, p = 0.75), and they scaled correspondingly (e.g., 1.19 × 0.5 + 1.16 × 0.5 ≈ 1.14). Together, these data indicate that PADREN lengths scale bidirectionally and in correspondence with the scaling of dendritic shafts, further suggesting that PADRENs are an integral dendritic component.
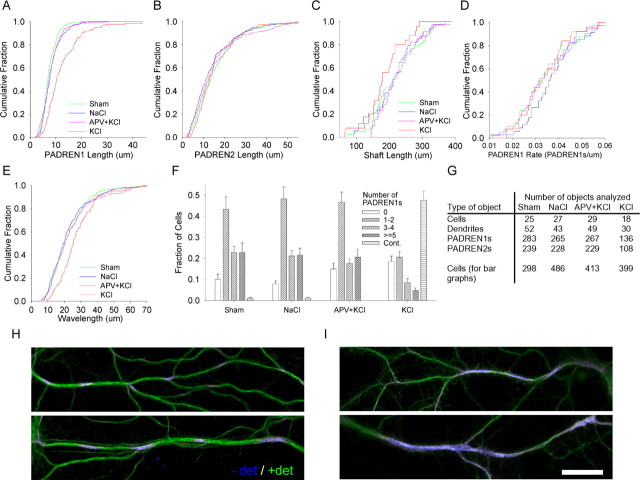
PADREN1 lengths are modified by neural activity
Extrinsically induced synaptic activity can sculpt dendritic arbors and change neuronal physiology. To test whether an acute depolarization would affect PADRENs, we applied KCl (20 mm, 15 min) to depolarize the plasma membrane. KCl treatment caused the average length of PADREN1s to increase by ∼70% over the control value (Fig. 5A; I, top). KCl treatment also caused long stretches (>50 μm) of immunostaining to develop, which we characterized using a new, “continuous” staining category (Fig. 5I, bottom). The degree of lengthening and continuity is consistent with the diffusion of a plasma membrane protein during KCl treatment (e.g., D ∼0.003–0.005 μm2/s; lower estimates) (for calculations, see supplemental material, available at www.jneurosci.org). The effects of KCl were completely blocked with the NMDA receptor antagonist APV (150 μm, 1 h pretreatment) and greatly reduced in the absence of extracellular calcium (data not shown). The effects were not blocked by the AMPA receptor antagonist CNQX (100 μm, 2 h pretreatment; data not shown). [In a single experiment, 2 μm TTX and 5 μm nimodipine (1 h pretreatment) did not block the effect of 40 mm KCl (15 min).] A mixture of APV and CNQX (200 and 100 μm, respectively) alone did not affect PADREN lengths (2 h treatment; two experiments; data not shown). Finally, glutamate (5–10 μm, 5–15 min) also caused PADREN1s to lengthen and the cells to acquire continuous immunostaining (16 DIV cultures; data not shown). These effects were completely blocked with APV (150 μm, 1 h pretreatment) but not by CNQX (100 μm, 2 h pretreatment; data not shown). Together, these results indicate that calcium influx through NMDA receptors is likely to modify PADRENs without affecting dendrite lengths.
Figure 5.
PADREN1 lengths are modified by activity. A, A cumulative distribution showing that applying KCl (20 mm, 15 min) increases the length of PADREN1s compared with cultures treated with APV (100 μm, 1 h pretreatment) and then KCl (p < 1 × 10−10). The block with APV was complete because the APV plus KCl group was similar to the NaCl control (p = 0.8). We did not detect a change in PADREN2 length (B), and measured wavelength increased (E) (p = 3.25 × 10−4). Shaft lengths (C) were unaffected (KCl vs NaCl; p = 0.11), as were segmentation rates (D). F, A bar graph showing that KCl also changes the fraction of cells containing different numbers of PADREN1s or having continuous immunostaining. The graph bars represent average fraction of cells per 40× field in each category; error bars represent SEM. G, A table showing the type (left column) and number (right columns) of objects analyzed under each condition to produce the data shown in A–F. Examples of PADRENs in control (H) and KCl-treated (I) dendrites show that PADREN1s lengthen (I, top) and become continuous (I, bottom) in response to KCl. Scale bar, 20 μm.
Because dendrites that exhibit continuous immunostaining after KCl are not patterned, it was not clear whether the continuous immunostaining represented the fusion of PADREN1s or a mechanistically distinct permeability. Suggesting the former, the increase in the fraction of cells exhibiting continuous immunostaining after KCl treatment can be explained by the decrease in the fraction of cells exhibiting some number of PADREN1s (Fig. 5F) (e.g., compare the fractions of patterned and continuous cells in the APV plus KCl group with the fractions of patterned and continuous cells in the KCl group).
Dendritic branch points preferentially associate with PADREN1s
We noticed that dendritic branch points preferentially associated with PADREN1 stripes (Fig. 6D, E). To quantify the degree of association between branch points and PADREN1s, we modeled the number of associations expected by chance within each cell as a binomial experiment, in which the probability of association is equal to the fraction of shaft length PADREN1s occupy. We then compared the number of associations expected by chance with the observed number of associations (for details, see Materials and Methods). At 8 DIV, ∼1.5 times more branches associated with PADREN1s than expected by chance (p = 1.8 × 10−6) (Fig. 6A, B). The slight decrease in the degree of association with cell age is likely attributable to branches near PADREN1 edges becoming associated with PADREN2s as PADREN1s shorten (supplemental material, available at www.jneurosci.org) and the period of branch addition passes. Importantly, PADREN1s are not a side effect of branching, because they are present in shafts with no branches, many PADREN1s do not contain branches, and some branch points originate from PADREN2s.
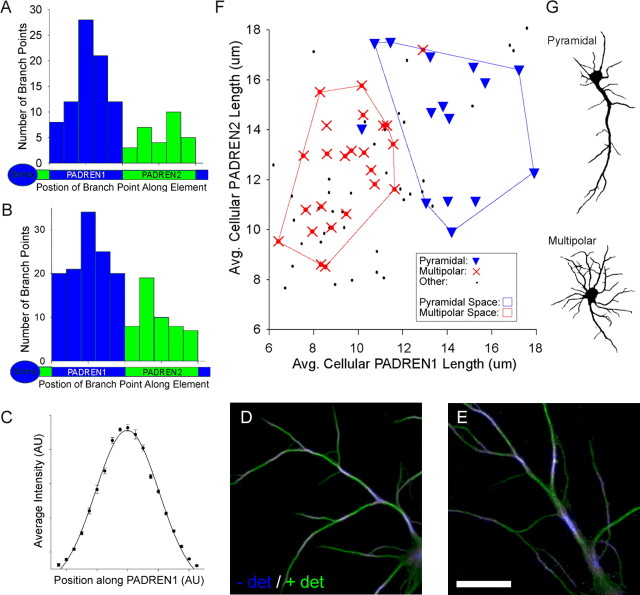
Figure 6.
Dendritic branch points preferentially associate with PADREN1s, and multipolar and pyramidal cells have distinct PADREN lengths. A, B, Frequency histograms showing the relative position of branch points along PADREN1s (blue) and PADREN2s (green) at 8 DIV (A) and 10 DIV (B). Relative position was computed as the distance from the proximal PADREN edge to the branch point divided by the length of the PADREN containing the branch point. “Soma” icons confer proximal–distal orientation to shaft icons. Branch points significantly associate with PADREN1s (p = 1.80 × 10−6, 8 DIV; p = 4.07 × 10−6, 10 DIV; custom test; for details, see Materials and Methods). Branch positions form a bell-shaped distribution along PADREN1s, which mirrors a Gaussian distribution of immunostaining intensity along PADREN1s (C). Points represent average immunostaining as a function of relative position after standardization and normalization from six randomly selected PADREN1s that did not contain branch points. D, E, Examples of the association between PADREN1s and branch points in 10 DIV neurons. Scale bar, 20 μm. F, Scatter plot of average cellular PADREN2 length versus average cellular PADREN1 length for each of 78 10 DIV cells. Point style indicates arbor type classification (pyramidal, multipolar, or other plotted as triangles, crosses, and dots, respectively). The shafts of pyramidal cells were approximately twice as long as the shafts of multipolar cells (pyramidal, 202 ± 14 μm; multipolar, 110 ± 4 μm; p = 1.75 × 10−8, t test). Showing PADREN dimensions and arbor types correspond, convex polygons enclosing pyramidal or multipolar cells delineate distinct PADREN dimension spaces. Both PADREN1s (p < 1 × 10−10) and PADREN2s (p = 0.006) are longer in pyramidal cells than multipolar cells. The chance of uniformly distributed pyramidal and multipolar cell types falling into the PADREN space areas they occupy is p ≪ 0.005 in both cases (χ2 test, df = 1). Additionally, average PADREN1 lengths and average PADREN2 lengths are correlated (β1 = 0.50; p(β1 = 0) = 2 × 10−6; simple linear regression; line not shown). G, Examples of arbor morphologies classified as pyramidal and multipolar. − det, Before the addition of detergent; + det, after the addition of detergent; AU, arbitrary units.
There is likely additional organization within PADREN1s, because the distribution of intensity of immunostaining along PADREN1s mirrors and aligns with the frequency distribution of branch points. The frequency distribution of branch points along PADREN1s is bell shaped, with the center of the distribution (e.g., place of highest branch frequency) corresponding to the center of PADREN1s (Fig. 6A, B). The distribution of intensity of immunostaining along PADREN1s is also bell shaped and greatest at PADREN1 centers (Fig. 6C). The shape of the intensity profile is not influenced by branching, because it is the same whether or not a given PADREN1 contains a branch point. The alignment between place of most frequent branch origin and position of greatest intensity of immunostaining suggests that branching may be sensitive to a PADREN1 property. Together, these data suggest that the arrangement of PADREN1s could influence the arrangement of dendritic branches.
Multipolar and pyramidal cells have distinct PADREN lengths
Hippocampal neurons grown in dissociated culture exhibit a number of arbor types that correlate with functional characteristics (Benson et al., 1994) and recapitulate arbor morphologies found in vivo (Banker and Cowan, 1979). Because dendritic branching patterns are a defining characteristic of morphological neuronal classification (Peters and Jones, 1984), we reasoned that PADREN dimensions and morphologically defined arbor types may correspond. From a population of 78 cells, at 10 DIV, we calculated the average PADREN1 length and average PADREN2 length for each cell and plotted the ordered pair as a point representing the cell (Fig. 6F). Next, we classified the cells (blind to the PADRENs) as “pyramidal” if they had a single predominant dendrite with smaller dendrites on the opposite side of the soma (20% of population), “multipolar” if they had at least four main shafts of approximately equal length evenly spaced around the soma (30% of population), or “other” if they met neither definition (Fig. 6G). We then labeled each point representing the PADREN lengths of a cell with the arbor classification of that cell. This analysis showed that pyramidal cells were characterized by having longer PADRENs, whereas multipolar cells exhibited shorter PADRENs (Fig. 6F). Strikingly, pyramidal cells and multipolar cells fell into distinct, essentially nonoverlapping “PADREN spaces” (Fig. 6F, outlined regions). These data suggest that specific PADREN lengths correspond to specific arbor types.
Evidence that PADRENs develop autonomously
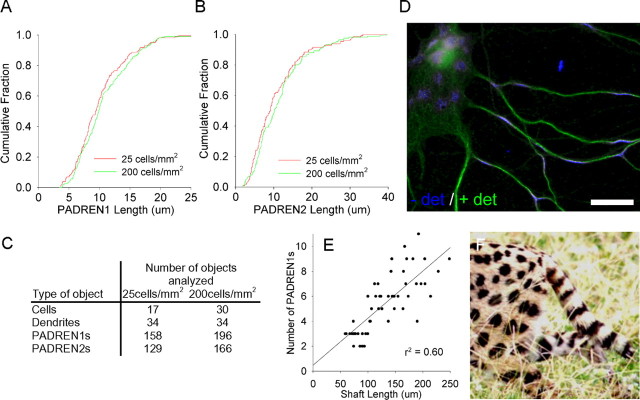
Cell-type-specific arbor patterns develop autonomously (Bartlett and Banker, 1984a). If PADRENs organize arbors, PADRENs must also be autonomously organized during development. To examine the influence of cell–cell interactions on PADRENs, we varied the number of such interactions by plating neurons over an eightfold range of densities. The lengths of PADRENs were then measured at 10 DIV. The lengths of the PADRENs were identical regardless of plating density (Fig. 7A, B). Additionally, in low-density (30 cells/mm2) 8 DIV cultures, in which neurites were sparse, we observed many cases of dendritic shafts that contained PADRENs but were not contacted by the neurites of another cell. Finally, a mixture of 1 μm TTX and 150 μm APV did not affect PADREN lengths (17 DIV cultures; 4 h treatment; two experiments; data not shown). Together, these data suggest that PADRENs develop autonomously.
Figure 7.
PADRENs develop autonomously and could be organized by a reaction-diffusion process. Cumulative distributions showing that changing the plating density eightfold across different wells of the same plate does not effect the length of PADREN1s (A) (p = 0.17) or PADREN2s (B) (p = 0.17) at 10 DIV. C, The table shows the type and number of objects analyzed under each condition. D, A 17 DIV hippocampal neuron with a particularly flat cell body illustrates the geometry-dependent transition of PADRENs from stripes in the narrow cylindrical dendrites to spots in the locally planar cell body. Scale bar, 20 μm. Such a transition is also observed in the coat markings of many animals, including the serval (F), and is consistent with a reaction-diffusion processes (serval photograph courtesy of Dr. Shonali Laha, Florida International University, Miami, FL). E, Further consistent with a reaction-diffusion process, a scatter plot showing a linear correlation between shaft length and the number of PADREN1s per shaft in 10 DIV hippocampal neurons.
A reaction-diffusion process could organize PADRENs
Because PADRENs are an intrinsically organized spacing pattern that may play a role in organizing dendritic branches, we wondered how PADRENs themselves may be organized. Many models have been proposed to explain the formation of biological spacing patterns (Held, 1992). A self-organizing feedback process between a short-range activator and long-range inhibitor can produce stripes and spots. This process can be formally described by coupled reaction-diffusion equations, so it is termed a reaction-diffusion process (Turing, 1951). To see whether such a process can quantitatively account for PADREN characteristics, we solved two coupled linear one-dimensional reaction-diffusion equations. Remarkably, a reaction-diffusion process can explain all of the characteristics of PADRENs that we have identified. First, diffusion constants comparable with those of membrane and cytosolic proteins are sufficient to produce the pattern wavelength that we observe (e.g., DAct = 0.01 μm2/s; DInh = 0.5 μm2/s produces a wavelength of ≥15 μm) (for details, see supplemental material, available at www.jneurosci.org). Second, the equations predict a linear correlation (Murray, 1981) between the number of wavelengths and field length (here, number of PADREN1s and shaft length, respectively), which we observe (Fig. 7E). Third, whether stripes or spots form depends on the geometry of the field. Spots form unless the circumference of the field is similar to the pattern wavelength, in which case, circumferential stripes form instead (Bard, 1981). We observe PADREN1 spots in the (large circumference) cell body and stripes in the dendrites, which have a circumference (∼5–10 μm) less than the wavelength (∼20 μm on average) of the pattern (Fig. 7D). A similar geometry-dependent transition from stripes to spots is observed in the coat markings of some animals (Fig. 7F). Together, these data suggest that a self-organizing reaction-diffusion process could organize PADRENs.
Discussion
Dendritic arbor organization is a critical aspect of neuronal circuitry. However, no hypothesis exists to explain how branch positions may be organized. Here, we suggest that a spacing pattern of local factors organized by a reaction-diffusion process could guide branch patterning. We observe that dendrites contain periodic and regular elements that are arranged into a spacing pattern. One of these elements, PADREN1s, delineate regions of increased branching. Moreover, specific PADREN dimensions correspond to specific arbor types. These data suggest that PADRENs could guide branch organization, a defining characteristic of distinct arbor morphologies.
Several lines of evidence suggest that PADRENs reveal an intrinsic patterned organization along dendritic shafts. First, PADRENs are readily observed in all neuronal types that we have examined. Second, PADREN1s preferentially contain dendritic branch points. Third, specific PADREN lengths correspond to specific arbor morphologies, and average cellular PADREN1 and PADREN2 lengths are correlated. Fourth, PADREN1 lengths decrease across development, whereas PADREN2 lengths increase but wavelength is conserved. Fifth, PADREN lengths scale in correspondence with pharmacologically induced increases or decreases in dendritic shaft lengths. Sixth, brief depolarization causes PADREN1 lengths to increase, and the increase is blocked by APV but not CNQX, whereas APV plus CNQX alone has no effect. Seventh, many characteristics of PADRENs can be explained by a reaction-diffusion process given the diffusion constants of biomolecules in a cellular environment. In total, these data strongly suggest that PADRENs reflect a level of intrinsic patterned organization along dendritic shafts rather than a physiologically irrelevant, nonbiological process.
PADRENs likely represent the organization of local factors along dendritic shafts. First, PADRENs are arranged into a spacing pattern, a ubiquitous form of intrinsic organization of local factors in biological systems. Examples include stripes of zebrin expression in the developing cerebellum (Herrup and Kuemerle, 1997), transcription factor expression in the developing midbrain (Agarwala et al., 2001), Shh and Bmp expression in the feather bud (Harris et al., 2005), and Hox gene expression in the developing hindbrain (Kiecker and Lumsden, 2005). Although these patterns organize a field of cells on a scale larger than PADRENs, during Drosophila development, pair-rule genes are patterned during the syncytial blastoderm stage [i.e., before cellular boundaries are present (Carroll and Scott, 1985)], and segment polarity gene patterns have a wavelength of ∼25 μm (Hafen et al., 1984), which is similar to the ∼20 μm wavelength of PADRENs. Interestingly, in the brains of Alzheimer’s patients, dendritic paired-helical filaments are organized into periodically alternating, 5- to 25-μm-long regions (PADREN1s are 5–25 μm long) that occur at “semiregular intervals along the dendrite [and] frequently at branch points” (Ashford et al., 1998). The analogy between PADRENs and spacing patterns in other systems supports the possibility that PADRENs reflect the organization of local factors along dendritic shafts.
Correlative evidence and further analogy with the function of other biological spacing patterns suggest that the function of PADRENs may be to position dendritic branches into cell-type-specific branching patterns. Our data show that branch points preferentially originate from the center of PADREN1s, mirror the distribution of immunoreactivity along PADREN1s, and that PADREN lengths correspond to specific arbor morphologies. [The branches that originate from PADREN2s may be the result of non-interstitial branching (Bray, 1973).] Further supporting a branch spacing function, PADREN wavelength is conserved across development, dendritic branching has been observed to be most frequent at specific dendritic locations (Wu et al., 1999), and developing biological systems often use spacing patterns of local factors to guide the formation of segmental morphologies (see the examples above). Notably, in plants, the concentration of the leaf-and-branch-growth-promoting hormone auxin is arranged into a spacing pattern. Thus, the distance between adjacent auxin concentration peaks determines the distance between adjacent branches, and this distance defines segmental units along the stem termed phytomers (Reinhardt et al., 2003; McSteen and Leyser, 2005). Analogously, PADREN1s are arranged into a spacing pattern, so the distance between adjacent PADREN1s (wavelength) may determine the distance between adjacent branches and thus define a “dendromer.” Such a similarity in patterning process may explain the strikingly similar arbor morphologies of plants and dendrites.
We are left to speculate about the components of PADRENs. These constituents may include endoplasmic reticulum (Nakamura et al., 2002; Bannai et al., 2004), ribosomes (Bartlett and Banker, 1984a; Tiedge and Brosius, 1996), RNA (Knowles et al., 1996; Rook et al., 2000), vesicles (Bartlett and Banker, 1984a), or mitochondria (Bartlett and Banker, 1984a), which are all known to be nonuniformly distributed along dendrites and associate with branch points. A spacing pattern of protein synthesis and trafficking machinery would be an attractive step before the elaboration of cell-type-specific dendritic branching patterns.
Footnotes
This work was supported by National Institutes of Health (NIH) Grants NS39321 and RR15578 (J.R.F.). A.B.T. was supported in part by NIH Predoctoral Training Grant T32MH20068. Initial observations were made in the laboratory of M. F. Bear (Department of Brain and Cognitive Sciences, Massachusetts Institute of Technology, Cambridge, MA). We thank S. Venkataramani and J. Zhang for assistance, and B. W. Connors, A. Dunaevsky, and M.R. Mehta for helpful discussion and comments on this manuscript.
References
- Agarwala S, Sanders TA, Ragsdale CW (2001). Sonic hedgehog control of size and shape in midbrain pattern formation. Science 291:2147–2150. [DOI] [PubMed] [Google Scholar]
- Agmon-Snir H, Carr CE, Rinzel J (1998). The role of dendrites in auditory coincidence detection. Nature 393:268–272. [DOI] [PubMed] [Google Scholar]
- Aizawa H, Hu SC, Bobb K, Balakrishnan K, Ince G, Gurevich I, Cowan M, Ghosh A (2004). Dendrite development regulated by CREST, a calcium-regulated transcriptional activator. Science 303:197–202. [DOI] [PubMed] [Google Scholar]
- Akum BF, Chen M, Gunderson SI, Riefler GM, Scerri-Hansen MM, Firestein BL (2004). Cypin regulates dendrite patterning in hippocampal neurons by promoting microtubule assembly. Nat Neurosci 7:145–152. [DOI] [PubMed] [Google Scholar]
- Ashford JW, Soultanian NS, Zhang SX, Geddes JW (1998). Neuropil threads are collinear with MAP2 immunostaining in neuronal dendrites of Alzheimer brain. J Neuropathol Exp Neurol 57:972–978. [DOI] [PubMed] [Google Scholar]
- Banker GA, Cowan WM (1979). Further observations on hippocampal neurons in dispersed cell culture. J Comp Neurol 187:469–493. [DOI] [PubMed] [Google Scholar]
- Bannai H, Inoue T, Nakayama T, Hattori M, Mikoshiba K (2004). Kinesin dependent, rapid, bi-directional transport of ER sub-compartment in dendrites of hippocampal neurons. J Cell Sci 117:163–175. [DOI] [PubMed] [Google Scholar]
- Bard JB (1981). A model for generating aspects of zebra and other mammalian coat patterns. J Theor Biol 93:363–385. [DOI] [PubMed] [Google Scholar]
- Bartlett WP, Banker GA (1984a). An electron microscopic study of the development of axons and dendrites by hippocampal neurons in culture. I. Cells which develop without intercellular contacts. J Neurosci 4:1944–1953. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bartlett WP, Banker GA (1984b). An electron microscopic study of the development of axons and dendrites by hippocampal neurons in culture. II. Synaptic relationships. J Neurosci 4:1954–1965. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benson DL, Watkins FH, Steward O, Banker G (1994). Characterization of GABAergic neurons in hippocampal cell cultures. J Neurocytol 23:279–295. [DOI] [PubMed] [Google Scholar]
- Blaser PF, Catsicas S, Clarke PG (1990). Retrograde modulation of dendritic geometry in the vertebrate brain during development. Brain Res Dev Brain Res 57:139–142. [DOI] [PubMed] [Google Scholar]
- Bray D (1973). Branching patterns of individual sympathetic neurons in culture. J Cell Biol 56:702–712. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brewer GJ, Torricelli JR, Evege EK, Price PJ (1993). Optimized survival of hippocampal neurons in B27-supplemented Neurobasal, a new serum-free medium combination. J Neurosci Res 35:567–576. [DOI] [PubMed] [Google Scholar]
- Carroll SB, Scott MP (1985). Localization of the fushi tarazu protein during Drosophila embryogenesis. Cell 43:47–57. [DOI] [PubMed] [Google Scholar]
- Danzer SC, McMullen NT, Rance NE (2001). Testosterone modulates the dendritic architecture of arcuate neuroendocrine neurons in adult male rats. Brain Res 890:78–85. [DOI] [PubMed] [Google Scholar]
- De Brabander MJ, Van de Veire RM, Aerts FE, Borgers M, Janssen PA (1976). The effects of methyl (5-(2-thienylcarbonyl)-1H-benzimidazol-2-yl) carbamate, (R 17934; NSC 238159), a new synthetic antitumoral drug interfering with microtubules, on mammalian cells cultured in vitro. Cancer Res 36:905–916. [PubMed] [Google Scholar]
- Gaudilliere B, Konishi Y, de la Iglesia N, Yao G, Bonni A (2004). A CaMKII-NeuroD signaling pathway specifies dendritic morphogenesis. Neuron 41:229–241. [DOI] [PubMed] [Google Scholar]
- Greenough WT, Chang FL (1988). Dendritic pattern formation involves both oriented regression and oriented growth in the barrels of mouse somatosensory cortex. Brain Res 471:148–152. [DOI] [PubMed] [Google Scholar]
- Grueber WB, Jan LY, Jan YN (2003). Different levels of the homeodomain protein cut regulate distinct dendrite branching patterns of Drosophila multidendritic neurons. Cell 112:805–818. [DOI] [PubMed] [Google Scholar]
- Hafen E, Kuroiwa A, Gehring WJ (1984). Spatial distribution of transcripts from the segmentation gene fushi tarazu during Drosophila embryonic development. Cell 37:833–841. [DOI] [PubMed] [Google Scholar]
- Harris MP, Williamson S, Fallon JF, Meinhardt H, Prum RO (2005). From the cover: molecular evidence for an activator-inhibitor mechanism in development of embryonic feather branching. Proc Natl Acad Sci USA 102:11734–11739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Held L (1992). In: Models for embryonic periodicity New York: Karger. [PubMed]
- Herrup K, Kuemerle B (1997). The compartmentalization of the cerebellum. Annu Rev Neurosci 20:61–90. [DOI] [PubMed] [Google Scholar]
- Horch HW, Katz LC (2002). BDNF release from single cells elicits local dendritic growth in nearby neurons. Nat Neurosci 5:1177–1184. [DOI] [PubMed] [Google Scholar]
- Kiecker C, Lumsden A (2005). Compartments and their boundaries in vertebrate brain development. Nat Rev Neurosci 6:553–564. [DOI] [PubMed] [Google Scholar]
- Knowles RB, Sabry JH, Martone ME, Deerinck TJ, Ellisman MH, Bassell GJ, Kosik KS (1996). Translocation of RNA granules in living neurons. J Neurosci 16:7812–7820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kossel A, Lowel S, Bolz J (1995). Relationships between dendritic fields and functional architecture in striate cortex of normal and visually deprived cats. J Neurosci 15:3913–3926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kossel AH, Williams CV, Schweizer M, Kater SB (1997). Afferent innervation influences the development of dendritic branches and spines via both activity-dependent and non-activity-dependent mechanisms. J Neurosci 17:6314–6324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee SH, Sheng M (2000). Development of neuron-neuron synapses. Curr Opin Neurobiol 10:125–131. [DOI] [PubMed] [Google Scholar]
- Li W, Wang F, Menut L, Gao FB (2004). BTB/POZ-zinc finger protein abrupt suppresses dendritic branching in a neuronal subtype-specific and dosage-dependent manner. Neuron 43:823–834. [DOI] [PubMed] [Google Scholar]
- Lohmann C, Myhr KL, Wong RO (2002). Transmitter-evoked local calcium release stabilizes developing dendrites. Nature 418:177–181. [DOI] [PubMed] [Google Scholar]
- Lu R, Wang H, Liang Z, Ku L, O’Donnell WT, Li W, Warren ST, Feng Y (2004). The fragile X protein controls microtubule-associated protein 1B translation and microtubule stability in brain neuron development. Proc Natl Acad Sci USA 101:15201–15206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mainen ZF, Sejnowski TJ (1996). Influence of dendritic structure on firing pattern in model neocortical neurons. Nature 382:363–366. [DOI] [PubMed] [Google Scholar]
- Malacinski G (1984). In: Pattern formation New York: Macmillan.
- Maletic-Savatic M, Malinow R, Svoboda K (1999). Rapid dendritic morphogenesis in CA1 hippocampal dendrites induced by synaptic activity. Science 283:1923–1927. [DOI] [PubMed] [Google Scholar]
- McSteen P, Leyser O (2005). Shoot branching. Annu Rev Plant Biol 56:353–374. [DOI] [PubMed] [Google Scholar]
- Morrison ME, Mason CA (1998). Granule neuron regulation of Purkinje cell development: striking a balance between neurotrophin and glutamate signaling. J Neurosci 18:3563–3573. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murray J (1981). A pre-pattern formation mechanism for animal coat markings. J Theor Biol 88:161–199. [Google Scholar]
- Murthy M, Garza D, Scheller RH, Schwarz TL (2003). Mutations in the exocyst component Sec5 disrupt neuronal membrane traffic, but neurotransmitter release persists. Neuron 37:433–447. [DOI] [PubMed] [Google Scholar]
- Nakamura T, Lasser-Ross N, Nakamura K, Ross WN (2002). Spatial segregation and interaction of calcium signalling mechanisms in rathippocampal CA1 pyramidal neurons. J Physiol (Lond) 543:465–480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nakayama AY, Harms MB, Luo L (2000). Small GTPases Rac and Rho in the maintenance of dendritic spines and branches in hippocampal pyramidal neurons. J Neurosci 20:5329–5338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Niblock MM, Brunso-Bechtold JK, Riddle DR (2000). Insulin-like growth factor I stimulates dendritic growth in primary somatosensory cortex. J Neurosci 20:4165–4176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pan L, Zhang YQ, Woodruff E, Broadie K (2004). The Drosophila fragile X gene negatively regulates neuronal elaboration and synaptic differentiation. Curr Biol 14:1863–1870. [DOI] [PubMed] [Google Scholar]
- Peters A, Jones E (1984). In: Cellular components of the cerebral cortex New York: Plenum.
- Polsky A, Mel BW, Schiller J (2004). Computational subunits in thin dendrites of pyramidal cells. Nat Neurosci 7:621–627. [DOI] [PubMed] [Google Scholar]
- Redmond L, Oh SR, Hicks C, Weinmaster G, Ghosh A (2000). Nuclear Notch1 signaling and the regulation of dendritic development. Nat Neurosci 3:30–40. [DOI] [PubMed] [Google Scholar]
- Reinhardt D, Pesce ER, Stieger P, Mandel T, Baltensperger K, Bennett M, Traas J, Friml J, Kuhlemeier C (2003). Regulation of phyllotaxis by polar auxin transport. Nature 426:255–260. [DOI] [PubMed] [Google Scholar]
- Rockwell PL, Storey BT (1999). Determination of the intracellular dissociation constant, K(D), of the fluo-3. Ca2+ complex in mouse sperm for use in estimating intracellular Ca2+ concentrations. Mol Reprod Dev 54:418–428. [DOI] [PubMed] [Google Scholar]
- Rook MS, Lu M, Kosik KS (2000). CaMKIIalpha 3′ untranslated region-directed mRNA translocation in living neurons: visualization by GFP linkage. J Neurosci 20:6385–6393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosso SB, Sussman D, Wynshaw-Boris A, Salinas PC (2005). Wnt signaling through Dishevelled, Rac and JNK regulates dendritic development. Nat Neurosci 8:34–42. [DOI] [PubMed] [Google Scholar]
- Schaefer AT, Larkum ME, Sakmann B, Roth A (2003). Coincidence detection in pyramidal neurons is tuned by their dendritic branching pattern. J Neurophysiol 89:3143–3154. [DOI] [PubMed] [Google Scholar]
- Shi SH, Jan LY, Jan YN (2003). Hippocampal neuronal polarity specified by spatially localized mPar3/mPar6 and PI 3-kinase activity. Cell 112:63–75. [DOI] [PubMed] [Google Scholar]
- Sin WC, Haas K, Ruthazer ES, Cline HT (2002). Dendrite growth increased by visual activity requires NMDA receptor and Rho GTPases. Nature 419:475–480. [DOI] [PubMed] [Google Scholar]
- Single S, Borst A (1998). Dendritic integration and its role in computing image velocity. Science 281:1848–1850. [DOI] [PubMed] [Google Scholar]
- Threadgill R, Bobb K, Ghosh A (1997). Regulation of dendritic growth and remodeling by Rho, Rac, and Cdc42. Neuron 19:625–634. [DOI] [PubMed] [Google Scholar]
- Tiedge H, Brosius J (1996). Translational machinery in dendrites of hippocampal neurons in culture. J Neurosci 16:7171–7181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turing A (1951). The chemical basis of morphogenesis. Philos Trans R Soc Lond B Biol Sci 237:37–72. [Google Scholar]
- Vaillant AR, Zanassi P, Walsh GS, Aumont A, Alonso A, Miller FD (2002). Signaling mechanisms underlying reversible, activity-dependent dendrite formation. Neuron 34:985–998. [DOI] [PubMed] [Google Scholar]
- Wu GY, Zou DJ, Rajan I, Cline H (1999). Dendritic dynamics in vivo change during neuronal maturation. J Neurosci 19:4472–4483. [DOI] [PMC free article] [PubMed] [Google Scholar]