Abstract
Mutations in SCN1A (encoding the neuronal voltage-gated sodium channel α1 subunit, NaV1.1, or SCN1A) are associated with genetic epilepsy syndromes including generalized epilepsy with febrile seizures plus (GEFS+) and severe myoclonic epilepsy of infancy. Here, we present the formulation and use of a computational model for SCN1A to elucidate molecular mechanisms underlying the increased persistent sodium current exhibited by the GEFS+ mutant R1648H. Our model accurately reproduces all experimentally measured SCN1A whole-cell biophysical properties including biphasic whole-cell current decay, channel activation, and entry into and recovery from fast and slow inactivation. The model predicts that SCN1A open-state inactivation results from a two-step process that can be conceptualized as initial gate closure, followed by recruitment of a mechanism (“latch”) to stabilize the inactivated state. Selective impairment of the second latching step results in an increase in whole-cell persistent current similar to that observed for the GEFS+ mutant R1648H. These results provide a deeper level of understanding of mutant SCN1A dysfunction in an inherited epilepsy syndrome, which will enable more precise computational studies of abnormal neuronal activity in epilepsy and may help guide new targeted therapeutic strategies.
Keywords: sodium channel, GEFS+, Markov model, SCN1A, epilepsy, computational neuroscience
Introduction
Mutations in genes encoding voltage-gated sodium channel subunits have been linked to several inherited disorders of membrane excitability including defects in skeletal muscle contraction, cardiac arrhythmias, and epilepsies (George, 2005). Currently, >150 SCN1A mutations have been associated with various genetic epilepsies (Mulley et al., 2005). Functional studies of these SCN1A mutants in heterologous systems have revealed an array of biophysical abnormalities that are difficult to fully reconcile with the observed clinical phenotype. In vivo SCN1A generates and propagates action potentials within an integrative environment consisting of multiple ionic conductances. Thus, establishing correlations between genotypes and biophysical phenotypes will likely require examination of SCN1A mutant behavior within such a context using either animal or computational models.
The majority of efforts to simulate sodium channel behavior using computational models [including SCN1A (Spampanato et al., 2004a,b; Barela et al., 2006)] have used the classic Hodgkin–Huxley (HH) formalism (Hodgkin and Huxley, 1952). These equations define sodium permeability in terms of multiple identical gates operating independently. However, this approach is unable to account for all channel behaviors (Hille, 2001). For instance, although sodium channels are constructed of four homologous domains (DI–DIV), each domain does not contribute identically to channel gating (Hille, 2001). In addition, inactivation and activation are coupled because channel inactivation preferentially immobilizes the DIII- and DIV-associated activation gating movements (Cha et al., 1999; Kuhn and Greeff, 1999). Additional discrepancies between HH-predicted and experimentally observed sodium channel behavior have also been described including gating currents, current fluctuation analysis, single-channel activity, and activation kinetics (Patlak, 1991; Hille, 2001; Baranauskas and Martina, 2006; Naundorf et al., 2006).
Attempts to reconcile the experimental voltage-gated sodium channel behavior to a mathematical description of channel activity have produced numerous thermodynamic and empirical models (for review, see Patlak, 1991; Hille, 2001). More recently, Markov chain models have been developed for excitability simulation studies that more faithfully approximate the biophysical activity of sodium channels (Vedantham and Cannon, 1998; Clancy and Rudy, 1999, 2002; Irvine et al., 1999; Clancy and Kass, 2004). Computational investigations with accurate sodium channel models promise to guide empirical experimentation and to predict novel mechanisms of abnormal excitability (Clancy et al., 2003).
In this study, we use an expanded Markov model for SCN1A to better define molecular mechanisms for an epilepsy-associated mutation. The model accurately reproduces all of the measured whole-cell biophysical characteristics of the human wild-type (WT) channel coexpressed with the human β1 and β2 accessory subunits and can be modified to simulate the behavior observed for the generalized epilepsy with febrile seizures plus (GEFS+) mutant R1648H. Moreover, both models provide theoretical insight into SCN1A gating. Our models predict that SCN1A open-state inactivation occurs by a biphasic mechanism that can be conceptualized by docking of the inactivation gate to the cytoplasmic face of the pore, followed immediately by gate stabilization (“latching”). Importantly, the increased persistent current exhibited by R1648H can be predicted by introducing a selective impairment of the latching mechanism, a previously unrecognized molecular mechanism for sodium channel dysfunction in epilepsy.
Materials and Methods
Electrophysiology.
All heterologously expressed WT-SCN1A and R1648H data used for the generation of the computational models has been reported previously by our laboratory (Lossin et al., 2002; Rhodes et al., 2004, 2005; Vanoye et al., 2006). Briefly, biophysical characterization of WT-SCN1A and R1648H was performed using human tsA201 cells (HEK293 cells stably expressing the SV40 large T antigen). Cells transiently coexpressed human WT-SCN1A or R1648H cDNA as well as the human β1 and β2 accessory subunits. Specific voltage-clamp protocols assessing channel activation, inactivation, and recovery from inactivation were used. Representations of all voltage protocols are included as figure insets, and all recordings were performed at room temperature. The average current recorded from multiple cells was used as a calibration standard to guide optimization of an accurate computational model response. SCN1A persistent current measurements were obtained by digital subtraction of currents recorded in the presence and absence of 10 μm tetrodotoxin (Sigma, St. Louis, MO). Heterologously expressed SCN1A data are presented as mean ± SEM (Lossin et al., 2002; Rhodes et al., 2004, 2005; Vanoye et al., 2006).
Computational modeling.
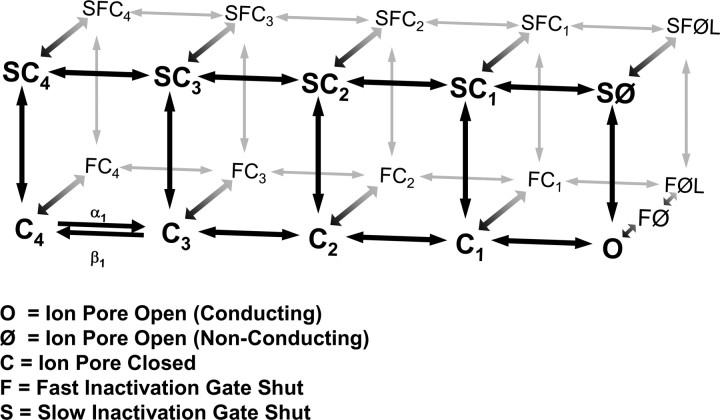
The computational model reported here for SCN1A is based on voltage-gated sodium channel modeling efforts by Clancy and Kass (2004), Clancy and Rudy (1999, 2002), and Horn and Vandenberg (Horn and Vandenberg, 1984; Vandenberg and Horn, 1984). Figure 1 illustrates the Markov model for SCN1A that includes states for the conditions: closed (C), open (O, conducting; Ø, non-conducting), fast inactivated (F), and slow inactivated (S). Transitions between states are reversible and described by continuous equations with an instantaneous solution that depends on the membrane voltage. In response to a voltage change, the channel distribution shifts to a new equilibrium over a time course determined by the new values of the rate constants. During SCN1A model optimization, the rate equations were constrained by the average whole-cell current recorded from heterologously expressed SCN1A.
Figure 1.
Diagram of SCN1A Markov model. The SCN1A Markov model consists of 21 states connected by 37 reversible transitions. The model includes states for the following conditions: closed (C), open (O), fast inactivated (F), and slow inactivated (S). The only ion-conducting state is O (Ø states are non-conducting because of inactivation gate closure). Supplemental Table S1 (available at www.jneurosci.org as supplemental material) includes a complete list of the voltage-dependent rate equations.
Voltage-gated ion channels do not exist at thermodynamic equilibrium at membrane voltages other than 0 mV (i.e., the imposed voltage gradient influences channel conformation) (Finkelstein and Peskin, 1984; Lauger, 1995; Colquhoun et al., 2004). Violations of the thermodynamic principle of detailed balance (microscopic reversibility) have been described previously for ion channels because of the influence of outside energies (ion electrochemical gradient or voltage gradient) on channel gating (Finkelstein and Peskin, 1984; Richard and Miller, 1990; Wyllie et al., 1996; Schneggenburger and Ascher, 1997). Thus, detailed balance was not imposed on the model for SCN1A for the following reasons: (1) nonthermodynamic equilibrium of SCN1A resulting from membrane voltage (Finkelstein and Peskin, 1984; Lauger, 1995; Colquhoun et al., 2004); (2) microscopic reversibility has not been demonstrated for SCN1A; (3) the absorbing nature of SCN1A inactivated states (low number of channel reopenings) limits the available information for assessing detailed balance (Vanoye et al., 2006); and (4) statistical tests for detailed balance lack sufficient power to test our complex and highly cyclic SCN1A model (Rothberg and Magleby, 2001; The et al., 2002). Rate equations for all transitions are reported in supplemental Table S1 (available at www.jneurosci.org as supplemental material).
The state O represents the conducting state, and the occupancy of O determines the sodium current by the following: INa = GNa_bar × O × (V − ENa), where INa is the sodium current, GNa_bar is the maximum sodium current density, O is the fractional occupancy of the open state, V is the membrane voltage, and ENa is the sodium reversal potential. For whole-cell simulations, the computational SCN1A model was expressed at a GNa_bar of 0.02 S/cm2. This corresponds to previously used sodium channel GNa_bar values between 0.01 and 0.2 S/cm2 (Clancy and Kass, 2004; Spampanato et al., 2004a,b; Barela et al., 2006). For single-channel simulations, a single model SCN1A channel was expressed with a conductance (GNa) of 17 pS. This value corresponds to the single-channel conductance previously reported for WT-SCN1A (17.2 ± 0.5 pS; n = 10) and R1648H (16.9 ± 0.9 pS; n = 7) (Vanoye et al., 2006). The average empirically calculated reversal potential observed for SCN1A was used for all simulations (ENa = 71.3 ± 1.5 mV; n = 14) (Rhodes et al., 2005).
Computational modeling was performed using NEURON (www.neuron.yale.edu) (Hines and Carnevale, 2001). All simulations were performed using the default integration strategy (Backward Euler) with an implicit fixed time step of 25 μs to maintain temporal accuracy and efficiency. Simulations were implemented on either a personal computer (PC) workstation using two parallel Intel Xeon dual-core 2.8 GHz processors or a PC desktop using an Intel Pentium 4, 3.0 GHz processor. All simulations were performed in Windows XP, and the simulation computer code is available on request.
For whole-cell simulations, we constructed an in silico single-compartment model of a tsA201 cell with a length of 20.0 μm, diameter of 12.1 μm, and membrane capacitance of 1 μf/cm2. The resulting computational surface area is equivalent to the average surface area measured for WT-SCN1A-expressing tsA201 cells (7.6 × 10−6 cm2; n = 15) (Rhodes et al., 2005). For single-channel simulations, we constructed an in silico single-compartment model of an outside-out membrane patch with a length of 0.5 μm, diameter of 0.5 μm, and membrane capacitance of 1 μf/cm2. The resulting computational surface area corresponds to a pipette tip diameter of 1 μm.
To minimize artifacts attributable to voltage protocol discrepancies, simulation protocols were identical to those used to experimentally characterize WT-SCN1A and R1648H (Lossin et al., 2002, 2003; Rhodes et al., 2004, 2005; Vanoye et al., 2006). This includes test voltage sequence as well as relaxation time. After the entire protocol had been recorded, the model was reinitialized to steady state (−120 mV) before the next simulation. Therefore, nonspecific protocol effects (e.g., accumulation of inactivation) should be identical between the model and the heterologously expressed channel.
The four previously reported SCN1A computational models were constructed using the published parameters (Clancy and Kass, 2004; Spampanato et al., 2004a,b; Barela et al., 2006). For simulation purposes, the GNa_bar of each model was reset to 0.02 S/cm2, the value used with our WT-SCN1A model. Because of the arbitrary nature of GNa_bar, all comparisons between the previously reported SCN1A computational models and the empirically recorded SCN1A biophysical data are performed using normalized data (with the exception of supplemental Figure S2A, available at www.jneurosci.org as supplemental material). The four previously reported SCN1A models include one Markov (model A) (Clancy and Kass, 2004) and three HH-style models (models B–D) (Spampanato et al., 2004a,b; Barela et al., 2006). The discrepancies between the previously reported activity of model A and our simulations most likely reflect differences in simulation environment differences. These considerations are not applicable to models B–D because these were previously constructed and reported using the NEURON simulation environment.
Data analysis.
Data analysis was performed using Clampfit 9.2, OriginPro 7, and GraphPad Prism 4. Channel inactivation was evaluated by fitting the decay phase of the whole-cell current with the two-exponential function I/Imax = Af × exp(−t/τf) + As × exp(−t/τs) + Ir, where τf and τs are the time constants (fast and slow components, respectively), A is a fractional amplitude, and Ir is the level of non-inactivating current. Whole-cell conductance was calculated by GNa = INa/(V − ENa) and normalized to the maximum conductance between −80 and +20 mV. Conductance-voltage and steady-state availability curves were fit with Boltzmann functions to determine the voltage for half-maximal activation/inactivation (V1/2) and the slope factor (k). The time-dependent entry into and the recovery from inactivation was evaluated by fitting the peak current with the two-exponential function I/Imax = Af × [1 − exp(−t/τf)] + As × [1 − exp(−t/τs)]. Persistent current was measured during the final 10 ms of a 200 ms depolarization to −10 mV and expressed as a percentage of peak current.
Using the same model parameters, sequential whole-cell simulations generate the identical model response. In contrast, single-channel simulations are stochastic, and sequential runs generate unique data. Thus, whole-cell results are reported as the value of the measured activity, and single-channel results are presented as mean ± SEM for independent simulation sequences. To allow direct comparison of the single-channel simulations with previously reported empirical data (Vanoye et al., 2006), single-channel events <0.1 ms were excluded from analysis.
Results
The majority of ion channel computational models rely on the quantitative descriptions of axonal ionic currents first introduced in 1952 by Hodgkin and Huxley. Subsequent work has shown that HH-style equations can only approximate neuronal voltage-gated sodium channel behavior (Patlak, 1991; Hille, 2001; Baranauskas and Martina, 2006; Naundorf et al., 2006). We developed enhanced Markov chain models for WT-SCN1A and the GEFS+ mutant R1648H that very accurately reproduce the observed biophysical characteristics of the corresponding heterologously expressed channels.
SCN1A Markov model
Figure 1 illustrates our Markov model for SCN1A. The model is composed of two interconnected layers of states: (1) a bottom layer containing the closed (C), open (O, conducting; Ø, open but non-conducting), and fast inactivated (F) states; and (2) a parallel upper layer containing the slow inactivated (S) states. Only the O state conducts ions as Ø states have undergone inactivation. Each state approximates a theoretical conformation SCN1A adopts during activation and inactivation. However, any direct correlation between a state within the diagram and a particular protein conformation is not possible. It is likely that many transient SCN1A protein conformations are grouped and represented as a single state within the model.
This scheme integrates many features of previous sodium channel models including multiple closed states, a single conducting state, closed state inactivation, and silent recovery from inactivation (Horn and Vandenberg, 1984; Vandenberg and Horn, 1984; Patlak, 1991; Hille, 2001). We positioned slow inactivation as a second upper layer because of the ex-perimental observations that fast and slow inactivation are discrete, although not entirely autonomous, mechanisms (Featherstone et al., 1996; Vedantham and Cannon, 1998). Featherstone et al. (1996) reported that removing fast inactivation increased the rate of entry into slow inactivation. As a result, the state of one inactivation gate (open vs closed) impacts the kinetics of the other, and parallel transitions in the model for SCN1A are not modeled with identical kinetics (e.g., C1 to SC1 compared with FC1 to SFC1). In the model, fast and slow inactivation mechanisms are able to independently terminate current flow through the pore (transitions out of O). The transitions O to FØ and O to SØ represent closure of the fast and slow inactivation gates, respectively. Both gates can be closed simultaneously (states labeled SF), but this requires two independent and sequential steps (e.g., closure of the fast gate followed by closure of the slow gate).
Transitions are described by rate equations that are instantaneously voltage dependent and were adjusted using previously recorded SCN1A whole-cell recordings as a calibration standard (Rhodes et al., 2005). The model reproduces many key features of voltage-gated sodium channel behavior. At the holding potential of −120 mV (under steady-state conditions), 97% of channels are located in C4. After depolarization, channels move through the four closed states (C4–C1) before entering the ion-conducting O state. Channels can enter fast inactivation (F states) from either open or closed states. For a depolarization to −10 mV, a transient equilibrium is established after 20 ms with 69% of channels occupying FØL and 24% in FC1. Long-lasting depolarizations drive channels from the F states into the upper layer of slow inactivated states (S states). After 10 s at −10 mV, channels predominately occupy the upper states (44% SFØL, 32% SFC1, and 6% SFC2). After repolarization, channels return to the lower layer re-establishing the steady-state equilibrium (either transitioning through the F states or moving directly into C states).
Open-state inactivation
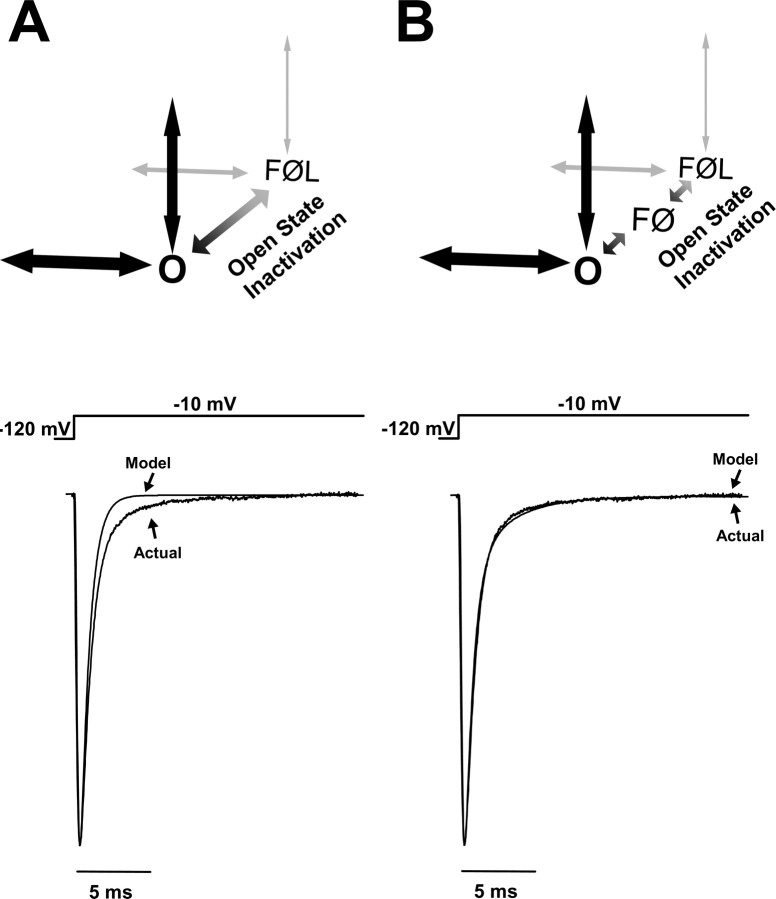
The whole-cell current carried by human SCN1A inactivates with a double-exponential time course (Lossin et al., 2002, 2003; Rhodes et al., 2004, 2005; Vanoye et al., 2006). Figure 2 illustrates theoretical investigations into possible mechanisms for generating this behavior. We first attempted to model open-state inactivation with a single step (O to FØL) (Fig. 2A). The resulting simulated whole-cell current (“Model”) decayed too quickly and followed a single exponential time course. For comparison with the current generated by heterologously expressed SCN1A, the average SCN1A whole-cell current recorded from multiple independent cells is depicted as “Actual” in Figure 2A (Rhodes et al., 2005). Integrating the Model and Actual current traces between the peak and 10 ms reveals that a single-step inactivation pathway conducts only 65.4% of the actual sodium influx. We next adjusted the rate constants for the O to FØL transition in an effort to introduce a second component to the whole-cell current inactivation. Slowing the O to FØL transition significantly increased the peak current amplitude and slowed the overall current decay without introducing a second time component (data not shown). Slowing inactivation by allowing channel reopening (increasing the FØL to O transition in Fig. 2A) increased the peak current and induced a significant persistent current without introducing a second inactivation component (data not shown).
Figure 2.
Secondary stabilization is essential for open-state inactivation. SCN1A open-state inactivation was explored by modeling different inactivation mechanisms. A, An open-state inactivation pathway consisting of a single step (O to FØL) was unable to reproduce the biphasic whole-cell current characteristic of SCN1A. B, A two-step inactivation pathway reproduces the SCN1A biphasic whole-cell current decay. The modeled inactivation pathway includes an unstable intermediate state FØ between the open state O and the stabilized latched inactivated state FØL.
We next attempted to model the biphasic whole-cell current decay with two parallel fast inactivation transitions (two transitions leading from O to the F states). Preliminary experiments with these models were unable to generate a whole-cell current decay that was well fit by a two-exponential equation (data not shown). Moreover, the mechanism of fast inactivation for voltage-gated sodium channels has been described in great detail and consists of pore occlusion by the DIII–DIV intracellular loop (Vassilev et al., 1989; Catterall et al., 2005). Introduction of a second fast inactivation pathway from O would imply a second fast inactivation gate that is not supported by the experimental data.
An alternative approach to reproduce the biphasic whole-cell current decay is to add an intermediate state in the open-state inactivation pathway. Figure 2B illustrates an inactivation mechanism for SCN1A that consists of two states in series (FØ and FØL). In this design, channels leaving O first enter the less stable fast inactivated state FØ. Most channels quickly transition into the absorbing fast inactivated locked state FØL. A small fraction of FØ channels transiently return to O, thereby reopening before inactivating again to FØ and finally arriving in FØL. The sodium current generated by this model overlays the current recorded for heterologously expressed SCN1A (Fig. 2B). Integrating the Model current trace between the peak and 10 ms reveals that a two-step open-state inactivation pathway conducts 98.5% of the actual sodium influx. All subsequent simulations were performed with models including the FØ state.
Model WT-SCN1A generates accurate whole-cell currents
To verify that the WT-SCN1A model reproduces the fundamental characteristics of SCN1A activity, we characterized the whole-cell sodium currents generated by the model and compared these results to those previously reported for SCN1A (Rhodes et al., 2005). Figure 3 illustrates a representative family of sodium current traces elicited by voltage steps to various potentials for a tsA201 cell heterologously expressing WT-SCN1A (A) and model WT-SCN1A (B). In both cases, the measured currents were inward and transient because of the rapid activation and inactivation of sodium influx. Overlaying the −10 mV current trace from Fig. 3, A and B, verifies that the model WT-SCN1A activates and inactivates with kinetics similar to those measured for WT-SCN1A (Fig. 3C). Figure 3D illustrates normalized current traces generated by the previously reported SCN1A models in response to a voltage step to −10 mV (Clancy and Kass, 2004; Spampanato et al., 2004a,b; Barela et al., 2006). In our simulation environment, each model displayed altered current kinetics compared with those actually measured for WT-SCN1A. Supplemental Figure S1 (available at www.jneurosci.org as supplemental material) illustrates the whole-cell current generated by the previously reported WT-SCN1A models in response to the voltage protocol in Figure 3A.
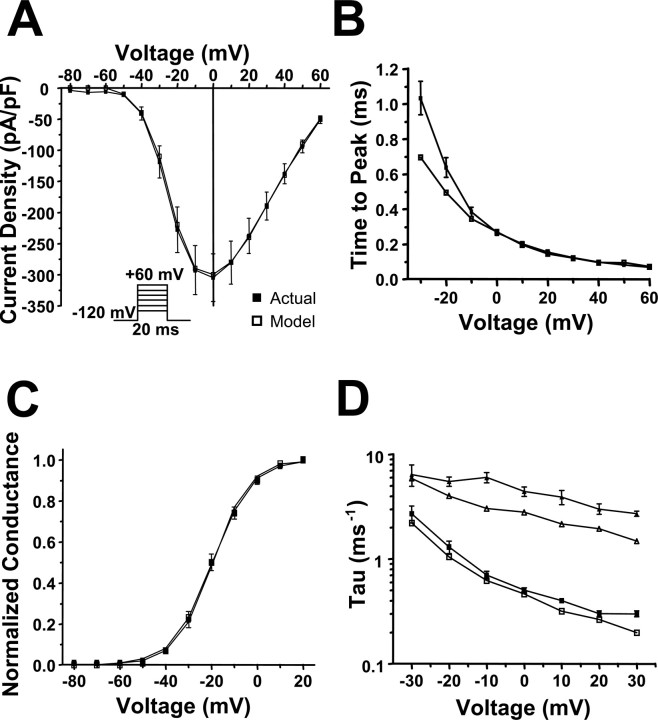
Figure 3.
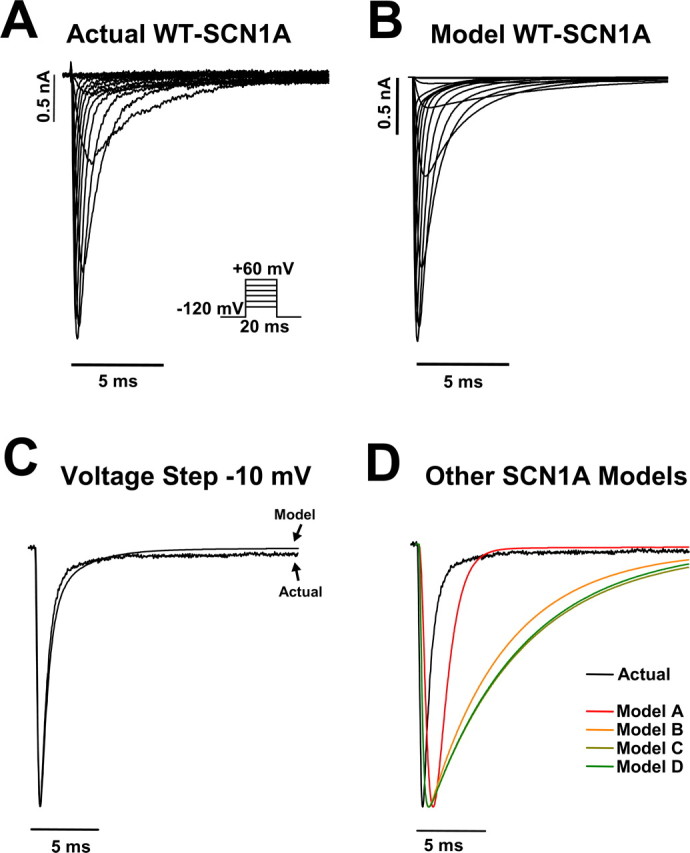
WT-SCN1A model generates accurate whole-cell currents. A, Representative whole-cell currents recorded from a tsA201 cell coexpressing the human WT SCN1A and the human β1 and β2 accessory subunits. Currents were elicited by voltage steps to potentials between −80 and +60 mV from a holding potential of −120 mV. B, Model WT-SCN1A whole-cell currents recorded in response to the stimulation protocol in A. C, Comparison of actual and model WT-SCN1A current traces for the −10 mV voltage step from A and B, respectively. D, Comparison of actual WT-SCN1A and all previously reported SCN1A computational models (Clancy and Kass, 2004; Spampanato et al., 2004a; Spampanato et al., 2004b; Barela et al., 2006) in response to the −10 mV voltage step.
To further demonstrate the accuracy of the whole-cell currents generated by model WT-SCN1A, we characterized their activation and inactivation kinetics. Figure 4A illustrates the peak current–voltage relationship for the whole-cell currents shown in Figure 3. There is minimal difference between the peak current generated by the WT-SCN1A model (open symbols) and actual SCN1A (filled symbols). At 0 mV, the model generates a peak current of −307 pA/pF compared with −305 ± 38 pA/pF (n = 14) for actual WT-SCN1A (Rhodes et al., 2005). We measured time to peak current for each voltage as an estimation of the rate of channel activation. Plotting the time to peak current for simulated and actual WT-SCN1A demonstrates that our model activates with a similar time course (Fig. 4B). At −10 mV, the time to peak current for model WT-SCN1A was 0.35 ms compared with 0.38 ± 0.03 ms (n = 14) for actual WT-SCN1A. Figure 4C illustrates that the voltage dependence of activation obtained from the normalized conductance values for simulated WT-SCN1A is similar to that directly measured for the heterologously expressed channel (fit parameters are listed in Table 1) (Rhodes et al., 2005). To quantitatively evaluate SCN1A current inactivation, the decay of the whole-cell current trace was fit with a two-exponential equation (Table 2). Figure 4D demonstrates that the fast and slow inactivation components (τf and τs, respectively) for model WT-SCN1A are comparable to those reported previously. The differences in τs most likely reflect the contribution (5 ms after voltage step) of nonspecific whole-cell currents in the heterologous recording system that are absent in silico (Fig. 3A). These results demonstrate that our WT-SCN1A model reproduces the fundamental properties of the whole-cell current (activation and inactivation) recorded from heterologously expressed SCN1A (Rhodes et al., 2005). For comparisons with our model, supplemental Figures S2–S4 (available at www.jneurosci.org as supplemental material) illustrate properties of the whole-cell currents generated by other previously reported WT-SCN1A models (Clancy and Kass, 2004; Spampanato et al., 2004a,b; Barela et al., 2006).
Figure 4.
Analysis of simulated WT-SCN1A whole-cell current. The WT-SCN1A computational model (open symbols) reproduces the whole-cell biophysical characteristics of WT-SCN1A heterologously expressed in tsA201 cells (n = 14; filled symbols). Whole-cell currents were elicited by the voltage protocol in the inset in A. A, B, Peak current amplitude and time to peak current were plotted for each potential, respectively. C, The voltage dependence of channel activation was calculated from the normalized conductance values. Data were fit using a Boltzmann equation, and fit parameters are provided in Table 1. D, Inactivation time constants were estimated by fitting the decay phase of the whole-cell current with a two-exponential function. Fit parameters are provided in Table 2, and the fast and slow inactivation time constants are plotted for each potential.
Table 1.
Biophysical parameters for activation and fast inactivation
| Activation |
Voltage dependence of fast inactivation |
Recovery from fast inactivationa |
|||||||
|---|---|---|---|---|---|---|---|---|---|
| V1/2(mV) | k (mV) | n | V1/2(mV) | k (mV) | n | τf(ms) | τs(ms) | n | |
| Actual WT-SCN1A | −19.4 ± 1.4 | 7.9 ± 0.2 | 13 | −62.7 ± 1.7 | −6.9 ± 0.2 | 14 | 2.4 ± 0.3 [85 ± 1%] | 41.0 ± 6.0 [15 ± 1%] | 14 |
| Model WT-SCN1A | −19.9 | 8.5 | −61.3 | −7.7 | 2.2 [82%] | 26.6 [18%] | |||
| Model R1648H | −19.9 | 8.5 | −61.3 | −7.8 | 2.1 [81%] | 23.0 [19%] | |||
aValues in brackets represent amplitude.
Table 2.
Whole-cell current inactivation time constants
| Fast componenta |
Slow componenta |
|||||
|---|---|---|---|---|---|---|
| Actual WT-SCN1A | Model WT-SCN1A | Model R1648H | Actual WT-SCN1A | Model WT-SCN1A | Model R1648H | |
| −30 mV | 2.73 ± 0.49 [69 ± 18%] | 2.20 [81%] | 2.22 [86%] | 6.4 ± 1.5 [31 ± 18%] | 5.9 [19%] | 7.0 [14%] |
| −20 mV | 1.34 ± 0.18 [86 ± 5%] | 1.04 [81%] | 1.03 [83%] | 5.5 ± 0.6 [14 ± 5%] | 4.0 [19%] | 3.8 [17%] |
| −10 mV | 0.72 ± 0.06 [93 ± 1%] | 0.62 [82%] | 0.68 [87%] | 6.0 ± 0.7 [7 ± 0.8%] | 3.0 [18%] | 3.3 [13%] |
| 0 mV | 0.47 ± 0.03 [94 ± 1%] | 0.46 [87%] | 0.46 [89%] | 4.4 ± 0.5 [6 ± 0.7%] | 2.8 [13%] | 2.6 [11%] |
| 10 mV | 0.37 ± 0.02 [94 ± 1%] | 0.32 [87%] | 0.33 [89%] | 3.9 ± 0.6 [6 ± 0.6%] | 2.2 [13%] | 2.2 [11%] |
| 20 mV | 0.31 ± 0.02 [92 ± 1%] | 0.26 [89%] | 0.23 [85%] | 3.0 ± 0.3 [8 ± 1.2%] | 1.9 [11%] | 1.6 [15%] |
| 30 mV | 0.28 ± 0.02 [90 ± 1%] | 0.20 [84%] | 0.19 [83%] | 2.7 ± 0.2 [10 ± 1.3%] | 1.5 [16%] | 1.4 [17%] |
aValues in brackets represent fractional amplitude.
Model WT-SCN1A replicates fast and slow inactivation
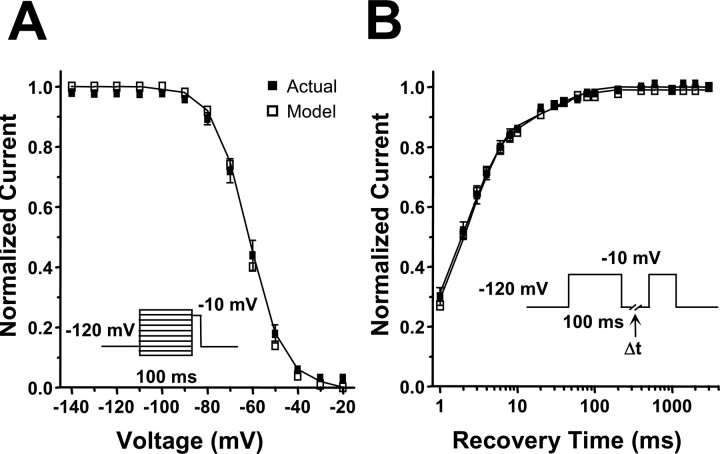
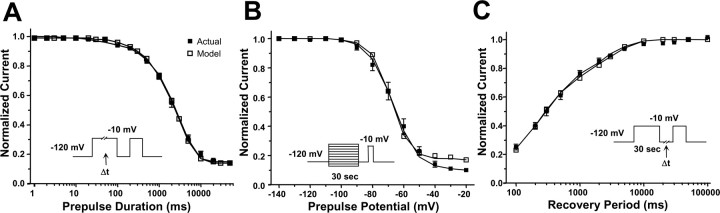
Sodium channel fast inactivation is critical for limiting sodium influx during excitation, and an accurate computational model should reproduce the fast inactivation properties of SCN1A. We examined both entry into (Fig. 5A) and recovery from (Fig. 5B) fast inactivation for our WT-SCN1A model using standard two-pulse voltage protocols. The results were compared with the parameters measured for WT-SCN1A (Table 1) (Rhodes et al., 2005). Figure 5A illustrates that our WT-SCN1A model (open symbols) simulates currents that entered fast inactivation with the same voltage dependence as actual WT-SCN1A (filled symbols). Similar to heterologously expressed WT-SCN1A, the model also exhibited recovery from fast inactivation that is well fit with a two-exponential equation.
Figure 5.
Analysis of simulated WT-SCN1A fast inactivation. The WT-SCN1A model (open symbols) reproduces the fast inactivation characteristics of channels heterologously expressed in tsA201 cells (n = 14; filled symbols). A, Voltage-dependent entry into fast inactivation was examined using a two-pulse protocol consisting of a 100 ms conditioning pulse at various potentials, followed by a test pulse at −10 mV. B, Time-dependent recovery from fast inactivation was examined using a two-pulse protocol consisting of a 100 ms inactivation pulse at −10 mV, followed by a variable length return to −120 mV and a second test pulse to −10 mV. Data were fit using either a Boltzmann (A) or two-exponential (B) equation; fit parameters are provided in Table 1.
Slow inactivation has been proposed to regulate channel availability and may play a significant role during periods of prolonged depolarization or repetitive stimulation. We used two-pulse voltage protocols to test the ability of our WT-SCN1A model to accurately emulate the time and voltage dependence of slow inactivation. The results were compared with the parameters actually measured for WT-SCN1A (Table 3) (Rhodes et al., 2005). Model WT-SCN1A (open symbols) exhibits the same time dependence of entry into slow inactivation as actual WT-SCN1A (Fig. 6A, filled symbols). Figure 6B shows that simulated WT-SCN1A enters slow inactivation with an equivalent voltage dependence compared with actual WT-SCN1A. In addition, simulated WT-SCN1A recovered from slow inactivation with the same biphasic time dependence of actual WT-SCN1A (Fig. 6C).
Table 3.
Biophysical parameters for slow inactivation
| Onset of slow inactivationa |
Voltage dependence of slow inactivation |
Recovery from slow inactivationa |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| τf(ms) | τs(ms) | Ir | n | V1/2(mV) | k (mV) | Ir | n | τf(ms) | τs(ms) | n | |
| Actual WT-SCN1A | 30 ± 7 [3 ± 1%] | 3029 ± 283 [83 ± 1%] | 14 ± 1 | 14 | −66.7 ± 2.0 | 7.8 ± 0.2 | 10 ± 1 | 11 | 238 ± 16 [65 ± 3%] | 2487 ± 240 [35 ± 3%] | 11 |
| Model WT-SCN1A | 30 [1%] | 2793 [84%] | 15 | −68.5 | 6.2 | 17 | 225 [63%] | 2647 [37%] | |||
| Model R1648H | 30 [1%] | 3112 [83%] | 16 | −68.6 | 6.1 | 18 | 221 [63%] | 2650 [37%] | |||
aValues in brackets represent amplitude.
Figure 6.
Analysis of simulated WT-SCN1A slow inactivation. The WT-SCN1A model (open symbols) reproduces the slow inactivation characteristics of heterologously expressed channels (n = 11; filled symbols). A, Time-dependent entry into slow inactivation was examined using a two-pulse protocol consisting of a variable length inactivation pulse to −10 mV, followed by a test pulse at −10 mV. Effects of fast inactivation were minimized using a 50 ms inter-pulse step to −120 mV to relieve fast inactivation. B, Voltage-dependent entry into slow inactivation was examined using a two-pulse protocol consisting of a 30 s conditioning pulse at various potentials, followed by a test pulse at −10 mV. Effects of fast inactivation were minimized using a 50 ms inter-pulse step to −120 mV to relieve fast inactivation. C, Time-dependent recovery from slow inactivation was examined using a two-pulse protocol consisting of a 30 s inactivation pulse to −10 mV, followed by a variable length inter-pulse step to −120 mV and a test pulse to −10 mV. Data were fit using either a two-exponential (A, C) or Boltzmann (B) equation; fit parameters are provided in Table 3.
Modeling increased persistent current
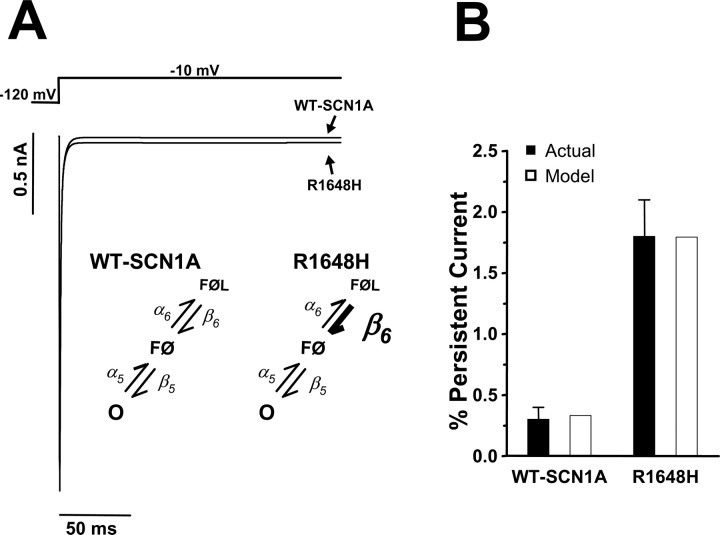
Beginning with the model for WT-SCN1A, we constructed a computational model for the GEFS+ mutant R1648H. The major biophysical defect exhibited by R1648H is an increased persistent current resulting from increased probability of late single-channel openings (Lossin et al., 2002; Rhodes et al., 2004; Vanoye et al., 2006). We were able to generate this biophysical phenotype by destabilizing the fast inactivated state FØL within the WT-SCN1A Markov model (Fig. 1). Increasing the rate constant for the transition from FØL to FØ (β6 in supplemental Table S1, available at www.jneurosci.org as supplemental material) allowed a small fraction of channels to transiently re-enter the open state O and generate the increased persistent current (Fig. 7A, inset). No other changes, such as additional states, were needed to generate this aberrant channel activity.
Figure 7.
Computational model of GEFS+ mutant R1648H. A, The model for R1648H was constructed by destabilizing the fast inactivated state FØL (6-fold increase in β6; inset). Whole-cell current simulations of R1648H reveal increased persistent sodium current compared with simulated WT-SCN1A. B, Levels of simulated persistent current for models WT-SCN1A (open bar; 0.3% of peak current) and R1648H (open bar; 1.8% of peak current) replicate the average persistent current empirically measured for heterologously expressed WT-SCN1A (filled bar; 0.3 ± 0.1% of peak current; n = 9) and R1648H (filled bar; 1.8 ± 0.3% of peak current; n = 6). Persistent current was measured during the final 10 ms of a 200 ms voltage step to −10 mV.
Figure 7A illustrates whole-cell current traces for the models WT-SCN1A and R1648H in response to a voltage step to −10 mV from a holding potential of −120 mV. R1648H exhibits a significant persistent current beginning 10 ms after the voltage step. The persistent current predicted between 190 and 200 ms after the voltage step for our R1648H model was 1.8% of peak current compared with 0.3% for the WT-SCN1A model. Figure 7B illustrates that the persistent current generated by both models (open bars) corresponds well with the persistent current measured for heterologously expressed WT-SCN1A (filled bar; 0.3 ± 0.1% of peak; n = 9) and R1648H (filled bar; 1.8 ± 0.3% of peak; n = 6) (Rhodes et al., 2004).
Complete characterization of simulated R1648H activation, fast inactivation, and slow inactivation was performed as described for the WT-SCN1A model. There was no difference between R1648H and WT-SCN1A (Tables 1–3), in agreement with the original study of this mutant (Lossin et al., 2002). Both computational models accurately reproduce the biophysical parameters that were measured for each channel. Using our simulation environment, previously reported SCN1A models predicted persistent current levels that varied widely between 0.6 and 2.3% of peak current (supplemental Fig. S5, available at www.jneurosci.org as supplemental material).
Simulated R1648H exhibits late channel openings
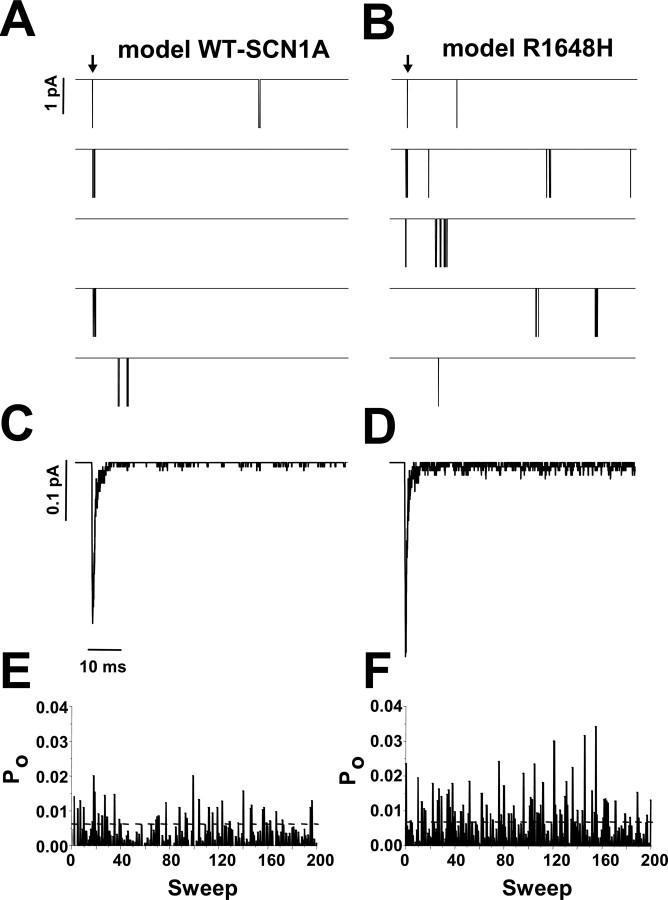
The computational models for WT-SCN1A and R1648H were generated using experimentally recorded SCN1A whole-cell data as a calibration standard to tune the voltage-dependent rate equations (supplemental Table S1, available at www.jneurosci.org as supplemental material). We next tested whether our models could reproduce the single-channel properties observed for WT-SCN1A and R1648H (Vanoye et al., 2006). We used the stochastic single-channel simulator in NEURON to test the single-channel characteristics of model WT-SCN1A and model R1648H in response to voltage steps to 0 mV. Figure 8, A and B, illustrates five consecutive voltage-step simulations for models WT-SCN1A and R1648H, respectively. The mean open time determined for simulated WT-SCN1A was 0.29 ± 0.02 ms (n = 3) compared with 0.30 ± 0.02 ms (n = 3) for that generated by the R1648H model. These open times compare well with the open times measured for heterologously expressed WT-SCN1A (0.25 ± 0.03 ms; n = 4) and R1648H (0.23 ± 0.02 ms; n = 5) (Vanoye et al., 2006).
Figure 8.
Late channel openings underlie model R1648H persistent current. A, B, Five consecutive single-channel simulations for WT-SCN1A and R1648H, respectively. Downward deflections represent channel openings, and arrows indicate onset of voltage step from −120 to −10 mV. C, D, Representative ensemble average of 200 consecutive simulations using WT-SCN1A and R1648H models, respectively. E, F, Open probability (Po) diary for each of the 200 simulations for WT-SCN1A and R1648H, respectively. Po was calculated 0–80 ms after the voltage step.
Model R1648H exhibits an increase in late single-channel openings (>10 ms after voltage step) compared with WT-SCN1A. Averaging 200 consecutive simulations reveals that WT-SCN1A exhibits a low level of late single-channel activity (Fig. 8C). In contrast, model R1648H opens late in many simulations (Fig. 8D). Figure 8, E and F, illustrates the open probability (Po) diary for the same 200 consecutive simulations of model WT-SCN1A and R1648H. The average probability of late channel opening (Po = 20–100 ms) for model R1648H (0.0036 ± 0.0002; n = 3) was sixfold greater than simulated WT-SCN1A (0.0006 ± 0.0002; n = 3; Student's t test, p < 0.0001). These results are very similar to the 7.4-fold increase in late Po measured for heterologously expressed R1648H compared with WT-SCN1A (Vanoye et al., 2006).
These data demonstrate that the whole-cell persistent current generated by model R1648H (Fig. 7) results from an increase in late single-channel openings as a direct result of destabilizing the fast inactivation locked state (FØL). Based on these findings, we propose that selective impairment of the latching step of fast inactivation is responsible for the increased persistent current observed for this GEFS+ mutant.
Discussion
Computational modeling is an effective experimental approach to explore alterations in ion channel behavior that result from disease-associated mutations. Here, we describe the construction of ion channel models for WT-SCN1A and R1648H that are based on previously recorded SCN1A whole-cell experimental data. We fully characterized each model to ensure biophysical accuracy. Moreover, our models provide novel insight into WT-SCN1A open-state inactivation and define a previously unrecognized molecular mechanism to explain increased persistent current exhibited by a GEFS+ mutant.
Comparison of SCN1A models
Previous attempts to generate computational models for WT-SCN1A have been based on either HH-style differential equations or Markov chains (Clancy and Kass, 2004; Spampanato et al., 2004a,b; Barela et al., 2006). We initially sought to modify an existing WT-SCN1A model to fit our experimentally recorded SCN1A activity. Each previously reported WT-SCN1A model was reconstituted, and the resulting whole-cell currents were compared with heterologously expressed human SCN1A coexpressed with both human β1 and β2 accessory subunits in human tsA201 cells (Fig. 3D and supplemental Figs. S1–S5, available at www.jneurosci.org as supplemental material). Although each previously reported WT-SCN1A model reproduced certain SCN1A activities, a rigorous characterization of the currently available models revealed that none were able to fully replicate the behavior of the channel (Fig. 3D and supplemental Figs. S1–S5, available at www.jneurosci.org as supplemental material). This may reflect the source of data used during the construction and calibration of each model. The models sharing the HH-equation architecture were calibrated using currents recorded from Xenopus laevis oocytes coexpressing rat Scn1a and only β1. In contrast, the previously reported SCN1A Markov model was constructed using human SCN1A data.
We chose to extend the efforts of Clancy and Kass (2004) to generate a Markov model for SCN1A that reproduces all of the experimentally recorded whole-cell properties of the heterologously expressed channels. A Markov design provides the parameter flexibility necessary to calibrate the rate equations to fit our experimental data. The major alterations to the previous model include the addition of a two-step open-state inactivation pathway and a second layer of slow inactivated states. All rate equations were modified to reproduce the previously recorded activity of heterologously expressed human SCN1A.
The computational models we developed for WT-SCN1A and R1648H generated whole-cell currents that are highly similar to the experimentally recorded data (Figs. 2, 3) (Lossin et al., 2002; Rhodes et al., 2004, 2005; Vanoye et al., 2006). Channel current was voltage dependent, inward, and transient. Characterization of the whole-cell currents revealed the proper biophysical parameters for the peak current amplitude (Fig. 4A), time course of activation (Fig. 4B), voltage dependence of activation (Fig. 4C), and biphasic whole-cell current inactivation (Fig. 4D). Moreover, the model WT-SCN1A and model R1648H reproduced the fast and slow inactivation processes for each channel, respectively. Specifically, the models exhibited virtually the same voltage dependence of fast inactivation (Fig. 5A), time-dependent recovery from fast inactivation (Fig. 5B), time-dependent entry into slow inactivation (Fig. 6A), voltage dependence of slow inactivation (Fig. 6B), and time-dependent recovery from slow inactivation (Fig. 6C) as experimentally determined channel properties. This comprehensive characterization confirms that the models WT-SCN1A and R1648H exhibit the proper biophysical parameters necessary to accurately emulate the heterologously expressed channel.
Open-state inactivation is a two-step process
Our SCN1A model incorporates a two-step pathway for open-state inactivation (Figs. 1, 2). This scheme was necessary to reproduce the biphasic decay of the SCN1A whole-cell current (Fig. 2) (Lossin et al., 2002, 2003; Rhodes et al., 2004, 2005; Vanoye et al., 2006). The cardiac voltage-gated sodium channel (SCN5A) also exhibits a two-component whole-cell current decay (Wang et al., 1996, 2000; Makita et al., 2000). Recent experiments have revealed SCN5A inactivation to be a multiple step process resulting from pore occlusion by the DIII–DIV inactivation loop, followed by inactivation gate stabilization by a second structure encoded in the proximal C-terminal tail (Cormier et al., 2002; Motoike et al., 2004; Glaaser et al., 2006). The sodium channel C-terminal tail also influences the rate of fast inactivation. In experiments involving SCN5A/SCN2A chimeras, the rate of whole-cell current inactivation was determined primarily by the C-terminal tail (Mantegazza et al., 2001).
Although the C terminus of SCN1A has not been linked directly to inactivation, a high homology exists between the neuronal isoforms SCN1A and SCN2A (∼90%) as well as the cardiac SCN5A (∼60%) (Catterall et al., 2005). Our SCN1A models predict that similar to SCN5A and SCN2A, a second molecular interaction is important for the stabilization of the inactivation gate. This stabilization could result from the SCN1A C terminus as has been proposed for SCN5A (Mantegazza et al., 2001; Cormier et al., 2002; Motoike et al., 2004; Glaaser et al., 2006). However, models alone cannot implicate structural interactions. The stabilization of inactivation may rely on additional channel regions or other associated proteins, such as the accessory β subunits.
It is worth noting that the biphasic open-state inactivation proposed here for SCN1A (Fig. 2B) should not be confused with (or compared with) the two-phase recovery from fast and slow inactivation (Figs. 5B, 6C). Extensive biophysical characterization of SCN1A as well as other voltage-gated sodium channels has demonstrated that inactivated channels do reopen during the recovery process (Kuo and Bean, 1994). Thus, recovery from inactivation is distinct from entry into inactivation. The mechanism(s) underlying the biphasic recovery from inactivation has not been completely explored.
Novel mechanism for increased persistent current
The persistent current model R1648H was constructed by altering a single rate constant in the WT-SCN1A model. The fast inactivated state FØL was destabilized by increasing the rate constant β6. This modification allows a small number of channels to re-enter the open state and generate the characteristic persistent current recorded for this GEFS+ mutant. Figure 7 illustrates that model R1648H exhibits a whole-cell persistent current that is comparable to the increased persistent current actually measured for this mutant (Rhodes et al., 2004). In agreement with actual observations, this abnormal activity results from model R1648H exhibiting an increase in late channel openings (Fig. 8) and not bursting behavior (Vanoye et al., 2006).
It is worth noting that the R1648H model did not generate Po values as large as those actually reported for R1648H (Vanoye et al., 2006). The large open probability for R1648H (0.1–0.3) observed for a subset of voltage sweeps partially reflects a second prolonged open time (Vanoye et al., 2006). Although the models for WT-SCN1A and R1648H accurately reproduce the SCN1A whole-cell biophysical activity, future versions of the models may need to include a second open state with a longer dwell time to improve the simulated single-channel behavior. Nevertheless, our models are sufficiently accurate at the whole-cell level to begin neuronal simulations investigating mechanisms of R1648H epileptogenesis.
The model for R1648H predicts a novel mechanism for the persistent current generated by this GEFS+ mutant. We were able to replicate the increased persistent current exhibited by R1648H by altering a single rate constant (β6) in the WT-SCN1A model. This implies that introducing a histidine at position 1648 within the S4 segment of DIV (R1648H) inhibits the secondary stabilization of fast inactivation. Experimental investigation will be necessary to confirm and characterize these theoretical predictions for open-state inactivation.
Our models of WT-SCN1A and R1648H generate whole-cell currents that very accurately recapitulate the currents measured for heterologously expressed channels (Fig. 3). This feature of our models will be highly valuable when constructing neuronal simulations. It is well accepted that proper in vivo excitability results from the integrated activity of a collection of ion conductances. Simulating accurate channel behavior is vital for engineering the next generation of neuronal excitability models.
Footnotes
This work was supported by a research grant from the National Institutes of Health (NS32387 to A.L.G.), an institutional training grant from the National Institute of Mental Health (T32-MH065215 to K.M.K.), and an Epilepsy Foundation research training fellowship (4-04-353-6242 to S.N.M.). A.L.G. is a recipient of a Javits Neuroscience Award from the National Institute of Neurological Diseases and Stroke. We thank Dr. Carlos Vanoye for critical review of this manuscript and Daniel Kaiser for help with computational model development.
References
- Baranauskas G, Martina M. Sodium currents activate without a Hodgkin-and-Huxley-type delay in central mammalian neurons. J Neurosci. 2006;26:671–684. doi: 10.1523/JNEUROSCI.2283-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barela AJ, Waddy SP, Lickfett JG, Hunter J, Anido A, Helmers SL, Goldin AL, Escayg A. An epilepsy mutation in the sodium channel SCN1A that decreases channel excitability. J Neurosci. 2006;26:2714–2723. doi: 10.1523/JNEUROSCI.2977-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Catterall WA, Goldin AL, Waxman SG. International union of pharmacology. XLVII. Nomenclature and structure-function relationships of voltage-gated sodium channels. Pharmacol Rev. 2005;57:397–409. doi: 10.1124/pr.57.4.4. [DOI] [PubMed] [Google Scholar]
- Cha A, Ruben PC, George AL, Jr, Fujimoto E, Bezanilla F. Voltage sensors in domains III and IV, but not I and II, are immobilized by Na+ channel fast inactivation. Neuron. 1999;22:73–87. doi: 10.1016/s0896-6273(00)80680-7. [DOI] [PubMed] [Google Scholar]
- Clancy CE, Kass RS. Theoretical investigation of the neuronal Na+ channel SCN1A: abnormal gating and epilepsy. Biophys J. 2004;86:2606–2614. doi: 10.1016/S0006-3495(04)74315-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clancy CE, Rudy Y. Linking a genetic defect to its cellular phenotype in a cardiac arrhythmia. Nature. 1999;400:566–569. doi: 10.1038/23034. [DOI] [PubMed] [Google Scholar]
- Clancy CE, Rudy Y. Na(+) channel mutation that causes both Brugada and long-QT syndrome phenotypes: a simulation study of mechanism. Circulation. 2002;105:1208–1213. doi: 10.1161/hc1002.105183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clancy CE, Tateyama M, Liu H, Wehrens XH, Kass RS. Non-equilibrium gating in cardiac Na+ channels: an original mechanism of arrhythmia. Circulation. 2003;107:2233–2237. doi: 10.1161/01.CIR.0000069273.51375.BD. [DOI] [PubMed] [Google Scholar]
- Colquhoun D, Dowsland KA, Beato M, Plested AJ. How to impose microscopic reversibility in complex reaction mechanisms. Biophys J. 2004;86:3510–3518. doi: 10.1529/biophysj.103.038679. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cormier JW, Rivolta I, Tateyama M, Yang AS, Kass RS. Secondary structure of the human cardiac Na+ channel C terminus: evidence for a role of helical structures in modulation of channel inactivation. J Biol Chem. 2002;277:9233–9241. doi: 10.1074/jbc.M110204200. [DOI] [PubMed] [Google Scholar]
- Featherstone DE, Richmond JE, Ruben PC. Interaction between fast and slow inactivation in Skm1 sodium channels. Biophys J. 1996;71:3098–3109. doi: 10.1016/S0006-3495(96)79504-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Finkelstein A, Peskin CS. Some unexpected consequences of a simple physical mechanism for voltage-dependent gating in biological membranes. Biophys J. 1984;46:549–558. doi: 10.1016/S0006-3495(84)84053-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- George AL., Jr Inherited disorders of voltage-gated sodium channels. J Clin Invest. 2005;115:1990–1999. doi: 10.1172/JCI25505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glaaser IW, Bankston JR, Liu H, Tateyama M, Kass RS. A carboxy terminal hydrophobic interface is critical to sodium channel function: relevance to inherited disorders. J Biol Chem. 2006;281:24015–24023. doi: 10.1074/jbc.M605473200. [DOI] [PubMed] [Google Scholar]
- Hille B. Ion channels of excitable membranes. Sunderland, MA: Sinauer; 2001. [Google Scholar]
- Hines ML, Carnevale NT. NEURON: a tool for neuroscientists. Neuroscientist. 2001;7:123–135. doi: 10.1177/107385840100700207. [DOI] [PubMed] [Google Scholar]
- Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol (Lond) 1952;117:500–544. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horn R, Vandenberg CA. Statistical properties of single sodium channels. J Gen Physiol. 1984;84:505–534. doi: 10.1085/jgp.84.4.505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Irvine LA, Jafri MS, Winslow RL. Cardiac sodium channel Markov model with temperature dependence and recovery from inactivation. Biophys J. 1999;76:1868–1885. doi: 10.1016/s0006-3495(99)77346-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuhn FJ, Greeff NG. Movement of voltage sensor S4 in domain 4 is tightly coupled to sodium channel fast inactivation and gating charge immobilization. J Gen Physiol. 1999;114:167–183. doi: 10.1085/jgp.114.2.167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuo CC, Bean BP. Na+ channels must deactivate to recover from inactivation. Neuron. 1994;12:819–829. doi: 10.1016/0896-6273(94)90335-2. [DOI] [PubMed] [Google Scholar]
- Lauger P. Conformational transitions of ion channels. In: Sakmann B, Neher E, editors. Single-channel recording. New York: Plenum; 1995. pp. 651–662. [Google Scholar]
- Lossin C, Wang DW, Rhodes TH, Vanoye CG, George AL. Molecular basis of an inherited epilepsy. Neuron. 2002;34:877–884. doi: 10.1016/s0896-6273(02)00714-6. [DOI] [PubMed] [Google Scholar]
- Lossin C, Rhodes TH, Desai RR, Vanoye CG, Wang D, Carniciu S, Devinsky O, George AL., Jr Epilepsy-associated dysfunction in the voltage-gated neuronal sodium channel SCN1A. J Neurosci. 2003;23:11289–11295. doi: 10.1523/JNEUROSCI.23-36-11289.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Makita N, Shirai N, Wang DW, Sasaki K, George AL, Jr, Kanno M, Kitabatake A. Cardiac Na(+) channel dysfunction in Brugada syndrome is aggravated by beta(1)-subunit. Circulation. 2000;101:54–60. doi: 10.1161/01.cir.101.1.54. [DOI] [PubMed] [Google Scholar]
- Mantegazza M, Yu FH, Catterall WA, Scheuer T. Role of the C-terminal domain in inactivation of brain and cardiac sodium channels. Proc Natl Acad Sci USA. 2001;98:15348–15353. doi: 10.1073/pnas.211563298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Motoike HK, Liu H, Glaaser IW, Yang AS, Tateyama M, Kass RS. The Na+ channel inactivation gate is a molecular complex: a novel role of the COOH-terminal domain. J Gen Physiol. 2004;123:155–165. doi: 10.1085/jgp.200308929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mulley JC, Scheffer IE, Petrou S, Dibbens LM, Berkovic SF, Harkin LA. SCN1A mutations and epilepsy. Hum Mutat. 2005;25:535–542. doi: 10.1002/humu.20178. [DOI] [PubMed] [Google Scholar]
- Naundorf B, Wolf F, Volgushev M. Unique features of action potential initiation in cortical neurons. Nature. 2006;440:1060–1063. doi: 10.1038/nature04610. [DOI] [PubMed] [Google Scholar]
- Patlak J. Molecular kinetics of voltage-dependent Na+ channels. Physiol Rev. 1991;71:1047–1080. doi: 10.1152/physrev.1991.71.4.1047. [DOI] [PubMed] [Google Scholar]
- Rhodes TH, Lossin C, Vanoye CG, Wang DW, George AL., Jr Noninactivating voltage-gated sodium channels in severe myoclonic epilepsy of infancy. Proc Natl Acad Sci USA. 2004;101:11147–11152. doi: 10.1073/pnas.0402482101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rhodes TH, Vanoye CG, Ohmori I, Ogiwara I, Yamakawa K, George AL., Jr Sodium channel dysfunction in intractable childhood epilepsy with generalized tonic-clonic seizures. J Physiol (Lond) 2005;569:433–445. doi: 10.1113/jphysiol.2005.094326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Richard EA, Miller C. Steady-state coupling of ion-channel conformations to a transmembrane ion gradient. Science. 1990;247:1208–1210. doi: 10.1126/science.2156338. [DOI] [PubMed] [Google Scholar]
- Rothberg BS, Magleby KL. Testing for detailed balance (microscopic reversibility in ion channel gating. Biophys J. 2001;80:3025–3026. doi: 10.1016/S0006-3495(01)76268-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schneggenburger R, Ascher P. Coupling of permeation and gating in an NMDA-channel pore mutant. Neuron. 1997;18:167–177. doi: 10.1016/s0896-6273(01)80055-6. [DOI] [PubMed] [Google Scholar]
- Spampanato J, Aradi I, Soltesz I, Goldin AL. Increased neuronal firing in computer simulations of sodium channel mutations that cause generalized epilepsy with febrile seizures plus. J Neurophysiol. 2004a;91:2040–2050. doi: 10.1152/jn.00982.2003. [DOI] [PubMed] [Google Scholar]
- Spampanato J, Kearney JA, de Haan G, McEwen DP, Escayg A, Aradi I, MacDonald BT, Levin SI, Soltesz I, Benna P, Montalenti E, Isom LL, Goldin AL, Meisler MH. A novel epilepsy mutation in the sodium channel SCN1A identifies a cytoplasmic domain for beta subunit interaction. J Neurosci. 2004b;24:10022–10034. doi: 10.1523/JNEUROSCI.2034-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- The YK, Wagner M, Timmer J. Method-independent effect in testing for detailed balance in ion channel gating. Biophys J. 2002;82:2275–2276. doi: 10.1016/S0006-3495(02)75573-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vandenberg CA, Horn R. Inactivation viewed through single sodium channels. J Gen Physiol. 1984;84:535–564. doi: 10.1085/jgp.84.4.535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vanoye CG, Lossin C, Rhodes TH, George AL., Jr Single-channel properties of human NaV1.1 and mechanism of channel dysfunction in SCN1A-associated epilepsy. J Gen Physiol. 2006;127:1–14. doi: 10.1085/jgp.200509373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vassilev P, Scheuer T, Catterall WA. Inhibition of inactivation of single sodium channels by a site-directed antibody. Proc Natl Acad Sci USA. 1989;86:8147–8151. doi: 10.1073/pnas.86.20.8147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vedantham V, Cannon SC. Slow inactivation does not affect movement of the fast inactivation gate in voltage-gated Na+ channels. J Gen Physiol. 1998;111:83–93. doi: 10.1085/jgp.111.1.83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang DW, Yazawa K, George AL, Jr, Bennett PB. Characterization of human cardiac Na+ channel mutations in the congenital long QT syndrome. Proc Natl Acad Sci USA. 1996;93:13200–13205. doi: 10.1073/pnas.93.23.13200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang DW, Makita N, Kitabatake A, Balser JR, George AL., Jr Enhanced Na(+) channel intermediate inactivation in Brugada syndrome. Circ Res. 2000;87:E37–E43. doi: 10.1161/01.res.87.8.e37. [DOI] [PubMed] [Google Scholar]
- Wyllie DJ, Behe P, Nassar M, Schoepfer R, Colquhoun D. Single-channel currents from recombinant NMDA NR1a/NR2D receptors expressed in Xenopus oocytes. Proc Biol Sci. 1996;263:1079–1086. doi: 10.1098/rspb.1996.0159. [DOI] [PubMed] [Google Scholar]