Abstract
Neocortical neurons in vivo exist in an environment of continuous synaptic bombardment, receiving a complex barrage of excitatory and inhibitory inputs. This background activity (by depolarizing neurons, increasing membrane conductance, and introducing fluctuations) strongly alters many aspects of neuronal responsiveness. In this study, we asked how it shapes neuromodulation of postsynaptic responses. Specifically, we examined muscarinic modulation of forelimb motor cortex, a brain area in which cholinergic stimulation is known to be necessary for modifications during motor skill learning. Using a dynamic clamp system to inject simulated conductances into pyramidal neurons in motor cortical slices, we mimicked in vivo-like activity by introducing a random background of excitatory and inhibitory inputs. When muscarinic receptors were stimulated with the agonist oxotremorine-M, several previously described currents were modified, and excitability was increased. However, the presence of the background conductances strongly attenuated most muscarinic agonist effects, with the notable exception that sustained firing responses to trains of inputs were well preserved. This may be important for promoting plasticity in vivo.
Keywords: motor cortex, forelimb, dynamic clamp, muscarinic, synaptic activity, slice
Introduction
Lesioning cholinergic input to neocortex impairs skilled motor learning in rodents and prevents experience-dependent motor map reorganization (Conner et al., 2003). This suggests that in motor cortex, as in other brain regions (Rasmusson, 2000; Kilgard, 2003), acetylcholine plays a permissive role in learning, a view that is further supported by evidence that synaptic plasticity here is difficult to elicit in the absence of cholinergic (and specifically muscarinic) stimulation (Castro-Alamancos et al., 1995; Hess and Donoghue, 1999).
At the cellular level, much progress has been made in documenting the effects of muscarinic receptor activation. An enormous body of work, encompassing different parts of the CNS, indicates that it modulates both intrinsic ion channels and synaptic transmission (McCormick, 1993; Hasselmo and McGaughy, 2004; Magistretti et al., 2004). This modulation is responsible for the varied response properties observed after muscarinic stimulation, which include depolarization, afterpotentials, and plateau firing. However, using this existing literature directly to understand the motor cortical circuit is problematic for two reasons. One is that the observed responses vary between different brain areas, different cell types, and even different cortical layers.
The other (less appreciated but perhaps more important) is that response properties have generally been examined under conditions very different from those cortical neurons experience in vivo. In a typical experiment, neurons reside in the quiet environment that characterizes the slice preparation, with hyperpolarized and stable resting potentials and very little synaptic activity; their responses are then probed by DC injections. But in the intact brain, neurons are under constant bombardment by a complex barrage of excitatory and inhibitory synaptic inputs, which act not by injecting current, per se, but by altering conductance (Destexhe and Pare, 1999; Anderson et al., 2000; Steriade et al., 2001). As a result, neurons in vivo experience depolarized and fluctuating membrane potentials, sharply reduced input resistances, shortened time constants, and irregular background firing (Destexhe et al., 2003). Experimental and theoretical studies over the last five years have demonstrated that this “high-conductance” condition alters neuronal response properties in important ways, including changes in sensitivity, synaptic integration, and gain (Ho and Destexhe, 2000; Brunel et al., 2001; Chance et al., 2002; Mitchell and Silver, 2003; Rudolph and Destexhe, 2003a; Shu et al., 2003; Zsiros and Hestrin, 2005). It should also significantly alter the response to neuromodulation.
Here, we examine this issue by using a dynamic clamp feedback system to introduce in vivo-like conductance activity into pyramidal neurons in slices of forelimb motor cortex. The dynamic clamp method allows researchers to use computer simulations to insert artificial synaptic or membrane conductances into biological neurons, thereby creating a hybrid circuit of real and model neurons (Robinson and Kawai, 1993; Sharp et al., 1993). Investigating muscarinic stimulation in this way, we found that random background conductances reduce most postsynaptic muscarinic effects but preserve sensitivity to sustained, correlated inputs. These are important for signaling forelimb movements, and this finding suggests one important cellular aspect of muscarinic modulation for motor skill learning.
Materials and Methods
Electrophysiology.
Coronal slices of 350 μm thickness containing the forelimb region of the primary motor cortex were prepared from Sprague Dawley rats 16–21 d of age. Animals were deeply anesthetized with isoflurane before decapitation, and their brains were quickly removed and sectioned in ice-cold artificial CSF (ACSF) containing the following (in mm): 124 NaCl, 3 KCl, 1.25 NaH2PO4, 26 NaHCO3, 2 MgCl2, 2 CaCl2, and 10 dextrose. The osmolality was adjusted to 310 mOsm with dextrose, and the pH level was buffered to 7.4 by bubbling with 95% O2/5% CO2. After sectioning, slices were transferred to oxygenated ACSF at 36°C and left to cool to room temperature after 10 min. Slices were allowed to equilibrate for at least 1 h before the start of experiments and were used for up to 7 h after preparation.
For recordings, slices were transferred one at a time to a submerged chamber mounted on a fixed-stage upright microscope (Leica DMLFSA; Leica, Nussloch, Germany). They were continuously perfused with warmed (31°C), oxygenated ACSF flowing at a rate of 3 ml/min. The flow rate and chamber size were such that the solution in the chamber could be completely exchanged in <30 s. Drugs were applied by dissolving them in the ACSF. In all experiments, synaptic transmission was blocked by 20 μm bicuculline and 1 mm kynurenate. Oxotremorine-M (Oxo-M) was normally used at a (nonsaturating) concentration of 1 μm; this was increased to 10 μm for voltage-clamp experiments. Other drugs used were tetrodotoxin (1 μm), carbachol (10 μm), and atropine (10 μm). All drugs and other chemicals were obtained from Sigma (St. Louis, MO), except for Oxo-M (Tocris Cookson, Bristol, UK).
Layer 5 pyramidal neurons in forelimb motor cortex were identified at 400× magnification using infrared DIC optics and an infrared-sensitive camera (Dage-MTI, Michigan City, IN). Whole-cell patch recordings were obtained with pulled glass micropipettes (4–5 MΩ; 1–2 μm tip diameter). The standard intracellular solution contained the following (in mm): 110 KMeSO4, 10 KCl, 10 (Na)phosphocreatine, 10 HEPES, 0.5 EGTA, 4 (Mg)ATP, 0.3 (Na)GTP, and 0.1% w/v biocytin, adjusted with KOH to pH 7.4 and with sucrose to 290–300 mOsm. To isolate different currents in the voltage-clamp experiments, the potassium in the internal solution was sometimes replaced by cesium, and the EGTA concentration was sometimes increased to 10 mm. Liquid junction potentials (5 mV) were left uncorrected. Recordings were accepted if, in control ACSF (i.e., without Oxo-M), input resistances were >100 MΩ, series resistances were <20 MΩ, and membrane potentials were more negative than −60 mV.
All electrophysiological recordings were made using a Multiclamp 700A amplifier (Molecular Devices, Union City, CA). Signals were filtered at 4 kHz and digitized at 10 kHz. Current-clamp and voltage-clamp data were acquired with a 16-bit input-output board (National Instruments, Austin, TX) using custom software written in MatLab (MathWorks, Natick, MA). Dynamic clamp data were acquired with a 16-bit digital signal processing board (dSpace), using custom software written in MatLab and Simulink (MathWorks). To minimize series resistance errors, the bridge was carefully balanced for current-clamp and dynamic clamp measurements, and series resistance compensation (60–80%) was used for voltage-clamp measurements.
All data analyses were performed using custom software written in MatLab. Numerical averages are presented as mean ± SEM. Unless otherwise stated, statistical tests for the effects of Oxo-M were made using the paired Student’s t test.
Dynamic clamp protocols.
Dynamic clamp was implemented via a digital signal processing board (DS1104; dSpace, Novi, MI). Models of synaptic and/or membrane conductances were constructed in Simulink, uploaded to the board using dSpace software, and controlled by custom software written in MatLab. All dynamic clamp simulations were run at 10 kHz. For each conductance g(t), a current I(t) was injected through the somatic electrode: I(t) = g(t)[V(t) − Erev], with V(t) being the measured membrane potential and Erev the reversal potential for that conductance. Seven types of conductances were simulated in different experiments: excitatory and inhibitory background inputs, AMPA and NMDA inputs grouped in trains, a potassium leak conductance, a potassium M conductance, and a calcium-dependent cation conductance.
Synaptic background activity was simulated using the “point conductance” method of Destexhe et al. (2001). Two conductance trains, one representing excitatory inputs and the other representing inhibitory inputs, were generated independently as Ornstein–Uhlenbeck processes. Each was determined by an equation of the form:
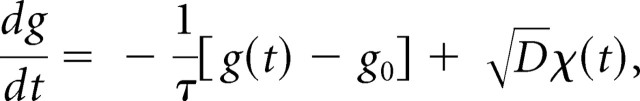 |
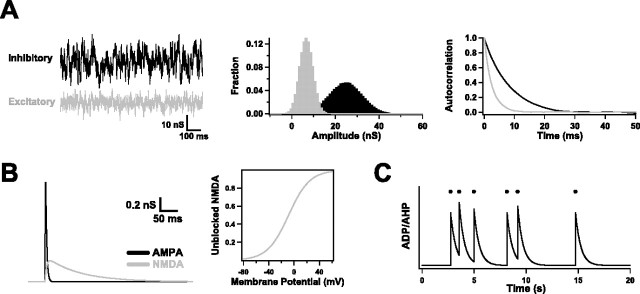
where g(t) is the value of the conductance, g0 is its mean value, τ is a time constant, D is a “diffusion” constant, and χ(t) is a Gaussian white noise term of zero mean and unit SD. As illustrated in Figure 3A, such an equation produces a random walk in time around the mean value, with a variance given by σ2 = Dτ/2. The reversal potentials were Eexc = 0 mV and Einh = −65 mV. As demonstrated previously (Destexhe et al., 2001; Fellous et al., 2003), background input to layer 5 pyramidal neurons can be well modeled by making the following parameter choices for the excitatory and inhibitory trains: τexc = 2.5 ms, τinh = 8 ms, ginh ≈ 5 gexc, and σinh ≈ 2.5 σexc. We followed these guidelines: normally, we set gexc between 5 and 15 nS and σexc between 2.5 and 7.5 nS, because these choices (and the corresponding ones for the inhibitory train) produced spike rates in control conditions of 1–7 Hz and membrane potential fluctuations of 3–5 mV.
Figure 3.
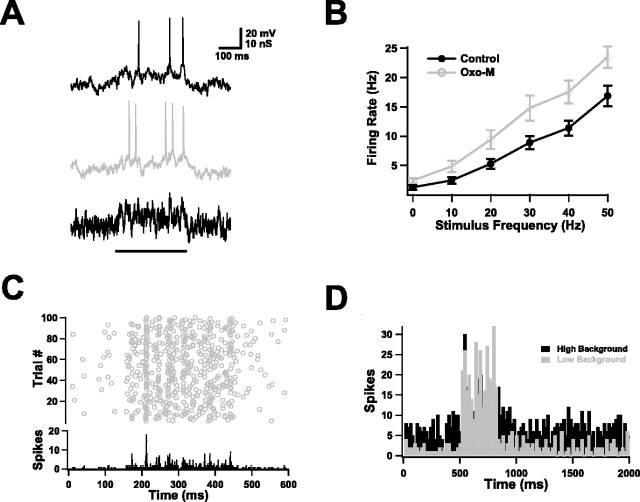
Dynamic clamp simulations. A, The noisy background input that motor cortical neurons receive in vivo was mimicked in vitro by injecting excitatory (gray) and inhibitory (black) conductance trains. These were generated independently as stochastic processes. Depicted at the left are typical examples. Fluctuations were normally distributed (middle) and were correlated at short times (right). B, Trains of synaptic inputs were generated by combining unitary AMPA and NMDA conductance transients. As shown, AMPA and NMDA transients were each modeled as a difference of exponentials and were activated simultaneously (left). The AMPA transients had much faster kinetics and were larger by a fixed amplitude ratio (10:1). The magnesium block of NMDA receptors was mimicked by multiplying NMDA conductances by a sigmoidal function (right). C, Slow ADP and AHP currents were introduced by simulating a spike-dependent conductance. Every time a neuron fired an action potential (black dots), this conductance was incremented. Between spikes, it decayed exponentially back to zero with a slow time constant (500 ms). The reversal potential was set to +50 mV (ADP) or −85 mV (AHP), depending on which current was being simulated.
Synaptic input trains were generated by combining unitary AMPA and NMDA conductances. Each unitary conductance was modeled by a difference of exponentials (Harsch and Robinson, 2000): g(t) = ḡ[exp(−(t − t0)/t) −exp(−(t − t0)/t)], for times t greater than or equal to the start time t0 of input and zero for earlier times (see Fig. 3B). Here, τr and τd are rise and decay time constants, and ḡ is a scaling factor. In addition, the magnesium block of NMDA receptors was approximated by multiplying its conductance by 1/[1 + K1exp(−K2V(t))], with K1 = 0.6 and K2 = 0.06/mV (Harsch and Robinson, 2000). The rise and decay time constants were set to 1 and 3 ms (AMPA) and 5 and 100 ms (NMDA). The scaling factor ḡ was varied between 0.5 and 4 nS for the AMPA conductance. We assumed that AMPA and NMDA conductances were always simultaneously activated, and that the NMDA scaling factor was always one-tenth the AMPA scaling factor, because this agrees with experimental measurements (Watt et al., 2000). The AMPA-NMDA reversal potential was 0 mV.
A potassium leak conductance was added (or subtracted) by setting gleak to a positive (or negative) constant value with reversal potential −85 mV. A potassium M conductance was modeled in the standard Hodgkin–Huxley way, with a conductance g(t) equal to gmaxm(t). The maximal conductance gmax was varied between −2 and 2 nS (negative values being used to subtract from the endogenous M current). The activation gating variable m(t) evolved according to the following:
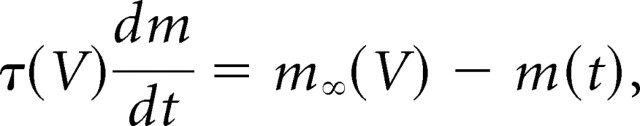 |
with τ(V) and m∞(V) given by the following (Fransen et al., 2002): τ(V) = {3.3exp[(V + 35)/40] + exp[−(V + 35)/20]}−1, m∞(V) = {1 + exp[−(V + 35)/5]}−1. Slow afterdepolarization (ADP) and afterhyperpolarization (AHP) conductances were simulated by a single conductance g(t). These are calcium-dependent conductances, but we were unable to simulate calcium dynamics in real time. Instead, we made the (reasonable) approximation of substituting spike dependence for calcium dependence:
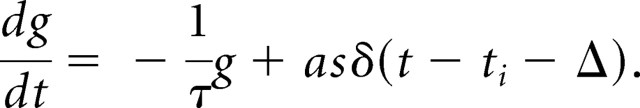 |
Here, τ is a decay time (=500 ms), {ti} are the spike times, Δ is a fixed delay (=10 ms), and δ(t) is the Dirac δ function. The amplitude by which the conductance was incremented with each spike was given by the product as, in which a scaling factor a varied between −1 and 2 nS and a saturation factor s = 5 × g/(5 + g). An example is shown in Figure 3C. The reversal potential was set either to +50 mV (ADP) or to −85 mV (AHP).
Results
We used a combination of current-clamp, voltage-clamp, and dynamic clamp techniques in these studies. The first two techniques were used to establish the basic muscarinic effects in forelimb motor cortical neurons and were similar to those used in previous studies in other brain areas (Magistretti et al., 2004). The third technique was used to introduce simulated synaptic or membrane conductances into neurons, allowing us to explore in a controlled and well-defined way the interaction between synaptic inputs and muscarinically modulated membrane conductances (Prinz et al., 2004). In the course of these studies, we simulated seven different conductances: excitatory and inhibitory synaptic inputs meant to mimic the noisy synaptic background activity cortical neurons experience in vivo; AMPA and NMDA conductance waveforms, which were combined to simulate synaptic trains; potassium leak and M conductances; and a spike-dependent conductance, which was used to approximate the effects of calcium-dependent conductances.
In all experiments, whole-cell patch recordings were obtained from regular spiking layer 5 pyramidal neurons in the forelimb region of postnatal day 16 (P16) to P21 primary motor cortex. We chose these neurons, because this is the class from which corticospinal neurons are drawn, their activity is closely tied to forelimb movements and is modified as rats learn fine motor skills, and data exist on the firing of these neurons in awake, behaving animals (Kaneko et al., 2000; Kleim et al., 2003; Kargo and Nitz, 2004). Moreover, in the motor cortex, a disproportionate share of cholinergic terminals is found near the somas of layer 5 neurons (Eckenstein et al., 1988). To activate muscarinic receptors, we bath applied the agonist Oxo-M (normally 1 μm), which is notable for its potency and its broad affinity for muscarinic receptors (Nishikawa et al., 1994). To verify this choice, we checked, in some experiments, that similar effects could be obtained by carbachol (n = 5) and could be blocked by atropine (n = 5).
Basic phenomena
Activation of muscarinic receptors modifies numerous postsynaptic ion channels and can alter intrinsic neuronal physiology in multiple ways, depending on cell type. In the case of pyramidal neurons, the effects, broadly speaking, can collectively be described as “increasing excitability” (Schwindt et al., 1988; McCormick, 1993; Barkai and Hasselmo, 1994; Fraser and MacVicar, 1996; Haj-Dahmane and Andrade, 1996, 1998; Klink and Alonso, 1997). However, this generalization masks differences in detailed effects between different brain areas and even between different cortical layers. It was therefore important, before beginning dynamic clamp experiments, to use standard current-clamp techniques to characterize muscarinic effects in the neurons under study here. We did this mainly for illustrative purposes, to provide a baseline of behavior to compare with previous studies of muscarinic modulation in other neurons and to contrast with muscarinic modulation when in vivo-like background activity is introduced. In these experiments, neurons were in the quiescent state typical of the slice preparation (a resting potential well below threshold, had a high input resistance, had very small membrane potential fluctuations), and were probed by the injection of DC steps.
Application of Oxo-M had several effects (n = 20 for all). The most consistent were a depolarization of the resting membrane potential (control, −69 ± 0.6 mV; Oxo-M, −62.6 ± 0.9 mV; p < 0.001) and an increase in the resting input resistance (control, 177 ± 11 MΩ; Oxo-M, 212 ± 13 MΩ; p < 0.001). The latter was quantified from the deflection produced by a small, hyperpolarizing current step. These two effects made it markedly easier for small inputs to initiate spike firing. When measured from a holding potential of −70 mV (and consequently reflecting the input resistance change alone), the threshold or rheobase current dropped from 88 ± 8 to 66 ± 7 pA (p < 0.05). In contrast, the threshold potential, estimated from the rate of rise of the membrane potential, was not measurably altered (control, 30 ± 1 mV above rest; Oxo-M, 31 ± 1 mV), presumably because sodium channels are only weakly affected by muscarinic activation. The sag potential, measured by delivering a −100 pA current step from a holding potential of −70 mV, was also unaltered (control, 2.2 ± 0.2 mV; Oxo-M, 2.4 ± 0.4 mV).
Two common effects of muscarinic activation in pyramidal neurons are to increase the number of action potentials generated by sustained currents and to reduce spike frequency adaptation (McCormick, 1993). We observed both phenomena after agonist application. Not only was the threshold current reduced, but neurons fired much more strongly to DC steps over a wide range of amplitudes. Average data on the numbers of spikes elicited by long steps are shown in Figure 1B (top panel) (n = 20); all differences above 40 pA are significant (p < 0.05), and all differences above 60 pA are highly significant (p < 0.01). These data actually underestimate the impact of muscarinic activation, because the steps were always delivered from a holding potential of −70 mV (maintained by DC) and thus do not reflect any contribution from the depolarization effect. To a considerable extent, the increase in spike number was the result of reduced spike frequency adaptation. Pyramidal neurons often show strong adaptation, with spike frequencies that are more than halved after only a few spike intervals. The neurons recorded here did this as well (Fig. 1B, bottom) (n = 20) in control conditions. After muscarinic activation, this drop-off in spike frequency was confined primarily to the first spike interval, with steady firing later in the train. In a few neurons, we found that not only was adaptation reduced, but for some current steps, it was actually reversed, with faster firing during later intervals (n = 5 of 20).
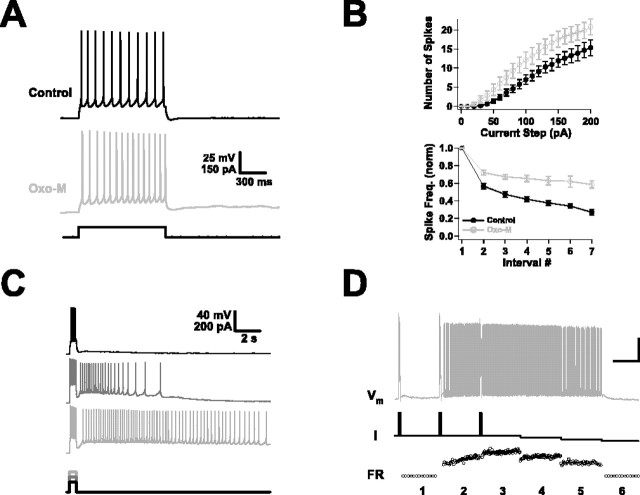
Figure 1.
Muscarinic effects in the absence of background activity. A, Firing of a layer 5 pyramidal neuron in forelimb motor cortex before (Control) and after (Oxo-M) application of Oxo-M in response to a DC step. In this case, muscarinic activation reversed spike frequency adaptation, causing the instantaneous frequency to increase rather than decrease over the course of the spike train. (In all figures, when data from control and Oxo-M conditions are plotted together, the former are in black, and the latter are in gray.) B, Muscarinic receptor activation increased the average number of spikes produced by a 1 s DC step consistently over a wide range of amplitudes (top panel). On average, it also reduced, but did not reverse, spike frequency adaptation. Plotted in the bottom panel are the instantaneous spike frequencies produced by a 200 pA current step as a function of spike interval number, normalized to the frequency for the first interval (n = 20 for both graphs). C, Muscarinic receptor activation replaced the burst afterhyperpolarization with a burst afterdepolarization. The size of the afterdepolarization varied with the intensity of the burst and could give rise to prolonged spike firing. Shown is the response of one neuron in the presence of Oxo-M to current injections of three different amplitudes (bottom traces). D, In some neurons, the afterdepolarization produced persistent graded activity. The top trace (Vm) shows spike firing induced by the current injections of the middle trace (I). Note that the instantaneous firing rate (FR) shown in the bottom trace could be ramped up or down in a controlled, step-like manner. Calibration: 25 mV, 100 pA; 6 Hz vertical; 10 s horizontal.
This kind of response is thought to be caused by slow calcium-dependent conductances, which also determine the afterpotentials that follow spike firing (Schwindt et al., 1992a,b). Modulation of these afterpotentials is perhaps the most striking feature of muscarinic activation. In control conditions, the firing of a small number of action potentials was typically followed by an AHP of a few millivolts, lasting for a few hundred milliseconds. After muscarinic activation, this AHP was eliminated and was replaced by an ADP (Fig. 1A). We found that the size and duration of the ADP depended strongly on the intensity of the firing that preceded it (Fig. 1C). Weak inputs, eliciting only two or three spikes, resulted in ADPs of 1 or 2 mV, lasting for a few hundred milliseconds; strong ones, in contrast, often blossomed into full-blown plateau potentials, keeping the neuron depolarized and firing spikes for periods ranging from seconds to minutes. In a small number of cases (n = 4 of 26), the plateau firing took on a special character: graded persistent activity (Egorov et al., 2002). Consecutive stimuli produced graded changes in firing rate that remained stable for seconds after each stimulus ended and could be moved up or down in a step-like manner (Fig. 1D).
Membrane currents modulated by muscarinic activation
Having established the basic phenomenology of muscarinic modulation using standard current-clamp techniques, we next used standard voltage-clamp techniques to identify the responsible postsynaptic membrane currents, guided in this by the existing literature (McCormick, 1993; Haj-Dahmane and Andrade, 1996, 1998; Klink and Alonso, 1997; Magistretti et al., 2004).
Two potassium currents were clearly affected by muscarinic activation: a leak current and the M current (McCormick, 1993; Shah et al., 2002). Both were measured in solution containing tetrodotoxin (1 μm) and cadmium (0.4 mm) to block sodium and calcium currents. The voltage step commands used to elicit these and other currents are depicted in the left-most column of Figure 2. The leak current was reduced by ∼25% (Fig. 2A) (35 ± 5 to 26 ± 2 pA; n = 12; p < 0.05), consistent with the increase in input resistance. This current is also primarily responsible for the depolarization effect. The M current was reduced by more than half (Fig. 2B) (198 ± 34 to 76 ± 28 pA; n = 12; p < 0.01), although these data overestimate its size because they were obtained with calcium currents blocked. Calcium influx tends to suppress the M current (Hu et al., 2002); in fact, we were not able to measure it when we did not include cadmium in the external solution (n = 3). This would argue against the M current being a major influence in the observed firing behavior, a point to which we discuss below.
Figure 2.
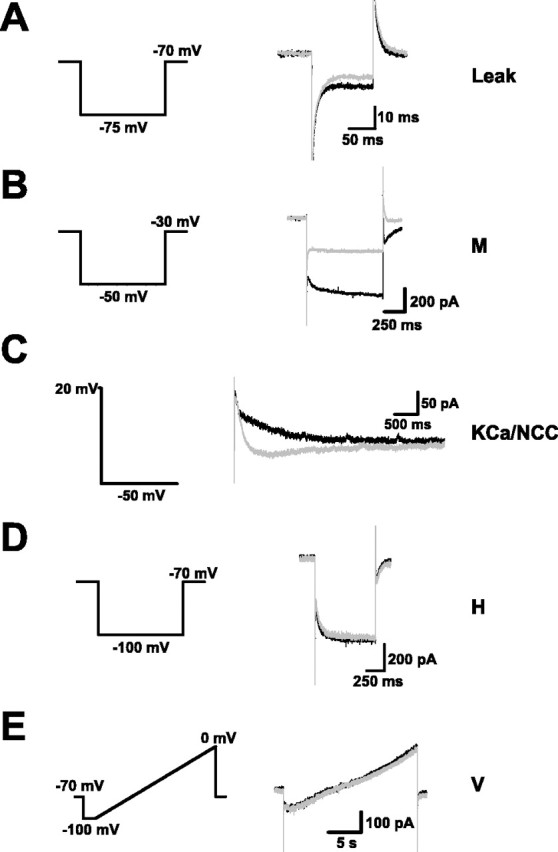
Voltage- and calcium-dependent currents responsible for observed effects. The voltage- and calcium-dependent currents responsible for the effects of muscarinic receptor activation were isolated and measured using standard voltage-clamp techniques. The traces at the left illustrate the voltage-clamp commands used to elicit different currents. Example currents of each type are shown at the right and include currents recorded before (black) and after (gray) application of Oxo-M. A, The potassium leak current was reduced by Oxo-M. B, The potassium M current was also reduced. C, A calcium-activated potassium current (KCa) was blocked and replaced by a calcium-activated nonspecific cation current (NCC). D, There was no effect on the hyperpolarization-activated current (H). E, There was no evidence for a voltage-dependent, nonspecific cation current (V).
As noted above, calcium-dependent currents are responsible for adaptation during spike firing and for afterpotentials. Quantifying them is difficult because they depend not on voltage, which is simple to control, but on calcium, which is not. With tetrodotoxin in the external solution, we elicited calcium-dependent currents by stepping the membrane potential briefly (100 ms) to +20 mV from a holding potential of −50 mV. We also used cesium substitution for potassium to identify ionic components. The results are shown in Figure 2C. In control conditions, currents were outward and carried by potassium and included fast/medium (<50 ms) and slow components (average peak current, 58 ± 12 pA; n = 13). After application of Oxo-M, the fast/medium component was essentially unaffected, but the slow component was entirely blocked and replaced by a slow inward current carried mainly by sodium (average peak current, −31 ± 11 pA; n = 13). This agrees well with previous studies (Schwindt et al., 1988) and with the current-clamp data, which show that, with muscarinic activation, spike frequency adaptation is confined to the earliest part of a spike train.
Some reports have identified the hyperpolarization-activated H current as a target of muscarinic modulation (Wischmeyer and Karschin, 1997; Zhu and Ulrich, 1998). However, we found that application of Oxo-M did not alter the H current (Fig. 2D) (control, 123 ± 33 pA; Oxo-M, 112 ± 30 pA; n = 12), a finding consistent with the unchanged sag potential. In the prefrontal cortex, a voltage-gated nonspecific cation conductance activated by muscarinic receptors has been identified (Haj-Dahmane and Andrade, 1996). It has been argued that it contributes to muscarinic depolarization and that previous studies in other parts of the cortex may have been misinterpreted, because it was not considered. We attempted to determine whether such a current exists in forelimb motor cortex by applying slow voltage ramps with other currents blocked, but we found no evidence for this (Fig. 2E) (n = 3).
Introducing in vivo background into in vitro neurons
Thus far, we characterized muscarinic modulation of forelimb motor cortical neurons in standard ways, using DC and voltage steps. These approaches are important and useful but, as we argue in the Introduction, they are also limited in that they fail to capture the high-conductance conditions of cortical neurons in vivo (Destexhe et al., 2003). In the intact brain, neurons receive a complex barrage of excitatory and inhibitory synaptic inputs. This synaptic background can take on a number of forms (e.g., sparse firing, rhythms, synchronous firing) depending on brain region and behavioral state. In choosing background inputs for our case, we were guided by single-unit recordings in forelimb motor cortex of behaving animals, which indicate that neurons generally fire irregularly at 1–10 Hz in the absence of forelimb movements (Kargo and Nitz, 2004).
A useful way of constructing background inputs consistent with this type of firing is offered by the “point conductance” method of Destexhe et al. (2001), which not only has been validated against in vivo recordings and model simulations but has the distinct advantage of physically meaningful parameters. One simulates excitatory and inhibitory background inputs by constructing two conductance trains, each generated by a stochastic (Ornstein-Uhlenbeck) process. As illustrated in Figure 3A, the resulting trains do a random walk in time around their mean, with fluctuations that are normally distributed and correlated at short times. To define each process, one must specify three parameters: a mean g0, an SD σ, and a decay time τ. We set the decay times at 2.5 ms (excitatory) and 8 ms (inhibitory), reflecting typical kinetics of glutamatergic and GABAergic synapses. The mean values and SDs were varied between neurons with two constraints: the inhibitory mean was four to five times larger than the excitatory one, with a deviation that was two to three times larger. These ratios were determined by fits to in vivo and model data (Destexhe et al., 2001; Fellous et al., 2003; Rudolph and Destexhe, 2003b). The preponderance of inhibitory conductance also makes physiological and anatomical sense: inhibitory interneurons tend to fire at higher rates, inhibitory synapses depress less and are more localized near the somatic/axonal site of spike generation, and the driving force (distance to the reversal potential) for inhibitory inputs is four to five times smaller than that for excitatory inputs at typical resting potentials.
The background conductances were introduced into neurons via a dynamic clamp circuit (Fig. 4A) (Robinson and Kawai, 1993; Sharp et al., 1993). As demonstrated previously (Fellous et al., 2003), the point conductance method reproduces several key features of the in vivo state: membrane potentials depolarized by ≈15 mV, membrane potential fluctuations of 3–5 mV (SD), and a threefold to fivefold drop in input resistance (Fig. 4B). We explored a range of conductance parameters, but normally we set them to achieve spontaneous firing rates in control conditions of 1–5 Hz.
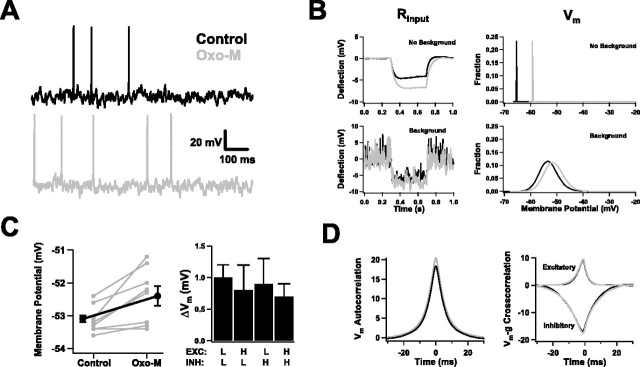
Figure 4.
Subthreshold behavior in the presence of background activity. A, Membrane potential recordings from one neuron before (Control; black trace) and after (Oxo-M; gray trace) application of Oxo-M. B, Examples of input resistance and membrane potential measurements, with and without background activity and/or muscarinic receptor activation. In the absence of background activity (top panels), the input resistance was large, and the membrane potential fluctuated only in a very narrow band. Application of Oxo-M produced marked changes in both (Control, black traces; Oxo-M, gray traces). Addition of background activity (bottom panels) reduced the input resistance, depolarized the membrane potential, and introduced wide fluctuations in its value. In this case, muscarinic effects were still stereotyped but much smaller. Input resistance was estimated from the voltage deflection produced by a hyperpolarizing current step (top, 20 pA; bottom, 150 pA). C, The effect of muscarinic receptor activation on membrane potential was small but reliable. Left, Values for individual cells before and after Oxo-M (gray traces) for one choice of excitatory/inhibitory parameters (those shown in Fig. 3A). The black trace is the average over all cells (n = 8). Right, Average change in membrane potential resulting from Oxo-M application for four different choices of background parameters. Excitatory and inhibitory mean conductances were independently varied between low (L) (gexc = 6 nS; ginh = 24 nS) and high (H) (gexc = 8 nS; ginh = 32 nS) values (n = 7). D, The autocorrelation of the membrane potential and its cross-correlation with the excitatory and inhibitory background conductances were similar before (black) and after (gray) muscarinic receptor activation. Correlations for a representative cell are shown.
Behavior in the presence of background activity
To investigate muscarinic modulation, we applied Oxo-M to neurons while introducing simulated background activity. Both subthreshold and suprathreshold effects were altered by the presence of the background.
What had been large, distinct effects on passive properties in the quiescent state were strikingly reduced in the active state. Without background, Oxo-M application increased resting input resistance by ∼30%. This was mainly through a block of leak channels, which removed 1–2 nS of conductance from the membrane, a significant fraction of the total 5–6 nS membrane conductance these neurons have absent synaptic inputs. However, in vivo, when embedded in an active network, total membrane conductance is dominated by synaptic conductances not by intrinsic ones. Basal synaptic activity increases total conductance by a factor of 4 or 5. To mimic in vivo firing patterns, we typically used excitatory and inhibitory conductances of 6 and 24 nS. These numbers reduced the muscarinic effect on input resistance substantially; it was still measurable but was now less 10% (Fig. 4B, left).
Muscarinic depolarization was similarly diminished (Fig. 4B, right), because the resting potential also was determined primarily by synaptic inputs. Without background, subthreshold resting potentials averaged −69 mV in control conditions and depolarized 6 mV when the agonist was applied. With background, however, the control average rose to −53.0 ± 0.1 mV, and the depolarization, while still a reliable muscarinic effect, was an order of magnitude smaller (0.7 ± 0.2 mV; p < 0.02) (Fig. 4C, left). These numbers were obtained using a single set of background parameters, but similar results could be obtained even if the parameters were varied by as much as a third (Fig. 4C, right). As long as the background was such that spontaneous firing was of order several spikes per second, the response to Oxo-M was not sensitive to the precise choice of parameters. Other features of the subthreshold membrane potential were not affected by muscarinic activation, including the size of its fluctuations, its autocorrelation, and its dependence on synaptic inputs (Fig. 4D). It is worth noting in Figure 4D how closely the membrane potential tracks the synaptic conductances: its autocorrelation decays exponentially with a time constant of ∼6 ms (i.e., intermediate between τexc and τinh), and it is determined predominantly by the inhibitory conductance, which is both larger than the excitatory one and correlated over longer times.
We investigated suprathreshold behavior by recording long sequences of spike firing (1–6 min long). In general, firing resulting from the synaptic background in control conditions was consistent and approximately random in time, without frequent burst firing or other strong temporal characteristics (Fig. 5A). Application of Oxo-M nearly doubled average firing rates, again independent of the exact choice of parameters (p < 0.01) (Fig. 5B,C). The firing remained approximately random: the coefficient of variation of interspike intervals (ISIs) in both control and Oxo-M conditions averaged just under 0.9, which is close to the value (one) expected of Poisson firing (Fig. 5B, inset). Likewise, interspike interval histograms were approximately Poissonian in shape, with Oxo-M histograms having higher average rates (Fig. 5D). There was no sign of plateau firing, as when the background was not present.
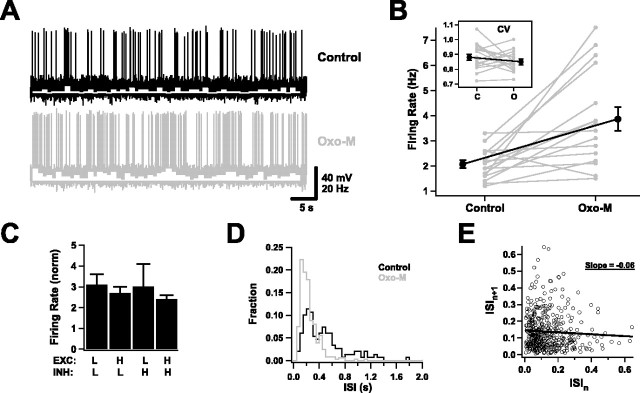
Figure 5.
Suprathreshold behavior in the presence of background activity. A, Spiking activity of a neuron in response to background inputs, before and after application of Oxo-M. Spike rate histograms are superimposed in white (bin size, 1 s). B, Average firing rates were reliably increased by muscarinic receptor activation. Gray traces are data for individual cells; the black trace is the average of all cells. The inset shows the coefficient of variation of ISIs (n = 16). C, The increase in firing rates was not sensitive to the exact choice of background parameters. The average firing rates in Oxo-M normalized to the control rates as the mean excitatory and inhibitory conductances were varied as in Figure 4C (n = 7). D, ISI histogram for a representative cell before and after Oxo-M. E, An example of an ISI return map, measured in the control condition. The circles are individual interspike intervals; the line is a linear fit, which has a negative slope.
Most of the effect of muscarinic activation on average firing rates was caused by the block of the potassium leak conductance. We demonstrated this by using the dynamic clamp circuit to reintroduce a simulated leak conductance (with a rever-sal potential of −85 mV) into neurons in an amount sufficient to reverse the changes Oxo-M had produced in resting input resistance and resting potential. Doing this reversed most of the increase in spike firing, which was reduced from 4.0 ± 0.7 to 2.6 ± 0.5 Hz (n = 7; p < 0.05). Likewise, subtracting 1–2 nS of potassium leak conductance with the dynamic clamp circuit boosted firing rates to levels only marginally smaller than those produced by Oxo-M application. Muscarinic block of the potassium leak had this effect not because its impact on overall conductance was so great (as noted above, it was not) but because it depolarized neurons by just under 1 mV. Although 1 mV sounds like a modest increase, the in vivo-like condition neurons are so depolarized, so close to threshold, that small fluctuations in membrane potential can trigger spikes. Consistent with this interpretation, depolarizing neurons with a small DC (≈50 pA, in addition to the background conductances) boosted firing rates substantially, whereas reducing membrane conductance without depolarizing (by setting the leak reversal potential of the dynamic clamp equal to the resting potential) had little effect.
However, the reduced leak conductance does not explain entirely the firing patterns observed in the presence of the muscarinic agonist. In particular, analysis of correlations between interspike intervals suggests that calcium-dependent conductances are also relevant. Although there were no gross temporal structures present in spike trains in control or Oxo-M conditions, which is why we describe firing as “random,” firing was weakly correlated. This was revealed by an analysis of ISI return maps (Wang, 1998). As illustrated in Figure 5E, such maps are constructed by plotting each interspike interval on the horizontal axis against the interspike interval that follows it on the vertical axis. If short intervals tend to be followed by long intervals, as they might if AHP currents are active, a linear fit to the points should be negatively sloped. In contrast, afterdepolarization currents, by making short intervals likely to be followed by even shorter intervals, should result in positively sloped fits. We found that, in our data, ISI return map slopes averaged −0.03 ± 0.02 in control conditions and +0.05 ± 0.03 in Oxo-M conditions (n = 16; p < 0.05). In 13 of 16 cells, application of Oxo-M made the return map slope more positive (p < 0.02; Fisher sign test). Thus, muscarinic replacement of slow AHP (calcium-dependent potassium) currents by slow ADP (calcium-dependent mixed cation) currents modulates, to a degree, the temporal pattern of background firing.
Conductance dominates background effects
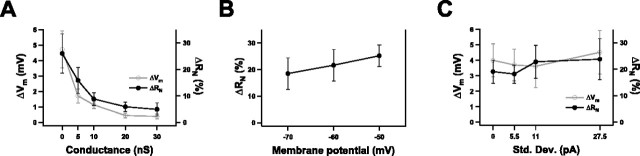
Background activity affects the neuronal resting state by introducing three distinct elements: an increase in overall conductance, a depolarization, and membrane potential fluctuations. To gauge the relative impact of these three elements on muscarinic modulation, we used the dynamic clamp circuit to introduce separately a DC conductance, a DC, and a fluctuating current.
These experiments demonstrated that the conductance increase was the most important aspect of the background. When the added conductance was 10 nS, Oxo-M application altered the resting potential by only 1 mV and the resting input resistance by only 10%. Increasing the DC conductance beyond 10 nS diminished muscarinically induced changes even more (Fig. 6A). In contrast, adding a DC had modest effects (Fig. 6B). Although the input resistance of these neurons was strongly voltage dependent, 36 ± 11% (n = 6; p < 0.05) larger at −50 mV than at −70 mV, there was only a small tendency toward larger muscarinically induced changes at the depolarized potential (McCormick and Prince, 1986). Adding current fluctuations, generated like the background conductances by an Ornstein-Uhlenbeck process, had essentially no effect on average resting potential or input resistance, whether in control or Oxo-M conditions (Fig. 6C).
Figure 6.
Dissecting the effects of conductance, depolarization, and fluctuations. Changes in membrane potential (ΔVm, in mV) and input resistance (ΔRN, as a percentage of control values) produced by Oxo-M application were measured as conductance, depolarization, and the size of membrane potential fluctuations were independently varied. A, A DC conductance reversing at the original resting potential was added (n = 7). B, A DC was used to fix the membrane potential at −70, −60, or −50 mV (n = 6). C, A fluctuating current was added (n = 5). The largest SD produced membrane potential fluctuations of ∼5 mV.
When a DC and a fluctuating current were combined (without the DC conductance), neurons fired irregular trains of action potentials. To compare these to firing patterns evoked by simulated background conductances, we first adjusted, in control conditions, the DC to depolarize neurons by 15 mV and the fluctuation amplitude to produce average spike rates of 2 Hz. We then applied Oxo-M. Doing so increased average firing rates by 295 ± 105%, more than twice the increase observed when background conductances were used (n = 7; p < 0.05). In addition, some neurons (n = 3 of 7) occasionally exhibited bouts of plateau firing, as were seen in quiescent conditions (Fig. 1C) but never with simulated background conductances.
Muscarinic activation increases sensitivity to correlated inputs
Forelimb movements are associated with transiently correlated firing of layer 5 neurons in rodent primary motor cortex. Usually, these neurons fire irregularly at 1–10 Hz, but when an animal makes a distinct forelimb movement (e.g., reaches for an object), neurons fire trains of action potentials, lasting several hundred milliseconds, averaging tens of spikes per second, and time locked on the reach. The learning of fine motor skills is closely tied to sharpening of the trains, with firing rates increasing and trains becoming significantly less variable from trial to trial (Kargo and Nitz, 2004). Learning is also closely tied to cholinergic innervation (Conner et al., 2003).
We therefore investigated how muscarinic activation affects the sensitivity of neurons to trains of synaptic inputs and ability to fire in a sustained manner. We did this by injecting simulated trains through the dynamic clamp circuit. This strategy allowed us complete control over and knowledge of the inputs, as well as the ability to focus on postsynaptic muscarinic effects independent of presynaptic ones. Synaptic trains were constructed by simulating varying numbers of presynaptic inputs (typically 20), each firing at a Poisson rate between 0 and 50 Hz. Synaptic conductance waveforms included both AMPA and NMDA components (Fig. 3B) (Harsch and Robinson, 2000). An example of a simulated train is shown in Figure 7A. Train duration was varied between 300 and 1000 ms. Trains were superimposed on background conductance activity that produced spontaneous spike rates of 1–3 Hz.
Figure 7.
Increased sensitivity to correlated inputs with muscarinic activation. A, Sensitivity to correlated inputs was probed by combining compound AMPA-NMDA transients in Poisson trains and adding these to the fluctuating background. An example of an excitatory conductance constructed in this way is shown in the bottom trace (the inhibitory background conductance is not shown); the simulated train is present during the time marked by the thick bar. Also shown are the responses of a neuron to this input before (top trace) and after (middle trace) activation of muscarinic receptors. B, Muscarinic receptor activation increased neuronal sensitivity to synaptic trains. Each train was constructed by simulating 20 presynaptic inputs, each with a maximal AMPA value of 1.5 nS, firing independently at a Poisson rate between 0 and 50 Hz. The response of each neuron to a train of a given frequency was measured over 10–50 trials, and a mean firing rate was calculated. Input trains lasted 300 ms. Shown are the firing rates, averaged over all cells, in response to trains of different frequencies. The rates at a stimulus frequency of 0 Hz are nonzero because of firing in response to background inputs (n = 9). C, Individual spike times were generally not precise because of the fluctuating background. The raster plot shows individual spikes elicited in one neuron by injecting the same train 100 times; it begins at time t = 150 ms and lasts 300 ms. The background was allowed to fluctuate randomly between trials. At the bottom is a spike histogram constructed using 1 ms bins. Only occasionally, as at t = 211 ms in this example, were spikes notably precise. D, Muscarinic inhibition of synaptic inputs might increase sensitivity to correlated inputs. Spike histograms constructed in response to 300 ms input trains (100 trials, 20 ms time bins) in the presence of high or low background activity.
Application of Oxo-M increased the response to trains over the entire range of stimulus frequencies examined (p < 0.01) (Fig. 7B), a result that is insensitive to the exact choice of parameters. Moreover, responses became more reliable, with less variability on repeated trials. We quantified this using the Fano factor, which is the variance in number of spikes per train divided by the average number. In Oxo-M, the Fano factor was significantly reduced. This was true even at the smallest stimulus frequency used (10 Hz), despite the presence of uncorrelated background firing that was higher in the Oxo-M condition (control, 0.90 ± 0.10; Oxo-M, 0.58 ± 0.09; p < 0.02; n = 9).
Although the number of spikes per train could be reliable, individual spike times were not. A sample spike rastergram, in which the same synaptic train is applied 100 times, is shown in Figure 7C. Only a minority of spikes were precisely timed. One can quantify this observation by calculating a reliability index (Harsch and Robinson, 2000), which is the fraction of spikes that appear in the same (5 ms) time bin in more trials than would be expected by chance. For both the control and Oxo-M conditions, the index averaged ∼0.2, with no difference between conditions (p > 0.25; n = 6).
Our focus is on how muscarinic activation affects postsynaptic membrane properties and how these, in turn, modulate neuronal response properties, but in the context of sensitivity to correlated inputs, it is worth noting one presynaptic effect: muscarinic activation tends to produce a general decrease in release probability at both excitatory and inhibitory synapses (Hasselmo and McGaughy, 2004). This might actually make neurons even more preferentially sensitive to correlated inputs, because although individual inputs themselves might be smaller, the background on which they sit would be smaller as well. Decreasing excitatory and inhibitory background inputs in a balanced way increases neuronal gain (Chance et al., 2002) and might allow correlated trains to stand out more, as it does in the example in Figure 7D.
Muscarinic activation improves sustained firing
With muscarinic activation, neurons became more sensitive to correlated inputs and responded by firing in spike trains of higher intensity. But what about the structure of the trains? As noted, spike frequency adaptation and spike afterhyperpolarizations are common response properties of pyramidal neurons, but these are produced mainly by slow AHP currents, which are blocked by muscarinic activation.
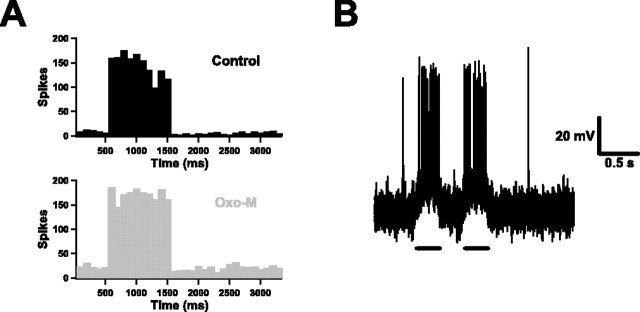
We addressed this question by constructing spike histograms after repeatedly (50–100 trials) delivering long synaptic input trains (Fig. 8A) and examining how sustained firing was during each train and whether firing was suppressed or enhanced immediately afterward. In control conditions, we found that neurons were not able to sustain firing at high rates (>10 Hz) over extended periods; there was a substantial drop-off in instantaneous firing rate toward the latter part of each train. The drop-off was not as dramatic as that seen in response to a DC step in the quiescent state (compare Fig. 1B) (Tang et al., 1997), but it was still striking. Also, spontaneous firing resulting from the fluctuating background was reduced for a short period (<300 ms) after the input terminated. However, both of these properties were eliminated by application of Oxo-M. With muscarinic activation, neurons were able to sustain firing at stable rates for as long as 1 s, and firing was slightly enhanced immediately afterward. On average, the ratio of the spike rate during the second half of a 1-s-long train to the rate during the first half was 0.79 ± 0.08 in control conditions but 1.04 ± 0.02 in Oxo-M conditions (n = 6; p < 0.05). The spike rate immediately after the train was 89 ± 18% of that immediately before the train in control conditions, but 129 ± 27% after muscarinic activation (n = 6; p = 0.10). On the basis of these data, we would argue that muscarinic activation greatly enhances the ability of neurons to signal in a sustained manner. The improved throughput accounts, in part, for the reduction in response variability (Fano factor data) (Fig. 7D).
Figure 8.
More sustained firing with muscarinic activation. A, Spike histograms for a neuron in the control condition and after application of Oxo-M (100 trials, 100 ms time bins). A 1 s input train was applied at t = 500 ms. Note the marked drop in numbers of spikes later in the train in the control case and contrast it with the stability of the muscarinic case. Note also that the spontaneous spike rate is depressed immediately after the input terminates in the control case. B, An example of the response of a neuron to two short inputs separated by 300 ms (10 trials are overlaid) in control conditions.
One of the most interesting roles suggested for the AHP current is to help mediate selective attention by allowing strong inputs to suppress the response to subsequent weak inputs (Wang, 1998). This is called forward masking and is illustrated, in the control condition, in Figure 8B. Two separate short-duration inputs are given with a small interval separating them; the response to the second is suppressed because of the presence of the first. This was also true on average: the second response was only 75% the size of the first response. In contrast, this was not true after application of Oxo-M (control, 74 ± 8%; Oxo-M, 115 ± 10%; n = 6; p < 0.01). If anything, the second response was slightly larger than the first, presumably because of the slow ADP current that muscarinic activation introduces. Therefore, it might be said that muscarinic activation replaces forward masking with priming, allowing for cooperation between separate inputs rather than competition. The time scale over which this is true is tight: unlike the quiescent state, when an afterdepolarization can last for seconds, with background activity the membrane potential is elevated for no >300 ms. Therefore, the time scale for synchronous inputs is widened by muscarinic activation, but not radically so.
Varying membrane conductances with the dynamic clamp
One limitation of using a pharmacological agent to investigate muscarinic effects is that it is difficult to titrate the level of activation. This is a concern, because one does not know a priori what activation level is the “real” one (i.e., pertains in vivo). In fact, there is no single true level: the concentration of acetylcholine undoubtedly fluctuates considerably even in the awake state as a result of variations in the firing of basal forebrain neurons and the actions of acetylcholinesterase. Moreover, the different conductances affected by muscarinic stimulation may be modulated to different degrees in different conditions. One way of addressing these concerns (of getting a sense of how sensitive neuronal response properties are to muscarinically modulated conductances) is to vary those conductances using the dynamic clamp circuit, achieving a degree of control that is not possible with pharmacology.
We focused on the effects on response properties of subtracting a potassium leak conductance and replacing the endogenous AHP conductance by a simulated ADP conductance. To simulate the calcium-dependent conductances, we made the useful approximation of substituting spike dependence for calcium dependence. That is, we assumed each conductance was triggered only by the calcium influx resulting from the firing of action potentials (Fig. 3C) (see Materials and Methods). To subtract the AHP conductance, its maximal conductance was made negative. As illustrated in Figure 9A, replacing the AHP by a simulated ADP reproduced basic features of spike firing in the presence of Oxo-M. We did not examine the role of the potassium M conductance in detail, because we found that subtracting it off with the dynamic clamp circuit, in an amount compatible with the voltage-clamp data, had only a small effect on neuronal responses (Fig. 9B).
Figure 9.
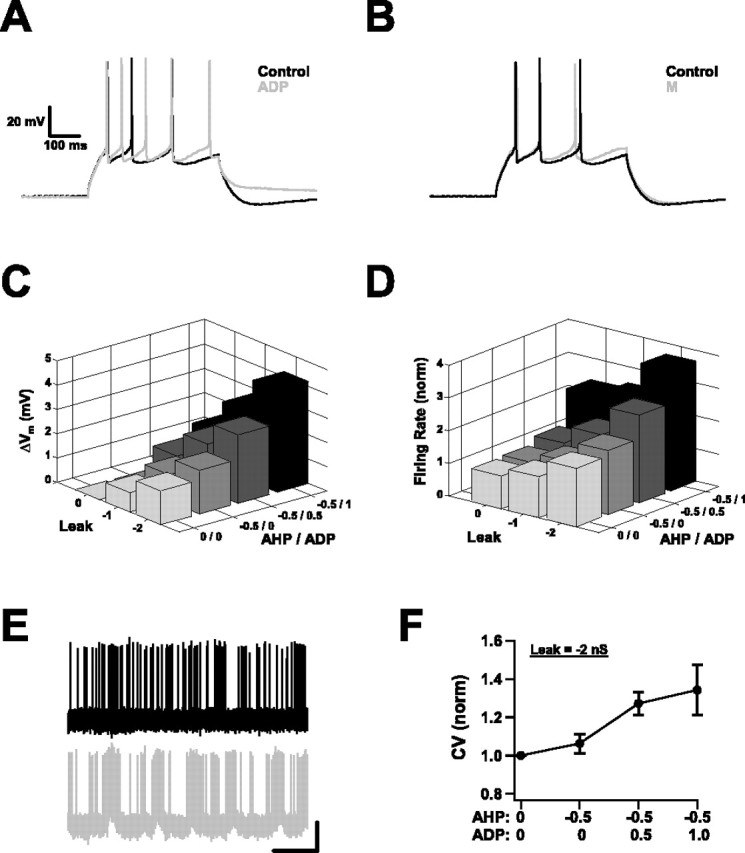
Varying membrane conductances with the dynamic clamp. A, A slow ADP conductance was introduced through the dynamic clamp and mimicked many aspects of the muscarinically activated slow ADP. The response of a neuron to a DC step (in the absence of background activity) before (Control) and after (ADP) introduction of the simulated conductance is shown. Note the reduced spike frequency adaptation and the appearance of an afterdepolarization. B, Mimicking the suppression of the potassium M conductance of Oxo-M, by subtracting a simulated M-type conductance through the dynamic clamp, had only small effects. Response to a DC step before and after subtraction of an M conductance (gmax = 1 nS). Scale bars are the same as in A. C, Change in membrane potential produced by systematically varying leak and AHP/ADP conductances through the dynamic clamp, with background activity set to produce 1–3 Hz spiking. Negative numbers indicate the specified conductance was being subtracted. Conductances are given in nanosiemen (n = 7). D, Effect on average firing rates of systematically varying leak and AHP/ADP conductances. Rates are shown relative to the rate when no conductance was added or subtracted (n = 7). E, Replacing the endogenous AHP conductance (black) by a strong, simulated ADP conductance (gray) introduced temporal correlations into firing trains produced by background activity. This neuron displayed an increased tendency to fire in sustained bouts as a result. Calibration: 25 mV vertical, 1 s horizontal. F, The correlations introduced by the simulated ADP conductance were reflected by changes in the coefficient of variation of interspike intervals (n = 7).
Several things were evident as we varied the leak and AHP/ADP conductances systematically, in the presence of background inputs sufficient to produce 1–3 Hz spike firing. One was that all of the effects previously obtained by Oxo-M application could also be obtained in this way by manipulating just two sets of conductances. Most effects varied smoothly as the conductances changed; there was a continuum of behavior. In particular, both the resting potential and the firing rate were sensitive to both the leak and the AHP/ADP levels (Fig. 9C,D). The strongest effects were obtained when the two sets of conductances were varied together. The largest parameter values we chose were at the high end of what was plausible given our previous pharmacological experiments. Even so, the effects were still smaller than those observed in the absence of background activity.
The most notable difference between these experiments and the ones using Oxo-M was the tendency, when the leak and AHP conductances had been subtracted and the highest simulated ADP conductance was used, for neurons to respond to the background inputs by sporadically firing in sustained trains. Figure 9E shows a particularly clear example. The temporal correlations this tendency introduced were reflected in the average data by coefficients of variation of interspike intervals >1 (Fig. 9F). This can be contrasted with firing during pharmacological stimulation, which remained Poissonian although there were weak hints of temporal correlations in the ISI return maps. What this underscores is the idea that the conductance changes produced by muscarinic activation increase the likelihood of short, sustained bouts of spike firing. In previous sections, this was reflected in the responses to transiently correlated inputs; here, chance combinations of background inputs that previously could not elicit trains of spikes can now do so.
Discussion
Understanding how neurons and neural circuits work requires probing them in multiple ways to observe how they respond and determine what kinds of behavior are possible. Injecting current (normally steps, but also ramps and sinusoidal waves) is a standard way of doing this and has long been used to evaluate neuronal input–output characteristics and classify neurons. It has the advantage of simplicity, but it also has significant limitations: neurons in vivo live in a noisy environment, and their synaptic inputs are not currents but conductances. These two differences, noise and conductance, alter neuronal response properties in important ways (Destexhe et al., 2003). Among other things, they make responses inherently stochastic, sharply reduce the membrane time constant with corresponding effects on temporal characteristics, and modulate the context in which intrinsic membrane conductances act.
The motivation for our study was to address this issue directly for the case of muscarinic modulation in the forelimb motor cortex. We wished to describe neuronal response properties in conditions that more accurately reflect those found in the intact brain. The dynamic clamp method offered a powerful way of doing this, a way of creating a hybrid system of computer simulations and biological neurons (Prinz et al., 2004). Our two main findings are as follows: (1) many of the previously reported effects of muscarinic activation can be strongly attenuated by a random synaptic background to the extent that their importance should be re-evaluated, and (2) one preserved muscarinic effect is its ability to facilitate sustained firing, which has implications for plasticity.
Quiescent versus active conditions
Activation of muscarinic receptors has multiple effects on postsynaptic membrane properties. When probed by DC steps from the quiescent state typical of the slice preparation, these include a pronounced depolarization and increase in input resistance, plateau potentials, and persistent spiking activity. These effects, seen in many parts of neocortex and hippocampus, are striking and have provoked speculation about possible muscarinic roles in delay activity, working memory, and neuronal excitability (Jensen and Lisman, 1996; Egorov et al., 2002; Fransen et al., 2002).
A different picture emerges when probed instead by conductance trains in the presence of in vivo-like background activity. The most dramatic effects are much reduced in magnitude or absent altogether, depending on choice of background (see below). For subthreshold behavior, this is because neuronal conductance is dominated primarily by synaptic conductance in the intact brain (Destexhe and Pare, 1999). Intracellular recordings in both awake and anesthetized animals suggest that approximately four-fifths of resting conductance in neocortical neurons is from the intense barrage of excitatory and inhibitory synaptic inputs (Destexhe et al., 2003). Consequently, the changes in input resistance and resting potential seen in the quiescent state are significantly compressed, smaller by a factor of 3–10.
Likewise, muscarinic effects on spontaneous spiking activity are also attenuated in the presence of a random background. As described, the background produces spike rates of several hertz, membrane potential fluctuations of several millivolts, and an increase in conductance of several-fold. This affects muscarinic modulation both because it increases noise and because it decreases input resistance and membrane time constant. Absent the background, dramatic consequences result from muscarinic activation: large afterdepolarizations, lasting for seconds, which can give rise to prolonged bouts of spike firing. These phenomena are not only visually impressive but suggest ways in which circuit functions like mathematical integration or delay activity might be implemented. However, the addition of uniform background inputs essentially eliminates them. The membrane potential closely tracks fluctuations in the background conductances, and spontaneous firing patterns are correspondingly stochastic.
In contrast, one muscarinic effect is well preserved: sustained firing in response to transiently correlated inputs. In the deep layers of motor cortex, forelimb movements are associated with trains of action potentials lasting hundreds of milliseconds. As we have shown, muscarinic activation increases the intensity of such firing in response to a given input. Moreover, it improves throughput. In control conditions, pyramidal neurons cannot maintain sustained firing at high rates in response to a sustained conductance injection. This adaptation is diminished compared with the quiescent state because of the noise the background creates (Tang et al., 1997), but it is still significant. Activation of muscarinic receptors allows for sustained signaling by replacing the AHP with an ADP current. By doing this, it also makes the response more reliable and increases cooperativity between inputs, with early inputs now facilitating rather than suppressing later inputs.
Choice of background activity
When interpreting these data, it is important to recognize that we made a particular choice of background activity: a random, uniform bombardment by a mixture of excitatory and inhibitory inputs. We made this choice because it fits well with what is known about the firing of neurons in forelimb motor cortex in behaving rats (Kargo and Nitz, 2004; unpublished observations). Except for distinct forelimb movements, spike firing is consistent and approximately uniform over time. However, this will not be true of all brain regions in all behavioral states. For example, there is considerable evidence that neural oscillations and network synchrony can be prevalent and may play important roles in brain processing (Llinas, 1988; Buzsaki and Draguhn, 2004). It remains to be determined what impact these kinds of input, perhaps combined with random synaptic background, would have on muscarinic effects. Indeed, it is tempting to speculate that the enhanced throughput of correlated inputs (described above) might reflect just this type of situation.
Another caveat concerns the fact that acetylcholine levels and background activity are not independent of each other. In fact, cholinergic modulation helps to create the spiking patterns that characterize the awake state. This raises the question of how compelling it is to ask, as we have done, what effect activation of muscarinic receptors has on neurons experiencing a pre-existing level of background activity. Might the two be so intertwined that it is problematic to treat them as separate entities? We would argue that the answer to this question is no, for several reasons. The most straightforward are that cholinergic neurons do not simply fire constantly or randomly in the awake state (Lee et al., 2005), and that active states can be elicited by other neurotransmitters or by other means entirely (Shu et al., 2003). A more indirect argument can be made based on what is known about cholinergic modulation of motor cortex in vivo. When cholinergic inputs from basal forebrain are chemically lesioned, learning of motor skills is impaired, but performance of previously learned skills is not (Conner et al., 2003). This suggests that acetylcholine has fairly specific effects in motor cortex; it is not responsible for the general activity of the circuit, but, rather, is more narrowly involved in plasticity associated with learning. This idea is supported by tetrode recordings in unanesthetized rats, which reveal substantial spiking activity in forelimb motor cortex even when animals are asleep (W. J. Kargo and D. A. Nitz, unpublished observations). As acetylcholine levels drop appreciably during sleep, this also suggests that general motor cortical activity can be usefully approximated as separate from cholinergic activation.
These arguments should not be overstated. Of course, acetylcholine shapes circuit activity. Most importantly, acetylcholine is known to have large and diverse effects on inhibitory interneurons, which in turn can strongly affect network behavior (Xiang et al., 1998; Bandyopadhyay et al., 2005). This is an issue not addressed by this study.
Trains of action potentials and plasticity
That sustained firing in response to correlated inputs should be the aspect of muscarinic modulation best preserved after the addition of a fluctuating background is interesting given the role that such firing plays in the learning of motor skills (Kargo and Nitz, 2004). The most attractive idea is that the cholinergic system acts as a gate on the learning (Kilgard, 2003).
The results presented here would fit in well with this idea. Motor cortex is notorious for being resistant to synaptic plasticity (Castro-Alamancos et al., 1995). Standard protocols for potentiating synapses, both rate-based and timing-based, that work robustly at synapses in sensory cortices do not appear to do so in motor cortex (Hess et al., 1996; our unpublished observations). Possibly, this is because the dense inhibitory connectivity of agranular cortex may not allow neurons to achieve the depolarization levels necessary for potentiation (Sjostrom et al., 2001). Muscarinic facilitation of trains of action potentials would tend to facilitate potentiation by boosting the postsynaptic depolarization achieved by a strong input, allowing for greater cooperativity between inputs, and improving the coupling between input and output.
A second possibility involves what has been called intrinsic plasticity (i.e., the plasticity of the intrinsic electrical properties of individual neurons) (Zhang and Linden, 2003). Repetitive firing or strong stimulation increases intrinsic neuronal excitability (Sourdet et al., 2003; Cudmore and Turrigiano, 2004), an effect likely mediated in part by a reduction in AHP currents. Muscarinic activation, by transiently suppressing AHP currents, intensifies repetitive firing. This might then trigger intrinsic plasticity and allow the improved repetitive firing to persist even in the absence of muscarinic stimulation.
Footnotes
This work was supported by the Neurosciences Research Foundation and the Mathers Foundation. We are grateful to Robert Cudmore, Eugene Izhikevich, Douglas Nitz, and William Kargo for useful discussions; Eugene Izhikevich and Gennady Cymbalyuk for help with the dynamic clamp system; and Tanya Casimiro for technical assistance.
References
- Anderson JS, Lampl I, Gillespie DC, Ferster D (2000). The contribution of noise to contrast invariance of orientation tuning in cat visual cortex. Science 290:1968–1972. [DOI] [PubMed] [Google Scholar]
- Bandyopadhyay S, Sutor B, Hablitz JJ (2006). Endogenous acetylcholine enhances synchronized interneuron activity in rat neocortex. J Neurophysiol in press. [DOI] [PubMed]
- Barkai E, Hasselmo ME (1994). Modulation of the input/output function of rat piriform cortex pyramidal cells. J Neurophysiol 72:644–658. [DOI] [PubMed] [Google Scholar]
- Brunel N, Chance FS, Fourcaud N, Abbott LF (2001). Effects of synaptic noise and filtering on the frequency response of spiking neurons. Phys Rev Lett 86:2186–2189. [DOI] [PubMed] [Google Scholar]
- Buzsaki G, Draguhn A (2004). Neuronal oscillations in cortical networks. Science 304:1926–1929. [DOI] [PubMed] [Google Scholar]
- Castro-Alamancos MA, Donoghue JP, Connors BW (1995). Different forms of synaptic plasticity in somatosensory and motor areas of the neocortex. J Neurosci 15:5324–5333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chance FS, Abbott LF, Reyes AD (2002). Gain modulation from background synaptic input. Neuron 35:773–782. [DOI] [PubMed] [Google Scholar]
- Conner JM, Culberson A, Packowski C, Chiba AA, Tuszynski MH (2003). Lesions of the basal forebrain cholinergic system impair task acquisition and abolish cortical plasticity associated with motor skill learning. Neuron 38:819–829. [DOI] [PubMed] [Google Scholar]
- Cudmore RH, Turrigiano GG (2004). Long-term potentiation of intrinsic excitability in LV visual cortical neurons. J Neurophysiol 92:341–348. [DOI] [PubMed] [Google Scholar]
- Destexhe A, Pare D (1999). Impact of network activity on the integrative properties of neocortical pyramidal neurons in vivo. J Neurophysiol 81:1531–1547. [DOI] [PubMed] [Google Scholar]
- Destexhe A, Rudolph M, Fellous JM, Sejnowski TJ (2001). Fluctuating synaptic conductances recreate in vivo-like activity in neocortical neurons. Neuroscience 107:13–24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Destexhe A, Rudolph M, Pare D (2003). The high-conductance state of neocortical neurons in vivo. Nat Rev Neurosci 4:739–751. [DOI] [PubMed] [Google Scholar]
- Eckenstein FP, Baughman RW, Quinn J (1988). An anatomical study of cholinergic innervation in rat cerebral cortex. Neuroscience 25:457–474. [DOI] [PubMed] [Google Scholar]
- Egorov AV, Hamam BN, Fransen E, Hasselmo ME, Alonso AA (2002). Graded persistent activity in entorhinal cortex neurons. Nature 420:173–178. [DOI] [PubMed] [Google Scholar]
- Fellous JM, Rudolph M, Destexhe A, Sejnowski TJ (2003). Synaptic background noise controls the input/output characteristics of single cells in an in vitro model of in vivo activity. Neuroscience 122:811–829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fransen E, Alonso AA, Hasselmo ME (2002). Simulations of the role of the muscarinic-activated calcium-sensitive nonspecific cation current INCM in entorhinal neuronal activity during delayed matching tasks. J Neurosci 22:1081–1097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fraser DD, MacVicar BA (1996). Cholinergic-dependent plateau potential in hippocampal CA1 pyramidal neurons. J Neurosci 16:4113–4128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haj-Dahmane S, Andrade R (1996). Muscarinic activation of a voltage-dependent cation nonselective current in rat association cortex. J Neurosci 16:3848–3861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haj-Dahmane S, Andrade R (1998). Ionic mechanism of the slow afterdepolarization induced by muscarinic receptor activation in rat prefrontal cortex. J Neurophysiol 80:1197–1210. [DOI] [PubMed] [Google Scholar]
- Harsch A, Robinson HPC (2000). Postsynaptic variability of firing in rat cortical neurons: the roles of input synchronization and synaptic NMDA receptor conductance. J Neurosci 20:6181–6192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hasselmo ME, McGaughy J (2004). High acetylcholine levels set circuit dynamics for attention and encoding and low acetylcholine levels set dynamics for consolidation. Prog Brain Res 145:207–231. [DOI] [PubMed] [Google Scholar]
- Hess G, Donoghue JP (1999). Facilitation of long-term potentiation in layer II/III horizontal connections of rat motor cortex following layer I stimulation: route of effect and cholinergic contributions. Exp Brain Res 127:279–290. [DOI] [PubMed] [Google Scholar]
- Hess G, Aizenman CD, Donoghue JP (1996). Conditions for induction of long-term potentiation in layer II/III horizontal connections of the rat motor cortex. J Neurophysiol 75:1765–1778. [DOI] [PubMed] [Google Scholar]
- Ho N, Destexhe A (2000). Synaptic background activity enhances the responsiveness of neocortical pyramidal neurons. J Neurophysiol 84:1488–1496. [DOI] [PubMed] [Google Scholar]
- Hu H, Vervaeke K, Storm JF (2002). Two forms of electrical resonance at theta frequencies, generated by M-current, h-current and persistent Na+ current in rat hippocampal pyramidal cells. J Physiol (Lond) 545:783–805. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jensen O, Lisman JE (1996). Novel lists of 7±2 known items can be reliably stored in an oscillatory short-term memory network: interaction with long-term memory. Learn Mem 3:257–263. [DOI] [PubMed] [Google Scholar]
- Kaneko T, Cho R, Li Y, Nomura S, Mizuno N (2000). Predominant information transfer from layer III pyramidal neurons to corticospinal neurons. J Comp Neurol 423:52–65. [DOI] [PubMed] [Google Scholar]
- Kargo WJ, Nitz DA (2004). Improvements in the signal-to-noise ratio of motor cortex cells distinguish early versus late phases of motor skill learning. J Neurosci 24:5560–5569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kilgard M (2003). Cholinergic modulation of skill learning and plasticity. Neuron 38:678–680. [DOI] [PubMed] [Google Scholar]
- Kleim JA, Bruneau R, Calder K, Pocock D, VandenBerg PM, MacDonald E, Monfils MH, Sutherland RJ, Nader K (2003). Functional organization of adult motor cortex is dependent upon continued protein synthesis. Neuron 40:167–176. [DOI] [PubMed] [Google Scholar]
- Klink R, Alonso A (1997). Ionic mechanisms of muscarinic depolarization in entorhinal cortex layer II neurons. J Neurophysiol 77:1829–1843. [DOI] [PubMed] [Google Scholar]
- Lee MG, Hassani OK, Alonso A, Jones BE (2005). Cholinergic basal forebrain neurons burst with theta during waking and paradoxical sleep. J Neurosci 25:4365–4369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Llinas R (1988). The intrinsic electrophysiological properties of mammalian neurons: insights into central nervous system function. Science 242:1654–1664. [DOI] [PubMed] [Google Scholar]
- Magistretti J, Ma L, Shalinsky MH, Lin W, Klink R, Alonso A (2004). Spike patterning by Ca2+-dependent regulation of a muscarinic cation current in entorhinal cortex layer II neurons. J Neurophysiol 92:1644–1657. [DOI] [PubMed] [Google Scholar]
- McCormick DA (1993). Actions of acetylcholine in the cerebral cortex and thalamus and implications for function. Prog Brain Res 98:303–308. [DOI] [PubMed] [Google Scholar]
- McCormick DA, Prince DA (1986). Mechanisms of action of acetylcholine in the guinea-pig cerebral cortex in vitro. J Physiol (Lond) 375:169–194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitchell SJ, Silver RA (2003). Shunting inhibition modulates neuronal gain during synaptic excitation. Neuron 38:433–445. [DOI] [PubMed] [Google Scholar]
- Nishikawa M, Munakata M, Akaike N (1994). Muscarinic acetylcholine response in pyramidal neurones of rat cerebral cortex. Br J Pharmacol 112:1160–1166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prinz AA, Abbott LF, Marder E (2004). The dynamic clamp comes of age. Trends Neurosci 27:218–224. [DOI] [PubMed] [Google Scholar]
- Rasmusson DD (2000). The role of acetylcholine in cortical synaptic plasticity. Behav Brain Res 115:205–218. [DOI] [PubMed] [Google Scholar]
- Robinson HPC, Kawai N (1993). Injection of digitally-synthesized synaptic conductance transients to measure the integrative properties of neurons. J Neurosci Meth 49:157–165. [DOI] [PubMed] [Google Scholar]
- Rudolph M, Destexhe A (2003a). Tuning neocortical pyramidal neurons between integrators and coincidence detectors. J Comp Neurosci 14:239–251. [DOI] [PubMed] [Google Scholar]
- Rudolph M, Destexhe A (2003b). Characterization of subthreshold voltage fluctuations in neuronal membranes. Neural Comp 15:2577–2618. [DOI] [PubMed] [Google Scholar]
- Schwindt PC, Spain WJ, Foehring RC, Chubb MC, Crill WE (1988). Slow conductances in neurons from cat sensorimotor cortex in vitro and their role in slow excitability changes. J Neurophysiol 59:450–467. [DOI] [PubMed] [Google Scholar]
- Schwindt PC, Spain WJ, Crill WE (1992a). Effects of intracellular calcium chelation on voltage-dependent and calcium-dependent currents in cat neocortical neurons. Neuroscience 47:571–578. [DOI] [PubMed] [Google Scholar]
- Schwindt PC, Spain WJ, Crill WE (1992b). Calcium-dependent potassium currents in neurons from cat sensorimotor cortex. J Neurophysiol 67:216–226. [DOI] [PubMed] [Google Scholar]
- Shah MM, Mistry M, Marsh SJ, Brown DA, Delmas P (2002). Molecular correlates of the M-current in cultured rat hippocampal neurons. J Physiol (Lond) 544:29–37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharp AA, O’Neil MB, Abbott LF, Marder E (1993). Dynamic clamp: computer-generated conductances in real neurons. J Neurophysiol 69:992–995. [DOI] [PubMed] [Google Scholar]
- Shu Y, Hasenstaub A, Badoual M, Bal T, McCormick DA (2003). Barrages of synaptic activity control the gain and sensitivity of cortical neurons. J Neurosci 23:10388–10401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sjostrom PJ, Turrigiano GG, Nelson SB (2001). Rate, timing and cooperativity jointly determine cortical synaptic plasticity. 32:1149–1164. [DOI] [PubMed] [Google Scholar]
- Sourdet V, Russier M, Daoudal G, Ankri N, Debanne D (2003). Long-term enhancement of neuronal excitability and temporal fidelity mediated by metabotropic glutamate receptor subtype 5. J Neurosci 23:10238–10248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steriade M, Timofeev I, Grenier F (2001). Natural waking and sleep states: a view from inside neocortical neurons. J Neurophysiol 85:1969–1985. [DOI] [PubMed] [Google Scholar]
- Tang AC, Bartels AM, Sejnowski TJ (1997). Effects of cholinergic modulation on responses of neocortical neurons to fluctuating input. Cereb Cortex 7:502–509. [DOI] [PubMed] [Google Scholar]
- Wang XJ (1998). Calcium coding and adaptive temporal computation in cortical pyramidal neurons. J Neurophysiol 79:1549–1566. [DOI] [PubMed] [Google Scholar]
- Watt AJ, van Rossum MC, MacLeod KM, Nelson SB, Turrigiano GG (2000). Activity coregulates quantal AMPA and NMDA currents at neocortical synapses. Neuron 26:659–670. [DOI] [PubMed] [Google Scholar]
- Wischmeyer E, Karschin A (1997). A novel slow hyperpolarization-activated potassium current (IK(SHA)) from a mouse hippocampal cell line. J Physiol (Lond) 504:591–602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xiang Z, Huguenard JR, Prince DA (1998). Cholinergic switching within neocortical inhibitory networks. Science 281:985–988. [DOI] [PubMed] [Google Scholar]
- Zhang W, Linden DJ (2003). The other side of the engram: experience-driven changes in neuronal intrinsic excitability. Nat Rev Neurosci 4:885–900. [DOI] [PubMed] [Google Scholar]
- Zhu JJ, Ulrich D (1998). Cellular mechanisms underlying two muscarinic receptor-mediated depolarizing responses in relay cells of the rat lateral geniculate nucleus. Neuroscience 87:767–781. [DOI] [PubMed] [Google Scholar]
- Zsiros V, Hestrin S (2005). Background synaptic conductance and precision of EPSP-spike coupling at pyramidal cells. J Neurophysiol 93:3248–3256. [DOI] [PubMed] [Google Scholar]