Hippocampal Sharp Waves and Reactivation during Awake States Depend on Repeated Sequential Experience

Abstract

Hippocampal firing patterns during behavior are reactivated during rest and subsequent slow-wave sleep. These reactivations occur during transient local field potential (LFP) events, termed sharp waves. Theories of hippocampal processing suggest that sharp waves arise from strengthened plasticity, and that the strengthened plasticity depends on repeated cofiring of pyramidal cells. We tested these predictions by recording neural ensembles and LFPs from rats running tasks requiring different levels of behavioral repetition. The number of sharp waves emitted increased during sessions with more regular behaviors. Reactivation became more similar to behavioral firing patterns across the session. This enhanced reactivation also depended on the regularity of the behavior. Additional studies in CA3 and CA1 found that the number of sharp waves emitted also increased in CA3 recordings as well as CA1, but that the time courses were different between the two structures.

Introduction

Damage to the hippocampal formation causes memory deficits in the storage of facts, episodes, and new spatial environments. Analogous deficits are observed in both humans and animals after hippocampal lesions (Scoville and Milner, 1957; O'Keefe and Nadel, 1978; Kesner and Novak, 1982; Morris et al., 1982; Redish, 1999; Clark et al., 2000; Fortin et al., 2002). Hippocampal firing patterns observed during behavior are reactivated during subsequent sleep states (Pavlides and Winson, 1989; Wilson and McNaughton, 1994; Kudrimoti et al., 1999; Nádasdy et al., 1999; Sutherland and McNaughton, 2000; Hoffmann and McNaughton, 2002; Lee and Wilson, 2002). Based on the effects of sleep on task learning (Smith, 1995; Gais and Born, 2004, 2006), theories have suggested that these reactivations may be involved in memory consolidation processes (Marr, 1971; Squire, 1987; Buzsáki, 1989; Redish and Touretzky, 1998; Hoffmann and McNaughton, 2002). In rodents, neural correlates of spatial aspects of memory are found in the strong spatial tuning of the hippocampal pyramidal neurons (place cells) (O'Keefe and Dostrovsky, 1971; Redish, 1999). Tasks with repetitive spatial components have been used to study reactivation of spatially dependent firing patterns during slow-wave sleep (Wilson and McNaughton, 1994; Skaggs and McNaughton, 1996; Kudrimoti et al., 1999; Nádasdy et al., 1999; Lee and Wilson, 2002).

In the hippocampus, network states are characterized by distinct oscillatory patterns in the local field potentials (LFPs). In rats, hippocampal LFPs show two clearly identifiable oscillatory patterns: (1) a 7–10 Hz regular oscillation (theta), seen during attentive behaviors, such as running, as well as REM sleep; and (2) a more broad-spectrum pattern [large-amplitude irregular activity (LIA)], seen during other behaviors, such as grooming, eating, and slow-wave sleep (Vanderwolf, 1971; O'Keefe and Nadel, 1978). LIA is punctuated by transient LFP events termed sharp wave–ripple complexes (SWRs), identified by high-frequency (100–250 Hz) ripple oscillations (O'Keefe and Nadel, 1978; Buzsáki et al., 1983; Ylinen et al., 1995). During wakefulness, LIA and SWR brain states similar to those activated during sleep are observed (Vanderwolf, 1971; O'Keefe and Nadel, 1978). During these awake sharp waves, ensemble firing patterns are reactivated, and this activity appears to grow with time (O'Neill et al., 2006).

Theories of hippocampal function (Buzsáki, 1989; Shen and McNaughton, 1996; Redish and Touretzky, 1998; Redish, 1999) predict that asymmetric plasticity (Levy and Steward, 1983; Bi and Poo, 2001) applied to recurrent connections within CA3 through experience of repeated spatial sequences during theta will lead to storage of sequences within the recurrent connectivity matrix (Levy and Steward, 1983; Muller et al., 1991; Blum and Abbott, 1996; Redish and Touretzky, 1998). During states in which the network was uncoupled from its entorhinal inputs (e.g., slow-wave sleep and LIA) (Chrobak and Buzsáki, 1994, 1996; Chrobak et al., 2000), uncorrelated noise in the system would then cascade across these strengthened synapses producing a replay of this stored information during sharp waves (Buzsáki, 1989; Ylinen et al., 1995; Redish and Touretzky, 1998; Redish, 1999; Csicsvari et al., 2000). These theories predict that the emission of awake sharp wave–ripple events should increase in number with experience within a session and that the organization of ensemble firing during those awake sharp waves should improve with experience. These increases in sharp wave emission and reactivation should depend on the level of repetition of spatial sequences. Because experimental evidence suggests SWR activity in CA3 can initiate CA1 SWs in vivo and in vitro (Buzsáki et al., 1983; Csicsvari et al., 1999; Ylinen et al., 1995; Behrens et al., 2005), any changes in SW activity in CA3 should be observable in CA1 as well.

Materials and Methods

In experiment I, we explicitly examined the task dependence of sharp wave emissions and hippocampal ensemble reactivation in well trained rats running three tasks with different spatial requirements. Hippocampal neural ensembles and local field potentials were recorded from the CA1 region of six rats as they ran three behavioral tasks daily. The tasks included shuttling back and forth along a linear track (LT), foraging for scattered pellets in a cylindrical arena [“cylinder-foraging” (CF)], and navigating to a goal for food reward in the same cylindrical arena [“cylinder-goal” (CG)]. In experiment II, we compared the experience dependence of SWR emission in CA1 and CA3 in data from six rats trained to run a multiple-choice sequence task (MT) (Schmitzer-Torbert and Redish, 2004).

Animals

Male Fisher–Brown–Norway hybrid rats (Harlan, Indianapolis IN), 7–14 months of age at the time of implantation, were maintained on a synchronous day/night cycle. Animals were handled for at least 1 week before beginning behavioral training. Rats were food deprived to no less than 80% of their body weight during behavioral training; water was freely available in the home cage at all times. All procedures were in accordance with National Institutes of Health guidelines for animal care and were approved by the Institutional Animal Care and Use Committee at the University of Minnesota.

Experiment I: behavior, surgery, and neurophysiological recordings

Food-deprived rats were trained to run on a series of multiple tasks, including shuttling back and forth along a 137 × 15 cm linear track (LT), foraging for scattered pellets in an 92-cm-diameter cylindrical arena (CF), or navigating to a small, invisible goal for food reward in the same cylindrical arena (CG). Linear track was similar to the shuttling tasks studied by O'Keefe and Recce (1993) and others: two to four (depending on the animal and session) 45 mg food pellets (TestDiet, Richmond, VA) were delivered via automated feeders (Med Associates, St. Albans, VT) when the animal reached the end of the track. Animals were required to alternate between track ends to receive food. Paths are highly repeatable on the linear track. The CF task was a variant of that studied by Muller et al. (1987) and others: food was delivered randomly into the cylinder at random intervals providing pellets approximately six times a minute. The 45 mg food pellets were delivered from one of three sites (randomly) above the cylinder. The food distribution that reached the cylinder floor was uniform and random. The CG task was a variant of that studied by Rossier et al. (2000) and Olypher et al. (2002): to receive food, the rat had to cross a 7-cm-diameter goal. Once the rat entered the goal region, a tone was played and three pellets were delivered from the automated feeders. Like the CF task, the food scattered randomly on dispensing. The goal was not rearmed until the rat had been outside a 14 cm surrounding region for 4 s. The goal was randomly placed on each session, but remained at a constant location within each session. Because the CF and CG tasks used the same arena, the arena was wiped down with 70% isopropyl alcohol before each CF and CG task to reduce carryover of odor cues.

Training began with 30–40 min sessions on a single task (task training order counterbalanced across rats) until an animal was proficient on that task: full coverage of arena on CF, at least 30 successful goal entries on CG, and at least 50 laps on LT. Animals were then trained on the next task to proficiency. This continued until animals had been trained on each task individually. This usually took ∼1 week per task. Next, animals were trained for at least 4 d on the three-task protocol such that they encountered each ordering at least once: LT–CF–CG, LT–CG–CF, CF–CG–LT, and CG–CF–LT. Thus, final-training and the postimplantation recording sessions consisted of 20 min exposure to each of the three tasks pseudorandomly ordered each day with a 5 min rest period before and after each task. Goal location also varied pseudorandomly each day.

Once a rat was running proficiently on all three tasks, it was implanted with a 14-tetrode microdrive (Kopf Neuro-Hyperdrive; 12 tetrodes and two references) at bregma, 3.8 mm posterior, 2.0–2.5 mm right mediolateral. Animals were allowed 2 d to recover, during which electrodes were advanced toward the CA1 pyramidal cell layer. Animals were retrained on the three-task protocol until electrodes were in place. Recordings were then taken from the pyramidal layer of the CA1 region of hippocampus. The pyramidal layer was identified by the presence of strong high-frequency (100–250 Hz) ripples (Ylinen et al., 1995). LFPs were recorded using 16 channels of a Neuralynx (Tucson, AZ) 64 channel Cheetah system and were sampled at 2 kHz and bandpass filtered from 1 to 425 Hz.

For experiment I, 1 ms, 32-sample spike waveforms were recorded to disk when extracellular potentials crossed a preset threshold. Waveform features were calculated and clustered using a combination of automatic and manual clustering algorithms (MClust; A. D. Redish et al.; http://mclust.sourceforge.net) (Klustakwik; K. D. Harris et al.; http://klustakwik.sourceforge.net). Only clusters with firing rates <2 Hz were used; these tended to have the characteristic bursting interspike interval (ISI) typical of hippocampal pyramidal neurons. Neurons whose waveforms were not stable enough across the entire session to reliably cluster or whose waveforms drifted toward the spike detection threshold were not clustered and were excluded from additional analysis. Clusters with very short interspike intervals (2 ms) were not clustered and were excluded from additional analysis. The data reported here were based on using all cells that met the above criteria. However, only including clusters with high quality (Schmitzer-Torbert et al., 2005) (L-ratio, <0.2; isolation distance, >15) produced qualitatively similar results. Figure 1 shows an example of seven hippocampal pyramidal neurons recorded simultaneously from one tetrode, their waveforms, clusters, ISI histograms, and cluster quality values.

Figure 1.

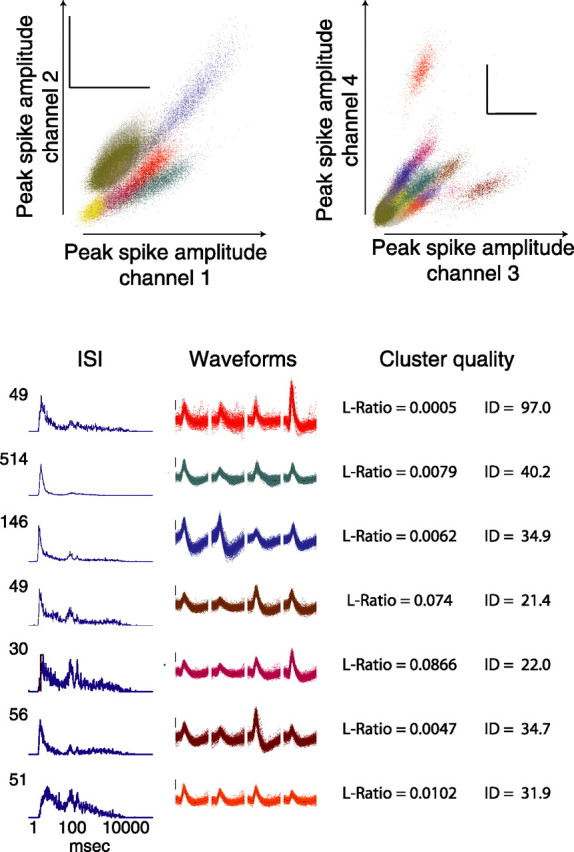
Example tetrode recordings: clustering, waveforms, and firing patterns. Spikes were clustered according to multiple waveform features including peak spike amplitude, energy, and principal components. Clustered spikes are shown with different colors for each cluster on two projections: peak spike amplitude on channel 1 versus channel 2, and peak amplitude on channel 3 versus channel 4. One millisecond waveforms for 7 of the 16 separable clusters are shown below color-coded by cluster color. ISI histograms from each neuron are typical of hippocampal pyramidal neurons. Calibration, 100 μV. ID, Isolation distance.

For all analyses and controls except the reactivation and transition entropy analyses versus experience, data from each session were transformed using a z-score analysis based on mean and SD over the first 30 laps. On the hidden-goal task (CG), the time between successful goal triggers, was considered a lap. These lap times were used for the analysis of the matching foraging task (CF) for that day. For each task, only sessions with 30 laps or more were considered on the three-task sessions (LT, n = 6 rats; CF, n = 7 rats; CG, n = 7 rats). See Table 1 for session and neuron yields. For the reactivation analysis, only sessions with >20 neurons recorded simultaneously were used (n = 10 sessions from three rats).

Table 1.

Session availability and neuron yields per rat for experiment I

Rat no.	No. sessions	No. neurons	No. interneurons	No. pyramidal
R031	6	107	11	96
R035	5	33	5	28
R039	7	23	2	21
R041	8	240	16	224
R044	3	0	0	0
R047	5	9	1	8
R048	7	284	25	259
Total	41	696	60	636

All rats ran the LT, CF, and CG tasks each day. No., Number.

Experiment II: behavior, surgery, and neurophysiological recordings

Food-deprived rats were trained to run for food on a multiple-choice sequence-learning task consisting of 4T choices with return rails after the final turn, making it a lap-based task (Schmitzer-Torbert and Redish, 2002, 2004). The track used for the multiple-T task consisted of an elevated (20 cm above the floor), 10 cm wide, carpet-covered, plywood track. The maze itself consisted of a set of three to five T-shaped tracks (stem, 30 cm; each choice arm, 18.5 cm) placed within a large outer rectangular track [140 cm (3Ts) to 220 cm (5Ts) × 142.5 cm]. Rats were required to run through the central sequence of Ts, making a final choice when they reached the top rail of the outer square. They then proceeded along the top rail of the outer square, back along a return rail, and returned to the start of the sequence. Food was provided at two sites on each return rail. An error on a T led to a deadend and required the animal to turn around to return to the correct path. The final choice entailed a decision about which return rail to use. On any specific day, only one pair of sites (i.e., the right or left return rail) was active and provided food reward. The other pair of feeders remained in their usual positions on the track but did not provide reward. The sequence of choices remained constant within a day, but changed between days. Rats were allowed to run for one 40 min session each day.

Rats were first trained on 3T sequences for 1 week, and then trained on 5T for 1 week. Once a rat was running proficiently on a five-choice task (>50 laps per day for at least 3 d), it was implanted with a 14-tetrode microdrive (Kopf Neuro-Hyperdrive; 12 tetrodes and two references) at bregma, 3.8 mm posterior, 2.0–4.0 mm right mediolateral. Recordings were taken from the pyramidal layer of the CA1 or CA3 regions of hippocampus (3× CA1, 2.0–2.5 mm right mediolateral; 3× CA3, 4.0 mm right mediolateral). For example recording locations (CA1 vs CA3), see Figure 2. Table 2 reports the number of sessions available from each animal and the recording location for each animal. The pyramidal layer was identified by the presence of strong high-frequency (100–200 Hz) ripples (Ylinen et al., 1995; Csicsvari et al., 1999). LFPs were recorded using 16 channels of a Neuralynx 64 channel Cheetah system, and were sampled at 2 kHz and bandpass filtered from 1 to 425 Hz.

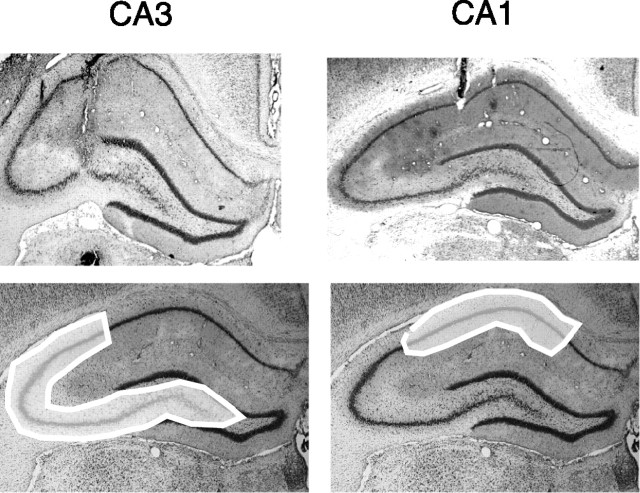
Figure 2.

Histology showing recording sites. The top panels show representative tetrode tracks in the CA3 (R057) and CA1 (R065) regions. The bottom panels show regions from which CA3 and CA1 recordings were taken.

Table 2.

Multiple-T session availability per rat for experiment II

Rat no.	No. sessions	Region
R048	19	CA1
R051	23	CA3
R057	24	CA3
R067	25	CA1
R069	18	CA3
R072	12	CA1
Total	56 CA1, 65 CA3

No., Number.

For multiple-T (MT), time passing the second feeder was identified as the start of a lap. (Thus, each lap consisted of a journey from the time the rat left the second feeder to the time the rat returned to the second feeder.) As above, sessions with at least 30 laps were considered (n = 3 CA3 rats, n = 3 CA1 rats on MT). One rat in the MT group was previously recorded in experiment I, and is therefore included in both experiments.

LFP analysis

Generally noisy channels were removed from the analysis. Any event of maximum/minimum voltage (during which the amplifiers reached the + or − rails) on any channel was removed from all channels including 0.5 s before and after.

SWR detection.

SWR events were extracted by down-sampling the LFP traces by a factor of 2 (using an anti-aliasing low-pass filter), and bandpass filtering from 100 to 250 Hz. Amplitude for each trace was found via Hilbert-transform and then averaged across traces. The distribution of log-transformed average amplitude was used to find samples >2.5σ from the mean power. Higher and lower values of σ (e.g., 2σ, 3σ, 4σ) yielded qualitatively similar results. Visual inspection of a subset of the data revealed ripple events synchronous across LFP channels. Threshold crossings <20 ms were removed; the remaining events were concatenated if <100 ms apart. Twenty milliseconds were added to the beginning and end of each SWR to capture the tails of the SWR. Raw threshold detections were also analyzed and yielded qualitatively similar results. Likewise, merging threshold crossings <100 ms apart before discarding short (<20 ms) events yielded qualitatively similar results. To reduce the possibility of non-LIA, high-frequency events contaminating the analysis, we removed all SWR events detected during high-theta/low-delta periods. Thus, the SWR represented in our analyses would be most analogous to the iSWR (immobile sharp wave–ripple) events of O'Neill et al. (2006). The results in this paper are from this conservative set; however, there was little qualitative difference introduced by including all SWR events.

SWR detection was done with wide-band filtering cutoffs of 100–250 Hz. Csicsvari et al. (1999) demonstrated a dissociation between regions CA1 and CA3 in the hippocampus and the characteristic frequency of sharp wave–ripples in these regions. We have observed a similar dissociation in our CA3 and CA1 recordings on MT (data not shown). The range of filters that were used detected SWRs robustly in either hippocampal region.

It is possible that volume conduction from ripples in CA1 could influence our detection in CA3; if CA3 was not emitting SW ripples, it may be that ripples occurring in CA1 could trigger SWR detection in CA3. This is unlikely because volume conductance drops off at higher frequencies (Niedermeyer and Lopes da Silva, 1999) and because CA3 showed additional, early SWRs not seen in CA1 (see Results).

Theta detection.

Theta times were extracted by down-sampling the LFP traces by a factor of 5 (using an antialiasing low-pass filter), and bandpass filtering from 6 to 10 Hz to obtain theta-band signals, and from 2 to 4 Hz to obtain delta-band signals. The amplitude for the band of each trace was found via Hilbert transform, and then averaged across traces to obtain two averaged signals: an average theta-band amplitude and an average delta-band amplitude. The distribution of the log-transformed ratio (theta/delta) of average amplitudes was used to identify samples with a low power-ratio > 1σ from the session mean; these were taken to be nontheta brain states. Higher and lower values of σ (e.g., 0.5σ, 1.5σ, 2σ) yielded qualitatively similar results. Visual inspection of a subset of the data revealed low theta amplitude epochs that clustered at locations of immobility (e.g., the linear track ends). These nontheta epochs were concatenated if <500 ms (the low-frequency cutoff for the delta band) apart, and events smaller than 100 ms (the high-frequency cutoff for the theta band) were removed. Raw threshold detections were also analyzed and yielded qualitatively similar results. Theta epochs were taken as the complementary set of times; these high theta-band power and low delta-band power epochs tended to coincide with times when the animal was moving. Because theta epochs were defined as times with theta/delta ratio either greater than the mean or no more than 1σ below the mean, some “theta” epochs may have had relatively lower theta power and may have corresponded to one or more intermediate states. However, visual inspection showed that the definition of “theta” epoch was relatively robust and tended to correspond to easily visually identifiable theta periods.

Statistics.

Linear regression was used to determine whether there was a change in SWR properties as a function of laps over the session. For per-lap measures in experiment I, only sessions in which the rat ran >30 laps were included, and only the first 30 laps of each session were included in the analyses. Because the number of laps run on the MT task in experiment II was much more variable the tasks in experiment I, sessions in which the rat ran >20 laps were included, and up to the first 60 laps of each session were included in the analyses to provide comparison with per-lap measures in experiment I. Because we looked at a number of regressions on the lap-dependent local field potential properties (time spent in nontheta, SWR emission rates, duration of SWR, etc.), we controlled for multiple comparisons with a Bonferroni correction (Zar, 1999) to define significance. This correction was only applied to the large number of lap-dependent analyses done.

Cofiring reactivation analysis

To measure reactivation at the ensemble level, we developed a new measure (see Appendix). Briefly, for an ensemble of n cells, this measure generates an n² binary representation (s_θ) of which cell pairs cofired within a theta cycle. A similar representation can be generated for cell pairs that cofired within a sharp wave (s_SW). These two binary strings can be compared by taking the exclusive OR (XOR) of the two. Under the null hypothesis H₀ that the strings are independent with respect to each other, the expected number of ones in the XOR string can be predicted from the binomial cumulative distribution as a function of the proportion of ones in each string and the length of the strings themselves. The deviation of the number of ones in the XOR string from the expected number indicates the extent to which the two strings are more similar than expected. Details of this procedure are given in Appendix.

The new analysis presented here uses the entire ensemble cofiring pattern, exploiting information about neurons that are not active on the task and pairs that did not have overlapping place fields. Thus, we are not measuring whether neuron pairs correlated in theta are increasing their correlation in SWR; we are testing whether the same cell assemblies are present in SWR that were present in theta. In other words, if neuron pairs were coactivated during theta but not during SWR, our measure would show a lower value than for matched coactivations in both states. Similarly, if neuron pairs were not coactive during theta but were coactive during SWR, our measure would also show a lower value than for matched coactivations in both states. Our application of this method here is not temporally biased, and is therefore insensitive to the firing ordering within the reactivated patterns. Furthermore, as noted in Appendix, any noise within the coactivation estimates reduces the similarity of the s_SW and s_θ patterns and argues in favor of the null hypothesis. However, to reduce the likelihood of clustering artifacts influencing the analysis (Quirk and Wilson, 1999), only neuron pairs recorded across tetrodes were included in the analysis.

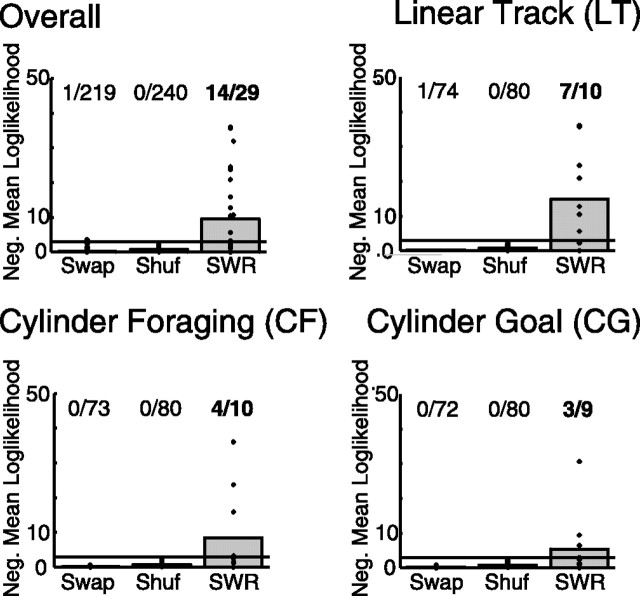
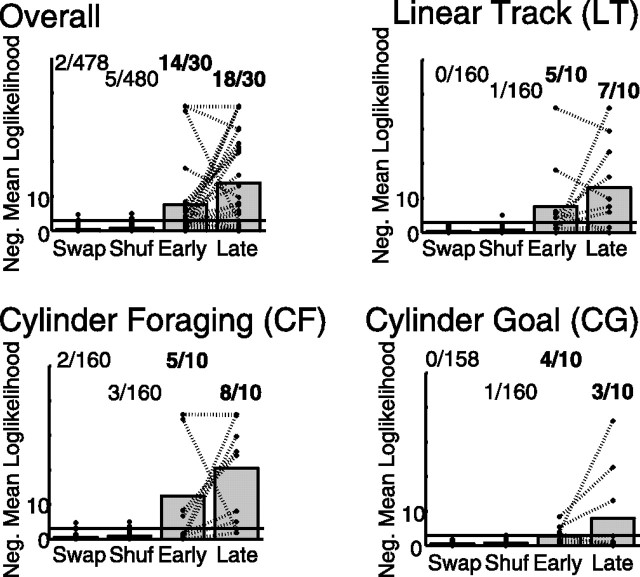
The null hypothesis in this analysis is that the cofiring patterns observed in theta and during SWRs are independent within a single session. To determine whether there is general reactivation, we must determine whether the number of sessions in which the null hypothesis will be rejected by chance. This can be found using a test which measures whether there are more sessions in which the null hypothesis can be rejected than would be expected by chance. This can be measured with a binomial test, asking whether there are more sessions with negative mean log-likelihoods less (more negative) than negative log(α) (Zar, 1999). We used α = 0.05 for these analyses. Thus, if (as seen in our data) (see Fig. 5), 14 sessions of 29 have significant reactivation (i.e., significance > α), this is highly significant (a binomial test would expect only 1.45 sessions of 29 to have reactivation by chance) with a value of p < 10⁻¹⁰.

Figure 5.

SWR complexes during awake behavior include the same cell assemblies as occur during theta. The similarity between cell cofiring during SWRs and during theta are shown for each condition (see Materials and Methods). Each session produced one · on each plot. For all four conditions, the cell assemblies active during SWR were more similar to those seen during behavior (theta) than would be expected from either random control, including SWAP (preserving timing and ensemble firing properties) and SHUFF (preserving the overall firing rate of each neuron). Note that the overall condition is an analysis over all sessions, not an average of the other three conditions. On each plot, the horizontal line at negative mean log-likelihood = 3 marks p = 0.05. The marks above this line imply significant reactivation on that session. The numbers above each column indicate the number of sessions with significant reactivation. The numbers in bold indicate more sessions with significant reactivation than would be expected by chance. ALL, Overall, including all three tasks, p < 10⁻¹⁰; LT, p < 10⁻⁸; CF, p < 0.00001; CG, p < 0.0001.

Randomized ensemble controls.

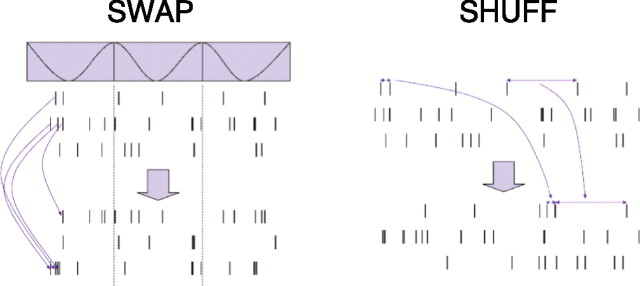
Two randomized controls were used for comparison with experimental reactivation. The first (SWAP) randomized spike identity across the ensemble while maintaining the overall ensemble state-dependent firing. The second (SHUFF) shuffled the ISIs of each neuron preserving first-order neuronal firing statistics but disrupting state-dependent firing and controlling for the contribution of silent cells to the reactivation analysis. Shuffles were conducted within each task (CF, CG, LT) across the entire task within each session (Fig. 3). Both randomizations were run eight times for each session, and the data for each session were averaged for within-session comparisons.

Figure 3.

Methods: randomized controls for cell assembly similarity (diagrammatic). The top three rasters represent spikes from three simulated neurons. Time runs along the x-axis are shown. SWAP, The spikes are shuffled across neurons preserving their timing but changing the neuron they are assigned to. This preserves the overall ensemble firing patterns with respect to the oscillatory state shown at the top. SHUFF, The intervals between spikes are shuffled within the spike train of each neuron in the bottom rasters, preserving the firing statistics of each neuron but disrupting ensemble state-dependent temporal firing patterns.

Video tracking and behavioral control

The positions of light-emitting diodes (LEDs) mounted on the headstage were recorded by a camera mounted in the center of the ceiling of the recording room. The video frame data were sampled at 60 Hz, digitized, and time stamped by a Cheetah recording system (Neuralynx); pixels that crossed thresholds set by the experimenter were recorded to disk. Real-time position data were accessed by in-house behavioral control software implemented in Matlab (The MathWorks, Natick, MA). This software used the serial ports to communicate with an experimental control box (constructed by J. C. Jackson) to trigger food delivery (45 mg pellets; Research Diets, New Brunswick, NJ) (food dispensers; Med Associates) and simultaneously signal the Cheetah recording system for a synchronous food delivery time stamp (each feeder had a unique digital identification).

Position data were then preprocessed for post hoc analysis by extracting the center of mass of all suprathreshold pixels. Video interlacing effects were removed from the data through linear interpolation of odd and even position samples (two 30 Hz time series) to produce two 60 Hz time series, which were then averaged to yield a single, stable 60 Hz time series.

Lap times: linear track.

Because the linear track was aligned along the x-direction of the video data, the x-position was taken as the linearized one-dimensional projection of the animal's behavior. The x-velocity was calculated using a 64th order low-pass FIR filter with a 2 Hz high-frequency cutoff by filtering forward and backward (to eliminate phase shifts). Plots of the x-position versus x-velocity displayed a clustering of low velocity at the track ends. These clusters were selected manually for each session and lap times were defined as the time from departure from one end of the track to the next departure from the same end. Interlap intervals were defined as the time spent in these low-velocity clusters at the track ends.

Goal entry times (laps): cylinder tasks.

When real-time tracking of the animal's position detected that the rat was in the goal region on CG, a tone was sounded and a TTL signal was sent to Cheetah via the experimental control module to time stamp the event. Trial division times were then taken as the delivery time of this qualifying tone. Because each day an animal ran both the CF task and CG task for 20 min each, the trial times from CG were applied to the CF task for a matched control. Throughout the text, we will also refer to these goal-entry times as “laps” for simplicity, because they serve as a temporal parcelation of the behavior.

Lap times (multiple-T).

On the multiple-T task, laps were defined as successfully triggering the second feeder on the correct return rail. This is consistent with previous analyses of the multiple-T task (Schmitzer-Torbert and Redish, 2002, 2004).

Spatial transition analyses

Behavioral entropy.

To determine the repetitive nature of the behavior, the entropy of the transitions between spatial positions was measured. For each task on each day, the x-, y-position data were binned into 40 × 40 pixel blocks (11 × 11 cm) and the transition probability from each bin into every other bin was calculated for each block of time. Thus, our 640 × 480 video capture yielded a 16 × 12 bin array and a 192 × 192 transition matrix, containing the transitions between the bins. The Shannon entropy of the transition matrix was calculated using all nonzero transitions as follows:

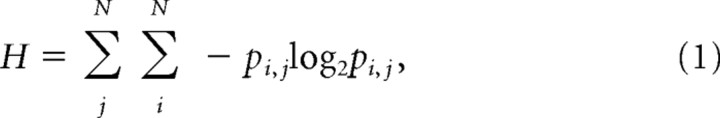where p_i,j is the time-independent probability of transition from bin j to bin i, and N = 16 × 12 = 192 is the total number of bins. This measures the variability in the distribution of transition probabilities between spatial positions. Highly variable behaviors will have a more uniform transition probability distribution and thus a high entropy. More regular behaviors will have a more limited transition probability distribution and thus a low entropy.

Reactivation and SWR emission given experience and behavior entropy.

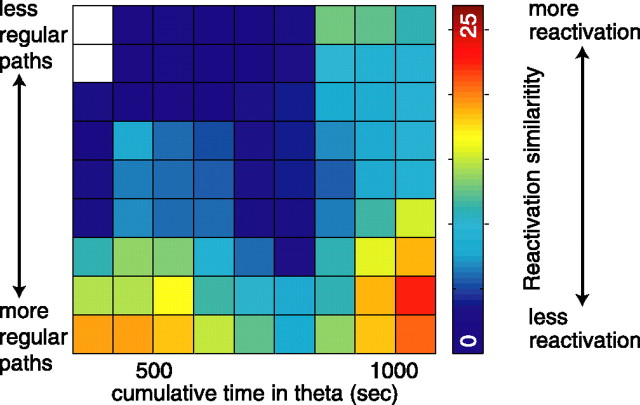
Measuring SWR emission by experience (number of laps) by entropy produced a three-dimensional data set of points. To show this distribution in graphical form (see Fig. 7), the lap and entropy axes were divided into 15 equally spaced bins and SWR emission rate was averaged within each bin. A square-root transform was applied to the SWR emission rate to stabilize the variance. For each bin, the plotted emission rate for that bin was then calculated from an ellipse with radii equal to twice the bin width of each axis for bins with five or more samples falling within this radius. This radial averaging technique made the bin-centered value estimation robust to spurious outliers encountered at the edges of sparse data regions and therefore reduced the dependence on choice of bin size and bin location. Cumulative spatial entropy was calculated as described above, taking the entropy of all behavior occurring before time t. For reactivation (see Fig. 8), the limited data sample available precluded using 15 bins, so entropy and time in theta were divided into nine equally spaced bins.

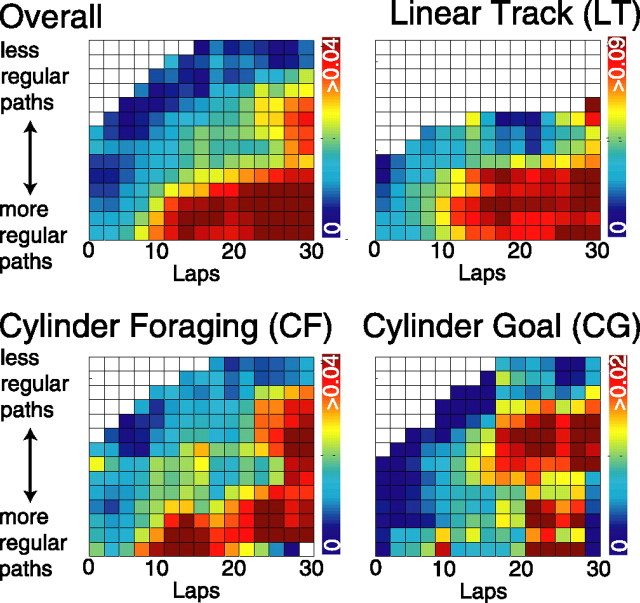
Figure 7.

Dependence of SWR emission on the sequential repetitiveness of the behavior. Number of SWR events normalized by time spent in nontheta states as a function of lap number and behavioral entropy. The color bar indicates SWR emission rate, measured as seconds⁻¹. SWR emission increased with lower entropy (more regular paths) and on later laps (with more experience). ALL, Each lap for each session on each task (LT, CF, or CG) contributed one three-dimensional point to the analysis. For each bin, points were radially averaged to determine average SW emission given the cumulative regularity and experience. Statistics: Stepwise regression on raw (i.e., unaveraged) data showed an effect of lap number, p < 0.00001; an effect of entropy, p < 0.00001; and an interaction between the two, p < 0.00001. LT, Same as ALL except only LT sessions were used. Statistics: Stepwise regression on raw data showed an effect of lap number, p < 0.00001; an effect of entropy, p < 0.0005; and an interaction between the two, p < 0.00001. CF, Same as ALL except only CF sessions were used. Statistics: Stepwise regression on raw data showed an effect of lap number, p < 0.002 (ns, by multiple comparisons); an effect of entropy, p < 0.001; and an interaction between the two, p < 0.00005. CG, Same as ALL except only CG sessions were used. Statistics: Stepwise regression on raw data showed an effect of lap number, p > 0.002 (ns, by multiple comparisons); an effect of entropy, p > 0.31 (ns); and an interaction between the two, p < 0.0005.

Figure 8.

Dependence of reactivation on the sequential repetitiveness of the behavior. Reactivation similarity (measured as negative log-likelihood of similarity relative to randomness) as a function of behavioral entropy and total time spent in theta. Statistics: Stepwise regression showed an effect of entropy, p < 0.005; for time in theta, p < 0.05; and an interaction between the two, p < 0.001.

Results

Experiment I: behavioral manipulations

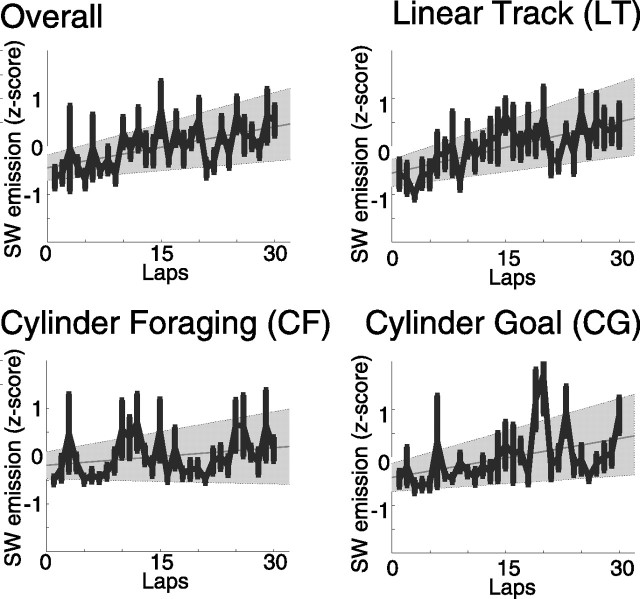
A total of 696 spike trains were recorded over 24 sessions in ensembles of up to 96 neurons/session (30 ± 31 neurons/session; mean ± SD); 17 additional sessions were included for which spike trains were unavailable. SWRs were identified by a threshold applied to the average amplitude across tetrodes of the Hilbert-transformed local field potentials, bandpass filtered from 100 to 250 Hz. As observed in previous experiments (O'Keefe and Nadel, 1978; Buzsáki et al., 1983; Christian and Deadwyler, 1986), SWR occurred during the tasks (LT, CF, CG) concentrated when the rat paused in running. Overall, the number of SWR events per time spent in nontheta states increased with laps on each task [slope > 0; p (slope = 0) < 0.0003] (Fig. 4).

Figure 4.

Experience-dependent changes in SW ripple events. Mean and SE of SW ripple events emission rate normalized by the time spent in nontheta were calculated from individual averages across animals. Linear regression line and 95% regression confidence intervals for all four conditions. ALL, Overall, including all three tasks, R² = 0.063, F = 14, p (slope = 0) < 0.0002; LT, R² = 0.098, F = 19, p (slope = 0) < 0.00002; CF, R² = 0.011, F = 2.3, p (slope = 0) > 0.12; CG, R² = 0.056, F = 10.3, p (slope = 0) < 0.002.

To determine whether these sharp wave–ripple events were also associated with experience-dependent changes in neuronal firing, we examined the cross-neuron cofiring probabilities. When averaged over the entire 20 min session, over all tasks, the pattern of neuron pairs that were coactive during awake SWRs were significantly more similar to the pattern that were coactive during theta than would be expected given random neuronal activity (binomial test, p < 10⁻¹²). These results were compared with two randomized controls: SWAP, in which the spike identity was swapped within the ensemble, preserving timing and ensemble firing properties, and SHUFF, in which the spike times were shuffled within spike train, preserving the overall firing rate of each neuron. Both randomizations removed the effect (Fig. 5).

The similarity between SWR firing and theta firing also increased across the session. For each session, this was measured by dividing the number of SWRs in the session in half (first half, second half), and comparing the similarity of coactive firing in each half with the coactive firing in theta. Overall, the similarity tended to increase (one-sided Wilcoxon's paired signed rank test comparing reactivation during the first n/2 SWR to reactivation during the second n/2 SWR, p < 0.02) (Fig. 6). Although there was an overall effect, the strength of the effect on each task differed. We next consider each task individually.

Figure 6.

The assemblies became more coherent through the session. The sharp wave–ripple complexes in each session were divided into two halves by the median occurring sharp waves, providing the same number of SWRs in two blocks (an early block and a late block). If the cell assemblies cofiring in the SWRs become more similar to the cell assemblies occurring during theta, we would expect the similarity to increase between the two blocks. The similarity did increase for the linear track, and for the overall condition. But the increase was not significant for the two-dimensional conditions. One-sided nonparametric Wilcoxon's signed rank tests were used (Zar, 1999). ALL, Overall, including all three tasks, p < 0.01; LT, p < 0.05; CF, p < 0.25; CG, p < 0.10.

Linear track

Sharp wave–ripple complexes occurred during the linear track task, concentrated at the ends of the track where the rat received food and paused between each lap (0.19 ± 0.11 SWR/s in nontheta; mean ± SE). The number of SWR events per lap increased throughout the session [slope > 0, p (slope = 0) < 0.00002] (Fig. 4). This increase in SWR emission could not be attributed to a change in performance, behavior at the track ends, changes in time spent in nontheta states, or changes in rate of transition between nontheta and theta (see below, controls). The duration of the SWR showed no detectable change across the session [p (slope = 0) = 0.30, nonsignificant (ns)]; however, there was a significant increase in the amplitude of the SWR [p (slope = 0) < 0.00005]. Awake SWRs are associated with reactivation of the ensembles active during theta (Foster and Wilson, 2006; O'Neill et al., 2006) as are SWRs that occur in slow-wave sleep after a session (Wilson and McNaughton, 1994; Kudrimoti et al., 1999; Nádasdy et al., 1999; Hoffmann and McNaughton, 2002). On the linear track task, the SWRs emitted during waking states were also associated with reactivation of firing patterns observed during the theta-associated components of behavior (p < 10⁻⁸) (Fig. 5). The proportion of neurons included in each SWR did not significantly change across each session [p (slope = 0) = 0.84, ns]. Nor did the average firing rates occurring within a SWR change across each session [p (slope = 0) = 0.94, ns]. The reactivation itself, however, did increase in similarity to cofiring patterns observed during theta across the task (one-sided Wilcoxon's paired signed rank test comparing reactivation during the first n/2 SWR to reactivation during the second n/2 SWR, p < 0.05) (Fig. 6).

Linear track controls.

The increase in SWR emission rate on the linear track could have been caused by an increase in the time spent resting between laps at the track ends; however, there was no detectable increase in lap duration [p (slope = 0) > 0.88, ns] nor in the resting time between laps [p (slope = 0) > 0.79, ns]. Neither was there a corresponding increase in the rate of transition out of theta [p (slope = 0) > 0.28, ns] nor in the time spent in nontheta brain states [p (slope = 0) > 0.14, ns]. Because we did not have video image data (only LED coordinates), an analysis of specific behaviors was not possible (e.g., grooming, resting, chewing, etc.). However, to test for changes in the activity level at the track ends, we compared how the mean and SD of the animal's speed while at the track ends changed across laps. There was no change in either of these measures of activity level [mean movement speed, p (slope = 0) > 0.55, ns; SD of movement speed, p (slope = 0) > 0.36, ns]. As a final control, to check for the possibility that increases in overall LFP power with experience could affect SWR detection, we ran the equivalent analyses with the bandpass filter set to the theta band power. No detectable increases in threshold crossings, neuronal recruitment, or firing rate were observed at the theta band, suggesting that the increase in SWR event detection is attributable to a specific enhancement in the SWR frequency band. Thus, the robust increase in SWR emission on LT cannot be explained by overt changes in the animal's state of arousal or intensity of behavior over the first 30 laps.

Two-dimensional tasks

Because the increase in SWR emission during awake states was obtained on a linear track where the animal repetitively traversed the same path, which presumably would allow for repeated strengthening of the connectivity of the network, we examined whether these increases occurred in more complex environments and tasks with less spatial behavioral regularity. Each day, in addition to the linear track session, each rat ran two additional 20 min sessions CF and CG (see Materials and Methods).

Sharp wave–ripple complexes also occurred on CF and CG, concentrated where the rat paused to consume food or rest (CF, 0.11 ± 0.10 SW/s in nontheta, mean ± SE; CG, 0.042 ± 0.061 SW/s in nontheta, mean ± SE). The rate of SWR emission did not increase significantly on the cylinder-foraging task [p (slope = 0) > 0.12], nor was there a detectable change in SW amplitude [p (slope = 0) > 0.16, ns]. As in LT, there was no detectable change in the duration of the SWR [p (slope = 0) > 0.10, ns]. When averaged over the entire 20 min session, the pattern of neuron pairs that were coactive during awake SWRs were significantly more similar to the patterns that were coactive during theta than would be expected given random neuronal activity for the task (p < 10⁻⁵) (Fig. 5). The similarity between cell assemblies active during SWR and theta showed no significant increase in the CF task (one-sided Wilcoxon's paired signed rank test, p = 0.28, ns) (Fig. 6).

On the CG task, the occurrence of SWR showed a trend [approaching, but not reaching significance when corrected for multiple comparisons, p (slope = 0) < 0.002 (Fig. 4); ns as a result of multiple comparisons]. As in CF, the duration of SWRs did not change significantly [p (slope = 0) > 0.57, ns], nor did the amplitude of SWRs [p (slope = 0) > 0.44, ns]. When averaged over the entire 20 min session, the set of neuronal pairs that were coactive during awake SWRs were significantly more similar to the set that were coactive during theta than would be expected given random neuronal activity for both tasks (p < 10⁻⁴) (Fig. 5). The similarity between cell assemblies active during SWR and theta on CG did not show a detectable increase (one-sided Wilcoxon's paired signed rank test, p = 0.10, ns) (Fig. 6).

Two-dimensional task controls.

For the two-dimensional tasks, there was no significant increase in lap duration [CG, p (slope = 0) > 0.70, ns; CF, p (slope = 0) = 0.02, ns as a result of multiple comparisons], neither was there a corresponding increase in the rate of transition out of theta [CG, p (slope = 0) > 0.74, ns; CF, p (slope = 0) = 0.01, ns as a result of multiple comparisons] nor in the time spent in nontheta brain states [CG, p (slope = 0) > 0.10, ns]. Thus, as with linear track, the increases in SWR emission rate and in reactivation similarity occurring across the session in the CG task could not be explained by changes in gross behavior.

Comparisons across tasks

A two-way ANOVA comparing SWR emission across laps and tasks revealed an effect of task (F = 19.1; p < 10⁻⁸). SWR emission rates were significantly higher on LT than on either CF or CG [p < 0.05, Tukey's honestly significant difference (HSD) criterion for multiple comparisons]; SWR emission rates were higher on CF than on CG (p < 0.05, Tukey's HSD criterion for multiple comparisons).

Because SWR emission rates and reactivation time courses differed across tasks, we tested whether those differences in SWR emission rates correlated with differences in spatial sequence behavior. To test this, each spatial task was binned into 40 × 40 pixel blocks (11 × 11 cm), and the transition probability from each bin into every other bin was calculated for each block of time (see Materials and Methods). As expected, an ANOVA comparing the entropy of these transition probabilities across tasks and time revealed an effect of task type (F = 101.3; p < 10⁻¹²) with LT having significantly lower transition entropy compared with either CF or CG. Consistent with the linear track being a one-dimensional task and both cylinder tasks being two-dimensional, LT had approximately one-half the spatial transition entropy of the behavior on CF and CG (LT, 27.4 ± 15.2 bits; CF, 53.7 ± 28.9 bits; CG, 56.2 ± 27.0 bits, mean ± SD).

Because sequential behavior is thought to engage hippocampal plasticity mechanisms (Mehta et al., 1997; Shen et al., 1997; Ekstrom et al., 2001), and both SWR emission and reactivation increased with time (Figs. 4, 6), we tested the extent to which SWR emission and reactivation were dependent on the interaction of the two factors of behavioral regularity. Because a sufficient number of SWRs were available to measure emission as a function of lap, the emission rate of SWRs in nontheta states was measured as a function of lap and the entropy of all behavior leading up to that lap (“cumulative entropy”). SWRs were more likely to be emitted earlier with more regular behavior (stepwise multiple linear regression: significant effect of lap number, p < 0.00001, and of entropy, p < 0.00001, with a significant interaction, p < 0.00001, F = 52.9) (Fig. 7).

This same trend could be seen in each task. On LT sessions, SWRs were more likely to be emitted earlier with more regular behavior (stepwise multiple linear regression: effect of lap number, p < 0.00001, and of entropy, p < 0.0005, with a significant interaction between the two, p < 0.00001, F = 15.0) (Fig. 7). On CF sessions, a similar interaction effect was observed (stepwise multiple linear regression: effect of lap number, p < 0.002; effect of entropy, p < 0.001; and a significant interaction between the two, p < 0.00005, F = 10.9) (Fig. 7). CG sessions demonstrated a similar interaction [stepwise multiple linear regression: effect of lap number, p < 0.002; no effect of entropy, p > 0.31 (ns)]; however, the interaction between the two was significant (p < 0.0005; F = 7.88) (Fig. 7).

Because reactivation could not be measured for each lap, the total time spent in theta was used as the temporal measure. Total time spent in theta was used because theories suggest that information storage in hippocampus occurs during theta, whereas information reactivation and replay occurs during sharp wave–ripples occurring in LIA (Buzsáki, 1989; Hasselmo and Bower, 1993; Redish, 1999). These theories predict that reactivation rate should depend on total time spent in theta. Reactivation similarity also increased with more regular behaviors and time spent in theta. This effect was significant (stepwise multiple linear regression: effect of entropy, p < 0.005, and of time spent in theta, p < 0.05, with a significant interaction p < 0.001). The low number of data points for this analysis was sufficient only for the pooled data from the three tasks, not for individual task comparisons of reactivation as a function of spatial regularity and experience (Fig. 8).

Effects of task order

On each day in experiment I, each rat ran all three tasks in one of the following orders: LT–CF–CG, LT–CG–CF, CG–CF–LT, or CF–CG–LT. There was no overall effect of order on number of laps (ANOVA, no effect of order, F = 0.04, p = 0.8447). Nor was there an effect on the entropy of behavior within each task (ANOVA, no effect of order, F = 0.92, p = 0.33), nor on the time spent in LIA during each task (ANOVA, no effect of order, F = 0.005, p = 0.81). Nor was there an effect of order on the number of SWR complexes emitted (ANOVA, no effect of order, F = 0.44, p = 0.51), nor on the duration of the SWRs emitted during each task (ANOVA, no effect of order, F = 0.1, p = 0.75). However, there was an effect of task order on the reactivation of ensembles.

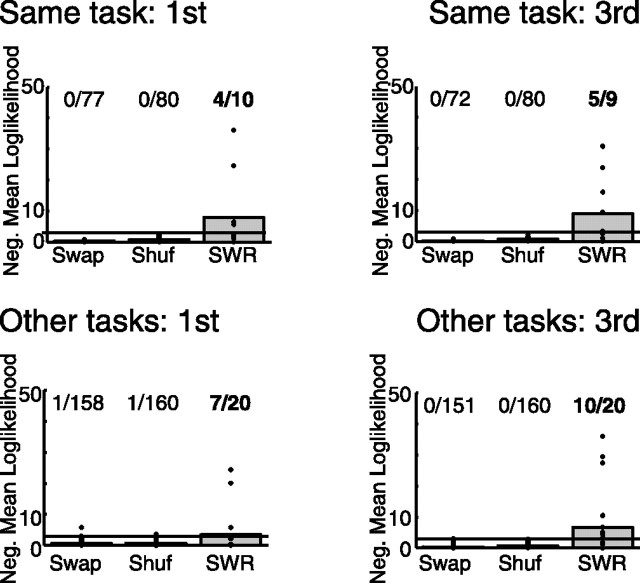
Because linear track was not run in the middle position, the first task was compared with the third. As can be seen in Figure 9, reactivation of the current task (i.e., LT while running LT, CF while running CF, CG while running CG) was strong whether the task was first or third (first, p < 0.0001; third, p < 0.0001). Reactivation of other tasks (that is, CF or CG when running LT, LT or CF when running CG, etc.) was weak, but significant (p < 0.0001) during the first task of the run. As can be seen in Figure 9, strong reactivation of other tasks was present during the third task of the run (p < 0.0001). Reactivation of the other tasks increased significantly with order (p < 0.0001, sign test), but the reactivation of the primary task did not change significantly with order (p = 0.09, sign test).

Figure 9.

Dependence of reactivation on the order of task experience. Reactivation similarity (measured as negative log likelihood of similarity relative to randomness) as a function of order of the tasks. The line indicates the significance threshold, p = 0.05. Statistics: All four conditions show significant reactivation, p < 0.001, binomial test. Significant increase in reactivation of other tasks with order (p < 0.001, sign test) but no increase in reactivation of the task being run (p = 0.09, sign test).

These data show that reactivation during awake states includes both the task being run as well as other tasks previously run by the animal. Reactivation of other tasks during the first run may reflect memories from previous days (Kudrimoti et al., 1999; Louie and Wilson, 2001). The increase in reactivation of other tasks from first to third, however, implies that representations of tasks recently run are reactivated during subsequent waking behavior in a manner similar to that known to occur during subsequent sleep sessions.

Experiment II: the multiple-T task: CA3 and CA1

The data in experiment I were all taken from the CA1 region while rats ran familiar tasks. SWRs have also been seen in recordings taken from the CA3 region (Csicsvari et al., 2000; Behrens et al., 2005). To determine the time course of changes in SWR generation with experience, we analyzed data from six animals running the multiple-T task. Although these animals had experience running on 3T and 5T tasks, this was their first experience on 4T mazes. Local field potential data were available from both CA3 (three animals) and CA1 (three animals).

Behavior on the MT task

Rats ran an average of 48 ± 26 (SD) laps per 40 min session. There was no significant difference between the number of laps run by CA1 or CA3 rats [CA1: 46 ± 2.4 (SE) laps; CA3: 49 ± 2.5 (SE) laps; p = 0.51, ns, t test], even taking differences between rats and sessions into account (ANOVA, F = 0.03, p = 0.87, ns). Nor were there differences in length of time spent in each lap between the two groups (ANOVA controlling for changes in length of lap over laps, F = 0.52, p = 0.47).

SWR emission on the MT task

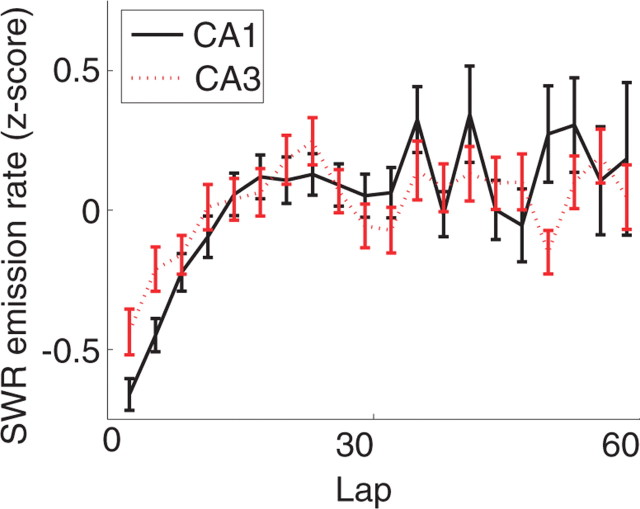
As can be seen in Figure 10, overall, the number of SWR complexes emitted per second of LIA increased over the first 20 laps, but then remained at an approximately constant rate over the subsequent laps. Although the number of SWR events emitted on each lap differed between rat, the pattern of lap-dependent change in SWR emission remained similar between rats (ANOVA, effect of rat, F = 15.0, p < 10⁻¹⁰; effect of lap, F = 1.72, p < 0.002; no interaction, F = 0.94, p = 0.75). A linear regression over the entire session showed a significant increase [F = 11.8; p (slope = 0) < 0.001]. A linear regression over the first 20 laps showed an even stronger effect (F = 82; p < 10⁻¹⁰). Both overall and over the first 20 laps specifically, the SWR amplitude also increased significantly (overall, F = 23.5, p < 10⁻⁷; first 20 laps, F = 15.4, p < 0.001). Interestingly, whereas the number of SWR complexes emitted per second of LIA after the first 20 laps remained constant, the SWR amplitude continued to increase.

Figure 10.

Change in SWR with experience on the multiple-T task. SWR emission in both CA3 and CA1 increased over the first 20 laps but then remained stable for the rest of the session. Error bars indicate SEM.

MT controls.

Unlike the tasks in experiment I, on the MT task, there was a significant increase in the proportion of time spent in LIA in each lap (F = 74; p < 10⁻¹⁰). Not surprisingly, given these results, there was a corresponding increase in the transition rate between theta and LIA in each lap (F = 35.0; p < 10⁻⁷). These effects may be attributable to the fact that the MT task was physically much larger than the other three tasks, and the animal had to run farther on the MT task to get food than on the other tasks. However, these effects remained significant even when restricted to the first 20 laps. Although these controls could explain the increase in SWR emission with experience on the MT task, based on the results from experiment I, we conclude that the increases in SWR emission were likely a result of experience, not of exhaustion.

Comparison of CA1 and CA3 SWR emission

Splitting by recording location, we found significant differences between SWR emission rates in CA1 and CA3. Both CA1 and CA3 showed strong changes in SWR emission rates (ANOVA; CA1, F = 3.57, p < 10⁻¹⁰; CA3, F = 2.04, p < 10⁻¹⁰). As can be seen in Fig. 10, in both structures, the SWR emission rate increased over the first 20 laps, and then remained approximately constant through subsequent laps [increase over all laps: CA1, p (slope = 0) < 0.00001; CA3, p (slope = 0) < 0.00001; over first 20 laps: CA1, p (slope = 0) < 10⁻¹⁰; CA3, p (slope = 0) < 10⁻⁸]. Controlling for session, rat, and changes over lap, there was a significant lap by structure interaction (F = 1.6; p < 0.008). As can be seen in Figure 10, CA3 showed an increased SWR emission rate on early laps (t test comparing emission rate over first five laps, p < 0.001).

Discussion

Together, these data confirm predictions that both SWRs and reactivation develop with experience across multiple behavioral tasks. This increased probability of SWR emission depended on repetition and the regularity of the behavior. SWR emission rates increased in both CA3 and CA1. Ensemble firing patterns during task performance were reliably reactivated during SWRs emitted on task. The similarity between the ensemble firing patterns in SWR and theta increased across the task and also depended on the regularity of the behavior.

The analyses presented here replicate and extend the recent work by O'Neill et al. (2006) and Foster and Wilson (2006) that the same cell assemblies that occur during theta are repeated during sharp wave–ripple complexes occurring during LIA, and that these assemblies become more likely to be reactivated with experience on an environment. These data support learning theories that suggest that experience-dependent mechanisms strengthen cell assemblies during tasks and that SWRs reactivate those cell assemblies in subsequent rest states. Such cell assemblies have been directly observed in theta during behavior (Wilson and McNaughton, 1993; Harris et al., 2003; Leutgeb et al., 2005; Wills et al., 2005) and reactivation of those assemblies have been observed during subsequent sleep states (Pavlides and Winson, 1989; Wilson and McNaughton, 1994; Kudrimoti et al., 1999; Nádasdy et al., 1999; Lee and Wilson, 2002). The fact that there was more reactivation of other tasks during the third task of each session than there was during the first task of each session (Fig. 9) implies that reactivation of recently experienced tasks also occurs during waking rest. These data indicate that reactivation is a cumulative process that incorporates information from all previous behavior (as opposed to place cell firing, which is task specific).

SWR detection: changes in amplitude versus increases in rate

Because SWRs were detected with a threshold detection mechanism, it is possible that the number of SWRs emitted remained constant, but the amplitude increased, bringing more SWRs above threshold. We find this unlikely, because SWR emission rate changes and SWR amplitude changes were uncoupled. For example, in experiment I, over all three tasks, the slope of SWR emission increased significantly, whereas SWR amplitude did not; whereas, in contrast, the SWR amplitude continued to increase in rats running the multiple-T task, even after the increase in SWR emission had stopped.

Implications for theories of SWR generation and function

Because the density of SWR emission during nontheta states depended on the behavioral structure of the task, our results are consistent with SWRs being generated by the sequential firing of neurons as a result of plasticity induced by sequential behavior (Skaggs and McNaughton, 1996; Csicsvari et al., 1999; Nádasdy et al., 1999; Redish, 1999). Our data are consistent with the SWR itself being a consequence of a noise-driven firing cascade across potentiated synapses within CA3 (Ylinen et al., 1995; Shen and McNaughton, 1996; Redish and Touretzky, 1998; Csicsvari et al., 1999, 2000; Behrens et al., 2005). Experimental evidence suggests SWR activity in CA3 initiates CA1 SWRs (Buzsáki et al., 1983; Ylinen et al., 1995; Csicsvari et al., 1999; Behrens et al., 2005). In our data, there was an experience-dependent increase in SWR emission in both CA1 and CA3 regions of the hippocampus. Theories of hippocampal function suggest that information is stored in the hippocampus during the theta state and replayed out via ripple activity during LIA (Marr, 1971; McNaughton et al., 1983; Buzsáki, 1989, 1996; Redish and Touretzky, 1998; Redish, 1999). Theories predict that asymmetric plasticity (Levy and Steward, 1983; Bi and Poo, 2001) applied to recurrent connections within CA3 through experience of repeated spatial sequences (Levy and Steward, 1983; Blum and Abbott, 1996; Redish and Touretzky, 1998) results in replay of this stored information. Our data strongly support this hypothesis; increases in SWR emission and reactivation were dependent on the level of repetition of regular spatial sequences.

On the linear track and multiple-T tasks, the animal's trajectories were highly repeated with specific reward delivery sites (back and forth along a thin track, around a loop on a track, respectively). In contrast, on the cylinder tasks, the trajectories were highly variable and the average reward distribution was uniform. These differences in behavior and reward distribution may account for the higher rate of SWR emission on LT and MT. On the goal-oriented task (CG), the repeated approach to the goal may account for the increase in SWR emission rate with experience, which was not observed in the foraging task (CF). It is possible that instrumental action required to obtain reward may also be important. Quantitative analysis of these variations in behavioral structure between LT, CF, and CG revealed a gradation in the repetition of spatially sequential behavior. As shown in Figure 7, combining the lap-to-lap variability of individual sessions across all tasks showed that an increase in the occurrence of SWR was strongly related to the cumulative sequential repetitiveness of behavior.

CA3 and CA1

As shown in Figure 10, SWR emission rates increased in both CA3 and CA1 with experience on the multiple-T task. Although this is consistent with theories suggesting that SWRs in CA1 reflect dynamics in CA3 projected to CA1 (Buzsáki, 1989; Ylinen et al., 1995; Redish and Touretzky, 1998; Csicsvari et al., 1999, 2000; Behrens et al., 2005), these recordings were not taken simultaneously. Therefore, we cannot measure the cross-coherence of CA3 and CA1 [as was done, for example, by Csicsvari et al. (2003)] and cannot conclude that CA3 “learns” earlier than CA1. Our data are also compatible with separate SWR generation mechanisms in CA3 and CA1, but with some additional, unknown process providing an early set of SWRs in CA3 but not CA1.

How much reactivation is based on internal input versus external input?

O'Neill et al. (2006) have reported that SWRs occurring during exploratory activity end with cells that reflect the current location of the animal. Similarly, Foster and Wilson (2006) have reported reverse sequences during awake SWRs on linear tracks that also end with cells that reflect the current location of the animal. The data from O'Neill et al. (2006) and Foster and Wilson (2006) may reflect self-localization phenomena (Touretzky and Redish, 1996; Redish and Touretzky, 1998; Redish, 1999). As shown computationally by Touretzky and Redish, reactivation and self-localization phenomena can co-occur in the same hippocampal network, depending on the amount of external input provided to the network during each SWR complex. Because our analyses did not examine the order of cell firing within the SWR, it is possible that some examples of “reactivation” seen on our tasks are actually examples of self-localization phenomena like those potentially seen by O'Neill et al. (2006) and Foster and Wilson (2006). However, reactivation of other tasks during a task (Fig. 9, bottom right panel) must be examples of reactivation rather than self-localization, because those reactivations do not reflect the current task the animal is in.

Appendix

Appendix: Cofiring reflectactivation analysis: pattern reactivation at the ensemble level

Using only spikes that occurred in strictly high theta states (see Materials and Methods, Theta detection), all neuron pairs that cofired more often within a median theta cycle than they did during 10 times the median theta cycle were considered to cofire. This was assessed by finding the maximum bin of the cross-correlation (binned at one-half the median theta cycle for the session). If the maximum of the cross-correlation was at the zero bin, that pair of neurons was declared to cofire during theta. To avoid potential clustering problems (Quirk and Wilson, 1999), only pairs from different tetrodes were included in the analysis. Each pair was only counted once.

The same cofiring criterion was then applied to spikes emitted during SWR complexes except that the median SWR duration was used for the bin width of the cross-correlations between nontetrode cell pairs. For each pair of neurons, the cross-correlation of all spikes fired during LIA by the pair was calculated, binned at one-half the median SW duration. If the maximum of the cross-correlation was at the zero bin, a pair of neurons was declared to cofire during SWRs. Any noise in determining this measure would only detract from the signal; therefore, this definition of cofiring enforces the conservative nature of the analysis below.

Computing the temporal cofiring for all cell pairs from different tetrodes yielded a pattern of 1's and 0's for the theta state s_θ and for the SWR state s_SW (1 = cofiring, 0 = not cofiring) (see example Eqs. 2 and 3).

These two ensemble cofiring patterns were compared as follows: (1) s_c was computed as the exclusive OR (XOR) of the two binary patterns s_SW and s_θ (see example Eq. 4):

(2) given the null hypothesis H₀ that s_SW and s_θ are independent with respect to each other and randomly related, the probability Prob(k ≤ n_c|N, p_c) of observing a particular number of 1's, where n_c = Σs_c or less (1's are mismatches between s_SW and s_θ) in the pattern s_c can be computed from the binomial cumulative distribution (Eq. 5) with parameters p_c (the probability of observing a 1) (Eq. 8), and the length N of pattern s_c.

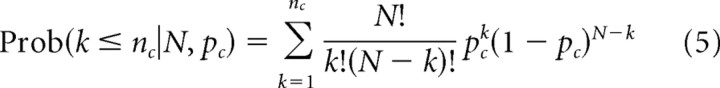p_c, the probability of observing a 1 in s_c, is determined from the proportion of ones p_SW in the SWR cofiring pattern and the proportion of ones p_θ in the theta cofiring pattern (8).

This is a one-tailed measure of how significantly different from random the similarity between two patterns is. If s_SW and s_θ are very similar, s_c has very few ones, and n_c is smaller than expected by random chance; therefore, Prob(k ≤ n_c|N, p_c) is low. Because the probability of a mismatch p_c is calculated from the proportion of 1's and 0's in the SWR and theta cofiring patterns, Prob(k ≤ n_c|N, p_c) is robust to differences in overall proportions of ones and zeros between the two patterns. Furthermore, because the null hypothesis assumes the patterns are randomly related, dependences between elements within either pattern are therefore expected to be randomly related. The result is that the individual elements of the output of the XOR operation are expected to be independent and identically distributed. Violations arising out of dependencies that occur in both sets argue for a rejection of the null hypothesis. Our analytical calculations and empirical simulations found that the binomial approximation is conservative and will underestimate significance levels. This is because of lower and upper limits to the number of possible matches, which reduces the possibility of seeing low probability events (i.e., events that argue for a rejection of the null hypothesis). These limits come increasingly into play as the proportion of 1's and 0's in the two patterns deviates from 50%, as is often the case in our data. Thus, as the proportion of 1's and 0's gets farther from even in either or both patterns, the measure becomes more conservative with n_c approaching either N × p_c or N × (1 − p_c).