Ca²⁺ from One or Two Channels Controls Fusion of a Single Vesicle at the Frog Neuromuscular Junction

Abstract

Neurotransmitter release is triggered by the cooperative action of approximately five Ca²⁺ ions entering the presynaptic terminal through Ca²⁺ channels. Depending on the organization of the active zone (AZ), influx through one or many channels may be needed to cause fusion of a vesicle. Using a combination of experiments and modeling, we examined the number of channels that contribute Ca²⁺ for fusion of a single vesicle in a frog neuromuscular AZ. We compared Ca²⁺ influx to neurotransmitter release by measuring presynaptic action potential-evoked (AP-evoked) Ca²⁺ transients simultaneously with postsynaptic potentials. Ca²⁺ influx was manipulated by changing extracellular [Ca²⁺] (Ca_ext) to alter the flux per channel or by reducing the number of open Ca²⁺ channels with ω-conotoxin GVIA (ω-CTX). When Ca_ext was reduced, the exponent of the power relationship relating release to Ca²⁺ influx was 4.16 ± 0.62 (SD; n = 4), consistent with a biochemical cooperativity of ∼5. In contrast, reducing influx with ω-CTX yielded a power relationship of 1.7 ± 0.44 (n = 5) for Ca_ext of 1.8 mm and 2.12 ± 0.44 for Ca_ext of 0.45 mm (n = 5). Using geometrically realistic Monte Carlo simulations, we tracked Ca²⁺ ions as they entered through each channel and diffused in the terminal. Experimental and modeling data were consistent with two to six channel openings per AZ per AP; the Ca²⁺ that causes fusion of a single vesicle originates from one or two channels. Channel cooperativity depends mainly on the physical relationship between channels and vesicles and is insensitive to changes in the non-geometrical parameters of our model.

Introduction

At fast-transmitting synapses, like vertebrate neuromuscular junctions (NMJs), release is stimulated by the influx of Ca²⁺ ions through voltage-gated channels. The cooperative action of three to five Ca²⁺ ions acting on the Ca²⁺ sensor(s) of the release machinery is believed to be required to trigger fusion of synaptic vesicles (Dodge and Rahamimoff, 1967; Augustine and Charlton, 1986; Stanley, 1986; Heidelberger et al., 1994; Bollmann et al., 2000; Schneggenburger and Neher, 2000). The requirement for simultaneous binding of multiple Ca²⁺ ions constitutes a “biochemical cooperativity” (Dodge and Rahamimoff, 1967). Although biochemical cooperativity has been supported universally by experimental findings, the number of channels that contribute Ca²⁺ to the fusion of a single vesicle is less clear and probably is synapse-specific (Stanley, 1997). Contribution of Ca²⁺ from more than one channel to fusion of a given vesicle is referred to in this study as “channel cooperativity” [equivalent to Ca²⁺ current cooperativity (Bertram et al., 1999)].

Theoretical and physiological experiments performed at many different synapses support the full spectrum of possibilities, from influx through one open channel to cooperative action of tens of channels for release of a single vesicle (Stanley, 1997). Good evidence exists for channel cooperativity at the immature calyx of Held synapse (Borst and Sakmann, 1996), which is reduced during maturation (Fedchyshyn and Wang, 2005). Also, different Ca²⁺ channel subtypes appear to couple to transmitter release with the same or different degrees of cooperativity (Mintz et al., 1995; Reid et al., 1997; Wu et al., 1999) in different synapses. Direct evidence that flux through a single channel can be sufficient for release of a vesicle was obtained at chick ciliary ganglion calyx (Stanley, 1993), and low channel cooperativity has been reported at mouse motor nerve terminal, squid giant synapse, and frog amygdala synapses (Llinás et al., 1981; Quastel et al., 1992; Mulligan et al., 2001). The number of channels that contribute Ca²⁺ to stimulate release of a given vesicle has implications for the physiology of the synapse. Although release driven by a single Ca²⁺ domain minimizes total influx, overlapping domains potentially can provide greater reliability and temporal fidelity (Stanley, 1997).

For >50 years frog skeletal NMJ has been used to study neurotransmitter release; consequently, much is known about the structure and neurophysiology of this synapse. Several putative Ca²⁺ channels are located within 100 nm of each vesicle (Heuser et al., 1974; Pumplin et al., 1981), so a high degree of channel cooperativity is possible. However, indirect electrophysiological analysis (Yoshikami et al., 1989; Augustine et al., 1991) and a recent Ca²⁺ imaging study (Wachman et al., 2004) are consistent with only a few channels opening with each action potential (AP), suggesting low cooperativity. We measured cooperativity by reducing the number of open channels with ω-conotoxin GVIA (ω-CTX) and monitoring Ca²⁺ influx fluorometrically while measuring postsynaptic potentials (PSPs). With estimates of Ca²⁺ channel positions from freeze fracture studies, we constrained the parameters of a high-resolution Monte Carlo simulation (Shahrezaei and Delaney, 2004) to determine the number and location of opened Ca²⁺ channels that would be consistent with our measurements. Our results indicate that, on average, only two to six Ca²⁺ channels open in response to an AP in each active zone (AZ) and are consistent with fusion of each vesicle resulting from Ca²⁺ influx through one or two nearby channels.

Materials and Methods

Tissue preparation.

Adult frogs (Rana pipiens) were immersed in anaesthesic (0.2% 3-aminobenzoic acid ethyl ester solution) for ∼15–20 min before being decapitated and pithed. The cutaneous pectoralis muscle, along with the innervating branch of the brachial nerve, was removed and immersed in normal frog Ringer's solution [containing the following (in mm): 116 NaCl, 2 KCl, 1.8 CaCl₂, 1 MgCl₂, 5 HEPES, buffered to pH ∼7.3] at all times during the remainder of the tissue preparation.

A pipette constructed from vinyl tubing was pinned onto a Sylgard ramp, and the nerve was cut, leaving ∼0.5–1 mm of nerve free of the muscle, which was sucked into the pipette. Then 100 mm EDTA (a Ca²⁺ and Mg²⁺ buffer) was applied immediately to the cut nerve end in an effort to prevent the cut axons from resealing. The buffer was removed after 1–2 min and replaced with a solution (0.1 mg/ml; ∼50 mm) of the dextran conjugate of the Ca²⁺-sensitive dye Oregon Green-1 BAPTA (OGB-1; Invitrogen, Burlington, Ontario, Canada). The Ca²⁺ dissociation constant of the dye lot used for this study was estimated by the manufacturer to be 188 nm in 100 mm KCl. The preparation was incubated in a moist chamber at room temperature for 4–6 h before the nerve was removed from the pipette and rinsed in normal frog Ringer's solution; the nerve/muscle preparation was left in the refrigerator overnight (∼4°C).

After axons were loaded with dye and after overnight incubation, the preparation was pinned to a small Sylgard-lined Petri dish, placed on a microscope stage, and maintained at ∼19°C with a Peltier cooling device throughout the imaging and electrophysiology component of the experiment.

Three sets of experiments were performed in which the Ca²⁺ influx into the presynaptic terminal was varied. In the first set the flux per channel was reduced by incrementally lowering external [Ca²⁺] (Ca_ext) from 1.8 to ∼0.45 mm. Two sets of experiments were performed in which the number of open channels was reduced by the application of 0.2 μm of the N-type Ca²⁺ channel blocker ω-CTX (Alomone Labs, Jerusalem, Israel). In one set ω-CTX was added to Ringer's containing 1.8 mm Ca²⁺, and in the other the Ca_ext was 0.45 mm. To avoid changes in the excitability of the tissue, which can occur in reduced Ca²⁺ solutions, we maintained the divalent cation concentration by a 1:1 substitution of Mg²⁺ for Ca²⁺.

Electrophysiology.

The cutaneous pectoralis nerve was stimulated at 3× threshold (determined by the onset of muscle twitch) via a constant current stimulus isolation device (SIU-90, A.M.P.I., Jerusalem, Israel), with the stimulation protocol controlled by a pulse generator (Master 8, A.M.P.I.). Depending on the Ca_ext, between 2 and 5 μm tubocurarine chloride (Sigma, St. Louis, MO) was added to the preparation to stop muscle twitching in response to a train of three nerve stimuli at 33 Hz. A terminal was chosen for Ca²⁺ imaging, and PSPs were recorded intracellularly from the muscle fiber on which it synapsed, using sharp microelectrodes (15–20 MΩ filled with 3 m KCl). Electrical recordings were prefiltered at 1 kHz and digitized at a 5 kHz sampling rate.

The recording electrode remained in the same muscle fiber throughout the remainder of the experiment. PSPs at the start of the experiment were adjusted to have an amplitude of 3–5 mV by the addition of curare before the addition of ω-CTX or the reduction of Ca_ext. Ringer's with different Ca_ext was prepared by mixing appropriate amounts of normal Ringer's with a Ringer's prepared with Mg²⁺ substituted for Ca²⁺ (Mg²⁺ = 2.8 mm). Normal Ringer's was exchanged with low Ca²⁺ Ringer's by washing 50 ml of solution through the 1.5 ml vol of the preparation chamber. After exchange the flow of saline was stopped, and the preparation was given 10–20 min to equilibrate. For experiments that used ω-CTX to block channels, aliquots of toxin were added directly to and gently mixed with the bath surrounding the muscle to a final concentration of 0.2 μm. PSPs and a series of Ca²⁺ influx measurements were collected every 5–10 min after the addition of toxin or after every change in Ca_ext.

Calcium imaging.

Terminals on the surface of a muscle fiber with fractional fluorescence changes of 15–25% and a peak-to-noise ratio of at least 10 for a single AP after averaging 10 trials were chosen for imaging. OGB-1 dextran conjugate was excited with 485 ± 6 nm light from a 75 W xenon arc lamp by using a switching monochromator (Polychrome II, TILL Photonics, Pleasanton, CA). Fluorescence was collected via a 60× 0.9 numerical aperture (NA) water-dipping lens (Leica Microsystems, Richmond Hill, Ontario, Canada), and images were obtained with an interline transfer CCD camera (PCO Imago, TILL Photonics) controlled by TILLVision (TILL Photonics). The camera was rotated to align the narrow axis of the terminal with the horizontal pixel rows of the camera. Images were binned on the chip before readout by a factor of 4× vertical by 15× horizontal to reduce the relative contribution of readout noise to the signal and were collected at a rate of 70 ms per frame in sets of 20. Stimuli were delivered at the onset of the 10th frame. Ten trials repeated at 5 s intervals then were averaged. The 5 s interval allowed enough time between stimulations to avoid facilitation or depression and for intracellular [Ca²⁺] to recover fully to prestimulus levels.

For measurement of fluorescence intensity the polygonal regions of interest were defined by delineating a portion of the endplate distal to the terminal Schwann cell that was in focus on the surface of the muscle fiber. Peak fractional fluorescence changes were calculated after correcting for background fluorescence from a region of the muscle fiber adjacent to the filled terminal, using the average resting fluorescence from nine frames before stimulation as a baseline. Thus, ΔF/F = (F (t) – F_rest)/(F_rest –F_bgnd), where F_rest and F_bgnd represent the fluorescence intensity of terminals in the absence of stimulation and background fluorescence, respectively. Imaging data were collected by using TILLVision, while most of the data analyses were performed with IgorPro (WaveMetrics, Lake Oswego, OR). A field stop aperture was used to restrict the illumination area around the terminal to reduce tissue background fluorescence and scattered fluorescence from out-of-focus structures.

For micrometer-sized structures like the presynaptic neuromuscular terminal, the measured fluorescence represents a spatial average of [Ca²⁺] across the entire volume. Ca²⁺ will reach spatial equilibrium in this volume within tens of milliseconds after a 1 ms duration Ca²⁺ current (Tank et al., 1995). The change in fluorescence that results is proportional to the total Ca²⁺ current. It is our hypothesis that, because of a small number of channels opening per AP, the relationship between total Ca²⁺ current and [Ca²⁺] at binding sites depends on the pattern of opening of channels within an AZ. Our method to test this hypothesis is to change the total Ca influx in two different ways, one of which changes the number of open channels and another that changes the flux per open channel. We then examine whether the same reduction of total Ca influx results in comparable reduction in release by these two methods. Calibration of fluorescence signals in terms of [Ca²⁺] is thus not necessary, but it is necessary to assume that, for each experiment in which the amplitude of AP-evoked fluorescence transients is compared with transmitter release, a reduction in AP-evoked fluorescence corresponds in an approximately linear manner to a reduction in total Ca²⁺ influx. Because the specific lot of OGB-1 dextran that we used is estimated to be a high-affinity indicator, we performed tests to confirm that it was not being saturated significantly by the incoming Ca²⁺ ions so that decreases in fluorescence would be essentially linear with decreases in [Ca²⁺] influx as influx was reduced by toxin or lowered Ca_ext. We compared the fluorescence change for a single AP with that produced by a pair of APs delivered at an interval of 30 ms. By assuming a single exponential decay and looking at fluorescence intensity for several frames after a single AP, we were able to estimate the fluorescence intensity decay time (τ ∼ 60 ms). Because the τ in our experiments is comparable to the frame rate (T = 70 ms), the response to a pair of APs should be less than twice that of a single AP. If we assume the fluorescence intensity after a single pulse follows a single exponential decay, we have the following:

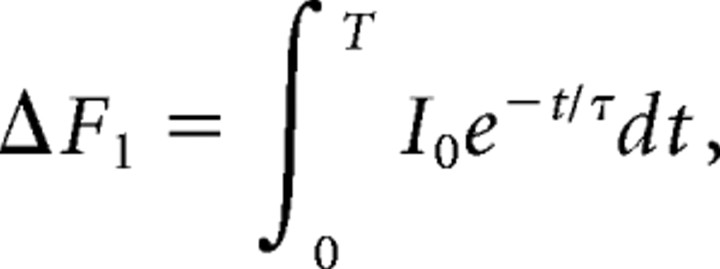where I₀ is a constant representing the total instantaneous increase in the fluorescence intensity that follows an AP. We assume the total Ca²⁺ influx produced in response to the second AP is the same as the first Ca²⁺ influx (i.e., there is no facilitation or inactivation of the Ca²⁺ channels). If the second influx follows the first after a time interval of T₁ and the response is linearly additive (no saturation of the dye), we have the following:

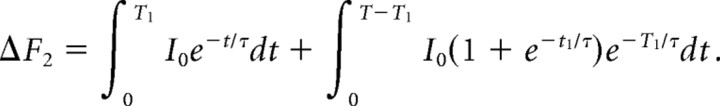Therefore, we arrive at a formula for the ratio of the response to a pair of pulses versus that of a single pulse as follows:

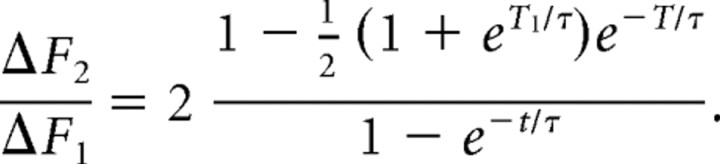For τ = 60 ms, T = 70 ms, and T₁ = 30 ms, this ratio is ∼1.7. We routinely observed this ratio for two versus one AP at the start our experiments, indicating that for single APs the change in Ca²⁺ in the terminals was small enough that we were working in an essentially linear regimen for this indicator, especially because our experiments involved manipulations that reduced Ca²⁺ influx from that present at the start of the experiment.

Monte Carlo simulation.

Monte Carlo simulation is a powerful method for studying reaction–diffusion problems. In this method the motion of each individual molecule (Ca²⁺ or buffer) is followed as it diffuses inside the nerve terminal. This is not done at the level of actual Brownian motion but rather at a coarser level, using random walk theory. The Monte Carlo method is efficient for simulating Ca²⁺ dynamics with high resolution when the number of molecules entering the system is small, which is the case for the brief channel openings resulting from AP-mediated depolarization. Also, using Monte Carlo simulations, we can store the identity of each Ca²⁺ molecule as it enters through a particular channel, diffuses throughout the terminal, and potentially interacts with a binding site on the release apparatus. As a consequence, this method naturally provides a powerful tool to study the Ca²⁺ channel cooperativity of release. In this paper we extended methods we previously developed to study the interaction between a single vesicle and the Ca²⁺ flux through a single channel (Shahrezaei and Delaney, 2004, 2005) to encompass an entire AZ of the frog NMJ. The AZ geometry in this terminal is well characterized, allowing for reasonable estimates of vesicle and potential Ca²⁺ channel positions.

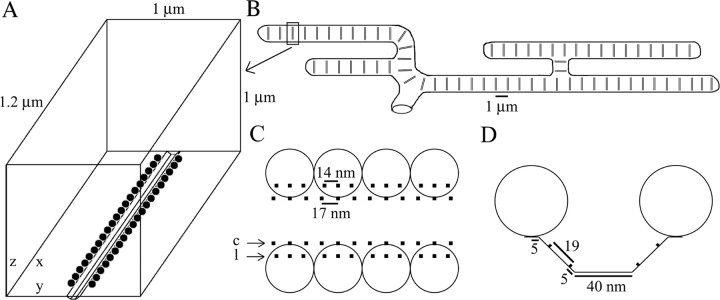
We simulated a single AZ, which consists of a transverse valley extending across the width of the terminal with Ca²⁺ channels situated on the walls bordered by two rows of synaptic vesicles (Heuser et al., 1974; Harlow et al., 2001). We have estimated the shape and geometrical parameters of the AZ based on a number of morphological studies (Pawson et al., 1998; Harlow et al., 2001; Stanley et al., 2003) (see Fig. 1). A typical NMJ of the pectoralis muscle consists of >100 AZs arranged parallel to each other with a spacing of ∼1 μm. We assumed an average AZ has 40 vesicles, each 50 nm in diameter, arranged in two parallel rows of 20. The AZ has a length of 1 μm and is separated by 100 nm from the walls of the terminal on each end. AZs at the frog NMJ are separated from each other by ∼1 μm, on average, so we assumed a width of 1 μm for the simulation box.

Figure 1.

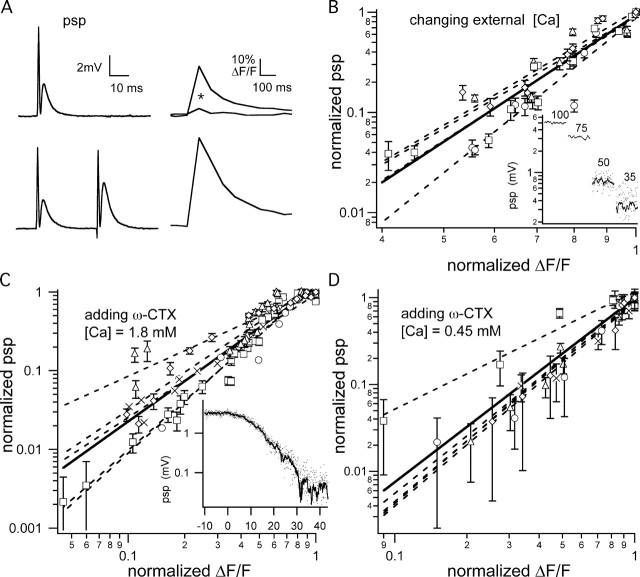
Relationship between the PSPs and Ca²⁺ influx. A, PSPs and presynaptic fluorescence transients produced by one and a pair of APs. Fluorescence transients in normal Ca_ext before and after (*) incubation with ω-CTX are shown. The observed increase in the size of the transient for a pair of APs is predicted from the linear summation of two equal transients spaced at 30 ms and decaying with an ∼70 ms time constant (see Materials and Methods), supporting our assumption that changes in F linearly correspond to changes in Ca²⁺ influx. B, Log–log plot of the relationship between the PSP and peak fractional fluorescence change (ΔF/F) for changing the Ca_ext. The data points for four experiments are shown with different symbols. Individual trials were fit by a power law function (dashed lines), and the average exponent (represented by the solid line) was 4.16 ± 0.62. Inset shows PSP data from one representative experiment. In all, 100 consecutive PSPs stimulated at 3.5 s intervals are plotted for each Ca_ext condition. For 50 and 35% of normal Ca_ext, the solid line plots the data as a continuous running average of 10 PSPs. C, Log–log plot of the relationship between the PSP and ΔF/F for channel-blocking experiments, with Ca_ext = 1.8 mm. The data points for five experiments are indicated by different symbols. Individual trials were fit with a power law function, and the average power was 1.70 ± 0.44. Inset shows PSP data from one representative experiment in which ω-CTX was added at T = 0 min, and PSPs were measured continuously over the ensuing 45 min to illustrate the slow time course of the buildup of the ω-CTX blockade. The solid line through individual data points is a 10 PSP running average. D, Log–log plot of the relationship between the PSP and the ΔF/F for channel-blocking experiments at [Ca²⁺] = 0.45 mm. Individual experiments (n = 5; different symbols) were fit with a power law function, and the average power was 2.12 ± 0.44. Error bars are ± SEM.

The valley between the two rows of vesicles has a depth of 25 nm and a width of 90 nm at the top and 40 nm at the bottom. There are four rows of Ca²⁺ channels in the valley between the vesicles, two on each side. We assumed six potential Ca²⁺ channels per vesicle, three in the medial row farthest from the vesicles and three in the lateral row nearest the vesicles (Pawson et al., 1998). Freeze fracture experiments generally show some particles are missing in the lateral row (Pawson et al., 1998; Stanley et al., 2003), so we randomly removed one-third of the channels in this row, leaving approximately five channels per vesicle for a total of 200 channels per AZ. All of the Ca²⁺ channels on the medial row are spaced equally, but the channels on the lateral row belonging to a single vesicle have a smaller spacing (Stanley et al., 2003).

Measurements of the endogenous Ca²⁺ buffer capacity in frog NMJ are limited, but there is some evidence that the buffer capacity may be as low as 50 (Suzuki et al., 2000). To test the dependence of our conclusions on endogenous buffer capacity, we assumed the presence of different amounts (0–0.5 mm) of a buffer with a rather high affinity (dissociation constant, K_D= 2 μm), fast kinetics (k_on= 3 × 10⁸ m⁻¹/s), and slow diffusion (27.5 μm²/s) (Burrone et al., 2002). This is equivalent to buffer capacities of up to 250. We did not consider any Ca²⁺ extrusion, sequestration, or release from internal stores, because their contribution to [Ca²⁺] profiles for short time intervals (∼1 ms) is negligible (Sala and Hernandez-Cruz, 1990).

The total Ca²⁺ rather than the Ca²⁺ current waveform determines the total release, if the time scales are smaller than the off-rate of the Ca²⁺ binding sites (Shahrezaei and Delaney, 2005). We assumed a simple square form for the single-channel Ca²⁺ current with a width of 1 ms and variable height to mimic different extracellular [Ca²⁺] levels. Also, as discussed in Results, we determined the effect of Ca²⁺ current duration and waveform on release and channel cooperativity.

Classic experiments at the frog NMJ revealed a strongly nonlinear relationship between Ca_ext and transmitter release (Dodge and Rahamimoff, 1967), suggesting that Ca²⁺-triggered release in this synapse requires simultaneous binding of multiple Ca²⁺ ions. Several models have been suggested for the Ca²⁺-dependent steps of release (Shahrezaei and Delaney, 2005). Here we use a high-affinity fast kinetic model suggested by Ca²⁺-uncaging experiments performed on the calyx of Held (Bollmann et al., 2000; Bollmann and Sakmann, 2005). We show that our results are robust against changes in the parameters of the release model.

Because we are interested in Ca²⁺ channel cooperativity for release, we tagged Ca²⁺ ions coming through different channels with the channel number (from 1 to 200). All of the boundary conditions are reflective for Ca²⁺ ions and buffer molecules. Ca²⁺ ions reflecting from the lateral walls of the AZ are approximately equivalent to Ca²⁺ ions coming from the adjacent AZ, so we changed the channel label of the Ca²⁺ ion to correspond to one of the channels in an imaginary adjacent AZ (1000–1200) if it is reflected from one of the lateral walls.

In the Monte Carlo simulations we assumed a Ca²⁺ diffusion coefficient of 220 μm²/s, Monte Carlo time steps of 10.2 ns, average jump sizes of 1.69 nm, and interaction range between Ca²⁺ ions and buffer molecules of 2 nm (Shahrezaei and Delaney, 2004). All simulations were implemented using the C programming language and parallelized by using the message-passing interface (MPI) library. Simulations were run on the Bugaboo cluster (96 dual 2.133 GHz Athlon processors) and Icarus, a 64 CPU (1.5 GHz Itanium 2) SGI (Mountain View, CA) Altix 3000 machine at Simon Fraser University. The simulations for this study required ∼2500 d of CPU time, but because we used parallel machines, the actual time taken was much shorter.

Results

Experiments

The cooperative relationship among Ca²⁺ ions, Ca²⁺ channels, and transmitter release has been studied at numerous synapses. A large body of evidence supports the concept that several Ca²⁺ ions must bind simultaneously, i.e., biochemically cooperate, to induce the fusion of a single vesicle. In principle, the ions that bind to the sites controlling the release of a single vesicle could enter the terminal through one or many channels. Experiments in which the amount of Ca²⁺ flowing through each open channel is changed can inform about the biochemical cooperativity but cannot indicate the number of Ca²⁺ channels supplying the ions that cause fusion of a given vesicle. Regardless of whether one or several channels contribute Ca²⁺ for fusion, reducing the flux per open channel will always result in a nonlinear (i.e., cooperative) relationship between total Ca²⁺ influx and release, because the [Ca²⁺] at all potential binding sites will be one-half normal if the flux per channel is reduced by one-half.

Ca²⁺ channel cooperativity can be explored by varying the number of channels that are opened during an AP. If many channels contribute Ca²⁺ to the release sites of one vesicle, then [Ca²⁺] at the binding sites will be reduced in direct proportion to the reduction in the number of open channels. Release thus will be reduced in superlinear proportion to the reduction in the number of open channels, because release probability is superlinearly related to [Ca²⁺]. On the other hand, if the Ca²⁺-stimulating release of a vesicle originates entirely from one channel, then release will be reduced linearly with the reduction in open channels. Vesicles adjacent to a channel that opens will experience normal [Ca²⁺] and have normal release probability, whereas those near closed channels will see no appreciable increase in [Ca²⁺] and experience no increase in release probability, so the overall release probability will change proportionally to the fraction of channels that are blocked. If a few channels contribute to triggering vesicle fusion, then a cooperativity between one and the limit set by the biochemical cooperativity is predicted.

We quantified the change in the number of open channels during the accumulation of ω-CTX blockade by measuring AP-induced fluorescence changes of OGB-1 dextran loaded into the presynaptic terminals of the NMJ of the frog cutaneous pectoralis nerve/muscle preparation. Figure 1A shows a typical profile of ΔF/F versus time, demonstrating that the increase in fluorescence in the terminal occurs concurrent with the delivered stimulus. For a non-ratiometric indicator like OGB-1, changes in fluorescence are related essentially linearly to changes in [Ca²⁺], provided that the [Ca²⁺] is at or below the K_D of the indicator. We repeatedly confirmed that ΔF was proportional to Δ[Ca²⁺] at the start of our experiments by doubling the total influx with a pair of APs delivered at an interval of 30 ms (as shown in Fig. 1A) (see Materials and Methods).

Changing the Ca_ext changes the single Ca²⁺ channel influx and, by monitoring the relationship between the change in AP-evoked fluorescence transients versus the change in the amplitude of the PSP, we can estimate the Ca²⁺ biochemical cooperativity. Plotting these two variables on log scales illustrates the power law relationship that exists between influx and release. Decreasing the Ca_ext from normal (1.8 mm) to near zero results in a rapid decrease in release, corresponding to an average power relationship between Ca²⁺ influx and release of 4.16 ± 0.62 (n = 4), slightly higher than Dodge and Rahamimoff's (1967) estimate (Fig. 1B). This suggests a biochemical cooperativity of five, similar to the value observed in the calyx of Held synapse (Bollmann et al., 2000; Schneggenburger and Neher, 2000).

To explore the effect of changing the number of open channels on release probability, we used ω-CTX to reduce the number of N-type Ca²⁺ channels that were opened by each AP without affecting the single-channel conductance of the unblocked fraction (Boland et al., 1994; McDonough et al., 2002). Blocking of N-type Ca²⁺channels completely abolishes AP-triggered release at the frog NMJ (Kerr and Yoshikami, 1984). By our applying a low concentration of ω-CTX (0.2–0.4 μm), the blocking accumulated exponentially, reaching a maximum over the course of 45–60 min (Fig. 1) (Zengel et al., 1993). This was slow enough that simultaneous measurements of Ca²⁺ influx and transmitter release, each requiring 1–3 min to complete, could be made at intervals during the course of channel blockade. Monitoring the relationship between PSP amplitude and Ca²⁺ influx while progressively blocking more channels reveals the cooperativity among the channels that are responsible for the vesicular release. In the presence of normal 1.8 mm Ca_ext the addition of ω-CTX reduces Ca²⁺ influx and release with an observed power relationship between influx and release of 1.70 ± 0.44 (n = 5), significantly different from the value of 4.16 obtained by reducing Ca_ext (Student's t test; df = 7; p < 0.01) (Fig. 1C). Cooperativity could be underestimated if the release process is saturated partially by Ca²⁺ influx at normal physiological levels of Ca_ext. However, with the preparation bathed in 25% Ca_ext (0.45 mm) solution, the addition of ω-CTX reduced Ca²⁺ influx and transmitter release with a slightly more nonlinear relationship of 2.12 ± 0.44 (n = 5), which was not different in a statistically significant way from the cooperativity observed with 1.8 mm Ca_ext for this sample size (Student's t test; df = 8; p ∼0.17) (Fig. 1D).

N-type Ca²⁺ channel heterogeneity has been reported at cultured NMJs on the basis of their susceptibility to reversal of ω-CTX binding (reversible in tens of minutes vs essentially irreversible). In our experiments low concentrations of ω-CTX were present for the duration of the experiment (Fig. 1), and in control experiments washout for 1 h showed no evidence for reversal of ω-CTX block (data not shown). The precise position of Ca channels within the two rows of particles associated with each row of vesicles has little influence on cooperativity (see Fig. 5). Therefore, we do not consider heterogeneity among the N-channels in the terminal as a likely explanation for our findings.

Figure 5.

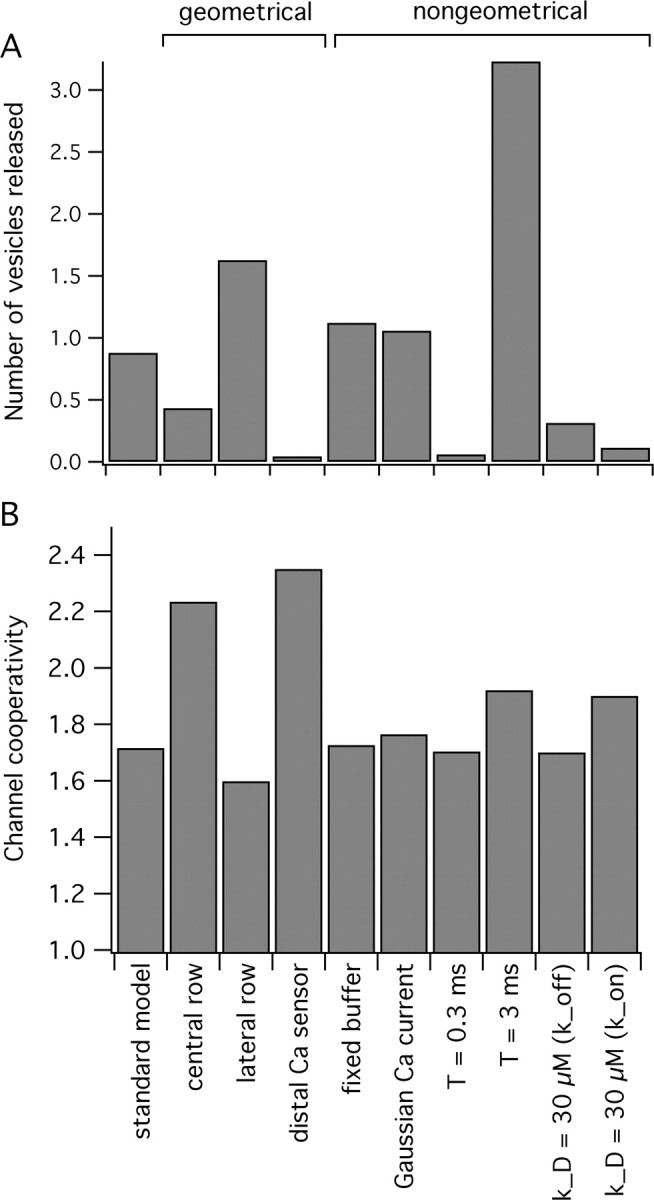
The number of vesicles released and channel cooperativity as a function of variation in model parameters. A, The average number of vesicles released for the standard model (4 open channels; single-channel I_Ca = 0.1 pA; mobile buffer concentration, 0.1 mm; K_D = 2 μm) compared with that when some of the geometrical and non-geometrical model parameters are varied. The geometrical variations that we explored were to constrain all of the open channels to the central row (far from vesicles) or lateral row (close to vesicles) or to restrict all of the Ca²⁺ binding sites to the side of the vesicle opposite the channels, as opposed to the side closest to the channels. The non-geometrical variations tested were to replace the mobile buffer with the fixed buffer (with the same amount and affinity), to decrease or increase the single-channel current duration (0.3 or 3 vs 1 ms), to use a Gaussian single-channel current waveform with the same total influx, to decrease or increase the single-channel current duration (0.3 or 3 vs 1 ms), and to increase the Ca²⁺ binding site dissociation constant to K_D = 30 μm (from 10 μm) by either increasing the off-rate or decreasing the on-rate as indicated. B, The channel cooperativity resulting from the parameter variations indicated in A as compared with the standard model.

We also do not believe that Ca²⁺-activated potassium (CaK) channels are confounding our conclusions regarding Ca²⁺ channel cooperativity. Using iberiotoxin and 0.45 mm Ca_ext (25% of normal), we confirmed an approximate doubling of release similar to the effect reported by Robitaille and Charlton (1992), who used saturating doses of charybdotoxin to block CaK with Ca_ext of 0.5 mm. Importantly, we also saw that iberiotoxin had a similar effect on release with normal 1.8 mm Ca_ext (data not shown), indicating that CaK channels are activated over the range of Ca²⁺ influx that we used to probe Ca²⁺ channel cooperativity. Also, we derive our conclusions regarding cooperativity by comparing data from two different treatments, both of which reduce Ca²⁺ influx, so they should have approximately similar effects (if any) on CaK. Finally, because AP broadening increases Ca²⁺ influx with only a moderate influence on release (e.g., a twofold increase in release for a 44% increase in Ca²⁺ influx with charybdotoxin) (Robitaille and Charlton, 1992) it would tend to compensate for the reduction of Ca²⁺ influx more than the reduction of release and therefore increase the apparent sensitivity of release to Ca²⁺, inconsistent with our observation of low cooperativity in these experiments.

Monte Carlo simulations

To relate the experimental findings to possible scenarios for the opening of Ca²⁺ channels in the AZ, we analyzed Ca²⁺ diffusion and its subsequent binding to receptors in the terminal by using a Monte Carlo simulation (Shahrezaei and Delaney, 2004). Previously, with the use of mathematical modeling, low channel cooperativity has been attributed to a small number of open channels driving individual release sites (Quastel et al., 1992; Bertram et al., 1999). By using a Monte Carlo simulation of Ca²⁺ diffusion in a realistic model of frog NMJ, we have attempted to relate the observed channel cooperativity of release to the number and position of open Ca²⁺ channels in the AZ. Frog NMJ is suitable for this type of modeling study because the morphology of the AZs in this terminal is well described. Figure 2A shows the geometry of a frog NMJ AZ that we used in our simulation. A typical-sized terminal may have >100 parallel AZs (Fig. 2B). We simulated a single typical AZ with 40 vesicles arranged in two parallel rows of 20 separated by a valley (Fig. 2A). Freeze fracture studies indicate that there are approximately five intramembranous particles associated with each vesicle, which reside in two rows on both sides of the valley between the rows of the vesicles. In the simulations we assumed these were all potentially Ca²⁺ channels. Assuming that only one-half or one-third of these particles were Ca²⁺ channels did not affect our analysis materially but, of course, changes our estimation of channel opening probability (see Discussion). For reference, we define the central row of channels as those that are farthest from the rows of vesicles and the lateral row as the row that is closest to the vesicles (Fig. 2C,D).

Figure 2.

Structure of frog NMJ relevant to our geometrically realistic Monte Carlo simulations. A, Simulation volume containing one AZ with associated vesicles and Ca²⁺ channels. B, Schematic view of a typical frog skeletal NMJ illustrating the parallel arrangement of its AZs. C, Top view (x–y plane) of part of an AZ showing the position of the two rows of vesicles and four rows of Ca²⁺ channels. The lateral and central rows are specified by c and l. D, Side view (y–z plane) showing the form of the valley between the rows of the vesicles and the position of the Ca²⁺ channels corresponding to the medial and lateral rows within the valley.

Figure 3A shows three examples of average [Ca²⁺] profiles in the AZ plane corresponding to different numbers of open channels. It is clear that a low number of open channels results in a highly nonuniform standing [Ca²⁺] profile, whereas many open channels flood the AZ with Ca²⁺ almost uniformly. Figure 3B shows the standing [Ca²⁺] at three different locations along the AZ and in a plane perpendicular to it for the case shown in Figure 3Ai. The three planes in Figure 3B are through the center of vesicles close to two open channels in Bi, through the center of an open channel in the central row in Bii, and through the center of an open channel in the lateral row close to vesicles in Biii. The last case in Figure 3B produces the greatest [Ca²⁺] at the vesicle and Ca²⁺ sensor.

Figure 3.

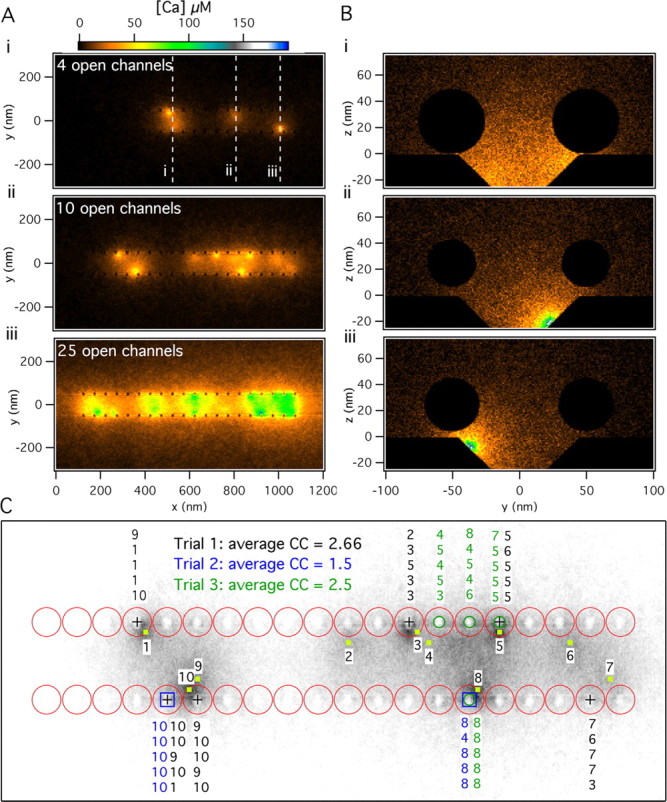
[Ca²⁺] profiles and Ca²⁺ channel cooperativity. A, Standing [Ca²⁺] (in the x–y plane at the z = 0) (see Fig. 2A) after 4, 10, or 25 channels remained open for 1 ms. B, Standing [Ca²⁺] profiles (in the y–z plane) (see Fig. 2A) for three different cross sections for the four open channels condition shown in Ai. Cross section i passes through the midline of vesicles adjacent to two nearby open channels, whereas cross sections ii and iii are centered on individual channels that open in the medial and lateral rows, respectively. C, Vesicles released in response to 10 open channels as shown in Aii for three different simulation trials. The specific Ca²⁺ channels that contributed the Ca²⁺ ions that bound to the Ca²⁺ sensor-binding sites for release of each vesicle are indicated above or below the released vesicle. The corresponding average number of channels involved in a release event (the channel cooperativity specified by CC in the panel) for each trial is obtained directly from these data.

Figure 3, A and B, illustrates that the standing [Ca²⁺] achieved inside the valley, where the putative Ca²⁺ channels reside and are surrounded by two rows of vesicles, is much higher than at the outside. The sharpness of the [Ca²⁺] profile at the boundaries of the valley is enhanced because of the blockage of free diffusion of Ca²⁺ ions by the vesicles (Shahrezaei and Delaney, 2004). Therefore, the geometry of the AZ in the frog NMJ prevents rapid spread of Ca²⁺ ions away from each AZ and enhances the [Ca²⁺] experienced by Ca²⁺ sensors.

In the Monte Carlo simulation each individual Ca²⁺ ion can be followed as it enters the terminal through a particular channel and binds to a binding site on the Ca²⁺ sensor responsible for release. Figure 3C shows the vesicles released in three different trials in which the same 10 channels were opened, as in Figure 3Aii (specified by the yellow squares and numbers in Fig. 3C). In each trial a different set of vesicles is released, and these are denoted by different symbols at the center of the released vesicles (square, circle, and plus signs). It is evident that vesicles closer to open channels are more likely to get released. Also, above (or below) each fused vesicle we have noted the channel identity for the channel or channels that supplied the Ca²⁺ ions that bound to the five binding sites of the Ca²⁺ sensor in each trial. In the illustrated case of 10 open channels, a single channel by itself rarely causes fusion of a vesicle (only channels 8 and 10 were ever solely responsible for a release). More often, cooperation of two or more channels was needed for release, although the majority of the ions originated from one channel. Using our simulations, we can determine directly the average number of Ca²⁺ channels that cause release in single trials and across several trials (Fig. 3C). We define the average number of channels that are needed for release across many trials as the channel cooperativity, which is functionally the same as the power relationship between Ca²⁺ influx and neurotransmitter release that is observed when influx is reduced by channel blocking and release is far from saturation.

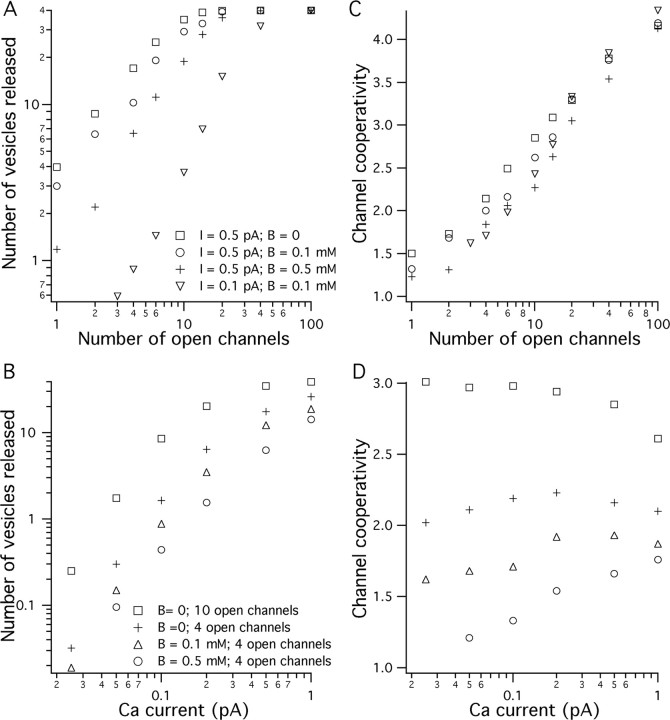
Figure 4 shows the dependence of release and channel cooperativity on the number of open Ca²⁺ channels and the single-channel current. Each data point is an average of at least 100 release events. The number of release events or the release probability is equivalent to the amplitude of the experimentally measured PSP, so the data in Figure 4A are equivalent to the experiments in which channels were blocked by ω-CTX, and those in Figure 4B correspond to experiments in which Ca_ext was changed. However, simulated release probabilities were performed over a larger range of Ca²⁺ influx than those measured experimentally. With many open channels or large Ca²⁺ currents, release is saturated with the number of released vesicles approaching 40 (the total number of docked vesicles). It has been observed experimentally that at normal Ca_ext the average number of vesicles released per AZ in frog NMJ is approximately one. Therefore, the limiting slopes for the simulated condition in Figure 4A with a small number of open channels are related to the chemical cooperativity measured experimentally. The limiting slopes of the data in Figure 4B for low Ca²⁺ influx are in the range of five for all conditions, which reflects the chemical cooperativity in the release model.

Figure 4.

Results of Monte Carlo simulations indicating the number of vesicles released and the channel cooperativity as a function of number of open channels and the channel influx. A, Average number of vesicles released (maximum possible of 40) as a function of the number of open channels in the AZ for different magnitudes of single-channel Ca²⁺ current and different amounts of mobile buffer. B, Average number of vesicles released as a function of single-channel Ca²⁺ current for different numbers of open channels and different amounts of mobile buffer. C, Average channel cooperativity (maximum possible of 5) as a function of the number of open channels in the AZ for different values of Ca²⁺ current and different amounts of mobile buffer present. D, Average channel cooperativity as a function of Ca²⁺ channel current for different numbers of open channels and different amounts of mobile buffer present.

Figure 4, C and D, shows the average number of Ca²⁺ channels involved in release (channel cooperativity) under each condition. Channel cooperativity is close to biochemical cooperativity (which is set to five in our release model) when many channels open and approaches unity with few open channels. The relationship between the channel cooperativity and number of open channels is approximately logarithmic. For our experimentally observed channel cooperativity for normal Ca_ext (1.7 ± 0.44) to match, the modeling results suggest that the number of open channels should be two to six (Fig. 4C). The magnitude of the single-channel Ca²⁺ current and the amount of mobile buffer present affect the simulated channel cooperativity (Fig. 4D). In general, buffer reduces the channel cooperativity by reducing the single-channel domain overlap. For example, for I_Ca = 0.5 pA and four open channels, the presence of 0.1 or 0.5 mm mobile buffer (K_D = 2 μm; k_on = 3 × 10⁸ m⁻¹/s) reduces the channel cooperativity by ∼7 or 14%, respectively (Fig. 4B).

Figure 4D shows that the channel cooperativity changes by only small amounts over 40-fold changes in Ca²⁺ influx, suggesting that the relative proportional contributions of different channels remain approximately constant. In the presence of 0 or 0.1 mm mobile buffer, reducing the channel current from 1 to 0.025 pA first increased the channel cooperativity and then decreased cooperativity by a small amount. In the presence of 0.5 mm mobile buffer, the channel cooperativity continuously decreased as channel current was reduced. We can understand the effect of buffer and channel current on channel cooperativity by considering the low and high buffer conditions. With little buffer present, channel cooperativity increases as channel current is reduced because the cooperation of more channels is required, on average, to contribute sufficient Ca²⁺ to evoke release. The presence of more buffer limits the contribution of channels farther away as the single-channel current is reduced and, therefore, lowers the channel cooperativity.

In our experiments we found no reduction in channel cooperativity but, instead, observed a slight increase at 25% of normal Ca_ext (Fig. 1). Therefore, we conclude that the total amount of buffer present in the terminals of NMJs under study (endogenous and added dye) was less than the equivalent of 0.5 mm concentration of our theoretical mobile buffer. This is consistent with the experimentally derived estimate of low buffer capacity in the frog NMJ (Suzuki et al., 2000) and also puts an upper limit on the amount of buffering provided by the addition of the Ca²⁺ indicator in our experiments.

The frog NMJ terminal consists of up to 100 parallel linear AZs separated from each other by ∼1 μm (Fig. 2B). Although we simulate only a single AZ, a Ca²⁺ ion bouncing off the lateral walls of our simulation box (parallel to the x–z plane in Fig. 2A) is equivalent to an ion entering the simulation volume from a neighboring AZ. We observed that these reflected Ca²⁺ ions rarely contribute to release. Therefore, we conclude that the Ca²⁺ influx from other AZs of the frog NMJ does not contribute significantly to release at a given AZ, although it may be important for residual Ca²⁺-dependent short-term synaptic plasticity.

It is known that the size of the Ca²⁺ transient at the release site can affect the synaptic delay (Bollmann et al., 2000; Schneggenburger and Neher, 2000; Bollmann and Sakmann, 2005). In our simulation we define the average time of fusion events as the delay of release. This counts only for the presynaptic portion of synaptic delay from opening of the Ca²⁺ channel to the beginning of the fusion event. In our simulations we observed that reducing Ca²⁺ influx, by reducing either the single-channel Ca²⁺ influx or the number of open channels, increases the delay to the onset of release. Simulations suggest that the maximum increase in delay expected in our experiments is ∼0.2 ms, by either changing Ca_ext or adding ω-CTX. We are using nerve stimulation several millimeters away from the terminal to elicit an AP; because we do not have an accurate measure of the time of AP invasion into the terminal, we are unable to determine changes of this magnitude in our experiments.

We tested the robustness of our simulations with regard to estimating the channel cooperativity by altering some of the geometrical parameters of our model, including the position of Ca²⁺ channels and Ca²⁺ binding sites, and non-geometrical parameters, including the duration of the current and the affinity of the Ca²⁺ sensor. Figure 5 shows that, although changes to most of these parameters significantly alter the total amount of release, channel cooperativity remains relatively constant. Changes in the Ca²⁺ current duration or in the affinity of the Ca²⁺ binding sites did not alter the channel cooperativity but did affect total release. We also tested the effect of having a very high Ca²⁺ affinity for binding sites. To increase the affinity from 10 to 1 μm, we increased the forward binding rate by a factor of three, to near the theoretical diffusion limit, and decreased the reverse binding rate a comparable amount. Total release tripled, consistent with the increase in forward binding rate, but the cooperativity remained low at 1.65. This result is consistent with the dominant contribution of Ca²⁺ from the nearest open channel to the binding sites for Ca²⁺, as previously seen with the slower forward rates used to achieve lower equilibrium affinity values. Using a Gaussian-like rather than a square single-channel current waveform with the same total influx did not change the channel cooperativity or release significantly, which justifies the use of simple square influx waveforms in this study. Also, replacing the mobile buffer with a fixed buffer of equal capacity did not affect the channel cooperativity. Changing the location of Ca²⁺ binding sites and Ca²⁺ channels had the largest effect on channel cooperativity. For example, moving the Ca²⁺ binding sites to the far side of the vesicle, away from the rows of postulated Ca²⁺ channels, increased the channel cooperativity by 46% while reducing the release probability by a factor of 20 because of the vesicles acting as a physical barrier for free diffusion of Ca²⁺ ions to the Ca²⁺ binding sites (Shahrezaei and Delaney, 2004). The blocking effect of vesicles also increased the channel cooperativity by increasing the relative contribution of channels located farther away from the Ca²⁺ binding sites. These results suggest that the main parameters determining channel cooperativity are the number and the geometrical organization of opened channels relative to the vesicles and their associated Ca²⁺ sensor(s).

Discussion

We examined the relationship between neurotransmitter release and Ca²⁺ influx through Ca²⁺ channels at the frog NMJ. Electrophysiology was used to measure PSPs, and the total Ca²⁺ influx was measured by monitoring the change in intracellular [Ca²⁺] produced by a single AP in the terminal with a fluorescent Ca²⁺ indicator dye. The degree of nonlinearity in the relationship between Ca²⁺ influx and release was dependent on how influx was altered. If the flux per channel was reduced by changing Ca_ext, we observed that release was proportional to Δ[Ca²⁺]ⁿ with n = 4.16 ± 0.62, which reflects the lower limit for the number of Ca²⁺ ions needed for release or the biochemical cooperativity (Dodge and Rahamimoff, 1967). If we reduced the number of open Ca²⁺ channels by blocking channels with ω-CTX, the data were fit with n = 1.70 ± 0.44. This observed value for the exponential relationship between Ca²⁺ influx and release reflects the average number of channels involved in a single release event or the channel cooperativity. This number is significantly smaller than the observed biochemical cooperativity and suggests that, on average, only one or a few channels contribute Ca²⁺ for a single release event. This is consistent with previous conclusions derived indirectly from experiments that used ω-CTX to block channels, which were performed without concurrent Ca²⁺ imaging at the frog NMJ (Yoshikami et al., 1989). We also found that channel cooperativity remains approximately the same (or possibly slightly higher) when Ca²⁺ influx is reduced to 25% of normal. Our measured channel cooperativity is lower than the estimate expected from the recently proposed phenomenological unified model of release (Gentile and Stanley, 2005).

It generally is understood that the channel cooperativity will depend on the specifics of AZ organization and Ca²⁺ buffering at a particular synapse (Stanley, 1997; Bertram et al., 1999). We constructed a Monte Carlo simulation with nanometer resolution based on existing morphological data for frog NMJ to reproduce Ca²⁺ dynamics and transmitter release in a realistic model of a typical AZ. Our simulations indicate that the organization of the AZ in frog NMJ, Ca²⁺ channels in the valley surrounded by two rows of vesicles, enhances the Ca²⁺ transient experienced by vesicles caused by blocking of free diffusion of Ca²⁺. Monte Carlo simulation is well suited to study of channel cooperativity, because individual Ca²⁺ ions can be tracked as they enter the terminal and diffuse via the simulation volume. Subsequently, the identity of all of the channels that contribute Ca²⁺ to a vesicle fusion event can be determined directly. Our modeling predicts that the channel cooperativity of 1.7 ± 0.4 that we observe can be achieved only if the number of open channels per AZ per AP is in the range of two to six. The low channel cooperativity results from the small number of channel openings and the tight colocalization of channels to vesicles in the AZ. With more open channels, cooperativity increases sublinearly until it equals the biochemical cooperativity set by the number of bound Ca²⁺ ions needed to trigger vesicle fusion. For example, if 10 channels open per AZ during an AP, a channel cooperativity of ∼2.4 is predicted in our model.

By regulating the spread of Ca²⁺ throughout the AZ, mobile buffers can change the extent of Ca²⁺ channel cooperativity. The influence of buffer on cooperativity depends on the topography of Ca²⁺ channels and vesicles. Bertram et al. (1999), using a model that included a rapid buffer approximation (Smith, 1996), predicted an increase in channel cooperativity with saturating amounts of a mobile buffer if channels were positioned equidistantly around the vesicle. However, modeling this channel–vesicle topography by using our Monte Carlo method, which does not require the rapid buffer approximation, we find no significant change in channel cooperativity in the presence or absence of mobile buffer (data not shown). This suggests that, with channels arranged equidistant from a vesicle, the relative contribution of each channel to the Ca²⁺ sensor remains the same regardless of the amount of buffer present.

Generally, however, channels are distributed at varying distances from vesicles. This is particularly true for the linear topography of the frog NMJ, in which only a small proportion of the channels is located near any given vesicle. This topography results in a different effect: increasing buffer capacity decreases cooperativity by disproportionately favoring channels that open near a vesicle. Our simulations indicate that, provided release is not saturated significantly (the number of vesicles released is less than the immediately releasable pool), channel cooperativity will be reduced by the experimental addition of exogenous buffer to AZs, with channels distributed unevenly around vesicles. Our simulations also indicate that increasing the number of open channels per AP (e.g., by widening APs pharmacologically or by lengthening voltage-clamp steps) should increase the cooperativity. It is believed that the frog NMJ has a relatively low buffer capacity of ∼50 (Suzuki et al., 2000), and our experimental and simulation results support this conclusion. In our simulations increasing buffer capacity by a factor of five above experimental estimates (using 0.5 mm of buffer) reduces the estimated channel cooperativity by <20%.

The prediction of a low number of open channels is not strongly dependent on our choices for various non-geometrical parameters, such as the channel current waveform or the Ca²⁺ binding site affinity. Some geometrical parameters can affect our estimate of the channel cooperativity. For example, by assuming active channels are located only in the central row farther from the vesicles or by positioning some of the Ca²⁺ binding sites on the side of the vesicle opposite the channels, cooperativity is increased.

A typical AZ in the frog NMJ is known to release somewhere between 0.5 and one vesicle per AP (Poage and Meriney, 2002). If we fix the geometry and the number of open channels in our model, then the total number of vesicles released depends on two parameters: the average single Ca²⁺ channel current during an AP and the affinity of the Ca²⁺ binding sites. Rapid high-resolution Ca²⁺ imaging of AP-mediated presynaptic Ca²⁺ transients at the frog NMJ indicates trial-to-trial variability in the spatial distribution of Ca²⁺ entry within single AZs (Wachman et al., 2004). This work suggests that an AP triggers the opening of a small number of Ca²⁺ channels per AZ, which is consistent with our experimental findings and the modeling. If all of the intramembranous particles seen in freeze fracture studies (∼200) are active N-type Ca²⁺ channels, then their opening probability must be <3% to match our results, which may be considered low for N-type Ca²⁺ channels even at room temperature (King and Meriney, 2005). A reasonable alternative, which would increase the opening probability, is that some of the particles observed in the freeze fracture are not functional N-type Ca²⁺ channels. There is evidence for CaK channels colocalized with the Ca²⁺ channels in the frog NMJ terminal (Robitaille and Charlton, 1992; Robitaille et al., 1993). It is therefore possible that perhaps 30–50% of the particles in the AZ are CaK channels, similar to the AZs of hair cells (Roberts et al., 1990).

The small number of open channels per AP per AZ and the low channel cooperativity that results have functional consequences for the physiology of the frog NMJ. Using a small number of open channels with tight colocalization between channels and Ca²⁺ binding sites to drive release reduces the energy needed to restore [Ca²⁺] after influx. So that release can be maintained during repetitive activity, it is advantageous for the frog NMJ to release only a small fraction of the available pool of vesicles with each AP. At the same time it must release enough transmitter reliably to bring the muscle fiber above threshold. Our experimental data and modeling suggest that this is achieved by having a relatively high probability of release for the vesicles adjacent to each of the small number of channels opened by each AP and virtually no likelihood for release of other vesicles. This contrasts to the alternative strategy by which release is limited to a small fraction of the readily releasable vesicle pool by a low probability of release for each of many vesicles exposed to Ca²⁺ entering through many channels. Interestingly, the amplitude of PSPs evoked by APs in normal Ca_ext varies less than expected for independent release events from the pool of docked vesicles (Del Castillo and Katz, 1954; Kreibel and Keller, 1999). An important problem that remains is to determine how the frog NMJ manages to achieve low release variability and how AZ geometry, or inhibitory intervesicular interactions, might function to improve the reliability of release at this synapse.