Abstract
Motor systems often require that superfluous degrees of freedom be constrained. For the oculomotor system, a redundancy in the degrees of freedom occurs during visually guided eye movements and is solved by implementing Listing’s law and the half-angle rule, kinematic constraints that limit the range of eye positions and angular velocities used by the eyes. These constraints have been attributed either to neurally generated commands or to the physical mechanics of the eye and its surrounding muscles and tissues (i.e., the ocular plant). To directly test whether the ocular plant implements the half-angle rule, critical to the maintenance of Listing’s law, we microstimulated the abducens nerve with the eye at different initial vertical eye positions. We report that the electrically evoked eye velocity exhibits the same eye position dependence as seen in visually guided smooth-pursuit eye movements. These results support an important role for the ocular plant in providing a solution to the degrees-of-freedom problem during eye movements.
Keywords: eye, torsion, muscles, pulleys, Listing’s law, pursuit
Introduction
Our limbs are controlled in the presence of kinematic redundancy. For example, when pointing to an object, one can rotate the arm torsionally about the index finger and still remain pointing at the same object. Similarly, the oculomotor system also faces kinematic redundancy during visually guided eye movements: objects in space project their images onto the retina, which in turn sends two-dimensional (i.e., horizontal and vertical) retinal error signals to the brain. These two-dimensional inputs must ultimately be used to rotate the eye, which is innervated by three pairs of muscles and thus has three degrees of freedom (i.e., horizontal, vertical, and torsional). This torsional third degree of freedom is often redundant and thus free to assume a range of values without affecting final gaze direction.
The oculomotor system solves this degree-of-freedom problem (i.e., it determines how much torsion to apply) by obeying Listing’s law and the half-angle rule (Fig. 1 A,B). Listing’s law states that “eye positions” have zero torsional components and are thus maintained in a planar range known as Listing’s plane (Fig. 1B, vertical dashed line). Mathematically, for this to hold, “angular eye velocities” must have non-zero torsional components such that they tilt out of Listing’s plane by half as much as eye position (Fig. 1B, near-vertical solid line). Although these principles have been shown to exist for over 100 years (Helmholtz, 1867), the mechanism(s) by which these rules are enforced has been a divisive issue.
Figure 1.
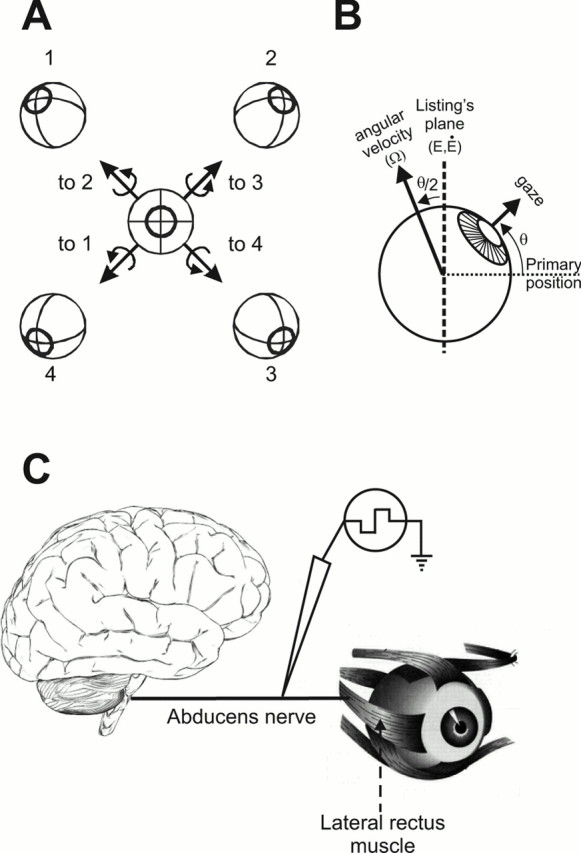
Three-dimensional ocular kinematics and methodology. A, A front view of the eye shows that any eye position can be defined as the axis of rotation (arrows 1- 4) that takes the eye from a reference position (center eye) to the new position (corresponding eye positions 1- 4). With such a representation, all such axes lie in a plane (i.e., the plane of the paper) known as Listing’s plane.B, From a side view of the eye, Listing’s plane can be viewed edge-on (vertical dashed line). Both eye positions (E) and the derivative of eye position (i.e., eye velocity = Ė) lie in Listing’s plane. But angular eye velocity, the axis about which the eye rotates when traveling from one position to the next, tilts out of Listing’s plane by half the angle of eye eccentricity from the primary position (the reference position in A). For example, if the eye is oriented upward by 20°, then angular eye velocity must tilt 10° away from Listing’s plane. C, Schematic of methodology. Stimulation was applied to the abducens nerve (cranial nerve VI), which carries neural commands from the brainstem to the lateral rectus muscle.
For the past decade, debate has centered around whether such three-dimensional rules are implemented neurally by brainstem circuits (Tweed and Vilis, 1987) or mechanically by the positioning of orbital pulleys (Miller, 1989; Miller et al., 1993; Quaia and Optican, 1998; Demer et al., 2000). In support of the former, Listing’s law is obeyed by saccades (Helmholtz, 1867; Tweed and Vilis, 1990), pursuit (Haslwanter et al., 1991; Tweed et al., 1992; Angelaki et al., 2003; Adeyemo and Angelaki, 2005) and vergence (Van Rijn and Van den Berg, 1993) eye movements, but not by others such as the rotational vestibulo-ocular reflex (Crawford and Vilis, 1991; Fetter et al., 1992; Angelaki, 2003; Angelaki et al., 2003). Listing’s law has also been shown to optimize both perceptual and motor aspects of vision (Glennand Vilis, 1992; Radau et al., 1994; Tweed, 1997; Schreiber et al., 2001). In support of the latter, histologically identified connective tissue has been proposed to have a pulley-like effect whereby extra-ocular muscles change their effective pulling direction with changes in eye position (Miller, 1989; Miller et al., 1993; Demer et al., 2000; Kono et al., 2002a,b; Demer, 2004), thus mechanically implementing the half-angle rule. Of course, the answer might also be found in an intermediate strategy in which brainstem circuits control an eye plant with pulleys (Tweed et al., 1994; Smith and Crawford 1998).
To directly test whether the half-angle rule can be implemented mechanically by the plant, we stimulated the abducens nerve (and, in some cases, the abducens nucleus) and subsequently measured the resultant three-dimensional eye movements (Fig. 1C). By stimulating so late in the oculomotor pathway, we essentially bypassed any neural circuits that could potentially contribute to the implementation of the half-angle rule. We show that the resultant movements exhibited an eye position dependence identical to that observed during visually guided pursuit, thus verifying a large role for the motor plant in providing a solution for the unwanted degree of freedom during eye movements.
Materials and Methods
Four rhesus monkeys (Macaca mulatta) and one cynomologous monkey (Macaca fascicularis) were chronically implanted with a delrin head ring that was attached to the skull via stainless steel or titanium screws and dental acrylic (Angelaki and Dickman, 2000) to restrain the head during experiments. In a separate surgery, two scleral search coils, designed for recording three-dimensional (i.e., horizontal, vertical, and torsional) eye movements using the magnetic search coil technique (Robinson, 1963; Judge, 1980), were surgically implanted under the conjuctiva. The first coil was 15–17 mm in diameter and was sutured to the sclera posterior to the limbus corneae and anterior to the eye muscle insertions (Hess, 1990), in a plane perpendicular to the line of sight. The second coil was ∼2 mm in diameter and sutured to the sclera on the inferior surface of the globe, lateral to the inferior rectus muscle insertion (the exact orientation of this coil is less important providing it is not coplanar with the first coil). After implantation, the larger pericorneal coil was approximately aligned with the optic axis of the eye, thereby capable of measuring the direction of the line of sight (i.e., horizontal and vertical). The axis of the smaller coil was approximately in the plane of the larger coil, thereby measuring the torsion of the eye about the line of sight. These surgeries were performed under isoflurane anesthesia and sterile conditions and conformed to the guidelines provided by Washington University School of Medicine and the National Institutes of Health.
The monkeys sat such that their heads were in the center of three mutually orthogonal magnetic fields alternating at 60, 90, and 135 Hz (CNC Engineering, Seattle, WA), and the signals generated by the magnetic fields in the search coils were detected by three axis phase-sensitive detectors (CNC Engineering). At the beginning of each experimental day, a calibration was performed in which the animals were required to fixate 13 laser-generated targets along the horizontal and vertical meridians (0, ±10, ±15, and ±20°). During each experimental day, using a stereotaxically implanted plastic grid, a 2 mm hole was drilled through the acrylic and skull that permitted the entry of a 26 gauge stainless steel guide tube and an imbedded tungsten microelectrode into the brain. The electrode was then lowered to the area of interest using a remote-controlled microdrive (FHC, Bowdoinham, ME).
The abducens nucleus was first identified by its characteristic burst–tonic activity during ipsilateral eye movements. Subsequently, the abducens nerve was found by searching for similar activity ∼2 mm anterior, lateral, and ventral to the abducens nucleus. Once identified, the following biphasic stimulation parameters were applied: pulse duration, 0.2 ms; train duration, 50 ms; frequency, 500 Hz. Note that we chose these short-duration, high-frequency parameters to generate high-velocity movements with small displacements. The stimulation current, which never exceeded 50 μA, was determined by finding the threshold current level and subsequently stimulating at 1.5 times the threshold.
The stimulation was applied when the monkey fixated a visual target at any one of 11 vertical eccentricities (25° up to 25° down in 5° intervals) located along the mid-sagittal plane. The targets were produced by a laser that was back-projected onto a plastic screen and positioned via two mirror galvanometers (GSI Lumonics, Moorpark, CA). Fixation was determined automatically by monitoring the location of the monkeys’ eyes relative to a theoretical window of 3 × 3°. After entering the fixation window, the target was extinguished, and the stimulation was delivered. A juice reward was given only after the stimulation-induced movement was complete. Stimulation at each target location was repeated three to five times. Stimulus presentation, juice delivery, and data acquisition were controlled with custom-written scripts in Spike2 (Cambridge Electronics Design, Cambridge, UK) using a CED Power 1401 (Cambridge Electronics Design). Data were anti-alias filtered (200 Hz, six-pole Bessel), digitized by the CED Power 1401 at a rate of 833.33 Hz (16-bit resolution), and recorded on a computer for off-line analysis.
Raw eye coil signals were first calibrated (Klier et al., 2005) and converted into rotation vectors (E = tan(p/2)n, where n is the normalized axis about which the eye rotates from a chosen reference position to the current position, and p is the angle of rotation about axis n). These eye positions were first computed in space coordinates (using straight-ahead as the reference position) but then converted into Listing’s coordinates (using primary position as the reference position). The transformation of data from space to Listing’s coordinates was made using equations described previously (Hess and Angelaki, 1997a,b). Briefly, during every experimental day, a data file was collected in which the monkeys made spontaneous movements in the light for a period of ∼1.5 min. According to Listing’s law, the computed eye position vectors are confined to a plane (Helmholtz, 1867). This plane, in space coordinates, was fit using a least-squares algorithm, and this fitted plane was then rotated to align with the monkey’s vertical upright (thereby minimizing torsion and placing the data in Listing’s coordinates). Data from stimulation trials underwent the same transformations as the spontaneous eye movement file to be visualized in Listing’s coordinates. Subsequently, Ė, the derivative of eye position, was calculated (Ė = dE/dt), and angular eye velocity was computed from eye velocity and eye position (Ω = 2/(Ė + E × Ė)/(1 + E2). Note that Ė is simply a mathematical value (only equivalent to eye velocity for movements in one dimension), whereas Ω is the accurate measure of eye velocity in three dimensions). Once the components of angular velocity were computed in Listing’s coordinates, plots of horizontal versus torsional eye velocity were constructed for each stimulation-induced eye movement. Linear fits were made to these eye velocity traces, and the tilt (in degrees) of these lines from Listing’s plane was then computed. The resultant tilt angles were then plotted against initial vertical eye position, and a linear regression was subsequently fit to these data. The slope of this regression line served as our measure of the corresponding eye position dependence (i.e., half-angle rule). This analysis was conducted three times: (1) for the entire velocity loop (i.e., stimulation-induced and passive eye movement that returned the eye back to its starting position); (2) only for the stimulation-induced eye movement; and (3) only for the passive return eye movement.
Finally, to compare the amount of eye position dependence observed in stimulation-induced eye movements with that resulting from self-generated, visually guided behavior, the monkeys performed smooth-pursuit eye movements while tracking small laser targets. These targets were displaced at five different vertical eccentricities (20° up to 20° down in 10° intervals) and moved horizontally ±5° (across the mid-sagittal plane) at a sinusoidal rate of 0.6 Hz. Eye positions and angular velocities for pursuit were computed as stated above.
Results
Effects of abducens nerve stimulation
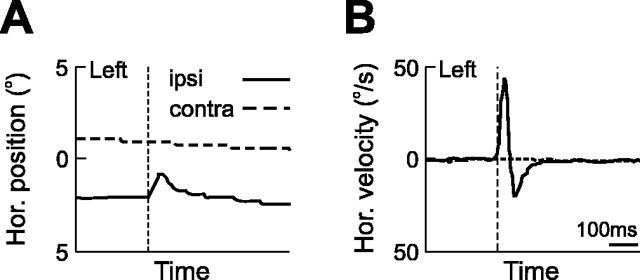
Figure 2A shows the typical effects of abducens nerve stimulation. Stimulation (vertical dashed line) causes excitation in the lateral rectus muscle of the ipsilateral eye (Fig. 2A, solid line) such that it assumes a new horizontal position. Because stimulation occurs downstream of the neural integrator (Skavenski and Robinson, 1973), the final position of the eye is not maintained and drifts back to its original position. There is no effect of stimulation on the contralateral eye (Fig. 2A, dashed line). The corresponding velocity traces are shown in Figure 2B, where a large velocity peak is seen during the stimulation-induced movement and a smaller velocity peak (in the opposite direction) is observed during the passive return movement (again, only the ipsilateral eye is affected).
Figure 2.
Horizontal eye position (A) and velocity (B) elicited during abducens nerve stimulation. Stimulation (dashed vertical line) causes a horizontal movement in the ipsilateral eye (ipsi; solid line) but not in the contralateral eye (contra; dashed horizontal line). The induced change in eye position does not hold but subsequently returns to its original position. The target viewing distance was 40 cm. Hor., Horizontal.
Do stimulation-induced movements follow the half-angle rule?
Figure 3A shows stimulation-evoked torsional and horizontal eye velocities in Listing’s coordinates from different initial eye positions: either straight ahead (green traces), 25° up (red traces), or 25° down (blue traces). Despite similar horizontal responses, torsional eye velocities differed depending on initial eye position. Clockwise (positive), torsion was observed when the eye looked up, whereas counterclockwise (negative), torsion was seen when the eye looked down. Figure 3B plots horizontal eye velocity as a function of torsional eye velocity during the stimulation-induced movement and the subsequent movement back to the null position of the eye (forming a velocity loop), for all vertical targets. Clearly, the data from different vertical eye eccentricities did not overlap, but rather tilted away from Listing’s plane (i.e., 0 torsion) (Fig. 3B, vertical dashed line) by various amounts, suggesting an eye position-dependent direction of action for the lateral rectus muscle.
Figure 3.
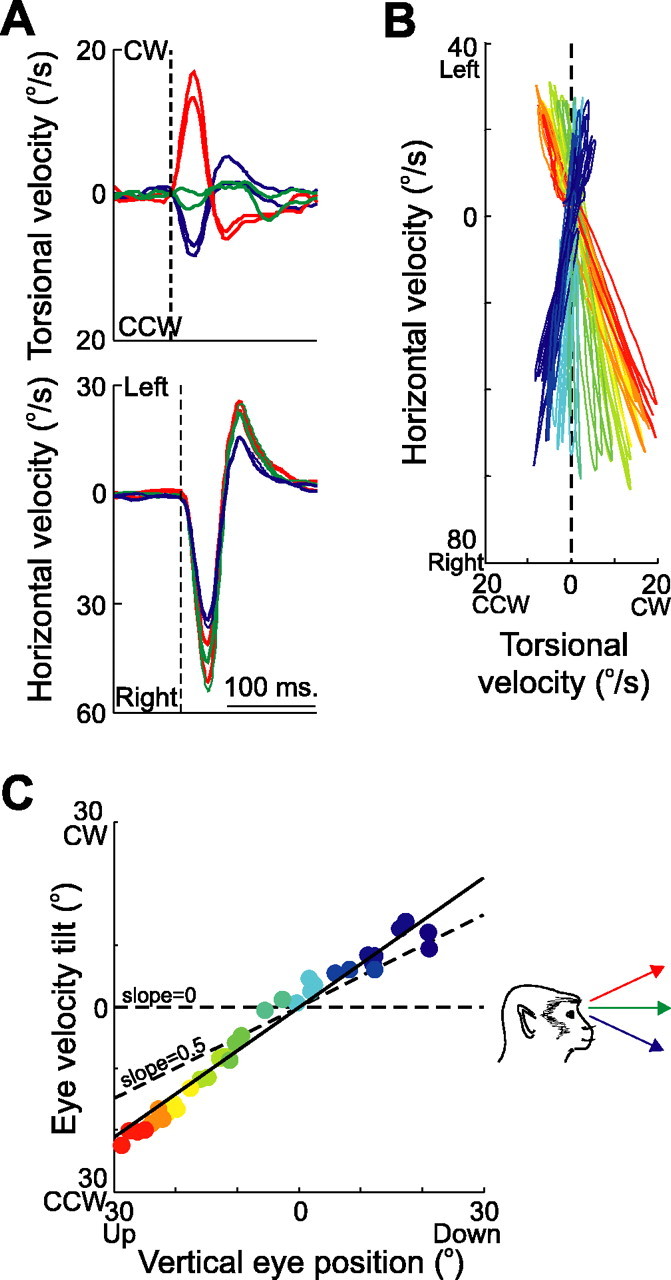
Characteristics of eye velocity during abducens nerve microstimulation. A, Temporal plots of eye velocity from different initial eye positions (green, straight ahead; red, 25° up; blue, 25° down) are similar in the horizontal domain (bottom) but differ in the torsional domain (top). Two traces of each are shown. B, Horizontal versus torsional velocity is plotted as the eye assumes different vertical positions. The orientation of the eye when the stimulation was delivered is illustrated by a color palette, ranging from 25° up (dark red) to 25° down (dark blue) in 5° intervals. The orientation of Listing’s plane is indicated by the vertical dashed line at 0° torsion. C, Measures of eye velocity tilt angle are plotted against initial vertical eye position. A slope of 0 (indicating fixed axes of rotation and a zero-angle rule) and a slope of 0.5 (indicating eye position-dependent axes of rotation and proper implementation of the half-angle rule) are also shown (dashed lines). CCW, counterclockwise; CW, clockwise.
Linear fits were made to the velocity loops in Figure 3B, and their tilts from Listing’s plane (vertical dashed line) was then computed. The resultant tilt angles are plotted against initial vertical eye position in Figure 3C, and a regression line (solid black) is fit through the data. This analysis was conducted three times: (1) for the entire velocity loop illustrated in Figure 3B (shown in Fig. 3C); (2) only for the stimulation-induced eye movement (data not shown); and (3) only for the passive return eye movement (data not shown). In this typical example, the three measures produced similar average (±SD) results [ slope 1, 0.70 ± 0.07; slope 2, 0.69 ± 0.07; slope 3, 0.47 ± 0.10] .
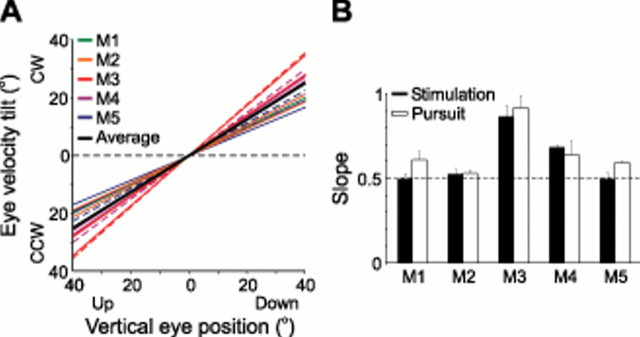
Figure 4A shows the computed regression lines from all tested sites in five animals. The average slope (±SD) for the entire velocity loop (Fig. 4A, black line) was 0.61 ± 0.15 (data not shown; the average slope for the stimulation-induced eye movement was 0.59 ± 0.12, and the average slope for the passive return eye movement was 0.56 ± 0.15). Compared with theoretical slopes of 0.5 for the half-angle rule and 0 for a zero-angle rule (in which the action of the muscle is independent of eye position), these slopes were not significantly different from the former (t test; p = 0.151) but significantly different from the latter (t test; p ≪ 0.001).
Figure 4.
Stimulation-evoked eye movements have the same eye position dependence as visually guided pursuit. A, For all sites tested with microstimulation, slopes closely approximate the half-angle rule (slope, 0.5) and not a zero-angle rule (slope, 0) (black dashed lines). This finding is observed for both nerve (solid lines) and nucleus (dashed lines) stimulation. CCW, counterclockwise; CW, clockwise. B, All monkeys were also required to pursue a horizontal, sinusoidally moving target (frequency, 0.6 Hz; amplitude, 5°) at five vertical eye positions (20° up to 20° down in 10° intervals). Computed half-angle rule slopes from pursuit (□) are compared with the median stimulation slopes (▪) for each of the five animals. The error bars indicate 95% confidence intervals. An ideal half-angle rule slope of 0.5 (black dashed line) is also shown. Note that differences in slopes from the ideal half-angle rule of 0.5 may be attributable to the number of eye coil surgeries in each animal: M1 had one eye coil surgery; M2 had one eye coil surgery; M3 had six eye coil surgeries; M4 had four eye coil surgeries; M5 had three eye coil surgeries.
Stimulation-induced versus smooth-pursuit eye movements
More importantly, we compared these stimulation-evoked eye velocity slopes with similar measures of the half-angle rule for these same animals during sinusoidal pursuit at different vertical elevations (Fig. 4B) [ pursuit eye movements have been shown to obey Listing’s law and the half-angle rule (Haslwanter et al., 1991; Tweed et al., 1992; Angelaki et al., 2003; Adeyemo and Angelaki, 2005)] . Although there was variability in the slope of the eye position dependence across animals (note that monkey M3 was our oldest animal who had had six eye coil surgeries, whereas M1, M2, and M5 were our newest monkeys, here participating in their first experiment), it is important to note that slope values during stimulation were not significantly different (paired t test; p = 0.190) from those obtained during pursuit (0.66 ± 0.17). The fact that the stimulation-induced tilt slopes covary with those of pursuit-evoked responses suggests a similar underlying mechanism for the implementation of Listing’s law.
Discussion
We have shown here that ocular plant mechanics are capable of implementing the half-angle rule in the absence of structured neural commands: the pulling direction of the lateral rectus muscle appeared to change as a function of vertical eye position, despite identical stimulation of the abducens nerve. This finding strongly supports the notion that the eye and its associated muscles and tissues play an important role in implementing the torsional constraints that help solve the degrees-of-freedom problem in situations in which the three-dimensional rotating eye is driven by a two-dimensional retinal error signal, such as during saccades and smooth-pursuit eye movements.
Motoneuron firing
These results, which demonstrate that the half-angle rule can be implemented peripherally, further advance recent findings that motoneurons do not appear to encode eye position-dependant torsion during pursuit eye movements (Ghasia and Angelaki, 2005). There it was shown that motoneurons innervating the superior and inferior oblique and rectus muscles do not modulate their activity as would be expected if they were to carry the eye position-dependent torsional drive necessary for the implementation of the half-angle rule by neural circuits. However, although these findings demonstrated the absence of an appropriate neural drive to the eye muscles for implementing the half-angle rule, they could only speculate that the plant itself could adequately deal with adding the appropriate amount of torsion. In light of the present findings, it is now clear why motoneurons encode the derivative of eye position (which is independent of current eye position) and not angular eye velocity (which is dependent on current eye position) (Tweed and Vilis, 1990): the motor plant can implement the eye position dependencies needed for the half-angle rule on its own.
The role of ocular muscle pulleys
These neurophysiological findings are consistent with ever-growing experimental evidence from both histological and imaging studies regarding oculomotor pulley involvement in the implementation of Listing’s law and the half-angle rule. Miller (1989) was the first to show that the pulling directions of the extraocular muscles are dependent on the position of the eye in the orbit, and since then, Demer and colleagues (Demer et al., 1995; for review, see Demer, 2004) have provided substantial and compelling support for the histological existence of muscle pulleys. It was then proposed that these pulleys change the effective pulling direction of the eye muscles and thus their axes of rotation (i.e., angular eye velocity), by half the change in ocular orientation (i.e., thereby implementing the half-angle rule) (Demer et al., 1995; Clark et al., 1997; Demer, 2004). Our results would be consistent with such a function.
Demer and colleagues (Demer et al., 1997, 2000; Kono et al., 2002a,b; Demer, 2004) have further proposed an “active pulley hypothesis,” according to which each eye muscle has two distinct layers: the global layer that inserts on the eye muscle tendon and thus moves the eye itself, and an orbital layer that connects to the collagen, elastin, and smooth muscle that surrounds the eye and forms the oculomotor pulley. In addition to the numerous aforementioned anatomical and imaging studies showing pulley-mediated position dependencies, support for this hypothesis has come from several studies that have found this type of muscle segregation in monkey, man, and other mammalian species (Khanna and Porter, 2001; Oh et al., 2001; Demer, 2004; Ruskell et al., 2005). In addition, differences in the types of muscle fibers projecting to either layer have also been noted (Collins, 1975; Spencer and Porter, 1981; Porter et al., 1995).
The extent of the independence between the global and orbital layers is still under investigation because there exists lateral transmission of extraocular muscle force from the orbital layer to the muscle tendon and from the global layer to the pulleys (Shall and Goldberg, 1995; Goldberg and Shall, 1999). In addition, it remains to be shown whether and how a unique pulse-slide-step firing pattern of motoneurons can possess and distribute differential information to the two fiber types (Scudder et al., 2002). Finally, some studies have claimed that the pulleys only serve passive orbital properties (Dimitrova et al., 2003) and that the orbital muscle fibers do not appear to terminate in the pulleys themselves (McClung et al., 2006), such that the pulleys are dragged along because of their physical attachment [ rather than being actively and independently controlled (Miller, 1989)] . Still, other studies strongly dispute this latter claim, showing that orbital layers terminate in the pulleys of man and monkey (Ruskell et al., 2005). Thus, despite extensive evidence for differences in the activity-dependent properties of orbital and global layers, more studies are required to understand their neurophysiological and dynamic functional properties.
A role for the brain
Although the ocular plant was able to produce eye movements that followed the half-angle rule, this finding does not absolve the brain from dealing with torsion altogether and does not necessarily relegate it to being a simple, two-dimensional, commutative operator (for review, see Crawford et al., 2003; Angelaki and Hess, 2004). For example, although eye movements such as pursuit and saccades, that redirect gaze when the head is stationary, follow the half-angle rule, other eye movements that stabilize the visual image during head movements, such as the vestibulo-ocular and optokinetic reflexes, do not obey Listing’s law (Crawford and Vilis, 1991; Fetter et al., 1992; Angelaki, 2003). The reason for this dichotomy is clear, because the former movements pose a degree-of-freedom problem (i.e., a two-dimensional retinal input must be converted into a three-dimensional motor output), whereas the latter do not (i.e., a three-dimensional input and a three-dimensional output). But it is only the brain that can decide when these rules must be followed and thus when the half-angle rule must be followed and when it must not. The ocular plant cannot make these decisions alone.
Perhaps the best example of what happens during movements that sometimes obey and sometimes disobey Listing’s law and the half-angle rule are those associated with head-free gaze shifts (Crawford et al., 1999). When the eyes and head are moving together toward a visual target, torsional eye position during the initial, saccadic part of the gaze shift is purposely driven out of Listing’s plane such that the subsequent slow-phase eye movement (caused by the eye landing on target first and waiting for the head to catch up) brings the eye back into Listing’s plane. Certainly, the plant has no a priori knowledge about the amplitude and direction of future head movements to violate the half-angle rule and implement the necessary pattern of intricate torsional eye movements by itself.
Situations such as these strongly implicate the neural activation of vertical motoneurons that innervate the superior and inferior oblique muscles that in turn generate the necessary torsional drive to move the eyes out of Listing’s plane. Magnetic resonance imaging of the rectus pulleys during static counterroll have shown that their positions change with torsional changes in eye position and thus the pulleys may allow for violations of Listing’s law when necessary (Demer and Clark, 2005). But note that these studies do not observe the pulleys during the rotational vestibulo-ocular reflex, and thus their role during dynamic head movements remains a matter of debate.
Several other behavioral studies have further shown that the brain requires knowledge about torsion and the ability to handle noncommutative mathematical operations for proper sensorimotor transformations. These include generating correct three-dimensional eye movements from head inputs during the vestibulo-ocular reflex (Tweed et al., 1999), updating the locations of visual targets in space after intervening torsional head rotations (Medendorp et al., 2002), accurately transforming two-dimensional retinal inputs into three-dimensional saccadic outputs (Klier and Crawford, 1998), and correctly dealing with the noncommutativity of whole-body rotations (Hess et al., 2005).
Finally, as with all motor control systems, the brain must have a realistic, three-dimensional internal model of the ocular plant to control it and to plan future eye movements. If the plant is involved with the torsional control of eye movements, then the brain must have an accurate representation of how the plant implements the half-angle rule to send out appropriate control signals. In fact, several computational models have shown that a plant capable of physically implementing Listing’s law [ such as the plant supported by Demer (2002) and our findings] nevertheless makes torsional errors if the neural system does not also implement a three-dimensional control strategy (Tweed et al., 1994; Smith and Crawford, 1998).
In summary, despite an unequivocal role for the brain in coordinating movement kinematics, the present results demonstrate that there exists an important peripheral contribution as well. The eye seems to be mechanically optimized to implement the kinematic constraints appropriate for visually guided eye movements, whereas neural signals have executive control: they have the critical role of deciding when, where, and how to violate these constraints in situations in which the third degree of freedom is not redundant and thus all three degrees of freedom are functionally appropriate.
Footnotes
This work was supported by the Human Frontier Science Program and National Institutes of Health Grants RO1-EY12814 and RO1-EY15271.
References
- Adeyemo B, Angelaki DE (2005). Similar kinematic properties for ocular following and smooth pursuit eye movements. J Neurophysiol 93:1710–1717. [DOI] [PubMed] [Google Scholar]
- Angelaki DE (2003). Three-dimensional ocular kinematics during eccentric rotations: evidence for functional rather than mechanical constraints. J Neurophysiol 89:2685–2696. [DOI] [PubMed] [Google Scholar]
- Angelaki DE, Dickman JD (2000). Spatiotemporal processing of linear acceleration: primary afferent and central vestibular neuron responses. J Neurophysiol 84:2113–2132. [DOI] [PubMed] [Google Scholar]
- Angelaki DE, Hess BJM (2004). Control of eye orientation: where does the brain’s role end and the muscle’s begin? Eur J Neurosci 19:1–10. [DOI] [PubMed] [Google Scholar]
- Angelaki DE, Zhou HH, Wei M (2003). Foveal versus full-field visual stabilization strategies for translational and rotational head movements. J Neurosci 23:1104–1108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clark RA, Miller JM, Demer JL (1997). Location and stability of rectus muscle pulleys. Muscle paths as a function of gaze. Invest Ophthalmol Vis Sci 38:227–240. [PubMed] [Google Scholar]
- Collins CC (1975). The human oculomotor control system. In: Basic mechanisms of ocular motility and their clilnical implications (Lennerstrand G, Bach-y-Rita P, eds) pp. 145–180. New York: Pergamon.
- Crawford JD, Vilis T (1991). Axes of eye rotation and Listing’s law during rotations of the head. J Neurophysiol 65:407–423. [DOI] [PubMed] [Google Scholar]
- Crawford JD, Ceylan MZ, Klier EM, Guitton D (1999). Three-dimensional eye-head coordination during gaze saccades in the primate. J Neurophysiol 81:1760–1782. [DOI] [PubMed] [Google Scholar]
- Crawford JD, Martinez-Trujillo JC, Klier EM (2003). Neural control of three-dimensional eye and head movements. Curr Opin Neurobiol 13:655–662. [DOI] [PubMed] [Google Scholar]
- Demer JL (2002). The orbital pulley system: a revolution in concepts of orbital anatomy. Ann NY Acad Sci 956:17–32. [DOI] [PubMed] [Google Scholar]
- Demer JL (2004). Pivotal role of orbital connective tissues in binocular alignment and strabismus. Invest Ophthalmol Vis Sci 45:729–738. [DOI] [PubMed] [Google Scholar]
- Demer JL, Clark RA (2005). Magnetic resonance imaging of human extraocular muscles during static ocular counter-rolling. J Neurophysiol 94:3292–3302. [DOI] [PubMed] [Google Scholar]
- Demer JL, Miller JM, Poukens V, Vinters HV, Glasgow BJ (1995). Evidence for fibromuscular pulleys of the recti extraocular muscles. Invest Ophthalmol Vis Sci 36:1125–1136. [PubMed] [Google Scholar]
- Demer JL, Poukens V, Miller JM, Micevych P (1997). Innervation of extraocular pulley smooth muscle in monkeys and humans. Invest Ophthalmol Vis Sci 38:1774–1785. [PubMed] [Google Scholar]
- Demer JL, Oh SY, Poukens V (2000). Evidence for active control of rectus extraocular muscle pulleys. Invest Ophthalmol Vis Sci 41:1280–1290. [PubMed] [Google Scholar]
- Dimitrova DM, Shall MS, Goldberg SJ (2003). Stimulation-evoked movements with and without the lateral rectus muscle pulley. J Neurophysiol 90:3809–3815. [DOI] [PubMed] [Google Scholar]
- Fetter M, Tweed D, Misslisch H, Fischer D, Koenig E (1992). Multidimensional descriptions of the optokinetic and vestibuloocular reflexes. Ann NY Acad Sci 656:841–842. [DOI] [PubMed] [Google Scholar]
- Ghasia F, Angelaki DE (2005). Do motoneurons encode the non-commutativity of ocular rotations? Neuron 47:281–293. [DOI] [PubMed] [Google Scholar]
- Glenn B, Vilis T (1992). Violations of Listing’s law after large eye and head gaze shifts. J Neurophysiol 68:309–317. [DOI] [PubMed] [Google Scholar]
- Goldberg SJ, Shall MS (1999). Motor units of extraocular muscles: recent findings. Prog Brain Res 123:221–232. [DOI] [PubMed] [Google Scholar]
- Haslwanter T, Straumann D, Hepp K, Hess BJM, Henn V (1991). Smooth pursuit eye movements obey Listing’s law in the monkey. Exp Brain Res 87:470–472. [DOI] [PubMed] [Google Scholar]
- Helmholtz H (1867). Southall JPC, trans. In: Treatise on physiological optics Rochester, NY: Optical Society of America.
- Hess BJ (1990). Dual-search coil for measuring 3-dimensional eye movements in experimental animals. Vision Res 30:597–602. [DOI] [PubMed] [Google Scholar]
- Hess BJ, Angelaki DE (1997a). Kinematic principles of primate rotational vestibulo-ocular reflex. I. Spatial organization of fast phase velocity axes. J Neurophysiol 78:2193–2202. [DOI] [PubMed] [Google Scholar]
- Hess BJ, Angelaki DE (1997b). Kinematic principles of primate rotational vestibulo-ocular reflex. II. Gravity-dependent modulation of primary eye position. J Neurophysiol 78:2203–2216. [DOI] [PubMed] [Google Scholar]
- Hess BJ, Klier EK, Angelaki DE (2005). Spatial updating is compromised after 3D yaw-roll rotations. Soc Neurosci Abstr 31:287–17. [Google Scholar]
- Judge SJ, Richmond BJ, Chu FC (1980). Implantation of magnetic search coils for measurement of eye position: an improved method. Vision Res 20:535–538. [DOI] [PubMed] [Google Scholar]
- Khanna S, Porter JD (2001). Evidence for rectus extraocular muscle pulleys in rodents. Invest Ohthalmol Vis Sci 42:1986–1992. [PubMed] [Google Scholar]
- Klier EM, Crawford JD (1998). Human oculomotor system accounts for 3-D eye orientation in the visual-motor transformation for saccades. J Neurophysiol 80:1760–1782. [DOI] [PubMed] [Google Scholar]
- Klier EM, Angelaki DE, Hess BJM (2005). Roles of gravitational cues and efference copy signals in the rotational updating of memory saccades. J Neurophysiol 94:468–478. [DOI] [PubMed] [Google Scholar]
- Kono R, Clark RA, Demer JL (2002a). Active pulleys: magnetic resonance imaging of rectus muscle paths in tertiary gazes. Invest Ophthalmol Vis Sci 43:2179–2188. [PubMed] [Google Scholar]
- Kono R, Poukens V, Demer JL (2002b). Quantitative analysis of the structure of the human extraocular muscle pulley system. Invest Ophthalmol Vis Sci 43:2923–2932. [PubMed] [Google Scholar]
- McClung JR, Allman BL, Dimitrova DM, Goldberg SJ (2006). Extraocular connective tissues: a role in human eye movements? Invest Ophthalmol Vis Sci 47:202–205. [DOI] [PubMed] [Google Scholar]
- Medendorp WP, Smith MA, Tweed DB, Crawford JD (2002). Rotational remapping in human spatial memory during eye and head motion. J Neurosci 22:RC196(1-4). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller JM (1989). Functional anatomy of normal human rectus muscles. Vision Res 29:223–240. [DOI] [PubMed] [Google Scholar]
- Miller JM, Demer JL, Rosenbaum AL (1993). Effect of transposition surgery on rectus muscle paths by magnetic resonance imaging. Ophthalmology 100:475–487. [DOI] [PubMed] [Google Scholar]
- Oh SY, Poukens V, Demer JL (2001). Quantitative analysis of rectus extraocular muscle layers in monkey and humans. Invest Ophthalmol Vis Sci 42:10–16. [PubMed] [Google Scholar]
- Porter JD, Baker RS, Ragusa RJ, Brueckner JD (1995). Extraocular muscles: basic and clinical aspects of structure and function. Surv Ophthalmol 39:451–484. [DOI] [PubMed] [Google Scholar]
- Quaia C, Optican LM (1998). Commutative saccade generator is sufficient to control a 3-D ocular plant with pulleys. J Neurophysiol 79:3197–3215. [DOI] [PubMed] [Google Scholar]
- Radau P, Tweed D, Vilis T (1994). Three-dimensional eye, head and chest orientations following large gaze shifts and the underlying neural strategies. J Neurophysiol 72:2840–2852. [DOI] [PubMed] [Google Scholar]
- Robinson DA (1963). A method of measuring eye movement using a scleral search coil in a magnetic field. IEEE Trans Biomed Eng 10:137–145. [DOI] [PubMed] [Google Scholar]
- Ruskell GL, Kjellevold Haugen IB, Bruenech JR, van der Werf F (2005). Double insertions of extraocular rectus muscles in humans and the pulley theory. J Anat 206:295–306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schreiber K, Crawford JD, Fetter M, Tweed D (2001). The motor side of depth vision. Nature 410:819–822. [DOI] [PubMed] [Google Scholar]
- Scudder CA, Kaneko CS, Fuchs AF (2002). The brainstem burst generator for saccadic eye movements: a modern synthesis. Exp Brain Res 142:439–462. [DOI] [PubMed] [Google Scholar]
- Shall MS, Goldberg SJ (1995). Lateral rectus EMG and contractile responses elicited by cat abducens motoneurons. Muscle Nerve 18:948–955. [DOI] [PubMed] [Google Scholar]
- Skavenski AA, Robinson DA (1973). Role of abducens neurons in vestibuloocular reflex. J Neurophysiol 36:724–738. [DOI] [PubMed] [Google Scholar]
- Smith MA, Crawford JD (1998). Neural control of rotational kinematics within realistic vestibuloocular coordinate systems. J Neurophysiol 80:2295–2315. [DOI] [PubMed] [Google Scholar]
- Spencer RF, Porter JD (1981). Innervation and structure of extraocular muscles in the monkey in comparison to those of the cat. J Comp Neurol 198:649–665. [DOI] [PubMed] [Google Scholar]
- Tweed D (1997). Visual-motor optimization in binocular control. Vision Res 37:1939–1951. [DOI] [PubMed] [Google Scholar]
- Tweed D, Vilis T (1987). Implications of rotational kinematics for the oculomotor system in three dimensions. J Neurophysiol 58:832–849. [DOI] [PubMed] [Google Scholar]
- Tweed D, Vilis T (1990). Geometric relations of eye position and velocity vectors during saccades. Vision Res 30:111–127. [DOI] [PubMed] [Google Scholar]
- Tweed D, Fetter M, Andreadaki S, Koenig E, Dichgans J (1992). Three-dimensional properties of human pursuit eye movements. Vision Res 32:1225–1238. [DOI] [PubMed] [Google Scholar]
- Tweed D, Misslisch H, Fetter M (1994). Testing models of the oculomotor velocity-to-position transformation. J Neurophysiol 72:1425–1429. [DOI] [PubMed] [Google Scholar]
- Tweed D, Haslwanter T, Happe V, Fetter M (1999). Non-commutativity in the brain. Nature 399:261–263. [DOI] [PubMed] [Google Scholar]
- Van Rijn LJ, Van den Berg AV (1993). Binocular eye orientation during fixations: Listing’s law extended to include eye vergence. Vision Res 33:691–708. [DOI] [PubMed] [Google Scholar]