Precise Long-Range Synchronization of Activity and Silence in Neocortical Neurons during Slow-Wave Sleep

Abstract

Slow-wave sleep is characterized by alternating periods of activity and silence in corticothalamic networks. Both activity and silence are stable network states, but the mechanisms of their alternation remain unknown. We show, using simultaneous multisite intracellular recordings in cats, that slow rhythm involves all neocortical neurons and that both activity and silence started almost synchronously in cells located up to 12 mm apart. Activity appeared predominantly at the area 5/7 border and spread in both anterior and posterior directions. The activity started earlier in fast-spiking cells and intrinsically bursting cells than in regular-spiking neurons. These results provide direct evidence for two mechanisms of active state generation: spread of activity from a local focus and synchronization of weaker activity, originating at multiple locations. Surprisingly, onsets of silent states were synchronized even more precisely than the onsets of activity, showing no latency bias for location or cell type. This most intriguing finding exposes a major gap in understanding the nature of state alternation. We suggest that it is the synchronous termination of activity and occurrence of silent states of the neuronal network that makes the EEG picture during slow-wave sleep so characteristic. Synchronous onset of silence in distant neurons cannot rely exclusively on properties of individual cells and synapses, such as adaptation of neuronal firing or synaptic depression; instead, it implies the existence of a network mechanism. Revealing this yet unknown large-scale mechanism, which switches network activity to silence, will aid our understanding of the origin of brain rhythms in normal function and pathology.

Introduction

A signature of the slow-wave sleep in the electroencephalogram (EEG) are large-amplitude fluctuations (Blake and Gerard, 1937), which reflect alternating periods of activity and silence in thalamocortical networks (Steriade et al., 1993a,b, 2001; Contreras and Steriade, 1995; Timofeev et al., 2001; Petersen et al., 2003). The active states are associated with neuronal depolarization, firing, and rigorous synaptic activity, whereas during the silent states, neurons are hyperpolarized and the network is inactive (Contreras et al., 1996; Timofeev et al., 1996, 2001; Wilson and Kawaguchi, 1996; Shu et al., 2003). The alternation of states is of intracortical origin because active and silent states are self-generated in the isolated cortical preparation (Steriade et al., 1993a; Sanchez-Vives and McCormick, 2000; Timofeev et al., 2000) and absent in the thalamus of decorticated animals (Timofeev and Steriade, 1996). Both activity and silence are stable states of the network, but the mechanisms of state alternation remain an enigma. One possibility is the origin of activity in a specific focus, or group of cells, with sequential lateral propagation (Sanchez-Vives and McCormick, 2000; Cossart et al., 2003). In its most conservative formulation, the propagation hypothesis predicts a reiterating pattern of activity initiation and spread, with systematic site-specific onset delays. For this scenario, focal activity must be strong enough to evoke discharges in target cells and thus to spread. Alternatively, weaker activity may originate occasionally at multiple locations and involve additional parts of the network if it appears to be sufficiently synchronous (Timofeev et al., 2000; Massimini et al., 2004). The synchronization hypothesis predicts a variable spatial pattern of activity initiation, no systematic delays between sites, and occurrence of occasional local episodes of activity at any site. To trigger a generalized active state by this mechanism, a sufficient number of sites must become active within an integration period of postsynaptic responses. These hypotheses propose two mechanisms that, either alone or in combination, underlie the origin of active states. Termination of activity and onset of silent states is ascribed to the intrinsic cellular properties and currents (Bazhenov et al., 2002; Compte et al., 2003; Hill and Tononi, 2004; Milojkovic et al., 2005). However, a mechanism relying exclusively on single-cell properties might lead to a high variability of silent state onsets in individual cells, because each neuron has a unique set of intrinsic currents. To test these predictions, we recorded simultaneously local field potentials (LFPs) and intracellular activity of two to four neurons in cat neocortex. We show that slow rhythm involves all neocortical neurons and that onsets of both activity and silence occur with high temporal precision in cells located up to 12 mm apart. Our results provide direct evidence for two mechanisms of active state generation: spread of activity from a restricted focus and synchronization of weaker activity, originating at multiple locations. Most surprisingly, onsets of silent states were synchronized even more precisely than onsets of activity. We suggest that the synchronous termination of activity and occurrence of silent states of the neuronal network are what make the EEG picture during slow-wave sleep so characteristic.

Materials and Methods

Surgery and recording.

All experimental procedures used in this study were performed in accordance with the Canadian guidelines for animal care and were approved by the committee for animal care of Laval University.

Experiments were conducted on adult cats under a mixture of ketamine–xylazine and thiopental anesthesia (0–15 mg/kg, i.m., ketamine; 2–3 mg/kg, i.m., xylazine; 10 mg/kg, i.v., thiopental). We opted for this type of anesthesia because it reproduces closely the typical natural sleep EEG patterns, including the slow-wave oscillations. Specifically, under this anesthesia, the slow-wave oscillations, spindles, and beta-gamma activities are reliably observed in the EEG. Details of the experimental procedures have been described previously (Crochet et al., 2005; Rosanova and Timofeev, 2005). Briefly, surgery was started after the EEG showed typical signs of general anesthesia and complete analgesia was achieved. Additional doses of anesthetics were administrated when the EEG showed changes toward activated patterns. A craniotomy to expose the suprasylvian gyrus was made at the following coordinates (in mm): anteroposterior (AP), −5 to +18; lateral, 3–12. Brain pulsations were reduced by bilateral pneumothorax, hip suspension, and drainage of the cisterna magna. End-tidal CO₂ was held at 3.5–3.7%, and body temperature was held at 37–38°C. To avoid possible respiration deficiency during deep anesthesia and improve further the stability of the recordings, animals were paralyzed with gallamine triethiodide (2 mg/kg, i.v.) and artificially ventilated.

Simultaneous recordings of the LFP and intracellular activity of two to four neurons were performed. Intracellular recordings were made with sharp electrodes, filled with 2.5 m potassium acetate and 2% Neurobiotin, and beveled to a resistance of 55–80 MΩ. Four electrodes for intracellular recording were positioned along the suprasylvian gyrus at 4 mm intervals, around the following coordinates (in mm): electrode 1, AP +12, area 5; electrode 2, AP +8, border between area 5 and area 7; electrode 3, AP +4, area 7; electrode 4, AP 0, border between area 7 and area 21. Lateral coordinates of all intracellular electrodes were between 8 and 9. LFPs were recorded with a coaxial bipolar tungsten electrode (SNE-100; Rhode Medical Instruments, Woodland Hills, CA), positioned between intracellular electrodes 2 and 3, at coordinates of anterior +6 mm, lateral between 7 and 8 mm.

After electrode positioning, the craniotomy was filled with 3.5–4% agar (Sigma, St. Louis, MO). With each intracellular electrode, several cells were sequentially recorded in one experiment. Some of the recorded cells were injected with Neurobiotin. To facilitate the morphological/electrophysiological correlation, we selected for injection only cells that were recorded for longer than 30 min and were separated well by cortical depth when recorded with the same electrode.

Intracellular signals were amplified with Neurodata IR-283 amplifiers (Cygnus Technology, Southport, NC). Both intracellular and LFP signals were digitized at 20 kHz and recorded on a Vision data acquisition system (Nicolet, Middletown, WI).

Morphological procedures.

After experiments, animals were perfused with 0.9% saline, followed by 3% paraformaldehyde. The brain around recorded sites was placed in 30% sucrose, sectioned, and then processed by standard procedures (Horikawa and Armstrong, 1988). Reconstruction of stained cells was done with a computerized Neurolucida system.

Data processing.

Off-line data processing was done with custom-written programs in Matlab (MathWorks, Natick, MA) environment.

Clusters of states.

We defined as “clusters” groups of states that fulfill two criteria: first, they occur in all simultaneously recorded cells; second, their onsets are separated by <200 ms. Thus, number of states in one cluster is equal to the number of simultaneously recorded cells. Within each cluster, we calculated delays of state onset in each cell relative to the cluster mean. After completing these calculations, we had the following: (1) for a set of simultaneously recorded cells, number of clusters; (2) for each cell, delays of state onsets in that cell relative to the cluster mean; and (3) for each cell, we calculated the proportion of the states contributed to clusters of the total number of states in this cell.

Statistical analysis.

For statistical analysis, we used subroutines of the Matlab Statistics Toolbox and SPSS for Windows (SPSS, Chicago, IL). Throughout the text, values are given as mean ± SD.

Results

We recorded simultaneously the LFP and intracellular activity of two to four neurons in cat neocortex. Data sample consists of 89 neurons, recorded in 10 sets of 4 cells, 13 sets of 3 cells, and 5 pairs. For the pairwise analysis, 104 pairs were composed of this data.

In membrane potential traces of four simultaneously recorded cells (Fig. 1A), the active, depolarized states are unambiguously distinguishable from the silent, hyperpolarized states. Two features are immediately apparent in the simultaneously recorded cells. First, all cells are involved in the rhythm of the slow LFP oscillations. Membrane potential traces of all four cells showed clear relation to the LFP signal, although occasionally a cell may skip a few activity cycles (Fig. 1B, shadowed period). Second, all simultaneously recorded neurons showed a very similar pattern of membrane potential changes. In all four cells, the alternation between active and silent states was synchronized on a coarse timescale, with common periods of activity or silence.

Figure 1.

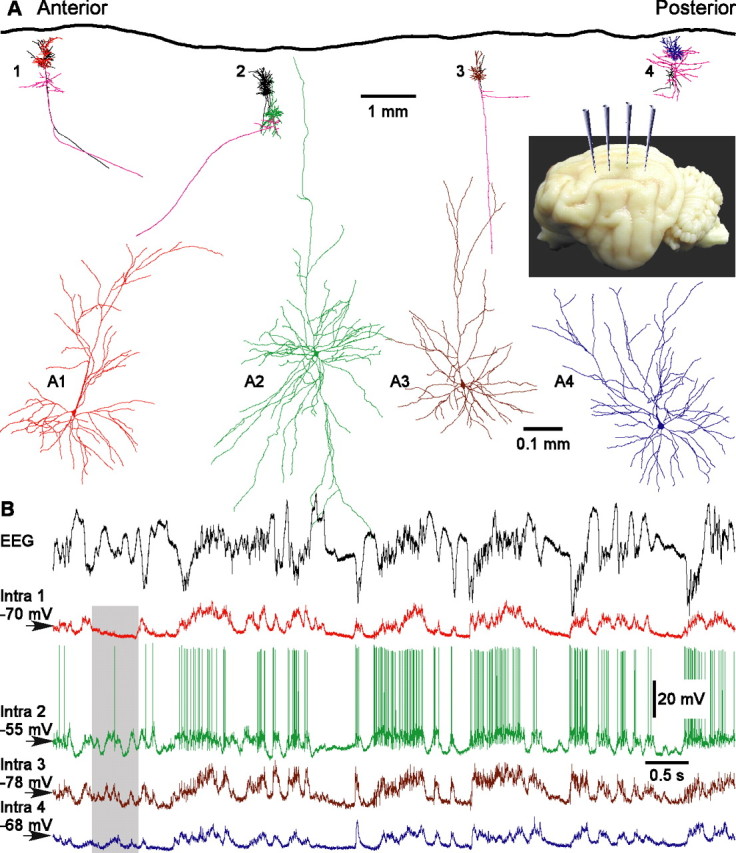
Active and silent states in four simultaneously recorded neurons and in the EEG. A, Location and morphology of cells recorded in one experiment. Four electrodes for intracellular recordings were positioned at 4 mm intervals along the suprasylvian gyrus, in areas 5, 7, and 21 (inset). With each intracellular electrode, several cells were sequentially recorded and stained. An overview shows reconstructions of all cells from this experiment. Colored are four simultaneously recorded neurons. The color code is the same for their dendritic trees in A and the intracellular traces in B. In the overview, pink lines show axons of these four neurons. Other neurons recorded in this experiment are drawn in black in the overview. In A1–A4, the four simultaneously recorded neurons are shown at expanded view. Cells in A1 and A3 were pyramids. Cells in A2 and A4 had nonpyramidal morphology but were also excitatory, as judged by their spiny dendrites (data not shown). B, Simultaneously recorded EEG and membrane potential of four cells, shown in A1–A4. The EEG electrode was positioned between the intracellular recording sites 2 and 3. Membrane potential traces are color coded as in A1–A4. The shadowed area shows a period of silence in cell 1, whereas the other cells were active.

To compare the timing of the onsets of activity and silence quantitatively, we detected active and silent states in the membrane potential traces of the 89 cells. We used two methods to detect and separate active and silent states.

The first method was based on clear bimodality of the membrane potential distributions during slow-wave oscillations. Two levels were set in the bimodal distribution of membrane potential values, which divided the interval between the peaks in three equal parts (Fig. 2A,B). The upper level was used as a threshold for the detection of active states, and the lower level was used for the detection of silent states. “States” were defined as periods during which the membrane potential remained above the threshold for active states or below the threshold for silent states. To avoid disturbances by transient membrane potential peaks, level crossings for periods shorter than 40 ms were not considered as states. Furthermore, if two active or two silent states were separated by <40 ms, the two states were extended to fill the gap and pasted together. During active states, cells were depolarized by 10.4 ± 4.94 mV (mean ± SD) relative to the silent states. Moreover, active states were also associated with stronger fluctuations of the membrane potential, as indicated by significantly higher values of its SD, 3.18 ± 1.27 mV during active states versus 1.11 ± 0.43 mV during silent states (n = 89; p < 0.001).

Figure 2.

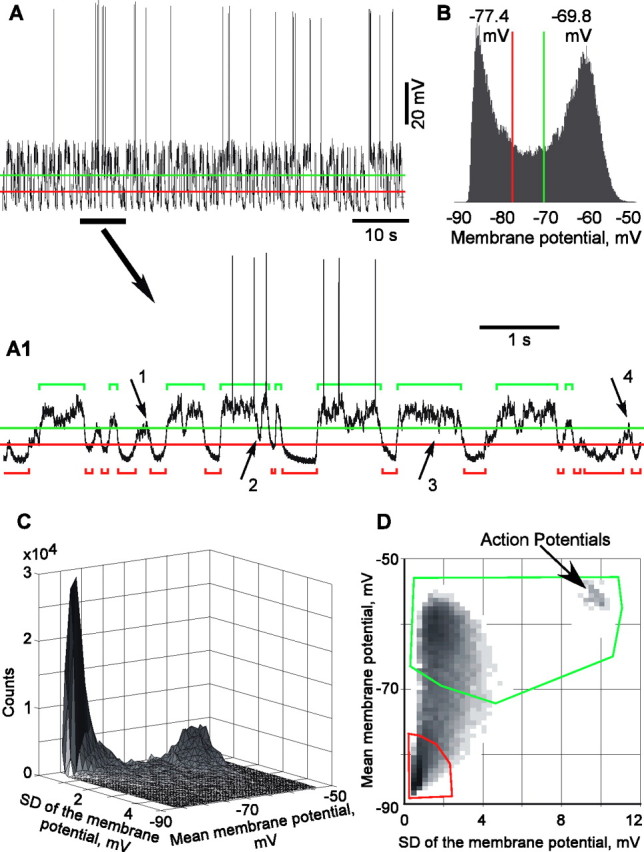
Two methods of state detection. The first method (A, B) uses membrane potential levels, whereas the second method (C, D) exploits, in addition to the levels, also the variability of the membrane potential to discriminate between active and silent states. A, Membrane potential trace of a neocortical cell and expanded view of its part (A1), with threshold levels for state detection and detected states (active, green; silent, red). States were defined as periods during which the membrane potential remained above the threshold for active states or below the threshold for silent states, for >40 ms. To avoid disturbances by transient membrane potential peaks, shorter level crossings were not considered as states (arrows 1, 4), and two active or two silent states separated by <40 ms were extended to fill the gap and pasted together (arrows 2, 3). The levels for state detection were set at equal distances between the peaks of bimodal distribution of the membrane potential values (B). C, Three-dimensional density distribution of the data from A. The mean membrane potential and its SD were calculated in a running window of 25 ms. These values were used as x and y coordinates; the z-axis is the frequency of their occurrence. D, Top view of the plot from C, with the regions used for detection of active (green) and silent (red) states outlined. The x-axis is extended compared with C to include the points with very high SD, which correspond to the windows containing action potentials. z-axis is gray level coded.

Our second method of state detection exploits this difference using two parameters by which active and silent state differ: (1) membrane potential value and (2) variability of the membrane potential. We calculated the mean membrane potential and its SD in a running window of 25 ms and plotted a three-dimensional distribution of the occurrence of pairs of mean and SD values (Fig. 2C,D). In this three-dimensional plot, silent states formed a sharp peak at hyperpolarized potentials and low SD values. Active states are represented in this plot by a broader hill at more depolarized potentials and higher SD values. Two regions, one containing the sharp peak representing silent states and another containing the peak representing active states, were delimited on the top view of this plot. Those periods, which were represented by data points within these regions, were classified as respective, active, or silent states. Because the location of the two peaks differs along both axes, the use of a combination of these two parameters improves detection and separation of active and silent states. For example, occasional periods of strong inhibition during active state of the network may hyperpolarize a cell below the membrane potential threshold of active state. However, because the network remains active, fluctuations of the membrane potential during such periods would still be strong, and this period will be correctly assigned as an active state. After this initial separation of active and silent states, the procedures against disturbances by occasional membrane potential peaks were applied: periods shorter than 40 ms were not considered as states, and two active or two silent states separated by <40 ms were extended to fill the gap and pasted together.

The two methods gave close results, with high coincidence of the states, detected in the same membrane potential traces. In 19 cells, in which results of state detection with both methods were compared quantitatively, coincidence indexes [calculated, for two state sequences, as percentage of the time of their intersection from their mean total length (for details, see Mukovski et al., 2006)] were 92.0 ± 4.9% for the active and 82.2 ± 7.0% for the silent states (n = 19). Because results of the second method, which exploited both the mean value of the membrane potential and its SD, corresponded better to the expert assessment, was used it for the analysis presented below. Averaged duration of active states detected in 89 cells was 266 ± 121 ms, ranging from 82 to 671 ms; average duration of silent state was 183 ± 57 ms, ranging from 101 to 385 ms.

Having detected the onsets of active and silent states, we could now address the following question: were there specific temporal patterns of involvement of neurons from different locations in active or silent states? Two strategies were used to investigate this.

First, we searched for possible patterns during generalized states in which all simultaneously recorded cells separated by 4 mm intervals in anteroposterior direction were involved (Fig. 3A). Such groups of active (or silent) states in simultaneously recorded cells will be referred to as clusters (Fig. 3B). We defined as clusters groups of states that fulfill two criteria: (1) they should occur in all simultaneously recorded cells, and (2) their onsets should be separated by <200 ms. Thus, number of states in one cluster is equal to the number of simultaneously recorded cells. When searching for clusters, states in one cell were taken as reference, and all other simultaneously recorded cells were assessed for state onsets within 200 ms from state onsets in the reference cell. During this search, only nearby neighbors were considered.

Figure 3.

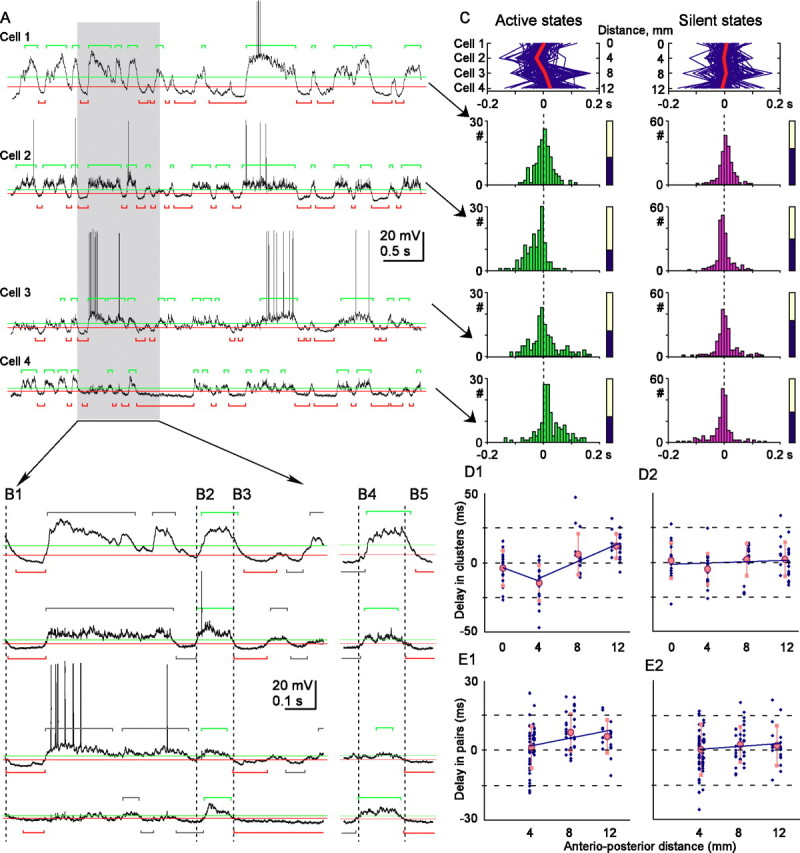
Clusters of active and silent states in simultaneously recorded cells. A, Membrane potential traces of four simultaneously recorded cells and expanded view of its part (B), with state detection levels and detected states (silent, red; active, green). States formed a cluster if they occurred in all recorded cells with the onsets separated by <200 ms. B1–B5 show examples of clusters, with clustered states (silent, B1, B3, B5; active, B2, B4) colored, and nonclustered states gray. Vertical broken lines, Onset of the first state in each cluster. C, In top panels, each cluster is represented by a blue line, connecting state onsets in all cells. Red line, Averaged delays of clustered states in four cells. Distance between recorded cells in the anteroposterior direction is indicated relative to the most anterior cell. For each cell, distributions of the onsets of clustered states and the portion of clustered states (filled part of the bars) are shown. D1, D2, Mean delay of clustered states plotted against the anteroposterior position of recorded cells. Data for 89 cells (blue symbols) and averages for four recording positions (pink indicates mean and SD). In D1, two trend lines are shown because the delays of active states in the cells recorded at 4 mm position were significantly different from both more anterior and more posterior positions. E1, E2, Mean delay of state onsets in simultaneously recorded cell pairs (n = 104) plotted against the anteroposterior distance between the cells. Mean delay of state onsets in a more posteriorly located cell was calculated relative to the state onsets in more anteriorly located cell. Other conventions are as in D.

After detecting clusters of states, we calculated for every cluster the delays of state onset in each cell relative to the cluster mean. If an active state would typically originate in a specific focus and then spread, as the propagation hypothesis predicts, the cell that is closest to that focus would be leading in the clusters and thus have a negative delay. Data in Figure 3C for the active state clusters supports this scenario. Cell 2 had a strong tendency to lead (averaged delay of −22.5 ± 27.5 ms), whereas cell 4 had a strong tendency to follow (averaged delay of +20.2 ± 46.1 ms; p < 0.001; n = 138). In cell 3, located between the neurons 2 and 4, the clustered active states had intermediate delays (average of −1.9 ± 49.7 ms). However, the above relationship was not absolute, and active state clusters with a “reversed” order, with cell 4 leading and cell 2 following, were occasionally observed (Fig. 3B4). Furthermore, the dispersion of the delays was high in every cell and all distributions covered 0, implying that any cell could be leading in some clusters (negative delays) although following in others (positive delays). Despite these reservations, the results strongly suggest that active states originated most often at, or close to, the cell 2 location and then spread in both directions. Population analysis of the sets of simultaneously recorded cells further supports this scenario (Fig. 3D1). In 21 neurons recorded at the border between area 5 and area 7 (position 2), averaged delays of clustered active states were negative (−14.6 ± 12.9 ms; n = 21) and significantly different from the positive delays in more posteriorly recorded cells (6.1 ± 14.8 ms, n = 17, p < 0.0016 at position 3; 11.9 ± 8.8 ms, n = 23, p < 0.001 at position 4). Moreover, the delays in neurons recorded at position 2 were more negative than the delays in more anteriorly recorded cells (position 1, −3.6 ± 12 ms, p = 0.0015).

In another approach, we analyzed state onset in 104 pairs of simultaneously recorded cells (Fig. 3E). Because more states contribute to a pairwise comparison, we consider it a useful supplement to the analysis of clusters. The pairwise analysis confirmed the results obtained for clustered states. When all possible pairs were pooled together, the cells, located 8–12 mm more posteriorly, were involved in active states with a delay of 7.8 ± 7.9 ms (8 mm; n = 33) and 6.1 ± 7.2 ms (12 mm; n = 18) relative to more anteriorly located reference cells (Fig. 3E1). At 4 mm distance, the delays were not significantly different from 0 (1.4 ± 9.0 ms; n = 53), apparently because active states did not originate from the most anterior position. To test for this latter possibility and to take into account the results of cluster analysis, which revealed preferential beginning of activity at recording position 2, we segregated the pairs of cells in two groups. The first group consisted only of pairs that contained cells recorded at the position of activity origin or more anterior to it (positions 1 and 2). The average delay of active state onsets in these pairs was negative (−5.1 ± 8.6 ms; difference from 0, p = 0.022; n = 18 pairs), indicating that activity started earlier at position 2. The second group consisted only of cells recorded at or more posterior to the preferential site of activity origin, at positions 2–4. For these pairs, the delays at either 4 or 8 mm distance were positive and significantly different from 0 (4.7 ± 7.3 ms, p = 0.001, n = 35; 10.5 ± 6.8 ms, p < 0.001, n = 21). Moreover, there was a significant correlation between the anteroposterior distance and delay of the active state onsets (r = 0.386; p = 0.003; n = 57 pairs). This result supports our conclusion that activity starts earlier at position 2 and spreads in the anterior direction, to position 1, and in the posterior direction, to positions 3 and 4.

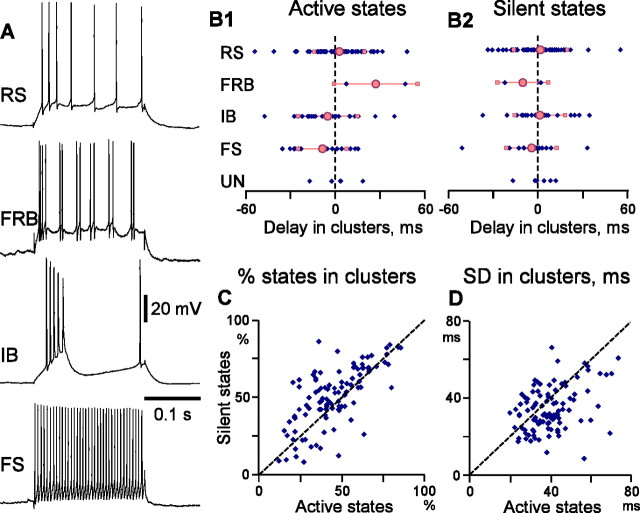
Did active states originate in cells of a specific type? We classified cells into four electrophysiological classes with differential intrinsic membrane properties (Connors and Gutnick, 1990; Gray and McCormick, 1996; Steriade et al., 1998; Steriade, 2004): regular-spiking (RS), fast-rhythmic bursting (FRB), intrinsic bursting (IB), and fast-spiking (FS) (Fig. 4A). This simplistic classification was made primarily on the basis of firing patterns in response to depolarizing current pulses. As additional criteria, action potential shape and firing pattern without stimulation were taken into account. For example, during both current-evoked firing and occasional spiking without stimulation, FS neurons generated very short action potentials, FRB cells generated characteristic duplets or triplets of action potentials, and IB cells produced typical bursts.

Figure 4.

Population analysis of the onsets of active and silent states in simultaneously recorded neurons. A, Electrophysiological identification of neurons. Responses of RS, FRB, IB, and FS cells to depolarizing current pulses. B, Relative delays of involvement of cells with different intrinsic membrane properties in clusters of active (B1) and silent (B2) states. Each diamond represents data for one cell; pink symbols are averages for cells of each class (circles, mean; squares, SD). UN, Unidentified cells. C, D, Comparison of the statistics of clustered active and silent states. Each point represents data for one cell, with the value for the silent states (ordinate) plotted against the respective value for active states (abscissa). C, Number of states involved in clusters, in percentage of the total number of states in a cell. D, SD of the onsets of clustered states in a cell.

Comparison of the timing of state onset in different electrophysiological cell classes revealed an interesting pattern of involvement of neurons in active states. On average, active states in clusters appeared first in the FS cells, then in IB neurons, and only later in the RS cells (Fig. 4B1). In FS cells, active states appeared with an averaged delay of −8.15 ± 16.2 ms (n = 14), which was significantly different from delays in cells of all other types (p = 0.051) and from delays in RS cells (p = 0.023). In IB neurons, active states appeared with an average delay of −4.42 ± 19.79 ms (n = 16). This delay was significantly different from the delay in RS neurons (p = 0.047) but not from FS cells or all other cell types pooled together (p > 0.1 for both comparisons). Pairwise comparison confirmed the results of analysis of state clusters. In the pairs consisting of an FS and an RS cell, the active states in the FS neurons started earlier, with an average delay of −6.14 ± 13.5 ms (p = 0.028; n = 26 pairs, consisting of 14 FS and 26 RS neurons). Also, in IB–RS pairs, the IB cells were leading with averaged delay of −11.5 + 7.9 ms (p < 0.01; n = 27 pairs, consisting of 16 IB and 27 RS neurons).

In marked contrast to the above results, similar analyses of silent state onsets provided no evidence for preferential origin at specific locus or specific cell type. The averaged delays of clustered silent states in cells 1–4 in Figure 3A–C were 5.3 ± 31.7 −2.5 ± 23.4, 3.9 ± 40.0, and −6.7 ± 37.2 ms (p > 0.1 for all pairs). Population analysis of silent state onsets in 23 sets and 104 pairs of simultaneously recorded neurons did not reveal any significant latency bias for any particular location (Fig. 3D2) or relative position of recorded cells (0.14 ± 11.0 ms at 4 mm distance, 2.3 ± 7.6 ms at 8 mm; and 1.9 ± 8.6 ms at 12 mm) (Fig. 3E2) or cell type (Fig. 4B2). For the silent states, the FS neurons had only a nonsignificant tendency to lead in clusters (−3.93 ± 16.4 ms) and in the FS–RS pairs (−1.53 ± 14.3ms; p > 0.1 in both cases).

Comparison between active and silent states revealed the most interesting point: namely, that silent states begin in simultaneously recorded cells more synchronously than active states. Several lines of evidence corroborate this conclusion. In state clusters, the SD of onset delays was lower for the silent states than for the active states (34.4 ± 11.2 vs 39.8 ± 11.0 ms; p < 0.001; n = 89) (Fig. 4D), showing that the silent states started with a higher temporal precision in different cells. This point is further stressed by the absence of significant dependencies of the onset of silent states on location (Fig. 3D2,E2) or cell type (Fig. 4B2). The proportion of states that formed clusters in simultaneously recorded neurons was higher for the silent than for the active states (52.5 ± 17.7 vs 46.0 ± 17.1%; p < 0.001; n = 89) (Fig. 4C). The higher percentage of clustered states implies that the cases when all simultaneously recorded cells entered the silent state were encountered more often than those cases when all cells became active together. Finally, the pairwise analysis also revealed lower SD of silent state onset than of the active states (28.7 ± 7.4 vs 33.6 ± 7.8 ms; p < 0.001; n = 104 pairs).

Discussion

Our analysis of slow sleep oscillation with simultaneous multisite intracellular recordings in cats showed the following: (1) all neocortical neurons are involved in the slow rhythm of alternating periods of activity and silence; (2) both activity and silence started almost synchronously in cells located up to 12 mm apart; and (3) most surprisingly, onsets of silent states were synchronized even more precisely than the onsets of activity.

The results provide direct evidence for both suggested mechanisms of active state generation: spread of activity from a specific focus (Sanchez-Vives and McCormick, 2000; Cossart et al., 2003; Massimini et al., 2004) and synchronization of weaker activity, originating at multiple locations (Timofeev et al., 2000; Massimini et al., 2004). The focal origin and spread hypothesis is supported by the finding that active states appear predominantly at the border between areas 5 and 7 and spread from there in both directions. Together with recent analysis of high-density EEG in humans (Massimini et al., 2004), our data suggests the presence of cortical regions with enhanced intrinsic excitability, which could primarily generate active states during sleep oscillations. Despite the difference in both experimental subjects and recording techniques, there are clear parallels between the results of Massimini et al. (2004) and our data. In both studies, activity was found to spread preferentially, although not exclusively, in the anteroposterior direction. Moreover, both studies report that activity originates predominantly at certain locations, although occasionally it may start at almost any location. These points indicate a possible similarity between the basic mechanisms underlying slow oscillations in higher mammals and in humans.

Earlier onset of activity in FS and IB cells than in other neurons shows that a specific cell type may underlie the origin of active states in cat neocortex (Sanchez-Vives and McCormick, 2000). The possibility that activity originates in IB cells, many of which are layer 5 large pyramids neurons, is consistent with previous in vitro results (Sanchez-Vives and McCormick, 2000). Moreover, bursts of action potentials generated by these cells may facilitate successful activation of additional cells and thus switching of the whole network into the active state. Earlier onset of activity in FS cells, which are inhibitory interneurons, is more difficult to interpret. Possible factors contributing to the earlier onset of active states in FS cells could be larger-amplitude and faster-onset dynamics of EPSPs in the FS cells than in pyramidal neurons (Povysheva et al., 2006). Occasional spontaneous release, which could be one of the reasons for the origin of active states (Timofeev et al., 2000), may depolarize the FS cells more effectively than neurons of other types. An additional factor could be the presence of electrical coupling among FS neurons (Galarreta and Hestrin, 1999; Gibson et al., 1999), which may facilitate detection of activity in electrically coupled neurons. One factor that could have led to an apparently earlier onset of active states in FS cells is a bias in our sample: of 14 FS cells, eight were recorded at the border between area 5 and 7, in which activity started most often. Definite resolution of the question which of the two factors (recording position vs cell type) contributed stronger to the relative timing of activity onset needs additional investigation.

Two observations cannot be explained by activity spread from a local focus but lend support to the hypothesis on multiple sources and synchronization of activity. At any recording site, we observed local activity episodes, not accompanied by activity in the other simultaneously recorded neurons. Moreover, “typical” sequences of involvement of cells in generalized active states occurred in line with alternative sequences, including reversed order. One important implication of the direct evidence for two mechanisms of active state generation is that the necessary requirements for both are fulfilled. Hence, during slow-wave sleep, thalamocortical networks can support both spread of activity from a local focus (Sanchez-Vives and McCormick, 2000; Cossart et al., 2003) and synchronization of activity originating from different foci (Timofeev et al., 2000; Massimini et al., 2004). It is tempting to speculate that the efficacy of these mechanisms may increase in pathology, eventually leading to seizures.

The most intriguing finding of our study is the high synchrony of the silent state onsets. It exposes a major gap in understanding the nature of state alternation. We suggest that it is the synchronous termination of activity and occurrence of silent states in the neuronal network that produces the characteristic EEG pattern of the slow-wave sleep. Our results allow the exclusion of several candidate mechanisms of activity termination. One candidate mechanism would be alternating activity of two mutually inhibiting neuronal subpopulations. Neurons belonging to one of these subpopulations would be active during active states and silent during silent states, but cells in the other subpopulation should express the opposite pattern, i.e., being active while the rest of the network is silent. This latter requirement is at odds with our results: we found that all cells, excitatory as well as inhibitory, were involved in the same slow rhythm, and we never observed a cell to be systematically active while other neurons were silent. Another candidate mechanism could be silencing of the network at a particular local focus, followed by a spread of silence in a kind of spreading depression. However, because we did not find evidence for preferential onset of silent states at any specific location, this possibility could be excluded as well. Finally, some recent hypotheses ascribe termination of activity and onset of silent states to the intrinsic cellular properties and currents or synaptic depression (Bazhenov et al., 2002; Compte et al., 2003; Hill and Tononi, 2004; Milojkovic et al., 2005). However, a mechanism relying exclusively on properties of individual cells and synapses might lead to a high variability of silent state onsets in neurons, because intrinsic properties are extremely nonuniform in different cells and synapses (Thomson and Deuchars, 1994; Markram et al., 2004). This allows to exclude intrinsic membrane properties of neurons or synaptic depression as major reasons for synchronous activity termination. Even not being the major players, intrinsic membrane currents and synaptic properties may nevertheless be instrumental in the organization of the slow EEG rhythm. For example, similarities in the properties of individual cells may facilitate synchronization of their activity.

The high synchrony of the silent state onsets implies the existence of a network mechanism that switches activity to silence. One possibility is synchronization among a subpopulation of inhibitory cells, which eventually discharge synchronously enough to silence the whole network. This would lead to termination of activity of both excitatory and inhibitory cells, including those cells that have generated the silencing discharge. The following considerations suggest several possible mechanisms, which are compatible with and may contribute to the above scenario. Fast-spiking and low-threshold-spiking cortical interneurons are electrotonically coupled (Galarreta and Hestrin, 1999; Gibson et al., 1999). During slow-wave oscillation, neuronal activity leads to a decrease of extracellular calcium concentration (Massimini and Amzica, 2001), thus facilitating electrotonical coupling of neurons and glial cells (Thimm et al., 2005). Finally, cortical activity can recruit intrinsic oscillatory mechanisms in thalamocortical neurons (Hughes et al., 2002), which could increase synchrony among inhibitory interneurons. Indeed, synchrony in silent state onset is disrupted in neocortical slabs (Timofeev et al., 2000). The above hypothesis predicts an increase of synchrony in membrane potential fluctuations of inhibitory interneurons toward the end of an active state. This could lead to the higher incidence of strong IPSPs in neocortical cells. Furthermore, if inhibitory neurons exert a synchronizing effect on activity in the neocortex, as they do in the hippocampus (Cobb et al., 1995), synchrony of the membrane potential fluctuations in all cells might also increase. Experimental testing of these predictions is a challenging task, but it will lead to additional insights into the mechanisms of slow-wave sleep and the origin of brain rhythms.