Interactions between Speed and Contrast Tuning in the Middle Temporal Area: Implications for the Neural Code for Speed

Abstract

A car driving through the fog appears to move more slowly than one driving on a clear and sunny day. In the laboratory, this observation has been confirmed as a pronounced reduction of perceived speed caused by a reduction in contrast.

We measured the influence of contrast on cells in the middle temporal area (MT) of the macaque, which has been hypothesized to underlie the perception of speed. The influence of contrast on the responsiveness and speed tuning of these cells was pervasive and highly regular. As expected, most cells responded less at low contrast. More importantly, the preferred speed of most cells shifted to lower speeds at lower contrasts. Moreover, approximately one-third of cells surprisingly responded more strongly to slow low-contrast stimuli than to slow high-contrast stimuli.

Current models of speed perception suggest that each MT cell votes for its preferred speed, with a vote determined by its firing rate. We tested a number of these labeled-line models by entering the neural responses we recorded from MT and comparing the predictions of the models with the perceptual reports of human subjects and monkeys. Contrary to the perceptual reports, the labeled-line models predicted that perceived speed should increase when contrast is decreased. We therefore conclude that perceived speed is not based on a labeled-line interpretation of MT cells.

Introduction

Contrast, the normalized difference in luminance between a moving object and its background, is known to affect our percept of speed (Thompson, 1982). We cannot think of a reason why this may be advantageous to the visual system but assume that it is a reflection of the inability of the system to entirely correct for changes in contrast. In other words, contrast gain control (Shapley et al., 1981), the neural mechanism that allows neurons to respond over the typically wide range of contrasts experienced in every day life, is not perfect. These imperfections induce contrast-dependent changes in neural responses, and presumably these neural changes evoke changes in the perception of speed.

The perception of speed has been linked to neural activity in the middle temporal area (MT) of the macaque brain. Lesion studies show that speed discrimination is impaired without MT (Rudolph and Pasternak, 1999), and microstimulation of MT changes speed perception (Liu and Newsome, 2005). Moreover, the typical speed tuning of MT cells suggests that these cells may code for their preferred speed. In other words, they may be labeled lines for their preferred speed. A complete model of speed perception needs to specify how multiple labeled lines are combined to arrive at a single speed percept. Lisberger and colleagues (Churchland and Lisberger, 2001; Priebe and Lisberger, 2004) have hypothesized that multiple labels are combined by vector averaging. According to this model, each MT cell votes for its preferred speed with a weight proportional to its firing rate. The speed that is perceived is the weighted average of all the votes. An alternative model, based mainly on psychophysical data, states that speed perception depends on the ratio of the response of a channel that prefers high speeds and a channel that prefers low speeds (Thompson, 1982). In neural terms, we interpret the low-speed channel as the cells in MT that prefer low speeds and the high-speed channel as the cells that prefer high speeds. Hence, in this model, MT cells vote for “fast” or “slow.” The essential difference with the vector average model is that the percept is not an average of the votes but the ratio of fast and slow votes.

A model of speed perception should not only be able to explain veridical speed perception but also errors in speed perception, such as those that occur with changes in contrast. In this project, we therefore aimed to quantify the relationship between stimulus contrast and neural responses in MT. With a detailed description of the contrast dependence of the neural response, we then tested the models. First, we documented contrast-dependent changes in perceived speed in humans and monkeys for stimuli matching our physiological studies. The results confirmed that lowering the contrast of a moving stimulus led to a reduction in perceived speed in both humans and monkeys. Second, we quantified in detail how contrast affected neural responses in area MT. We found not only the expected overall reduction in firing rate for low-contrast stimuli but also a reduction in preferred speed. Third, we used the MT responses in the vector average and ratio models to predict speed percepts. In contradiction with the perceptual reports of our subjects, the model predicted that low-contrast stimuli should look faster. Because the contrast-induced changes in the neural data were highly consistent and predicted qualitatively different perceptual effects, this contradiction could not be resolved by simple parameter choices in the models.

Materials and Methods

Subjects

Two adult male rhesus monkeys (Macaca mulatta; monkeys M and S) were used in the electrophysiological experiments. Monkey M performed the behavioral experiments. Experimental and surgical protocols were approved by The Salk Institute Animal Care and Use Committee and conformed to United States Department of Agriculture regulations and National Institutes of Health guidelines for humane care and use of laboratory animals. Surgical procedures have been described in detail previously (Dobkins and Albright, 1994).

Five naive human subjects and one author participated in the human psychophysical experiments. Participants gave informed consent, and all procedures were in accordance with international standards (Declaration of Helsinki) and National Institutes of Health guidelines. All subjects had normal or corrected-to-normal visual acuity.

Visual stimulation

All visual stimuli were generated with in-house OpenGL software using a high-resolution graphics display controller (Quadro Pro Graphics card, 1024 × 768 pixels, 8 bits/pixel) operating in a Pentium class computer. In the experiments with monkeys, stimuli were displayed on a 21 inch monitor (75 Hz, non-interlaced, 1024 × 768 pixels; model GDM-2000TC; Sony, Tokyo, Japan). In the experiments with human subjects, we used a 19 inch Sony Trinitron E500 monitor (75 Hz, non-interlaced, 1024 × 768 pixels). The output of the video monitor was measured with a PR650 photometer (Photo-Research, Chatsworth, CA), and the voltage/luminance relationship was linearized independently for each of the three guns in the cathode ray tube. Stimuli were viewed from a distance of 57 cm in a dark room (<0.5 cd/m²) in both the human and monkey experiments.

Monkeys were seated in a standard primate chair (Crist Instruments, Germantown, MD) with the head post rigidly supported by the chair frame. Eye position was sampled at 60 Hz using an infrared video-based system (IScan, Burlington, MA), and the eye position data were monitored and recorded with the CORTEX program (Laboratory of Neuropsychology, National Institute of Mental Health, Bethesda, MD; http://www.cortex.salk.edu/), which was also used to implement the behavioral paradigm and to control stimulus presentation.

Stimuli and experimental paradigms

We used random dot patterns consisting of 100 dots moving coherently in one direction within a 10° diameter circular aperture. Dots had infinite lifetime and were randomly repositioned after leaving the aperture. Dots were 0.15° in diameter and always more luminous than the gray background (5 cd/m²). In the physiological experiments, the direction of motion was adjusted to match the neuronal preferred direction rounded to the nearest multiple of 45°.

The luminance of every dot in a given pattern was 5.53, 6.11, 7.5, or 30 cd/m². Compared with the 5 cd/m² background, this resulted in a Michelson point contrast of 5, 10, 20, or 70%. Note, however, that because the background luminance was never changed, this manipulation simultaneously changed the overall luminance level. Given the dot density, the spatially averaged luminance of the patch varied from 5.01 cd/m² at 5% point contrast to 5.56 cd/m² at 70% point contrast. Because the concomitant luminance manipulation is small (<11%), we refer to the stimulus manipulation as a change in contrast. Moreover, the psychophysical data were obtained under identical stimulus conditions; hence, this confound of average luminance and contrast did not have any adverse effect on our efforts to relate perceptual changes to neural changes. Other studies (Pack et al., 2005) have used a metric based on the average deviation from mean luminance to describe contrast in random dot patterns (Moulden et al., 1990). For comparison with such studies, our Michelson point contrasts of 5, 10, 20, and 70% correspond to 0.006, 0.03, 0.14, and 13.75, respectively.

Psychophysical paradigm.

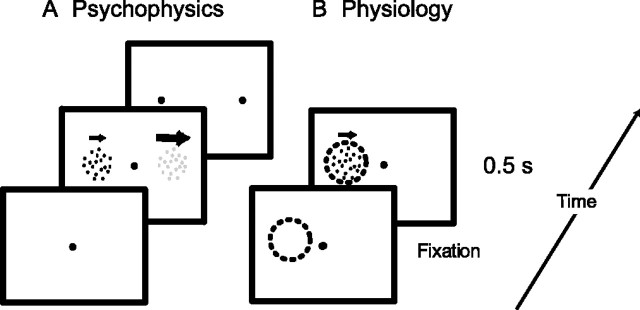
Figure 1A shows the paradigm we used to investigate how contrast affected perceived speed. Subjects fixated a small dot at the center of the screen. Two patches of random dots appeared 10° left and right of fixation. In one patch, the reference stimulus, dots moved rightward at the reference speed and had a contrast chosen from 5, 10, 20, or 70%. In the other patch, the test stimulus, dots also moved rightward, but contrast was fixed to 70% and speed was slower or faster than the reference speed by 0, 10, 40, or 80%. These 28 test conditions (four contrasts × seven speeds) were randomly interleaved. In one block of conditions, reference speed was 2, 5, or 40 °/s (randomly interleaved). In the second block, reference speed was 10 or 20°/s (also randomly interleaved). After the 500 ms stimulus presentation, the dot patterns were extinguished and subjects answered the question “Which pattern moved faster?” by pressing one of two keys on the keyboard. The human subjects received no feedback on their performance, and the next trial started immediately after the subjects’ response. The positions of test and reference stimuli were counterbalanced. Each comparison of reference speed and test speed at a given contrast was repeated 20 times.

Figure 1.

Experimental paradigms. A, Sequence of events in the behavioral paradigm. Subjects fixated a central red spot and then two random dot patterns appeared for 500 ms. In this example, the right pattern is a low-contrast reference stimulus, moving rightward at a fixed reference speed. The left pattern is a high-contrast test pattern moving at low speed (indicated by arrow length). In the monkey behavioral experiments, two dots appeared after stimulus offset. The monkey fixated one of these to indicate which stimulus moved faster. In the human psychophysical experiments, subjects pressed one of two buttons to indicate which of the two patterns was moving faster. B, The physiological experiments used a similar stimulus configuration, but those parts of the display that were not in the receptive field of the cell were not shown. The dashed circle indicates the receptive field of the cell under study. The only behavioral requirement was that fixation be maintained for the duration of each trial.

The psychophysical paradigm was adapted so that monkey M could report his percept with an eye movement. Once the stimuli were extinguished, two small green dots appeared 10° left or right of fixation. First, we trained the monkey extensively on the speed discrimination task with stimuli of equal contrast. In these experiments, the reference stimulus speed was 4, 16, or 64°/s. The test stimuli were slower or faster than the reference stimuli by 5, 10, 20, 40, or 80%. A small liquid reward was given if, after the stimuli and the central fixation point had been extinguished, the monkey directed its gaze to the green dot at the position where the faster stimulus had been. Once the monkey reached a stable level of performance (∼80% correct for a 40% speed difference), we introduced a condition in which the test and reference stimulus had the same physical speed but the test stimulus was at 70% contrast and the reference stimulus was at 20% contrast. In these trials, reward was given randomly in 60% of the trials. The positions of test and reference stimuli were counterbalanced, and monkey M performed this task on 5 consecutive days for a total of >10,000 trials.

Electrophysiological paradigm.

We recorded the activity of single units in area MT using tungsten microelectrodes (3–5 MΩ; Frederick Haer Company, Bowdoinham, ME), which were driven into cortex using a hydraulic micropositioner (model 650; David Kopf Instruments, Tujunga, CA). Neurophysiological signals were filtered, sorted, and stored using the Plexon (Dallas, TX) system. We identified area MT physiologically by its characteristically high proportion of cells with directionally selective responses, receptive fields (RFs) that were small relative to those of neighboring medial superior temporal area, and its location on the posterior bank of the superior temporal sulcus. The typical recording depth agreed well with the expected anatomical location of MT that was determined from structural magnetic resonance scans.

We used automated methods to determine the directional selectivity and receptive fields of the cells (for details, see Krekelberg and Albright, 2005). The RF center and the preferred direction of motion revealed by these methods were used to optimize stimuli for subsequent neuronal response measurements. To measure the speed tuning curves of MT cells at various levels of contrast, we centered a single random dot pattern on the receptive field. These patterns appeared 250 ms after the monkey started fixating a central red dot. After moving in the preferred direction of the neuron for 500 ms, the pattern was extinguished. For each cell, the range of test speeds was 1, 2, 4, 8, 16, 32, and 64°/s, and the range of test pattern contrasts was 5, 10, 20, or 70%. These 28 conditions were randomly interleaved. Trials in which eye position deviated from a 2° wide square window centered on the fixation spot were aborted and excluded from analysis. Each condition was typically repeated 15 times.

Data analysis

Psychophysical data.

Separately for each combination of reference and test stimuli, we calculated the percentage of trials in which subjects responded that the test stimulus was faster. We used the “psignifit” Matlab (MathWorks, Natick, MA) toolbox (Wichmann and Hill, 2001) to fit these data with cumulative Gaussians. This fit provided an estimate of the point of subjective equality (PSE) defined as the speed at which the fitted curve crossed 50% “test faster.”

Physiological data.

We analyzed neuronal responses with custom in-house software, written in Matlab. The measure of neuronal response was mean spike rate computed within a window of 500 ms (test stimulus duration) after response onset. To determine response onset, we first calculated the mean and SD of the baseline firing rate. This was defined as the average response during the 250 ms interval in which fixation was maintained but no stimulus was presented in the RF. Response onset was defined as the start of the first 20 ms bin in which firing rate exceeded the baseline firing rate by 3 SDs. The latency of the cell for a given stimulus was then defined as the time between stimulus onset and response onset. We used the minimum response latency across all conditions as the start of the 500 ms window in which we determined the response. This allowed us to analyze conditions in which the response did not exceed the (arbitrary) statistical threshold. (For each cell, there was at least one condition in which the threshold was reached.)

Significance of the speed and contrast dependence, and their interaction, was assessed using a standard two-way ANOVA. We used a nonlinear least squares method to fit functions of the following log-Gaussian form to the speed tuning data:

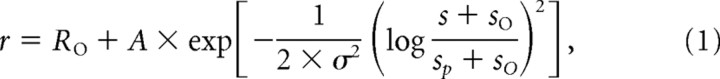where r is the firing rate and s the stimulus speed in degrees per second. The function has five free parameters: R₀, the spontaneous firing of the cell; A, the peak amplitude; σ, the (logarithmic) tuning width; s₀, an offset speed; and s_p, the preferred speed (Nover et al., 2005).

Results

We divided the results into three parts. First, we document how changes in contrast affect perceived speed in humans and monkeys. Second, we describe how changes in contrast change the responsivity and speed tuning of MT neurons. Finally, we test whether the vector average model of speed representation in MT can link the neural data of part 2 with the perceptual data of part 1.

Contrast dependence of speed perception

Although the effects of contrast on speed perception are well known (Thompson, 1982), we wanted to quantify these effects for the particular stimuli we used in the physiological experiments. Because we planned to characterize contrast effects in MT neurons over a range of speeds, we also needed to quantify the perceptual effect over a range of speeds. Moreover, we wanted to ascertain whether the effect of contrast on speed perception in monkeys is similar to that in humans. To achieve these goals, we performed behavioral experiments in human subjects and one rhesus monkey. The details of the behavioral paradigm are described in Materials and Methods. Briefly, both the human subjects and monkeys viewed two patches of moving random dots and reported which of the two moved faster (Fig. 1 A).

In the experiments with human subjects, the contrast in one patch (reference stimulus) was variable (5, 20, 40, or 70%; see definition of contrast in Materials and Methods) and the speed was fixed. In the other patch (test stimulus), the dots always had 70% contrast and their speed equaled that of the reference stimulus or it was 10, 40, or 80% faster or slower than the reference stimulus. Note that contrast was manipulated by changing the luminance of the dots while keeping the background luminance constant. Although this introduced a confound between the contrast and the average luminance of the stimulus patches, the overall change in luminance was minimal (see Materials and Methods), and we refer to the stimulus manipulation as a change in contrast. Moreover, the confound of luminance and contrast has no effect on our attempts to relate neural and behavioral data because identical stimuli were used in the behavioral and electrophysiological experiments.

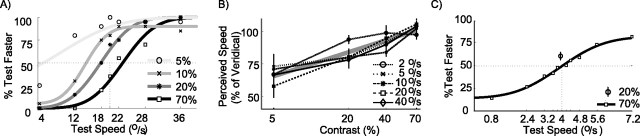
Figure 2A shows results obtained from one human subject. In this experiment, the reference stimulus moved at 20°/s. The speed of the test stimulus is shown on the horizontal axis. The vertical axis represents the percentage of trials in which the subject reported the test stimulus to be faster than the reference stimulus. The squares show performance for trials in which both test and reference stimuli had 70% contrast. The darkest curve, a cumulative Gaussian fitted to the data points, crosses the 50% line at 22.8°/s. Hence, the PSE is 22.8°/s, which suggests that a test stimulus moving at 22.8°/s looked as fast as the reference stimulus moving at 20°/s.

Figure 2.

Perceptual contrast effects. A, Psychometric curves from a single human subject comparing a reference speed of 20°/s with a range of test speeds (horizontal axis) at four levels of contrast (color of the data point/curve; see legend). The point at which the psychometric curves cross the horizontal dashed line (Test Faster is 50%) defines the PSE for that contrast. The solid curves are cumulative Gaussians that were fitted to the data points (see Materials and Methods). B, Average data from human subjects (n = 6) illustrating the change in PSE with contrast for various speeds. All PSE changes are expressed as a ratio of perceived to reference speed. The thick gray line represents a linear regression to the data averaged over all reference speeds. Error bars represent the SE in the population mean. C, Psychometric curve from a single macaque subject (monkey M) comparing a reference speed of 16°/s to a range of test speeds. The squares represent comparisons between equal (70%) contrast stimuli. The open circle shows the percentage of trials (recorded over multiple days; n = 1100) in which a 20% contrast reference stimulus was reported to be faster than the 70% test stimulus moving at the physically identical speed. Error bars show 95% confidence intervals.

The main goal of this experiment was to quantify how a reduction in contrast of the reference stimulus changed its perceived speed, as measured by the point of subjective equality. Figure 2A shows that the PSE was shifted to lower speeds for reference stimuli of lower contrast. For instance, the PSE of the lightest gray curve (representing the reference stimulus at 5% contrast), was 6°/s. This means that, for this subject, the 5% contrast reference stimulus moving at 20°/s looked as fast as the 70% contrast test stimulus moving at 6°/s. In other words, the perceived speed of a low-contrast stimulus was much reduced.

Next, we wanted to quantify how the reduction in perceived speed depended on contrast and the physical speed of the stimulus. We measured a complete set of psychometric curves as in Figure 2A for six human subjects and at a range of reference speeds. For each subject, reference speed, and contrast, we determined the points of subjective equality. In Figure 2B, these PSEs are expressed as a percentage of physical reference speed: 50% corresponds to a stimulus that looks half the speed it really is, and 100% refers to a stimulus that appears veridical. The figure shows that, at 70% contrast, the average perceptual report for all reference speeds was near veridical. For lower contrasts, the perceived speed was reduced. The fact that the perceptual reports at a given contrast overlap considerably for the different reference speeds suggests that the percept depended very little on the physical speed of the reference stimulus. A two-way ANOVA confirmed this: there was a significant main effect of contrast (p < 0.01) but no significant effect of reference speed (p = 0.63). Given the absence of a significant effect of reference speed, we averaged the data over all speeds and determined a best-fitting linear regression between perceived speed (ŝ), the veridical speed (s), and the logarithm (base 2) of the contrast (c). This regression is given by the following formula: ŝ = (44% + 9% × log₂ (c)) × s. For the range 5–70% contrast, this formula means that, regardless of actual stimulus speed, a reduction of contrast by one octave will lower perceived speed by ∼9%.

Finally, Figure 2C shows the results from a rhesus monkey subject. The reference speed in this experiment was 4°/s; test speeds are shown on the horizontal axis. The data points show the monkey’s performance when comparing two patches at 70% contrast. The PSE for this curve is 4°/s, showing that the monkey’s percept was veridical. However, the shallower slope of the psychometric curve and the fact that the asymptotes do not reach 100% shows that the monkey did not perform as well as most of our human subjects (Fig. 2A, solid black curve). A reduced absolute level of performance for this particular kind of speed discrimination in monkeys compared with humans has been observed previously (Liu and Newsome, 2005; Krekelberg et al., 2006).

In contrast to the human experiments, we did not measure complete psychometric curves for different levels of contrast. The reason for this was that, in trials with patches with different contrast, it is not a priori clear what the monkey should see. Hence, in such trials, reward can only be given on a random (response-independent) schedule. Because the animal’s only true goal in the experiment is to maximize its reward, random rewards will often cause the animal to search (in vain) for response strategies that lead to more reward. The success of our experiment, however, relied on the animal pursuing only a single response strategy: speed discrimination. To encourage this strategy, we mainly (83% of trials) presented patches with the same contrast; in these trials, the animal was rewarded for veridical speed discrimination. In the remaining 17% of trials, both reference and test stimuli moved at the same speed, but the reference stimulus was lowered to 20% contrast. From these trials, which were rewarded randomly, we could determine whether the monkey perceived low-contrast stimuli faster or slower than high-contrast stimuli.

The data point shown as an open circle in Figure 2C shows the animal’s performance when comparing the 70% test stimulus with a 20% contrast reference stimulus, both moving at 4°/s. This data point is based on ∼1000 trials. Although these stimuli moved at identical physical speeds, the animal reported in 62% of trials that the 70% contrast test stimulus was faster than the 20% contrast reference stimulus. In other words, as for the human subject, the monkey reported that the low-contrast stimulus moved slower than the high-contrast stimulus. Lacking data on the full psychometric curve, these numbers are difficult to translate into a quantitative estimate of the underestimation of speed. If we ignore possible changes in the slope and assume that the psychometric curve at low contrast is a purely shifted version of the psychometric curve at high contrast, the PSE at 20% contrast would be ∼3.2 °/s. This corresponds to a perceived speed that is 80% of veridical and is in the same range as the human data shown in B. In two additional experiments, the monkey also reported a reduction in perceived speed for low-contrast stimuli moving at 16 and 64°/s (data not shown). Together, these behavioral data clearly support the view that the influence of contrast on perceived speed is similar in monkeys and humans.

These behavioral results demonstrate that a reduction in perceived speed with a reduction in contrast applies to the random dot stimuli used in our paradigm, as it does to the more commonly used gratings (Thompson, 1982) and a wide range of other stimuli (Blakemore and Snowden, 1999). Over the range of speeds at which we measured this effect, we never observed an increase in perceived speed. The reduction in perceived speed was evident in humans as well as in our macaque subject. Combined with the fact that random dot stimuli drive MT cells well, this provides a good basis for exploring neural correlates of this perceptual illusion in macaque MT.

Contrast dependence of neuronal speed tuning

We recorded from 109 cells in area MT of two monkeys. The mean RF eccentricity and its SD was 8 ± 4.3° (range of 3–15°). This eccentricity range is well matched to the position of the stimuli used in the behavioral experiments (10°). As expected and in agreement with previous findings (Rodman and Albright, 1987; Lagae et al., 1993), a majority of the cells (96 of 109; 88%) was significantly speed tuned (as defined in Materials and Methods). We restricted our analyses to these 96 cells (monkey S, 41 cells; monkey M, 55 cells). Using the definitions for speed tuning of Liu and Newsome (2003), 7% of the cells were classified as low pass, 68% bandpass, and 25% high pass over the tested range. The distribution of preferred speeds of these cells was broad: the quartile range extended from 10 to 31°/s, with a median of 20°/s. There were few cells with a preferred speed above 40°/s or below 2°/s. These properties are of course influenced by our particular choice of stimuli, but they are in general agreement with other studies (Van Essen, 1985; Churchland and Lisberger, 2001; DeAngelis and Uka, 2003; Liu and Newsome, 2003).

To investigate the interaction of contrast and speed tuning, we presented patches of moving dots centered on the receptive field of the cell that moved in the preferred direction at a range of speeds. Stimulus duration was 500 ms. Dot luminance was adjusted such that the contrast of a single dot with the 5 cd/m² background was 5, 10, 20, or 70%. Neural response was quantified as the average firing rate during stimulus presentation, corrected for latency of the cell (see Materials and Methods).

Illustrative example cells

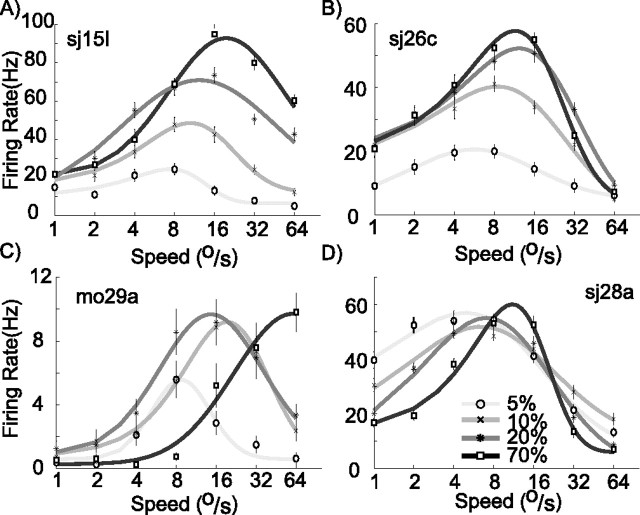
Figure 3 shows speed tuning curves recorded at four contrast levels for a selection of cells. The logarithmically scaled horizontal axis represents speed; the vertical axis represents neural response. For each stimulus contrast, we fitted a log-Gaussian function with five free parameters to the data (see Materials and Methods). These fits are represented by the curves in Figure 3, and the contrast of the curves was used to indicate the contrast of the stimulus. The log-Gaussian function provided a good fit to the speed tuning curves; the median explained variance for all cells, and all contrasts was 95%. This close match allowed us to use the free parameters to quantify three aspects of the response properties: peak firing rate, preferred speed, and tuning width. Figure 3A shows a cell that responded vigorously to the moving dots at 70% contrast (darkest curve). When contrast was lowered from 70 to 5%, the peak of the response was reduced from 90 to 20 Hz. The second notable feature found in this example cell is that the preferred speed was 24°/s at 70% contrast but decreased with a decrease in contrast: at 5% contrast, preferred speed was only 8°/s. This feature can be observed to a greater or lesser extent in the other example cells. A third interesting aspect of the tuning curves is their width. Whereas some cells show an increase in (logarithmic) tuning width at high contrast (e.g., C) others show a decrease (D). The final feature of interest is most dramatically illustrated by the cell in C: for low speeds, this cell responded more vigorously to slow patterns of low contrast (5%; left side of lightest gray curve) than to a pattern of high contrast (70%; darkest curve). Although initially unexpected, this stronger response to low-contrast stimuli can be seen as an extreme case of the shift in preferred speed. For this cell, the preferred speed decreased so much with a lowering in contrast that the peak response at low contrast became higher than the off-peak firing rate evoked by the high-contrast pattern.

Figure 3.

Examples of speed tuning curves at different contrasts. A–D, Four cells that span the range of effects found in area MT. The fitted curves provided quantitative estimates of peak rate, preferred speed, and amplitude. Error bars indicate SEM.

Cell-by-cell analysis

To quantify the effects illustrated by the example cells in Figure 3, we analyzed the basic tuning properties of our sample using a two-way ANOVA, with speed and contrast as the main factors. In our sample of speed-tuned cells, 87 (90%) showed significant contrast tuning (main effect of contrast, p < 0.05) and 76 (79%) showed a statistically significant interaction between the main effects of contrast and speed (p < 0.05). The remainder of this section is devoted to illustrating the interaction between speed and contrast tuning in more detail. Specifically, we compare tuning curve parameters (peak rate, preferred speed, and tuning width) obtained at the four levels of contrast.

Contrast effects on firing rates.

Figure 4 shows how firing rate changes with contrast. In Figure 4A, we analyzed the changes in the peak firing rate. Each cell is represented by three points in this plot. On the horizontal axis is the peak firing rate evoked by a 70% contrast stimulus. On the vertical axis is the peak firing rate evoked by 5% (circles), 10% (crosses), or 20% (asterisks) contrast stimuli. Nearly all data points lie below the diagonal, showing that the peak firing rate decreased with a decrease in contrast for most cells. The inset in Figure 4A shows the population median peak firing rate at each contrast, confirming that the peak firing rates tended to decrease with a decrease in contrast (Kruskal–Wallis ANOVA on ranks, p < 0.01). The error bars in the inset represent quartile ranges.

Figure 4.

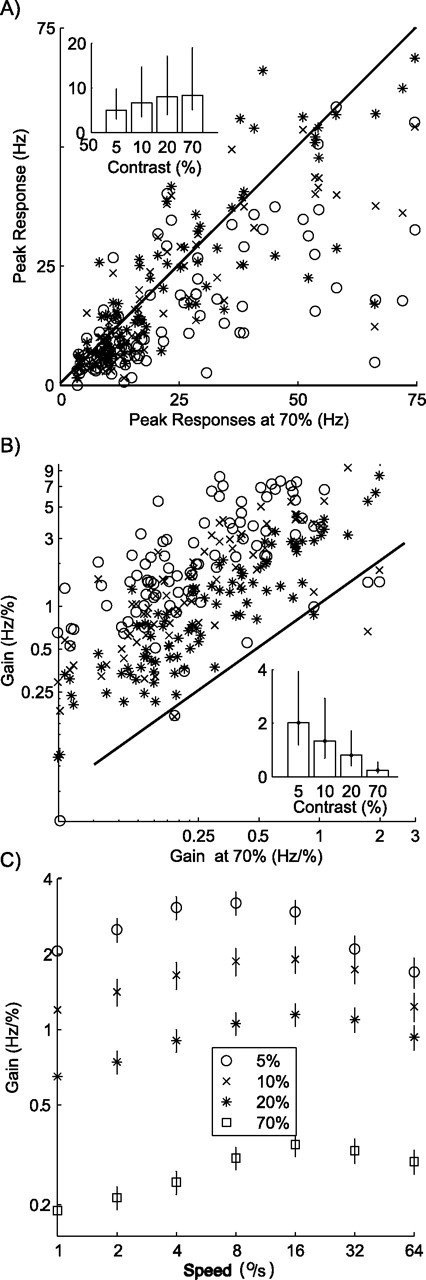
Changes in firing rate and gain with contrast. A, Peak rate. Each data point represents peak firing rate elicited by stimuli of low contrast (circles, 5%; cross, 10%; asterisk, 20%) as a function of peak rate at high contrast (70%, x-axis). Inset shows median peak firing rate at the four levels of contrast. Error bars extend from the 25th to the 75th percentile of peak firing rates. Firing rate is weaker, on average, at lower contrast. B, Gain changes. Gain is defined as the ratio of firing rate to contrast. Data points compare gain at lower contrasts with gain at high contrast (70%, x-axis). Inset shows median gain at four levels of contrast, with error bars extending from the 25th to the 75th percentile of the gain distribution. Gain is greatest, on average, at low contrast. Graphical conventions as in A. C, Gain changes as a function of stimulus speed. The average gain over all cells is shown for each contrast and stimulus speed. This figure shows that the reduction in firing rate that occurred with a reduction in contrast could be partially described as a multiplicative effect on the gain. This effect, however, was not the same for all speeds.

Figure 4A shows that there is considerable spread in the peak rate increase with contrast. We investigated whether other tuning properties were predictive of the increase and found that neither preferred speed nor tuning width was significantly correlated with the change in peak rate. Next, we analyzed whether the reduction in firing rate that occurs with a reduction in contrast is consistent with a simple multiplicative gain control mechanism.

We defined gain as the neural response divided by stimulus contrast. In other words, the gain is the spike count per unit of contrast. In Figure 4B, we show the gain (for each cell and stimulus speed) at low-contrast levels as a function of gain at high (70%) contrast. Fitting lines through these data points and the origin allows us to estimate the relationship between gain and contrast. When the contrast was reduced from 70 to 20%, gain increased 3.3-fold. For this contrast change, a gain increase described the change very well: a linear regression through the origin explained 95% of the variance in the gain. For the larger contrast reductions from 70 to 10% and from 70 to 5%, the gain increased by a factor of 4.8 and 8.4, respectively. The simple linear gain increase model, however, was less appropriate here, as witnessed by the lower explained variance in the regression of 30 and 75%, respectively. Hence, for small contrast reductions, the neural response gain change can be described as a purely multiplicative gain change. For reductions to contrast values below 20%, however, this simple description failed.

We therefore analyzed whether gain changes depended on the stimulus speed. For Figure 4C, we calculated the gain for each level of contrast and speed and then averaged over cells. Clearly, the gain was reduced for higher contrast. Moreover, consistent with the changes in preferred speed observed in the example cells, the peak of the population gain curve shifted toward higher speeds at higher contrasts.

Rate changes at fixed speed.

Figure 3C shows an example of a cell with a peak firing rate that is lower for low contrast (thus falling below the diagonal line in Fig. 4A), but at 8°/s the cell responded more strongly at low contrast.

We did a statistical analysis to quantify how prevalent this property was. For each cell with a statistically significant effect of speed and contrast (two-way ANOVA, p < 0.05) we did a post hoc test comparing the responses to the stimuli with different contrasts but the same speed. This test told us whether a low-contrast pattern could evoke a significantly higher firing rate than a high-contrast pattern moving at the same speed. This was the case in 29 of 96 cells (30%). Visual inspection of these tuning curves showed that the typical effect was like that shown in Figure 3C. Although the peak firing rate was lower for a low-contrast pattern, the preferred speed was so much lower that the firing rate at the low and/or intermediate contrast peak was higher than the off-peak firing rate evoked at high contrast.

Preferred speed.

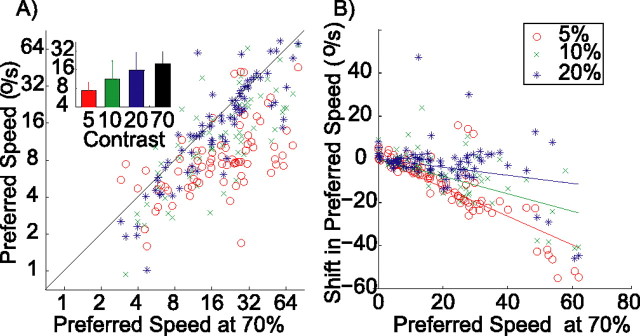
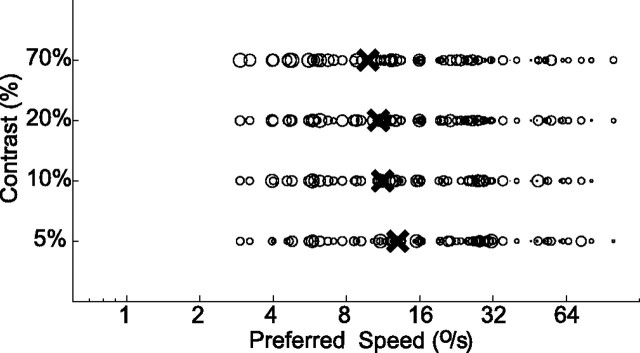
Figure 5 shows how preferred speed changes with contrast. The horizontal axis in Figure 5A represents the preferred speed found at 70% contrast, and the vertical axis represents the preferred speed found at lower levels of contrast. For visual clarity, this figure uses color in addition to marker styles to identify the stimulus contrast (see legend). Again, most data points lie below the diagonal (e.g., 85% of the data points at 5% contrast), showing that, for most cells, the preferred speed decreased with decreasing contrast. The inset shows how the median preferred speed across the population changed with contrast (Kruskal–Wallis ANOVA on ranks, p < 0.01).

Figure 5.

Changes in preferred speed with contrast. A, Preferred speed at low contrast (y-axis; red circles, 5%; green crosses, 10%; blue asterisks, 20%) compared with the preferred speed at high contrast (x-axis, 70%). Inset shows the median preferred speed for each contrast level. Error bars represent the 25th and 75th percentile. Although graphical conventions are the same as in Figure 4, color was added for visual clarity. B, Relationship between the shift in preferred speed with contrast and the preferred speed at high contrast. Across the population, preferred speed decreases with a decrease in contrast. This decrease is largest for cells with a high preferred speed at high contrast.

It appears from Figure 5A that cells with higher preferred speeds also had the largest decreases in preferred speed with a decrease in contrast. We analyzed this by comparing the changes in preferred speed with the preferred speed of the cell at 70% contrast. This relationship turned out to be highly linear. Figure 5B shows the preferred speed of the cells on the horizontal axis and the change in preferred speed on the vertical axis. Fitting straight lines through the origin to these data points allowed us to quantify the change in preferred speed as a simple multiplicative factor. For instance, the red data points show the shift in preferred speed that occurred when the contrast was changed from 70 to 5%. The linear regression through the origin resulted in a curve with a slope of −0.60, and this linear model explained 64% of the variance (r = 0.82; p < 0.01). Hence, on average, when contrast was reduced from 70 to 5%, the preferred speed was reduced by 60% of the original (high-contrast) preferred speed. For smaller contrast changes, there were correspondingly smaller preferred speed changes. Reducing the contrast from 70 to 10% (green data points) generated a curve with slope −0.37 (explained variance, 39%; r = 0.64; p < 0.01), and reducing the contrast from 70 to 20% (blue data points) generated a curve with slope −0.15 (explained variance, 13%; r = 0.38; p < 0.01).

Tuning width.

A recent study by Pack et al. (2005) reported that cells with low preferred speeds increased their tuning width with an increase in contrast, whereas cells with high preferred speeds decreased their tuning width with an increase in contrast. We could not confirm this in our sample of MT cells. The width of the log-Gaussian tuning function (parameter σ; see Materials and Methods) was essentially independent of contrast (Kruskal–Wallis test, p = 0.93). The median tuning width was 0.9 octaves. We have no explanation for this discrepancy.

Population tuning curves

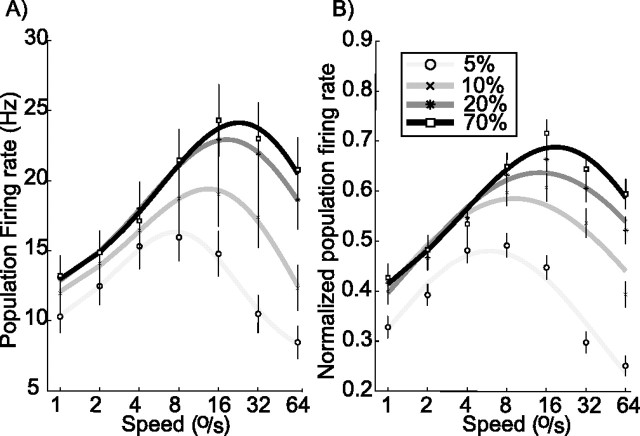
Figures 4 and 5 give overviews of the changes that take place for individual cells in our sample. We also wanted to gain some insight into how population activity changed with contrast. We averaged firing rate for each contrast and speed over the whole sample. This resulted in the tuning curves of Figure 6A, which represent average firing rate for a given speed and contrast. In this raw population average, cells with high firing rates could have a disproportionate influence. In Figure 6B, we therefore show the normalized population average: for this plot, the response of each cell was first normalized to its maximum firing rate and then averaged with the rest of the population.

Figure 6.

Population speed tuning. A, Raw population average. Responses to the speed shown on the horizontal axis were averaged, separately for each stimulus contrast, over all 96 cells. Error bars show SEMs. On average, the MT population response is weaker at low contrast, and preferred speed is lower. B, Normalized population average. For this plot, the firing rate of each cell was normalized to its peak before determining the population average. Graphical conventions are as in previous plots.

Both the raw and the normalized population tuning curves reiterate some of the main points made in the previous section, and they show that those properties extend to the population as a whole. Specifically, peak firing rate and preferred speed both increased with increasing contrast. Additionally, the increase in firing rate with contrast was largest for fast stimuli. The only single-cell finding that we did not find at the population level is the observation that some cells prefer low-contrast stimuli at low speeds (Fig. 3C). We attribute this to the fact that only 30% of cells (see above) exhibited this effect.

Testing labeled-line models

The previous section documents the relationship between neural responses, speed, and contrast in MT. The effects of contrast on response were surprisingly consistent across cells. Similarly, effects of contrast on speed perception were consistent across subjects and species and were described by a simple linear relationship. These properties (consistency and linearity) make the phenomenon of contrast-induced changes in speed perception an ideal candidate to explore the relationship between neural responses and perception.

The vector average model

In previous work, a vector average model of speed perception has been shown to successfully relate neural responses to changes in speed perception (Churchland and Lisberger, 2001; Priebe et al., 2003; Priebe and Lisberger, 2004; Price et al., 2005; Krekelberg et al., 2006). In this section, we test whether this model can also relate our neural and perceptual data. The vector average model assumes that every MT cell votes for its preferred speed with a weight proportional to its normalized firing rate. In other words, it assumes that cells are labeled lines; a spike from a given cell is always interpreted as evidence for the presence of the preferred speed of that cell (its label).

We formalized the vector average model as follows (Priebe and Lisberger, 2004):

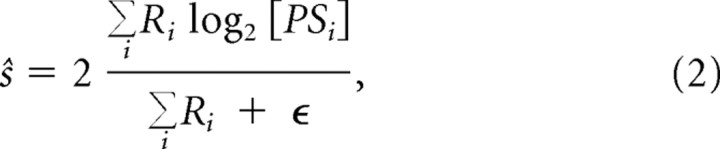where ŝ is the speed estimate, and PS_i denotes the preferred speed of the cell as measured with a 70% contrast stimulus. To give all cells equal voting power, the firing rate R_i is normalized to the peak rate of the cell. The bias term (ε) prevents the estimate from exploding for small firing rates and has been used to generate the documented bias in human perception toward low speed estimates (Priebe and Lisberger, 2004). In the model results below, we set ε = 0 for simplicity (see Discussion). Figure 7A shows the vector average model in action. Each data point represents data from a single cell. The horizontal position of a point corresponds to the label of the cell (PS_i). Following Priebe and Lisberger, the diameter of a point scales with the relative firing rate (R_i). The top row represents the population response to a 70% contrast stimulus that moves at 4°/s. Consistent with this, most data points near the right end of the figure (cells that prefer speeds much higher than 4°/s) are relatively small. Cells that prefer lower speeds have high firing rates and are marked by larger circles. The black cross shows the centroid of the distribution calculated by Equation 2. This centroid represents the speed estimate ŝ. Although the real speed is 4°/s, the speed estimate is 9.6°/s. The reason for this is that few cells have preferred speeds in the lower range; hence, although neurons with low preferred speeds fire most, there are more neurons with higher preferred speeds; this pulls the centroid of activity toward the overrepresented speeds. In our population, the preferred speed of ∼20°/s was most prevalent; hence, speeds below 20°/s were overestimated and speeds above 20°/s were underestimated (data not shown). This bias in the estimation could easily be corrected by using either a population with a homogeneous distribution of preferred speeds or a weighted or nonlinear average of the labels. Following Priebe and Lisberger (2004), however, we will ignore the bias in the estimation of absolute speed that inevitably arises from a nonflat population distribution. This is justified because, even using a model with a speed bias, one can still investigate how a change in some stimulus parameter evokes a change in the vector average speed representation. Such relative speed measures are not strongly affected by the bias in the population.

Figure 7.

Vector average model of speed perception. Population activity diagram for a 70% contrast stimulus moving at 4°/s. Each cell is represented by an open circle whose diameter is proportional to the normalized firing rate of the cell. Position of the circle on the horizontal axis is given by the preferred speed of the cell at 70% contrast, which we interpreted to be the label of the cell. Vector average of the population activity was calculated with Equation 2 and is represented by the black cross. The vector average model incorrectly predicts that perceived speed (the centroid) increases when contrast decreases.

Figure 7 also shows the decoded speed for stimuli at lower levels of contrast. They were estimated with the vector average model, now using the rates evoked by the stimulus moving at 4°/s but at lower contrast. Because the label of a cell is assumed to be constant in the vector average model, the preferred speed that enters Equation 2 was kept the same. When the contrast was lowered to 20% (second row from the top), all cells responded less (in agreement with Fig. 4A: the peak of the tuning curve is lower). However, this overall reduction is not systematically related to the preferred speed of the cell (see above). Hence, this merely scales the value of R_i and has no influence on the vector average as calculated by Equation 2. Following the results shown in Figure 4B, however, contrast reduction caused cells to respond relatively more vigorously for speeds below their originally preferred speed. In Figure 7, this is, for instance, reflected by a gradual increase in size of the circles near 32°/s when the contrast is lowered from 70 to 5% and the concomitant shift in the centroid of population activity toward higher speeds. As a consequence, the decoded speed for low-contrast stimuli resulting from the vector average model (the centroid, represented by the cross in Fig. 7) is higher than that for high-contrast stimuli. This is clearly opposite to the perceptual reports of our subjects.

Note that these results do not depend on the details of the assumptions in the model. The main, qualitative finding (a decrease in contrast leads to an increase in decoded speed) is found in all variants of the model that we investigated. This includes models that determined the population answer with a winner-take-all algorithm, models that used a nonlinear function to normalize the firing rate, and a model with a non-zero bias term (ε in Eq. 2). The reason that a non-zero bias term cannot save the model is quite simple. At low contrast, the tuning curves peak at approximately half of their high-contrast preferred speed (Fig. 6). In the vector average model with ε = 0, this causes an overestimate of the speed by a factor of ∼2. To undo this overestimate, ε would have to be at least 100% of the population activity (Σ_iR_i) at low contrast. At high contrast, the total population activity is higher by approximately a factor of 2 (Fig. 6); hence, the influence of ε is reduced somewhat, but, because ε is so large, it will nevertheless lead to underestimates of perceived speed whose magnitude (∼33%) is inconsistent with the perceptual data.

Also, the failure of the model does not depend on the assumptions about the contrast at which the “true” preferred speed (the label of the cell) is determined. If we had assumed that the label is determined at low contrast, then at higher contrast the cell would fire more for a stimulus faster than the label of the cell. That high speed would thus be interpreted as the (low) label. Hence, even when the label is determined at low contrast, an increase in contrast would lead to a decrease in decoded speed. The assumption that inevitably leads to a contradiction with the perceptual report is that cells always cast their vote for the same speed.

The ratio model

In psychophysical work, perceived speed is often equated with the ratio of the response of a fast (“flicker”) channel and a slow (“pattern”) channel. With appropriate parameter choices for the channels, this model can explain why low-contrast gratings look slower and even why high temporal frequency gratings with low contrast look faster (Thompson et al., 2006). To test whether a similar ratio model based on MT cells could explain the speed perception of random dot stimuli, we divided our sample of MT cells in two groups: those with low preferred speeds (<8°/s) and those with high preferred speeds (>8°/s). Figure 8A shows the total response of these two “channels,” normalized to their maximum at high contrast. The solid black line is the average normalized response of MT cells with high preferred speeds (the fast channel). The dotted black line is the response of the MT cells with low preferred speed at high contrast (the slow channel). The gray lines show the response of the same channels at 5% contrast. Both channels responded less by ∼50%. Additionally, however, both channels became more bandpass with peaks at lower speeds. This is of course a consequence of the fact that MT cells preferred lower speeds at lower contrast (Fig. 5) and matches the behavior of model channels (Perrone, 2005).

Figure 8.

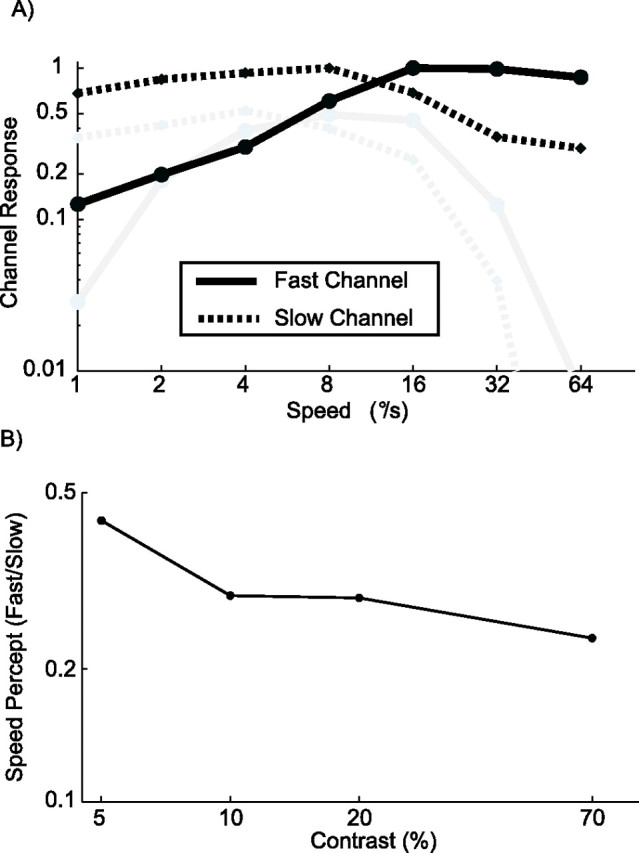
An MT-based ratio model of speed perception. The solid lines show the total normalized response of all cells with a preferred speed above 8°/s; they form the fast channel. The dotted lines show the total normalized response of all cells with a preferred speed less than or equal to 8°/s; they form the slow channel. The black lines show responses at 70% contrast, and gray lines are at 5% contrast. B, Predictions of the MT-based ratio model for the perceived speed of a stimulus moving at 4°/s. The ratio of the activity of the fast and slow channel is shown for four levels of contrast. The ratio model predicts that the perceived speed (ratio of fast/slow) decreases with an increase in contrast. Hence, the ratio model based on our sample of MT cells is inconsistent with our behavioral data on the contrast dependence of speed perception.

Using these channels, we next calculated perceived speed as the ratio of the fast and the slow channel. Figure 8B depicts this ratio (vertical axis) at four levels of contrast (horizontal axis), for a stimulus moving at 4°/s. The ratio model based on our MT population predicts that perceived speed decreases with an increase in contrast. Again, this is clearly inconsistent with the behavioral data of Figure 2. This inconsistency did not depend on the (arbitrary) threshold of 8°/s that we used to divide cells into the slow and fast channel: for every threshold speed we chose, the same qualitatively incorrect prediction was found (data not shown). Also, a similarly incorrect prediction was found for other stimulus speeds. As can be seen in Figure 8A, the ratio of fast/slow (the vertical signed distance between the solid and the dashed lines in this logarithmic plot) is almost always larger for the high-contrast black lines than the low-contrast gray lines. The only exception is the 1°/s stimulus whose perceived speed is correctly predicted to be slower at low contrast.

Discussion

We documented the regularity of the influence of stimulus contrast on neural responses in macaque MT. We measured speed tuning curves over a wide range of contrast and quantified how these curves changed. First, we found that peak firing rates increased with contrast. Second, we found that the preferred speeds of the cells also increased with contrast. Third, we found that, at low speeds, ∼30% of cells prefer low- to high-contrast random dots. We then used these data to test the labeled-line models of speed perception based on MT cells. All models predicted that many low-contrast stimuli should appear faster than high-contrast stimuli, in clear contradiction with the psychophysical literature as well as our own replication of those experiments in humans and monkeys. We conclude that the perception of speed is not based on fixed speed labels attached to MT cells.

Speed tuning and contrast

Priebe and Lisberger (2004) reported that a change in contrast did not lead to a change in preferred speed in MT. At first sight, this may appear contradictory with our findings. Priebe and Lisberger, however, used sine-wave gratings and thus measured the effect of contrast on speed tuning at a single spatial and temporal frequency at a time. These measurements showed that the response increases with grating contrast, but it does not change the preferred speed of the cells. This finding would contradict our data only if, first, the effect of contrast were the same at all spatial and temporal frequencies, and second, the responses of the MT cells to stimuli with multiple spatial frequencies were the linear sum of the responses to the spatial frequency components. The first assumption can be rejected from the data shown by Priebe and Lisberger (2004, their Fig. 6): the effect of contrast for a high spatial and temporal frequency stimulus is larger than for a low spatial and temporal frequency stimulus with the same speed. The second assumption would be observable as perfectly speed-tuned (and not spatiotemporal frequency-tuned) MT cells. Although MT cells are speed tuned to some extent (Perrone and Thiele, 2002), recent work shows that only a minority of MT neurons is speed tuned in the sense that preferred speed is independent of spatial frequencies (Priebe et al., 2003). Together, the interactions among speed preference, spatial frequency, and the contrast response predict an interaction between contrast and speed preference when the latter is measured with a broadband spatial frequency stimulus. We conclude therefore that our data are at least qualitatively compatible with those of Priebe and Lisberger (2004).

The neural code for speed

Although our data are consistent with those of Priebe and Lisberger (2004) and Pack and Born (2005), our conclusions about the neural code for speed are quite different. Priebe and Lisberger showed that the vector average model (with a bias term) could relate their neural data to speed perception. Pack and Born found the same shifts in preferred speed that we report but suggested that the vector average model could be saved by introducing a bias term. Our data, however, demonstrate that the model fails to capture the relationship between MT activity, perceived speed, and stimulus contrast.

In the Bayesian model of speed perception (Ascher and Grzywacz, 2000; Weiss et al., 2002), the reduction in perceived speed at low contrast is the result of an increasing reliance on the built-in “slow-and-smooth” prior when the stimulus-related evidence is weak because of the low signal strength at low contrast. Although this is an attractive explanation for the behavioral data, it is not clear how Bayesian priors and likelihoods can be mapped onto neural responses. Therefore, our data have no direct bearing on the Bayesian model. We note, however, that under the simplest mapping assumption, namely that the output of an MT cell represents the likelihood of its preferred stimulus (its label), the Bayesian model would make the same errors as any other labeled-line model. This shows that the influence of the prior, as assumed in the Bayesian model of speed perception, is not seen in MT responses.

The ratio model (Thompson, 1982; Perrone, 2005; Thompson et al., 2006) is a labeled-line model with two labels: fast and slow. These labels accrue votes proportional to the response of the fast and slow channel. The crucial difference with the vector average model is that the votes are not averaged, but a ratio is taken. Therefore, in this model, a reduction in perceived speed would be observed at low contrast if the response of the fast channel were reduced more than the slow channel response. With the channels defined by our population of MT cells, this is not the case: for almost all speeds, the fast channel is affected less by the contrast reduction (Fig. 8A). As a consequence, the model incorrectly predicts an increase in perceived speed with a reduction in contrast.

Finally, even if a single MT cell were a labeled line and responsible for all of the animal’s percept, a reduction in preferred speed with a reduction in contrast would result in an increase, not a decrease, in perceived speed. From this observation, it is clear that the discrepancy between perceptual data and predictions of the various labeled-line models is attributable to the fixed nature of the labels. The details of how the multiple labels are combined (be it by a simple average, a Bayesian average weighted by a prior, or by determining a ratio) have no great effect on this discrepancy. Hence, we interpret our data as evidence against the idea of a labeled line for speed in MT.

The popularity of the labeled-line MT model presumably stems from the successes of previous studies of speed perception (Churchland and Lisberger, 2001; Priebe and Lisberger, 2004) but also from the analogy with the successful MT model of direction perception, which have been confirmed quite convincingly with microstimulation evidence (Salzman et al., 1992). For speed perception, however, the literature is less unequivocal. The strongest evidence in favor of a labeled line for speed in MT was provided in a recent microstimulation study. Liu and Newsome (2005) reported that stimulation in a region with cells preferring high speeds led to an increase in perceived speed, whereas stimulation in an area with low-speed-preferring cells led to a decrease in perceived speed. This is at least consistent with the view that those cells “vote” for slow speeds. Previous studies, however, reported no correlation between the speed preference in a region of MT and the effect that microstimulation of that region has on pursuit (Groh et al., 1997; Born et al., 2000). This may in part be explained by the relatively weak clustering of speed preferences in MT (Liu and Newsome, 2003). We note, however, that another study (Komatsu and Wurtz, 1989) reported that microstimulation in MT always evoked an increase in pursuit speed. Moreover, that increase was proportional to the total injected current. This result would be unexpected if MT cells were labeled lines for speed because the current spread associated with a strong stimulation current should lead to equal stimulation of all preferred speeds and therefore have no effect on the behavior (Murasugi et al., 1993). Instead, the finding of Komatsu and Wurtz suggests that speed is proportional to the total activity in area MT. This, however, would only make sense if only a subset of cells (those whose firing rate increases monotonically with stimulus speed) are used for speed perception. Evidence supporting this view comes from a choice-probability study: Liu and Newsome (2005) showed that, on average, for a stimulus slower than their preferred speed, MT cells have a choice probability significantly larger than 0.5. When those same cells are confronted with stimuli above their preferred speed, however, the choice probability was significantly reduced and no longer distinguishable from chance (0.5).

There are four qualitatively different inferences one could draw from this discussion. First, one could argue that MT cells are not used for this type of speed discrimination. Given the evidence cited above, and the lesion studies in particular (Rudolph and Pasternak, 1999), this seems unlikely. The second inference is that different subpopulations of MT neurons are used for different tasks. Given the large fraction of cells for which preferred speed increases with contrast, we doubt, however, that a substantial subpopulation of MT could be found in which a labeled-line model would predict the perceptual data of Figure 2. The third possibility is that labels of MT cells change depending on contrast. Although it is not clear how or in which area this relabeling could be done, the required information (an estimate of current contrast and the contrast-dependent speed response) are clearly available in the visual system. The fourth possibility is that, although their speed tuning functions suggest that MT cells are labels for preferred speed, the brain does not use labels to relate MT activity to perceptual speed. The microstimulation (Komatsu and Wurtz, 1989) and choice probability (Liu and Newsome, 2005) data suggest to us that speed may instead be encoded by the total firing rate of (possibly a subset of) MT cells.