Summary
Two goals motivate treating diseases with drug combinations: reduce off-target toxicity by minimizing doses (synergistic potency), and improve outcomes by escalating effect (synergistic efficacy). Established drug synergy frameworks obscure such distinction, failing to harness the potential of modern chemical libraries. We therefore developed Multidimensional Synergy of Combinations (MuSyC), a formalism based on a generalized, multi-dimensional Hill-equation which decouples synergistic potency and efficacy. In mutant-EGFR driven lung cancer, MuSyC reveals that combining a mutant-EGFR inhibitor with inhibitors of other kinases may only result in synergistic potency, whereas synergistic efficacy can be achieved by co-targeting mutant-EGFR and epigenetic regulation or microtubule polymerization. In mutant-BRAF melanoma, MuSyC determines whether a molecular correlate of BRAFi insensitivity alters a BRAF inhibitors potency, efficacy, or both. These findings showcase MuSyC’s potential to transform the enterprise of drug-combination screens by precisely guiding translation of combinations towards dose reduction, improved efficacy, or both.
Graphical Abstract
eTOC Blurb:
Meyer CT et al. developed a framework for measuring drug combination synergy. The framework, termed MuSyC, distinguishes between two types of synergy. The first quantifies the change in the maximal effect with the combination (synergistic efficacy) and the second measures the change in a drug’s potency due to the combination (synergistic potency). By decoupling these two synergies conflated in prior methods, MuSyC rationally guides discovery and translation of drug combinations for the improvement of therapeutic efficacy and reduction of off target toxicities via dose reduction.
Introduction
Recent decades have witnessed an exponential expansion of available drugs for the treatment of disease (Gong et al., 2017). This expansion has been concomitant with an evolving understanding of disease complexity; complexity commonly necessitating combination therapy (He et al., 2016). However, clinical applications of combination therapy are often limited by tolerable dose ranges, and, therefore, it is desirable to identify combinations that enable dose reduction (Tallarida, 2011), i.e., synergistic potency. Additionally, combining drugs does not guarantee a priori an increase in efficacy over the single agents, and, therefore, it is desirable to identify combinations with effects greater than achievable with either drug alone (Foucquier and Guedj, 2015), i.e., synergistic efficacy. To assess a combination’s performance toward these goals, several drug synergy metrics have been proposed (Foucquier and Guedj, 2015). The roots of current synergy metrics can be traced back to either Loewe, who advanced the Dose Additivity Principle (Loewe, 1926) or Bliss who first described the Multiplicative Survival Principle (Bliss, 1939). Nearly a century later, methods to quantify drug synergy continue to appear (Chou et al., 1983; Yadav et al., 2015; Twarog et al., 2016; Zimmer et al., 2016; Schindler, 2017) based on these two principles. However, none of these methods distinguish between synergistic potency and synergistic efficacy. Instead, they either make no distinction or tacitly assume the only form of synergism is through potency.
Nevertheless, this distinction is essential to arrive at an unambiguous definition of synergy and properly rationalize the deployment of drug combinations, e.g. in personalized medicine. Indeed, conflating them may mislead drug combination discovery efforts. For instance, a search for improved efficacy based on traditional synergy frameworks may be confounded by an inability to sort out synergistically potent combinations.
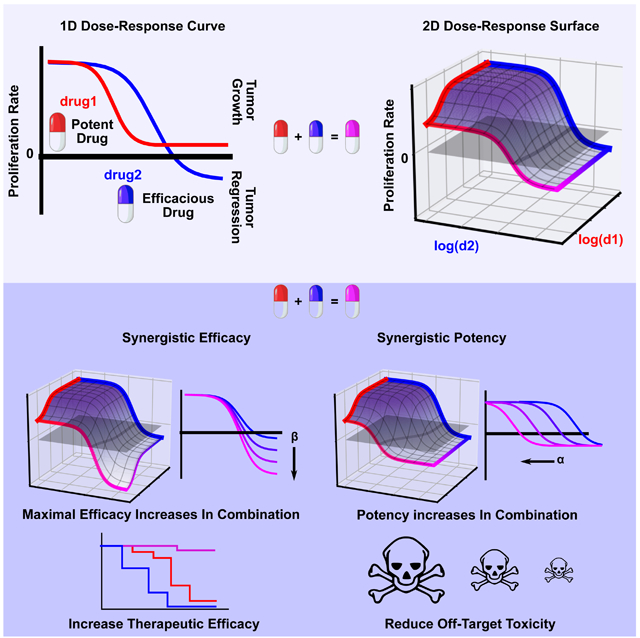
To address this critical shortcoming and resolve these two independent types of synergy, herein we propose a synergy framework termed Multi-dimensional Synergy of Combinations (MuSyC), which is based on a two-dimensional (2D) extension of the Hill equation derived from mass action kinetics. The 2D Hill equation extends dose-response curves to dose-response surfaces.
MuSyC distinguishes between synergistic potency and synergistic efficacy based on parameters in the 2D Hill equation. These synergy parameters are extensions of standard pharmacologic measures of potency and efficacy, and define a dose-response surface onto which changes in potency and efficacy are orthogonal. We visualize synergy of potency and efficacy on Drug Synergy Diagrams (DSDs) which globally stratify drug combinations along orthogonal axes of synergy facilitating comparisons between the synergistic profiles of many combinations.
To demonstrate the value of MuSyC, we investigate a panel of anti-cancer compounds in combination with a third-generation mutant-EGFR inhibitor, osimertinib, in EGFR-mutant non-small cell lung cancer (NSCLC). We find that drugs targeting epigenetic regulators or microtubule polymerization are synergistically efficacious with osimertinib. In contrast, drugs co-targeting kinases in the MAPK pathway affected potency, not efficacy of osimertinib. These conclusions have implications for drug combination deployment in NSCLC where increasing the efficacy of EGFR-inhibitors has historically relied on trial and error with no overarching principles to guide development (Schiffmann et al., 2016).
We also apply MuSyC to study the well-established, clinically-relevant combination targeting RAF and MEK in BRAF-mutant melanoma (Long et al., 2014).We find this combination to be synergistically efficacious, though in several cases at the cost of potency. We then identify NOX5 as a previously unsuspected molecular determinant of sensitivity to BRAF inhibition (BRAFi) in BRAF-mutant melanoma. Applying MuSyC, we find that NOX5 expression levels affect BRAF inhibition efficacy, but not potency.
In direct comparisons, we found that traditional synergy frameworks are biased and ambiguous even for the most synergistically efficacious of the NSCLC and melanoma combination studies, leading to misclassifications of combination synergy. We further show how MuSyC addresses and corrects these problems by generalizing the traditional models.
Results
2D Hill equation decouples synergy of efficacy from synergy of potency.
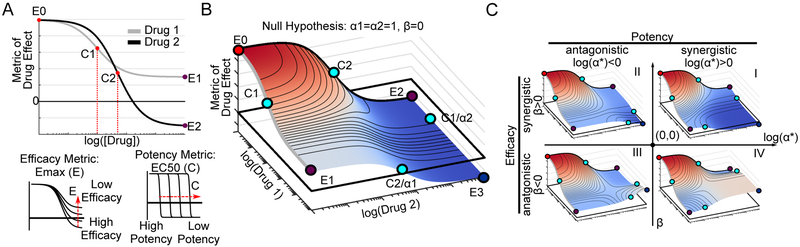
The dose-effect relationship of a single drug is traditionally quantified by the Hill equation, which contains parameters describing efficacy (Emax) and potency (EC50) of a dose-response curve (see STAR Methods section Methods Details for equation derivation and Table 1 for definitions) (Figure 1A). The Hill equation is derived from a phenomenological 2-state model of drug effect (Figure S1A). Therefore, to characterize the dose-effect relationship for drug combinations, we extended this model to a 4-state model (Figure S1B) to derive a 2D generalization of the Hill equation, using principles of mass action kinetics (see STAR Methods section Methods Details). The 2D Hill equation parameterizes a dose-response surface (Figure 1B, Table S1 for parameter descriptions) (Greco, Bravo and Parsons, 1995), a 2D extension of 1D dose-response curves (Figure 1A). In this equation, the changes in the efficacy and potency resulting from the combination are quantified by parameters for synergistic efficacy, denoted by β, and synergistic potency, denoted by α (Table S1). These parameters govern the shape of the dose-response surface and can capture complex patterns in experimental data.
Table 1:
Key Definitions
| Potency | The amount of drug required to produce a specified effect. A highly potent drug is active at low concentrations. Classically quantified as the required concentration to achieve half the maximal effect (EC50). |
| Efficacy | The degree to which a drug can produce a beneficial effect. Classically quantified as the maximal effect (Emax). |
| Synergistic Potency | The magnitude of the change in the drug potency, due to the presence of another drug. |
| Synergistic Efficacy | The percent change in the maximal efficacy of the combination compared to the most efficacious single agent. |
Figure 1: 2D Hill equation parameterizing dose-response surfaces distinguishes synergistic efficacy and synergistic potency.
A) Sigmoidal dose-response curves relating drug concentration to a measured effect are commonly fit to the Hill equation, derived from a 2-state model of drug effect (Figure S1A). The equation contains parameters for calculating a drug's potency, (C) equal to the concentration required for half-maximal effect, and efficacy (Emax), equal to the maximal effect. Here, Drug 1 is more potent than Drug 2 (C1<C2) while Drug 2 is more efficacious (E2<E1). For simplicity, in this diagram we only depict a metric of drug effect for which increasing drug concentration results in lower values (e.g., anti-proliferative drugs). However, the same equation is valid for metrics which increase in value (Emax>E0) (e.g. percent effect). B) A dose-response surface for Drugs 1 and 2, based on the 2D Hill equation derived from a 4-state model of combination drug treatment (Figure S1B), under the null hypothesis of no synergy of efficacy (β=0) or potency (α1=α2=1). C) Representative dose-response surfaces for each quadrant on a Drug Synergy Diagram (DSD). The vertical axis is divided into antagonistic (β<0) and synergistic (β>0) efficacy. The horizontal axis is divided into antagonistic (log(α*)<0) and synergistic (log(α*)>0) potency where α* can be either α1 or α2. Quadrant I corresponds to synergistic potency and efficacy. In contrast, combinations in quadrant IV have synergistic potency, but antagonistic efficacy corresponding to a blunting in efficacy at lower doses. See Supplemental Movie 1 a depiction of the orthogonal effects of α and β on the dose-response surface.
The parameter β is defined as the percent increase in a drug combination’s effect beyond the most efficacious single drug. For instance, in the case of synergistic efficacy (β>0), the effect at the maximum concentration of both drugs (E3) exceeds the maximum effect of either drug alone (E1, E2) (Figure 1C Quadrants I, II). For antagonistic efficacy (β<0) (Figure 1C Quadrants III, IV), at least one or both drugs are more efficacious as single agents than in combination. See Supplemental Movie 1 for an animated example of how the dose-response surface changes as a function of β.
The parameter α quantifies how the effective dose of one drug is altered by the presence of the other. In the case of synergistic potency (α>1), the EC50 (denoted C in Figure 1B) decreases due to the addition of the other drug (Figure 1C Quadrants I, IV) corresponding to an increase in potency. In the case of antagonistic potency (0≤α<1), the EC50 of the drug increases as a result of the other drug (Figure 1C Quadrants II, III) corresponding to a decrease in potency. See Supplemental Movie 1 for an animated example of how the dose-response surface changes as a function of α. Since each drug can modulate the effective dose of the other independently (Zimmer et al., 2016), the 2D Hill equation contains two α values (α1 and α2) (Figure S1B, bottom and right edges of surface). This separation of α values in the 2D Hill equation makes it possible for a given drug combination to have synergism of potency in one direction (α1>1), and antagonism of potency in the other (α2<1), or vice versa (see Figure S1C for example surfaces).
Both MuSyC parameters for synergy of efficacy (β) and synergy of potency (α) correspond to geometric transformations of the dose-response surface, analogous to the parameters for efficacy (Emax) and potency (EC50) that transform the single-drug dose-response curve in classic pharmacology. We surveyed eight synergy methods to understand how they might account for these distinct types of synergy, including traditional methods of Bliss, Loewe, and Highest Single Agent (HSA)(Gaddum, 1940), as well as more recent frameworks including Combination Index (CI)(Chou et al., 1983), Zimmer et al.’s Equivalent Dose Model (Zimmer et al., 2016), Schindler’s PDE-Hill Model (Schindler, 2017), ZIP (Yadav et al., 2015), and BRAID (Twarog et al., 2016). We find Bliss, Loewe, HSA, PDE-Hill, ZIP, and BRAID conflate synergy of efficacy and potency (Figure S2A-F), so that a drug combination with high synergistic potency scores identical to a combination with high synergistic efficacy (Figure S2A). This conflation, even in methods classically regarded as quantifying exclusively changes in efficacy, such as HSA, underscores the necessity of considering the entire topology of the dose-response surface in order to decouple synergistic efficacy from synergistic potency.
In other methods (Equivalent Dose and CI), only synergistic potency is tacitly assumed by asserting the maximal effect of each drug and of the combination is equal to zero (Figure S2G-J). (see STAR Methods section Methods Details subsection “Comparison to alternative synergy models” for a case-by-case comparison of MuSyC with other synergy frameworks.)
By using the Hill equation as the basis for MuSyC, the metric of drug effect is not bounded to range between 0 and 1, as is the case for Bliss, CI, and Equivalent Dose Model, providing a greater versatility for application to other systems. Indeed, the challenges in applying prior synergy frameworks to our recently proposed metric of drug effect, the drug-induced proliferation (DIP) rate (Harris et al., 2016), provided the initial impetus for developing this framework.
In summary, the 2D Hill equation enables a formalism, termed Multi-dimensional Synergy of Combinations (MuSyC), in which synergistic efficacy and synergistic potency are orthogonal and quantified by the parameters β and α, respectively. We have provided an interactive MuSyC demo (see STAR Methods, Data and Software Availability section) to facilitate an intuitive understanding of the relationship between different parameter values and shape of the dose-response surface.
MuSyC quantifies synergy of potency and efficacy in a drug combination screen.
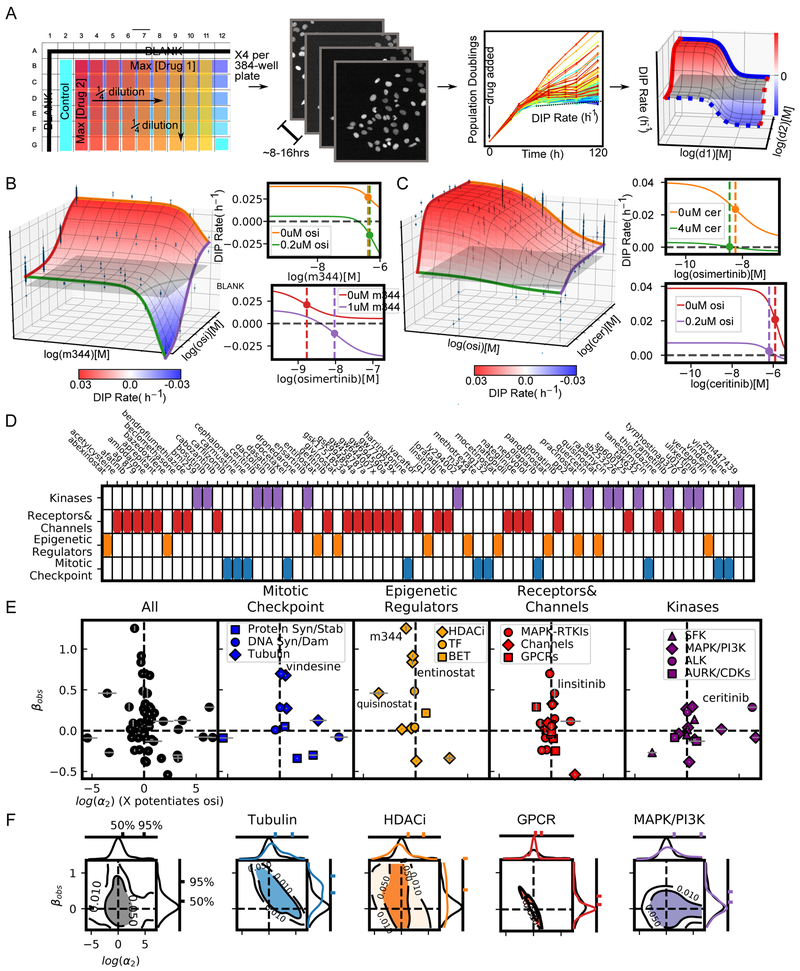
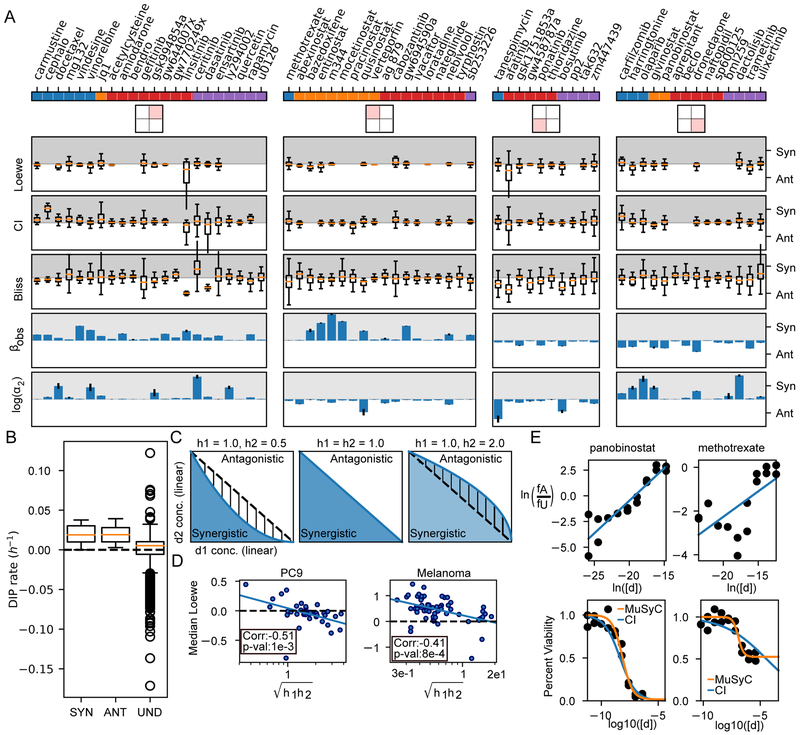
We applied MuSyC to evaluate the synergistic potency and efficacy of a 64 drug panel (See Table S2 for drugs, drug classes, nominal targets, and tested concentration ranges) in combination with osimertinib, a mutant EGFR-tyrosine kinase inhibitor recently approved for first-line treatment of EGFR-mutant NSCLC (Soria et al., 2018). The selected drugs span a diverse array of cellular targets that can be broadly grouped into four categories: kinases, receptors and channels, epigenetic regulators, and mitotic check-points (Figure 2D), each with several sub-categories. The combinations were tested in PC9 cells, a canonical model of EGFR-mutant NSCLC (Jia et al., 2013) using a high-throughput, in vitro, drug-screening assay (Figure 2A). We quantified drug effect using the DIP rate metric (Harris et al., 2016), a metric which avoids temporal biases characteristic of traditional endpoint assays (see STAR Methods section Quantification and Statistical Analysis).
Figure 2: High throughput screen of 64 drugs combined with osimertinib (mutant EGFR-TKI) reveals drug class dependence of synergistic potency and efficacy in NSCLC.
A) High-throughput pipeline for generating dose-response surfaces. Initial drug matrix is prepared on a 384-well plate and transferred to cells seeded at sub confluent densities. Cells are engineered to express a fluorescently tagged histone (H2B-RFP) allowing for cell counts using automated segmentation software (See STAR Methods section Quantification and Statistical Analysis). Each condition is imaged every 6-8 hours resulting in growth curves. The growth curves are fit for the DIP rate (slope of dotted line) (Harris et al., 2016) to quantify drug effect. This matrix of DIP Rates is fit to the 2D Hill equation to extract synergy parameters. B) Combination surface of M344, an HDACi, and osimertinib (osi). Grey plane indicates a cytostatic growth rate (i.e., DIP rate=0 h−1). Left are the dose-response curves for each drug alone (orange and red curves) and each drug with the maximum tested concentration of the other (green and purple). Colors correspond to the colored lines on the combination surface. The dotted lines demarcate the EC50 for each curve. C) Combination surface for ceritinib (cer), an ALK, in combination with osimertinib. Ceritinib increases the potency of osimertinib at maximum tested concentration, as observed in the shift of the EC50 between orange and green curves in the top left panel. The shift is proportional to the concentration used and would, therefore, increase at higher concentrations; however, such concentrations are not physiologically realizable due to the low potency of ceritinib in this system (EC50=2.02 uM) highlighting the importance of interpreting synergistic potency in the context of the absolute potency. D) Drug panel used in combination with osimertinib grouped in 4 categories (see Table S2 for details). E) DSDs for drug combinations. The vertical axis quantifies the observed synergistic efficacy, (βobs). The horizontal axis (log(α2)) quantifies how osimertinib's potency is modulated by each drug (see Figure S4C for α1- α2 plot). Error bars represent the parameter uncertainty based on the MCMC optimization (See STAR Methods for description of fitting algorithm). F) 2D density plots and associated marginal distributions for βobs (vertical axis) and α2 (horizontal axis) for all drugs (black) and selected category subclasses. Colored tick marks indicate the 50% and 95% probability density intervals for each distribution.
To fit the resulting dose-response surfaces, we developed a Bayesian fitting algorithm, using a Particle Swarm Optimizer (PSO) to seed priors for a Markov Chain Monte Carlo (MCMC) optimization (Figure S3A-B, STAR Methods section Quantification and Statistical Analysis). The algorithm also accounts for non-optimal drug dosage selection, since dose-ranges which are insufficient to observe saturating effects – due to limited solubility or potency of the drug – result in a commensurate increase in the uncertainty of MuSyC’s synergy parameters (Figure S3C-E).
Applying this algorithm, we extracted synergy parameters (α1, α2, and βobs) from fitted surfaces for all osimertinib combinations (βobs is the observed synergistic efficacy at the maximum tested dose range) (see STAR Methods section Methods Details).
As single agents, the drug panel displays wide ranges of efficacy (E2) and potency (C) (Figure S4A). The efficacy and potency of the single agents have no relationship with the synergistic efficacy and synergistic potency when combined with osimertinib (p-value>0.2) (Figure S4B) confirming MuSyC’s synergy parameters are independent of single-agents’ dose-response curve and therefore, as expected, cannot be predicted from the single-agent, pharmacologic profiles.
Inspection of dose-response surfaces from this combination screen, highlight the significance of resolving synergistic potency and efficacy. For instance, the dose-response surface for the osimertinib combination with M344 (a histone deacetylase (HDAC) inhibitor) exhibits synergistic efficacy (βobs=1.25±0.03, reflecting a 125% increase in efficacy over osimertinib alone) (Figure 2B,E). However, this improved efficacy comes at the cost of potency (log(α2)=−0.90±0.01) as observed in the shift in the EC50 of osimertinib in the presence of 1uM M344 (Figure 2B red to purple dotted line). In contrast, ceritinib, an ALK inhibitor with off-target effects on IGF1R (Shaw et al., 2014), increases osimertinib’s potency (log(α2)=6.25±0.50) (Figure 2C green to orange dotted line) at 4uM (maximal tested concentration), but with inconsequential improvement of efficacy (βobs=0.28±0.003)
To visualize synergy globally, we plotted drug combinations on DSDs, with observed synergistic efficacy (βobs) and potency on the vertical and horizontal axes, respectively (Figure 2E). These DSDs reveal distinguishing trends between the four drug categories tested.
Within the mitotic checkpoint drugs, tubulin destabilizers (including vindesine and vinorelbine) showed an upward shift along the axis of synergistic efficacy (Figure 2E). The marginal distribution confirmed this trend in comparison to all the drugs (Figure 2F, blue versus black vertical distributions). Similar results were obtained for the HDACi subgroup within the epigenetic regulators (Figure 2E, F). As expected, we observed limited synergistic/antagonistic efficacy for drugs targeting G-protein coupled receptors (GPCRs) (Figure 2E,F red versus black distributions). We also observed limited synergistic efficacy in directly co-targeting kinases in the MAPK pathway suggesting this may be an unproductive avenue in EGFR-mutant NSCLC (Figure 2E,F purple to black comparison along vertical axis).
In summary, by quantifying synergy of potency separate from synergy of efficacy, MuSyC reveals drug-class trends which can be used to guide subsequent screens and drug combination deployment in NSCLC.
MuSyC validates co-targeting RAF and MEK in BRAF-mutant melanoma.
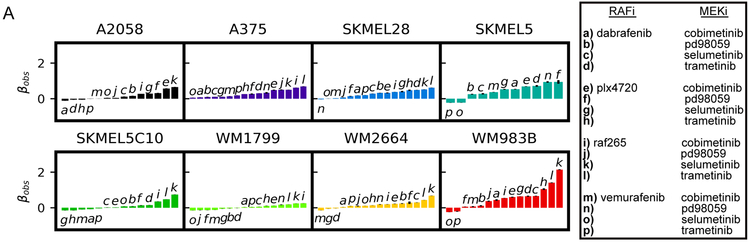
The NSCLC drug screen (Figure 2) suggests combinations targeting molecules within the same signaling pathway may not be productive avenues for increasing efficacy. However, a combination used clinically in BRAF-mutant melanoma co-targets kinases BRAF and MEK in the MAPK pathway (Long et al., 2014; Eroglu and Ribas, 2016). To investigate this combination in more detail, we screened a panel of 8 BRAFV600-mutant melanoma cell lines (See (Paudel et al., 2018) for cell-line information) against 16 BRAFi/MEKi combinations (see Table S2 for drug information and tested dose ranges).
Based on the mean βobs across cell-lines, all 16 combinations were synergistically efficacious (Figure 3A, Figure S5C) indicating MuSyC would have identified this treatment strategy prospectively. In contrast, conventional methods produce ambiguous results (Figure S6, top 3 panels in each cell line group), such that this combination strategy could have not been identified. Furthermore, MuSyC detected variations in synergistic efficacy between cell lines (Figure 3A, S5C), underscoring its sensitivity and pointing to heterogeneous, cell-intrinsic mechanisms modulating the efficacy of BRAF/MEK inhibition. In particular, A2058 displayed low average synergistic efficacy, suggesting that its canonical insensitivity to BRAFi does not depend on MEK reactivation, but rather on altered metabolic phenotype (Parmenter et al., 2014; Hardeman et al., 2017).
Figure 3: Synergistic efficacy and/or potency of drug combinations in BRAF-mutant melanoma.
A) 8 BRAF-mutant melanoma cell lines were treated with all possible pairwise combinations of 4 RAF and 4 MEK inhibitors (Table S2) for a total of 128 unique combinations. Waterfall plots of βobs for each cell line with all combinations which converged in fitting. Drug combinations noted by letter in the legend to right. (Also see Figure S5).
MuSyC also provides information on synergistic potency for these combinations. A clinically deployed combination (dabrafenib and trametinib) is synergistically efficacious, but antagonistically potent in all cell lines except one (Figure S5), a trade-off that may be relevant in the clinic.
Together, MuSyC analyses of NSCLC and of melanoma combination screens indicate the magnitude of a drug combination’s synergistic efficacy depends upon the oncogenetic context, i.e., co-targeting within the MAPK pathway may work for mutant-BRAF melanoma, not for mutant-EGFR NSCLC.
MuSyC reveals whether molecular correlates of insensitivity alter synergistic efficacy, or potency.
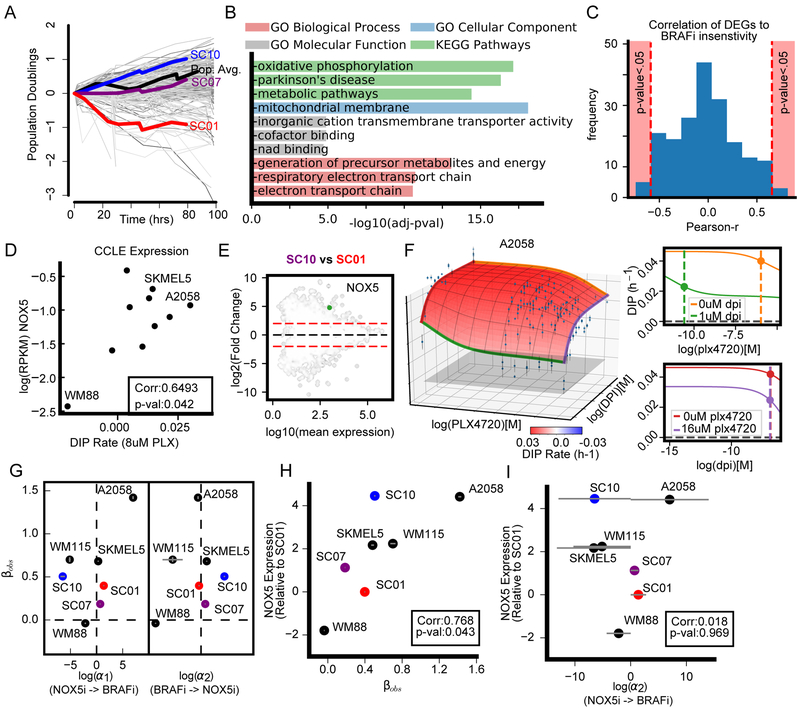
While drug combinations are commonly identified from top-down approaches, e.g., high throughput drug screens, others, including BRAFi/MEKi, were discovered from a bottom-up approach via investigating molecular correlates of insensitivity. However, these molecular correlates may alter either the potency or the efficacy of the primary drug (or both). MuSyC can distinguish among these possibilities, enabling an informed choice between improving either efficacy or potency. As an example, we looked for molecular correlates of BRAFi insensitivity between subclones of a BRAF-mutant melanoma cell line (SKMEL5) with differential sensitivity to BRAFi (Figure 4A). Specifically, we quantified gene expression using RNAseq and identified the top 200 differentially expressed genes (DEGs) (FDR<0.001, see STAR Methods section Quantification and Statistical Analysis). This gene set was significantly enriched in processes, cellular components, and molecular functions relating to metabolism (Figure 4B), aligning with previous reports on the relationship between altered metabolism and resistance to BRAFi (Parmenter et al., 2014; Hardeman et al., 2017). We computed the correlation of the 200 DEGs’ expression to BRAFi sensitivity across a 10 cell line panel (see STAR Methods) using expression data from (Subramanian et al., 2017). NADPH oxidase 5 (NOX5) stood out as one of five genes with a significant, positive correlation with BRAFi insensitivity (Pearson r=0.65, p-val=0.042) (Figure 4C-D, Table S3 for quantification of BRAFi insensitivity and Table S4 for genes correlated with BRAFi insensitivity) and was significantly up-regulated in the BRAFi insensitive subclone (SC10) compared with the sensitive subclone (SC01) (Figure 4E). Previously unconsidered, NOX5 is an interesting target due to its convergent regulation on metabolic and redox signaling at mitochondria (Lu et al., 2012), processes significantly enriched in the DEGs (Figure 4B).
Figure 4: NOX5, a molecular correlate of insensitivity to BRAFi, is a synergistically efficacious cotarget in BRAF-mutant melanoma.
A) Growth curves of differentially sensitive, single-cell-derived subclones from SKMEL5 treated with 8uM PLX4720. Grey curves represent colony growth according to the clonal fractional proliferation assay (Tyson et al., 2012). The average population response indicated in black curve. SC01, SC07, and SC10 were subsequently used to identify 200 DEGs. B) Top gene set enrichment terms for 200 DEGs (see STAR Methods section Quantification and Statistical Analysis). C) Distribution of the correlation between 200 DEGs expression and BRAFi insensitivity. Drug sensitivity was quantified as DIP rate measured in 8μM PLX4720 (Table S3). Significance threshold of p-value<0.05 annotated in pink. D) NOX5 expression correlates with BRAFi sensitivity in 10 BRAF-mutant melanoma cells. E) Pairwise comparison between SC01 and SC10 of DEGs (FDR<0.001) identified using DESeq2 (Love, Huber and Anders, 2014). The 200 identified DEGs (ANOVA between three subclones) are in black. Dotted red lines denote plus/minus 4-fold change. F) Dose-response surface for PLX4270+DPI (NOX5 inhibitor) in A2058. G) DSD for NOX5i (DPI) plus BRAFi (PLX4720). H) Correlation (Pearson r) of NOX5 expression with observed synergistic efficacy (βobs). I) Correlation (Pearson r) of NOX5 expression with synergistic potency (α2=DPI’s effect on PLX4720 potency).
To study NOX5’s contribution to the potency or efficacy of BRAF inhibition, we tested PLX4720 in combination with a NOX5 inhibitor, DPI (Jaquet et al., 2011), in a panel of 7 melanoma cell lines selected based on differential NOX5 expression. We found synergistic efficacy correlated with NOX5 expression (Pearson r=0.77, p-value=0.043) (Figure 4G-H); however, synergistic potency did not (Pearson r=0.01, p-value=0.96) (Figure 4G,I). Of note, A2058, well-known for its resistance to BRAFi exhibited the highest NOX5 expression among the cell lines and the highest synergistic efficacy (βobs=1.42±0.05) (Figure 4F) which was more synergistically efficacious than all tested MEKi/BRAFi combinations (Figure 3A).
Taken together, these results suggest co-targeting NOX5 in BRAF-mutant melanoma could lead to improved outcomes for BRAF-mutant melanoma patients with a unique metabolic program for which NOX5 is a biomarker. Furthermore, this study demonstrates the utility of MuSyC for distinguishing a molecular constituent’s role in modulating the potency or efficacy of a drug.
MuSyC generalizes traditional synergy metrics and removes biases and ambiguities.
To investigate how results from MuSyC compare with the most frequently used synergy metrics, we calculated synergy using Loewe additivity, Combination Index (CI), and Bliss on data from the NSCLC (Figure 2) and the melanoma (Figure 3A) screens. Loewe synergy was calculated directly from the DIP rate data, while CI and Bliss, which require percent metrics, were calculated from 72-hour percent viability (Barretina et al., 2012) imputed from the growth curves (see STAR Methods section Quantification and Statistical Analysis) . Unlike MuSyC, these metrics are evaluated at every concentration resulting in dose-dependent distributions of synergy (Figure 5A, S6) commonly resulting in ambiguous classification of a combination. By the median of each distribution, none of the metrics can statistically discriminate between the MuSyC DSD quadrants (Figure 5A, S6, Kruskal-Wallis p-value > 0.05).
Figure 5: Biases and limitations of Loewe, CI, and Bliss.
A) Drugs are separated based on their DSD quadrant from Figure 2, and distributions of synergy calculated by Loewe, CI, and Bliss are shown. Loewe was calculated directly from DIP rates, while CI and Bliss were calculated from 72-hour viability (See STAR Methods section Methods Details). Overall, most combinations span synergism and antagonism when quantified by Loewe, CI, or Bliss. Conditions for which synergy could not be defined were removed. Traditionally, Loewe and CI are synergistic between 0 and 1, and antagonistic for values >1; however, for visualization, we transformed them to −log(Loewe) and −log(CI), so synergism (Syn) corresponds to positive numbers (grey region), antagonism (Ant) to negative (white region). α2 is the change in osimertinib’s potency due to the other drug. Error bars for βobs and log(α2) calculated from MCMC optimization. B) Loewe is undefined (Und) for all concentrations which achieved a net negative DIP rate. C) Loewe and CI assume the dose-response surface contours (i.e., the DIP rate axis comes out of the page) are linear (middle panel). The blue and white areas indicate regions which are synergistic and antagonistic respectively by MuSyC. When (left panel), Loewe and CI misclassify the hatched region as synergistic, while when (right panel), they misclassify the hatched region as antagonistic. D) As predicted, the median values of synergy calculated by Loewe are anti-correlated with the geometric mean of the hill slope in both the NSCLC and BRAF-mutant melanoma datasets. E) CI poorly fits drugs whose max effect is not equal to 0. The top panel shows linear dose-response fit by the CI algorithm, bottom shows the quality of fit in a standard dose-response view. The CI fit works well for drugs for which Emax ~= 0, like panobinostat (left, Emax=0.016, C=7.13 nM, h2=0.99 for orange fit, Emax=0, C=4.42 nM, h2=0.63 by CI). However, drugs with Emax >> 0, like methotrexate (right) lead to poor fits (Emax=0.52, C=0.119 uM, h2=1.88 by orange fit, Emax=0, C=34.7 uM, h2=0.23 by CI).
Examining the models underlying these metrics revealed several limitations and biases accounting for their ambiguity. For Loewe additivity, synergy is undefinable for many tested concentrations as Loewe cannot be calculated at combination conditions with effects exceeding the maximum effect of the weaker drug (Foucquier and Guedj, 2015). This is particularly limiting for synergistically efficacious combinations, which, by definition, achieve greater effect than either drug alone. In the NSCLC screen, because osimertinib alone was not sufficient to achieve a negative DIP rate (i.e., regressing population), Loewe is undefinable for all conditions where DIP rate was less than zero (Figure 5B). For conditions where Loewe is defined, Loewe additivity has been reported to be most appropriate for combinations of mutually exclusive inhibitors (Chou and Talalay, 1984). Accordingly, we found Loewe emerges from MuSyC as a special case under the conditions of both α1=α2=0 (i.e., the drugs are mutually exclusive) and h1=h2= 1 (see STAR Methods section Methods Details subsection 2.1). If the condition h1=h2=1 is not satisfied (Figure 5C), MuSyC predicts that when the geometric mean of the hill slopes is less than one (), the linear model of Loewe will overestimate synergy and when , Loewe will underestimate synergy (Figure 5C). Correspondingly, we found the median value of Loewe synergy was negatively correlated with the geometric mean of the hill coefficients in both the NSCLC and melanoma screens (Figure 5D, spearman r= −0.51 and −0.41, p-value=1e-3 and 8e-4 respectively). That is, the synergy of a combination according to Loewe additivity could be estimated based on the hill slope of a single drug alone in contrast to MuSyC where synergistic potency and efficacy are decoupled from the single drug's pharmacologic profile (Figure S3B).
CI is a special case of Loewe additivity which adds the additional condition that E0=1, E1=E2=E3=0, such that the drug effect is equated with percent inhibition (Chou et al., 1983). The condition on effect range assumes all drugs achieve the same maximum effect, and thus, unlike Loewe additivity, CI range is not limited by the weaker drug. However, in percent viability data, many drugs do not achieve 0% viability (e.g., methotrexate, which reaches a maximum effect of 52% viability)(Figure 5E). In these cases, fits for the single-drug dose-response curves used to calculate CI are poor (Figure 5E). CI is thus inappropriate for cell-based assays of drug effect where the correspondence between percent inhibition and cell viability is not one-to-one.
Bliss, like CI, can only be applied to percent metrics with the condition E0=1, E1=E2=E3=0. As with CI, because most drugs in combination do not satisfy this condition, Bliss is also an inappropriate model to use. However, if this condition is satisfied, Bliss emerges as a special case of MuSyC under the conditions α1=α2=1 (see STAR Methods section Methods Details subsection 2.2)
In summary, MuSyC subsumes Loewe (and therefore CI) and Bliss into a single framework satisfying both the Dose Additivity and the Multiplicative Survival Principles under certain conditions. For combinations that do not satisfy these conditions, we show the traditional metrics lead to biased and ambiguous results, while MuSyC’s generality resolves these limitations. Specifically these limitations are: traditional methods cannot distinguish synergy of potency from synergy of efficacy (Figure 5A,S2); Loewe is undefined for combinations with synergistic efficacy (Figure 5B); Loewe (and by extension CI) contain an artificial bias toward synergy for drugs with hill slopes much less than one (Figure 5C,D); and, CI leads to poor fits because it disregards synergistic efficacy by assuming that maximal effect of a drug reaches 0%, even when this is not the case (Figure 5E).
Discussion
The goal of using synergistic drugs is to achieve more with less. It is therefore intuitive that two types of synergy exist: one corresponding to how much more is achievable (synergistic efficacy), the other to how much less is required (synergistic potency). Finding such combinations is vital for optimizing therapeutic windows, as there exists a fundamental trade-off between clinical efficacy and tolerable doses. Diseases for which singledrug efficacy is sufficient would benefit from synergistically potent combinations to drive down toxicity and/or side effects. Diseases with treatments of insufficient efficacy are in pressing need of synergistically efficacious combinations in order to improve depth and durability of response. By stratifying synergy along distinct axes of potency and efficacy using MuSyC, informed choices can be made about this trade-off. The distinction facilitates identifying drug-class trends that can be iteratively expanded in future screens to optimize synergistic efficacy or synergistic potency, whichever is desirable for a particular disease.
In this respect, MuSyC provides a global view of the synergistic behavior of whole classes of drugs, e.g., from a high-throughput drug screen, via DSDs. In this work, MuSyC revealed a subclass of epigenetic regulators as potentially interesting targets for combination therapy in an EGFR-oncogene addicted background. Epigenetic regulators have previously been suggested to prime NSCLC for sensitivity to EGFRi (Schiffmann et al., 2016) and the HDACi entinostat in combination with erlotinib (first generation EGFR-TKI) has been shown to increase overall survival in EGFR-mutant, NSCLC cases with high expression of E-cadherin (Witta et al., 2006, 2012). Consistent with this, we also observe entinostat was synergistically efficacious with osimertinib (βobs=0.84±0.027) in PC9 cells, an E-cadherin high expressing cell line (Shimoyama et al., 1992). As is typical of high-throughput screens, there were results of undetermined significance, including dronedarone (an anti-arrhythmic sodium channel inhibitor) and GW694590a (an antiangiogenesis compound targeting the TIE2 receptor) which were the most antagonistic and synergistically efficacious compounds out of the Receptors and Channels drug class respectively. Further studies are needed to verify these results. Nonetheless, MuSyC provides a quantitative foundation to further investigate unsuspected combinations.
The global views provided by the MuSyC DSDs also reveal synergistic trends that vary according to disease context. For example, co-targeting the MAPK pathway in NSCLC or BRAF-mutant melanoma yields different outcomes: in the former, only synergistic potency is observed, while in the latter synergistic efficacy, and sometimes potency, is registered. The disparity emphasizes that synergistic trends require data-driven metrics that distinguish between synergy of efficacy and potency.
MuSyC dose-response surfaces facilitate evaluating the significance that combination synergy should be assigned. That is, MuSyC’s synergy parameters quantify the relative increase in efficacy or potency of the combination, with respect to single agents, and therefore the improvements should be interpreted in the context of the absolute potency and efficacy. This information is directly conveyed in the topology of the dose-response surface. As an example, in the NSCLC screen, the combination of osimertinib with quisinostat exhibited the greatest total efficacy. However, since quisinostat is already significantly efficacious on its own, that combination ranks lower than the M344-osimertinib combination along the axis of synergistic efficacy on a DSD. Thus, DSDs are useful to rank relative increase in potency or efficacy, whereas surfaces convey the absolute efficacy and potency achieved by a combination.
MuSyC is also useful for investigating a molecular species’ contribution to the potency and efficacy of a compound. Here we demonstrated NOX5 activity modulates the efficacy, but not the potency, of BRAFi. However, the NOX5i used, DPI, is known to have off-target effects (AltenhÖfer et al., 2015); therefore, further evidence for the role of NOX5 in BRAFi efficacy will require extending MuSyC to studies combining drugs and gene silencing technology (e.g., RNAi or CRISPR).
To fit the dose response surface and extract synergy parameters, MuSyC utilizes a Bayesian approach combining PSO and a multi-tier MCMC walk in order to track uncertainty in the values for synergistic potency and efficacy. The sources for this uncertainty include noise, partial dose-response curves, and data density. A similar Bayesian approach was previously implemented for Loewe (Hennessey et al., 2010).
Loewe additivity and Bliss independence have maintained dominance in the field, along with the related work of Chou and Talalay. Yet there is no consensus regarding the appropriate use of these methods because they are based on distinct foundational principles, often leading to incompatible results (Greco et al., 1992). MuSyC removes these sources of confusion by unifying these methods into a consensus framework, within which Loewe and Bliss emerge as special cases.
There has been much critical analysis over the past twenty-five years on the term ‘synergy’ (Greco et al., 1992), arguably rooted in the practice of defining synergy with respect to arbitrary expectations of drug additivity implicitly codified in previous methods’ foundational principles. In contrast, ambiguity about the meaning of ‘synergy’ disappears in MuSyC, because its synergy parameters relate directly to the textbook pharmacology concepts of efficacy and potency. Indeed, a major advance of MuSyC is the decisive shift toward synergy calculations directly related to an observable change in efficacy and/or potency. Thus, ambiguous questions, such as “Is there synergy?” can be recast into more precise questions, such as “How much does efficacy/potency of drug X change when drug Y is added?” Such precise language should promote a move away from arbitrary cut-offs for “significant synergy” which are context dependent.
While we focused on the DIP rate as our metric of effect, MuSyC may be applied to any quantifiable phenotype whose dose-response is suitable to be fit by a Hill equation. In contrast, all other synergy models we surveyed impose strict constraints on the type and/or magnitude of the drug effect metric. Thus, MuSyC opens up the potential to study synergy of drug effects previously impossible to address by existing methods. Examples of metrics include immune activation, growth in 3 dimensional culture, or second messenger efflux. The flexibility is particularly critical in translating drug combinations to the clinic by using models of increasing complexity, such as organoids, which better represent drug sensitivity of a patient (Jabs et al., 2017). Indeed, that most clinical combinations can be explain by patient-to-patient variability (Palmer and Sorger, 2017) is strong rationale for translating combination screens to more complex, pre-clinical models. Subsequent work will be devoted to scaling the combination drug screening pipeline developed here to pre-clinical experimental models of increasing complexity, such as organoids.
In conclusion, we have presented MuSyC, a drug synergy framework that maintains a distinction between two intuitive types of pharmacological synergy and that may be applied to any drug effect metric. We showed this framework allows for a richer understanding of drug interactions, with practical, translational consequences. We foresee this approach will streamline drug discovery pipelines and facilitate the deployment of precision approaches to therapeutic combinations.
STAR Methods
CONTACT FOR REAGENT AND RESOURCE SHARING
Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Vito Quaranta (vito.quaranta@vanderbilt.ed)
EXPERIMENTAL MODEL AND SUBJECT DETAILS
PC9 (previously PC-14, gender unknown) cells were obtained from W. Pao (U Penn.) and were cultured in RPMI 1640 medium containing 10% FBS at 37C and 5% CO2. Cells were engineered to express histone 2B-mRFP via lenti-viral transfection using the pHIV-H2B-mRFP plasmid (Welm et al., 2008) as previously described (Tyson et al., 2012). A single-cell derived clonal population demonstrated to exhibit proliferation characteristic of the parental population was then selected by limiting dilution. BRAFV600-mutant melanoma lines cells (A2058 (M), WM1799 (U), A375 (F), WM983B (M), SKMEL5 (F), SKMEL28 (M), WM2664 (F), M=Male, F=Female, U=Unknown) were obtained from ATCC or M. Herlyn (Wistar Institute)(see Key Resources Table) and were cultured in DMEM media containing 2 mM glutamine, 4.5 g/L glucose, 10% FBS and no sodium pyruvate (catalog 11965-092) as previously described (Hardeman et al., 2017). SKMEL5.SC10, SKMEL5.SC07, and SKMEL5.SC01 are single cell-derived subclones from SKMEL5 (Paudel et al., 2018). Cell lines were tested for mycoplasma before each experiment.
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Antibodies | ||
| Bacterial and Virus Strains | ||
| Biological Samples | ||
| Chemicals, Peptides, and Recombinant Proteins | ||
| Trizol | Invitrogen | 15596026 |
| DMSO | Sigma | D8418 |
| FBS | Gibco | 10437-028 |
| PBS | Corning | 21-040-CV |
| DMEM | Gibco | 11965-092 |
| RPMI | Corning | 10-040-CV |
| TryplE | Gibco | 12604-013 |
| DMEM/F12 | Gibco | 11330-032 |
| SytoxGreen | ThermoFisher | S7020 |
| 5-Iodotubericidin | ENZO | EI-293 |
| Abexinostat (PCI-24781) | SelleckChem | S1090 |
| Acetylcysteine | SelleckChem | S1623 |
| Afatinib (BIBW2992) | LC Laboratories | A8644 |
| AG-879 | ENZO | EI-258 |
| Alisertib (MLN8237) | MedChemExpress | HY-10971 |
| Amiodarone HCl | SelleckChem | S1979 |
| Aprepitant | SelleckChem | S1189 |
| Bazedoxifene HCl | SelleckChem | S2128 |
| Beclomethasone dipropionate | Light Biologicals (NIH Clinical Collection II) | MZ-3012 |
| Bendroflumethiazide | Light Biologicals (NIH Clinical Collection II) | B-8008 |
| BML-259 | ENZO | EI-344 |
| Bosutinib (SKI-606) | LC Laboratories | B-1788 |
| Brigatinib (AP26113) | SelleckChem | S8229 |
| Buparlisib (BKM120, NVP-BKM120) | SelleckChem | S2247 |
| Cabozantinib | LC Laboratories | C-8901 |
| Carfilzomib | LC Laboratories | C-3022 |
| Carmustine | NCI Chemotherapeutic Agents Repository | 409962 |
| Cephalomannine | SelleckChem | S2408 |
| Ceritinib (LDK378) | SelleckChem | S7083 |
| Cisplatin | Sigma | 470306 |
| Cobimetinib | MedChemExpress | HY-13064 |
| Crizotinib | LC Laboratories | C-7900 |
| Dabrafenib | LC Laboratories | D-5678 |
| Dactolisib | LC Laboratories | N-4288 |
| Dasatinib | LC Laboratories | D-3307 |
| Docetaxel | SelleckChem | S1148 |
| Dronedarone HCl (Multaq) | SelleckChem | S2114 |
| Ensartinib (X-396) | SelleckChem | S8230 |
| Entinostat (MS-275) | SelleckChem | S1053 |
| Erlotinib | LC Laboratories | E-4007 |
| Everolimus (RAD001) | LC Laboratories | E-4040 |
| Foretinib (GSK1363089) | SelleckChem | S1111 |
| Gefitinib (ZD1839) | LC Laboratories | G-4408 |
| Givinostat (ITF2357) | SelleckChem | S2170 |
| GSK1751853A | GSK PKIS | N/A |
| GSK994854A | GSK PKIS | N/A |
| GW458787A | GSK PKIS | N/A |
| GW644007X | GSK PKIS | N/A |
| GW694590A | GSK PKIS | N/A |
| GW770249X (GW770249A) | GSK PKIS | N/A |
| Homoharringtonine (Omacetaxine mepesuccinate) | Sequoia Research Products Ltd. (NIH Clinical Collection II) | SRP02125h |
| Ivacaftor (VX-770) | SelleckChem | S1144 |
| (+)-JQ1 | SelleckChem | S7110 |
| Linsitinib (OSI-906) | SelleckChem | S1091 |
| Loratadine | SelleckChem | S1358 |
| LY294002 | ENZO | ST-420 |
| M344 | SelleckChem | S2779 |
| Methotrexate | MedChemExpress | OL-14377 |
| MG-132 | SelleckChem | S2619 |
| ML-9-HCl | ENZO | EI-153 |
| Mocetinostat (MGCD0103) | SelleckChem | S1122 |
| Naftopidil | SelleckChem | S2126 |
| Nateglinide | SelleckChem | S2489 |
| Nebivolol HCl | SelleckChem | S1549 |
| Olaparib (AZD2281, Ku-0059436) | LC Laboratories | O-9201 |
| Osimertinib (AZD9291) | SelleckChem | S7297 |
| Paclitaxel | Sigma | 17191 |
| Panobinostat | NCI Chemotherapeutic Agents Repository | 761190 |
| 2'-Amino-3'-methoxyflavone | LC Laboratories | P-4313 |
| Pimobendan | SelleckChem | S1550 |
| PLX-4720 | SelleckChem | S1152 |
| Ponatinib (AP24534) | LC Laboratories | P-7022 |
| PP2 | ENZO | EI-297 |
| Pracinostat (SB939) | SelleckChem | S1515 |
| Primaquine Diphosphate | SelleckChem | S4237 |
| Quercetin | ENZO | AC-1142 |
| Quisinostat (JNJ-26481585) | SelleckChem | S1096 |
| RAF-265 | MedChemExpress | HY-10248 |
| Rapamycin (Sirolimus) | SelleckChem | S1039 |
| SB-253226 | GSK PKIS | N/A |
| Selumetinib (AZD-6244) | LC Laboratories | S-4490 |
| SP 600125 | ENZO | EI-305 |
| Sunitinib Malate | SelleckChem | S1042 |
| TAK-632 | SelleckChem | S7291 |
| Tanespimycin (17-AAG) | SelleckChem | S1141 |
| Thioridazine hydrochloride | SelleckChem | S5563 |
| Trametinib | LC Laboratories | T8123 |
| AG-370 | ENZO | EI-229 |
| U-0126 | ENZO | EI-282 |
| Ulixertinib (BVD-523, VRT752271) | SelleckChem | S7854 |
| Vemurafenib (PLX4032) | SelleckChem | S1267 |
| Verteporfin | SelleckChem | S1787 |
| Vindesine | Sequoia Research Products Ltd. (NIH Clinical Collection) | SRP01038v |
| Vinorelbine Tartrate | SelleckChem | S4269 |
| ZM 447439 | SelleckChem | S1103 |
| Critical Commercial Assays | ||
| Tru-Seq stranded mRNA sample prep kit | Illumina | Cat # RS-122-2101 |
| Reverse Transcription Kit | QuantiTect | Cat # 205311 |
| IQTM SYBR Green Supermix | BioRad | Cat # 170 |
| Deposited Data | ||
| Fitted combination surface plots | This Paper |
https://github.com/QuLab-VU/MuSyC_Cell.git
In folder(s): Code_Paper_Figures/Fig2(3)/html |
| Code for Generating Paper Plots | This Paper |
https://github.com/QuLab-VU/MuSyC_Cell.git
In folder(s): Code_Paper_Figures/ |
| Table of fitted parameters for all experiments | This Paper |
https://github.com/QuLab-VU/MuSyC_Cell.git
In folder: Data Files: MasterResults.csv & MasterResults_plx_dpi_melPanel |
| RT-qPCR quantification of NOX5 expression | This Paper |
https://github.com/QuLab-VU/MuSyC_Cell.git
In file: Data/nox5Expr.csv |
| DIP Rate Calculations | This Paper |
https://github.com/QuLab-VU/MuSyC_Cell.git
In folder(s): Data Files: −HTS018_rates −HTS022_timeavg_rates_sub2.csv −03-27-2018-dpi+plx-cm_bp_timeavg_preCalcDIP_timSub.csv −dasatinib_osimertinib_cellavista_cm_8-24-17.csv −linsitinib_osimertinib_cellavista_cm_8-24-17.csv −HTS015_017_Combined.csv |
| cFP Raw Data | This Paper |
https://github.com/QuLab-VU/MuSyC_Cell.git
In folder(s): Data/SKMEL5_cFP |
| List of DEGS | This Paper |
https://github.com/QuLab-VU/MuSyC_Cell.git
In folder(s): Data/DEGs_GO_Analysis |
| Raw RNAseq data for subclones | GEO | GSE122041 |
| This data is also available from Mendeley Data at the following doi | This Paper | doi:10.17632/n8bp8db5ff.1 |
| Experimental Models: Cell Lines | ||
| PC9-H2B.RFP | Tyson et. al. 2012 (W. Pao at UPenn) | N/A |
| SKMEL5-H2B.RFP | Paudel et al. 2018 (ATCC) | HTB-70 |
| WM1799-H2B.RFP | Paudel et al. 2018 (M. Herlyn at Wistar Institute) | N/A |
| WM983B-H2B.RFP | Paudel et al. 2018 (M. Herlyn at Wistar Institute) | N/A |
| A375-H2B.RFP-FUCCI | Paudel et al. 2018 (ATCC) | CRL-1619 |
| SKMEL28-H2B.RFP-FUCCI | Paudel et al. 2018 (ATCC) | HTB-72 |
| WM2664-H2B.RFP | Paudel et al. 2018 (M. Herlyn at Wistar Institute) | N/A |
| A2058-H2B.RFP | Paudel et al. 2018 (ATCC) | CRL-11147 |
| SKMEL5.SC10-H2B.RFP | Paudel et al. 2018 Derived Subclone from SKMEL5-H2B.RFP | N/A |
| SKMEL5.SC07-H2B.RFP | Paudel et al. 2018 Derived Subclone from SKMEL5-H2B.RFP | N/A |
| SKMEL5.SC01-H2B.RFP | Paudel et al. 2018 Derived Subclone from SKMEL5-H2B.RFP | N/A |
| Experimental Models: Organisms/Strains | ||
| Oligonucleotides | ||
| NOX5_Forward Primer: GGCTCAAGTCCTACCACTGGA |
This paper | N/A |
| NOX5_Reverse Primer: GAACCGTGTACCCAGCCAAT |
This paper | N/A |
| HPRT_Forward Primer: TGCTCGAGATGTGATGAAGGAG |
This paper | N/A |
| HPRT_Reverse Primer: TGATGTAATCCAGCAGGTCAGC |
This paper | N/A |
| 36B4_Forward Primer: CATGTTGCTGGCCAATAAGG |
This paper | N/A |
| 36B4_Reverse Primer: TGGTGATACCTAAAGCCTGGAA |
This paper | N/A |
| PGC1a_Forward Primer: TGCCCTGGATTGTTGACATGA |
This paper | N/A |
| PGC1a_Reverse Primer: TTTGTCAGGCTGGGGGTAGG |
This paper | N/A |
| Recombinant DNA | ||
| pHIV-H2B-mRFP | Addgene, Welm et al Cell Stem Cell. 2008 | Plasmid #:18982 |
| Software and Algorithms | ||
| Scikit-learn | van der Walt et al. 2014 | N/A |
| RabbitMQ/Celery | www.celeryproject.org | N/A |
| GNU parallel | Tange, 2011 | N/A |
| Scipy | Jones, Oliphant and Peterson, 2001 | N/A |
| Matplotlib | Hunter, 2007 | N/A |
| Pandas | McKinney, 2010 | N/A |
| Numpy | Oliphant, 2006 | N/A |
| Pymc3 | Salvatier, Wiecki and Fonnesbeck, 2016 | N/A |
| HISAT2 | Kim, Langmead and Salzberg, 2015 | N/A |
| featureCounts | Liao, Smyth and Shi, 2014 | N/A |
| Bioconductor (R) | www.bioconductor.org | N/A |
| ENRICHR (R) | Kuleshov et al., 2016 | N/A |
| DESeq2 | Love, Huber and Anders, 2014. | N/A |
| Other | ||
METHODS DETAILS
Key Equations
For full derivation of these equations, see subsection 4 Derivation of generalized 2-dimensional hill equation. This section is meant to serve as a quick reference guide for the main equations used in the paper.
If the behavior of the drugs in the model formulation of Figure S1B obey detailed balance, then the effect of the combination (i.e., the height of combination surface) is described by
| (1) |
where Ed represents the expected effect for a given dose pair d1, d2 and is specified with 9 parameters defined in Table S1. In addition, detailed balance enforces the constraint that
| (2) |
α is a unitless scalar transforming dose d into an effective dose a ⋅ d and is used to quantify synergistic potency in MuSyC.
Synergistic efficacy (β) is calculated from E0, E1, E2, E3. β is defined in equation 3 and is interpreted as the percent increase in maximal efficacy of the combination over the most efficacious single agent. The observed β at the maximum of tested concentrations is defined in eq. 4.
| (3) |
| (4) |
Equation 1 can be re-written to include β explicitly by replacing E3 with min(E1, E2) – β * (E0 − min(E1, E2) resulting in the following equation.
| (5) |
For drugs that do not follow detailed balance, we have derived a more general formulation with 12 parameters:
| (6) |
where again E3 can be replaced to include β explicitly.
Because we do not know a priori whether combinations will follow detailed balance, we use an information theoretic approach to pick the best model for the data. We have defined six tiers of model complexity, and the best model is selected based on minimizing the deviance information criterion. (See section Quantification and Statistical Analysis, subsection 1 Fitting Dose-response Surfaces for description of fitting algorithm and Table S5 for description of model tiers).
Comparison to alternative synergy models
Several other methods for calculating synergy exist, including long-standing traditional methods Loewe (Loewe, 1926, 1927) , Bliss (Bliss, 1939), HSA (Gaddum, 1940; Greco, Bravo and Parsons, 1995), and CI (Chou and Talalay, 1984), as well as more recent methods such as ZIP (Yadav et al., 2015), BRAID (Twarog et al., 2016), the effective dose model (Zimmer et al., 2016), and Schindler’s Hill-PDE model (Schindler, 2017). All of these methods, as well as our own, define a null surface. Combinations with effects greater than or less than expected based on the null surface are deemed synergistic or antagonistic respectively. These methods broadly use one of two approaches to quantify synergy. Loewe, Bliss, CI, HSA, Schindler’s Hill-PDE, and ZIP quantify synergy at every concentration based on how the experimentally measured response deviates from the null surface. BRAID, the effective dose model, and MuSyC provide equations with synergy parameters describing the entire surface which is fit to experimental data using non-linear curve-fitting techniques.
Here, we briefly compare our model to each of these others and show that our model (1) describes distinct combination surfaces, (2) results in synergy parameters which are straight forward to interpret, (3) is not restricted to a special class of effects with bounded scales, and (4) reduces to many of these other approaches in special cases thereby unifying and generalizing seemingly disparate synergy principles.
The Dose Equivalence Principle: Loewe and CI
The first prevalent foundational principle, established by Loewe (Loewe, 1926) and subsequently expanded on by CI (Chou and Talalay, 1984), is the Dose Equivalence Principle. This principle states that for a given effect magnitude E achieved by dose x of drug X alone or dose y of drug Y alone, there exists a constant ratio such that using Δx less of drug X can always be compensated for by using Δy = RΔx more of drug Y. Therefore, the null surface is only defined for combinations whose magnitude of effect is less than the weaker drug’s maximal effect. This is because for combination effects greather than the effect of the weakest drug, no amount of the weaker drug can compensate for reducing the dose of the stronger drug.
The resulting null surfaces have linear isoboles. Our model recovers this under the constraint that the two drugs are maximally antagonistic. This can be seen by setting α 0, and reducing eq. 6 to
By this it is easy to see when h1 = h2 = 1, iso-effect lines () are represented by the linear isoboles characteristic of Loewe Additivity and the CI null models. However, even in this case MuSyC is not limited by the weaker drug, and can therefore extend Loewe’s isoboles to any combination doses.
The requirement that α = 0 means the Loewe and CI null models assumes infinite potency antagonism (α1 = α2 = 0). Therefore, combinations with (0 < α < 1) may be deemed synergistic by Loewe or CI. However, these values directly reflect a decrease in potency, and our formulation accurately identifies this as antagonistic. Finally, their null model also ignores the possible effect of hill slopes not equal to 1. For drugs with h < 1, they will tend to overestimate synergy, while drugs with h > 1 will lead to underestimated synergy (Figure 5C,D). Because their null model relies on such specific assumptions, which are not true for many drugs, it is generally impossible to know whether their results reflect true underlying synergy/antagonism, or simply stem from an inappropriate null surface.
The Multiplicative Survival Principle: Bliss and Effective Dose Model
The other prevalent foundational synergy principle is multiplicative survival, described by Bliss (Bliss, 1939). Bliss’ null model assumes the probability of a cell being unaffected by drug 1 (U1) is independent of the probability of a cell being unaffected by drug 2 (U2). From this, the null surface states the probability of being unaffected by both drug 1 and drug 2 in combination is U1,2 = U1 ⋅ U2. When there is no potency synergy or antagonism, MuSyC reproduces this behavior in the following manner.
Setting α1 = α2 = 1, consider the fraction of unaffected cells, U, for each drug in isolation:
And for the two drugs in combination, solving eq. 67 for U we get
From this, it is easy to verify that U1,2 = U1 ⋅ U2, which is equivalent to Bliss Independence. However, the Bliss method explicitly requires the effect being measured in the combination surface is "percent affected", such as percent of cells killed vs. percent of cells remaining. For drugs which induce different maximum effects, Bliss is unable to account for the difference between being affected by drug 1 (E1), drug 2 (E2), and or both (E1,2), and may give unreliable results. Our model addresses this by decoupling the effect of a drug (E0, E1, E2, E3) and the "percent affected" by a drug (U, A1, A2, A1,2). If the effect itself is measuring percent (un)affected, that corresponds to the case where E0 = 1, E1 = E2 = E3 = 0, in which case MuSyC’s null model is identical to Bliss’.
Zimmer et. al. introduced the effective dose model (Zimmer et al., 2016) as a parameterized version of Bliss, and shares the same null surface. However, while Bliss defines synergy at every concentration independently, the effective dose model introduces a parameter ai,j to quantify synergy, similar to MuSyC’s potency synergy (α). The ai,j parameter reflects how the presence of drug i modulates the potency of drug j. However, like Bliss, the effective dose model can only be applied to drug responses where the measured drug effect is "percent affected" thereby implicitly requiring the maximum effect of both drugs and the combination is 100% affected which is commonly not observed in dose-response studies (Fallahi-Sichani et al., 2013).
ZIP
Like the equivalent dose model (Zimmer et al., 2016), as well as our potency synergy (α), ZIP (Yadav et al., 2015) works by quantifying how one drug shifts the potency of the other. ZIP is formulated for arbitrary E0 and Emax; however, it assumes Emax is the same for both drugs, as well as the combination (explicitly E1 = E2 = E3). To identify potency shifts, the ZIP method fixes the concentration of one drug, then fits a Hill-equation dose response for the other drug. However, for combinations with efficacy synergy or antagonism, dose responses can have non-Hill, and even non-monotonic shapes. In our data, several drugs displayed this behavior. Because our method accounts explicitly for efficacy synergy, our surfaces are able to describe such complex drug combination surfaces where ZIP fails.
Furthermore, ZIP calculates synergy at every concentration. This is similar to the approach taken by Bliss, Loewe, and CI, and can be used to find doses which “maximize” the observed synergy. However, quantifying synergy on a dose-by-dose basis confounds synergy of potency and efficacy which emerge only on inspection of the global dose-response surface. Additionally, this dose dependent synergy often leads to ambiguous results about whether a given combination is synergistic or not, as it synergizes at some concentrations, and antagonizes at others (Figure 5A).
BRAID
Like ZIP, BRAID (Twarog et al., 2016) assumes that each drug alone has a sigmoidal dose-response, and constructs a Hill-like equation for the combination. This equation uses a single dose parameter κ which combines the doses of both individual drug. To uniquely solve for κ, this formalism, like Loewe additivity, adds the constraint that a drug in combination with itself must be neither synergistic nor antagonistic. By adjusting κ, BRAID is able to fit complex drug combination surfaces, including non-monotonic responses. Because BRAID fits the whole combination surface using a single parameter, it can be used to make unambiguous statements about whether the combination is synergistic or antagonistic. Nevertheless, BRAID does not account for differences in synergy due to efficacy vs. potency, whereas we find many combinations that are synergistic with respect to one, but antagonistic with respect to the other. Further, the biochemical interpretation of κ is not straightforward. And finally, the BRAID model is unable to fit combination surfaces with synergistic efficacy, as it assumes that the maximum effect of the combination is equal to the maximum effect of the stronger singledrug.
Highest Single Agent (HSA)
HSA, originally proposed by Gaddum in 1940 (Gaddum, 1940) and then revived later by Greco (Greco, Bravo and Parsons, 1995), is a simple heuristic which argues synergy is any combination effect which exceeds the effect of either single agent. While β is conceptually similar to HSA, β provides a global view of the possible increase in effect rather than a point-by-point dose comparison as done in HSA. Because HSA is calculated at every dose it cannot distinguish between synergistically efficacious combinations and synergistically potent combinations as both will increase the effect at intermediate doses (Figure S2). Additionally, as HSA is only defined on a dose-by-dose basis with no model fit, it is sensitive to the dose range selected.
Schindler 2D-Partial Differential Equation (PDE) Model
Schindler’s Hill PDE was derived to impute the dose-response surface from the single dose-response curves alone (Schindler, 2017). Therefore, it does not contain any fit parameters, but rather defines a null surface for which synergy results in deviations in the surface. While Schindler did not specify how to account for these devations, he postulates some implementation of perturbation theory would be sufficient. Like CI and the Equivalent Dose Model, Schindler’s framework requires effects in a range between 0 and 1, based on the assumption that the metric is a percent. Therefore, Schindler cannot be applied to data collected with other types of metrics (e.g., DIP Rates). Additionally, Schindler’s maximum effect of the combination (E3) is set equal to the average of the single drug maximal effect. This allows for smooth transitions between the two single dose-response curves but results in some non-intuitive solutions. For example, if drug 1 has a maximal effect of 50% and drug 2 has a maximal effect of 70% the expected additive effect of the combination in the null model is 60% which is less than the maximal effect of drug 1. Therefore, an effect of 65% in combination, though less than achievable with one drug, is designated synergistic by Schindler.
Sham Experiment
It is common for synergy metrics to examine the special case in which the two drugs being combined are actually the same drug in a so called sham experiment first postulated by Chou (Chou and Talalay, 1984). Famously, Loewe, Combination Index, and other methods based on the Dose Equivalence Principle are sham compliant while Bliss and other methods based on the Multiplicative Survival Principle are not. Because our method distinguishes between two types of synergy, we tested sham compliance for each independently. It is immediately apparent synergistic efficacy is sham complaint in all conditions. This can be observed by substituting E1 = E2 = E3, as the maximum effect of the drug remains constant, into the definition for β in equation 3
| (7) |
To test the sham compliance of synergistic potency, we can write the full dose response surface as a direct 2D extension of the 1D dose-response curve in equation 12 by replacing d with d1 + d2.
| (8) |
Our 2D generalization of equation 12, given by equation 1 can be rewritten for the case of 2 identical drugs by observing that C1 = C2 = C, h1 = h2= h, and E1 = E2 = E3 = Em, resulting in
| (9) |
Setting equations 8 and 9 equal to one another, we find
| (10) |
This equality is true when α2 = α1 = 0 and h = 1. This makes sense as our model reduces to Loewe additivity under those conditions, and Loewe additivity was developed to explicitly address the sham-combination case. In conclusion, MuSyC satisfies the sham experiment in all conditions where Loewe is the appropriate model.
Derivation of generalized 2-dimensional hill equation
One-dimensional sigmoidal dose-response curve
In pharmacology, the effect of a drug is usually described by the Hill equation, which arises from the equilibrium of a reversible transformation between an unaffected population (U) and an affected population (A)
| (11) |
Here, [d] is the concentration of the drug, h is the Hill slope, and r1 and r−1 are constants corresponding to its rate of action. Solving for the equilibrium results in
When , then half the population is affected, and half is unaffected (A = U). This dose is the EC50, denoted as . Adding the constraint that U + A = 1, which states that 100% of the population is either unaffected or affected, we find the classic Hill equation :
If the unaffected and affected populations differ phenotypically by some arbitrary effect (e.g., proliferation rate), the observed effect over the whole population at dose d of some drug will be a weighted average of the two effects by the percent affected and unaffected. Namely,
where E0 is the effect characteristic of the unaffected population, and Em is the effect characteristic of the affected population. From this we find the final form of a 4-parameter sigmoidal equation describing dose-response due to Hill-kinetics:
| (12) |
Extending the mass action paradigm to simple four-state model assuming detailed balance
Consider a cell type U that can transition into a “drugged” state A1 in the presence of drug d1 and into a different drugged state A2 in the presence of drug d2 (Figure S1B). We can write these transitions as
| (13) |
| (14) |
where [di] denotes concentration of drug di. At equilibrium, the forward and reverse rates of these processes are equal, i.e.,
| (15) |
| (16) |
where [Ai] is the population of cell state Ai. Defining Θx as the ratio of forward and reverse rates (Θx ≡ r−x/rx) and assuming the system obeys detail balance, we find
| (17) |
| (18) |
Now assume that a fourth state exists, A1,2, corresponding to a “doubly” drugged state (Figure S1B). A1 cells can transition into this state in the presence of drug d2 and A2 cells can transition into this state in the presence of drug d1. We can write these processes as
| (19) |
| (20) |
Note that without loss of generality, we set the forward rate constant for (19) equal to the same value in (14) multiplied by a factor α1 > 0. Similarly, the rate constant for (20) is the same as in (13) multiplied by a factor α2 > 0. Here α represents how each drug potentiates the action of the other and can be interpreted as a change in the “effective” dose of one drug given the presence of the other. When α=1 the effective dose of the first drug is the same given the presence of the second drug. When α<1, more of the first drug is required to observe the same effective concentrations due to the presence of the second drug. Finally, when α>1 the same concentration of the first drug is effectively increased by the second drug.
Again asserting the system obeys detailed balance at equilibrium, we have
| (21) |
| (22) |
We can derive the relationship between the multiplicative factors α1 and α2 by rearranging Eq. (17) as
| (23) |
Substituting for [A1] from Eq. (21) gives
| (24) |
Substituting for [A1,2] from Eq. (22) gives
| (25) |
Finally, substituting for [A2] from Eq. (18) gives
| (26) |
i.e., α1 = α2 = α . Note this equality only holds for systems obeying detailed balance. In general, we do not assume this (See Section 4.4 ‘Generalized derviation without assuming detailed balance’) and α1 and α2 are independent (Figure S4). However, assuming detailed balance facilitates in deriving a more intuitive form of the 2D Hill equation (eq. 1) compared to the full form (eq. 6).
Now, we define the total cell count
| (27) |
Substituting for [A1], [A2], and [A1,2] from Eqs. (17), (18), and (24), respectively, gives
| (28) |
Solving for [U] gives
| (29) |
Substituting Eq. (29) into Eq. (17) and rearranging gives
| (30) |
Similarly, from Eq. (18) we get
| (31) |
and from Eq. (24)
| (32) |
As in the derivation of the 1D Hill equation, the measured effect (Ed) is then the relative proportion of cells in each state multiplied by the effect characteristic of that state as in
| (33) |
Here we define the effect of each state (E0, E1, E2, E3) to be proliferation rate in the following way.
We assume that cells in each state can divide and die at rates characteristic of the state, i.e.,
| (34) |
| (35) |
where Ci is specific state of the cell.
We define the drug-induced proliferation (DIP) rate for each state as the difference between the division and death rate constants, i.e.,
| (36) |
Using Eq. (27), the rate of change of the total cell population is
| (37) |
From (13), (14), (19), (20), (34)-(36), we get
| (38) |
Substituting Eqs. (29)-(32) and rearranging, we get
| (39) |
with
| (40) |
Note that with a slight modification, Eq. (40) can be written as
| (41) |
Therefore, if [d2] = 0 (i.e., single-drug treatment) we get
| (42) |
Rearranging gives
| (43) |
Comparing to Eq. (12), we see that Eq. (43) is a one-dimensional sigmoidal dose-response curve with , , , C = Θ1, and h = 1. By analogy, we surmise that eq. (40) is a 9 parameter, two-dimensional generalization of Eq. (12), i.e.,
| (44) |
with , , , , , C1 = Θ1, C2 = Θ2, h1 = 1, h2 = 1, and the additional parameter α2. Note that under the assumption of detailed balance we found α1 = α2 for the case when h = 1. Therefore, in the general case when h ≠ 1, . By fitting the eq. 44, α1 is uniquely determined.
Four-state model with multiple steps between states
Let us assume instead of occurring in a single step, the cell state transitions are h step processes, i.e.,
| (45) |
p
Assuming that all steps are in rapid equilibrium, it is straightforward to show that
| (46) |
where Θx, m ≡ r−x,m/rx,m. Defining , Eq. (46) can be written as
| (47) |
which is the well-known Median-Effect Equation from Chou (Chou et al., 1983; Chou and Talalay, 1984; Chou, 2010). Replacing reactions (13) and (14) with multi-step processes of the form (45), gives us
| (48) |
| (49) |
Similarly, we replace reactions (19) and (20) with the same multi-step process except with the rate constant for the transition (entry into the cascade) equal to αyrx,1[dx], giving
| (50) |
| (51) |
Note, we assume that the number of steps in the cascade (45) is dependent on the drug type (i.e., U → A1 and A2 → A1,2, both driven by d1, take h1 steps, while U → A2 and A1 → A1,2, both driven by d2, take h2 steps). Using Eqs. (48)-(51) and again defining the total cell count CT as in Eq. (27), we derive
| (52) |
| (53) |
| (54) |
| (55) |
Therefore, in the same way that we arrived at Eq. (40), we can derive
| (56) |
which is of the form Eq. (44) with , , , , , C1 = Φ1, and C2 = Φ2. From this it is clear the hill coefficent (h) is related to the number of intermediate steps in the system.
The derivation of Eq. (56) assumes that the populations of all intermediate cell states in (45) are small (≈ 0).1 We can satisfy this assumption by requiring that all rx,m, r−x,m ⪢ 1 (m ∈ {1 …h}) and Θx,1 ⪢ Θx,2 ≈ ⋯ ≈ Θx,h−1 ⪢ Θx,h. To see this, consider cell state U and all of its intermediate states between states A1 and A2. Let us define
| (57) |
From (45), we see that , , etc. Therefore,
| (58) |
p
If Θ1,1 ⪢ 1, Θ1, Θ1,m ⪡ 1 (m ∈ {2 … h1 − 1}) and Θ2,1 ⪢ 1, Θ2,m′, ⪡ 1 (m′ ∈ {2 … h2 − 1}), we get UT ≈ [U], i.e., the populations of all intermediate states are ≈ 0. Now consider cell state A1 and all of its intermediate states between cell state A1,2. Similar to above, we have
| (59) |
and
| (60) |
Thus, as before, if Θ2,1 ⪢ 1 and Θ2,m, ⪡ 1 (m ∈ {2 … h2 − 1}) we have . However, from (45) we also have
| (61) |
Since, from above, Θ1,1 ⪢ 1 and Θ1, m ⪡ 1 (m ∈ {2 … h1 − 1}), we must require that Θ1,h1 ⪡ 1 and Θ1,m ⪢ 1 (m ∈ {2 … h1 − 1}) in order to offset the large value of Θ1,1 and to ensure that [A1] ≈ 0, and to ensure. The latter condition means that Θ1,m ≈ 1 (m ∈ {2 … h1 − 1}). Therefore, we have the condition that Θ1,1 ⪢ Θ1,2 ≈ ⋯ ≈ Θ1,h1−1 ⪢ Θ1,h1 . Similarly, we can derive that Θ2,1 ⪢ Θ2,2 ≈ ⋯ ≈ Θ2,h2−1 ⪢ Θ2,h2 by considering cell state A2 and all of its intermediate states between cell state A1,2 (not shown).
Generalized derivation without assuming detailed balance
More generally if we do not assume detailed balance, the state occupancy of U, A1, A2, A1,2 are defined by the partial equilibrium equations
| (62) |
| (63) |
| (64) |
| (65) |
A final constraint is
| (66) |
At equilibrium, the equations 62 through 65 must be equal to zero; however, the system only defines a rank 3 matrix, necessitating equation 66. Thus we find
| (67) |
Equations of the form
can be solved as
Thus we find the expected effect, as in the 1D case, is the weighted average of the characteristic effect of each state weighted by the state occupancy as governed by the 2D Hill Equation.
| (68) |
This is derived assuming mass action from the reaction rules U + d → A1 + d, A1 → U. If instead we assume a multi-step transition as in section 4.3, we can simply replace the following in 68
resulting in
| (69) |
Equation 69 has the following twelve explicit parameters: r1 r−1, r2, r−2, E0, E1, E2, E3, h1, h2, α1 and α2. There is a relationship defined between a drug’s EC50 (C in our derivation), the transition rates (ri, r−i), and the hill slope (hi), given by .
Combination experiments protocol
Experiments were conducted in the Vanderbilt High Throughput Screening Facility. Cells were seeded at approximately 300 cells per well in 384-well plates and allowed to adhere overnight. A preliminary image of each plate was taken approximately 8 hours after seeding to verify sufficient numbers of cells for each experiment. Images were taken on either the ImageXpress Micro XL (Molecular Devices) or CellaVista. The matrix of drug concentrations was prepared using a row-wise and column-wise serial 2X or 4X dilution in 384 well plates using a Bravo Liquid Handling System (Agilent) or manually in 96-well plates. See Table S2 for dose ranges tested. After allowing to adhere overnight, medium containing drugs and 5 nM Sytox Green (to detect dead cells) was added (time = 0) and replaced after 72 hours. Images were obtained at intervals ranging from every 4 to 8 h, depending on the experiment, for >120 hours. Cell counts were determined using custom-image segmentation software developed in Python using scikit-image package (van der Walt et al., 2014) and run in parallel using RabbitMQ/Celery (http://www.celeryproject.org/).
RNA-seq of melanoma cell lines
Total RNA was isolated from untreated SKMEL5 single-cell derived sublines, each in triplicate, using Trizol isolation method (Invitrogen) according to the manufacturer’s instructions. RNA samples were submitted to Vanderbilt VANTAGE Core services for quality check, where mRNA enrichment and cDNA library preparation were done with Illumina Tru-Seq stranded mRNA sample prep kit. Sequencing was done at Paired-End 75 bp on the Illumina HiSeq 3000. Reads were aligned to the GRCh38 human reference genome using HISAT2 (Kim, Langmead and Salzberg, 2015) and gene counts were obtained using featureCounts (Liao, Smyth and Shi, 2014). All downstream analyses were performed in R (https://www.r-project.org) using the Bioconductor framework (https://www.bioconductor.org)
RT-qPCR quantification of NOX5 expression
Total RNA was extracted using Trizol isolation method (Invitrogen) according to the manufacturer’s instructions. cDNA synthesis was performed with QuantiTect Reverse Transcription Kit (Cat# 205311) from Qiagen. RT-qPCR was performed using the IQTM SYBR Green Supermix from BioRad (Cat# 1708880). Amplifications were performed in BioRad CFX96 TouchTM Real-Time PCR Detection System. All experiments were done at least in 3+ technical replicates. Log2 of the transcript expressions were normalized to SKMEL5 subline SC01. HPRT or 36B4 were used as housekeeping gene in all the experiments. Primers used in RT-qPCR are listed in Key Resources Table.
QUANTIFICATION AND STATISTICAL ANALYSIS
Fitting Dose-response Surfaces
We developed a fitting algorithm, implemented in Python, to fit the combinations experiments to the 2D Hill equation. The fitting is done in three steps, first estimates of the single dose-response parameters (C1,C2,h1,h2,E0,E1,E2) are extracted from fits to the single dose-response curves using the Pythonic implementation of a Levenburg-Marquart (LM) least squares optimization (scipy.optimize.curve_fit). The fit uncertainty (σ) is then the square root of the covariance matrix which is approximated as the inverse of the Hessian matrix (equal to JTJ in LM where J is the Jacobian) at the solution. In the second step, a Particle Swarm Optimizer (10,000 particles, 100 iterations) fits the full 2D Hill equation using the single parameter fits and uncertainties as initial values and bounds (±2σ). In the last step, the PSO optimized values are used to construct priors for a Metropolis-Hastings Monte-Carlo Markov Chain (MCMC) Optimization (Metropolis Hastings 10,000 iterations). Convergence is tested by checking all parameters’ Geweke Z-score. If the Z-score range is (−2,2) over the sampling time frame, the optimization is considered to converge (Figure S3D,E). We found it necessary to use both the PSO and MCMC in order to fit a wide range of dose-response surfaces (Figure S3). To test the sensitivity of our fitting algorithm, we generated in silico data for 125 different dose-response surfaces at different data densities. The density of data tested were square matrixes of rank 5, 7, 10, 15, and 25. At each density 25 different dose-response surfaces were sampled across a 5×5 grid of log(α) and β values ranging from [−2,2] and from [−0.5,0.5], respectively. The parameters for E0, the single drug hill slope, EC50, and maximal effects were held constant at (0.3, 1, 10e-5, and 0.0), respectively. Random noise equal to the average uncertainty in the DIP Rate fits from the NSCLC screen was added to the data (0.001). In all conditions we observed a PSO particle count of 10,000 converged to a minimum in <60 iterations (Figure S3A). However, this minimum was not the optimal solution. The addition of an MCMC walk further improved fits (Figure S3B) (Pymc3 package). The MCMC walk calculates the posterior distribution for each parameter from which each parameter’s value (mean of trace) and uncertainty (standard deviation of trace) is calculated. Uncertainty in (E0, E1, E2, and E3) was propagated when calculating β using the equation
Where Ex and σEx are min(E1,E2) and σ(min(E1, E2)) respectively. All other uncertainty propagations were handled with python package uncertainties (Lebigot, 2011). By calculating the uncertainty in the synergy parameters from the posterior distributions, the significance of synergy can be assessed in an unbiased way. Multiple factors contribute to increasing uncertainty in the fitted parameters. Dose-selection, an important consideration in all drug response profiling, changes the certainty of the fits (Figure S3C-E). While we are unable to observe saturating effects implicit in the model for some of our drug combinations – due to limited solubility or potency of the drug – by keeping careful account of the uncertainty in our synergy calculations we can still interpret the synergy of non-optimal dose-regimes. To demonstrate this, we generated the same 25 dose-response surfaces with varying log(α) and β values ranging from [−2,2] and from [−0.5,0.5] respectively but at different coverage of the dose-response curve. The uncertainty in the synergy parameters increases for decreased dose range (Figure S3C and D). It is important to note that in general the uncertainty is a function of many different aspects other than data density including the hill slope of the single curves (high hill slopes can result in higher uncertainty in log(α)), noise of experimental data, and quality of priors resulting from the single-drug fits. We posit the rigorous approach taken here accounts for all these sources resulting in a true estimate of confidence in a particular synergy value.
To prevent over fitting the data, we have defined six different model tiers which have increasing degrees of freedom (Table S5). To select the correct model tier, we penalize models with higher degrees of freedom by selecting the model based on minimizing the deviance information criterion (DIC) (Berg, Meyer and Yu, 2004). Fits for each nest are used to inform priors for subsequent nests. Only drug combinations which converged to the full model (tier 5 with fits for all 12 parameters – equation 69 in section 4.4 of Methods Details) were used for subsequent analysis. The MCMC optimization additionally allows for quantification of parameter confidence given the data. The following packages were used for fitting, data analysis, or visualization: GNU parallel (Tange, 2011), SciPy (Jones, Oliphant and Peterson, 2001), Numpy (Oliphant, 2006), Pandas (McKinney, 2010), Matplotlib (Hunter, 2007). Pymc3 (Salvatier, Wiecki and Fonnesbeck, 2016).
Calculating the DIP Rate
Traditionally, the efficacy of an anti-proliferative compound is measured as the percent of viable cells (relative to control) after a treatment interval (Fallahi-Sichani et al., 2013); however, it has been recently shown this metric is subject to temporal biases (Hafner et al., 2016; Harris et al., 2016). To address these biases, we previously developed an unbiased metric of drug effect termed the drug-induced proliferation (DIP) rate (Harris et al., 2016). The DIP rate is defined as the steady state proliferation rate after drug equilibration. A positive DIP rate indicates an exponentially growing population, while a negative DIP rate indicates a regressing one. A rate of zero indicates a cytostatic effect, which may result from cells entering a non-dividing state or from balanced death and division (Paudel et al., 2018). We used the available findDIP R package for calculating DIP rates from growth curves which automatically selects the interval after drug equilibration (https://github.com/QuLab-VU/DIP_rate_NatMeth2016.git).
Calculating Loewe, CI, Bliss, and HSA
To compare our method to the prevailing methods for computing synergy, we calculated Loewe, CI, Bliss for the data from the osimertinib screen in Figure 2 and melanoma BRAF/MEK data of Figure 3. Loewe is agnostic to effect metric, and so we applied it directly to the DIP rate. To calculate CI and Bliss, we imputed the percent viability at 72 hours from the DIP rate for each condition. Percent viability is defined as in equation 1.
| (70) |
Estimates of percent viability are sensitive to even small differences between initial cell counts in the control and treated wells due to exponential amplification (Harris et al., 2016). To correct for this the bias, a ‘matching’ control cell count at 72-hours for each treated condition was calculated using equation
| (71) |
where Control Growth Rate is the median of the fitted growth rates for all control wells. Because the automated microscope did not image all the conditions at exactly zero or seventy two hours, we extrapolate and interpolate respectively the cell count at these times from the measured time series.
The Bliss metric only requires marginal data. For each experiment, individually, we calculated a Bliss score as
| (72) |
where PVi∣di is the %-viability measured for treatment with drug i alone at dose di, and PV1,2∣d1, d2 is the %-viability measured for the combination treatment. The first term corresponds to the expected viability, assuming independence, while the second term is the measured viability. By this definition, Bliss>0 is synergistic, and Bliss<0 is antagonistic.
Loewe and CI require parameterization of a 1D Hill equation for each drug alone.
| (73) |
CI, as per standard calculations (Chou and Talalay, 1984), further requires that E0 = 1 and Emax = 0 and is fit to a linearized, log-transformed version of the hill equation(Chou, 2010) which has been previously critiqued for artificial compression of uncertainty in experimental data leading to poor model fits compared with nonlinear regression (Ashton, 2015). CI dose-response curves were fit using the scipy.stats.linregress module. All data points with percent viability greater than 1 were excluded from the CI fit, as becomes complex.
For some drugs, this left too few points to fit a line, such that CI was undefined for combinations with those drugs. In other drugs, the fit hill coefficient was negative, and likewise all CI values were undefined for those drugs. For Loewe, we used the single-drug parameters fit by MuSyC.
From these parameterized hill equations, Loewe and CI were calculated using
| (74) |
where Di is the amount of drug i which, alone, achieves an effect equal to the combination effect, and is calculated from the Hill equation fit for that drug. We take the negative log to transform the synergy values to match Bliss, such that S>0 is synergistic, while S<0 is antagonistic. Because Loewe allows the two drugs to have different Emax, Loewe synergy cannot be calculated for measurements which exceed the weaker drug's Emax because no amount of the weaker drug alone would be sufficient to achieve that effect; therefore, those conditions are undefined.
For calculating HSA (Gaddum, 1940), we calculate the difference between the observed effect at each combination concentration and the most efficacious single agent effect at those doses. This difference is integrated across the surface to yield a single value for a particular combination.
Fitting ZIP, BRAID, Schindler’s Hill PDE, and Equivalent Dose Models
Theoretical dose-response surfaces with different combinations of synergistic potency and efficacy were generated then fit to estimate the synergy according to these methods (Figure S2). Both ZIP and BRAID were calculated using the R packages available for each method (ZIP’s R code is in the supplemental file 1 of the manuscript (Yadav et al., 2015) and BRAID’s package is available from:https://cran.r-project.org/web/packages/braidReports/braidReports.pdf). Schindler’s Hill PDE model contains no fitting parameters as the dose-response surface is derived purely from the marginal data. In fact, Schindler does not propose a method to estimate synergy from experimental data, but postulates some implementation of perturbation theory could be used to fit experimental data (Schindler, 2017). Therefore, to calculate the synergy of this model, we defined the sum of residuals between the null surface and the experimental data to the metric of synergy. Finally, to fit Zimmer et al.’s Equivalent Dose Model we used the curve_fit() module of the scipy.optimization package in python. Specifically, the Equivalent Dose Model, equation 2 in (Zimmer et al., 2016), contains parameters for C1,C2, a12, a21, h1, and h2 where the C parameters are the EC50 of the single agents, the ai,j parameters are the synergy values corresponding to a change in potency, and the h parameters are the hill slopes of the single agents. In the model, there are no parameters for efficacy because it is assumed the drug effect ranges between zero and one. When this is not true, the Effective Dose Model results in poor fits to the data (Figure S2) similar to CI.
Identifying DEGs for GO Enrichment Analysis
Differentially Expressed Genes (DEGs) were selected by ANOVA on baseline gene expression data on three clones based on a statistical cutoff of Likelihood Ratio Test (LRT) (p-values < 0.001). Functional enrichment analyses, including GO Term Enrichment and Pathway Enrichment Analysis were done using CRAN Package “Enrichr” (https://cran.r-project.org/web/packages/enrichR/index.html), based on a web-based tool for analyzing gene sets and enrichment of common annotated biological functions (Kuleshov et al., 2016). The enriched GO terms and enriched KEGG pathways were restricted to those with p-values corrected for multiple testing less than 0.001. The top GO Biological Processes included generation of precursor metabolites and energy, electron transport chain, inorganic cation transmembrane transport, and metabolic process. The top GO Molecular Function terms included inorganic cation transmembrane transporter activity, cofactor binding, NAD binding, and ATPase activity. The top GO Cellular Component term was the mitochondria membrane. Top KEGG pathways enriched in the DEGs included metabolic pathways, oxidative phosphorylation, carbon metabolism and TCA cycle (Figure 3B). Overall, these enriched GO terms and pathways point toward differences in the regulators of metabolic function in the three subclones. This is consistent with previous reports that suggest altered metabolism is implicated in drug sensitivity and melanoma resistance to BRAFi (Parmenter et al., 2014; Hardeman et al., 2017).
Correlation of BRAFi insensitivity was computed for each identified DEG according to DIP Rate at 8uM PLX-4720 for a 10 cell line panel (Table S3) Pair-wise comparisons of DEGs was performed on genes (after low count genes were removed) using DESeq2 pipeline (Love, Huber and Anders, 2014).
DATA AND SOFTWARE AVAILABILITY
All raw cell counts, calculated DIP rates, DEGs between subclones, and expression data are available in the github repo: https://github.com/QuLab-VU/MuSyC_Cell.git in the folder Data. Additionally, the repo contains all the code required to reproduce all the figures and supplemental figures from the data and is found in the Code_Paper_Figures folder. The subfolders Fig2 and Fig3 contain html folders with interactive plots of all the screened combinations. Open the .html files using a browser. The raw RNAseq is available from GEO at the accession number GSE122041. The software for interactive manipulation of the different parameters to study their contribution to the contours of the dose-response surface is also available in the github repo in the folder MuSyC_App. This folder contains both the matlab source code and a compiled application for the different operating systems. A copy of the github repo at the time of publication is also available from Mendeley Data via the following http://dx.doi.org/10.17632/n8bp8db5ff.
Supplementary Material
Movie S1: The orthogonal effects of β and α on the topology of the dose-response surface. Related to Figure 1. Synergy of potency and efficacy (α and β) correspond to orthogonal geometric transformations of the dose-response surface and are therefore analogous to the geometric translations of the single-drug dose-response curve described by classic pharmacology parameters quantifying a drug’s potency and efficacy (EC50 and Emax).
Highlights:
MuSyC is a synergy framework applicable to any metric of drug combination effect
Unlike other methods, MuSyC decouples synergy of potency and efficacy
It subsumes traditional synergy methods resolving ambiguities and biases in the field
MuSyC reveals optimal co-targeting strategies in NCSLC and melanoma
Acknowledgments:
The authors would like to thank Corey Hayford, Sarah Maddox, Carlos Lopez, and Chris Wright for insightful conversations. Additionally, the authors would like to thank Jing Hao for the help with experimental preparation and reagent procurement. Finally, the authors would like to thank James Pino and Alexander Lubbock for the pythonic implementation of PSO and findDIP libraries respectively.
Experiments were performed in the Vanderbilt HTS Core Facility, an institutionally supported core with assistance provided by Debbie Mi, Page Vinson, and Joshua Bower.
This work was supported by the following funding sources: CTM was supported by National Science Foundation (NSF) Graduate Student Fellowship Program (GRFP) [Award #1445197]. VQ was supported by the National Institutes of Health (NIH) [U54-CA217450, R01-186193, and U01-CA215845]; JAB was supported by the National Cancer Institute (NCI) [R50-CA211206]. DW was supported by Ruth L. Kirschstein National Research Service Award (2T32HL094296-06A1). CML was supported in part by the NIH [P30-CA086485, R01-CA121210, and P01-CA129243]. CML additionally was supported by a V Foundation Scholar-in-Training Award, an AACR-Genentech Career Development Award, a Damon Runyon Clinical Investigator Award, a LUNGevity Career Development Award, and a Lung Cancer Foundation of America / International Association for the Study of Lung Cancer Lori Monroe Scholarship.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
This is most evident in our use of Eq. (27) for the total cell population, where we only consider the end states. However, it is also implicit in our use of Eq. (46), which is used to derive Eqs. (52)-(55) that lead to Eq. (56) via Eq. (38). In other words, we are assuming that the intermediate states do not significantly contribute to the dynamics of the total cell population. Since it is not reasonable to assume that cells in these states do not divide and die, we must assume the percent occupancy of these states is near zero.
Declaration of Interests
The authors declare no competing interests.
Bibliography
- AltenhÖfer S et al. (2015) ‘Evolution of NADPH Oxidase Inhibitors: Selectivity and Mechanisms for Target Engagement’, Antioxidants & redox signaling. Mary Ann Liebert, Inc., 23(5), pp. 406–27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ashton JC (2015) ‘Drug Combination Studies and Their Synergy Quantification Using the Chou–Talalay Method—Letter’, Cancer Research, 75(11), pp. 2400–2400. [DOI] [PubMed] [Google Scholar]
- Barretina J et al. (2012) ‘The Cancer Cell Line Encyclopedia enables predictive modeling of anticancer drug sensitivity’, Nature, 483(7391). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berg A, Meyer R and Yu J (2004) ‘Deviance Information Criterion for Comparing Stochastic Volatility Models’, Journal of Business & Economic Statistics, 22(1). [Google Scholar]
- Bliss CI (1939) ‘The Toxicity of Poisons Applied Jointly’, Annals of Applied Biology, 26(3), pp. 585–615. [Google Scholar]
- Chou T-C (2010) ‘Drug Combination Studies and Their Synergy Quantification Using the Chou-Talalay Method’, Cancer Research, 70(2), pp. 440–446. [DOI] [PubMed] [Google Scholar]
- Chou T-CT-C et al. (1983) ‘Analysis of combined drug effects: a new look at a very old problem’, Trends in Pharmacological Sciences. Cambridge University Press, Cambridge, 4, pp. 450–454. [Google Scholar]
- Chou TC and Talalay P (1984) ‘Quantitative analysis of dose-effect relationships: the combined effects of multiple drugs or enzyme inhibitors.’, Advances in enzyme regulation, 22, pp. 27–55. [DOI] [PubMed] [Google Scholar]
- Eroglu Z and Ribas A (2016) ‘Combination therapy with BRAF and MEK inhibitors for melanoma: latest evidence and place in therapy’, Therapeutic advances in medical oncology. SAGE Publications, 8(1), pp. 48–56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fallahi-Sichani M et al. (2013) ‘Metrics other than potency reveal systematic variation in responses to cancer drugs’, Nature Chemical Biology, 9(11), pp. 708–714. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foucquier J and Guedj M (2015) ‘Analysis of drug combinations: current methodological landscape’, Pharmacology research & perspectives. Wiley-Blackwell, 3(3), p. e00149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gaddum JH (1940) Pharmacology. London: Oxford University Press. [Google Scholar]
- Gong Z et al. (2017) ‘Compound Libraries: Recent Advances and Their Applications in Drug Discovery’, Current Drug Discovery Technologies, 14(4), pp. 216–228. [DOI] [PubMed] [Google Scholar]
- Greco W et al. (1992) ‘Consensus on Concepts and Terminology for Combined-action Assessment: The Saariselka Agreement’, Archives of Complex Environmental Studies, 4(3), pp. 65–69. [Google Scholar]
- Greco WR, Bravo G and Parsons JC (1995) ‘The search for synergy: a critical review from a response surface perspective.’, Pharmacological reviews, 47(2), pp. 331–85. [PubMed] [Google Scholar]
- Hafner M et al. (2016) ‘Growth rate inhibition metrics correct for confounders in measuring sensitivity to cancer drugs’, Nature Methods, 13(6), pp. 521–527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hardeman KN et al. (2017) ‘Dependence On Glycolysis Sensitizes BRAF-mutated Melanomas For Increased Response To Targeted BRAF Inhibition’, Scientific reports. Nature Publishing Group, 7, p. 42604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris LA et al. (2016) ‘An unbiased metric of antiproliferative drug effect in vitro’, Nature Methods, 13(6), pp. 497–500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He B et al. (2016) ‘Combination therapeutics in complex diseases’, Journal of cellular and molecular medicine. Wiley-Blackwell, 20(12), pp. 2231–2240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hennessey VG et al. (2010) ‘A Bayesian approach to dose-response assessment and synergy and its application to in vitro dose-response studies.’, Biometrics. NIH Public Access, 66(4), pp. 1275–83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hunter JD (2007) ‘Matplotlib: A 2D Graphics Environment’, Computing in Science & Engineering, 9(3), pp. 90–95. [Google Scholar]
- Jabs J et al. (2017) ‘Screening drug effects in patients-derived cancer cells links organoid responses to genome alterations’, Molecular Systems Biology. Wiley-Blackwell, 13(11), p. 955. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jaquet V et al. (2011) ‘NADPH oxidase (NOX) isoforms are inhibited by celastrol with a dual mode of action’, British journal of pharmacology. Wiley-Blackwell, 164(2b), pp. 507–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jia P et al. (2013) ‘Next-generation sequencing of paired tyrosine kinase inhibitor-sensitive and -resistant EGFR mutant lung cancer cell lines identifies spectrum of DNA changes associated with drug resistance’, Genome research. Cold Spring Harbor Laboratory Press, 23(9), pp. 1434–45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones E, Oliphant T and Peterson P (2001) SciPy: Open Source Scientific Tools for Python. Available at: http://www.scipy.org/. [Google Scholar]
- Kim D, Langmead B and Salzberg SL (2015) ‘HISAT: a fast spliced aligner with low memory requirements’, Nature Methods, 12(4), pp. 357–360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuleshov MV et al. (2016) ‘Enrichr: a comprehensive gene set enrichment analysis web server 2016 update’, Nucleic Acids Research, 44(W1). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lebigot EO (2011) Uncertainties: a Python package for calculations with uncertainties. Available at: http://pythonhosted.org/uncertainties/. [Google Scholar]
- Liao Y, Smyth GK and Shi W (2014) ‘featureCounts: an efficient general purpose program for assigning sequence reads to genomic features’, Bioinformatics, 30(7), pp. 923–930. [DOI] [PubMed] [Google Scholar]
- Loewe S (1926) ‘uber Kombination swirkungen’, Arch fur Exp Pathology, 114, pp. 313–326. [Google Scholar]
- Loewe S (1927) ‘Versuch einer allgemeinen Pharmakologie der Arznei- kombinationen.’, Klinische Wochenschrift, 6(23), pp. 1078–1085. [Google Scholar]
- Long GV et al. (2014) ‘Combined BRAF and MEK Inhibition versus BRAF Inhibition Alone in Melanoma’, New England Journal of Medicine, 371(20), pp. 1877–1888. [DOI] [PubMed] [Google Scholar]
- Love MI, Huber W and Anders S (2014) ‘Moderated estimation of fold change and dispersion for RNA-seq data with DESeq2.’, Genome biology. BioMed Central, 15(12), p. 550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu W et al. (2012) ‘Novel Role of NOX in Supporting Aerobic Glycolysis in Cancer Cells with Mitochondrial Dysfunction and as a Potential Target for Cancer Therapy’, PLoS Biology. Edited by Schartl M. Public Library of Science, 10(5), p. e1001326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McKinney W (2010) ‘Data Structures for Statistical Computing in Python’, pp. 51–56. [Google Scholar]
- Oliphant TE (2006) ‘Guide to NumPy’. [Google Scholar]
- Palmer AC and Sorger PK (2017) ‘Combination Cancer Therapy Can Confer Benefit via Patient-to-Patient Variability without Drug Additivity or Synergy Theory Combination Cancer Therapy Can Confer Benefit via Patient-to-Patient Variability without Drug Additivity or Synergy’, Cell, 171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parmenter TJ et al. (2014) ‘Response of BRAF-mutant melanoma to BRAF inhibition is mediated by a network of transcriptional regulators of glycolysis’, Cancer discovery. American Association for Cancer Research, 4(4), pp. 423–33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paudel BP et al. (2018) ‘A Nonquiescent "Idling" Population State in Drug-Treated, BRAF-Mutated Melanoma’, Biophysical Journal. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salvatier J, Wiecki TV and Fonnesbeck C (2016) ‘Probabilistic programming in Python using PyMC3’, PeerJ Computer Science. PeerJ Inc., 2, p. e55. [Google Scholar]
- Schiffmann I et al. (2016) ‘Epigenetic therapy approaches in non-small cell lung cancer: Update and perspectives’, Epigenetics. Taylor & Francis, 11(12), pp. 858–870. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schindler M (2017) ‘Theory of synergistic effects: Hill-type response surfaces as “null-interaction” models for mixtures’, Theoretical Biology and Medical Modelling, 14(1), p. 15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shaw AT et al. (2014) ‘Ceritinib in ALK -Rearranged Non–Small-Cell Lung Cancer’, New England Journal of Medicine. Massachusetts Medical Society, 370(13), pp. 1189–1197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shimoyama Y et al. (1992) ‘Cadherin dysfunction in a human cancer cell line: possible involvement of loss of alpha-catenin expression in reduced cell-cell adhesiveness.’, Cancer research, 52(20), pp. 5770–4. [PubMed] [Google Scholar]
- Soria J-C et al. (2018) ‘Osimertinib in Untreated EGFR -Mutated Advanced Non–Small-Cell Lung Cancer’, New England Journal of Medicine, 378(2), pp. 113–125. [DOI] [PubMed] [Google Scholar]
- Subramanian A et al. (2017) ‘A Next Generation Connectivity Map: L1000 Platform and the First 1,000,000 Profiles’, Cell. Elsevier, 171(6), p. 1437–1452.e17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tallarida RJ (2011) ‘Quantitative methods for assessing drug synergism’, Genes & cancer. Impact Journals, LLC, 2(11), pp. 1003–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tange O (2011) ‘GNU Parallel: The Command-Line Power Tool’, ;login;, 36(1), pp. 42–47. [Google Scholar]
- Twarog NR et al. (2016) ‘BRAID: A Unifying Paradigm for the Analysis of Combined Drug Action’, Scientific Reports. Nature Publishing Group, 6(1), p. 25523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tyson DR et al. (2012) ‘Fractional proliferation: a method to deconvolve cell population dynamics from single-cell data.’, Nature methods, 9(9), pp. 923–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van der Walt S et al. (2014) ‘scikit-image: image processing in Python’, PeerJ, 2, p. e453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Welm BE et al. (2008) ‘Lentiviral Transduction of Mammary Stem Cells for Analysis of Gene Function during Development and Cancer’, Cell Stem Cell, 2(1), pp. 90–102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Witta SE et al. (2006) ‘Restoring E-Cadherin Expression Increases Sensitivity to Epidermal Growth Factor Receptor Inhibitors in Lung Cancer Cell Lines’, Cancer Research, 66(2), pp. 944–950. [DOI] [PubMed] [Google Scholar]
- Witta SE et al. (2012) ‘Randomized phase II trial of erlotinib with and without entinostat in patients with advanced non-small-cell lung cancer who progressed on prior chemotherapy’, Journal of Clinical Oncology. American Society of Clinical Oncology, 30(18). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yadav B et al. (2015) ‘Searching for Drug Synergy in Complex Dose–Response Landscapes Using an Interaction Potency Model’, Computational and Structural Biotechnology Journal. Elsevier, 13, pp. 504–513. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zimmer A et al. (2016) ‘Prediction of multidimensional drug dose responses based on measurements of drug pairs’, Proceedings of the National Academy of Sciences of the United States of America. National Academy of Sciences, 113(37), pp. 10442–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Movie S1: The orthogonal effects of β and α on the topology of the dose-response surface. Related to Figure 1. Synergy of potency and efficacy (α and β) correspond to orthogonal geometric transformations of the dose-response surface and are therefore analogous to the geometric translations of the single-drug dose-response curve described by classic pharmacology parameters quantifying a drug’s potency and efficacy (EC50 and Emax).
Data Availability Statement
All raw cell counts, calculated DIP rates, DEGs between subclones, and expression data are available in the github repo: https://github.com/QuLab-VU/MuSyC_Cell.git in the folder Data. Additionally, the repo contains all the code required to reproduce all the figures and supplemental figures from the data and is found in the Code_Paper_Figures folder. The subfolders Fig2 and Fig3 contain html folders with interactive plots of all the screened combinations. Open the .html files using a browser. The raw RNAseq is available from GEO at the accession number GSE122041. The software for interactive manipulation of the different parameters to study their contribution to the contours of the dose-response surface is also available in the github repo in the folder MuSyC_App. This folder contains both the matlab source code and a compiled application for the different operating systems. A copy of the github repo at the time of publication is also available from Mendeley Data via the following http://dx.doi.org/10.17632/n8bp8db5ff.