Taking advantage of external mechanical work to reduce metabolic cost: the mechanics and energetics of split-belt treadmill walking

Abstract

In everyday tasks such as walking and running, we often exploit the work performed by external sources to reduce effort. Recent research has focused on designing assistive devices capable of performing mechanical work to reduce the work performed by muscles and improve walking function. The success of these devices relies on the user learning to take advantage of this external assistance. Although adaptation is central to this process, the study of adaptation is often done using approaches that seem to have little in common with the use of external assistance. We show in 16 young, healthy participants that a common approach for studying adaptation, split-belt treadmill walking, can be understood from a perspective in which people learn to take advantage of mechanical work performed by the treadmill. Initially, during split-belt walking, people step further forward on the slow belt than the fast belt which we measure as a negative step length asymmetry, but this asymmetry is reduced with practice. We demonstrate that reductions in asymmetry allow people to extract positive work from the treadmill, reduce the positive work performed by the legs, and reduce metabolic cost. We also show that walking with positive step length asymmetries, defined by longer steps on the fast belt, minimizes metabolic cost, and people choose this pattern after guided experience of a wide range of asymmetries. Our results suggest that split-belt adaptation can be interpreted as a process by which people learn to take advantage of mechanical work performed by an external device to improve economy.

Introduction

The neuromotor system can learn to take advantage of external assistance to produce and sustain motion. In everyday tasks such as walking and running, we often exploit the passive dynamics that arise from the interaction between the body and gravity to reduce the need for muscle force (Mochon & McMahon, 1980; McGeer, 1990). External assistance of our motion is not restricted to gravity in common tasks such as in downhill waking (Hunter et al., 2010). In more skilled tasks such as wave surfing we learn to harvest the assistance of waves and in wind surfing we learn to harvest the assistance of the wind. The ability of the neuromotor system to harness energy is critical if we are to take advantage of assistance from devices like powered prostheses and exoskeletons. Specifically, exoskeletons for the lower limbs are often designed to reduce muscular work, reduce effort, and increase endurance during walking (Ferris et al., 2007; Ferris, 2009; Herr, 2009). These devices commonly use powered actuators (Gordon & Ferris, 2007; Sawicki & Ferris, 2008; Gordon et al., 2013; Malcolm et al., 2013; Jackson & Collins, 2015; Koller et al., 2015; Selinger & Donelan, 2016; Galle et al., 2017), designed to reduce metabolic cost by performing mechanical work that would otherwise need to be generated by muscles. However, the degree to which these assistive devices reduce metabolic cost depends not only on the amount of work performed by the device, but also on the individual’s ability to exploit adaptive learning processes to take advantage of the external assistance (Zhang et al., 2017).

Although learning is key to maximizing the benefits from external assistance, the study of locomotor learning is often done in contexts that do not seem to have much in common with the study of assistive devices. For example, much of the work on adaptive locomotor learning uses a split-belt treadmill paradigm where individuals walk on a treadmill with two belts that move at different speeds (Dietz et al., 1994; Prokop et al., 1995; Reisman et al., 2005). Upon initial exposure to walking with the belts moving at different speeds, the distance between the feet at leading limb heel-strike—referred to here and in the split-belt literature as step length—becomes asymmetric. The step at foot strike on the slow belt becomes longer than the step length at foot-strike on the fast belt, because the fast belt pulls the leg into a more extended position. This asymmetry in step lengths is gradually reduced over the course of 10 to 15 minutes (Reisman et al., 2005) and is accompanied by a reduction in positive mechanical work performed by the legs (Selgrade et al., 2017) and a reduction in metabolic cost (Finley et al., 2013). The gradual reduction in step length asymmetry occurs in parallel with an increase in step time asymmetry (Finley et al., 2013), while stance times remains asymmetric thought the entire split-belt walking period (Reisman et al., 2005). A potential explanation for these observations is that individuals may adapt their gait during split-belt walking to minimize metabolic cost (Finley et al., 2013; Selinger et al., 2015).

Here we use principles from mechanics and experimental evidence to illustrate that, like exoskeletons, split-belt treadmills can provide assistance during walking. As we detail in the Theory and Predictions section, gaining assistance in the form of net mechanical work on the person from the treadmill is unique to the split-belt treadmill and is not possible on a normal “tied-belt” treadmill, or when walking over ground. Walking at a constant speed in any of these situations requires that the person generates braking and propulsive impulses that are balanced throughout the gait cycle. On a split belt treadmill, however, people can choose how to distribute braking and propulsion between the two belts to take advantage of the difference in belt speeds. If the forces and work generated by the legs are redistributed properly, the work performed by the treadmill on the person could be used to reduce the positive work required by the person’s muscles and ultimately reduce metabolic cost.

Split-belt treadmills provide a unique approach to study how to gain advantage of external assistance, as individuals could reduce the energetic cost of walking by stepping further forward on to the fast belt relative to the slow belt (Sánchez et al., 2017). As we describe in Theory and Predictions, this pattern would generate a larger braking force on the fast belt, which would be balanced by more propulsive force applied to the slow belt. Because of the difference in belt speeds, this results in net negative work performed by the person on the belts, and net positive work performed by the belts on the person. It is not guaranteed that the person benefits from this positive treadmill work—they may dissipate it by performing additional negative work. But it is also possible that they allow the positive work from the belts to assist walking by increasing their mechanical energy, reducing the positive mechanical work required from their muscles, and reducing their metabolic cost. This can only occur if individuals learn to take advantage of the treadmill work by reducing positive muscle work. Here, we show that individuals can learn to adapt their coordination to take advantage of the resulting positive work performed by the treadmill and reduce metabolic cost.

Theory and Predictions

Here we consider three walking conditions: overground walking, walking on side-by-side treadmills with belts “tied” to move at the same speed, and walking on side-by-side treadmills with belts “split” to move at different speeds. In overground walking, the ground is level and the person walks at a constant average speed relative to the ground. In the two treadmill cases, the treadmills are level and the person keeps the same average position on the treadmills equating to zero average speed relative to the stationary ground. Here, the reference frame is fixed to the ground, yet the arguments hold for other reference frames, as long as they are not accelerating and as long as one does not switch between reference frames. In the treadmill conditions, we consider three systems: the person, the left belt, and the right belt. The left and right belts move at the same speed in the tied-belt condition, and at different speeds in the split-belt condition. In the overground walking condition, the ground has zero speed resulting in only two systems: the person and the ground. In all of the above walking conditions, the following two constraints must be fulfilled.

• C1.The sum of the external forces acting on the person must be zero on average. Otherwise, there would be net acceleration or net vertical displacement violating the requirements of steady-state speed and level walking.
• C2.The net mechanical work on the person must be zero on average. Otherwise, there would be a net gain in kinetic or potential energy, again violating the steady-state speed and level walking requirements. Importantly, these two constraints taken together do not mean that external forces (e.g. treadmill forces) cannot perform net mechanical work on the person. Indeed, they could perform net negative or net positive work while still summing to zero net system acceleration as long as forces internal to the person system (e.g. muscle forces) perform the opposite amount of work.

These constraints affect the three walking conditions in different ways. For overground walking, they mean that the work performed by the person must be zero on average. This is because the ground cannot perform work on the person—relative to the ground-fixed reference frame, there is no displacement at the ground point of force application and thus the person must perform no net work (C2). Performing no net work can be accomplished by performing zero work, but more likely it is accomplished with equal amounts of positive and negative work. We consider the person as a point mass body with legs that are massless pistons that generate forces on the ground (or treadmill belts as in Figure 1A & B) and equal but opposite forces on the point mass. In this model, all the work performed by the person is performed by the legs. In overground walking, the legs can perform both positive and negative work as long as they sum to zero.

Figure 1.

A. We model the person as a point mass body with massless legs that can extend or compress. B. Free-body diagram of the person and treadmill systems. Blue represents the leg on the slow belt and red represents the leg on the fast belt when the belt velocities are split. Large open arrows represent forces, line arrows represent velocities. C. Power generated by the treadmill on the legs. We use the individual limbs method to calculate the power generated by the treadmill on each leg during a stride (not shown). Dashed arrows represent velocities rotated by 90 degrees to facilitate visualization of the power generated by the treadmill. The positive power generated by the treadmill on the legs is visualized with open rectangles above the point of force application, and negative power with closed rectangles below the point of force application. D. Power generated by the treadmill on the legs. During tied belt walking, the positive power generated by the treadmill on the legs is always equal to the negative power generated within a stride, at all step length asymmetries (SLA). This is true even though the total power generated during the long step is greater than that generated during the short step, at asymmetric step lengths. We can observe this through the rectangles shown to the right of each condition, where the sum of the top open rectangles always equals the sum of the bottom closed rectangles. However, when walking on split-belt treadmill, we see that at positive step length asymmetries (bottom row), the treadmill generates net positive power on the legs during the long step that is greater than the net negative power it generates during the short step. This leads to a net positive power on the person over the stride.

The constraints explained above also require the person to perform zero net work during tied-belt treadmill walking. Unlike overground walking, the person performs work on the belts during treadmill walking when considered from a ground-fixed reference frame. At heel contact, for example, the force exerted by the leading leg opposes the belt velocity at the point of contact (Figure 1B). Since the velocity at the point of force application only has a fore-aft component, the power generated by the treadmill on the leg is the dot product of the horizontal fore-aft force from the treadmill and the treadmill velocity. It is positive when the force and velocity are in the same direction, and negative when the two are opposite. At heel contact, this force will perform negative work on the belt. The belt does not slow down because its motor simultaneously does an equal amount of positive work on the belt. The reaction force of the belt on the person is equal and opposite to the force of the person on the belt (Figure 1B), but the velocity of the point of force application is the same—when a person does negative work on a belt, the belt does an equal amount of positive work on the person (Figure 1C).

When the belts are moving at the same speed, as is the case for the tied-belt condition, the positive and negative work done by the person on the belts, and that done by the belts on the person, both must sum to zero. This is because of the constraint that the external forces must sum to be zero on average (C1). Since the belt speeds are equal, balancing forces also means balancing the work done by the person on the belts, and by the belts on the person. Thus, a person walking on tied belts cannot benefit from net work performed by the belts on the person—it will always sum to zero (Figure 1D).

In split-belt walking, the belts can do net work on the person, and the work done by the person does not need to sum to zero. The external forces acting on the person must still average zero (C1), and the net work on the person must also average zero (C2). This zero net work may be accomplished with net positive or negative work by the person and net negative or positive work by the treadmills (Figure 1D). For example, the person’s leg on the fast belt might provide net propulsive force on the fast belt resulting in net positive fast leg work, and then the person’s slow leg might provide an equal amount of net braking force on the slow belt to bring the average horizontal force to zero. However, because of the differences in belt speeds, this braking force would require the slow leg to perform less net negative work on the slow belt than the net positive work that the fast leg had to perform on the fast belt for the same magnitude horizontal force. Together, the person’s legs would perform net positive work on the belts, and consequently, the belts would perform net negative work on the person. Alternatively, if the fast leg was responsible for more of the braking, and the slow leg for more of the propulsion, the person would perform net negative work and the person would gain net positive work from the treadmill belts.

Based on these predictions, a split-belt treadmill can be viewed as an assistive device—similar to an exoskeleton—where the person has to learn how to coordinate their legs to maximize the assistance from the motors and reduce the positive work generated. Positive muscle mechanical work is metabolically expensive relative to negative muscle mechanical work requiring roughly five times the ATP per Joule (Burdett et al., 1983; Umberger et al., 2003). To decrease the relatively expensive positive mechanical work, a person should decrease the propulsive forces generated by the fast leg on the fast belt by lifting off the fast belt with less hip extension, and instead rely on the slow leg to perform more propulsion for less positive work by lifting off at a larger hip extension angle and contacting at a smaller angle during heel strike. This effect will shorten the distance between the feet at slow-leg heel-strike (slow step length: SL_Slow ) and lengthen the distance between the feet at fast-leg heel-strike (fast step length SL_Fast). If we consider step length asymmetry as a measure of the difference between the fast step length and the slow step length, this change in coordination will shift asymmetry to more positive values.

To summarize, we predict that as an individual adopts a more positive step length asymmetry, the split-belt treadmill will perform more positive work on the person, reducing the positive work required by their muscles. Because of the relative expense of positive work, we also predict a reduction in the metabolic cost of walking as step length asymmetry becomes more positive, consistent with the findings from previous adaptation experiments (Finley et al., 2013). However, we do not attempt to predict the metabolically optimal step length asymmetry as positive muscle mechanical work is only one contributor to metabolic cost, and it is not clear how other contributors, such as the cost of step timing (Ellis et al., 2013), the cost to swing the legs (Doke et al., 2005), or the cost of maintaining an upright posture (Huang et al., 2012), change with step length asymmetry.

Materials and Methods

Experiment Protocol

Sixteen healthy participants (7 female, 9 male, age 27 +/− 3.5 years) completed our study. All experimental procedures were approved by the University of Southern California Institutional Review Board and each participant provided written informed consent before testing began. All aspects of the study conformed to the principles described in the Declaration of Helsinki.

We used a biofeedback-based protocol to map the relationship between mechanical work, metabolic cost, and step length asymmetry during split-belt walking (Figure 2B). Participants first walked on an instrumented split-belt treadmill (Fully Instrumented Treadmill, Bertec Corporation, OH) with both belts at 1.0 m/s while we measured their baseline step lengths and metabolic cost. In the next trial, we introduced the visual feedback and participants walked with both belts at 1.0 m/s, while matching their step lengths to the visual targets (see below). For the next seven trials, we set the belt speeds to a 3:1 ratio, with the left belt at 1.5 m/s and the right belt at 0.5 m/s. Participants performed the split-belt trials with visual feedback providing target step length asymmetries of 0.00, +/− 0.05, +/− 0.10 and +/−0.15 (see below). These asymmetries were relative to each participant’s baseline and we presented these trials in random order. To determine whether mechanical work or energetic cost increased at extreme positive asymmetries, two participants performed two additional trials at asymmetries of +0.20 and +0.25. Each of these trials was six minutes in duration.

Figure 2:

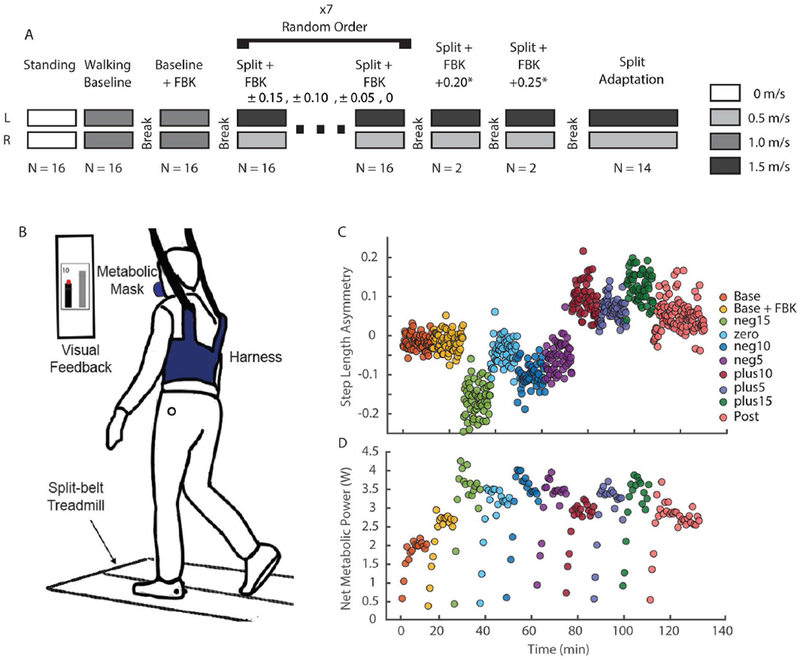
Experimental protocol and setup. A) Detailed experimental protocol. We randomized the order of the split-belt trials during which feedback of step lengths was provided to obtain seven different levels of asymmetry. Two participants performed two additional trials for levels of 0.20 and 0.25 step length asymmetry. All participants performed the split-belt adaptation trial last. The adaptation trial was performed freely for 10 minutes, with no feedback of step length and no instructions; all other trials lasted six minutes with four-minute breaks in between. B) Experimental setup. Reflective markers were placed bilaterally on the lateral malleoli to measure step lengths in real time. Two additional markers were placed on left and right greater trochanters to measure hip width for the visual feedback. An overhead harness was used to prevent falls without providing body weight support. No handrail was provided. Metabolic cost was measured using expired gas analyses. C) Raw values of step length asymmetry for all walking trials for a representative participant. Average step length asymmetry was binned every 10s to illustrate performance in the time domain. D) Raw net metabolic power values measured for each walking trial for the participant in panel C. All values were baseline corrected to standing baseline. Data were averaged every three breaths for metabolic cost to reduce the number of data points for visualization purposes. The last three steady state minutes of the metabolic cost data in each trial were used for analyses.

After the visual feedback trials, participants completed a 10-minute split-belt adaptation trial with no visual feedback of their step lengths and no explicit instructions of the step lengths they should maintain. The purpose of the final trial was to test whether participants would converge towards the metabolically or mechanically optimal level of asymmetry observed during the previous split-belt trials. During all walking trials, participants wore a harness designed to prevent falls while providing no body weight support. Participants did not hold on to handrails during any portion of the trials. After each walking trial, participants sat down and rested for at least four minutes, and we visually inspected measured metabolic cost to ensure that it had returned to resting levels before beginning the next trial.

For all feedback conditions, participants relied on a monitor located at eye-level in front of the treadmill to target the desired step length targets. We measured the position of ankle markers placed bilaterally on the lateral malleoli at 100 Hz using an 11 camera Qualisys Oqus camera system (QTM, Sweden) and the visual display was controlled by custom software written in Vizard (Worldviz, Santa Barbara, CA). A fourth-order low-pass digital Butterworth filter smoothed marker data using a cut-off frequency of 10 Hz. We defined peak fore-aft position of the filtered ankle marker trajectories as heel-strike, and step length as the distance between right and left ankle markers at this instance. The monitor displayed the ankle position for the intervals where the ground reaction forces were less than 20N (Zeni et al., 2008), which corresponded to swing phase. At foot-strike, defined as the point when the ground reaction force exceeded 20N, the ankle marker disappeared from the visual feedback. We instructed participants to step such that the location of the ankle marker at heel-strike would match the top a vertical bar in the visual display (Figure 2B). Participants targeted the left bar for the left leg and the right bar for the right leg. We constrained the sum of the step lengths to be equal to the baseline stride length (Equation 1), therefore participants adjusted the individual step lengths while maintaining stride length equal to that measured during the baseline trial. Note that the baseline speed was 1.0 m/s, which is the average of the individual belt speeds during the split-belt condition:

$$S{L}_{fast}+S{L}_{slow}=Strid{e}_{baseline}$$ (1)

We constrained the desired stride length so that the desired step lengths would be fixed for a given level of step length asymmetry. To reinforce performance, the display provided participants with a score for each step at heel-strike, according to the following equation, rounded to the nearest integer:

$$Score=10-20*abs\left(1-\frac{StepLength}{TargetStepLength}\right)$$ (2)

Participants only received a score if their step lengths were within eight standard deviations from the target. For example, for a representative participant, the average step length measured on the baseline trial was 560mm, thus, the achieved step length must be within 14 mm of the target to obtain a score of 10 on each side. For this same participant, the standard deviation was 17mm. If the step length was off-target by more than 136 mm, the participant did not receive a score. We verbally encouraged participants to obtain the maximum score of 10 points for all steps. Participants were successful at maintaining scores of above 8 points for each stride and maintaining each leg on its corresponding belt.

The target step lengths were selected to correspond to different levels of step length asymmetry which, per convention (Finley et al., 2013; Sánchez et al., 2017), was defined as follows:

$$StepLengthAsymmetry=\frac{S{L}_{fast}-S{L}_{slow}}{S{L}_{fast}+S{L}_{slow}}$$ (3)

Here SL_fast is the step length at the instant the leading leg heel-strikes on the fast belt, and SL_slow is the step length at the instant the leading leg heel-strikes on the slow belt. Negative values correspond to longer steps with the slow (right) leg and positive values correspond to longer steps with the fast (left) leg. We used the last 100 strides of each trial to obtain the average step length asymmetry. Participants’ baseline step length asymmetry ranged from −0.039 to 0.032, with a mean and standard deviation of 0.007 and 0.018.

There may be more direct methods to change leg coordination to gain positive work from the treadmill than manipulating step length asymmetry. We choose to use step length asymmetry for two reasons. First, prior research has shown that during split-belt walking, people increase fast step lengths by stepping further forward on the fast belt and decrease slow step length by lifting the trailing fast leg sooner, both during adaptation and when increasingly more positive asymmetries are enforced with visual feedback (Reisman et al., 2005; Roemmich et al., 2016a; Sánchez et al., 2017; Leech & Roemmich, 2018). Second, the literature on adapting to split-belts is primarily focused on considering adaptation as a process that minimizes step length asymmetry error (Roemmich et al., 2016b; Leech & Roemmich, 2018) and keeping our manipulation in terms of step length asymmetry helps make clear that there are alternative explanations for why the neuromotor system may adapt to reduce negative step length asymmetries. We anticipate that stepping further forward on the fast belt will lead to more braking force by the fast leg around heel-strike, and thus more positive work on the person by the belt. We also anticipate that short steps with the slow leg will be associated with reduced propulsive force generated by the fast leg around toe-off, and thus less positive work generated by that leg. In addition, longer steps with the fast belt will also lead the slow leg to lift off at a greater hip angle, generating increased propulsion.

Analysis

We assessed metabolic cost by determining the rates of oxygen consumption (V_O2) and carbon dioxide production (V_CO2) using a TrueOne® 2400 system (Parvomedics, UT). The metabolic cart recorded data on a breath-by-breath basis and subsequently, we re-sampled these data at a frequency of 0.1 Hz and averaged for smoothing in 10s bins. Since it takes approximately three minutes for oxygen consumption and carbon dioxide production by the body to reach steady-state in a task, we first identified the time point closest to the third minute of the trial (Selinger et al., 2015) . We then measured the total V_O2 consumed and the V_CO2 produced from that time point onwards until the end of the trial, where the cost was at a steady state and when participants had already achieved a steady performance of the task. We then estimated the energy consumed during the last three minutes using the standard Brockway equation (Brockway, 1987) as follows:

$$E_{met,gross}=\left(16.48\frac{J}{ml{O}_2}{V}_{O_2}\cdot 1000\right)+\left(4.48\frac{J}{mlC{O}_2}{V}_{C{O}_2}\cdot 1000\right)$$ (4)

From here, we dived E_met,gross by the exact duration (T) over which it was calculated to obtain an estimate of the gross metabolic rate P_met,gross measured in Watts. Finally, we subtracted each participants’ standing metabolic rate from each walking trials. Thus, all metabolic rate values presented here are net metabolic rate. The addition of visual feedback during the second baseline trial increased metabolic rate by 11 +/− 11% compared to the cost of walking without feedback (p<0.001) despite there being no changes in step length asymmetry (p=0.359). We expect this added cost to remain constant for all trials that required visual feedback.

We estimated the mechanical work performed by the legs using an extension of the individual limbs method (Donelan et al., 2001; Selgrade et al., 2017). This method approximates the legs as massless pistons and the entire body as a point mass acting at the center of mass (Figure 1A). We use a reference frame attached to the stationary ground—the belt speeds and center of mass velocity are relative to this reference frame. We measured individual leg ground reaction forces from the instrumented treadmill at 1,000 Hz and filtered this signal with 20 Hz cut-off low-pass zero-lag digital Butterworth filter. We segmented the ground reaction forces into strides using a vertical ground reaction force threshold of 32N (Selgrade et al., 2017) to identify the beginning and end of each stride and performed the following analysis on a stride-by-stride basis.

We calculated the medio-lateral, fore-aft and vertical center of mass velocities by first calculating the center of mass accelerations as the sum of the forces acting on the body normalized for body mass (Donelan et al., 2001; Selgrade et al., 2017). We estimated body mass as the average vertical force during the final 100 strides of the trial, divided by the acceleration due to gravity (9.81 m/s²). We calculated center of mass velocities from the time integral of the center of mass accelerations. We determined the integration constants by requiring the average center of mass velocity over a stride to be zero in each direction because net movement in any direction must on average be small on a treadmill.

The total mechanical power generated by each leg is composed of power generated by the leg on the body and the power generated by the leg on the treadmill’s belts. We define the mechanical power generated on the body by a leg as the dot product of the ground reaction force from that leg and the center of mass velocity. Similarly, we define the mechanical power generated by a leg on a belt as the dot product of the force generated by the leg on the belt, which is equal and opposite to the ground reaction force measured by the treadmill, and the velocity of the corresponding belt. The medio-lateral and vertical components of belt velocity are zero, and the fore-aft component is either −0.5 m/s (slow belt), −1.5 m/s (fast belt), or −1.0 m/s (tied belts). For each leg, we then calculated the instantaneous sum of the two powers to obtain the total instantaneous mechanical power generated by that leg (Figure 1B). We calculate the instantaneous power generated by the slow and fast belts on the body as the dot product of the ground reaction force measured from that belt with that belt’s velocity.

To determine the total positive and negative work performed by a leg or a belt, we calculated the time integral of the positive or negative portion of its instantaneous power over the stride cycle (Selinger & Donelan, 2014). The net work performed by a leg or a belt is the time integral of the full instantaneous power over the stride cycle. We express all measures of work as work rates by dividing each measure by stride duration. As with step length asymmetry, measures of work rate for each trial are the average values over the last 100 strides.

We converted the metabolic rate and mechanical work rate to dimensionless units to reduce variability between subjects. We divided each individual’s values by ml^0.5g^1.5 here m is their body mass, l is their leg length and g is gravity (9.81 m/ŝ2). Thus, using the average body mass (75.4 kg) and average leg length (0.88 m) of our participants, all reported dimensionless values can be approximately redimensionalized to the average values in Watts by multiplying by 2.17 × 10³.

Statistical Analyses

A participant’s mechanical work and metabolic cost depend not only on the conditions that we control but also on differences between individuals. Our purpose here is to test predictions about the former—we do not, for example, seek to explain the differences in metabolic cost between individuals for a given condition. Consequently, we used mixed-effect regression models that allowed individualized intercepts but shared a fixed dependence on the independent variables of interest These models captured the relationship between 1) measure of foot placement and step length asymmetry, 2) measures of mechanical work and step length asymmetry, 3) measures of mechanical work performed by the legs and the mechanical work performed by the treadmill, 4) metabolic power and mechanical work performed by the treadmill, and 5) metabolic power and step length asymmetry. Although the target levels of step length asymmetry were set at discrete values (0.00, +/−0.05, +/−0.10, +/−0.15), the actual step length asymmetry used in our regression models was a continuous variable since each participant’s actual performance differed from the target asymmetry. All models included a random intercept for each participant to account for unknown, subject-specific effects. We used a modified version of the marginal R² for linear mixed effect models (Nakagawa & Schielzeth, 2013) to compute the variance explained by the fixed components of our linear models. We computed R² as the ratio of the variance computed from the fixed effects and the sum of the variance from both the fixed effects and residuals from the regression model. We used this approach in lieu of the conditional R², which accounts for the variance explained by both the fixed and random effects, because we were only interested in quantifying the explanatory value of the fixed effects. To make our figures consistent with our statistical analysis approach, we removed the individualized intercepts from each participant’s data before generating each scatterplot. Lastly, we determined if participants plateaued at a step length asymmetry that differed from baseline during the adaptation period using a paired-samples t-test. We conducted all statistical analyses in Matlab R2017a (Mathworks, Natick, MA) and set statistical significance level to p < 0.05.

Results

Modulation of Foot Position to Achieve Target Step Length Asymmetry

Participants modified the position of both the leading limb and the trailing limb at initial contact of the leading limb as they varied step length asymmetry throughout the experiment (Figure 3). As step length asymmetry became more positive, participants increased the length of their steps when stepping on the fast belt and decreased the length of their steps when stepping on the slow belt. To take longer steps on the fast belt, participants placed their leading foot farther forward on the fast belt (β = 243.4, 95% CI [212.2, 274.6], p=2.22e-29) and extended their trailing foot farther behind the body on the slow belt (β = −356.1, 95% CI [−385.1, −327.1], p=4.43e-46). To take shorter steps on the slow belt, participants placed the leading leg closer to the body (β = −348.5, 95% CI [−385.3, −311.6], p=5.00e-36) but only made minor reductions in trailing limb extension on the fast belt (β = 85.4, 95% CI [56.5, 114.3], p=5.17e-8).

Figure 3.

Distance from the leading and trailing foot to the center of mass at heel strike. The x-axes show the achieved step length asymmetry for all participants. Positive values indicate that the foot is anterior to the center of mass while negative values indicate that the foot is posterior to the center of mass. Closed and open points correspond to the fast and slow limb, respectively. The distance between the leading and trailing feet at heel strike constitutes the step length. A) Fast step lengths. To increase the fast step length as asymmetry increased from negative to positive, participants increased both leading foot distance to the center of mass and trailing foot distance to the center of mass. B) Slow step lengths. To decrease the slow step length as asymmetry increased from negative to positive, participants primarily decreased the distance from the leading foot to the center of mass while maintaining a relatively consistent trailing foot position.

Mechanical Work Performed by the Legs and the Treadmill Varies with Step Length Asymmetry

Consistent with our hypothesis, participants transitioned from performing net positive work with the legs at negative step length asymmetries to performing net negative work at positive asymmetries. This change in work performed by the limbs can be appreciated by understanding how the mechanical power generated by each limb changes across levels of asymmetry. The fast leg transitioned from generating a large amount of positive power during push-off at −15% asymmetry to performing a large amount of negative work during weight acceptance at an asymmetry of +15% (Figure 4A). In contrast, there were negligible changes in mechanical power in the slow leg across levels of asymmetry (Figure 4B). Overall, the amount of positive work performed by the legs decreased by ~13% between −15% and +15% step length asymmetry (Figure 5A, β = −0.009, 95% CI [−0.013, −0.006], p=3.52e-7). In contrast, the amount of negative work performed by the legs increased by ~33% over the full range of step length asymmetries (Figure 5B, β = −0.019, 95% CI [−0.0220, −0.0151], p=7.59e-19). As a result of these combined changes, the legs ultimately performed more negative work than positive work at positive asymmetries (Figure 5C, β = −0.028, 95% CI [−0.029, −0.027], p=1.66e-67).

Figure 4:

Mechanical power generated by the A) fast leg, B) slow leg, C) fast belt, and D) slow belt throughout the stride cycle. The power generated by the treadmill belts represents the rate of mechanical work performed by each belt on the body. During the early portion of the stride cycle (~0-15%), the leading, fast leg generated a large peak negative peak in power while the trailing, slow leg generated a relatively smaller positive peak. This relationship reversed during the later portion of the stride cycle (~40-70% of the gait cycle) such that the fast leg generated a burst of positive power while the slow leg generated a smaller burst of negative power. Each trace is an average of all participants (n = 16). The stride cycle begins and ends at foot-strike of the fast limb. Blue, yellow, and red traces correspond to split-belt walking at step length asymmetries of −15%, 0%, and +15%, respectively.

Figure 5:

Average rate of work performed by the legs and the treadmill belts as a function of step length asymmetry. A) Positive work performed by the legs, B) negative work performed by the legs, and C) total work performed by the legs. D) Positive work performed on the body by the treadmill, E) negative work performed on the body by the treadmill, and F) total work performed by the treadmill on the body. Work rate is expressed in dimensionless units on the left y-axis and in Watts on the right y-axis. Each data point represents a single trial for an individual participant and each color represents a different participant.

We predicted that the treadmill would act as an assistive device at positive step length asymmetries by performing net positive work on the body, and our observations were consistent with this prediction (Figure 4C). As asymmetry became more positive, there was a ~28% increase in the amount of positive work performed by the belts on the body (Figure 5D, β =0.016, 95% CI [0.014, 0.018], p=1.64e-29) and a ~15% decrease in the amount of negative work performed by the belts on the body (Figure 5E, β =0.011, 95% CI [0.010, 0.013], p=1.58e-23). Together, these changes resulted in a shift from the treadmill performing mostly negative work on the body and extracting energy from the person at negative asymmetries to performing mostly positive work on the body and adding energy to the person at positive asymmetries (Figure 5F, β =0.028, 95% CI [0.026, 0.029], p=4.76e-67).

The legs’ shift toward performing net negative work at positive step length asymmetries was primarily driven by changes in the fast leg. Across participants, we observed both a ~30 % reduction in positive work (Figure 6A, β =0.010, 95% CI [−0.012, 0.008], p=7.34e-17) and a ~36% increase in negative work performed by the fast leg (Figure 6C, β = −0.012, 95% CI [−0.014, −0.009], p=7.63e-14) at increasingly positive asymmetries. In contrast, there were no changes in positive work performed by the leg on the slow belt (Figure 6B, p=0.53), but there was a ~21% increase in negative work by the slow leg at positive asymmetries (Figure 6D, β = −0.007, 95% CI [−0.010, −0.004], p=4e-5).

Figure 6:

Average rate of work performed by the individual legs across levels of step length asymmetry. A) Positive work performed by the fast leg, B) positive work performed by the slow leg, C) negative work performed by the fast leg, and D) negative work performed by the slow leg. Work rate is expressed in dimensionless units on the left y-axis and in Watts on the right y-axis. Each data point represents a single trial for an individual participant and each color represents a different participant.

As the treadmill performed increasingly more positive work on the body, there was a proportional reduction in positive work performed by the legs (Figure 7, β = −0.33, 95% CI [−0.43, −0.23], p=2.8e-9). The slope of this relationship suggests that participants exploited the work performed by the treadmill belts with an effectiveness of approximately 33%. That is, for every 3 Joules of positive work performed by the belts on the person, the person reduced the positive work performed by the legs by about 1 Joule.

Figure 7:

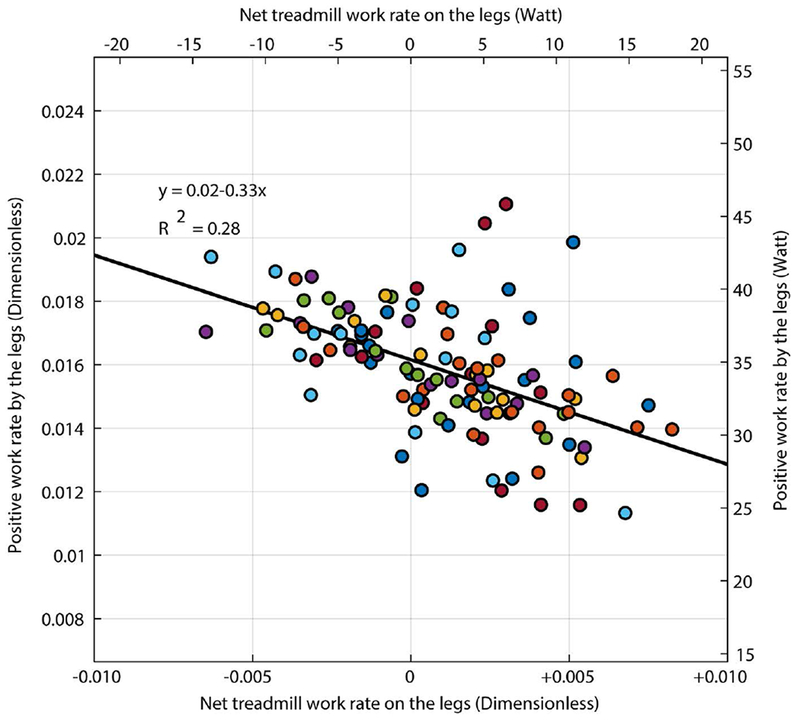
Relationship between the average rate of positive work performed by the legs and the average rate of work performed by the treadmill on the body. Work rate is expressed in dimensionless units on the lower x-axis and the left y-axis and in Watts on the upper x-axis and right y-axis. Each data point represents a single trial for an individual participant and each color represents a different participant.

Assistance Provided by the Treadmill Led to a Reduction in Metabolic Cost

The assistance provided by the treadmill at positive step length asymmetries was not only associated with a reduction in positive work performed by the legs but was also associated with a reduction in metabolic cost (Figure 8A, β = −1.54, 95% CI [−2.07, −1.02], p=5.34e-8). Since the assistance provided by the treadmill was associated with a reduction in positive work performed by the legs, we also found that metabolic power was strongly correlated with the total positive work performed by the legs (Figure 8B, β = 0.105, 95% CI [0.091, −0.119], p=1.89e-27). The slope of this relationship suggests that positive work was performed at an efficiency of about 10%. Overall, by exploiting the assistance provided by the treadmills, participants achieved an approximately 14% reduction (8 to 18% reduction, 95% CI) in metabolic cost relative to the most costly level of step length asymmetry (Figure 8C).

Figure 8:

Metabolic power, mechanical work, and asymmetry. A) Metabolic power as a function of the rate of work performed by the treadmill on the body. B) Positive work rate versus metabolic power. C) Metabolic power as a function of step length asymmetry. Each data point represents a single trial for an individual participant.

The Ability to Use Step Length Asymmetry to Exploit Assistance Provided by the Treadmill is Bounded

Although the increase in positive work performed by the treadmill led to a reduction in metabolic cost, we also wanted to determine if this ability to exploit the work performed by the treadmill increased indefinitely or whether there was a specific level of asymmetry that minimized metabolic cost. Our results supported the existence of an energetically optimal level of step length asymmetry as a regression model including both linear and quadratic terms explained the relationship between metabolic cost and step length asymmetry better than a simple linear model (LRStat = 4.83, p=0.028, adjusted R² = 0.27, Figure 8C). Bootstrap analyses indicated that the asymmetry that minimized metabolic cost had a 95% confidence interval of 0.06 and 0.38, which is consistent with our prediction that positive asymmetries minimize energetic cost.

Although metabolic cost generally decreased with increasingly positive asymmetries as is predicted in our model, experimentally we expected that metabolic cost would increase again at large positive asymmetries given biomechanical constraints associated with walking with extreme positive asymmetries. We confirmed this finding in two participants, who each completed two additional trials where they walked at target levels of 0.20 and 0.25 step length asymmetry. The metabolic cost for three out of four of these trials was 0.027 ± 0.022 greater than the minimum cost predicted from the regression fit. These increases in metabolic cost at extreme positive asymmetries support the quadratic relationship that we determined in our analysis.

Participants Chose Positive Step Length Asymmetries When Allowed to Freely Adapt

Lastly, we found that participants chose to walk at a level of step length asymmetry near that which minimized metabolic cost when they were allowed to freely select their walking pattern. After experiencing a range of asymmetries during the cost mapping trials, participants tended to plateau at step length asymmetries that were more positive than their natural baseline asymmetry (Figure 9, mean: 0.028, 95% CI [0.0018, 0.0434], p=0.010) though they had shorter stride lengths during adaptation (95% CI [929 mm, 999 mm]) than they did when walking at similar levels of asymmetry during the split-belt trials with visual feedback (95% CI [47, 93] mm shorter strides during adaptation, p= 1.03e-05). This positive step length asymmetry markedly differs from the behavior typically observed within a single session of adaptation where participants most often plateau at slightly negative asymmetries (Leech et al., 2018a, 2018b). In addition, there was no significant difference between the metabolic cost measured at the end of the adaptation trial (0.086, 95% CI [0.074, 0.10]) and the minimum predicted from the regression fit (0.096, p=0.12).

Figure 9:

Adaptation of step length asymmetry during the adaptation trial in the absence of visual feedback. Participants consistently selected positive asymmetries near those which minimized metabolic cost during the cost mapping trials. The dark blue line represents the average asymmetry as a function of stride number when averaged across all participants and the light blue area represents the standard deviation about this average. The final error represents the average ± standard deviation level of asymmetry at the end of the split-belt adaptation trial. The step length asymmetry achieved during the last 50 strides was significantly different from their baseline step length asymmetry (p=0.010).

Discussion

Learning to gain assistance from external sources is a general problem for the neuromotor system. We explored this problem using a split-belt treadmill paradigm to determine whether people learn to harness energy from the differences in belt speeds to reduce the metabolic cost of walking. People exploited the assistance provided by the treadmill by changing their step lengths such that the treadmill performed net positive work on the body, thereby allowing the legs to perform net negative work. This shift toward performance of negative work by the legs was associated with a reduction in metabolic cost which likely reflects the energetic benefits of negative work (Herzog, 2018). Therefore, the reductions in asymmetry commonly observed during split-belt walking can be interpreted as a strategy generated by the neuromotor system to take advantage of the work performed by the treadmill to reduce energetic cost (Finley et al., 2013; Sánchez et al., 2017).

Similar to using a powered exoskeleton, individuals can learn to coordinate their movement to maximize the assistance from the treadmill’s motors. We find that individuals use the assistance from the split-belt treadmill with an effectiveness of 33%, i.e. they reduce their positive work by 1 J for every 3 J of positive work done by the treadmill. While this is not a commonly reported metric in exoskeleton use, Sawicki and Ferris (Sawicki & Ferris, 2008) used a similar metric to show that their ankle exoskeletons reduced joint mechanical power by 41% relative to the mechanical power provided by their ankle exoskeleton—similar to our results. We focus on this metric because while the maximum effectiveness possible in powered exoskeletons may be system-dependant and hard to quantify, we can provide a reasoned estimate of the maximum possible effectiveness for split-belt treadmill walking. When the treadmill does positive work on the person, it applies a negative force on the person that has to be cancelled out by an equal positive propulsive force applied by the trailing leg on the treadmill. In applying this propulsive force, the trailing leg has to perform positive work on the treadmill. In fact, the minimum amount of positive work necessary depends on the ratio of the belt speeds. In our experiment, the fast belt moved three times faster than the slow belt. Since work is the time integral of the dot product of force and velocity, this means that the trailing leg on the slow belt has to at least perform positive work that is roughly one third of the negative work performed by the leading leg on the fast belt. This means that the participants in our study could have at most achieved an effectiveness of ~67%. We only include the fast step in this calculation because any braking force on the slow belt, only further decreases this value.

It is possible that individuals cannot, in practice, exploit the positive work from the treadmill to the degree we have suggested here. One strategy to improve effectiveness in split-belt walking is for individuals to use more positive step length asymmetries. However, the extreme positive asymmetries needed to maximize the positive work performed by the treadmill likely challenge anatomical constraints. In addition, even at less extreme positive asymmetries, an individual might choose to perform more positive work, and consequently also negative work, than necessary simply to feel safe in the new gait (Hunter et al., 2010). We suspect that with practice and appropriate guidance, the effectiveness observed in our study can be improved from that observed here. This is one of the goals of our future research.

The reduction in positive mechanical work we observed was accompanied by a reduction in metabolic cost of 14%. This reduction is comparable to that observed in powered lower-limb exoskeletons that can currently achieve reductions up to 17% (Ding et al., 2018). Both effectiveness and energetic benefits incurred as a result of learning to walk in lower-limb exoskeletons are similar to that observed in split-belt walking. As described earlier, we suspect that people can be taught to improve their effectiveness and maximize energetic benefits in split-belt walking and when using powered exoskeletons. Because split-belt treadmills are becoming more common in biomechanics labs, split-belt walking could become a model experimental paradigm to understand how the human neuromotor system learns to walk in environments where it is possible to take advantage of external assistance.

Traditionally, studies of split-belt adaptation have shown that after 10-20 minutes of adaptation, individuals converge to step length asymmetries near zero (Reisman et al., 2005; Finley et al., 2013). This adaptation toward a step length asymmetry of zero is consistent with the hypothesis that step length asymmetry is treated as an error by the nervous system. In this hypothesis, the difference between expected and achieved sensory feedback during movement, known as sensory prediction error, drives motor adaptation (Shadmehr et al., 2010; Vazquez et al., 2015; Roemmich et al., 2016b). Reductions in step length asymmetry are also consistent with the hypothesis that individuals converge towards habitual behaviors when exposed to novel environments (de Rugy et al., 2012; Loeb, 2012). Based on this hypothesis, people adopt steps of equal length because this is the habitual pattern they use regularly. One challenge to both of these notions is that people adopt asymmetric step times in order to take steps of equal length (Finley et al., 2015) and thus, it is not immediately apparent why the nervous system would choose to reduce errors in step length but not in time. In addition, these asymmetries in step time could lead to sensory prediction errors and are non-habitual behaviors in the time domain. Further evidence that adaptation is not purely driven by sensory prediction errors related to step length asymmetry was provided by a recent study showing that sensory recalibration and motor recalibration have different timescales (Leech et al., 2018c). In this study, the authors postulated that if we recalibrate motor commands in response to sensory prediction errors, then error perception is also updated (Izawa et al., 2008). Therefore, if the same neural processes drive motor and perceptual recalibration during locomotor adaptation, they would change over a similar timescale. However, the authors found that motor and perceptual adaptation to differences in belt speeds occurred over different timescales and are likely independent of each other. The authors also found that after multiple days of adaptation, individuals plateau at positive step length asymmetries. These results, together with our findings that individuals adopt positive asymmetries after being exposed to the cost landscape, refute the idea that split-belt adaptation is explained by the nervous system’s desire to minimize perceived errors in step length asymmetry or converge towards habitual behaviors. Instead, energy optimization explains both why people reduce step length asymmetry during single sessions of split-belt adaptation and why they adopt positive asymmetries when provided with more extensive experience.

A logical follow-up question is, if energetic optimization is the goal of split-belt adaptation, why are positive asymmetries that minimize mechanical work and metabolic cost not observed during adaptation? One potential explanation is that the energetic savings for positive asymmetries are minor compared to the cost of symmetry, and this might impede the optimization process. Given that the confidence interval for the step length asymmetry associated with the lowest metabolic cost ranged from 6 to 38%, the energetic gradient might be too shallow for people to obtain meaningful energetic reductions from walking with positive asymmetries. In fact, our results show that the optimal step length asymmetry reduced metabolic cost by only 2% compared to symmetry. Despite these small savings, after exposure to the step length asymmetry landscape, participants in our study plateaued at positive asymmetries during adaptation. This suggests that people may be willing to adjust how they walk for savings of less than 5% as reported in previous work (Selinger et al., 2015).

Alternatively, positive asymmetries may not have been observed during typical locomotor adaptation studies because energetic optimization occurs over a timescale that is longer than that commonly used in adaptation studies (Balasubramanian et al., 2009; Huang et al., 2012). To date, most locomotor adaptation studies have been performed using single session paradigms of 10 to 20 minutes in duration (Reisman et al., 2005; Finley et al., 2013). Thus, short, single bout studies may not provide enough time or experience for individuals to fine tune their steps lengths to achieve the more energetically optimal positive asymmetries. Consistent with the interpretation that energy optimization occurs over a longer timescale, people tend to reach positive asymmetries when allowed to adapt to a split-belt treadmill over multiple days (Leech et al., 2018c). Surprisingly, the visual feedback in our experiment, which exposed participants to positive asymmetries, accelerated the convergence towards positive asymmetries in a single session to that which occurs during multi-day adaptation. The longer timescale for energetic optimization is further supported by work in the upper extremity, which shows that improvements in task performance and fine tuning of upper extremity muscle activation, occurred over a faster timescale than energy minimization (Balasubramanian et al., 2009; Huang et al., 2012). Overall, we conclude that the symmetric steps commonly observed at the conclusion of previous split-belt adaptation studies and the associated reductions in energetic cost (Finley et al., 2013; Selgrade et al., 2017), may be only a partial picture of a slower energetic optimization process that plateaus at positive asymmetries.

One of the features of our study is that we constrained stride lengths to those measured during baseline with the belts tied at 1.0 m/s. Given this constraint, the metabolic optima that we found in this study is a local minimum for that specific stride length and may not be a global minimum. We imposed this constraint as it would not be practical to characterize the metabolic cost landscape across both the dimensions of step length asymmetry and stride length. Moreover, post-hoc analysis of data from a previous adaptation study (Sánchez et al., 2017) showed that there was no change in stride length during split-belt adaptation compared to baseline walking (p=0.389). Our constraint on stride length is particularly relevant given the results of the adaptation trial in the current study, where 15/16 participants adapted to the split-belt treadmill using shorter stride lengths. Whether optimization of stride length can further reduce positive work and metabolic cost during locomotor adaptation remains to be seen.

In conclusion, the process by which people adapt to walking on a split-belt treadmill is just one example of a broad class of tasks in which the neuromotor system learns to exploit external assistance to improve economy. A common feature of these types of tasks is that the process of optimizing the use of assistance may proceed quite gradually in the absence of guided experience. Ultimately, understanding how best to guide people through a range of experiences capable of accelerating the learning and optimization process has important implications for maximizing the utility of assistive devices such as exoskeletons and prostheses.

Key points summary.

• The neuromotor system generates flexible motor patterns that can adapt to changes in our bodies or environment and also take advantage of assistance provided by the environment.

• We ask how energy minimization influences adaptive learning during human locomotion to improve economy when walking on a split-belt treadmill. We use a model-based approach to predict how people should adjust their walking pattern to take advantage of the assistance provided by the treadmill, and we validate these predictions empirically.

• We show that adaptation to a split-belt treadmill can be explained as a process by which people reduce step length asymmetry to take advantage of the work performed by the treadmill to reduce metabolic cost.

• Our results also have implications for the evaluation of devices designed to reduce effort during walking, as locomotor adaptation may serve as a model approach to understand how people learn to take advantage of external assistance.