Hierarchical Rough-to-Fine Model for Infant Age Prediction based on Cortical Features

Abstract

Prediction of the chronological age based on neuroimaging data is important for brain development analysis and brain disease diagnosis. Although many researches have been conducted for age prediction of older children and adults, little work has been dedicated to infants. To this end, this paper focuses on predicting infant age from birth to 2 years old using brain MR images, as well as identifying some related biomarkers. However, brain development during infancy is too rapid and heterogeneous to be accurately modeled by the conventional regression models. To address this issue, a two-stage prediction method is proposed. Specifically, our method first roughly predicts the age range of an infant and then finely predicts the accurate chronological age based on a learned, age-group-specific regression model. Combining this two-stage prediction method with another complementary one-stage prediction method, a Hierarchical Rough-to-Fine (HRtoF) model is built. HRtoF effectively splits the rapid and heterogeneous changes during a long time period into several short time ranges and further mines the discrimination capability of cortical features, thus reaching high accuracy in infant age prediction. Taking 8 types of cortical morphometric features from structural MRI as predictors, the effectiveness of our proposed HRtoF model is validated using an infant dataset including 50 healthy subjects with 251 longitudinal MRI scans from 14 to 797 days. Comparing with 5 state-of-the-art regression methods, HRtoF model reduces the mean absolute error of the prediction from >48 days to 32.1 days. The correlation coefficient of the predicted age and the chronological age reaches 0.963. Moreover, based on HRtoF, the relative contributions of the 8 types of cortical features for age prediction are also studied.

I. Introduction

THE HUMAN brain changes dynamically during the prenatal and early postnatal development [1–4]. Based on non-invasive brain MR imaging, studying brain developmental trajectories becomes possible and promising. Besides measuring the longitudinal change of brain features [5, 6], age prediction based on brain MRI features and machine learning methods is one of the most effective ways for brain development analysis [7]. Identifying the mapping from brain MRI features to chronological age may also provide important biomarkers to supervise the brain development or cognitive performance [8]. On the other hand, the gap between the predicted age and the chronological age provides an index of deviation from the normal developmental trajectory, which may indicate neurodevelopmental disorders [9]. Furthermore, age prediction also helps discerning possible environmental influences on the human brain [10, 11].

Various age ranges of subjects have been used for studying age prediction. For example, the subjects of 3–20 years of age were chosen for assessment of biological maturity based on age prediction [12]; the study of the advanced BrainAGE in patients with type 2 diabetes mellitus was conducted based on the subjects of 20–86 years of age [13]; the subjects of 21–65 years of age were chosen for studying the brain ageing in schizophrenia [9]; the age range of 65–85 years was used for the discussion of the dependence between brain age and Alzheimer’s disease [14]. Nonetheless, little research has been done on the age prediction of infants before 2 years of age. To the best of our knowledge, the only study about the infant age prediction involved subjects from 5 to 590 days and reached the mean absolute error of the prediction as 72 days [15]. However, this study relied on image features obtained by difference-of-Gaussian scale space transformation. Its results are less useful for analyzing the dynamic changes of the cortical features on the infant brain, which is crucial for many psychiatric and neurodevelopmental disorders [16]. Actually, many infant-tailored methods have been proposed to address the challenges in infant brain MRI processing, i.e., poor tissue contrast, large within-tissue intensity variations, and dynamic appearance changes [6]. Consequently, the quantitative analysis of the development of the infant brain cortical measures, such as cortical volume, gyrification, cortical thickness, and surface area [16–20], has been conducted and many insightful results of infant brain development have been discovered. But these group-level comparison results are often not enough for precise identification of abnormal brain development in individuals [21]. Leveraging the infant-specific computational pipelines [4], infant age prediction based on neurobiologically meaningful cortical measures becomes possible.

Previously, many machine learning based regression algorithms have been used for age prediction, such as support vector regression [22], convolutional neural network [23], Gaussian process regression [24], relevance vector regression [25], and multiple linear regression with elastic-net penalty [8]. However, directly applying them on infant age prediction is not feasible, because the brain anatomical changes during infancy are too rapid and spatiotemporally heterogeneous to be accurately captured by a single regression model. Although a covariate-adjusted restricted cubic spline regression model [26] is able to handle the complicated changes of brain development, it is more suitable for the regression with a single predictor variable. Nonstationary regression, such as nonstationary support vector machine [27] and nonstationary Gaussian process regression [28, 29], focuses on time-dependent processes and may have the potential to deal with the heterogeneous and dynamic infant brain development. However, most of nonstationary regression algorithms were specifically developed for nonstationary time series analysis. Some particular variables, such as the current time or the driving force of the process, should be incorporated into many nonstationary regression models. These variables are not suitable for the age prediction that does not consider any longitudinal information. Herein, to specifically address the challenge in infant age prediction, we propose a two-stage prediction method to split the heterogeneous brain development process into several adjacent age groups and carry out fine age prediction based on several age-group-specific regression models, and thus construct a Hierarchical Rough-to-Fine (HRtoF) model by further introducing an ordinary one-stage prediction method as the complement for alleviating the influence of the possible age range prediction deviation. The effectiveness of HRtoF is verified by comparing with 5 state-of-the-art regression methods based on an infant dataset. In addition, we also discuss the relative contribution of 8 types of cortical features in infant age prediction based on our HRtoF model.

II. Materials and methods

A. Subjects and MR image acquisition

The Institutional Review Board (IRB) of the University of North Carolina (UNC) School of Medicine approved this study. Healthy infants were recruited by the UNC hospitals based on the written informed consents from both parents. Each subject was scanned unsedated in natural sleep with oxygen saturation and heart rate monitored by a pulse oximeter. Detailed information on subjects and imaging acquisition can be found in [30, 31].

50 infants were longitudinally scanned by a Siemens 3T head only MRI scanner with 32 channel heal coil at seven scheduled time points (i.e., around 1, 3, 6, 9, 12, 18 and 24 months of age). T1-weighted images (144 sagittal slices) were acquired with the imaging parameters: TR/TE = 1900/4.38 ms, flip angle = 7, acquisition matrix = 256 × 192, and resolution with 1 × 1 × 1 mm³. T2-weighted images (64 axial slices) were acquired with the imaging parameters: TR/TE = 7380/119 ms, flip angle = 150, acquisition matrix = 256×128, and resolution with 1.25×1.25×1.95 mm³. Totally, 251 longitudinal scans were included in our study after removing the images with insufficient quality. The demographic information of these scans is illustrated in Table I.

Table I.

Subject demographics of the dataset.

	1 month	3 month	6 month	9 month	12 month	18 month	24 month
Scans (Female/Male)	39 (17/22)	36 (17/19)	41 (20/21)	36 (17/19)	36 (16/20)	40 (17/23)	23 (14/9)
Age (days)	14–48	81–116	169–225	251–309	352–418	507–613	666–797
Age Mean±SD	27.3±9.0	94.6±8.6	190.0±12.8	278.1±13.9	375.5±14.5	556.8±19.8	738.2±27.3

B. Image preprocessing

As the predictors for age prediction, several morphological features of the cerebral cortex were computed based on an infant-specific computational pipeline as detailed in [32]. Briefly, it included the following major preprocessing steps: i) skull stripping by a learning-based method [33]; ii) cerebellum and brain stem removal by registration [34] with a volumetric atlas [35]; iii) intensity inhomogeneity correction by N3 [36]; iv) longitudinally consistent tissue segmentation using a learning-based multi-source integration framework [37, 38]; v) non-cortical structures filling and left/right hemisphere separation [19]. After that, for each hemisphere of each scan, the topologically-correct and geometrically-accurate inner (white/gray matter interface) and outer (gray matter/cerebrospinal fluid interface) cortical surfaces were reconstructed using a topology-preserving deformable surface method based on tissue segmentation results [19]. Given the reconstructed cortical surfaces, 8 types of morphological features on each vertex were calculated, including sulcal depth measured in Euclidean distance (SDE), sulcal depth measured in streamline distance (SDS), local gyrification index (LGI), average convexity, sharpness, cortical thickness, surface area, and cortical volume.

Directly using the morphological features of all vertices is computationally expensive, since the vertex number on each hemisphere is too large. To reduce the feature dimension, many studies use the regions of interest (ROIs) based features by leveraging the anatomical structures of the brain and has been proved to be an effective strategy. In this work, to generate the brain ROIs, we aligned each individual cortical surface onto the UNC 4D Infant Cortical Surface Atlas (https://www.nitrc.org/projects/infantsurfatlas/) [32, 39] using Spherical Demons [40]. Then, 35 cortical ROIs from the Desikan parcellation [41] were propagated onto each individual cortical surface of each hemisphere. With the ROIs on each surface of each hemisphere, 6 types of features (SDS, SDE, LGI, thickness, sharpness, and convexity) were obtained by averaging the corresponding values of all vertices inside each ROI; and 2 types of features (area and volume) were obtained by summing the corresponding values of all vertices inside each ROI. Therefore, for each scan, totally 560 features (8 feature types × 70 ROIs) were acquired for two hemispheres.

C. Machine learning based age prediction model

Since different cortical morphological features contribute differentially to the age prediction during different developmental phases [12], it is an effective strategy to partition the first 24 months after birth with heterogeneous brain development to several sequential age groups and then model the relation between age and features in each specific age group. Based on this idea, i) the entire time range (24 months after birth) is partitioned into K age groups randomly at first, which will then be optimized by minimizing the error of the prediction; ii) K age-group-specific regression models are learned; iii) a two-stage prediction method is proposed, which first predicts the age group of an infant in the rough prediction stage, and then further finely predicts the accurate chronological age based on the predicted age group and the age-group-specific regression model in the fine prediction stage; iv) a complementary one-stage prediction is activated if the belief level of the two-stage age prediction is lower than a given threshold, which predicts the infant age in the ordinary way. Of note, the conventional age prediction methods are called one-stage prediction methods to be distinguished with the two-stage prediction method proposed in this paper. These 4 parts constitute a new age prediction model: Hierarchical Rough-to-Fine (HRtoF) model. The architecture of HRtoF is shown in Fig. 1.

Fig. 1.

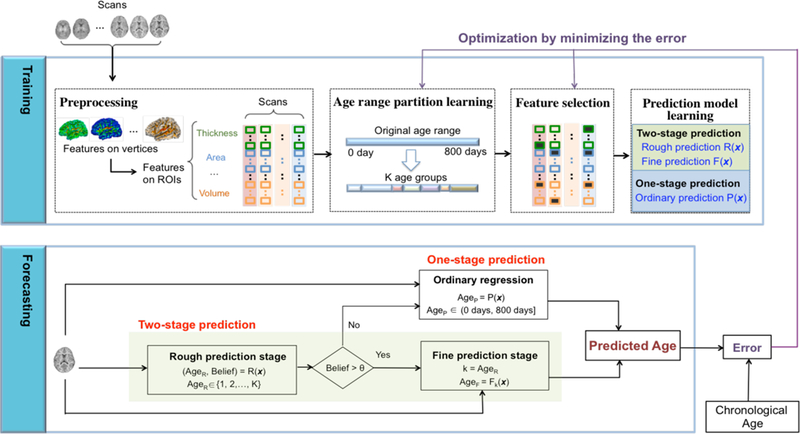
The architecture of the proposed age prediction model: HRtoF.

Training of HRtoF

The training process of HRtoF mainly comprises three steps: 1) age range partition learning, 2) feature selection, and 3) prediction model learning.

1). Age range partition learning

The partition of the age range, (0, 800) in days, will be set randomly at the beginning and then be learned by minimizing the mean absolute error (MAE) of the age prediction. Herein, MAE is the mean of the absolute value of the difference between the predicted ages and chronological ages. In this step, an optimal partition-nodes set {y₁,⋯,y_k−1,y_k,y_k+1,⋯,y_K−1}will be learned, where y₁ < ⋯ < y_k−1 < y_k < y_k+1 < ⋯ < y_K−1. This partition nodes set leads to the partition of (0, 800) as {(0, y₁), [ y₁, y₂), ⋯ , [ y_k−1, y_k), [ y_k, y_k+1), ⋯ , [ y_k−1, 800), which corresponds to K age groups. The scans with their ages lie in [ y_k−1, y_k) form the k^th age group, with y₀ = 0, y_K = 800, and k = 1,2, ⋯ , K. The detailed process of the partition learning is shown in supplementary material.

2). Feature selection

Since there is obvious redundant information due to complex correlation among the 560 features (8 types of features on 70 ROIs) adopted for age prediction, feature selection is necessary to improve the prediction accuracy. Of note, in HRtoF model, the rough prediction part focuses on classifying a scan into the correct age group, the fine prediction part dedicates on the prediction in the determined age group, and the one-stage prediction directly predicts the infant age with respect to the whole age range in a conventional way. The features applied in the rough prediction, fine prediction and one-stage prediction are required to be selected separately, since they are totally different prediction tasks. For the rough prediction part, sparse logistic regression, which is a regular multi-class logistic regression with ${\ell }_{2,1}$ -norm penalty [42], was chosen for feature selection. Sparse logistic regression dedicates to perform feature selection as an embedded part of the statistical multi-classification procedure and avoid overfitting at the same time, which makes it a good feature selection algorithm for rough prediction. As for fine prediction and one-stage prediction, the linear regression with the elastic-net penalty [43] was chosen for feature selection, because it is designed for regression and particularly useful when the number of observations is smaller than the number of predictors.

3). Prediction model learning

After feature selection, different selected dedicated feature sets are adopted for learning the rough prediction, fine prediction and one-stage prediction model, respectively. For the rough prediction, Bayesian linear discriminant analysis [44] is chosen, because the essence of this part is to determine the age group that a scan should belong to, which is a classification problem indeed. A given scan is represented by its corresponding morphological feature values and denoted as x. Bayesian linear discriminant analysis first models the prior probability p(k) of the age group k, and the multivariate normal density function p(x | k ) of the predictors in each age group k. Then it estimates the posterior probability $\widehat{p}\left(k|\mathbf{x}\right)$ that the scan x is in age group k based on Bayes rule. Finally, it determines the predicted age group Age_R that is with the maximal posterior probability for the given scan x, i.e., $Ag{e}_R=\underset{k=1,\cdot \cdot \cdot ,K}{\text{argmax}}\widehat{p}\left(k|\mathbf{x}\right)$ The ‘Belief’ of Age_R is $\widehat{p}\left(Ag{e}_R|\mathbf{x}\right)$. Actually, when the distributions of the predictors are assumed to be Gaussian distribution, the model of Bayesian linear discriminant analysis is very similar in form to logistic regression. This consistency guarantees that the feature set selected by sparse logistic regression maintains its superiority in the classification based on Bayesian linear discriminant analysis. Note that, sparse logistic regression is only used for feature selection rather than classification, because the parameters estimated by Bayesian linear discriminant analysis is more stable than logistic regression when the sample size is small and the distributions of the predictors are approximately Gaussian distribution [44]

For the fine prediction and one-stage prediction, because we only have 251 scans for the whole model and only 20–40 scans in each age group, as illustrated in Table I, the support vector regression [45] was adopted due to its superior performance on small samples.

Forecasting process in HRtoF

The forecasting process in HRtoF uses the following 3 parts to predict the age of the scan.

1. Rough prediction stage ( Age_R, Belief ) = R(x) : the rough prediction aims to accurately determine the age group that the scan belongs to. Age_R is the age group which Bayesian linear discriminant analysis classifies the given scan x into. ‘Belief’ is the estimated posterior probability and equals $\widehat{p}\left(Ag{e}_R|\mathbf{x}\right)$.

2. Fine prediction stage Age_R = F_k(x) from the rough prediction stage is larger than a predetermined belief threshold θ, which means the model provides high confidence for the rough prediction, HRtoF goes to the fine prediction stage. In the fine prediction stage, each age group has its specific regression model F_k (k = 1, ⋯ , K) that characterizes how the cortical features change along with age in the corresponding age group. According to the Age_R determined by the rough prediction, HRtoF uses the regression model $F_{Ag{e}_R}$ to get the final predicted age.

3. One-stage prediction Age = P(x) : if ‘Belief’ is equal to or smaller than θ, using Age_R for the further fine prediction may be risky. Therefore, HRtoF switches to a conventional one-stage prediction model P(x), when the scan could not be assigned to any subgroup with enough belief.

D. Evaluation of age prediction

To evaluate the effectiveness of the age prediction and analyze the relative contribution of features, 100 times of 10-fold cross validation was implemented. All the hyperparameters in HRtoF were learned by minimizing the mean absolute error of the prediction. Furthermore, since the 251 scans included in our experiments were acquired from 50 infants longitudinally, each infant has 5 scans on average. To control the non-independence of the scans in the cross validation, the scans of the same subjects were put in the same fold. Thus, the 50 infants were split into ten folds and the scans of the subjects in 9 folds were collected as the training set and the remaining scans were used as the testing set. The age prediction model was assessed by 3 criteria, i.e., the mean absolute error (MAE), the mean relative absolute error (MRAE), and the correlation value r between the predicted ages and the chronological ages. Of note, MRAE is the mean of the absolute error divided by the corresponding chronological age and expressed in terms of per 100. For the correlation value r, the 95% confidence interval of the r was computed by the 2.5 and 97.5 percentiles of correlation values obtained from 1,000 samples bootstrap method. Each 10-fold cross validation brought an MAE, an MRAE and a confidence interval of the correlation. The 10-fold cross validation procedure was repeated 100 times, yielding 100 random 10-fold partitions of the experimental data. The mean and standard deviation of the 100 MAEs, MRAEs and confidence intervals of the correlation were used to validate the age prediction model. The same bootstrap samples were adopted for the 100 times of 10-fold cross validation when computing the confidence interval of the correlation. This guarantees that the bootstrap selection is unbiased for each of the 10-fold cross validation.

We also compared the proposed hierarchical rough-to-fine (HRtoF) model with 5 state-of-the-art age prediction methods, i.e., partial least squared regression (PLSR), support vector regression (SVR), Gaussian process regression (GPR), elastic net penalized linear regression (ENLR), and nonstationary Gaussian process regression (NonS-GPR), quantitatively based on MAE, MRAE and correlation value.

E. The relative contribution of the features

The relative contributions of the features to age prediction were analyzed based on 3 aspects, i.e., 1) relative importance, 2) relative performance, and 3) relative irreplaceable contribution.

1). Relative importance of the features

Relative importance depicts the contribution of each feature to age prediction when using 8 types of feature together as the predictors. It is measured by the coefficients of decision boundaries in Bayesian linear discriminant analysis (BLDA) at the rough prediction stage of HRtoF. In BLDA, the analytic expression of decision boundary between k^th and k + 1^th (k = 1, ⋯ , k − 1) age groups is shown as

$$\text{log}\left(\frac{p\left(k|\mathbf{x}\right)}{p\left(k+1|\mathbf{x}\right)}\right)=w_0+{\mathbf{w}}^T\mathbf{x}$$

where and w are the coefficients and intercept of the boundary and learned from scans in k^th and k + 1^th age groups [46]. Like logistic regression, BLDA models the log odds as a linear function of the predictors. The exponential coefficient in the decision boundary represents the change in odds, when the corresponding predictor increases a unit with other predictor increases a unit with other predictors being fixed. Thus, ${\mathbf{b}}_{k,k+1}=|\exp \left(\mathbf{w}\right)-1|$ was used to measure the relative importance of the features in discriminating the subjects in k^th and k+ 1^th age group. The longitudinal changes of the relative importance of the features from 1 month to 24 months was captured by the sequential values of $\left\{{\mathbf{b}}_{k,k+1}|k=1,\cdot \cdot \cdot ,K-1\right\}$, which was obtained from the k − 1 sequential decision boundaries among the K age groups. Each type of feature (SDE, LGI, SDS, convexity, sharpness, thickness, area and volume) includes 70 features (from 70 ROIs). The relative importance of each type of feature was obtained by summing the relative importance of the corresponding 70 ROI features.

2). Relative performance of the features

Except for evaluating the contribution of each feature type in the model that uses all 8 feature types together as predictors, each feature type was also evaluated by adopting it as the sole predictor in the age prediction model. Suppose MAE_f is obtained by the age prediction based on an individual feature type f. Its relative performance is defined as

$$\left(-MA{E}_f+\frac{1}{8}{\sum }_{f\prime }\text{MA}{\text{E}}_{f\prime }\right)/\left(\frac{1}{8}{\sum }_{f\prime }\text{MA}{\text{E}}_{f\prime }\right),$$

where f′ is one of the 8 feature types. Positive or negative relative performance respectively indicates whether the capability of this individual type of feature on age prediction is bigger or smaller than the average level.

3). Relative performance of the features

When removing a specific type of feature out of the feature set, the change on the accuracy of age prediction shows the contribution of the feature type that could not be replaced by the remaining feature types. The relative irreplaceable contribution of the individual feature type f is defined as.

$$\left(\text{MA}{\text{E}}_{\overline{f}}-\frac{1}{8}{\sum }_{f\prime }\text{MA}{\text{E}}_{\overline{f}\prime }\right)/\left(\frac{1}{8}{\sum }_{f\prime }\text{MA}{\text{E}}_{\overline{f}\prime }\right)$$

where $\text{MA}{\text{E}}_{\overline{f}}$ is the MAE by using the feature set without f, and f′ is one of the 8 feature types. Positive and negative relative irreplaceable contribution respectively indicates whether the irreplaceable contribution of this individual feature type on age prediction is bigger or smaller than the average level.

III. Results

A. The prediction performance of HRtoF

The HRtoF model was mostly programmed based on Matlab. The regularized sparse logistic regression for feature selection in the rough prediction stage was implemented by SLEP toolbox [42]. The criteria MAE, MRAE and the 95% confidence interval of the correlation value r were used to compare HRtoF with other 5 regression models, i.e., partial least squared regression (PLSR), support vector regression (SVR), Gaussian process regression (GPR), elastic net penalized linear regression (ENLR), and nonstationary Gaussian process regression (NonS-GPR) with dot-product as the nonstationary kernel. The results obtained from 100 times of 10-fold cross validation were presented in Table II. r_L and r_R are the left and right endpoints of the 95% confidence interval of r. Scatter plots of the predicted age and chronological age are shown in Fig. 2, in which the subfigures were obtained by HRtoF, PLSR, SVR, GPR, ENLR, and NonS-GPR, respectively.

Table II.

The comparison of HRtoF, PLSR, SVR, GPR, ENLR, and NonS-GPR, in terms of MAE, MRAE, and the 95% confidence interval of correlation value. Mean and standard deviation of the values were obtained from the 100 times of 10-fold cross validation.

	MAE(days)	MRAE(%)	rL	rR
HRtoF	32.1±1.2	16.2±0.5	0.945±0.008	0.981±0.003
PLSR	51.7±1.8	39.6±1.5	0.939±0.004	0.963±0.002
SVR	52.1±1.7	36.4±1.8	0.934±0.004	0.960±0.002
GPR	48.5±1.0	23.8±0.6	0.937±0.002	0.962±0.001
ENLR	59.9±2.7	47.8±2.3	0.928±0.007	0.951±0.004
NonS-GPR	53.6±1.5	36.2±1.6	0.931±0.003	0.958±0.004

Fig. 2.

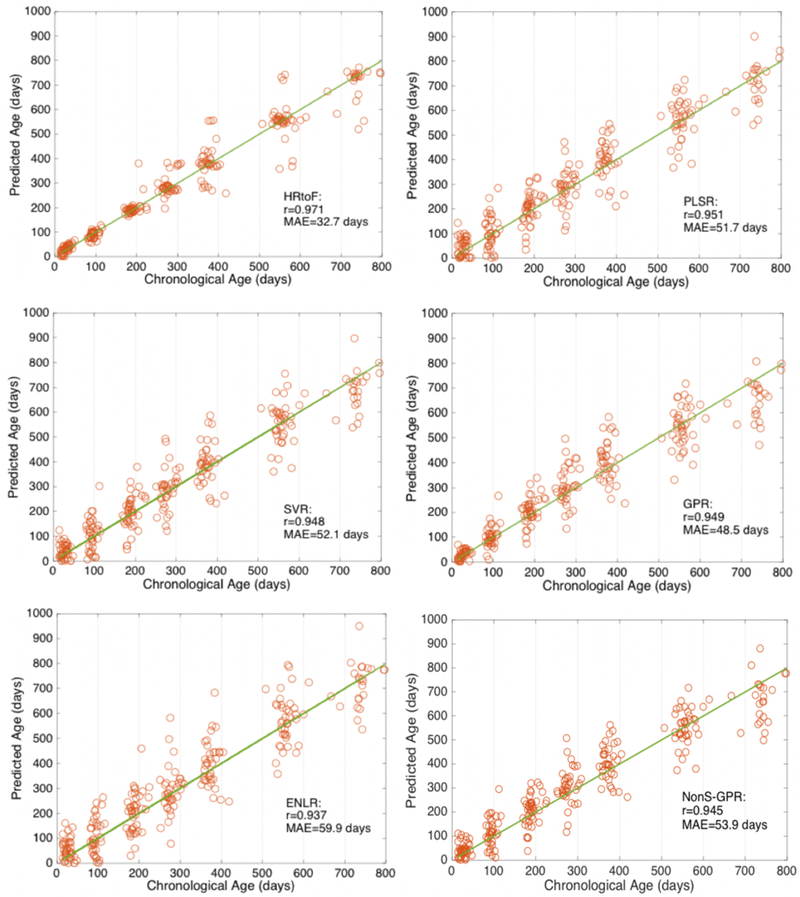
Scatter plots of the chronological age and predicted age obtained by HRtoF, PLSR, SVR, GPR, ENLR, and NonS-GPR are shown in the 6 subfigures, respectively. The solid line describes the best predictions.

PLSR, SVR, GPR, ENLR, and NonS-GPR performed similarly on age prediction. The MAE obtained by them was around 48.5 days to 59.9 days; the MRAE was around 23.8% to 47.8%; and the average correlation r was around 0.938 to 0.951. HRtoF model improved the prediction performance considerably. Specifically, the MAE and MRAE were respectively reduced to 32.1 days and 16.2%, while the average of the 95% confidence interval of r increased to 0.963.

Since the images in our experiments were collected at around 1, 3, 6, 9, 12, 18, and 24 months of age, the MAE and MRAE of prediction were broken down at these 7 time points to show the detailed prediction performance, as shown in Tables III and IV. From Table II, GPR and ENLR respectively are the best and worst out of the 5 conventional one-stage methods. Tables III and IV show more details about the prediction at each time point. These four one-stage prediction methods perform differently at different time points, especially at the youngest and oldest time points. GPR outperforms the other 4 models at 1, 3 and 6 months, while performs not as well as the others at the rest of the time points. Especially at 24 months, the MAE of the prediction obtained by GPR increases to 84.7 days, while the MAE of ENLR is 61.5 days. ENLR performs worse than the other 4 methods at most of the time points except 24 months. Therefore, a fact could not be neglected is that even a one-stage prediction method is chosen for age prediction due to its better overall performance across the whole time range, the prediction effectiveness is not guaranteed at some specific ages. Compared with these 5 methods, HRtoF consistently shows better prediction performance at all time points. Focusing on the variance of the 7 MRAEs from 1 month to 24 months, the standard deviation (S.D.) of MRAE obtained from HRtoF is 13.16%, while the values of PLSR, SVR, ENLR and Nons-GPR are from 35.49% to 54.52%. Although the standard deviation of the 7 MRAEs obtained from GPR is as small as the one obtained from HRtoF, the standard deviation of MRAE along with the 6 time points (from 3 months to 24 months) obtained from GPR is 6.84%, while the one obtained from HRtoF is only 1.65%. This result shows that HRtoF also outperforms the other four models on the stability of the prediction at the 7 time points.

Table III.

The broken down MAE (days) obtained by HRtoF, PLSR, SVR, GPR, ENLR, and NonS-GPR at the 7 time points. Mean and standard deviation were obtained from the 100 times of 10-fold cross validation; ‘M’ is short for ‘month’.

	HRtoF	PLSR	SVR	GPR	ENLR	NonS-GPR
1M	11.1±0.3	30.4±1.7	24.3±1.8	11.7±0.5	37.5±2.9	24.2±1.5
3M	11.0±0.4	48.8±2.5	48.6±2.6	28.1±1.0	59.6±3.5	49.1±2.8
6M	17.8±1.9	44.9±2.5	47.8±2.4	39.3±1.2	58.7±3.3	45.2±2.0
9M	29.9±3.1	51.8±2.7	52.1±2.9	59.1±1.5	59.5±4.4	53.0±2.6
12M	52.9±3.9	65.0±3.0	64.7±3.0	68.7±1.7	67.7±4.2	64.3±2.7
18M	58.5±4.7	62.8±2.8	63.5±3.1	62.9±1.6	77.8±4.3	61.6±2.1
24M	60.7±5.8	61.3±3.4	70.1±3.0	84.7±2.2	61.5±5.3	74.1±3.5

Table IV.

The broken down MRAE (%) obtained by HRtoF, PLSR, SVR, GPR, ENLR and NonS-GPR at the 7 time points. Mean and standard deviation of the values were obtained from the 100 times of 10-fold cross validation. S.D. is short for standard deviation; ‘M’ is short for ‘month’.

	HRtoF	PLSR	SVR	GPR	ENLR	NonS-GPR
1M	45.18±1.48	130.24±6.86	108.49±7.38	49.43±19.7	162.28±13.59	109.21±6.52
3M	11.68±0.44	51.75±2.64	51.03±2.73	29.44±1.02	62.29±3.70	53.14±2.05
6M	9.20±1.04	23.57±1.34	25.03±1.30	20.68±0.66	30.95±1.76	22.67±1.28
9M	10.69±1.49	18.70±0.99	18.72±1.04	21.17±0.54	21.57±1.59	18.91±1.32
12M	13.97±1.54	17.16±0.80	17.06±0.80	18.16±0.46	17.89±1.12	17.16±0.75
18M	10.46±1.21	11.29±0.52	11.42±0.57	11.21±0.29	14.06±0.77	11.27±0.49
24M	8.25±1.22	8.35±0.46	9.51±0.41	11.49±0.30	8.38±0.71	10.03±0.58
S. D. (1M~24M)	13.16	43.40	35.49	13.19	54.52	36.65
S. D. (3M~24M)	1.99	15.64	15.19	6.84	19.39	15.92

B. The relative contributions of features

As mentioned in section II-E, the relative contribution of the features for age prediction was analyzed by relative importance, relative performance, and relative irreplaceable contribution. Based on the age range partition learning, the partition of the age range was obtained as: {[0,136), [136,244), [244,332), [332,462), [462,645), [645,800]}.

The number of the age groups is K = 6. (1~3M, 6M), (6M, 9M), (9M, 12M), (12M, 18M), (18M, 24M) represent the 5 sequential decision boundaries of the 6 age groups. ‘M’ is short for ‘month’. The sequential change of the exponential coefficients in the 5 decision boundaries shows the longitudinal variation of the features’ relative importance. The longitudinal trajectories of the relative importance of 8 types of cortical features are obtained by $\left\{{\mathbf{b}}_{k,k+1}|k=1,\cdot \cdot \cdot ,5\right\}$ and shape preserving piecewise cubic interpolation as shown in Fig. 3. From the trajectories in Fig. 3, the relative importance of LGI is always the biggest one from 1 month to 24 months, while cortical thickness is nearly the most insignificant contributor to the rough prediction. Although SDS has low contribution in the middle range of the time, it is the second important feature type at the beginning and the end of the time. Furthermore, when the relative importance of convexity and SDS decrease in the decision boundaries of (6M, 9M) and (12M, 18M), the relative importance of sharpness and SDE increase. When the relative importance of convexity and SDS increase in the decision boundaries of (9M, 12M) and (18M, 24M), the relative importance of sharpness and SDE decrease. This phenomenon shows that the two feature sets “convexity and SDS” and “sharpness and SDE” may be mutually complementary with each other in the age prediction at different time points.

Fig. 3.

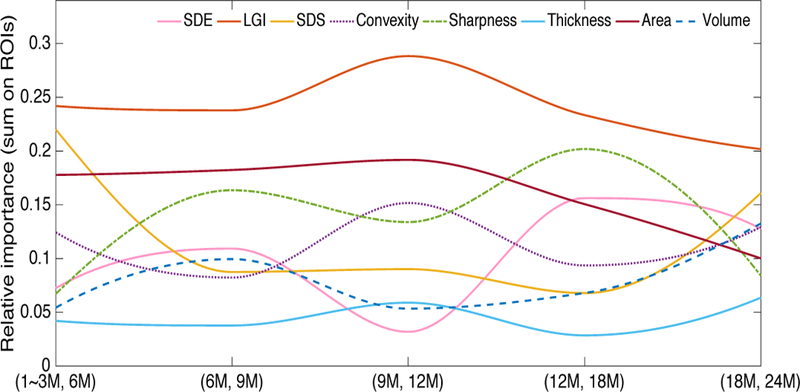
The relative importance of the 8 types of features varies from 1~3 months to 24 months. The relative importance of each feature type in each decision boundary was computed by summing the values of its related ROI features and normalized by dividing the total relative importance of the 8 feature types in the decision boundary.

The longitudinal relative importance of the feature types shown in Fig. 3 was obtained in the model that includes all 8 types of features as predictors. To further study the relative contribution of each feature type, the 8 feature types were included into the age prediction model HRtoF separately. For each feature type, MAE, MRAE and the 95% confidence interval of the correlation value r obtained from 100 times of 10-fold cross validation are presented in Table V. When applied to the age prediction model HRtoF individually, volume shows as the best predictor (MAE=51.2 days), while LGI is the worst one (MAE=94.2 days). The prediction capabilities of SDE, SDS, convexity, thickness and area are similar. The MAEs obtained by them are from 59.5 days to 66.9 days. Sharpness is not a very good predictor for age, because the MAE obtained by it is as high as 75.5 days. Meanwhile, the biggest average correlation value obtained by a single feature is 0.92, which is reached by volume.

Table V.

The comparison among 8 types of features when applying them individually for age prediction based on the criteria MAE, MRAE and the 95% confidence interval of correlation value. The values in this table are the corresponding mean obtained from the 100 times of 10-fold cross validation.

	SDE	LGI	SDS	Convexity	Sharpness	Thickness	Area	Volume
MAE (days)	61.4	94.2	62.5	59.5	75.5	66.9	64.2	51.2
MRAE (%)	26.36	54.56	28.59	26.67	36.16	33.14	30.09	23.46
rL	0.876	0.664	0.859	0.877	0.804	0.851	0.883	0.896
rR	0.927	0.810	0.921	0.932	0.888	0.915	0.928	0.945

Comparing the relative importance obtained from the prediction using all the 8 feature types and the performance obtained from the prediction using a single feature type, a wide difference shows up. For example, LGI has the biggest relative importance when predicting age together with other 7 features and the smallest accuracy when predicting the age individually. To uncover the reason for this difference, an experiment was further implemented. Each feature type was removed from the feature set and the rest 7 feature types were used to predict the infant age based on HRtoF model. The prediction capabilities of the 8 feature sets, respectively without a certain feature type, were also assessed and presented in Table VI.

Table VI.

The comparison of the age prediction based on the feature sets without a certain feature type. The values of MAE, MRAE and the 95% confidence interval of correlation in the table are the corresponding mean obtained from 100 times of 10-fold cross validation.

	SDE	LGI	SDS	Convexity	Sharpness	Thickness	Area	Volume
MAE (days)	34.6	38.1	33.7	35.3	36.3	34.5	32.3	35.2
MRAE (%)	16.88	18.41	16.48	17.06	17.45	17.33	16.10	17.29
rL	0.934	0.935	0.938	0.938	0.931	0.932	0.940	0.929
rR	0.970	0.968	0.973	0.972	0.969	0.972	0.976	0.971

After removing a feature type from the original feature set, the change of the prediction performance represents whether the contribution of the feature type in age prediction could be replaced by the remaining feature types or not. The more the prediction accuracy decreases the feature type is more irreplaceable in the original feature set. As shown in Table II, the MAE of the age prediction when using the 8 types of features together is 32.1 days. The MAE obtained by the feature set without ‘area’ is almost unchanged. On the contrary, after removing LGI out of the feature set, the MAE of age prediction increased most. Sharpness is another feature that leads to a 4-day increase on the MAE when using the feature set without it for age prediction.

The comparison between the prediction results obtained by individual feature type against the feature sets without this individual feature type could uncover some important facts about how the feature type works on the age prediction. As defined in section 2.5, the relative performance and relative irreplaceable contribution of the 8 types of features are computed and shown in Table VII.

Table VII.

The relative performance and relative irreplaceable contribution of the 8 types of features (SDE, LGI, SDS, convexity, sharpness, thickness, area and volume).

	SDE	LGI	SDS	Convexity	Sharpness	Thickness	Area	Volume
Relative performance	0.083	−0.408	0.066	0.111	−0.128	0.000	0.041	0.235
Relative irreplaceable contribution	−0.011	0.089	−0.037	0.009	0.037	−0.014	−0.077	0.006

The values of the relative performance and the relative irreplaceable contribution help us to classify the 8 types of features into four classes, which are described in Table VIII. LGI and sharpness belong to class IV, which means that they have strong irreplaceability on age prediction, although they could not predict the age very well by themselves. SDE, SDS, thickness and area belong to class I. These 4 feature types could individually predict the age well, but some features in the remained feature set could mostly replace their contributions in age prediction, because the MAE only changed a little when removing them. Convexity and volume belong to class II. They could individually predict age at higher than the average level of accuracy and also have more than the average amount of irreplaceable contribution for age prediction. Comparing the irreplaceable contribution with the relative importance analysis, their results are highly consistent. The high relative importance of LGI and sharpness shown in Fig. 3 meets the big irreplaceable contribution of them for the age prediction. Although LGI and sharpness could not predict the infant age very well individually, they still have a big potential to increase the accuracy of prediction when cooperating with other feature types. Thus, when building an age prediction model, only including the feature types with high individual prediction power may not definitely lead to an ideal model, because the contribution of the feature types may be heavily overlapped. On the other side, including some feature types of class IV into the prediction model may be crucial for the improvement of the performance.

Table VIII.

The classification of the 8 types of features (SDE, LGI, SDS, convexity, sharpness, thickness, area and volume) based on relative performance and relative irreplaceable contribution.

Class	Description	Feature types
Class I	Relative performance>0, Relative irreplaceable contribution<0	SDE, SDS, Thickness, Area
Class II	Relative performance>0, Relative irreplaceable contribution>0	Convexity, Volume
Class III	Relative performance<0, Relative irreplaceable contribution<0
Class IV	Relative performance<0, Relative irreplaceable contribution>0	LGI, Sharpness

C. The ROIs involved in the rough prediction stage

The rough prediction stage is a crucial part of HRtoF model. After the feature selection based on sparse logistical regression, only 58 features are chosen out of the original 560 features (8 feature types on 70 ROIs). The numbers of the ROIs related to different feature types were broken into left and right hemispheres and were shown in Fig. 4. 14 ROIs related to LGI were chosen and used as predictors in the rough prediction stage, while only 3 ROIs related to thickness and volume were chosen for the rough prediction. These 58 features distribute asymmetrically on the left and right hemispheres. The ROIs on the right hemisphere involved more in the rough prediction stage than the ROIs in the left hemisphere. Although there have been some reports [47, 48] about longitudinal hemispheric structural symmetries of the human cerebral cortex form birth to 2 years of age, they studied different cortical features independently. The structural asymmetry showed in our study was from the viewpoint of age group discrimination, and the interaction between different cortical features were considered. Because the degree of feature change is closely related to the discriminability of age groups, the asymmetrical distribution of these 58 features likely indicates that the right hemisphere may has higher development rate than the left hemisphere in the first two years of life. To some extent, this result is consistent with the report of “the right brain hemisphere is dominant in human infants”[49].

Fig. 4.

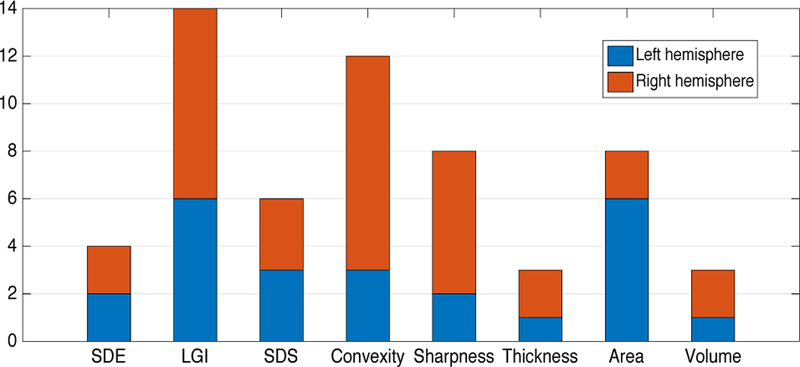
The number of the ROIs related to each feature type (SDE, LGI, SDS, convexity, sharpness, thickness, area and volume).

For clarity, the selected 58 features are shown on ROIs according to the 8 types of features in Fig. 5. The ROIs that are most frequently involved in the rough prediction are bilateral medial orbitofrontal, bilateral parahippocampal, bilateral temporal pole, right superior parietal and right posterior cingulate cortex. Each of them participated in the rough prediction with more than 3 feature types.

Fig. 5.

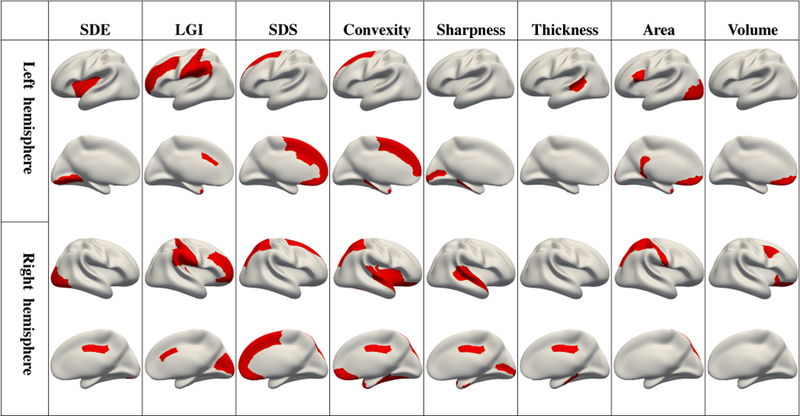
The 58 selected most contributive features used in rough prediction stage are shown as red regions according to 8 feature types, i.e., SDE, LGI, SDS, convexity, sharpness, thickness, area and volume.

IV. Discussion

1). HRtoF model having good performance on age prediction

Although many useful strategies have been employed to address the complex relationship between the predictors and the age in conventional one-stage regression methods, the accuracy does not improve much improvement in infant age prediction. The MAE of the prediction obtained by PLSR, SVR, GPR, nonstationary GPR, and ENLR is around 48.5 to 59.9 days, and the correlation value is around 0.939–0.949. The reason is that the heterogeneity of early brain development is forcibly represented by a single model and the discrimination capability of the cortical features cannot be thoroughly mined. By splitting the long time range with heterogeneous early brain development and introducing a two-stage prediction method, HRtoF reaches a considerably higher accuracy.

Furthermore, with the age range partition learning of HRtoF, the age group, in which the relationship between the change of the cortical features and age is relatively stable, can be discovered. In our experiment, we find that the subjects belong to 1 month and 3 months were combined into a single age group, while the MAE obtained by HRtoF at 1 month and 3 months are smaller than the MAEs obtained by the other 4 methods. This shows that the relationship between the cortical features and chronological age is similar for the subjects belonging to 1 month and 3 months.

From the prediction scatter plot shown in Fig. 2, we can find that the prediction error obtained by HRtoF is getting bigger along the time, especially from 1 to 2 years of age. This prediction error pattern is mainly due to heterogeneous brain development rates during the first two years. The developmental trajectories of the 8 types of features were mapped by covariate-adjusted restricted cubic spline regression [26] and shown in Fig. 6. As can be seen, the development of these global features show that the infant brain goes through a dramatic development from birth to 1 years of age, and then a relatively stationary development during the second year. When the age becomes larger, the cortical feature differences across age groups become smaller, therefore their distinguishability becomes lower. Since the rough prediction stage of our proposed model uses the discrimination capability of the data, the relative stationary brain development in year 2 is the main reason of higher prediction error. Thus, different prediction accuracies at different phases could also reveal different rates of brain development.

Fig. 6.

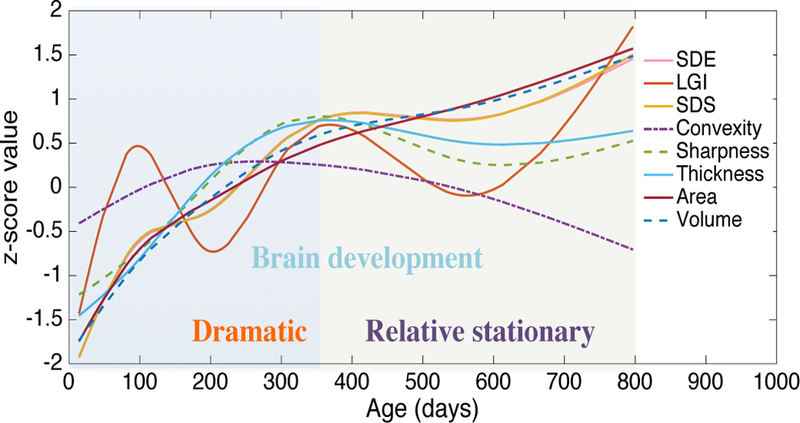
The development trajectories of the 8 types of global features from birth to 2 year of age. SDE, LGI, SDS, Convexity, Sharpness, and Thickness shown in this figure were obtained by averaging the corresponding values on all brain vertices; Area and Volume were obtained by summing the corresponding values on all brain vertices. Of note, these values were all normalized as z-scores for comparison.

Furthermore, although there are not enough data for the training of the 6 models in the fine prediction stage, they still learned some useful prediction knowledge from the limited data. To evaluate the prediction effectiveness of these 6 models trained by SVR, they were used for age prediction in their own age group and also neighboring age groups. The correlations between the predicted ages and the chronological ages were shown in Table S1 in supplementary material. Model 1~3M and Model 12M can predict the age with high accuracy in both its own and neighboring age groups, while Model 12M cannot work well in all age groups. Actually, from Fig. 6, we can find that 12M is a very special period, when almost all the cortical features are changing the development rates. For the phases at 1~3 months and 24 months, the variation of all the feature types is keeping at a determinative situation.

2). Parameter selection of HRtoF

There are 4 groups of parameter required to be determined in HRtoF. They are: i) the nodes of the partition; ii) the regulation parameter ρ in sparse logistic regression for the feature selection in the rough prediction stage; iii) the weight of penalty α and regulation parameters λ in linear regression with elastic-net penalty for the feature selection in fine prediction stage and one-stage prediction; iv) the belief threshold θ. All of them were selected by minimizing the averaged MAE from 10 times of inner 10-fold cross validation.

The belief threshold θ balances the usage of the two-stage prediction and the ordinary one-stage prediction. It determines whether a scan should be further predicted by the fine prediction stage or by the ordinary one-stage prediction. Thus, the choice of θ is related to the reliability of the rough prediction. The detailed information of the age prediction obtained by our proposed model, HRtoF, is shown in Fig. 7. We can see that, most of the failed-predicted scans were resulted from the incorrect classification at the rough prediction stage. Actually, the classification accuracy of the rough prediction stage is 0.83±0.01 in our experiment.

Fig. 7.

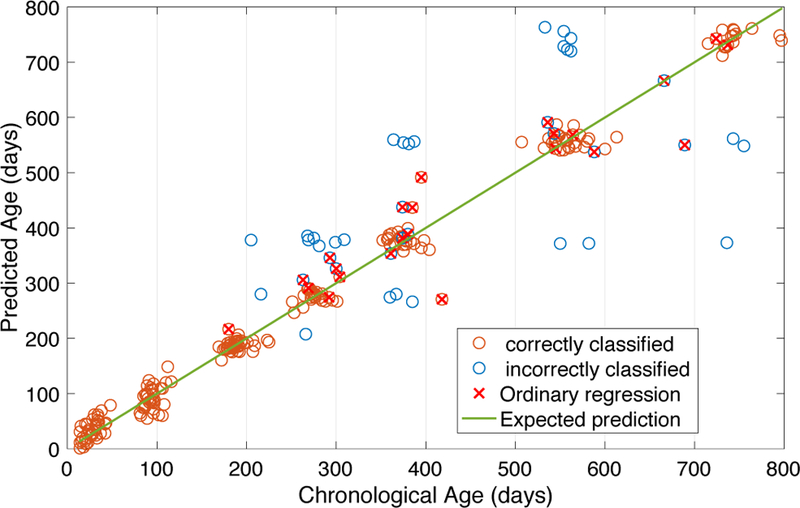
The detailed information in the scatter plot of the chronological ages and predicted ages obtained by HRtoF. The circles with red crosses represent the prediction ages obtained by the ordinary prediction (Belief≤ θ). The circles without red crosses on it represent the prediction ages obtained by the two-stage prediction (Belief> θ). Red circles represent the corresponding scans, which were correctly classified by the rough prediction stage, while blue circles represent the corresponding scans that were incorrectly classified by the rough prediction stage.

From 0.5 to 1, the parameter θ was assessed by the averaged MAE obtained from 10 times of 10-fold cross validation. The relationships between θ and detailed information of the prediction are shown in Table IX. Specifically, the detailed information includes i) the percentage of the scans predicted by the fine prediction stage (Belief>θ); ii) the percentage of the scans correctly classified by rough prediction stage and further predicted by the fine prediction stage (correct & Belief> θ); and iii) the corresponding prediction MAE. When all the scans were predicted by the two-stage prediction, i.e., θ= 0, the MAE was around 36.9 days. When θ= 0.89, 11% scans were predicted by the ordinary one-stage prediction model and the MAE was reduced to 32.1 days. It is obvious that the introduction of the ordinary one-stage prediction does alleviate the influence of the possible age range prediction deviation and improve the accuracy. However, larger θ may lead to strong dependence on the one-stage prediction and reduce the advantage of two-stage prediction. Therefore, the choice of θ is important. Finally, θ =0.89 was chosen as the belief threshold in our experiment. To guarantee the fairness of the comparison between HRtoF and the other 5 methods, Lasso regression was used for the feature selection of PLSR, SVR, GPR, and NonS-GPR, and all the relevant parameters in these 5 methods were chosen based on minimizing the average MAE obtained from the 10 times of 10-fold cross validation. Actually, an independent validation set may be better for the parameter selection. However, currently, we only have 251 scans in the dataset and only 23~41 scans in each time point. This amount of data is not large enough for us to get an independent validation data set that has the same distribution with the training data. When more infant data are increasingly acquired, the independent external validation will be possible, which will be our future work.

Table IX.

The sensitivity analysis of the belief threshold θ. %(> θ) represents the percentage of the scans predicted by the fine prediction stage; %(Correct & > θ) represents the percentage of the scans correctly classified by the rough prediction stage and further predicted by the fine prediction stage. MAE represents the MAE obtained by HRtoF accoring to the belief threshold θ. Mean and standard deviation of the values were obtained from the 10 times of 10-fold cross validation.

	% (> θ)	%(Correct & > θ)	MAE
θ = 0.99	0.71±0.021	0.69±0.008	40.1±1.8
θ = 0.89	0.89±0.007	0.74±0.005	32.1±1.2
θ = 0.90	0.91±0.007	0.76±0.008	32.7±1.5
θ = 0.80	0.93±0.008	0.78±0.012	34.8±1.7
θ = 0.60	0.97±0.008	0.81±0.014	35.6±1.8
θ = 0.50	0.98±0.005	0.82±0.012	36.7±2.4
θ = 0	1	0.83±0.010	36.9±2.9

3). The potential applications of HRtoF

Splitting the long time range with heterogeneous brain development and using a collection of group-specific regression models have the potential to perform better than the conventional methods. Thus, HRtoF may be useful for age prediction of any other age ranges, since the brain changes of different stages of life follows different trajectories.

It is worth noting that the scans used for our study have a characteristic that the infants were all required to take the scans at specific time points. Although there are variations of the ages that the subjects were scanned, as shown in Table I, the ages of these scans could be discretely partitioned into 7 discrete time points. However, the two-stage age prediction model is still useful for the subjects with continuous age distribution. First, the partition learning part could still automatically learn the nodes of the partition no matter how the ages of the scans are distributed. Second, the one-stage prediction part and the belief threshold in HRtoF could be very effective for the continuous age distribution. On one hand, when a scan belongs to the boundary of the partition, the posterior probability of the scan belongs to every age group is always lower than the belief threshold θ. Thus, the one-stage prediction part will be activated for the age prediction of the subject. On the other hand, when a scan does not belong to the boundary of the partition, the posterior probability of the scan belongs to a certain age group is always higher than the belief threshold θ, which leads to the activation of the local regression model in the fine prediction stage. Thus, the one-stage prediction part and the belief threshold will guarantee the effectiveness of HRtoF for the age prediction of the subjects with continuous age distribution.

4). Limitation and future direction

Although we have compared our proposed HRtoF with a nonstationary GPR, we only used dot-product nonstationary kernel. Some other nonstationary kernels and nonstationary regression models may still have high potentials in age prediction, although they are not specifically designed for and never used in age prediction. We should investigate how to design specific kernels for age prediction and incorporate the nonstationary regression into our proposed HRtoF model. Furthermore, although some important brain regions have been chosen for age prediction and reach good performance in our model, it is still unclear neurobiologically why these regions are so tightly related to the age prediction. More discussions should be done in our future work. Finally, based on the HRtoF model proposed in this paper, infant age prediction based on complementary multi-modal images should also be studied in the future.

V. Conclusion

In summary, this paper proposes a novel two-stage age prediction method and builds a hierarchical rough-to-fine (HRtoF) model to capture the rapid and heterogeneous changes of the brain development and achieves a high accuracy on infant age prediction. Partitioning the rapid brain development into several age groups, mining the discrimination capability of cortical features and using a collection of age-group-specific regression models are efficient and promising strategies to conduct the regression on a long time range. Furthermore, the high correlation coefficient (r = 0.962) between the predicted and chronological ages also shows that the cortical maturation has a strong relationship with the chronological age.