Abstract
The evaluation of head malformations plays an essential role in the early diagnosis, the decision to perform surgery and the assessment of the surgical outcome of patients with craniosynostosis. Clinicians rely on two metrics to evaluate the head shape: head circumference (HC) and cephalic index (CI). However, they present a high inter-observer variability and they do not take into account the location of the head abnormalities. In this study, we present an automated framework to objectively quantify the head malformations, HC, and CI from three-dimensional (3D) photography, a radiation-free, fast and non-invasive imaging modality. Our method automatically extracts the head shape using a set of landmarks identified by registering the head surface of a patient to a reference template in which the position of the landmarks is known. Then, we quantify head malformations as the local distances between the patient’s head and its closest normal from a normative statistical head shape multi-atlas. We calculated cranial malformations, HC, and CI for 28 patients with craniosynostosis, and we compared them with those computed from the normative population. Malformation differences between the two populations were statistically significant (p<0.05) at the head regions with abnormal development due to suture fusion. We also trained a support vector machine classifier using the malformations calculated and we obtained an improved accuracy of 91.03% in the detection of craniosynostosis, compared to 78.21% obtained with HC or CI. This method has the potential to assist in the longitudinal evaluation of cranial malformations after surgical treatment of craniosynostosis.
Keywords: Non-invasive, computational quantification, cranial malformations, three-dimensional photography, craniosynostosis, computer-aided diagnosis
1. INTRODUCTION
Craniosynostosis is a congenital defect that affects 1 in 2,100 live births in which one or more cranial sutures fuse early [1]. It typically results in abnormal cranial morphology due to cranial growth constraints and, if untreated, patients can present increased intracranial pressure or cognitive delays among other symptoms [2]. Although the diagnosis is made from the observations of fused sutures in computed tomography (CT) images, the evaluation of the head shape plays an important role in the decision to perform surgical treatment and in the longitudinal evaluation after surgery [3], [4]. To this end, the head circumference (HC) and cephalic index (CI) are often used clinically [5], [6]. However, they do not describe accurately the location of malformations and they present high inter-observer variability [7]. In this study, we present a reproducible method to assess cranial shape abnormalities quantitatively using three-dimensional (3D) photography, a non-invasive and radiation-free imaging modality.
Most image-based methods [3], [8], [9] quantify cranial shape abnormalities from CT images, which involve ionizing radiation in young children [10][11]. For that reason, 3D photography has gained popularity for the evaluation of cranial morphology [12]. Using 3D photographs, a method based on principal component analysis (PCA) to model the variations observed in a population over the mean head shape was proposed in [13]. Similarly Tu et al. [14] proposed to quantify 3D head malformations using a statistical shape atlas, to characterize the morphological abnormalities of patients with craniosynostosis. However, previous methods could only analyze head malformations globally and not separately on different areas of interest (i.e. frontal, parietal, or occipital bone areas), since 3D photography cannot image cranial bones. To facilitate the understanding and interpretation of head abnormalities, we overcome previous limitation in this work by creating a normative statistical shape atlas of the head using CT images, where both the skin and the bones are imaged and, therefore, the head skin of these subjects can be parcellated using the underlying bone information. This allows identifying bone areas in a new 3D photograph of a patient by propagating the ones parcellated on its closest normal shape from the statistical head shape multi-atlas. Thus, head malformations can be calculated at the area of each cranial bone to identify patients with head abnormalities related to craniosynostosis.
2. MATERIALS AND METHODS
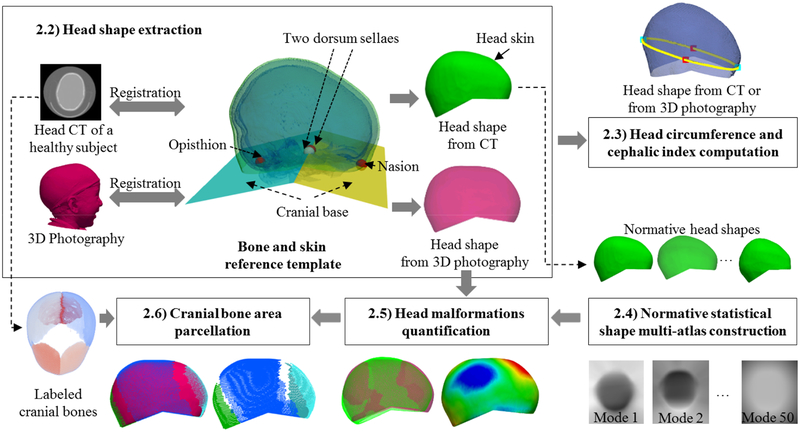
In the following sections, we will describe each component of our framework to automatically quantify local head malformations in patients with craniosynostosis from 3D photography, which are shown in Fig. 1.
Fig. 1.
Schematic of the proposed method. The head malformations were quantified above the cranial base automatically defined by four landmarks (nasion, opisthion and the two clinoid processes of the dorsum sellae).
In previous work, Mendoza et al. [3] quantified cranial malformations at each cranial bone from CT images using a statistical shape multi-atlas. They employed a landmark free shape descriptor, signed distance functions (SDF), to represent the cranial bone shapes of a normative population, and they used PCA to create a normative multi-atlas based on the SDFs. They showed that cranial shape abnormalities could be accurately quantified by comparing the cranial shape of a patient with its closest normal in the multi-atlas. Inspired by that study, we aim at automatically quantifying head malformations on patients with craniosynostosis from 3D photography, using a statistical atlas of the head shape instead of the cranial bones. Unlike other methods based on 3D photography, we build a statistical shape atlas using CT images, which let us identify the area of each cranial bone in the head skin. Fig.1 shows the workflow of our method divided into five steps.
2.1. Data description
A set of head 3D photographs was acquired using the 3dMD head System (3dMD, Atlanta, GA) from 28 patients (average age 3 ± 2 months, range 1–8 months, 10 female) with different types of craniosynostosis (17 sagittal, 4 left coronal, 4 right coronal, and 3 metopic) before surgical treatment.
We also used a set of retrospective CT axial images of 50 subjects (average age 4 ± 3 months, range 0–10 months, 26 female) without cranial pathology to build the normative statistical shape multi-atlas. The CT image in-plane resolution ranged 0.26–0.49 mm, with axial spacing ≤ 3mm.
2.2. Head shape extraction
We extracted the head shape from the CT image of the subjects without cranial pathology using thresholding to segment the head volume (including the skin, Hounsfield units, HU > −200) and the cranial bones (HU >100). Then, we extracted the largest connected component using morphological opening [15] to get a binary mask defining the head of a patient, and we reconstructed their surface using the marching cubes algorithm [10]. Next, we obtained two continuous surfaces representing the skin and the cranial bones of the head using the ShrinkWrap method [16]. The cranial bones obtained from the CT image were registered (optimizing translation, rotation, and scaling) to the cranial bones of a reference template, in which a set of four landmarks at the nasion, clinoid processes of the dosum sellae, and the opisthion had been manually placed [3] (see Fig. 1). These four landmarks were propagated to the head of the subject and used to define two cutting planes at the cranial base (Fig. 1), which were used to extract the head surface at the cranial vault area (represented in green in Fig. 1) [3].
Given the 3D photograph of a new patient, we registered it to the skin of the reference template using a rigid transformation with isotropic scaling, which we subsequently refined using both affine and B-spline-based non-rigid transformations. Similar to previous head extraction from CT, the positions of the landmarks in the reference template were used to extract the head shape from the 3D photograph (magenta surface in Fig. 1).
2.3. Head circumference and cephalic index computation
We shifted the plane defined by the nasion and clinoid processes of the dorsum sellae (yellow in Fig. 1) along its normal direction to find the maximum frontal-occipital extension and obtain a closed curve around the head to calculate the HC. We calculated the CI as the ratio between the two principal axes of the closed curve. To compensate for age, we normalized the HC of all subjects to the normative references provided by the National Center of Health Statistics for each age (www.cdc.gov) [17].
2.4. Normative statistical shape multi-atlas construction
We aligned all the head shapes (i.e. skin shapes) from the normative population optimizing for rotation, translation, and isotropic scaling, and we obtained their SDF representation [3], thus creating a volumetric image for each one (resolution 280*320*280 voxels, with isotropic spacing of 0.5 mm). Then, we created a statistical shape model of the SDFs of the normative cases using PCA and obtained a 50-dimensional normative multi-atlas, similar to [3].
2.5. Head malformations quantification
To quantify head shape malformations from 3D photography, we projected the SDF of the head shape into the PCA space and we identified the head shape of the closest normal using Euclidean distances [3] in that space. Then, we defined malformations at each point as the Euclidean distance to its closest point from the closest normal head shape, as proposed in [3] for the cranial bones.
2.6. Cranial bone area parcellation
For each CT image of the normative population, we segmented the five cranial bones (two frontal, two parietal, and occipital) using the graph-cut-based technique presented in [3], and we projected those regions in their head skin shape. Given the 3D photograph of a new patient, since no bone information is available, we parcellated the head shape propagating the cranial bone areas from its closest normal.
3. RESULTS
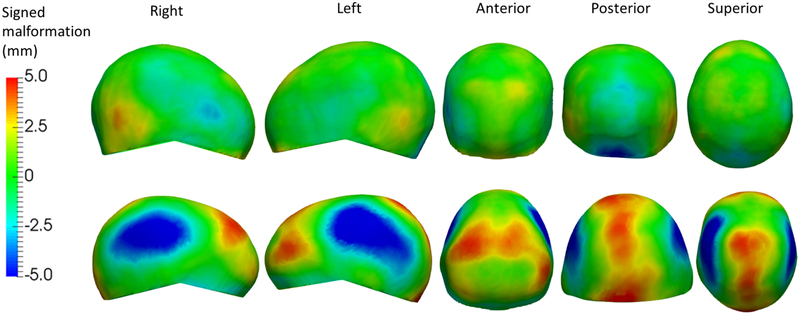
Table 1 shows the normalized HC (denoted as HC*), CI, average, and maximum cranial malformations for both the patients with craniosynostosis and the normative population. To calculate the average and maximum malformations, we discarded the 10% of points with the highest and lowest values at each head area to minimize the effect of outliers. Patients with sagittal craniosynostosis presented significantly higher (p<0.05 using Student’s t-test) HC* and lower CI than normal subjects, as well as significantly higher malformations at all bone areas (Fig. 2). Patients with coronal craniosynostosis showed significantly higher CI and maximum malformations in the frontal bones, but HC* for right coronal craniosynostosis was not significantly different to normal subjects. The HC* and CI of patients with metopic craniosynostosis were not significantly different than normal subjects, but they presented significantly higher average malformations in the frontal bones. Importantly, the areas where significant differences of malformations between patients with craniosynostosis and subjects without cranial pathology were found coincide with reported clinical findings [18]. Fig. 2 shows the example of a patient with sagittal craniosynostosis with its map of malformations showing head narrowing at the parietal bone areas and frontal-occipital enlargement, which is typical of these patients [18].
Table 1.
Normalized head circumference (HC*), cephalic index (CI, in %), average and maximum malformations (in mm) at the five cranial bone areas: left/right parietal bone (LP/RP), left/right frontal bone (LF/RF), and occipital bone (O) for all subject groups. The p-values (p) were computed between normal and each type of craniosynostosis. ●: significant (p<0.05), ○: non-significant.
| Normal | Sagittal (p) | Left coronal (p) | Right coronal (p) | Metopic (p) | Accuracy | |
|---|---|---|---|---|---|---|
| HC* | 1.07±0.05 | 1.11±0.03 (●) | 1.09±0.04 (●) | 1.06±0.04 (○) | 1.06±0.02 (○) | 78.21% |
| CI | 80.76±4.67 | 72.60±5.47 (●) | 87.75±4.10 (●) | 90.85±6.14 (●) | 82.24±4.18 (○) | 78.21% |
| LP average | 1.00±0.34 | 3.19±0.93 (●) | 1.27±0.22 (○) | 1.40±0.19 (●) | 1. 10±0. 31 (○) | |
| RP average | 0.96±0.44 | 2.42±0.63 (●) | 1. 18±0. 15 (○) | 1.27±0.07 (○) | 1.31±0.63 (○) | |
| LF average | 1.00±0.36 | 3.56±3.32 (●) | 1.62±0.59 (●) | 2.17±1.16 (●) | 1.48±0.43 (●) | 83.33% |
| RF average | 0.98±0.40 | 3.39±3.28 (●) | 1.41±0.68 (○) | 1.77±0.36 (●) | 1.68±0.42 (●) | |
| O average | 1.48±0.63 | 3.65±0.95 (●) | 1.61±0.32 (○) | 1.31±0.40 (○) | 1.83±0.37 (○) | |
| LP max | 2.11±0.66 | 6.88±1.58 (●) | 2.64±0.75 (○) | 3.16±0.76 (●) | 2.43±0.46 (○) | |
| RP max | 2.11±0.84 | 5.66±1.02 (●) | 2.40±0.27 (○) | 2.67±0.31 (○) | 2.63±1.01 (○) | |
| LF max | 2.17±0.90 | 7.11±6.22 (●) | 4.67±0.44 (●) | 4.29±2.37 (●) | 3. 12± 1.32 (○) | 91.03% |
| RF max | 2.10±0.76 | 6.33±6.58 (●) | 2.98±1.38 (●) | 4.03±1.31 (●) | 3.51±0.57 (●) | |
| O max | 3.07±1.29 | 6.62±1.45 (●) | 3.02±0.38 (○) | 3.03±1.56 (○) | 3.64±0.54 (○) |
Fig. 2.
Five views of the signed malformations on the head shape of a healthy subject (top) and a patient with sagittal craniosynostosis (bottom). Blue represents underdevelopment with respect to the closest normal, while red represents overdevelopment.
We trained a support vector machine classifier using the maximum malformations calculated at the area of each cranial bone on the head shapes and we evaluated its performance in classifying patients with craniosynostosis from normative subjects, obtaining an accuracy of 91.03% (sensitivity 85.71%, specificity 94.00%). We also identified the thresholds on the normalized HC and CI that provided the optimal classification between the two populations, obtaining a maximum accuracy of 78.21% (sensitivity 75.00%, specificity 80.00%) and 78.21% (sensitivity 50.00%, specificity 94.00%), with normal ranges of [0.94, 1.07] and [70.67, 88.17]% for the normalized CH and CI, respectively. Importantly, the classification accuracy using head malformations was significantly higher than using CH or CI, obtaining a p-value of 0.02 using a Fisher’s exact test.
4. CONCLUSIONS
We proposed a novel automatic framework to quantify head malformations locally at the area of each cranial bone on patients with craniosynostosis from 3D photography. These malformations were significantly higher in patients with craniosynostosis than on a normative population at the areas of the head where growth is abnormal due to suture fusion. Our results also show that the local malformations provide a more accurate identification of head shape abnormalities in patients with craniosynostosis than the clinically used HC and CI. The proposed framework has the potential to provide an objective, low-cost, fast, reproducible, and radiation-free evaluation of the surgical outcome and the evolution of malformations in patients with craniosynostosis.
ACKNOWLEDGEMENTS
This work was partly funded by the National Institutes of Health, Eunice Kennedy Shriver National Institute of Child Health and Human Development under grant NIH R42HD081712.
References
- [1].Lajeunie E, Le Merrer M, Bonaïti-Pellie C, Marchac D, and Renier D, “Genetic study of nonsyndromic coronal craniosynostosis,” Am. J. Med. Genet, vol. 55, no. 4, pp. 500–504, 1995. [DOI] [PubMed] [Google Scholar]
- [2].Sloan GM, Wells KC, Raffel C, and McComb JG, “Surgical treatment of craniosynostosis: outcome analysis of 250 consecutive patients,” Pediatrics, vol. 100, no. 1, p. e2 LP–e2, July 1997. [DOI] [PubMed] [Google Scholar]
- [3].Mendoza CS, Safdar N, Okada K, Myers E, Rogers GF, and Linguraru MG, “Personalized assessment of craniosynostosis via statistical shape modeling,” Med. Image Anal, vol. 18, no. 4, pp. 635–646, 2014. [DOI] [PubMed] [Google Scholar]
- [4].Porras AR, Paniagua B, Ensel S, Keating R, Rogers GF, Enquobahrie A, and Linguraru MG, “Locally affine diffeomorphic surface registration and its application to surgical planning of fronto-orbital advancement,” IEEE Trans. Med. Imaging, vol. 37, no. 7, pp. 1690–1700, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Martini M, Klausing A, Lüchters G, Heim N, and Messing-Jünger M, “Head circumference - a useful single parameter for skull volume development in cranial growth analysis?,” Head Face Med, vol. 14, no. 1, p. 3, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Fischer S, Maltese G, Tarnow P, Wikberg E, Bernhardt P, and Kölby L, “Comparison of intracranial volume and cephalic index after correction of sagittal synostosis with spring-assisted surgery or pi-plasty,” J. Craniofac. Surg, vol. 27, no. 2, 2016. [DOI] [PubMed] [Google Scholar]
- [7].Schaaf H, Wilbrand J-F, Bödeker R-H, and Howaldt H-P, Accuracy of photographic assessment compared with standard anthropometric measurements in nonsynostotic cranial deformities, vol. 47 2010. [DOI] [PubMed] [Google Scholar]
- [8].Paniagua B, Emodi O, Hill J, Fishbaugh J, Pimenta LA, Aylward SR, Andinet E, Gerig G, Gilmore J, van Aalst JA, and Styner M, “3D of brain shape and volume after cranial vault remodeling surgery for craniosynostosis correction in infants,” in Proc. of SPIE Medical Imaging, 2013, vol. 8672, p. 86720V–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Porras AR, Zukic D, Equobahrie A, Rogers GF, and Linguraru MG, “Personalized optimal planning for the surgical correction of metopic craniosynostosis,” in Medical Image Computing and Computer-Assisted Intervention, Workshop on Clinical Image-based Procedures: Translational Research in Medical Imaging, LNCS, Springer Cham, vol. 9958, 2016, pp. 60–67. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Miglioretti DL, Johnson E, Williams A, Greenlee RT, Weinmann S, Solberg LI, Spencer Feigelson H, Roblin D, Flynn MJ, Vanneman N, and Smith-Bindman R, “The use of computed tomography in pediatrics and the associated radiation exposure and estimated cancer risk,” JAMA Pediatr, vol. 167, no. 8, pp. 700–707, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Brody AS, Frush DP, Huda W, and Brent RL, “Radiation risk to children from computed tomography,” Pediatrics, vol. 120, no. 3, p. 677 LP–682, September 2007. [DOI] [PubMed] [Google Scholar]
- [12].van Veelen M-LC, Jippes M, Carolina J-CA, de Rooi J, Dirven CMF, van Adrichem LNA, and Mathijssen IM, “Volume measurements on three-dimensional photogrammetry after extended strip versus total cranial remodeling for sagittal synostosis: A comparative cohort study,” J. Cranio-Maxillofacial Surg, vol. 44, no. 10, pp. 1713–1718, 2016. [DOI] [PubMed] [Google Scholar]
- [13].Meulstee JW, Verhamme LM, Borstlap WA, Van der Heijden F, De Jong GA, Xi T, Bergé SJ, Delye H, and Maal TJJ, “A new method for three-dimensional evaluation of the cranial shape and the automatic identification of craniosynostosis using 3D stereophotogrammetry,” Int. J. Oral Maxillofac. Surg, vol. 46, no. 7, pp. 819–826, June 2017. [DOI] [PubMed] [Google Scholar]
- [14].Tu L, Porras AR, Oh A, Lepore N, Mastromanolis M, Tsering D, Paniagua B, Enquobahrie A, Keating R, Rogers GF, and Linguraru MG, “Radiation-free quantification of head malformations in craniosynostosis patients from 3D photography,” in Proceedings of SPIE Medical Imaging 2018: Computer-Aided Diagnosis, 2018, vol. 10575, p. 105751U–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Gonzalez RC and Woods RE, Digital image processing (3rd ed.). Upper Saddle River, N.J.: Prentice Hall, 2008. [Google Scholar]
- [16].Pope P, “Shrinkwrap: 3d model abstraction for remote sensing simulations,” in Proc. of the 2009 ASPRS Annual Meeting, 2009, pp. 9–13. [Google Scholar]
- [17].Kuczmarski RJ, Ogden CL, Guo SS, Grummer-Strawn LM, Flegal KM, Mei Z, Wei R, Curtin LR, Roche AF, and Johnson CL, “2000 CDC growth charts for the United States: Methods and development.,” Natl. Cent. Heal. Stat. Vital Heal. Stat, vol. 11, no. 246, 2002. [PubMed] [Google Scholar]
- [18].Sharma RK, “Craniosynostosis,” Indian Journal of Plastic Surgery : Official Publication of the Association of Plastic Surgeons of India, vol. 46, no. 1 India, pp. 18–27, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]