Abstract
Isolating the role(s) of microstructural pathological features in affecting diastolic filling is important in developing targeted treatments for heart diseases. We developed a microstructure-based constitutive model of the myocardium and implemented it in an efficient open-source finite element modeling framework to simulate passive inflation of the left ventricle (LV) in a representative 3D geometry based on experimentally measured muscle fiber architecture. The constitutive model was calibrated using previous tissue-level biaxial mechanical test data derived from the canine heart and validated with independent sets of measurements made at both the isolated constituent and organ level. Using the validated model, we investigated the load taken up by each tissue constituent and their effects on LV passive inflation. The model predicts that the LV compliance is sensitive to the collagen ultrastructure, specifically, the collagen fiber azimuthal angle with respect to the local muscle fiber direction and its waviness. The model also predicts that most of the load in the sub-epicardial and sub-endocardial regions is taken up, respectively, by the muscle fibers and collagen fiber network. This result suggests that normalizing LV passive stiffness by altering the collagen fiber network and myocyte stiffness is most effective when applied to the sub-endocardial and sub-epicardial regions, respectively. This finding may have implication for the development of new pharmaceutical treatments targeting individual cardiac tissue constituents to normalize LV filling function in heart diseases.
Keywords: cardiac mechanics, microstructural constitutive model, collagen fiber network, finite element modeling, left ventricle
1. Introduction
Passive filling capacity of the left ventricle (LV) is a major determinant of the heart’s pumping performance [1], [2]. Heart failure with preserved ejection fraction (HFpEF) (referred previously as diastolic heart failure) is associated with abnormalities in LV filling that can be detected from clinical imaging [3], [4]. Because HFpEF accounts for about one-half of all chronic HF patients [5], understanding how LV filling is affected by the many microstructural pathological features associated with this syndrome (e.g., cardiac fibrosis [6], myocyte passive stiffening [7], and collagen ultrastructure alterations [8] is very important. As such, the development of a 3D LV mechanics model that includes myocardial tissue constituents and their microstructure will enable one to isolate and quantify the impact of each constituent on LV filling.
Current constitutive models used to describe the mechanical behavior of the myocardium can be broadly categorized into two types: i.e., phenomenological and microstructural models. In phenomenological constitutive models, the tissue’s mechanical behavior is usually described by a mathematical expression of its strain energy function (SEF) with the form of a polynomial [9], an exponential [10], [11] or a zero-pole function [12] of either the invariants or components of the strain tensor. While able to represent the bulk cardiac tissue mechanical behavior, these phenomenological models cannot distinguish between contributions of tissue constituents’ intrinsic mechanical behavior and ultrastructure (e.g., collagen waviness) to the LV mechanics and function. Moreover, model parameters in the phenomenological models can only be obtained by fitting with experimental measurements of stress-strain relationships and have no direct physical meaning.
First developed by Lanir, microstructural constitutive models take into account the tissue constituents’ morphology and structural arrangement in a stochastic manner as well as their intrinsic mechanical behavior [13]. One advantage of microstructural constitutive models is that their morphometric parameters, in addition of being physiologically meaningful, can be directly measured. With the significant advancement in microscopy imaging (e.g., multiphoton microscopy) techniques that enable the tissue constituent’s (e.g., elastin, collagen, cells) morphology and structure to be accurately measured, these models can be exploited to directly isolate and quantify the effects of microstructural changes on the overall tissue mechanical behavior and organ function.
Microstructural constitutive models have been applied to describe the mechanics of various tissues, such as skin [14], heart valves [15], arteries [16] as well as the passive myocardium [17]. The solution of the mechanical equilibrium boundary value problem using these models, however, were obtained semi-analytically and their applications were therefore confined to simple idealized geometries such as thick-walled cylinder [18]. Quantification of three-dimensional tissue mechanics in a realistic organ geometry requires an efficient finite element (FE) implementation of the microstructural constitutive model, which is, to the best of our knowledge, currently lacking and limited to tissue mechanics of a thin myocardial strip [19], a thick single-element myocardial wall segment[20], as well as a thin membrane [21].
To address this gap, we developed a microstructural FE model of the LV with a representative 3D geometry and muscle fiber architecture to describe the passive mechanics of myocardial tissue during inflation. The model was implemented using an open-source FE library FEniCS [22]. Additionally, we estimated the microstructural constitutive model parameters using previous biaxial mechanical test measurements of the canine myocardial tissue. These model parameters were also validated using independent sets of measurements made on isolated cardiac tissue constituents and the intact LV during passive filling. Based on the calibrated parameters, we investigated the load taken up by each constituent during passive filling. The FE model shows that the global LV filling function is sensitive to the tissue microstructure.
2. Materials and Methods
2.1. Microstructural constitutive model formulation.
The myocardium has two major load-bearing elements: collagen fibers and muscle fibers. Arranged in a fibrous network, collagen fibers form a network of “struts” interconnecting adjacent myocytes and fibrous weaves surrounding groups of myocytes [23], [24]. Both types of fibers are embedded in an interstitial fluid matrix. The fibers carry tensile forces, while the fluid matrix sustains only hydrostatic pressure. On the other hand, the myocardium also contains a non-fibrous ground matrix consisting of non-load bearing substances such as fibroblasts, plasma cells, as well as a gel-like ground substance composing of glycosaminoglycans and glycoproteins.
Following Horowitz et al. [17], we developed a microstructure-based constitutive model to describe the passive mechanical behavior of the myocardium based on the following assumptions:
The myocardium is treated as an incompressible pseudo-hyperelastic composite material [25], namely, there exists a strain energy function from which the stresses are derived. The viscoelastic aspect of the tissue is not considered in our study due to the relatively short duration of the cardiac cycle (≤ 1s) compared with the characteristic relaxation time of the myocardium (> 100 s) [26].
The fibers are thin and perfectly flexible. They can only carry tensile loads and have no compressive strength and if contracted will buckle under zero load.
Each fiber is subjected to a uniaxial strain that is the tensorial transformation of the overall strain in the fiber’s direction (affine deformation). This is intuitively justified by the numerous interconnections between muscle and collagen fibers [17], [27], [28].
Correspondingly, the total strain-energy function Wtotal of the myocardium can be represented by the volume-weighted summation of the strain energy function of its constituents, i.e.:
| (1) |
where ϕg, ϕm and ϕc are the volume fraction of the ground matrix, muscle fibers and collagen fibers, respectively, with ϕg + ϕm + ϕc = 1. On the other hand, Wg, Wm and Wc are the corresponding SEF of the ground matrix, muscle fibers and collagen fibers, respectively. In Eq. (1), J is the determinant of deformation gradient tensor F, and p is the Lagrange multiplier to enforce incompressibility due to the negligible fluid flow within the tissue for the pertinent time intervals. Correspondingly, we assume that the last term − p (J − 1) in Eq. (1) represents the contribution to Wtotal by the interstitial fluid matrix. The deformation gradient tensor is defined by F = I + ∇u, where u is the displacement field and I is the identity tensor. In the following, we describe the mechanical behavior of each constituent.
Non-fibrous ground matrix
Following a previous study [29], we modeled the non-fibrous ground matrix as an isotropic hyperelastic Neo-Hookean material with the SEF defined as:
| (2) |
where I1 = tr(C) is the first invariant of the right Cauchy-Green deformation tensor C = FT F, and C1 is a material constant. The resulting second Piola-Kirchhoff (PK2) stress tensor associated with the non-fibrous ground matrix is then given by:
| (3) |
where is the right Cauchy-Green strain tensor.
Muscle fibers.
Because the isolated myocyte exhibits a non-linear stress-strain relationship of an exponential form [30], we used an SEF [31] that is given as:
| (4) |
to describe the muscle fiber’s passive mechanical behavior. In Eq. (4), is the uniaxial stretch of the muscle fiber, ef is a unit vector describing the local muscle fiber direction in the undeformed configuration, whereas C2 and C3 are the material constants. The corresponding PK2 stress tensor associated with the muscle fibers is given by:
| (5) |
Collagen fiber network
For simplicity, different hierarchies of collagen fibers (perimysial, epimysial and endomysial or struts) are lumped into one inclusive system in the model. Because straightened individual collagen fiber exhibits a linear stress-strain relation [32], uniaxial stress Sc of a single straightened collagen fiber is prescribed to be a linear function of its strain taken with respect from its initial straightened configuration with a slope or elastic modulus C4. Collagen fibers, however, are observed to be undulated and slack in the unstressed state in the myocardium [23]. Because of their crimped structural feature, the individual wavy collagen’s true fiber strain ϵt taken with respect from its initial straightened configuration is given by:
| (6) |
where ϵc is the total strain of the collagen fiber taken with respect from its initial wavy configuration and ϵs is the strain at which the collagen fiber first straightens; i.e., straightening strain. Assuming that the collagen fiber doesn’t show any resistance to stretch before becoming straightened (or reaching their straightening strain ϵs), the resulting SEF for a single wavy collagen fiber is given by:
| (7) |
The extent of collagen fiber undulation can vary, however, across collagen fibers in the myocardium [28]. To stochastically account for the gradual recruitment of wavy collagen fibers, we assume a truncated normal distribution with the density function:
| (8) |
where is a truncated parameter with Φ denoting the cumulative normal distribution function, whereas, mc and σc denote the mean and variance of the collagen fiber straightening strain, respectively. Thus, the resulting SEF for a uniaxial ensemble of collagen fibers over all possible waviness (weighted by the waviness distribution) is given by:
| (9) |
The mechanical behavior of the overall collagen fiber ensemble is the sum of the contributions from all uniaxial ensembles over all collagen fiber orientation s. Following Horowitz et al.[17], we assume that the collagen fibers are symmetrically distributed around the muscle fiber to which they are attached, with the muscle fiber serving as an axis of symmetry (Fig. 1). Following this assumption, the collagen fibers are ascribed a uniform distribution R(θ) in the circumferential θ – direction (0 ≤ θ ≤ 2π), and a bimodal normal distribution R(ϕ) in the azimuthal ϕ – direction(0 ≤ ϕ ≤ π). Thus, the overall spatial distribution function is given by:
| (10) |
where (mϕ, π − mϕ) are the means and (σϕ, σϕ) are the standard deviations of the bimodal distribution of the azimuthal angle ϕ. Since the arrangement of the collagen fibers is referred to the muscle fibers to which they are attached, the uniaxial strain of a local collagen fiber oriented with respect to the local muscle fiber that it is attached to can be related to the local muscle fiber strains by a tensorial transformation as:
| (11) |
where Nc = {cosϕ, cosθsinϕ, sinθsinϕ] and Em is the Green-Lagrange strain tensor in the local material coordinate system. The components of Em are related to the Green-Lagrange strain tensor E in the global coordinate system by:
| (12) |
with the subscript (i,j) ∈ (f,s,n) denoting the muscle fiber ef, cross muscle fiber es, tissue sheet normal en directions.
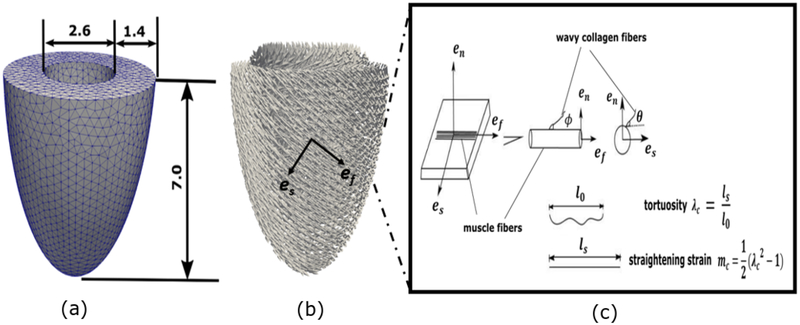
Fig. 1.
(a) Unloaded canine LV FE geometry (all dimensions are in cm). (b) Muscle fiber orientation with a linear transmural variation from 70° at the endocardium to − 40° at the epicardium. (c) Schematic representation of the local arrangement of muscle fiber and collagen fiber network. The muscle fiber defines an axis of symmetry for the spatial arrangement of collagen fiber that attached to it. Collagen fiber dispersion is prescribed by a continuous function with the angle θ and ϕ. An azimuthal angle ϕ = 0 corresponds to the axial fiber family whereas a circumferential angle ϕ ≠ 0 corresponds to the radial fiber family.
If the waviness density distribution function D (x) is assumed to be homogeneous over all spatial orientations, the total collagen fiber SEF is given by:
| (13) |
Correspondingly, the PK2 stress tensor associated with the collagen network is given by:
| (14) |
We note that the approach here to describe the collagen network stress tensor in Eq. (14) differs from the generalized structure tensor (GST) approach [33], which assumes that the dispersion of fiber orientation (as described by a structure tensor) is separable from the dispersion of tortuosity. No such assumption is made in this approach, which is also referred as the “angular integration” (AI) approach [33]. For a detail comparison of the GST and AI approaches, refer to Holzapfel and Odgen [34]. From Eq. (1), the total PK2 stress tensor of the myocardium is given as:
| (15) |
2.2. Parameter estimation
We used the biaxial mechanical test data obtained from 6 canine mid-wall myocardium in a previous experimental study [35] to estimate the model’s parameters. In that study, equi-biaxial stretching and constant α tests, where cross-fiber stretch was varied at a constant muscle fiber stretch of α, were performed on thin slab of tissues taken from the mid ventricular wall. We fixed the volume fraction of the tissue constituents to be ϕm = 0.7, ϕc = 0.026, ϕa = 0.274 based on previous experimental measurements [36], [37]. The collagen spatial distribution variance σϕ was also fixed at 0.1 rad (or equivalently 6°) based on a quantitative analysis of the collagen orientation in the canine LV [8]. This leaves the remaining 7 unknown model parameters to be estimated, namely, material constants of the constituents C1, C2, C3, C4, mean value of the collagen spatial distribution function mϕ, and the mean mc and variance σc of the collagen waviness distribution. These model parameters were fitted to the experimental data with an objective function defined as the sum of squared residuals (SSEs) between the model predictions and experimental measurements, i.e.,
| (16) |
In Eq. (16), N is the total number of data points and are the measured values of the Cauchy stresses. We also imposed constraints to our model parameters, especially those related to the microstructural features, to vary within physiological ranges based on previous studies (Table 1). A nonlinear programming solver “fmincon” in MATLAB (The Mathworks, Inc., Natick, MA, USA) was used to find parameters that lie between the imposed physiological lower and upper bounds, and minimize the objective function. An optimal solution was obtained when the change in parameters or the objective function was less than 10−9 Different sets of initial guesses were randomly generated between the lower bounds and upper bounds in order to eliminate parameter dependence on the initial guess values. Details of the plane stress formulation for fitting the biaxial test data is given in Appendix A.
Table 1:
List of model parameters with the corresponding lower/upper bounds according to literature references
To investigate the identifiability and correlation of the fitted model’s parameters, we estimated the asymptotic correlation matrix R associated with these parameters using the scaled inverse of the hessian matrix H evaluated at the optimal solution [38]. Specifically, components of the estimated correlation matrix R was defined as:
| (17) |
The closer the absolute value of the off-diagonal terms Rij to 1, the stronger the correlation between the íth and jth parameters.
2.3. Finite element simulation of left ventricular passive filling
Unloaded geometry and microstructure
The unloaded LV geometry was modeled as a half prolate ellipsoid with geometric dimensions that are based on measurements of isolated arrested canine hearts (Fig. 1) [39]. Specifically, the unloaded LV cavity volume is about 20 ml. The geometry is meshed with 17600 quadratic tetrahedral elements and 83799 nodes. The local muscle fiber orientation in the LV is prescribed based on the mean values reported in an experiment [39], which shows that the helical angle varied linearly in the transmural direction from about 70° at the endocardium to − 40° at the epicardium.
Finite element formulation
Passive filling of the LV was simulated by incrementally increasing the pressure at endocardium as a Neumann boundary condition. The weak form of the mechanical equilibrium equation is given by:
| (18) |
where P = FStotal = F(Sg + Sm + Sc) − pJF−T is the first Piola-Kirchhoff stress tensor, Pendo is the prescribed LV cavity pressure at the endocardial surface ∂Ωendo with unit outward normal of N, whereas v and q are the variation of the displacement field u and the Lagrange multiplier p, respectively, Thus, the Euler-Lagrange problem becomes one of finding u ∈ H1(Ω0), p ∈ L2(Ω0) that satisfies . The basal deformation is constrained to be in-plane (i.e., u·n|base = 0) and the endocardial basal nodes are fixed in all directions to account for the relative stiff valve annuli [40]. The nonlinear FE problem was solved using Newton-Raphson method and implemented based on the parallel open-source FE library FEniCS. The code is freely available at https://cexi@bitbucket.org/cexi/microstructure_lv.git. Convergence of the numerical solution for the nonlinear FE problem was accepted when the normalized two-norm of the residual vector is smaller than 10− 9 Analyses of the mesh sensitivity and computational efficiency were also performed.
Post-processing of myocardial strains and stresses
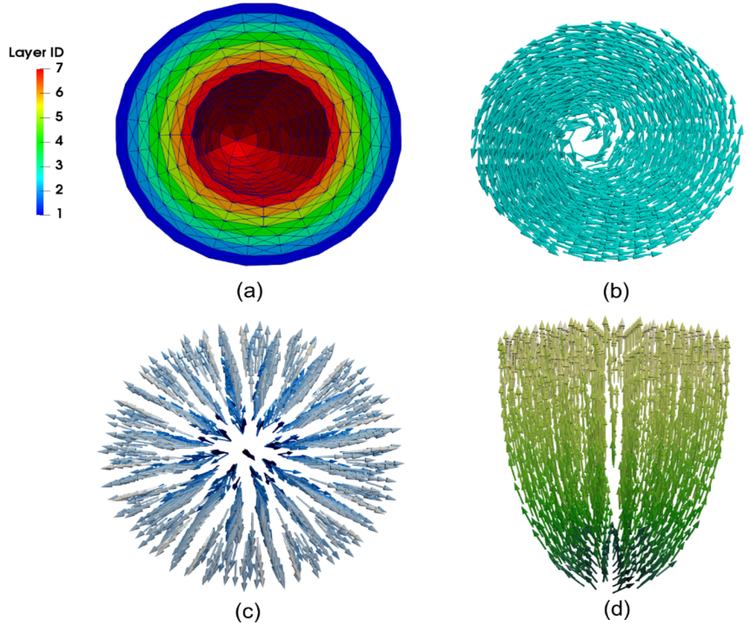
To compare with strain measurements and estimate myocardial stress, we computed strains and stress components in the circumferential ec, longitudinal el and radial er directions, as well as fiber ef and cross-fiber es directions (Fig. 2). We also divided the LV FE mesh into 7 layers with equal thickness. The strain and stress components were averaged over the volume of each layer to determine their transmural variations (Fig. 2).
Fig. 2.
(a) Transmural division of mesh into 7 layers with the same wall thickness. (b) Circumferential direction. (c) Radial direction. (d) Longitudinal direction.
Post-processing of collagen fiber tortuosity.
Volume-averaged 2D tortuosity λc (fiber arc length/midline length) of the collagen fiber network was computed at a given ventricular pressure P as:
| (19) |
where is the initial tortuosity for a collagen fiber with an initial straightening strain x, is the tortuosity of deformed local collagen fiber with spatial orientation (θ, ϕ) at ventricular pressure P and Ω0 is the whole material volume at the reference configuration.
2.4. Statistical Analysis
Categorical variables are expressed as number and percentage, and continuous variables as mean ± standard deviation (SD). Nonlinear regression analysis was performed to correlate model-predicted biaxial stresses with corresponding stress-strain measurements in canine LV midwall myocardium (n = 6).
3. Results
3.1. Biaxial tests
Table 2 lists the best fitted model parameters for 6 specimens with corresponding root mean square errors. About eighty iterations were required to obtain the optimized model parameters for each specimen. In general, our microstructural model shows very good fit to the measurements. Except for C1, the spreads of all other parameter values are relatively small across the specimens. The large SD of C1 may be related to the fact that the stiffness modulus and volume fraction for the ground matrix are much smaller than other the myocardial constituents [41]. The average correlation coefficient of the fit between the measurements and model-predicted stresses in the muscle fiber and cross-fiber directions are 0.980 and 0.999, respectively. The maximum root mean square errors is 0.152 kPa, which is less than 2% of the range of stress reached in the biaxial tests. We also note that increasing the lower and upper bounds of the mean collagen waviness to 0.22 ≤mc≤ 0.78, which corresponds to the collagen tortuosity range of 1.2 – 1.6 as found in the skin [14], led to a larger mean square error and increased both the mean value of mc and C4 by about 2 times. A comparison between the measurements and model predictions of the equi-biaxial and constant α test using the best-fit material parameters for a representative specimen is shown in Fig. 3a. Corresponding stresses in the muscle fiber and cross-fiber directions associated with each constituent in the equi-biaxial test of the representative specimen is shown in Fig. 3b. Taking all the specimens into account, we found that the collagen fiber network accounts, on average, for 57% and 99.4% of the total stress in the muscle fiber and cross-fiber directions, respectively, at a stretch of 1.32. The muscle fiber, on the other hand, accounts on average for about 43% of the total stress in the fiber direction at that stretch value. At stretch lower than 1.1, however, the collagen fiber network contributes very little to the total stress. For the results of all other specimens, refer to Appendix B.
Table 2:
Best-fit model parameters and root mean square error (RMSE) for biaxial tests of six canine mid-wall LV myocardium
| Specimen | C1 (kPa) | C2 (kPa) | C3 | C4 (MPa) | mc | σc | mϕ(rad) | RMSE (kPa) |
|---|---|---|---|---|---|---|---|---|
| 0118 | 1.255 | 0.204 | 10.874 | 6.624 | 0.117 | 0.094 | 0.930 | 0.122 |
| 0119 | 0.1 | 0.261 | 10.911 | 3.818 | 0.117 | 0.052 | 0.901 | 0.152 |
| 0124 | 0.1 | 0.151 | 12.870 | 4.587 | 0.124 | 0.057 | 0.919 | 0.152 |
| 0217 | 0.438 | 0.596 | 6.579 | 4.287 | 0.116 | 0.084 | 0.915 | 0.084 |
| 0303 | 1.786 | 0.717 | 5.196 | 3.426 | 0.140 | 0.100 | 0.938 | 0.055 |
| 0330 | 0.1 | 0.392 | 8.451 | 7.816 | 0.123 | 0.075 | 0.959 | 0.134 |
| Mean | 0.630 | 0.387 | 9.147 | 5.093 | 0.123 | 0.077 | 0.927 | 0.122 |
| SD | 0.722 | 0.227 | 2.921 | 1.736 | 0.009 | 0.019 | 0.020 | 0.089 |
Fig. 3.
(a) Comparison of the fitted and experimental Cauchy stress-stretch data for equibiaxial and constant α = 1.1, 1.15 and 1.2 tests of specimen 0118. (b) Contribution of the collagen fiber network, muscle fibers, non-fibrous ground matrix and interstitial fluid matrix to the total stress in the fiber direction (top) and the cross-fiber (bottom) directions in the equi-biaxial test of specimen 0118.
Table 3 compares the microstructural model parameters that are directly related to the constituents’ structure and mechanical behaviors with measurements from experiments conducted on the isolated constituents. Specifically the average fitted values of the collagen fiber elastic modulus C4, mean collagen fiber straightening strain mc, and the stiffness and uniaxial stress computed from the material constants of the muscle fiber C2, C3 are within the range of reported values [30], [42]-[44]. We computed the uniaxial stress and the resulting stiffness modulus (see Appendix C for details) at an engineering strain ϵ ≈ 0.158, which is associated with the stretch imposed on the muscle fibers in the experiments. Measurements of the mean inclination angle of the collagen fibers with respect to the muscle fibers mϕ are not available, however, for comparison with the fitted value of 53.1°.
Table 3:
Comparison of fitted parameters with measurements of isolated myocytes and collagen fibers.
| Description | Fitted model parameters | Reported Values |
|---|---|---|
| Cardiac muscle stiffness modulus | 13.49 ± 1.92kPa* | Guinea pig:16.4 ± 11.0 kpa [42]; Hamster: 7.48 ± 1.73 kpa [30]; |
| Cardiac muscle uniaxial stress | 1.36 ± 0.28 kPa* | Guinea pig: 2.1 ± 1.4 kpa [42]; Hamster: 0.88 ± 0.48 kpa [30]; |
| Collagen fiber stiffness C4 | 5.1 ± 1.7MPa | Skin: 0 ~ 50 MPa [43] |
| Collagen fiber mean tortuosity | 1.116** | Canine: 1.01~1.2 [44] |
Cardiac muscle stiffness and uniaxial stress were computed at 2.2 μm sarcomere length. Based on a resting sarcomere length of 1.9 μm, this translates at an engineering strain ϵ ≈ 0.158
The collagen fiber mean tortuosity was computed from the collagen fiber straightening strain mc by where mc = 0.12
Table 4 shows the estimated average correlation matrix R of the model parameters from all the specimens. Parameters C2 and C3 describing the muscle fiber mechanical behavior has the greatest interaction and are inversely related with correlation coefficient ≈ −0.93. Large positive correlation between the collagen elastic modulus C4 and mean straightening strain mc is also found (correlation coefficient ≈ 0.75). Interactions between the parameter pairs (C1,C2), (C4, σc) and(mc,σc) are moderate; their largest correlation coefficient is 0.55.
Table 4:
Average correlation matrix of fitted model parameters
| C1 | C2 | C3 | C4 | mc | σc | mϕ | |
|---|---|---|---|---|---|---|---|
| C1 | 1 | −0.52 | 0.33 | 0.04 | 0.49 | −0.09 | −0.35 |
| C2 | 1 | −0.93 | 0.27 | −0.04 | 0.09 | 0.07 | |
| C3 | 1 | −0.37 | −0.03 | −0.07 | 0.23 | ||
| C4 | 1 | 0.75 | 0.54 | −0.22 | |||
| mc | 1 | 0.55 | −0.04 | ||||
| σc | 1 | 0.07 | |||||
| mϕ | 1 |
3.2. Finite element simulation of passive filling
Differences of the transmural fiber stress distribution and pressure-volume relationship are found to be < 2% between FE meshes containing 17,600 and 38,985 elements in the mesh sensitivity analysis. (Appendix E). With 16 processors (Intel® Xeon (R) CPU E5–1660 v3@ 3.00GHz × 16), the computing time for simulating the inflation of an LV model with 17,600 elements is about 13 hours. The FE implementation (that utilizes the domain decomposition method in FEniCS) also exhibits an approximately linear scalability (Appendix E), which indicates that the computing time can be reduced substantially with more processors. An estimation of the simulation time for solving active mechanics over a cardiac cycle is also provided in Appendix E.
Inflation pressure-volume relations.
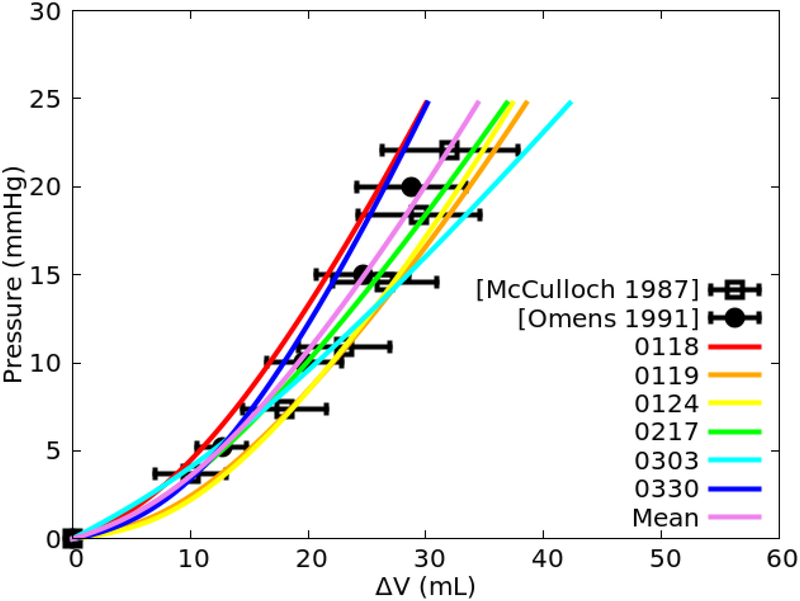
Figure 4 shows the relationships between the change in LV cavity volume AV with respect to the LV pressure using the fitted parameters in Table 2 for all the 6 specimens. Compared to the measurements from the experiments on isolated canine hearts [39], [45], the pressure-volume curves derived from all 6 sets of parameter values fell largely within1 SD of the mean measurements.
Fig. 4.
Comparison of the inflation pressure-volume curves derived from the 6 sets of fitted model parameter values (Table 2) and their mean values with measurements (plotted as mean ± SD).
Local ventricular wall strains
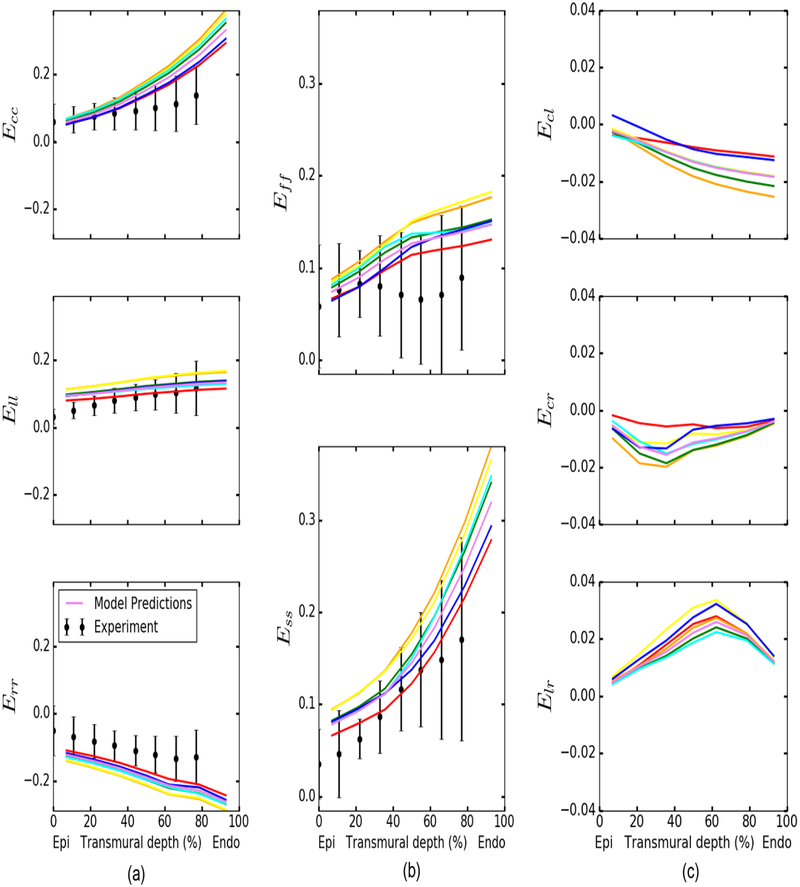
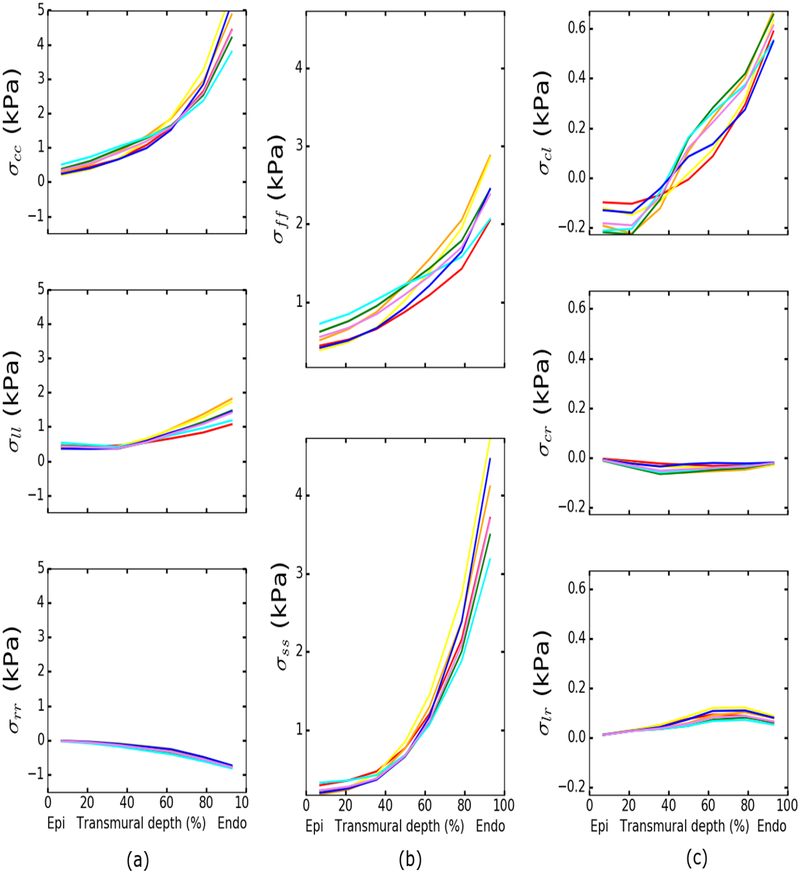
Figure 5 shows the comparison of transmural distribution of normal strains at a LV pressure of 8 mmHg with measurements [39]. Consistent with the experiments, the model predicted both circumferential strain Ecc and longitudinal strain Ell to increase from the epicardium to endocardium, and the radial strain Err to be negative and decrease from epicardium to endocardium (Fig. 5a). Model prediction of the Ell transmural distribution is closest to the experiments, whereas the predicted transmural distribution of Err has an offset of ~ 0.08 with respect to the measured mean values. Both muscle fiber strain Eff and cross fiber strain Ess are predicted to increase from the epicardium to the endocardium, and both are largely within 1 SD of the measurements (Fig. 5b). In-plane shear Ecl is negative and its magnitude increases from the epicardium to the endocardium. Compared to the normal strains, the magnitude and transmural gradient of shear strains are small (Fig. 5c). We also compared model predictions of the normal and shear strains as a function of the change in LV cavity volume ΔV with measurements at the subepicardial, midwall, and sub-endocardial [39] (Appendix D). Overall, model predictions of the relationship between strains and AV are comparable to the measurements. Of all the normal strains, the relationship between Ell and ΔV is closest to the measurements at all 3 transmural locations, whereas Ecc at ΔV = 20 ml in the sub-endocardial region has the largest discrepancy with the measurements (measured: 0.126; model: 0.257). The predicted relationship between the shear strains and AV are largely within the 1 SD of the measurements.
Fig. 5.
Transmural distributions of the strain components at a LV pressure of 8 mmHg. Colored solid lines: model predictions using best-fit and mean parameters in Table 2. Measurements of strains at LV pressure of 8 ± 4 mmHg [39] are plotted as means ± SD. Note: shear strain results from experimental data are not shown as the measured values are small and difficult to digitize.
Local ventricular wall stresses
Figure 6 shows the transmural distribution of stresses corresponding to a LV pressure of 8 mmHg. The results show that both circumferential stress σcc and longitudinal stress σll increase from the epicardium to the endocardium (Fig. 6a). The magnitude of σcc is larger than σll at all transmural depth. Radial stress is negative and increases in magnitude towards the endocardium. Both fiber stress σff and cross-fiber stress σss increase from the epicardium to the endocardium (Fig. 6b). Magnitude of the shear stress components are small compared to the normal stresses. In-plane shear stress σcl has a larger transmural gradient than the other transverse shear stresses, increasing from −0.2 kPa at the epicardium to 0.6 kPa at the endocardium (Fig. 6c).
Fig. 6.
Transmural distributions of the stresses at a ventricular pressure of 8 mmHg. Colored solid lines: model predictions using best-fit and mean parameters in Table 2.
Contribution of the tissue constituents to the wall stress
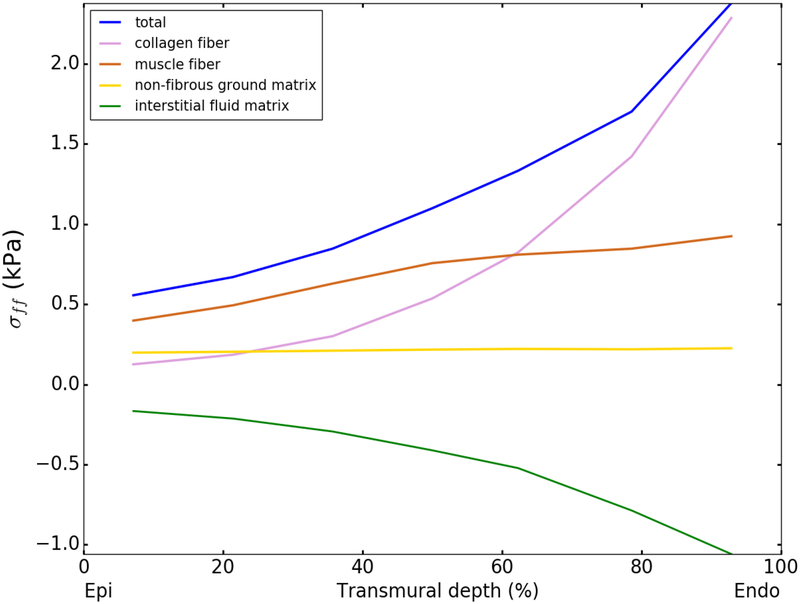
Figure 7 shows the transmural variation of the contribution of each tissue constituent to the total normal stress in the mean muscle fiber direction σff at an LV pressure of 8 mmHg as predicted by the model using the mean value of the fitted parameters in Table2. The contribution of the interstitial fluid matrix to σff is simply −p based on Eq. (15). The results show that the contribution of muscle fiber is substantial at all transmural locations, accounting between 40 – 70% of the total stress. The contribution of collagen fibers to the total stress increases from 22% at the epicardium to 96% at the endocardium. Interestingly, the results also show that at 60% transmural depth, where Eff ≈ 0.13 or fiber stretch ≈ 1.12, the contribution of collagen fibers starts to exceed that of the muscle fibers; i.e., the collagen fibers become the dominant load-bearing constituent at a transmural depth > 60%. We also note that the contribution to σff by each constituent remains largely unchanged using model parameters fitted from the biaxial test data with larger lower and upper bounds of the mean collagen waviness at 0.22 ≤mc≤ 0.78.
Fig. 7.
Transmural variation of the contribution of the collagen fiber network, muscle fibers, non-fibrous ground matrix and interstitial fluid matrix to the total normal stress in the local muscle fiber direction at an LV pressure of 8 mmHg using the mean fitted parameter values from Table 2.
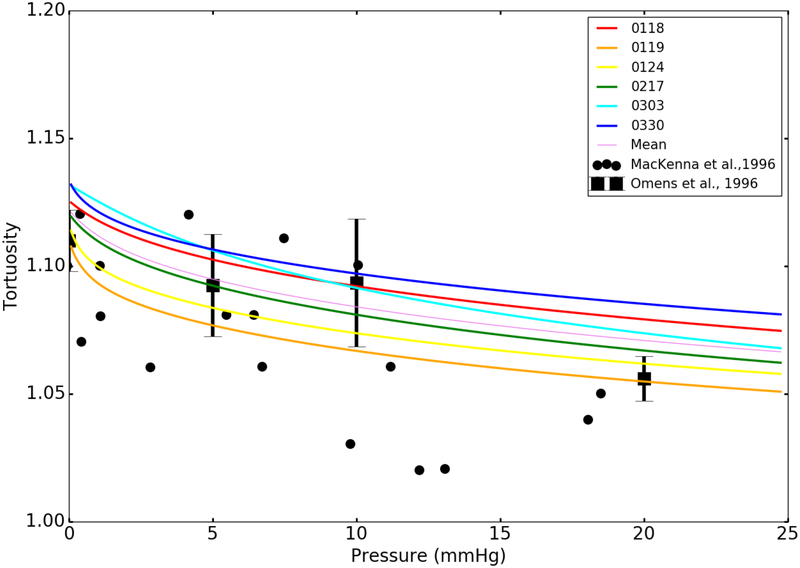
Collagen fiber tortuosity
Figure 8 shows the comparison of the model predictions of the relationship between collagen fiber tortuosity and LV pressure with the measurements [46], [47]. Our model predicts that the collagen fiber tortuosity decreases from 1.123 ± 0.009 to 1.066 ± 0.01 when LV pressure is increased from 0 to 25 mmHg. The model predictions are mostly within the measured ranges when the LV pressure is less than 10 mmHg. Discrepancy between model prediction and measurement is generally larger at higher pressure.
Fig. 8.
Collagen fiber tortuosity as a function of LV pressure. Colored solid lines: model predictions using the best-fit and mean parameters in Table 2. Black scattered dots: measurements of the perimysial collagen fiber tortuosity in rat hearts [46]. Black square marker with error bars (mean ± SD): measurements of collagen tortuosity in normal rat LV [47].
Parameter sensitivity analysis
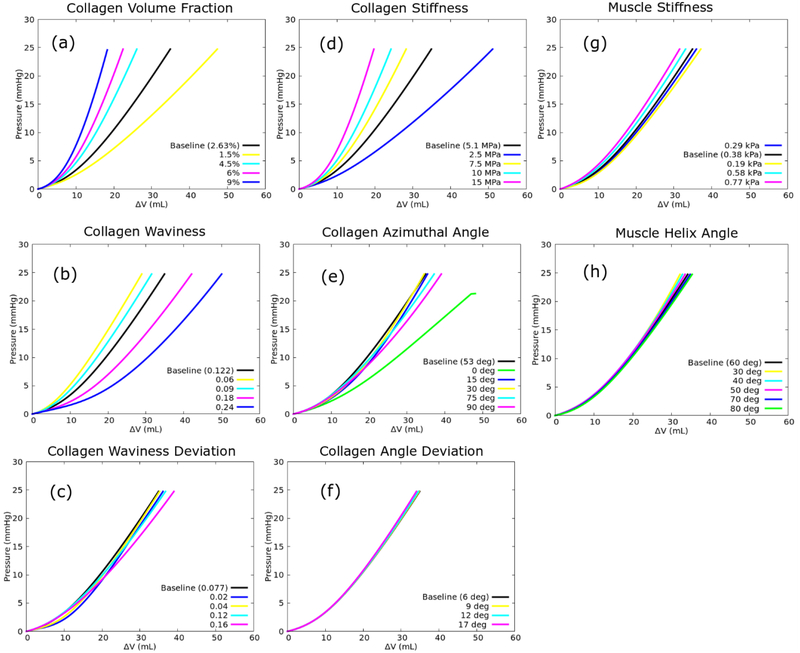
Sensitivity analysis of the model’s parameters revealed that the passive filling pressure-volume curve is very sensitive to the collagen volume fraction ϕc, collagen waviness mc, collagen stiffness modulus C4, collagen azimuthal angle mϕ and muscle fiber stiffness C2 (Fig. 9). The LV becomes less compliant as ϕc, C4, C2 are increased or as the collagen fiber waviness mc is decreased. On the other hand, the relationship between the LV chamber stiffness and mean collagen azimuthal angle mϕ is non-monotonic for the range 0° ≤ mϕ≤ 90°. The effects on the pressure-volume curve are less for the other parameters.
Fig. 9.
Sensitivity of (a) collagen volume fraction ϕc, (b) collagen waviness mc, (c) collagen waviness deviation σc, (d) collagen stiffness modulus C4, (e) collagen azimuthal angle mϕ, (f) collagen azimuthal angle deviation σϕ, (g) muscle stiffness C2 and (h) muscle fiber helix angle to the pressure-volume curve.
Table 5 shows the percentage of absolute change in ΔV at LV pressures of 20 and 30 mmHg when each model parameter is changed 100% with respect to the corresponding mean value (baseline). Our results show that the collagen ultrastructure (i.e., waviness and azimuthal angle) has a substantial impact on the ΔV. Collagen volume fraction and the stiffness of individual collagen fiber roughly have the same effects on ΔV. On the other hand, the muscle fiber stiffness and orientation have lesser influence on ΔV compared to the collagen network. The sensitivities of ΔV to the model parameters are relatively the same at both pressures.
Table 5:
Percentage of absolute change in ΔV at a LV pressure of 20 and 30 mmHg with 100% change in each model parameter about its mean fitted value.
| Model parameters | Percentage of absolute change in ΔV at 20 mmHg | Percentage of absolute change in ΔV at 30 mmHg |
|---|---|---|
| Collagen Azimuthal Angle | 48.3 | 44.7 |
| Collagen Waviness | 46.7 | 39.9 |
| Collagen Volume Fraction | 29.5 | 31.5 |
| Collagen Stiffness | 29.6 | 31.6 |
| Collagen Waviness Deviation | 11.1 | 11.6 |
| Muscle Stiffness | 9.83 | 6.5 |
| Muscle Helix Angle | 4.4 | 7.5 |
| Collagen Angle Deviation | 0.84 | 1.1 |
Sensitivity analysis of the muscle fiber helix angle was evaluated for a change between a symmetric transmural variation of helix angle of (30°/−30°) (baseline) to (60°/−60°).
Current constitutive models describing the tissue mechanical behavior of the myocardium are largely phenomenological. While able to represent the bulk tissue mechanical behavior, these models cannot distinguish the contribution of the tissue constituents and their ultrastructure to heart function. Although microstructure-based constitutive models can be used to isolate the role of tissue ultrastructure, they have not been implemented in a computational framework that can accommodate realistic 3D organ geometry. The present study addresses these issues by developing and validating a microstructure-based computational modeling framework, which is used to investigate the role of tissue constituents and their ultrastructure in affecting heart function.
4. Discussion
We have developed and validated a microstructure-based constitutive model of the passive myocardium in a three-dimensional FE modeling framework, and have shown that the LV filling function is sensitive to the collagen ultrastructure and the load taken up by the tissue constituents varies depending on the LV transmural location. To the best of our knowledge, this is the first FE implementation of a microstructural constitutive model to simulate passive filling of a LV in a representative 3D geometry with experimentally measured transmural muscle fiber orientation. Calibrated against the tissue-level biaxial test data derived from the mid-wall of the canine myocardium [35], we show that the fitted parameter values are consistent with microscale measurements made on individual cardiac tissue constituents and the FE model predictions using these values are largely in agreement with independent measurements from experiments on the intact canine LV. This study, therefore, provides a rigorous comparison of the microstructural constitutive model predictions with measurements made across multiple scales; i.e., at the constituent, tissue and organ levels.
At the constituent’s level, the calibrated myocyte stiffness modulus and tension at a sarcomere length of 2.2 μm are comparable to the reported values of other species such guinea pig [42] and hamster [30] since we are not able to find any passive mechanical tests conducted on canine myocytes. For the collagen fiber network, the calibrated mean elastic modulus of a straightened collagen fiber C4 is ~ 5 MPa, which is within the reported values of 0 – 50 MPa for collagen fibers in the skin tissue [43] and comparable to the mean fitted value of 3.76 MPa in the rat right ventricle [38]. Direct measurements of the collagen fiber elastic modulus are, to the best of our knowledge, not available. In terms of the collagen fiber network microstructural features, the model’s calibrated mean collagen fiber tortuosity of 1.116 is well within the histological measurements of 1.01 – 1.2 [44]. While the calibrated mean inclination angle of 0.927 rad or 53.1 ° cannot be quantitatively compared with measurements, histological studies have reported qualitatively that the collagen fibers are inclined relative to the muscle fibers [24].
At the tissue level, the constitutive model is able to fit the measurements derived from all the biaxial testing protocols very well for each canine specimen (fiber direction: R=0.98; cross-fiber direction: R=0.999). An assessment of the relative contribution by each constituent to the total stress reveals that the collagen fiber network bears most of the load in the cardiac tissue, accounting for about 57% of the total load when cardiac tissue is stretched beyond 1.3. The cardiac muscle fibers, on the other hand, still accounts for a significant portion (~ 43%) of the total load. This finding is consistent with a recent study which shows that the mechanical contribution of muscle fibers is significant at all physiological ranges of stretch [38].
At the organ level, the FE implementation of the microstructural constitutive model in a representative 3D LV geometry enables comparison with measurements of the pressure-volume curves, strains and collagen tortuosity during inflation. The pressure vs. volume change curves predicted using the fitted model’s parameters all fell within 1 SD of the measurements in canine hearts [39], [45]. Prediction of the relationship between collagen fiber tortuosity and LV pressure is also comparable with the measurements [46], [47], showing that the collagen fibers are not all fully stretched over the range of diastolic filling pressures (0 – 25 mmHg). Moreover, model predictions of the strains as a function of LV cavity volume change and their transmural distribution across the LV wall are also largely in agreement with the measurements [39].
The generally good agreement between model predictions of tissue-level strain, collagen fiber tortuosity and pressure-volume relationship of the LV with measurements using the fitted parameters from biaxial mechanical data provide confidence of the model’s ability to predict multiscale features associated with LV filling. More significantly, the consistency of the fitted parameters with microscale mechanical and structural measurements of isolated tissue constituents substantiate, to some level, the validity of the model prediction of the contribution of each constituent to the total stress during LV inflation. Specifically, the model predicts that the contribution of muscle fibers to the total stress is significant at low strain, but its contribution diminishes at higher strain. Conversely, the contribution of collagen fiber network to the total stress is small at low strain but its contribution increases due to the gradual recruitment of wavy collagen fibers at higher strain. As a result, the collagen fiber becomes the dominant load-bearing constituent at high strain, accounting for more than half of the normal stress in the local muscle fiber direction at a stretch of 1.32. This result supports the suggestion made in a previous study [48] that myocytes, where titin is the primary contributor to its passive stress response, may be the major component of the myocardial stiffness at low LV pressure.
Interestingly, this result is also reflected in the transmural variation of the constituent’s contribution to the total fiber stress (Fig. 7). At a LV pressure of 8 mmHg, the simulations show that the cardiac muscle fiber accounts for most of the load in the local muscle fiber direction between the transmural depth of 0% (epicardium) - 60% of the ventricular wall. The collagen fiber, on the other hand, is the dominant load-bearing constituent between the transmural depth of 60%−100% (endocardium) (i.e., the subendocardial region). This finding has implications on pharmaceutical therapies under investigation for treating HFpEF that targets specific tissue individual constituent; e.g., attenuating myocardial fibrosis [49] and reducing myocyte titin stiffness [50]. In particular, our finding suggests that reducing LV passive stiffness by altering the collagen fiber network may be most effective when applied to the sub-endocardial region. Conversely, altering the myocyte stiffness to reduce LV passive stiffness may be most effective when applied to the sub-epicardial region. Although we have demonstrated that the microstructural model can be applied to predict load sharing of the constituents that cannot be experimentally measured, caution must be exercised in directly applying these results for optimizing treatments as they were obtained based on 1) normal LV geometry, 2) assumptions that the LV has homogeneous material properties and collagen fiber waviness and 3) omission of residual stresses. The model needs to be calibrated using more data, especially those from humans that consider sex-differences in the LV passive behavior [51], before predictions can be reliably applied in the clinics.
Through a parameter sensitivity study, we show that the LV passive stiffness is not only sensitive to the stiffness of the individual tissue constituents (particularly, muscle and collagen fiber), but it is also sensitive to the collagen fiber network ultrastructure; i.e., the mean waviness mc, the mean azimuthal angle mϕ with respect to the muscle fibers. These findings underscore the importance of quantifying changes in the collagen fiber network ultrastructure during remodeling, particularly in diseases where fibrosis is a key feature such as HFpEF [52].
The microstructural FE LV model is not without limitations. First, we adopt a linear transmural variation of the muscle fiber helix angle without any planar splay. This framework can be extended to include physiological distributions of muscle fiber splay in future. Second, the assumptions of homogeneous 1) axisymmetrical distribution of collagen fibers around local muscle fiber direction, 2) bimodal normal distribution to describe the collagen fiber spatial orientation and 3) truncated normal distribution to describe the collagen fiber waviness need to be validated against microscopy measurements of the myocardium, which to the best of our knowledge, is not available. Third, due to the lack of histological or microscopy measurements of the myocardial tissue ultrastructure, we had to fit most of the model’s parameters using the biaxial test data, including morphometric parameters that should, in principle, be prescribed using values directly measured in experiments. This is not ideal as some of the parameters are highly correlated to each other (Table 4). Nevertheless, we have attempted to minimize this issue by imposing physiological bounds on the model’s parameters in the fitting process and validating our fitted model parameters against independent measurements of the constituents and organ-scale LV inflation experiments. Fourth, we have, for simplicity, ignored the presence of residual strains and stresses in simulating passive filling of the intact LV that may produce a more uniform transmural distribution of stress [10]. The presence of residual stresses and residual strains in the LV may also be responsible for the transmural differences of collagen waviness as observed in some histological studies [46]. Finally, the microstructural model formulation ignores any direct mechanical or physical interactions between the myocytes and collagen fibers, which a recent study suggests to be present in the LV [53].
In conclusion, we have developed a microstructural constitutive model in an efficient FE framework, and used it to investigate the contribution of individual tissue constituent to LV mechanics during passive inflation. This framework can be readily extended to increase the model’s realism, such as by incorporating a more realistic biventricular geometry and an active contraction constitutive model of the myocyte to simulate active mechanics in the LV as well as by calibrating the model using human data.
Supplementary Material
6. Acknowledgement
This work was supported by NIH R01 HL134841, NSF 1702987, AHA 17SDG33370110.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
5. Conflict of Interest
The authors have no conflict of interest to declare.
7. References
- [1].Diamond G, Forrester JS, Hargis J, Parmley WW, Danzig R, and Swan HJC, “Dlastolic Pressure-Volume Relationship in the Canine Left Ventricle,” Circ. Res, vol. 29, no. 3, pp. 267–275, 1971. [DOI] [PubMed] [Google Scholar]
- [2].Gilbert JC and Glantz SA, “Determinants of left ventricular filling and of the diastolic pressure-volume relation.,” Circ. Res, vol. 64, no. 5, pp. 827–852, May 1989. [DOI] [PubMed] [Google Scholar]
- [3].Golman M, Padovano W, Shmuylovich L, and Kovács SJ, “Quantifying Diastolic Function: From E-Waves as Triangles to Physiologic Contours via the ‘Geometric Method,’” Cardiovasc. Eng. Technol, 2018. [DOI] [PubMed] [Google Scholar]
- [4].Pedrizzetti G et al. , “On estimating intraventricular hemodynamic forces from endocardial dynamics: A comparative study with 4D flow MRI,” J. Biomech, 2017. [DOI] [PubMed] [Google Scholar]
- [5].Oktay AA, Rich JD, and Shah SJ, “The emerging epidemic of heart failure with preserved ejection fraction.,” Curr. Heart Fail. Rep, vol. 10, no. 4, pp. 401–410, December 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Su M-YM et al. , “CMR-Verified Diffuse Myocardial Fibrosis Is Associated With Diastolic Dysfunction in HFpEF,” JACC Cardiovasc. Imaging, vol. 7, no. 10, pp. 991–997, 2014. [DOI] [PubMed] [Google Scholar]
- [7].Borbély A et al. , “Cardiomyocyte stiffness in diastolic heart failure,” Circulation, vol. 111, no. 6, pp. 774–781, 2005. [DOI] [PubMed] [Google Scholar]
- [8].Neumann T, Vollmer A, Schaffner T, Hess OM, and Heusch G, “Diastolic dysfunction and collagen structure in canine pacing-induced heart failure,” J. Mol. Cell. Cardiol, 1999. [DOI] [PubMed] [Google Scholar]
- [9].Humphrey JD, Strumpf RK, and Yin FC, “Determination of a constitutive relation for passive myocardium: I. A new functional form.,” J. Biomech. Eng, vol. 112, no. 3, pp. 333–339, 1990. [DOI] [PubMed] [Google Scholar]
- [10].Guccione JM, McCulloch AD, and Waldman LK, “Passive Material Properties of Intact Ventricular Myocardium Determined From a Cylindrical Model,” J. Biomech. Eng, vol. 113, no. 1, pp. 42–55, February 1991. [DOI] [PubMed] [Google Scholar]
- [11].Holzapfel GA and Ogden RW, “Constitutive modelling of passive myocardium: a structurally based framework for material characterization,” Philos. Trans. R. Soc. A Math. Phys. Eng. Sci, vol. 367, no. 1902, p. 3445 LP–3475, September 2009. [DOI] [PubMed] [Google Scholar]
- [12].Hunter PJ, Nielsen PM, Smaill BH, LeGrice IJ, and Hunter IW, “An anatomical heart model with applications to myocardial activation and ventricular mechanics.,” Crit. Rev. Biomed. Eng, vol. 20, no. 5–6, pp. 403–26, January 1992. [PubMed] [Google Scholar]
- [13].Lanir Y, “A structural theory for the homogeneous biaxial stress-strain relationships in flat collagenous tissues.,” J. Biomech, vol. 12, pp. 423–436, 1979. [DOI] [PubMed] [Google Scholar]
- [14].Jor JWY, Nash MP, Nielsen PMF, and Hunter PJ, “Estimating material parameters of a structurally based constitutive relation for skin mechanics,” Biomech. Model. Mechanobiol, vol. 10, no. 5, pp. 767–778, 2011. [DOI] [PubMed] [Google Scholar]
- [15].Billiar KL and Sacks MS, “Biaxial Mechanical Properties of the Native and Glutaraldehyde-Treated Aortic Valve Cusp: Part II—A Structural Constitutive Model,” J. Biomech. Eng, vol. 122, no. 4, pp. 327–335, March 2000. [DOI] [PubMed] [Google Scholar]
- [16].Chen H, Luo T, Zhao X, Lu X, Huo Y, and Kassab GS, “Microstructural constitutive model of active coronary media,” Biomaterials, vol. 34, no. 31, pp. 7575–7583, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Horowitz A, Lanir Y, Yin FCP, Perl M, Sheinman I, and Strumpf RK, “Structural Three-Dimensional Constitutive Law for the Passive Myocardium,” J. Biomech. Eng, vol. 110, no. 3, pp. 200–207, August 1988. [DOI] [PubMed] [Google Scholar]
- [18].Nevo E and Lanir Y, “The effect of residual strain on the diastolic function of the left ventricle as predicted by a structural model,” J. Biomech, vol. 27, no. 12, pp. 1433–1446, 1994. [DOI] [PubMed] [Google Scholar]
- [19].Horowitz A, Sheinman I, Lanir Y, Perl M, and Sideman S, “Nonlinear Incompressible Finite Element for Simulating Loading of Cardiac Tissue—Part I: Two Dimensional Formulation for Thin Myocardial Strips,” J. Biomech. Eng, vol. 110, no. 1, pp. 57–61, February 1988. [DOI] [PubMed] [Google Scholar]
- [20].Horowitz A, Sheinman I, and Lanir Y, “Nonlinear Incompressible Finite Element for Simulating Loading of Cardiac Tissue—Part II: Three Dimensional Formulation for Thick Ventricular Wall Segments,” J. Biomech. Eng, vol. 110, no. 1, pp. 62–68, February 1988. [DOI] [PubMed] [Google Scholar]
- [21].Fan R and Sacks MS, “Simulation of planar soft tissues using a structural constitutive model: Finite element implementation and validation,” J. Biomech, vol. 47, no. 9, pp. 2043–2054, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Alnæs M et al. , “The FEniCS Project Version 1.5,” Arch. Numer. Softw, vol. 3, no. 100, December 2015. [Google Scholar]
- [23].Caulfield JB and Borg TK, “The collagen network of the heart.,” Lab. Invest, vol. 40, pp. 364–372, 1979. [PubMed] [Google Scholar]
- [24].Robinson TF, Cohen-Gould L, and Factor SM, “Skeletal framework of mammalian heart muscle. Arrangement of inter- and pericellular connective tissue structures,” Lab. Invest, vol. 49, no. 4, pp. 482–498, 1983. [PubMed] [Google Scholar]
- [25].Fung Y, Biomechanics: mechanical properties of living tissues. Springer Science & Business Media, 2013. [Google Scholar]
- [26].Sommer G et al. , “Biomechanical properties and microstructure of human ventricular myocardium,” Acta Biomater, vol. 24, pp. 172–192, 2015. [DOI] [PubMed] [Google Scholar]
- [27].Fan R and Sacks MS, “Simulation of planar soft tissues using a structural constitutive model: Finite element implementation and validation,” J. Biomech, vol. 47, no. 9, pp. 2043–2054, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Lanir Y, “Constitutive equations for fibrous connective tissues,” J. Biomech, vol. 16, no. 1, pp. 1–12, 1983. [DOI] [PubMed] [Google Scholar]
- [29].Buchanan RM and Sacks MS, “Interlayer micromechanics of the aortic heart valve leaflet.,” Biomech. Model. Mechanobiol, vol. 13, no. 4, pp. 813–826, August 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Fish D, Orenstein J, and Bloom S, “Passive stiffness of isolated cardiac and skeletal myocytes in the hamster.,” Circ. Res, vol. 54, no. 3, pp. 267–276, March 1984. [DOI] [PubMed] [Google Scholar]
- [31].Humphrey JD and Yin FCP, “On Constitutive Relations and Finite Deformations of Passive Cardiac Tissue: I. A Pseudostrain-Energy Function,” J. Biomech. Eng, vol. 109, no. 4, pp. 298–304, November 1987. [DOI] [PubMed] [Google Scholar]
- [32].Shen ZL, Dodge MR, Kahn H, Ballarini R, and Eppell SJ, “Stress-Strain Experiments on Individual Collagen Fibrils,” Biophys. J, vol. 95, no. 8, pp. 3956–3963, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Holzapfel GA, Niestrawska JA, Ogden RW, Reinisch AJ, and Schriefl AJ, “Modelling non-symmetric collagen fibre dispersion in arterial walls,” J. R. Soc. Interface, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Holzapfel GA and Ogden RW, “Comparison of two model frameworks for fiber dispersion in the elasticity of soft biological tissues,” Eur. J. Mech. A/Solids, 2017. [Google Scholar]
- [35].Humphrey JD, Strumpf RK, and Yin FC, “Determination of a constitutive relation for passive myocardium: II. Parameter estimation.,” J. Biomech. Eng, vol.112, no. 3, pp. 340–346, August 1990. [DOI] [PubMed] [Google Scholar]
- [36].Frank JS and a Langer G, “The myocardial interstitium: its structure and its role in ionic exchange.,” J. Cell Biol, vol. 60, no. 3, pp. 586–601, March 1974. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Bashey RI, Martinez-Hernandez A, and Jimenez SA, “Isolation, characterization, and localization of cardiac collagen type VI. Associations with other extracellular matrix components.,” Circ. Res, vol. 70, no. 5, pp. 1006–1017, May 1992. [DOI] [PubMed] [Google Scholar]
- [38].Avazmohammadi R, Hill MR, Simon MA, Zhang W, and Sacks MS, “A novel constitutive model for passive right ventricular myocardium: evidence for myofiber--collagen fiber mechanical coupling,” Biomech. Model. Mechanobiol, vol. 16, no. 2, pp. 561–581, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Omens JH, May KD, and McCulloch a D., “Transmural distribution of three-dimensional strain in the isolated arrested canine left ventricle.,” Am. J. Physiol, 1991. [DOI] [PubMed] [Google Scholar]
- [40].Choi HF, D’hooge J, Rademakers FE, and Claus P, “Influence of left-ventricular shape on passive filling properties and end-diastolic fiber stress and strain.,” J. Biomech, vol. 43, no. 9, pp. 1745–53, June 2010. [DOI] [PubMed] [Google Scholar]
- [41].Humphrey JD, “Cardiovascular Solid Mechanics: Cells, Tissues and Organs. 35 Springer-Verlag,” New York, 2002. [Google Scholar]
- [42].Brady AJ, “Length dependence of passive stiffness in single cardiac myocytes,” Am. J. Physiol. Circ. Physiol, vol. 260, no. 4, pp. H1062–H1071, April 1991. [DOI] [PubMed] [Google Scholar]
- [43].Yang W et al. , “On the tear resistance of skin.,” Nat. Commun, vol. 6, p. 6649, March 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].MacKenna DA, Vaplon SM, and McCulloch AD, “Microstructural model of perimysial collagen fibers for resting myocardial mechanics during ventricular filling.,” Am. J. Physiol, vol. 273, no. 3 Pt 2, pp. H1576–86, September 1997. [DOI] [PubMed] [Google Scholar]
- [45].McCulloch AD, Smaill BH, and Hunter PJ, “Left ventricular epicardial deformation in isolated arrested dog heart.,” Am. J. Physiol, vol. 252, no. 1 Pt 2, pp. H233–41, January 1987. [DOI] [PubMed] [Google Scholar]
- [46].MacKenna DA, Omens JH, and Covell JW, “Left ventricular perimysial collagen fibers uncoil rather than stretch during diastolic filling,” Basic Res. Cardiol, vol. 91, no. 2, pp. 111–122, 1996. [DOI] [PubMed] [Google Scholar]
- [47].Omens JH, Miller TR, and Covell JW, “Relationship between passive tissue strain and collagen uncoiling during healing of infarcted myocardium,” Cardiovasc. Res, vol. 33, no. 2, pp. 351–358, February 1997. [DOI] [PubMed] [Google Scholar]
- [48].Linke WA, Popov VI, and Pollack GH, “Passive and active tension in single cardiac myofibrils.,” Biophys. J, vol. 67, no. 2, pp. 782–792, August 1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Zouein FA, De Castro Brás LE, Da Costa DV, Lindsey ML, Kurdi M, and Booz GW, “Heart failure with preserved ejection fraction: Emerging drug strategies,” J. Cardiovasc. Pharmacol, vol. 62, no. 1, pp. 13–21, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50].Krüger M et al. , “Protein kinase G modulates human myocardial passive stiffness by phosphorylation of the titin springs,” Circ. Res, vol. 104, no. 1, pp. 87–94, 2009. [DOI] [PubMed] [Google Scholar]
- [51].Dal Lin C, Tona F, and Osto E, “The heart as a psychoneuroendocrine and immunoregulatory organ,” in Advances in Experimental Medicine and Biology, 2018. [DOI] [PubMed] [Google Scholar]
- [52].Mohammed SF, Hussain S, Mirzoyev SA, Edwards WD, Maleszewski JJ, and Redfield MM, “Coronary microvascular rarefaction and myocardial fibrosis in heart failure with preserved ejection fraction.,” Circulation, vol. 131, no. 6, pp. 550–559, February 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].Grobbel MR, Shavik SM, Darios E, Watts SW, Lee LC, and Roccabianca S, “Contribution of left ventricular residual stress by myocytes and collagen: existence of inter-constituent mechanical interaction,” Biomech. Model. Mechanobiol, vol. 17, no. 4, pp. 985–999, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54].Glantz SA and Kernoff RS, “Muscle stiffness determined from canine left ventricular pressure-volume curves.,” Circ. Res, vol. 37, no. 6, pp. 787–794,1975. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.