Abstract
Limit of detection (LOD) issues are ubiquitous in exposure assessment. While there is an extensive literature on modeling exposure data under such imperfect measurement processes, including likelihood-based methods and multiple imputation, the standard practice continues to be naïve single imputation by a constant (e.g. ). In this paper, we consider the situation where, due to the practical logistics of data accrual, sampling, and resource constraints, exposure data are analyzed in multiple batches where the LOD and the proportion of censored observations differ across batches. Compounding this problem is the potential for non-random assignment of samples to each batch, often driven by enrollment patterns and biosample storage. This issue is particularly important for binary outcome data where batches may have different levels of outcome enrichment. We first consider variants of existing methods to address varying LODs across multiple batches. We then propose a likelihood-based multiple imputation strategy to impute observations that are below the LOD while simultaneously accounting for differential batch assignment. Our simulation study shows that our proposed method has superior estimation properties (i.e., bias, coverage, statistical efficiency) compared to standard alternatives, provided that distributional assumptions are satisfied. Additionally, in most batch assignment configurations, complete-case analysis can be made unbiased by including batch indicator terms in the analysis model, although this strategy is less efficient relative to the proposed method. We illustrate our method by analyzing data from a cohort study in Puerto Rico that is investigating the relationship between endocrine disruptor exposures and preterm birth.
Introduction
Estimating the effect of an environmental contaminant (X) on a health outcome (Y) is frequently affected by measurement issues related to the quantification of low concentrations in biologic samples. These concentration levels are often subject to a left-censoring mechanism called the limit of detection (LOD), which is defined as the smallest concentration that can be reliably distinguished from a reference with no contamination.1 Thus far, the LOD literature has focused on one or multiple contaminants, each of which is uniformly subject to a single LOD across all analyzed samples.2-4 However, in large cohort studies, it is often not feasible to assess all concentrations in one batch and, furthermore, recalibration of the LOD between batches can cause the LOD to change. Moreover, samples are typically assayed on a rolling basis, implying that certain subject-level characteristics which increase the likelihood of early enrollment may be overrepresented in initial batches. In retrospective assaying of archived biosamples, simple storage strategies (for example, storing “diseased” samples in one freezer) may create different enrichment of outcomes in batches. Non-random assignment of samples to batches complicates matters by inducing a dependency between batch characteristics and the censoring mechanism itself.
The problem under consideration is motivated by an ongoing birth cohort study, The Puerto Rico Test site for Exploring Contamination Threats (PROTECT), which is a multi-institutional effort to identify and understand the environmental risk factors contributing to a higher incidence of preterm birth in Puerto Rico, where 11.5% of live births occur prematurely.5 Preterm birth is the second leading cause of neonatal mortality in the United States and is associated with chronic respiratory complications, intestinal scarring, impaired cognitive development, and an elevated risk for sudden unexpected infant deaths.6-10 Urine samples of expecting mothers were collected at each trimester on a continuous basis but were analyzed in batches because of funding constraints and scientific interest in preliminary exposure data collection. For the present example, we focus on six of the 31 phthalate, phenol, paraben, and antibacterial agent concentrations that have two or more distinct LODs. The LOD changes were attributable to assay recalibration before analyzing each batch.
As a practitioner, it is natural to adapt existing statistical methods for handling LODs to this context. They can be divided into the following four broad classes: complete-case analysis, single imputation with a constant value, likelihood-based estimation, and multiple imputation. Ignoring non-detects (i.e., complete-case analysis) is usually not pragmatic, as it considerably reduces the number of available observations and can lead to major efficiency losses. Popular choices of constant imputation, such as , LOD/2, E[X∣X < LOD], and E[X∣X > LOD], do not properly account for sampling variability below the LOD.3,4,11-13 Consequently, constant imputation results in biased parameter estimates, improperly estimated standard errors, and less than nominal coverage probabilities, particularly when the fraction of observations below the LOD is large.4,12,14,15
Two preferred methods are to either directly obtain regression parameter estimates by maximizing a proper censored likelihood2,12,16-19 or to multiply impute values below the LOD and pool inference across imputed datasets.14,17,20-24 If distributional assumptions are satisfied, censored likelihood maximization has marginally better statistical efficiency compared to multiple imputation, but is more computationally expensive and requires a separate implementation for each outcome model.21 In contrast, imputing non-detects conditional on multiple health outcomes of interest has a major practical advantage, in that epidemiologic investigators can multiply impute the exposure once and use the resulting imputed datasets for multiple outcome models. The imputation approach is also naturally amenable for extension to multiple pollutants.
Sequential multiple imputation strategies, such as multiple imputation (MI) using chained equations, are routinely used due to their availability in standard statistical software. However, a straightforward implementation of MI using chained equations that ignores the LOD structure does not guarantee that imputed values will fall below the LOD. To ensure that imputed values are below the LOD, we consider censored likelihood multiple imputation (censored likelihood MI). The main idea behind censored likelihood MI is to construct a censored likelihood function derived from the conditional distribution of an exposure X (censored at LOD if X < LOD) given an outcome Y and a vector of covariates C and randomly generate samples from the fitted distribution of {X∣X < LOD, Y, C}.17,21-23 Censored likelihood MI strategies for handling non-detects have been examined in the context of generalized linear models and M-regression, with potentially multiple exposures;14,17,21,23,24 however, little work has been done to extend these concepts to varying detection limits. Arunajadai et al. (2012) investigated multiple LODs, but did not consider potential structural bias induced by differential batch enrichment.22
The goal of this paper is to evaluate the performance of common LOD solutions under changing LODs and different mechanisms for sample allocation to batches. Specifically, we propose an extension of the censored likelihood MI strategy outlined in Lubin et al. (2004) for handling such data and compare this method, via extensive simulation study, to complete-case analysis, substitution by , and MI using chained equations.14 We then apply these methods to the PROTECT dataset to assess the relationship between endocrine disruptor exposures and preterm birth.
Methods
We first briefly review existing methods for handling the LOD problem in exposure assessment, and then propose new remedies for the situation in which the LOD changes across batches. Let Xjl denote the true exposure for the l-th observation in batch j(j = 1, …, m and l = 1, …, nj), with a known distribution. For simplicity, we assume Xjl is normally distributed. Suppose that the underlying model for the binary outcome, Yjl, is given by
| (1) |
where πjl = P(Yjl = 1 ∣ Xjl, Cjl); Cjl = (Cjl1, Cjl2) where Cjl1 is the set of confounders, and Cjl2 is the set of precision variables that are correlated with Yjl but unrelated to Xjl. Our focus is to find a consistent estimator for βE and its corresponding standard error estimate when the Xjl’s are below the LOD for batch j (denoted as LODj).
Existing Methods for Analyzing Data Subject to LOD
To characterize the impact of multiple LODs, we define the underlying conceptual variable Zjl:
That is, we assume that observations above LODj have no measurement error, i.e., . Although this assumption may be violated in practice, the goal of this paper is to understand the impact of changing LODs across multiple batches on the resultant inference, not the joint impact of multiple LODs and exposure measurement error (which is also an important issue).
Complete-case analysis removes observations where Xjl < LODj and fits a logistic model on only. Constant imputation replaces with a batch-specific constant, i.e., , and fits a logistic model on plus imputed values. Multiple imputation generates multiple random draws from the stochastic distribution of conditional on , outcomes, batch indicators, and other covariates.
For each single or multiply imputed dataset, an estimate of the outcome-exposure association is then obtained by fitting a logistic regression model {Yjl∣Zjl, Cjl}. However, the issue of multiple batches subject to differential enrichment of disease states (and/or potentially important confounders) introduces a new complexity to the problem. One way to control for this in the analysis model is to include batch indicators such that the post-imputation analysis model becomes,
| (1) |
where θjl = P(Yjl = 1∣Zjl, Cjl, Batchjl). For multiple imputation, the estimates are then pooled, properly accounting for imputation uncertainty within and between the imputed datasets.25-27 Going forward, we will denote the estimate of αE from analysis model (1) with batch indicators as and the estimate of αE from analysis model (1) with no batch indicators (i.e., setting αb2 = ⋯ = αbm = 0) as , to explicitly establish the link between our analysis models and the true model. Both outcome models (with and without batch indicators) will be considered throughout the simulation study. Since our proposed framework is multiple imputation based on censored likelihood maximization, we will discuss that approach in greater detail.
Proposed Method: Censored Likelihood Multiple Imputation (censored likelihood MI)
The main goal of censored likelihood MI is to estimate the conditional cumulative distribution function of {Xjl∣Yjl, Cji1}, draw random values from the conditional distribution {Xjl∣Yjl, Cjl1, Xjl < LODj}, and fit a logistic regression on each imputed dataset. Suppose that {Xjl∣Yjl, Cjl1} ~ N(γ0+γ1Yjl+γTCjl1, σ2). That is, we assume the distribution of underlying contaminant concentrations does not depend on batch assignment. The likelihood can be written as:
where δ(Xjl) = I(Xjl < LODj) is the censoring indicator function for observation l in batch j and ϕXjl(·) and ΦXjl(·) are the probability density function and cumulative distribution function of the conditional distribution of {Xjl∣Yjl, Cjl1}. Note that it is important to condition on disease status (Y) in the likelihood. A likelihood ignoring Y will result in regression parameters biased towards the null, when a true association between Y and X conditional on C exists.
To obtain one imputed dataset:
Draw a bootstrapped dataset {, , } of the same size as the original dataset.
Using the censored likelihood, obtain maximum-likelihood estimates , , , and for the bootstrapped dataset. The estimate of ΦXjl, , is the cumulative distribution function corresponding to a distribution.
For every observation in the bootstrapped dataset such that , randomly draw and obtain the corresponding quantile .
Repeat this procedure K times to get K imputed datasets. Pooled inference follows from Rubin’s combination rules.25-27
Simulation Design
We consider moderately-sized (N = 1,000) and large (N = 5,000) cohort studies, both of which have two distinct batches. Within each study, both batches will have three choices for the extent of censoring: light (15% below the LOD), moderate (30% below the LOD), and heavy censoring (60% below the LOD). For notational convenience, we will denote P1 and P2 as the percentage of observations below LOD1 and LOD2, respectively.
Generative models.
Suppose we have a contaminant of interest (X) that depends on two binary covariates, say smoking (S) and gender (G), such that:
Further, suppose that the true generative model for the binary outcome is given by:
where πi = P(Yi = 1∣Xi, Si, Gi). The intercept was determined by fixing the marginal prevalence of the outcome in the overall simulated population at P(Yi = 1) = 0.1.
Batch Assignment.
There are four assignment schemes of individuals to batches: (a) completely at random, (b) dependent on Y, (c) dependent only on covariates, and (d) dependent on both Y and covariates. The general form of the allocation model is:
We discuss the results for scenarios (a), (b), and (c); the results for scenario (d) are expected to be very similar to (b). For (b), η0 = −0.13, ηY = 1.5, and ηS = ηG = 0, so that the two batches have an equal number of subjects and P(Batch 1 ∣Yi = 1) =0.8. As a sensitivity check, we also considered a modified (b) setting where P(Batch 1 ∣Yi = 1) = 0.6 (see eAppendix 1 for detailed results). For (c), η0 = 0.73, ηY = 0, ηS = 1.5, and ηG = −2, such that the two batches have an equal number of subjects and P(Batch 1 ∣Yi = 1) ≈ 0.5. That is, we selected coefficients in (c) such that batch assignment conditional on covariate values did not inadvertently introduce a dependency on outcome status. Note that the single batch scenario, a special case where both batches have the same LOD, can be ascertained from assignment scheme (a) when P1 = P2 (see eTable 1).
Using 1,000 simulated datasets, we will compare the proposed censored likelihood MI with complete-case analysis, constant imputation with for batch j (denoted as ), and MI using chained equations by fitting analysis model (1) with and without batch indicators. Specifically, we will evaluate the methods in terms of relative bias (denoted as ), mean-squared error (denoted as ), and 95% coverage probability (denoted as ) of and . Explicit evaluation metric definitions are provided in eAppendix 1.
Data Example: Application to the PROTECT Cohort
The PROTECT study is a prospective cohort study in Puerto Rico that is investigating the relationship between exposure to environmental contaminants and preterm birth. For the present analysis, we are specifically interested in phthalates, phenols, parabens, and antibacterial agents, which are commonly found in industrial plastics, cosmetics, and pesticides. Exposure typically occurs through the use of personal care products, such as shampoos and deodorants, and the consumption of packaged food/beverages. Endocrine disruptors have been linked to a plethora of adverse health outcomes, including earlier onset of puberty, infertility, adverse birth outcomes and neurodevelopment, diabetes, and altered sex steroid and thyroid hormone levels.28-32 The dataset contains 1004 participants, with 31 different contaminants measured longitudinally at three different visits, with median gestational age of 18, 22, and 26 weeks, respectively. Recruitment was initiated in 2010 and, since then, samples were shipped to the US Centers for Disease Control and Prevention (CDC) on a rolling basis for measurement of urinary phthalate metabolite and phenol concentrations by solid phase extraction high-performance liquid chromatography–isotope dilution tandem mass spectrometry.33 Batches were analyzed in the order that they were received. Because of this study protocol, a subset of contaminants had multiple LODs, six of which we use in our illustrative data example. Further details regarding study design and data collection can be found in Cantonwine et al. (2014) and Meeker et al. (2013).33,34 Ethics and Research Committees at the University of Puerto Rico, the University of Michigan School of Public Health, Northeastern University, and the participating clinics reviewed and approved the study protocol. The involvement of the CDC laboratory was determined not to constitute engagement in human subjects research. The study was thoroughly explained to every study participant and all participating women gave informed consent before enrolling.
Analytic Dataset.
We consider log-transformed mono-(2-ethylhexyl) phthalate (MEHP), mono-(3-carboxypropyl) phthalate (MCPP), butylparaben (BPB), bisphenol F (BPF), triclosan (TCS), and triclocarban (TCC) measured at visits 1 and 2. Since visit 1 and visit 2 do not necessarily contain the same subjects, we include the maximum number of subjects available at each visit in our analysis models. For MEHP, MCPP, BPB, and TCS, visit 1 consists of 43 spontaneous preterm deliveries and 583 full-term deliveries, whereas visit 2 has 42 spontaneous preterm deliveries and 598 full-term deliveries. BPF and TCC were only measured on a subset of subjects; therefore, visit 1 contains 31 spontaneous preterm deliveries and 355 full-term deliveries, while visit 2 consists of 31 spontaneous preterm deliveries and 351 full-term deliveries.
Statistical Analysis.
To illustrate the use of complete-case analysis, , MI using chained equations, and censored likelihood MI, we fit analysis model (1) with a batch indicator at each visit. For the censored likelihood MI, C1 corresponds to specific gravity, while C2 contains maternal age, employment status, and parity. All simulations and analyses were performed using R statistical software, version 3.3.1. An R implementation of the censored likelihood MI is available at: https://github.com/bossjona/Single-Pollutant-Multiple-LODs.
Results
Simulation Study
Here we present results for the moderately sized study under analysis models with and without batch indicators. For the large study, general trends across the methods were similar, and hence are relegated to eTable 2, eFigure 1a, and eFigure 1b.
Random Batch Assignment.
Panels A and B in eFigure 1c present relative bias results, panels A and B in eFigure 1d present mean squared error (MSE) results, and Table 1 presents the empirical coverage probabilities.
Table 1.
Empirical Coverage Probabilities of 95% Confidence Intervals with N = 1,000.
| Empirical Coverage Probability |
||||||||
|---|---|---|---|---|---|---|---|---|
| LOD Info | With Batch Indicator () | Without Batch Indicator () | ||||||
| CCA | MICE | CLMI | CCA | MICE | CLMI | |||
| Random a | ||||||||
| (15, 15) b | 0.958 | 0.959 | 0.952 | 0.958 | 0.960 | 0.959 | 0.950 | 0.957 |
| (15, 30) | 0.953 | 0.957 | 0.957 | 0.956 | 0.957 | 0.957 | 0.956 | 0.954 |
| (15, 60) | 0.952 | 0.951 | 0.949 | 0.961 | 0.955 | 0.950 | 0.922 | 0.961 |
| (30, 15) | 0.962 | 0.961 | 0.961 | 0.961 | 0.963 | 0.963 | 0.963 | 0.958 |
| (30, 30) | 0.963 | 0.957 | 0.951 | 0.962 | 0.964 | 0.960 | 0.951 | 0.963 |
| (30, 60) | 0.959 | 0.942 | 0.953 | 0.962 | 0.955 | 0.945 | 0.946 | 0.963 |
| (60, 15) | 0.959 | 0.950 | 0.965 | 0.956 | 0.957 | 0.957 | 0.942 | 0.955 |
| (60, 30) | 0.963 | 0.945 | 0.957 | 0.957 | 0.964 | 0.951 | 0.952 | 0.956 |
| (60, 60) | 0.962 | 0.910 | 0.942 | 0.955 | 0.964 | 0.912 | 0.943 | 0.953 |
| Outcome-Dependent c | ||||||||
| (15, 15) | 0.958 | 0.952 | 0.957 | 0.953 | 0.961 | 0.960 | 0.957 | 0.958 |
| (15, 30) | 0.955 | 0.954 | 0.957 | 0.955 | 0.933 | 0.958 | 0.928 | 0.958 |
| (15, 60) | 0.949 | 0.953 | 0.947 | 0.951 | 0.762 | 0.912 | 0.511 | 0.958 |
| (30, 15) | 0.953 | 0.948 | 0.945 | 0.954 | 0.935 | 0.956 | 0.931 | 0.953 |
| (30, 30) | 0.962 | 0.951 | 0.955 | 0.958 | 0.961 | 0.959 | 0.955 | 0.959 |
| (30, 60) | 0.951 | 0.949 | 0.943 | 0.956 | 0.823 | 0.942 | 0.772 | 0.955 |
| (60, 15) | 0.965 | 0.933 | 0.960 | 0.948 | 0.666 | 0.847 | 0.870 | 0.956 |
| (60, 30) | 0.958 | 0.929 | 0.965 | 0.956 | 0.763 | 0.833 | 0.880 | 0.958 |
| (60, 60) | 0.955 | 0.917 | 0.948 | 0.950 | 0.957 | 0.895 | 0.947 | 0.961 |
| Covariate-Dependent d | ||||||||
| (15, 15) | 0.955 | 0.959 | 0.955 | 0.956 | 0.957 | 0.962 | 0.957 | 0.956 |
| (15, 30) | 0.956 | 0.965 | 0.957 | 0.956 | 0.961 | 0.964 | 0.957 | 0.957 |
| (15, 60) | 0.953 | 0.952 | 0.961 | 0.952 | 0.961 | 0.954 | 0.940 | 0.952 |
| (30, 15) | 0.955 | 0.958 | 0.954 | 0.955 | 0.955 | 0.957 | 0.952 | 0.955 |
| (30, 30) | 0.959 | 0.962 | 0.954 | 0.954 | 0.964 | 0.964 | 0.952 | 0.956 |
| (30, 60) | 0.957 | 0.943 | 0.963 | 0.962 | 0.958 | 0.949 | 0.958 | 0.962 |
| (60, 15) | 0.953 | 0.954 | 0.944 | 0.961 | 0.957 | 0.953 | 0.942 | 0.963 |
| (60, 30) | 0.958 | 0.941 | 0.953 | 0.963 | 0.957 | 0.946 | 0.954 | 0.961 |
| (60, 60) | 0.967 | 0.911 | 0.953 | 0.952 | 0.965 | 0.911 | 0.956 | 0.951 |
Abbreviations: CCA, complete-case analysis; CLMI, censored likelihood multiple imputation; LOD, limit of detection; MICE, multiple imputation using chained equations; , constant imputation with .
“Random” refers to random batch assignment.
The notation (A, B) means that approximately A% of observations in batch 1 were below the batch 1 LOD and approximately B% of observations in batch 2 were below the batch 2 LOD.
“Outcome-Dependent” refers to batch assignment that depends on Y when P(Batch 1 ∣Yi = 1) = 0.8.
“Covariate-Dependent” refers to batch assignment that depends on S and G.
Regardless of the inclusion of a batch indicator, complete-case analysis and censored likelihood MI are generally unbiased across all scenarios, while is almost always biased. The resulting bias induced by increased as more observations became censored, regardless of whether a batch indicator was included. In analysis model (1) without a batch indicator, a naïve implementation of MI using chained equations results in biases when either P1 ≪ P2 or P2 ≪ P1 (e.g., , when P1 = 60% and P2 = 15%; eFigure 1c, panel A).
In general, MI using chained equations has the largest MSE, which is primarily driven by the large standard deviations associated with pooled parameter estimates. eFigure 1d shows that, when P1 = 60% and P2 = 60%, this method results in . In comparison, complete-case analysis (, ( and ), and censored likelihood MI () have smaller MSEs (see eFigure 1d). Note that complete-case analysis still has larger MSE, because deleting observations below the LOD is inefficient, especially when exposure data are subject to heavy censoring. For , the reduction in MSE is due to smaller variation (MSE for is mainly driven by the bias). Censored likelihood MI has a uniformly smaller MSE compared to complete-case analysis, MI using chained equations, and .
In analysis model (1) with and without a batch indicator, complete-case analysis and censored likelihood MI have proper coverage probabilities. MI using chained equations occasionally has less than nominal coverage for the analysis model without a batch indicator when the fraction of censored observations differs across batches (for instance, when P1 = 15% and P2 = 60%, ; Table 1), but has improved coverage when a batch indicator is included (when P1 = 15% and P2 = 60%, ; Table 1). falls below the nominal coverage probability when P1 = P2 = 60%, whether or not a batch indicator is included in the analysis model (, ; Table 1).
Outcome-Dependent Batch Assignment.
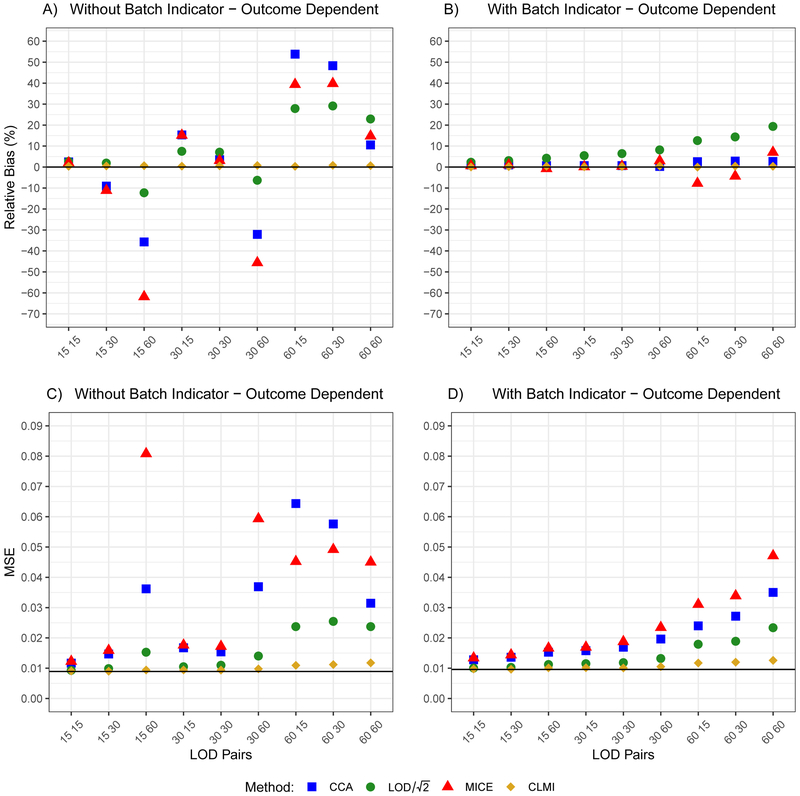
Panels A and B in Figure 1 present relative bias results, panels C and D in Figure 1 present MSE results, and Table 1 presents the empirical coverage probabilities when P(Batch 1 ∣Yi = 1) = 0.8. Results for the analysis model with a batch indicator were similar to the random batch assignment scenario. Therefore, the following discussion will focus on the analysis model without a batch indicator.
Figure 1.
Relative bias and mean-squared error (MSE) at various LOD combinations in a simulated, moderately-sized cohort study (N = 1,000) with outcome-dependent batch assignment (P(Batch 1 ∣Yi = 1) = 0.8). The first and second numbers in the LOD pair correspond to the percent of observations below batch 1 LOD and batch 2 LOD, respectively. Panels A and C correspond to an analysis model without a batch indicator and panels B and D correspond to an analysis model with a batch indicator. In panels A and B, the bolded black line indicates a relative bias of 0% (true βE = log(1.5)). In panels C and D, the bolded black line indicates the gold standard MSE (no observations subject to censoring).
Abbreviations: CCA, complete-case analysis; CLMI, censored likelihood multiple imputation; LOD, limit of detection; MICE, multiple imputation using chained equations; , constant imputation with .
Under moderate and heavy censoring, complete-case analysis and MI using chained equations have very large biases. For example, when P1 = 15% and P2 = 60%, is −35.7% for CCA, while is −61.8% for MI using chained equations (see Figure 1A). Relative biases for are large across all LOD pairs, however, outperforms CCA with respect to bias whenever , when P1 = 15% and P2 = 60%; Figure 1A). Censored likelihood MI leads to drastically lower relative biases compared with CCA, MICE, and when P1 = 15% and P2 = 60%; Figure 1A). Figure 1C shows that, across all (P1, P2) pairs, complete-case analysis and MI using chained equations have larger MSE than . Censored likelihood MI uniformly outperforms MI using chained equations, complete-case analysis, and .
Our proposed method has nominal coverage probabilities across all LOD pairs, whereas complete-case analysis, MI using chained equations, and often fall well below the nominal coverage probability. Notably, when P1 = 60% and P2 = 30%, the coverage probabilities are for complete-case analysis, for MI using chained equations, for , and for censored likelihood MI (see Table 1).
When P(Batch 1 ∣Yi = 1) = 0.6, the relative bias and MSE patterns are virtually identical to the to the P(Batch 1∣Yi = 1) = 0.8 case, the only exception being that the magnitude of the relative bias and MSE are smaller (see eFigures 2a and 2b).
Covariate-Dependent Batch Assignment.
Panels E and F in eFigure 1c present relative bias results, panels E and F in eFigure 1d present MSE results, and Table 1 presents the empirical coverage probabilities. Results were comparable to random batch assignment. Recall that the covariate-dependent batch allocation model did not introduce differential batch assignment by outcome, implying that outcome-dependent batch assignment is particularly problematic for complete-case analysis, , and MI using chained equations.
Summary.
Table 2 summarizes the simulation study results presented in Figure 1, eFigures 1c and 1d, and Table 1. Complete-case analysis and censored likelihood MI have low bias and accurate coverage probability when batch indicators are included in the analysis model. However, censored likelihood MI provides an efficiency gain and is the uniformly preferred method when more than 15% of observations fall below the LOD (in terms of both bias and MSE). and MI using chained equations are not recommended, as they can have large biases, improperly estimated or inflated standard errors, and less than nominal coverage.
Table 2.
LOD Simulation Study Properties when a Batch Indicator is Included in the Analysis Model.
| % Below LOD |
||||
|---|---|---|---|---|
| Method | 0%-15% | 15%-30% | 30%-60% | |
| CCA | Absolute Rel. Bias | 1.0%-1.8% | 0.7%-1.8% | 0.3%-3.6% |
| Rel. Variance a | 1.2x-1.3x | 1.2x-1.7x | 1.3x-2.8x | |
| MSE Ratio b | 1.2x-1.3x | 1.2x-1.7x | 1.3x-2.8x | |
| Coverage | 95%-96% | 95%-96% | 94%-97% | |
| Absolute Rel. Bias | 2.4%-3.0% | 3.1%-7.1% | 4.3%-20.2% | |
| Rel. Variance | 1.0x | 1.0x-1.1x | 1.1x-1.4x | |
| MSE Ratio | 1.0x-1.1x | 1.1x-1.5x | 1.1x-4.2x | |
| Coverage | 94%-96% | 91%-97% | 69%-95% | |
| MICE | Absolute Rel. Bias | 0.6%-1.4% | 0.0%-1.8% | 0.6%-7.8% |
| Rel. Variance | 1.2x-1.4x | 1.3x-1.9x | 1.4x-4.1x | |
| MSE Ratio | 1.2x-1.4x | 1.3x-1.9x | 1.4x-4.1x | |
| Coverage | 95%-96% | 95%-96% | 93%-98% | |
| CLMI | Absolute Rel. Bias | 0.0%-0.8% | 0.1%-0.9% | 0.0%-1.3% |
| Rel. Variance | 1.0x | 1.0x | 1.0x | |
| MSE Ratio | 1.0x | 1.0x | 1.0x | |
| Coverage | 95%-96% | 95%-96% | 95%-96% | |
Abbreviations: CCA, complete-case analysis; CLMI, censored likelihood multiple imputation; LOD, limit of detection; MSE, mean-squared error; Rel, relative; , constant imputation with .
Relative variance is reported with respect to CLMI. As an example, relative variance ranging between 1.2x-1.3x for CCA means that, depending on the simulation setting, CCA is between 1.2 and 1.3 times less efficient compared to CLMI.
Ratio of MSEs is reported with respect to CLMI. As an example, MSE ratio ranging from 1.2x-1.3x for CCA means that, depending on the simulation setting, CCA has between a 1.2 and 1.3 times higher MSE compared to CLMI.
PROTECT Data Analysis
At both visits 1 and 2, women that had spontaneous preterm deliveries were older on average, had a higher rate of unemployment, and had proportionately higher parity compared to women with full-term deliveries (see eTable 3). LOD summary information for contaminants, provided in eTable 4, shows that MEHP, MCPP, TCS, and TCC all have approximately 10% – 15% samples below two distinct LODs, while BPF has 51.0% below the LOD at visit 1 and 52.1% at visit 2 (see eFigure 3 for contaminant distributions). BPB is the only contaminant with four distinct LODs and has a sizable overall percent of samples below the LOD (37.4% at visit 1 and 43.3% at visit 2).
Table 3 shows that, as the percent of samples below LOD increased, the point estimates of the log-odds ratios differed more across methods, while censored likelihood MI had the uniformly smallest standard error and, consequently, the narrowest confidence intervals (CI). For BPF, the only contaminant with over 50% below the LOD in both visits 1 and 2, we observed that the point estimate using complete-case analysis was numerically quite different from the other estimates. This could be because complete-case analysis retained few spontaneous preterm deliveries in visit 1 and 2, making estimation of the analysis model unstable. One noteworthy clinical finding is that all four methods identified a significant association between TCC exposure and spontaneous preterm delivery at visit 1 (censored likelihood MI: , 95% CI: 0.084, 0.425; Table 3); for a more detailed discussion see Aker et al. (2019).35
Table 3.
Log-odds Ratio Estimates for one Log-ng/ml Higher Contaminant Exposure with Respect to Spontaneous Preterm Delivery at Visit 1 and Visit 2 in the PROTECT Cohort, Puerto Rico, 2010 – 2017.
| Visit 1 (N = 626, 43 SPD, 583 FTD) | Visit 2 (N = 640, 42 SPD, 598 FTD) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Pollutant | Method | % Below LOD |
95% CI | % Below LOD |
95% CI | ||||
| BPB | CCA | 37.4% | −0.006 | 0.104 | −0.214, 0.196 | 43.3% | −0.004 | 0.116 | −0.239, 0.218 |
| −0.031 | 0.078 | −0.191, 0.117 | 0.046 | 0.084 | −0.127, 0.206 | ||||
| MICE | −0.063 | 0.105 | −0.273, 0.146 | 0.038 | 0.100 | −0.161, 0.237 | |||
| CLMI | −0.023 | 0.065 | −0.152, 0.105 | 0.042 | 0.064 | −0.083, 0.167 | |||
| BPF a,b | CCA | 51.0% | 0.154 | 0.205 | −0.290, 0.537 | 52.1% | 0.140 | 0.209 | −0.306, 0.528 |
| 0.098 | 0.161 | −0.248, 0.391 | 0.035 | 0.165 | −0.321, 0.334 | ||||
| MICE | 0.080 | 0.217 | −0.364, 0.525 | 0.061 | 0.179 | −0.295, 0.417 | |||
| CLMI | 0.038 | 0.137 | −0.235, 0.311 | 0.020 | 0.135 | −0.250, 0.289 | |||
| MCPP | CCA | 8.9% | −0.011 | 0.172 | −0.363, 0.313 | 10.8% | 0.287 | 0.180 | −0.079, 0.632 |
| 0.065 | 0.157 | −0.255, 0.364 | 0.234 | 0.163 | −0.096, 0.545 | ||||
| MICE | 0.006 | 0.175 | −0.337, 0.349 | 0.301 | 0.193 | −0.082, 0.684 | |||
| CLMI | 0.064 | 0.153 | −0.237, 0.365 | 0.230 | 0.161 | −0.087, 0.546 | |||
| MEHP | CCA | 13.1% | −0.289 | 0.247 | −0.784, 0.184 | 14.4% | −0.095 | 0.235 | −0.574, 0.347 |
| −0.238 | 0.202 | −0.638, 0.152 | −0.086 | 0.192 | −0.470, 0.282 | ||||
| MICE | −0.301 | 0.266 | −0.828, 0.227 | −0.116 | 0.237 | −0.584, 0.352 | |||
| CLMI | −0.211 | 0.191 | −0.586, 0.165 | −0.053 | 0.180 | −0.407, 0.302 | |||
| TCC a | CCA | 11.4% | 0.249 | 0.094 | 0.069, 0.438 | 12.6% | 0.092 | 0.097 | −0.099, 0.283 |
| 0.262 | 0.089 | 0.090, 0.442 | 0.086 | 0.090 | −0.092, 0.264 | ||||
| MICE | 0.238 | 0.093 | 0.055, 0.421 | 0.081 | 0.100 | −0.117, 0.279 | |||
| CLMI | 0.254c | 0.087 | 0.084, 0.425 | 0.093 | 0.085 | −0.075, 0.261 | |||
| TCS | CCA | 12.9% | −0.093 | 0.090 | −0.275, 0.081 | 13.3% | −0.157 | 0.095 | −0.352, 0.025 |
| −0.102 | 0.079 | −0.261, 0.049 | −0.118 | 0.081 | −0.284, 0.037 | ||||
| MICE | −0.097 | 0.091 | −0.277, 0.083 | −0.159 | 0.097 | −0.349, 0.032 | |||
| CLMI | −0.092 | 0.071 | −0.232, 0.047 | −0.100 | 0.073 | −0.243, 0.044 | |||
Abbreviations: BPB, butylparaben; BPF, bisphenol F; CCA, complete-case analysis; CI, confidence interval; CLMI, censored likelihood multiple imputation; FTD, full-term delivery; LOD, limit of detection; MCPP, mono-(3-carboxypropyl) phthalate; MEHP, Mono-(2-ethylhexyl) phthalate; MICE, multiple imputation using chained equations; SE, standard error; SPD, spontaneous preterm delivery; , constant imputation with ; TCC, triclocarban; TCS, triclosan.
TCC and BPF were measured in a subset of subjects: N = 386 (31 SPDs, 355 FTDs) for visit 1 and N = 382 (31 SPDs, 351 FTDs) for visit 2.
There were not enough complete spontaneous preterm deliveries to fit an analysis model including a batch indicator using CCA for BPF. Therefore, all BPF analysis models do not include a batch indicator. All models for the other contaminants include batch indicators.
Example interpretation of coefficients: for CLMI at visit 1, one log-ng/ml higher in TCC exposure is associated with a 0.25 higher log-odds of having a preterm delivery adjusted for parity, maternal age, maternal employment status, and specific gravity.
Discussion
In this paper, we proposed censored likelihood MI, a multiple imputation scheme to reconstruct the left-tail of a multiply-censored contaminant distribution such that proper statistical inference is made. Across a range of simulation scenarios, censored likelihood MI resulted in unbiased parameter estimates and correct coverage probabilities. Furthermore, censored likelihood MI was more efficient than other approaches such as complete-case analysis and MI using chained equations, evidenced by uniformly smaller standard deviations over all simulation settings.
When dealing with exposures assayed across multiple batches, observations may be unevenly assigned to batches with respect to the outcome of interest or potential confounders. Investigators should be mindful of the sample allocation scheme for exposure assays in order to minimize potential bias related to outcome enrichment. If imbalance occurs in batch allocation, censored likelihood MI is robust to such disparities, even when there are many distinct batches (see eAppendix 2 for an additional simulation study exploring the robustness of censored likelihood MI to the total number of batches).
Another natural question that arises is the robustness of censored likelihood MI to distributional misspecification. Our simulations evaluating the impact of a misspecified distribution of X (X generated from a mixture of normal distributions or a gamma distribution) show that our method has at most an 8% relative bias across all LOD pairs (see eAppendix 3).
In the data example, we illustrated our method and compared the results against complete-case analysis, , and MI using chained equations, where each pollutant was analyzed separately. One promising future research direction is whether censored likelihood MI can be extended to the multivariate scenario where we want to model all six contaminants jointly. This is an important consideration, given the shift in environmental epidemiology towards large-scale multipollutant studies.36,37 One could easily conceptualize censored likelihood MI in a multipollutant setting with p contaminants by constructing a conditional censored likelihood under a multivariate normal distributional assumption, i.e., {Xi1, …, Xip∣Yi, Ci1}~MVN(μ, Σ). However, as the number of pollutants gets large, the multivariate normal assumption becomes tougher to satisfy and, even if it is satisfied, high-dimensional censored-likelihood maximization can be computationally challenging.
One theme throughout the simulation study that deserves further comment is the general unbiasedness of complete-case analysis, despite the LOD being a non-ignorable missing data mechanism. Little and Rubin (2002) claim that complete-case analysis results in unbiased regression parameter estimates if the probability of being a complete case depends only on the observed contaminant concentration and adjustment covariates (i.e., missing at random).13 In our simulation study, generating batch conditional on a binary health outcome Y implicitly introduced confounding by batch, which, when unaccounted for in the analysis model, biased parameter estimates obtained from complete-case analysis. It is important to note that complete-case analysis without batch indicators can produce biased estimates.
Conclusion
Although and complete-case analysis are convenient, inference can be heavily distorted or have low power to detect a true signal, respectively. These issues are amplified in the multiple batch scenario with differential batch enrichment if a batch indicator is not included in the analysis model. Censored likelihood MI generates efficient, unbiased parameter estimates when parametric assumptions are correct. It is imperative that researchers in environmental epidemiology understand the biases and efficiency losses of commonplace LOD solutions in the presence of differential batch enrichment and place a methodological emphasis on statistically rigorous solutions to rectify left-censored exposure data.
Supplementary Material
Acknowledgments:
We would like to thank Huixia Judy Wang for her helpful comments and suggestions.
Source of Funding: This work was supported by the Superfund Research Program of the National Institute of Environmental Health Sciences (NIEHS), National Institutes of Health (NIH; grant number P42ES017198). Additional support was provided from NIH grant number P30ES017885 and the NIH Environmental influences on Child Health Outcomes (ECHO) program grant number UG3OD023251. Funding for B. Mukherjee was provided by the NSF Division of Mathematical Sciences grant number 1712933. Funding for K. Ferguson was provided by the Intramural Research Program of NIEHS.
Footnotes
Conflict of interest: None declared
Availability of Data and Computing Code: A general implementation of censored likelihood multiple imputation, example code, and an artificial dataset can be found at: https://github.com/bossjona/Single-Pollutant-Multiple-LODs. The dataset used in the data example is not publicly available due to the sensitive nature of demographic information and biological measurements, but is available from the corresponding author on reasonable request.
References
- 1.MacDougall D, Crummet WB, Joginder L, Amore FJ. Guidelines for data acquisition and data quality evaluation in environmental chemsitry. Anal Chem. 1980;52(14):2242–2249. [Google Scholar]
- 2.Kong S, Nan B. Semiparametric approach to regression with a covariate subject to a detection limit. Biometrika. 2016;103(1):161–174. [Google Scholar]
- 3.Richardson DB, Ciampi A. Effects of exposure measurement error when an exposure variable is constrained by a lower limit. Am J Epidemiol. 2003;157(4):355–363. [DOI] [PubMed] [Google Scholar]
- 4.Schisterman EF, Vexler A, Whitcomb BW, Liu A. The limitations due to exposure detection limits for regression models. Am J Epidemiol. 2006;163(4):374–383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.March of Dimes. 2017. Premature Birth Report Cards. https://www.marchofdimes.org/mission/prematurity-reportcard.aspx. Accessed November 5, 2017.
- 6.Centers for Disease Control and Prevention. Infant Mortality. https://www.cdc.gov/reproductivehealth/maternalinfanthealth/infantmortality.htm. Accessed November 5, 2017.
- 7.Ostfeld BM, Schwartz-Soicher O, Reichman NE, Teitler J. Prematurity and sudden unexpected infant deaths in the United States. Pediatrics. 2017;140(1):e20163334. [DOI] [PubMed] [Google Scholar]
- 8.Vento M, Cheung P-Y, Aguar M. The first golden minutes of the extremely-low-gestational-age neonate: A gentle approach. Neonatology. 2009;95(4):286–298. [DOI] [PubMed] [Google Scholar]
- 9.Voss W, Hobbiebrunken E, Ungermann U, Wagner M. The development of extremely premature infants. Dtsch Arztebl Int. 2016;113(51–52):871–878. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Caplan MS, Miller-Catchpole R, Kaup S, Russell T. Bifidobacterial supplementation reduces the incidence of necrotizing enterocolitis in a neonatal rat model. Gastroenterology. 1999;117(3):577–583. [DOI] [PubMed] [Google Scholar]
- 11.Hornung RW, Reed LD. Estimation of average concentration in the presence of nondetectable values. Appl Occup Environ Hygenie. 1990;5(1):46–51. [Google Scholar]
- 12.Nie L, Chu H, Liu C, Cole SR. Linear regression with an independent variable subject to a detection limit. Epidemiology. 2010;21(Suppl 4):S17–S24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Little RJA, Rubin DB. Statistical Analysis with Missing Data. 2nd ed. Hoboken, NJ: John Wiley & Sons, Inc.; 2002. [Google Scholar]
- 14.Lubin JH, Colt JS, Camann D, Davis S. Epidemiologic evaluation of measurement data in the presence of detection limits. Environ Health Perspect. 2004;112(17):1691–1696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Helsel DR. Fabricating data: How substituting values for nondetects can ruin results, and what can be done about it. Chemosphere. 2006;65(11):2434–2439. [DOI] [PubMed] [Google Scholar]
- 16.Thompson M Lou, Nelson KP. Linear regression with Type I interval and left-censored response data. Environ Ecol Stat. 2003;10(2):221–230. [Google Scholar]
- 17.Lynn HS. Maximum likelihood inference for left-censored HIV RNA data. Stat Med. 2001;20(1):33–45. [DOI] [PubMed] [Google Scholar]
- 18.Cole SR, Chu H, Nie L, Schisterman EF. Estimating the odds ratio when exposure has a limit of detection. Int J Epidemiol. 2009;38(6):1674–1680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.May RC, Ibrahim JG, Chu H. Maximum likelihood estimation in generalized linear models with multiple covariates subject to detection limits. Stat Med. 2011;30(20):2551–2561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.van Buuren S, Groothuis-Oudshoorn K. mice: Multivariate Imputation by Chained Equations in R. J Stat Softw. 2011;45(3):1–67. [Google Scholar]
- 21.Bernhardt PW, Wang HJ, Zhang D. Statistical methods for generalized linear models with covariates subject to detection limits. Stat Biosci. 2015;7(1):68–89. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Arunajadai SG, Rauh VA. Handling covariates subject to limits of detection in regression. Environ Ecol Stat. 2012;19(3):369–391. [Google Scholar]
- 23.Chen H, Quandt SA, Grzywacz JG, Arcury TA. A distribution-based multiple imputation method for handling bivariate pesticide data with values below the limit of detection. Environ Health Perspect. 2011;119(3):351–356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Wang HJ, Feng X. Multiple Imputation for M-Regression With Censored Covariates. J Am Stat Assoc. 2012;107(497):194–204. [Google Scholar]
- 25.Barnard J, Rubin DB. Small-Sample Degrees of Freedom with Multiple Imputation. Biometrika. 1999;86(4):948–955. [Google Scholar]
- 26.Dong Y, Peng C-YJ. Principled missing data methods for researchers. Springerplus; 2013;2(222). doi: 10.1186/2193-1801-2-222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Rubin DB. Multiple Imputation for Nonresponse in Surveys. New York: John Wiley & Sons, Inc.; 1987. [Google Scholar]
- 28.Binder AM, Corvalan C, Calafat AM, et al. Childhood and adolescent phenol and phthalate exposure and the age of menarche in Latina girls. Environ Heal. 2018;17(1):32. doi: 10.1186/s12940-018-0376-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Huo X, Chen D, He Y, Zhu W, Zhou W, Zhang J. Bisphenol-A and Female Infertility: A Possible Role of Gene-Environment Interactions. Int J Environ Res Public Health. 2015;12(9):11101–11116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Lee D-W, Kim M-S, Lim Y-H, Lee N, Hong Y-C. Prenatal and postnatal exposure to di-(2-ethylhexyl) phthalate and neurodevelopmental outcomes: A systematic review and meta-analysis. Environ Res. 2018;167:558–566. [DOI] [PubMed] [Google Scholar]
- 31.Gore AC, Chappell VA, Fenton SE, et al. Executive Summary to EDC-2: The Endocrine Society’s Second Scientific Statement on Endocrine-Disrupting Chemicals. Endocr Rev. 2015;36(6):593–602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Lind PM, Lind L. Endocrine-disrupting chemicals and risk of diabetes: an evidence-based review. Diabetologia. 2018;61(7):1495–1502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Cantonwine DE, Cordero JF, Rivera-Gonzalez LO, et al. Urinary phthalate metabolite concentrations among pregnant women in Northern Puerto Rico: distribution, temporal variability, and predictors. Environ Int. 2014;62:1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Meeker JD, Cantonwine DE, Rivera-Gonzalez LO, et al. Distribution, Variability, and Predictors of Urinary Concentrations of Phenols and Parabens among Pregnant Women in Puerto Rico. Environ Sci Technol. 2013;47(7):3439–3447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Aker AM, Ferguson KK, Rosario ZY, et al. The associations between prenatal exposure to triclocarban, phenols and parabens with gestational age and birth weight in northern Puerto Rico. Environ Res. 2019;169:41–51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Braun JM, Gennings C, Hauser R, Webster TF. What Can Epidemiological Studies Tell Us about the Impact of Chemical Mixtures on Human Health? Environ Health Perspect. 2016;124(1):A6–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Dominici F, Peng RD, Barr CD, Bell ML. Protecting human health from air pollutation: Shifting from a single-pollutant to a multi-pollutant approach. Epidemiology. 2010;21(2):187–194. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.