Abstract
The evaluation of cranial malformations plays an essential role both in the early diagnosis and in the decision to perform surgical treatment for craniosynostosis. In clinical practice, both cranial shape and suture fusion are evaluated using CT images, which involve the use of harmful radiation on children. Three-dimensional (3D) photography offers non-invasive, radiation-free, and anesthetic-free evaluation of craniofacial morphology. The aim of this study is to develop an automated framework to objectively quantify cranial malformations in patients with craniosynostosis from 3D photography. We propose a new method that automatically extracts the cranial shape by identifying a set of landmarks from a 3D photograph. Specifically, it registers the 3D photograph of a patient to a reference template in which the position of the landmarks is known. Then, the method finds the closest cranial shape to that of the patient from a normative statistical shape multi-atlas built from 3D photographs of healthy cases, and uses it to quantify objectively cranial malformations. We calculated the cranial malformations on 17 craniosynostosis patients and we compared them with the malformations of the normative population used to build the multi-atlas. The average malformations of the craniosynostosis cases were 2.68 ± 0.75 mm, which is significantly higher (p<0.001) than the average malformations of 1.70 ± 0.41 mm obtained from the normative cases. Our approach can support the quantitative assessment of surgical procedures for cranial vault reconstruction without exposing pediatric patients to harmful radiation.
Keywords: Radiation-free, computational quantification, cranial malformations, three-dimensional photography, craniosynostosis, computer-aided diagnosis
1. INTRODUCTION
Cranial shape abnormalities are a common complaint in the pediatric clinic, since 25% of infants of single pregnancies and 50% of multiple pregnancies have some degree of skull malformation at birth that causes head shape abnormalities in the first weeks or months of lives [1]. While babies with positional malformations (i.e. positional plagiocephaly) do not generally need to be exposed to the harmful ionizing radiation of computed tomography (CT), this image modality is generally used to confirm the diagnosis of children with craniosynostosis and to plan the treatment [2][3].
Although diagnosis of craniosynostosis relies on the presence of a fused cranial suture, the evaluation of cranial malformations plays an important role in the decision to perform surgical treatment [4]. In particular, in the case of metopic craniosynostosis, the metopic suture fuses early in healthy children too, so diagnosis cannot be made only based on the fusion of the metopic suture [5][6]. During surgery, the cranial bones are cut, reshaped, and repositioned to achieve a normal cranial shape. The lack of objective metrics to quantify cranial malformations leaves an unsettling diagnostic and treatment ambiguity that can result in over-treatment or under-treatment. Thus, it would be desirable to have objective and quantitative descriptors of cranial shape abnormalities to assist surgeons in deciding if surgical treatment is necessary and planning cranial vault reconstructive surgery.
Most methods [7][8][9][10] that quantify cranial shape abnormalities are based on segmentation from CT images. Recently, three-dimensional (3D) photography has become an increasingly attractive modality to various applications, such as cranial shape variation assessment [11][12] and facial analysis [13][14], since it offers radiation-free, non-invasive, and anesthetic-free imaging. Wilbrand et al. [15] demonstrated that 3D photography has great potential to track and quantify the clinical course of surgical correction of craniosynostosis. Freudlsperger et al. [16] used 3D photography to capture pre- and post-operative scans of children with metopic craniosynostosis to compare head volume changes before and after surgery. Tu et al. [17] demonstrated that intracranial volume can be accurately quantified from 3D photography.
However, cranial malformations assessment is not possible either with current 3D photography systems or with existing methods. The purpose of this study is to create a novel computational framework to quantify cranial malformations from 3D photography, and use them to characterize cranial shape abnormalities objectively and quantitatively in patients with craniosynostosis.
2. MATERIALS AND METHODS
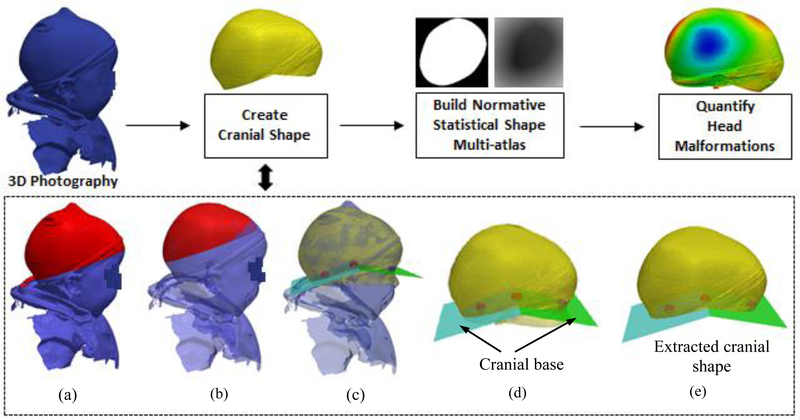
In the following sections, we will describe each component of our framework to automatically quantify head malformations in patients with craniosynostosis from 3D photography, which are shown in Fig. 1.
Fig. 1.
Schematic of the proposed method. (a) A 3D photograph in which the region depicted in red includes bumps due to the use of a hat. (b) The same 3D photograph from (a) after eliminating the bumps. (c) Landmarks (see Fig. 2 for more details about these landmarks) detected to define the cranial base, together with the area of the head used to estimate them (in yellow). (d) The 2 planes calculated from the landmarks that define the cranial base. (e) The cranial shape used to quantify malformations by calculating its signed distance function (SDF) representation and comparing it with a normative shape multi-atlas.
In previous works, Mendoza et al. [8] presented a method to quantify cranial malformations from CT images using a statistical shape multi-atlas. They employed a landmark free shape descriptor, signed distance functions (SDF), to represent the cranial shapes of a healthy population, and they used principal component analysis (PCA) to create a normative statistical shape multi-atlas based on the SDFs. They showed that cranial shape abnormalities could be accurately quantified by comparing the cranial shape of a patient with its closest normal shape in the multi-atlas. Specifically, they proposed two descriptors: (1) malformations, which are the local Euclidean distances between correspondent points of the two cranial shapes, and (2) curvature discrepancies, defined as the absolute local curvature differences. Inspired by their experiments, we aim to automatically quantify head malformations on patients with craniosynostosis using radiation-free 3D photography. Fig.1 shows the workflow of our method.
2.1. Data description
A set of head 3D photographs was acquired using the 3dMD head System (3dMD, Atlanta, GA) from 45 subjects (average age 17 ± 14 months, range 1–48 months), in which 28 subjects had clinical indication noted as cleft palate (average age 24 ± 12 months, range 7–48 months), and 17 had a variety of types of craniosynostosis (8 sagittal, 6 single coronal, 2 bicoronal, and 1 metopic; average age 5 4 months, range 1–16 months).
These subjects were then categorized into two groups. The first group included the 28 subjects with cleft palate, which did not present cranial pathology and were used as normative cases. The second group included the 17 subjects with craniosynostosis, for which 3D photography was acquired before surgical intervention.
2.2. Create cranial shape
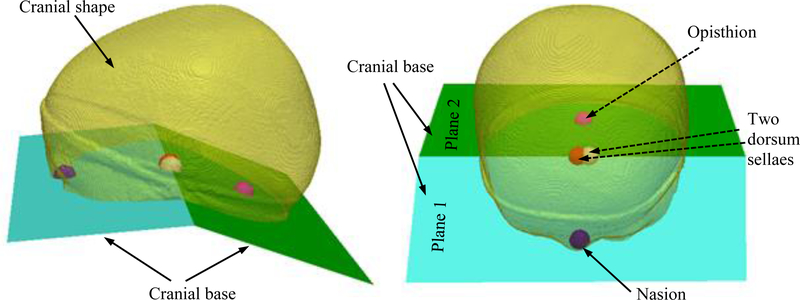
To extract the cranial shape, we first identified a set of four landmarks (the cranial base landmarks, as shown in Fig. 2) defining two cutting planes (cranial base) that divide the cranial vault from the rest of the head, as presented in previous work [8]. In summary, we registered the head shape from the 3D photograph of a healthy subject to its corresponding head CT image. Then, the four landmarks defining the cranial vault in the CT image at the nasion, opisthion and the two clinoid processes of the dorsum sellae were projected onto the 3D photograph, which was subsequently used as a reference template (£).
Fig. 2.
The graphic illustration of the four landmarks (nasion, opisthion and the two clinoid processes of the dorsum sellae) that define the cranial base.
Given the 3D photograph of a new subject, similarity registration (rigid with isotropic scaling) was used to transform £ to match the 3D photograph. After registration, we projected the position of the four landmarks from £ onto the head of the new patient. This yielded an initial position of the landmarks for the head, which were then refined using affine registration and a B-splines based non-rigid transformations. The landmarks were used to identify two planes that defined the cranial base on the 3D photograph. The cranial vault could then be defined as the section above the base. A morphological opening was applied to the top region (see Fig. 1, the top part of the head as highlighted in red) of the cranial vault to remove bumps caused by the hat used to contain hair during the acquisition of photography. Then the cranium was warped by a sphere using a technique called ShrinkWrap [18] to fill any holes or artifacts in the photograph.
2.3. Build normative statistical shape multi-atlas
Similarly to the method presented in [8], we adopted SDF representations to describe cranial shapes. The cranial shape meshes aligned to the template through similarity registration are then converted to binary volumes. All these binary images were resampled to have the same size. Then a SDF representation was computed for each image. Using this SDF representation, each subject was turned into a high-dimensional vector (as many components as voxels in the volume). We build a statistical shape model of the SDFs of the normative cases using PCA.
2.4. Quantify head malformations
To quantify head malformations, the closest normal shape in the multi-atlas was identified and used for comparison. Given a subject with craniosynostosis, we quantified its shape malformation by projecting its SDF representation into the 28-dimensional normative PCA space, and we compared its projection coefficients with those from multi-atlas references. The similarity of the projection between a subject and its closest normal references was defined as their Euclidean distance.
We quantified malformations in term of signed distance, defined as
where pi is a point on the subject’s head surface, qi is the correspondent point on the closest normal’s head surface, d(pi, qi ) is the distance malformations used in [8], and θ is the angle between the normal vector at pi and the vector pointing from pi to a closest point on its closest normal head surface.
We also computed the curvature discrepancies in terms of relative difference between local curvatures at corresponding points pi and qi. The local curvature was estimated by fitting a plane minimizing the squared distance and averaging the distance to the plane based on neighborhood points.
3. RESULTS
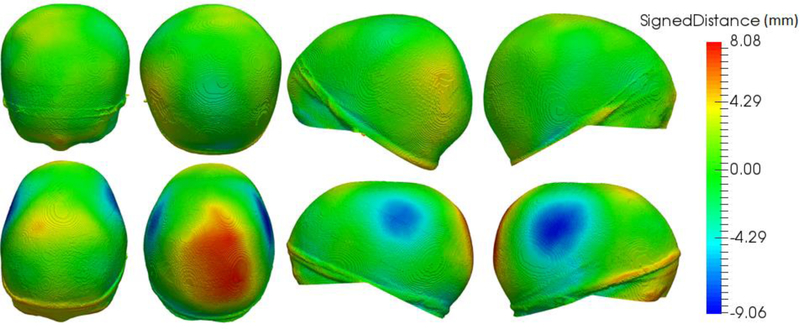
We quantified head malformation in the group of 17 cases with craniosynostosis using the proposed framework. We obtained average head malformations on the patients with craniosynotsis of 2.68 ± 0.75 mm, compared to 1.70 ± 0.41 mm obtained for the normative group. Differences between the two groups were statistically significant (p<0.001 using Student’s t-test). Our values are similar to those reported in earlier papers [9][8], but computed from CT images. As an example, Fig. 3 shows the head shape of a normal subject compared to a patient with sagittal craniosynostosis and its computed malformations. Note that the highest malformation values are concentrated on occipital regions (for sagittal craniosynostosis), similarly to the results reported from CT images in [8]. This is explained by the compensatory growth of the cranium in the direction parallel to the fused suture.
Fig. 3.
Head shape of a healthy subject (first row) and head malformations of a sagittal craniosynostosis subject (second row) in four different views. From left to right columns: anterior, posterior, left and right.
The average curvature discrepancy of the craniosynostosis patients was 0.23 ± 0.03, compared with 0.21 ± 0.06 of the normative data (p=0.086). A limitation of the proposed method is that the quantified malformation and curvature discrepancy are averaged over the whole head, while craniosynostosis may affect only certain cranial bones. This limitation could be overcome by analyzing each cranial bone, which is in our plan for near future.
4. CONCLUSIONS
We proposed a novel automatic framework to quantify head malformations from 3D photography, and we used it to assess cranial malformation on patients with craniosynostosis. The results show significant differences (p<0.001) between normative cases and craniosynostosis patients, which suggests the ability of our radiation-free framework to quantify cranial malformation from 3D photography. We reported that the head malformations on craniosynostosis patients were significantly higher than on patients with a healthy cranial shape. Our framework has the potential to support the quantitative assessment of surgical procedures for cranial vault reconstruction without exposing pediatric patients to harmful radiation. The proposed method could minimize the use of radiation in the diagnosis and surgical planning of craniosynostosis.
ACKNOWLEDGEMENTS
This work was partly funded by the National Institutes of Health, Eunice Kennedy Shriver National Institute of Child Health and Human Development under grant NIH R42HD081712.
REFERENCES
- [1].Ghizoni E, Denadai R, Raposo-Amaral CA, Joaquim AF, Tedeschi H, and Raposo-Amaral CE, “Diagnosis of infant synostotic and nonsynostotic cranial deformities: a review for pediatricians,” Rev. Paul. Pediatr, vol. 34, no. 4, pp. 495–502, October 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Miglioretti DL, Johnson E, Williams A, Greenlee RT, Weinmann S, Solberg LI, Spencer Feigelson H, Roblin D, Flynn MJ, Vanneman N, and Smith-Bindman R, “The use of computed tomography in pediatrics and the associated radiation exposure and estimated cancer risk,” JAMA Pediatr, vol. 167, no. 8, pp. 700–707, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Zhang S, Takaku M, Zou L, Gu A-D, Chou W, Zhang G, Wu B, Kong Q, Thomas SY, Serody J, Chen X, Xu X, Wade P, Cook DN, Ting JPY, and Wan Y, “Reversing SKI–SMAD4-mediated suppression is essential for TH17 cell differentiation,” Nature, vol. 551, pp. 105–109, October 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Porras AR, Paniagua B, Enquobahrie A, Ensel S, Shah H, Keating R, Rogers GF, and Linguraru MG, “Locally affine diffeomorphic surface registration for planning of metopic craniosynostosis surgery BT - Medical Image Computing and Computer-Assisted Intervention − MICCAI 2017: 20th International Conference, Quebec City, QC, Canada, September 11–13, 2017,” Descoteaux M, Maier-Hein L, Franz A, Jannin P, Collins DL, and Duchesne S, Eds. Cham: Springer International Publishing, 2017, pp. 479–487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Wood BC, Mendoza CS, Oh AK, Myers E, Safdar N, Linguraru MG, and Rogers GF, “What’s in a name? Accurately diagnosing metopic craniosynostosis using a computational approach,” Plast. Reconstr. Surg, vol. 137, no. 1, pp. 205–213, 2016. [DOI] [PubMed] [Google Scholar]
- [6].Rodriguez-Florez N, Ö. Göktekin K, Bruse JL, Borghi A, Angullia F, Knoops PGM, Tenhagen M, O’Hara JL, Koudstaal MJ, Schievano S, Jeelani NUO, James G, and Dunaway DJ, “Quantifying the effect of corrective surgery for trigonocephaly: A non-invasive, non-ionizing method using three-dimensional handheld scanning and statistical shape modelling,” J. Cranio-Maxillofacial Surg, vol. 45, no. 3, pp. 387–394, 2017. [DOI] [PubMed] [Google Scholar]
- [7].Paniagua B, Emodi O, Hill J, Fishbaugh J, Pimenta LA, Aylward SR, Andinet E, Gerig G, Gilmore J, van Aalst JA, and Styner M, “3D of brain shape and volume after cranial vault remodeling surgery for craniosynostosis correction in infants,” in Proc. of SPIE Medical Imaging, 2013, vol. 8672, p. 86720V–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Mendoza CS, Safdar N, Okada K, Myers E, Rogers GF, and Linguraru MG, “Personalized assessment of craniosynostosis via statistical shape modeling,” Med. Image Anal, vol. 18, no. 4, pp. 635–646, 2014. [DOI] [PubMed] [Google Scholar]
- [9].Porras AR, Zukic D, Equobahrie A, Rogers GF, and Linguraru MG, “Personalized optimal planning for the surgical correction of metopic craniosynostosis,” in Medical Image Computing and Computer-Assisted Intervention, Workshop on Clinical Image-based Procedures: Translational Research in Medical Imaging, LNCS, Springer; Cham, vol. 9958, 2016, pp. 60–67. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Ezaldein HH, Metzler P, Persing JA, and Steinbacher DM, “Three-dimensional orbital dysmorphology in metopic synostosis,” J. Plast. Reconstr. Aesthetic Surg, vol. 67, no. 7, pp. 900–905, July 2014. [DOI] [PubMed] [Google Scholar]
- [11].van Veelen M-LC, Jippes M, Carolina J-CA, de Rooi J, Dirven CMF, van Adrichem LNA, and Mathijssen IM, “Volume measurements on three-dimensional photogrammetry after extended strip versus total cranial remodeling for sagittal synostosis: A comparative cohort study,” J. Cranio-Maxillofacial Surg, vol. 44, no. 10, pp. 1713–1718, 2016. [DOI] [PubMed] [Google Scholar]
- [12].Meulstee JW, Verhamme LM, Borstlap WA, Van der Heijden F, De Jong GA, Xi T, Bergé SJ, Delye H, and Maal TJJ, “A new method for three-dimensional evaluation of the cranial shape and the automatic identification of craniosynostosis using 3D stereophotogrammetry,” Int. J. Oral Maxillofac. Surg, vol. 46, no. 7, pp. 819–826, June 2017. [DOI] [PubMed] [Google Scholar]
- [13].Booth J, Roussos A, Ponniah A, Dunaway D, and Zafeiriou S, “Large scale 3D morphable models,” Int. J. Comput. Vis, April 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Weinberg SM, Raffensperger ZD, Kesterke MJ, Heike CL, Cunningham ML, Hecht JT, Kau CH, Murray JC, Wehby GL, Moreno LM, and Marazita ML, “The 3D Facial Norms Database: Part 1. A Web-Based Craniofacial Anthropometric and Image Repository for the Clinical and Research Community,” Cleft Palate-Craniofacial J, vol. 0, no. August, pp. 15–199, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Wilbrand J-F, Szczukowski A, Blecher J-C, Pons-Kuehnemann J, Christophis P, Howaldt H-P, and Schaaf H, “Objectification of cranial vault correction for craniosynostosis by three-dimensional photography,” J. Cranio-Maxillofacial Surg, vol. 40, no. 8, pp. 726–730, 2012. [DOI] [PubMed] [Google Scholar]
- [16].Freudlsperger C, Steinmacher S, Bächli H, Somlo E, Hoffmann J, and Engel M, “Metopic synostosis: Measuring intracranial volume change following fronto-orbital advancement using three-dimensional photogrammetry,” J. Cranio-Maxillofacial Surg, vol. 43, no. 5, pp. 593–598, June 2015. [DOI] [PubMed] [Google Scholar]
- [17].Tu L, Porras AR, Ensel S, Tsering D, Paniagua B, Enquobahrie A, Oh A, Keating R, Rogers GF, and Linguraru MG, “Intracranial volume quantification from 3D photography,” Med. Image Comput. Comput. Interv. Work. Clin. Image-based Proced. Transl. Res. Med. Imaging, LNCS, Springer New York, vol. 10550, pp. 116–123, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Pope P, “Shrinkwrap: 3d model abstraction for remote sensing simulations,” in Proc. of the 2009 ASPRS Annual Meeting, 2009, pp. 9–13. [Google Scholar]