Evaluating arcuate fasciculus laterality measurements across dataset and tractography pipelines

Abstract

The arcuate fasciculi are white‐matter pathways that connect frontal and temporal lobes in each hemisphere. The arcuate plays a key role in the language network and is believed to be left‐lateralized, in line with left hemisphere dominance for language. Measuring the arcuate in vivo requires diffusion magnetic resonance imaging–based tractography, but asymmetry of the in vivo arcuate is not always reliably detected in previous studies. It is unknown how the choice of tractography algorithm, with each method's freedoms, constraints, and vulnerabilities to false‐positive and ‐negative errors, impacts findings of arcuate asymmetry. Here, we identify the arcuate in two independent datasets using a number of tractography strategies and methodological constraints, and assess their impact on estimates of arcuate laterality. We test three tractography methods: a deterministic, a probabilistic, and a tractography‐evaluation (LiFE) algorithm. We extract the arcuate from the whole‐brain tractogram, and compare it to an arcuate bundle constrained even further by selecting only those streamlines that connect to anatomically relevant cortical regions. We test arcuate macrostructure laterality, and also evaluate microstructure profiles for properties such as fractional anisotropy and quantitative R1. We find that both tractography choice and implementing the cortical constraints substantially impact estimates of all indices of arcuate laterality. Together, these results emphasize the effect of the tractography pipeline on estimates of arcuate laterality in both macrostructure and microstructure.

1. INTRODUCTION

The arcuate fasciculus is a bilateral white‐matter (WM) pathway that connects cortical regions in the frontal and temporal lobes (Bernal & Ardila, 2009; Catani & Mesulam, 2008; Reil, 1812). Previous in vivo research shows an association between the arcuate and language behavior (Catani et al., 2007; Lopez‐Barroso et al., 2013; Meyer, Obleser, Anwander, & Friederici, 2012). In particular, many of these studies describe a leftward laterality of the arcuate, such as greater fascicle volume (Thiebaut de Schotten et al., 2011) or higher values for local indices such as fractional anisotropy (FA; Beaulieu, 2002). Leftward asymmetry of the arcuate also has been related to leftward activation asymmetry during sentence processing (Meyer et al., 2012; Ocklenburg, Hugdahl, & Westerhausen, 2013), which agrees with the wider literature regarding the laterality of the language network in general (Broca, 1865; Corballis, 2014; Geschwind, 1965; McAvoy et al., 2016; Vigneau et al., 2006; Wernicke, 1874). In order to identify the arcuate in vivo and measure its laterality, a tractography analysis is performed on diffusion magnetic resonance imaging (dMRI) data. However, different tractography pipelines can give different estimates of WM bundles, which would then impact inferences about the underlying anatomy and subsequent laterality measures (Jones, 2010; Maier‐Hein et al., 2017; Thomas et al., 2014). Therefore, the aim of this study is to assess how tractography and related methodological choices influence measurements of arcuate laterality.

One factor that can impact assessments of arcuate laterality in vivo is the type of tractography used, and the freedoms and constraints endemic to each. At the more permissive end of the spectrum are tracking methods that employ probabilistic tracking or that can allow for multiple fiber orientations within a voxel (Behrens, Berg, Jbabdi, Rushworth, & Woolrich, 2007; Tournier, Calamante, & Connelly, 2007). Such methods can yield a great diversity of streamlines, for example, by resolving some of the inherent uncertainty in the data or by accounting for fiber crossing within voxels, a prevalent issue in WM modeling (Jeurissen, Leemans, Tournier, Jones, & Sijbers, 2013; Jones, 2008; Wedeen et al., 2012). However, these permissive methods may introduce spurious streamlines and thus be susceptible to false positives. In many cases, a more conservative tractography method may be preferred. This includes deterministic tracking or the use of the older and simpler tensor model (Basser, Pajevic, Pierpaoli, Duda, & Aldroubi, 2000; Mori, Crain, Chacko, & van Zijl, 1999). Indeed, for the case of arcuate laterality, we find more studies that employ a more limited deterministic tractography (Allendorfer et al., 2016; Budisavljevic et al., 2015; Takao, Hayashi, & Ohtomo, 2013) than we do studies that employ more permissive probabilistic methods (De Santis, Drakesmith, Bells, Assaf, & Jones, 2014; Zhao, Thiebaut de Schotten, Altarelli, Dubois, & Ramus, 2016). Instead of false‐positive errors, however, these limited deterministic methods may be more prone to false‐negative errors, as true streamlines may be aborted or prematurely terminated due to smaller sensitivity in deterministic tracking or the tensor model.

Beyond the tractography itself, there are other methodological constraints that can impact the assessment of arcuate laterality in vivo. One option is to define the arcuate by constraining the fascicle endpoints to a predefined set of regions of interest (ROIs; Powell et al., 2006; Rilling, Glasser, Jbabdi, Andersson, & Preuss, 2012; Rilling et al., 2008). This definition may be susceptible to false‐negative errors if anatomically feasible regions are excluded from the set of ROIs. The other option is to model the whole brain's streamlines (also called a tractogram) and then extract arcuate streamlines from them. One way to constrain the tractogram is by using anatomical priors such as WM waypoint planes (Wakana et al., 2007) to identify the arcuate (Budisavljevic et al., 2015; Yeatman et al., 2011). Another possible constraint, even before the arcuate is extracted from the tractogram, is to use an evaluation method on the tractogram to discard problematic streamlines or rank the importance of kept streamlines set (Daducci, Dal Palù, Lemkaddem, & Thiran, 2015; Pestilli, Yeatman, Rokem, Kay, & Wandell, 2014). The ROIs and tractogram strategies have been suggested to yield different results for WM tracking (Bauer et al., 2013; O'Donnell, Golby, & Westin, 2013; Sydnor et al., 2018), but it is unresolved how such constraints in both tractography and fascicle extraction can impact measures of arcuate laterality in vivo.

When assessing arcuate laterality in vivo, we highlight two important scales, the macrostructure and the microstructure. Macrostructure can be assessed through the gross volume of the tract, for example, through measurements such as streamline count and fiber density (Nucifora, Verma, Melhem, Gur, & Gur, 2005; Thiebaut de Schotten et al., 2011). Microstructure, on the other hand, gives a more local measurement of fiber properties, which can be interpreted as reflecting underlying biological properties of the tissue itself. These microstructure measurements include diffusion‐based indices such as FA, which is thought to be sensitive to a number of biophysical properties such as fiber orientation and myelination (Beaulieu, 2002; Jones, Knösche, & Turner, 2013). Microstructure also includes quantitative nondiffusion indices such as the quantitative relaxation rate R1, which is thought to be sensitive to myelin content (Lutti, Dick, Sereno, & Weiskopf, 2014; Stuber et al., 2014). Studies employing deterministic methods usually identify arcuate laterality in both macrostructure and microstructure (Buchel et al., 2004; Klingberg et al., 2000; Thiebaut de Schotten et al., 2011). On the other hand, the results with probabilistic methods tend to be more mixed (De Santis et al., 2014; Lebois, 2014; Talozzi et al., 2018; Zhao et al., 2016). Importantly, as research detailing human brain anatomy is still inconclusive, such studies that do not find a strong left lateralization of can cast some doubt as to the true nature of the arcuate fasciculus.

In this study, we evaluate arcuate laterality in vivo, comparing multiple tractography pipelines. Importantly, there is no gold standard with which the results of in vivo tractography can be verified. Instead, we assess the reliability of our analyses by comparing two independent datasets: one that we collected and one that is publicly available. We report arcuate laterality differences between datasets and tractography types, as consistent with the mixed state of the literature; importantly, we show a reduction of variability with the implementation of different types of constraints. We propose a new method for constraining the definition of the arcuate, incorporating aspects of both tractogram‐ and ROI‐based strategies.

In addition to highlighting the added value of anatomically based cortical constraints on measures of arcuate laterality, we report the following findings: First, that deterministic tracking is less variable and yields a more consistent leftward arcuate laterality. Second, that probabilistic tracking is more susceptible to noise when evaluating arcuate laterality, but that the laterality effect can still be extracted with additional constraints, such as a global evaluation method or added anatomical information. Third, that arcuate laterality is multifaceted and arises from multiple biophysical sources which exhibit different spatial characteristics, as illustrated by independent laterality signatures for different measures such as FA and R1.

2. MATERIALS AND METHODS

2.1. Datasets

The first set of subject data was taken from a larger dataset (Yeatman, Wandell, & Mezer, 2014) collected at Stanford University. For this study, we selected subjects from the larger dataset using the following criteria: adults between the ages of 18 and 55 years, self‐reported right‐handed, and with HARDI data (see Section 2.2). From the original 102 subjects, this yielded a selection of 33 (17 men, 16 women; mean age 33.55 ± 11.72 years, range 18–55 years: four subjects aged 18–20, 10 subjects aged 21–30, 10 subjects aged 31–40, six subjects aged 41–50, three subjects aged 51–55). We use the label STAN33 to refer to these subjects. Data collection procedures were approved by the Stanford University Institutional Review Board. Subjects were recruited from the San Francisco area and were screened for neurological, cognitive, and psychiatric disorders. All subjects provided informed consent.

To replicate our findings, we performed the same analyses on data from the Human Connectome Project (Van Essen et al., 2013). We analyzed the data subset consisting of 100 unrelated subjects (46 men, 54 women; 17 subjects aged 22–25, 40 subjects aged 26–30, 42 subjects aged 31–35, 1 subject aged 36+). The handedness of these subjects was scored using the Edinburgh Handedness Inventory (EHI; Oldfield, 1971). For these subjects, 79 were right‐handed (50 < EHI < 100), 11 were left‐handed (−100 < EHI < −50), and 10 were ambiguous (−50 < EHI < 50). We found similar results using the 79 right‐handed subjects compared to all 100 subjects (Figures A1–A5), so we will use the entire sample in the following analyses. We use the label HCP100 to refer to these subjects.

2.2. Scanning and preprocessing

2.2.1. STAN33

The STAN33 data were collected at Stanford University's Center for Cognitive and Neurobiological Imaging (http://www.cni.stanford.edu/), using a 3T General Electric Discovery 750 (General Electric Healthcare, Milwaukee, WI) equipped with a 32‐channel head coil (Nova Medical, Wilmington, MA).

Quantitative MRI

Quantitative MRI (qMRI) derives tissue properties from biophysical models of the MRI signal. One particular qMRI metric we used is the quantitative relaxation rate R1, which is the inverse of the quantitative spin–lattice relaxation time T1 and which was shown to be highly sensitive to myelin content (Stuber et al., 2014).

To calculate each subject's R1 map, we used four high‐resolution spoiled gradient echo (SPGR) R1 scans and corrected for the transmit‐coil inhomogeneities using four low‐resolution spin echo inversion recovery (SEIR) R1 scans (Mezer et al., 2013; Mezer, Rokem, Berman, Hastie, & Wandell, 2016). The SPGR images had a resolution of 1 × 1 × 1 mm³ and flip angles of 4, 10, 20, and 30°, with repetition time and echo time of 14 and 2.4 ms, respectively. The SEIR images had a resolution of 2 × 2 × 4 mm³ and inversion times of 50, 400, 1,200, and 2,400 ms, with a repetition time of 3 ms and echo time set to “minimum full.” For the analysis of the quantitative data, we used the mrQ software (version 2.0, https://github.com/mezera/mrQ). mrQ calls ANTs (version 2.1.0; Avants et al., 2011) to align the SPGR and SEIR images. Then, we calculated the transmit‐coil inhomogeneities, and calculated the R1 maps using a weighted linear least squares fitting algorithm (Chang, Koay, Basser, & Pierpaoli, 2008).

We also used mrQ to calculate two additional quantitative brain maps: the lipid and macromolecular tissue volume (MTV) map (Mezer et al., 2013, 2016), which uses the proton density signal to determine the amount of nonwater per voxel; and the water‐surface interaction rate (SIR) map, which estimates the spin‐lattice relaxation rate normalized by nonwater tissue volume and reflects differences in tissue composition (Mezer et al., 2013). Finally, we used mrQ to synthesize a bias‐free T1‐weighted image from the qMRI data (Berman, West, Does, Yeatman, & Mezer, 2017; Gomez et al., 2017; Yeatman, Wandell, & Mezer, 2014).

Diffusion MRI

The dMRI data for each subject were comprised of a twice refocused spin‐echo sequence (Reese, Heid, Weisskoff, & Wedeen, 2003) with full‐brain coverage and yielded HARDI data. These scans included 96 noncollinear diffusion‐weighted directions with a b‐value of 2,000 s/mm², and eight nondiffusion‐weighted images with a b‐value of 0 s/mm². The diffusion images had a resolution of 2 × 2 × 2 mm³, with a repetition time of 7,800 ms and an echo time of 93.6 ms. The gradient strength was 53 mT/m and the slew rate was 200 mT/m/ms. We used the Vistasoft (http://github.com/vistalab/vistasoft/mrDiffusion) and MRtrix (version 0.2.12, https://www.nitrc.org/projects/mrtrix/) software packages for preprocessing, which included a correction for subject motion using a rigid‐body transformation algorithm. For this sequence, the long delay between the excitation pulse and image collection in the dual spin‐echo sequence allows for the eddy currents to dephase, meaning that we did not need to perform an eddy current correction (Reese et al., 2003; see Figure A6).

One use of the dMRI data was tractography (see Section 2.3). Another use was the computation of dMRI parameters maps. We fit a tensor model (Pierpaoli & Basser, 1996) to the diffusion data and used it to compute the FA and mean diffusivity (MD) maps. We also fit a more complex model called the sparse fascicle model (SFM). In contrast to the diffusion tensor model, SFM can fit multiple fascicles per voxel (Rokem et al., 2015). We used the SFM implemented in Dipy (Garyfallidis et al., 2014; http://nipy.org/dipy), and also available as a Docker image (https://hub.docker.com/r/arokem/dipy-sfm/), to create a brain map of the dispersion index (DI), a metric that quantifies the amount of fascicle crossing per voxel. The DI metric ranges from 0 to 1, where a higher DI value suggests more fiber crossing. We define the Fiber Coherence Index (FCI), FCI = 1‐DI, so that the directionality of the FCI metric matches with that of FA, as a higher FA is thought to indicate greater fiber coherence.

2.2.2. HCP100

We downloaded the HCP100 data that already had been passed through the HCP preprocessing pipeline (Glasser et al., 2013). For each subject, the data included T1‐weighted and T2‐weighted images with resolution of 0.7 × 0.7 × 0.7 mm³. No quantitative maps are included in the HCP data, so we created a T1w/T2w ratio image, a semiquantitative image that is considered to reflect myelin content (Glasser & Van Essen, 2011). To correct for spatial biases in these images, we used the N4 algorithm in ANTs (Tustison et al., 2010). The dMRI data consisted of 90 noncollinear diffusion‐weighted directions with a b‐value of 2,000 s/mm², and six nondiffusion‐weighted images with a b‐value of 0 s/mm². The diffusion images had a resolution of 1.25 × 1.25 × 1.25 mm³. We tested the effect of the differing dMRI resolution between the two datasets by downsampling HCP100's diffusion data to STAN33's diffusion resolution of 2 × 2 × 2 mm³ (see Figure A7). Finally, we downloaded the output files of bedpostx (Behrens et al., 2007), which were used to run probabilistic tractography with probtrackx2, part of FSL (https://fsl.fmrib.ox.ac.uk/fsl/fslwiki/FSL).

2.3. Tractography algorithms

Starting with the same diffusion data in each subject, we used three tractography pipelines to generate three different tractograms. First, we used STT to perform deterministic tracking on a tensor model of the data (Basser et al., 2000). We implemented tracking with STT with Vistasoft functions, placing eight seeds in every voxel within a smoothed FA mask and using the following parameters: step size 1 mm, angle threshold 30°, stopping criterion FA < 0.20. For the STAN33 data, this yielded 199,802 ± 35,425 (mean ± SD) streamlines per STT tractogram; for HCP100, these numbers were 813,820 ± 128,857 streamlines. We label this tractogram “DET.”

For our second tractogram, we used a probabilistic tractography algorithm on a constrained spherical deconvolution (CSD) model of the data (Tournier et al., 2007). We used MRtrix with a maximum harmonic order (l _max) of 6 to fit a multilobe shape (instead of a single tensor) to represent the fiber orientation distribution in each voxel, and then to generate 500,000 streamlines using the sd_prob method (Tournier, Calamante, & Connelly, 2012). To compute the whole‐brain tractogram in MRtrix, we used a WM mask as both the seed and mask regions, with the default MRtrix parameters (step size 0.2 mm, curvature radius 1 mm, stopping criterion FA < 0.1). We label this tractogram “PROB.”

For our third tractogram, we used LiFE, a tractography‐evaluation method (Pestilli et al., 2014 and https://github.com/francopestilli/life). In this global method, a set of streamlines is reduced by assigning each streamline a weight that corresponds to its contribution to predicting the original diffusion data. Here, we started with the 500,000‐streamline tractogram generated with MRtrix and then constrained it using LiFE. After discarding all the streamlines that do not contribute at all to predicting the original data, the LiFE‐reduced tractograms contained around 51,605 ± 5,369 streamlines (10.32 ± 1.07%) in the STAN33 data, and 125,021 ± 11,025 streamlines (25.00 ± 2.21%) in the HCP100 data.

This step successfully eliminates all nonpredictive streamlines, but it does not account for the weights that the LiFE model assigns to the kept streamlines. The number of streamlines is used for two post‐tractography analyses: calculating the asymmetry in number of streamlines and calculating the arcuate fiber core using automated fiber quantification (AFQ, see Section 2.3). In the other two tractograms (DET and PROB), all streamlines are valued equally, so counting the number of streamlines in a fiber bundle is possible. However, merely counting the number of LiFE streamlines neglects the information carried by the weight assigned to each streamline. Since the nonzero LiFE weights are linear coefficients, we account for the LiFE weights by including multiple copies of each remaining streamline, where the number of copies for each streamline is its weight divided by the smallest weight and rounded. This duplication yielded an effective tractogram of around 949,985 ± 102,215 streamlines in the STAN33 data, and 1,799,689 ± 139,945 streamlines in the HCP100 data. We label this evaluated tractogram “ePROB” (see Figures A8 and A9).

We used WM seeding when generating each of the three tractograms (indirectly for ePROB, as it uses the PROB tractogram as an input). As a comparison, we added an alternative seeding approach by implementing anatomically constrained tractography (Smith, Tournier, Calamante, & Connelly, 2012) using MRtrix3 (https://github.com/MRtrix3/mrtrix3). With this method, the brain is segmented into five tissue types, and tractography seeding is initiated at the gray matter – WM boundary (see Figure A10).

2.4. Arcuate identification and property mapping

For each of the three tractograms, we used MATLAB (MATLAB, 2017) to run the software package AFQ (Yeatman, Dougherty, Myall, Wandell, & Feldman, 2012 and https://github.com/yeatmanlab/AFQ) to investigate the arcuate. We used AFQ to identify the left and right arcuate from the tractogram. AFQ uses the Mori atlas (Wakana et al., 2007) to define 20 known major WM tracts, including the left and right arcuate. A streamline is included in the left or right arcuate if it passes through two WM waypoint ROI planes in its respective hemisphere, one in the axial plane and one in the coronal plane (Figure A11). AFQ's cleaning procedure then removes outlier streamlines, defined as five standard deviations away from the fiber tract core or four standard deviations above the mean streamline length.

AFQ calculates a fiber “core” for each arcuate, which spans the region between the two waypoint ROI planes. The part of each arcuate streamline between the two ROI planes is resampled into 100 equidistant points, and the coordinates of corresponding points across all streamlines were averaged to yield a fiber core with 100 equidistant nodes. Next, AFQ takes each of the brain maps (from the FA, MD, FCI, R1, MTV, SIR, and T1w/T2w metrics) and interpolates a value onto each of the 100 points along each arcuate streamline. Importantly, before projecting these brain maps onto the arcuate, we first had to bring the STAN33 nondiffusion quantitative maps (R1, MTV, and SIR) to the diffusion space, because the diffusion images were collected with an echo‐planar imaging (EPI) readout scheme and the quantitative maps with a non‐EPI readout scheme. Since different readout schemes produce different geometrical artifacts, we used ANTs to warp the nondiffusion quantitative maps into the diffusion space. (For further discussion and examples, see Berman et al., 2017; Yeatman, Wandell, & Mezer, 2014). Finally, the tract profile for each metric was calculated by performing a weighted averaging of the corresponding points, such that points closer to the core count more than points farther away.

2.5. Arcuate identification: Preselected‐ROI analyses

In the methodology described above, the arcuate fasciculus was identified by first performing whole‐brain tractography and then extracting arcuate streamlines by the use of an anatomical prior (Wakana et al., 2007). While many studies (Budisavljevic et al., 2015; Yeatman, Weiner, et al., 2014) use a similar approach, other studies (e.g., Powell et al., 2006; Rilling et al., 2008, 2012) identify the arcuate by performing tractography solely between preselected ROIs.

In order to determine the effect of these ROIs on arcuate identification and subsequent laterality, we first needed to define the ROIs in our datasets. In Rilling et al. (2012), the arcuate was tracked between a temporal ROI (consisting of the banks of the superior temporal sulcus (bSTS), posterior superior temporal gyrus (pSTG), and posterior middle temporal gyrus (pMTG)) and a frontal ROI (consisting of areas 44, 45, and 47l). We identified these ROIs using two brain atlases: We took the larger, gyrification‐based, temporal ROIs from the Desikan–Killiany atlas (Desikan et al., 2006), and the smaller, multimodal‐based, frontal ROIs from the HCP multimodal parcellation (Glasser et al., 2016). These ROIs are illustrated in Figure A11. We resampled each atlas from template space into subject space using surface‐based registration in FreeSurfer (version 5.3.0, http://surfer.nmr.mgh.harvard.edu/).

With these ROIs computed for all subjects, we used two approaches to evaluate the effect of cortical ROI constraints on arcuate definition and laterality. First, we used FSL's probtrackx2 function on the HCP100's bedpostx data to perform probabilistic tractography solely between the two ROI groups. We tracked twice, once from the frontal ROI to the temporal ROI, and once the reverse. We tracked 5,000 samples from each seed voxel. In each hemisphere, the arcuate was defined as the volumetric intersection of the two sets of tracks, and selecting all voxels that had been visited by at least the mean number of total samples.

In a second preselected ROI approach, we sought to use the information about the arcuate's cortical endpoints to augment the analysis performed on the whole‐brain tractogram. Therefore, we added another constraint to the definition of the arcuate: Inclusion as an arcuate streamline required not only the intersection of both Mori waypoint planes, but also that the streamline connect to one of the regions in both the temporal and frontal ROI groups. This constraint yielded a new arcuate bundle that is a subset of the initial arcuate bundle.

2.6. Arcuate laterality calculations

For the streamlines created with AFQ, we operationalized arcuate macrostructure laterality in two ways: by counting the number of streamlines in the left and right arcuate, and by counting the number of unique voxels occupied by those streamlines between the ROI waypoint planes. For the arcuate fasciculi created with probtrackx2, we operationalized laterality by counting the number of arcuate voxels.

For these laterality measures, we then computed the laterality index, LI = (left – right)/(left + right), where a positive LI indicates leftward laterality and a negative LI indicates rightward laterality. We also tested for an effect of sex and age: For sex, we used an independent‐sample two‐tailed t test, with α = .05 Bonferroni‐corrected to control for multiple comparisons (Bonferroni, 1936). For age, we used both linear (LI = β₀ + β₁ × Age) and quadratic (LI = β₀ + β₁ × Age + β₂ × Age²) models for the STAN33 data, while for the HCP100 data (where age is binned into three ranges) we used an analysis of variance.

We used the tract profiles to calculate the group arcuate asymmetry in microstructure metrics (e.g., FA, R1). For each metric, we calculated the mean of all subjects' left arcuate and right arcuate, and computed the group's LI at each of the nodes along the tract profiles. To identify regions of statistically significant laterality among these nodes, we randomly permuted the labels (left and right) of the subjects' tract profiles, and used a permutation test (Nichols & Holmes, 2002) with 1,000 permutations to calculate a familywise error‐corrected alpha value (initially α = .05) for pointwise comparisons.

3. RESULTS

The choice of tractography method can have profound effects on the anatomical properties of the estimated WM tracts (Takemura, Caiafa, Wandell, & Pestilli, 2016). In this work, we evaluated the effect of tractography and different constraints on measures of arcuate WM laterality. We compared three tractography pipelines: DET, which uses deterministic tracking on a tensor model of the data; PROB, which uses probabilistic tracking on a CSD model of the data; and ePROB, which uses the LiFE algorithm to discard nonpredictive streamlines from the PROB output. We investigated the effects of these tractography pipelines on two classes of WM asymmetry: macrostructure and microstructure. For macrostructure, we measured both the number of arcuate streamlines and the number of voxels occupied by those streamlines between the ROI waypoint planes. For microstructure, we computed the arcuate laterality profiles for both diffusion (FA, MD, FCI) and nondiffusion (R1, MTV, SIR, T1w/T2w) measurements. To test the stability of the methods, we compare the results across two independent datasets (STAN33 and HCP100).

3.1. Arcuate macrostructure lateralization

Figure 1 shows the analysis pipeline for an example subject for all three tractography methods (additional example subjects can be viewed in Figure A12). First, we generated a tractogram of streamlines across the whole brain, and then extracted arcuate streamlines from the tractogram by selecting the streamlines that intersect both Mori planes in each hemisphere (first column). This yielded an arcuate bundle in each hemisphere (second column). We identified a left and right arcuate for all subjects in all tractography pipelines in both datasets (Table 1).

Figure 1.

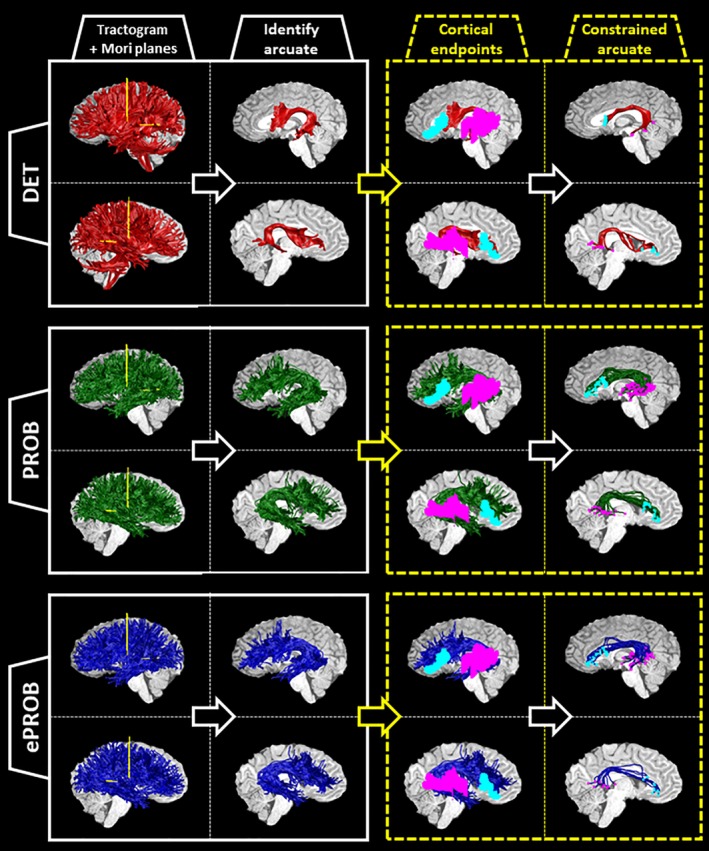
Pipeline for identifying the arcuate fasciculus from three whole‐brain tractograms, illustrated on a sample subject. For each subject, a whole‐brain set of streamlines is generated three times: (1) with deterministic, tensor‐based tracking, labeled DET (red); (2) with a probabilistic, spherical‐deconvolution–based tracking, labeled PROB (green); and (3) with the application of a global evaluation algorithm to reduce the PROB tractogram, labeled ePROB (blue). After the tractogram is generated, two Mori waypoint planes (yellow) are inserted into each hemisphere (first column; see also Figure A11). The streamlines that intersect both planes in each hemisphere are labeled arcuate streamlines (second column). To incorporate additional anatomical information about the cortical destinations of the arcuate, we choose only those arcuate streamlines that connect to both the frontal and temporal cortical regions of interest (ROIs; cyan and magenta, respectively, in the third column). By implementing this constraint, we define a new, subset arcuate bundle (last column, with the endpoints marked in cyan and magenta). For each tractography, we show the left hemisphere on top and the right hemisphere on the bottom [Color figure can be viewed at http://wileyonlinelibrary.com]

Table 1.

Group macrostructure laterality calculations for number of voxels and number of streamlines in the arcuate bundle. For both the STAN33 and HCP100 datasets, we tested for laterality for the three tractography methods DET, PROB, and ePROB using paired‐sample, one‐tailed t tests. The * indicates p‐values smaller than α = .05 (Bonferroni‐corrected). The three numbers for N indicate the number of subjects for whom only a left arcuate, both a left and a right arcuate, and only a right arcuate, respectively, could be identified

		STAN33			HCP10
		DET	PROB	ePROB	DET	PROB	ePROB
N (left/both/right)		0/33/0	0/33/0	0/33/0	0/100/0	0/100/0	0/100/0
Voxel count	Left mean	510.2	2,623.6	1,211.1	1,508.1	7,037.1	4,788.4
	Left SD	142.2	570.9	323.7	523.5	1,391.7	949.3
	Right mean	416.9	2,507.3	1,100.9	1,019.2	7,062.0	4,707.4
	Right SD	182.5	541.7	256.0	531.8	1,425.4	967.0
	p‐Value	2.49E‐03*	6.62E‐02	8.41E‐03*	<10E‐06*	5.94E‐01	1.49E‐01
	t‐Value	3.017	1.544	2.523	9.183	‐0.237	1.046
	LI	0.13	0.02	0.05	0.22	0.0	0.01
Streamline count	Left mean	2,047.2	3,300.1	1,974.9	10,439.8	7,801.1	8,570.7
	Left SD	1,049.6	890.9	724.6	4,463.3	1,557.9	2,082.8
	Right mean	1,022.7	3,075.5	1,408.9	5,563.4	5,779.3	6,755.3
	Right SD	908.2	928.6	503.3	4,704.0	1,572.5	1,814.6
	p‐Value	1.35E‐06*	2.57E‐02	<10E‐06*	<10E‐06*	<10E‐06*	<10E‐06*
	t‐Value	5.723	2.025	5.597	9.542	14.095	10.180
	LI	0.44	0.04	0.16	0.38	0.16	0.12

Abbreviations: LI = laterality index; SD = standard deviation.

In Figure 2, we illustrate group patterns for arcuate macrostructure laterality. As expected, we detect a general trend of leftward laterality. However, we also report a dependency on the choice of tractography. Of the three tractography pipelines we tested, only DET showed consistent laterality across all analysis variations: The leftward laterality effect with DET is robust to dataset differences, and also remains when the HCP100 dMRI data is downsampled to the resolution of the STAN33 dMRI data (Figure A7). The leftward laterality effect with DET is consistent for both macrostructure measurements, and is preserved for two different classes of tractography seeding (Figure A10). These findings are consistent with earlier studies that use deterministic tracking to identify the arcuate (Catani et al., 2007; Glasser & Rilling, 2008; Matsumoto et al., 2008; Nucifora et al., 2005). On the other hand, for PROB and ePROB, we find variation in arcuate macrostructure laterality. The PROB arcuate often does not show any laterality, and while the effect sometimes can be restored through the use of an evaluation algorithm like LiFE, the laterality effect with ePROB is not consistent, either. Similarly, in contrast to the effect with DET, neither the PROB nor ePROB arcuate shows a laterality effect that is consistent across both seeding types (Figure A10). This suggests a sensitivity in these newer tractography methods to factors such as dataset or seeding strategy.

Figure 2.

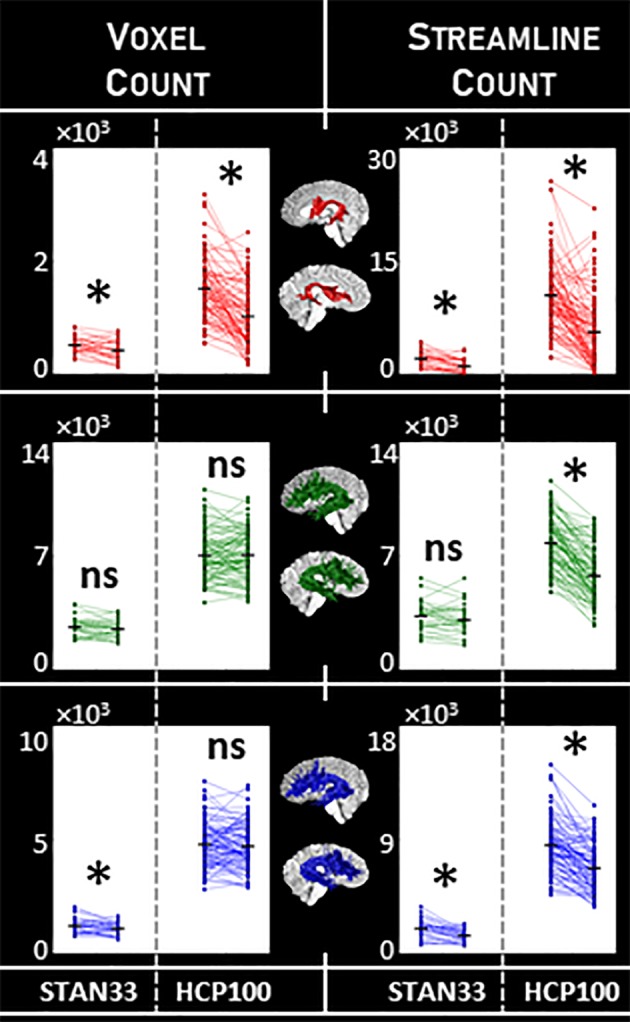
Macrostructure laterality for the arcuate. We measured arcuate macrostructure using voxel count and streamline count (columns) for the three tractography classes DET, PROB, and ePROB (red, green, and blue, respectively). We tested for laterality using paired‐sample one‐tailed t tests; comparisons marked with * indicate p < α = .05, Bonferroni‐corrected, while nonsignificant comparisons are marked “ns.” We compare the two independent datasets STAN33 and HCP100, and identify the most consistency with DET. Measurements provided in Table 1. (Compare to Figure 4, and see also Figures A7 and A10) [Color figure can be viewed at http://wileyonlinelibrary.com]

The above results are based on an arcuate bundle where the streamlines are not limited to where in the brain they may terminate. The Mori atlas defines the arcuate based on the space between the two planes, and was designed for deterministic tractography. Alternatively, other definitions of the arcuate focus on which cortical areas these streamlines are connecting. It is possible to define the arcuate using only its cortical endpoints, and for both datasets we identify the arcuate by selecting those streamlines that link areas 44, 45, and 47l in the frontal cortex with bSTS, pSTG, and pMTG in the temporal cortex. This method can lead to false positive streamlines traveling ventrally (Figure A13), but overall we still detect a leftward macrostructure laterality across most tractography methods (Figures A14–A16). In a related analysis, we used FSL's probtrackx2 to perform probabilistic tracking between the frontal and temporal ROIs, similar to Rilling et al. (2012). We did indeed replicate previous results and detect a leftward macrostructure laterality effect (Figure 3).

Figure 3.

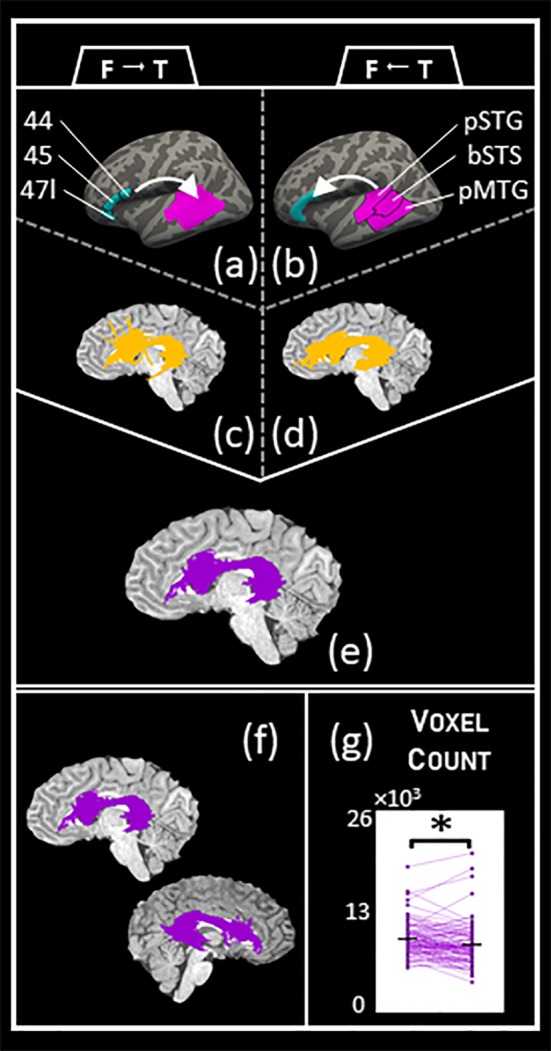
Arcuate laterality with probtrackx2. (a,b) Schematic of probtrackx2 tracking. Each arcuate was tracked twice: once by seeding in the frontal region and tracking to the temporal region (a) and once by seeding in the temporal region and tracking to the frontal region (b). The frontal region is comprised of areas 44, 45, and 47l, while the temporal region is comprised of the posterior part of the superior temporal gyrus (pSTG), the banks of the superior temporal sulcus (bSTS), and the posterior part of the middle temporal gyrus (pMTG). We tracked 5,000 samples from each seed voxel. (c,d) The resulting arcuate voxels from the tracking described (a,b), respectively. The output of probtrackx2 is not a set of streamlines but rather the voxels that were visited in tracking from the seed to the target region, and we set a threshold on the voxels by selecting those that had been visited by at least the mean number of total samples. (e) Final arcuate voxels for probtrackx2 analysis, which is the overlap of (c) and (d). (f) Left and right probtrackx2 arcuate for the same sample subject as in Figure 1. (g) Testing for macrostructure laterality for the probtrackx2 arcuate. We identified the left and right arcuate in 95 of the 100 HCP100 subjects, and used a paired‐sample, one‐tailed t‐test to check for volume laterality. We found more voxels in the left arcuate (M = 9,480.2, SD = 2,157.5) than in the right arcuate (M = 8,744.9, SD = 2,704.1); t(94) = 3.88, p = 9.80 × 10⁻⁵. The significant leftward laterality effect in this probabilistic, region‐to‐region tracking is similar both to existing literature and to our findings with the cortically constrained arcuate (Table 2) [Color figure can be viewed at http://wileyonlinelibrary.com]

We sought to combine these two approaches together, employing both a tractogram‐based framework and the anatomical specificity of known arcuate endpoints. To do so, we added another constraint to the arcuate identification pipeline (Figure 1, third column), selecting only those streamlines that intersected both the frontal and temporal ROI groups as described above. Implementing this additional constraint yields a smaller, subset arcuate (Figure 1, last column). Macrostructure results for the constrained arcuate are summarized in Table 2, and illustrated in Figure 4. For the constrained arcuate method, the results show an opposite trend compared to those with the original method: With DET, we do not detect a significant laterality effect, and at times even find a trend for rightward laterality. Meanwhile, with PROB and ePROB, we find a leftward laterality effect that is consistent across datasets and measurement types. As expected, the constrained PROB arcuate bundles look similar to the FSL (probabilistic) arcuate (Figure 3), and the streamline laterality value of 0.44 is similar to the 0.42 reported in Rilling et al. (2012). Thus, while probabilistic tracking with an unconstrained whole‐brain tractogram approach may not always detect arcuate laterality, with the addition of the cortical constraint we can identify a consistent leftward laterality effect in arcuate macrostructure. Conversely, we find that deterministic tracking best captures arcuate laterality in the unconstrained case.

Table 2.

Group macrostructure laterality calculations for number of voxels and number of streamlines in the cortically constrained arcuate bundle. For both the STAN33 and HCP100 datasets, we tested for laterality for the three tractography methods DET, PROB, and ePROB using paired‐sample, one‐tailed t‐tests. The * indicates p‐values smaller than α = .05 (Bonferroni‐corrected). The three numbers for N indicate the number of subjects for whom only a left arcuate, both a left and a right arcuate, and only a right arcuate, respectively, could be identified

		STAN33			HCP100
		DET	PROB	ePROB	DET	PROB	ePROB
N (left/both/right)		6/9/7	0/33/0	5/27/1	26/35/19	0/100/0	0/100/0
Voxel count	Left mean	104.7	735.4	173.8	327.8	2,086.2	1,108.8
	Left SD	72.4	169.3	97.5	178.3	438.2	308.6
	Right mean	146.4	568.0	75.5	331.8	1,384.2	465.0
	Right SD	63.2	158.3	45.3	189.0	458.1	222.6
	p‐Value	8.87E‐01	1.20E‐05*	1.39E‐05*	5.64E‐01	<10E‐06*	<10E‐06*
	t‐Value	−1.309	4.934	5.073	−0.164	13.145	19.626
	LI	−0.14	0.13	0.44	0.09	0.21	0.42
Streamline count	Left mean	187.9	138.4	107.2	667.9	216.1	415.8
	Left SD	268.2	72.1	66.0	645.1	102.4	174.9
	Right mean	192.0	76.6	27.5	563.6	82.9	96.4
	Right SD	184.1	43.7	25.0	724.4	50.1	60.7
	p‐Value	3.76E‐01	2.24E‐05*	<10E‐06*	3.78E‐01	<10E‐06*	<10E‐06*
	t‐Value	0.326	4.720	6.404	0.313	13.632	19.223
	LI	−0.09	0.29	0.59	0.15	0.44	0.62

Abbreviations: LI = laterality index; SD = standard deviation.

Figure 4.

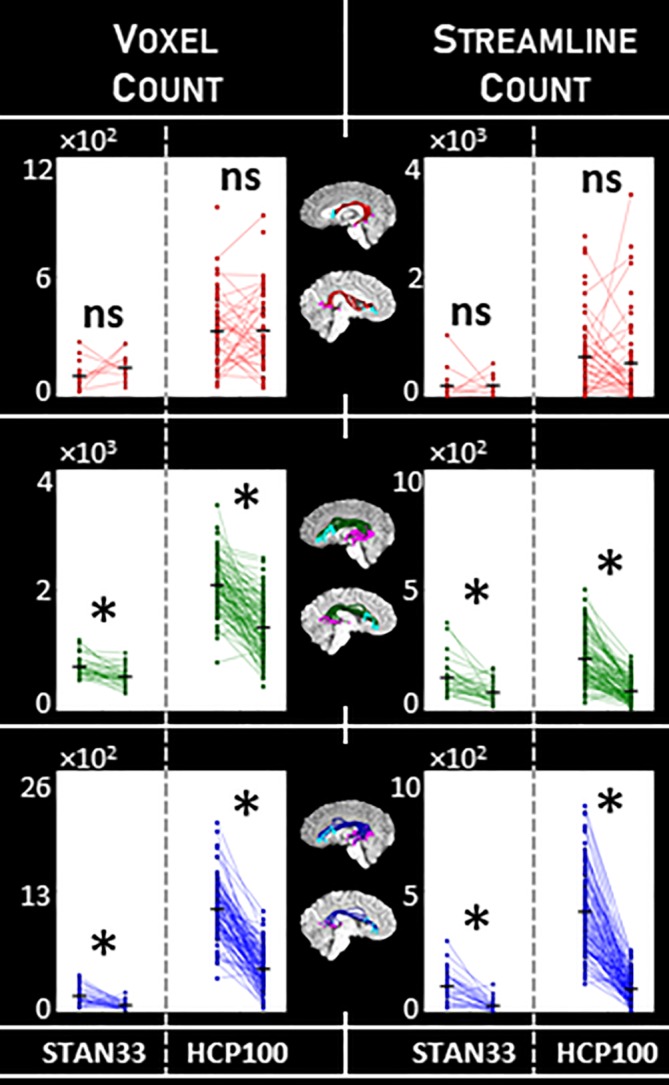
Macrostructure laterality for the arcuate with the cortical endpoints constraint. We measured arcuate macrostructure using voxel count and streamline count (columns) for the three tractography classes DET, PROB, and ePROB (red, green, and blue, respectively). We tested for laterality using paired‐sample one‐tailed t tests; comparisons marked with * indicate p < α = .05, Bonferroni‐corrected, while nonsignificant comparisons are marked “ns.” We compare the two independent datasets STAN33 and HCP100, and find PROB and EPOB show a consistent laterality effect while DET no longer does. Measurements provided in Table 2 [Color figure can be viewed at http://wileyonlinelibrary.com]

Previous research describes arcuate macrostructure laterality as a function of sex or age, mainly finding no significant impact of either (Allendorfer et al., 2016; Budisavljevic et al., 2015; Lebel & Beaulieu, 2009). Here, we test across all these methods and datasets, specifically evaluating whether arcuate macrostructure laterality index scores were influenced by subject sex (Tables A1 and A2) or age (Figure A17 and Table A3). We detected no significant effects, and this is consistent with the literature (Allendorfer et al., 2016; Budisavljevic et al., 2015; Lebel & Beaulieu, 2009). We also tested whether subjects' arcuate laterality index scores with one methodology correlated with their laterality index scores from another. We identified some significant correlations but no one‐to‐one relationship (Figures A18 and A19). The strongest LI relationship is found between PROB and ePROB, which are both derived from the same starting tractogram.

3.2. Arcuate microstructure lateralization

In addition to describing laterality in arcuate macrostructure, previous studies also identify laterality in indices of arcuate microstructure, for example, a leftward effect for FA (Allendorfer et al., 2016; Buchel et al., 2004; Lebel & Beaulieu, 2009). However, these measurements are usually presented as an average, and this can neglect the arcuate's shape, size, and geometry, which we showed in the previous section to be sensitive to different methodological choices (Figure 1). Therefore, we estimated the spatial profiles of several arcuate microstructure indices as a complement to our estimation of arcuate macrostructure laterality. For both the STAN33 and the HCP100 subjects, we used the AFQ software to calculate a tract profile for each subject's left and right arcuate as identified with the DET, PROB and ePROB pipelines, and we repeated these analyses for the cortically constrained arcuate. In both datasets, we assessed the tract profiles for three diffusion measurements: the single‐tensor measurements FA and MD, and the multitensor coherence measurement FCI, where a low value indicates a large number of tensors with large crossing angles. For the STAN33 subjects, we added the tract profiles for R1, MTV, and SIR, as calculated from the quantitative nondiffusion maps. For the HCP100 subjects, we added the tract profile of a T1w/T2w ratio image.

In Figure 5, we illustrate the results of the tract profile analysis for the STAN33 dataset using DET. The left and center columns show the raw traces for all subjects in the left and right arcuate, respectively. The right column shows the group laterality index profiles, with the shaded areas denoting the segments along the tract profile that display an asymmetry that is statistically significant. In this figure, we highlight the results with DET; in the supplementary material, we provide the results for PROB and ePROB with STAN33 data (Figures A20 and A21) and for DET, PROB, and ePROB with the HCP100 data (Figures A22–A24).

Figure 5.

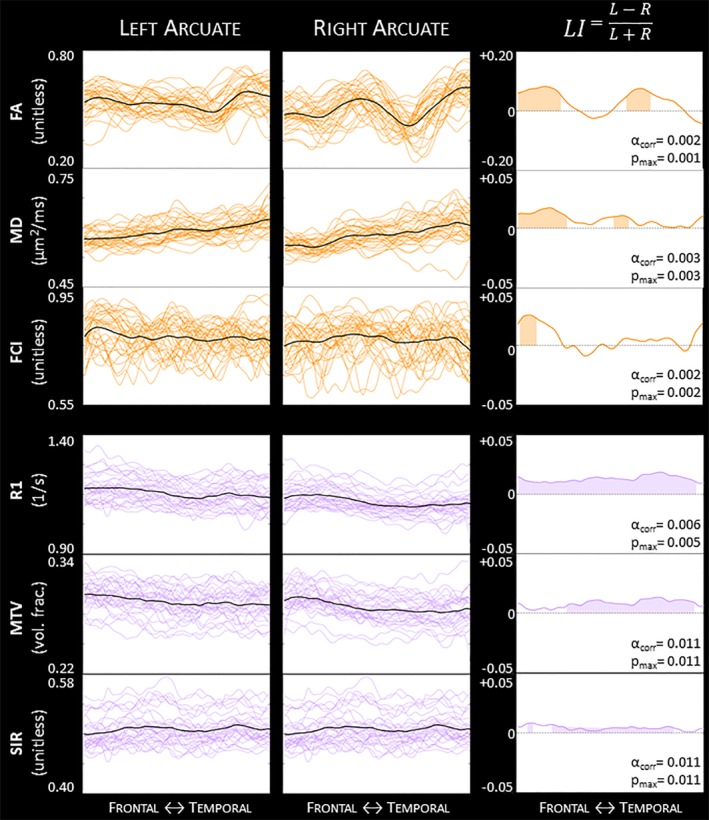
DET arcuate individual tract profiles and LI profiles for the STAN33 dataset. We illustrate microstructure laterality for the diffusion measurements FA, MD, and FCI (orange) and the quantitative nondiffusion measurements R1, MTV, and SIR (purple). Individual tract profiles for subjects' left and right arcuate are displayed in the thin colored lines, while the group mean is displayed with a thick black line. The right column shows the group LI profiles, whereby a positive LI score indicates a leftward asymmetry and a negative LI score indicates a rightward laterality. (Note the different y axis for the first LI profile.) The shaded areas denote segments along the profile that display statistically significant asymmetry, as calculated with a permutation test; α _corr is the new alpha value after correcting initial α = .05; and p _max is the largest p‐value within the shaded area. See also Figures A20–A24. FA = fractional anisotropy; FCI = Fiber Coherence Index; MD = mean diffusivity; MTV = macromolecular tissue volume; SIR = surface interaction rate [Color figure can be viewed at http://wileyonlinelibrary.com]

In Figure 5, we show that both the subject profiles of individual estimates and the group laterality index profiles exhibit a variance in space (from the arcuate's frontal end to its temporal end). Previous studies identified an average leftward asymmetry in the deterministic arcuate in the microstructure index FA (Allendorfer et al., 2016; Buchel et al., 2004; Lebel & Beaulieu, 2009). We replicate this average FA asymmetry (Figure A25). Nevertheless, in Figure 5, we demonstrate that this FA laterality is not constant in space, as we detect two left‐lateralized regions on either side of a nonlateralized center. Importantly, we find that each measurement's tract profile exhibits a different spatial variance, though the laterality effect is largest for FA. The profile of the fiber coherence parameter FCI corresponds somewhat to the FA profile, yet it is mainly nonlateralized. This difference may be related to the fact that FA laterality cannot be explained by differences in crossing, or alternatively by the notion that FCI may be similar to FA but more sensitive to overfitting error as it relies on fitting multiple compartments. In addition to FA and FCI, which are highly sensitive to local fiber configuration, we evaluated relaxometry parameters from the quantitative nondiffusion measurements for complementary laterality profiles. We found that R1 exhibits a constant leftward laterality while other measurements show more fluctuations and only specific subregions of significant laterality.

To assess the stability of these findings across datasets, we compared the microstructure laterality profiles of STAN33 and HCP100. In Figure 6a, we highlight the results for the DET arcuate, where we also detected a strong leftward macrostructure laterality. We identify the greatest similarity for FA, where in both datasets we identify two left‐lateralized peaks surrounding a nonlateralized center. The FCI profiles are also similar, with both datasets showing significant leftward lateralization at the frontal section and a nonlateralized segment thereafter. The MD profile shows the biggest difference between the two datasets, as STAN33 shows a positive effect and HCP100 a negative effect. For the quantitative nondiffusion measurements, although we have a quantitative nondiffusion maps for STAN33 only, we compared the STAN33 quantitative R1 profile to the HCP100 semiquantitative T1w/T2w profile, as both have been theorized to be sensitive to myelin content (Glasser & Van Essen, 2011; Schurr et al., 2018; Stuber et al., 2014). We find that the R1 profile has a constant leftward laterality, while the T1w/T2w profile shows a stronger leftward laterality at the frontal part of the profile but no significant lateralization thereafter.

Figure 6.

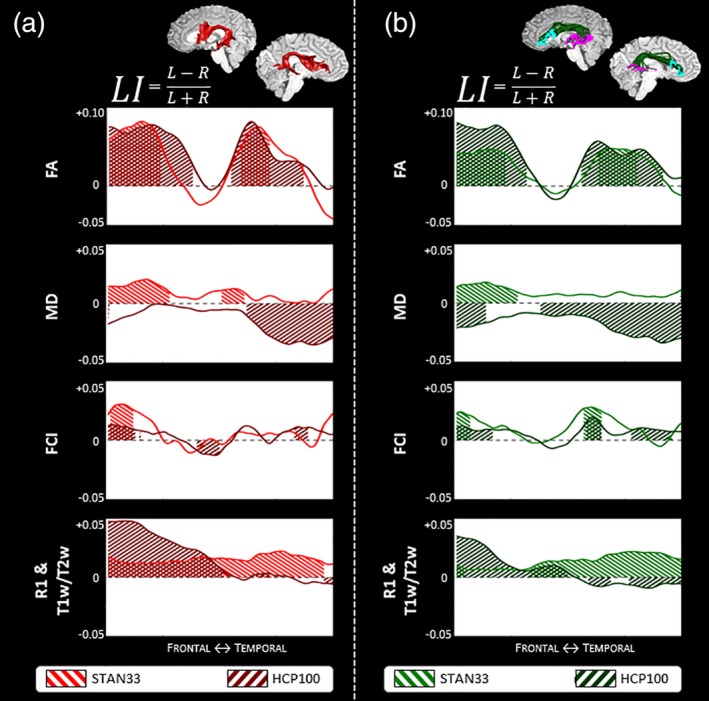
Comparing arcuate microstructure laterality profiles between datasets. We compare the STAN33 and HCP100 datasets using both the DET arcuate (a) and the PROB constrained arcuate (b). We illustrate microstructure laterality for the diffusion measurements FA, MD, and FCI and the nondiffusion measurements quantitative R1 (STAN33 data only) or semiquantitative T1w/T2w (HCP100 data only). A positive LI score indicates a leftward asymmetry and a negative LI score indicates a rightward laterality, with shaded areas denoting segments along the profile that display statistically significant asymmetry, as calculated with a permutation test. See also Figures A26–A28. FA = fractional anisotropy; MTV = macromolecular tissue volume [Color figure can be viewed at http://wileyonlinelibrary.com]

Next we compare the STAN33 and HCP100 laterality profiles with the DET arcuate (Figure 6a) to their counterparts with the constrained PROB arcuate (Figure 6b), as this method also exhibited a reliable leftward laterality effect for arcuate macrostructure. We find similar laterality profiles between these two methods. Here, again we find the FA profile as showing the strongest consistency between datasets. In Figures A26–A28, we provide results for all three tractography analyses as well as with and without the cortical constraints.

Though we find some similarities between STAN33 and HCP100 profiles (Figure 6), we also sought to control for potential sources of differences, such as sample size and data resolution. To that end, we matched the HCP100 to the STAN33 by randomly selecting 33 subjects and using dMRI data downsampled to the same resolution as in STAN33. After performing this random selection 200 times, we found these results were still more similar to the original HCP100 than to STAN33 (Figure A29). In another attempt to reconcile the differences between the two datasets, particularly in MD, we used the N4 algorithm in ANTs to correct for potential spatial biases. First, we applied the spatial bias correction to the diffusion image itself; however, this did not affect subsequent calculations of FA or MD. Then, we applied the spatial bias correction to the FA and MD maps directly. In both datasets, the FA LI profiles' shapes were preserved, while the MD LI profiles show a modest increase in similarity between datasets (Figures A30 and A31). The fact that the differences between datasets are maintained, in particular for MD, suggests that other sources of differences between these two datasets also impact the measured arcuate microstructure laterality.

4. DISCUSSION

In this work, we assessed a multitude of methods for identifying and constraining the in vivo arcuate and tested their effect on measurements of arcuate laterality (Figure 1). Overall, we tend to identify a leftward arcuate laterality. This is consistent with previous literature, both ex vivo and in vivo (Catani & Mesulam, 2008; de Jong et al., 2009; Glasser & Rilling, 2008; Takaya et al., 2015; Thiebaut de Schotten et al., 2011). In this work, we hypothesize that the mixed result in the literature regarding arcuate laterality is due to the greater variability in probabilistic tractography, and that it can be addressed by using additional constraints on the track identification process. Furthermore, we assumed that multiple microstructural laterality can be identify along the arcuate, revealing additional laterality information that is not evident from just the average values. In this work, we base our conclusions on the agreement of different methods across datasets, since a gold standard, postmortem, detailed delineation of the human brain arcuate fasciculi and their laterality is still not available. On the macrostructure scale, we identify leftward arcuate laterality in general, and this is qualified by a sensitivity to the choice of both tractography pipeline and segmentation method. We find that the tensor‐based method DET reliably identifies a leftward laterality effect using the WM waypoint planes only, and that the effect is consistent across datasets and macrostructure measurement types (Figure 2). On the other hand, the PROB and ePROB arcuate, which employ newer tracking and modeling techniques, exhibit an inconsistent effect for macrostructure laterality across these different analysis variations. Using WM waypoint planes only, the PROB and ePROB arcuate may be susceptible to false‐positive streamlines, which can dilute the laterality effect.

The potential washout of arcuate macrostructure laterality with probabilistic tracking can be mitigated with the implementation of additional constraints. Borrowing from the work that tracks only between ROIs (Rilling et al., 2012), we further stipulated that arcuate streamlines already identified from the whole‐brain tractogram must terminate in preselected ROIs in the frontal and temporal lobes. Implementing these constraints helped reveal a consistent (and expected) leftward arcuate laterality in the PROB and ePROB data (Figure 4). Conversely, adding the preselected ROIs to the DET pipeline negates the leftward laterality effect and even introduces a trend toward rightward laterality. This is because the DET arcuate does not always reach the expected cortical ROI and therefore, for many subjects, the constrained DET arcuate could not be identified, and those that were identified had a drastic reduction in number of streamlines (Table 2). This is an expected, erroneous overconstraining of using cortical ROI for deterministic tractography. These results highlight the dependence of arcuate macrostructure laterality on the interplay of both tractography choice and segmentation choice, and the susceptibility of each to different types of errors. With these cortical constraints, false negatives may be more impactful, as laterality with DET may be lessened by the tracks not detected; on the other hand, without these cortical constraints, the laterality with PROB and ePROB may be weakened by the high diversity of streamlines which includes false positives. Both tractography and segmentation should be considered when designing an analysis of arcuate macrostructure laterality and when evaluating published results in the literature. The importance of cortical endpoints when identifying the arcuate is supported by postmortem work that shows the left arcuate innervates the left pars opercularis more than the right arcuate does to the right pars opercularis (Fernandez‐Miranda et al., 2014). Similarly, postmortem work with gray matter shows a number of cellular differences between Broca's area and its right‐hemisphere homolog (Amunts et al., 1999; Amunts, Schleicher, Ditterich, & Zilles, 2003; Zilles, Bacha‐Trams, Palomero‐Gallagher, Amunts, & Friederici, 2015).

Besides tractography and segmentation, we found that arcuate macrostructure laterality is also affected by dataset, dMRI resolution, and seeding strategy (Figures A7 and A10). These factors can add more complexity to the identification of arcuate macrostructure laterality in vivo, especially with probabilistic methods, and reminds us of the absence of a gold standard for verifying dMRI tractography results.

Another measure of arcuate laterality is its microstructure profiles. We measured multiple microscale tissue indices along the arcuate length, and found that the profiles for the different dMRI and qMRI measurements demonstrate different patterns of spatial variation laterality (Figure 5). This illustrates that arcuate laterality is not one homogenous entity, but rather that the arcuate is diverse and exhibits different biophysical sources at different points in space. In Figure 6, we compare the DET arcuate and the PROB constrained arcuate for two datasets, and present two important observations: First, we note that the DET arcuate and the PROB constrained arcuate, which have similar macrostructure laterality, also exhibit similar trends of microstructure laterality. Second, we identify similar patterns for the two independent datasets, strengthening the reliability of these findings.

The microstructure laterality profiles reveal potential biophysical asymmetries in the underlying arcuate tissue itself. Among diffusion measurements, we identify a consistent laterality profile with FA. A general trend of leftward FA asymmetry is reported in the literature (Buchel et al., 2004; Lebel & Beaulieu, 2009; Takao et al., 2013); here, we describe a leftward laterality that varies in space, with a robust two‐peak signature. These findings provide additional spatial information for the localization of FA differences. Further research might try to determine what anatomical or biophysical effect is driving this hemispheric asymmetry at these particular points of the arcuate, as FA is thought to be sensitive to a number of microstructure properties such as fiber orientation or myelination (Jones et al., 2013).

The FA laterality signature features one peak in the anterior part of the arcuate and a second peak at the temporal part. These signals may represent a contribution from two arcuate sub‐segments, the anterior segment and the posterior segment, respectively (Catani, Jones, & ffytche, 2005). In this sub‐bundle nomenclature, the long segment corresponds to the arcuate as we define it in this work; the anterior and posterior segments are identified using an additional ROI, located in the sagittal plane near the supramarginal gyrus. These three segments exhibit considerable overlap in space. These separate segments have been theorized to correspond to three components of a model of working memory (Baddeley, 2007), and disruptions or reductions in these segments have been linked to disorders such as autism (Catani et al., 2016) and auditory hallucinations (Benetti et al., 2015). A comprehensive analysis of the anterior and posterior segments is beyond the scope of this work, but an understanding of the segments' laterality, and component microstructure signatures for measures such as FA, may enrich the story of arcuate laterality we describe here.

We also detected a leftward laterality in nondiffusion measurements, specifically in measurements thought to reflect myelin content. In the STAN33 dataset, we identify a leftward R1 laterality effect that spans the length of the tract. An increase in quantitative measurement R1 has been linked to an increase in myelination (Berman et al., 2017; Stuber et al., 2014), suggesting higher myelin in the left arcuate than in the right. For the HCP100 dataset, we found a leftward asymmetry in the T1w/T2w ratio, a related and semi‐quantitative measurement also thought to be sensitive to myelin content (Glasser & Van Essen, 2011). However, this lateralization is localized in the frontal part of the tract. This suggests these two measurements, R1 and T1w/T2w, are capturing nonidentical aspects of arcuate microstructure laterality. For MD, we detected a laterality effect that differed between the two datasets. This result was not due to differences in sample size, data resolution, or potential spatial bias (Figures A29–A31). Arcuate MD laterality should be interpreted with caution, and future research should determine the source of the MD differences. In combining the different diffusion and quantitative nondiffusion microstructure profiles together, we find that the full story of the different microstructure measurements, and how they are interconnected, remains to be written. Future work is needed to understand how tissue properties such as myelination (R1), fiber crossing (FCI), tissue volume (MTV), and others contribute to the complex, plural lateralities of the arcuate.

Such arcuate lateralities as we report them agree with published findings of leftward laterality in both macrostructure (Buchel et al., 2004; Nucifora et al., 2005; Thiebaut de Schotten et al., 2011) and microstructure (Catani et al., 2007; Lebel & Beaulieu, 2009; Lebois, 2014). A recent study (Talozzi et al., 2018) compared arcuate laterality with three tractography pipelines but found results that are different from ours. These include a lack of volume asymmetry for the deterministic arcuate as well as significant regions of rightward asymmetry in the FA profile. These findings may be attributable to acquisition differences such as scanner strength (1.5 T), diffusion paradigm (anisotropic voxels with size 1.25 × 1.25 × 3 mm³, b = 900 s/mm²) and sample size (29 subjects). The fact that such different results are achieved with a somewhat similar approach highlights the need to verify diffusion outcomes with independent datasets. Indeed, here, we compare the STAN33 results to that with the larger HCP100 to assess the stability of results across independent datasets.

A limitation of the present study is the lack of a gold standard for verifying the results. We cannot determine how accurate our dMRI models of the arcuate truly are (Daducci, Dal Palú, Descoteaux, & Thiran, 2016; Jones et al., 2013; Thomas et al., 2014). We note that LiFE (and life) is not perfect: while evaluation algorithms such as LiFE (Pestilli et al., 2014) or COMMIT (Daducci et al., 2015) constrain the tractography results and find a better solution than the initial tractogram in terms of predicting the raw dMRI data, they do not necessarily reach a unique global minimum. Multiple solutions could minimize the objective function, and these solutions would depend not only on the evaluation algorithm's implementation but also on the initial tractogram and the quality of the data (Daducci et al., 2015; Takemura et al., 2016).

Additionally, the formulation of ePROB streamline laterality depended on our choice of how to incorporate the LiFE model weights. While this choice could impact the estimate of streamline count laterality, we report arcuate streamline lateralization with ePROB regardless of whether we implement the LiFE model weights (Figures A8 and A9). Importantly, we also find ePROB arcuate macrostructure asymmetry when using voxel count, a measure that does not depend on the LiFE model weights. Future research is needed to determine how best to express the LiFE model parameters in a tractogram in a biologically meaningful manner. Finally, since streamlines are not axons (Jones et al., 2013), we observe that the macrostructure estimate of streamline count should not be seen as absolute but rather as a heuristic for understanding the arcuate bundle as modeled with tractography.

5. CONCLUSION

We report a substantial impact of tractography pipelines on biological inferences from dMRI data. We assess laterality of the arcuate fasciculus in vivo, which we define using different tracking, identification, and seeding approaches. We describe the effects for two known tractography methods as well as for a third, new method which attempts to remove potential false‐positive streamlines. We also describe the effect of arcuate identification choice, whereby arcuate laterality is impacted by the addition of constraints specifying which cortical regions are valid streamline destinations. Implementing such additional constraints can help mitigate inconsistencies in probabilistic data and reduce variability between datasets where such data are used. Importantly, we highlight multiple lateralized aspects of WM microstructure, in both dMRI and other qMRI measurements. We conclude that a better understanding of these methodologies can contribute to an understanding of the mixed results in the literature and will provide a better understanding of asymmetry in the brain and of the language network as a whole.

CONFLICT OF INTEREST

The authors have no conflict of interest to declare.

AUTHOR CONTRIBUTIONS

J.D.Y. and A.R. collected data and provided software and analysis methodology; R.S. performed formal analysis and visualization; and J.S.B. and A.A.M. performed analysis and wrote the manuscript.

Supporting information

Appendix S1: Supplementary Material Appendix A

Bain JS, Yeatman JD, Schurr R, Rokem A, Mezer AA. Evaluating arcuate fasciculus laterality measurements across dataset and tractography pipelines. Hum Brain Mapp. 2019;40:3695–3711. 10.1002/hbm.24626

DATA AVAILABILITY

The HCP100 dataset is available from the Human Connectome Project website (https://db.humanconnectome.org/), as the subject group “100 unrelated subjects.” The STAN33 dataset is part of a larger dataset that has not been released as it is currently being used for additional analyses, and the larger database is planned to be released within the next year.