Interplay between the persistent random walk and the contact inhibition of locomotion leads to collective cell behaviors

Abstract

Cell migration plays an important role in physiology and pathophysiology. It was observed in experiments that cells, such as fibroblast, leukocytes, and cancer cells, exhibit a wide variety of migratory behaviors, such as persistent random walk, contact inhibition of locomotion, and ordered behaviors. To identify biophysical mechanisms for these cellular behaviors, we developed a rigorous computational model of cell migration on a two-dimensional non-deformable substrate. Cells in the model undergo motion driven by mechanical interactions between cellular protrusions and the substrate via the balance of tensile forces. Properties of dynamic formation of lamellipodia induced the persistent random walk behavior of a migrating cell. When multiple cells are included in the simulation, the model recapitulated the contact inhibition of locomotion between cells at low density without any phenomenological assumptions or momentum transfer. Instead, the model showed that contact inhibition of locomotion can emerge via indirect interactions between the cells through their interactions with the underlying substrate. At high density, contact inhibition of locomotion between numerous cells gave rise to confined motions or ordered behaviors, depending on cell density and how likely lamellipodia turn over due to contact to other cells. Results in our study suggest that various collective migratory behaviors may emerge without more restrictive assumptions or direct cell-to-cell biomechanical interactions.

1. Introduction

Cell migration is a coordinated process, playing an important role in physiology and pathophysiology (Horwitz and Webb 2003), including embryogenesis and morphogenesis (Aman and Piotrowski 2010; Weijer 2009), cancer metastasis (van Zijl et al. 2011), and wound healing (Friedl and Gilmour 2009). Studies focused on identifying the mechanisms of cell migration suggest that the motility of cells on a two-dimensional (2D) substrate arises from coordinated actions of various cytoskeletal structures in five steps (Blanchoin et al. 2014; Bravo-Cordero et al. 2013; Yamashiro and Watanabe 2014). A cell (i) polarizes spontaneously or in response to sensed signals, (ii) explores surrounding spaces by forming lamellipodial or filopodial protrusions at the leading edge, (iii) anchors the protrusions to the substrate via focal adhesions, (iv) breaks old focal adhesions at rear positions by forces generated from myosin motors, and (v) slide forward. The steps from (ii) through (v) are repeated during cell migration.

The trajectory of a single cell migrating on a 2D substrate seems random but does not exactly follow a random walk; a migrating cell shows both diffusive and ballistic motions (Svensson et al. 2018). Super-diffusive migratory behaviors of diverse cell types on a 2D substrate have been described well by the Persistent Random Walk (PRW) model (Dieterich et al. 2008; Gruver et al. 2010; Harms et al. 2005; Li and Gundersen 2008). The PRW is different from purely random walk in that the current direction (i.e. polarity) of cells is correlated with the direction of cell movement, which results in a super-diffusive motion. The PRW is mainly attributed to cell polarity and the biased formation of protrusions toward the front part of migrating cells. When there are multiple cells migrating on a 2D substrate at high density, the cells make contact, pause briefly after contact, and change directions to move away from each other. This tendency is called the Contact Inhibition of Locomotion (CIL) (Abercrombie 1970; Abercrombie 1979). The CIL can lead to highly confined or ordered motions. Some of the previous studies hypothesized that CIL is attributed to biochemical signaling (Mayor and Carmona-Fontaine 2010; Roycroft and Mayor 2016), but lack of a space for persistent migration also seems to play a critical role for the CIL (Vedel et al. 2013).

Cell migration is a mechanical process that requires force generation and interactions with the environment and with other migrating cells. To study the mechanism of migration, a wide variety of mechanical models have been developed to recapitulate individual and collective cell migration. Each of the models employs distinct simplification schemes with assumptions that are often phenomenological. For example, the Cellular Potts model can simulate individual and collective cell migration with or without environmental sensing by compartmentalizing cells into lattices (Graner and Glazier 1992). The Vicsek model was developed to explain collective cell migration as a dynamic non-equilibrium system consisting of cells with repulsive and adhesive forces (Mehes and Vicsek 2014; Szabo et al. 2006; Vicsek et al. 1995). Particle dynamics models with simplification of cells as propelled particles have also been developed and used to test mechanisms of collective cell migration (Rey and Garcia-Aznar 2013; Sepulveda et al. 2013; Vedel et al. 2013).

Although these modeling studies have provided insights into understanding the mechanisms of cell migration, they have a number of shortcomings that motivate the development of a new migration model. First, the existing cell migration models focus primarily on intercellular interactions but do not account for interactions between cells and the substrate by which the cells move. In addition, the models can be improved to better account for cell physiology and the processes that lead to cell migration such as the polarization, morphology, and dynamic lamellipodial activity of cells. Moreover, most of the previous models can capture only either individual or collective cell migration, not both. For example, the Vicsek model is designed only for collective migration, whereas the models developed for PRW of a single cell based on the Langevin equation cannot reproduce collective migration. These shortcomings prevent us from gaining critical insights into multi-scale cell migration from those models.

Here, we present a rigorous computational model to study both individual and collective cell migration on a 2D non-deformable substrate. Using the model, we show how properties of dynamic formation of lamellipodia affect migratory behaviors of a single cell. Then, we recapitulate the CIL of several cells at low density without any phenomenological assumptions. Based on our results, we propose an alternative mechanism for the CIL. We found that the collective migration of numerous cells at very high density spontaneously emerges from the CIL and show effects of cell density and contact-induced turnover of lamellipodia on collective migration including nematic ordering.

2. Methods

2.1. Simplification of cells and substrate

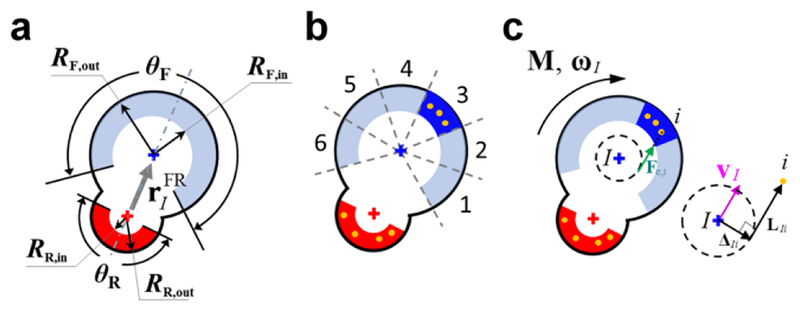
A non-deformable substrate is simplified into immobile points uniformly located on an equilateral triangle lattice. The number of substrate points per unit area can be varied by changing the size of triangles of the lattice. A cell is modeled as a machine consisting of front and rear cell-points (Fig. 1a). The two cell-points representing the front and rear parts of a polarized cell are connected by an elastic spring to maintain an equilibrium distance between the cell-points. Polarity and orientation of cells are represented by a vector from the rear cell-point to the front one. Each cell-point has its own adhesion region defined by a partial donut shape with outer/inner radii and an angular span defined with respect to a segment connecting the two cell-points (Fig. 1a). The adhesion region of the rear cell-point is a half donut with the angular span of θ_R = 180° and relatively small outer (R_R,out) and inner radii (R_R,in). The adhesion region of the front cell-point is relatively large with outer (R_F,out) and inner radii (R_F,in). We tested three different angular spans for the front adhesion region (θ_F): 180, 240, and 300°. Values of all parameters used in the model are listed in Online Table 1.

Fig. 1.

Simplification of modeled features of cells, a substrate, and cell-substrate interactions. a A cell consists of front (“F”, blue cross) and rear (“R”, red cross) cell-points. A dot-dashed line represents the direction of cell orientation, and a gray arrow is a vector from the rear cell-point to the front one ($r_I^{\text{FR}}$) indicating cell polarity. Each cell-point has its own adhesion region defined by a partial donut shape with outer (R_out) and inner radii (R_in) and an angular span. The angular span of a rear adhesion region is θ_R = 180°, whereas the angular span of a front adhesion region is set by a variable, θ_F. b The front adhesion region is divided into angular sections to represent dynamic formation of lamellipodia. A portion of lamellipodia are activated (blue) stochastically and then deactivated (light blue) due to their finite duration (or contact to other cells in some of the simulations). A non-deformable substrate is simplified into immobile substrate points uniformly located on an equilateral triangle lattice. Substrate points within active adhesion regions immediately become focal adhesion (FA) points (orange dots). c Contractile forces exerted on a cell-point I by a FA point i (F_c,i) are directed such that they are tangent to a circle centered at the cell-point with a radius equal to half of the average distance between the cell-point I and all FA points that belong to the cell-point. Δ_Ii is a vector from the center of the circle to the tangential point, and L_Ii is a vector from the tangential point to the substrate point. Directions of the torque (M), angular velocity (ω_I), and velocity of the cell-point (v_I) are shown in the diagram

2.2. Lamellipodial protrusions and interactions between cells and substrate

To represent dynamic formation of lamellipodial protrusion, we divided the adhesion region of the front cell-point into several sections (Fig. 1b). A portion of the sections are activated in a stochastic manner and can stay active during their duration, and the number of simultaneously active sections cannot be greater than the maximum number. While they are active, the sections do not rotate with respect to the substrate even if a cell changes its orientation, which is explained in detail in Fig. S2. If a section is deactivated due to its finite duration or contact to other cells, another section is chosen randomly and then activated. By contrast, it is assumed that the entire adhesion region of the rear cell-point always remains active.

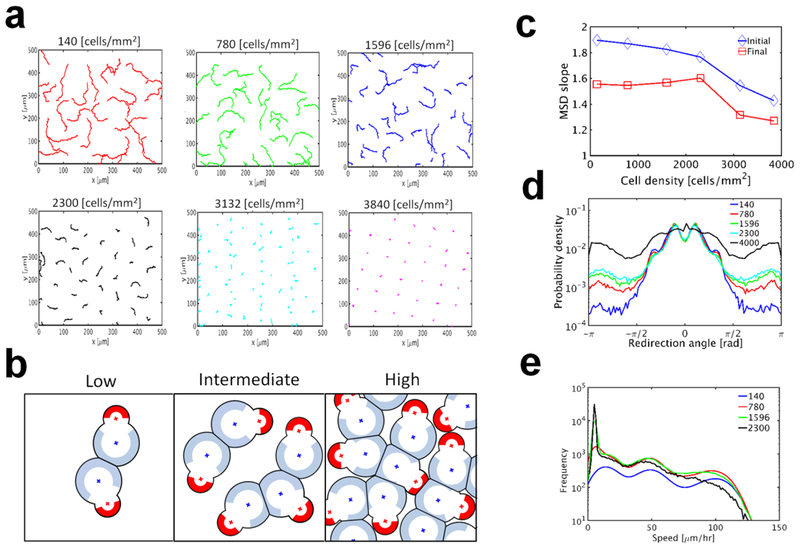
If substrate points are located within an active adhesion region (which is an entire rear adhesion region or an active section of the front adhesion region), they can be turned into focal adhesion through which the cell exerts traction forces on the substrate (Figs. 1b, 1c). If a substrate point is located within more than one active adhesion regions, it belongs to the adhesion region of a cell-point the closest to the substrate point. Thus, if cells are located adjacently to each other, the number of substrate points interacting with their active adhesion regions can be limited. If an active section of the front adhesion region comes to interact with a smaller number of substrate points than a critical level, it can be deactivated immediately, regardless of its duration. The critical level is determined by a parameter called “sensitivity to contact”. For example, if the sensitivity is large, the active section can be deactivated even by a small decrease in the number of substrate points interacting with the active section.

2.3. Formulation of the system

The front and rear points of each cell generate constant torques (Fig. 1c). To account for the cell polarity, it is assumed that the magnitude of torque generated by the front cell-point (M^F) is much greater than that generated by the rear cell-point (M^R). Each focal adhesion i within an adhesion region R_I exerts tensile force F_c,i on the cell-point I. Note that F_c,i is not a centripetal force. Indeed, directions of contractile forces exerted on a substrate by a cell are not centripetal as seen in actin retrograde flow (Gardel et al. 2010). In the model, F_c,i is parallel to a tangent line drawn between the focal adhesion point and a circle centered at the cell-point with a radius equal to half of the average distance between the cell-point I and all focal adhesion points that belong to the cell-point, which results in a finite torque. We assumed that rotational inertia of cell-points is negligible, and that there is resistance of the cell-points to rotation, which is characterized by an angular drag coefficient, γ. Then, the total torque acting on front and rear cell-points should be approximately zero:

$$\begin{gathered} M^{\text{F}}-\gamma {\omega }_I^{\text{F}}+\sum _{i\in R_I^{\text{F}}}{\mathrm{\Delta }}_{Ii}^{\text{F}}\times F_{\text{c},i}=0 \\ {M}^{\text{R}}-\gamma {\omega }_I^{\text{R}}+\sum _{i\in R_I^{\text{R}}}{\mathrm{\Delta }}_{Ii}^{\text{R}}\times F_{\text{c},i}=0 \end{gathered}$$ (1)

where Δ_Ii is a vector from the cell-point I to the tangential point, ω_I is an angular velocity of the cell-point, and superscripts “F” and “R” indicate front and rear cell-points, respectively.

Force balance for front and rear cell-points with an assumption of negligible inertia is:

$$\begin{gathered} F_I^{\text{FR}}-\alpha \left(v_I^{\text{F}}-v_I^R\right)-\sum _J\beta \left(v_I^{\text{F}}-v_J\right)-\eta v_I^{\text{F}}+\sum _{i\in R_I^{\text{F}}}{F}_{c,i}=0 \\ -F_I^{\text{FR}}-\alpha \left(v_I^{\text{R}}-v_I^{\text{F}}\right)-\sum _J\beta \left(v_I^{\text{R}}-v_J\right)-\eta v_I^{\text{R}}+\sum _{i\in R_I^{\text{R}}}{F}_{c,i}=0 \end{gathered}$$ (2)

where the first and second terms represent spring force and viscous drag force acting between the front and rear cell-points of a single cell, the third term is viscous drag force acting between the cell-point and other cell-points located within a short distance (r_crit), the fourth term is viscous drag force originating from an underlying substrate and a surrounding medium, and the last term is the sum of tensile forces exerted between focal adhesions and the cell-point. The spring force $F_I^{\text{FR}}$ is:

$$F_I^{\text{FR}}=-\kappa \left(\left|r_I^{\text{FR}}\right|-r_0^{\text{FR}}\right)\frac{r_I^{\text{FR}}}{\left|r_I^{\text{FR}}\right|}$$ (3)

where κ is a spring constant, $r_0^{\text{FR}}$ is an equilibrium distance between front and rear cell-points, and $r_I^{\text{FR}}$ is a vector from a rear cell-point to a front cell-point (Fig. 1a). α, β, and η are constant drag coefficients.

It is assumed that the magnitudes of F_c,i for all focal adhesion points of a cell-point are identical to each other, but the magnitude is updated at each time step. To calculate the magnitude, we devised a kinematic constraint between the angular and linear velocities of cell-points, which replicates the mechanism by which cells propel themselves on a substrate. For each cell-point, one of the substrate points is randomly selected. The velocity of the cell-point is related to ω_I and Δ_Ii as follows (Fig. 1c):

$$\begin{gathered} v_I^{\text{F}}={\mathrm{\Delta }}_{Ii}^{\text{F}}\times {\omega }_I^{\text{F}} \\ {v}_I^{\text{R}}={\mathrm{\Delta }}_{Ii}^{\text{R}}\times {\omega }_I^{\text{R}} \end{gathered}$$ (4)

This kinematic constraint makes the direction of ω_I the same as that of M. Then, to satisfy Eq. 1, the third term in Eq. 1 must be negative, indicating that forces F_c,i are tensile forces pointing in the direction shown in Fig. 1c. Thus, the solution of Eqs. 1, 2, and 4 always results in tensile forces for F_c,i. This is consistent with the mechanism of cell migration; cells propel themselves forward by exerting tensile forces on focal adhesions.

2.4. Overall flow and implementation of computations in the model

At each time step, we employed the cell list scheme to efficiently assign substrate points to adhesion regions of cell-points for finding FA points and to find neighboring pairs of cells for calculating drag forces. Based on the identified proximity between cell-points and between cell-points and substrate points, Eqs. 1, 2, and 4 can be formulated in the form of a matrix equation:

$$Ku=f$$ (5)

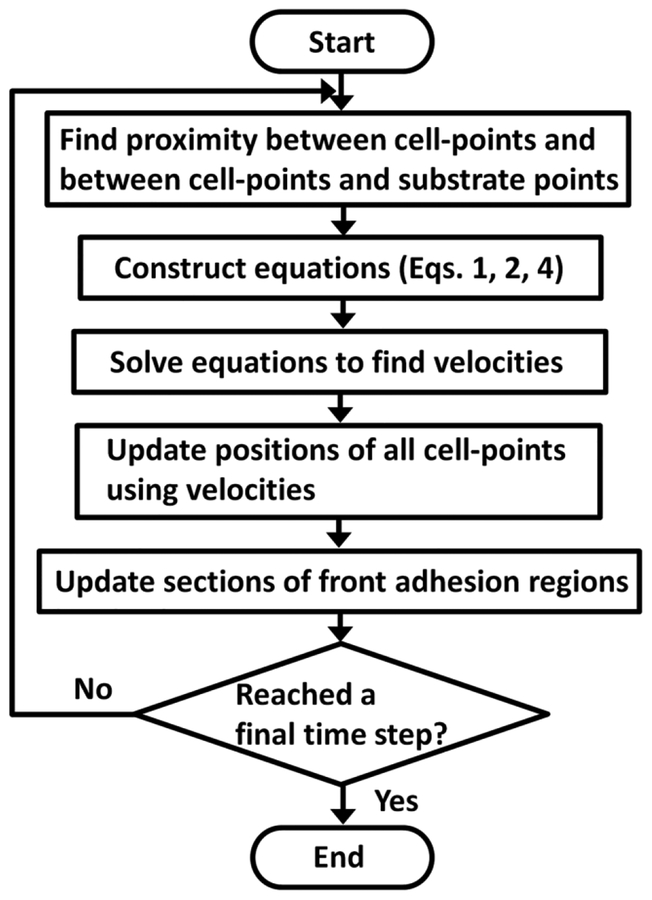
where K is a coefficient matrix built based on the relative locations of cell-points and substrate points, u is a vector which contains all unknown variables, and f is a vector containing constant torques and forces determined by Eq. 3. Fig. S1 shows the overall structure and elements of the matrix equation, and Supplementary Text and Fig. S3 show an example of the matrix equation for a very simple system. Velocities of all cell-points for a next time step are calculated by solving the matrix equation via Intel Pardiso linear solver, and positions are updated using the calculated velocities via the Adams-Bashforth fourth-order integration scheme (Hayes 2011). Finally, activation and deactivation of sections of the adhesion region of each front cell-point are considered. A flow chart in Fig. 2 summarizes the flow of computations in simulations. Typically, each simulation was run with Intel CPU cores between 16 and 24, and most of the computations were performed in parallel via OpenMP.

Fig. 2.

Overall flow of computations. Neighboring pairs of cells are identified, and substrate points are assigned to active adhesion regions of cell-points. Based on the identified proximity, the matrix equation is constructed using Eqs. 1, 2, and 4. Then, the matrix equation is solved to find velocities of all cell-points. Positions of all cell-points are updated using the velocities for a next time step. Finally, the activation and deactivation of sections of the front adhesion regions are considered. These steps are repeated until a final time step

2.5. Analysis of trajectories of cell motions

To characterize motions of cells, we calculated the mean squared displacement (MSD) by tracking positions of rear points of all cells:

$$MSD(\tau )=\frac{1}{N}\sum _I^N\left(\frac{1}{T-\tau }\underset{0}{\overset{T-\tau }{\int }}{\Vert r_I(t+\tau )-r_I(t)\Vert }^{2}dt\right)$$ (6)

where N is the number of cells, T is the duration of simulation, τ is a lag time, r_I is a position vector of the rear point of I th cell. We also measured the logarithmic slope of MSD curves:

$$S=\frac{\text{d ln }MSD}{\text{d ln }\tau }$$ (7)

If cell motion is ballistic, the slope is equal to 2, whereas it is equal to 1 if motion is purely diffusive. In addition, a slope between 1 and 2 indicates persistent motion, and the slope below 1 is indicative of sub-diffusive motion.

Also, we quantified a change in the direction of migration at each time step and named it a redirection angle. We measured the probability distribution of the redirection angle.

2.6. Analysis of directional order of cells

To quantify the directional ordering behaviors of multiple cells, we calculated the ordering tensor, The Q, using the directional property of each cell, u_I:

$$Q=\frac{1}{2N_C}\left[\sum _I\left(3u_I\otimes u_I-I\right)\right]$$ (8)

where N_C is the total number of cells, I is a unit tensor, and ⊗ is a tensor product operator. The eigenvector corresponding to the highest eigenvalue of Q is a preferred direction for all cells, n. Then, the directional order parameter is calculated as follows (Saupe 1968):

$$h=\frac{1}{2N_{\text{C}}}\left[\sum _I\left(3{\left(u_I\cdot n\right)}^2-1\right)\right]$$ (9)

where h = 1 indicates perfect ordering, whereas h = 0 is indicative of no order. The directional order parameter, h_p, was calculated for cell polarity using a vector between the rear and front cell-points (i.e. $u_I=r_I^{\text{FR}}$). In addition, the directional order parameter, h_v, was calculated using the velocity of the rear cell-point (i.e. $u_I=v_I^{\text{R}}$).

3. Results

3.1. Cell polarity with dynamic formation of lamellipodia give rise to a persistent random walk (PRW)

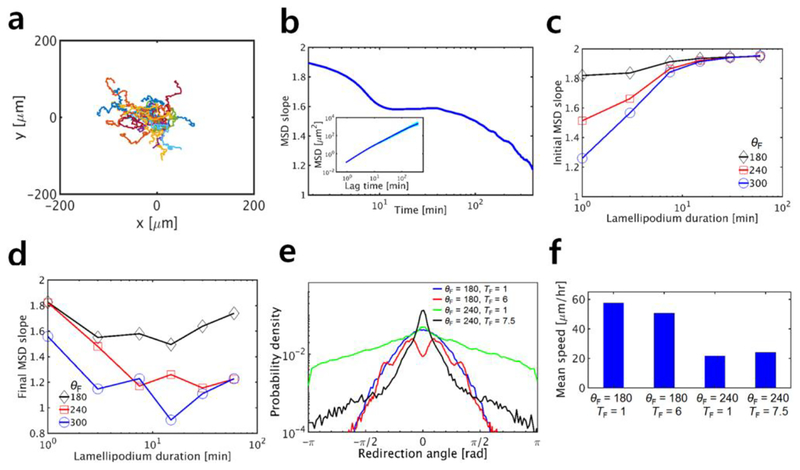
First, we performed simulations with only one cell. Fig. 3a shows examples of migration trajectories from simulations performed under the same condition. To analyze characteristics of cell motions, we quantified the mean squared displacement (MSD) (Fig. 3b, inset) and logarithmic slope of MSD (Fig. 3b) under various conditions. In this example, the slope is nearly 2 at small lag times but continuously decreases as the lag time increases. This implies that cells move in a ballistic manner at short time scales but tend to exhibit diffusive motions at longer time scales. These results correspond well to PRW of single cells observed in experiments (Harms et al. 2005; Li and Gundersen 2008; Weiger et al. 2010).

Fig. 3.

Dynamic formation of lamellipodia highly affects migratory behaviors of a single cell. In each case, we varied the total angular span of a front adhesion region (θ_F) and the duration of a lamellipodium represented by an active section in the front adhesion region (T_F) to evaluate their effects on migration. In all cases, there are 6 sections in the front adhesion region, and only one of them can be activated at once. a Examples of trajectories of cells migrating for 30 hr with θ_F = 240° and T_F = 6 min. b The logarithmic slope of mean squared displacement (MSD, shown in the inset) calculated using the cases in a. The MSD slope in this example implies that cells move in a ballistic manner at short time scales and exhibit diffusive motions at longer time scales, indicative of the persistent random walk. c Initial MSD slope measured at very small lag time, depending on T_F and θ_F. d Final MSD slope measured at lag time of 400 min with the same values of T_F and θ_F as those in c. Interestingly, the final slope shows biphasic dependence on T_F. e Distribution of the redirection angle with four sets of T_F and θ_F. f Average speed of cells with the same four sets of T_F and θ_F as those used in e

To understand how lamellipodial dynamics affects individual cell migration, we evaluated effects of a change in two important parameters on the initial slope of MSD measured at short lag times (Fig. 3c). We varied the total angular span of the front adhesion region between 180° and 300° and the duration of active sections of the front adhesion region between 1 min and 60 min. Under each condition, 10 simulations were run for 60 h. The initial MSD slope is generally smaller with shorter duration and wider angular span of lamellipodia; shorter duration leads to a more frequent change in the direction of the velocity of the front cell-points at short time scales, and wider angular span allows a cell to change the direction of the velocity drastically at once. Regardless of the angular span, the initial slope is almost 2 if the duration is very large; long-lasting lamellipodia result in very persistent motion of the cell in one direction, corresponding to a ballistic motion.

In addition, we probed influences of the same two parameters on the final slope of MSD measured at τ = 400 min (Fig. 3d). As the initial slope, the final slope is smaller, regardless of duration of lamellipodia, if the total angular span of the front adhesion region is larger; if lamellipodia can be formed in any direction independent of cell polarity, cells show more diffusive motions, resulting in a smaller final MSD slope. Interestingly, the final MSD slope shows biphasic dependence on the duration of lamellipodia. Since our model explicitly accounts for polarity of cells determined by positions of front and rear cell-points with drag coefficients, it takes time for the cells to change the orientation of polarity. If the direction of lamellipodia varies very frequently due to their small duration, the instantaneous velocity of front cell-points may change at relatively the same frequency, but the cell polarity does not vary much because there is not a sufficient time for the cell to reorient toward the direction of lamellipodia. Thus, lamellipodia with short duration result in rather persistent cell motions in one direction with noisy oscillation, leading to greater final MSD slope than the initial one. By contrast, if the duration is too long, cells persistently move in one direction for long time, leading to less diffusive motion. Therefore, the final MSD slope becomes minimal at intermediate duration of lamellipodia. Since time required for cells to reorient is determined primarily by drag coefficients of cell-points, the duration at which the minimal final slope emerges is not dependent much on the angular span of the front adhesion region.

We further examined cell trajectories by calculating the probability distribution of the redirection angle (Fig. 3e). Although active sections of the front adhesion region that represent lamellipodia are randomly selected, probability of the redirection angle is not likely to be uniform because of the cell polarity mentioned above. It was found that the probability tends to be higher at angles whose magnitudes are smaller. This tendency is affected by the angular span and duration of lamellipodia. The probability at angles near 0° is higher with shorter duration of lamellipodia because a change in a direction would not occur frequently if the duration of lamellipodia is long. This probability distribution shows the significance of the cell polarity for PRW.

Although changes in the migrating direction occur at various time scales, the speed of migrating cells does not vary noticeably over time, which has been observed in experiments (Abercrombie and Heaysman 1953; Li and Gundersen 2008). Net movement of cells in our model is attributed mostly to a difference between torques generated by the front and rear cell-points. Since the magnitudes of two torques are fixed, the speed does not change much over time. The average speed of cells is affected much more by the angular span of lamellipodia than by the duration (Fig. 3f).

3.2. Competition between cells for a substrate space induces the contact inhibition of locomotion (CIL)

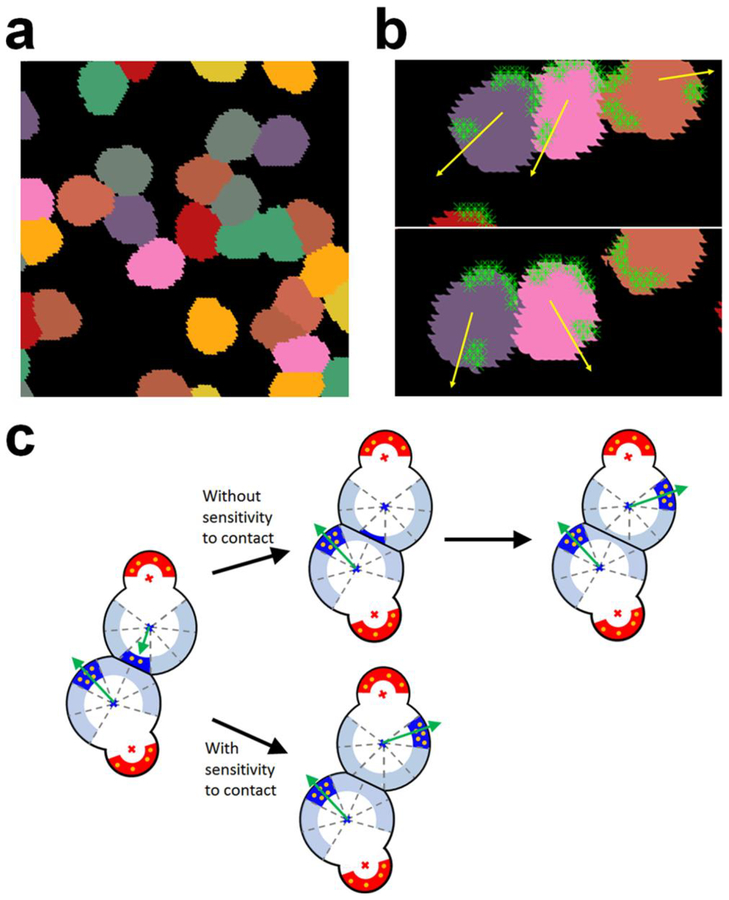
To understand interactions between cells migrating on a substrate, we simulated migration of multiple cells with dynamic formation of lamellipodia at intermediate cell density (Fig. 4a and Online Movie 1). We found that the cells do not overlap with each other and change a direction after making contact to other cells, indicative of CIL. Note that we did not impose a repulsive force that explicitly prevents cells from overlapping. As shown earlier, cells with dynamic lamellipodia explore a substrate space via PRW. If two cells approach each other by chance, a substrate space between the two cells becomes limited (Fig. 4b). Then, a decrease in the number of substrate points interacting with lamellipodia makes the cells slow down and eventually stop. After pause, activation of another section of the front adhesion region toward an open space with available substrate points enables the cells to move away from each other. This result suggests that CIL can emerge from indirect interaction between cells via the underlying substrate without explicit area exclusion between the cells, and that dynamic formation of lamellipodia can lead to redirection of cells after CIL.

Fig. 4.

Interactions between cells and a substrate lead to the contact inhibition of locomotion (CIL). a A snapshot showing migration of multiple cells on a substrate at intermediate cell density. Cells are represented by different colors for distinction. Without repulsive forces or explicit area exclusion, cells do not overlap substantially with each other. b A snapshot showing interactions between three cells. Yellow arrows indicate the directions of cell velocities, and light green symbols represent substrate points interacting with cells. The middle cell wants to migrate toward the left, but the movement is frustrated gradually due to competition with the left cell for substrate points. It eventually changes the direction toward the right due to the turnover of lamellipodia. c Emergence of CIL from competition for a substrate space. If two cells approach each other, the top cell slows down due to a decrease in the number of substrate points in the active section of a front adhesion region. Without sensitivity to contact, the top cell keeps moving and eventually stops if there is no substrate point to interact with. If a new section is activated in the front adhesion region in a different direction, the top cell finally moves away from the bottom one. By contrast, if the active section is deactivated earlier due to imposed sensitivity to contact, a new section is activated in a different direction before the cell makes full contact to the bottom cell, which enhances the efficiency of CIL

3.3. Cell density affects the migratory behaviors of cells

To examine relative importance of PRW and CIL, we simulated multiple cells with dynamic lamellipodia at various cell densities. Fig. 5a shows trajectories of cells for 15 h, depending on cell density. With higher cell density, cell motions are confined more (Online Movie 2). At low cell density, a cell may encounter another cell occasionally (Fig. 5b). However, as the cell density increases, a cell will overlap with more cells much more frequently, resulting in an insufficient substrate space for the cell to exert forces. Thus, cells at high density can migrate slowly over only a very short distance. Highly confined motions of cells at very high cell density are reminiscent of jamming that emerges in confluent cell layers (Abercrombie and Heaysman 1953; Garcia et al. 2015; Nnetu et al. 2012; Vedel et al. 2013). To quantify effects of cell density on migratory behavior of individual cells, we calculated the logarithmic slope of MSDs of migrating cells simulated under the same condition except the cell density (Fig. 5c). The initial MSD slope is slowly reduced as cell density increases up to a critical density (2400 cells/mm²), and then it drops faster at higher cell density. By contrast, the final MSD slope does not change much up to the same critical density, and then it decreases rapidly. Based on these observations, it is likely that cells experience a phase transition at critical cell density.

Fig. 5.

Effects of cell density on migration of cells without sensitivity to contact. In these cases, there are 6 sections in the front adhesion region with θ_F = 180°, and only one of them can be activated at once and lasts for T_F = 6 min. a Examples of trajectories of migrating cells at a wide range of cell density. Cell motions are confined more as the cell density increases. b Schematic diagrams showing the frequency of contacts between cells and available substrate spaces around cells at low, intermediate, and high cell density. The front active adhesion region was not shown for simplicity. c Initial and final slopes of MSD depending on cell density. Both slopes are more sensitivity to a change in cell density if the density is higher than critical level, 2,300 cells/mm². d Distribution of the redirection angle with various cell densities (in cells/mm²). Cells tend to change directions more drastically if cell density is higher. e Distribution of average speed depending on cell density (in cells/mm²). All cases show anomalous speed distributions. Speed tends to be lower with higher cell density because of confined cell motions

We also quantified the probability distribution of the redirection angle with various cell densities (Fig. 5d). With higher cell density, the probability for angles with large magnitudes significantly increases, indicating frequent, drastic redirection events. This is consistent with results shown in a previous modeling study (Vedel et al. 2013). Note that an increase in cell density beyond the critical level identified in Fig. 5c highly changes the probability distribution. These results can be explained based on interplay between PRW of individual cells and CIL. Dynamic formation of lamellipodia leads to a change in migration direction at a frequency corresponding to the duration of lamellipodia. When there are multiple cells, the persistent motion of a cell can be inhibited by contact to the other cells at a certain average frequency determined by cell density. At cell densities below the critical level, redirection of cells by dynamic formation of lamellipodia takes place more frequently than inhibition induced by contact. By contrast, at cell densities beyond the critical level, cells enter a jamming state where CIL events play a dominant role. Thus, MSD slopes and the probability density of the redirection angle change at the critical cell density.

To evaluate the extent of CIL, we measured the distribution of speed of all cells at various cell densities (Fig. 5e). In general, the speed is smaller at higher cell density because of CIL. We found that the distribution is highly dependent on cell density and has long tails. The distribution does not correspond to an equilibrium distribution, but it is similar to anomalous speed distributions observed in previous studies (Masuzzo et al. 2017; Rink et al. 2015; Selmeczi et al. 2005; Souza Vilela Podesta et al. 2017; Vedel et al. 2013). The anomalous speed distribution originates from the non-equilibrium nature of collectively migrating cells. In both reality and our model, a system of cells migrating on a substrate is an actively-driven, dissipative, and open system. In addition, cells do not have a way to collectively reach equilibrium since they do not exchange momentum unlike gas molecules. Therefore, the system should not have canonical speed distributions.

In sum, cell density determines the relative importance of PRW and CIL. At low cell density, PRW of cells largely determines characteristics of their migration. However, as the cell density increases, CIL plays a more dominant role for migratory behaviors of cells.

3.4. Contact-induced turnover of lamellipodia leads to distinct collective behaviors

To further investigate the collective behavior of cells in our model, we sought to determine how contact-induced turnover of lamellipodia impacts CIL and PRW. In experiments, it was observed that a cell can form a different lamellipodium if the area of an older lamellipodium is reduced much due to contact to another cell (Stramer and Mayor 2016). This is known to be regulated by various factors, receptors, polarity proteins, and cytoskeletal elements. To illuminate the role of contact-induced turnover, we implemented the parameter called sensitivity to contact as explained earlier. If the sensitivity is higher, a small decrease in the number of interacting substrate points can result in the turnover of active sections of the front adhesion region (i.e. lamellipodia). Then, a cell does not need to wait until an active lamellipodium expires, which helps cells promptly redirect toward an open space with available substrate points after contact to other cells.

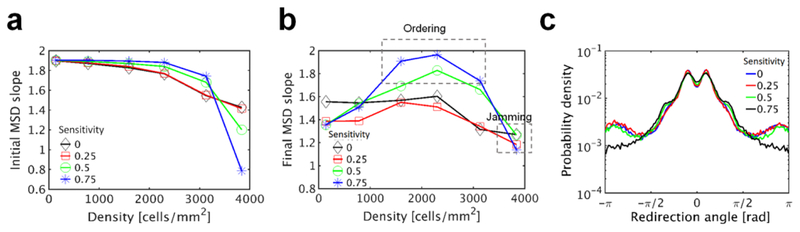
We calculated the initial and final slopes of MSD with 4 different values for sensitivity to contact (Fig. 6a). At low cell density, the initial slope shows weak dependence on sensitivity since CIL does not play an important role for cell migration. However, as cell density increases, the initial slope shows stronger dependence on the sensitivity to contact. If the sensitivity is high, the initial slope decreases very slowly as the cell density increases up to the critical level (2400 cells/mm²), and it drops very sharply at higher cell density. With higher sensitivity, cells adjust their directions earlier via turnover of lamellipodia before they make deep contact to other cells. Thus, if cell density is not very high, the high sensitivity to contact helps the cells collectively migrate more efficiently by finding an available space at higher frequency. The probability distribution of the redirection angle measured at the critical cell density shows that cells with high sensitivity tend to make a less drastic change in their migrating direction (Fig. 6c), which supports the positive role of contact-induced turnover of lamellipodia for collective migration. However, if the cell density becomes too high, the high sensitivity makes cells almost stationary because the cells experience very rapid contact-induced turnover of lamellipodia without any persistent motion in one direction.

Fig. 6.

Cell density and sensitivity to contact regulate collective migration. In all cases, there are 6 sections in the front adhesion region with θ_F = 180°, and only one of them can be activated at once for up to T_F = 6 min. Numbers in all legends represent the sensitivity of lamellipodia to contact; higher numbers mean that lamellipodia making contact to other cells are deactivated faster. a Initial MSD slope depending on cell density and sensitivity to contact. b Final slope of MSD. At intermediate cell density and high sensitivity to contact, the final MSD slope is close to 2, indicative of ordered behaviors. At very high cell density, cells show more diffusive behaviors because they are severely jammed. c Distribution of the redirection angle at cell density of 2,300 cells/mm² with four values of sensitivity to contact

The final MSD slope measured at lag time of 400 min shows rather complex dependence on cell density and sensitivity to contact (Fig. 6b). At low cell density, the final slope does not vary much with the sensitivity to contact because CIL does not play an important role. As the cell density increases up to the critical density, the final slope shows a rise to an extent proportional to the sensitivity. The final slope with the high sensitivity becomes nearly 2 at the critical cell density. Such an increase in the final slope suggests more efficient collective migration of cells. Indeed, we found that nematic ordering emerges spontaneously at higher sensitivity and critical cell density (Online Movie 3), which is very similar to experimental observations that fibroblasts exhibit ordering behaviors at high cell density (Duclos et al. 2017; Duclos et al. 2014). Thus, more persistent motions of cells indicated by the final MSD slope close to 2 stem from a state where cells collectively move in a preferred direction. If the cell density becomes too high, the final MSD slope converges to the same low value because cells cannot move efficiently at long time scales in a jamming state.

3.5. The duration and sensitivity of lamellipodia regulate nematic ordering

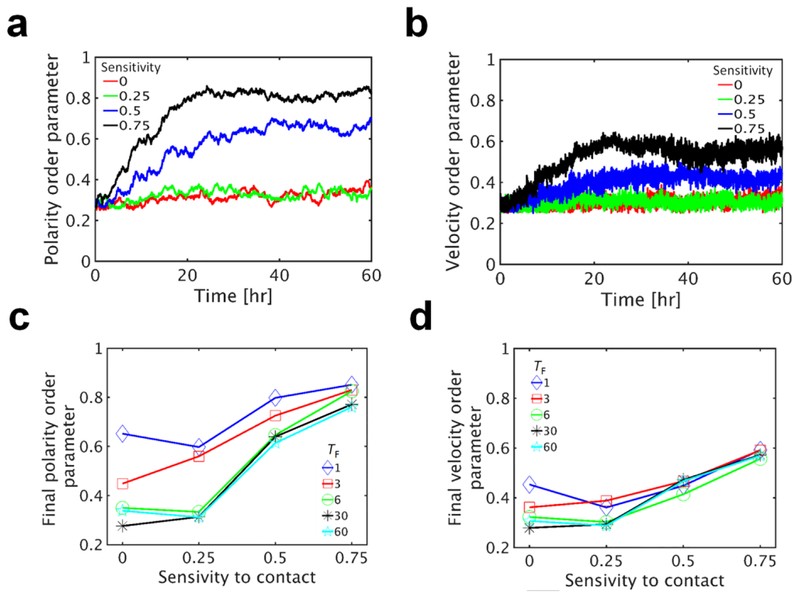
To quantify the extent of nematic ordering, we calculated the directional order parameter using cell polarity (h_p) and velocity (h_v) as an indicator for nematic ordering (Figs. 7a, 7b). In cases with low sensitivity to contact, h_p and h_v do not increase much over time, indicating no nematic ordering. However, with higher sensitivity, h_p and h_v highly increase over time and reach asymptote after 20 h, implying the emergence of nematic ordering of the polarity and velocity of cells. Increasing rates and asymptotic values of h_p and h_v are consistent with experimental results (Duclos et al. 2014) and also proportional to the sensitivity. With higher sensitivity, h_p and h_v reach larger asymptotic values faster.

Fig. 7.

Ordered behaviors originate from lamellipodia that turn over very frequently. In all cases, the front adhesion region with θ_F = 180° is divided into 6 sections, and only one of them can be activated at once for up to T_F = 6 min. Cell density is 2300 cells/mm². a, b Time evolution of order parameters measured for the polarity and velocity of cells depending on sensitivity to contact. Numbers in the legends represent the sensitivity of lamellipodia to contact. Ordered behaviors are more apparent with higher sensitivity to contact. c, d Asymptotic values of ordered parameters for the polarity and velocity of cells, averaged over last 6 hours depending on the duration and sensitivity of lamellipodia. Numbers in the legends indicate the duration of lamellipodia (T_F). Higher sensitivity to contact or shorter duration (i.e. fast turnover of lamellipodia) leads to more ordered behaviors

To better understand how the nematic ordering emerges, we systematically altered the duration and sensitivity of lamellipodia on asymptotic values of the order parameters averaged over the last 6 hours (Fig. 7c, 7d). The order parameters are generally increased with higher sensitivity to contact because the sensitivity accelerates the nematic ordering via CIL. The order parameters are higher with shorter duration of lamellipodia. This is consistent with our conclusion that cells that frequently change directions more efficiently explore the substrate space and reach nematic ordering.

Interestingly, the nematic ordering of velocity is always less than the nematic ordering of cell polarity (Figs. 7a, 7b). Even when cells are aligned in a specific direction, the cells attempt to explore a space in other directions because lamellipodia consistently turn over due to finite duration. This leads to a change in the velocity of the cells temporarily, but the cells are not reoriented in other directions since new lamellipodia formed in other directions are deactivated rapidly due to contact to other cells. Thus, the order parameter of cell polarity that does not vary much after emergence of the nematic order tends to be higher than the order parameter of cell velocity that keeps changing at relatively high frequency.

In summary, we found that the nematic ordering can emerge spontaneously via CIL occurring indirectly through the underlying substrate without direct force interaction between cells.

4. Discussion

In this study, we present a versatile computational model for cell migration on a 2D non-deformable substrate. In the model, cells are simplified into machines with components that reflect cellular structures crucial for migration. In contrast to previous models, we explicitly account for interactions between cells and the underlying substrate. Since cell-cell adhesion is not incorporated, our model represents mesenchymal migration of specific types of cells, such as fibroblast that forms minimal cell-cell adhesion. The model can recapitulate a wide variety of migratory behaviors from individual migration to collective migration.

First, we show how individual cells undergo the PRW based on one cell interacting with the substrate. Cells in reality form lamellipodial or filopodial protrusion in random directions for exploring a surrounding space. However, the directions of protrusions are biased toward the front part of migrating cells because of cell polarity, which results in a rather persistent migration trajectory, not a purely diffusive motion. Our model took into account the cell polarity and biased formation of lamellipodial protrusion, so PRW spontaneously emerged. In addition, we found that interplay between cell polarity and dynamic formation of lamellipodia regulates characteristics of PRW. For example, it is shown that the reduction of the bias in directions of protrusion formation leads to more diffusive motions. We also showed that lifetime of each lamellipodium can highly affect cell motions at both short and long time scales.

In order to mimic dynamic formation of lamellipodia, we assumed that only the front adhesion region is divided into several sections, and a portion of the sections are active for formation of FA points. Considering that FA points are also observed at trailing edges of highly polarized cells even without lamellipodia, it was assumed that the entire rear adhesion region in the model is always active. The radius of the front adhesion region is larger than that of the rear one. In addition, the magnitude of torque exerted by front cell-point is much higher than that exerted by rear cell-point. Thus, the sum of contractile forces exerted on FA points by the front cell-point is much larger, so effects of forces acting on FA points in the rear adhesion region are negligible. Therefore, it is expected that our results would not change much even if we divide the rear adhesion region into multiple sections like the front cell-point.

Interestingly, CIL emerged between cells through indirect interactions between cells and an underlying substrate. Because of the assumption for an overdamped system, cells without any inertia can move only in the direction where focal adhesions were established. Since we assumed that each substrate point can interact with only one cell-point, two cells making contact compete for substrate points located between them. Thus, a decrease in the number of adhesion points reduces propulsion forces and thus makes the cells slow down. If the overlap between them becomes substantial, the two cells will completely stop and wait for turnover of lamellipodia. This is consistent with the empirical description of CIL in (Abercrombie 1970): “Contact inhibition of movement is here defined simply as the stopping of the continued locomotion of a cell in the direction which has produced a collision with another cell; so that one cell does not use another as a substratum.” Thus, we substantiated that partitioning the substrate space located between adjacent cells is sufficient for inducing CIL. Note that we did not include explicit area exclusion between cells in the model that were included in many of the previous models (Zimmermann et al. 2016).

This finding provides an alternative view for CIL. The mechanism of CIL presented in this study indicates that CIL is not caused by an elastic collision. In the case of an elastic collision, we can predict directions of motions of two objects after collision, using momentum conservation. By contrast, the absence of inertia in the over-damped system makes collision-induced momentum transfer between cells negligible. Directions of motions of the two cells after contact are determined by a direction where a new lamellipodium appears toward an available space. In addition, the body of cells is not elastic; the cells are likely to deform as incompressible soft material similar to a viscous fluid droplet subject to force fields. Cells migrating on a substrate are usually spread very widely compared to those in suspension. Outer parts of such wide cells are very thin and thus unlikely to exert strong repulsive forces even if the cells make some contact to other cells. Therefore, the alternative view for CIL explained here seems more physiologically relevant than that based on elastic collision.

However, if cells overlap with each other significantly, cytoskeletal structures that can effectively resist compression, such as microtubules and intermediate filaments, and a stiffer nucleus may exert repulsive forces to preclude further overlap. Therefore, it is reasonable to assume that a critical distance below which strong repulsive force starts acting between two cell-points is much smaller than the sum of inner radii (R_in) of the two cell-points in our model. However, cells would stop migrating due to lack of substrate points even before a distance between the two cell-points becomes smaller than the critical distance. Thus, it expected that the inclusion of repulsive forces would not affect CIL significantly.

We also investigated effects of contact-induced turnover of lamellipodia which is known to be regulated by biochemical signaling pathways (Stramer and Mayor 2016). Sensitivity of lamellipodia to contact implemented in our model represents that cells do not want to sustain their lamellipodial protrusions if there is a physical constraint and thus form another lamellipodium in a different direction with a minimal delay. Thus, cells with high sensitivity can explore a surrounding substrate space more efficiently via lamellipodia that quickly turn over.

We showed how the sensitivity of lamellipodia to contact affects migratory behaviors of multiple cells, depending on cell density. At low cell density below critical level, dynamic turnover of lamellipodia plays a main role for determination of migrating directions because PRW dominates CIL. By contrast, at high cell density, redirection of cells via CIL occurs more frequent than that via dynamic turnover of lamellipodia. Thus, the sensitivity to contact shows a greater effect on migratory behaviors at cell density above critical level. This implies that experiments and models designed for studying CIL may not neglect influences of PRW driven by dynamic formation of lamellipodia if cell density in the system is not high enough.

Interestingly, we found that cells with lamellipodia highly sensitive to contact show nematic ordering behaviors, which is quite analogous to flocking behavior of cells in epithelial and endothelial confluent layers (Vedula et al. 2012). It was observed that cells located at the interior of the confluent layers exert traction stress on the substrate without distinct lamellipodial protrusions when they collectively move (Trepat et al. 2009). Based on our results, we speculate that cadherin-based physical adhesions between cells in the confluent layer may not play an important role during collective motions, other than inducing effective frictions between them which are considered viscous drag force in our model.

Our model has a few limitations. The first limitation is related to spatial distribution and dynamics of FAs. Our model does not account for force-dependent maturation of FA points; we assumed that substrate points are turned into FAs instantaneously as they are located within adhesion regions of cell-points. In reality, it will take some time for FAs to be matured by applied forces and thus become stable enough to transmit forces between the substrate and cells. This may play an important role for guiding cell migration if forces acting on FA points differ from each other due to spatially heterogeneous stiffness or non-linear deformation of the substrate. However, our model assumes an infinitely rigid substrate, so it is assumed that forces exerted on FA points by the lamellipodium of a certain cell-point are always identical to each other in magnitude. Thus, the extent of FA maturation on the substrate points would occur to a similar extent if we include the force-dependent FA dynamics. Thus, it is expected that inclusion of the complicated force-dependent FA dynamics would not change migratory behaviors of a single cell on a rigid substrate significantly. In addition, we account for only FA points underneath lamellipodia although FA points are observed more uniformly in the leading edge of migrating cells (Choi et al. 2008). However, it is likely that much larger contractile forces are exerted on FAs beneath lamellipodia. We assumed that contributions of forces on FAs outside protruding lamellipodia to migration are negligible, and that transient links formed by FAs located outside the lamellipodia are reflected by viscous drag force acting on each cell-point with η.

The second limitation is the assumption of our model based on torque generation. We assumed that front and rear cell-points of cells generate constant torque, and this torque is balanced by the sum of torques resulting from non-centripetal contractile forces exerted by FA points. The actin retrograde flow observed primarily in lamellipodia is induced by forces generated from myosin motors. The direction of the retrograde flow is not centripetal, indicating that contractile forces are not centripetal either. We devised the torque-based assumption from such non-centripetal contractile forces generated by cells. Although previous models designed for simulating cell migration did not assume constant torque for each cell, most of them assumed that a certain mechanical quantity is fixed at constant level, such as the magnitude of force exerted by each protrusive structure (Kim et al. 2013; Vedel et al. 2013). Likewise, we assumed that torque generated by each cell-point, whose dimension is the same as that of elastic energy, is constant. It was shown that the strain energy in a substrate induced by a single cell is nearly constant (Gardel et al. 2010).

The last limitation is the description of lamellipodial dynamics. It was shown that lamellipodia are activated by biochemical wave patterns within a cell, implying that lamellipodia might be formed sequentially rather than randomly (Weiner et al. 2007). However, our model assumes random formation of lamellipodia. It is possible that the lamellipodia formation may not occur very sequentially despite the intracellular wave propagation. If lamellipodia are formed very sequentially, the trajectory of a migrating cell would show a certain repeated pattern. However, many experiments have shown that trajectories are rather random with some persistency. In addition, since the shape of a cell keeps changing during migration, patterns of wave propagation would also change over time, possibly leading to non-sequential lamellipodia formation. Moreover, considering that most of the previous models assuming stochastic lamellipodia formation successfully reproduced cell migration (Kim et al. 2013; Vedel et al. 2013), our assumption seems to be valid. Note that our model already accounts for some aspects of lamellipodial protrusion driven by biochemical wave propagation. The reorientation of migrating cells induced by a physical barrier is related to the intracellular wave propagation (Weiner et al. 2007). The sensitivity to contact used in our model reflects such contact-induced turnover of lamellipodia.

In conclusion, we developed a highly versatile computational model for migration of cells on a 2D non-deformable substrate. Using the model, we recapitulated representative migratory behaviors including PRW, CIL, and nematic ordering behaviors and quantitatively showed how properties of cells regulate individual and collective cell migration.