Patient-Specific Modeling of Heart Valves: From Image to Simulation

Abstract

Heart valves play a very important role in the functioning of the heart and many of the heart failures are related to the valvular dysfunctions, e.g. aortic stenosis and mitral regurgitation. As the medical field is moving towards a patient-specific diagnosis and treatment procedures, modeling of heart valves with patient-specific information is becoming a significant tool in medical field. Here we present the ingredients for valve simulation specifically the aortic valve, with a main focus on a novel spline-based mapping technique which solves many issues in generating patient-specific models – the microstructural mapping, the pre-strain calculations, prescribing dynamic boundary conditions, validation and inverse-modeling to obtain material parameters.

1. Introduction

Heart valves are mechanical components of heart that regulate the direction of blood flow. Structurally they are made of up of multiple layers with highly nonlinear elastic behavior and carry around 3 × 10⁹ cycles of very high pressure loads over a human lifetime [1,2]. A lot of heart related problems are related to the valves, with most of the repairs/replacements being performed on aortic and mitral valves, for problems like aortic stenosis, aortic insufficiency, endocarditis, aneurysm, mitral regurgitation etc [3]. Traditionally, the diagnosis and treatment of these problems used to be solely based on the imaging information available to the clinicians. However, that doesn’t suffice in many cases, specially for heart valves which carry out such an intricate structural role with their microstructure details varying widely over the human population. Here we present the ingredients needed for generating patient-specific heart valves models from three-dimensional echocardiographic (3DE) imaging. We address the challenges and present a novel spline-based mapping technique. We apply this technique to the specific case of normal (tricuspid) aortic valve and its congenital anomalous version – bicuspid aortic valve.

In the next section, we give details about the imaging modality used here and layout the steps for generating model from the images. We also, briefly mention the problems and then present the novel spline-based microstructural mapping technique which is the main focus of this paper. Then we present the other components for simulation – namely displacement boundary conditions and material modeling, pointing out the importance of spline technique in defining those as well. We, then, end with a discussion about the results and future possibilities.

2. Imaging to Simulation

Ultrasound is the safest and most-commonly used imaging modality in medical diagnosis. We used novel in vivo real-time transesophageal three-dimensional echocardiographic (3DE) data obtained with the iE33 platform (Philips Medical Systems Andover, MA). Electrocardiographically gated full-volume 3D images were acquired using a 2–7 MHz matrix-array transducer over four cardiac cycles with a frame rate of 17–30 Hz and imaging depth of 12–16 cm along a midesophageal view. The images were then exported in Cartesian format (≈ 200 × 200×200 voxels), with an approximately isotropic resolution of 0.6–0.8 mm. The images were then hand-digitized by a trained eye.

The imaging data gives us the valve geometry during cardiac cycle in the form of a point cloud. However, the points tracked are not material points and, thus, it doesn’t provide us any information about the strain and curvature changes as valve leaflets go through cyclic loading. Also, it doesn’t include any details about the microstructure of the valve. To solve these two problems in the next section a spline-fitting technique is presented which closely approximates the material points on valve. We also use it to map the microstructure determined on ex-planted leaflets to in vivo valve geometry and correct the material models using pre-strain between in vivo and ex-planted in vitro configurations. In addition, defining patient-specific boundary and loading conditions is also facilitated by using a common spline parameter space.

3. Spline Based Fitting and Microstructural Mapping

Splines are the standard tools in computer aided design for geometric representations and have been recently integrated into the finite element analysis of structures and fluids [4]. For soft tissues, in addition to their macro-level geometry, there are other microstructural details, e.g. fiber alignment, orientation, crimp and stiffness. As the biomedical engineering is making progress, there is a need for developing a tool which can integrate all this information into one framework. In this section, a spline-based method is presented for soft tissue (here applied to aortic valve) which facilitates mapping of the fiber structure from any aortic valve specimen to any other aortic valve geometry through a common parameter space. Spline based models for heart valves have been developed before [5,6]. However, in their methods the emphasis has been on motion tracking by machine learning algorithms. They do not have specialized spline representation as represented here which can be used to map microstructures because of the direct connection between control points and the valve shape (see next section for more details). Thus using a common parameter space, this techniques also has the ability to calculate mean tissue microstructure of representative population as will be shown next.

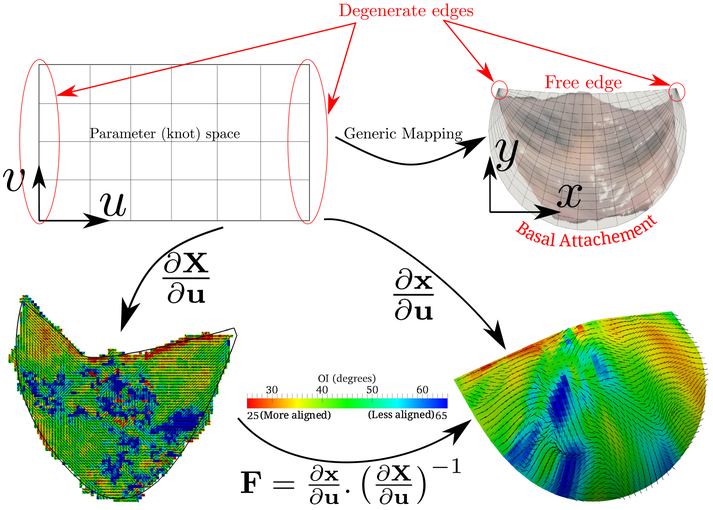
3.1. Mapping Idea

The most easily recognizable features of aortic valve are, first of all, it’s commissure points and then its two edges – the free edge and basal attachment. The spline surface is parameterized in the knot space with (u, v) = [0, 1] [0, 1] [7]. As the spline surface has four edges, for mapping we degenerate the two edges of spline space (u = 0 and u = 1) to the two commissure points (see top row in Fig. 1). Direct surface fitting leads to oscillation at the boundary. To avoid that, a C²-continuous spline curve with two C⁰ points (the commissures) is first fitted to the boundary. Then the closed curve is converted into an open surface. To do this we have to make sure that the two continuous parts of the boundary curve have equal number of control points and same knot intervals. Then the spline surface is fitted to the valve geometry keeping the boundary fixed eliminating the oscillation problem.

Fig. 1.

(Top row) Generic mapping for aortic valve where two edges in the parameter space are degenerated to commissure points and (bottom row) example of mapping fiber structure from 2D to 3D using the spline parameter space

3.2. Mathematical Formulation

For fitting a spline surface to the hand-digitized point cloud, norm of the difference between the input points x_i and their projection on the spline surface $x_i^p$ is minimized to find the control points C_j:

$$\text{min}\sum _i\Vert x_i-x_{ip}{\Vert }^2\equiv \text{min}\sum _i\Vert x_i-\sum _j{N}_j\left(u_i^p,v_i^p\right)C_j{\Vert }^2$$ (1)

where N_j are the shape functions associated with j-th control point, calculated at projection points $\left(u_i^p,v_i^p\right)$. This least square problem can be solved by the linear system C = (A^T A)⁻¹A^T x, where C is vector of control points and A is the matrix of shape functions $N_j\left(u_i^p,v_i^p\right)$. Projection points $\left(u_i^p,v_i^p\right)$ are calculated by the condition that closest/projection point should be normal to the curve. Therefore, it can be found by solving the equation $\left(x_i-x_i^p\right)\cdot \frac{d{x}_i^p}{du}=0$ using Newton’s method.

The spline is initialized with few control points (usually 4) and progressively refined to better fit the given geometry. Once a spline curve is fit satisfactorily to the boundary, the two C² parts of the curve are separated and the second part is reversed. Then, the control points of two curves are interpolated linearly to get control points in between these two. Using this matrix of control points of the spline surface defined by parameter space shown in Fig. 1 gives us an initial approximation of the spline-surface to the input data. Then, keeping the edge control points fixed, the interior ones are varied to minimize the difference similar to formulation described for 1D in (1) – L₂-minimization of the difference between input points and their projection. Upon convergence, this gives us the spline surface representation of the input point cloud data. However, it should be noted that the projection operator (for calculating $x_i^p$) becomes more involved compared to curve fitting because of higher dimensions and having an open surface (i.e. boundary points may not satisfy the normality condition) but the details are skipped here because of limited space.

3.3. Population Average Fiber Structure

For patient-specific modeling, ex-planted leaflets are not available for fiber structure determination. In many studies the fiber structure is assumed to be orthotropic with fibers running along the circumfrential direction of valve tissue [8,9]. However, this might not be always true, specially for anomalous or diseased valves. To get a population average fiber structure, ex-planted 6 normal tricuspid aortic valves (TAV) and 6 bicuspid aortic valves (BAV) were sampled from humans and their microstructure was determined using small angle light scattering (SALS) [10]. Spline surface was fitted to each of the SALS output to parameterize the fiber data. A common template of simulated heart valve geometry was used and a spline surface was fitted to that (RMSD of fitting < 0.04 mm). The knot space parameterization was used to map the fiber structure from any ex-planted valve to the SHV (see bottom row of Fig. 1 for an example). The common template then allowed us to calculate the average fiber structure of the sampled TAV and BAV data (Fig. 2) – clearly showing a difference in the fiber structure. A simple statistical analysis of three regions (Fig. 2 right panel) shows that the fiber structure is less aligned in the bicuspid case specially around the regions A and B where two leaflets are fused together. Also to be noted in the plot is that both TAV and BAV structures are pretty consistent and we can find the averages with high confidence. This is the first time such population average structures have been calculated.

Fig. 2.

(left) Average TAV and BAV fiber structure of representative population (lines show the fiber preferred direction and color shows their orientation index – how aligned they are) and (left) statistical mean and 95% bootstrap confidence interval in three regions of the valve

3.4. Matched Leaflet Mapping

To illustrate the mapping on real data set, instead of using a simulated heart valve geometry, in vivo shape at just-coapted configuration (when the transvalvular pressure is approximately zero) was determined from 3DE for a sheep heart. The valve leaflets of the sheep were then ex-planted and their fiber structure was determined. The fiber structure was then mapped onto the in vivo “reference” configuration (Fig. 3).

Fig. 3.

(Top) 3D echocardiograph image of sheet heart with normal aortic valve segmentation shown in black, (bottom right) ex-planted leaflets and their fiber structure from SALS and (bottom left) spline surface fit to the segmentation with fiber structure mapped from ex-planted leaflets

4. Material Model

The valve tissues are made up of multiple layers (fibrosa, ventricularis etc.) with different types of fibers embedded in a matrix for each of them [1,2]. However it is very hard to take into account the contribution of each layer separately. Therefore, here we take one of the most realistic material models developed where tissue is idealized as a planar network of collagen fibers (main load bearing component) embedded in a ground substance (glycosaminoglycans, elastin, water) [11]. Thus, the strain energy is assumed to be a sum of the contributions from fibrillar (anisotropic) and non-fibrillar (isotropic) components expressed in terms of the tissue level Green-Lagrange strain E:

$$\psi ={\psi }_{\text{iso}}^{\text{M}}(E)+{\psi }_{\text{aniso}}^{\text{F}}(E)$$ (2)

where, ${\psi }_{\text{iso}}^{\text{M}}$ and ${\psi }_{\text{aniso}}^{\text{F}}$ are strain energy functions representing ground-matrix and fiber contributions respectively. The ground-matrix function describes low-strain behavior and provides stiffness in the unloaded state. Tissue response to large strains is accommodated by the anisotropic term characterizing the fibrillar microstructure averaged through the thickness. The isotropic contribution is assumed to be neo-Hookean. Following the formulation in [11], the ensemble 2^nd Piola-Kirchhoff stress in a single fiber is

$$S_{\text{e}ns}\left(E_{\text{e}ns}\right)=\frac{\partial {\psi }_{\text{e}ns}}{\partial E_{\text{e}ns}}=\eta \underset{0}{\overset{E_{\text{e}ns}}{\int }}D(x)\frac{E_{\text{e}ns}-x}{{(1+2x)}^2}dx$$ (3)

where, η is the fiber stiffness, D is the fiber recruitment function and E_ens is the uniaxial Lagrangian strain in single fiber aligned in direction N so that E_ens = N^T EN. For a distribution of fibers in a planar biaxial state, we get the planar stress by integrating over the distribution

$$S(E)=\frac{\partial {\psi }_{\text{iso}}^{\text{M}}}{\partial E}+\frac{\partial {\psi }_{\text{aniso}}^{\text{F}}}{\partial E}=\mu I+\underset{-\pi /2}{\overset{\pi /2}{\int }}R(\theta )S_{\text{e}ns}(E(\theta ))N\otimes Nd\theta -p{C}^{-1},$$ (4)

where μ is determined from the flexure experiments and p is the Lagrange multiplier for incompressibility condition. The fiber distribution was determined at every point of the tissue using SALS setup [10]. The parameters in the above expression were obtained using a standard biaxial experimental setup for both TAV and BAV tissue samples. However, these experiments were performed in vitro on ex-planted tissues. In general in dynamic biological systems, it is ambiguous which state should be taken as the reference or stress-free configuration. Entities on all the scales from virus shells [12] to heart valves [13] have been shown to have some pre-strain in their native state. This renders all the material models unrealistic, as the reference configuration in simulations is taken from the ultrasound images which is not, in reality, strain or stress free.

From the spline mapping method described in the last section, we get a mapping between the ex-planted (or in vitro) to in vivo shape giving us a measure of pre-strain at every point of the valve (Fig. 4). This effect can be included into the material model by replacing the Green-Lagrange strain E by $F_p^{-T}E{F}_p^{-1}$, where F_p is the pre-strain deformation gradient at every point calculated from the 2D to 3D mapping.

Fig. 4.

Mapping from 2D to 3D gives us a strain map which was used to correct the material models developed in vitro. Jacobian is the third invariant of the Green’s strain tensor indicating the change in area upon deformation. Clearly, the in vivo configuration is stretched.

5. Boundary and Loading Conditions

In addition to the geometry, microstructure and material parameters, we define the boundary conditions and loading to complete the problem definition. The aortic valve is attached to the aortic root through basal attachment. The basal attachment was manually digitized in all the 3DE frames and a C² spline curve was fit to it with knot space of u = [0, 1]. For making the boundary conditions dynamic we need to prescribe velocity and acceleration of the basal attachment as well. To achieve, that the corresponding control points of spline curves at different time steps can be interpolated using another C² spline in time domain. This will give us the velocity and acceleration (since second derivative of C²-continuous curve does exist) of the basal attachment to be prescribed as a boundary condition. For prescribing the load, in vivo transvalvular pressure was measured experimentally. The parameterization of this loading curve in terms of the measurable patient-specific blood pressures is not clear at this time. Further experiments will reveal the appropriate scaling. For now, a piecewise constant pressure is assumed which provides a good approximation.

6. Discussion

In summary, we presented a different components of creating patient-specific models of heart valves from 3DE data. The novel idea here was the spline-based mapping which is a simple yet surprisingly robust method for mapping the microstructure – the fiber directions and alignment, of tissues. Such a mapping usually requires physical markers limiting its use [14]. However, using the method presented here eliminates the need for any physical markers. Although spline based models have been developed before [5,6], they are not specialized to map the microstructure. In our knowledge, this is the first time population averaged microstructures have been obtained.

It should also be noted that in the AV model generated (Fig. 3) instead of the matched leaflet microstructure, the population average microstructure previously calculated could also be mapped to the 3DE configurations. Thus this technique allows us to use any fiber architecture to be used in any valve model. This is a very useful tool in understanding which structural features lead to the valve disease e.g. bicuspid aortic valve leads to an accelerated growth of calcific aortic valve disease. The method presented here will be helpful in providing insights into such phenomenon. Also, this method allows us to connect the in vivo state to the in vitro measurements through pre-strain map which was used in constitutive modeling of valve tissues (Fig. 4). Also, the spline maps with C² continuity allow us to calculate velocity and acceleration from point cloud at different time points.

The other novel aspect of this work is our ability to get patient-matched leaflets and 3DE data. This allows for the validation of material models as well as creating a benchmark case of valve motion of population average which will be a very useful tool in the clinical diagnostics of abnormal valve motion. The strains calculated using cardiac cycle might also enable us to determine valve’s material properties from 3DE images using inverse modeling.