Critical Role of Dynamic Flexibility in Ge‐Containing Zeolites: Impact on Diffusion

Abstract

Incorporation of germanium in zeolites is well known to confer static flexibility to their framework, by stabilizing the formation of small rings. In this work, we show that the flexibility associated to Ge atoms in zeolites goes beyond this static effect, manifesting also a clear dynamic nature, in the sense that it leads to enhanced molecular diffusion. Our study combines experimental and theoretical methods providing evidence for this effect, which has not been described previously, as well as a rationalization for it, based on atomistic grounds. We have used both pure‐silica and silico‐germanate ITQ‐29 (LTA topology) zeolites as a case study. Based on our simulations, we identify the flexibility associated to the pore breathing‐like behavior induced by the Ge atoms, as the key factor leading to the enhanced diffusion observed experimentally in Ge‐containing zeolites.

Introduction

Zeolites are nanoporous framework inorganic materials widely used in industry as catalysts, ion exchangers, adsorbents and molecular sieves.1 The incorporation of Ge in their framework is a very useful route to tune their functionality. For example, the performance of zeolites in various applications is closely related to their topological features, and in the last two decades much attention has been focused on the discovery of new large‐pore frameworks, which can be stabilized by the inclusion of Ge atoms in tetrahedral sites.2 Furthermore, in gas separation applications, the effectivity of the materials is largely reduced by the presence of extra‐framework cations or acid sites needed for charge compensation when Al or other trivalent cations are part of the framework.3 Much effort has therefore been devoted to the preparation of zeolites containing Ge, which is isovalent with Si, thus permitting the creation of new zeolites with neutral frameworks.4 Brunner and Maier proposed that the presence of small rings favors the formation of large‐pore zeolites,5 which explains the role of Ge in the synthesis of large‐pore zeolites. Both experimental and theoretical studies have shown that Ge atoms preferentially locate in these small rings, particularly 3‐ and 4‐member rings (MR), which has been interpreted as a consequence of the higher flexibility of the GeO₄ tetrahedra, allowing stress release in these small units.4b, 4c, 6 It is worth noting that the flexibility associated to Ge has been always linked to a static picture, that is, the accommodation of otherwise strained bonds.

In this study, we use a combination of experimental and computer simulation methods to show that the flexibility associated to Ge atoms in zeolites is not only static, but also has a dynamic nature, leading to enhanced molecular diffusion. As a case study, we have carried out a comparative investigation of isomorphous ITQ‐29 zeolites (LTA code from IZA), both pure silica (Si‐ITQ‐29) and silico‐germanate (SiGe‐ITQ‐29) frameworks.7 Small‐pore zeolites have been previously investigated for their potential application in the separation of propene from propane.8 Purified olefins are highly in demand for the large‐scale production of polymers, but propane/propene separation is difficult, due to their very similar volatilities (their boiling points differ by only 6 K) and molecular sizes (their effective diameters differ by ca. 0.2 Å, from 4.3 Å for propane to 4.5 Å in propene according to Breck,9 although other authors indicate a reverse order of size and give values for propene of around 3.810 or 4.0 Å11).

Using transient uptake techniques, it has been found that C3 (propene and propane) hydrocarbons diffuse through the 8‐MR channels of CHA, ITQ‐3 and ZSM‐58 pure‐silica zeolites, even when the reported crystallographic window apertures of the zeolite are smaller than the kinetic diameters of the molecules.12 By comparing the behavior observed for CHA in relation to the other two zeolites, it can be concluded that for pore diameters of around 3.8 Å any small pore size variation induces a dramatic change in diffusivity. Zeolite 5A (LTA) has a pore diameter of 4.5 Å, and propane molecules diffuse through it despite the presence of extra‐framework cations.13 Molecular dynamics (MD) studies have predicted differences of several orders of magnitude in the diffusion coefficients for small pore‐size variations around the kinetic diameters of the diffusing molecules.14 The very high differences predicted by these studies can be partially attributed to the use of rigid‐framework models in the MD simulations. It is well known that when the atomic coordinates of the framework atoms are allowed to vary during the simulation, that is, a flexible‐framework model is used, the sensitivity of the diffusion coefficients to the pore size around the critical value decreases, although it remains high.14, 15 Despite progress in this area, there are still several unclarified points about the physical processes that determine alkane diffusivity in zeolites with pore openings similar to the guest molecular size. For example, in a recent paper16 the diffusion of linear hydrocarbons, from methane to butane, has been studied at a theoretical level by means of transition path sampling, a technique that makes use of transition state theory (TST) to calculate the diffusion activation energies. This is a valuable method to study diffusion in slow‐motion systems, but it does not take into account the effects of molecule–molecule interactions on diffusion.17 On the other hand, previous studies that consider zeolites with different pore diameters, have used solids with different topologies,12, 15 which makes it difficult to isolate the effect of pore windows size on the diffusion behavior.

For the present work, the choice of two systems with the same topology and slightly different pore sizes (SiGe‐ITQ‐29 has nearly circular pores of 4.23 Å×4.28 Å, while Si‐ITQ‐29 has slightly narrower pores of 3.95 Å×4.17 Å),7 appeared as optimal for investigating the effects described above. We chose to study the diffusion of C3 hydrocarbons on ITQ‐29 zeolites using MD simulations, in order to overcome the stated limitations of TST‐based approaches. In addition, the ability of MD simulations to capture anharmonic vibrations, and eventually large distortions of the pore windows, is an important advantage when modeling diffusion in these systems. While the original focus of our research was on critical pore‐size effects, in the course of this study we found that the presence of Ge in the ITQ‐29 framework had an unexpected impact on molecular diffusion, driven by the flexibility that it conferred to the structure. Since this effect has not been identified so far, and considering the importance it can have in the design of zeolites that exploit this flexibility for advanced applications, we have explored this phenomenon in detail. Then, this report focuses on the elucidation of the role of Ge in the flexibility of Ge‐bearing ITQ‐29. The adsorption and diffusion simulations have been performed to study the impact of Ge on the zeolite flexibility and its concomitant effect on molecular diffusion.

It is interesting that the role of framework flexibility on molecular transport was anticipated early on by Barrer and Vaughan18 as the most likely explanation for the adsorption of molecules with kinetic diameter larger than the pore entrance of the zeolites. Experimental results published during the last few years on trap‐door or gate behavior of zeolite pore windows and its impact on molecular sieving19 have triggered a renewed interest in zeolite flexibility. For example, a recent study combining Monte Carlo, energy minimization and MD techniques allowed a detailed description of the complex behavior of the highly flexible zeolite RHO.20 Based on information gained by simulations with no symmetry constraints, the impacts of the nature of the extra‐framework cations, temperature and degree of hydration on the size of the pore windows of the zeolite were determined and associated to the nano‐valve effect of this zeolite in molecular sieving. In this scenario, computer modeling, supported by experimental results, can provide relevant insight into the role of Ge atoms in the dynamic flexibility of zeolites.

Results and Discussion

Samples of both pure Si‐ITQ‐29 and SiGe‐ITQ‐29 were prepared with similar average crystal size of approximately 3 μm, as estimated from scanning electron microscopy (SEM) images (Figure 1 a and b). In order to experimentally verify that the enhanced diffusion is mainly attributable to changes that have occurred in the bulk of the solids (the presence of Ge atoms) a sample of SiGe‐ITQ‐29 having a much smaller crystal size (average 0.6 μm) was also prepared (Figure 1 c). The crystals in the two Ge‐containing samples have different average sizes but similar morphologies, which are also similar to the morphology of the pure silica crystals, as can be seen in the SEM images in Figure 1.1

Figure 1.

SEM micrographs of synthesized samples of: a) Si‐ITQ‐29 with average crystal size of 3 μm, b) SiGe‐ITQ‐29 with average crystal size of 3 μm, and c) SiGe‐ITQ‐29 with average crystal size of 0.6 μm.

We performed uptake kinetics experiments to study the diffusion of propane through these samples, in particular focusing on the diffusivity parameter (D/r ²).21 Figure 2 reveals that in Ge‐containing ITQ‐29 samples the diffusivity parameter of propane was not affected by the size of the crystals. A substantial difference is found, however, with respect to the kinetics of propane diffusion in pure Si‐ITQ‐29, which is significantly lower. These results suggest that the speed‐up in diffusion upon Ge incorporation is not due to differences in the rate of external surface diffusion. A possible explanation could be that pore‐blocking defects are present and affecting the diffusion in pure‐Si‐ and SiGe‐ITQ‐29 zeolites differently. However, this does not seem to be the case, based on our study of Si‐ITQ‐29 by means of ²⁹Si‐MAS‐NMR spectroscopy for measuring the concentration of silanols. The ratio of the integrated intensities of the resonances at −113 (Q ₄) and at −100 (Q ₃) is 0.985. This indicates that this sample is essentially defect‐free, as seen in previous work.22 Unfortunately, the calcined SiGe‐ITQ‐29 is not stable upon exposure to ambient moisture, and therefore quantitative ²⁹Si‐MAS‐NMR spectroscopy experiments cannot be carried out for a proper comparison. But from the present results it is already clear that the slower diffusion in the pure‐Si sample is not due to defects. Thus, from the overall analysis of the experimental results, we conclude that diffusion in these samples takes place predominately through the internal micropores, and it is not significantly affected by defects or by external–surface diffusion. Consequently, the molecular simulations showed in the following only deal with intracrystalline molecular diffusion.2

Figure 2.

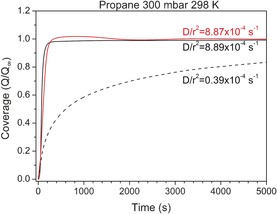
Propane uptake kinetics in ITQ‐29 zeolites with different crystal sizes and compositions. Red solid: SiGe‐ITQ‐29 with 3 μm crystal size; solid black: SiGe‐ITQ‐29 with 0.6 μm crystal size; black dashed: Si‐ITQ‐29 with 3 μm crystal size.

Prior to the computational study of the effect of Ge atoms in the flexibility of ITQ‐29 type zeolites and the diffusion and adsorption behaviors, we present and discuss the incorporation of Ge into the frameworks. Since ITQ‐29 zeolites have just one tetrahedral site in the asymmetric unit cell, we would not expect any significant degree of ordering in the Ge incorporation into the framework, in contrast with what has been observed upon incorporation of heteroatoms in zeolites with symmetrically distinct tetrahedral sites.23 Thus, we employed the SOD code24 to generate 100 Si–Ge configurations that were not symmetry‐equivalent. The Si/Ge ratio was set to 2.4:1, similar to that of the experimental samples. This ratio was achieved by using a unit cell with 17 Si and 7 Ge atoms. In order to consider the possible effects of the Ge–Ge interactions, a wide range of Ge–Ge distances were explored, including those having multiple Ge atoms condensed in the same double‐4‐MRs. This is similar to what has been previously done for Al‐containing zeolites.25 The ion positions and cell parameters of the as‐built structures were then fully optimized, by means of electronic structure calculations performed with VASP.26

Upon energy minimization, the cell parameters of the relaxed configurations do not show any significant differences among the different structures (the differences are all lower than 3 %). This can be regarded as evidence of static flexibility of Ge atoms, which can adopt a range of local environments at low energetic cost. We cannot carry out ab initio MD simulations of the 100 configurations because the computational cost would be prohibitive, so we selected three configurations that cover the whole range of structures likely to appear experimentally: a) the most stable structure, b) a structure the energy of which is the highest (less stable) out of the 25 % most stable structures, c) and one structure the energy of which is the highest out of the 50 % more stable structures. These structures are labeled as S1, S2 and S3, respectively. The Ge‐free structure, Si‐ITQ‐29, has been labeled as S0. All their crystal structures are supplied in the Supporting Information. The energy differences between the configurations are rather small, just 0.012 eV per tetrahedron, which suggests that the distribution of Ge atoms is largely disordered. The calculated average T−O distances and cell volumes of SiGe‐ITQ‐29 are larger than those of Si‐ITQ‐29, in agreement with experimental results (Table 1).1

Table 1.

Geometric parameters of simulated and experimental ITQ‐29 zeolites. Cell volume; T−O mean distance (T=Si, Ge); pore volume (PV) per unit cell; surface area (SA) per unit cell. The values of PV and SA obtained in the simulations are computed using He and N₂ probe molecules, respectively. The experimental Si/Ge ratio of SiGe‐ITQ‐29 is 2.4.^[a]

	S0	S1	S2	S3
cell volume [Å3]	1692	1771	1744	1744
T−O mean distance [Å]	1.62	1.67	1.67	1.67
pore volume [Å3]	685.3	776.4	759.0	760.5
surface area [Å2]	236.1	250.8	245.8	244.6
	Exp. Si‐ITQ‐29		Exp. Ge‐ITQ‐29
cell volume [Å3]	1668		1734
T−O mean distance [Å]	1.60		1.62
pore volume [Å3]	765		801
surface area [Å2]	158		171

[a] Pore volume and surface area are given in absolute values per unit cell, that is, ų and Ų, respectively, in order to allow for a direct comparison between the samples, due to the large mass difference between Si and Ge atoms.

It is worth noting that despite the fact that the individual Ge−O distances are 10 % larger than Si−O distances (1.74 vs.1.60 Å), the overall structure of SiGe‐ITQ‐29 is very similar to that of Si‐ITQ‐29 (Figure 3). This is due to the smaller T‐O‐T angles in the presence of Ge, which allows absorbing the distortions “locally”, without large distortions beyond the GeO₄ tetrahedra, as shown in Figure 3. This is in line with the calculated energy dependences on T‐O‐T angles (T=Si or Ge) in cristobalite and zeolites, which show that angles having Ge atoms can be much lower than the analogous Si‐O‐Si at very low energetic cost.27, 3

Figure 3.

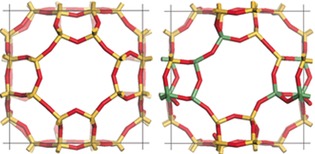
Unit cells of modeled Si‐ITQ‐29 (left) and the configuration S1 of SiGe‐ITQ‐29 (right). Atom color labels: O red, Si yellow and Ge green. We show the largest structural deformation in both cases.

The pore volume of SiGe‐ITQ‐29 zeolites (both in experiment and simulation) is slightly larger than that of Si‐ITQ‐29. This fact alone would mean that a less negative value of adsorption heat should be expected for the Ge‐containing zeolites. However, there is a competing effect, since the polarizability of Ge⁴⁺ is twice that of Si⁴⁺.28 It is then expected that small molecules will be adsorbed with similar strength in both frameworks, perhaps even slightly favoring the adsorption in SiGe‐ITQ‐29 zeolites, since the large difference in polarizability is likely to dominate. This is what both calculated and experimental adsorption heats and Henry's constants reflect (Table 2): the guest molecules are attracted more strongly by the SiGe‐ITQ‐29 frameworks. In this context, we stress that for the correct description of this effect, it is essential to introduce a correction in the interatomic potentials to account for the larger dispersion interaction of Ge, as compared to Si, with the molecules (see details in Experimental Section). Neglecting this correction, the calculated heats of adsorption in SiGe‐ITQ‐29 are smaller than those in Si‐ITQ‐2

Table 2.

Experimental and calculated heats of adsorption, Q _st [kJ mol⁻¹] and Henry's constants, K _H [mol (kg Pa⁻¹)⁻¹×10⁴], of propane in ITQ‐29 zeolites.

	S0	S1	S2	S3
Q st	−26.3	−27.1	−27.5	−27.6
K H	1.78	2.07	2.37	2.41
	Exptl Si‐ITQ‐29		Exptl SiGe‐ITQ‐29 (Si/Ge=2)
Q st	−21.2		−27.4
K H	2.42		3.85

Since the geometric hindrance towards diffusion within the structures is not very different, an analysis based on a static picture of the systems would predict that the molecules diffuse more slowly in SiGe‐ITQ‐29 where they are bound more tightly. However, the experimental findings show the opposite, that is, the diffusion parameters (D/r ²) of propane in Si‐ITQ‐29 and SiGe‐ITQ‐29 are 0.4×10⁻⁴ and 8.9×10⁻⁴ s⁻¹, respectively, as shown in Figure 2. Considering that the enhanced diffusion experimentally observed in SiGe‐ITQ‐29 cannot be explained based on the analysis of the adsorption energies and static structural data, we will center our attention on the dynamic features of the solids. First, we study the intrinsic dynamics of the frameworks, that is, the dynamics of the frameworks without adsorbate molecules. To do this, we have chosen ab initio molecular dynamics (AIMD) simulations, as implemented in VASP. These simulations are computationally very expensive, but they are able to provide a reliable view of the dynamic behavior at an atomistic level, with an accurate description of framework deformations.

The simulation performed for Si‐ITQ‐29 reveals the typical behavior of most zeolites, with all atoms vibrating around their equilibrium positions, the vibrations of the O atoms being more pronounced than those of Si atoms. However, the behavior is remarkably different in SiGe‐ITQ‐29, where the deformations of the windows are so large that the pores show a breathing‐like behavior, as can be seen in the snapshot of Figure 3 (right). The full movies of the simulations are supplied as Supporting Information.

In order to quantify the framework structural changes related to the diffusion paths, we consider the 8‐member rings (8‐MR) of the zeolites. Histograms of the area of these 8‐MRs, as well as histograms of their minimum aperture, are shown in Figure 4. Analysis of the behavior of the different frameworks reveals that a common feature of the three Ge‐containing zeolites is that the width of the curves of the minimum aperture is about 0.4 Å higher than in the pure silica counterpart. This cannot be explained on the basis of the slightly larger cell parameters of SiGe‐ITQ‐29, and this is therefore an indication of the flexibility induced by the presence of Ge atoms. Moreover, the detailed features vary from one solid to another, which indicates that the distribution of Ge within the framework has an impact on this behavior. It is worth noting that, while S0, S1 and S3 have minimum apertures of similar size (ca. 3.95 Å), the minimum aperture of S2 is 0.2 Å lower. The window area is also an important structural feature related with molecular transport. The areas of the windows observed during the simulations are around the values found for the corresponding minimum energy structures (Figure 4, right), which are represented by vertical bars. S1 and S3 exhibit distributions of areas wider than that of S0, again suggesting that they display a larger flexibility. The average areas for the Ge‐containing zeolites are very similar, and they are larger than that for Si‐ITQ‐29. In order to understand why the relative ordering of the window apertures is different from the ordering of the widow areas we have to consider the flexibility of the structure, which induces a degree of instantaneous ellipticity of the Ge‐containing zeolites.4

Figure 4.

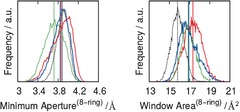
Histograms of the minimum aperture of 8‐MRs (left) and window area of the 8‐MRs (right), obtained from the AIMD simulations. Color code: S0 dashed black, S1 red, S2 green, and S3 blue. Vertical lines show the corresponding values for rigid models.

The observed structural differences affect the probability of intercage molecular crossing, as they can induce a large difference in the energy barrier for intercage hops.29 The joint analysis of Figure 3 and Figure 4 suggests that the Ge‐imprinted flexibility could be exploited to make a molecular sieving valve that might be useful for a number of separation processes. It is important to consider that experimentally the features of the windows are likely to be a blended behavior of those shown in Figure 4, as a consequence of the disorder in the distribution of Ge atoms, which would increase the flexibility of Ge‐bearing zeolites.

Since the calculation of diffusion coefficients requires very long simulation times and larger simulation cells, AIMD simulations are not adequate to this purpose. Therefore, we use classical MD simulations, as implemented in the RASPA code,30 to model methane and propane diffusion. In this way, a simulation time of 20 ns was achieved. Attention was paid to the choice of the forcefields used, as this is an important point for obtaining a realistic picture of the phenomena that take place in the systems, particularly for tight diffusion processes in nanopores, as has been recently pointed out by O'Malley and Catlow.31 In a recent study, it was reported that propane diffusion at 300 K in Si‐LTA was very slow.16 While the diffusion coefficient could not be computed directly by MD in their study, the authors used the transition path sampling method and obtained values of D of around 10⁻¹³ m² s⁻¹. In contrast to our experimental results and those reported in other experimental and theoretical studies,12, 15 they found that propene diffuses more slowly than propane in this zeolite. In this work, we studied the diffusion using MD simulations using both rigid frameworks and fully flexible forcefields. It is known that computing the diffusion coefficients in pure silica zeolites using rigid framework models yields values that are much lower than those obtained when framework atoms are allowed to move.29a, 32 We include here the results of the simulations with rigid frameworks, as a complementary element to show how the presence of Ge influences the dynamics of the diffusing molecules, by affecting both the host–guest interactions and the framework flexibility. The common understanding of linked adsorption–diffusion processes would lead to the prediction of a higher diffusivity in the pure silica zeolite (S0), considering that the heats of adsorption in SiGe‐ITQ‐29 zeolites are higher than in Si‐ITQ‐29. However, the opposite case would be expected if we considered the static picture of the systems, since Ge‐containing zeolites have larger pore window areas, which would suggest that diffusion is faster in Ge‐bearing ITQ‐29 zeolites. It is therefore not possible to predict what results the MD simulations will yield.

Efforts to compute diffusion coefficients of propane in ITQ‐29 zeolites using rigid framework models in our classical MD simulations failed to offer reliable data, due to the very slow diffusion; that is, diffusion coefficients at these conditions are lower than those currently attainable by this technique. However, the use of flexible framework models at temperatures above 450 K does allow us to compute the diffusion coefficients from the linear diffusive regime region of the mean square displacement (MSD) curves. In Figure 5 (left), we show the MSD curves of the simulations performed at 450 K for the four systems (S0–S3). Before comparing simulations and experiments in the context of diffusion, it is worth noting that our experiments measure the molecular uptake at a macroscopic scale, which provides a reliable characterization of the diffusion performance.21 However, we can still compare simulation and experiment by calculating the ratios between computed and measured values, for the different materials.5

Figure 5.

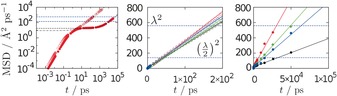
Mean square displacement (MSD) as a function of time, for methane (open symbols) and propane (solid symbols) in S1 at 450 K. We can identify four diffusion regimes for both compounds.33 Center and right: MSD as a function of time for methane (center) and propane (left) in S0–S3. We show the linear regressions for the MSD in the IV‐regime for both compounds. Diffusivity coefficients have an error of less than 0.5 % in the case of methane and less than 3 % in the case of propane. Color labels: S0 black, S1 red, S2 green, and S3 blue. We have added, as horizontal dashed‐blue lines, the values of (λ/2)² and λ ², where λ is the distance between the centers of consecutive cages; λ can be regarded as a reference for the distance of molecular transit between cages.

As mentioned above, it is not possible to study the diffusion of propane in rigid zeolite framework models using MD for ITQ‐29 zeolites. Since our main goal is to show the impact of the Ge atoms in the flexibility of the framework as the source of the enhanced diffusivity, simulations with rigid frameworks are desirable. We want to show that the computed, much larger, diffusion coefficients are not associated to the well‐known observation in simulation studies of faster diffusion when passing from rigid to flexible framework models. We use here methane as molecular probe for this purpose. The experimentally determined diffusivities and the theoretically computed diffusion coefficients of methane and propane in ITQ‐29 zeolites are presented in Table 3.3

Table 3.

Computed diffusion coefficients [m² s⁻¹×10⁻⁸] of methane and propane in modeled ITQ‐29 zeolites, and diffusivity [s⁻¹] of propane in experimental samples.

Modeled, rigid framework[a]
	S0	S1	S2	S3
methane	2.49	2.13	1.22	1.89
propane	–	–	–	–
Modeled, flexible framework[a]
	S0	S1	S2	S3
methane	5.01	6.48	5.62	5.69
propane	0.0083	0.0310	0.0187	0.0149
Experimental (10−4)[b]
	Si‐ITQ‐29		SiGe‐ITQ‐29 (Si/Ge=2)
propane	0.4		8.9

[a] Modeled at 450 K. [b] Experimental D/r ² parameter at 298 K and 300 mbar.

The experimental findings demonstrate that diffusion in Ge‐bearing materials is much faster than in the pure silica zeolite. In contrast with this experimental result, the simulations performed using rigid frameworks show higher methane diffusivities for the Si‐ITQ‐29 zeolite. So, in this scenario of rigid framework, the higher host–gest attractive interactions induced by the much larger Ge polarizability in SiGe‐ITQ‐29 has a larger effect than that caused by the decrease of the geometrical hindrance for diffusion in Si‐ITQ‐29. On the other hand, the simulations carried out using a non‐rigid framework are in agreement with experiment, showing faster diffusion in SiGe‐ITQ‐29, which confirms the role of Ge atoms in imprinting dynamic flexibility to the framework. It should be noted that, in our simulations of methane diffusion in pure silica zeolite, the ratio between the diffusion coefficients calculated with the non‐rigid and rigid framework models is about 2. However, for SiGe‐ITQ‐29 this ratio is in between 3 and 4.6, which indicates that the calculated enhanced diffusion is due primarily to the greater flexibility induced by the Ge atoms. The ratio between the computed diffusion coefficients of germanium‐containing and pure‐silica ITQ‐29 zeolites (Table 3) is between 1.8 and 3.7, while the experimental ratio of the diffusivities is 22.2. To find a rationalization for this discrepancy, the first point to address is that in Table 3 the theoretical data were calculated at 450 K, since the much slower diffusion at 300 K would require extremely long simulation times, while experiments were conducted at room temperature. We then performed MD simulations at different temperatures, in order to extrapolate the data for S0 and S1 to room temperature, by using an Arrhenius‐type dependence of the diffusion coefficients (shown in Supporting Information). The estimated ratio thus obtained at room temperature is 15.0, which compares reasonably well with the value of 22.2 obtained experimentally.

Conclusions

Our combined experimental and theoretical study has been successful in showing that the presence of Ge atoms in zeolites confers flexibility to the frameworks, not only by favoring the formation of small rings, as it is well known in synthetic chemistry, but also by incorporating dynamic flexibility to the framework, which results in extensive, breathing‐like pore behavior. This effect has a direct impact on molecular diffusion, and in the case of the zeolite framework type LTA we observe an enhancement of the diffusion coefficient by at least a factor of 3. Based on the consideration of the frameworks’ “breathing dynamics” picture, our findings can actually explain a number of observations that were in contradiction with the traditional picture, where the description of the dynamics of the flexible frameworks is based on the oscillating atomic movements around equilibrium positions. In particular, we have shown that large pore window deformations, which are linked to the breathing dynamics, lead to faster diffusion in SiGe‐ITQ‐29 compared the pure silica ITQ‐29, despite the fact that diffusing molecules are attracted more strongly to the zeolite framework in the presence of Ge. We expect that this study will open new avenues towards a more precise control of molecular diffusion speed in zeolites, which could also optimize their performance in areas of practical interest, including catalysis and adsorption.

Experimental Section

The initial lattice parameters and atomic coordinates employed in our simulations were taken from the experimental structure.7 The number of atoms in the simulation cell was 72, of which 24 are Si atoms and 48 are O atoms. The replacement of seven Si atoms by Ge atoms to reach a Si/Ge ratio of 2.4 was considered in the calculations, in order to approach the experimental composition (Si/Ge=2.2). Obtaining a closer agreement would require an increase of the simulation cell that would make the quantum mechanical calculations infeasible. Nevertheless, we believe that the very small mismatch will not alter the conclusions obtained here. Due to the high symmetry of the LTA framework, 100 different Si/Ge configurations were constructed for considering a wide range of local structures. The SOD code24 was used to guarantee that non‐symmetry equivalent configurations were selected. The configurations were then fully relaxed by means of density functional theory (DFT) calculations. All DFT calculations (both geometry optimizations and ab initio molecular dynamics) were carried out with the VASP program,26 which uses periodic boundary conditions. The simulations were performed using the PAW potentials,34 with the PBEsol exchange‐correlation functional,35 taking into account the van der Waals interactions with the DFT‐D2 method of Grimme.36 Considering the large size of the unit cell (cubic system with a lattice parameter of ca. 11.9 Å), the simulation cell for the DFT simulations was composed of only a single unit cell. This was also large enough to allow the use of just the gamma point for sampling the Brillouin zone. The energy cut‐off for the plane‐wave expansion of the wave‐functions was 400 eV. The AIMD simulations were run for 40 ps, with a time step of 1 fs, computing the results for the last 30 ps.

The calculation of the adsorption properties and classical molecular dynamics simulations were carried out in full atomistic detail with the RASPA code.30 The silica‐hydrocarbon interactions were modeled using calibrated classical forcefields.37 The polarizability of Ge cations is twice that of Si cations,28 which has an effect on the long‐range van der Waals host–guest interactions. In the forcefield developed by Calero et al., the contributions of the Si atoms to the van der Waals interactions are embedded into those of the oxygen atoms.37 Therefore, we added the additional individual contribution arising from the Ge ions, based on the C₆ formula by Grimme.36 We have thus the Ge*−CH₄, Ge*−CH₃ and Ge*−CH₂ interaction parameters, described as (sigma, epsilon) Lennard–Jones potentials with parameters (3.97, 41.00), (3.98, 37.293) and (4.02, 25.565), respectively. Sigma and epsilon are expressed in Å and K, respectively. Note that the * on the Ge indicates that the strength of the interactions only covers the surplus with respect to Si, to avoid double counting, since the parameters for oxygen are already enlarged to include the contribution from the silicon atoms. For the molecular dynamics simulations, framework flexibility was considered using the forcefield developed by Nicholas et al.38 This is a valence forcefield, which allows a simple modification to incorporate the Ge contribution, by considering Ge−O distance of 1.74 Å, an equilibrium distance obtained from our DFT results. Molecular dynamics simulations were conducted in the NVT ensemble, using a time step of 1 fs. Since the pore windows of ITQ‐29 zeolites are close to the molecular size of the diffusing molecules (methane and propane), a long simulation time was used (20 ns) to allow the accurate computation of the diffusion coefficient by the Nerst–Einstein relation. The equilibration time was set to 1 ns.

The syntheses of Si‐ITQ‐29 and large crystals of SiGe‐ITQ‐29 zeolites were performed as described in reference 7. Small crystals of SiGe‐ITQ‐29 zeolite were obtained by seeding the synthesis gel with previously obtained SiGe‐ITQ‐29. In this case the autoclave was heated up to 398 K in rotating conditions. Kinetic measurements of propane adsorption were performed in an IGA‐3 gravimetric analyzer (Hiden Isochema). Approximately, 50 mg of the sample were placed in the balance. Due to the lack of stability of the calcined Ge‐containing LTA zeolite upon exposure to ambient moisture, the sample was calcined in situ inside the IGA‐3 thermobalance, under dry O₂/He=20:80 flow at 823 K for 5 h. The Si‐ITQ‐29 sample was calcined at 973 K in ambient air in a muffle furnace for 5 h. Before each adsorption experiment, the sample was outgassed at 673 K under a final pressure lower than 10⁻⁴ mbar, during four hours. Diffusional studies were performed at 300 mbar and 298 K, and the gas uptake was continuously monitored versus time.

When crystals are not of uniform size and geometry, as it is our case regarding size, the diffusion ability of a particular gas or vapor within a porous crystalline material is usually measured in terms of their characteristic D/r ² values. In this parameter, D is Fick's diffusion coefficient and r is the averaged radius representative of their crystal size, assuming spherical particles. D/r ² can be derived from adsorption kinetic measurements by using the first 20 terms of the Crank solution for diffusion:39

$$\frac{Q}{Q_{\infty }}=1-\frac{6}{{\pi }^2}\sum _{n=1}^{\infty }\frac{1}{n^2}exp\left(-n^2{\pi }^{2}t\frac{D}{r^2}\right)$$ (1)

where Q represents the gas uptake at a time, t, and Q _∞ is the uptake at equilibrium.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supplementary

Supplementary

Supplementary

Supplementary

Supplementary

J. J. Gutiérrez-Sevillano, S. Calero, S. Hamad, R. Grau-Crespo, F. Rey, S. Valencia, M. Palomino, S. R. G. Balestra, A. R. Ruiz-Salvador, Chem. Eur. J. 2016, 22, 10036.