Computer‐Aided Production of Scaffolded DNA Nanostructures from Flat Sheet Meshes

Abstract

The use of DNA as a nanoscale construction material has been a rapidly developing field since the 1980s, in particular since the introduction of scaffolded DNA origami in 2006. Although software is available for DNA origami design, the user is generally limited to architectures where finding the scaffold path through the object is trivial. Herein, we demonstrate the automated conversion of arbitrary two‐dimensional sheets in the form of digital meshes into scaffolded DNA nanostructures. We investigate the properties of DNA meshes based on three different internal frameworks in standard folding buffer and physiological salt buffers. We then employ the triangulated internal framework and produce four 2D structures with complex outlines and internal features. We demonstrate that this highly automated technique is capable of producing complex DNA nanostructures that fold with high yield to their programmed configurations, covering around 70 % more surface area than classic origami flat sheets.

Since its introduction in the 1980s,1 DNA nanotechnology has been a rapidly growing and diversifying field. This growth has accelerated since the introduction of scaffolded DNA origami in 2006.2 In a DNA origami structure, a long strand, called the scaffold, traverses the entire structure pairing with hundreds of oligonucleotides, called staple strands, that hold the structure together. The structures are often based around a square or honeycomb lattice3 where finding the scaffold path and designing staples is relatively easy, especially when using software like caDNAno.4 DNA nanostructures based on small polyhedra have been demonstrated with both scaffolded5 and non‐scaffolded6 designs. Scaffolded DNA nanostructures based on meshwork designs have also been demonstrated with crossing four‐arm junctions,7 with others containing meshes with two DNA double helices per edge.8 However, no general strategy for producing arbitrary wireframe 2D structures has been demonstrated.

A major branch of research has been the addition of functional elements to DNA nanostructures to give them novel properties. Carbon nanotubes and metal nanoparticles have been added for electronic9 and plasmonic10 applications. Proteins have been added for templating enzymatic reactions11 or cell signaling studies.12 Fluorophores have been added to study energy transfer13 and to create nanoscale barcodes.14 DNA origami structures have also been used to control the shape of metal particles15 and graphene sheets.16 Demonstrations of drug loading17 and lipid encapsulation18 indicate that DNA nanostructures could serve as drug delivery tools. Many applications rely on single layer DNA objects as they offer the largest 2D canvas for functionalization and are rigid when immobilized on surfaces.

Building on Rothemund's method2 for scaffolded DNA nanostructures, we recently developed a method for automatically generating wireframe structures from polyhedral meshes.19 This method relies on an algorithm for finding an Eulerian scaffold path through the mesh and then automatically generating the staple strands needed for folding the structure. For the algorithmic process to work, the method was previously restricted to inflatable meshes (that can be smoothly transformed into a ball); herein we expand this method to allow the generation of scaffolded DNA nanostructures from arbitrary 2D meshes. We first generate rectangular meshes based on the three regular tessellations (the tiling of a plane with one or more repeating polygons) and investigate their properties with AFM. Then, we use the triangulated 3‐tesselation to generate four DNA designs from 2D meshes.

In the pipeline, the mesh is first reconditioned to remove odd degree vertices (those with an odd number of incident edges) by the introduction of double edges,20 meaning that in the final design, some edges may be converted into two parallel double helices. This is necessary since it is not possible to find an Eulerian circuit scaffold routing through a mesh with odd degree vertices.21 Next, a routing algorithm finds an A‐trail22 route through the mesh, visiting all edges once (except for the double edges) and transiting at the vertices by only exiting on an edge that is a cyclical neighbor to the entering edge (i.e. never crossing across the vertex). A‐trail routing ensures that the scaffold routing does not cross at the vertices and that the designed scaffold path is not knotted.19

After a scaffold route has been found through the mesh, a first approximation of the DNA design is created as a set of rigid cylinders representing the DNA helices connected by springs. This model is simulated in a physical simulation engine19 and the strain of all springs is calculated. Then, the lengths of the edges are iteratively modified to minimize the strain of the springs. When this has finished, the structure is imported to vHelix,28 our custom plug‐in for Autodesk Maya for staple design and export.

The A‐trail routing algorithm requires as input the local order of rotation of edges around the vertices, and for polyhedral graphs, this order can be obtained uniquely using a planar embedding algorithm.23 However, multiple planar embeddings may exist for the graph of a flat sheet (see Figure S1 in the Supporting Information). These embeddings will not share the cyclic ordering of edges in all vertices, and an A‐trail route found in one embedding may not be an A‐trail route for another embedding (see Figure S2). On the other hand, we can fetch the correct local rotation from the face descriptions in the mesh description file (PLY, see below) when the following two conditions are met: 1) all the faces must be described with a consistent orientation, either clockwise or counter‐clockwise, as viewed from one side; 2) the design should not contain any vertex with two incident holes (for example, if two holes of the three‐hole disc in Figure 1 shared a common vertex). We have now implemented a new algorithmic pipeline, described in detail in the Supporting Information, incorporating these changes to also allow flat sheets to be used as an input.

Figure 1.

Example pipeline for the production of a 2D DNA structure from a mesh. A) First, an arbitrarily sized mesh (gray) is created in a 3D graphics software program. From this canvas, the desired mesh (red) is produced by deleting the extra edges and vertices. B) The edges and vertices of the mesh can then be remodeled to create the desired shape. C) An uninterrupted scaffold path through the mesh is then found algorithmically. D) A physical simulation where the DNA helices are represented by rigid cylinders connected by springs is used to generate a DNA model with minimized internal tension. E) This DNA model is imported to vHelix where the final DNA staple design and sequences are generated.

As demonstrated in Figure 1, meshes can be easily created in 3D graphics software. If a mesh with a complex outline and/or complex internal features is required, a large regular mesh can first be created as a canvas. The user can then sculpt the desired mesh by deleting faces from the larger canvas mesh. Standard modeling functions such as extrusions can be used to add extra features to the mesh. In combination with this, the user can move vertices and rescale faces or edges to fine tune the mesh that will template the DNA design. Next, the user exports the mesh to the PLY format and our software28 automatically finds a scaffold route through the mesh and creates a DNA model with minimal tension. The size of the final DNA model is determined by a user specified scaling value.28

First, we investigated the effect of varying the vertex geometries by producing rectangular structures with different internal tessellations. A tessellation where the geometry of every vertex is identical is called a regular tessellation. Only three regular tessellations exist: the 6‐tesselation, consisting of a honeycomb tiling of hexagons, the 4‐tessellation, consisting of a tiling of squares, and the 3‐tesselation, consisting of a tiling of triangles. In these tessellations, the number of edges entering every vertex, or the vertex degree, is identical for all vertices: three for the 6‐tessellation, four for the 4‐tessellation, and six for the 3‐tesselation. This means that the different tessellation will have different vertex degrees and different vertex geometries. Because it is not possible to find a scaffold routing in a mesh containing odd degree vertices, this means that the 6‐tessellation will have its vertices converted into four‐degree vertices by the introduction of double edges. Despite this, the three different tessellations give rectangular sheets with clear differences of internal structure as is visible in Figure 2.

Figure 2.

DNA 2D sheets based on regular tessellations. A) Internal frameworks of DNA 2D structures based on the 6‐tesselation (left), 4‐tesselation (center), and 3‐tesselation (right). Insets: full design structures (drawn to scale). B) 2×2 μm field‐of‐view AFM images of the structures folded with 10 mm MgCl₂. C, D) 250×250 nm AFM images of the structures folded with 10 mm MgCl₂ buffer (C) or PBS (D). E) 100×40 nm expanded portions of areas marked by boxes in (D). F) Histograms, with data measured from AFM images, where the x‐axis is area per base pair measured in nm² and the y‐axis shows the number of structures (n). Additional data provided in Figure S5 and Table S1. All scale bars=100 nm.

First, we folded the structures in a standard DNA origami folding buffer containing 10 mm MgCl₂ (see the Supporting Information for all buffer components) and assayed the folding quality using agarose gel electrophoreses (Figure S4). This assay revealed monodisperse folding with no visible aggregation. Next, we undertook atomic force microscopy (AFM) of the structures in folding buffer. This further revealed that the flat sheet structures had successfully folded into monodisperse structures with a high degree of similarity to the designs. AFM also revealed internal features of the structures, further indicating that the structures had truly folded as predicted (Figure 2).

AFM also revealed that the overall shapes of the sheets based on the 6‐ and 4‐tessellation did not fully spread out (Figure 2 C). The 6‐tesselation spread well along its long axis but did not fully stretch out along its short axis. The 4‐tesselation did not fully stretch to a regular square but instead appeared to form a rhombus shape. In the DNA designs both of these structures consist of vertices connecting four DNA double helices that is, Holliday junctions. The structure of Holliday junctions is well studied and it is known to exist in stacked or unstacked conformations.24 In the unstacked conformation (represented in Figure 2 A, center), the four DNA helices form a planar cross with right angles. This conformation is however mostly present in the absence of divalent cations. When divalent cations, like Mg²⁺, are present, the Holliday junction will tend to transition into its stacked conformation where the arms of the junctions form a 60° angle. As the structures were folded and imaged in the presence of 10 mm MgCl₂ it is not surprising that the junctions conform into this angled form, leading to a deformation of the overall shape.

Wireframe origami has been shown to fold and remain stable in buffers containing only monovalent salts;19, 25 this may be of great importance for applications where a high concentration of divalent cations is detrimental. Close‐packed origami can be folded with monovalent salts only26 but the concentrations required there are significantly higher than what can be found in physiological buffers.

We tested folding the structures in phosphate‐buffered saline (PBS), a buffer with around 150 mm Na⁺ that is commonly used in cell‐culture studies. Unfortunately, it is very challenging to perform AFM imaging on DNA origami structures in liquid without divalent salts as they form a charge bridge with the negatively charged mica leading to immobilization. We were able to image structures that were first folded in PBS and then subsequently imaged in a buffer containing 10 mm NaCl and 1–3 mm NiSO₄. This demonstrated that the structures could indeed fold in buffers containing only monovalent cations. The AFM data also seem to indicate that the 6‐tesselation, and in particular the 4‐tesselation, stretched out more, consistent with previous findings of unstacking of junctions in the absence of divalent cations.

One of the main motivations for using flat sheet nanostructures for applications is the relatively large 2D canvas offered for functionalization. However, the scaffold raster fill used in classic DNA origami flat sheets may not offer the largest possible surface coverage for a given scaffold strand. Herein, we use the AFM data to measure the areas of the new flat sheets (Figure 2; Figure S5) and compare them with a twist corrected version of the rectangle flat sheet originally published by Rothemund.2 This sheet has an average surface area of 6600 nm². The new mesh‐based flat sheets have significantly larger surface areas of 13 800, 15 100, and 12 800 nm² (absolute areas of the sheets) for the 6‐, 4‐, and 3‐tessellations, respectively. These new sheets, however, use 10–17 % more bases in their scaffold. Still, taking this into account, the mesh‐based sheets offer 70–95 % more surface area per scaffold base (Table S1). Here, the 3‐tesselation with a 70 % larger relative surface coverage may be the most relevant comparison as it folds to its programmed shape.

As the design based on the triangulated 3‐tesselation folded into its predicted shape in both buffer conditions, we used this tessellation to create four more structures with both external and internal features. First, a simple ring made from triangulated double faces and an internal diameter of circa 80 nm was designed (Figure 3 A). Inspired by the original work on DNA origami, we designed a triangulated three‐hole disc with a diameter of circa 120 nm. We also made a hand‐shaped sheet with thin finger features made from single triangulated faces, as well as a nanostructured shape representation of the map of Scandinavia, showing Norway, Sweden, and Finland, where internal helices also outline the borders between the countries.

Figure 3.

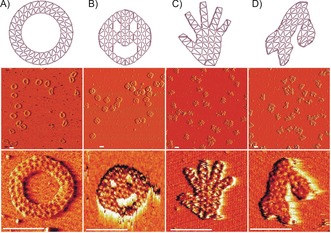
2D sheets based on a triangulated mesh. A) A ring with an inner diameter of 80 nm. B) A three‐hole disc with a diameter of 120 nm. C) A hand‐shaped mesh. D) A mesh shape with an outline representing Norway, Sweden, and Finland. Middle row: 2×2 μm field‐of‐view AFM images of the structures. Bottom row: 200×200 nm AFM images of the structures. All scale bars=100 nm.

These structures folded well into their shapes as indicated by agarose gel electrophoresis (Figure S4), which demonstrated a clean monomeric folding except for the three‐hole disc where some dimerization is seen. AFM was again employed to investigate the folding (Figure 3). As these structures contained finer features, like the fingers on the hand, than the regular sheets, some deformation can be seen in some of the meshes in AFM. However, many structures appeared well‐formed (Table S2).

In conclusion, we have demonstrated that producing 2D DNA nanostructures from meshes is a simple yet powerful method, yielding novel structures with interesting properties. We find that the rigidity of the structures is highly dependent on the meshwork design. Multiple meshworks can be combined in one mesh; this could be utilized to create structures with both rigid and flexible segments. The recent advances in the simulation27 of DNA nanostructures indicate that it may soon be possible to predict the properties of such structures. We find that triangulated meshes fold successfully to their programmed shape and at the same time give 70 % more surface coverage for a given scaffold strand compared to classic DNA origami flat sheets, and in addition can be folded and remain stable under physiological salt conditions.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supplementary

E. Benson, A. Mohammed, A. Bosco, A. I. Teixeira, P. Orponen, B. Högberg, Angew. Chem. Int. Ed. 2016, 55, 8869.