Ultraefficient thermophotovoltaic power conversion by band-edge spectral filtering

Significance

Thermophotovoltaic conversion utilizes thermal radiation to generate electricity in a photovoltaic cell. On a solar cell, the addition of a highly reflective rear mirror maximizes the extraction of luminescence, which in turn boosts the voltage. This has enabled the creation of record-breaking solar cells. The rear mirror also reflects low-energy photons back into the emitter, recovering the energy. This radically improves thermophotovoltaic efficiency. Therefore, the luminescence extraction rear mirror serves a dual function; boosting the voltage, and reusing the low-energy thermal photons. Owing to the dual functionality of the rear mirror, we achieve a thermophotovoltaic efficiency of 29.1% at 1,207 °C, a temperature compatible with furnaces, and a new world record at temperatures below 2,000 °C.

Abstract

Thermophotovoltaic power conversion utilizes thermal radiation from a local heat source to generate electricity in a photovoltaic cell. It was shown in recent years that the addition of a highly reflective rear mirror to a solar cell maximizes the extraction of luminescence. This, in turn, boosts the voltage, enabling the creation of record-breaking solar efficiency. Now we report that the rear mirror can be used to create thermophotovoltaic systems with unprecedented high thermophotovoltaic efficiency. This mirror reflects low-energy infrared photons back into the heat source, recovering their energy. Therefore, the rear mirror serves a dual function; boosting the voltage and reusing infrared thermal photons. This allows the possibility of a practical >50% efficient thermophotovoltaic system. Based on this reflective rear mirror concept, we report a thermophotovoltaic efficiency of 29.1 ± 0.4% at an emitter temperature of 1,207 °C.

Photovoltaic devices generate electricity from thermal radiation (1–6). In thermophotovoltaic energy conversion, first described (7) in 1956, photovoltaic cells convert thermal radiation from a local heat source to electricity. The key is to find a way to exploit the great majority of low-energy thermal photons that would otherwise be unusable in a photovoltaic system.

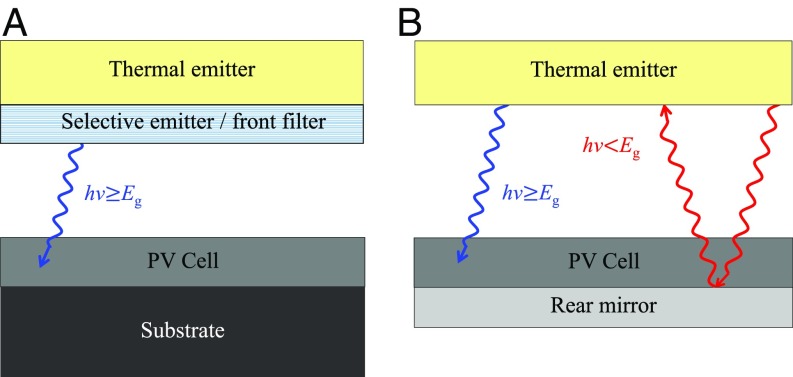
Most effort in this regard has been directed toward engineering the hot emitter, making it spectrally selective such that it suppresses the emission of low-energy photons (8, 9). In this arrangement, the spectral emissivity of the thermal source is tailored to the absorption edge of the photovoltaic cell (10, 11), as illustrated in Fig. 1A. The spectral filter has been implemented by photonic crystals (12–17), metamaterials (18–22), and rare-earth oxides (23, 24).

Fig. 1.

Increasing the efficiency of thermophotovoltaics by managing the low-energy thermal photons that cannot be absorbed by the semiconductor. There are two approaches for doing this. (A) Use a spectrally selective coating that will ideally emit high-energy photons or (B) exploit the semiconductor band edge itself as the spectral filter. The presence of a rear mirror ensures that any unabsorbed photons are reflected back to the emitter and are rethermalized.

We present a different approach. All new record-breaking solar cells now include a rear mirror to assist in the extraction (25) of band-edge luminescence from the photovoltaic cell. For high-quality photovoltaic materials, the rate of internal photon generation is high. However, in devices with poor photon management, this is typically wasted by a poorly reflecting electrode at the rear of the device. When a highly reflective mirror is inserted, a bright internal photon gas develops, maximizing the observed external luminescence flux associated with a large carrier concentration. This provides a voltage boost of ∼0.1 V at open circuit (26). Indeed, the development of a highly reflective rear mirror has been the main driver of recent efficiency records in solar photovoltaics (27–29).

Serendipitously, such a rear mirror could also reflect below-bandgap photons (Fig. 1B). Unprecedented thermophotovoltaic efficiency can be achieved by reflecting low-energy photons back to reheat the blackbody emitter, while utilizing the high-energy photons for photovoltaic electricity generation. In effect, the semiconductor band edge itself provides spectral selectivity, without the need for a spectrally selective thermal emitter. This idea, first patented in 1967 (30), relies on the reuse of low-energy photons (31), thus wasting no energy. We will call this process “regenerative thermophotovoltaics.”

Here, we present experimental results on a thermophotovoltaic cell with 29.1 ± 0.4% power conversion efficiency at an emitter temperature of 1,207 °C. This is a record for thermophotovoltaic efficiency. Our cells have an average reflectivity of 94.6% for below-bandgap photons, which is the key toward recycling subbandgap photons. We predict that further improvements in reflectivity, series resistance, material quality, and the radiation chamber geometry will push system efficiency to >50%. Such a highly efficient thermophotovoltaic system can have significant impact as a power source for hybrid cars (32), unmanned vehicles (33), deep-space probes (34–36), and energy storage (37, 38), as well as enabling efficient cogeneration systems (39–41) for heat and electricity.

The Regenerative Thermophotovoltaic System

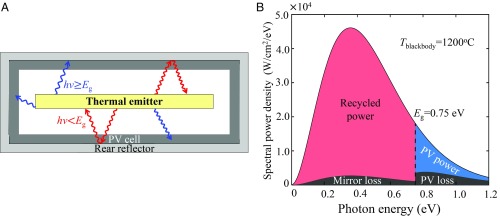
In an ideal thermophotovoltaic system employing photon reuse (Fig. 2A), a hot emitter is surrounded by photovoltaic cells lining the walls of the chamber, collecting light from the emitter. For efficient recovery of unused photons, the photovoltaic cells are backed by highly reflective rear mirrors. Such mirrors are needed, in any case, to provide the voltage boost associated with luminescence extraction. As shown in Fig. 2B, the below-bandgap recycled component of the radiated spectrum rethermalizes within the heat source after being reflected from the photovoltaic cell.

Fig. 2.

An ideal regenerative thermophotovoltaic system formed by a thermal radiation chamber, and power conversion inside the chamber. (A) High-energy (blue) photons from the emitter are converted to carriers in the photovoltaic cell, while low-energy (red) photons are reflected back to the emitter and rethermalized. (B) A highly reflective rear mirror is essential since a photon will need to be reflected many times before emerging in the high-energy tail of the Planck spectrum, for absorption in the semiconductor. Other losses in the photovoltaic cell arise due to poor material quality, as well as thermalization of high-energy carriers.

Photon reuse in this chamber—enabled by high mirror reflectivity—results in high system efficiency. The system power conversion efficiency, η, is defined (42, 43) as the electrical power generated by the photovoltaic cell, divided by the total thermal radiative power absorbed,

$$\eta =\frac{P_{\text{electrical}}}{P_{\text{incident}}-P_{\text{reflected}}}=\frac{P_{\text{electrical}}}{P_{\text{absorbed}}},$$ [1a]

where P_incident is the incident power on the photovoltaic cell, and P_reflected is the power reflected from the cell. Eq. 1a is analogous to the efficiency definition of a solar cell, except that it accounts for the fact that reflected radiation is not lost but is rethermalized at the thermal source. P_reflected is taken from the measured reflectivity spectrum of the photovoltaic cell, while P_incident is obtained from an accurate calibration of emitter temperature.

Alternately,

$$\eta =\frac{P_{\text{electrical}}}{P_{\text{absorbed}}}\hspace{0.17em}=\frac{P_{\text{electrical}}}{P_{\text{electrical}}+Q_{\text{waste}}},$$ [1b]

which is the conventional definition of heat engine efficiency, where Q_waste is the waste heat.

Eqs. 1a and 1b assume that the internal surfaces of the radiation chamber are completely covered by photovoltaic cells as shown in Fig. 2. To the extent that the internal walls are not fully covered by photovoltaic cells, the remaining area of bare walls needs excellent reflectivity to produce a good net “effective reflectivity” that controls the system efficiency.

The incident power P_incident(T_s) at an emitter temperature T_s can be defined as the incident black body radiation flux b_s(E, T_s) corrected by the spectral emissivity ε(E) of the emitter [∼0.91 for graphite (44)], integrated over energy and area,

$$P_{\text{incident}}\left(T_s\right)={\displaystyle \underset{0}{\overset{\infty }{\mathrm{\int }}}\epsilon \left(E\right)b_s\left(E,T_s\right)\cdot EdEA},$$ [2]

where E is the photon energy and A is the surface area of the photovoltaic cell. The cell absorptivity spectrum a(E), used to determine P_absorbed, which is the denominator in the efficiency expressions (Eqs. 1a and 1b), can be directly known by measuring the cell reflectivity R(E), since a(E) = 1 − R(E).

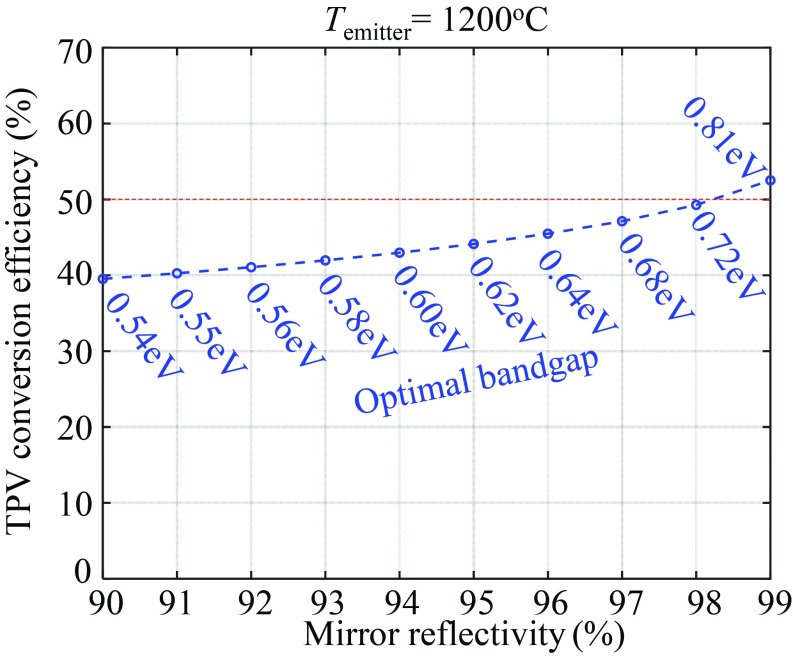
We can estimate the realistic thermophotovoltaic efficiency based on the quality of the existing III-V materials that contributed to the current record-holding solar cells. The projected thermophotovoltaic efficiency is shown in Fig. 3, which represents a realistic efficiency projection rather than ideal Shockley−Queisser (45) performance. The optimum bandgap increases slightly upon improving the rear reflectivity, to minimize thermalization losses from photons at the high-energy tail of the emitter Planck spectrum. With an optimal bandgap, thermophotovoltaic efficiency can reach as high as >50%. For these calculations, we parameterized the material quality by the internal luminescence efficiency η_int—probability that carriers undergo radiative recombination—with a value η_int = 98%. Such luminescence efficiency has been reported for GaAs (46).

Fig. 3.

Projected thermophotovoltaic (TPV) system conversion efficiency versus effective mirror reflectivity. As reflectivity rises, the optimum bandgap rises. In absence of a rear mirror, only 8.5% efficiency is possible. For this calculation, internal luminescence efficiency was assumed to be 98%, along with zero series resistance and unity emissivity.

Since the simple addition of a rear reflector can offer such high efficiencies, it is tempting to consider the possibility of combining the rear reflector photovoltaic cells, with a spectrally tuned emitter. For a spectrally tuned emitter with subbandgap reflectivity r (≡1−ε)_, and a photovoltaic cell reflectivity R, the total loss due to parasitic absorption is dependent on both of these reflectivities, as obtained through geometric progression of multiple reflections between the emitter and the photovoltaic cell,

$$a_{\text{parasitic}}=\hspace{0.17em}\frac{\left(1-r\right)\left(1-R\right)}{1-rR}.$$ [3]

We can lower parasitic absorption a_parasitic fraction by reflecting low-energy photons using rear mirror (R ≈ 1), and by suppressing emission of low-energy photons with spectral control of emitter radiation (r ≈ 1).

With R ≈ 1, the denominator of Eq. 3 becomes 1 − r, leaving the total parasitic absorptivity dependent on the quality of the rear mirror. On the other hand, if r ≈ 1, implying excellent spectral emissivity control, then the total parasitic absorptivity a_parasitic ≈ 1 − r. Hence, in the presence of excellent emissivity control, the performance is almost entirely dominated by the high thermal emitter spectral reflectivity r. Whichever of R or r is more ideal, is closer to unity, will dominate, and further improvements in the other, nondominant reflectivity, r or R will not contribute significantly. Therefore, it is sufficient to simply aim for the best rear reflectivity R, and to dispense with spectral emissivity control.

Efficiency Calibration

The purpose of this section is to validate the experimentally measured regenerative thermophotovoltaic efficiency. Under the regenerative principle, the reflected photon flux from the photovoltaic cell reheats the thermal emitter and does not count against the measured efficiency. Hence, the measurement (42, 43) of the power conversion efficiency $\eta =P_{\text{electrical}}/\left(P_{\text{incident}}-P_{\text{reflected}}\right)=P_{\text{electrical}}/P_{\text{absorbed}}$ of a thermophotovoltaic device requires measurement of the total generated power (P_electrical), the incident power P_incident, and the reflected thermal power (P_reflected) by the device.

In an absolute calibration, the numerator is the electrical power, which is straightforward to measure. However, the power absorbed is difficult to know, since it depends on multiple parameters. We now indicate how to measure the incident photon flux and the fraction of it that is absorbed.

To measure the incident photon flux, we need to know 1) the emissivity of the emitter, 2) the geometrical view factor F_eff; the fractional solid angle subtended by the emitter as viewed from the photovoltaic cell as well as the multiple reflections between the photovoltaic cell, emitter, and the baffle used in our chamber; and 3) the temperature of the emitter.

We establish methods to measure each of these parameters.

• 1)The emissivity ε of graphite was measured experimentally (details in SI Appendix), obtaining a value of ε ≈ 0.91, similar to other literature reports (44).
• 2)The geometrical view factor determines the short-circuit current from a black body. We calibrate the emitter temperature at 1,085 °C by slowly increasing the supplied electrical power until a copper bead that was previously placed on top of the emitter reaches its solid-to-liquid transition. Thus, by measuring the short-circuit current at exactly 1,085 °C, we obtain the geometrical view factor. The relationship between the short-circuit current, view factor, using Eq. 4, and Planck spectrum can be expressed:

$$I_{SC}\left(T_s\right)=qA{F}_{\text{eff}}{\displaystyle \underset{0}{\overset{\infty }{\int }}{\epsilon }_{\text{eff}}\left(E\right)EQE\left(E\right)b_s\left(E,T_s\right)dE}.$$ [4]

For calibration of F_eff, we use the black body Planck spectrum b_s(E, T_s) at a calibrated emitter temperature T_s = 1,085 °C, EQE(E) is the measured external quantum efficiency, and ε_eff(E) is the effective emissivity spectrum. (For our calculations, we use an effective emissivity ε_eff instead of using the emissivity ε of graphite to take into account multiple reflections between the cell and the emitter. The effective emissivity, ε_eff is given by ε/[1 − R(E)(1 − ε)], where the reflectivity spectrum, R(E), changes sharply when transitioning to energies above the bandgap. The emissivity difference is (ε_eff – ε)/ε = 5%, which leads to a shift of thermophotovoltaic efficiency from 29.7 to 29.1%.) From this, we extract a view factor F_eff = 0.31.

• 3)Since the above procedure calibrates the geometrical view factor, which is temperature-independent, we can then solve Eq. 4 to find the emitter temperature when T_s ≠ 1,085 °C.

Now, since we know the effective emissivity, geometrical view factor, and emitter temperature, we can accurately measure the incident flux, $P_{\text{incident}}\left(T_s\right)=A{F}_{\text{eff}}{\displaystyle \underset{0}{\overset{\infty }{\int }}{\epsilon }_{\text{eff}}\left(E\right)b_s\left(E,T_s\right)\cdot EdE}.$

We need to convert the incident spectrum to absorbed spectrum, since any unabsorbed portion of the incident spectrum will be reflected back to the thermal emitter. For this, we measure the device’s absorptivity spectrum as (1 − reflectivity), which also includes the parasitic free carrier absorption of low-energy photons. The total absorbed power in the photovoltaic device is then

$$P_{\text{absorbed}}\left(T_s\right)=P_{\text{incident}}-P_{\text{reflected}}=A{F}_{\text{eff}}{\displaystyle \underset{0}{\overset{\infty }{\int }}{\epsilon }_{\text{eff}}\left(E\right)\left(1-R\left(E\right)\right)b_s\left(E,T_s\right)\cdot EdE}.$$ [5]

With 1) emissivity calibration, 2) view factor calibration, and 3) temperature calibration, we can now accurately characterize the device thermophotovoltaic efficiency.

Experiment

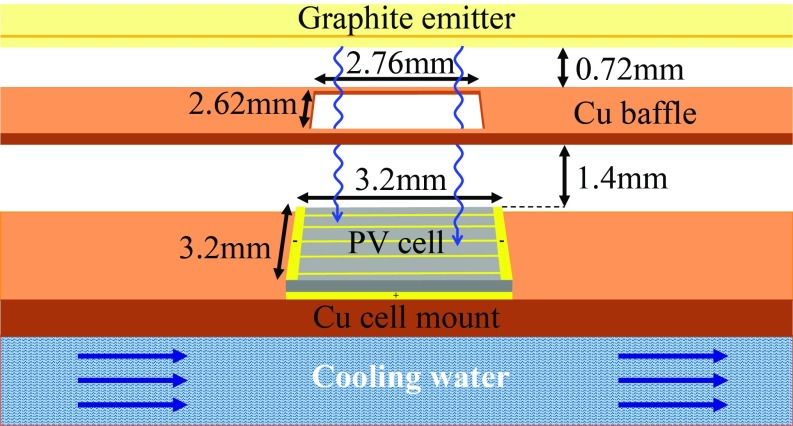
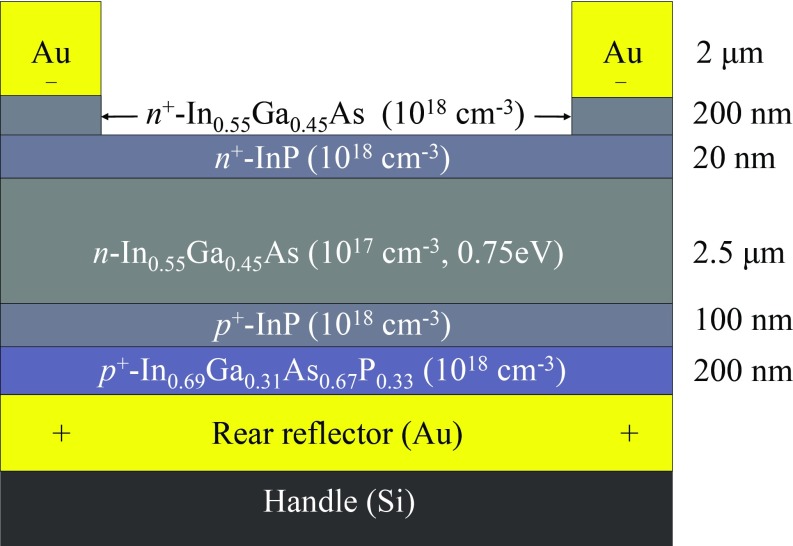
The experimental chamber used for thermophotovoltaic measurements is shown in Fig. 4. The thermal emitter is a graphite ribbon. Current is injected into the ribbon through its short ends to raise the temperature by Joule heating. Beneath the ribbon, the photovoltaic cell is placed on a copper mount using thermally conductive epoxy. For our experiment, we use an In_0.55Ga_0.45As photovoltaic cell with a bandgap of 0.75 eV, as shown in Fig. 5.

Fig. 4.

In our experiment, a planar graphite emitter is Joule-heated by a large electric current. Beneath the emitter, a copper baffle is used to limit the area of the photovoltaic cell exposed to illumination. The photovoltaic cell is mounted on a copper base, with water at 20 °C flowing through the copper mount.

Fig. 5.

The cross-section of the photovoltaic cell is shown here. The InGaAs active layer has a bandgap of 0.75 eV. The rear Au layer acts as the reflective mirror. Electrons are collected by the front electrode grid, while holes are collected by the rear Au layer.

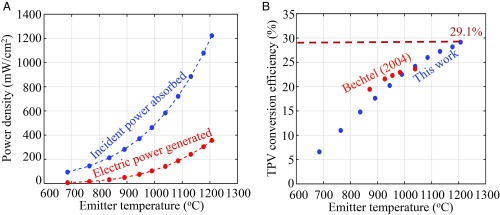
The total radiant power absorbed at different emitter temperatures and the corresponding electric power generated are given in Fig. 6A. The thermophotovoltaic conversion efficiency, the ratio between the electric power and the absorbed radiant power, is shown in Fig. 6B, reaching a maximum of 29.1%, at 1,207 °C. At this temperature, we obtain J_sc, V_oc, and fill factor of 918 mA/cm², 529 mV, and 0.73, respectively. This is for a photovoltaic cell with an active area of 10 mm², and corresponding external luminescence efficiency of 3.5%, and with a corresponding internal luminescence efficiency of ∼82%. The detailed procedure for extracting the luminescence efficiencies is given in SI Appendix. We limit our emitter temperature to 1,200 °C, even though an increase in efficiency is possible at higher temperatures. This is to test the performance of the proposed regenerative thermophotovoltaics within the temperature ranges of practical furnaces.

Fig. 6.

(A) Black body power absorbed (blue) and electrical power (red) extracted by the photovoltaic cell. (B) Thermophotovoltaic (TPV) efficiency at different emitter temperatures. The maximum efficiency is 29.1% at an emitter temperature of 1,207 °C. Results from our experiment are compared with similar results reported by Bechtel Bettis Inc. (42). Our results present the maximum thermophotovoltaic efficiency reported in the literature.

Our result is compared with results from Wernsman et al. (42), where they used similar emitter temperature ranges, with a corresponding photovoltaic cell bandgap of 0.63 eV. We get a similar efficiency as Bechtel at 1,039 °C (peak efficiency in Bechtel’s experiment), even though our cells are not optimized for operation at that temperature. Moreover, we achieve 29.1% efficiency at 1,207 °C, at a much lower temperature (2,027 °C) than the one used by Swanson et al. (31) to obtain similar efficiency with silicon. This is due to 2 key improvements of our device compared with previous results: 1) The reflectivity of our mirror reached 94.6% versus 90% in prior work (42), and 2) we have a better match of material bandgap to the Planck spectrum, leading to superior performance. The optimum bandgap for a particular emitter temperature is a trade-off between reducing the parasitic absorption of low-energy photons and the thermalization loss of high-energy photons. We reduce the absorption of low-energy photons by using a highly reflective mirror. Then we use an InGaAs active layer with bandgap = 0.75 eV, well matched to an emitter temperature of ∼1,207 °C for reducing the thermalization loss.

Although we achieved a record for thermophotovoltaic cell efficiency (29.1%), a pathway to translate this into a complete high-efficiency system would require further work on furnaces, combustion product circulation, thermal management, geometrical view factor, etc.

The rear mirror reflectivity is a key determinant of thermophotovoltaic cell efficiency. Since the absorbed power is proportional to (1 − R), where R is close to 1, the subbandgap reflectivity, R, of the cell needs to be measured very accurately. We used bare evaporated gold as our reference for calibrating all other reflectivity measurements, using a Nicolet iS50 spectrometer. The observed reflectivity of bare gold was very reproducible. The optical constants of bare gold (47, 48) are used to calibrate the Au reflectivity to 98.0%, when averaged over ±36° from the normal, and over both polarizations.

The spectrally averaged measured reflectivity of our InGaAs/Au devices is 94.6%, versus 94.4% calculated for an InGaAs/Au reflector [using known optical constants (47, 48)]. The standard deviation of the average reflectivity is 94.6 ± 0.2%, after averaging 70 runs over the specified random measurement error, ±1%, of the spectrometer. This results in a thermophotovoltaic efficiency error of ∼29.1 ± 0.4%, due to reflectivity uncertainty. Note that the reflectivity from the optical constants and the measured reflectivity agree with one another within our reflectivity measurement accuracy window. We also analyzed the contribution to uncertainty from temperature dependence of emissivity and the EQE measurement. The statistical error in the reflectivity measurement was by far the dominant contribution to error in the thermophotovoltaic efficiency. Full details of this error analysis can be found in SI Appendix.

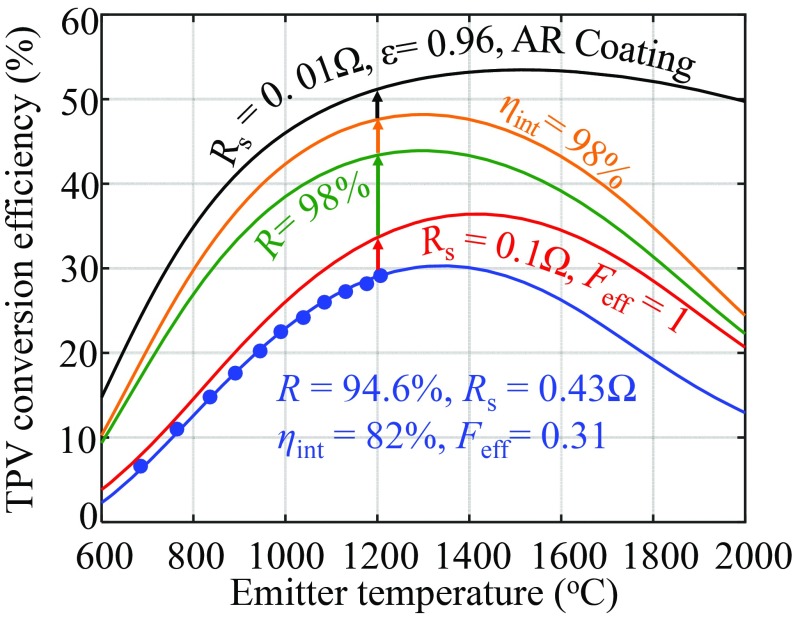
Now we project further improvements in thermophotovoltaic efficiency, as key device and chamber parameters improve. The key device parameters are the internal luminescence efficiency η_int, series resistance R_s, and the rear mirror reflectivity R_rear = 94.6%. A poor η_int is linked to significant loss of open-circuit voltage in the photovoltaic cell (27). From our current−voltage curves, we extract a series resistance R_s = 0.43 Ω and estimate η_int ≈ 82%, corresponding to η_ext ≈ 3.5%. Based on these values of η_int, R_rear, and R_s, we project the thermophotovoltaic efficiency of our cell at different temperatures (blue line in Fig. 7) and also compare it with the experimentally measured values (dots). The efficiency begins to diminish at emitter temperatures of >1,350 °C. Series resistance limits the performance of the device in that temperature range, where the brighter illumination gives rise to a larger short-circuit current, and therefore larger resistive voltage drop. The detailed procedure for estimating η_int and R_s from the current−voltage data is given in the SI Appendix.

Fig. 7.

Projection of thermophotovoltaic (TPV) efficiency. Effects of device and material quality, emitter, and chamber geometry on the system efficiency are illustrated. With the realistic projection of improvement in these key device and chamber parameters, more than 50% thermophotovoltaic conversion efficiency is possible.

Our setup differs from a thermophotovoltaic system in a full chamber (as shown in Fig. 1A) in 2 key factors: 1) the geometric view factor, which should be unity in the full chamber, and 2) the internal series resistance, which should be limited by the inherent series resistance of the device. The latter can be approached via improved interconnect metallization in commercial devices. High series resistance penalizes the cell’s fill factor due to a resistive voltage drop. In our case, the device had an inherent internal R_s ≈ 0.1 Ω, but we had an excess 0.33 Ω introduced by the wire bonds. If these technical difficulties are resolved, we project that such a system, using a photovoltaic cell identical to ours, would have a power conversion efficiency of 33.6% at 1,207 °C. This projection is shown by the red line in Fig. 7.

The projected effect of improved subbandgap reflectivity, from an average value of 94.6 to 98%, is shown by the green curve in Fig. 7. This improvement in reflectivity can be obtained by adding a layer of low refractive index dielectric between the rear gold layer and the semiconductor (49).

Improving the material quality of the photovoltaic device, which we parameterize with the internal luminescence efficiency η_int, leads to an enhancement in both operating and open-circuit voltages. The internal luminescence efficiency of InGaAs is mainly affected by defect-mediated Shockley−Read−Hall recombination and, to a lesser extent, by intrinsic Auger recombination. The best reported (50) values for InGaAs films reached τ_SRH ≈ 47 μs, with a corresponding Auger coefficient ∼8.1 × 10⁻²⁹ cm⁶⋅s⁻¹. For our projection, we use a more moderate Shockley−Read−Hall lifetime τ_SRH ≈ 10 μs, ∼2 orders of magnitude longer than the lifetime τ_SRH ≈ 60 ns in our device. This would increase the value of η_int to 98%. This improvement in the internal luminescence efficiency leads to a larger voltage in the photovoltaic cell, raising the thermophotovoltaic efficiency to ∼48%, as shown by the orange curve in Fig. 7.

Further efficiency gains can be achieved using an antireflection coating, and by maximizing the emitter emissivity using silicon carbide as the thermal radiation source instead of graphite, since the former has an emissivity ε = 0.96 versus ε = 0.90 of the latter. This full set of improvements can lead to >50% power conversion efficiency in an InGaAs thermophotovoltaic system, as shown by the black line in Fig. 7.

Although we have achieved a record for thermophotovoltaic cell efficiency (29.1%), to translate this into a full thermophotovoltaic system would require further work on furnaces, combustion product circulation, thermal management, and other elements.

Conclusion

We have achieved 29.1 ± 0.4% thermophotovoltaic power conversion efficiency, by reuse of unabsorbed subbandgap photons. We provide a roadmap to achieve higher efficiencies by separately considering the realistic improvements of material, device, and chamber parameters. With the improvement of these parameters, it is possible to achieve >50% power conversion efficiency using InGaAs photovoltaic cells. A highly efficient thermophotovoltaic heat engine would be an excellent choice for hybrid automobiles, unmanned vehicles, and deep space probes.