Skip to main content
PMC home page
ACS Omega logoLink to ACS Omega
. 2019 Jul 19;4(7):12385–12392. doi: 10.1021/acsomega.9b01566

11B NMR Chemical Shift Predictions via Density Functional Theory and Gauge-Including Atomic Orbital Approach: Applications to Structural Elucidations of Boron-Containing Molecules

Peng Gao †,‡, Xingyong Wang †,‡, Zhenguo Huang §, Haibo Yu †,‡,∥,*
PMCID: PMC6682094  PMID: 31460356

Abstract

graphic file with name ao-2019-01566n_0006.jpg

11B nuclear magnetic resonance (NMR) spectroscopy is a useful tool for studies of boron-containing compounds in terms of structural analysis and reaction kinetics monitoring. A computational protocol, which is aimed at an accurate prediction of 11B NMR chemical shifts via linear regression, was proposed based on the density functional theory and the gauge-including atomic orbital approach. Similar to the procedure used for carbon, hydrogen, and nitrogen chemical shift predictions, a database of boron-containing molecules was first compiled. Scaling factors for the linear regression between calculated isotropic shielding constants and experimental chemical shifts were then fitted using eight different levels of theory with both the solvation model based on density and conductor-like polarizable continuum model solvent models. The best method with the two solvent models yields a root-mean-square deviation of about 3.40 and 3.37 ppm, respectively. To explore the capabilities and potential limitations of the developed protocols, classical boron–hydrogen compounds and molecules with representative boron bonding environments were chosen as test cases, and the consistency between experimental values and theoretical predictions was demonstrated.

1. Introduction

The electron deficiency of boron enables fascinating chemistry. The studies of the structure and reactivity of boron-containing molecules have formed the basis of many important chemical concepts.1 Over the years, boron containing compounds have found a wide range of applications in metallomimetic chemistry,2 materials science,3−5 and medicinal chemistry.6,7 The rapid development of boron chemistry is tightly coupled with the application of 11B nuclear magnetic resonance (NMR) spectroscopy, which has been proved to be one of the most reliable and efficient methods for structural elucidation.8−10 Such an analysis enables effective elucidations of the chemical environment of boron within a molecule, structural assignments of possible intermediate states, as well as kinetics analysis of the reactions of interest.1111B NMR chemical shift analysis helps convincingly in structural assignment, particularly in the cases for which the X-ray crystallography study is challenging. For instance, Marwitz et al. reported the first isolation and characterization of 1,2-dihydro-1,2-azaborine, a hybrid organic/inorganic benzene isoelectronic structure through NMR analysis.12 Recently, by monitoring the temperature-dependent 11B chemical shifts, we have conclusively demonstrated that ammonium aminodiboranate, a long-sought isomer of diammoniate of diborane and ammonia borane dimer, is stable at −18 °C and decomposes at elevated temperatures.13

The development of various computational methods for chemical shift predictions further improves the capabilities of NMR spectroscopy in structural assignments.8,14−18 With the introduction of density functional theory (DFT)19−23 and gauge-including atomic orbital (GIAO)-based approach,24 the calculations of boron isotropic shielding constants become accessible. At the same time, the application of linear regression correlating calculated isotropic shielding constants and experimental NMR values has also proved effective to improve the prediction accuracy for 1H, 13C, and 15N chemical shifts at relatively low computational costs.25−30 The linear regression between computed isotropic shielding constants (σ) and experimental chemical shifts (δ) was performed via the following equation

1. 1

There are two empirical scaling factors that need to be fitted: slope and intercept. The former is a correction to the systematic error (the ideal value is −1), whereas the latter corresponds to the choice of reference applied in the NMR measurement. Through these two scaling factors, the calculated isotropic shielding constants can be converted into chemical shifts with sufficient accuracy, for instance, to allow distinguishing between different stereoisomers.29

In this work, effective predictions of 11B NMR chemical shifts based on linear regression were investigated. First, a database of boron-containing molecules was constructed. Second, we conducted calculations of boron isotropic shielding constants via eight different levels of theory along with two implicit solvent models for comparison. To be consistent with the experimental data, tetrahydrofuran (THF) was included as the solvent in our calculations. Third, the corresponding linear regression scaling factors were derived, and the ones with the best performance were subjected to further tests on a diverse set of boron-containing molecules including a series of boron–hydrogen compounds. Together with the previous work on 1H,25,2613C,26,30,31 and 15N,28,29,31 accurate NMR chemical shift predictions for molecules containing these elements can be achieved.

2. Results and Discussions

2.1. The Performance of the Adopted Methods

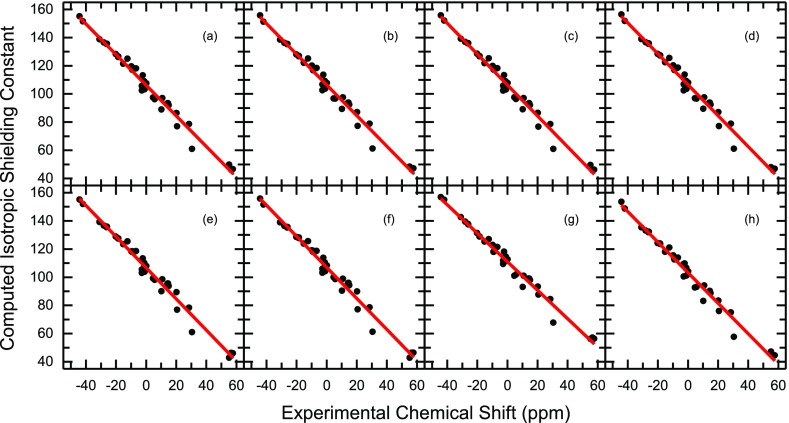
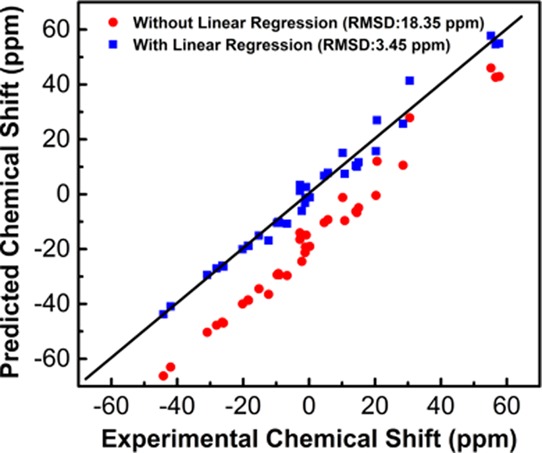
The fitted empirical scaling factors are listed in Table 1, and their performances are summarized in Table 2. The linear regressions are shown in Figure 1. For all eight methods with implicit solvent models, the values of R2 were close to 1.0 (Table 1), indicating that the applied data are suitable for linear regression. At the same time, the deviation of the slope from −1 indicates the existence of systematic errors in the adopted DFT/GIAO-based calculations.26 From the root-mean-square deviation (RMSD) values, we can see that all eight methods performed reasonably well. By the linear regression, they predicted 11B chemical shifts with errors of 3.40–3.50 and 3.37–3.50 ppm with respect to the experimental data using the solvation model based on density (SMD) and conductor-like polarizable continuum model (CPCM) solvent models, respectively (Table 2 and Figure S2 in the Supporting Information). In contrast, the corresponding errors of the results obtained without linear regression are substantially larger (>18 ppm) (Table 2), demonstrating the effectiveness of the fitted scaling factors in improving prediction accuracy. It is worth noting that the boron atoms bonded with halogen atoms have a large error, which has also been noted in 13C chemical shift predictions and is likely due to the deficiency in the adopted DFT method for this class of compounds.26

Table 1. The Eight Methods Adopted for Calculating 11B Isotropic Shielding Constants and the Fitted Empirical Scaling Parameters (Slope and Intercept) in THF.

      SMDc
 CPCMd
method geometrya (opt & freq) NMRb (GIAO) slope intercept slope intercept
1 B3LYP/6-31+G(d,p) mPW1PW91/6-311+G(2d,p) –1.0869 106.19 –1.0851 106.02
2 B3LYP/6-311+G(2d,p) mPW1PW91/6-311+G(2d,p) –1.0877 106.40 –1.0867 106.25
3 B3LYP/6-31+G(d,p) PBE0/6-311+G(2d,p) –1.0959 106.32 –1.0941 106.15
4 B3LYP/6-311+G(2d,p) PBE0/6-311+G(2d,p) –1.0967 106.53 –1.0956 106.37
5 M062X/6-31+G(d,p)g mPW1PW91/6-311+G(2d,p) –1.1050 106.67 –1.0903 106.65
5′ M062X/6-31+G(d,p)g mPW1PW91/6-311+G(2d,p) –1.1170e 107.52e –1.1386f 107.76f
6 M062X/6-311+G(2d,p)g mPW1PW91/6-311+G(2d,p) –1.1014 106.94 –1.1003 106.79
7 B3LYP/cc-pVDZ B3LYP/cc-pVDZ –1.0104 110.96 –1.0078 110.79
7′ B3LYP/cc-pVDZ B3LYP/cc-pVDZ –1.0386e 111.96e –1.0442f 111.80f
8 B3LYP/cc-pVTZ B3LYP/cc-pVTZ –1.0824 103.20 –1.0823 103.09
Open in a new tab
a

The geometry optimization and vibrational frequency calculations were performed with this method.

b

The GIAO calculations24 were performed with this method together with the implicit solvent models in Gaussian 09.

c

The fitted empirical scaling factors (slope and intercept in eq 1) for the chemical shift calculations with the SMD model.32 The linear fitting is shown in Figure 1.

d

The fitted empirical scaling factors (slope and intercept in eq 1) for the chemical shift calculations with the CPCM model.33 The linear fitting is shown in Figure S2 in the Supporting Information.

e

The fitted empirical scaling factors (slope and intercept in eq 1) for the chemical shift calculations with the SMD model included in the optimization step. The linear fitting can be seen in Figure S3 in the Supporting Information.

f

The fitted empirical scaling factors (slope and intercept in eq 1) for the chemical shift calculations with the CPCM model included in the optimization step. The linear fitting can be seen in Figure S3 in the Supporting Information.

g

int=ultrafine was included in all calculations with the M06 functionals.

Table 2. The Performance of the Fitted Empirical Scaling Factors for the Eight Methods in Table 1.

method R2a RMSDb RMSDc R2a RMSDb RMSDc
  SMD CPCM
1 0.9812 3.40 19.52 0.9813 3.38 19.41
2 0.9811 3.40 19.18 0.9812 3.40 19.07
3 0.9812 3.40 19.57 0.9813 3.39 19.45
4 0.9811 3.41 19.22 0.9812 3.40 19.11
5 0.9807 3.45 18.35 0.9803 3.48 18.32
5′d 0.9796 3.55 18.11 0.9818 3.34 18.49
6 0.9801 3.50 18.10 0.9800 3.50 17.99
7 0.9811 3.41 20.17 0.9815 3.37 20.06
7′d 0.9821 3.31 19.51 0.9832 3.21 19.45
8 0.9807 3.45 22.38 0.9808 3.44 22.30
Open in a new tab
a

R2 is the coefficient of determination for the linear regression.

b

RMSD for the predicted chemical shifts of the boron-containing molecules in the database (see Table S1 in the Supporting Information) with respect to their respective experimental values (in ppm) with linear regression.

c

RMSD for the predicted chemical shifts of the boron-containing molecules in the database (see Table S1 in the Supporting Information) with respect to their respective experimental values (in ppm) without linear regression (using BF3OEt2 as reference).

d

Implicit solvent models (CPCM or SMD) were included in the optimization step.

Figure 1.

Figure 1

Open in a new tab

Linear regression between the experimental 11B chemical shifts and calculated isotropic shielding constants with method 1–8 with the SMD solvent model for NMR GIAO calculations. (a) Method 1; (b) method 2; (c) method 3; (d) method 4; (e) method 5; (f) method 6; (g) method 7; and (h) method 8. See Figure S2 in the Supporting Information for more details for the linear regression with the CPCM solvent model for NMR GIAO calculations.

Based on the above results, it can be seen that all of the eight methods display comparably good performances. PBE0 and mPW1PW91 provide similar accuracy for 11B NMR chemical shift predictions (method 1 vs 3 and 2 vs 4). Method 5 and 7, with geometry optimization at M062X/6-31+G(d,p) or B3LYP/cc-pVDZ in the gas phase and NMR GIAO calculations at mPW1PW91/6-311+G(2d,p) or B3LYP/cc-pVDZ, were proved to be effective for not only 11B, but also for 1H, 13C, and 15N chemical shift predictions as discussed before.26,28−30 In particular, the important advantage of method 5 (with the SMD solvent model) is that it could provide chemical shift predictions for 1H, 13C, 15N, and 11B with a consistent accuracy in one set of calculation via the corresponding changes of the applied solvents.27,29

For the two implicit solvent models (SMD and CPCM), we found that their prediction errors of 11B NMR chemical shifts are very similar (Table 2). Moreover, we investigated the potential benefit of including the implicit solvent models in the geometry optimization (method 5′ and 7′ in Table 2 and Figure S3 in the Supporting Information) in contrast to those in vacuo (method 5 and 7). Only minor changes were observed (RMSD changes less than 0.15 ppm), indicating that the inclusion of implicit solvent models in geometry optimization may not improve the result significantly. Specifically, for the SMD model, the prediction error for method 5′ increases slightly from 3.45 to 3.55 ppm, whereas the error decreases from 3.41 to 3.31 ppm with method 7′. The result obtained with the CPCM model shows a slight difference, where the errors for both method 5 and 7 decrease. Considering their increased computational costs and the corresponding gain in accuracy, we recommend to use gas phase geometry optimization and only include the solvent model for the NMR calculation step.

2.2. Applications of 11B Chemical Shift Predictions for Boron–Hydrogen Compounds

We applied the developed protocol to illustrate its possible assistance for experimental work in the field of hydrogen storage. In recent years, because of the high content of hydrogen,34,35 the studies of boron–hydrogen compounds have attracted increasing interest from the community of hydrogen storage. Nevertheless, effective identification of the intermediates during hydrogen evolution remains a challenge. From the perspective of the NMR analysis, merely relying on 1H NMR spectroscopy is not sufficient.36 Combining 1H and 11B NMR spectroscopies can be a powerful strategy in resolving the structure of boron–hydrogen compounds.

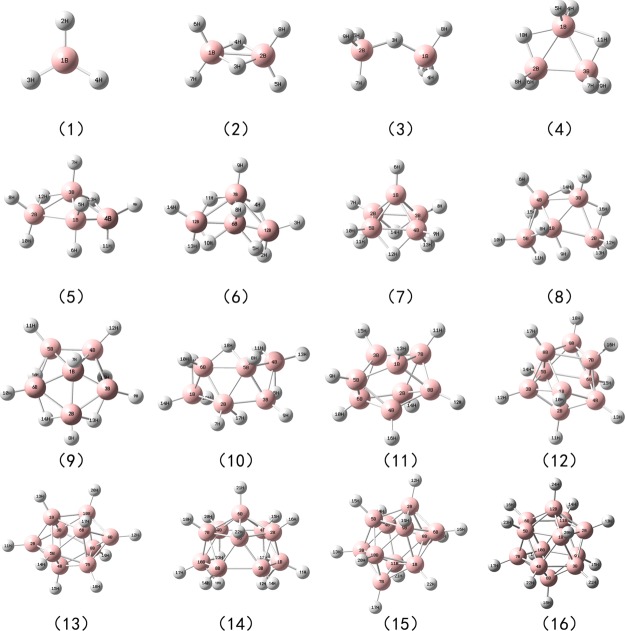
In this study, we tested 16 classical boron–hydrogen compounds (Figure 2), for which experimental data are available (Table 3). We conducted the NMR GIAO calculations via method 5 and 7 in vacuo following the same procedure as above. Table 3 and Figure 3 show an excellent agreement between the predicted values and experimental data.37 For both method 5 and 7, scaling factors derived from both SMD and CPCM models work equally well, and most of the prediction errors are within 1.0 RMSD.

Figure 2.

Figure 2

Open in a new tab

Boron–hydrogen compounds included in the application study.

Table 3. Experimental and Predicted 11B NMR Chemical Shifts (in ppm) for Selected Boron–Hydrogen Compoundsa.

      δpred.
  Pos.b Exp.c 5d 7e 5f 7g
BH3 δB-1 86.0 84.22 83.16 85.34 83.20
B2H6 δB-1,2 16.6 17.84 15.98 18.06 15.85
B2H7– δB-1,2 –24.6 –24.51 –23.48 –24.86 –23.71
B3H8– δB-1–3 –30.4 –26.99h –28.16h 27.37h 28.40h
B4H9– δ(1)B-1 –54.5 –54.41 –56.46 –55.16 –56.77
  δ(2)B-2,4 –10.2 –11.65 –12.72 –11.83 –12.92
  δ(3)B-3 0.8 0.06 –1.41 0.05 –1.58
B4H10 δ(1)B-6,7 –6.9 –6.85 –7.51 –6.97 –7.70
  δ(2)B-12 –41.8 –40.18 –42.75 –40.74 –43.03
B5H9 δ(1)B-1 –13.4 –14.17 –15.47 –14.38 –15.68
  δ(2)B-2–5 –53.1 –50.65 –55.75 –51.35 –56.06
B5H11 δB-1–5 –55.3 –51.38 –53.43 –52.09 –53.74
B6H10 δ(1)B-3–6 18.6 14.77 14.98 14.95 14.85
  δ(2)B-2 –6.5 –8.23 –11.13 –8.36 –11.33
  δ(3)B-1 –51.8 –48.95 –51.64 –49.63 –51.94
B6H12 δ(1)B-1,4 22.6 22.56 20.43 22.85 20.32
  δ(2)B-3,6 7.9 11.04 10.15 11.17 10.01
B8H82– δB-1–8 –6.8 –1.55 –3.60 –1.59 –3.78
B9H92– δ(1)B-3,4,9 –2.9 –3.60 –6.40 –3.67 –6.59
  δ(2)B-1,2,5–8 –20.5 –21.98 –22.22 –22.30 –22.45
B10H102– δ(1)B-1,3–8,10 –30.9 –28.38 –28.85 –28.78 –29.10
  δ(2)B-2,9 0.9 –2.47 –3.18 –2.52 –3.36
B10H14 δ(1)B-5,6 13.5 12.66 12.20 12.81 12.06
  δ(2)B-1,10 10.7 8.18 7.62 8.27 7.47
  δ(3)B-3,4,8,9 1.6 0.65 0.42 0.64 0.25
  δ(4)B-2,7 –35.2 –33.14 –34.95 –33.60 –35.21
B11H112– δB-1–11 –16.9 –17.10 –17.63 –17.35 –17.85
B12H122– δB-1–12 –15.6 –13.82 –14.62 –14.03 –14.83
Open in a new tab
a

All of the NMR calculations were conducted in vacuo.

b

Positions for the boron of interest, more details can be seen in Table S6 in Supporting Information.

c

Experimental data were taken from refs.37,41,46−49

d

The predicted chemical shifts via the linear regression model by method 5 (the SMD set).

e

The predicted chemical shifts via the linear regression model by method 7 (the SMD set).

f

The predicted chemical shifts via the linear regression model by method 5 (the CPCM set).

g

The predicted chemical shifts via the linear regression model by method 7 (the CPCM set).

h

For B3H8–, our calculations predicted two different chemical shifts for boron atoms, and the averaged value was used to compare with the experimental value.

Figure 3.

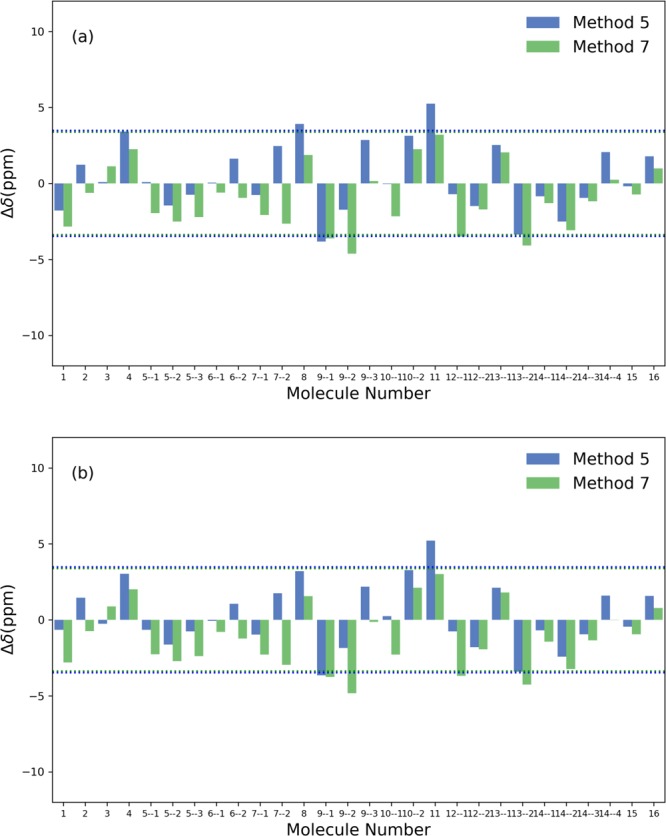
Figure 3

Open in a new tab

The deviations between the predicted and experimental 11B NMR chemical shifts of molecules listed in Table 3. (a) The isotropic shielding constants were calculated with method 5 and 7 with the SMD model, and were converted to chemical shifts with the scaling factors of the SMD set listed in Table 1. The RMSD value is marked by the dashed line. (b) The isotropic shielding constants were calculated with method 5 and 7 with the CPCM model, and were converted to chemical shifts with the scaling factors of the CPCM set listed in Table 1. The RMSD value is marked by the dashed line.

The diborane, B2H6, which has two bridging hydrogen atoms and features a ring structure (structure 2 in Figure 2), is a highly reactive reagent that has versatile applications. As can be seen from Figure 2, the optimized structure shows a planar ring of diborane with the dihedral angle between Hb–B–Hb–B at 0°, matching well with the experimental measurement38,39 and previous computational work.37 The deviations of the predicted values from the experimental data are within 1.5 ppm. The anion B3H8– (structure 4 in Figure 2) has attracted a lot of attention due to its stability and high content of hydrogen.40,41 This anion may adopt different structures in solution.42 Indeed, solution NMR studies have shown that the transformation between possible structures can happen via the migration of hydrogen.43−45 Considering the fluxional behavior of B3H8–, we applied the same procedure by Sethio et al.37 to average the two predicted values of 11B NMR chemical shifts, and then compare the average with experimental data. From Table 3, we found that the deviations are within 3.4 and 2.2 ppm for method 5 and 7, respectively, which is in a reasonable agreement with the experimental data. In contrast, Sethio et al. reported errors ∼6–9 ppm for three different DFT methods without linear regressions.37

2.3. Applications of 11B Chemical Shift Predictions for Structural Elucidations of Boron Containing Molecules

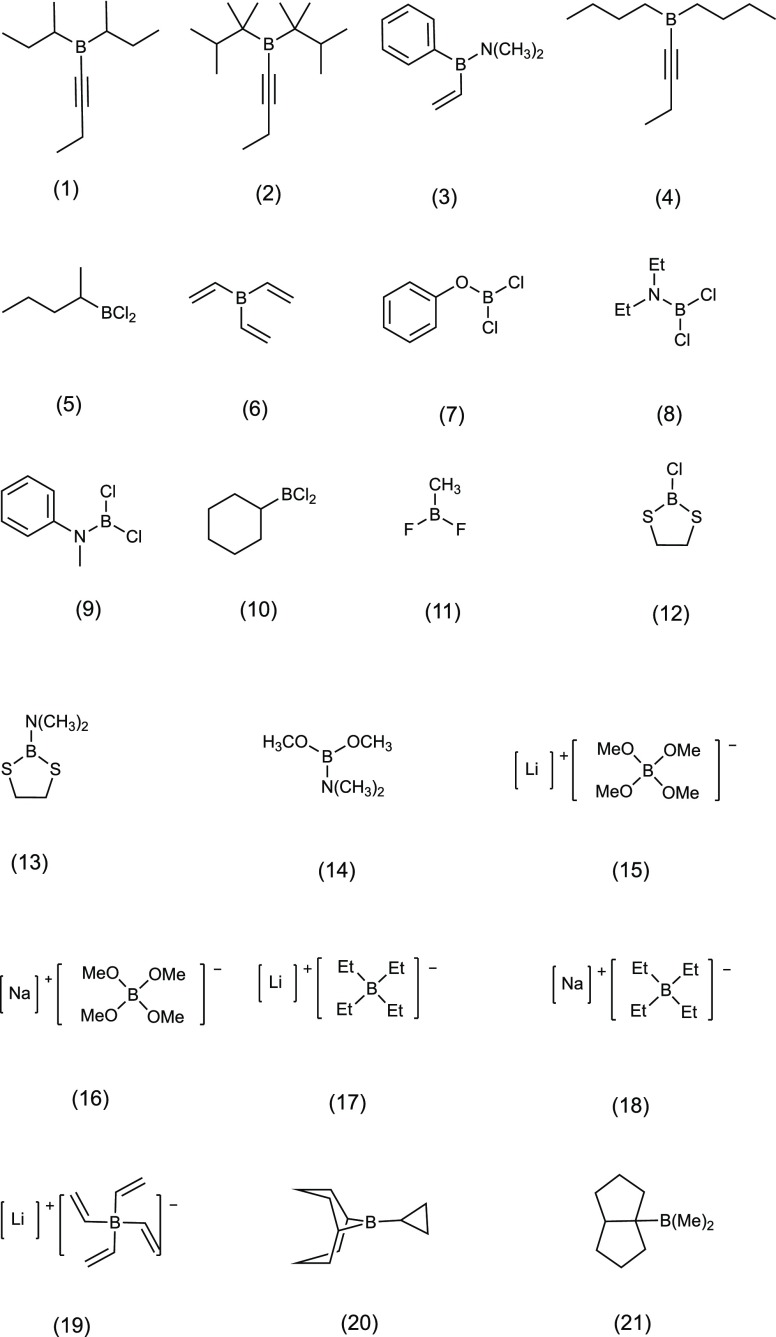
We also applied our protocol to further test some other boron containing molecules with diverse bonding environments and investigate their overall applicability (Figure 4). From the results listed in Table 4 and deviations shown in Figure 5, we can see that the agreement between the predicted values and experimental data is excellent, indicating the robustness of our protocol for structural elucidations of boron containing molecules with different bonding features. It is worth pointing out that, some of these experimental 11B chemical shift values were measured in pure liquids or solvents other than THF (Table 4). We infer that there exists a reasonable transferability for scaling factors among different solvents. This is consistent with our previous work on nitrogen NMR chemical shift predictions.29

Figure 4.

Figure 4

Open in a new tab

Boron containing molecules included in the application study.

Table 4. Experimental and Predicted 11B NMR Chemical Shifts (in ppm) for Selected Boron Containing Moleculesa.

  Exp.b 5c 7d 5e 7f
    δpred.
1 72.2 67.32 67.89 68.22 67.94
2 81.1 76.99 81.02 78.67 81.83
3 40.0 37.88 38.83 38.38 38.76
4 72.0 66.94 66.90 67.82 66.90
5 65.3 61.98 64.78 62.80 64.77
6 55.2 51.21 51.06 51.88 51.02
7 33.0 32.72 31.82 33.14 31.74
8 31.6 31.76 33.38 32.17 33.29
9 30.8 32.31 32.69 32.73 32.60
10 67.6 61.37 64.30 62.18 64.30
11 28.1 30.43 25.27 30.85 25.16
12 62.7 59.53 62.98 60.32 62.97
13 45.3 43.30 45.44 43.86 45.39
14 21.3 21.10 17.71 21.37 17.59
15 3.0 3.51 1.23 3.52 1.06
16 2.7 3.07 0.86 3.11 0.72
17 –17.5 –17.29 –17.03 –17.41 –17.07
18 –16.6 –18.08 –17.92 –18.25 –18.10
19 –16.1 –12.91 –12.52 –13.19 –12.79
20 84 79.37 80.94 80.591 81.29
21 82.3 80.70 77.75 82.17 78.24
Open in a new tab
a

Details of the calculations can be found in Tables S9 and S10 in the Supporting Information.

b

Experimental data.50

c

The difference between experimental values and calculated chemical shifts with the linear regression model by method 5 (the SMD set).

d

The difference between experimental values and calculated chemical shifts with the linear regression model by method 7 (the SMD set).

e

The difference between experimental values and calculated chemical shifts with the linear regression model by method 5 (the CPCM set).

f

The difference between experimental values and calculated chemical shifts with the linear regression model by method 7 (the CPCM set).

Figure 5.

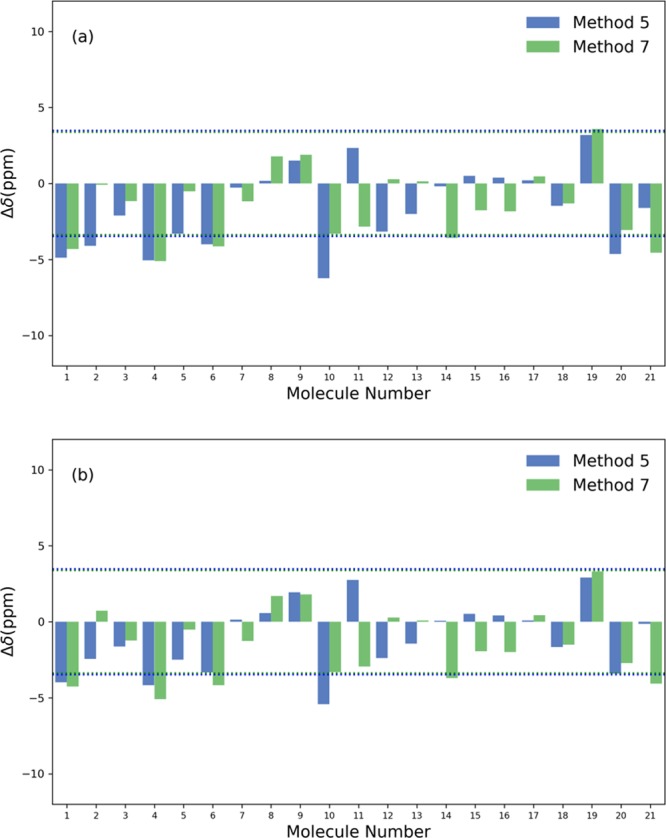
Figure 5

Open in a new tab

The deviations between the predicted and experimental 11B NMR chemical shifts of molecules listed in Table 4. (a) Isotropic shielding constants were calculated with methods 5 and 7 with the SMD model and were converted to chemical shifts with the scaling factors of the SMD set listed in Table 1. The RMSD value is marked by the dash. (b) Isotropic shielding constants were calculated with method 5 and 7 with the CPCM model and were converted to chemical shifts with the scaling factors of the CPCM set listed in Table 1. The RMSD value is marked by the dash line.

3. Methodology

3.1. Database of Boron-Containing Molecules

There are 36 molecules and 36 chemical shifts in total included in our database (see Table S1 in the Supporting Information for more details). The two criteria for selection of molecules include (a) reliable experimental data available, preferably in THF;50 and (b) having relatively rigid boron skeletons. As discussed in ref (29), the reason for the second criterion is to avoid the potential challenges in dealing with flexible molecules when developing linear regression models, which require Boltzmann averaging of the calculated isotropic shielding constants on the basis of relative energies of all available conformers. However, the developed scaling factors are expected to be applicable for flexible molecules, provided that the relative energies of their relevant conformers can be calculated accurately.26

3.2. Computational Details

To be consistent with the procedure proposed by Tantillo and co-workers26,27 and our previous study on 15N NMR chemical shifts,29 we first carried out geometry optimization in vacuo to locate the minima on the potential energy surface. These optimized structures were verified by vibrational frequency calculations. Second, we conducted NMR single-point calculations in THF with both the SMD32 and CPCM33 solvent models. It has been shown that the inclusion of the implicit solvent model in the NMR calculation step is crucial to improve the prediction accuracy of 1H and 13C chemical shifts.25−27 Another study by Xin et al. focusing on 13C chemical shift predictions adopted the CPCM solvent model.30 The inclusion of the explicit solvent model may further improve the prediction accuracy of chemical shifts,51,52 with a substantial increase of the computational cost. For consistency with the previous studies,26−30 implicit solvent models were adopted in the current work. The GIAO approach was applied to calculate 11B isotropic shielding constants.24 All of the calculations were carried out with Gaussian 09.53 The first six levels of theory (Table 1, method 1–6) are to follow Tantillo and co-workers’ work on 1H and 13C chemical shifts26,27 and our previous study on 15N chemical shifts.29 In addition, two methods (Table 1, method 7 and 8), which have been shown to provide accurate predictions for both 15N28 and 13C30 chemical shift calculations, were also included for comparison. To further investigate the solvent effects, additional calculations with an implicit solvent model included in the geometry optimization step were carried out for two levels of theory (method 5′ and 7′).

4. Conclusions

In this study, empirical scaling techniques for accurate prediction of 11B NMR chemical shifts have been proposed by comparing eight different levels of theory with two solvent models, based on the calculated isotropic shielding constants in THF. The protocol of 11B NMR chemical shift prediction is consistent with the procedure proposed by Tantillo and co-workers26,27 for 1H and 13C chemical shifts and our previous work for 15N chemical shift.29 The two sets of scaling factors for two different solvent models (SMD and CPCM) were compared. Among the eight levels of theory, method 5 and 7 show the best performance, with geometry optimization in the gas phase at M062X/6-31+G(d,p) or B3LYP/cc-pVDZ and NMR GIAO calculation at mPW1PW91/6-311+G(2d,p) or B3LYP/cc-pVDZ with an implicit solvent model. At the same time, the effect of including solvent model in the optimization step was also investigated. In summary, we recommend method 5 and 7 for 11B chemical shift prediction together with those for 1H, 13C, and 15N in one set of calculations. For boron–hydrogen compounds or other boron-containing molecules, the predicted 11B chemical shifts with method 5 and 7 agree well with the experimental data, indicating the robustness and broad applicability of this protocol for structural elucidation. It is worth noting that the fitted scaling factors in THF can provide a reasonable prediction for 11B chemical shifts measured in either pure liquids or in other solvents. This is consistent with the finding of our previous research on 15N chemical shift.29 We expect that this work on 11B chemical shift can serve as a useful tool for elucidating or confirming the structure of boron-containing compounds.

Acknowledgments

H.Y. is the recipient of an Australian Research Council Future Fellowship (project number FT110100034) and X.W. is the recipient of a University of Wollongong Vice-Chancellor’s Postdoctoral Fellowship. We wish to acknowledge the Australian Government for an Australian International Postgraduate Award scholarship for P.G. This research was in part supported under the Australian Research Council’s Discovery Projects funding scheme (project number DP170101773). We wish to acknowledge that this research was undertaken with the assistance of resources provided at the NCI National Facility systems at the Australian National University through the National Computational Merit Allocation Scheme supported by the Australian Government (Project id: v15).

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsomega.9b01566.

  • Experimental 11B NMR chemical shifts used in this study and figures for linear regression between the experimental 11B NMR chemical shifts and the calculated isotropic shielding constants with the CPCM solvent model (PDF)

The authors declare no competing financial interest.

Supplementary Material

ao9b01566_si_001.pdf (880.4KB, pdf)

References

  1. Bregadze V. I.; Xie Z. Boron Chemistry - A Rapidly Expanding Research Field. Eur. J. Inorg. Chem. 2017, 2017, 4348–4349. 10.1002/ejic.201701175. [DOI] [Google Scholar]
  2. Légaré M.-A.; Pranckevicius C.; Braunschweig H. Metallomimetic Chemistry of Boron. Chem. Rev. 2019, , in press 10.1021/acs.chemrev.8b00561. [DOI] [PubMed] [Google Scholar]
  3. Demirci U.; Miele P.; Yot P. Boron-Based (Nano-)Materials: Fundamentals and Applications. Crystals 2016, 6, 118. 10.3390/cryst6090118. [DOI] [Google Scholar]
  4. Huang Z.; Autrey T. Boron-nitrogen-hydrogen (BNH) compounds: recent developments in hydrogen storage, applications in hydrogenation and catalysis, and new syntheses. Energy Environ. Sci. 2012, 5, 9257. 10.1039/c2ee23039a. [DOI] [Google Scholar]
  5. Wang X.; Yu L.; Inakollu V. S. S.; Pan X.; Ma J.; Yu H. Molecular Quantum Dot Cellular Automata Based on Diboryl Monoradical Anions. J. Phys. Chem. C 2018, 122, 2454–2460. 10.1021/acs.jpcc.7b11964. [DOI] [Google Scholar]
  6. Leśnikowski Z. J. Challenges and Opportunities for the Application of Boron Clusters in Drug Design. J. Med. Chem. 2016, 59, 7738–7758. 10.1021/acs.jmedchem.5b01932. [DOI] [PubMed] [Google Scholar]
  7. Issa F.; Kassiou M.; Rendina L. M. Boron in Drug Discovery: Carboranes as Unique Pharmacophores in Biologically Active Compounds. Chem. Rev. 2011, 111, 5701–5722. 10.1021/cr2000866. [DOI] [PubMed] [Google Scholar]
  8. Todd L. J.; Siedle A. R. NMR studies of boranes, carboranes and hetero-atom boranes. Prog. Nucl. Magn. Reson. Spectrosc. 1979, 13, 87–176. 10.1016/0079-6565(79)80001-1. [DOI] [Google Scholar]
  9. Wrackmeyer B.Nuclear Magnetic Resonance Spectroscopy of Boron Compounds Containing Two-, Three- and Four-Coordinate Boron. In Annual Reports on NMR Spectroscopy; Webb G., Ed.; Academic Press, 1988; Vol. 20; pp 61–203. [Google Scholar]
  10. Siedle A.11B NMR Spectroscopy. In Annual Reports on NMR Spectroscopy; Webb G., Ed.; Academic Press, 1988; Vol. 20; pp 205–314. [Google Scholar]
  11. Noeth H.; Wrackmeyer B.. Nuclear Magnetic Resonance Spectroscopy of Boron Compounds, 1st ed.; Springer-Verlag: Berlin, Heidelberg, New York, 1978. [Google Scholar]
  12. Marwitz A. J. V.; Matus M. H.; Zakharov L. N.; Dixon D. A.; Liu S.-Y. A Hybrid Organic/Inorganic Benzene. Angew. Chem. 2009, 121, 991–995. 10.1002/ange.200805554. [DOI] [PubMed] [Google Scholar]
  13. Chen W.; Yu H.; Wu G.; He T.; Li Z.; Guo Z.; Liu H.; Huang Z.; Chen P. Ammonium Aminodiboranate: A Long-Sought Isomer of Diammoniate of Diborane and Ammonia Borane Dimer. Chem.—Eur. J. 2016, 22, 7727–7729. 10.1002/chem.201601375. [DOI] [PubMed] [Google Scholar]
  14. Buhl M.; Gauss J.; Hofmann M.; Schleyer P. v. R. Decisive electron correlation effects on computed boron-11 and carbon-13 NMR chemical shifts. Application of the GIAO-MP2 method to boranes and carbaboranes. J. Am. Chem. Soc. 1993, 115, 12385–12390. 10.1021/ja00079a020. [DOI] [Google Scholar]
  15. Buehl M.; Von Ragué Schleyer P. Application and Evaluation of ab Initio Chemical Shift Calculations for Boranes and Carboranes. How reliable Are accurate Experimental Structures?. J. Am. Chem. Soc. 1992, 114, 477–491. 10.1021/ja00028a013. [DOI] [Google Scholar]
  16. McKee M. L.; Lipscomb W. N. Ab initio study of the transient boron hydrides B3H7, B3H9, B4H8, and B4H12 and the fluxional anion B3H8-. Inorg. Chem. 1982, 21, 2846–2850. 10.1021/ic00137a060. [DOI] [Google Scholar]
  17. Łodziana Z.; Bloński P.; Yan Y.; Rentsch D.; Remhof A. NMR Chemical Shifts of 11B in Metal Borohydrides from First-Principle Calculations. J. Phys. Chem. C 2014, 118, 6594–6603. 10.1021/jp4120833. [DOI] [Google Scholar]
  18. Tian S. X. Ab Initio and Electron Propagator Theory Study of Boron Hydrides. J. Phys. Chem. A 2005, 109, 5471–5480. 10.1021/jp050067e. [DOI] [PubMed] [Google Scholar]
  19. Kohn W.; Sham L. J. Self-Consistent Equations Including Exchange and Correlation Effects. Physical Review 1965, 140, A1133–A1138. 10.1103/physrev.140.a1133. [DOI] [Google Scholar]
  20. Becke A. D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. 10.1063/1.464913. [DOI] [Google Scholar]
  21. Perdew J. P.; Ernzerhof M.; Burke K. Rationale for mixing exact exchange with density functional approximations. J. Chem. Phys. 1996, 105, 9982–9985. 10.1063/1.472933. [DOI] [Google Scholar]
  22. Adamo C.; Barone V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. 10.1063/1.478522. [DOI] [Google Scholar]
  23. Zhao Y.; Truhlar D. G. Density Functional for Spectroscopy: No Long-Range Self-Interaction Error, Good Performance for Rydberg and Charge-Transfer States, and Better Performance on Average than B3LYP for Ground States. J. Phys. Chem. A 2006, 110, 13126–13130. 10.1021/jp066479k. [DOI] [PubMed] [Google Scholar]
  24. Ditchfield R. Self-consistent perturbation theory of diamagnetism. Mol. Phys. 1974, 27, 789–807. 10.1080/00268977400100711. [DOI] [Google Scholar]
  25. Jain R.; Bally T.; Rablen P. R. Calculating Accurate Proton Chemical Shifts of Organic Molecules with Density Functional Methods and Modest Basis Sets. J. Org. Chem. 2009, 74, 4017–4023. 10.1021/jo900482q. [DOI] [PubMed] [Google Scholar]
  26. Lodewyk M. W.; Siebert M. R.; Tantillo D. J. Computational Prediction of 1H and 13C Chemical Shifts: A Useful Tool for Natural Product, Mechanistic, and Synthetic Organic Chemistry. Chem. Rev. 2012, 112, 1839–1862. 10.1021/cr200106v. [DOI] [PubMed] [Google Scholar]
  27. CHESHIRE CCAT, the Chemical Shift Repository for computed NMR scaling factors, with Coupling Constants Added Too. 2017, http://cheshirenmr.info/index.htm (accessed May 20, 2019).
  28. Xin D.; Sader C. A.; Fischer U.; Wagner K.; Jones P.-J.; Xing M.; Fandrick K. R.; Gonnella N. C. Systematic investigation of DFT-GIAO 15N NMR chemical shift prediction using B3LYP/cc-pVDZ: application to studies of regioisomers, tautomers, protonation states and N-oxides. Org. Biomol. Chem. 2017, 15, 928–936. 10.1039/c6ob02450e. [DOI] [PubMed] [Google Scholar]
  29. Gao P.; Wang X.; Yu H. Towards an Accurate Prediction of Nitrogen Chemical Shifts by Density Functional Theory and Gauge-Including Atomic Orbital. Adv. Theory Simul. 2019, 2, 1800148. 10.1002/adts.201800148. [DOI] [Google Scholar]
  30. Xin D.; Sader C. A.; Chaudhary O.; Jones P.-J.; Wagner K.; Tautermann C. S.; Yang Z.; Busacca C. A.; Saraceno R. A.; Fandrick K. R.; Gonnella N. C.; Horspool K.; Hansen G.; Senanayake C. H. Development of a 13C NMR Chemical Shift Prediction Procedure Using B3LYP/cc-pVDZ and Empirically Derived Systematic Error Correction Terms: A Computational Small Molecule Structure Elucidation Method. J. Org. Chem. 2017, 82, 5135–5145. 10.1021/acs.joc.7b00321. [DOI] [PubMed] [Google Scholar]
  31. Jaźwiński J.; Stefaniak L. Structural studies on mesoionic 1,2,3,4-thiatriazolo-5-aminides and 1,2,3,4-thiatriazolo-5-methylides by nitrogen and carbon NMR. Magn. Reson. Chem. 1993, 31, 447–450. 10.1002/mrc.1260310506. [DOI] [Google Scholar]
  32. Marenich A. V.; Cramer C. J.; Truhlar D. G. Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B 2009, 113, 6378–6396. 10.1021/jp810292n. [DOI] [PubMed] [Google Scholar]
  33. Barone V.; Cossi M. Quantum Calculation of Molecular Energies and Energy Gradients in Solution by a Conductor Solvent Model. J. Phys. Chem. A 1998, 102, 1995–2001. 10.1021/jp9716997. [DOI] [Google Scholar]
  34. Züttel A.; Borgschulte A.; Orimo S.-I. Tetrahydroborates as new hydrogen storage materials. Scr. Mater. 2007, 56, 823–828. 10.1016/j.scriptamat.2007.01.010. [DOI] [Google Scholar]
  35. Orimo S.-i.; Nakamori Y.; Eliseo J. R.; Züttel A.; Jensen C. M. Complex Hydrides for Hydrogen Storage. Chem. Rev. 2007, 107, 4111–4132. 10.1021/cr0501846. [DOI] [PubMed] [Google Scholar]
  36. Hwang S.-J.; Bowman R. C.; Reiter J. W.; Rijssenbeek; Soloveichik G. L.; Zhao J.-C.; Kabbour H.; Ahn C. C. NMR Confirmation for Formation of [B12H12]2-Complexes during Hydrogen Desorption from Metal Borohydrides. J. Phys. Chem. C 2008, 112, 3164–3169. 10.1021/jp710894t. [DOI] [Google Scholar]
  37. Sethio D.; Lawson Daku L. M.; Hagemann H. A theoretical study of the spectroscopic properties of B2H6 and of a series of BxHyz-species (x=1-12, y=3-14, z=0-2): From BH3 to B12H12–2. Int. J. Hydrogen Energy 2016, 41, 6814–6824. 10.1016/j.ijhydene.2016.02.121. [DOI] [Google Scholar]
  38. Duncan J. L.; Harper J. The structure of the diborane molecule. Mol. Phys. 1984, 51, 371–380. 10.1080/00268978400100251. [DOI] [Google Scholar]
  39. Bartell L. S.; Carroll B. L. Electron-Diffraction Study of Diborane and Deuterodiborane. J. Chem. Phys. 1965, 42, 1135–1139. 10.1063/1.1696092. [DOI] [Google Scholar]
  40. Huang Z.; Lingam H. K.; Chen X.; Porter S.; Du A.; Woodard P. M.; Shore S. G.; Zhao J.-C. Synthesis, structural analysis, and thermal decomposition studies of [(NH3)2BH2]B3H8. RSC Adv. 2013, 3, 7460–7465. 10.1039/c3ra22836c. [DOI] [Google Scholar]
  41. Yan Y.; Remhof A.; Rentsch D.; Lee Y.-S.; Whan Cho Y.; Züttel A. Is Y2(B12H12)3 the main intermediate in the decomposition process of Y(BH4)3?. Chemical Communications 2013, 49, 5234–5236. 10.1039/c3cc41184b. [DOI] [PubMed] [Google Scholar]
  42. Olson J. K.; Boldyrev A. I. Ab initio characterization of the flexural anion found in the reversible dehydrogenation. Comput. Theoret. Chem. 2011, 967, 1–4. 10.1016/j.comptc.2011.04.011. [DOI] [Google Scholar]
  43. Bushweller C. H.; Beall H.; Grace M.; Dewkett W. J.; Bilofsky H. S. Temperature dependence of the proton nuclear magnetic resonance spectra of copper(I) borane complexes, B3H8- salts, and icosahedral carboranes. Quadrupole-induced spin decoupling. Fluxional behavior. J. Am. Chem. Soc. 1971, 93, 2145–2149. 10.1021/ja00738a009. [DOI] [Google Scholar]
  44. Beall H.; Bushweller C. H.; Dewkett W. J.; Grace M. Intramolecular exchange and ″thermal″ decoupling in B3H8-compounds. J. Am. Chem. Soc. 1970, 92, 3484–3486. 10.1021/ja00714a053. [DOI] [Google Scholar]
  45. Chong M.; Karkamkar A.; Autrey T.; Orimo S.-i.; Jalisatgi S.; Jensen C. M. Reversible dehydrogenation of magnesium borohydride to magnesium triborane in the solid state under moderate conditions. Chem. Commun. 2011, 47, 1330–1332. 10.1039/c0cc03461d. [DOI] [PubMed] [Google Scholar]
  46. Contreras R.; Wrackmeyer B. Application of 11B nuclear magnetic resonance spectroscopy to the study of hydroboration-III. 11B Nuclear magnetic resonance study of exchange reactions of triorganyl boranes with borane in tetrahydrofurane and dimethyl sulfide. Spectrochim. Acta Part A: Mol. Spect. 1982, 38, 941–951. 10.1016/0584-8539(82)80119-0. [DOI] [Google Scholar]
  47. Greatrex R.; Greenwood N. N.; Millikan M. B.; Rankin D. W. H.; Robertson H. E. The molecular structure of hexaborane(12) in the gas phase as determined by electron diffraction. Dalton Trans. 1988, 2335–2339. 10.1039/dt9880002335. [DOI] [Google Scholar]
  48. Huang Z.; King G.; Chen X.; Hoy J.; Yisgedu T.; Lingam H. K.; Shore S. G.; Woodward P. M.; Zhao J.-C. A Simple and Efficient Way to Synthesize Unsolvated Sodium Octahydrotriborate. Inorg. Chem. 2010, 49, 8185–8187. 10.1021/ic101543v. [DOI] [PubMed] [Google Scholar]
  49. Heřmánek S. NMR as a tool for elucidation of structures and estimation of electron distribution in boranes and their derivatives. Inorg. Chim. Acta 1999, 289, 20–44. 10.1016/s0020-1693(99)00055-9. [DOI] [Google Scholar]
  50. Boron NMR Chemical Shifts. 2015, http://www.chemistry.sdsu.edu/research/BNMR (accessed May 20, 2019).
  51. Zhu T.; Zhang J. Z. H.; He X. Automated Fragmentation QM/MM Calculation of Amide Proton Chemical Shifts in Proteins with Explicit Solvent Model. J. Chem. Theory Comput. 2013, 9, 2104–2114. 10.1021/ct300999w. [DOI] [PubMed] [Google Scholar]
  52. Exner T. E.; Frank A.; Onila I.; Möller H. M. Toward the Quantum Chemical Calculation of NMR Chemical Shifts of Proteins. 3. Conformational Sampling and Explicit Solvents Model. J. Chem. Theory Comput. 2012, 8, 4818–4827. 10.1021/ct300701m. [DOI] [PubMed] [Google Scholar]
  53. Frisch M. J.; et al. Gaussian 09, Revision E.01; Gaussian Inc.: Wallingford CT, 2009.

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao9b01566_si_001.pdf (880.4KB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES