Studies on Bed Density in a Gas-Vibro Fluidized Bed for Coal Cleaning

Abstract

Dry coal beneficiation has played a vital role during the initial stage of coal cleaning in recent years. Successful utilization of a gas–solid fluidized bed for >6 mm coal cleaning motivates scholars to explore the possibility of fine coal cleaning using dry beneficiation methods. In this study, pulsed flow was introduced into a fluidized bed to optimize bubble behavior, thus improving the density stability. The equation of minimum fluidization velocity (U_mfp) in a gas-vibro fluidized bed for coal preparation was investigated theoretically. An equation has been proposed for predicting U_mfp while considering changes in the friction coefficient (C_f) in the gas-vibro fluidized bed. Based on two-phase theory, the correlation of bed density was determined by analyzing the bubble behavior in the gas-vibro fluidized bed. The theoretical bed density was then compared with experimental data of the bed density and separation density. The predicted bed density in monodisperse and binary dense medium systems was found to be consistent with the experimental results. Overall, the equation of bed density is suitable for estimating the separation density in the gas-vibro fluidized bed.

1. Introduction

Coal is the largest energy resource in China, accounting for about 63% of total energy consumption in 2017.¹ It is noted that combustion of raw coal generally produces amount of ash, which causes serious air pollution, e.g., fog and haze. Coal beneficiation technologies are commonly used to remove gangue during the initial stage of coal cleaning. Traditionally, coal and gangue are often segregated, depending on the difference in their densities, surface properties, and dielectric constants.² Gravity methods, such as cyclone and dense medium separation system, still play a crucial role in coal cleaning.³⁻⁶ However, water shortage is an important problem in the western arid regions of China. In addition, investments are another factor for consideration when evaluating the technical feasibility. Thus, dry beneficiation methods have drawn the scholars’ attention in recent years because of the advantages of no water consumption and lower investments. At present, different technologies have been put into production in the industry.^7,8 An air-jig separator, FGX separator, and air dense medium fluidized bed (ADMFB) are representative beneficiation technologies. It is worth noting that the separation principles of air-jig and FGX separators are primarily based on differences in the settling velocity of coal and gangue.^9,10 It is noticeable that the settling velocity is directly related to the particle size and density. It is difficult to remove gangue if coal and gangue have the same settling velocity. ADMFB primarily relies on the bed density for segregation of coal and gangue. In the separation procedure, magnetite powder is suspended by gas in the bed and the fluidized bed has pseudofluid properties with stable density. The gangue density is higher than the bed density; thus, gangue sinks to the bottom of the bed while coal floats to the surface.¹¹⁻¹⁴ In recent years, ADMFB has been used for >6 mm coal separation on an industrial scale.¹⁵

The successful use of ADMFB for >6 mm coal separation motivates scholars to explore its possible use for fine coal separation with dry beneficiation methods. Because additional energy can reduce the bubble size and increase the bubble residence time in the fluidized bed, the bed density fluctuation decreases significantly. Other scholars have attempted to introduce additional energy, such as vibration and pulsed flow energy, into the bed to optimize bubble behavior and improve density stability.¹⁶⁻²⁰ It is important to point out that the gas-vibro fluidized bed was widely studied in recent years, including its separation mechanism, density distribution, separation theory, and its use for fine coal separation. However, many density models are mainly based on the empirical methods through the separation experiments. A few studies have been conducted on the theoretical analysis of bed density in a gas-vibro fluidized bed. Compared to the previous models, the density model based on the two-phase theory can generally predict the bed density well in the fluidized bed. Therefore, minimum fluidization velocity and the fluid mechanics in the gas-vibro fluidized bed were initially investigated in this study. The equation of the minimum fluidization velocity was also proposed by analyzing the relationship between the friction coefficient (C_f) and the frequency of gas flow. During the second stage, the theoretical bed density models were put forward depending on the two-phase theory in a gas-vibro fluidized bed. The theoretical density was then compared with experimental data on the bed density and separation density to verify the accuracy of the model.

2. Experimental System and Materials

2.1. Experimental Apparatus

Figure 1 shows the experimental apparatus of the gas-vibro fluidized bed. The apparatus includes a gas supply system, a gas flow control system, a pulsed flow generator system, a fluidized bed separator, feedstock, and a data acquisition system. The fluidized bed system includes an air chamber, a distributor, and a cylindrical column. The pore size of the distributor is 5 mm, and the cylindrical column is made of organic glass with 120 mm inner diameter and 400 mm height. Pulsed gas flow was provided by installing a butterfly valve driven by an electric motor, and an inverter was used to control the speed of the motor corresponding to the pulsed frequency of gas flow. A pressure transducer was used to measure the pressure drop in the fluidized bed. During the separation process, fine magnetite powder, coal powder, and quartz sand powder were used as dense medium in the fluidized bed. Raw coal was then placed in the fluidized bed from feedstock. Coal with lower density floats to the surface, while gangue with a higher density sinks to the bottom.

Figure 1.

Schematic diagram of the gas-vibro fluidized bed system. (1) Air generator; (2) flow meter; (3) air valve; (4) electric motor; (5) butterfly; (6) cylindrical column; (7) feedstock; (8) pressure transducer; and (9) data acquisition system.

2.2. Dense Medium and Coal Sample Properties

Because magnetite powder can be easily recovered and reused, it is primarily used for coal beneficiation in the gas-vibro fluidized bed. The bed density normally ranges from 1.8 to 2.3 g/cm³ if magnetite powder is used as the dense medium. As shown in Figure 2, due to the high bed density in a monodisperse particle system, it is necessary to investigate a method for decreasing separation density in the gas-vibro fluidized bed. Traditionally, a mixture of binary particle is an effective method to decrease the separation density and broaden the range of density adjustment. As shown in Table 1, magnetite powder, fine coal, and quartz sand powder were used to investigate the fluidization characteristics and conduct separation experiments in the gas-vibro fluidized bed. One should note that magnetite powders with average sizes of 232 and 110 μm were used to investigate the fluidization characteristics in a single dense medium system. The mixture of magnetite powder and fine coal powder or quartz sand powder were used to study the fluidization behavior in a binary dense medium system. To apply fluidization theory in the binary particle systems, it is important to define the particle diameter and density of the binary particles. In this study, an effective density and effective diameter of mixture are defined as²¹

1

2

where ρ̅ is the equivalent density of binary particles, w₁ and w₂ are the proportions of each type of particle, and d̅ is equivalent diameter of the binary particles.

Figure 2.

Single and binary dense medium systems for coal beneficiation.

Table 1. Properties of the Dense Medium.

material type	ρs (kg/m3)	dp (μm)	voidage
magnetite powder	4600	232	0.45
magnetite powder	4590	110	0.48
quart sand powder	2600	250	0.45
fine coal powder	1400	400	0.40

In this study, a −6 + 3 mm coal sample from Xinjiang, China was used for separation experiments. Table 2 shows the density distribution and ash content, which were determined through float-and-sink experiments. The ash content exhibits an increasing tendency as the density increases, and the average content of raw coal is 25.13%. Meanwhile, the average ash content of coal with −1.6 g/cm³ is 4.30%. In addition, coal with a density of −1.6 g/cm³ accounts for the highest proportion, 72.53% of all samples. The aim of coal separation is to decrease the ash content to about 5%, while the separation density should be maintained near 1.6 g/cm³. Therefore, we also attempted to explore the possibility of separation at a lower density in the gas-vibro fluidized bed.

Table 2. Results of Float-and-Sink Test of −6+3 mm Coal.

			cumulative float		cumulative sink		separation density ± 0.1
density (g/cm3)	fraction (%)	ash (%)	fraction (%)	ash (%)	fraction (%)	ash (%)	density (g/cm3)	fraction (%)
<1.3	1.74	2.83	1.87	2.83	100.00	25.13	1.30	59.50
1.3–1.4	57.76	2.86	59.50	2.86	98.25	25.53	1.40	67.89
1.4–1.5	10.13	8.60	69.63	3.69	40.49	57.86	1.50	13.03
1.5–1.6	2.90	18.91	72.53	4.30	30.37	74.28	1.60	5.43
1.6–1.8	2.53	38.37	75.06	5.45	27.46	80.13	1.70	2.53
1.8–2.0	2.23	50.13	77.30	6.74	24.93	84.37	1.90	2.23
>2.0	22.70	87.74	100.00	25.13	22.70	87.74
total	100	25.13

3. Results and Discussion

3.1. Minimum Fluidization Velocity in the Gas-Vibro Fluidized Bed

The minimum fluidization velocity (U_mf) is a crucial parameter for identifying the transition from a fixed bed to a fluidized bed. When the gas velocity U < U_mf, the particles are in a quiescent state and the pressure drop increases linearly as the gas velocity increases. In contrast, the particles are suspended in the gas, the pressure drop remains constant, and the bed enters a fluidized state when U > U_mf. In a laboratory scale, experimental methods are used to determine U_mf using pressure drop and gas velocity data. However, one should note that exploring U_mf on an industrial scale using experimental methods is difficult due to difficulty in data collection. Thus, theoretical analysis is necessary to determine correlations in the experimental data when predicting U_mf. In a traditional gas–solid fluidized bed, researchers consider particles in the fluidized bed like an inclined pipe.²² Through an analysis of the relationship between the friction coefficient (C_f) and Reynolds number (Re), the pressure drop (ΔP) in a fluidized bed can be described as shown in eq 3

3

where μ is the gas viscosity, L is the height of particles in the bed, d is the particle size, U is the gas velocity, ε is the particle voidage, and λ is a constant.

Carman considered λ = 180 in a traditional fluidized bed.²³ However, Ergun proposed that C_f in eq 3 can be used to calculate ΔP at lower Re values and modified the friction coefficient is as follows²⁴

4

Thus, ΔP in a fluidized bed becomes

5

The gravity and drag are balanced when U = U_mf, namely, the weight of particles is equal to the pressure drop in the fluidized bed, as shown in eq 6

6

where ρ_s is the particle density, ε_mf is the particle voidage in the minimum fluidization state, and g is the gravitational acceleration. Therefore, U_mf can be calculated by combining eqs 3 and 6, or eqs 5 and 6.

Compared to a traditional fluidized bed, a gas-vibro fluidized bed relies on variations in gas flow to encourage gas vibration, which produces variations in C_f. It was found in previous studies that U_mf varies with different gas pulse frequencies in the fluidized bed.²⁰ Traditional equations of U_mf do not work well in a gas-vibro fluidized bed. It is necessary to determine a new equation of U_mf in a gas-vibro fluidized bed. For particles in a gas-vibro fluidized bed, the force balance is defined as

7

where F_D is the drag force and F_m is the weight of the particles. Kozeny’s method can be used at lower Re to simplify C_f in a gas-vibro fluidized bed. Thus, combining eqs 3, 6, and 7 yields

8

where U_mfp is the minimum fluidization velocity in the gas-vibro fluidized bed.

Due to disturbances in the pulsed gas flow, λ is directly related to the frequency of the pulsed gas flow as follows

9

Thus, eq 8 can written as follows

10

Finally, U_mfp can be written as follows

11

Table 3 shows detailed information about U_mfp with different particles and λ at different gas pulsed frequencies. Figure 3 shows a curve for fitting the value of k(f), where the equation is defined as

12

One should notice that λ is about 180, as proposed by Carman,²³ when the gas pulse frequency is 0. Meanwhile, values of λ are similar at the same gas pulse frequency, proving the credibility of the assumption of λ in the gas-vibro fluidized bed. Meanwhile, error analysis yields an overall R² value of 80.65% compared with the experimental data, showing higher precision in the gas-vibro fluidized bed. Based on theoretical C_f values, experimental data on U_mfp were compared with theoretical U_mfp values, as shown in Figure 4. The results show that the predicted minimum gas velocities are consistent with the experimental data, with a relative deviation of less than 10%. This means that the new equation of U_mfp is consistent with the experimental data. Therefore, equations of U_mfp are suitable for predicting the minimum gas fluidization velocity in a gas-vibro fluidized bed when considering pulsed gas flow. Meanwhile, the new equation has wide applications, which can be accurately used to predict U_mfp for monodisperse and binary particle systems.

Table 3. Minimum Gas Velocity in Gas-Vibro Fluidized Bed.

	dense medium				gas
type	material	ρs (kg/m3)	dp (μm)	voidage	ρf (kg/m3)	viscosity (kg/(m s))	f (Hz)	Umfp (cm/s)	k(f)
monodispersed dense medium	magnetite powder	4600	232	0.45	1.205	17.9 × 10–6	0	12.3	182.78
		4600	232	0.45	1.205	17.9 × 10–6	0.87	11.2	200.72
		4600	232	0.45	1.205	17.9 × 10–6	1.75	10.8	208.16
		4600	232	0.45	1.205	17.9 × 10–6	2.62	10.7	210.10
		4600	232	0.45	1.205	17.9 × 10–6	3.49	10.3	218.27
		4600	232	0.45	1.205	17.9 × 10–6	4.36	10.1	222.59
		4600	232	0.45	1.205	17.9 × 10–6	5.24	10.2	220.41
		4600	232	0.45	1.205	17.9 × 10–6	6.11	10.5	214.11
	magnetite powder	4590	110	0.48	1.205	17.9 × 10–6	0	3.5	184.96
		4590	110	0.48	1.205	17.9 × 10–6	0.85	3.3	196.16
		4590	110	0.48	1.205	17.9 × 10–6	1.70	3.1	208.82
binary mixture dense medium	magnetite powder + quart sand (40%)	3514	158	0.47	1.205	17.9 × 10–6	0	5.5	171.24
		3514	158	0.47	1.205	17.9 × 10–6	0.85	5.2	181.12
		3514	158	0.47	1.205	17.9 × 10–6	1.70	4.9	192.21
		3514	158	0.47	1.205	17.9 × 10–6	2.55	4.4	200.39
		3514	158	0.47	1.205	17.9 × 10–6	3.40	4.2	209.29
		3514	158	0.47	1.205	17.9 × 10–6	4.25	4.1	214.05
	magnetite powder + fine coal powder (10%)	3738	136	0.46	1.205	17.9 × 10–6	0	4	170.75
		3738	136	0.46	1.205	17.9 × 10–6	0.85	3.8	179.74
		3738	136	0.46	1.205	17.9 × 10–6	1.70	3.6	189.73
		3738	136	0.46	1.205	17.9 × 10–6	2.55	3.3	206.98
		3738	136	0.46	1.205	17.9 × 10–6	3.40	3.2	213.45
		3738	136	0.46	1.205	17.9 × 10–6	4.25	3	227.68

Figure 3.

Variation of constant value (λ) at different frequencies of pulsed gas flow.

Figure 4.

Error analysis of the proposed correlation for the available experimental data.

3.2. Estimation of Bed Density Based on Two-Phase Theory in the Gas-Vibro Fluidized Bed

Traditionally, for Geldart B particles, bubbles begin to arise in the fluidized bed when U > U_mf. Two phases (bubble phase and emulsion phase) appear in the fluidized bed simultaneously,²⁵ as shown in Figure 5. Generally, it is considered that bubbles carry extra gas away from the bed. Thus, the bubble phase volume can be described as follows

13

where Q is the extra gas flow, A is the cross-sectional area of the fluidized bed, and ΔU is the extra gas velocity. The bubble holdup at one certain bed height can calculated using eq 14

14

Thus, the bed height occupied by bubbles is

15

The total bed height is

16

When the bubbles are stable and U_b exhibits little variation at a certain height, eq 16 simply becomes

17

In the gas-vibro fluidized bed, the bubble size and diameter are important parameters for understanding the distribution of the bubble and emulsion phases. Many researchers experimentally investigated the bubble behavior in gas-vibro fluidized beds.²⁶⁻³¹Regarding the bubble size, Sobrino et al. and Dong et al. observed the variation of bubble size in gas-vibro fluidized beds and found some difference in the bubble size between a traditional fluidized bed and a gas-vibro fluidized bed.^26,27 In addition, Sobrino et al. proposed the bubble size equation in the gas-vibro fluidized bed²⁶

18

where r_bd is the initial bubble radius, A₀ is cross-sectional area per hole in the distributor, and ω is the angular velocity of the butterfly valve.

Figure 5.

Schematic diagram of two-phase theory of fluidization.

Thus, the bubble diameter becomes

19

For estimating the bubble size, Bizhaem et al. attempted to use Mori and Wen’s bubble size equations in a gas-vibro fluidized bed.^31,32 The equations can be described as follows

20

21

where d_eq,m is the maximum equivalent bubble diameter of a bubble and D is the fluidized bed diameter.

Regarding the bubble size, Köksal et al. found that the bubble velocity in a gas-vibro fluidized bed is lower than that in a traditional fluidized bed,²⁹ which increases the bubble residence time and bed expansion in a gas-vibro fluidized bed. The equations can be described as follows

22

The total bed height is

23

Thus, average bubble holdup, , can be calculated as

24

The bed density in a fluidized bed at a given height is

25

Thus, combining eq 24 with eq 25, the bed density in a fluidized bed at a given height is

26

For high-density separation of coal in a gas-vibro fluidized bed, magnetite powder is only used as the dense medium with the separation density ranging from approximately 1.8 to 2.2 g/cm³. In this study, 232 and 110 μm magnetite powders were chosen for density analysis. Dong previously used the 232 μm magnetite powder and reported the effect of the gas pulse frequency on density variations at a fluidization number, N, of 1.2.²⁰ Thus, for the former particles, data were collected from the previous study for comparison. For the 110 μm magnetite powder, the bed density was analyzed at different pulse frequencies and gas velocities. As shown in Figures 6 and 7, experimental data for the 110 and 232 μm magnetite powders were compared with the theoretical value calculated by eq 26 in the fluidized bed, respectively. One should note that the error between the theoretical density and the experiment data are approximately ±0.1 g/cm³, which meets the required density prediction accuracy in an industrial process. Thus, the equation can be used to estimate the density in monodispersed particle systems. The small difference may arise due to errors in estimating the bubble behavior and gas exchange between the emulsion and bubble phases.

Figure 6.

Prediction for the bed density of magnetite powder (110 μm).

Figure 7.

Prediction for the bed density of magnetite powder (232 μm).

For a binary particle system in a gas-vibro fluidized bed, magnetite powder (110 μm) was mixed with fine coal (400 μm) and quartz sand (250 μm). Figures 8 and 9 show that the theoretical bed density calculated with eq 26 is consistent with the experimental data in a binary particle system. In most cases, the error between the theoretical density and experimental data are within ±0.1 g/cm³, which shows that the bed density model provides very accurate density predictions in a binary particle system. Therefore, the equation can also be used to estimate the bed density in a binary particle system.

Figure 8.

Prediction for the bed density of a mixture of magnetite powder (110 μm) and 40% quartz sand (250 μm).

Figure 9.

Prediction for the bed density of mixture of magnetite powder (110 μm) and 10% fine coal (400 μm).

Figure 10 shows the error between the experimental data and predicted values. The relative deviation between the theoretical and experimental data is within ±10%. It is worth noting that better agreement can be found between the calculated and experimental values with a relative deviation of less than 15%. Thus, the theoretical bed density determined from two-phase theory is consistent with the experimental data. Based on the above analysis, the proposed equation is suitable for predicting the bed density in the gas-vibro fluidized bed.

Figure 10.

Error analysis of correlation for the bed density.

3.3. Comparison between Bed Density and Separation Density

Traditionally, the bed density can be measured with pressure transducers and calculated by analyzing the distribution of the bubble and dense phase in the fluidized bed. The separation density is determined through coal beneficiation experiments. Because the bubble behavior or dense medium can affect the coal movement, the separation density may be slightly different from the bed density. To analyze the relation between the bed density and separation density, fine coal separation experiments must be conducted to explore the reliability of eq 26. At present, much work on coal separation using a high-density gas-vibro fluidized bed has been conducted.^{18−20,27,30} Separation density data were collected for comparison. For low-density separation of fine coal, magnetite powder (110 μm) and quartz sand (200 μm, 40%) were mixed to decrease the separation density in the study.

A partition curve is often used to analyze the separation density in an industrial process during actual coal separation experiments.^15,17,20 The X-coordinate is the density and the Y-coordinate is the mass fraction of the misplaced coal, whose density is lower than the density corresponding to the X-coordinate value. The partition coefficient, δ₅₀, refers to the separation density when the partition coefficient is 50%. Figures 11 and 12 show the separation density at different gas velocities and gas pulse frequencies. The results show that the separation densities are approximately 1.6 g/cm³, which are very close to the theoretical bed density in the gas-vibro fluidized bed.

Figure 11.

Separation results at different gas velocities.

Figure 12.

Separation results at different frequencies of pulsed gas flow.

The separation densities from many publications were then collected for comparison with the theoretical bed density determined using the above equations, as shown in Table 4. The error between the separation densities and theoretical values is compared in Figure 13. It is worth noting that the predicted bed densities are consistent with the experimental data with a relative deviation of less than 10%. In addition, fairly better agreement can be found between the calculated and experimental values with a relative deviation of less than 15%. The agreement between the experimental and predicted values further illustrates the reliability of the predicted density. Based on above analysis, the theoretical bed density based on the two-phase theory can be used to predict the separation density in a gas-vibro fluidized bed.

Table 4. Literature Summary of Separation Density in the Gas–Solid Fluidized Bed.

		medium properties
refs	bed diameter (mm)	type	density (g/cm3)	size (μm)	medium height (mm)	ΔU (m/s)	sep. density (g/cm3)	notes
(20)	200	magnetite powder	4600	232	100	0.0246	1.85
							2.03
(33)	40	magnetite powder	5200	53–106	50	0.145	1.6
(34)	120	magnetite powder	4500	150–300	80	0.0412	1.82
(35)	120	magnetite powder	4500	150–300	90	0.048	1.83
(36)	290	zircon sand	4200	238	150	0.008	2.85
(37)a	290	zircon sand + iron powder	bulk density: 2900 (zircon sand) + 4400 (iron powder)	100–300 (zircon powder) + 100 (Iron powder)	200	0.0155	2.75	V (iron) = 0
						0.031	2.55
						0.0465	2.45
						0.0095	3.25	V (iron) = 25%
						0.019	3.05
						0.0285	2.90
						0.0075	3.55	V (iron) = 50%
						0.015	3.50
						0.0225	3.25
						0.008	3.90	V (iron) = 100%
						0.016	3.60
						0.024	3.50

^aThe reference gives the bulk densities of zircon powder and iron powder. The average density can be calculated as ρ̅ρ_bulk1V₁ + ρ_bulk2V₂.

Figure 13.

Error analysis of correlation for separation density and theoretical bed density.

4. Conclusions

A theoretical analysis of the minimum fluidization velocity and bed density is necessary to establish relative equations. It is noted that the gas pulse frequency influences U_mfp. An equation for predicting U_mfp that considers changes in the friction coefficient (C_f) in the gas-vibro fluidized bed has been proposed. The predicted minimum gas velocities are consistent with the experimental data with a relative deviation of less than 10%. The bed density was defined in terms of the bubble size and velocity in the gas-vibro fluidized bed based on the two-phase theory. Compared with the experimental bed density, prediction density errors are less than 0.10 g/cm³ in major situations, which illustrates accurate bed density prediction in monodisperse and binary particle systems. Compared with the separation density, the theoretical values are consistent with the experimental data with a relative deviation of less than 15%, illustrating the reliability of the theoretical density. Thus, the predicted bed density determined from two-phase theory can be used for predicting the separation density in a gas-vibro fluidized bed.

Glossary

NOMENCLATURE

A₀

section area of the hole, m²

A

section area of the fluidized bed, m²

C_f

friction coefficient

d

particle size, m

d̅

particle diameter of binary particles, μm

d_eq,m

maximum equivalent diameter of the bubble, m

d₀

diameter of the hole in the distributor, m²

d_b

bubble diameter, m

D

fluidized bed diameter, m

ε

particle voidage

ε_b

bubble holdup at a certain bed height

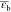
average bubble holdup

ε_mf

particle voidage at the minimum fluidization state

F_D

drag force, N

F_m

mass force, N

g

gravitational acceleration, m/s²

Re

Reynolds number,

λ

constant value

H

total bed height, m

H_b

bed height occupied by bubbles, m

H_mf

minimum bed height, m

L

bed height of particles, m

N

fluidization number, N = U/U_mf

ΔP

pressure drop, Pa

ρ_g

gas density, kg/m³

ρ_s

dense medium density, kg/m³

ρ̅

particle density of binary particles, g/cm³

Q

gas flow, m³/h

μ

gas viscosity, kg/(m s)

U

gas velocity, m/s

U_mf

minimum fluidization velocity in the normal fluidized bed

U_mfp

minimum fluidization velocity in the gas-vibro fluidized bed, m/s

ΔU

extra gas velocity, m/s

V (iron) = 0

bulk volume percentage of iron powder, %

δ₅₀

separation density when the partition coefficient is 50%

w₁

fraction of one particle, %

w₂

fraction of another particle, %

ω

angular velocity of the butterfly,

Author Contributions

^∥ C.Z. and L.D. contributed equally to the work and can be considered co-first author.

The authors declare no competing financial interest.