Single-neuron perturbations reveal feature-specific competition in V1

Abstract

We developed a method – influence mapping – that uses single-cell perturbations to reveal how local neural populations reshape representations. We used two-photon optogenetics to trigger action potentials in a targeted neuron and calcium imaging to measure the effect on neighbors’ spiking in awake mice viewing visual stimuli. In V1 layer 2/3, excitatory neurons on average suppressed other neurons and had a center-surround influence profile over anatomical space. A neuron’s influence on a neighbor depended on their similarity in activity. Notably, neurons suppressed activity in similarly tuned neurons more than dissimilarly tuned neurons. Also, photostimulation reduced the population response, specifically to the targeted neuron’s preferred stimulus, by ~2%. Therefore, V1 layer 2/3 performed feature competition, in which a like-suppresses-like motif reduces redundancy in population activity and may assist inference of the features underlying sensory input. We anticipate influence mapping can be extended to uncover computations in other neural populations.

We studied how local groups of neurons in layer 2/3 of mouse primary visual cortex (V1) reshape representations, by perturbing identified neurons and monitoring resulting changes in the local population. Layer 2/3 encodes various features of visual stimuli, including stimulus orientation, which are also encoded in its inputs from layer 4^1–3. Studies have proposed that layer 2/3 reshapes these inherited representations through ‘feature amplification’ to increase the magnitude and reliability of a stimulus response^4,5. Amplification is based on the idea that activity in one neuron enhances the activity of similarly tuned neurons more than dissimilarly tuned neurons. Findings that excitatory neurons with similar tuning have stronger and more frequent monosynaptic connections^5–9 support this hypothesis. Alternatively, theoretical work^10–13 and related experimental findings^14–16 have suggested that competition is critical for the computational goals of V1. We can generalize the predictions of this work as ‘feature competition’: the activity of a neuron suppresses similarly tuned neurons more than dissimilarly tuned neurons. Feature competition can reduce redundancy in a population representation¹⁰, and differentiate representations of similar stimuli that cause overlapping sensory receptor activity, thus assisting inference of the properties of external stimuli^12,17. Feature amplification and feature competition could also co-exist in a population between different subsets of neurons.

These hypotheses make direct predictions of how the activity of one neuron affects nearby neurons. This effect is difficult to measure with existing methods because it is both causal and functional. For example, from monosynaptic connectivity^5,8,9,18 it is challenging to predict how one neuron’s spiking affects another’s because connectivity profiles are typically incomplete (often limited to < 50 µm) and contributions from all polysynaptic pathways (e.g. disynaptic inhibition^19–21) must be simultaneously considered. Also, from activity measurements alone, as in functional connectivity studies²², it is difficult to establish causality. Therefore, we extended previous work^21,23–29 and developed a method – influence mapping – in which we optically triggered action potentials in a targeted neuron to directly measure its functional influence on neighboring, non-targeted neurons with known tuning (Fig. 1a).

Figure 1:

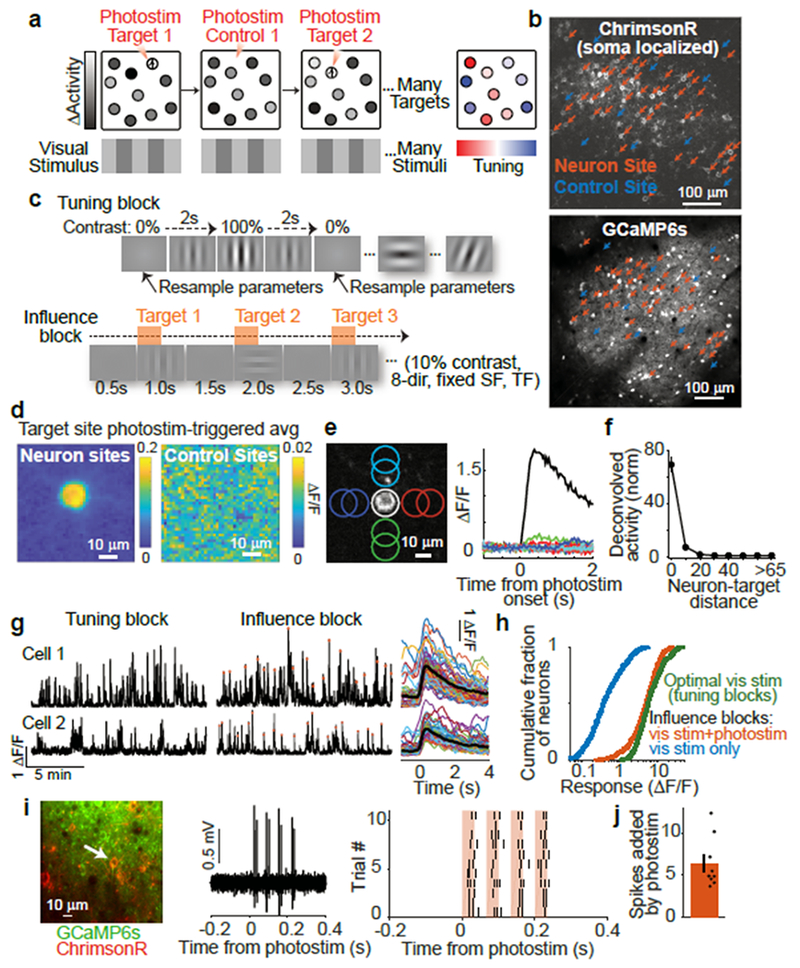
Photostimulation of targeted neurons

(a) Influence mapping schematic.

(b) Example field-of-view with neuron (red) and control (blue) photostimulation sites.

(c) Top: Tuning blocks measured responses to drifting gratings with varying direction, spatial frequency, and temporal frequency. Bottom: Influence blocks presented 10% contrast visual stimuli simultaneous to single-neuron photostimulation.

(d) Photostimulation-triggered average fluorescence changes from raw images centered on targeted neuron sites (n = 31) and control sites (n = 10). n = 153 trials per site.

(e) Left: Photostimulation sites (colored circles) near isolated C1V1-expressing neuron. Right: Fluorescence transients following photostimulation at sites in left panel.

(f) Response vs. distance between centers of photostimulation and soma (normalized by median at > 65 μm). n = 9 experiments, 3 mice, 98 targets at 16,019 sites, 25 trials/site. Compared to > 65 μm (n = 13,367 sites): p < 1.3 × 10⁻³ for each bin ≤ 15-25 μm (n = 774); p > 0.17 for each bin ≥ 25-35 μm (n = 300), Mann-Whitney U-test.

(g) Left: Activity traces during tuning and influence blocks. Red dots mark photostimulation times. Right: Single-trial traces for all photostimulation events during an influence block (smoothed for display). Black lines, mean.

(h) Responses to optimal visual stimuli during tuning block (green) and to visual stimuli during influence block with (red) or without (blue) photostimulation. Influence block with photostimulation vs. optimal visual stimulus: p < 3.1×10⁻⁶, Mann-Whitney U-test, n=518 neurons.

(i) Example cell-attached electrophysiology during photostimulation. Left: Cell recorded and targeted for photostimulation, white arrow. Middle: Single trial trace during photostimulation. Right: Raster plot of spikes across all trials. Photostimulation (red): four 32 ms-long sweeps at 15 Hz.

(j) Spikes added over four photostimulation sweeps in ~250 ms. Mean ± sem: 6.38 ± 1.01 spikes added per trial. n = 9 cells.

Photostimulation of targeted neurons

We co-expressed GCaMP6s and a red-shifted channelrhodopsin (C1V1-t/t or ChrimsonR)^30,31 in layer 2/3 V1 neurons (Fig. 1b). Opsin expression was restricted to excitatory neurons using the CaMKIIα promoter. We targeted localization of channelrhodopsin to the soma using a motif from the Kv2.1 channel³² (Extended Data Fig. 1a). This localization should improve the specificity of influence measurements by reducing photostimulation of non-targeted neurons’ axons and dendrites near the target site³³. In tuning measurement blocks, we measured neural responses to contrast-modulated gratings with varying drift direction, spatial frequency, and temporal frequency (Fig. 1c, top). In influence measurement blocks, we independently scanned two lasers of different wavelengths to simultaneously image neuronal activity across the population and photostimulate individual targeted neurons with two-photon excitation (Extended Data Fig. 1b). Photostimulation was time-locked to the onset of low contrast (10%) drifting gratings (eight directions, fixed spatial and temporal frequencies) to measure influence in the context of visual stimulus processing (Fig. 1c, bottom). Photostimulation induced cell-shaped increases in fluorescence at the target site, indicating selective photostimulation of the targeted neuron (Fig. 1d–f; Extended Data Fig. 1c,e; Supplementary Videos 1–2).

To examine the resolution of photostimulation, we limited opsin expression to a very sparse set of neurons and monitored photostimulation responses in an isolated opsin-expressing neuron. Responses decreased with distance between the neuron and photostimulation target, and were not significant beyond 25 μm (Fig. 1e–f, Extended Data Fig. 1d). To be conservative, all subsequent analyses excluded neuron pairs with < 25 μm lateral separation. To further control for off-target photostimulation, in influence mapping experiments, we expressed channelrhodopsin in a moderately sparse subset of excitatory neurons (~20–60 neurons in 0.3 mm²; Fig. 1b) to reduce opsin-expressing neurons adjacent to photostimulation targets. Furthermore, we interleaved trials targeting opsin-expressing neurons with trials targeting control sites that lacked an opsin-expressing cell (Fig. 1b). Control sites accounted for effects arising from nonspecific photostimulation (including in the axial dimension). Control photostimulation triggered no fluorescence changes near the target (Fig. 1d, Extended Data Fig. 1c).

To estimate the amplitude of activity induced by photostimulation, we performed cell-attached electrophysiological recordings in anesthetized animals, without presented visual stimuli. Photostimulation added approximately six spikes in the targeted neuron within the ~250 ms photostimulation window (Fig. 1i–j). During influence measurement blocks in awake mice, photostimulation concurrent with low contrast visual stimuli elevated the activity of targeted neurons above the levels evoked by the visual stimuli alone, as expected (Figure 1h). The targeted neuron’s activity following photostimulation during low contrast visual stimuli was slightly smaller than responses to optimal gratings in the tuning measurement block (Figure 1g–h). Photostimulation therefore induced activity that did not exceed physiologically relevant levels. The magnitude of photostimulation did not vary strongly with other properties of the cell, including visual stimulus tuning (Extended Data Fig. 1f–g).

The magnitude of influence in layer 2/3 of V1

We quantified the change in each non-targeted neuron’s activity following photostimulation. Using the deconvolved activity of non-targeted neurons, we calculated an influence metric ΔActivity: the response on individual photostimulation trials minus the average response on control trials with the same visual stimulus, normalized by the standard deviation of this difference over all trials (Fig. 2a, left). We averaged a neuron’s ΔActivity over all trials for individual photostimulation targets to obtain an influence value for each pair of targeted and non-targeted neuron. We identified positive (excitatory) and negative (inhibitory) influence (Fig. 2a). Influence values corresponded to soma-shaped fluorescence changes in raw images centered on the non-targeted neuron (Fig. 2b). We also developed a metric that expressed influence as a probability that a non-targeted neuron was excited or inhibited following photostimulation. This metric was robust to the varyingly asymmetric and heavy-tailed distributions of individual neurons’ activity, and revealed similar findings (Extended Data Fig. 3).

Figure 2:

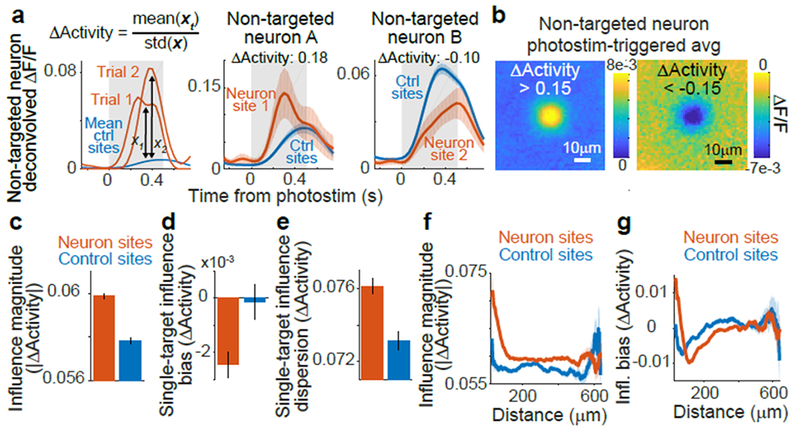
Measurement and characterization of influence

(a) Left: calculation of ΔActivity: activity in a non-targeted neuron on single trials following photostimulation of neuron site 1 (red) and on control trials (blue) with matched visual stimulus (gray box). x_t, values for all trials with photostimulation of site t. Center, Right: ΔActivity and traces for example pairs. Traces smoothed for display, shading is mean ± sem

(b) Photostimulation-triggered average fluorescence changes from raw images centered on all non-targeted neurons for pairs with ΔActivity > 0.15 (left) or < −0.15 (right).

(c) Influence magnitude (average of |ΔActivity| values) following neuron site (n = 153,689 pairs) or control site (n = 90,705) photostimulation. The non-zero value for control sites is expected because of noise due to random sampling of neural activity and potential off-target effects. Error bars, mean ± sem calculated by bootstrap. Neuron vs. control: p = 1.23 × 10⁻¹⁹, Mann-Whitney U-test.

(d) Influence bias (average of signed ΔActivity values) for a single target was the mean ΔActivity across all non-targeted neurons. Error bars, mean ± sem across targets. n = 518 neuron targets, 295 control targets. p = 0.0023, Mann-Whitney U-test.

(e) Same as for (d), except for influence dispersion for a single target, which was the standard deviation of ΔActivity across all non-targeted neurons. p = 2.1 × 10⁻⁶, Mann-Whitney U-test.

(f) Influence magnitude vs. distance between the target site and non-targeted neuron for pairs with neuron site (n=153,689) or control site (n=90,705) photostimulation, shading is mean ± sem

(g) Influence bias vs. distance, as in (h).

We compared influence following neuron and control site photostimulation, using a leave-one-out procedure to calculate ΔActivity for control sites. Control values deviated from zero because of random sampling of neural activity and potential off-target effects. However, the magnitude of influence values following neuron photostimulation were ~4% larger than for control photostimulation (Fig. 2c). This effect arose in part because individual excitatory neurons had an average inhibitory effect on other neurons (Fig 2d). In addition, for individual targeted neurons, influence values had ~4% greater dispersion than expected based on control sites (Fig. 2e). This larger dispersion indicated that a neuron differentially affected specific non-targeted neurons, potentially governed by similarities between targeted and non-targeted neurons.

We tested this idea by analyzing influence as a function of the anatomical distance between neurons. The magnitude of influence decreased with distance, although it remained above control levels for all distances (Fig. 2f). The relative strength of excitatory and inhibitory influence varied: on average, neurons < 70 μm apart had excitatory influence, maximum inhibitory influence was present around 110 μm, and net influence was balanced at longer distances > 300 μm (Fig. 2g). Influence therefore had a center-surround relationship with distance. Because there are fewer pairs at smaller distances, the average influence we observed was negative. Influence was most suppressive at distances where neurons’ receptive fields partially overlap (~12° receptive field width, ~10 μm/° retinotopic magnification)³⁴. Influence following control site photostimulation exhibited weak spatial structure, consistent with small off-target excitation (Fig. 2f–g).

To put these effects on a functional scale, we compared influence to single-trial variability in a neuron’s response. Influence values in units of ΔActivity were by definition a fraction of trial-to-trial variability. Moreover, the variance of the true effect of one neuron’s activity on another can be calculated as the difference in variance of influence values following neuron and control photostimulation. This calculation revealed that single-neuron photostimulation caused a 2.1% change in another neuron’s activity relative to trial-to-trial variability (quantified by the ratio of standard deviations). We similarly computed changes in activity as a fraction of average activity, and observed a 5.4% effect on other neurons, with a net ~0.5% decrease in population activity.

Considering that a neuron exhibits variability driven by thousands of synaptic inputs, yet we added a few spikes to a single neuron that typically will not be monosynaptically connected^5,8,19, these effects are substantial and underscore the strength of polysynaptic pathways^19,21. Despite this large effect from the perspective of brain function, our measurement for individual pairs was noisy: we performed 150–200 repeats per pair, yet ~2,500 repeats would be needed for a single-pair signal-to-noise ratio of ~1. However, by pooling data across > 10,000 pairs in each experiment, we obtained highly significant results at the population level.

Average influence effects could result from strong influence in a small fraction of pairs or weaker influence distributed across the population. Removing pairs with the largest positive or negative influence did not qualitatively change the population results (Extended Data Fig. 1a–c). Also, influence relationships were not significantly affected by a neuron’s baseline activity level or other properties (Extended Data Fig. 2d–i). Therefore, the addition of a few spikes to a targeted neuron had a distributed effect across many non-targeted neurons.

Tuning similarity is inversely related to influence

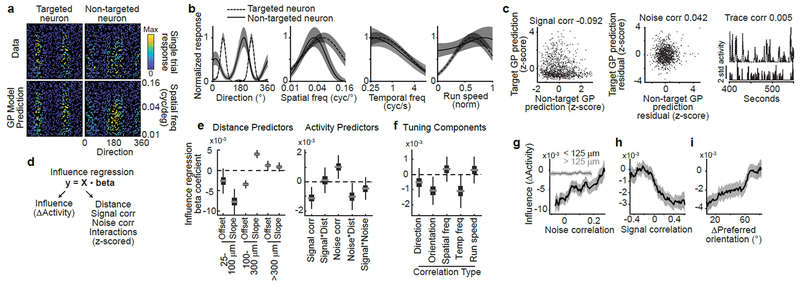
To test hypotheses of feature amplification and feature competition, we related visual tuning and influence in the same pairs of neurons. In blocks without photostimulation, we measured the tuning of neurons to gratings with randomly sampled drift direction, spatial frequency, and temporal frequency. To estimate neural tuning in the absence of identical stimulus repeats, we used a Bayesian nonparametric smoothing method, Gaussian Process regression (GP) (Fig. 3a–b, Extended Data Fig. 4). This method creates a tuning curve by approximating responses via comparisons to trials with a similar stimulus, assuming that neural responses are a smooth function of stimulus parameters. GP smoothing yielded similar tuning results to a conventional model and better predictions of neural activity (Extended Data Fig. 5).

Figure 3:

Relationship of influence to activity similarities between neurons

(a) Tuning for spatial frequency and direction for a pair of neurons. Each dot is a single trial color-coded by the mean activity throughout the visual stimulus. Data (top) and GP model predictions on held-out trials (bottom) showed high correspondence.

(b) One-dimensional tuning curves for the pair in (a), predicted from the GP model. Shading, mean ± sem.

(c) Signal correlation (left), noise correlation (middle), and trace correlation (right) for the pair in (a-b).

(d) Design of influence regression. Predictors were z-scored so that coefficients indicate the change in influence for 1std increase in predictor.

(e) Influence regression coefficient estimates based on bootstrap. Gray line, median; box, 25-75% interval; whiskers, 1-99% interval. Left: piece-wise linear distance predictors. 25-100 μm, offset p=0.048 (bootstrap), slope p<1×10⁻⁴; 100-300 μm, offset p<1×10⁻⁴, slope p<1×10⁻⁴; >300 μm, offset p=0.009, slope p=0.078. Right: activity predictors from the same model. Signal correlation, p=0.0004; signal*distance, p=0.77; noise correlation p=0.0024; noise*distance, p=0.013; signal*noise, p=0.17; n=64,485 pairs.

(f) Coefficient estimates from separate models, based on (d), using the specified correlation instead of signal correlation and pairs in which both neurons exhibited tuning. Direction, p = 0.18, n = 36,565 pairs; orientation, p = 0.0058, n = 36,565; spatial frequency, p = 0.32, n = 47,810; temporal frequency, p = 0.020, n = 26,526; running speed, p = 0.41, n = 46,634.

(g) Influence vs. noise correlation, for nearby (black, n=8,538) or distant (gray, n=56,307) pairs. Percentile bins, 20% half-width. Similar results with different distance thresholds (not shown). Shading, mean ± sem calculated by bootstrap.

(h) Influence vs. signal correlation. Percentile bins, 15% half-width.

(i) Influence vs. difference in preferred orientation. Bin half-width, 12.5 degrees.

For each pair of neurons, we computed similarity in tuning as a signal correlation, measured as the correlation between single-trial GP predictions of each neuron’s visual stimulus response (Fig. 3c). We also computed similarity in trial-to-trial variability as a noise correlation, using the correlation between single-trial residuals after subtraction of GP predictions (Fig. 3c). A model-free ‘trace correlation’ was computed as the correlation between the neurons’ activity throughout the tuning measurement block (Fig. 3c).

We used multiple linear regression to determine how distance, signal correlation, and noise correlation metrics related to the influence between neurons (Fig. 3d). Regression coefficients revealed the sign and magnitude of a metric’s relationship to influence, after controlling for the effects of other similarity metrics. We used this approach because there were correlations between metrics, such as higher activity correlations at shorter anatomical distances and a positive correlation between signal and noise correlations (Extended Data Fig. 6a–b). We included terms for interactions between metrics to consider non-linear effects, such as a changing relationship between signal correlation and influence at different anatomical distances. We complemented the regression analysis (Fig. 3e–f) by plotting influence as a function of single activity metrics (Fig. 3g–i) and comparing these plots to regression-based predictions (Extended Data Fig. 6c–f).

The regression results confirmed that influence had a center-surround pattern as a function of distance: near pairs had a negative slope, intermediate pairs a positive slope, and distant pairs a slope near zero (Fig. 3e, left; cf. Fig. 2g). Furthermore, influence was positively related to a neuron pair’s noise correlation (Fig. 3e, right). However, the noise correlation-by-distance interaction coefficient was negative, indicating the relationship between influence and noise correlations decayed with anatomical distance (Fig. 3e, right). Therefore, there existed a positive relationship between influence and noise correlation for nearby pairs, and little relationship for distant pairs (Fig. 3g). This suggests that noise correlations for nearby pairs partially reflected local influence, whereas noise correlations over a broad spatial range may reflect shared external inputs³⁵.

We then considered the relationship between influence and signal correlation. A positive regression coefficient would support feature amplification, whereas a negative coefficient would support feature competition. Influence had a significant negative relationship with signal correlation (Figure 3e, right). The signal correlation-by-distance interaction term was close to zero, indicating that this relationship did not vary with anatomical distance (Figure 3e, right). Influence also appeared more negative for higher signal correlation values by direct examination (Figure 3h). Therefore, similarly tuned neurons suppressed each other’s activity more than dissimilarly tuned neurons, across all distances examined.

To test which tuning features contributed to this relationship, we replaced signal correlation in the influence regression with correlations of individual tuning features. Orientation tuning recapitulated the negative relationship with influence, as did temporal frequency, indicating that representations of these features were reshaped by recurrent computation (Fig. 3f,i). Influence appeared unrelated to tuning similarity for running speed and spatial frequency, despite robust neural tuning to both of these features (Fig. 3f, Extended Data Fig. 4c–d). Local processing may therefore selectively shape only a subset of features present in its inputs.

Multiple factors therefore contributed to influence: (1) a center-surround effect of distance, (2) a positive effect of noise correlation that decayed with distance, and (3) a spatially-invariant negative effect of signal correlation, with specificity for distinct stimulus features. We verified that these influence patterns were not due to data processing or analysis artifacts by analyzing ΔF/F traces directly (Extended Data Fig. 7a–e). Because photostimulation likely caused weak activation of neurons near the targeted neuron, including axially displaced neurons^23,24,36 (Fig. 1f, Fig. 2f–g), we tested for effects due to off-target photostimulation. We repeated influence regression, but using the average activity similarity between the non-targeted neuron and multiple neurons near the target site. We found no significant effects of local activity (Extended Data Fig. 7f). Thus, our findings reflect a genuine relationship between an individual photostimulated neuron’s characteristics and its influence.

Functional significance on population encoding

Our results so far revealed feature competition based on trial-averaged pairwise relationships. However, these analyses did not quantify the functional consequence of influence on the brain’s ability to discriminate stimulus properties like orientation, using population responses on single trials. Feature competition led to a surprising prediction: due to greater suppression between similarly tuned neurons, photostimulation during a neuron’s preferred orientation should suppress the population response and reduce information about orientation in non-targeted neurons more than when presenting non-preferred orientations.

We analyzed responses in non-targeted neurons to drifting gratings in influence measurement blocks. We built decoders to estimate the population’s information about orientation on single trials, and examined accuracy as a function of similarity between visual stimulus orientation and the photostimulated neuron’s preference. Consistent with our prediction, we observed a significant decrease in decoding performance of ~2% when orientations matched (Fig. 4a).

Figure 4:

Effects of feature competition on population encoding of orientation

(a) Naïve-Bayes decoding of orientation from population activity during influence blocks. Error bars, mean ± sem, logistic regression mixed-effects model, non-overlapping bins. Line, logistic regression on non-binned data with a continuous similarity predictor; p = 0.00056, n = 54,187 trials, F-test.

(b) Population activity (deconvolved ΔF/F) along dimension for 0-degree oriented stimuli on control trials, example experiment. Activity along this dimension was high only during 0-degree stimuli, showing that population dimensions allow orientation discrimination. Shading, mean ± sem (bootstrap)

(c) Following (b), population activity along the 0-degree dimension during a 0-degree stimulus was decreased by photostimulation of example neurons preferring a similar stimulus (10-degrees) but not neurons preferring alternate stimuli (45-degrees).

(d) Following (b-c), photostimulation triggered little change along dimensions not aligned (0-degree dimension) with the presented stimulus (45-degrees).

(e) Changes in population encoding as a function of similarity between the orientation of visual stimulus and a photostimulated neuron’s preference. Dots, mean ± sem for 5 non-overlapping bins; line, linear regression on non-binned data using a single continuous predictor. The population response along the dimension of presented stimulus (‘gain’ dimension) was suppressed when orientations were similar, c = 0.0115, p = 0.0076, Spearman rank correlation. n = 54,187 trials.

(f) Responses along other directions were not affected, orthogonal orientation projection, c = 0.0045, p = 0.2974, n = 54,187 trials.

(g) Responses along the uniform dimension were not affected, c = −0.0046, p = 0.2880, n = 54,187 trials.

(h) Rate-network model. Neuron i receives feedforward input u_i and has functional connection w_i,j with neuron j.

(i) Model neuron responses for a 90 degree stimulus (dashed line). Feedforward inputs were identical for all networks.

(j) Model neuron responses for a linear sum of 60 and 120 degree stimuli. Gray lines, summed network response to the stimuli presented individually. Feedforward inputs have maxima ~70 and 110 degrees.

We then analyzed how photostimulation changed population encoding of orientation. For each of the four presented orientations, we defined a dimension of population activity that helped isolate the change in population activity specific to that orientation. In addition, we defined a non-selective ‘uniform’ dimension that weighted all neurons equally. Single-trial population responses were projected onto these dimensions (Fig. 4b–d, Extended Data Fig. 8b; Methods). When the targeted neuron’s preferred orientation was similar to the presented stimulus, we observed a ~2% decrease in activity along the dimension of the presented orientation (response gain) (Fig. 4c,e). Activity along the uniform dimension and other encoding dimensions was not significantly changed (Fig. 4d,f,g). In summary, suppression was selective for population activity encoding a visual stimulus matching the targeted neuron’s preference, and had physiological significance for the brain’s ability to discriminate visual stimuli.

Feature competition can support perceptual inference

One implication of feature competition is the reduction of redundant stimulus information in the population, which has benefits for sensory codes^10,11. We developed a ‘toy’ rate-network model to qualitatively explore this and other potential functions, guided by previous studies^13,17. Model neurons received orientation-tuned feedforward inputs (U) and had recurrent functional connections (W) that were similar in effect to influence (Fig. 4h). The functional connections were linearly proportional, with constant s, to the similarity in the connected neurons’ inputs. We modeled a competition network with a negative relationship between functional connections and input similarity (s < 0) and an ‘untuned’ network (s = 0) with the same level of overall inhibition (see Extended Data Fig. 9 for more detail).

Untuned and competition networks responded with a similar bump of activity to a single visual stimulus (Fig. 4i). To probe the impact of feature competition, we tested responses to stimuli with mixtures of different orientations. The competition network demixed feedforward inputs into components closely matching the responses to individual inputs (Fig. 4j). In contrast, the untuned network responded as a thresholded version of its input (Fig. 4j). Thus, the competition network inferred the underlying causes of feedforward input. Due to the negative relationship between recurrent connections and tuning similarity in the competition network, the recurrent connections counteracted input drive to each neuron that was better explained by another neuron’s activity^12,17. For example, in Fig. 4j, neurons preferring 60 or 120 degrees were driven strongly by feedforward input and inhibited neurons driven by overlap with the 60 and 120 degree stimuli but that preferred different orientations (e.g. 90 degrees). This effect is the statistical principle known as ‘explaining away’¹⁷: when an observed phenomena (e.g. feedforward input to a neuron preferring 90 degrees) could be caused by alternative sources (e.g. 60+120 degree or 90 degree stimuli), evidence for one cause typically decreases the likelihood of the other (e.g. suppression of the 90 degree cause due to evidence for the 60+120 degree cause). In the competition network, feedforward input was ‘observed’, and neural activity encoded an estimate of the stimulus features responsible for the input.

Non-competitive influence

The presence of feature competition on average does not exclude other possible structure in the neural population. We looked for structure consistent with strong monosynaptic connections between excitatory neurons with highly correlated moment-by-moment activity during stimulus presentation⁵ (trace correlation). The distribution of trace correlations was heavily weighted at small values, with pronounced positive and negative tails (Fig. 5a). Influence was excitatory for the most strongly correlated pairs (Fig. 5b). Pairs with high trace correlations had high signal and noise correlations, as well as fine-timescale correlations not captured by our signal and noise metrics, as expected for neurons with diverse locations and phases of receptive fields (Fig. 5c). For all other pairs, including even weakly positively correlated pairs, influence was inhibitory. The strongest negative influence was between highly anti-correlated neurons (Fig. 5b).

Figure 5:

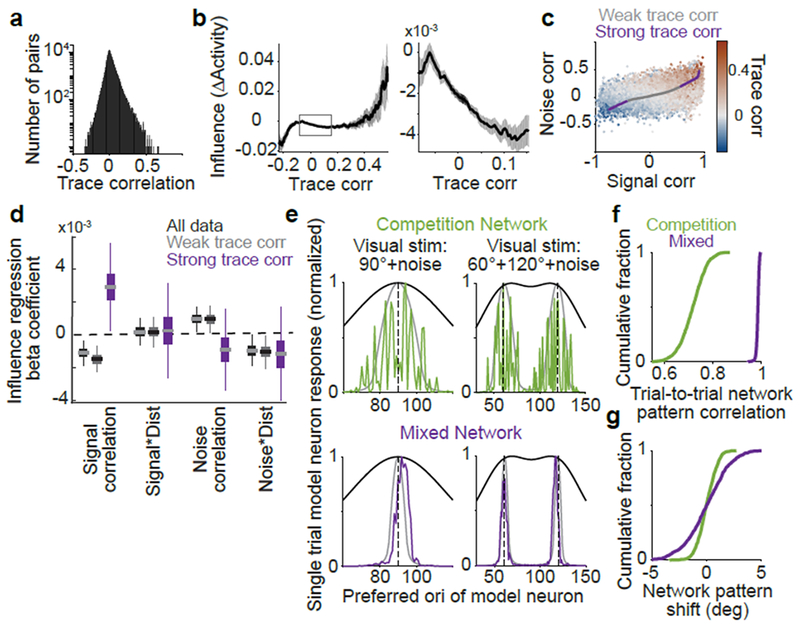
Strongly-correlated pairs exhibit non-competitive influence

(a) Histogram of trace correlations.

(b) Influence vs. trace correlation. Bin half-width, 0.1. Right: zoom on central 95% of trace correlations. Shading, mean ± sem (bootstrap), n=153,689 pairs.

(c) Signal and noise correlations colored by trace correlation. Line, average signal and noise correlations for the trace correlation bins in (b), colored by weak (central 95%) or strong (top, bottom 2.5%) trace correlations. Trace correlation is related, but not identical to, the sum of signal and noise correlations.

(d) Influence regression coefficients, as in Figure 3e. All data, black; pairs with weak (gray) or strong (purple) trace correlations. Distance predictors were included (not shown, see Extended Data Fig. 10). For strong trace correlations: signal correlation, p = 0.011 (bootstrap), n = 3,242 pairs; other coefficients, p > 0.32.

(e) Single trial rate-network model neuron responses to a 90 degree stimulus (left) or sum of 60 and 120 degree stimuli (right), with noisy inputs. Gray lines, responses without added noise. Black lines, feedforward inputs (without noise).

(f) Cross-correlation of single-trial responses on 1000 simulated noisy trials to the noiseless response (maximum value over all shifts in orientation).

(g) As in (f), but for the shift in network response due to noise in the input (orientation center-of-mass of activity relative to the noiseless response).

Influence had a non-monotonic relationship with trace correlation that suggested distinct regimes. The central 95% of trace correlations had a negative correlation with influence. For the extrema of the distribution, influence was positively correlated with trace correlation. We thus compared the rules governing influence for these two regimes, by re-fitting our influence regression (Fig. 3d–e) separately for weak (central 95% of data) and strong trace correlations (top and bottom 2.5%) (Extended Data Fig. 10). Pairs with weak trace correlations gave similar results to those for the entire dataset (Fig. 5d), but for pairs with strong trace correlations, influence and signal correlation were positively related (Fig. 5d). Thus, although feature competition dominated on average, it was replaced by amplification for the sparse pool of highly correlated pairs.

We tested potential impacts of sparse feature amplification between strongly correlated pairs in a network with feature competition on average. In our ‘toy’ competition model, we incorporated sparse like-to-like connectivity between neurons with the most correlated input (‘mixed’ model). On simulations of single trial responses to noisy inputs, this added structure preserved the stimulus demixing capacity of the competition motif, and resulted in a smoother bump of population activity whose shape was consistent across trials (Fig. 5e–g). Thus sparse amplification between near-identical neurons in our network model smoothed population representations of orientation, but additional investigation will be needed to fully understand the rules and function of this non-competitive influence in the brain.

Discussion

We have shown that adding a few spikes to a targeted neuron had substantial effects on the local population, including ~2% modulations of responses to visual stimuli and changes in decoding of stimulus properties. These effects included major contributions from inhibition³⁷, including an average inhibitory influence between neurons and an enhanced competition between similarly tuned neurons, forming a like-suppresses-like motif. Feature competition was embedded in a complex network structure; however, direct analysis of population activity confirmed key predictions of feature competition and did not reveal widespread amplification. Feature competition is thus an important, but incomplete, account of function in layer 2/3 of V1. Further examination in different physiological contexts, and with different perturbations, is needed to elaborate this structure.

In support of single-unit recordings in V1^15,38,39, our results provide some of the first causal evidence that local circuitry in V1 suppresses redundant information in a visual scene to create a sparse and efficient code^10,11. Feature competition is consistent with the principle of ‘explaining away’ and may assist inference of visual stimulus properties underlying sensory inputs^12,13,17. The computational goal of feature competition generalizes to any sensory system and thus could be a common motif of sensory processing⁴⁰.

Our functional influence results suggest biophysical implications for V1 microcircuitry. Because competition varied depending on tuning similarities, inhibition is likely more finely structured than generally appreciated^4,18,41–43 (but see^44–47). Our results are consistent with studies in multiple species showing similar tuning of excitatory and inhibitory inputs to individual cells^48–50. However, the absence of widespread feature amplification suggests reconsidering the function of like-to-like excitatory connections⁵. We speculate competition might operate over small neural pools, rather than on individual neurons, with strong intra-pool excitation. However, when multiple visual stimulus dimensions are considered, it is rare for two neurons to be similar along all dimensions, suggesting that amplification in pools could be quite restricted.

Influence mapping has the potential to be a general tool to probe computation in local neural populations. It potentially allows longitudinal studies over timescales of development, behavioral learning, and changes in brain state. Further, its causal, functional estimates are amenable to direct comparison with network modeling and thus could bridge computational and biophysical investigations of cortical function.

Methods

Soma localization:

Soma-localized ChrimsonR and C1V1(t/t) plasmids and sequence data will be made available on Addgene (presently available upon request). Soma-localization was achieved by appending a motif from Kv2.1⁵¹ after the sequence for the fluorescent protein. Construct sequences were synthesized by GenScript, and AAV2/9 virus was prepared by Boston Children’s Hospital Viral Core.

Mice and surgeries:

All experimental procedures were approved by the Harvard Medical School Institutional Animal Care and Use Committee and were performed in compliance with the Guide for Animal Care and Use of Laboratory Animals. Male C57BL/6J mice were obtained from Jackson Laboratory at ~8 weeks old, with surgeries performed 1-16 weeks after arrival. Mice were given an injection of dexamethasone (3 μg per g body weight) 4-12 hours before the surgery. A cranial window surgery was performed with a 3.5 mm-diameter window centered at 2.25 mm lateral and 3.1 mm posterior to bregma. The window was constructed from bonding two 3.5 mm-diameter coverslips to each other and to an outer 4 mm-diameter coverslip (#1 thickness, Warner Instruments) using UV-curable optical adhesive (Norland Optics NOA 65). A virus mixture was created by diluting into phosphate-buffered saline AAV2/1-synapsin-GCaMP6s⁵² (obtained from U. Penn Vector Core), AAV2/9-CamKIIa-Cre, and one of either channelrhodopsin construct AAV2/9-Ef1a-ChrimsonR-mRuby2-Kv2.1 or AAV2/9-Ef1a-C1V1(t/t)-mRuby2-Kv2.1. Mixture composition was adjusted slightly over the course of experiments, with final and optimal ratios (compared to undiluted stock) of 1/12.5 GCaMP (~4e12 gc/ml), 1/180 channelrhodopsin (~2.22e11 gc/ml), and 1/2,100 cre (~1.33e10 gc/ml). Virus was injected on a 3×3 grid of 600 μm spacing over the posterior lateral quadrant of the craniotomy, corresponding to V1, with ~40 nL injection at each site at 250 μm below the pia surface. Injections were made using a glass pipette and custom air-pressure injection system and were gradual and continuous over 2-5 minutes, with the pipette left in place after each injection for an additional 2-3 minutes. After injections and before insertion of the glass plug, a durectomy was performed, as we observed improved peak optical clarity and a prolonged period of optimal window clarity with this step. An intact dura often showed slight increases in thickness and vascularization 1-2 months from surgery visible under our surgical microscope. The plug was then sealed in place using Metabond (Parkell) mixed with india ink (5% vol/vol) to prevent light contamination. Ten mice were used for the primary dataset combining tuning and influence mapping (6 ChrimsonR, 6 C1V1-t/t). Three mice with C1V1-t/t opsin were used for experiments mapping out photostimulation resolution and false-positive influence (Fig. 1e–f); in these mice cre was diluted to 1/10,000 (~3e9 gc/ml) in order to produce highly sparse channelrhodopsin expression. Experiments were performed on mice typically 6–8 weeks after surgery, occasionally ranging as short as 4 or up to 12 weeks. Experiments were terminated when GCaMP expression appeared high, with some neurons exhibiting GCaMP in the nucleus.

Microscope design:

Data were collected using a custom-built two-photon microscope with two independent scan paths merged through the same Nikon 16× 0.8 NA water immersion objective. One scan path used a resonant-galvanometric mirror pair separated by a scan lens-based relay to achieve fast imaging frame acquisitions of 30 Hz. The other path, used for photostimulation, used two galvanometric mirrors with an identical relay. The two paths were merged after the scan lens – tube lens assembly before the objective via a shortpass dichroic mirror with 1000 nm cutoff (Thorlabs DMSP1000L), with small adjustments made to co-align pathways by imaging a fluorescent bead sample through both pathways. A light-tight aluminum box housed collection optics to prevent contamination from visual stimuli. Green and red emission were separated by a dichroic mirror (580 nm long-pass, Semrock) and then bandpass filtered (525/50 or 641/75 nm, Semrock) before collection by GaAsP photomultiplier tube (Hamamatsu). A Ti:sapphire laser (Coherent Chameleon Vision II) was used to deliver pulsed excitation at 920 nm through the resonant-galvo pathway for calcium imaging, and a Fidelity-2 fiber laser (Coherent) was used to deliver pulsed excitation at 1070 nm through the galvo-galvo pathway. A small number of initial experiments used a 1040 nm Ytterbium-based solid-state laser (YBIX, Lumentum) for the galvo-galvo pathway. The mouse was head-fixed atop a spherical treadmill, as previously described⁵³, which was mounted on an XYZ translation stage (Dover Motion) that moved the entire treadmill assembly underneath the microscope’s stationary objective. Microscope hardware was controlled by Scanimage 2015 (Vidrio Technologies). Rotation of the spherical treadmill along all three axes was monitored by a pair of optical sensors (ADNS-9800) embedded into the treadmill support communicating with a microcontroller (Teensy, 3.1), which converted the four sensor measurements into one pulse-width-modulated output channel for each rotational axis.

Visual stimulus:

All visual stimuli were generated using Psychtoolbox 3 in Matlab. A 27-inch gaming LCD monitor running at 60 Hz refresh was gamma-corrected and used to display all stimuli (ASUS MG279Q). The screen was positioned so that the closest point on the monitor was 22 cm from the mouse’s right eye, such that visual field coverage was 107° in width and 74° in height. Before each experiment, coarse retinotopy was mapped out via online observation of imaging data using a movable spot stimulus, and monitor position was adjusted so that centrally-presented spots drove the largest responses in the imaged field-of-view. Drifting grating stimuli were different in ‘influence measurement’ and ‘tuning measurement’ blocks. Influence measurement blocks used square-wave gratings at 10% contrast, 0.04 cycles per degree, and 2 cycles per second, presented for 500 ms with 500 ms of grey between presentations (i.e. 1 Hz stimulus presentation rate). Stimuli discretely tiled direction space with 45 degree spacing. Tuning measurement blocks used sine-wave gratings presented for 4 s, during which contrast linearly increased from 0% to 100% and back to 0%. Grating parameters were each sampled from a uniform distribution covering: direction 0–360 degrees, spatial frequency 0.01–0.16 cycles per degree, and temporal frequency 0.5–4 cycles per second. In a subset of experiments (e.g. the example in Fig. 3), the range of temporal frequencies was adjusted such that a constant range of grating speeds was tested at each spatial frequency (with 0.5–4 Hz temporal frequency used for the central spatial frequency of 0.04 cycles per degree). All grating stimuli were windowed gradually with a gaussian aperture of 44 degree standard deviation to prevent artifacts at the monitor’s edges. Stimuli were presented on a gray background such that average luminance of the monitor was constant throughout all grating presentations and contrasts in the experiment. In influence-measurement blocks, a digital trigger was output from the computer controlling visual stimuli to initiate photostimulation simultaneous to the psychtoolbox screen ‘flip’ command. In all blocks, digital triggers output from the computer controlling visual stimuli were recorded simultaneous to the output of Scanimage’s frame clock for offline alignment.

Experimental protocol:

Mice were habituated to handling, the experimental apparatus, and visual stimuli for 2-4 days before data collection began. A field-of-view was selected for an experiment based on co-expression of GCaMP6s and channelrhodopsin. 920 nm excitation used for GCaMP6s imaging was between 40–60 mW (average with pockels cell blanking at image edges, measured after the objective). Multiple experiments performed in the same animal were performed at different lateral locations within V1 or at different depths within layer 2/3 (110-250 μm from brain surface). Once a field-of-view was selected, images were acquired from both laser paths. The 920 nm-excitation resonant pathway image (~680 × 680 μm) was stored and used throughout the experiment to correct for brain drift during the experiment (described below). The 1070 nm excitation photostim galvo pathway image (~550 × 550 μm) was used to visualize channelrhodopsin expression and select regions-of-interest (ROIs) for photostimulation (parameters described below). Experiments began with a tuning-measurement block of ~40 minutes, followed by three photostimulation blocks of 50 minutes each, and finally a second tuning-measurement block of ~40 minutes. Within each photostimulation block, each photostimulation target was activated once in a randomized permutation at 1 Hz, and this process was then repeated throughout the block, such that all targets in an experiment were activated in near-random order with exactly the same number of repeats. The total number of photostimulation trials per experiment was typically ~8,400, split into ~180 per site.

We found that, over these long experimental durations, both deformation of the brain and/or air bubble formation in the objective immersion fluid could lead to contamination of data. Thus between each experimental block, we used the alignment image captured before any experiment blocks and overlaid this image with a live-stream of the current FOV and adjusted the stage as necessary to bring the two into alignment. This alignment usually required shifts of < 10 μm laterally and axially over the full experiment duration, and was typically no more than 3μm between individual blocks. We also found that boiling the water used for objective immersion to remove dissolved gas (cooling to room temperature before use) prevented formation of bubbles. Post-hoc verification of drift and image quality stability were confirmed by examining 1000× sped-up movies of the entire experiment after motion correction and temporal down-sampling. Insufficiently stable experiments were discarded without further analysis. Additionally, single-neuron stimulation was observed and subjectively judged online, so that experiments with generally poor stimulation efficacy were excluded from further analysis. All inclusion and exclusion decisions were made before data analysis, and after all experiments had been performed, and were not altered once analysis began.

The complete dataset consisted of 28 experiments from 10 mice, with 295 control photostimulation sites and 539 neuron photostimulation sites, 518 of which were significantly photostimulated. A total of 8,552 neurons were recorded, of which 6,061 passed criteria for GP regression fit quality (see below). This resulted in 156,759 pairs of neuron photostimulation and non-targeted neuron response, from which 1,440 were excluded by our 25 μm distance threshold, and 1,630 were excluded by spatial overlap (see below on CNMF filter overlap). This left 153,689 pairs for analysis, from which 64,845 further passed criteria for GP regression fit quality for both targeted and non-targeted neurons. All data from experiments were managed and analyzed using a custom built pipeline in the DataJoint framework⁵⁴ for MATLAB.

Photostimulation:

Our photostimulation protocol was a modification of a ‘spiral scan’ approach³⁶. After selecting areas for stimulation, we initialized a circular target around each area slightly broader than the targeted neuron in order to account for brain motion in vivo (12-15 μm diameter). We used the microscope’s galvo-galvo pathway to rapidly sweep a diffraction-limited-spot across the cross-sectional area of a photostimulation target. This area was covered uniformly in time using a sweep trajectory combining a 1 kHz circular rotation of the spot around the photostimulation target with an irrational frequency oscillation of the spot’s displacement magnitude from target center ($1∕(2\pi -\frac{2}{3})\mathrm{kHz}$), which was found to rapidly fill the circular cross-section (see Extended Data Fig. 1b). The oscillation of displacement magnitude was a sawtooth wave modified with a square root transform to spend greater time at greater displacements, to account for the increasing circular area at larger displacement. A single sweep trajectory was set to 32 ms in duration. Photostimulation consisted of a 15 Hz train of 4 sweeps, with sweep onset aligned to the onset of imaging frames. Power was typically ~50 mW (measured without pockels blanking, after the objective), but was increased in some experiments if stimulation efficacy was observed to be low (min 36mW, max 67.5mW, mean 52.7mW).

Cell-attached Recordings:

Two mice were injected with virus using the same protocols used for experimental animals. 4-8 weeks after injection, the cranial window was removed and replaced with a 3mm glass window laser with a 0.5mm diameter access hole. This custom window was laser cut from a sheet of quartz glass. Two-photon targeted recordings⁵⁵ were obtained using borosilicate glass pipettes pulled to a resistance of 5-7 M ohms and filled with extracellular solution. Signals were amplified on a Axopatch 200B (Molecular Devices), filtered with a lowpass bessel filter w/ cutoff at 5 kHz,and recorded at 10 kHz. Signals were later high-pass filtered offline and a manual threshold was used to identify spike times. Photostimulation was performed using the same protocol used in all experiments (described above, 45 mW power, 1070 nm excitation). Spikes added by photostimulation was calculated as the average number of spikes observed 0-250 ms after photostimulation onset, minus one-fourth the average spikes observed in the 1,000 ms preceding photostimulation. No recorded neurons exhibited changes in spiking activity more than 250 ms after photostimulation onset.

Pre-processing of imaging data:

Imaging data were processed offline using custom Matlab code described below. Code is available online: https://github.com/HarveyLab/Acquisition2P_class for motion correction, https://github.com/Selmaan/NMF-Source-Extraction for source extraction. Motion correction was implemented as a sum of shifts on three distinct temporal scales: sub-frame, full-frame, and minutes- to hour-long warping. First, sequential batches of 1000 frames were corrected for rigid translation using an efficient subpixel two-dimensional fft method⁵⁶. Then rigidly-corrected imaging frames were corrected for non-rigid image deformation on sub-frame timescales using a lucas-kanade method⁵⁷. To correct for non-rigid deformation on long (minutes to hours) timescales, a reference image was computed as the average of each 1000-frame batch after correction, one being selected as a global reference for the alignment of all other batches. This alignment was fit using a rigid two dimensional translation as above, followed by an affine transform after the rigid shift (imregtform in Matlab), followed by a nonlinear warping (imregdemons in Matlab). We found that estimating alignment in this iterative way gave much more accurate and consistent results than attempting nonlinear alignment estimation in one step. However interpolating data multiple times can degrade quality, and so all image deformations (including sub- and full-frame shifts within batch) were converted to a pixel-displacement format and summed together to create a single composite shift for each pixel for each imaging frame. Raw data were then interpolated once using bi-cubic interpolation (interp2 in Matlab).

Because single experiments were much too large to load into a conventional computer’s memory (~250 GB per experiment), frames were temporally binned by a factor of 25 (from 30 Hz to 1.2 Hz) after motion correction but before source extraction. GCaMP6s transients were still easily resolved, and previous work has suggested that source extraction is improved by temporal down-sampling⁵⁸. The constrained non-negative matrix factorization (CNMF) framework^59,60 was then used to identify spatial footprints for all sources using the down-sampled data. Some modifications were made to the publicly distributed implementation. First, because the approximation of imaging noise needed for CNMF is biased at low temporal frequencies in which imaging noise and signal are not temporally separable, we used full-resolution data to approximate pixel noise and divided this value by the square-root of the down-sampling factor. We also used three unregularized (‘background’) components (default is one), because we observed that spatial footprints of neuropil activity were distinct from the true ‘background’ fluorescence of baseline GCaMP6s brightness. An initial rank-one background component was temporally filtered (1000-frame median filter) such that all high-frequency fluctuations were isolated into one component. The remaining low-frequency component was then split between two components which linearly ramped up from or down to zero over the experiment’s duration, to account for slight background changes over hours. Spatial and temporal profiles for each component were then estimated ordinarily on all subsequent CNMF iterations after this initialization procedure.

We further modified the initialization method used by CNMF in order to model sources independent of their spatial profile (i.e. neural processes as well as cell bodies), using a normalized cuts-based procedure similar to that used in previous work⁶¹, which clusters pixels into maximally similar groups based on temporal activity correlations. As ordinary for CNMF, our initialization operated on overlapping square sub-regions of the field-of-view (~70 μm, 52 pixel edge length, 6 pixel overlap). We then calculated the correlation coefficient of all pixel pairs (i, j) in this sub-region over all time points in the down-sampled data, and used these values to construct a graph with edge weight $W(i,j)=\exp (-\frac{1-\mathit{corr}(i,j)}{\sigma })$. The parameter σ was set to median(1 − C), where C is the correlation coefficients for all pixel pairs in the subregion. We obtained a clustering of the resulting graph using a non-negative factorization as described⁶². These initial source estimates were then further refined via initialization of a spatially-sparse NMF decomposition of the down-sampled subregion data, and merging of any ‘over split’ components (when projections of data, after removal of background component, onto two source masks had temporal correlation coefficients greater than 0.9). The resulting sources were then used as initializations for all future iterations of the core CNMF algorithm. After running CNMF for three iterations on temporally down-sampled data, the resulting spatial footprints were used to extract activity traces for each source from the full temporal resolution data. Fluorescence traces of each source were then deconvolved using the constrained AR-1 OASIS method⁶³; decay constants were initialized at 1 s and then optimized for each source separately. ΔF/F traces were obtained by dividing CNMF traces by the average pixel intensity in the movie in the absence of neural activity (i.e. the sum of background components and the baseline fluorescence identified from deconvolution of a source’s CNMF trace). Deconvolved activity was also rescaled by this factor, in order to have units of ΔF/F.

Because our implementation of CNMF resulted in non-cell-body fluorescence sources being modeled, we trained a 2-layer convolutional network in Matlab using manually annotated labels to identify whether each fluorescence source was one of: (i) a cell body, (ii) an axially-oriented neural process appearing as a bright spot, (iii) a horizontally-oriented neural process appearing as an extended branch, (iv) an unclassified source or imaging artifact. The network operated on source-centered windows 25×25 pixels wide (at ~1.2μm/pixel), and consisted of ReLU units with two convolutional layers (32 18×18×1 filters followed by 3 5×5×32 filters), a 256-unit fully connected layer, and a 4-unit softmax output. Only sources identified as cell bodies were used in this paper, although we note that neural processes frequently revealed quite similar signals in terms of quality and encoding properties. However the inclusion of non-cell-body sources in CNMF for this project was intended only to reduce contamination of cellular fluorescence signals. The network was trained on 8,700 sources which were further augmented 30-fold by rescaling, rotation, and reflection. There is no ground-truth accuracy to compare with, but agreement with human annotation on held-out datasets ranged from 80-90%, which was qualitatively similar to human variability. We provide example predictions of this network on a held-out mouse and session compared to typical human annotation in Extended Data Fig. 1h.

For analysis of traces without neuropil subtraction, we projected imaging data onto the spatial filters obtained by CNMF (i.e. without any demixing or subtraction), analogous to averaging pixel intensities for each ROI, to obtain fluorescence traces for each neuron. All subsequent processing stages were handled identically to the ‘demixed’ fluorescence traces.

Photostimulation-specific pre-processing:

A number of additional pre-processing steps were introduced for specific purposes related to photostimulation. For each photostimulation target, we calculated a photostimulation-triggered-average (PTA) image for the entire field-of-view of fluorescence changes for 50-frames after versus before photostimulation of that target (Extended Data Fig. 1c). This PTA was then used at a number of stages of the processing pipeline. First, when initializing source extraction from imaging data using the algorithm described above, we added the largest connected component from PTAs to assist the algorithm’s detection of photostimulated neurons. Second, we used PTAs for post-hoc confirmation of matches between cellular sources identified by CNMF and photostimulation targets. Specifically, we manually examined all sources identified near the location of each photostimulation target, and overlaid these with the PTA image for that target, as well as plotting the PTA trace of each source’s activity. This was necessary because axial blurring of in vivo two-photon calcium imaging data can lead to fluorescence signals from distinct cells with partial lateral overlap. Whenever we did not observe an unambiguous pairing of source and intended target, we labeled a target as ‘unmatched’ (418 photostimulation sites), and excluded it from further analysis. Finally we observed that, due to imperfect axial-resolution, the processes of a stimulated neuron, as identified in a PTA image, could sometimes overlap with the spatial footprint of other cellular sources. This overlap could lead to an erroneous measurement of influence between the pair, if the photostimulated neuron’s activity was not properly demixed by CNMF and so contaminated the activity trace of the other neuron. We note that this issue is a generic property of in vivo two-photon calcium imaging, and not specific to influence mapping or photostimulation per se. Given the limitations of current algorithms for demixing, we directly estimated the spatial overlap of each cell’s spatial profile (as used in CNMF) with each photostimulated target’s processes (taken to be the largest connected component in a binarized PTA) and excluded from analysis any pairs with detected overlap. This affected pairs generally < 100 μm apart, and had no qualitative impact on results, although quantitatively the relationship between influence and distance (Fig. 2f–g) exhibited a more pronounced excitatory center without removing overlapping pairs.

Photostimulation causes a minor artifact by directly exciting GCaMP6s or from autofluorescence, causing calcium imaging data collected simultaneously to be biased in a photostimulation-target-specific manner. Though this artifact was small with 1070 nm photostimulation, it became quite noticeable when hundreds of trials were averaged. Thus, we leveraged the fact that our photostimulation protocol consisted of pulses aligned to imaging frame onsets, and pulses were sub-frame-length, and replaced original data from single-frames containing a photostimulation artifact with linearly interpolated values from the frame immediately before and after. This interpolation was performed on all source’s activity traces, prior to deconvolution.

Gratings and Photostimulation Response Magnitude:

The magnitude of response to optimal visual stimuli during tuning blocks was measured with a model-free approach, which did not assume any particular tuning structure or contrast sensitivity. We measured the difference between the 99th and 1^st percentiles of each neuron’s ΔF/F trace over each 4 s-long trial during tuning measurement blocks, and then quantified gratings response magnitude as the 95% percentile of this distribution over all trials. For this analysis only, the ΔF/F trace of each neuron for the entire tuning measurement blocks was smoothed with a Savitzky-Golay filter of order five and frame-length 2 s (using MATLAB sgolayfilt) to reduce the impact of imaging noise on this measure.

Photostimulation response magnitude was estimated as average ΔF/F for 300-600 ms following photostimulation minus ΔF/F −500 to −100 ms before photostimulation. We observed no differences between photostimulation magnitudes when using C1V1 or ChrimsonR (0.61 vs 0.6 ΔF/F, p = 0.304, n = 283 C1V1 neurons, 235 ChrimsonR neurons, Mann-Whitney U-test).

Influence measurement:

We used two complementary metrics to quantify influence. For both approaches, single-trial responses for each neuron were computed as the average value of deconvolved traces over 11 imaging frames (367 ms) beginning with the onset of photostimulation (Activity_i,n for neuron n on trial i). Our first metric computed the difference between single trial and average control trial activity:

$$\Delta {\text{Activity}}_{i,n}={\text{Activity}}_{i,n}-{\langle {\text{Activity}}_{j,n}\rangle }_j$$

where trials j corresponds to all control site photostimulation trials with the same visual stimulus as presented on trial i (and excluding all trials where any site within 25 μm was photostimulated). We then normalized ΔActivity_i,n by dividing by the standard deviation over all trials i. This was important because it is difficult to determine absolute levels of spiking activity from calcium imaging data. The normalization ensured that we measured effects relative to each neuron’s variability, and furthermore that results would not be improperly influenced by misestimation of absolute activity levels in some neurons. Influence values for an individual photostimulation target were then computed as the average ΔActivity_i,n over all trials where that target was photostimulated. For analysis of influence from control site photostimulation we used a leave-one-out procedure, where a single control site was excluded from trials j used to calculate expected activity and influence values for that site were obtained as above, and we obtained influence values for all control sites by repeating this procedure for each control site in an experiment.

Our second influence metric converted the data into a probabilistic framework using a non-parametric shuffle procedure, which controls for the asymmetric and heavy-tailed distributions of single-trial neural activity. This metric was used to confirm results of the simpler metric above, and was further used to identify ‘significant’ influence values (Extended Data Fig. 2a–c). We began by computing single-trial residuals as described above (i.e. ΔActivity_i,n). Average photostimulation responses to individual targets were then computed over all trials and compared to 100,000 averages computed via random permutations of trial number and photostimulation target, and excluding any trials with photostimulation of a target within 25 μm of a cell (‘shuffle distribution’). Our second metric was computed as the log-odds ratio that non-targeted neuron n’s average response to targeted neuron t photostimulation (ΔActivity_t,n) was greater- versus less-than the shuffle distribution:

$${\mathit{InfOdds}}_{t,n}={\mathit{log}}_{10}\left(\frac{p(\Delta {\text{Activity}}_{t,n}>{\text{shuffle}}_n)}{p(\Delta {\text{Activity}}_{t,n}<{\text{shuffle}}_n)}\right).$$

InfOdds_t,n was capped at ±5 because we used a finite number of shuffles (this occurred for 57 out of 64,845 pairs in the primary dataset).

We used InfOdds_t,n to determine the significance of influence values for individual pairs, against the null hypothesis of random sampling of activity (Extended Data Fig. 2a–c). We performed independent tests for whether a neuron’s activity was increased or decreased relative to random sampling. These values were then used to determine a p-value threshold using the positive false discovery rate procedure⁶⁴, as implemented in MATLAB’s function mafdr. We set p-value thresholds corresponding to false discovery rates of 5% and 25% (respectively 0.15% and 0.42% of all pairs passed these thresholds).

We also computed an influence measure ΔFluorescence that could be computed directly from a neuron’s fluorescence traces without deconvolution, or in some cases without neuropil subtraction. ΔFluorescence was computed as for ΔActivity, except a vector of timepoints aligned to photostimulation onset were used instead of a single scalar value of single-trial activity. ΔFluorescence was normalized as for ΔActivity, using the standard deviation of fluorescence values averaged 300-600 ms after photostimulation onset.

Note that we use the phrase ‘non-targeted neuron’ throughout the text with respect to the specific subset of trials on which another neuron was targeted. That is, a ‘non-targeted neuron’ on some trials could be a ‘targeted’ neuron on other trials (and vice versa).

Gaussian process tuning model:

Our tuning measurement protocol sampled responses over a broad range of stimulus parameters, however it results in no repeats of exactly identical stimuli. This improves our sampling efficiency compared to repeating an identical stimulus multiple times, but complicates analysis. We thus needed a method to interpolate between highly similar trials. Gaussian process regression is a principled, probabilistic approach to both determine smoothing parameters and to perform this interpolation. The use of a Gaussian process, as opposed to a conventional regression with basis function expansion, allowed us to specify high-level properties of neural tuning without assuming any particular parametric form of the tuning function, and to reason probabilistically about uncertainties in estimating the latent tuning.

Single-trial responses of individual neurons during the tuning-measurement block were computed by averaging deconvolved activity over 112 frames of visual stimulus presentation (~4 s, excluding the first and last 4 frames within a contrast cycle), then taking the square-root transform in order to stabilize response variability across the range of average response magnitudes⁶⁵. These responses were considered as noisy observations of a 4-dimensional latent function f(x) with dimensions of: grating drift direction, grating spatial frequency, grating temporal frequency, and the mouse’s running speed (which is known to modulate responses in V1). This latent function defines the tuning of an individual neuron, and was fit using a Bayesian non-parametric Gaussian process regression model built using the GPML toolbox 4.0⁶⁶ in Matlab.

The model is specified by the form and hyperparameters of a covariance function K(x, x′), which determines smoothness by specifying the similarity of function values between any two points in the 4-dimensional tuning space. We chose the commonly used squared-exponential covariance:

$$K(\mathit{x},{\mathit{x}}^{\prime })={{\sigma }_c}^2\exp (-{(\mathit{x}-{\mathit{x}}^{\prime })}^T{\mathit{P}}^{-1}(\mathit{x}-{\mathit{x}}^{\prime }))$$

The hyperparameters here include σ_c² as the scale of the covariance function, and P as a diagonal matrix with entries λ₁², …, λ₄² defining an independent length scale for each dimension. Shorter distances correspond to functions which are sharply ‘tuned’ to particular dimensions. Note that distances for grating drift direction were calculated after projection into the complex plane. We then used a Gaussian likelihood function with hyperparameter σ_n² as the level of response variability, such that any number of finite samples of the latent function f and noisy observations y at locations X have joint Gaussian distributions:

$$\mathit{f}\mid \mathit{X}~\mathcal{N}(0,\mathit{K})$$

$$\mathit{y}\mid \mathit{f}~\mathcal{N}(\mathit{f},{{\sigma }_n}^2)$$

where K is a matrix specifying the covariance between all samples. Thus by conditioning on a set of observed data points (the ‘training set’), we obtain a posterior distribution over function values at any set of unobserved locations, either held-out data points (the ‘test set’) or untested locations (see⁶⁶ for details). All hyperparameters were optimized by maximizing the marginal likelihood of the data p(y|X) = ∫ p(y|f)p(f|X)df, as ordinary for a Gaussian process model. This procedure is a Bayesian alternative to regularization which does not require cross-validation.

We divided each neuron’s responses (~1000 trials) into 20-folds, and predicted responses for each fold using ‘training’ data from the other 19 folds. These ‘test’ predictions were then correlated with actual data as a metric for model accuracy. We also compared accuracy when predictions were made on ‘test’ versus ‘training’ data as a metric for model over-fitting, which we observed was generally quite low (Extended Data Fig. 4b). Test predictions from the model were then used to calculate single-trial residuals. Pearson’s linear correlation coefficient was computed between test predictions of two neurons to determine signal correlation, and between residuals to determine noise correlation. Because our separation of signal and noise correlation was model-based, all analysis involving either or both quantities needed to exclude from consideration any neurons with inaccurate models. To pass inclusion criteria, both the photostimulation targeted neuron’s model and the non-targeted neuron’s model had to have model accuracies, defined as the pearson correlation between predicted and actual responses, above 0.4 as well as a difference between train and test accuracies of < 0.15 (to exclude possible over-fitting). Analysis of neuron versus control influence, distance, and trace correlation relationships (Fig. 2 and 5b) did not apply these criteria because signal and noise were not considered, however results for both were similar when analyzing the subset of data which passed tuning criteria.

The Gaussian process model fits neural responses with a nonlinear 4-dimensional tuning function, which is not necessarily separable by dimension. To extract 1-d tuning curves, we thus employed the canonical neurophysiological approach of studying tuning to a stimulus which optimally drives a neuron. In other words, we examined spatial frequency tuning at the drift direction, temporal frequency, and running speed that best activated a neuron, as determined by the GP model, and so on for all individual dimensions. Specifically, we identified the location x where latent response f was maximal, by starting from the location of the maximal single-trial prediction and then performing a grid-search over all nearby locations in 4-d. Given this location, we then fixed three dimensions and varied a 4^th to obtain a tuning curve. We further used these tuning curves to determine whether each neuron was significantly tuned to each tuning dimension by calculating a depth-of-modulation dom_d as follows:

$${\mathit{dom}}_d=\frac{\max ({\mathit{t}}_d)-\min ({\mathit{t}}_d)}{\mathit{sqrt}({\sigma }_{\max ({\mathit{t}}_d)}^2+{\sigma }_{\min ({\mathit{t}}_d)}^2)}$$

where t_d is a neuron’s tuning curve for the d^th dimension, and ${\sigma }_{\max ({\mathit{t}}_d)}^2$, ${\sigma }_{\min ({\mathit{t}}_d)}^2$ are the variance of the posterior distribution at the locations of maximum and minimum tuning values. Neurons were considered tuned to dimension d when dom_d > 2, corresponding to statistically significant evidence for tuning modulation along this dimension, and analysis was restricted to these neurons whenever tuning along individual dimensions was considered (Fig. 3f,i; Fig. 4). Preferred stimulus values were also extracted from 1-d tuning curves. Fractions of tuned neurons for each dimension, tuning curves, and depth-of-modulation values are presented in Extended Data Fig. 4.

Comparison of GP and conventional tuning model:

We adapted a recent parametric tuning model⁴⁶ to compare with the GP model described above. This model approximated single-trial neural responses during tuning measurement blocks, as analyzed above for the GP model, as a product of one-dimensional gaussian tuning curves to each stimulus dimension (drift direction, spatial frequency, temporal frequency, and running speed). Tuning to drift direction was a sum of two gaussians, separated by 180-degrees, with a scaling parameter r which adjusted the relative strength of the two gaussians to account for directional preference. All other tunings were single gaussians, with a parameter for center and width, and the model included an additional additive response offset. All parameters were optimized using MATLAB’s Isqnonlin.

To compare model accuracies, we used all neurons from a single experiment, and divided trials into 10 cross-validation folds. All parameters for both GP and parametric tuning models were fit to 90% of the data and used to predict responses on held-out trials. Model accuracy was quantified as the pearson correlation coefficient between predicted and actual data.

Correlations used as similarity metrics:

Four correlation types were used in this study. (1) ‘Trace correlation’ was defined as the Pearson’s linear correlation of two neuron’s deconvolved activity throughout tuning measurement blocks, after downsampling from 30 Hz to 3 Hz to reduce the influence of noise and imaging artifacts. We considered this analogous to what has been termed ‘total’ or ‘response correlation’ in the literature⁵. (2) ‘Signal correlation’ was defined as the Pearson’s linear correlation of GP model single-trial predictions on held-out data (using 20-fold cross-validation to form predictions for all trials). We considered this analogous to signal correlations computed on average responses to a discrete set of stimuli, because the GP model predictions are the mean response inferred by interpolating between trials with similar stimulus parameters. (3) ‘Noise correlation’ was defined as the Pearson’s linear correlation of residuals between a neuron’s actual single-trial responses and GP model-predictions (using the same procedure on held-out data as above). We considered this analogous to noise correlations computed as residuals of average responses to a discrete set of stimuli by the same logic as for signal correlations. (4) ‘Response correlation’ was defined as the Pearson’s linear correlation of the single-trial neural responses to which GP models were fit. This is similar to trace correlation, but averages over 4 s periods, and is aligned to visual stimulus presentation. Single-trial correlation was used only for visualization purposes in Extended Data Fig. 6e–f.

Analysis of influence values:

Influence resulting from photostimulation of neuron sites was only analyzed for targets where we could confirm effective stimulation (average response > 5 standard deviations greater than expected in shuffled distribution described above, Extended Data Fig. 1E). We used two analysis procedures: a one-dimensional running average (e.g. Fig. 3g–i), and multiple linear regression (e.g. Fig. 3d–f). For running average analyses, we chose center locations to span the full range of observed values and a manually specified bin width. Bin parameters were specified in percentile space for signal and noise correlations, and in real space for distance and trace correlation analysis to better sample the sparse tails of these distributions, as described in figure legends for each plot. For all plots, x-values were the mean value of the smoothed variable (e.g. distance) within a bin, which typically deviates slightly from the nominal bin center. We estimated standard errors for each bin by bootstrap resampling. Because this analysis introduces arbitrary parameters that could affect results, we considered smoothing analyses as qualitative and exploratory. All statistical claims were thus verified by analysis of correlation coefficients or the regression procedure described below.

Multiple linear regression was used to estimate the relationship between similarity metrics (distance, signal-, noise-, and trace-correlations) and influence values. We constructed a design matrix whose columns included piece-wise linear terms for distance (< 100 μm, 100–300 μm, and > 300 μm segments), linear terms for signal and noise correlations and their interaction, and linear interactions for both signal and noise correlation with log-transformed distance. Each distance segment included terms for both offset and slope. All predictors were z-scored to facilitate comparison of coefficient magnitudes. We then resampled our data points 10,000 times and estimated regression coefficients for each. Median coefficients, confidence intervals, and p-values were obtained from this bootstrap distribution as described below. For the tuning-components regression in Fig. 3f, we constructed five alternate regression models, in which signal correlation and its interactions were replaced by tuning curve correlations for one of the five tuning features. For each feature, data were restricted to the subset of pairs for which both the photostimulated target neuron and non-targeted neuron exhibited significant tuning (see above). Because our model predicted grating drift direction over 360°, we obtained orientation-specific tuning curves by averaging tuning curves across both directions for each orientation, and direction-specific tuning curves by taking the difference across both directions for each orientation.

For model prediction plots of Extended Data Fig. 6c–f, data were first smoothed as described above. Then we used the influence regression model above to predict influence values for each data point, using either the full model or a subset of coefficients. The interaction term of signal or noise correlations with distance were considered a part of the ‘signal’ and ‘noise’ component of the model for these plots. These predicted values were then smoothed identically to the data. Note that predictions thus appear nonlinear, despite a linear prediction model, because of complex interdependencies between the distributions of signal correlation, noise correlation, and distance.

For analysis of influence directly on ΔF/F traces in Extended Data Fig. 7, we fit influence regression models for each frame of ΔFluorescence values, obtaining a temporal vector of influence regression coefficients for each predictor. This analysis was otherwise identical to the regression analysis of ΔActivity.

‘Nearby Neuron’ Analysis:

We designed this analysis to confirm that influence effects were specific to the relationship of non-targeted neurons and the precise identity of a photostimulated neuron (Extended Data Fig. 7f). To accomplish this, for each photostimulation site we identified the closest 2.5% of all neurons to the photostimulation site (typically ~10-30 μm away), and averaged their signal and noise correlations with individual non-targeted neurons. This captures any spatially broad similarities in tuning shared by neurons near the targeted neuron. The influence from this photostimulation site was then analyzed using the influence regression model described above, using this locally-averaged similarity of each non-targeted neuron to neurons nearby the photostimulation site (including all criteria mentioned above). This procedure scrambled the relationship between a photostimulated neuron’s activity and influence, except for properties which vary smoothly in space and thus would be shared by accidentally activated, non-targeted neurons (either laterally or axially). However distances and the statistical structure of our data (e.g. correlations between similarity metrics) were unaltered. Thus effects related to the precise tuning of individual neuron targets, but not those caused by low-resolution photostimulation of a small volume, were disrupted by this procedure. We present results of this analysis (Extended Data Fig. 7f) applied to neuron photostimulation data analyzed throughout this manuscript. We also performed this analysis for all photostimulation sites (including unmatched and control photostimulation sites, where we could not verify neuronal activation) and obtained similar results (data not shown).

Decoding analysis:

For decoding and population projection (below) analyses, we analyzed trials from ‘influence mapping’ blocks on which orientation-tuned neuron targets were photostimulated. For each neuron targeted for photostimulation, orientation-tuning significance and preference was determined as detailed above, using the GP model and data exclusively from the ‘tuning measurement’ experimental blocks. We used a naïve Bayes decoder to predict which of the four orientations of gratings were presented on single trials in influence mapping blocks. The decoder makes the approximation:

$$p(\mathit{ori}\mid \mathit{r})\approx {\Pi }_{i}p(\mathit{ori}\mid r_i)={\Pi }_i\frac{p(r_i\mid \mathit{ori})p(\mathit{ori})}{p(r_i)}$$

where r is a vector whose entries r_i are neural responses from the i^th neuron on a single-trial. Thus this decoder is suboptimal because it ignores noise correlations between neurons. Because we were interested in predicting the best grating orientation on each trial, we ignored the term in the denominator, and because all orientations were equally likely to be presented, we ignored p(ori) in the numerator, resulting in the following function for prediction of single trial orientation $\widehat{or\iota }$:

$$\widehat{or\iota }=\underset{\mathit{ori}}{\mathrm{argmax}}{\Pi }_{i}p(r_i\mid \mathit{ori})$$

which is a simple maximum likelihood predictor. We estimated p(r_i|ori) non-parametrically, since many neurons had a response of precisely zero on a large fraction of trials, which severely limited accuracy when a parametric, exponential family distribution was used as the likelihood model. Specifically, non-zero responses across all trials were discretized to be in one of four equal-width percentile bins, and p(r_i, ori) was calculated directly for the percentile and zero bins. To prevent our decoder from fitting to the effects of photostimulation, we used a leave-one-out procedure in which all trials for a single photostimulation target were predicted using a model with these data excluded from model fitting. Additionally, all photostimulated neurons were excluded from the decoder, so that decoder accuracy was not trivially altered by excluding different neurons for different photostimulation targets.

Precise levels of decoding accuracy were variable from experiment to experiment, depending on the number and tuning of imaged cells as well as overall signal quality. Furthermore cardinal orientations tended to be slightly over-represented in neural tuning (Extended Data Fig. 4d) and thus easier to predict than oblique orientations. This is of note because the tuning bias also causes different grating orientations to be more or less likely to be matched to the tuning preferences of photostimulated neurons. To control for these factors when analyzing combined data, we used a generalized linear mixed-effects model for logistic regression. Mixed-effects models allow estimation of ‘fixed’ effects (as in conventional regression) in the presence of confounding ‘random’ effects caused by variation attributable to various groupings. In our application, the angular difference of presented grating and photostimulated neuron’s preferred orientations (‘Orientation Misalignment’) was a fixed effect, and both experiment ID and grating orientation were random effects. We modeled single-trial accuracy of the decoder as:

$$\mathit{acc}~\text{Bernoulli}(p)$$

$$\log \left(\frac{p}{1-p}\right)=X\beta +\mathit{Zb}$$

$${\mathit{b}}_{\mathit{ID}}~\mathcal{N}(0,{\sigma }_{\mathit{id}}^2\mathit{I})$$

$${\mathit{b}}_{\mathit{ori}}~\mathcal{N}(0,{\sigma }_{\mathit{ori}}^2\mathit{I})$$

where Xβ are the design matrix and coefficients for fixed effects, and Zb are the same for random effects, and random effects terms for each experimental ID (b_ID and grating orientation (b_ori) have independent Gaussian priors with variance fit to the data. For plots in Fig. 4, we fit two model variants: one in which orientation misalignment was divided into five equally spaced, discrete bins; a second in which misalignment was treated as a single continuous value. The model was fit and p-values were estimated in Matlab using the glme class.

Population-projections analysis:

We decomposed single-trial population responses during influence-measurement blocks into projections along five axes: one each corresponding to the average response to each grating orientation, and a fifth ‘uniform’ projection that simply averaged the response of all neurons. In contrast to previous analyses, to define a population projection, it was necessary to separate out neurons with a large increase in activity in response to gratings from neurons with a high, tonic level of activity. Thus the activity of each neuron across all trials was normalized by calculating pre-trial activity (~467-100 ms before gratings onset), subtracting this value from single trial responses (0-367ms after gratings onset), and dividing the result by the standard deviation of pre-trial responses (i.e. single trial responses were z-scored relative to pre-trial activity). We then computed response directions to each orientation as the average response, normalized to unit length, and all responses for each orientation were scaled by a single factor so that the average projection of responses onto this direction was one, and single trial projections were then obtained by the inner product of normalized single-trial responses and each of the five population directions.

Because the four average response dimensions were not entirely orthogonal, on each trial, we termed the population direction associated with the presented grating as that trial’s ‘gain direction’, and orthogonalized projections onto the other orientation directions with respect to that trial’s gain (outlined in Extended Data Fig. 8b). As for the decoding analysis, all photostimulated neurons were excluded from this analysis to prevent trivial effects due to changing the composition of the analyzed population on different trials. For this analysis, in contrast to decoding, by design grouping variables of experiment and visual stimulus orientation had no predictive power. We thus used ordinary least-squares regression and non-parametric rank correlation analysis to estimate effects and significance in the main text.

Rate network simulations:

Our network model was modified from that studied previously¹⁷. It consisted of one layer of generic neurons with linear input and a rectifying output nonlinearity, and instantaneous functional connections which could be both positive and negative. Precisely, the network dynamics obeyed the following discrete time equations:

$${\stackrel{.}{\mathit{r}}}_t=-{\mathit{r}}_t+{\mathit{Wr}}_t+\mathit{h}$$

$${\mathit{r}}_{t+1}=\max (0,{\mathit{r}}_t+{\stackrel{.}{\mathit{r}}}_t\cdot \mathit{dt})$$

$$\mathit{h}={\mathit{U}}^T\mathit{y}$$

where r_t is a vector of firing rates in the network at time t, W is a matrix of functional connections between neurons (with all diagonal entries set to 0), and h is a vector of feedforward inputs to each neuron, given by the product of neural tuning U (with columns u_i of individual neuron’s tuning) and network input y. Individual neuron tuning was given by a von Mises function:

$${\mathit{u}}_{\mathit{i}}=\alpha \cdot \exp (k\cdot \cos (2\cdot (\theta -{\theta }_i))$$

where θ_i is the preferred orientation of a neuron (uniformly tiling 0-180°), and α is selected such that ‖u_i‖₂ = 1. Tuning width as specified by k was set to 1. As outlined in Fig. 4h and Extended Data Figure 9a, we constructed the W matrix as a sum of 3 components:

$$\mathit{W}=s{\mathit{U}}^T\mathit{U}+c+ℇ$$

where s controls the relationship between feedforward inputs and functional connectivity, c controls overall excitatory-inhibitory levels, and ℇ is a matrix of i.i.d. values. ℇ was 0 for all analyses except for Extended Data Fig. 9b, for which it was uniformly distributed between −0.25 and 0.25. Our ‘amplification’ network used s = 0.5, ‘competition’ used s = −0.5, and ‘untuned’ used s = 0, but similar results were obtained for a wide range of values. For each network, c was adjusted so that overall inhibition was similar. Without this adjustment, it would be impossible to compare networks, since ‘amplification’ networks would exhibit explosive growth of activity. Specifically, we used c = −0.7 for ‘amplification’, c = 0 for ‘competition’, and c = −0.35 for ‘untuned’ networks. For results in Figure 4, the network contained 100 neurons and, for Figure 5, 180 neurons, although network behavior was largely unaffected by this choice. For all simulations, dt was set to 0.001, the simulation was initialized with r = 0 and run for 4,000 time steps (i.e. 4× the neural time-constant), and network responses were taken as the summed rate over all timesteps for each neuron.

For the analysis of Extended Data Fig. 9b, we simulated variable responses by varying inputs between single simulation runs (‘trials’). We varied both the gain of the feedforward input (uniformly distributed between 0.75 and 1.25) and an additive offset to the input of each individual neuron (uniformly distributed between −β/2 and β/2, where β was 10 times the average neural activity of all neurons over all stimuli). We note that gain variability was not necessary for the results demonstrated; however, adding it led to a positive relationship between signal and noise correlations in all modeled networks, in agreement with data. We generated 1000 simulated responses for each of 18 orientations uniformly tiling orientation space, for each network type. Regression coefficients were then obtained by linear regression of signal and noise correlations, calculated using simulated responses, against the entries of matrix W. This was intended to verify that our general findings from analysis of influence in Fig. 3 were consistent with our ‘competition’ model network.

For simulations involving single-neuron stimulation (results in Extended Data Fig. 9e,f), we clamped the activity of a single neuron to a high value (0.1) from the beginning of a simulation run, and normalized network responses by their response magnitude without clamping. The gain of network responses was measured by projecting single trial responses onto the direction of network activity on trials without clamping. We note that the small bump in gain for all networks in Extended Data Fig. 9f for <10° is due to the simplified ‘clamping’ approach to modeling single-neuron stimulation, as it corresponds to a slightly reduced increase in activity due to clamping for stimuli which ordinarily drive the clamped neuron to fire.

We created a ‘mixed’ network, used in Figure 5, by adding an ‘amplification’ pattern of functional connectivity (with s = 0.5) calculated with tuning width k = 100 to the ‘competition’ pattern (s= −0.5, k = 1). To match experimental data, we also subtracted this same pattern from functional connectivity of oppositely tuned neurons (i.e. after rotating the columns of the connectivity matrix by 90° of preferred orientation), although we observed no differences between networks when performing this latter step or not. We generated noisy responses by adding random values uniformly distributed between −0.015 and 0.015 to each neuron’s input on each simulation run. We measured trial-to-trial network pattern correlations and network pattern shifts by comparing network responses on simulated noisy trials to a template response with no noise but identical visual stimulus. Our objective was to quantify the observation that ‘mixed’ networks exhibited a stereotypical smooth bump of activity in orientation-space in the presence of noise, unlike ‘competition’ networks. We thus computed the cross-correlation in orientation space between template and single-trial responses; the maximum correlation across all shifts was the ‘network pattern correlation’, and the change in center-of-mass was ‘network pattern shift’.

Simplified network equations:

The network described above can be analytically re-expressed as a function of a comparison between inputs and an internal representation, as presented in Extended Data Fig. 9g. The equations presented are derived and explained in detail here. We first examine the linear part of the network dynamics given above, focusing on changes in an individual neuron’s activity indexed by i:

$${\stackrel{.}{r}}_{i,t}=-r_{i,t}+\sum _{j\ne i}{w}_{i,j}{r}_{j,t}+h_i$$

Subsequent equations suppress temporal indices for simplicity. Substituting for w_i,j (with no weight variability, i.e. ℇ = 0) and h_i and rearranging terms we obtain:

$${\stackrel{.}{r}}_i=-r_i+{\mathit{u}}_i^T\left(\mathit{y}+s\cdot \sum _{j\ne i}{\mathit{u}}_j{r}_j\right)+c\cdot \sum _{j\ne i}{r}_j$$

We then define ${\mathit{y}}_{-i}^{\mathit{net}}={\Sigma }_{j\ne i}{\mathit{u}}_j{r}_j$ as a linear ‘reconstruction’ or internal representation of the network input excluding neuron i. Similarly, we define $r_{-i}^{\mathit{sum}}={\Sigma }_{j\ne i}{r}_j$ as total activity in the network excluding neuron i. We then obtain the simplified equation:

$${\stackrel{.}{r}}_i=-r_i+{\mathit{u}}_i^T(\mathit{y}+s\cdot {\mathit{y}}_{-i}^{\text{net}})+c\cdot r_{-i}^{\text{sum}}$$

This derivation was demonstrated previously¹⁷ for the special case of s = −1 and c = 0. In this scenario, each neuron is driven by the overlap of the residual of $\mathit{y}-{\mathit{y}}_i^{\mathit{net}}$ with its tuning u_i, implementing a dynamic ‘explaining away’ of the network’s inputs.

Statistical Procedure:

Statistical tests used are specified in figure legends. We generally used non-parametric tests. We also used a bootstrap procedure both to calculate standard errors and for certain hypothesis tests. For standard error calculation, we re-calculated a test statistic (e.g. mean or standard deviation of a sample) on subsets of our data sampled 1,000 times from the full dataset with replacement. The standard deviation over bootstraps was used as the standard error of the test statistic. For hypothesis testing, used for calculating significance of influence regression coefficients, we performed influence regression 10,000 times on resampled data. The percentiles of the distribution for each coefficient are used for box and whisker plots, and the p-values reported are double the fraction of the bootstrap distribution in which the coefficient was 0 or of opposite sign to the median value. The reported p-values from this bootstrap procedure are thus ‘two-sided’.

Extended Data

Extended Data Figure 1:

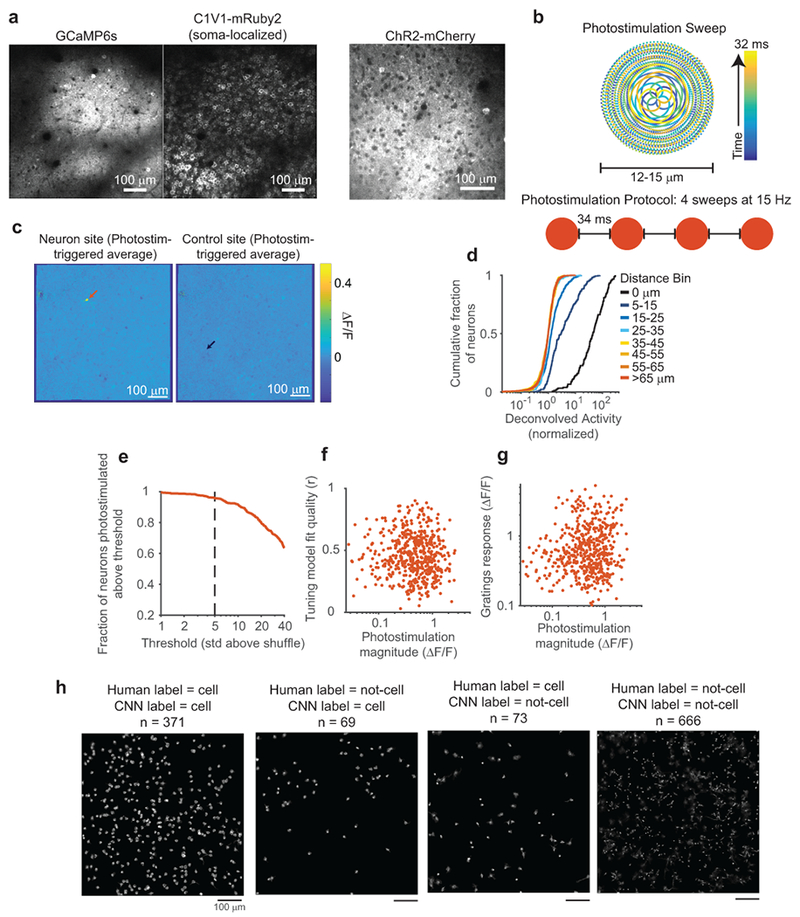
Photostimulation characterization and methods

(a) Left, images showing GCaMP6s and densely expressed, soma-localized C1V1 in the same neurons. Right, an image of Channelrhodopsin-2 tagged with mCherry, obtained from a different mouse. Note that non-localized channels are prominent in the neuropil background compared with soma-localized channels.

(b) Photostimulation protocol schematic. Top: beam position as a function of time, samples of mirror trajectory plotted at 100 kHz. Bottom: Four repeats of an identical sweep were used to photostimulate neurons.

(c) Photostimulation triggered average images, for a neuron (left) and control (right) site from the experiment in Fig. 1b. Arrows mark the location of both sites.

(d) Cumulative density plots of photostimulated neuron responses for different lateral displacements of target location from the neuron’s center. Same data as in Fig. 1e, but note log scale of x-axis. The 15-25 μm offset caused responses that were not present at greater distances.

(e) Fraction of neurons that could be photostimulated as a function of the threshold for this classification. At a threshold of 5 std above shuffle, more than 96% of neurons (n=518) could be photostimulated. Shuffle distributions were computed by bootstrap resampling of activity from trials the neuron was not targeted.

(f) Fit quality of the GP tuning model vs. photostimulation magnitude. Each dot is a single targeted neuron (n = 518 neurons). Spearman correlation, c = 0.084, p = 0.055.

(g) Mean gratings response of a neuron vs. photostimulation magnitude. Each dot is a single targeted neuron (n = 518 neurons). Spearman correlation, c = 0.11, p = 0.009.

(h) A CNN was trained with human-labeled data to predict whether CNMF sources were identified as a cell body or an alternative source, including distinct neural processes, excessively blurry or out-of-plane cells, or artefactual sources (see Methods). Note that many non-soma sources exhibited similar calcium transient signals as cell body sources. Because there is no objective ground-truth for this classification, held-out datasets were hand labeled, and compared to CNN labeling. One example dataset is shown here. The large majority of sources were labeled identically, however there are borderline cases where labels differed; many cases appear to be either human error in labeling, due to finite human time and inconsistencies in making borderline judgments, or an overly conservative CNN criteria for cell classification. Neither of these errors are expected to impact results presented in this manuscript.

Extended Data Figure 2:

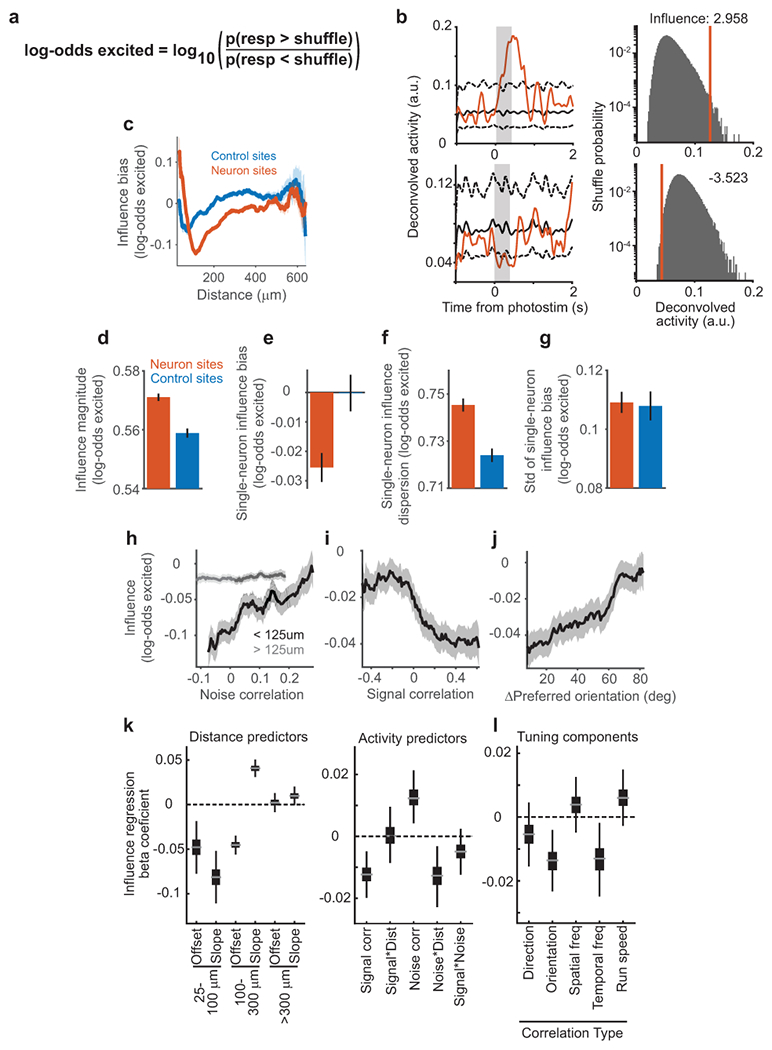
Influence measured as probability excited/inhibited (log-odds excited).

(a) Log-odds excited metric. This metric uses a non-parametric bootstrap procedure to estimate the chance of observing average responses to photostimulation of a target from random sampling of a neuron’s activity (see Methods). An influence value of 0.1 corresponds to a log-odds of ~1.259, or a probability of being excited above shuffles of ~0.557. This metric adapts to the varyingly sparse, heavy-tailed, and skewed response distributions of each neuron’s activity, and so complements the ΔActivity measure. Key analyses from Fig. 2 and Fig. 3 were repeated using this log-odds metric.

(b) Calculation of influence using the activity of a non-targeted neuron. Examples are shown for two pairs of neurons. Left: Deconvolved activity of a non-targeted neuron on trials photostimulating a different neuron (red). Black lines indicate 5% and 95% bounds from resampling all trials. Data were smoothed with a 67 ms std gaussian filter for display only. Right: Mean deconvolved activity for non-targeted neuron averaged over 0.367 s following photostimulation of target (red). Probabilities for obtaining a given deconvolved activity from the shuffle distribution of the non-targeted neuron are shown (black).

(c) Influence bias (average of signed influence values) as a function of distance between the targeted site and non-targeted neurons., plotted for both neuron and control photostimulation targets. Shading is mean ± sem. Same pairs as Fig. 2g, n = 153,689 neuron site pairs, 90,705 control site pairs.

(d) Influence magnitude measured as the absolute value of influence values for all pairs following neuron or control site photostimulation. The non-zero value for control sites is expected because of noise due to random sampling of neural activity and potential off-target effects. Error bars indicate mean ± sem. n = 153,689 neuron site pairs, 90,705 control site pairs. Neuron vs. control: p = 2.31 × 10⁻⁵, Mann-Whitney U-test.

(e) Influence bias for a single-target was the mean of influence values for the targeted neuron across all non-targeted neurons. Error bars indicate mean ± sem across targets. n = 518 neuron targets, 295 control targets. p = 7.40 × 10⁻⁴, Mann-Whitney U-test.

(f) Influence dispersion for a single-target was the standard deviation of influence values for the targeted neuron across all non-targeted neurons. Error bars indicate mean ± sem across targets. n = 518 neuron targets, 295 control targets. p = 2.3 × 10⁻⁶, Mann-Whitney U-test.

(g) The mean influence for all values for a single-target was calculated. Plotted is the standard deviation of these values for neuron sites and control sites. The similar values indicate that it is unlikely that some neurons tended to have much larger positive or negative influence than expected based on control sites. n = 518 neuron sites, 295 control sites. p = 0.88, two-sample F-test.

(h) Running average of influence with noise correlation, for nearby (black) or distant (gray) pairs, with bin half-width of 20% (percentile bins).

(i) Running average of influence with signal correlation, with bin half-width of 15% (percentile bins).

(j) Running average of influence with difference in preferred orientation, with bin half-width of 12.5 degrees.

(k) Coefficient estimates for linear regression of influence values. Plots show bootstrap distribution with median estimate as gray line, 25–75% interval as box, 1–99% interval as whiskers. Left: coefficients for piece-wise linear distance predictors from the model. Significance estimated by bootstrap: 25–100 μm, offset p = 0.0006, slope p < 1×10⁻⁴; 100–300 μm, offset p < 1×10⁻⁴, slope p < 1×10⁻⁴; > 300 μm, offset p = 0.68, slope = 0.056. Right: coefficients for activity predictors from the same model. Signal correlation, p = 0.0002; signal-distance interaction, p = 0.96; noise correlation p = 0.0010; noise-distance interaction, p = 0.0024; signal-noise interaction p = 0.14; n = 64,485 pairs.

(l) Coefficient estimates from separate models in which the specified tuning correlation replaced signal correlation in the influence regression model of (i). Same bootstrap and boxplot convention as (i). Each model used only pairs in which targeted and non-targeted neurons exhibited tuning. Direction, p = 0.21, n = 36,565 pairs; orientation, p = 0.0026, n = 36,565; spatial frequency, p = 0.30, n = 47,810; temporal frequency, p = 0.011, n = 26,526; running speed, p = 0.11, n = 46,634.

Extended Data Figure 3:

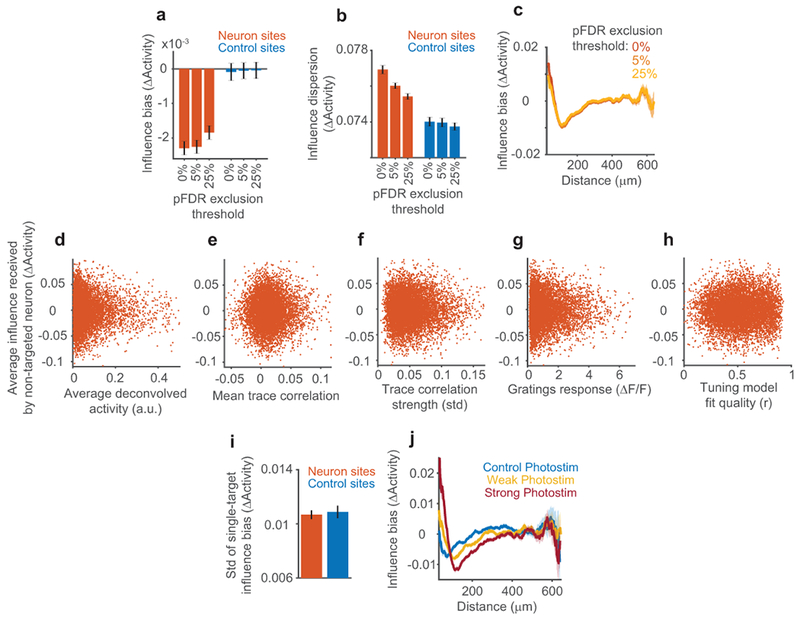
Extended comparison of photostimulation of neuron sites and control sites.

(a) Influence bias (mean ΔActivity) comparison between neuron and control site photostimulation, after exclusion of pairs with individually significant influence values. Significance of each individual pair’s influence was determined with a non-parametric bootstrap (Extended Data Fig. 3, Methods), and a p-value threshold for significance was chosen to restrict the fraction of false positives below 5% or 25% (pFDR, Methods). For 0%, n=153,689 neuron and 90,705 control pairs. 225 neuron and 26 control pairs were excluded for 5% pFDR, 638 neuron and 50 control pairs were excluded for 25% pFDR. Influence following neuron photostimulation was significantly negative for all thresholds, Mann-Whitney U-test, 0% p = 8.90 × 10⁻¹⁶, 5% p = 7.24 × 10⁻¹⁵, 25% p = 5.72 × 10⁻¹².

(b) As in (a) but for influence dispersion (std of ΔActivity). Influence dispersion was greater following neuron than control photostimulation for all thresholds, two-sample F-test, 0% p = 6.84 × 10⁻³⁹, 5% p = 6.04 × 10⁻²⁰, 25% p = 2.63 × 10⁻¹⁴.

(c) As in (a-b), but for influence bias as a function of distance. A quantitatively similar center-surround pattern was observed for all thresholds.

(d) Average influence values for a non-targeted neuron (over all photostimulated neurons) vs. that neuron’s average deconvolved activity during non-photostimulated trials in influence mapping blocks. Each dot is a single non-targeted neuron. n = 8552 neurons. Spearman correlation, c = −0.00003, p = 0.99.

(e) Same as in (c), except for mean trace correlation during tuning measurement blocks. c = 0.0068, p = 0.53.

(f) Same as in (d), except for trace correlation strength. c = 0.0099, p = 0.36.

(g) Same as in (d), except for gratings response. c = 0.0092, p = 0.38.

(h) Same as in (d), except for GP tuning model fit quality. c = 0.011, p = 0.29.

(i) The mean influence for all values for a single-target was calculated. The standard deviation of these values for neuron sites and control sites is plotted. The similar values indicate that it is unlikely that some neurons tended to have much larger positive or negative influence than expected based random sampling of the group mean (which was lower for neuron than control sites, see Fig. 2). Error bars, mean ± sem across targets. n = 518 neuron targets, 295 control targets, p = 0.72, two-sample F-test.

(j) Running average of influence with pairwise distance using bin half-width of 30 μm. Shading corresponds to mean ± sem calculated by bootstrap. Data are divided into influence from photostimulation sites with stronger versus weaker direct photostimulation responses in the targeted neuron, using a median split of photostimulation significance, as well as for control site photostimulation. Mean photostimulation response was 0.36 ΔF/F and 0.85 ΔF/F for weak and strong groups. Note the weak distance-dependence observed for control site photostimulation is consistent with greatly reduced, but non-zero, neural excitation when targeting control sites. This may result from a number of factors including suboptimal resolution and brain movement in vivo, and indicates the necessity of control site photostimulation.

Extended Data Figure 4:

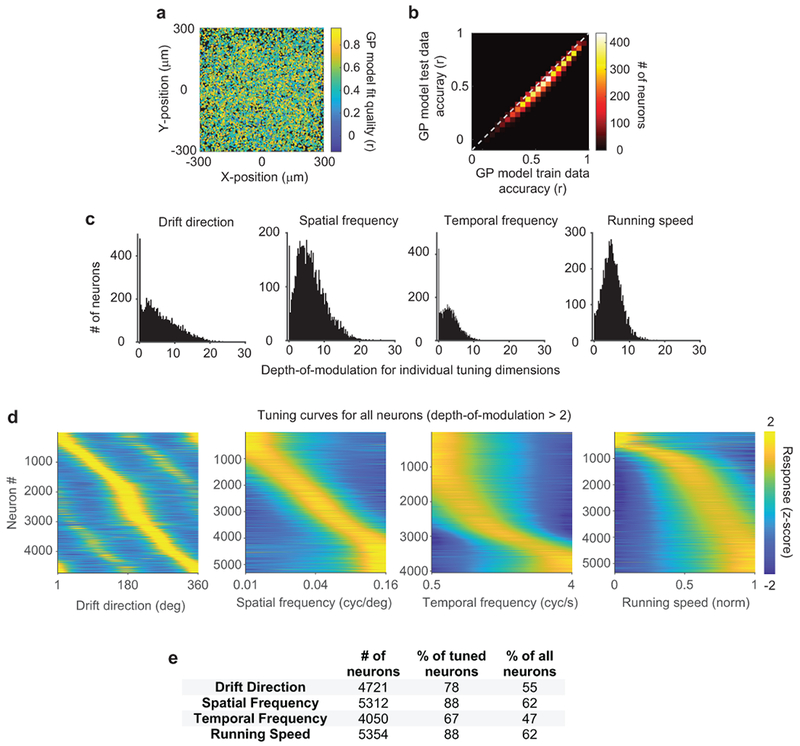
Characterizing neural tuning in V1 using Gaussian process (GP) regression.

(a) GP model fit quality (pearson correlation with held-out data). Each neuron plotted at its relative position in an individual experiment’s field-of-view. Neurons at all positions were similarly well fit.

(b) Two-dimensional histogram of GP model fit quality (‘test accuracy’) and prediction quality on not-held-out data (‘train accuracy’). Major overfitting was not observed.

(c) Depth-of-Modulation (see Methods) for each individual tuning dimension, for all neurons that passed model fit criteria. Dimensions exhibited qualitatively distinct distributions. Left: many neurons had almost no drift direction modulation, with many others exhibiting extremely pronounced modulation (> 10). Right: Almost all neurons exhibited a moderate degree of modulation (~5) by the mouse’s running speed.

(d) Z-scored tuning curves for each individual tuning dimension, for all neurons passing model fit criteria and with significant modulation (> 2) for the plotted dimension. Tuning was qualitatively different for different dimensions. Spatial frequency tuning was distributed evenly over our stimulus set and generally bandpass. Running speed tuning was distributed more tightly into a few neurons preferring stillness, versus many broadly preferring running.

(e) Significance of tuning for each dimension as determined by GP regression.

Extended Data Figure 5:

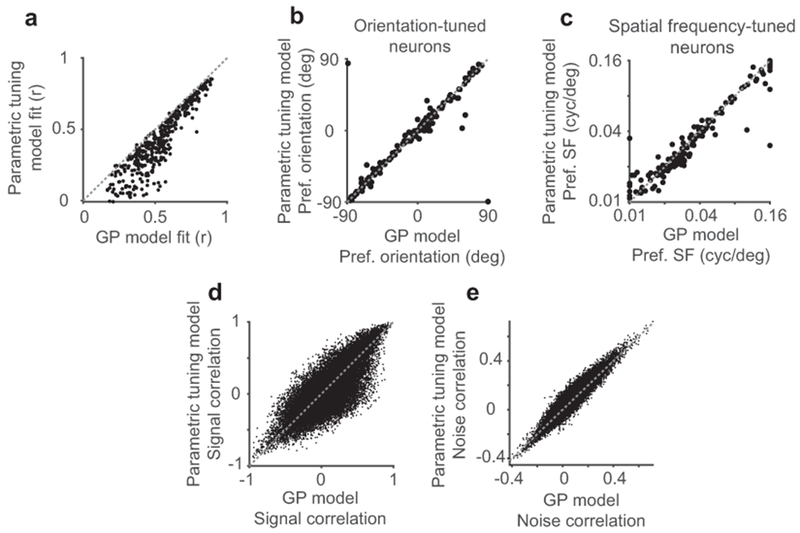
Comparison of GP tuning model and conventional parametric tuning model.

(a) Model fit qualities for an example session, assessed on left-out data. Each dot is a single neuron, n = 358 neurons. GP model fit qualities were higher than those from the parametric tuning model, mean difference of 0.11, p = 5.02 × 10⁻⁶⁰, Mann-Whitney U-test.

(b) Estimated preferred orientations of neurons were similar between models. Pearson correlation c = 0.88, calculated using only neurons significantly tuned to orientation.

(c) Estimated spatial frequency preferences of neurons were similar between models, c = 0.95 calculated using only neurons significantly tuned to spatial frequency.

(d) Signal correlations calculated from the two models were similar, c = 0.80.

(e) Noise correlations calculated from the two models were similar, c = 0.94.

Extended Data Figure 6:

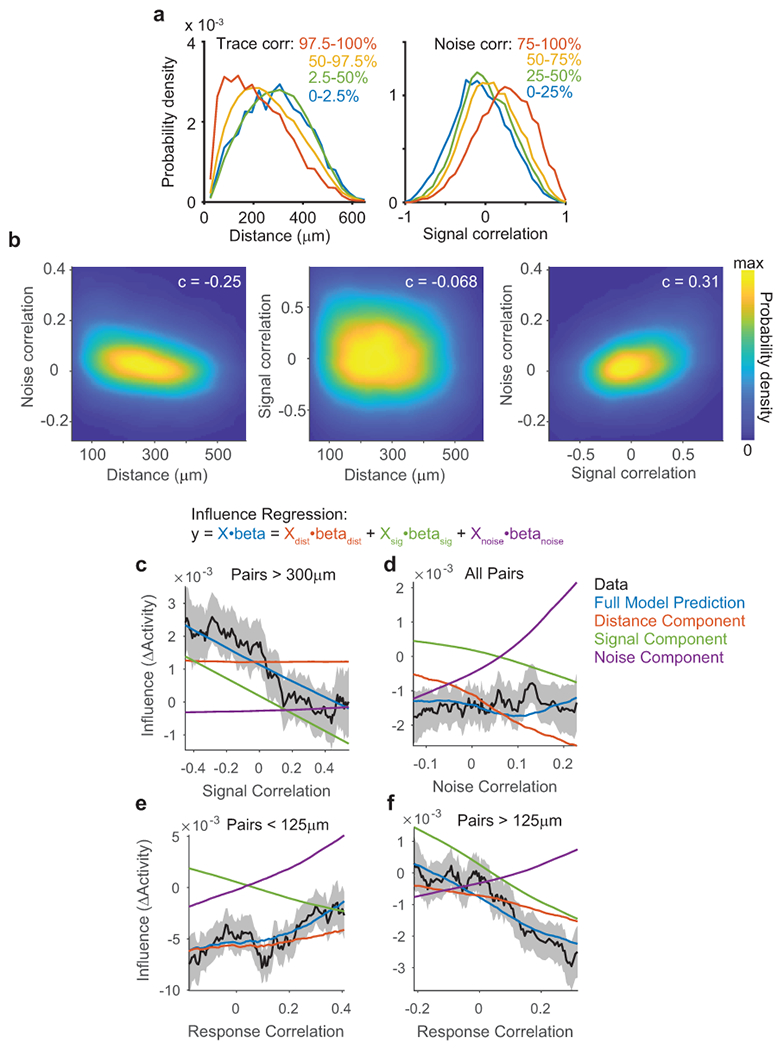
Influence regression separates contributions of correlated similarity metrics

(a) Probability density functions estimated by kernel smoothing for distance (left) and signal correlation (right), for all data used in influence regression (n = 64,485 pairs). Separate densities were estimated for pairs exhibiting varying trace correlation (left) or noise correlation (right). The plots show that pairs with high trace correlations occurred at all distances, but more often for nearby neurons. Similarly signal correlations for pairs with high versus low noise correlations were distinct but overlapping distributions. This highlights the importance and feasibility of influence regression to disambiguate the contributions of distance, signal, and noise correlation.

(b) Two-dimensional probability density functions for pairs of similarity metrics, estimated using kernel smoothing, for all data used in influence regression. Spearman correlation values for each pair of similarity metrics are overlaid. All correlations were significant with p < 1×10⁻⁶⁰, n=64,845 pairs.

(c) Running average of influence data (black) and predictions (colored lines) from influence regression model, using a bin half-width of 15% (percentile bins). Dashed lines are mean ± sem of data by bootstrap. Signal correlation is plotted against mean influence, for the subset of pairs more than 300 μm apart. Model predictions are computed using a full influence regression model (blue), or using subsets of coefficients from the same model (distance-red, signal-green, noise-purple). The full model prediction is equal to the sum of the three components. The running average analysis here accurately reflects the signal component of the influence regression model, plus a tonic offset from the distance component.

(d) Running average as in (a), but for noise correlation and pairs at all distances. Note that signal and noise interaction coefficients with distance are included in signal and noise components, respectively. The running average analysis here confusingly indicates a flat slope of noise correlation and influence. Our model predicts this relationship because pairs with higher noise correlations were located at shorter distances, and also had increased signal correlations, and these effects together canceled out increases in influence due to noise correlation.

(e) Running average as in (a), but for model-free correlations of single-trial responses, and for pairs separated by less than 125 μm. At short distances, the positive effect of noise correlations dominated the negative effect of signal correlations.

(f) Running average as in (a), but for model-free correlations of single-trial responses, and for pairs separated by more than 125 μm. At long distances, the negative effect of signal correlations dominated the positive effect of noise correlations.

Extended Data Figure 7:

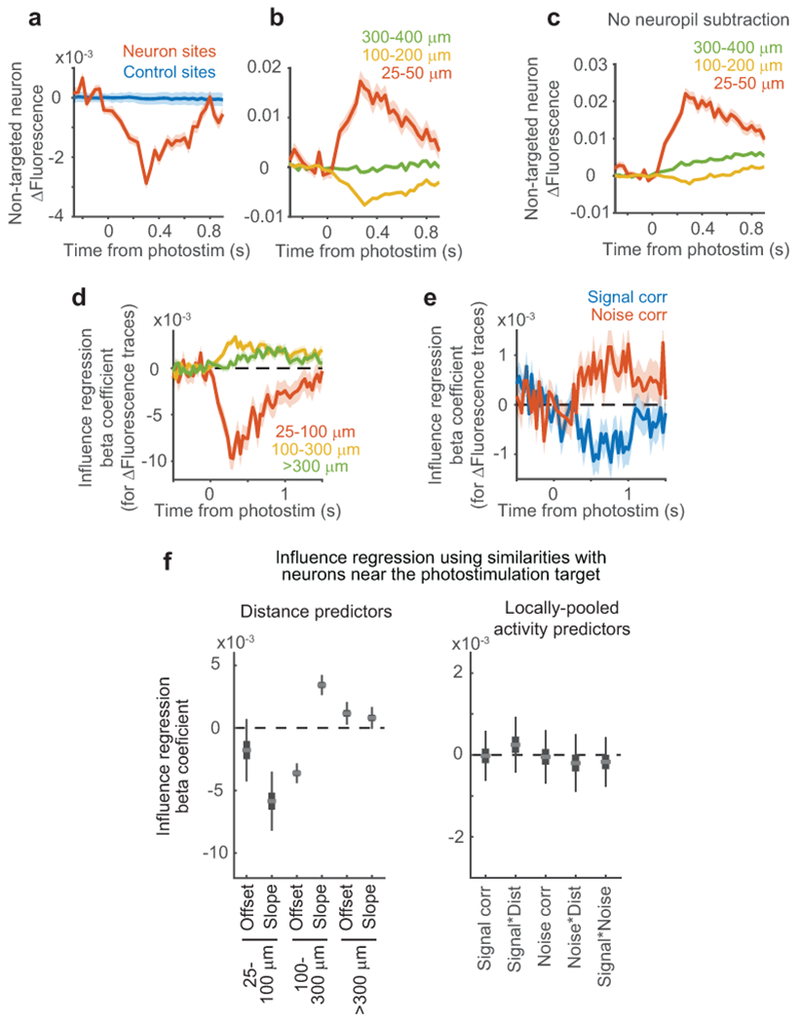
Results of influence regression are robust to potential artifacts from data processing and off-target photostimulation

(a) Analysis of influence effects directly in ΔF/F traces. ΔFluorescence was calculated as for ΔActivity, but using ΔF/F traces rather than trial-averaged deconvolved activity. ΔFluorescence was significantly negative in the 1 s following neuron photostimulation relative to control, n = 153,689 neuron site pairs and 90,705 control site pairs. Neuron vs. control site: p = 6.79 × 10⁻¹⁵, Mann-Whitney U-test. Shading for all plots is mean ± sem calculated by bootstrap.

(b) ΔFluorescence in non-targeted neurons following photostimulation of neurons at varying distances. n = 1,822 near pairs, 35,541 mid-range pairs, 35,882 far pairs. Near vs. mid-range: p = 7.62 × 10⁻¹⁹; near vs. far: p = 5.0 × 10⁻⁶; mid-range vs. far: p = 1.21 × 10⁻⁴⁷, Mann-Whitney U-test.

(c) As in (b), but without neuropil subtraction, or any source de-mixing from CNMF; traces were extracted by projecting raw movies onto neuron ROIs. n = 1,822 near pairs, 35,541 mid-range pairs, 35,882 far pairs. Near vs. mid-range: p = 5.96 × 10⁻²⁸; near vs. far: p = 5.21 × 10⁻³⁸; mid-range vs. far: p = 4.15 × 10⁻¹³, Mann-Whitney U-test. This indicates that distance-dependent influence effects were not an artifact of source extraction algorithms.

(d) The influence regression from Fig. 3d was applied to ΔFluorescence traces. This regression resulted in beta coefficients for traces at each time frame relative to photostimulation onset, which are plotted over time. Coefficients for slopes for the three distance bins are plotted. The same size and ordering of effects is apparent as when using deconvolved data and the ΔActivity metric, compare to Fig. 3. Shading corresponds to mean ± sem, calculated using 10,000 coefficient estimates by bootstrap resampling. All coefficients were significantly different from zero, averaged over 0–1,000 ms from photostimulation onset, with p < 1×10⁻⁴ by bootstrap.

(e) Same as in (a) except for signal and noise correlation coefficients. Averaged over 0–1,000 ms from photostimulation onset, signal correlation coefficients were significantly less than zero with p = 0.0008 and noise correlation was greater than zero with p = 0.0154, estimated by bootstrap.

(f) Similar to regression analysis in Fig. 3d–e, except as a test of potential off-target effects. Instead of using only the photostimulated neuron’s activity and tuning properties to calculate correlations with the non-targeted neuron, properties of multiple nearby neurons were used, to test if off-target photostimulation of nearby cells could underlie the observed effects (see Methods). This is equivalent to influence regression using identical influence values and distance predictors as in Fig. 3e, but changing all activity predictors. Only distance effects were apparent, as expected, whereas activity-related effects were absent. This suggests that the properties of the individually targeted neuron were responsible for the influence relationships we observed. Plots show bootstrap distribution with median estimate as gray line, 25–75% interval as box, 1–99% interval as whiskers. Left: coefficients for piece-wise linear distance predictors from the model. Significance estimated by bootstrap: 25–100 μm, offset p = 0.0982, slope p < 1×10⁻⁴; 100–300 μm, offset p < 1×10⁻⁴, slope p < 1×10⁻⁴; > 300 μm, offset p = 0.0018, slope = 0.0316. Right: coefficients for activity predictors from the same model. Signal correlation, p = 0.9370; signal*distance interaction, p = 0.4072; noise correlation p = 0.8772; noise*distance interaction, p = 0.5138; signal*noise interaction p = 0.5260; n = 64,485 pairs.

Extended Data Figure 8:

Population analysis of gratings responses during influence mapping blocks

(a) The orientation information content of all neurons during influence mapping blocks, calculated using the same binning approach used for population decoding. Information is color coded, and plotted as a function of a neuron’s directional modulation and preferred spatial frequencies estimated during tuning measurement blocks. This demonstrates that tuning estimated in tuning and influence measurement blocks were concurrent (gratings during influence mapping were always 0.04 cyc/deg), but that responses to full-field, low-contrast gratings in influence measurement blocks were sparse.

(b) Schema indicating the orthogonalization procedure used for population analysis. Briefly, because average responses to each grating orientation were not entirely orthogonal, and because photostimulation evoked highly significant changes in response gain in our dataset, we wished to isolate potential changes along alternative population activity dimensions independent of gain changes. To accomplish this we orthogonalized projections along non-gain dimensions relative to the gain projection observed on individual trials. This ensured that changes in response gain could not trivially produce changes along non-gain population dimensions.

Extended Data Figure 9:

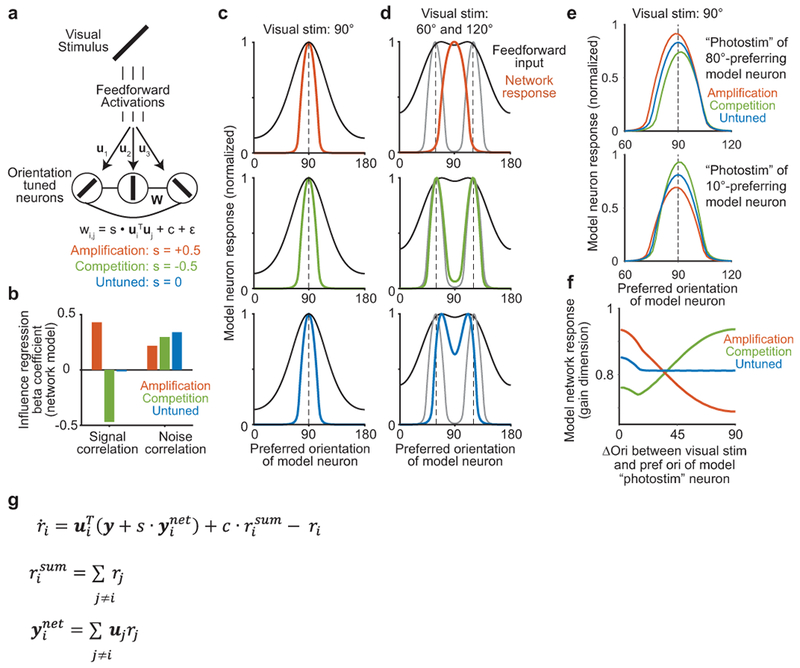
‘Toy’ model of feature competition and its functional implications.

(a) Diagram of rate-network model, in which each neuron i receives feedforward input u_i driven by the orientation of a visual stimulus and has functional connection w_i,j with neuron j. Neurons were modeled as rectified-linear units.

(b) Influence regression coefficients for the rate-network model. Signal and noise correlations were estimated from noisy simulated trials and regressed against functional connections W, similar to Fig. 3d–e. To be consistent with experimental data, random trial-to-trial fluctuations in gain as well as single-neuron-specific noise were added to simulations (see Methods), such that all networks exhibited a positive correlation between signal and noise correlations. However results were similar without simulated gain fluctuations.

(c) Model neuron responses following presentation of a 90 degree stimulus. Feedforward inputs were identical for all networks. Colors are the same as in panel (a). Dashed line indicates orientation of the visual stimulus.

(d) Model neuron responses following presentation of a linear sum of 60 and 120 degree stimuli. Gray lines are the average response of each network to the two stimuli presented individually. Note that neurons preferring 70 and 110 degrees receive the maximum feedforward input.

(e) Model neuron responses to a visual stimulus (90 degrees) with simulated photostimulation of a neuron. Responses (in non-stimulated neurons) are shown when the “photostimulated” neuron had preference for similar (top, 80 degrees) or dissimilar (bottom, 10 degrees) orientations relative to the visual stimulus, color coded by network type. Responses are normalized to activity without simulated photostimulation.

(f) Model network responses to visual stimuli with simultaneous “photostimulation”, as a function of difference in orientation between visual stimulus and “photostimulated” neuron’s preference. The response gain dimension was calculated as the normalized response to the visual stimulus in the absence of “photostimulation”.

(g) Analytical solution for the linear aspect of network dynamics (see Methods for derivation). This indicates that the network performs a comparison between inputs y and an internal estimate y^net, which when s is negative corresponds to dynamical explaining away of network inputs.

Extended Data Figure 10:

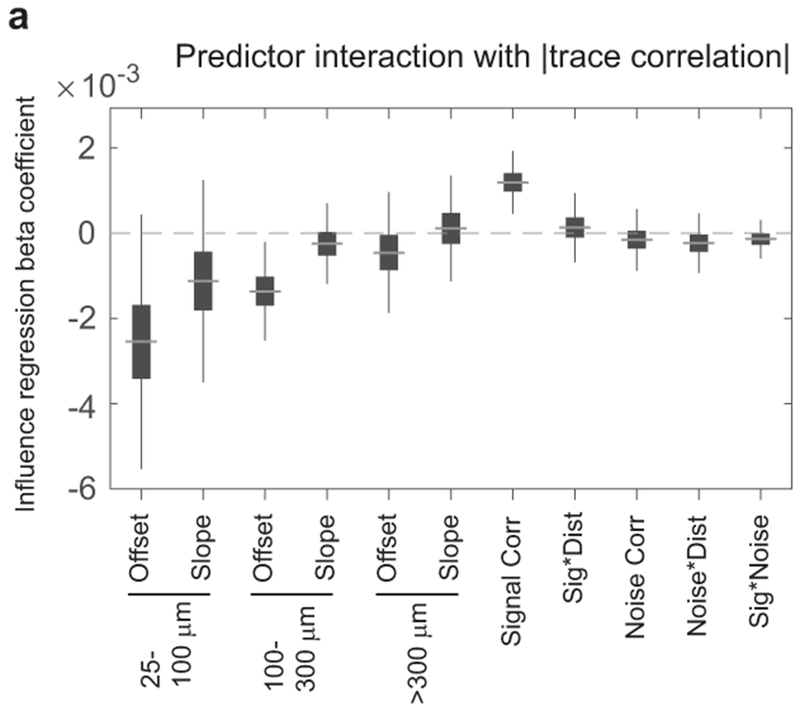
Interaction of trace correlation with influence regression model coefficients

(a) Further characterization of the effects of trace correlation on feature competition vs. amplification (compare to Fig. 5d). Influence regression (as in Fig. 3d) was performed after including an interaction of each predictor with the magnitude of trace correlation. Coefficient estimates for each interaction plotted with uncertainty from bootstrap: gray line, median; box, 25–75% interval; whiskers, 1–99% interval. This analysis used no manually-specified division between ‘strong’ and ‘weak’ correlations, and considered whether trace correlation changed the relationship between influence and any predictors in the influence regression. Signal correlation exhibited a highly significant positive interaction, indicating a transition from competition (negative slope) to amplification (positive slope) as the magnitude of trace correlation increased, n = 64,845 pairs, p = 0.0002 (bootstrap). Interactions with all other activity predictors were not significant with p > 0.444. Interactions with the slopes of distance predictors were not significant with p > 0.2716. There were weak interactions with offsets for near (p = 0.0486) and mid (p = 0.0076) distance bins, but not far (p=0.4738). These results indicate that the magnitude of trace correlation had a substantial effect on the relationship between signal correlation and influence.