Abstract
Background:
The Gail model and the model developed by Tyrer and Cuzick are two questionnaire–based approaches with demonstrated ability to predict development of breast cancer in a general population.
Methods:
We compared calibration, discrimination and net-reclassification of these models, using data from questionnaires sent every 2 years to 76,922 participants in the Nurses’ Health Study between 1980 and 2006, with 4,384 incident invasive breast cancers identified by 2008 (median follow-up 24 years; range 1–28 years). In a random one-third sample of women, we also compared the performance of these models with predictions from the Rosner-Colditz model estimated from the remaining participants.
Results:
Both the Gail and Tyrer-Cuzick models showed evidence of mis-calibration (Hosmer-Lemeshow P<0.001 for each) with notable (P<0.01) over-prediction in higher risk women (2-year risk above about 1%) and under-prediction in lower risk women (risk below about .25%). The Tyrer-Cuzick model had slightly higher C-statistics both overall (P<0.001) and in age-specific comparisons than the Gail model (overall C 0.63 for Tyrer-Cuzick versus 0.61 for the Gail model). Evaluation of net reclassification did not favor either model. In the one-third sample, the Rosner-Colditz model had better calibration and discrimination than the other two models. All models had C-statistics <0.60 among women age ≥70.
Conclusion:
Both the Gail and Tyrer-Cuzick models had some ability to discriminate breast cancer cases and non-cases, but have limitations in their model fit.
Impact:
Refinements may be needed to questionnaire-based approaches to predict breast cancer in older and higher risk women.
Breast cancer prediction rules, based solely on questionnaire information without data from biomarkers or mammograms, can be implemented non-invasively and at minimal cost in large populations. While these prediction rules have limitations in their overall ability to distinguish women who will and will not develop breast cancer (1–3), they have been utilized for risk stratification for chemoprevention and screening protocols (4–6).
Information on the relative performance of the alternative risk models in general populations is still somewhat limited, with available evidence indicating modest concordance in risk classification and limited discrimination in external validation (3, 7). Perhaps the two most widely evaluated models that do not require biomarker or mammographic data are the Breast Cancer Risk Assessment Tool (BCRAT) developed by Gail and colleagues (8–12) and the International Breast Cancer Intervention Study (IBIS) risk score developed by Tyrer and Cuzick (13). Explicit comparisons of discrimination, calibration, and classification performance between these two models have used selected populations of higher risk women enriched for family history or risk factors such as high rates of delayed childbirth (1, 14, 15). Further, these studies included relatively small numbers of breast cancer cases (<250 in each study), limiting the ability to evaluate the accuracy of classification of women across a wide range of clinical risk categories. All three found better calibration and discrimination with the Tyrer-Cuzick model relative to the Gail model. The impact of enrichment of the study populations with women who have a positive family history is unclear.
In this paper, we compare metrics of model performance, including calibration, discrimination, and ability to re-classify cases into higher clinical risk categories and non-cases into lower risk categories (net-reclassification indices) between the Gail and Tyrer-Cuzick models in the broad population of US nurses participating in the Nurses’ Health Study, including a higher percentage of women at average risk. Also, we compare the performance of these models with that of an updated version of the alternative Rosner-Colditz risk prediction model, as developed in a sample of participants in the Nurses’ Health Study, and evaluated in an independent sample (16–19).
Materials and Methods
The Nurses’ Health Study cohort was established in 1976 when 121,701 female registered nurses aged 30–55 years responded to a mailed questionnaire inquiring about risk factors for breast cancer, including reproductive factors, menopausal hormone therapy use, anthropometric variables, benign breast disease, and family history of breast cancer. The risk factor data have been updated by means of repeat questionnaires sent every 2 years up to the present time (20).
Alcohol consumption, both current and at age 18 years, was ascertained in 1980, with information updated in 1984, and then every 4 years from 1986 to 2006. Measures of family history of breast and ovarian cancer, utilized in the Tyrer-Cuzick model, were assessed at several times during follow-up (21). Information on breast cancer in a woman’s mother and the number of her sisters with breast cancer was collected first in 1976, then updated in 1982, 1988, 1992, 1996, 2000, and 2004, with updates on age at diagnosis for each in 1996, 2000, and 2004. Women were asked about breast cancer in their maternal and paternal grandmothers in 1988; in their daughters in 2000 and 2004; and about ovarian cancer in their mothers and sisters in 1992, 1996, and 2000, and in their daughters in 2004.
Identification of breast cancer cases
On each questionnaire, women were asked whether breast cancer had been diagnosed and, if so, the date of diagnosis. All women (or their next of kin, if deceased) were contacted for permission to review their medical records so as to confirm the diagnosis. Cases of invasive breast cancer from 1980 to 2008 for which we had a pathology report were included in these analyses. We excluded women with types of menopause other than natural menopause or bilateral oophorectomy because of the inability to determine the true age at menopause and menopausal status, prevalent cancer (other than nonmelanoma skin cancer) in 1980, or missing data for weight at age 18 years, age at first birth, parity, age at menarche, age at menopause, or menopausal hormone therapy use.
During follow-up of 76,922 (768,948 2-year intervals) women with complete data on baseline risk factors from 1980 to 2006, 4,384 women developed invasive breast cancer. We censored women who developed another type of cancer (except non-melanoma skin cancer) at their diagnosis date.
Analysis
All estimates of risk from the Gail, Tyrer-Cuzick, and Rosner-Colditz models used 2-year risk windows. This was expected to maximize predictive performance, as all models used time-varying covariates which were updated at 2-year intervals. Thus, for a woman still cancer free at the beginning of a follow-up interval, her risk over the subsequent 2 years was estimated based on her risk factor profile at that time. For variables not updated at each questionnaire, including family history and alcohol use information, we carried forward responses from prior questionaires. This approach parallels previous strategies used to evaluate time-varying risk (22–24).
Rockhill et al (25) previously evaluated the fit and discriminatory ability of the BCRAT model in the Nurses’ Health Study, based on data from 1992 through 1997. We used the BRCa_RAM SAS macro developed by the Division of Cancer Epidemiology and Genetics at the National Cancer Institute (http://dceg.cancer.gov/tools/risk-assessment/bcrasasmacro) to estimate a woman’s Gail-model risk of developing breast cancer over a 2-year period, separately for every 2-year interval with updated risk factor information, beginning in 1980 and continuing as long as a woman was alive, reporting risk factor information, and free of breast cancer and other cancer types except nonmelanoma skin cancer. The variables in the Gail model and their assessment in the Nurses’ Health Study are described in Supplemental Table 1. As in Rockhill et al (25), presence of hyperplasia was coded as missing because this variable was only assessed in a small group of participants in the Nurses’ Health Study. While imputation of hyperplasia status can be useful, we chose not to apply models that include the outcome (breast cancer development) in the imputation of hyperplasia status and have been found to have a small impact on the C-statistic for prediction (26). Also, we were able to classify women at the beginning of an interval only with regard to ever/never history of previous benign breast biopsy, rather than 0, 1, or greater than or equal to two biopsies as specified in the Gail model.
We also estimated a woman’s 2-year risk of breast cancer, separately for each of the time intervals she contributed to the analysis based on her updated information from the Tyrer-Cuzick model, as implemented from a command line version downloaded from http://www.ems-trials.org/riskevaluator/software/v7/winBatch/IBIS_RiskEvaluator_CL_v8.zip, as directed by a personal communication from the authors. Variables included in the Tyrer-Cuzick and Gail models and their assessment in the Nurses’ Health Study are described in Supplemental Table 1. As for the Gail model, we set to missing the indicators of hyperplasia status and also did not have information on a woman’s Ashkenazi heritage, her expected future duration of hormone therapy, bilaterality of breast cancer in relatives, or on her genetic testing or that of her relatives. We also invoked the model’s missing data option for family history variables in a woman’s second or third degree relatives (except for available information on grandmothers which was utilized).
Evaluation of calibration of the models compared observed and expected risks within deciles of predicted risks for each of the Tyrer-Cuzick and Gail models. The unit of analysis for these comparisons was the observed and predicted outcome within a 2-year interval. We used the large sample confidence interval for the ratio of expected to observed events based on log transformation of this ratio and the delta method, as previously applied by Park et al (27). Consistent with this confidence interval, we used the Z-statistic defined as log(E/O)/sqrt(1/O) to test the null hypothesis that the expected to observed ratio (E/O) was equal to 1 within a decile of predicted risk. In addition to decile-specific ratios and confidence intervals of observed to expected event ratios, we used the Hosmer-Lemeshow test statistic as an indicator of calibration. Graphical display of the observed versus expected numbers of cases within each decile of risk included 95% confidence intervals for the observed count, with use of a log transformation for variance stabilization, as above. Subgroup analyses evaluated calibration for each model separately using intervals in women age <50, 50–59, 60–69, and ≥70 when the interval started.
We also compared discrimination between the two models, both overall and within age groups with age defined at the beginning of each 2-year interval. Estimates of standard errors of overall, age-adjusted, and age-specific C-statistics between models used the approach of Rosner and Glynn (28).
To evaluate risk re-classification based on alternative models, we used four a priori chosen absolute 2-year risk categories suggested by Tice et al (29): 0-<.4%; .4-<.67%; .67-<1.0%; and ≥1.0%. Following recommendations of Kerr et al (30), we report reclassification percentages separately for breast cancer cases and non-cases, again with 2-year time windows as the unit of analysis. Additional subgroup analyses considered risk reclassification separately among intervals in each of the four age groups defined above. As additional subgroup analyses, we considered calibration, discrimination, and reclassification in intervals among women with a family history of breast cancer in a first degree relative.
We also compared calibration and discrimination of the Gail and Tyrer-Cuzick models to that of the Rosner-Colditz model. Estimates of the parameters of the Rosner-Colditz model were obtained using all available study time in a two-thirds random sample of study participants, and its calibration and discrimination were evaluated in the other third of the study population over the same time period from 1980 until 2008 (19). Herein, we also use this one third sample of the study population to compare calibration and discrimination of the Gail and Tyrer-Cuzick models with that of the Rosner-Colditz model.
Results
In the 768,948 2-year intervals during the time period from 1980 to 2008, 4,384 women developed incident, invasive breast cancer for an average 2-year risk of 0.57%. Supplemental Table 2 compares distributions of characteristics at the beginning of intervals among all women, those with a history of breast cancer in a first degree relative, and those who developed breast cancer during that interval.
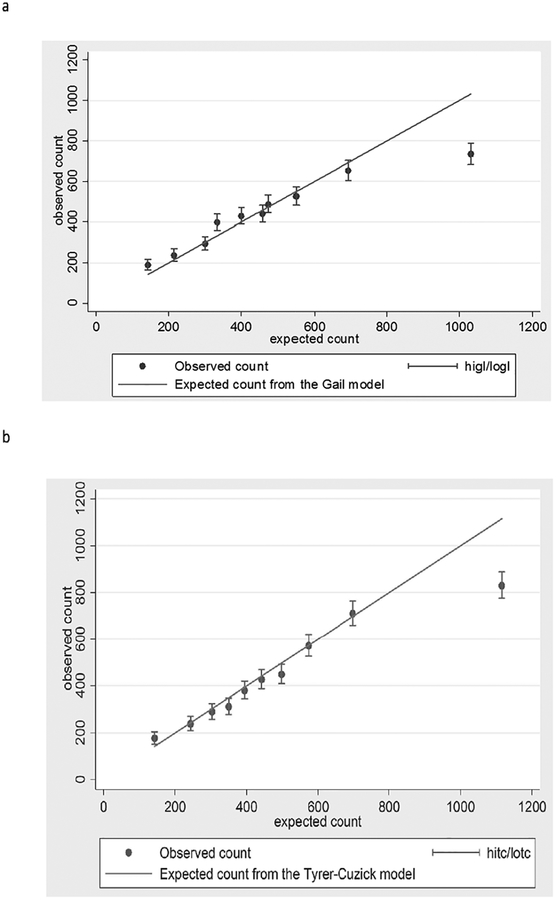
Overall, both the Gail model and the Tyrer-Cuzick model slightly overestimated the number of incident breast cancer cases in the Nurses’ Health Study. Specifically, the average 2-year predicted risk from the Gail model was 0.60%, and this model predicted 5% more cases than observed (95% CI: 2%−8%) (Table 1). The average 2-year predicted risk from the Tyrer-Cuzick model was 0.62% and this model predicted 9% more cases than observed (95% CI: 5%−12%) (Table 1). However, agreement between observed and predicted numbers of cases varied substantially according to predicted risk. Both models substantially underestimated the number of cases in the lowest decile of their predicted risk (24% fewer expected cases than observed for the Gail model and 19% fewer expected cases than observed for the Tyrer-Cuzick model). Conversely, both models substantially overestimated the number of cases in the highest decile of their predicted risk (40% more expected than observed for the Gail model and 34% more expected than observed for the Tyrer-Cuzick model). Graphical comparisons of observed versus expected counts illustrated these differences but showed good agreement for predictions within deciles 2–9 of each model (Figure 1a and b). For both models, the Hosmer-Lemeshow test of the null hypothesis that the model is adequately calibrated was highly significant, suggesting some miscalibration.
Table 1.
Calibration of predictions from the Gail and Tyrer-Cuzick models in the Nurses’ Health Study: 4,384 incident breast cancer cases in 764,564 2-year intervals
| Gail model | Gail model calibration | Tyrer-Cuzick model | Tyrer-Cuzick model calibration | ||||
|---|---|---|---|---|---|---|---|
| Risk decile cutpoints | Intervals, expected and observed cases | Risk decile cutpoints | Intervals, expected and observed cases | ||||
| Predicted risk (%)* | N | E/O | Ratio, (95% CI) | Predicted risk (%)* | N | E/O (ratio) | Ratio, (95% CI) |
| .0249–.2485 | 78,871 | 143.2/189 | 0.76, (0.66, 0.87)‡ | .0258-.2644 | 76,894 | 142.8/176 | 0.81, (0.70, 0.94)‡ |
| .2486–.3474 | 71,461 | 215.8/237 | 0.91, (0.80, 1.03) | .2644-.3604 | 76,895 | 243.3/238 | 1.02, (0.90, 1.16) |
| .3480–.4020 | 80,932 | 301.1/294 | 1.02, (0.91, 1.15) | .3604-.4262 | 76,895 | 303.4/289 | 1.05, (0.94, 1.18) |
| .4023–.4755 | 75,874 | 334.3/398 | 0.84, (0.76, 0.93)‡ | .4262-.4837 | 76,895 | 350.0/311 | 1.13, (1.01, 1.26)‡ |
| .4757–.5313 | 78,763 | 400.7/429 | 0.93, (0.85, 1.03) | .4837-.5428 | 76,895 | 394.5/381 | 1.04, (0.94, 1.14) |
| .5314–.6097 | 81,484 | 473.0/486 | 0.97, (0.89, 1.06) | .5428-.6089 | 76,895 | 442.2/427 | 1.04, (0.94, 1.14) |
| .6098–.6902 | 70,139 | 457.9/439 | 1.04, (0.95, 1.15) | .6089-.6909 | 76,895 | 498.3/449 | 1.11, (1.01, 1.22)‡ |
| .6904–.8001 | 74,505 | 549.9/525 | 1.05, (0.96, 1.14) | .6909-.8101 | 76,894 | 573.5/572 | 1.00, (0.92, 1.09) |
| .8002–.9941 | 79,868 | 694.0/652 | 1.06, (0.99, 1.15) | .8101–1.042 | 76,896 | 698.8/711 | 0.98, (0,91, 1.06) |
| .9948–4.289 | 77,051 | 1032.1/735 | 1.40, (1.31, 1.51)‡ | 1.042–5.141 | 76,894 | 1115.8/830 | 1.34, (1.26, 1.44)‡ |
| Overall | 768,948 | 4,602/4,384 | 1.05, (1.02, 1.08)‡ | 768,948 | 4762.4/4384 | 1.09, (1.05, 1.12)‡ | |
| Average (SD), min–max predicted risk (%) | 0.60 (0.34), 0.0249–4.289 | 0.62 (.36), .0258–5.141 | |||||
| Hosmer-Lemeshow Chi square =121.36, d.f.=8, P<0.001 | Hosmer-Lemeshow Chi square =92.15, d.f.=8, P<0.001 | ||||||
E/O denotes expected number of breast cancer cases/observed number of cases
Predicted 2-year risk
P<0.01 for test of the null hypothesis that E/O=1
Figure 1.
a. Scatterplot of observed versus expected counts over deciles of risk based on the Gail model with 45 degree line*
*higl and logl denote the upper and lower 95% confidence interval limits for the observed count
b. Scatterplot of observed versus expected counts over deciles of risk based on the Tyrer-Cuzick model with 45 degree line*
*hitc and lotc denote the upper and lower 95% confidence interval limits for the observed count
Separate analyses of calibration for the two models restricted to women within each of four age groups (<50, 50–59, 60–69, and ≥70) found evidence for misclassification of each model within each age group (Supplemental Tables 3–6). In particular, under-prediction of risk was noted for both models among lower risk women younger than 50, and over-prediction of risk was seen in higher risk women in the two age groups age 60 or above.
Discrimination, as measured by the C-statistic, was better for the Tyrer-Cuzick model (0.629) than for the Gail model (0.608) (Table 2). When discrimination was examined separately in each of four age groups, discrimination was slightly better by the Tyrer-Cuzick model in each age-group. A weighted average of the age-specific C-statistics, which somewhat adjusts for age, found lower C-statistics from each model (0.600 for the Tyrer-Cuzick model and 0.574 for the Gail model).
Table 2:
Comparison of age-specific, and weighted averages of age-specific C-statistics for the Gail and Tyrer-Cuzick breast cancer prediction models in the Nurses’ Health Study: 4,384 incident breast cancer cases in 764,564 2-year intervals
| Cases | Gail model | Tyrer-Cuzick model | Difference | ||
|---|---|---|---|---|---|
| Age group | N | C ±SE | C ±SE | C ±SE | P-value |
| <50 years | 616 | .587±.011 | .599±.011 | .012±.006 | 0.032 |
| 50–59 years | 1441 | .579±.008 | .599±.007 | .020±.007 | 0.002 |
| 60–69 years | 1575 | .568±.007 | .607±.007 | .039±.007 | <0.001 |
| ≥70 years | 752 | .564±.010 | .587±.010 | .024±.009 | 0.011 |
| Weighted average† | 4384 | .574±.004 | .600 ± .004 | .023±.003 | <0.001 |
| Overall‡ | 4384 | .608±.004 | .629±.004 | .021±.002 | <0.001 |
Weighted average of the age-group specific C-statistic
Based on prediction in the entire dataset without age adjustment
A comparison of the ability to reclassify cases into meaningfully higher risk groups and non-cases into meaningfully lower risk groups found different conclusions for these two comparisons (Table 3). The Tyrer-Cuzick model reclassified 27.3% of incident cases into a higher risk category than the Gail model, while the Gail model reclassified 15.1% of cases into a higher risk category than the Tyrer-Cuzick model, for a net reclassification of cases of 12.2%. Conversely, the Gail model reclassified 22.4% of non-cases into a lower risk category than the Tyrer-Cuzick model, while the Tyrer-Cuzick model reclassified 16.2% of non-cases into a lower risk category, for a net reclassification of non-cases of 6.2%. Some heterogeneity in this reclassification pattern was observed when reclassification was evaluated separately in each of four age groups (Supplemental Tables 7–10). Specifically, while in the three younger age groups (women under age 70), the Tyrer-Cuzick model reclassified a higher percentage of cases to a higher risk category and the Gail model reclassified a higher percentage of non-cases to a lower risk category, for women age ≥ 70 the Gail model reclassified a higher percentage of cases to a higher risk category and the Tyrer-Cuzick model reclassified a higher percentage of non-cases to a lower risk category.
Table 3.
Cross-classification of predicted and observed risk by the Gail model and the Tyrer-Cuzick model based on 4,384 incident breast cancer cases over 768,948 2-year intervals in the Nurses’ Health Study
| Tyrer-Cuzick model 2-yr risk | ||||
|---|---|---|---|---|
| Gail model 2–yr risk | 0–<.4% | .4–<.67% | .67–<1.0% | ≥1.0% |
| 0–<.4%, n | 160,388 | 62,664 | 2,584 | 165 |
| Cases (risk*) | 428 (2.7) | 252 (4.0) | 19 (7.4) | 1 (6.1) |
| .4–<.67%, n | 33,107 | 189,243 | 73,117 | 6,554 |
| Cases (risk*) | 127 (3.8) | 949 (5.0) | 547 (7.5) | 80 (12.2) |
| .67–<1.0%, n | 4,272 | 65,039 | 70,035 | 27,080 |
| Cases (risk*) | 10 (2.3) | 363 (5.6) | 593 (8.5) | 296 (10.9) |
| ≥1.0%, n | 140 | 5,813 | 16,191 | 52,556 |
| Cases (risk*) | 2 (14.3) | 25 (4.3) | 137 (8.5) | 555 (10.6) |
2-year risk × 1,000
Net reclassification index (cases): Gail model: (127+10+363+2+25+137)/4384 = 15.1%;
Tyrer-Cuzick model: (252+19+1+547+80+296)/4384 = 27.3%
Net reclassification index (non-cases): Gail model: (62412+2565+164+72570+6474+26784)/764564 = 22.4%;
Tyrer-Cuzick: (32980+4262+64676+138+5788+16054)/764564 = 16.2%
In addiditional subgroup analyses of intervals in women who had a family history of breast cancer (Supplemental Tables 11–13), risk remained over-estimated among women in the highest risk groups for both models. The magnitude of over-estimation was greater in this subgroup than observed in the whole population (Supplemental Table 11 and Supplemental Figures 1a and 1b). Discrimination remained better for the Tyrer-Cuzick model relative to the Gail model, but it was overall weaker for both models in this restricted population relative to the results in the entire cohort. As for the overall analyses, the Tyrer-Cuzick model reclassified more cases to higher risk categories while the Gail model reclassified more non-cases to lower risk categories among women with a family history.
In the one third sample of women set aside for validation of the re-fitted Rosner-Colditz model, 1,418 incident breast cancer cases occurred in 254,767 2-year intervals for a 2-year risk of 0.56%. In this validation sample, the Rosner-Colditz model had an average 2-year risk of 0.58% (Table 4), which yielded an overall ratio of expected to predicted numbers of events of 1.04 (95% CI: 0.98–1.09). Overall, calibration of the Rosner-Colditz model was adequate in this independent sample (Hosmer-Lemeshow Chi square P=0.18). Both the Gail and Tyrer-Cuzick models showed the same patterns seen in the entire dataset of fewer predicted than observed events in the lowest risk decile and more predicted than observed events in the highest risk decile within this valildation sample (Table 4).
Table 4.
Calibration of predictions from the Gail, Tyrer-Cuzick and re-fitted Rosner-Colditz models in the Nurses’ Health Study: 1,418 incident breast cancer cases in 254,767 2-year intervals among women in the validation sample for the Rosner-Colditz model
| Gail model calibration | Tyrer-Cuzick calibration | Rosner-Colditz calibration | ||||||
|---|---|---|---|---|---|---|---|---|
| Intervals, expected and observed cases | Intervals, expected and observed cases | Intervals, expected and observed cases | ||||||
| Risk* (%) | N, E/O | Ratio, (95% CI) | Risk (%) | N, E/O | Ratio, (95% CI) | Risk (%) | N, E/O | Ratio, (95% CI) |
| .027–.249 | 26,244, 47.5/76 | 0.63, (0.50,0.78)‡ | .040–.264 | 25,476, 47.1/71 | 0.66, (0.53,0.84)‡ | .062–.250 | 25,476, 50.9/44 | 1.16, (0.86,1.55) |
| .249–.346 | 23,509, 71.0/66 | 1.08, (0.85,1.37) | .264–.360 | 25,477, 80.5/67 | 1.20, (0.95,1.53) | .250–.321 | 25,477, 73.1/53 | 1.38, (1.05,1.81)† |
| .348–.402 | 26,780, 99.7/103 | 0.97, (0.80,1.17) | .360–.426 | 25,477, 100.5/85 | 1.18, (0.96,1.46) | .321–.384 | 25,477, 89.9/86 | 1.05, (0.85,1.29) |
| .402–.476 | 24,834, 109.4/114 | 0.96, (0.80,1.15) | .426–.483 | 25,476, 115.8/100 | 1.16, (0.95,1.41) | .384–.444 | 25,477, 105.4/114 | 0.92, (0.77,1.11) |
| .476–.531 | 26,032, 132.4/146 | 0.91, (0.77,1.07) | .483–.543 | 25,477, 130.6/128 | 1.02, (0.86,1.21) | .444v.509 | 25,476, 121.4/115 | 1.06, (0.88,1.27) |
| .531–.610 | 26,957, 156.5/160 | 0.98, (0.84,1.14) | .543–.608 | 25,477, 146.4/126 | 1.16, (0.98,1.38) | .509–.581 | 25,477, 138.6/150 | 0.92, (0.79,1.08) |
| .610–.690 | 24,734, 162.1/156 | 1.04, (0.89,1.22) | .608–.691 | 25,477, 165.0/155 | 1.06, (0.91,1.25) | .581–.666 | 25,477, 158.5/158 | 1.00, (0.86,1.17) |
| .690–.800 | 23,318, 172.9/154 | 1.12, (0.96,1.31) | .691–.811 | 25,477, 190.1/199 | 0.96, (0.83,1.10) | .666–.784 | 25,477, 183.8/172 | 1.07, (0.92,1.24) |
| .800–.994 | 26,653, 231.8/215 | 1.08, (0.94,1.23) | .811–1.05 | 25,476, 232.1/236 | 0.98, (0.87,1.12) | .784–.981 | 25,477, 222.3/226 | 0.98, (.86,1.12) |
| .995–4.29 | 25,706, 345.6/228 | 1.52, (1.33,1.73)‡ | 1.05–4.47 | 25,477, 371.4/251 | 1.48, (1.31,1.67)‡ | .981–5.93 | 25,476, 325.3/300 | 1.08, (0.97,1.21) |
| Overall | 254,767, 1529/1418 | 1.08, (1.02,1.14)‡ | Overall | 254767, 1579/1418 | 1.11, (1.06,1.17)‡ | Overall | 254767, 1469/1418 | 1.04 (0.98, 1.09) |
| Average (SD), min–max 2–yr risk (%) | 0.600 (0.34), 0.0268–4.289 | 0.620 (.37), .0403–4.473 | 0.577 (.32), .062–5.93 | |||||
| Hosmer-Lemeshow Chi square =62.76, d.f.=8, P<0.001 | Hosmer–Lemeshow Chi square =61.95, d.f.=8, P<0.001 | Hosmer-Lemeshow Chi square =11.40, d.f.=8, P=0.18 | ||||||
O/E denotes observed number of breast cancer cases/expected number of cases
Predicted 2-year risk
P<0.05 for test of the null hypothesis that E/O=1;
P<0.01 for test of the null hypothesis that E/O=1
Comparisons of model discrimination within the one-third validation sample showed that the Rosner-Colditz model had higher overall C-statistic than the Gail model (0.65 versus 0.60) and also higher than the Tyrer-Cuzick model (0.65 versus 0.63, Table 5). As seen for the other two models in the entire dataset, the Rosner-Colditz model also had the weakest age-group specific discrimination among women age 70 years or older (0.59).
Table 5:
Comparison of age-specific, and weighted averages of age-specific C-statistics for the Gail, Tyrer-Cuzick and Rosner-Colditz breast cancer prediction models in the Nurses’ Health Study: 1,418 incident breast cancer cases in 254,767 2-year intervals among women in the validation sample for the Rosner-Colditz model
| Cases | Gail model | Tyrer–Cuzick model | Rosner Colditz model | RC-Gail* | P–value | RC–TC* | P–value | |
|---|---|---|---|---|---|---|---|---|
| Age group | N | C ±SE | C ±SE | C ±SE | ||||
| <50 years | 196 | .549±.021 | .565±.020 | .626±.020 | .078±.016 | <0.001 | .061±.016 | <0.001 |
| 50–59 years | 469 | .580±.013 | .605±.013 | .636±.013 | .056±.014 | <0.001 | .030±.011 | 0.005 |
| 60–69 years | 503 | .564±.013 | .603±.013 | .630±.012 | .066±.014 | <0.001 | .026±.009 | 0.006 |
| ≥70 years | 250 | .556±.018 | .583±.018 | .594±.018 | .038±.020 | 0.055 | .011±.014 | 0.42 |
| Weighted average† | 1418 | .566±.0080 | .595±.0080 | .625±.0070 | .061±0.008 | <0.001 | .030±.006 | <0.001 |
| Overall‡ | 1418 | .602±.0075 | .627±.0074 | .649±.0073 | .047±.0061 | <0.001 | .021±.0049 | <0.001 |
RC denotes predicted risks from the Rosner Colditz model; TC predicted risks from the Tyrer-Cuzick model; SE denotes standard error
Weighted average of the age-group specific C-statistic
Based on prediction in the entire evaluation dataset without age adjustment
Discussion
We used data from 26 years of experience in the Nurses’ Health Study to compare the performance of alternative simple models, based only on information obtained from questionnaires, to predict the occurrence of invasive breast cancer. Overall, we confirmed that each of the Gail, Tyrer-Cuzick, and Rosner-Colditz models has only moderate ability to predict breast cancer (1–3, 13–15). New findings from our study include evidence of mis-calibration in the Gail and Tyrer-Cuzick models, especially among women in the lowest and highest risk groups, better re-classification of cases to higher risk categories by the Tyrer-Cuzick model relative to the Gail model, and better re-classification of non-cases to lower risk categories by the Gail model relative to the Tyrer-Cuzick model.
Additional testing, including measures of mammographic density and testing for relevant genetic variation can somewhat improve model discrimination (29, 31–34). Addition of mammographic density and risk factor-based prediction models could be easily accommodated with appropriate referral of women according to level of risk – to consider chemoprevention or lifestyle changes (weight loss/physical activity, etc.). SNP assessment and polygene score generation is not yet routine and still has hurdles to overcome before integration into a routine breast cancer risk assessment at first screening mammogram. Other costly and logistically complex measures such as endogenous hormones improve prediction (measured by the C-statistic) in the Rosner-Colditz model by about 5%, but only in analyses restricted to postmenopausal women not using postmenopausal hormones at blood collection (35). Also, while models including only information from questionnaire are probably not sensitive enough to excuse a woman from screening on the basis of a low predicted risk, they are explicitly used in cross-national guidelines to direct clinical decisions (4–6, 36).
Three previous studies made direct comparisons of predictions from the Gail and Tyrer-Cuzick models, each conducted in study populations enriched for family history or risk factors such as delayed childbirth (1, 14, 15). In all three, the Gail model was found to underestimate risk (as indexed by a ratio of expected to observed events significantly below 1), whereas the confidence interval for the expected to observed ratio from the Tyrer-Cuzick model included 1 for each. Further, each of these comparisons found better discrimination (as indexed by higher C-statistics) from the Tyrer-Cuzick relative to the Gail model. However, the relatively small number of incident cases included in each of these studies (<250) limited the power to detect deviations between observed and expected event counts, especially within deciles of risk such as the lowest and highest risk women. Further, over-sampling of high risk women, and particularly those with a positive family history, may have favored the performance of the Tyrer-Cuzick model which particularly focuses on this component of risk.
Our study among a larger population spanning all levels of risk agreed with this previous literature in finding slightly better discrimination with the Tyrer-Cuzick relative to the Gail model, and extended the previous work by showing the discrimination under the Tyrer-Cuzick model was slightly better within each of four age groups. We also extended previous work by finding decreased discrimination under both models in older women. In contrast to previous studies, we found evidence for mis-calibration of both models, and that predicted risks differed from observed risks particularly in the lowest and highest risk women. Specifically, both models under-estimated risk among women in their lowest predicted decile of risk, and over-estimated risk among women in their highest predicted decile of risk, particularly among women with a family history of breast cancer. With respect to risk re-classification across established categories of clinical risk, we found that the Tyrer-Cuzick model more likely re-classified women who developed breast cancer during the 2-year interval to a higher risk category, but the Gail model more likely re-classified women who did not develop breast cancer to a lower risk category. These overall patterns of risk re-classification were different among women age 70 or older. Even when re-classification is separately considered among cases and non-cases, interpretation of these indices is problematic when models exhibit some level of miscalibration (37).
Relative to an evaluation of a previous version of the Gail model performed within the Nurses’ Health Study at a time when no women were age 75 or older, and hence average breast cancer risk was lower (25), we found a slightly higher level of discrimination (C statistic 0.61 [95% CI: 0.60–0.62], compared with 0.58 [95% CI: 0.56–0.60] in Rockhill et al (25)). Consistent with that report, we found the ratio of expected to observed cases under the Gail model to be less than 1 for lower risk women and greater than 1 for higher risk women, but the magnitude of this heterogeneity was greater in our updated analysis (ranging from 0.76 in the lowest decile to 1.40 in the highest decile of predicted risk, as seen in Table 1). Also, while Rockhill et al observed that the risk among women in the highest decile of estimated risk was 2.83 times that of women in the lowest decile, the corresponding relative risk in the current analysis was 3.95 (Table 1). These trends likely reflect the greater range of risks corresponding to the wider age range in our updated data.
Our comparison of the Tyrer-Cuzick and Gail models with the Rosner-Colditz model in a separate sample of Nurses’ Health Study participants found better discrimination and calibration in the Rosner-Colditz model. These three models include several common variables, but also involve different parameterizations of some of these variables, including interactions involving menopausal status in the Rosner-Colditz model. The models also include some different variables, such as extended family history information in the Tyrer-Cuzick model and consideration of alcohol consumption history and more details on postmenopausal hormone therapy in the Rosner-Colditz model. Although the Nurses’ Health Study has maintained a focus on risk factors for breast cancer since its inception, several components of the Gail and Tyrer-Cuzick model were not measured. Also, key variables including measures of family history were not updated at each questionnaire. While the unmeasured components were not highly prevalent characteristics, their unavailability somewhat limited our comparisons. It is likely that a small group of women had their risk of breast cancer under-estimated because of this missing information, but overall risk in the entire study population was slightly but significantly over-estimated by both the Tyrer-Cuzick and Gail models. A future question is whether simpler models are possible that would attain nearly equivalent performance in prediction and be more easily integrated into routine breast health services. Considerable effort is currently underway to improve simple models, while limiting the burden of data collection to maximize participation and enhance generalizability (38–40).
In summary, our comparison of three readily implemented risk prediction rules for breast cancer found somewhat better discrimination in the Rosner-Colditz model. We also saw evidence for mis-calibration of the Gail and Tyrer-Cuzick models, particularly among the highest and lowest risk women in the Nurses’ Health Study. The Rosner-Colditz model includes more variables which take longer for their assessment. For women in the extreme deciles of risk, prediction from the Rosner-Colditz model is somewhat more accurate than prediction in the Tyrer-Cuzick and Gail models.
Supplementary Material
Funding
This project was funded by a cohort infrastructure Grant (UM1 CA186107), and a program project Grant (P01 CA87969) from the National Cancer Institute.
Footnotes
Conflict of interest
The authors declare that they have no conflict of interest.
References
- 1.Amir E, Evans DG, Shenton A, Lalloo F, Moran A, Boggis C, Wilson M, Howell A. Evaluation of breast cancer risk assessment packages in the family history evaluation and screening programme. J Med Genet. 2003; 40(11):807–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Meads C, Ahmed I, Riley RD. A systematic review of breast cancer incidence risk prediction models with meta-analysis of their performance. Breast Cancer Res Treat. 2012; 132: 365–77. [DOI] [PubMed] [Google Scholar]
- 3.Quante AS, Whittemore AS, Shriver T, Hopper JL, Strauch K, Terry MB. Practical problems with clinical guidelines for breast cancer prevention based on remaining lifetime risk. J Natl Cancer Inst. 2015; 107(7). pii: djv124. doi: 10.1093/jnci/djv124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Bevers TB, Anderson BO, Bonaccio E, Buys S, Daly MB, Dempsey PJ, Farrar WB, Fleming I, Garber JE, Harris RE, Heerdt AS, Helvie M, Huff JG, Khakpour N, Khan SA, Krontiras H, Lyman G, Rafferty E, Shaw S, Smith ML, Tsangaris TN, Williams C, Yankeelov T; National Comprehensive Cancer Network. NCCN clinical practice guidelines in oncology: breast cancer screening and diagnosis. J Natl Compr Canc Netw. 2009; 7(10):1060–96. [DOI] [PubMed] [Google Scholar]
- 5.National Institute for Health and Care Excellence. NICE guideline CG164. Familial breast cancer: classification, care and managing breast cancer and related risks in people with a family history of breast cancer. Available at https://www.nice.org.uk/guidance/cg164. [PubMed]
- 6.Moyer VA; U.S. Preventive Services Task Force. Ann Intern Med. 2013; 159(10):698–708. [DOI] [PubMed] [Google Scholar]
- 7.Anothaisintawee T, Teerawattananon Y, Wiratkapun C, Kasamesup V, Thakkinstian A. Risk prediction models of breast cancer: a systematic review of model performances. Breast Cancer Res Treat. 2012; 133(1):1–10. [DOI] [PubMed] [Google Scholar]
- 8.Gail MH, Brinton LA, Byar DP, Corle DK, Green SB, Shairer C, Mulvihill JJ: Projecting individualized probabilities of developing breast cancer for white females who are being examined annually. J Natl Cancer Inst 1989; 81: 1879–86. [DOI] [PubMed] [Google Scholar]
- 9.Costantino JP, Gail MH, Pee D, Anderson S, Redmond CK, Benichou J, Wieand HS. Validation studies for models projecting the risk of invasive and total breast cancer incidence. J Natl Cancer Inst 1999; 91: 1541–8. [DOI] [PubMed] [Google Scholar]
- 10.Gail MH, Costantino JP, Pee D, Bondy M, Newman L, Selvan M, Anderson GL, Malone KE, Marchbanks PA, McCaskill-Stevens W, Norman SA, Simon MS, Spirtas R, Ursin G, and Bernstein L. Projecting Individualized Absolute Invasive Breast Cancer Risk in African American Women. J Natl Cancer Inst 99(23):1782–1792, 2007. [DOI] [PubMed] [Google Scholar]
- 11.Matsuno RK, Costantino JP, Ziegler RG, Anderson GL, Li H, Pee D, Gail MH. Projecting individualized absolute invasive breast cancer risk in asian and pacific islander american women. JNCI 2011; 103:951–61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Division of Cancer Epidemiology and Genetics. Breast cancer risk assessment macro BrCa_RAM.sas. Downloaded from http://dceg.cancer.gov/tools/risk-assessment/bcrasasmacro.
- 13.Tyrer J, Duffy SW, Cuzick J. A breast cancer prediction model incorporating familial and personal risk factors. Stat Med 2004; 23: 1111–30. [DOI] [PubMed] [Google Scholar]
- 14.Quante AS, Whittemore AS, Shriver T, Strauch K, Terry MB. Breast cancer risk assessment across the risk continuum: genetic and nongenetic risk factors contributing to differential model performance. Breast Cancer Res 2012; 14(6):R144. doi: 10.1186/bcr3352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Powell M, Jamshidian F, Cheyne K, Nititham J, Prebil LA, Ereman R. Assessing breast cancer risk models in Marin County, a population with high rates of delayed childbirth. Clin Breast Cancer. 2014. June;14(3):212–220.e1. doi: 10.1016/j.clbc.2013.11.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Rosner B, Colditz GA. Nurses’ health study: log-incidence mathematical model of breast cancer incidence. J Natl Cancer Inst 1996; 88: 359–364. [DOI] [PubMed] [Google Scholar]
- 17.Colditz GA, Rosner B. Cumulative risk of breast cancer to age 70 years according to risk factor status: data from the Nurses’ Health Study. Am J Epidemiol 2000; 152: 950–964. [DOI] [PubMed] [Google Scholar]
- 18.Colditz GA, Rosner BA, Chen WY, Holmes MD, Hankinson SE. Risk factors for breast cancer according to estrogen and progesterone receptor status. J Natl Cancer Inst 2004; 96: 218–228. [DOI] [PubMed] [Google Scholar]
- 19.Glynn RJ, Colditz GA, Tamimi RM, Chen WY, Hankinson SE, Willett WW, Rosner B. Extensions of the Rosner-Colditz breast cancer prediction model to include older women and type-specific predicted risk. Breast Cancer Res Treat. 2017; 165(1): 215–223. doi: 10.1007/s10549-017-4319-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Colditz GA, Hankinson SE. The Nurses’ Health Study: lifestyle and health among women. Nat Rev Cancer 2005; 5:388–396. [DOI] [PubMed] [Google Scholar]
- 21.Colditz GA, Kaphingst KA, Hankinson SE, Rosner B. Family history and risk of breast cancer: nurses’ health study. Breast Cancer Res Treat. 2012; 133: 1097–104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Prentice RL, Gloeckler LA. Regression analysis of grouped survival data with application to breast cancer data. Biometrics 1978; 34(1):57–67. [PubMed] [Google Scholar]
- 23.Wu M, Ware JH. On the use of repeated measurements in regression analysis with dichotomous responses. Biometrics 1979; 35(2):513–21. [PubMed] [Google Scholar]
- 24.D’Agostino RB, Lee ML, Belanger AJ, Cupples LA, Anderson K, Kannel WB. Relation of pooled logistic regression to time dependent Cox regression analysis: the Framingham Heart Study. Stat Med 1990; 9(12):1501–15. [DOI] [PubMed] [Google Scholar]
- 25.Rockhill B, Spiegelman D, Byrne C, Hunter DJ, Colditz GA: Validation of the Gail et al. model of breast cancer risk prediction and implications for chemoprevention. J Natl Cancer Inst 93(5):358–66, 2001. [DOI] [PubMed] [Google Scholar]
- 26.Tamimi RM, Rosner B, Colditz GA. Evaluation of a breast cancer risk prediction model expanded to include category of prior benign breast disease lesion. Cancer 2010; 116: 4944–53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Park Y, Freedman AN, Gail MH, Pee D, Hollenbeck A, Schatzkin A, Pfeiffer RM. Validation of a colorectal cancer risk prediction model among white patients age 50 years and older. J Clin Oncol. 2009; 27(5):694–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Rosner B, Glynn RJ. Power and sample size estimation for the Wilcoxon rank sum test with application to comparisons of C statistics from alternative prediction models. Biometrics 2009; 65: 188–97. [DOI] [PubMed] [Google Scholar]
- 29.Tice JA, Cummings SR, Smith-Bindman R, Ichikawa L, Barlow WE, Kerlikowske K. Using clinical factors and mammographic breast density to estimate breast cancer risk: development and validation of a new predictive model. Ann Intern Med. 2008; 148: 337–47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Kerr KF, Wang Z, Janes H, McClelland RL, Psaty BM, Pepe MS. Net reclassification indices for evaluating risk prediction instruments: a critical review. Epidemiology. 2014; 25: 114–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Boyd NF, Guo H, Martin LJ, Sun L, Stone J, Fishell E, Jong RA, Hislop G, Chiarelli A, Minkin S, Yaffe MJ. Mammographic density and the risk and detection of breast cancer. N Engl J Med. 2007; 356: 227–36. [DOI] [PubMed] [Google Scholar]
- 32.Barlow WE, White E, Ballard-Barbash R, Vacek PM, Titus-Ernstoff L, Carney PA, Tice JA, Buist DS, Geller BM, Rosenberg R, Yankaskas BC, Kerlikowske K. Prospective breast cancer risk prediction model for women undergoing screening mammography. J Natl Cancer Inst 2006; 98:1204–14. [DOI] [PubMed] [Google Scholar]
- 33.Wacholder S, Hartge P, Prentice R, Garcia-Closas M, Feigelson HS, Diver WR, Thun MJ, Cox DG, Hankinson SE, Kraft P, Rosner B, Berg CD, Brinton LA, Lissowska J, Sherman ME, Chlebowski R, Kooperberg C, Jackson RD, Buckman DW, Hui P, Pfeiffer R, Jacobs KB, Thomas GD, Hoover RN, Gail MH, Chanock SJ, Hunter DJ. Performance of common genetic variants in breast-cancer risk models. N Engl J Med. 2010. March 18;362(11):986–93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Pharoah PD, Antoniou AC, Easton DF, Ponder BA. Polygenes, risk prediction, and targeted prevention of breast cancer. N Engl J Med. 2008; 358: 2796–803. [DOI] [PubMed] [Google Scholar]
- 35.Tworoger SS, Zhang X, Eliassen AH, Qian J, Colditz GA, Willett WC, Rosner BA, Kraft P, Hankinson SE. Inclusion of endogenous hormone levels in risk prediction models of postmenopausal breast cancer. J Clin Oncol. 2014; 32: 3111–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Visvanathan K, Hurley P, Bantug E, Brown P, Col NF, Cuzick J, Davidson NE, Decensi A, Fabian C, Ford L, Garber J, Katapodi M, Kramer B, Morrow M, Parker B, Runowicz C, Vogel VG 3rd, Wade JL, Lippman SM. Breast cancer follow-up and management after primary treatment: American Society of Clinical Oncology clinical practice guideline update. J Clin Oncol 2013; 31: 2942–62. [DOI] [PubMed] [Google Scholar]
- 37.Pepe MS, Fan J, Feng Z, Gerde T, Hilden J. The net reclassification index (NRI): a misleading measure of prediction improvement even with independent test data sets. Stat Biosci 2015; 7: 282–295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Pfeiffer RM, Park Y, Kreimer AR, Lacey JV Jr, Pee D, Greenlee RT, Buys SS, Hollenbeck A, Rosner B, Gail MH, Hartge P. Risk prediction for breast, endometrial, and ovarian cancer in white women aged 50 y or older: derivation and validation from population-based cohort studies. PLoS Med 2013;10(7):e1001492. doi: 10.1371/journal.pmed.1001492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Eriksson M, Czene K, Pawitan Y, Leifland K, Darabi H, Hall P. A clinical model for identifying the short-term risk of breast cancer. Breast Cancer Res 2017; 14:19(1):29. doi: 10.1186/s13058-017-0820-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Brentnall AR, Cuzick J, Buist DSM, Bowles EJA. Long-term Accuracy of Breast Cancer Risk Assessment Combining Classic Risk Factors and Breast Density. JAMA Oncol 2018; 4(9):e180174. doi: 10.1001/jamaoncol.2018.0174 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.