Shift models for dose finding in partially ordered groups

Abstract

Background:

Limited options are available for dose finding clinical trials requiring group specific dose selection. While conducting parallel trials for groups is an accessible approach to group specific dose selection, this approach allows for maximum tolerated dose selection that does not align with clinically meaningful group order information.

Methods:

The two-stage continual reassessment method is developed for dose-finding in studies involving three or more groups where group frailty order is known between some but not all groups, creating a partial order. This is an extension of the existing continual reassessment method shift model for two ordered groups. This method allows for dose selection by group, where maximum tolerated dose selection follows the known frailty order among groups. For example, if a group is known to be the most frail, the recommended maximum tolerated dose for this group should not exceed the maximum tolerated dose recommended for any other group.

Results:

With limited alternatives for dose finding in partially ordered groups, this method is compared to two alternatives: 1) an existing method for dose finding in partially ordered groups which is less computationally accessible and 2) independent trials for each group using the two-stage continual reassessment method. Simulation studies show that when ignoring information on group frailty, using independent continual reassessment method trials by group, 30% of simulations would result in maximum tolerated dose selection that is out of order between groups. In addition, the two-stage continual reassessment method for partially ordered groups selects the maximum tolerated dose more often and assigns more patients to the maximum tolerated dose compared to using independent continual reassessment method trials within each group. Simulation results for the proposed method and the less computationally accessible approach are similar.

Conclusion:

The proposed continual reassessment method for partially ordered groups ensures appropriate maximum tolerated dose order and improves accuracy of maximum tolerated dose selection, while allowing for trial implementation that is computationally accessible.

Background

This work is motivated by a clinical trial presented by Innocenti et al.¹ with the aim of identifying the maximum tolerated dose (MTD) of irinotecan for three groups of cancer patients. Information provided for irinotecan indicates that UGT1A1^⋆28 is a biomarker for neutropenia and that a reduced first dose should be considered in patients who are homozygous for this allele (^⋆28/^⋆28). For this trial, groups 1, 2, and 3 are defined by their genotypes: ^⋆1/^⋆1, ^⋆1/^⋆28, and ^⋆28/^⋆28, respectively. Group 3 is anticipated to require the lowest dose among the three groups. It is unknown if the MTD should differ between groups 1 and 2. Therefore, MTD₃ ≤ MTD₁ and MTD₃ ≤ MTD₂ are known without it being possible to specify the relationship between MTD₁ and MTD₂, creating a partial order among the three groups.²

In Innocenti et al.¹, a modified 6 + 6 design was used in parallel trials for each group. The trials concluded with different MTDs selected for each group, with the lowest MTD for group 3 and the highest MTD for group 1. While these results followed the known group order information, that the MTD for group 3 should not have a MTD at a dose level higher than that of groups 1 and 2, using parallel trials to determine group specific MTDs allows for MTD determination in reverse of the expected group order.

Methods to allow for group specific MTD selection are limited. Two methods proposed by Conaway^3,4 allow for more than two groups with complete and partial ordering. Both methods combine order restricted inference with the continual reassessment method (CRM) to make recommendations for each group. Yuan and Chappell⁵ offer a method that allows for consideration of more than two groups but only for complete group ordering, where the order of MTD selection is known between all groups. Several methods are available for two groups, including the shift model, which was introduced by O’Quigley⁶ and discussed in greater detail by O’Quigley and Conaway⁷ and O’Quigley and Iasonos⁸. This model is based on the idea that the MTD in one group is “shifted” one or more levels away from the MTD in the other group. The overall strategy is to first estimate a parameter characterizing the shift between the two groups, followed by estimation of the DLT probabilities under the estimated shift. This approach can be situated with other dose-finding methods in a hierarchical modeling framework in which model selection precedes estimation of the DLT probabilities under the chosen model^9–11. The proposed method generalizes the two group shift model allowing for more than two groups with partial orders. Wages et al.¹² describe the design of a dose-finding trial using the previously mentioned shift model to allow for dose selection in two groups of patients identified as having “good” and “poor” prognosis. Other methods available for MTD estimation in two groups include O’Quigley et al.¹³, O’Quigley and Paoletti¹⁴, Ivanova and Wang¹⁵, and Conaway and Wages¹⁶.

There is a strong need for methods that allow for more than two groups with partial group ordering, as conducting parallel trials by group allows for MTD selection that does not align with clinically meaningful group order information. In addition to the concern of observing MTD selection that contradicts known group ordering, independent trials by group ignore information that, if shared in a single trial, can lead to observing improvements in properties associated with selecting the best dose. The simulation section provides comparison of the proposed method with parallel trials using the CRM and a method proposed by Conaway³ for partially ordered groups. The methods by Conaway^3,4 are less accessible computationally and there is no publicly available code. Programming these methods rely upon the ability of researchers to compute Hwang and Peddada estimation¹⁷, which depends on the sequential classification of nodal and non-nodal parameters among the doses that have been tried up to a certain point in the study. A nodal parameter is one whose ordering with respect to all other parameters is known, whereas a non-nodal parameter is simply one that is not nodal. At each dosing decision point, evaluating which DLT probabilities are nodal and which are non-nodal among the tried doses can be a complex programming task, making it difficult to produce general user-friendly code that would be available to researchers in a broad range of partial order situations. Our motivation for this work is based on the notion that a more straightforward method, building more directly off of the well-known CRM, would be useful, provided that the new methodology performs well when compared with the Conaway methodology.

The aim of this manuscript is to provide a computationally accessible method for dose finding with partially ordered groups. This work shows similar properties as the method proposed by Conaway³ and demonstrates superiority over the use of parallel trials for partially ordered groups. The code necessary to implement the proposed method uses repeated calls to R package ‘dfcrm’¹⁸ and can be easily adapted to allow for a variety of partially ordered group settings. In this manuscript, we will first describe the proposed method, followed by a description of the simulations considered and discussion of the simulation results.

Methods

Design for Partially Ordered Groups

The proposed method is a generalization of the shift model described by O’Quigley and Iasonos⁸. In general, there are K pre-specified dose levels and the trial is to be conducted with G groups. Let d_gk denote the dose at level k and group number, such that k = 1, …, K and g = 1,…, G. The target toxicity rate, θ, is pre-specified. In the motivating example where there are three groups and 4 dose levels, G = 3 and K = 4. Group 3 is known to be the most frail and the order of frailty between groups 1 and 2 is unknown. In this example, the probability of toxicity observed in group 3 for a particular dose level will be greater than or equal to the probability of toxicity seen at that dose level in groups 1 and 2.

Implementation of the proposed shift model is carried out in two stages. The first stage is rule based, using cohorts of size 1. Once heterogeneity is observed, at least one DLT and non-DLT, the second stage begins where dose allocation is based on estimation from a working model.

Stage 1 Allocation

The first stage consists of rule-based allocation with cohort size of 1. Single patient cohorts are assigned escalating doses, continuing until one DLT and one non-DLT are observed. Once heterogeneity of responses is observed, the trial proceeds into the second stage using model-based allocation. A trial is terminated if the first two patients experience a DLT. Due to the known clinically meaningful group information, patient group must be considered during dose allocation in the first stage. Patients enter the study in random order with respect to group. The first patient will be allocated to the first dose level, regardless of group identity. Subsequent patients entering in either of the two less frail groups, groups 1 and 2, will be allocated to one dose higher than the current maximum dose level observed among all groups. Patients entering the study in the most frail group, group 3, will be allocated to one dose higher than current maximum dose level observed within patients in group 3. The first patient in group 3 will be allocated to dose level 1, regardless of the number of dose levels considered in the less frail groups.

Let $d_g^{max}$ indicate the maximum dose level assigned to previously accrued patients in group g. The first patient entering the study and the first patient entering the study in group 3 will be assigned to the first dose level. The next dose allocation depends on group and is given in Table 1.

Table 1.

Dose level allocation by group

Group	Dose allocation
1 (less frail)	$\text{min}\left\{\text{max}\left(d_1^{max},d_2^{max},d_3^{max}\right)+1,K\right\}$
2 (less frail)	$\text{min}\left\{\text{max}\left(d_1^{max},d_2^{max},d_3^{max}\right)+1,K\right\}$
3 (most frail)	$\text{min}\left\{d_3^{max}+1,K\right\}$

Consider an example of within trial dose allocation for the first stage in Table 2. Here, we can see dose allocation following the guidance given above:

1. the first patient is assigned to dose level 1,

2. patients 2, 3, and 5 are associated with a less frail group and are assigned the next dose level greater than the highest dose level observed in the trial at that time, and

3. patient 4, from the most frail group, is allocated to the next dose level greater than doses considered within this group, dose level 2.

Once heterogeneity of DLT responses is observed with patient 5, the first stage ends and modeling is used in the second stage to identify dose allocation for remaining trial patients.

Table 2.

Within trial dose allocation

Patient	Group	$d_1^{max}$	$d_2^{max}$	$d_3^{max}$	Dose allocated	DLT
1	3 (most frail)	-	-	-	1	no
2	2 (less frail)	-	-	1	2	no
3	2 (less frail)	-	2	1	3	no
4	3 (most frail)	-	3	1	2	no
5	1 (less frail)	-	3	2	4	yes

End stage 1. Begin stage 2 modeling.

Stage 2 Allocation

In order to describe the relationship between MTDs for different groups, we use the idea of a shift to indicate the number of dose levels separating the MTD for two groups. For the motivating example described in the background section, there are two shifts to consider: a shift in MTD between groups 3 and 1 and between groups 3 and 2, given by Δ₃₁ and Δ₃₂, respectively. The assumed partial order dictates that shifts in the MTD range in magnitude from 0 dose levels to 3 dose levels, such that Δ₃₁ = {0, 1, 2, 3} and Δ₃₂ = {0, 1, 2, 3}. At any point in the trial n_gk patients have been observed in group g at dose level k with y_gk patients who have experienced a DLT. In general, for a trial with K dose levels, 2 × K − 1 skeleton values are generated, where skeleton values are an initial guess of the probability of toxicity for each dose level. For the motivating example, 4 dose levels would lead to 7 skeleton values generated to allow for all possible magnitudes of shift in the MTD between groups. Using the ‘getprior’ function within the ‘dfcrm’ package for the motivating example, the 7 dose level skeleton is given by (0.10, 0.19, 0.30, 0.42, 0.54, 0.64, 0.73). Here, the halfwidth is 0.06, a target DLT rate of 0.3, and MTD located at the third dose level. In this particular example, there are m = 1,…, 16 possible shift models that account for all possible shifts where group 3 is known to be the most frail and the frailty order between groups 1 and 2 is unknown. Shift models are given in Table 3. Note that due to the partial ordering in the motivating example, the relationship between the MTDs for groups 1 and 2 is unknown. With the unknown order of MTD between groups 1 and 2, shift models m = 11,…, 16 are found by exchanging the probability of toxicity profiles for groups 1 and 2 in shift models m = 5,…, 10.

Table 3.

Shifts considered in the probability of toxicity by dose level and group

Skeleton value by dose level
m	Group	1	2	3	4
Δ32 = 0, Δ31 = 0
1	3 (most frail)	0.10	0.19	0.30	0.42
	2 (less frail)	0.10	0.19	0.30	0.42
	1 (less frail)	0.10	0.19	0.30	0.42
Δ32 = 1, Δ31 = 1
2	3 (most frail)	0.19	0.30	0.42	0.54
	2 (less frail)	0.10	0.19	0.30	0.42
	1 (less frail)	0.10	0.19	0.30	0.42
Δ32 = 2, Δ31 = 2
3	3 (most frail)	0.30	0.42	0.54	0.64
	2 (less frail)	0.10	0.19	0.30	0.42
	1 (less frail)	0.10	0.19	0.30	0.42
Δ32 = 3, Δ31 = 3
4	3 (most frail)	0.42	0.54	0.64	0.73
	2 (less frail)	0.10	0.19	0.30	0.42
	1 (less frail)	0.10	0.19	0.30	0.42
Δ32 = 0, Δ31 = 1
5	3 (most frail)	0.19	0.30	0.42	0.54
	2 (less frail)	0.19	0.30	0.42	0.54
	1 (less frail)	0.10	0.19	0.30	0.42
Δ32 = 0, Δ31 = 2
6	3 (most frail)	0.30	0.42	0.54	0.64
	2 (less frail)	0.30	0.42	0.54	0.64
	1 (less frail)	0.10	0.19	0.30	0.42
Δ32 = 0, Δ31 = 3
7	3 (most frail)	0.42	0.54	0.64	0.73
	2 (less frail)	0.42	0.54	0.64	0.73
	1 (less frail)	0.10	0.19	0.30	0.42
Δ32 = 1, Δ31 = 2
8	3 (most frail)	0.30	0.42	0.54	0.64
	2 (less frail)	0.19	0.30	0.42	0.54
	1 (less frail)	0.10	0.19	0.30	0.42
Δ32 = 1, Δ31 = 3
9	3 (most frail)	0.42	0.54	0.64	0.73
	2 (less frail)	0.30	0.42	0.54	0.64
	1 (less frail)	0.10	0.19	0.30	0.42
Δ32 = 2, Δ31 = 3
10	3 (most frail)	0.42	0.54	0.64	0.73
	2 (less frail)	0.19	0.30	0.42	0.54
	1 (less frail)	0.10	0.19	0.30	0.42
Δ32 = 1, Δ31 = 0
11	3 (most frail)	0.19	0.30	0.42	0.54
	2 (less frail)	0.10	0.19	0.30	0.42
	1 (less frail)	0.19	0.30	0.42	0.54
Δ32 = 2, Δ31 = 0
12	3 (most frail)	0.30	0.42	0.54	0.64
	2 (less frail)	0.10	0.19	0.30	0.42
	1 (less frail)	0.30	0.42	0.54	0.64
Δ32 = 3, Δ31 = 0
13	3 (most frail)	0.42	0.54	0.64	0.73
	2 (less frail)	0.10	0.19	0.30	0.42
	1 (less frail)	0.42	0.54	0.64	0.73
Δ32 = 2, Δ31 = 1
14	3 (most frail)	0.30	0.42	0.54	0.64
	2 (less frail)	0.10	0.19	0.30	0.42
	1 (less frail)	0.19	0.30	0.42	0.54
Δ32 = 3, Δ31 = 1
15	3 (most frail)	0.42	0.54	0.64	0.73
	2 (less frail)	0.10	0.19	0.30	0.42
	1 (less frail)	0.30	0.42	0.54	0.64
Δ32 = 3, Δ31 = 2
16	3 (most frail)	0.42	0.54	0.64	0.73
	2 (less frail)	0.10	0.19	0.30	0.42
	1 (less frail)	0.19	0.30	0.42	0.54

The probability of dose-limiting toxicity for a given shift model, group, and dose level is given by R_mg such that

$$\begin{gathered} R_{mgk}\left(d_{gk}\right)=\text{ Pr} \left(Y_{gk} \\ =1|d_{gk},g,m\right)={\psi }_{mgk}\left(d_{gk},a_m\right)=p_{mgk}^{\text{exp}\left(a_m\right)}, \end{gathered}$$ (1)

where ψ_mgk (x_gk, a_m) is a one parameter model and a_m is defined on the set. $\mathcal{A}$ For every dose, d_gk there exists some $a_m\in \mathcal{A}$ such that R_mgk (d_gk) = ψ_mgk (d_gk, a_m) for a specified group and shift model. We use the one parameter power model as a working model for the probability of toxicity for each group and dose level. Specifically, the power model, $p_{mgk}^{\text{exp}\left(a_m\right)}$ is used where k = 1,…, K denotes the dose level, g = 1, …, G denotes the group number, m identifies the particular shift model (m = 1, …, M) in which M is the maximum number of potential models, and p_mgk skeleton values are ordered such that 0 < p_mg1 < p_mg2 <⋯ < p_mgK < 1.

The logarithm of the likelihood function is given by

$${\mathcal{l}}_m\left(a_m\right)=\sum _{g=1}^G\sum _{k=1}^K\left\{y_{gk}\text{ log }{\psi }_{mgk}\left(d_{gk},a_m\right)+\left(n_{gk}-y_{gk}\right)\text{ log }\left(1-{\psi }_{mgk}\left(d_{gk},a_m\right)\right)\right\}$$ (2)

For each patient accrued in the second stage, the most appropriate shift model is selected by considering the log-likelihood function in (2) evaluated at the maximum likelihood estimate ${\widehat{a}}_m$ for each shift model m. Let m^* indicate the shift model which maximizes the log-likelihood function evaluated at ${\widehat{a}}_m$, then

$$m^{*}=\underset{m}{\text{ argmax }}{\mathcal{l}}_m\left({\widehat{a}}_m\right).$$

Once the shift model, m^*, is chosen, dose allocation for the next patient, or MTD selection if at the end of the trial, by group is found by selecting the dose which minimizes the difference in the probability of toxicity and the target DLT rate, $\left|{\widehat{R}}_{m^{*}g}\left(d_{gk}\right)-\theta \right|$.

Reversals

A reversal occurs when independent trials are implemented by group and MTD selection does not follow the known group frailty order. This is an issue arising with the use of independent trials for groups and the proposed method does not allow for reversals in dose selection. Consider the motivating trial setting where three groups are identified and partial group ordering is known, with group 3 known to have a greater probability of toxicity at a specified dose compared to groups 1 and 2. For each dose, the probability of toxicity for patients in group 3 is greater than patients from groups 1 and 2. Independent trials for each group allow for selecting the group 3 MTD at a higher dose level than in groups 1 or 2. In practice there would need to be an additional level of decision making such as: 1) decreasing the selected MTD in group 3 to the MTD in group 1 or 2; or 2) increasing the MTD in groups 2 and 3 to be at least as high as the MTD selected for group 3. In either case there is great concern for incorrect dose selection either by selecting a dose associated with a DLT rate that is unacceptably high or selecting a dose with a DLT rate too low that is not effective. Although the only method compared in these simulations uses independent CRM trails, it is anticipated that independent group trials for any dose finding method would result in reversals. In this case, two types of reversals are possible in each simulation: between groups 1 and 3 and between groups 2 and 3. Although there are 4 dose levels, it is possible to see a reversal of magnitude 4 if the trial for either group 1 or 2 result in all doses being deemed too toxic and the MTD for group 3 is dose level 4.

Simulation setup

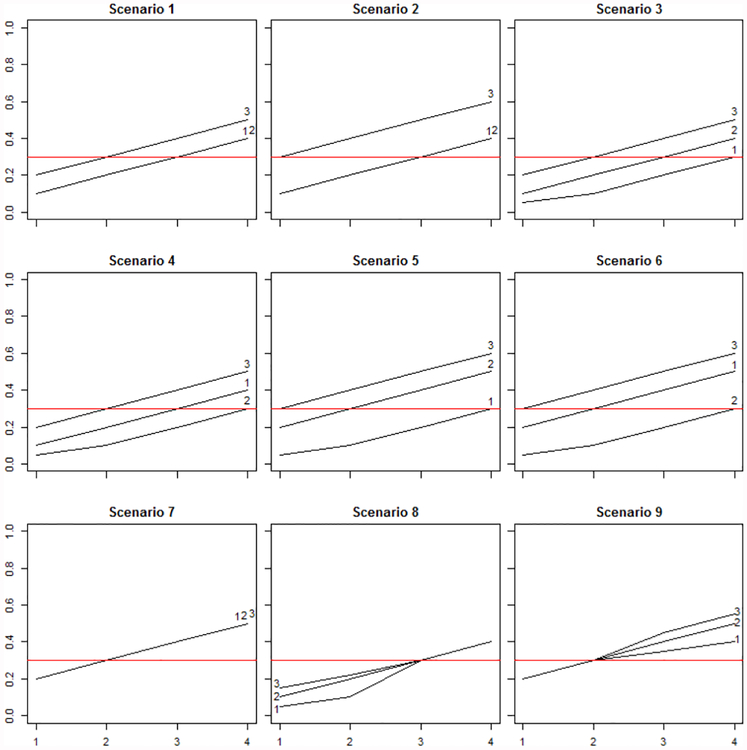
In this section, we present the design of the simulations and discuss the simulation results. For comparison, we also consider the use of independent trials for each group using the continual reassessment method (CRM). In all simulations, the target toxicity rate is θ = 0.3 and 1, 000 simulated trials were generated. Nine dose-toxicity curves are considered with 4 dose levels, shown in Figure 1. While patients in group 3 are considered to be the most frail, their probability of toxicity at a specific dose should be greater than or equal to the probability of toxicity for patients in groups 1 and 2. The dose-toxicity curves considered allow for a variety of order of severity between groups 1 and 2 and spacing of the true MTD for each group. Overall sample sizes of 45 and 72 were considered and group specific sample sizes were randomly generated. Results from samples of size 72 are given in the Supplemental Material. Both methods use the same simulated data, allowing for direct comparison of MTD and other information for each simulation. Percentage of correct selection and accuracy index are used to compare the methods. Percentage of correct selection is defined as the proportion of simulations selecting the correct dose as MTD. Accuracy index, outlined by Cheung¹⁹, was calculated for both dose selection and subject allocation, as used by Horton et al.²⁰. Accuracy index is given by $A_n=1-K\times \frac{{\sum }_{i=1}^K{\rho }_i\times p_i}{{\sum }_{i=1}^K{\rho }_i}$, where p_i gives the probability that dose i is selected as the MTD and ρ₁ is a distance measure between the true probability of toxicity as dose level i and the target toxicity rate. Figures and tables with the prefix “S” are presented in the supplemental material.

Figure 1.

Dose Toxicity Curves

Parallel CRM trials by group

The continual reassessment method (CRM), given by O’Quigley et al.²¹, run independently by group, is used to compare to the proposed method. The simulations utilize the two-stage likelihood version of CRM given by O’Quigley and Shen²². This design uses a one-parameter working model for the probability of toxicity at dose d_k that assumes a monotonically increasing dose-toxicity relationship. A practical choice is the power model, given by:

$$\psi \left(d_k,a\right)=p_k^{\text{exp}(a)},$$ (4)

where k = 1,…, K denotes the dose level, a is a scalar parameter, and 0 < p₁ < p₂ < ⋯ < p_K < 1 are pre-specified constants referred to as the skeleton values. The likelihood version of CRM requires heterogeneity in DLT responses before the second stage sequential approach can begin. These simulations allow for a first stage consisting of a rule-based design with cohort size of 1, where single patient cohorts are assigned escalating doses, beginning with the first dose, and continuing until one DLT and one non-DLT are observed. Once heterogeneity of responses is observed, the trial proceeds into the second stage where the estimate of the parameter a is found by maximizing the likelihood, given by:

$$L\left(a,n_k,y_k\right)=\prod _{k=1}^K{\left(p_k^{\text{exp}(a)}\right)}^{y_k}{\left(1-p_k^{\text{exp}(a)}\right)}^{n_k-y_k}.$$ (5)

Simulation results for the CRM design were obtained using the crm function in R package ‘dfcrm’, specifying the ‘mle’ method and ‘empiric’ model. The skeleton was specified using the getprior function within the ‘dfcrm’ package^18,23, specifying a halfwidth of 0.06 and prior guess of MTD of dose 3. Iasonos and O’Quigley²⁴ and Jia et al.²⁵ provide additional information on design aspects of CRM. Both the proposed method and independent CRM trials by group terminate a trial early if the first two patients indicate a DLT.

Order restricted CRM

In the method proposed by Conaway³, estimates $\widehat{a}=\left({\widehat{a}}_1,{\widehat{a}}_2,{\widehat{a}}_3\right)$ are found by maximizing the likelihood, using the CRM working model, separately within each group. The j^th diagonal element of the observed information matrix based on the log of the likelihood, evaluated at $\left({\widehat{a}}_1,{\widehat{a}}_2,{\widehat{a}}_3\right)$, is denoted by $v_j\left({\widehat{a}}_j\right)$. Once the individual group estimates are obtained, the estimation procedure of Hwang and Peddada¹⁷ is applied to $\widehat{a}=\left({\widehat{a}}_1,{\widehat{a}}_2,{\widehat{a}}_3\right)$ using weights $\frac{1}{v_j\left({\widehat{a}}_j\right)}$. The resulting estimates are denoted by ${\widehat{a}}^{HP}=\left({\widehat{a}}_1^{HP},{\widehat{a}}_2^{HP},{\widehat{a}}_3^{HP}\right)$, and satisfy

$${\widehat{a}}_1^{HP}\ge {\widehat{a}}_3^{HP};{\widehat{a}}_2^{HP}\ge {\widehat{a}}_3^{HP}$$ (6)

After “isotonizing” the estimates, estimates of the probabilities of a DLT for dose d in group g are based on substituting the order restricted estimates into the CRM working model. The next patient in group g is assigned to the dose level in group g with the estimated DLT probability closest to the target probability. Specifications for the skeleton are the same as those given for parallel CRM trials by group in the previous section.

Results

Reversals

Figure S1, in the supplemental material, displays the proportion of simulations having at least 1 reversal. Figure S2 and Table S1, in the supplemental material, display the percentage of maximum reversal magnitude observed among simulations with at least 1 reversal. The scenarios with greater distance between the MTDs for group 3 and groups 1 and 2 (scenarios 2, 3, 4, 5, and 6) show a lower incidence of reversals. Even with this level of MTD separation, 2 dose levels between the MTDs of group 3 and groups 1 and 2, 13.8% of simulations observe at least 1 reversal for scenario 2. Although a greater percentage of reversals have magnitude of 1 dose level difference in these scenarios, reversals of magnitude 4 are observed. A reversal of magnitude 4 indicates that the MTD for group 3 (the most frail group) is dose level 4 and all doses were considered too toxic for either group 1 or 2. The greatest percentage of reversals is seen in scenarios where all groups have the same MTD (scenarios 7, 8 and 9) and the magnitude of these reversals tends to be greater than in scenarios with more distance between group MTDs.

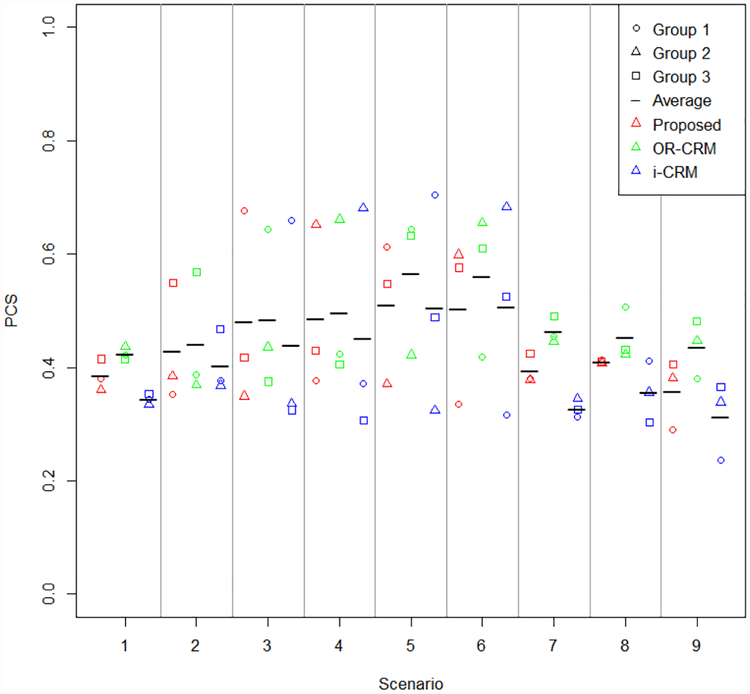
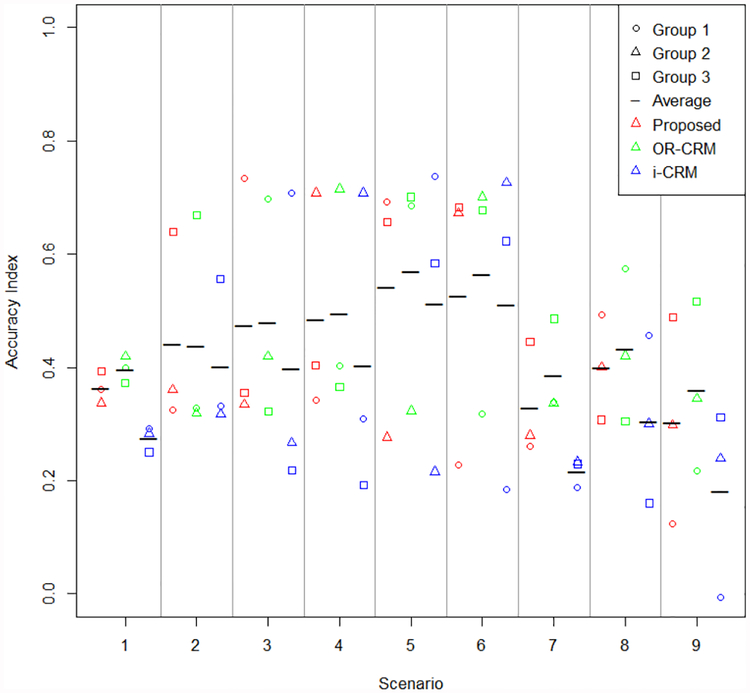
Percentage of correct selection and accuracy index

Percentage of correct selection and accuracy index for dose selection are given in Figures 2 and 3, respectively. Accuracy index for subject allocation is presented in Figure S7, in the supplemental material. Methods displayed in figures are specified as the proposed method, OR-CRM to indicate the order restricted method proposed by Conaway³, and i-CRM to indicate independent parallel CRM trials. These figures display the group specific summary measures as well as the average across groups for an overall summary measure. In every scenario considered, the average summary measure for the proposed method either meets or exceeds that of the independent CRM trials by group. Average performance between the proposed method and that of Conaway³ is similar, with a slight edge in performance of Conaway’s method over the proposed. Scenarios 5 and 6 contain the greatest differences in the correct group dose with a difference of three doses between group 3 and either group 1 or 2 for the partially ordered group methods compared to independent parallel CRM trials. In these scenarios, there is very little difference in the average percentage of correct selection between the two methods. A distinct advantage is seen in average percentage of correct selection for the proposed method for all other scenarios in comparing the proposed method to independent parallel CRM trials. In many scenarios the greatest gain in percentage of correct selection for proposed method versus independent CRM trials by group is seen in group 3, where the partial ordering information is focused. A similar pattern is seen in accuracy index for dose selection. The gains in accuracy index for subject allocation for the proposed method compared to individual CRM trials by group appear to be similar in all groups for most scenarios.

Figure 2.

Percentage of correct selection

Figure 3.

Accuracy index for dose selection

Figures for summary measures with trial size of 72 are given in the supplemental material. Although there are fewer reversals with the increased sample size, reversals are not uncommon and show a similar pattern by scenario as seen with trial sizes of 45. The magnitude of reversals also has a similar pattern, except in scenario 6 where there is a much great proportion of discrepancies of 1 dose level. As expected, percentage of correct selection and accuracy index for both dose selection and subject allocation are increased with the greater trial size. The patterns observed between the groups and the scenarios is similar in both trial sizes.

Discrepancies

Discrepancies between group MTDs can occur when the MTD for at least 2 groups is equal, indicating that there is no group effect between the specified groups²⁶. In these cases, the MTD selection within the trial indicates a group effect where none exists. As seen in Figure 1, the MTDs for groups 2 and 3 are equal for scenarios 1 and 2. In scenarios 7, 8, and 9, the MTDs for all groups are equal. Discrepancies occur in both the proposed method and independent CRM trials by group. Table S2 indicates the magnitude and frequency in which discrepancies occur in the 5 scenarios where no group effect is indicated between at least 2 groups. Maximum magnitude is reported for scenarios 7, 8, and 9 where discrepancies can occur between groups 1 and 2, groups 1 and 3, and groups 2 and 3 due to there being no group effect overall. Discrepancies are less common when using the proposed method. The magnitude of discrepancies is worse when using independent CRM trials. Note that discrepancies of magnitude 4 do not occur in the proposed method but are seen for all scenarios when using independent CRM trials.

Conclusion

This manuscript proposes a shift model for dose finding in clinical trials with more than two groups, where group frailty order is known between some but not all groups, creating a partial order. While methods exist for dose finding trials for two groups, only two methods are known to exist for dose finding trials with more than two groups which are partially ordered^3,4.

Simulations consider two additional approaches to compare with the proposed shift model: 1) a method by Conaway³ for partially ordered groups and 2) parallel trials using CRM, which ignore the known group orders. By ignoring the known partial ordering of groups with parallel CRM trials, some trials end with reversals, where MTD selection does not follow the known group frailty order. Simulations show that reversals are common in the parallel CRM trials. In the scenarios considered, reversals were present in 30% of trials, on average. Raphal et al.²⁶ considered use of independent designs in phase I trials in pediatric oncology, concluding that independent designs should be avoided. Both the proposed shift model for partially ordered groups and the method proposed by Conaway³ achieve MTD selection without reversals.

Designs considered for partially ordered groups outperformed parallel CRM trials, as shown by the operating characteristics. The proposed shift model and the method proposed by Conaway³ performed similarly, with a slight edge to the method proposed by Conaway. The proposed shift model is more computationally accessible and R code is available for this method.

The proposed shift model for dose finding in partially ordered groups can be easily adapted to a variety of settings involving more than two groups. Complete ordered settings, where the group frailty order is known between all groups, can be implemented by restricting the shift models to only those that are relevant. Other partially ordered settings can also be considered by selecting shift models which follow the known group frailty order. For example, consider the setting with four groups, where group 1 is known to be the least frail and group 4 is known to be the most frail. It is unknown if the MTD should differ between groups 2 and 3. Therefore, MTD₄ ≤ MTD₂ ≤ MTD₁ and MTD₄ ≤ MTD₃ ≤ MTD₁. Doses considered can also vary by group with the proposed method.

In summary, this manuscript provides a computationally accessible method for dose finding with partially ordered groups, allowing for MTD selection that follows the known frailty order among groups. We are exploring the use of this method for varying partially ordered group structures, including consideration of more than 3 groups. Additionally, varying doses by group are being considered.