Mechanism of Catalytic O₂ Reduction by Iron Tetraphenylporphyrin

Abstract

The catalytic reduction of O₂ to H₂O is important for energy transduction in both synthetic and natural systems. Herein, we report a kinetic and thermochemical study of the oxygen reduction reaction (ORR) catalyzed by iron tetraphenylporphyrin (Fe(TPP)) in N,N′-dimethylformamide using decamethyl-ferrocene as a soluble reductant and para-toluenesulfonic acid (pTsOH) as the proton source. This work identifies and characterizes catalytic intermediates and their thermochemistry, providing a detailed mechanistic understanding of the system. Specifically, reduction of the ferric porphyrin, [Fe^III(TPP)]⁺, forms the ferrous porphyrin, Fe^II(TPP), which binds O₂ reversibly to form the ferric-superoxide porphyrin complex, Fe^III(TPP)($\left({{\text{O}}_2}^{•-}\right).$ The temperature dependence of both the electron transfer and O₂ binding equilibrium constants has been determined. Kinetic studies over a range of concentrations and temperatures show that the catalyst resting state changes during the course of each catalytic run, necessitating the use of global kinetic modeling to extract rate constants and kinetic barriers. The rate-determining step in oxygen reduction is the protonation of Fe^III(TPP)($\left({{\text{O}}_2}^{•-}\right)$ by pTsOH, which proceeds with a substantial kinetic barrier. Computational studies indicate that this barrier for proton transfer arises from an unfavorable preassociation of the proton donor with the superoxide adduct and a transition state that requires significant desolvation of the proton donor. Together, these results are the first example of oxygen reduction by iron tetraphenylporphyrin where the pre-equilibria among ferric, ferrous, and ferric-superoxide intermediates have been quantified under catalytic conditions. This work gives a generalizable model for the mechanism of iron porphyrin-catalyzed ORR and provides an unusually complete mechanistic study of an ORR reaction. More broadly, this study also highlights the kinetic challenges for proton transfer to catalytic intermediates in organic media.

Graphical Abstract

INTRODUCTION

Many diverse biological and energy processes involve the catalytic reduction of dioxygen (O₂). ^1,2–5 In nature, cytochrome c oxidase reduces O₂ to drive ATP synthesis in cellular respiration,⁶ and cytochromes P450 couple the reduction of O₂ to the oxidations of endogenous and xenobiotic substances in numerous synthetic and metabolic processes.^7–9 In energy conversion technologies such as fuel cells, the oxidation of a fuel (dihydrogen, methanol, etc.) is coupled to the oxygen reduction reaction (ORR, eq 1), producing usable electrochemical work for portable and stationary applications.¹⁰ For such approaches to be practical, the ORR must be performed at fast rates and with high selectivity and energy efficiency over thousands of hours of operation.

$${\text{O}}_2+4{\text{H}}^{+}+4{\text{e}}^{-}\to 2{\text{H}}_2\text{O}$$ (1)

Widespread commercialization of fuel cell technologies requires the identification of inexpensive and efficient electrocatalysts capable of delivering 4H⁺ and 4e⁻ to O₂ and cleaving the O=O bond. Much research effort has been focused on developing new catalytic systems and improving previously known ORR electrocatalysts.^3,4,11,12 Given their biological relevance as active sites, iron porphyrins have been widely studied as ORR catalysts under electrocatalytic conditions.^13,14 Notably, graphite-embedded iron porphyrinic-like materials have been shown to exhibit ORR activity rivaling that of platinum metal in acidic media; however, the exact nature of their active sites remains a continued discussion.^15–17

Further improvement of ORR cathodic materials will require an understanding of the catalyst identity and turnover-limiting step(s) in the catalytic cycle. Such a detailed understanding is difficult to achieve for heterogeneous electrode surfaces, where the nature and catalytic activities of specific sites and intermediates are difficult to determine. Studying molecular ORR electrocatalysts that have been physisorbed or chem-isorbed onto electrode surfaces can circumvent some of these complications, especially with the use of in situ spectroscopic characterization.^18–23

Reaction mechanisms are more easily analyzed in systems with homogeneous molecular catalysts because these catalysts can be prepared in pure form and are readily examined using standard spectroscopic and kinetic methods for solution species. Optical spectroscopies have been extensively used to study iron porphyrins in the biomimetic context of dioxygen binding^24–26 and the oxidation of organic molecules.^27,28 However, surprisingly few studies have investigated the catalytic reduction of O₂ by iron porphyrins using soluble reductants.¹¹

Nearly 30 years ago, two reports by Fukuzumi described the first mechanistic investigations of O₂ reduction by iron tetraphenylporphyrin (abbreviated herein as Fe(TPP) if the oxidation state and axial ligand(s) are not specified). These studies were performed in acetonitrile (MeCN) using substituted ferrocenes (Fc) as the source of electrons and perchloric acid (HClO₄) as the source of protons.^29,30 Under these conditions, the rate-determining step was proposed to be outer-sphere electron transfer from the reductant to [Fe^III(TPP)]ClO₄, based upon the first-order dependence on [Fc] and the zero-order dependences on [O₂] and [HClO₄]. In this example, the strongly acidic medium with relatively weak reductants resulted in no detectable intermediates within the catalytic cycle.

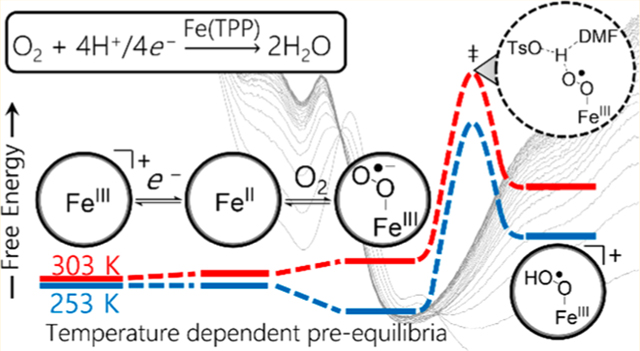
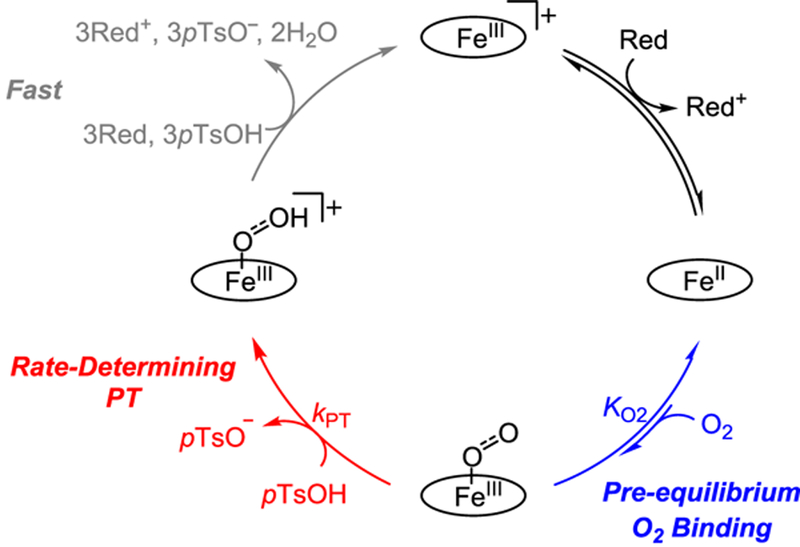
More recently, kinetic studies examined O₂ reduction catalyzed by Fe^III(TPP)Cl and other porphyrin derivatives in acidic acetonitrile and N,N′-dimethylformamide solutions containing decamethylferrocene (Fc*) as a soluble reductant.^31,32 With excess of this stronger reductant, the rate law for catalysis via Fe^III(TPP)Cl was zero order in reductant because electron transfer from Fc* to Fe^III(TPP)Cl was initially rapid and favorable. Under these conditions, the rate of ORR catalysis was first order in O₂, acid, and catalyst.³¹ The same rate law and rate constant were obtained under electrocatalytic conditions. Subsequent studies found this rate law to be general for electrocatalytic O₂ reduction using substituted iron porphyrins³² and in the presence of proton donors of varying acidity (pK_a).³³ The rate law implicates a mechanism of initial reduction of Fe^III to Fe^II, pre-equilibrium O₂ binding to Fe¹¹, and rate-limiting proton transfer from the acid to the Fe^m-superoxo intermediate (Scheme 1). However, efforts to decrease the proton-transfer barrier by appending proton relays to the iron porphyrins did not result in rate enhancements.³² To obtain direct support for the proposed mechanism and to better understand the factors affecting catalytic rates, a more thorough mechanistic analysis was needed.

Scheme 1.

Proposed Mechanism for Oxygen Reduction Catalyzed by Fe(TPP), with TPP Abbreviated as an Oval^a

^aRed = Fc* or electrode.

Herein, we report a much more complete and nuanced analysis of the 4H⁺/4e⁻ reduction of O₂ to H₂O catalyzed by iron tetraphenylporphyrin, prepared as the triflate salt ([Fe^III(TPP)]OTf). The ferrous and ferric-superoxide porphyrin species are identified and observed as catalytic intermediates for the first time, and their temperature-dependent speciation is reported. This includes measurements of the equilibrium constants for electron transfer from Fc* to [Fe^III(TPP)]OTf and for O₂ binding to Fe^II(TPP). These shifting equilibria and speciation play critical and previously unappreciated roles in the kinetics of catalysis in which the catalyst resting state varies among three different species during the course of the reaction. The temperature dependence of these equilibria, combined with measurements of catalytic rates and catalyst speciation by optical stopped-flow and electrochemical methods, provides an unusually rich data set. Modeling these results gives a detailed view of the catalytic mechanism under different conditions. The model yields the activation parameters for protonation of the ferric-superoxo intermediate, the rate-determining step in the catalytic cycle. These results are used in conjunction with computational modeling to analyze the underlying factors limiting proton transfer to the ferric-superoxide intermediate. Such a detailed mechanistic understanding provides critical insight into iron porphyrin-catalyzed oxygen reduction and should enable further improvements in catalytic systems.

$$\begin{gathered} {\text{O}}_2+4p\text{TsOH}+4\text{Fc*} \\ \stackrel{[\text{Fe}(\text{TPP})]\text{OTf}}{\to }2{\text{H}}_2\text{O}+4p{\text{TsO}}^{-}+4{\text{Fc*}}^{+} \end{gathered}$$ (2)

EXPERIMENTAL SECTION

Materials.

Iron tetraphenylporphyrin chloride, Fe^III(TPP)Cl, was synthesized by the metalation of meso-tetraphenylporphyrin with iron(ll) chloride in refluxing DMF as previously reported³² (SI, Figures S1 and S2). [Fe^III(TPP)]OTf was generated in situ from Fe(TPP)Cl and TlOTf in acidified DMF (SI, Figures S3 and S4). Fe^II(TPP) was prepared from the well-known reduction of Fe^III(TPP) Cl by Zn/Hg amalgam and was recrystallized from toluene/THF mixtures.^34,35 This compound was also prepared using modified literature procedures (SI, Figures S7 and S8). All solvents and electrolytes were purchased in high purity and purified as needed, as further described in section 1.2 of the Supporting information.

Optical Equilibrium and Kinetics Measurements.

Equilibrium measurements were performed with optical spectroscopy using a temperature-controlled Unisoku Unispeks cryostat. Equilibrium constants for electron transfer were made by fitting the UV–vis spectra of DMF solutions containing 0.1 M $\left[n-{\text{Bu}}_4\text{N}\right]\left[{\text{PF}}_6\right]$ and equimolar (100 μM) amounts of [Fe^III(TPP)]OTf, Fe^II(TPP), Fc*, and Fc*⁺ between 213 and 293 K. Likewise, equilibrium constants for O₂ binding were made by fitting the UV–vis spectra of O₂-saturated DMF solutions initially containing 0.1 M $\left[n-{\text{Bu}}_4\text{N}\right]\left[{\text{PF}}_6\right]$ and 60 μM Fe^II(TPP) between 213 and 238 K. Both sets of equilibrium data were analyzed using van ′t Hoff plots to yield enthalpic and entropic parameters. See Sections 2 and 3 of the Supporting information for complete details.

Stopped-flow kinetics measurements were performed by mixing N₂-saturated DMF solutions of Fc* in one syringe with air-saturated DMF solutions containing [Fe^III(TPP)]OTf and pTsOH in a second syringe. The reaction progress was monitored by following the appearance of Fc*⁺ over time. Experiments were performed at various [pTsOH], [catalyst], and temperatures (253–303 K). Changes in catalyst speciation over time were determined by fitting optical spectra to linear combinations of three catalyst species: [Fe^III (TPP)]-OTf, Fe^II(TPP), and Fe^III(TPP)$\left({{\text{O}}_2}^{•-}\right).$ The concentration time courses were modeled to obtain thermodynamic and kinetic parameters. See Sections 5 and 6 of the Supporting Information for complete details.

Kinetic Modeling.

The time course data from the stopped-flow catalytic experiments were fit to a multistep kinetic model in the COPAS1 program.³⁶ The thermodynamic parameters $\left(\mathrm{\Delta }{H}^{°}\text{and}\mathrm{\Delta }{S}^{°}\right)$ for electron transfer and O₂ binding and the activation parameters $\left(\mathrm{\Delta }{H}^{‡}\text{and}\mathrm{\Delta }{S}^{‡}\right)$ for proton transfer were optimized in order to minimize the sum of square deviations between the experimental concentrations and fitted time course concentrations. See Section 6 in the Supporting Information for complete details.

Computational Modeling.

The present density functional theory (DFT) calculations build on previously reported work.³² Stationary points were optimized using the PBE exchange and correlation functional.³⁷ The Stuttgart/Dresden basis set with a relativistic effective core potential (SDD) was used for the Fe center, and the 6–31G** basis set^38,39 was used for all atoms except sulfur. Diffuse functions and additional polarization functions (6–31++G(2df,2pd)) were used on sulfur in order to capture the sulfur–oxygen bonding correctly. Justification for this can be found in Section 8 of the SI. Single-point solvation energies in DMF were modeled using the SMD continuum solvent.⁴⁰ Harmonic vibrational frequencies, calculated at the same level of theory, were used to estimate the zero-point energy (ZPE) and the thermal contributions to free energies. Free energies are referenced to the standard state concentration of 1 M for the solute and 12.9 M for solvent DMF at T = 298 K. See Section 8 of the Supporting Information for complete details.

RESULTS

Electron-Transfer Equilibrium.

The proposed mechanism involves the initial reduction of [Fe^III(TPP)]OTf to Fe^II(TPP) by decamethylferrocene (Fc*). Qualitatively, the addition of excess Fc* to [Fe^III(TPP)]OTf results in the predominant formation of Fe^II(TPP) (Figures S9 and S10). Adding Fc*⁺ to this solution reoxidizes some Fe^II(TPP) and confirms the equilibrium nature of this ET process (eq 3, Figure S11). Equilibrium constants in DMF were measured by preparing solutions containing the four species and 0.1 M [n-Bu₄N][PF₆] to make the conditions similar to those used in the electrocatalytic and optical measurements. Analysis of the optical spectra gave the ratio of [Fe^III(TPP)]OTf to Fe^II(TPP) (SI).

$$\text{Fc}*+{\text{Fe}}^{\text{III}}{(\text{TPP})}^{+}\rightleftharpoons {\text{Fc*}}^{+}+{\text{Fe}}^{\text{II}}(\text{TPP})$$ (3)

$$K_{\text{ET}}=\frac{[{\text{Fc}*}^{+}][{\text{Fe}}^{\text{II}}(\text{TPP})]}{[\text{Fc}*]{[[{\text{Fe}}^{\text{III}}(\text{TPP})]}^{+}]}$$ (4)

Following eq 4, K_ET was determined at 293 K to be 0.16 ± 0.03. This K_ET could also be determined from electrochemical measurements: $E_{1/2}\left({\text{Fe}}^{\text{III}}{(\text{TPP})}^{+}/{\text{Fe}}^{\text{II}}(\text{TPP})\right)=-0.538\text{V}$ vs Fc⁺/Fc (vide infra) and $E_{1/2}\left({\text{Fc}*}^{+}/\text{Fc}*\right)=-0.484\text{V}$ vs Fc⁺/Fc in DMF³¹ containing 0.1 $\text{M}\left[n{\text{-Bu}}_{\text{4}}\text{N}\right]\left[{\text{PF}}_{\text{6}}\right].$ The 0.054 V difference in reduction potentials gives K_ET = 0.12 (SI Section 2.2), very close to the K_ET = 0.16 from optical measurements. The optical measurements were repeated at temperatures between 213 and 293 K to investigate the temperature dependence of K_ET (Figure 1a). The resulting van ′t Hoff plot yielded the enthalpy and entropy for the electron transfer from Fc* to [Fe^III(TPP)]OTf: $\mathrm{\Delta }{H^{°}}_{\text{ET}}=2.8\pm 0.1\text{kcal}{\text{mol}}^{-1}$ and $\mathrm{\Delta }{S^{°}}_{\text{ET}}=6\pm 2{\text{cal mol}}^{-1}{\text{K}}^{-1}$ (Figure 1b).

Figure 1.

(a) Spectra of a DMF solution containing 100 μM [Fe^III(TPP)]OTf, Fe^II(TPP), Fc*, and Fc*⁺ and 0.1 M [n-Bu₄N][PF₆] in the Q-band region at temperatures between 293 and 213 K. (b) van ′t Hoff analysis of ln(K_ET) derived from the data in panel a.

Oxygen-Binding Equilibrium.

To test the hypothesis that O₂ binding follows the initial reduction of [Fe^III(TPP)]OTf, a genuine Fe^II(TPP) sample was prepared and exposed to O₂ at low temperatures in DMF. The addition of 1 atm of O₂ to DMF solutions of Fe^II(TPP) at 213 K resulted in the quantitative conversion of Fe^II(TPP) to a new species with Q-band absorbance features at 542 and 580 nm, characteristic of a ferric tetra-arylporphyrin superoxide complex, Fe^III(TPP)-$\left({{\text{O}}_2}^{•-}\right).$^41,42 The chemically generated ${\text{Fe}}^{\text{III}}(\text{TPP})\left({{\text{O}}_2}^{•-}\right)$ complex was relatively stable (~30 min) at 213 K but decomposed quickly at temperatures above 238 K to the well-known μ-oxo dimer, [Fe^III(TPP)]₂O.⁴²

The stoichiometry of O₂ binding was measured by titrating a DMF solution of Fe^II(TPP) at 213 K with a room-temperature DMF solution containing 1 atm of O₂ (3.1 mM [O₂]).⁴³ With substoichiometric concentrations of O₂, the Q bands of Fe^II(TPP) incrementally shifted to those of ${\text{Fe}}^{\text{III}}(\text{TPP})\left({{\text{O}}_2}^{•-}\right)$ (Figure 2a). At 213 K, slightly more than 1 equiv of O₂ was necessary to reach the end point of the titration, after which no additional changes occurred in the spectra (Figures S13 and S15).

Figure 2.

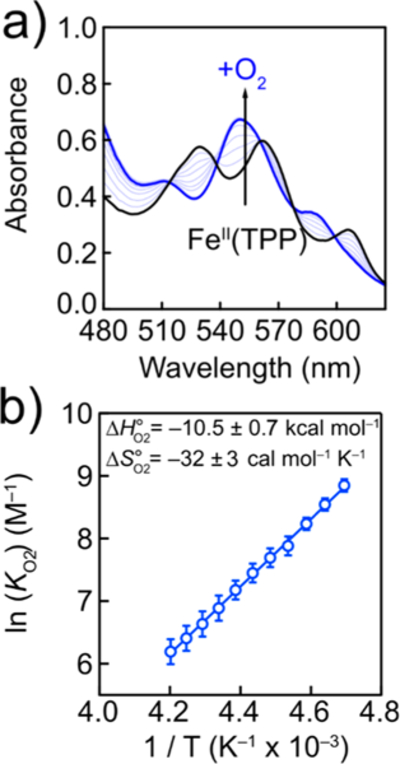
(a) Optical spectra (corrected for dilution) of a titration at 213 K of a DMF solution containing 50 μm Fe^II(TPP) and 0.1 M [n-Bu₄N][PF₆] with DMF containing dissolved O₂. (b) van ′t Hoff analysis of O₂ binding to ${\text{Fe}}^{\text{II}}(\text{TPP})\left(K_{{\text{O}}_2}{\text{in M}}^{-1}\right).$

The reversibility of O₂ binding to Fe^II(TPP) was investigated by sparging a solution of the generated ${\text{Fe}}^{\text{III}}(\text{TPP})\left({{\text{O}}_2}^{•-}\right)$ adduct with argon at 213 K. A spectrum collected after 5 min of sparging closely matched the initial anaerobic spectrum of Fe^II(TPP) with some residual contributions from remaining ${\text{Fe}}^{\text{III}}(\text{TPP})\left({{\text{O}}_2}^{•-}\right)$ (Figure S16. The fact that Fe^II(TPP) could be formed from ${\text{Fe}}^{\text{III}}(\text{TPP})\left({{\text{O}}_2}^{•-}\right)$ demonstrated O₂ binding reversibility and enabled us to measure equilibrium constants (eq 5).

$$K_{{\text{O}}_2}\left({\text{M}}^{-1}\right)=\frac{\left[{\text{Fe}}^{\text{III}}(\text{TPP})\left({{\text{O}}_2}^{•-}\right)\right]}{\left[{\text{Fe}}^{\text{II}}(\text{TPP})\right]\left[{\text{O}}_2\right]}$$ (5)

The equilibrium constants for O₂ binding to Fe^II(TPP)($K_{{\text{O}}_{\text{2}}},$ eq 5) were measured at various temperatures. With excess O₂, a solution of ${\text{Fe}}^{\text{III}}(\text{TPP})\left({{\text{O}}_2}^{•-}\right)$ was prepared at 213 K and incrementally warmed to 238 K. Upon warming, the initial spectrum gradually changed to contain Q bands of both ${\text{Fe}}^{\text{III}}(\text{TPP})\left({{\text{O}}_2}^{•-}\right)$ and ${\text{Fe}}^{\text{II}}(\text{TPP})$ (Figure S17). The UV–vis spectrum at each temperature was fit to a linear combination of independently measured ${\text{Fe}}^{\text{III}}(\text{TPP})\left({{\text{O}}_2}^{•-}\right)$ and ${\text{Fe}}^{\text{II}}(\text{TPP})$ spectra (SI Section 3.3). The concentrations of ${\text{Fe}}^{\text{II}}(\text{TPP})$, ${\text{Fe}}^{\text{III}}(\text{TPP})\left({{\text{O}}_2}^{•-}\right)$, and dissolved O₂ from mass balance were then used to calculate at each temperature (eq 5). At 213 K, the free energy of formation for ${\text{Fe}}^{\text{III}}(\text{TPP})\left({{\text{O}}_2}^{•-}\right)$ is exergonic, $\mathrm{\Delta }{G}_{{\text{O}}_2}^{°}=-3.68\text{kcal}{\text{mol}}^{-1}.$ The slope and intercept of the resulting van ′t Hoff plot (Figure 2b) yielded the enthalpy and entropy for the binding of O₂ to form ${\text{Fe}}^{\text{III}}(\text{TPP})\left({{\text{O}}_2}^{•-}\right):\mathrm{\Delta }{H^{°}}_{{\text{O}}_2}=-10.5\pm 0.7\text{kcal}{\text{mol}}^{-1}\text{and}\mathrm{\Delta }{S^{°}}_{{\text{O}}_2}=-32\pm 3\text{cal}{\text{mol}}^{-1}{\text{K}}^{-1}.$ By extrapolating the van ′t Hoff plot to 298 K, the equilibrium constant for O₂ binding at room temperature was determined to be ca. 5 M⁻¹. A t-test gave a 95% confidence interval for this extrapolated value at 298 K to be between 0.21 and 110 M⁻¹ (details in the SI).⁴⁴

Electrochemical Kinetics of Catalytic Oxygen Reduction.

Our previous studies have shown that the rate of ORR catalyzed by iron tetra-arylporphyrins exhibits first-order dependences on the concentrations of catalyst, O₂, and acid.³² To verify that the same rate law applies to the system studied here, we investigated the kinetics of ORR catalyzed by $\left[{\text{Fe}}^{\text{III}}(\text{TPP})\right]\text{OTf}$ using cyclic voltammetry.

1n anaerobic DMF solutions containing [Fe^III(TPP)]OTf and 0.1 M [n-Bu₄N][PF₆], a chemically reversible, diffusioncontrolled reduction was observed at −0.538 V vs Fc⁺/Fc (Figure 3a (black trace), Figure S20). This wave is diagnostic of the reduction of [Fe^m(TPP)]⁺ to Fe¹¹(TPP), as previously reported by Saveant⁴⁵ and later by our group.^32,33 The addition of pTsOH did not affect $E_{1/2}\left({\text{Fe}}^{\text{III}}{(\text{TPP})}^{+}/{\text{Fe}}^{\text{II}}(\text{TPP})\right)$ (Figure S21), in contrast to what has been observed for Fe(TPP) in the presence of chloride salts.³¹ These results are consistent with the preferred binding of DMF solvent over triflate, in both Fe(III) and Fe(II) redox states, as previously observed.^32,45 For simplicity, we exclude explicit solvent molecules from the abbreviated formulas and continue to abbreviate these redox states as [Fe^III(TPP)]OTf and Fe^II(TPP).

Figure 3.

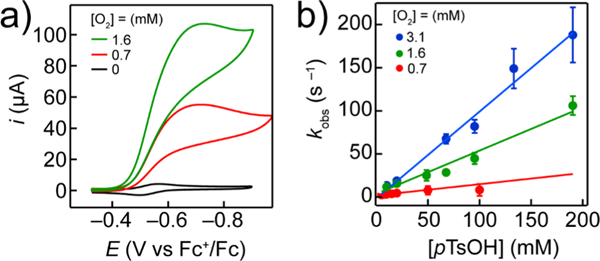
(a) Electrochemical response of 0.3 mM [Fe^III(TPP)]OTf in the presence of 1 M pTsOH and 1.6 mM O₂ (green), 0.7 mM O₂ (red, air sparged), and 0 mM O₂ (black, N₂ sparge) at 298 K. (b) Dependence of k_obs from FOWA on [pTsOH] at different O₂ concentrations. All CVs were taken in the presence of 0.1 M [n-Bu₄N][PF₆] electrolyte.

When DMF solutions containing $\left[{\text{Fe}}^{\text{III}}(\text{TPP})\right]\text{OTf},p\text{TsOH},$ and $\left[n-{\text{Bu}}_4\text{N}\right]\left[{\text{PF}}_6\right]$ were sparged with 1 atm of air (0.7 Mm O₂ in DMF),⁴³ the voltammograms displayed significant current enhancements (> 10×) centered above $E_{1/2}({\text{Fe}}^{\text{III}}/{\text{Fe}}^{\text{II}})$ (Figure 3a, red trace). The magnitude of this irreversible current was linear with the square root of the scan rate, which suggests that the catalytic current arises from an electro-generated, homogeneous catalyst. Rotating ring-disk electrochemistry (RRDE) was used to quantify the amount of H₂O₂ produced during turnover. The RRDE measurements demonstrated that catalysis is selective for the $4{\text{H}}^{+}/4{\text{e}}^{-}$ reduction of O₂ to water and produces ~1.5% H₂O₂ (n_cat = 3.9) under these conditions (Figure S50–S51).

The pseudo-first-order rate constant k_obs for ORR was quantified using foot-of-the-wave analysis (FOWA, eq 7),⁴⁶ where n_cat = 3.9 (determined by RRDE, see above). FOWA allows the determination of catalytic rate constants under conditions where the concentrations of the substrates in the reaction-diffusion layer (O₂ and pTsOH in this case) are essentially identical to the bulk solution concentrations (see S1).⁴⁶ The linearity of the foot-of-the-wave plots (Figure S22) indicated that the reaction was first order in catalyst. Additionally, k_obs was linearly dependent on both [O₂] and [pTsOH] (Figure 3), indicating the third-order rate law in eqs 6 and 8. The quotient of k_obs and the reactant concentrations then afforded the third-order rate constant, k_cat. Considering the upper and lower bounds for σ in eq 7 (see S1), k_cat ranged from 3.2 × 10⁵ to 6.4 × 10⁵ M⁻² s⁻¹.

$$\text{rate}=n_{\text{cat}}{k}_{\text{obs}}[\text{Fe}(\text{TPP})]$$ (6)

$$\frac{i_{\text{c}}}{i_{\text{p}}}=\frac{2.24{n_{\text{cat}}}^{\sigma }\sqrt{\frac{RT}{Fv}{k}_{\text{obs}}}}{1+\exp \left[\frac{F}{RT}\left(E-E_{1/2}\right)\right]}$$ (7)

$$k_{\text{obs}}=k_{\text{cat}}\left[{\text{O}}_2\right][p\text{TsOH}]$$ (8)

Optical Kinetics.

The kinetics of Fe(TPP)-catalyzed ORR were also studied by optical spectroscopy over a range of temperatures. These experiments were performed in DMF using pTsOH as the proton source and Fc* as the soluble reductant. During optical measurements, all solutions also contained 0.1 $\left[n-{\text{Bu}}_4\text{N}\right]\left[{\text{PF}}_6\right]$ to mirror the electrochemical conditions. In a typical experiment, a solution of air-saturated $\text{DMF}\left(0.7\text{mM}{\text{O}}_2\right)$ containing $\left[{\text{Fe}}^{\text{III}}(\text{TPP})\right]\text{OTf}(60\mu \text{M})$ and pTsOH (50 mM) was rapidly mixed in a stopped-flow instrument with an equal volume of an anaerobic DMF solution of Fc* (6 mM, higher concentrations were limited by solubility), with all concentrations being halved upon mixing (SI). After mixing, optical spectra showed the growth of a broad absorbance feature between 600 and 700 nm, diagnostic of decamethylferrocenium (Fc*⁺) formation, along with various changes in the porphyrin Q-band region (Figures 4a and S24, discussed further below). Control experiments performed under identical conditions but in the absence of [Fe^III(TPP)]OTf catalyst formed a much smaller amount of Fc*⁺ (~10%) over the same time course (Figure 4b). The small amount of Fc* autooxidation likely results from unfavorable pre-equilibrium electron transfer with O₂ followed by irreversible chemical reactions of ${{\text{O}}_2}^{•-}.$⁴⁷ When pTsOD was substituted for pTsOH, the rate of Fc*⁺ formation did not change $(\text{KIE}\approx 1,$ see Figure S25).

Figure 4.

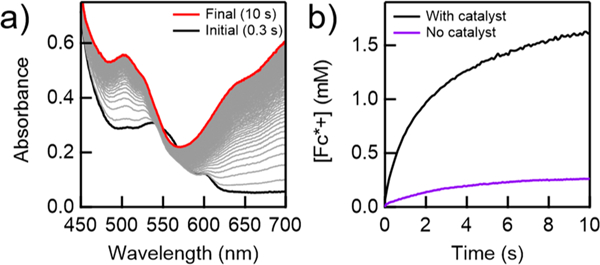
(a) Spectral changes measured for the reaction of O₂ (0.33 mM) with pTsOH (50 mM) and Fc* (3 mM), catalyzed by [Fe^III(TPP)]OTf (30 μM) over a 30 s reaction at 298 K. (b) Rate of Fc*⁺ formation during the first 10 s of reaction (a) (black trace), compared to the same reaction conducted in the absence of added [Fe^III(TPP)]OTf catalyst (purple trace). Concentrations of Fc*⁺ were calculated at 700 nm after the removal of the absorbance contributions from [Fe^III(TPP)]OTf (SI, Section 5.3).

The kinetics of Fe(TPP)-catalyzed ORR were examined by stopped-flow methods at temperatures between 253 and 303 K. In these experiments, the air-saturated syringe was prepared at room temperature so that the initial concentration of dissolved O₂ remained constant for all catalytic runs. Notably, as shown in Figure 5, the spectrum collected 1 s after mixing was temperature-dependent. At 253 K, absorbance features at 542 and 580 nm were immediately present (Figure 5a). These features match those of the independently prepared ferric superoxide, ${\text{Fe}}^{\text{III}}(\text{TPP})\left({{\text{O}}_2}^{•-}\right)$, described above. However, at temperatures above 273 K, the initial spectrum resembled a mixture of Fe^II(TPP) and ${\text{Fe}}^{\text{III}}(\text{TPP})\left({{\text{O}}_2}^{•-}\right)$ (Figure 5b). At all temperatures, the initial traces decayed with the formation of [Fe^III(TPP)]OTf and Fc*⁺.

Figure 5.

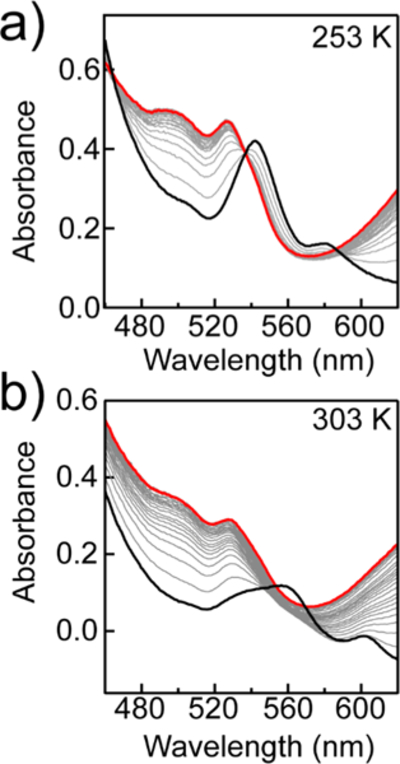
(a) Spectral changes after stopped-flow mixing of [Fe^III(TPP)]OTf (30 μM), pTsOH (35 mM), Fc* (3 mM), and O₂ (0.33 mM) at 253 K. Black trace = initial spectrum after mixing (1 s) Red trace = final spectrum after mixing (50 s). (b) Same conditions as in panel a at 303 K. Black trace = initial spectrum after mixing (1 s) Red trace = final spectrum after mixing (20 s).

The temperature dependence of the initial stopped-flow kinetic traces reflects the temperature-dependent equilibrium constant for O₂ binding. The initial spectra showed exclusively ${\text{Fe}}^{\text{III}}(\text{TPP})\left({{\text{O}}_2}^{•-}\right)$ at low temperatures and a mixture of Fe^II(TPP) and ${\text{Fe}}^{\text{III}}(\text{TPP})\left({{\text{O}}_2}^{•-}\right)$ at higher temperatures, consistent with the independent O₂ binding measurements described above. While the electron-transfer equilibrium also shows a temperature dependence, ΔG_ET changes by only ~0.3 kcal mol⁻¹ between 253 and 303 K. Thus, the observed spectral differences are dominated by the difference in O₂-binding favorability across this temperature range. Additionally, the observation of Fe^II(TPP) or ${\text{Fe}}^{\text{III}}(\text{TPP})\left({{\text{O}}_2}^{•-}\right)$ as the initial catalyst resting state also supports the proposed mechanism in which the rate of ORR is limited by the protonation of ${\text{Fe}}^{\text{III}}(\text{TPP})\left({{\text{O}}_2}^{•-}\right)$ rather than initial electron transfer or O₂ binding (Scheme 1).

Over the course of the stopped-flow kinetics runs, the speciation of the iron catalyst changed, with [Fe^III(TPP)]OTf becoming the predominant species at the end of the reaction (when limiting O₂ is completely consumed). The changes in catalyst speciation reflect the positions of the time- and temperature-dependent equilibria among [Fe^III(TPP)]OTf, Fe^II(TPP), and ${\text{Fe}}^{\text{III}}(\text{TPP})\left({{\text{O}}_2}^{•-}\right)$ during catalytic turnover, as discussed in more detail in the next section. In the absence of a constant catalyst resting state, the rate law for Fc*⁺ formation needs to be defined with respect to the total amount of catalyst in solution, ${[\text{Fe}(\text{TPP})]}_{\text{total}}.$ The resulting rate law (eq 9) includes the two pre-equilibria (K_ET and $K_{{\text{O}}_2}$) and the turnover-limiting protonation step, k_PT. The complexity of this rate law arises from the uphill electron-transfer equilibrium between Fc* and [Fe^III(TPP)]OTf (K_ET < 1). As such, even with a large excess of Fc* (e.g., >40:1 ratio of [Fc*]:[O₂]), the growth of oxidized product Fc*⁺ shifts the initial electron-transfer reaction away from the formation of catalytically active Fe^II(TPP), as demonstrated independently in Section I above. The complexity of this rate law and the inability to find experimental conditions under which it simplifies have precluded simple fitting and the determination of a simple reaction order in [Fc*] (SI).

$$\frac{\text{d}[{\text{Fc}*}^{+}]}{\text{d}t}=\frac{n_{\text{cat}}{K}_{\text{ET}}{K}_{{\text{O}}_2}{k}_{\text{PT}}{[\text{Fe}(\text{TPP})]}_{\text{total}}[{\text{O}}_2][\text{Fc}*][p\text{TsOH}]}{K_{\text{ET}}[\text{Fc}*](1+K_{{\text{O}}_2}[{\text{O}}_2])+[{\text{Fc}*}^{+}]}$$ (9)

Longer-time-scale catalytic experiments were conducted by combining a large excess of Fc* (10 mM) and pTsOH (260 mM) relative to [Fe^III(TPP)]OTf (1 μM) and stirring the solution in ambient air. Over 15 min, significantly larger amounts of Fc*⁺ were produced than an identical experiment conducted in the absence of [Fe^III(TPP)]OTf. Iodometric titrations of the resulting solution were used to quantify the amount of H₂O₂ produced during the catalyzed reaction and revealed that ~15% H₂O₂ (n_cat = 3.7 e⁻/O₂, Figure S51) was formed under such conditions, in good agreement with the selectivity values obtained electrochemically $(n_{\text{cat}}\approx 3.9{\text{e}}^{-}/{\text{O}}_2).$ These results demonstrate that the catalyst remains active for ORR for at least 15 min and permit a rough estimation of the catalyst turnover number over 15 min, TON = 2000 mol O₂ consumed per mole of catalyst (Figure S26).

Kinetic Modeling.

The constantly evolving catalyst speciation during ORR by Fe(TPP), observed by stopped-flow measurements, required us to use a kinetic model to fit the data. The model yielded the thermodynamic parameters for the ET and O₂-binding pre-equilibria and the kinetic parameters for the turnover-limiting step.

Fitting the optical data to a kinetic model first required the concentration of each catalyst species at every time point to be determined. These concentrations were obtained using Beer’s law and a system of linear equations that considered absorbance contributions from [Fe^III(TPP)]OTf, Fe^II(TPP), ${\text{Fe}}^{\text{III}}(\text{TPP})\left({{\text{O}}_2}^{•-}\right)$, and Fc*⁺. Absorbance contributions from Fc* were negligible in the wavelength region of interest and could be ignored (SI Section 5.3).

Global modeling of stopped-flow kinetic runs was performed with COPASI³⁶ software using the kinetic model in Scheme 2 and the corresponding rate law (eq 9). The only input parameters in the model were the fast rate constants (10⁷ M⁻¹ s⁻¹) for (1) electron transfer from Fc* to Fe^III(TPP)⁺ and (2) O₂ binding to Fe^II(TPP). This was done to ensure that these steps were fast pre-equilibria, as observed experimentally (see above). Step 4 was included to account for mass balance in the reaction and was set to a fast enough rate to be kinetically invisible.

Scheme 2.

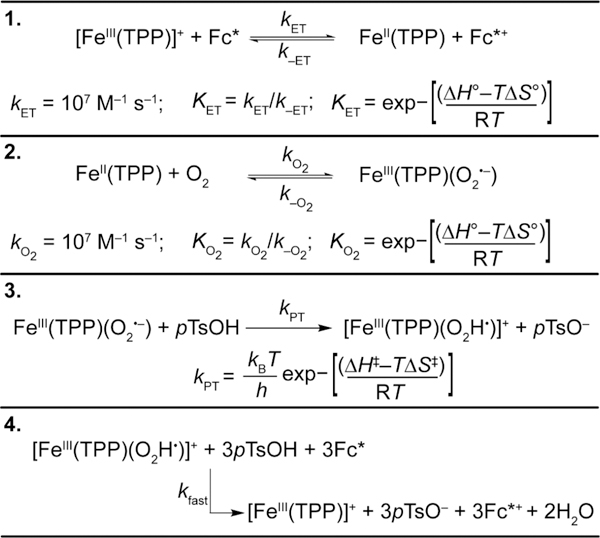
Kinetic Model and Parameters Used for the Global Fitting of the Stopped-Flow Kinetic Data and the Attainment of ΔH°_ET, ΔS°_ET, ΔH°_O2, ΔS°_O2, ΔH^‡_PT, and ΔS^‡_PT

The model used in Scheme 2 attempted to fit both the rate of decamethylferrocenium formation $\left(\text{d}[{\text{Fc}*}^{+}]/\text{dt}\right)$ and the catalyst speciation to the experimental data by varying the thermodynamic parameters for electron transfer $\mathrm{\Delta }{H^{°}}_{\text{ET}}\text{and}\mathrm{\Delta }{S^{°}}_{\text{ET}},$ step 1), the thermodynamic parameters for O₂ binding $((\mathrm{\Delta }{H^{°}}_{{\text{O}}_2}\text{and}\mathrm{\Delta }{S^{°}}_{{\text{O}}_2},$ step 2), and the activation parameters for proton transfer $(\mathrm{\Delta }{H^{‡}}_{\text{PT}}\text{and}\mathrm{\Delta }{S^{‡}}_{\text{PT}},$ step 3). The six parameters were optimized to fit all stopped-flow data simultaneously, including experiments between 253 and 303 K with varied concentrations of substrate (50–100 mM pTsOH) and catalyst (30–50 μM [Fe(TPP)]_total). The experiments have some uncertainty in the catalyst speciation with time as a result of the overlapping absorbance features, low concentrations of the different Fe(TPP) species, and uncertainties in the experimental ε values (in part due to high air sensitivity at low concentrations and the instability of the materials). Therefore, we sought a model that fit the general trends in catalyst speciation rather than the exact concentration profiles (Figure 6). The fits are good for the [Fc*⁺] time courses and agree with the general trends in catalyst speciation. Notably, the model fits well to changes in initial [Fe^II(TPP)] and [${\text{Fe}}^{\text{III}}(\text{TPP})\left({{\text{O}}_2}^{•-}\right)$] concentrations across a variety of temperatures and is representative of the temperature-dependent O₂ binding equilibrium. Across the whole temperature range, the model also correctly predicts that [Fe^III(TPP)]OTf is the predominant catalyst species at the end of the reaction, even when excess Fc* is used.

Figure 6.

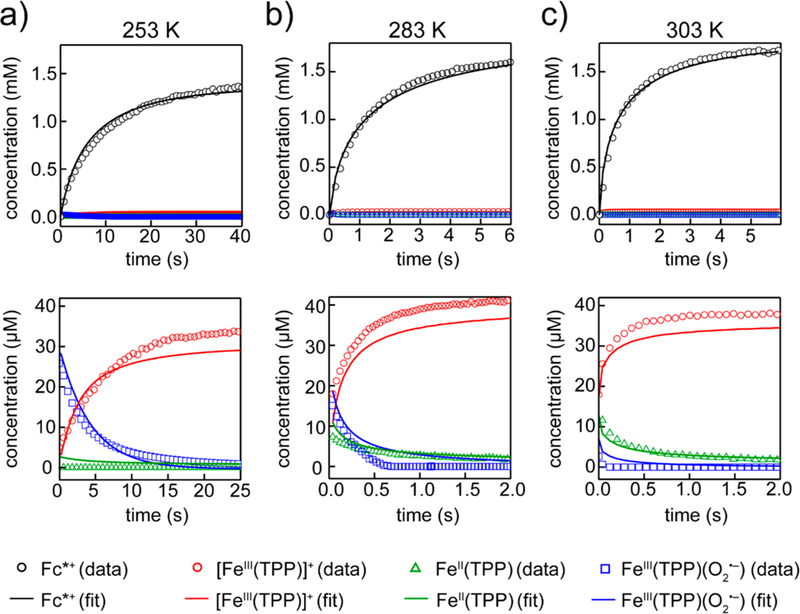
Data (points) and fits (lines) for three stopped-flow ORR time courses (0.3 μM Fe(TPP), 50 mM pTsOH, 0.33 mM O₂, 3 mM Fc*,varied temperatures): (a) 253 K, (b) 283 K, and (c) 303 K. For each temperature column, the top figure shows the Fc*⁺ concentrations, and the bottom figure shows an expansion for the Fe(TPP) speciation.

The accuracy of the model is evidenced by the agreement with experimental data for both the thermodynamic and kinetic parameters (Table 1). The modeled values for $\mathrm{\Delta }{H^{°}}_{\text{ET}},\mathrm{\Delta }{H^{°}}_{{\text{O}}_2},\text{and}\mathrm{\Delta }{S^{°}}_{\text{ET}}$ very closely match the experimentally determined values from Sections I and II above. The modeled value for $\mathrm{\Delta }{S^{°}}_{{\text{O}}_2}$ is somewhat less negative than the experimental value, which is similar to typical entropies for O₂ binding in polar organic solvents.⁴⁸ The inconsistencies between modeled and experimental $\mathrm{\Delta }{S^{°}}_{{\text{O}}_2}$ could be due to an unrecognized catalyst complex in the spectral fitting. Although we cannot rule out such a contribution, we believe the higher than expected modeled $\mathrm{\Delta }{S^{°}}_{{\text{O}}_2}$ may instead be related to error balancing with the activation parameters for proton transfer. Consistent with a balancing of errors, the model accurately predicts the rate constant k_cat at 298 K: $k_{\text{cat},\text{model}}=(2-20)\times {10}^5{\text{M}}^{-2}{\text{s}}^{-1},\text{and}{k}_{\text{cat,experimental}}=(3.2-6.4)\times {10}^5{\text{M}}^{-2}{\text{s}}^{-1}.$ This experimental rate constant was calculated under electrochemical conditions, where k_cat is the product of $K_{{\text{O}}_2}$ and k_PT. Although $\mathrm{\Delta }{S^{°}}_{{\text{O}}_2}$ and the activation parameters are not significantly correlated according to the COPASI statistical analysis, there is evidence that these parameters are not all known completely independently from one another. We can achieve similarly strong fits of the data with different parameter values when they are tightly constrained the to the experimental results (see SI, Section 6).

Table 1.

Results of COPASI Global Fitting of Stopped-Flow Optical Kinetic Results and Comparison with Experimental Values^a

reaction	parameterb	model	experimentalc
$\text{Fc}*+{\text{Fe}}^{\text{III}}{(\text{TPP})}^{+}\rightleftharpoons {\text{Fc}}^{*+}+{\text{Fe}}^{\text{II}}(\text{TPP})$	KET (298 K)	0.055(7)	0.18(3)
	ΔH°ET	2.9(1)	2.8(1)
	ΔS°ET	4.1(4)	6(2)
FeII(TPP) + O2 ⇌ FeIII(TPP)(${{\text{O}}_2}^{•-}$)	KO2 (250 K, M−1)d	(2.7–6.4) × 104	(0.205–11.5) × 102e
	ΔH°O2	−9.5(1)	−l0.5(7)e
	ΔS°O2	−16.9(4)	−32 (3)e
FeIII(TPP)(${{\text{O}}_2}^{•-}$) + pTsOH → FeIII(TPP)(O2H•)+ + pTsO−	kPT (298 K)	1.5(3)×103 M−1 s−1	2.0(9)f × 105 M−1 s−1
	ΔH‡PT	12.0(1)
	ΔS‡PT	−3.1(2)
FeII(TPP) + O2 + pTsOH → FeIII(TPP)(O2H•)+ + pTsO−g	kcat (298 K, M−2 s−1) = KO2kPT	(2–20) × 105h	(3.2–6.4) × 105i

^aOptimized values from COPASI analysis of data at 253–303 K, 50–100 mM pTsOH, 30–50 μM Fe(TPP). COPASI values and experimental equilibrium parameters are given with the uncertainty in parentheses representing 1 standard deviation.

^b$\mathrm{\Delta }{H}^{°}\text{and}\mathrm{\Delta }{H}^{‡}$ values in kcal mol⁻¹; ΔS° and ΔH° values in cal K⁻¹ mol⁻¹.

^cDirect experimental measurements of equilibrium parameters from optical spectra and van ′t Hoff analyses (sections I and II).

^dValues extrapolated from thermodynamic parameters from kinetic data (model) or lower-temperature equilibrium measurements (experiment).

^eThe 95% confidence limits from a t test are for $K_{{\text{O}}_2}$ at 298 K, 0.21 to 110 M⁻¹; for $\mathrm{\Delta }{H^{°}}_{{\text{O}}_2},$ −9.6 to −11.8 kcal mol⁻¹; and for $\mathrm{\Delta }{S}_{{\text{O}}_2},$ −28 to −38 cal K⁻¹ mol⁻¹, SI Section 3.4).

^fCalculated as $k_{\text{cat}(\text{echem})}/K_{{\text{O}}_2(\text{experimental})},$ where $K_{{\text{O}}_2}$ was defined as the mean value, 5 M⁻¹.

^gChemical steps involved in defining the catalytic rate constant, k_cat, determined electrochemically.

^hCalculated as $K_{{\text{O}}_2}(\text{model})\times k_{\text{PT}}\text{(model)}.$

ⁱCalculated from foot-of-the-wave analysis, vide infra.

Computational Analysis of the Barrier for the Protonation of Fe^III(TPP)$\left({{\text{O}}_2}^{•-}\right)$ by pTsOH.

Prior DFT and experimental studies identified the protonation of ${\text{Fe}}^{\text{III}}(\text{TPP})\left({{\text{O}}_2}^{•-}\right)$ as the rate-limiting step for the ORR by Fe(TPP) in DMF with [H-DMF]OTf as the acid.³² This section extends that computational analysis to evaluate the thermochemistry and kinetics of protonation of ${\text{Fe}}^{\text{III}}(\text{TPP})\left({{\text{O}}_2}^{•-}\right)$ by pTsOH, the acid used in this study.

The thermochemistry and kinetics of ${\text{Fe}}^{\text{III}}(\text{TPP})\left({{\text{O}}_2}^{•-}\right)$ protonation are dictated by interactions among the proton source, solvent, and superoxide adduct.³² As such, DFT analysis was performed to quantify the energetics of interactions among explicit pTsOH, pTsO⁻, and DMF molecules in DMF solvent. Calculations show that the free energy of the $p\text{TsOH}\cdots \text{DMF}$ pair is stabilized by 1.6 kcal mol⁻¹ relative to its constituent parts (separate pTsOH and DMF molecules). Formation of the ${[p\text{TsOH}\cdots p\text{TsO}]}^{-}$ homoconjugate is even more stable, favored by 5.9 kcal mol⁻¹ relative to separate pTsOH and pTsO⁻ molecules; however, the experimental conditions $([\text{DMF}]\gg [p{\text{TsO}}^{-}])$ favor the pTsOH···DDMF heteroconjugate. Therefore, the thermochemistry and kinetics of proton transfer to ${\text{Fe}}^{\text{III}}(\text{TPP})\left({{\text{O}}_2}^{•-}\right)$ were investigated using pTsOH···DDMF as the proton donor.

The computed free-energy profiles for the protonation of ${\text{Fe}}^{\text{III}}(\text{TPP})\left({{\text{O}}_2}^{•-}\right)$ (1) by pTsOH···DMF are shown in Figure 7a, wherein all energetics are referenced to 1. The free-energy profile for protonation by pTsOH···DMF first features the formation of a preassociation complex, 2, in which the acid approaches ${\text{Fe}}^{\text{III}}(\text{TPP})\left({{\text{O}}_2}^{•-}\right)$ (1). The formation of 2 involves solvent reorganization and the establishment of a three-center site and has an overall energetic penalty of 8.5 kcal mol⁻¹. This energetic cost results from unfavorable entropic $(-T\mathrm{\Delta }S=10.7{\text{kcal mol}}^{-1}\text{at}298\text{K})$ and solvation terms (7.8 kcal mol⁻¹) that are only partially balanced by being electronically favorable (−9.9 k_cal mol⁻¹). Proton transfer then yields the perhydroxyl (3) species, which was calculated to be 9.8 k_cal mol⁻¹ uphill from 1. This result indicates that the proton transfer is unfavorable and is consistent with the experimental data.

Figure 7.

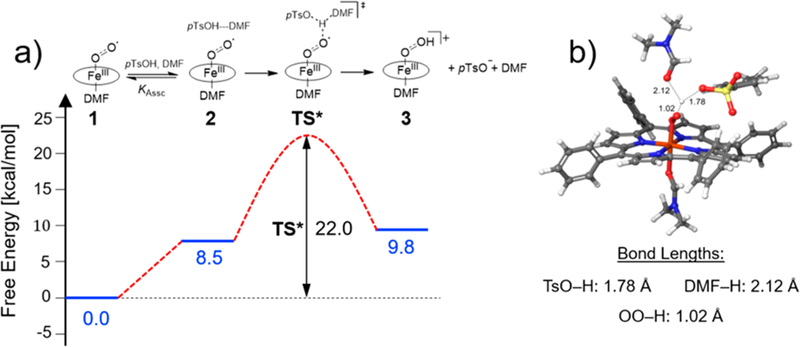
(a) Computed free-energy profile for association (K_assc) and protonation of Fe^III(TPP)(${{\text{O}}_2}^{•-}$) by the pTsOH···DMF heteroconjugate pair. (b) Optimized structure for the proton-transfer transition state (k_PT) and the corresponding O−H bond lengths for the proton-transfer donor (pTsOH), solvent (DMF), and acceptor Fe^III(TPP)(${{\text{O}}_2}^{•-}$). All distances are in angstroms.

To further understand the kinetics of proton transfer, the barrier for protonation from the heteroconjugated pair pTsOH···DMF was sought. As shown in Figure 7, the transition state (TS*) involves proton transfer from the preassociation complex (2) and has an overall barrier of 22.0 kcal mol⁻¹ relative to ${\text{Fe}}^{\text{III}}(\text{TPP})\left({{\text{O}}_2}^{•-}\right)$. This calculated barrier is an upper bound because it does not compensate for the errors in computing sulfonate group energetics. Taking into account these errors as discussed in the SI, the estimated lower bound of this barrier is about 17.0 kcal mol⁻¹. The energetic contributions for the energy change between 2 and TS* show that the transition-state energy is enthalpically driven. Additionally, in the transition state, the proton is closer to the acceptor ${\text{Fe}}^{\text{III}}(\text{TPP})\left({{\text{O}}_2}^{•-}\right)$ than the donor pTsOH···DMF, as evidenced by the O-H bond lengths in the optimized structure (Figure 7b). The kinetic isotope effect for this transition state was calculated using pTsOD-DMF as the proton donor, affording a KIE of 0.94 (Section 8 in the SI).

DISCUSSION OF THE MECHANISM OF ORR CATALYSIS BY FE(TPP)

The results of the spectroscopic, electrochemical, and computational experiments described above support the mechanism illustrated in Scheme 1. In this mechanism, Fc* or an electrode rapidly reduces [Fe^m(TPP)]OTf to the ferrous porphyrin, Fe^II(TPP). Fe^II(TPP) then binds O₂ reversibly $\left(K_{{\text{O}}_2}\right)$ to form the ferric superoxide, ${\text{Fe}}^{\text{III}}(\text{TPP})\left({{\text{O}}_2}^{•-}\right)$. The rate-determining step is the protonation of ${\text{Fe}}^{\text{III}}(\text{TPP})\left({{\text{O}}_2}^{•-}\right)\left(k_{\text{PT}}\right)$ to form the perhydroxyl-iron(III) complex, ${\left[{\text{Fe}}^{\text{III}}(\text{TPP})\left({\text{O}}_2{\text{H}}^{•}\right)\right]}^{+}.$ The perhydroxyl complex is rapidly reduced and protonated under the catalytic conditions to produce 2 equivalents of H₂O and restart the catalytic cycle. The evidence in support of this mechanism is discussed below.

The reduction of [Fe^m(TPP)]OTf to Fe^II(TPP), the first step in the proposed catalytic cycle, was found to be a fast pre-equilibrium between [Fe^III(TPP)]OTf and the reductant in both electrochemical and spectroscopic measurements. The cyclic voltammograms during electrocatalytic O₂ reduction fit well to a mechanism in which rapid pre-equilibrium electron transfer from the electrode $({[{\text{Fe}}^{\text{III}}(\text{TPP})]}^{+}+{\text{e}}^{-}\rightleftharpoons {\text{Fe}}^{\text{II}}(\text{TPP}))$ is followed by a rate-limiting catalytic step, k_obs (an EC′ mechanism). With Fc* as a chemical reductant, this pre-equilibrium is thermodynamically uphill in the standard state $\left(\mathrm{\Delta }{G^{°}}_{\text{ET}}=+1.01(8)\text{kcal}{\text{mol}}^{-1}\right).$ Spectroscopic studies of the reduction of [Fe^III(TPP)]OTf by Fc* at different temperatures have yielded the $\mathrm{\Delta }{H^{°}}_{\text{ET}}\text{and}\mathrm{\Delta }{S^{°}}_{\text{ET}}$ for this equilibrium (Results Section I). Those values are consistent with the electrochemically measured difference in reduction potentials between [Fe(TPP)]+/Fe^II(TPP) and ${\text{Fc}*}^{+/0}$ at ambient temperatures. In the room-temperature stopped-flow kinetics, the initial spectra show an almost complete reduction of [Fe^III(TPP)]OTf only because the starting concentration of Fc*+ is very small, ~0 mM, and the [Fc*]/[Fc*+] ratio is very large. As catalysis progresses, however, the ratio of Fc* to Fc*+ decreases, quickly shifting this equilibrium so that [Fe^III(TPP)]⁺ is the resting state of the catalyst for much, if not most, of the reaction (Figures 6 and S34–S49).

Spectroscopic experiments have also quantified the rapid pre-equilibrium O₂ binding to Fe^II(TPP), which is proposed to follow initial electron transfer. The distinct optical spectrum of ${\text{Fe}}^{\text{III}}(\text{TPP})\left({{\text{O}}_2}^{•-}\right)$ enabled measurements of the equilibrium constants for binding $\left(K_{{\text{O}}_2}\right)$ at low temperatures in the absence of reductant and acid. Low temperatures are required to avoid the decomposition of ${\text{Fe}}^{\text{III}}(\text{TPP})\left({{\text{O}}_2}^{•-}\right)$ to the well-known μ-oxo dimer.⁴² The measured $\mathrm{\Delta }{H^{°}}_{{\text{O}}_2}\text{and}\mathrm{\Delta }{S^{°}}_{{\text{O}}_2}$ could then be used to predict values of K_O2 at the higher temperatures of catalysis. The μ-oxo dimer is not formed under the catalytic conditions because of the presence of strong acid, as indicated by the reaction of independently prepared μ-oxo dimer with pTsOH (see SI, Section 5.4) and by prior reports.^49,50 Consistent with these equilibrium measurements, ${\text{Fe}}^{\text{III}}(\text{TPP})\left({{\text{O}}_2}^{•-}\right)$ is observed as the predominant initial catalyst resting state in catalytic stopped-flow experiments at low temperatures (e.g., 253 K). Under such conditions, [Fe^III(TPP)]OTf is completely converted to ${\text{Fe}}^{\text{III}}(\text{TPP})\left({{\text{O}}_2}^{•-}\right)$ within 0.1 s (Figure S29). As the reaction proceeds, both [O₂] and the ratio of $[\text{Fc}*]/[{\text{Fc}*}^{+}]$ decrease, leading to a change in the resting state from reduced porphyrin intermediates to ${[{\text{Fe}}^{\text{III}}(\text{TPP})]}^{+}$ (Figures 6 and S34–S49).

The kinetics of the electrocatalysis are not complicated by the shifts in the pre-equilibrium reduction or O₂-binding steps observed in the stopped flow data. The catalytic voltammo-grams are fit using FOWA, which yields rate constants for reactions catalyzed by the reduced Fe^II(TPP) catalyst resting state. Additionally, because the current is analyzed at the “foot” of the wave, the concentration of substrates in the reaction—diffusion layer is the same as the bulk solution (true pseudo-first-order conditions). For these reasons, the electrocatalytic kinetics yield a simple third-order rate law, as previously reported,³¹ obtained by removing the K_ET, [Fc*], and [Fc*⁺] terms from the complex rate law required for the stopped-flow data (eq 9). Despite the complex rate law using Fc* as a chemical reductant, the similarities between the k_cat values obtained electrochemically and chemically confirm that electron-transfer kinetics are not involved in the rate-limiting steps and remain a fast pre-equilibrium step under all conditions. Furthermore, the first-order dependences on O₂, pTsOH, and [Fe(TPP)] exclude bimolecular pathways involving peroxo (Fe–O₂–Fe) or μ-oxo (Fe–O–Fe) dimeric intermediates, pathways that are observed in the absence of strong acids.^51–54

Catalytic turnover requires the addition of four protons and three more electrons to ${\text{Fe}}^{\text{III}}(\text{TPP})\left({{\text{O}}_2}^{•-}\right)$, ultimately forming water and [Fe^III(TPP)]OTf. A number of initial steps could be imagined for this transformation, but only those which have an acid dependence were considered because the rate of the ORR is first order in [pTsOH]. Within that constraint, the two possible pathways for the reaction of the superoxide complex involve (i) proton transfer (PT) from pTsOH to form perhydroxyl or (ii) concerted proton-coupled electron transfer (CPET) with pTsOH and a reductant to give a hydroperoxo complex. While option ii should be thermodynamically advantageous, it is formally a termolecular CPET reaction and preassociation with the proton donor.^55,56 Because DFT calculations show that the preassociation of pTsOH with ${\text{Fe}}^{\text{III}}(\text{TPP})\left({{\text{O}}_2}^{•-}\right)$ is uphill by 8.5 kcal mol⁻¹ (Figure 7), pathway ii is unlikely, and rate-limiting proton transfer from pTsOH to ${\text{Fe}}^{\text{III}}(\text{TPP})\left({{\text{O}}_2}^{•-}\right)$ is the more plausible mechanism. Previous studies of ORR by Fe(TPP) under different conditions, using HClO₄ as the acid and in the presence of excess chloride, indicated a zeroth-order dependence of turnover frequency for the concentration of Fc*.³¹ In the model used successfully here (Scheme 2), the concentration of the electron donor appears only in the first pre-equilibrium. The rate-determining step cannot be CPET because that would require a molecule of reductant.

The strongest support for the proposed mechanism is the close agreement between the equilibrium parameters determined by COPASI fits to the stopped flow data and the directly measured equilibrium values of $\mathrm{\Delta }{H^{°}}_{\text{ET}}/\mathrm{\Delta }{S^{°}}_{\text{ET}}\text{and}\mathrm{\Delta }{H^{°}}_{{\text{O}}_2}/\mathrm{\Delta }{S^{°}}_{{\text{O}}_2}.$ In addition, the idealized third-order rate constant predicted by the COPASI fit, $(2-20)\times {10}^5{\text{M}}^{-2}{\text{s}}^{-1},$ is in excellent agreement with the value determined by electrocatalysis, $k_{\text{cat}}=(3.2-6.4)\times {10}^5{\text{M}}^{-2}{\text{s}}^{-1}.$

The computational conclusions qualitatively agree with the experimental results and show that proton transfer is the turnover-limiting step. The barrier extracted from the COPASI fits, $\mathrm{\Delta }{G^{‡}}_{\text{PT}}\cong 11\text{kcal}{\text{mol}}^{-1},$ is significant but smaller than the computed barrier. However, the COPASI barrier is higher than would be expected based on the k_PT derived from the electrochemical rate constant. Still, good agreement between theory and experiment was obtained for the change in barrier heights upon changing the acid from pTsOH to ${[\text{DMF}-\text{H}]}^{+}.$ The same value for this Bronsted $\alpha =\mathrm{\Delta }\mathrm{\Delta }{G^{‡}}_{\text{PT}}/\mathrm{\Delta }\mathrm{\Delta }{G^{°}}_{\text{PT}}=0.3$ was obtained from both experiment and theory.^32,33

In this system, both the computational and experimental results highlight the challenges of proton delivery to the iron—dioxygen adduct. Even when using a relatively strong proton donor such as pTsOH (pK_a = 2.3 in DMF), the protonation of ${\text{Fe}}^{\text{III}}(\text{TPP})\left({{\text{O}}_2}^{•-}\right)$ is computed to be uphill by >5 kcal mol⁻¹. This shows the poor basicity of ${\text{Fe}}^{\text{III}}(\text{TPP})\left({{\text{O}}_2}^{•-}\right)$, which has an estimated pK_a of −1.7 in DMF.³²

Beyond the endoergic nature of the proton-transfer step, the computations and experiments implicate a significant kinetic barrier for the protonation of ${\text{Fe}}^{\text{III}}(\text{TPP})\left({{\text{O}}_2}^{•-}\right)$. The computational results shown in Figure 7 allow k_PT to be expressed as the product of preassociation (K_assc, Figure 7a) and a unimolecular proton transfer step. The computed preassociation free energy of +8.6 kcal mol⁻¹ is due to the fact that the unfavorable entropy (−TΔS = 10.7 kcal mol⁻¹ at 298 K) and partial desolvation penalty for pTsOH···DMF (7.8 kcal mol⁻¹) are only partially offset by the hydrogen bonding between the superoxide moiety and pTsOH $(\mathrm{\Delta }E=-9.9\text{kcal}{\text{mol}}^{-1}).$ This unfavorable interaction contributed almost 50% to the overall reaction barrier height from ${\text{Fe}}^{\text{III}}(\text{TPP})\left({{\text{O}}_2}^{•-}\right)$ determined computationally. These results are consistent with the first-order dependence of k_obs on the [pTsOH] determined electrochemically (Figure 3b), which further supports the fact that the preassociation of the proton donor to ${\text{Fe}}^{\text{III}}(\text{TPP})\left({{\text{O}}_2}^{•-}\right)$ is unfavorable.

From the preassociated adduct, the transition state is achieved from a decrease in the O–H–O dihedral angle in the pTsOH···DMF adduct, yielding a species where the proton is shared among the $p{\text{TsO}}^{-},\text{DMF},$ and ${\text{Fe}}^{\text{III}}(\text{TPP})\left({{\text{O}}_2}^{•-}\right)$ oxygen atoms (Figure 7b). These results are consistent with a previous computational study that examined ${[\text{DMF}-\text{H}]}^{+}$ as the proton source.³² The calculated barrier for proton transfer to ${\text{Fe}}^{\text{III}}(\text{TPP})\left({{\text{O}}_2}^{•-}\right)$ is smaller with the stronger acid ${[\text{DMF}-\text{H}]}^{+},$ as expected. Still, even with the stronger cationic acid, preassociation is again unfavorable by >6 kcal mol⁻¹. As with pTsOH···DMF, there is a significant desolvation penalty for the ${[\text{DMF}-\text{H}]}^{+}···\text{DMF}$ proton donor that is not offset by hydrogen bonding to the ${\text{Fe}}^{\text{III}}(\text{TPP})\left({{\text{O}}_2}^{•-}\right)$ intermediate.

A surprising feature of this ORR mechanism is that the slow, turnover-limiting step is proton transfer from one oxygen atom to another. The proton donor is para-toluenesulfonic acid, pTsOH, and the oxygen acceptor is the superoxide complex, ${\text{Fe}}^{\text{III}}(\text{TPP})\left({{\text{O}}_2}^{•-}\right)$. Proton transfers between oxygen atoms are typically fast, although that is not always the case.^57–60 Physical organic studies of proton-transfer reactions have discussed preassociation, nonsynchronicity, and other factors to explain slow PT rate constants, particularly for carbon acids.^57,59,61,62

Taken together, these results suggest that barriers to proton transfer can be an important component of ORR catalysis in DMF and perhaps other polar organic solvents. Given that preassociation dynamics have been shown to play a major role in the catalytic rates of the reduction of H⁺ to H₂ by nickel phosphine—amine complexes,⁶³ our results suggest that preassociation for proton transfer to ${\text{Fe}}^{\text{III}}(\text{TPP})\left({{\text{O}}_2}^{•-}\right)$ may be more facile in media where the proton donor preferentially interacts with the ${\text{Fe}}^{\text{III}}(\text{TPP})\left({{\text{O}}_2}^{•-}\right)$ adduct over the solvent. These conditions may be realized by working with strong proton donors in solvents with dielectric constants lower than that of DMF or MeCN (e.g., THF, CH₂Cl₂). More broadly, using the medium to target preassociation dynamics could be a general approach to improving PCET reactions that are limited by proton-transfer steps, particularly for reactions containing nonpolar adducts, such as the ORR.

CONCLUSIONS

[Fe^III(TPP)]OTf is a rapid catalyst and electrocatalyst for the oxygen reduction reaction (ORR). This report describes a detailed mechanistic study of the catalytic chemical reduction of O₂ with decamethylferrocene (Fc*) and p-toluenesulfonic acid (pTsOH) in DMF, forming Fc*⁺, $p{\text{TsO}}^{-},$ and (predominantly) water. The various results indicate a mechanism initiated by pre-equilibrium electron transfer to form Fe^II(TPP), followed by O₂ binding to form the superoxide complex ${\text{Fe}}^{\text{III}}(\text{TPP})\left({{\text{O}}_2}^{•-}\right)$ in a second pre-equilibrium step. Both of these equilibria were studied independently as a function of temperature, and their equilibrium constants and enthalpies and entropies are reported. Optical stopped-flow monitoring of the reaction kinetics showed that the resting state of the iron catalyst varies substantially during the reactions and with temperature and reaction conditions. The complexity of the kinetics required global analysis of a large set of kinetic runs under different conditions using the COPASI software. This analysis gave an independent measure of the thermodynamic parameters for the pre-equilibria. The agreement between these kinetic-fit values and the directly measured equilibrium parameters provides very strong evidence for the proposed mechanism. In addition, parallel electrochemical kinetics showed complementary kinetic behavior and rate constants, further supporting the proposed mechanism.

The turnover-limiting step in catalysis is the protonation of ${\text{Fe}}^{\text{III}}(\text{TPP})\left({{\text{O}}_2}^{•-}\right)$. Computational studies of this step showed that there is substantial energetic cost to assembling the preassociation complex of the acid and ${\text{Fe}}^{\text{III}}(\text{TPP})\left({{\text{O}}_2}^{•-}\right)$ and that there is a substantial barrier to proton transfer within this complex. This study is a rare example of a mechanistic investigation of the ORR that directly observes and quantifies the pre-equilibria and rate-determining steps of three catalytic intermediates. The ability to correlate thermodynamic, chemical kinetic, electrochemical kinetic, and computational data provides an unusual level of detail about a multistep proton-coupled electron transfer catalytic process. In particular, the results highlight the importance of improving proton transfer dynamics during catalytic transformations involving nonpolar small-molecule adducts in organic solvents.