Abstract
In recent years, a consensus has emerged about the development of the ventral visual pathway in humans: although scene- and body-selective regions are mature by middle childhood, face-selective regions are not. This conclusion has rested primarily on comparisons of the relative size and univariate selectivity of these neural regions in both children and adults. In contrast, considerably less work has used multivariate methods, such as representational similarity analysis, to track the developmental trajectory of more distributed activation patterns within and across neural regions. Here, we scanned both children (ages 5–7) and adults to test the hypothesis that distributed representational patterns arise before category selectivity (for faces, bodies, or scenes) in the ventral pathway. Consistent with this hypothesis, we found mature representational patterns in several ventral pathway regions (e.g., FFA, PPA, etc.), even in children who showed no hint of the univariate selectivity. These results suggest that representational patterns emerge first in each region, perhaps forming a scaffold upon which univariate category selectivity can subsequently develop. More generally, our- findings demonstrate an important dissociation between category selectivity and distributed response patterns, and raise many questions about the relative roles of each in development and adult cognition.
1. Introduction
The functional organization of the ventral visual pathway is strikingly similar across people (Kanwisher, 2010), raising the obvious question of how this highly systematic structure arises in development (Golarai, 2007; Deen, 2017). A consensus has emerged that although some regions like the parahippocampal place area (PPA) and extrastriate body area (EBA) are adultlike by middle childhood (Golarai et al., 2010; Scherf et al., 2007; Peelen et al., 2009; Pelphrey et al., 2009, but see Golarai et al., 2007; Chai et al., 2010), the fusiform face area (FFA) is still developing at this age (Passarotti et al., 2003; Golarai et al., 2007; 2010; 2015; Scherf et al., 2007, 2011; Peelen et al., 2009; Natu et al., 2016; but see Pelphrey et al., 2009 and Cantlon et al., 2011). However, this work has focused almost exclusively on the relative size and univariate selectivity of these regions. By contrast, a growing literature in adults has argued that multivariate analyses can provide a richer, finer-grained characterization of the neural representations within and across cortical regions (Haxby et al., 2014; Kriegeskorte and Kievit, 2013). In particular, representational similarity analysis offers a window into the representations contained within a cortical region by comparing the similarities of the response patterns between all possible stimulus pairs. To the extent that this method can reveal neural representations, it should be an important tool for characterizing cortical development.
Here, we examined the developmental time course of pattern-based information using representational similarity matrices within and across regions of ventral visual cortex, and asked how they relate to the development of univariate category selectivity in these regions. Only a few studies have examined the development of representational similarity of the ventral visual pathway, finding that it is not adultlike at six months (Deen et al., 2017) but adultlike by age 7–11 (Golarai et al., 2010; 2015). Our study differs from these previous studies in two key respects: First, we tested 5 to 7 year-old children, an age between the infants and older children tested previously. Second, rather than exclusively examining large swaths of cortex, we quantified both representational similarity and univariate selectivity in numerous regions (e.g., FFA, PPA, EBA, etc.).
The central hypothesis tested in this study was that mature representational similarity patterns would arise before univariate selectivity in each cortical region. To test this hypothesis, we scanned adults and children with functional magnetic resonance imaging (fMRI) while they passively viewed a variety of object categories. For each participant, we first measured the size of several category-selective regions: FFA, PPA, EBA, as well as the occipital face area (OFA), the face selective portions of the superior temporal sulcus (STS), the occipital place area (OPA), and retrosplenial cortex (RSC). For each region we then selected every child with zero category-selective voxels for the defining contrast of that region, and we identified every adult with at least 100 category-selective voxels in each region. Within these participants, we asked whether the representational similarity patterns (i.e., the matrix of similarities in the pattern of responses across voxels between each pair of stimulus categories) were correlated between children and adults in each region. This procedure enabled us to ask whether children who lacked any voxels showing the defining univariate selectivity for a given region nonetheless showed mature representational similarity patterns in that region.
What might we predict about the relationship between category selectivity and representational similarity across development? One possibility is that the univariate structures arise first, with the finer-grained pattern information developing later. If this were true, we would expect to find extremely low correlations between children and adult similarity matrices because we explicitly selected the children with zero category-selective voxels. In contrast, our hypothesis that representational similarity precedes category selectivity within each region predicts strong correlations between children and adults using representational similarity analysis even in children with no category-selective voxels. Here, we found strong support for this second prediction for each region in the ventral visual pathway. This finding raises new questions about how these univariate structures and multivariate patterns develop, their relationship to each other, and their respective causal roles in development and behavior.
2. Materials and Methods
2.1. Subjects
We scanned 38 adults (mean 25.1 years old; standard deviation 4.48 years) and 41 children, ages 5–7 years old (mean 6.6 years old; standard deviation 0.91 years). Excessive amounts of motion in 4 of the children resulted in their data being excluded from all further analyses due to an inability to reconstruct the images. All participants had normal or corrected-to-normal vision and no known neurological or psychiatric conditions or structural brain abnormalities. Adult participants and the parents of children participants provided written, informed consent and all children gave verbal assent to participate in the experiment. The Massachusetts Institute of Technology (MIT) Institutional Review Board approved of all experimental protocols.
2.2. Stimuli
In order to hold the interest of children we used colored movie clips as stimuli, which showed movies of faces, bodies, scenes, objects, and scrambled objects (Pitcher et al., 2011). Movies of faces and bodies were filmed on a black background, and framed closeup so that only the faces or bodies of 7 children were visible as they danced, or played with toys or adults that were out of frame. The scene stimuli were mostly pastoral scenes shot from the window of a car that drove through suburbs. There were also some stimuli that were clips of flying over canyons or walking through tunnels. Moving objects were selected that minimized any suggestion of animacy of the object itself or of a hidden actor pushing the object. Examples of these objects included mobiles, windup toys, toy planes and tractors, balls rolling down sloped inclines. The scrambled objects were created by dividing each object clip into a 15×15 box grid and rearranging the location of each of the resulting frames. Finally, rather than using a stationary fixation point as baseline, we used six uniform color fields that were designed to maintain the interest of children, while approximating a fixation baseline condition by avoiding any patterned visual input. All stimuli were created using MATLAB and Psychtoolbox (Brainard, 1997; Pelli, 1997) and were presented by a liquid crystal display projector onto a screen in the scanner, which subjects viewed via a mirror attached to the head coil.
2.3. fMRI Acquisition
All participants were scanned using functional magnetic resonance imaging (fMRI) at the Athinoula A. Martinos Imaging Center at the McGovern Institute for Brain Research, MIT on a Siemens 3T MAGNETOM Trim Trio Scanner (Siemens AG Healthcare). Two weeks before a child’s visit, he or she received a CD and illustrated booklet that introduced the experimenters to the child, described the MRI procedure, and included recordings of scanner sounds. Earbuds similar to those the child would wear in the scanner were also included so that he or she could become accustomed to them. Parents were encouraged to review all materials with their child and asked to help him or her practice lying still while listening to the noises of the scanner. Immediately before their scanning session, all children were trained for 15 to 30 min in a “mock” scanner, designed to simulate the appearance, noise, and confinement of the actual scanner. During these training sessions, children practiced lying still while watching a movie. The movie was turned off by a motion tracking system any time children moved too much in order to teach them how still they had to be to get “good brain pictures.”
For the children, functional images were acquired using a custom made 32-channel phased array head-coil (Keil et al., 2011) optimized to the average head size of 5 to 7 year olds, and a gradient echo single-shot echo-planar imaging sequence (32 slices, repetition time (TR) = 2 s, echo time (TE) = 30 ms, voxel size = 3×3×3 mm, and 0.6 mm inter-slice gap). For the adults, functional imaging parameters were identical to the children, with the exception of using a commercially available Siemens 32-channel phased array head-coil, which is ideally suited for an adult head. For all scans, slices encompassed the whole brain aligned to the AC/PC line. Prior to each scan, four “dummy” scans were acquired and discarded to allow longitudinal magnetization to reach equilibrium. High-resolution T1-weighted anatomical images were also acquired for each participant.
2.4. Experimental Design
Functional data were acquired over four blocked-design functional runs lasting 234 seconds each. Each functional run contained three 18-second rest blocks, at the beginning, middle, and end of the run, during which a series of six uniform color fields were presented for three seconds each. Each run contained two sets of five consecutive stimulus blocks (i.e., faces, bodies, scenes, objects, or scrambled objects) sandwiched between the rest blocks, to make two blocks per stimulus category per run. Each block lasted 18 seconds and contained six 3-second movies clips from each of the five stimulus categories. The order of stimulus category blocks in each run was palindromic (e.g., fixation, faces, objects, scenes, bodies, scrambled objects, fixation, scrambled objects, bodies, scenes, objects, faces, fixation), and counterbalanced across runs. Participants were asked to passively view the stimuli.
2.5. fMRI Data Analysis
All fMRI data were analyzed using the Freesurfer software package (Dale et al., 1999; Fischl et al., 1999; 2001) and custom MATLAB scripts. Preprocessing steps included 3-dimensional motion correction, linear trend removal, temporal high-pass filtering (0.01 Hz cutoff), slice scan-time correction, and spatial smoothing (5 mm FWHM kernel). To ensure that this smoothing process did not artificially inflate our results, we also conducted a variety of key analyses on unsmoothed data (see Supplementary Data). In addition, both children and adult scans were spatially registered using the combined volume and surface-based (CVS) non-linear registration method (Postelnicu et al., 2009) via the T1-weighted MRI images. The surfaces were constructed from a 1 mm isotropic MPRAGE with real-time motion correction using nVas (van der Kouwe et al., 2008; Tisdall et al., 2012). This allowed for direct comparisons between the two groups since this transformation into a common space normalizes for absolute brain volume. All statistical analyses were based on the general linear model (GLM). GLM analyses all included boxcar regressors for each stimulus block, which were convolved with a gamma function to approximate the idealized hemodynamic response. For each experimental protocol, separate GLMs were computed for each participant, yielding regression-weights (i.e., beta maps) for each condition for each subject.
2.6. Defining, characterizing, and measuring category-selective regions of interest
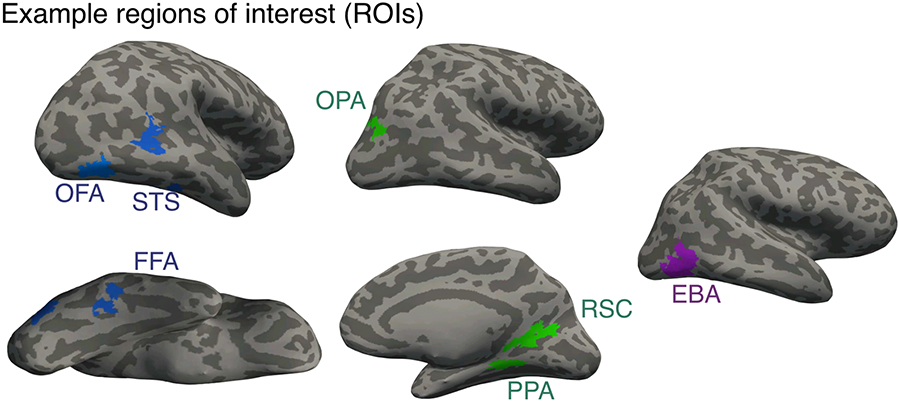
Because category-selective regions of interest (ROIs) are sometimes ambiguous, such as when a subject has two FFAs (Weiner and Grill-Spector, 2012), traditional methods of identifying functionally defined ROIs sometimes require judgment calls about which activation cluster should be taken as the ROI in question, raising the possibility of bias. To minimize the subjectivity inherent in hand picking ROIs, our primary analysis used an algorithmic method for ROI selection. All category-selective ROIs were defined using a Group-Constrained Subject Specific (GSS) Method (Fedorenko et al., 2010). This analysis is based on a previously published parcel atlas that was derived from 42 human subjects to constrain the definition of numerous ROIs (Julian et al., 2012). These parcels are identified as relatively large swaths of the cortical surface in which most subjects show activation for a particular contrast. Therefore, each of our category-selective ROIs was defined by conjoining contrast maps (e.g., faces vs. objects) with a particular parcel. The particular contrasts used to define our ROIs were faces vs. objects for FFA, OFA, and STS, scenes vs. objects for PPA, OPA, and RSC, and bodies vs. objects for EBA (Figure 2). In all cases, for our primary analyses, we combined regions across the two hemispheres to form one bilateral region of interest.. For all contrasts, we used a statistical threshold of P<0.001 uncorrected.
Figure 2.
Example of each of the category selective regions we identified on representative adult participants.
To define and characterize every ROI, two runs were always used to select the voxels for a particular region, while the remaining two runs were used to obtain an independent measure of the response profile of that region. When quantifying the volume of a region, we would measure the number of voxels that passed our statistical threshold within each subject for the odd runs and the even runs separately and then average them together. For example, in the FFA, if a participant had 500 significant voxels from the two odd runs and 300 significant voxels from the two even runs, we would ultimately say that participant has an average of 400 significant FFA voxels. Meanwhile, to characterize a region, we would use the held out runs (i.e., define on odd runs, measure on even runs; and define on even runs, and measure on odd runs), and the results from those analyses were then averaged together. These steps were taken to ensure that we avoided any issues of statistical non-independence: data used to define a region were never also used to characterize a region (Kriegeskorte et al., 2009; Vul et al., 2009).
2.8. Statistical analysis: Representational similarity analysis
To compare the similarity structures between adults and children, we used representational similarity analysis to compute a series of brain/brain correlations focused on a variety of subdivisions within the visual hierarchy. This analysis requires the formation of a representational similarity matrix from neural measures in both adults and children that could then be directly compared to one another (Kriegeskorte and Kievit, 2013). A representational similarity matrix is the set of pairwise similarities (i.e. correlations) between the pattern of response of voxels in a given region to two stimulus classes (e.g., the correlation across voxels between the patterns of response to faces and scenes in FFA). Once these similarity matrices were computed for each child and each adult, they were averaged within each group to create a child group similarity matrix and an adult group similarity matrix. We then measured the correlation between those group-level matrices. The statistical significance of the observed correlations between two correlation matrices, one from adults and the corresponding one from children, was assessed using group-level analyses. That is, the condition labels of the data of each group-level matrix were shuffled, the newly labeled matrices were correlated with one another, and the resulting correlation value was Fisher z-transformed. This procedure was repeated 10,000 times, resulting in a distribution of correlation values. A particular correlation between representational similarity matrices was considered significant if it fell within the top 5% of values in this distribution.
When correlating the representational similarity matrices between adults and children, it is possible that we would see artificially low correlations simply because of unreliable neural data. To assess this possibility, for every correlation we observed between adults and children, we also computed a reliability-adjusted correlation. The first step of computing these adjusted correlations requires determining the split-half reliability for each particular participant. To compute two similarity matrices, we would first use one set of runs (i.e., runs 1 and 3) to define an ROI and the other runs (i.e., runs 2 and 4) to generate a similarity matrix. We would then switch the runs to generate a second similarity matrix (i.e., define an ROI with runs 2 and 4 and generate the matrix with runs 1 and 3). The result of this process was an odd and even similarity matrix for each participant and ROI. Once these matrices were computed for each participant, they were averaged together to form a group level odd and even similarity matrix for both the adults and the children. Those group level odd and even similarity matrices were then correlated with one another to get an estimate of the reliability of the data for each group of participants. These correlation values were then adjusted using the Spearman-Brown formula to estimate the reliability of the full data set (Spearman, 1910; Brown, 1910). Finally, to adjust the observed correlations as a function of the reliability of the data, we used the correction for attenuation formula: the observed correlation between adults and children from a given neural region divided by the square root of the product of reliability of the data in that region from both adults and children (Nunnally and Bernstein, 1994; Cohen et al., 2017).
2.9. Similarity analysis in category-selective regions and participant selection
Rather than perform our analyses in every participant we scanned, we examined only those children who had zero category-selective voxels for each region and those adults who had at least 100 category-selective voxels for each region. The rationale for these selection criteria is as follows: If we find significant correlations between the representational similarity matrices of children and adults with these two groups, it would provide the strongest evidence that representational similarity precedes category selectivity in the ventral pathway. If, for example, we find strong correlations between children that do not have a single FFA voxel and adults that have at least 100 FFA voxels, then it suggests that distributed representational structures develop before category-selective regions, since there are no category-selective voxels in these particular children.
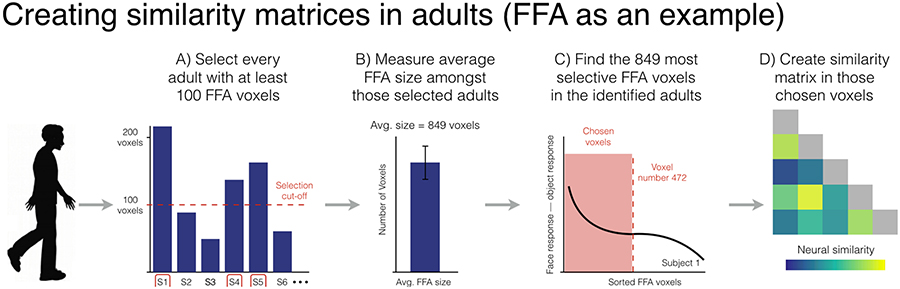
To select the voxels we want to use for these analyses, we first counted the number of category-selective voxels in each individual adult and only selected those adults with at least 100 voxels (Figure 3A). Once we identified those adults, we then computed the average number of category-selective voxels within that group (Figure 3B). In the case of the FFA, we found that our selected adults had on average 849 significant voxels. Then, in order to have the same number of voxels across individuals, we went back to our contrast maps and selected the same number of voxels for each individual. Thus, for the FFA, this meant selecting the 849 most face-selective voxels in each individual adult (Figure 3C). It should be noted that in some cases this meant selecting some voxels that did not reach statistical significance in some people and excluding some voxels that did reach statistical significance in others. For example, imagine a participant with only 800 significant FFA voxels (P<0.001 uncorrected). To get to 849 voxels, we chose those significant 800 voxels and we also chose the 49 voxels with the lowest P-values even though those values were all P>0.001. Conversely, imagine a participant with 900 significant FFA voxels. To get to 849 voxels with this participant, we would excluded the 51 voxels with the lowest P-values even though those voxels all had P-values that were still P<0.001. It was with these selected voxels that we would create a similarity matrix (Figure 3D) for each individual participant, which we then averaged together to make a single group-level matrix for the adults.
Figure 3.
Visualization of the method used to form representational similarity matrices in adults. In this case, we use the FFA as an example. A) First, we measured the size of the FFA in every adult and only selected adults with at least 100 voxels. B) Then we determined the average size of the FFA across the selected adults (i.e., 849 voxels). C) Next, we selected the top 849 voxels in every adult such that we had the exact same number of voxels in every participant. D) Once those voxels were selected, we created a similarity matrix in each individual participant, which we then averaged together across participants to make one adult group-level matrix.
Once we identified the adults we wanted to examine and determined how many voxels were in each category-selective region for those adults, we then selected our children and the voxels we want to use within those children. Since the goal of our analyses is to examine representational similarity in children with no category-selective voxels, the first step of this process is to identify every child that has zero category-selective voxels in a given region, again with a threshold of P<0.0001 uncorrected (Figure 4A). We then consulted the number of category-selective voxels we found in a given region amongst the adults that we selected above (Figure 4B). In the case of the FFA, for example, we found an average of 849 FFA voxels. Similar to the procedure described above, we then selected that exact number of voxels in every child even though none of those voxels were above our statistical threshold. (Figure 4C). In other words, we selected the 849 most “selective” FFA voxels in children in spite of the fact that none of those voxels are reliably more responsive to faces than objects.
Figure 4.
Visualization of the method used to form representational similarity matrices in children. A) First, we measured the size of the FFA in every child and only selected children with 0 voxels. B) Then we consulted how many FFA voxels we found across our group of selected adults (i.e., 849 voxels). C) Next, we selected the top 849 voxels in every child (even though none of those voxels reached statistical significance) such that we had the exact same number of voxels in every participant. D) Once those voxels were selected, we created a similarity matrix in each individual participant, which we then averaged together across participants to make one child group-level matrix.
It should be noted that even though we selected voxels in the children that did not significantly respond to faces over objects, it is still possible that once grouped together across participants, we would still find significant activation to the preferred category over objects in a particular region. For example, imagine that every FFA voxel we selected in children had a hypothetical P-value of 0.06 in terms of faces vs. objects. In that case, while no single voxel is significantly responsive to faces, once averaged together within and across participants, it is likely we would find that the group-level response to faces is greater than the group-level response to objects. Such a finding would defeat the purpose of these analyses, as the primary goal is to identify children that have zero category selectivity. Thus, with the selected children, we performed group-level comparisons of the average response to faces/scenes/bodies and the average response to objects. If the overall difference between the selected category and objects was P<0.50, we removed the participants with the greatest effect size until we reached P>0.50 for the group. This procedure was intended to ensure that we not only had selected individual children with no category-selective voxels, but that the children we did analyze did not even have a trend of a significant preference as a group for the selected category over objects in the different category-selective regions. Once we identified those children and those voxels in every individual child, we then performed our similarity analyses within those voxels for each child and then averaged them together to form a group similarity matrix that we could compare to adults (Figure 4D).
3. Results
3.1. Size of category-selective region and participant selection
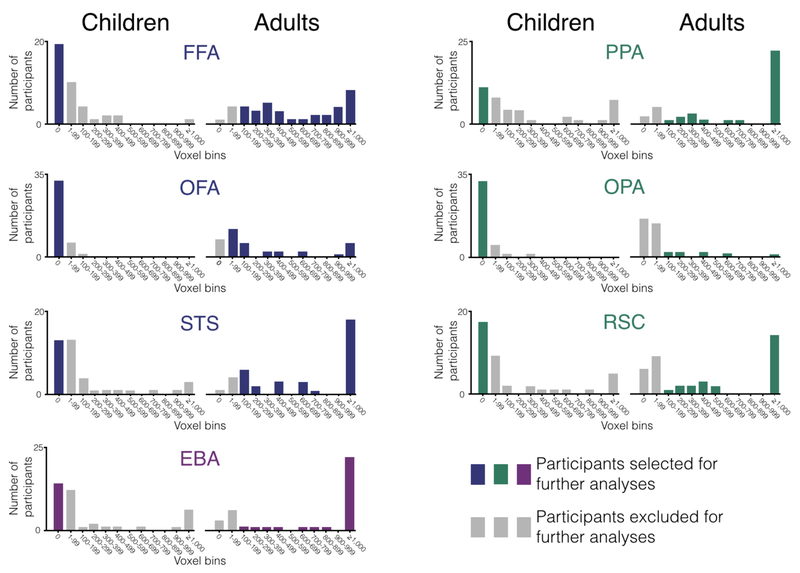
The number of significant voxels we found in each child and adult for each of our seven category selective-regions is presented below (Figure 5). For the children, this resulted in the selection of 19 participants for the FFA, 31 for the OFA, 13 for the STS, 11 for the PPA, 32 for the OPA, 17 for the RSC, and 14 for the EBA. For the adults, this resulted in the selection of 33 participants for the FFA, 19 for the OFA, 33 for the STS, 29 for the EBA, 31 for the PPA, 8 for the OPA, and 23 for the RSC.
Figure 5.
Summary distribution of the size of the category-selective regions in every participant. On the x-axis of every plot is a series of voxel bins in which we group the number of voxels into discrete bins of 100 voxels. On the y-axis is the number of participants whose category-selective region land within a given bin. Across all plots, the colored bars mark the participants selected for further analyses (i.e., children with no category-selective voxels and adults with at least 100 category-selective voxels), while the grey bars mark participants excluded for further analyses (i.e., children with any category-selective voxels and adults with fewer than 100 category selective voxels).
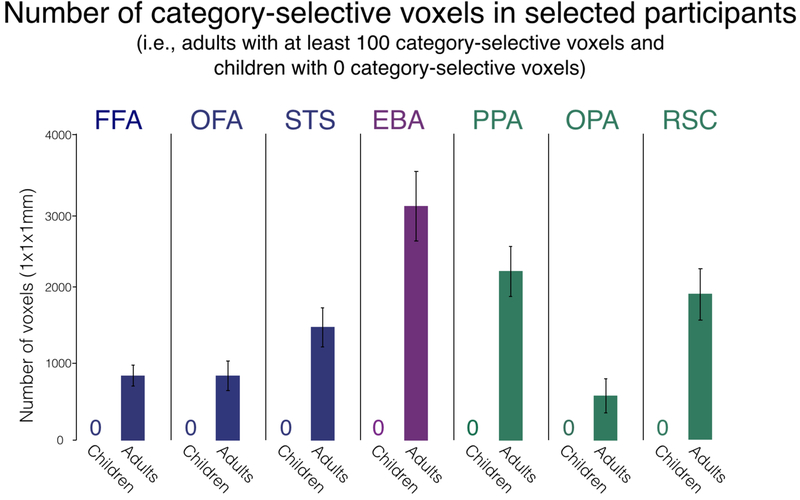
Overall, this selection process resulted in our identifying a group of adults within each category-selective region with an average total of 849 voxels in the FFA, 836 in the OFA, 1,463 in the STS, 2,257 in the PPA, 561 in the OPA, 1,901 in the RSC, and 3,056 in the EBA (Figure 6). Naturally, since we selected children with no category-selective voxels, there was an average of zero category-selective voxels in each region.
Figure 6.
Size of each category-selective region. The number of voxels in each region was measured for both children and adults and is shown here on the y-axis. Each region was defined using a statistical threshold of P<0.001 uncorrected. There are no bars for the children since we purposefully selected children with no category-selective voxels. The error bars for adults denote the standard error of the mean.
3.2. Response properties of category selective regions
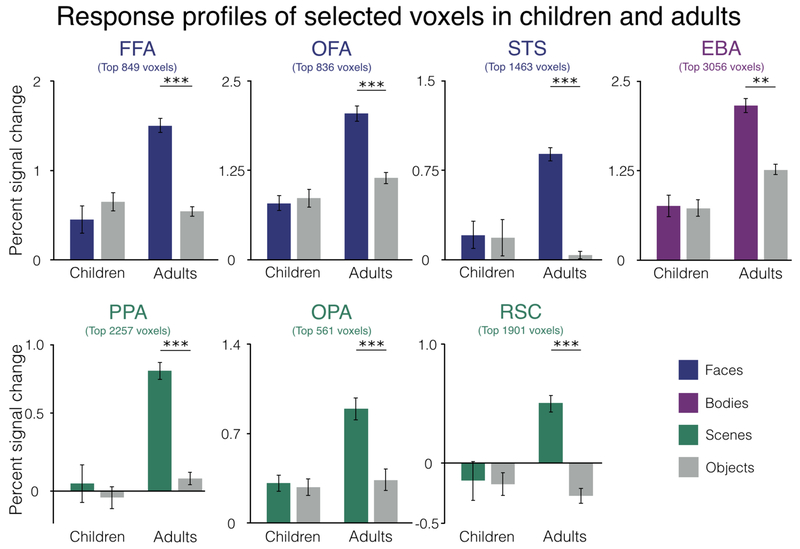
Even though we selected children with no category-selective voxels, it is still possible that on average, the response to the selective category (e.g., scenes in PPA or bodies in EBA) will still be significantly higher than to the control category (objects) in the group analysis. Indeed, we found this exact pattern of results in several of our category-selective regions in children: PPA: t(10)=2.32, P<0.05; OPA: t(31)=2.62, P<0.01; RSC: t(16)=3.70, P<0.01. For OFA, STS, and EBA, the selective category (i.e., faces and bodies) were not significantly greater than objects: OFA: t(30)=0.68, P=0.50; STS: t(12)=0.91, P=0.38; EBA: t(13)=1.66 P=0.12. Interestingly, in FFA, we actually found that the response to objects was slightly higher than the response to faces in the children selected with zero FFA voxels, though this effect was not significant (FFA: t(18)=1.25, P=0.23). For those category-selective regions in which the difference between the preferred category and objects was P<0.50, we identified the children with the largest preferences for the selective category over objects (i.e., faces greater than objects in OFA, bodies greater than objects in EBA) and removed them one by one until we obtained P>0.50. After removing certain subjects, all category-selective regions showed no preference for the selective category over objects in children: STS: t(10)=0.17, P=0.87; EBA: t(10)=0.30, P=0.77; PPA: t(6)=0.52, P=0.62; OPA: t(24)=0.57, P=0.58; RSC: t(6)=0.42, P=0.69. Meanwhile, in adults, each region showed a strong preference for the selective category relative to objects: FFA: t(32)=7.26, P<0.001; OFA: t(18)=13.48, P<0.001; STS: t(32)=14.58, P<0.001; EBA: t(28)=19.23, P<0.001; PPA: t(30)=15.39, P<0.001; OPA: t(7)=7.88, P<0.001; RSC: t(22)=12.41, P<0.001 (Figure 7).
Figure 7.
Univariate responses to selective categories (i.e., faces in FFA, OFA, and STS, bodies in EBA, and scenes in PPA, OPA, and RSC) in the selected voxels of children and adults. These data show the responses in each group after iteratively removing any children until the group analysis across children showed no univariate selectivity for the region-defining contrast. In all cases, the grey bars are the response in those regions to objects, while the colored bar are the response to the preferred category for the region in question, in data independent of those used to define the region. Percent signal change is represented on the y-axis. **P<0.01, ***P<0.001
3.3. Representational similarity in category selective regions
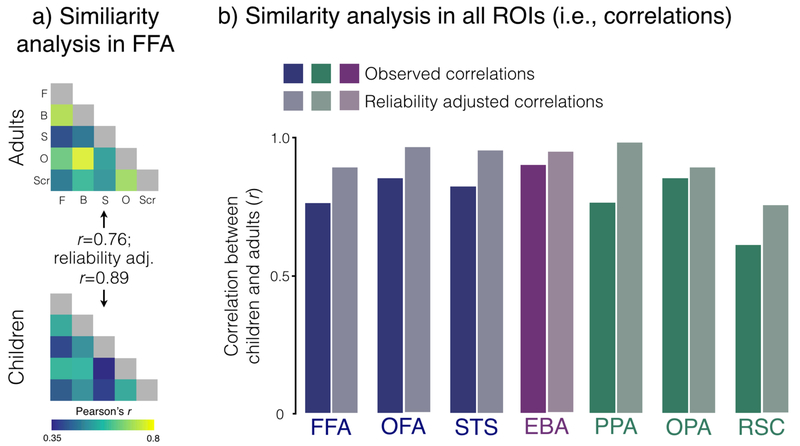
Once we identified a group of children with no discernable category selectivity and a group of adults with strong selectivity (Figures 6 and 7), we then asked if there is a significant correlation between the representational similarity matrices of these two groups. Again, to perform this analysis in children, we selected the most “selective” voxels for each region even though none of those voxels responded significantly more to the preferred category for that region than to objects. To determine how many voxels to select, we used the size of the adults’ category-selective regions as our benchmark (i.e., the top 849 voxels in FFA since on average the adults had 849 FFA voxels). After selecting these voxels in both groups, we created representational similarity matrices by correlating the responses for each pairing of categories across all voxels in a particular neural region (e.g., the correlation across voxels between the patterns of response to faces and scenes in FFA, etc.).
Our results were unambiguous. In every category-selective region, we found strong correlations between childrens’ and adults’ matrices: FFA: r=76, P<0.05, reliability-adjusted r=0.89; OFA: r=0.85, P<0.05, reliability-adjusted r=0.96; STS: r=0.82, P<0.05, reliability-adjusted r=0.95; EBA: r=0.90, P<0.05, reliability-adjusted r=0.94; PPA: r=0.76, P<0.05, reliability-adjusted r=0.98; OPA: r=0.85, P<0.05, reliability-adjusted r=0.89 (Figure 8). The one region in which there was a trend, of a correlation that did not reach significance was in RSC (r=0.60, P=0.05). However, this relatively low correlation is likely due to unreliable data since the reliability-adjusted correlation is also quite high (r=0.75). Taken together, these data strongly suggest that even in children with no discernable selectivity for the defining contrast for that region, distributed representational structures are already mature in those regions.
Figure 8.
Representational similarity analysis comparing children and adults. A) Visualization of the similarity matrices based on distributed activation patterns in the FFA voxels in adults (top matrix) and children (bottom matrix). Each cell corresponds to the correlation of the activation patterns within a particular region for two stimulus categories (e.g., the correlation between the pattern of response across voxels to objects and bodies in FFA, etc.). B) Correlations between children and adults in each of our neural regions. The y-axis shows the correlation between the two groups. For each neural region, the saturated bar represents the observed correlation between children and adults while the desaturated bar represents the reliability adjusted correlation (see Methods).
Because we found such strong correlations between adult and child similarity matrices in every category-selective region, a natural question is whether these regions have different representational structures from one another. Are the strong correlations between adults and children across all category-selective regions driven by a common representational structure? Or do the different regions have dissociable structures that vary across the cortex? To address these questions, we calculated the correlations between each of our neural regions within our two groups (i.e., correlate FFA and PPA within children, or EBA and RSC within adults, etc.). In children, approximately two thirds of the neural regions were not significantly correlated with one another: 15 out of 21 possible pairings. In adults, meanwhile, approximately half of the neural regions were not correlated with one another: 10 out of 21 possible pairings. Thus, while there appears to be some common representational structures between certain neural regions, it does not appear as if our strong correlations between adults and children are driven entirely by our measuring one single structure.
3.4. Does category selectivity ever precede representational similarity?
We have focused so far on the development of representational similarity amongst a group of children who were specifically chosen because they have no discernable selectivity on the defining contrast for the region in question. We have shown that despite their total lack of univariate category selectivity, these children nonetheless show mature representational similarity patterns in the same regions. Is the opposite true? Do children who have no representational similarity with adults have any hint of category selectivity? To answer this question, we first correlated the matrix from each individual child from our original group (N=37) with the group-level adult similarity matrix, for each category selective region. We then selected every child whose individual correlation with the adults was r ≤ 0.00 in the region in question (i.e., one group of children were selected for FFA, another for PPA, etc.). Next, we measured the average size of the category-selective regions in the selected group of children using a statistical threshold of P<0.001 uncorrected. Overall, we found that for children that did not show a positively correlated representational similarity pattern in the region in question, the size of the category-selective region was never significantly greater than 0 (FFA: 88 voxels, t(7)=1.62, P=0.15; OFA: 7 voxels, t(10)=1.06, P=0.31; STS: 69 voxels, t(7)=1.64, P=0.15; PPA: 42 voxels, t(2)=1.0, P=0.42; OPA: 1 voxel, t(4)=1.0, P=0.36; RSC: 55 voxels, t(5)=1.10, P=0.32; EBA: 200 voxels, t(4)=1.18, P=0.30). In other words, this analysis revealed that children who have not developed any representational structures that are correlated with adults have also not begun to develop category-selective regions (e.g., FFA, PPA, EBA, etc.). Thus, representational similarity patterns are present in children who lack the corresponding univariate selectivity for the region in question, but not vice versa. Of course, these analyses should be interpreted with some caution since for several regions we were only able to identify a small number of children whose similarity matrices were negatively correlated with adults (e.g., PPA). However, the fact that so few children are negatively correlated with adults is itself consistent with our broader claim that distributed activation patterns mature earlier than category selective regions.
4. Discussion
Here, we report a developmental dissociation between univariate category selectivity and distributed similarity patterns: even in children that have no discernable selectivity for the defining contrast of a given region (e.g., no voxels that respond significantly more to faces than objects in the FFA), the representational similarity patterns in that region are already mature. These findings highlight a key dissociation in the development of the human visual system: rather than developing in perfect sync with one another, each region’s fine-grained activation patterns apparently develop before that region’s defining univariate selectivity. These results are consistent with those of Golarai and colleagues (2010; 2015), who showed more mature representational similarity across the ventral visual pathway in 7–11 year old children. However, our findings build on the earlier results by further showing that this more mature representational similarity a) is present at the younger age of 5–7, b) exists within each developing category-selective region, and c) is present even when the defining category selectivity of a region is absent altogether. These results reveal an important dissociation between category selectivity and representational similarity
Our findings raise numerous questions. First, what is the precise time-course of the development of distributed representational structures in the ventral visual pathway? Deen and colleagues (2017) showed that representational similarity structures are very different from adults at 6 months of age, so they could mature any time between infancy and the 5–7 year old range studied here. Second, what are the neurobiological mechanisms that construct representational similarity during development? Third, given that representational similarity appears to mature first, does it play a causal role in the development of category selectivity? None of these important questions is answerable with the current data set, but in principle all could be addressed in future work.
A major obstacle in speculating about these questions comes from the fact that we do not understand the relative significance and causal roles of representational similarity and univariate selectivity, or their neurobiological basis, even in adults. Empirically, univariate selectivity in the ventral visual pathway is among the most robust and replicated phenomena in human cognitive neuroscience, and extensive evidence shows that category-selective regions play specific causal roles in behavior (Wada and Yamamoto, 2001; Pitcher et al., 2008; Dilks et al., 2013; Schalk et al., 2017). But computationally, we do not know what goal might be served by category selectivity of specific neural populations, or by the spatial clustering of these neural populations at a sufficient grain to produce category-selective regions detectable with fMRI. Similarly, representational similarity patterns are robust and widely replicated. However, the window they offer into neural/mental representations and their causal role in behavior is unclear. The fact that a given stimulus classification can be performed based on patterns of response across voxels within a particular region of cortex does not guarantee that this information is used (i.e. read out by other brain regions Williams et al., 2007). Although representational similarity is sometimes correlated with behavior (e.g., Cohen et al., 2014; 2015; 2017), evidence from patients and stimulation studies raise questions about its causal role. For example, despite the many studies showing decoding abilities and replicable similarity matrices for non-faces objects in the FFA, intracranial electrical stimulation of the FFA appears to affect only face percepts, not the perception of non-face objects (Parvizi et al., 2012; Schalk et al., 2017), suggesting that the pattern information about non-face objects in the FFA may not be causally related to perceptual experience.
Even if representational similarity is sometimes epiphenomenal in terms of its role in adult perception and cognition, it may nonetheless play an important role in development. But how differences in representational similarity could lead to a later change in the univariate selectivity of a given region is far from clear. One possibility is that early-developing representational similarity in the ventral pathway reflects a “protomap” of cortical organization that serves as a scaffold upon which further development is built (Hasson et al., 2002; Deen et al., 2017, Livingstone et al., 2017). These representational similarities could further reflect retinotopic and featural biases (e.g., for curvature versus rectilinearity) inherited from earlier stages of visual processing, with these biases determining which regions of the ventral pathway will take on which function. Of course, it may be that representational similarity plays a relatively minor role in determining a region’s selectivity. Instead, that role may be better accomplished by structural connectivity, which develops very early, varies systematically across functionally different regions (Saygin et al., 2012; Osher et al., 2015), and in at least one case identifies the locus of a functionally distinct region before that region’s univariate selectivity arises (Saygin et al 2016).
The many questions raised by this study about the role of representational similarity in development can be addressed in future work by deriving more detailed similarity matrices from a larger set of stimulus types both within and between categories. Richer matrices might reveal differences between adults and children that were not evident in our study. It will also be important to scan children between the ages of 6 months and five years to learn more about the timeline of the development of representational similarity structures across distributed populations of voxels and neurons. Finally, to understand the role of distributed activation patterns in development, we need to better understand its causal role in adult perception, including the fundamental question of the spatial scale of the neural codes that are read out in behavior.
Figure 1.
Sample stimuli. Example frames from movies used as dynamic stimuli
Acknowledgements
This study was supported by funds from the Ellison Medical Foundation. Thanks to Harris Hoke for assistance with data analysis and Caroline Robertson and Leyla Isik for helpful comments on the project.
Footnotes
Note: this version is not the absolute most final version f the paper, but it is close.
References
- Brainard DH, 1997. The Psychophysics Toolbox. Spat. Vis 10, 433–436. [PubMed] [Google Scholar]
- Cantlon JF, Pinel P, Dehaene S, Pelphrey KA, 2011. Cortical representations of symbols, objects, and faces are pruned back during early childhood. Cereb. Cortex 21, 191–1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chai XJ, Ofen N, Jacobs LF, Gabrieli JDE 2010. Scene complexity: influence on perception, memory, and development in the medial temporal lobe. Front. Hum. Neuro 4, 21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen MA, Konkle T, Rhee J, Nakayama K, Alvarez GA, 2014. Processing multiple visual objects is limited by overlap in neural channels. Proc. Natl. Acad. Sci 111, 8955–8960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen MA, Nakayama K, Konkle T, Stantic M, Alvarez GA, 2015. Visual awareness is limited, by the representational architecture of the visual system. J. Cogn. Neuro 27, 2240–2252. [DOI] [PubMed] [Google Scholar]
- Cohen MA, Alvarez GA, Nakayama K, Konkle T, 2017. Visual search for object categories can be predicted across all of higher-level visual cortex. J. Neurophysiol 117, 388–402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dale AM, Fischl B, Sereno MI 1999. Cortical surface-based analysis. I. Segmentation and surface reconstruction. Neuroimage 9, 179–194. [DOI] [PubMed] [Google Scholar]
- Deen B, Richardson H, Dilks DD, Takahashi A, Keil B, Wald LL, Kanwisher N, Saxe R, 2017. Organization of high-level visual cortex in human infants. Nat. Commun 8, 13995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Desikan RS, Segonne F, Fischl B, Quinn BT, Dickerson BC, Blacker D, Buckner RL, Dale AM, Maguire RP, Hyman BT, Albert MS, Killiany RJ, 2006. An automated labeling system for subdividing the human cerebral cortex on MRI scans into gyral based regions of interest. Neuroimage 31, 968–980. [DOI] [PubMed] [Google Scholar]
- Dilks DD, Julian JB, Paunov AB, Kanwisher N, 2013. The occipital place area is causally and selectively involved in scene perception. J. Neurosci 33, 1331–1336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fedorenko E, Hsieh P-J, Nieto-Castanon A, Whitfield-Gabrieli S, Kanwisher N, 2010. A new method for fMRI investigations of language: Defining ROIs functionally in individual subjects. J. Neurophysiol 104, 1177–1194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischl B, Sereno MI, Dale AM, 1999a. Cortical surface-based analysis II: Inflation, flattening, and a surface-based coordinate system. Neuroimage 9, 195–207. [DOI] [PubMed] [Google Scholar]
- Fischl B, Liu A, Dale AM, 2001. Automated manifold surgery, constructing geometrically accurate and topologically correct models of the human cerebral cortex. I.E.E.E. Trans. Med. Imaging, 20, 70–80. [DOI] [PubMed] [Google Scholar]
- Golarai G, Ghahremani DG, Whitfield-Gabrieli S, Reiss A, Eberhardt JL, Gabrieli JD, Grill-Spector K, 2007. Differential development of high-level visual cortex correlates with category-specific recognition memory. Nat. Neuro 10, 512–22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golarai G, Liberman A, Yoon JMD, Grill-Spector K, 2010. Differential development of the ventral visual cortex extends through adolescence. Front. Hum. Neurosci 3, 80. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golarai G, Liberman A, Grill-Spector K, 2015. Experience shapes the development of neural substrates of face processing in human ventral temporal cortex. Cereb. Cortex 27, 1229–1244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hasson U, Levy I, Behrmann M, Hendler T, Malach R, 2002. Eccentricity bias as an organizing principle for human high-order object areas. Neuron 34, 479–490. [DOI] [PubMed] [Google Scholar]
- Haxby JV, Connolly AC, Guntupalli JS, 2014. Decoding neural representational spaces using multivariate pattern analysis. Annu. Rev. Neurosci 4, 435–456. [DOI] [PubMed] [Google Scholar]
- Julian JB, Fedorenko E, Webster J, Kanwisher N, 2012. An algorithmic method for functionally defining regions of interest in the ventral visual pathway. Neuroimage 60, 2357–2364. [DOI] [PubMed] [Google Scholar]
- Kamps FS, Morris E, & Dilks DD (2019). A face is more than just the eyes, nose, and mouth: fMRI evidence that face-selective cortex represents external features. NeuroImage, 184, 90–100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kanwisher N, 2010. Functional specificity in the human brain: a window in- to the functional architecture of the mind. Proc. Natl. Acad. Sci 107, 11163–11170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keil B, Alagappan V, Mareyam A, McNab JA, Fujimoto K, Tountcheva V, Triantafyllou C, Dilks DD, Kanwisher N, Lin W, Grant PE, Wald LL, 2011. Size-optimized 32-channel brain arrays for 3 T pediatric imaging. Magn. Reson. Med 66, 1777–1787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koldewyn K, Yendiki A, Weigelt S, Gweon H, Julian J, Richardson H, Malloy C, Saxe R, Fischl B, Kanwisher N, 2014. Differences in the right inferior longitudinal fasciculus but no general disruption of white matter tracts in children with autism spectrum disorder. Proc. Natl. Acad. Sci 111, 1981–1986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Konkle T, Caramazza A 2013. Tripartite organization of the ventral stream by animacy and object size. J. Neurosci 33, 10235–10242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kriegeskorte N, Mur M, Ruff DA, Kiani R, Bodurka J, Esteky H, Tanaka K, Bandettini PA, 2008. Matching categorical object representations in inferior temporal cortex of man and monkey. Neuron. 60, 1126–1141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kriegeskorte N, Mur M, Bandettini P, 2008. Representational similarity analysis-connecting the branches of systems neuroscience. Front. Sys. Neurosci 2, 4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kriegeksorte N, Simmons WK, Bellgowan PSF, Baker CI, 2009. Circular analysis in systems neuroscience, the dangers of double dipping. Nat. Neuro 12, 535–540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kriegeskorte N, Kievit RA, 2013. Representational geometry, integrating cognition, computation, and the brain. Trends. Cogn. Sci 17, 401–412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Livingstone MS, Vincent JL, Arcaro MJ, Srihasam K, Schade PF, Savage T, 2017. Development of the macaque face-patch system. Nat. Comm 8, 14897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Natu VS, Barnett MA, Hartley J, Gomez J, Stigliani A, Grill-Spector K, 2016. Development of neural sensitivity to face identity correlates with perceptual discriminability. J. Neurosi 36, 10893–10907 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nishimoto S, Vu AT, Naselaris T, Benjamini Y, Yu B, Gallant JL 2011. Reconstructing visual experiences from brain activity evoked by natural movies. Curr. Biol 21, 1641–1646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Norman-Haignere S, Albouy P, Caclin A, McDermott JH, Kanwisher N, Tillmann B, 2016. Pitch-responsive cortical regions in congenital amusia. J. Neurosci 36, 2986–2994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Osher DE, Saxe R, Koldewyn K, Gabrieli JDE, Kanwisher N, Saygin ZM, 2016. Structural connectivity fingerprints predict cortical selectivity for multiple visual categories across cortex. Cereb. Cortex 26, 1668–1683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parvizi J, Jacques C, Foster BL, Withoft N, Rangarajan V, Weiner KS, Grill-Spector K, 2012. Electrical stimulation of human fusiform face-selective regions distorts face perception. J. Neurosci 32, 14915–14920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Passarotti AM, Paul BM, Bussiere JR, Buxton RB, Wong EC, Stiles J, 2003. The development of face and location processing, An fMRI study. Dev. Sci 6, 100–117. [Google Scholar]
- Peelen MV, Glaser B, Vuilleumier P, Eliez S, 2009. Differential development of selectivity for faces and bodies in the fusiform gyrus. Dev. Sci F16–F25. [DOI] [PubMed] [Google Scholar]
- Pelli DG 1997. The VideoToolbox software for visual psychophysics: transforming numbers into movies. Spat. Vis 10, 437–442. [PubMed] [Google Scholar]
- Pelphrey KA, Lopez J, Morris JP, 2009. Developmental continuity and change in responses to social and nonsocial categories in human extrastriate visual cortex. Front. Hum. Neurosci 3, 25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pitcher D, Charles L, Devlin JT, Walsh V, Duchaine B, 2008. Triple dissociation of faces, bodies, and objects in extrastriate cortex. Curr. Biol 19, 319–324. [DOI] [PubMed] [Google Scholar]
- Pitcher D, Dilks DD, Saxe R, Triantafyllou C, Kanwisher K, 2011. Differential selectivity for dynamic versus static information in face-selective cortical regions. Neuroimage 56, 2356–2363. [DOI] [PubMed] [Google Scholar]
- Postelnicu G, Zollei L, Fischl B, 2009. Combined volumetric and surface registration. I.E.E.E. Trans. Med. Imaging 28, 508–522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saugin ZM, Osher DE, Norton ES, Youssoufian DA, Beach SD, Feather J, Gaab N, Gabrieli JDE, Kanwisher N, 2016. Connectivity precedes function in the development of the visual word form area. Nat. Neuro 19, 1250–1255 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saygin ZM, Osher DE, Koldewyn K, Reynolds G, Gabrieli JDE, Saxe RR, 2012. Anatmoical connectivity patterns predict face-selectivity in the fusiform gyrus. Nat. Neuro 15, 321–327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schalk G, Kapeller C, Guger C, Ogama H, Hiroshima S, Lafer-Sousa R, Saygin Z, Kamada K, Kanwisher N, 2017. Facephenes and rainbows: Causal evidence for functional and anatomical specificity of face and color processing in the human brain. Proc. Natl. Acad. Sci 114, 12285–12290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scherf KS, Behrmann M, Humphreys K, Luna B, 2007. Visual category-selectivity for faces, places, and objects emerges along different developmental trajectories. Dev. Sci 10, F15–F30. [DOI] [PubMed] [Google Scholar]
- Scherf KS, Luna B, Avidan G, Behrmann M, 2011. “What” precedes “which”, Developmental neural tuning in face- and place-related cortex. Cereb. Cortex 21, 1963–1980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tisdall MD, Hess AT, Reuter M, Meintjes EM, Fischl B, van der Kouwe AJ, 2012. Volumentric navigators for prospective motion correction and selective reacquisition in neuroanatomical MRI. Magn. Reson. Med 68, 389–399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van der Kouwe AJW, Benner T, Salat DH, Fischl B, 2008. Brain morphometry with multiecho MPRAGE. Neuroimage 40, 559–569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vul E, Harris C, Winkielman P, Pashler H, 2009. Puzzilingly high correlations in fMRI studies of emotion, personality, and social cognition. Perspect. Psychol. Sci 4, 274–290. [DOI] [PubMed] [Google Scholar]
- Wada Y, Yamamoto T, 2001. Selective impairment of facial recognition due to a haematoma restricted to the right fusiform and lateral occipital region. J. Neurol. Neurosurg. Psychiatry 71, 254–257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wiener K, Grill-Spector K, 2012. The improbable simplicity of the fusiform face area. Trends. Cogn. Sci 16, 251–254. [DOI] [PubMed] [Google Scholar]