Distinguishing genetic correlation from causation across 52 diseases and complex traits

Abstract

Mendelian randomization (MR), a method to infer causal relationships, is confounded by genetic correlations reflecting shared etiology. We developed a model in which a latent causal variable (LCV) mediates the genetic correlation; trait 1 is partially genetically causal for trait 2 if it is strongly genetically correlated with the LCV, quantified using the genetic causality proportion (gcp). We fit this model using mixed fourth moments $E({\alpha }_1^2{\alpha }_1{\alpha }_2)$ and $E({\alpha }_2^2{\alpha }_1{\alpha }_2)$ of marginal effect sizes for each trait; if trait 1 is causal for trait 2, then SNPs affecting trait 1 (large ${\alpha }_1^2$) will have correlated effects on trait 2 (large α₁α₂), but not vice versa. In simulations, our method avoided false positives due to genetic correlations, unlike MR. Across 52 traits (average N=331k), we identified 30 causal relationships with high gcp estimates. Novel findings included a causal effect of LDL on bone mineral density, consistent with clinical trials of statins in osteoporosis.

Introduction

Mendelian Randomization (MR) is widely used to identify potential causal relationships among heritable traits, potentially leading to new disease interventions[1-12]. Genetic variants that are significantly associated with one trait, the ``exposure," are used as genetic instruments to test for a causal effect on a second trait, the ``outcome." If the exposure is causal, then variants affecting the exposure should affect the outcome proportionally. For example, LDL[3, 13] and triglycerides[4] (but not HDL[3]) causally affect coronary artery disease risk. However, pleiotropy presents a challenge for MR, especially when it produces a genetic correlation and when the exposure is highly polygenic[2,11,12,14-16]. Sometimes, this challenge can be addressed using curated genetic variants without pleiotropic effects; this approach is most appropriate for molecular traits (e.g. LDL). For other complex traits, statistical approaches have been used to reduce the likelihood of confounding, such as MR-Egger [7] and bidirectional MR [11,17,18]. However, these approaches have their own limitations.

We introduce a latent causal variable (LCV) model, under which the genetic correlation between two traits is mediated by a latent variable having a causal effect on each trait. We define trait 1 as partially genetically causal for trait 2 when it is strongly correlated with the causal variable, implying that part of the genetic component of trait 1 is causal for trait 2. We quantify partial causality using the genetic causality proportion. We showed in simulations that LCV has major advantages over MR methods, and we applied it to 52 diseases and complex traits.

Results

Overview of methods

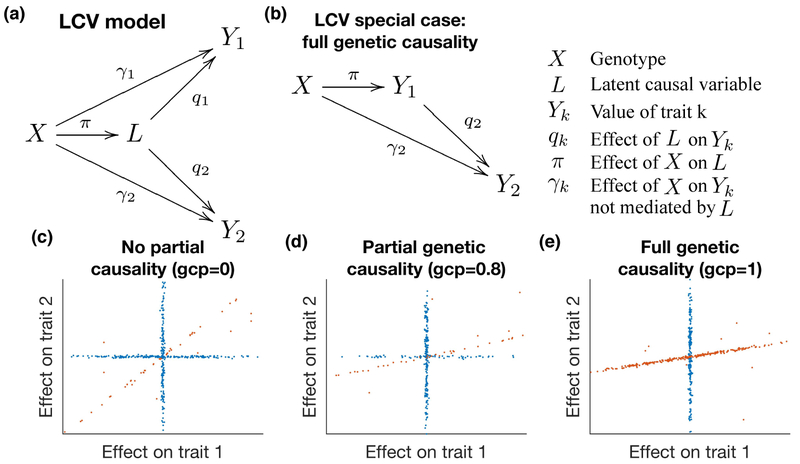
The latent causal variable (LCV) model is based on a latent variable L that mediates the genetic correlation between the two traits (Figure 1a). Under the LCV model, trait 1 is fully genetically causal for trait 2 if it is perfectly genetically correlated with L; ``fully" means that the entire genetic component of trait 1 is causal for trait 2 (Figure 1b). More generally, trait 1 is partially genetically causal for trait 2 if the latent variable has a stronger genetic correlation with trait 1 than with trait 2; ``partially" means that part of the genetic component of trait 1 is causal for trait 2. In order to quantify partial causality, we define the genetic causality proportion (gcp) of trait 1 on trait 2. The gcp ranges between 0 (no partial genetic causality) and 1 (full genetic causality). A high value of gcp (even if it is not exactly 1) implies that interventions targeting trait 1 are likely to affect trait 2. An intermediate value implies that some interventions targeting trait 1 may affect trait 2. (However, we caution that an intervention may fail to mimic genetic perturbations, e.g. due to its timing relative to disease progression.) For example, a recent study suggested either a fully causal effect of age at menarche (AAM) on height or a shared hormonal pathway affecting both traits[11]. If this shared pathway (modeled by L) has a large effect on AAM but a small effect on height, then AAM would be strictly partially genetically causal for height. Indeed, LCV produced an intermediate gcp estimate ($\widehat{\text{gcp}}$ = 0.43(0.10), see below). We caution that low gcp estimates are not evidence of full genetic causality, and we refer to trait pairs with low gcp estimates as having limited partial genetic causality. LCV p-values test the null hypothesis that gcp=0, and a highly significant p-value does not imply a high gcp.

Figure 1:

Illustration of the latent causal variable model. We display the relationship between genotypes X, latent causal variable L and trait values Y₁ and Y₂. (a) Full LCV model. The genetic correlation between traits Y₁ and Y₂ is mediated by L, which has normalized effects q₁ and q₂ on each trait. (See Supplementary Table 17 for a list of random variables vs. parameters.) (b) When q₁ = 1, Y₁ is perfectly genetically correlated with L (so L does not need to be shown in the diagram), and we say that Y₁ is fully genetically causal for Y₂. (c) Example genetic architecture of genetically correlated traits with no genetic causality (gcp = 0, i.e. q₂ = q₁ < 1). Slight noise is added to SNP effects for illustration. Orange SNPs have correlated effects on both traits via L, while blue SNPs do not. (d) Example genetic architecture of genetically correlated traits with partial genetic causality (gcp = 0.8, i.e. q₂ < q₁ < 1). (e) Example genetic architecture of genetically correlated traits with full genetic causality (gcp = 1, i.e. q₂ < q₁ = 1).

In order to test for partial genetic causality and to estimate the gcp, we exploit the fact that if trait 1 is partially genetically causal for trait 2, then most SNPs affecting trait 1 will have proportional effects on trait 2, but not vice versa (Figure 1c-e). Instead of using thresholds to select subsets of SNPs[11], we compare the mixed fourth moments $E({\alpha }_1^2{\alpha }_1{\alpha }_2)$ and $E({\alpha }_2^2{\alpha }_1{\alpha }_2)$ of marginal effect sizes for each trait. The rationale for utilizing these mixed fourth moments is that if trait 1 is causal for trait 2, then SNPs with large effects on trait 1 (large ${\alpha }_1^2$) will have proportional effects on trait 2 (large α₁α₂), so that $E({\alpha }_1^2{\alpha }_1{\alpha }_2)$ will be large; conversely, SNPs with large effects on trait 2 (large ${\alpha }_2^2$) will generally not affect trait 1 (small α₁α₂), so that $E({\alpha }_2^2{\alpha }_1{\alpha }_2)$ will be smaller. Thus, estimates of the mixed fourth moments can be used to test for partial genetic causality and to estimate the gcp. We note that LCV, unlike MR, does not distinguish between the “exposure” and the “outcome”; trait 1 and trait 2 are interchangeable labels.

LCV assumes that joint effect size distribution for two traits is a sum of two independent distributions: (1) a shared genetic component corresponding to L, whose values are proportional for both traits; and (2) a distribution that does not contribute to the genetic correlation (see Methods). We interpret the first distribution as ``mediated" effects (corresponding to π; Figure 1a) and the second distribution as ``direct" effects (corresponding to γ). The LCV model assumption is strictly weaker than the ``exclusion restriction" assumption of MR (see Methods).

Under the LCV model, the genetic causality proportion is defined as the number x such that:

$$\frac{q_2^2}{q_1^2}=({\rho }_g^2{)}^x,$$ (1)

where q_k is the normalized effect of L on trait k (Figure 1a), and ρ_g is the genetic correlation[16] (note that ρ_g = q₁q₂). When the gcp is equal to 1, trait 1 is fully genetically causal for trait 2; when it is positive but less than 1, trait 1 is partially genetically causal. When it is negative, trait 2 is partially genetically causal. The gcp can be defined without making LCV (or other) model assumptions (see Methods).

In order to estimate the gcp, we utilize the following relationship between the mixed fourth moments of the marginal effect size distribution and the parameters q₁ and q₂:

$$E({\alpha }_1^3{\alpha }_2)={\kappa }_{\pi }{q}_1^3{q}_2+3{\rho }_g,$$ (2)

where π is the effect of a SNP on L and κ_π = E(π⁴) − 3 is the excess kurtosis of π (see Methods). This equation implies that if $\mid E({\alpha }_1^3{\alpha }_2)\mid \ge \mid E({\alpha }_1{\alpha }_2^3)\mid$, then $q_1^2\ge q_2^2$ and gcp ≥ 0.

We calculate statistics S(x) for each possible value of gcp=x, using equation (2). These statistics also depend on the heritability[19], the genetic correlation[16], and the cross-trait LDSC intercept[19]. We estimate the variance of these statistics using a block jackknife and obtain an approximate likelihood function for the gcp. We compute a posterior mean gcp estimate (and a posterior standard deviation) using a uniform prior. We test the null hypothesis (that gcp=0) using S(0). Details of the method are provided in the Methods section. We have released open source software implementing the LCV method (see URLs).

Simulations

To compare the calibration and power of LCV with existing causal inference methods, we performed a wide range of null and causal simulations involving simulated summary statistics with no LD. We compared four main methods: LCV, random-effect two-sample MR[5,9] (denoted MR), MR-Egger[7], and Bidirectional MR[11] (see Methods). We also compared with the weighted median estimator (MR-WME)[8] and mode-based estimator (MR-MBE)[10] (whose performance was roughly similar to MR and to MR-Egger respectively; results using these methods are reported in supplementary tables). We applied each method to simulated GWAS summary statistics (N=100k individuals in each of two non-overlapping cohorts; M=50k independent SNPs[20]) for two heritable traits (h²=0.3), generated under the LCV model. LCV uses LD score regression [19]; for simulations with no LD, we use constrained-intercept LD score regression (simulations with LD are described below). A detailed description of all simulations is provided in the Supplementary Note, and simulation parameters are described in Supplementary Table 1.

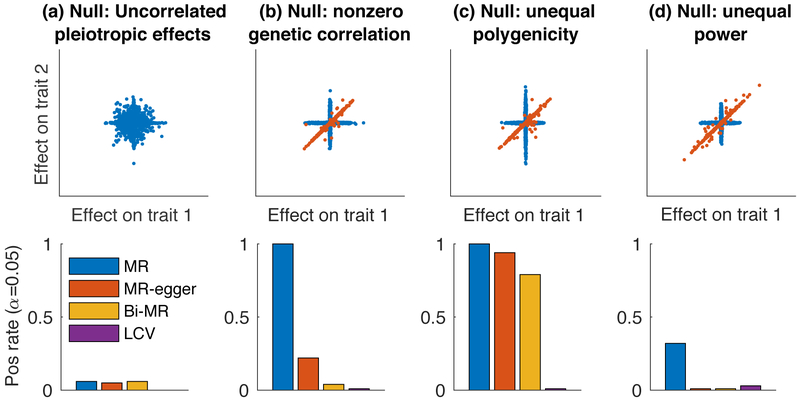
First, we performed null simulations (gcp=0) with uncorrelated pleiotropic effects (via γ; Figure 1a) and zero genetic correlation. 1% of SNPs were causal for both traits (with independent effect sizes, explaining 20% of heritability for each trait), and 4% of SNPs were causal for each trait exclusively (Figure 2a, Supplementary Table 2a-d). LCV produced conservative p-values (0.0% false positive rate at α = 0.05); our normalization of the test statistic can lead to conservative p-values when the genetic correlation is low (see Methods). All three main MR methods produced well-calibrated p-values. Even though the ``exclusion restriction" assumption of MR is violated here, these results confirm that uncorrelated pleiotropic effects do not confound random-effect MR at large sample sizes[21]. (Such pleiotropy is known to cause false positives if a less conservative fixed-effect approach is used[22].) In these simulations, all methods except LCV used the set of approximately 170 SNPs (on average) that were genome-wide significant (p < 5 × 10⁻⁸) for trait 1 (or approximately 330 SNPs that were genome-wide significant for either trait, in the case of Bidirectional MR).

Figure 2:

Null simulations with no LD to assess calibration. We compared LCV to three main MR methods (two-sample MR, MR-Egger and Bidirectional MR). We report the positive rate (α = 0.05) for a causal (or partially causal) effect. Scatterplots illustrate the bivariate effect size distribution. (a) Null simulation (gcp=0) with uncorrelated pleiotropic effects and zero genetic correlation. (b) Null simulation with nonzero genetic correlation. (c) Null simulation with nonzero genetic correlation and differential polygenicity between the two traits. (d) Null simulation with nonzero genetic correlation and differential power for the two traits. Results for each panel are based on 4000 simulations. Numerical results are reported in Supplementary Table 1.

Second, we performed null simulations with a nonzero genetic correlation. 1% of SNPs had causal effects on L, and L had effects $q_1=q_2=\sqrt{0.2}$ on each trait (so that ρ_g = 0.2). 4% of SNPs were causal for each trait exclusively (Figure 2b, Supplementary Table 2). MR and MR-Egger both produced excess false positives, while Bidirectional MR and LCV produced well-calibrated p-values. These simulations violate the MR-Egger assumption that the magnitude of pleiotropic effects on trait 2 are independent of the magnitude of effects on trait 1 (the ``InSIDE" assumption) [7], as SNPs with larger effects on L have larger effects on both trait 1 and trait 2 on average, consistent with known limitations [22].

Third, we performed null simulations with a nonzero genetic correlation and differential polygenicity in the non-shared genetic architecture between the two traits. 1% of SNPs were causal for L with effects $q_1=q_2=\sqrt{0.2}$ on each trait, 2% were causal for trait 1 but not trait 2, and 8% were causal for trait 2 but not trait 1 (Figure 2c, Table S2h-j). Thus, the likelihood that a SNP would be genome-wide significant was higher for causal SNPs affecting trait 1 only than for causal SNPs affecting trait 2 only. As a result of this imbalance, Bidirectional MR (as well as other MR Methods) produced excess false positives, unlike LCV.

Fourth, we performed null simulations with a nonzero genetic correlation and differential power for the two traits, reducing the sample size from 100k to 20k for trait 2. 0.5% of SNPs were causal for L with effects $q_1=q_2=\sqrt{0.5}$ on each trait, and 8% were causal for each trait exclusively (Figure 2d, Table S2k-m). Because per-SNP heritability was higher for shared causal SNPs than for non-shared causal SNPs, shared causal SNPs were more likely to reach genome-wide significance in the smaller trait 1 sample (N=20k), leading to a similar imbalance as in Figure 2c. As a result, Bidirectional MR (as well as other MR Methods) produced excess false positives, while LCV produced well-calibrated p-values.

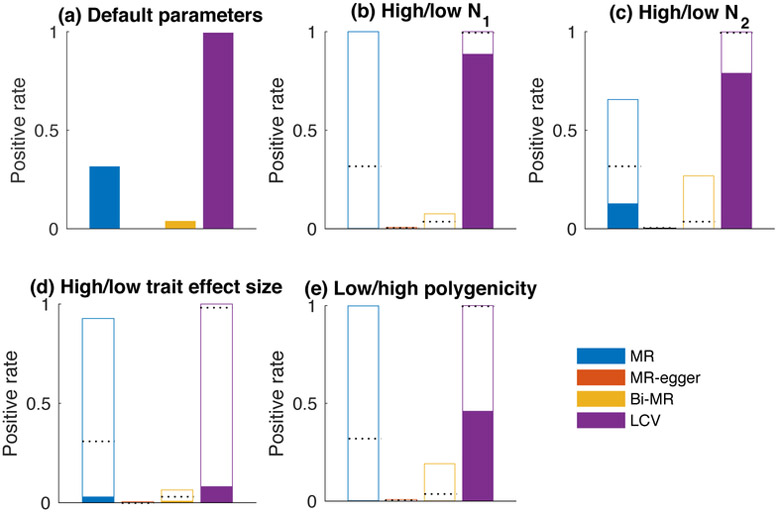
Next, we performed causal simulations (with full genetic causality) to assess whether LCV is well-powered to detect a causal effect. We caution that LCV had lower power in simulations with LD (see below). First, we chose a set of default parameters: N=25k for each trait, 5% of SNPs causal for trait 1 (the causal trait), a (fully) causal effect of size q₂ = 0.2 of trait 1 on trait 2, and 5% of SNPs causal for trait 2 only (Figure 3a). There were ~15 genome-wide significant SNPs on average, explaining ~2% of h². LCV was well-powered to detect a causal effect at α = 0.001, while MR had lower power and bidirectional MR and MR-Egger had low power.

Figure 3:

Causal simulations with no LD to assess power. We compared LCV to three main MR methods (two-sample MR, MR-Egger and Bidirectional MR). We report the positive rate (α = 0.001) for a causal (or partially causal) effect. (a) Causal simulations with default parameters: N₁ = N₂ = 25k; M = 50k; q₁ = 1, q₂ = 0.2 (results also displayed as dashed lines in panels b-e). (b) Higher (unfilled) or lower (filled) sample size for trait 1 (N₁ = 50k and N₁ = 12.5k respectively). (c) Higher (unfilled) or lower (filled) sample size for trait 2 (N₂ = 50k and N₂ = 12.5k respectively). (d) Higher (unfilled) or lower (filled) causal effect size of trait 1 on trait 2 (q₂ = 0.4 and q₂ = 0.1 respectively). (e) Lower (unfilled) or higher (filled) polygenicity for trait 1. Results for each panel are based on 1000 simulations. Numerical results are reported in Supplementary Table 3.

Second, we reduced the sample size for trait 1 (Figure 3b, Supplementary Table 3b-d), finding that LCV had high power while the MR methods had very low power, owing to the small number of genome-wide significant SNPs. We caution that for real traits, heritability estimates can be noisy at very low sample size, potentially leading to unreliable results (see below).

Third, we reduced the sample size for trait 2 (Figure 3c, Supplementary Table 3e-g). LCV had high power, while other methods had low power. The effect of trait 2 sample size on MR power was more modest than the effect of trait 1 sample size, suggesting that the number of genome-wide significant SNPs (ascertained using trait 1) is the primary limiting factor for MR power.

Fourth, we reduced the causal effect size of trait 1 on trait 2 (Figure 3d and Supplementary Table 3h-j). LCV had low power, and other methods had very low power. Fifth, we increased the polygenicity of the causal trait (Figure 3e, Supplementary Table 3k-m). LCV had moderate power while the MR methods had very low power, again owing to the low number of genome-wide significant SNPs. We also simulated a partially genetically causal relationship (gcp=0.25-0.75), with similar results (Supplementary Table 3p-r). We compared our gcp estimates in fully causal simulations with our gcp estimates in partially causal simulations, finding that LCV reliably distinguished the two cases, unlike existing methods (Supplementary Table 3a,p-r).

In order to investigate potential limitations of our approach, we performed null and causal simulations under genetic architectures that violate LCV model assumptions. These simulations and their results are described in detail in the Supplementary Note. We simulated four types of LCV model violations: (1) null simulations with a bivariate Gaussian mixture model, where one of the mixture components generates imperfectly correlated effect sizes on the two traits; (2) null simulations with two latent causal variables; (3) causal simulations with a bivariate Gaussian mixture model; and (4) causal simulations with an additional latent confounder. LCV produced well-calibrated p-values under models of type (1) (Supplementary Figure 1a-c); in addition, these simulations recapitulated the limitations of existing methods (Figure 2). Models of type (2) sometimes caused LCV (and existing Methods) to produce false positives (Supplementary Figure 1d-e); however, extreme values of the simulation parameters were required in order for LCV to produce high gcp estimates, implying that results with high gcp estimates are extremely unlikely to be false positives (Supplementary Figure 2). Causal models of type (3-4) lead to reduced power for LCV (and other Methods) (Supplementary Figure 1f-g), as well as downwardly biased gcp estimates for LCV (Supplementary Tables 4-5).

Next, we performed simulations with real LD patterns to further assess the robustness of the LCV method. These simulations and their results are described in detail in the Supplementary Note. In null simulations with a wide range of parameter settings, LCV produced approximately well-calibrated or conservative false positive rates, except for simulations at low sample size with noisy heritability estimates (Supplementary Table 6 a-s and Supplementary Table 7). (We exclude real datasets with noisy heritability estimates). We determined that LCV can be confounded by uncorrected population stratification (Supplementary Table 8). In non-null simulations, LCV was usually well-powered to detect a causal or partially causal effect (Supplementary Table 6 t-bb). In simulations with a range of gcp values, we determined that our posterior mean gcp estimates are approximately unbiased and that our posterior standard errors are approximately well-calibrated (Supplementary Figure 3 and Supplementary Table 9).

Application to real traits

We applied LCV and the MR methods to GWAS summary statistics for 52 diseases and complex traits, including summary statistics for 37 UK Biobank traits[27,28] computed using BOLT-LMM[29] (average N=429k) and 15 other traits (average N=54k) (see Supplementary Table 10 and Methods). These traits were selected based on the significance of their heritability estimates (Z_h > 7), and trait pairs with very high genetic correlations (∣ρ_g > 0.9) were pruned. As in previous work, we excluded the MHC region from all analyses, due to its unusually large effect sizes and long-range LD patterns[19].

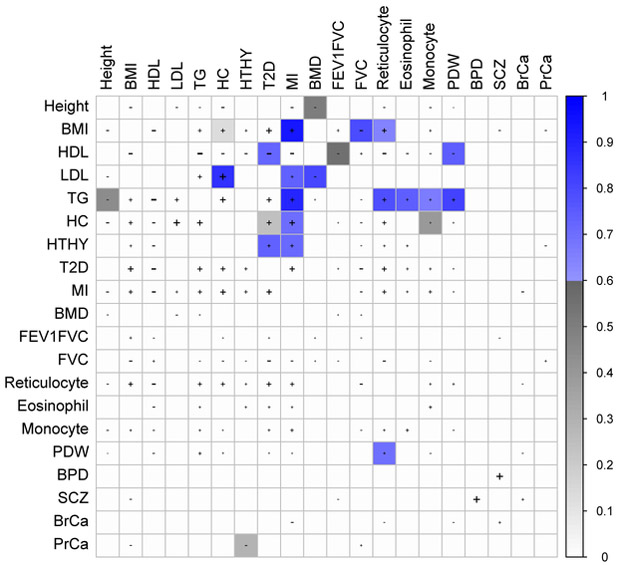
We applied LCV to the 429 trait pairs (32% of all trait pairs) with a nominally significant genetic correlation (p<0.05), detecting significant evidence of full or partial genetic causality for 59 trait pairs (FDR < 1%), including 30 trait pairs with $\widehat{\text{gcp}}>0.6$. We primarily focus on trait pairs with high gcp estimates, which have greater biological interest (and are extremely unlikely to be false positives; see Simulations). Results for selected trait pairs are displayed in Figure 4; results for the 30 trait pairs with $\widehat{\text{gcp}}>0.6$ are reported in Table 1; results for all 59 significant trait pairs are reported in Supplementary Table 11; and results for all 429 genetically correlated trait pairs are reported in Supplementary Table 12. To investigate the possibility that these results could be affected by model misspecification, we developed an auxiliary test for partial genetic causality that does not rely on LCV model assumptions (Supplementary Note). This test, though underpowered, produces highly concordant results on these trait pairs, confirming that LCV is unlikely to be affected by model misspecification

Figure 4:

Partially or fully genetically causal relationships between selected complex traits. Shaded squares indicate significant evidence for a causal or partially causal effect of the row trait on the column trait (FDR <1%). Color scale indicates posterior mean $\widehat{\text{gcp}}$ for the effect of the row trait on the column trait; blue color indicates $\widehat{\text{gcp}}$ > 0.6, grey color indicates $\widehat{\text{gcp}}$ < 0.6. ``+" or ``−" signs indicate trait pairs with a nominally significant (positive or negative) genetic correlation (p<.05), and the size of the "+" or "-" size is proportional to the genetic correlation. Results for the 30 trait pairs with $\widehat{\text{gcp}}>0.6$ are reported in Table 1, results for all 59 significant trait pairs are reported in Supplementary Table 11, and results for all 429 genetically correlated trait pairs are reported in Supplementary Table 12. HTHY: hypothyroidism. FG: fasting glucose. PDW: platelet distribution width. BPD: bipolar disorder. SCZ: schizophrenia. BrCa: breast cancer: PrCa: prostate cancer.

Table 1:

Fully or partially genetically causal relationships between complex traits. We report all significant trait pairs (1% FDR) with high gcp estimates ($\widehat{\text{gcp}}>0.6$). p_LCV is the p-value for the null hypothesis of no partial genetic causality; ${\widehat{\rho }}_g$ is the estimated genetic correlation, with standard error; $\widehat{\text{gcp}}$ is the posterior mean estimated genetic causality proportion, with posterior standard error. We provide references for all MR studies supporting causal relationships between these traits that we are currently aware of. Results for all 59 significant trait pairs are reported in Supplementary Table 11, and results for all 429 genetically correlated trait pairs are reported in Supplementary Table 12.

Trait 1	Trait 2	pLCV	${\widehat{\rho }}_g$ (std err)	$\widehat{\text{gcp}}$ (std err)	MR ref
Triglycerides	Hypertension	1 × 10−38	0.25 (0.04)	0.95 (0.04)
BMI	Heart attack	5 × 10−9	0.34 (0.09)	0.94 (0.11)	[32,38]
Triglycerides	Heart attack	2 × 10−31	0.30 (0.06)	0.90 (0.08)	[4]
Triglycerides	BP – systolic	1 × 10−40	0.13 (0.03)	0.89 (0.08)
HDL	Hypertension	1 × 10−21	−0.29 (0.06)	0.87 (0.09)
LDL	Hi cholesterol	2 × 10−6	0.77 (0.07)	0.86 (0.11)
Triglycerides	Mean cell volume	2 × 10−18	−0.20 (0.04)	0.86 (0.11)
Triglycerides	BP – diastolic	9 × 10−39	0.11 (0.04)	0.86 (0.10)
Mean platelet volume	Platelet count	1 × 10−9	−0.66 (0.03)	0.84 (0.10)
BMI	Hypertension	3 × 10−16	0.38 (0.03)	0.83 (0.11)	[11,38]
Triglycerides	Platelet distribution width	1 × 10−16	0.19 (0.04)	0.81 (0.13)
LDL	Bone mineral density – heel	7 × 10−34	−0.12 (0.05)	0.80 (0.12)
BMI	FVC	9 × 10−13	−0.22 (0.03)	0.79 (0.17)
Hi cholesterol	RBC count	0.002	0.08 (0.03)	0.79 (0.15)
Triglycerides	Reticulocyte count	5 × 10−10	0.33 (0.05)	0.79 (0.14)
Type 2 Diabetes	Mean cell volume	0.004	−0.15 (0.03)	0.77 (0.20)
HDL	RBC count	0.003	−0.13 (0.05)	0.76 (0.34)
Triglycerides	Eosinophil count	6 × 10−17	0.14 (0.05)	0.75 (0.16)
Balding4	Number children – male	3 × 10−30	−0.16 (0.05)	0.75 (0.13)
HDL	Platelet distribution width	2 × 10−16	−0.14 (0.04)	0.75 (0.16)
RBC distribution width	Type 2 Diabetes	7 × 10−4	0.11 (0.03)	0.73 (0.19)
LDL	Heart attack	4 × 10−31	0.17 (0.08)	0.73 (0.13)	[3,13]
Hi cholesterol	Lymphocyte count	0.004	0.18 (0.04)	0.73 (0.22)
Platelet distribution width	Platelet count	2 × 10−7	−0.47 (0.04)	0.73 (0.15)
Hypothyroidism	Type 2 Diabetes	4 × 10−4	0.22 (0.05)	0.73 (0.29)
HDL	Type 2 Diabetes	5 × 10−7	−0.40 (0.06)	0.72 (0.17)
Heart attack	Breast cancer	0.01	−0.16 (0.05)	0.72 (0.24)
Hypothyroidism	Heart attack	1 × 10−11	0.26 (0.05)	0.72 (0.16)
Hi cholesterol	Heart attack	5 × 10−4	0.52 (0.12)	0.71 (0.19)
HDL	BP – diastolic	9 × 10−17	−0.12 (0.06)	0.70 (0.18)

Myocardial infarction (MI) had a nominally significant genetic correlation with 31 other traits, of which six had significant evidence (FDR <1%) for a fully or partially genetically causal effect on MI (Table 1); there was no evidence for a genetically causal effect of MI on any other trait. Consistent with previous studies, these traits included LDL[3,13], triglycerides[4] and BMI[30], but not HDL[3]. The effect of BMI was also consistent with prior MR studies [30-33], although these studies did not attempt to account for pleiotropic effects (also see ref. [34], which detected no effect). There was also evidence for a genetically causal effect of high cholesterol, which was unsurprising (due to the high genetic correlation with LDL) but noteworthy because of its strong genetic correlation with MI, compared with LDL and triglycerides. The result for HDL and MI did not pass our significance threshold (FDR <1%), but was nominally significant (p=0.02, Supplementary Table 12); we residualized HDL summary statistics on summary statistics for three established causal risk factors (LDL, BMI and triglycerides), determining that residualized HDL showed no evidence of genetic causality (p=0.8). On the other hand, most of the other traits remained significant (Supplementary Table 13).

We also detected evidence for a fully or partially genetically causal effect of hypothyroidism on MI (Table 1). Although hypothyroidism is not as well-established a cardiovascular risk factor as high LDL, its genetic correlation with MI is comparable (Table 1), and this effect is mechanistically plausible[40,41]. While this result was robust in the conditional analysis (Supplementary Table 13), and there was no strong evidence for a genetically causal effect of hypothyroidism on lipid traits (Supplementary Table 12), it is possible that this effect is mediated by lipid traits. A recent MR study of thyroid hormone levels, at ~20 × lower sample size than the present study, provided evidence for a genetically causal effect on LDL but not CAD [42]. On the other hand, clinical trials have demonstrated that treatment of subclinical hypothyroidism leads to improvement in several cardiovascular risk factors [43-47]. We also detected evidence for a fully or partially genetically causal effect of hypothyroidism on T2D (Supplementary Table 11), consistent with a longitudinal association between subclinical hypothyroidism and diabetes incidence [48], as well as an effect of thyroid hormone withdrawal on glucose disposal in athyreotic patients [49].

We detected evidence for a (negative) genetically causal effect of LDL on bone mineral density (BMD; Table 1). A meta-analysis of randomized clinical trials reported that statin administration increases BMD[50]. Moreover, familial defective apolipoprotein B leads to high LDL and low BMD [51]. We performed two-sample MR using 8 SNPs that were previously curated (in ref. 3; see Supplementary Note), finding modest evidence for a negative causal effect (p=0.04). Because these variants are not likely to have pleiotropic effects, this analysis provides separate evidence for a genetically causal effect. Additional trait pairs with high gcp estimates are discussed in the Supplementary Note.

Approximately half of significant trait pairs had low to medium gcp estimates (<0.6). Given that there is lower power to detect trait pairs with low gcp values (Supplementary Table 3a,p-r), it is likely that partial genetic causality with gcp<0.6 is more common than full or nearly-full genetic causality with gcp>0.6. Trait pairs with low gcp estimates can suggest plausible biological hypotheses. For example, we identified a partially genetically causal effect of age at menarche (AAM) on height ($\widehat{\text{gcp}}=0.43(0.10)$, Table S11), suggesting that these traits are influenced by a shared hormonal pathway that is more strongly correlated with AAM than with height, as recently hypothesized [11].

A recent study reported genetic correlations between various complex traits and number of children in males and females[52]. We identified only one trait (balding in males) with a fully or partially causal effect on number of children (in males; Table 1). For college education, which has a strong negative genetic correlation with number of children (${\widehat{\rho }}_g$ = −0.31(0.07) and −0.26(0.06) in males and females respectively), we obtained low gcp estimates with low standard errors ($\widehat{\text{gcp}}$ = 0.00(0.09) and $\widehat{\text{gcp}}$ = 0.04(0.21) respectively, Supplementary Table 12). Thus, a genetic correlation with number of children does not imply direct selection. This result does not contradict the conclusion of reference [52] that complex traits are affected by natural selection, as pleiotropic selection can also affect a trait [53].

Polygenic autism risk is positively genetically correlated with educational attainment[16] (and cognitive ability[54], a highly genetically correlated trait[57]), possibly consistent with the hypothesis that common autism risk variants persist in the population due to compensatory effects on cognitive ability [55,56]. If so, then most common variants affecting autism risk would also affect educational attainment, leading to a partially genetically causal effect of autism on educational attainment. However, we detected evidence against such an effect ($\widehat{\text{gcp}}$ = 0.13(0.13), ${\widehat{\rho }}_g$ = 0.23(0.07); Supplementary Table 12). Additional trait pairs with negative results are reported in the Supplementary Note and in Supplementary Table 14.

In order to evaluate whether the limitations of MR observed in simulations (Figure 2) are also observed in analyses of real traits, we applied MR, MR-Egger and Bidirectional MR to all 429 genetically correlated trait pairs (Supplementary Table 12). MR reported significant causal relationships (1% FDR) for 271/429 trait pairs, including 155 pairs of traits for which each trait was reported to be causal for the other trait. This implausible result confirms that MR frequently produces false positives in the presence of a genetic correlation, as predicted by our simulations (Figure 2). In contrast, LCV reported a significant partially or fully genetically causal relationship for only 59 trait pairs (Supplementary Table 11), and it never reports a causal effect in both directions. Similarly, Bidirectional MR reported a significant causal relationship for only 45 trait pairs (including 17 pairs of traits that overlapped with LCV; Supplementary Table 15).

Discussion

We have introduced a latent causal variable (LCV) model to identify causal relationships among genetically correlated pairs of complex traits. We applied LCV to 52 traits, finding that many trait pairs do exhibit partially or fully genetically causal relationships. Our method represents an advance for two main reasons. First, unlike existing MR methods, LCV reliably distinguishes between genetic correlation and full or partial genetic causation. Positive findings using LCV are more likely to reflect true causal effects. Second, we define and estimate the genetic causality proportion (gcp) to quantify the degree of causality. This parameter, which provides information orthogonal to the genetic correlation or the causal effect size, enables a non-dichotomous description of the causal architecture.

This study has two important limitations (additional limitations are discussed in the Supplementary Note). First, the LCV model includes only a single intermediary and can be confounded in the presence of multiple intermediaries. However, the 30 trait pairs with $\widehat{\text{gcp}}$ > 0.6 are unlikely to be false positives (see Supplementary Note and Supplementary Figure 2). Second, because LCV models only two traits at a time, it cannot be used to identify conditional effects given observed confounders[4,60]. This approach was used, for example, to show that triglycerides affect coronary artery disease risk conditional on LDL[4]. However, it is less essential for LCV to model observed genetic confounders, since LCV explicitly models a latent genetic confounder.

Despite these limitations, for most pairs of complex traits we recommend using LCV instead of MR, as MR methods (including MR Egger) are easily confounded by genetic correlations. MR is more reliable when it is possible to identify variants that are likely to represent valid instruments. For example, an MR analysis identified a causal effect of vitamin D on multiple sclerosis, utilizing genetic variants near genes with well-characterized effects on vitamin D synthesis, metabolism and transport [66]. As another example, cis-eQTLs can be used as genetic instruments, as they are unlikely to be confounded by processes mediated in trans [62-64]; however, this approach has other limitations [63,65].

Methods

LCV model

The LCV random effects model assumes that the distribution of marginal effect sizes for the two traits can be written as the sum of two independent bivariate distributions (visualized in Figure 1c-e in orange and blue respectively): (1) a shared genetic component (q₁π, q₂π) whose values are proportional for both traits; and (2) an even genetic component (γ₁, γ₂) whose density is mirror symmetric across both axes. Distribution (1) resembles a line through the origin, and we interpret its effects as being mediated by a latent causal variable (L) (Figure 1a); distribution (2) does not contribute to the genetic correlation, and we interpret its effects as direct effects. Informally, the LCV model assumes that any asymmetry in the shared genetic architecture arises from the action of a latent variable.

In detail, the LCV model assumes that there exist scalars q₁, q₂ and a distribution (π, γ₁, γ₂) such that

$$\begin{gathered} ({\alpha }_1,{\alpha }_2)=(q_1\pi +q_2\pi )+({\gamma }_1,{\gamma }_2), \\ \text{where}\pi \perp ({\gamma }_1,{\gamma }_2) \\ \text{and}({\gamma }_1,{\gamma }_2)~(-{\gamma }_1,{\gamma }_2)~({\gamma }_1,-{\gamma }_2). \end{gathered}$$ (3)

Here α_k is the random marginal effect of a SNP of trait k, π is interpreted as the marginal effect of a SNP on L, and γ_k is interpreted as the non-mediated effect of a SNP on trait k. α and π (but not γ) are normalized to have unit variance, and all random variables have zero mean. (The symbol ``~" means ``has the same distribution as.") q₁, q₂ are the model parameters of primary interest, and we can relate them to the mixed fourth moments, which are observable (equation 2). In particular, this implies that the model is identifiable (except when the excess kurtosis κ_π = 0; see Supplementary Note). We do not expect that κ_π will be exactly zero for any real trait, but there will be lower power for traits with higher polygenicity. Note that we have avoided assuming any particular parametric distribution.

The LCV model assumptions are strictly weaker than the assumptions made by MR. Like LCV, a formulation of the MR assumptions is that the bivariate distribution of SNP effect sizes can be expressed in terms of two distributions. In particular, it assumes that the effect size distribution is a mixture of (1') a distribution whose values are proportional for both traits (representing all SNPs that affect the exposure Y₁) and (2') a distribution with zero values for the exposure Y1 (representing SNPs that only affect the outcome Y₂). These two distributions can be compared with distributions (1) and (2) above. Because (1") is identical to (1) and (2") is a special case of (2), the LCV model assumptions are strictly weaker than the MR assumptions (indeed, much weaker). We also note that the MR model is commonly illustrated with a non-genetic confounder affecting both traits. Our latent variable L is a genetic variable, and it is not analogous to the non-genetic confounder. Similar to MR, LCV is unaffected by nongenetic confounders (such a confounder may result in a phenotypic correlation that is unequal to the genetic correlation).

The genetic causality proportion (gcp) is defined as:

$$\text{gcp}=\frac{\log \mid q_2\mid -\log \mid q_1\mid }{\log \mid q_2\mid +\log \mid q_1\mid }$$ (4)

which satisfies equation (1). gcp is positive when trait 1 is partially genetically causal for trait 2. When gcp = 1, trait 1 is fully genetically causal for trait 2: q₁ = 1 and the causal effect size is q₂ = ρ_g (Figure 1b,e). The LCV model is broadly related to dimension reduction techniques such as Factor Analysis[67] and Independent Components Analysis[68], although it differs in its modeling assumptions as well as its goal (causal inference); our inference strategy (mixed fourth moments) also differs.

Under the LCV model assumptions, we derive the estimation equation (2) as follows:

$$\begin{gathered} E({\alpha }_1^3{\alpha }_2)=E(({\gamma }_1+q_1\pi {)}^3({\gamma }_2+q_2\pi )) \\ =q_1^3{q}_{2}E({\pi }^4)+3q_1{q}_{2}E({\pi }^2{\gamma }_1^2) \\ =q_1^3{q}_{2}E({\pi }^4)+3q_1{q}_{2}E({\pi }^2)E({\gamma }_1^2) \\ =q_1^3{q}_{2}E({\pi }^4)+3q_1{q}_2(1)(1-q_1^2) \\ =q_1^3{q}_2(E({\pi }^4)-3)+3q_1{q}_2. \end{gathered}$$

In the second line, we used the independence assumption to discard cross-terms of the form γ_pπ³ and ${\gamma }_1^3\pi$, and we used the symmetry assumption to discard terms of the form ${\gamma }_1{\gamma }_2^3$. In the third and fourth lines, we used the independence assumption, which implies that $E({\gamma }_1^2{\pi }^2)=E({\gamma }_1^2)E({\pi }^2)=E({\gamma }_1^2)=1-q_1^2$. The factor E(π⁴) – 3 is the excess kurtosis of π , which is zero when π follows a Gaussian distribution; in order for the estimation equation to be useful, E(π⁴) – 3 must be nonzero (see Supplementary Note).

Estimation under the LCV model

In order to estimate the gcp and to test for partial causality, we utilize six steps. First, we use LD score regression[19] to estimate the heritability of each trait; these estimates are used to normalize the summary statistics. Second, we apply cross-trait LD score regression[16] to estimate the genetic correlation; the intercept in this regression is also used to correct for possible sample overlap when estimating the mixed fourth moments. Third, we estimate the mixed fourth moments of the bivariate effect size distribution. Fourth, we compute test statistics for each possible value of the \gcp, based on the estimated genetic correlation and on the estimated mixed fourth moments. Fifth, we jackknife on these test statistics to estimate their standard errors, similar to ref. 19, obtaining a likelihood function for the gcp. Sixth, we obtain posterior means and standard errors for the gcp using this likelihood function and a uniform prior distribution. These steps are detailed below.

First, we apply LD score regression to normalize the test statistics. Under the LCV model, the marginal effect sizes for each trait, α₁ and α₂, have unit variance. We use a slightly modified version of LD score regression[19] with LD scores computed from UK10K data [58]. In particular, we run LD score regression using a slightly different weighting scheme, matching the weighting scheme in our mixed fourth moment estimators; the weight of SNP i was:

$$w_i=\frac{1}{\max (1,{\ell }_i^{\text{HapMap}})}$$ (5)

where ${\ell }_i^{\text{HapMap}}$ was the estimated LD score between SNP i and other HapMap3 SNPs (this is approximately the set of SNPs that were used in the regression). This weighting scheme is motivated by the fact that SNPs with high LD to other regression SNPs will be over-counted in the regression (see ref. 19).

Similar to ref. 16, we improve power by excluding large-effect variants when computing the LD score intercept; for this study, we chose to exclude variants with χ² statistic 30 × the mean, exploiting the fact that genome-wide significant SNPs are not due to population stratification (these variants are not excluded in subsequent steps). Then, we divide the summary statistics by $s=\sqrt{{\chi }_{\text{avg}}^2-{\chi }_0^2}$, where ${\chi }_{\text{avg}}^2$ is the weighted mean χ² statistic and ${\chi }_0^2$ is the LD score intercept, obtaining estimates $\widehat{\alpha }$ of α. (We also divide the LD score intercept by s².) We assess the significance of the heritability by performing a block jackknife on s, defining the significance Z_h as s divided by its estimated standard error.

Second, to estimate the genetic correlation, we apply cross-trait LD score regression [16]. Similar to above, we use a slightly modified weighting scheme (equation 5), and we exclude large-effect variants when computing the cross-trait LD score intercept. We assess the significance of the genetic correlation using a block jackknife.

Third, we estimate the mixed fourth moments $E({\alpha }_1{\alpha }_2^3)$ using the following equation:

$$E({\widehat{\alpha }}_1{\widehat{\alpha }}_2^3\mid {\alpha }_1,{\alpha }_2)={\alpha }_1{\alpha }_2^3+3{\alpha }_1{\alpha }_2{\sigma }_2^2+{\alpha }_2^2{\sigma }_{12}+3{\sigma }_{12}{\sigma }_2^2,$$ (6)

where ${\sigma }_2^2$ is the LD score regression intercept for trait 2 (normalized by dividing by $s_2^2$) and σ₁₂ is the cross-trait LD score regression intercept (normalized by dividing by s₁s₂). For simulations with no LD, we fix ${\sigma }_2^2=1∕s_2^2$ and σ₁₂ = 0. Thus, we obtain an estimate ${\widehat{\kappa }}_k$ of ${\kappa }_k=E({\alpha }_k^2{\alpha }_1{\alpha }_2)-3{\rho }_g$ by computing the weighted average of ${\widehat{\alpha }}_1{\widehat{\alpha }}_2^3$ over SNPs (with weights given by equation 5), and subtracting $3{\widehat{\alpha }}_1{\widehat{\alpha }}_2{\sigma }_2^2+{\alpha }_2^2{\sigma }_{12}+3{\sigma }_{12}{\sigma }_2^2$.

Fourth, we define a collection of statistics S(x) for x ∈ X = {−1, −.01, −.02,…,1} (corresponding to possible values of gcp):

$$\begin{gathered} S(x)=\frac{A_1(x)-A_2(x)}{\max \left(\frac{1}{\mid {\rho }_g\mid },\sqrt{A_1(x{)}^2+A_2(x{)}^2}\right)} \\ \text{where}{A}_{\mathrm{k}}(\mathrm{x})=\mid {\rho }_{\mathrm{g}}{\mid }^{-x}{\widehat{\kappa }}_k. \end{gathered}$$ (7)

The motivation for utilizing the normalization by $\sqrt{A_1(x{)}^2+A_2(x{)}^2}$ is that the magnitude of A₁(x) and A₂(x) tend to be highly correlated, leading to greatly increased standard errors if we only use the numerator of S. However, the denominator tends to zero when the genetic correlation is zero, leading to instability in the test statistic and false positives. The use of the threshold leads to conservative, rather than inflated, standard errors when the genetic correlation is zero or nearly zero. We recommend only analyzing trait pairs with a significant genetic correlation, and this threshold usually has no effect on the results. Another reason not to analyze trait pairs whose genetic correlation is non-significant is that for positive LCV results, the genetic correlation provides critical information about the causal effect size and direction.

Fifth, we estimate the variance of S(x) using a block jackknife with k = 100 blocks of contiguous SNPs, resulting in minimal non-independence between blocks. Blocks are chosen to include the same number of SNPs, and the jackknife variance is:

$${\sigma }_{S(x)}^2=101\sum _{j=1}^{100}(S_j(x)-S_{\text{avg}}(x){)}^2$$ (8)

where S_j(x) is the test statistic computed on blocks 1,…,j − 1, j + 1,…100 and S_avg(x) is the mean of the jackknife estimates. We compute an approximate likelihood, L(S∣gcp = x), by assuming (1) that L(S∣gcp = x) = L(S(x)∣gcp = x) and (2) that if gcp = x then S(x)/σ_S(x) follows a T distribution with 98 degrees of freedom.

Sixth, we impose a uniform prior on the gcp, enabling us to obtain a posterior mean estimate:

$$\widehat{\text{gcp}}=\frac{1}{\mid X\mid }\sum _{x\in X}xL(x)$$ (9)

The estimated standard error is:

$$\mathrm{se}=\frac{1}{\mid X\mid }\sum _{x\in X}(S_j(x)-S_{\text{avg}}(x){)}^2$$ (10)

In order to compute p-values, we apply a T-test to the statistic S(0).

Outlier removal

In a secondary analysis, we applied an outlier removal procedure to determine whether our results on real traits using LCV were unduly influenced by individual loci. We computed the LCV test statistic S(0) for each of the 100 jackknife blocks, discarded jackknife blocks that were >20 standard deviations from the mean, and re-ran the procedure iteratively until no outliers remained. For most trait pairs, this process results in the removal of 0 blocks; for a handful of trait pairs, it results in the removal of one or a few.

We do not recommend the broad use of this procedure, because outlier loci may contain valuable information. In particular, if any SNP affects trait 1 without affecting trait 2 proportionally, this suggests that trait 1 is not causal for trait 2. An alternative explanation is that its effect on trait 2 is masked by an opposing pleiotropic effect, either of the same causal SNP or of a different causal SNP at the same locus. If an outlier locus is to be removed, we recommend manually examining it and determining whether its removal can be justified or whether it provides competing statistical evidence against a causal effect.