Abstract
Humans exhibit evidence of a mental number line (MNL) that suggests a left to right, or sometimes right to left, representation of smaller to larger numbers. The Spatial Numerical Association of Response Codes (SNARC) effect is one example of this mental number line and has been investigated extensively in humans. Less research has been done with animals, and results have been inconclusive. Rugani et al. (2015) found that young chicks showed a bias to respond to small quantities presented to their left and large quantities presented to their right when forced to move toward those stimuli to gain food reward. We replicated this design with rhesus macaques and capuchin monkeys using a computerized task, but we did not find this outcome. We also trained monkeys to choose between two arrays of dots, and then assessed biases in terms of choice location and response latency on trials with a numerical difference and on trials with equal numbers of items in both sets. There was no evidence of SNARC-like effects in equal trials, although when arrays differed in number, 12 of 19 monkeys showed differential performance depending on whether the smaller array was at left or at right onscreen. These results indicate that SNARC-like effects may not emerge in all contexts and may not be phylogenetically widespread. More effort is needed to broaden the number of species assessed and match other methods that are used with human participants so that we can better define the presence and extent of such effects.
Keywords: Numbers, space, SNARC effect, mental number line, monkeys
Humans naturally and frequently make judgments about the numerical properties of stimuli, such as by counting, estimating, comparing, and operating on sets of items (Cohen Kadosh & Dowker, 2015; Geary, Berch, & Mann Koepke, 2015; Henik, 2016). Humans also naturally and frequently make judgments about the spatial arrangements of stimuli and encode and use spatial relations in various ways. The representations of space and number (and perhaps also time) may share not only processing mechanisms but also neural architecture, specifically with regards to the intraparietal sulcus (e.g., Cohen Kadosh, Lammertyn, & Izard, 2008; de Hevia & Spelke, 2009; de Hevia, Girelli, & Macchi Cassia, 2012; Dehaene, Piazza, Pinel, & Cohen, 2003; Hubbard, Piazza, Pinel, & Dehaene, 2005; Lourenco, 2016; Lourenco & Longo, 2010; Walsh, 2003). The hypothesis that representing space and number are similar processes comes in part from evidence that numerical and spatial processing often overlap when individuals make numerical judgments. Restle (1970) provided some of the earliest evidence for a mental number line (MNL) that acts as a spatial map to assist in numerical processing when participants had to compare numerical values. For English speakers, the MNL typically would run from left-to-right, but would go from right-to-left in cultures that read in that direction (e.g., Shaki & Fischer, 2008; Shaki, Fischer, & Petrusic, 2009; Shaki, Petrusi, & Leth-Steensen, 2012). Small numbers, for left-to-right readers, are oriented on the left side of the MNL and large numbers are oriented on the right. Although the MNL theoretically runs in a direction that mirrors reading direction, it also may be more idiosyncratic across individuals even within the same culture (Nuerk, Wood, & Willmes, 2005; Wood, Nuerk, & Willmes, 2006), and some have argued that the MNL is more a cultural phenomenon than an innate part of human experience of magnitude (e.g., Núñez, 2011).
The MNL is predicated on the idea that there should be quicker (and perhaps more accurate) responses to one side of a spatial array for small numbers and another side for large numbers when making numerical judgments (e.g., Dehaene, Bossini, & Giraux, 1993). This effect, termed the Spatial Numerical Association of Response Codes (SNARC), has been found to be robust although it varies in direction across individuals (e.g., Nuerk et al., 2005; Wood et al., 2006; Wood, Willmes, Nuerk, & Fischer, 2008). In a seminal study of the SNARC effect, Dehaene et al. (1993) discovered that French speakers were faster at responding with their left hand when presented with small numbers but were faster at responding with their right hand when presented with large numbers. Conversely, speakers that typically read in a right-to-left direction either showed a diminished or reversed SNARC effect (e.g., Shaki & Fischer, 2008; Shaki & Gevers, 2011; Zebian, 2005). Hung, Hung, Tzeng, and Wu (2008) reported that Chinese participants showed a left-to-right SNARC effect when looking at Arabic numerals, but when they looked at Chinese characters they showed an up-down SNARC effect. The influence of reading direction has prompted questions of the cultural impact on numerical and spatial processing (e.g., Shaki & Fischer, 2008; Shaki et al. 2009, 2012). And, there is inconsistent reporting for when it first emerges in children, with some studies showing that it emerges near nine years of age (e.g., Berch, Foley, Hill, & Ryan, 1999) but others reporting the effect much earlier, such as in 4-year-old children who have not yet learned to read (van Galen & Reitsma, 2008; Patro & Haman, 2012) and even among 8- to 9-month old infants (Bulf, de Hevia, & Macchi Cassia, 2016).
The SNARC effect has been seen in tasks where a particular number (e.g., ‘7’) may be associated with the right side of space when paired with smaller numbers (e.g., 1 to 6), but may be associated with the left side of space when paired with larger numbers (e.g., 8 to 12). This flexibility in shifting the space-number association for a numeral is not limited to its relative position to other numbers. Bächtold, Baumüller, and Brugger (1998) altered the left-to-right orientation of the SNARC effect in their participants by asking them to imagine the numbers on a clock face, which are arranged in the opposite direction to a standard number line, as opposed to a ruler in which numbers are represented according to the MNL. This difference in task instruction resulted in a reversed SNARC effect. Further examples include priming bilingual participants to read either left-to-right or right-to-left, which influences the direction of the SNARC effect (Shaki & Fischer, 2008), and SNARC effects have been reported with non- numerical but sequentially ordered stimuli, such as letters (Gevers, Reynvoet, & Fias, 2003).
Although the SNARC effect is robust, there is still vigorous debate over the mechanisms behind it (e.g., Gevers, Verguts, Reynvoet, Caessens, & Fias, 2006; Mapelli, Rusconi, & Umiltà, 2003; Rusconi, Umiltà, & Galfano, 2006). Long-term memory was thought to account for the SNARC effect (see Ginsburg & Gevers, 2015), but further investigation has revealed that working memory plays a large role. For example, van Dijck and Fias (2011) found that the SNARC effect occurs based on the sequential position of an item in working memory, with the first numbers being associated with the left and the last numbers associated with the right. In addition, working memory load can reduce or eliminate the SNARC effect (van Dijck, Gevers, & Fias, 2009). Other theories propose that brain lateralization is responsible, and the MNL follows a general right hemisphere dominance for processing spatial and numerical attributes of visual stimuli that leads to differential attention to stimuli in the left and right hemifield (e.g., Rugani, Vallortigara, Priftis, & Regolin, 2015). Another possibility is that SNARC effects are related to the actual topographical arrangement of numerical magnitudes in human parietal cortex (Harvey, Klein, Petridou, & Dumoulin, 2013), although this arrangement is not well-documented and has not been seen in nonhuman animals (Drucker & Brannon, 2015). The cultural influences of reading direction and various possible biological mechanisms have created conflicting accounts of the origins of the SNARC effect. Research with non-human animals has thus sought to inform this debate and to provide insight into whether the SNARC effect is a generalized processing mechanism or a result of human language, development or unique cultural experiences.
To assess whether the SNARC effect is a uniquely human phenomenon, Rugani et al. (2015) presented chicks with a two-choice discrimination task after first exposing them to a central quantity value. This training involved five as the target number, and chicks had to physically circumnavigate a panel to retrieve a reward and did so repeatedly to gain experience with the procedure and the target number. Then, two identical dot arrays of equal quantity and spatial arrangement were presented on the left and the right sides of the enclosure. The chicks were allowed to move behind either the left or right panel to retrieve a reward. When presented with a smaller number relative to the target quantity (two items), the chicks preferentially circumnavigated the left array, but they moved to the right panel when presented with a larger quantity (eight items) on both sides. Further, it was demonstrated that the SNARC effect was reflected in relative quantities for the chicks as well, meaning that absolute numerical values were not assigned to the left or right sides so much as the relative values presented after experiences. When chicks were instead trained with the target number 20 (rather than five), they then moved to the left when presented with eight items on both sides, but to the right when presented with 32 items on both sides. This evidence suggested that chicks spontaneously approached identical choices according to a left-to-right MNL that was anchored to the recent experiences with a central value (e.g., five items, in the case of the 2–2 or 8–8 comparison, and 20 items in the case of the 8–8 or 32–32 comparison).
Other research with nonhuman primates has provided similar results that may suggest a SNARC effect. Following training to match dot arrays with colors on either side of a screen and to associate small arrays with the left side of the screen and large arrays with the right side, rhesus monkeys were more accurate in matching on the left when the arrays were small, and this effect was reversed when trained in the opposite direction (Diamond, Gazes, & Hampton, 2015). Apes also have shown the SNARC effect. Adachi (2014) trained chimpanzees to touch Arabic numerals presented on a computer screen in order from one to nine. When presented with two numerals, chimpanzees were faster to touch the smaller of the two numbers when it was positioned on the left and the larger of the two numbers when it was positioned on the right than when the reverse arrangement was presented. Further, gorillas and orangutans were faster to touch small arrays on the left and large arrays on the right when making relative quantity judgments in a two-choice discrimination task, although there were individual differences in the direction of the SNARC effect (Gazes et al., 2017). This effect differed across individuals in terms of the direction of the SNARC effect (some were left-to-right as described, others were right-to-left); but importantly, the direction of the effect reversed when the apes were then trained to touch the smaller array (or the larger array depending upon the order of conditions). A subsequent assessment of gorillas, humans, and black bears also showed some evidence of SNARC-like effects (Johnson-Ulrich & Vonk, 2018), although there again was variability in the direction of shift in performance and response time across conditions and individuals. Importantly, this was true even for humans, who in this case completed the same task as that given to bears and gorillas. These data suggested a continuity for SNARC-like effects across species.
Although the existence of the SNARC effect in some studies with nonhuman animals suggests an evolutionary origin of this phenomenon in humans, the direction of this effect is still under debate, and this is still an under-investigated phenomenon in comparative research. Adachi (2014) posited that the SNARC effect is more about the general association of numbers and space and less about the technical aspects of which direction those stimulus dimensions are mapped. Because culture can influence the direction of the SNARC effect in humans, it stands to reason that training can do the same in nonhuman primates, and that the left-to-right orientation may be innate but also able to be altered through experience. In may even be that the SNARC effect is fully determined through experience, in terms of its spatial direction. However, there are reports of SNARC-like effects in human children from early infancy, suggesting that some type of spatial representation of magnitude may be innate in humans (see Rugani & de Hevia, 2017). For example, 8- to 9-month-old infants orient their visual attention in ways that suggest a left-to-right mental mapping of magnitude that exists well before cultural or experiential contributions would establish that mapping (e.g., Bulf et al., 2016). This evidence also would align well with the idea such spatial representations are shared with other species and have a long evolutionary history.
To our knowledge, only two attempted replications of Rugani et al. (2015) have been undertaken. The first was another assessment of two-day-old chicks (Noyek, 2016). This study closely followed the procedures in Rugani et al. for the test where five was the trained quantity and then two arrays both had two items or both had eight items at left and right on test trials. In this replication, no evidence of side biases was found overall, or for the first trials from each chick. Noyek concluded that those chicks did not show a SNARC effect. Another conceptual replication was with cleaner fish (Triki & Bshary, 2018). In that study, the fish first showed that, when two visual arrays differed in number, they could discriminate the smaller array from the larger array. In the crucial test of the SNARC effect, fish first moved repeatedly to a single array (five items) that was centrally located, and then were given trials where two arrays (at left and right) each had either two or eight items on them. The fish showed no bias to move to either side as a function of array size, thereby failing to replicate the Rugani et al. outcome. This again was true for all trials and looking only at the first-trial performance. Triki and Bshary noted that their result showed a clear need for a broader species assessment of the MNL using this type of approach.
The design and results of Rugani et al. (2015) have been challenged in other ways also. Shaki and Fischer (2015) noted that although Rugani et al. attempted to control for non- numerical stimulus cues in their third experiment, the approach they took still allowed for a confounding factor (either density or area) to exist in the different trial types. And, density and area are both known to be associated with specific spatial left-right biases. More dense arrays attract attention to the right (and, when density is not controlled, denser arrays are numerically larger). Furthermore, a smaller area that leads to lighter background coloration attracts attention to the left and would be expected in cases where the smaller number also was at left. Thus, these confounds with number may have accounted for the chicks’ response biases. Harshaw (2015) argued that precocial chicks have natural perceptual and motoric biases that align with SNARC- like effects but for reasons unrelated to processing of numerical or quantitative information, and concerns were raised about the analyses that were applied to repeated measures data collected from the chicks (Mangalam & Karve, 2015).
Given the reported commonalities in human and nonhuman primates’ quantitative and numerical cognition in behavioral tests (e.g., Cantlon & Brannon, 2005, 2006) and in terms of underlying neurobiology (Nieder & Merten, 2007; Nieder & Miller, 2003, 2004), additional studies with nonhuman primates that specifically assess the SNARC effect offer great value. This is especially true given some of the previous reports with great apes that indicated SNARC-like effects using other methods (Gazes et el., 2017; Johnson-Ulrich & Vonk. 2018). Even with the noted concerns about the design of Rugani et al. (2015), there is still good reason to assess whether SNARC-like effects appear in other species using varied methods. Given the interest in the Rugani et al. approach, both in terms of its original results, and also in terms of the contrast seen when fish and other chicks were given a similar test, we chose to design a conceptual replication based on that design that could be given to nonhuman primates. We also incorporated features of Gazes et al. (2017) and Triki & Bshary (2018).
Capuchin monkeys and rhesus macaques were given a series of discrimination tasks. In the first experiment, they had to choose between identical quantities (2 vs. 2 or 8 vs. 8) following training with a target quantity of five, and then choose between identical quantities (8 vs. 8 or 32 vs. 32) following additional training with a target quantity of 20 items presented on a computer screen. A significant preference for one spatial location over the other (left or right) that varied as a function of the training target value (5 or 20) would be evidence of a SNARC effect in these monkeys that matched the effect as shown in chicks (Rugani et al., 2015). The second task required the same monkeys to make relative quantity judgments of smaller or larger sets of dots onscreen from the range 2 to 8 items. These judgments allowed us to assess possible SNARC effects in the presence of numerical differences. For example, if a left-to-right SNARC effect is evident, monkeys should perform more accurately and more quickly when larger sets were on the right side of the screen and smaller sets were on the left side of the screen than in other spatial arrangements. And, in some trials, two identical arrays of either two items (the lowest possible values ever seen in this phase) or eight items (the highest possible values seen in this phase) could appear at left and right positions onscreen, and we recorded which of those arrays were selected. A SNARC effect would be evident if there was a bias to choose one side (left-right) of the screen more often for one set size and the other side (left-right) for the other set size. Traditionally, this would mean choosing the left more often for the 2–2 comparison and choosing the right more often for the 8–8 comparison, although we anticipated that the MNL did not need to run from left to right in these nonhuman species, given the past work with other primates as well as the variability documented among humans.
We acknowledge the concerns noted about the approach of Rugani et al. (Harshaw, 2015; Mangalam & Karve, 2015; Shaki & Fischer, 2015), but we wanted to present as close an approach in our first computerized experiment to what was done with the chicks in the open field test. And, our use of a computerized task, with highly proficient users of that apparatus, minimized or eliminated any concerns about specific motor and perceptual biases evident in chicks (Harshaw, 2015). Our subsequent experiments were designed and motivated in large part by the results of our first experiment, and those results suggested that these concerns were secondary to what was anticipated to be a greater struggle to demonstrate SNARC-like effects than to need to control confounds in an effort to isolate such effects.
Method
Participants
We tested five adult male rhesus monkeys between the ages of 15 and 36 years. We tested 14 adult capuchin monkeys (9 females) between the ages of 9 and >40 years (see Table 1 for more information). Two additional monkeys were presented the task, but joystick malfunctions led to severe one-directional responding during the experiment, and so we removed all data from those monkeys because of uncertainty about the reliability of apparatus. All monkeys previously had been trained to use a computerized apparatus to respond to game-like tasks (Evans, Beran, Chan, Klein, & Menzel, 2008; Richardson, Washburn, Hopkins, Savage- Rumbaugh, & Rumbaugh, 1990). Rhesus monkeys had access to the task for time blocks ranging from 4 to 8 hours during which time the software program was available onscreen, and capuchin monkeys had access to the task for blocks ranging from 3 to 5 hours. Monkeys worked on the task as they chose, taking breaks when they chose. Monkeys always had access to water and were given a daily meal each afternoon independent of whether they worked on the computer task. Meals were adjusted based on the number of pellets consumed from the computer task so as to maintain the monkeys on daily levels of caloric intake that were established by the veterinary staff. When not working on computerized tasks, capuchin monkeys lived in multi-male, multi-female social groups with indoor-outdoor access. Rhesus monkeys also had indoor and outdoor access when not working, and in some cases had a companion monkey with whom they were compatible and could spend time grooming or otherwise engaging socially.
Table 1.
Information about the monkeys and their training in Phase 3
| Sex | Age in Years | Choice Rule | Trials to Criterion | |
|---|---|---|---|---|
|
Capuchin Monkeys | ||||
| Bias | Female | 30 | Smaller | 2,127 |
| Gambit | Female | 21 | Smaller | 2,952 |
| Gonzo | Female | 11 | Smaller | 315 |
| Gretel | Female | 13 | Larger | 266 |
| Griffin | Male | 20 | Larger | 323 |
| Lexi | Female | 9 | Larger | 147 |
| Liam | Male | 12 | Smaller | 229 |
| Logan | Male | 12 | Larger | 93 |
| Mason | Male | 18 | Smaller | 2,338 |
| Nala | Female | 15 | Larger | 510 |
| Nkima | Male | 9 | Smaller | 268 |
| Star | Female | 40+ | Larger | 7,230 |
| Widget | Female | 9 | Smaller | 1,061 |
| Wren | Female | 14 | Larger | 643 |
|
Rhesus Monkeys | ||||
| Chewie | Male | 17 | Larger | 183 |
| Han | Male | 15 | Larger | 42 |
| Hank | Male | 36 | Larger | 176 |
| Lou | Male | 26 | Larger | 151 |
| Murph | Male | 26 | Smaller | 836 |
A joystick stopped working properly and would only go in one direction during one test session with one rhesus monkey, and so we had to exclude the data from this monkey. Given that the aim was to assess potential choice biases and speed of responding to left and right-side stimuli, this error precluded any meaningful data contribution from this monkey because of the long run of trials he completed with the malfunctioning joystick, and how that might have impacted any future performance on the task. We also attempted to train one additional rhesus monkey, but this animal refused to engage in the task for multiple sessions in a row, and so he was not forced to continue in this experiment.
Apparatus
All monkeys completed the experiment using the Language Research Center’s Computerized Test System (LRC-CTS). This system consisted of a personal computer, digital joystick, color monitor, and pellet dispenser (Evans et al., 2008; Richardson et al., 1990). Monkeys used their hands to manipulate a digital joystick so that they could move a red, circular cursor onscreen during trials. Monkeys earned 45-mg banana-flavored chow pellets as food rewards (Bio-Serv, Frenchtown, NJ), and those pellets were delivered via a pellet dispenser that was connected to the computer. Trials were presented using software programmed in Visual Basic 6.0.
Design and Procedure.
Monkeys completed trials using the LRC-CTS. They manipulated their joystick to control a cursor onscreen. Each monkey continued to work on the program until all four phases of the experiment were completed. Because monkeys worked as much or as little as they chose during work sessions, and because there was a training criterion in place for Phase 3, they required variable numbers of trials to complete the experiment.
Phase 1.
In this phase, the monkeys completed 30 trials. The first 20 trials were identical. Centered onscreen was an array of five black dots placed within a grey square, that was itself on a white background screen (Figure 1, top panel). These dots had a radius of 4.5 mm and were randomly selected from an 8 × 8 grid of potential locations. Each of the 20 trials presented a uniquely random distribution of five dots, different from the previous trial. The monkeys simply moved the cursor upwards onscreen into contact with that grey rectangle, and then a pellet was dispensed. A 1 s inter-trial interval (ITI) occurred, and then the next trial was presented. Monkeys rapidly progressed through these 20 trials.
Figure 1.
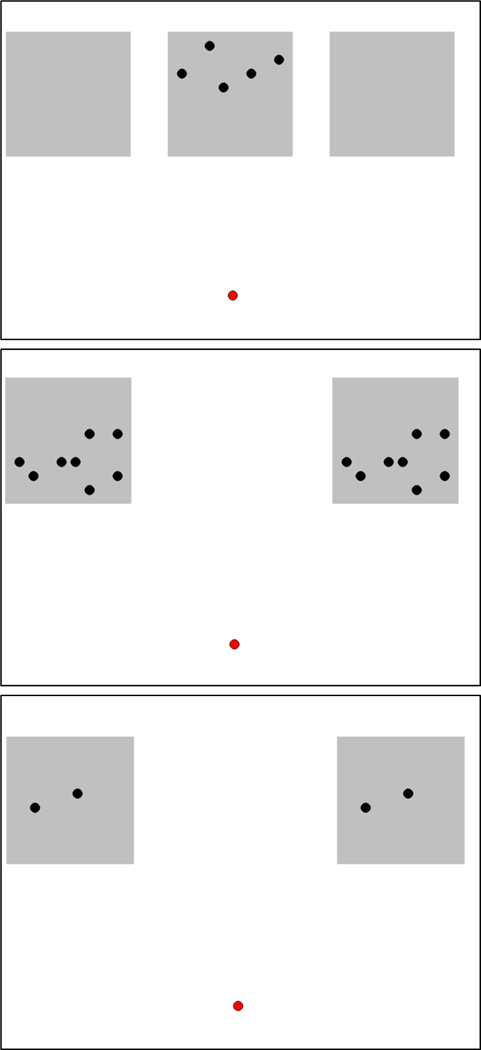
The stimuli presented in Phase 1. At top is an example of the first 10 trials, where touching the center stimulus with five dots on it led to reward. At middle and bottom are trials in which equal quantities in the same arrangement were placed at left and at right and contacting either stimulus led to food reward.
Then, 10 trials were presented in which the center square was empty (no dots) and dots appeared instead in squares located at center left and center right onscreen (Figure 1). In each of these rectangles appeared either two dots or eight dots (Figure 1, middle and bottom panel). There were five trials of each quantity (2 vs. 2 or 8 vs. 8). For these trials, there was an identical distribution of dots, and thus the arrays were identical across the right-left array. Each trial was unique in that the spatial layout of dots varied across trials. Selection of either array resulted in a single pellet reward, and a 1 s ITI before the next trial appeared. The program recorded which array (left or right) was selected and the latency to make a response.
Phase 2.
This phase also consisted of 30 trials, presented in the same manner as in Phase 1. The difference was that the first 20 trials presented an array of 20 dots in the center of the screen (randomized dot location within an 8 by 8 grid for each trial), and the last 10 trials consisted of presenting either eight dots in each of the two side arrays or 32 dots in each of the two side arrays. In this phase, there was an identical distribution and spatial arrangement of dots within a trial, but each trial was unique in that the spatial layout of dots across trials varied. The program again recorded which array (left or right) was selected and the latency to respond.
Phase 3.
In this phase, every trial presented an array at left and an array at right. These arrays contained any quantity between two and eight dots, and one array (left or right, randomly determined) always contained more dots that the other. Unlike Phase 1 and Phase 2, the spatial arrangement of dots within each array was randomized within and across trials, within an 8 by 8 grid. These arrays looked similar to those shown in Figure 1 but the left-right arrays were not identical in this phase. Some monkeys were trained to choose the larger quantity, and others were trained to choose the smaller quantity (training criterion below).
Correct choices led to the delivery of a single food pellet and a 1 s ITI before the next trial was presented. Incorrect choices led to a blank screen and a 20 s timeout period before the next trial was presented. For all trials, the number of dots presented on both sides of the array was recorded, the latency to contact an array with the cursor was recorded, and the choice (i.e., array size and location on the screen) was recorded. Monkeys continued to work in this phase until they were correct for at least 40 of the last 50 trials completed. When this criterion was met, they immediately began Phase 4.
Assignment of capuchin monkey to the condition in which they were to choose the larger array or the smaller array was random. The assignment of the rhesus monkeys also was intended to be random, but due to experimenter error, more monkeys were assigned to the condition of choosing larger (five of six monkeys). The assignment of each monkey is presented in Table 1.
Phase 4.
Monkeys completed at least 1,000 trials in this phase. Only the first 1,000 trials were analyzed, but because monkeys worked and rested at their choosing, we allowed the program to continue to be accessible through the end of the test session even after they exceeded 1,000 trials, so that they might still have the choice to work or not. One monkey (Lexi) completed only 793 trials in this phase due to experimenter error.
In this phase, two arrays of dots again were presented at left center and right center. For approximately 80% of trials, the same dot comparisons were presented as in Phase 3, with differences in the numbers of dots in the arrays (randomly assigned to left or right sides of the screen). On approximately 10% of trials, both arrays had two dots, presented in the same spatial configuration in each array. On approximately 10% of trials, both arrays had eight dots, presented in the same spatial configuration. Thus, on these equal quantity trials, the same stimuli were presented at both sides, and the program recorded whether a monkey selected the left array or the right array. These equal trials were identical to Phase 1 and Phase 2. On equal trials, any response was rewarded. For all trials, the number of dots presented on both sides of the array was recorded, the latency to contact an array with the cursor was recorded, and the choice (i.e., array size and location on the screen) was recorded.
Data Analyses.
For Phase 1 and Phase 2, we first assessed the responses of screen side. Here, the independent variable was the quantity of items at each side of the screen. In Phase 1, this was two items versus eight items, and for Phase 2 this was eight items versus 32 items. The first dependent variable we assessed was the proportion of choices of one side of the screen versus the other. For Phase 1 and Phase 2, we conducted a repeated-measures ANOVA to examine the proportion selection of the left array as a function of the number of dots in the arrays and as a function of species. A SNARC effect would require a significant difference in these proportions as a function of the number of items in the arrays.
Time to complete a response was evaluated to determine whether a SNARC-like effect can be found in the monkeys’ response latencies. A SNARC-like effect would be evident if response latencies differed as a function of the number of items in the arrays. To examine any differences in response time (RT) in Phase 1 and Phase 2 as a function of set size and the side of the screen selected, we developed a generalized linear mixed effects model using R (utilizing the lme4 package in R; Bates et al., 2016). For these RT analyses we looked at the independent variables of Species (capuchin and macaque monkeys), Condition (Test 1: 2-item arrays; Test 1: 8-item arrays; Test 2: 8-item arrays; Test 2: 32-item arrays), Selection (Left or Right), and any interactions. The model analyzed the natural log of the RT values to accommodate for a positive skew and the independent variables were effect-coded to account for possible multicollinearity. Finally, subject was specified as a random effect and the condition and selection factors (but not species factor) were allowed to vary between subjects to meet the repeated measures assumption (Gelman & Hill, 2007).
For Phase 3, we reported the descriptive information about the number of trials required for each monkey to meet the training criterion given that this was a training phase.
For each species in Phase 4, we first correlated performance and the numerical ratio of the two quantities when there was a numerical difference between the two arrays. This was done to confirm that more similar quantity comparisons were more difficult. We then focused on trials with equal numbers of dots in both arrays. We conducted a repeated measures ANOVA with the independent variables of species (rhesus and capuchin) and array size (two dots or eight dots) with the dependent measure of proportion of trials the left array was selected. For Phase 4 RT analyses we again used the linear mixed effects modeling to look at the effect of Species (capuchin and macaque monkeys), Condition (2-item or 8-item arrays), Selection (Left, Right), and any interactions on response times. We also examined performance on trials with quantity differences in Phase 4, to determine if the left-right presentation of those sets affected performance. To do this, we calculated difference scores for the proportion of trials correctly completed when the smaller quantity was on the left compared to when it was one the right. These difference scores were compared to a hypothetical difference of 0 using one-sample t-tests. SNARC-like effects, in either direct (right to left or left to right) would be evident if a monkey showed better performance whenever one such arrangement pattern was presented versus the other arrangement.
Results
Phase 1.
Figure 2 shows the percentage of trials in which each species selected the left array, as a function of the number of dots on both sides of the screen. If a SNARC effect was present, there would be a significant difference for 2-dot arrays compared to 8-dot arrays in the proportion of left choices onscreen following the 5-item target array. The ANOVA indicated no effect of size of the dot arrays, F (1, 17) = 0.07, p = .78, ƞp2 = .01. There also was no effect of species, F (1, 17) = 0.38, p = .55, ƞp2 = 02, and no interaction of species and dot array size, F (1, 17) = 2.79, p = .11, ƞp2 = 14. The monkeys did not differentially select either array (left or right) as a function of the number of dots presented.
Figure 2.
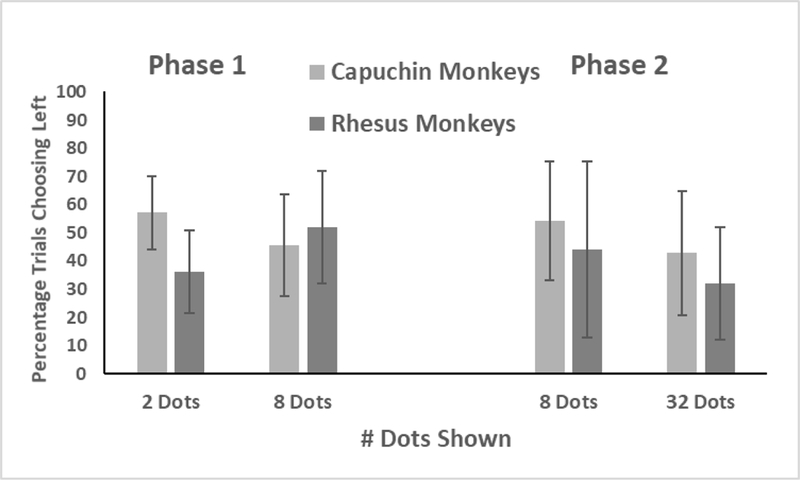
Performance of each species on trials in Phase 1 and Phase 2 in which two arrays presented the same number of dots. Shown are the mean percentages in which the monkeys chose the array at left. There were no significant differences for either species in either phase for those percentages as a function of the number of dots in each array. Error bars indicate 95% CIs.
Phase 2.
Figure 2 also shows the percentage of trials in which each species selected the left array, as a function of the number of dots on both sides of the screen (8 vs. 8 or 32 vs. 32) following the 20-item target array. The ANOVA indicated no effect of size of the dot arrays, F (1, 17) = 2.25, p = .15, ƞp2 = 12. There also was no effect of species, F (1, 17) = 0.32, p = .58, ƞp2 = .02, and no interaction of species and dot array size, F (1, 17) = 0.001, p = .97, ƞp2 = 00. The monkeys again showed no differential selection of either array (left or right) as a function of the number of dots presented.
Phase 1 and Phase 2.
The Wald Chi Squared Test did not report any statistically significant model parameters on RT as a function of species, condition, choice, or the interaction of any of these variables (Figure 3 and Table 2). Thus, the monkeys did not show a side-bias (left-right) or a response time bias as a function of set size across either phase.
Figure 3.
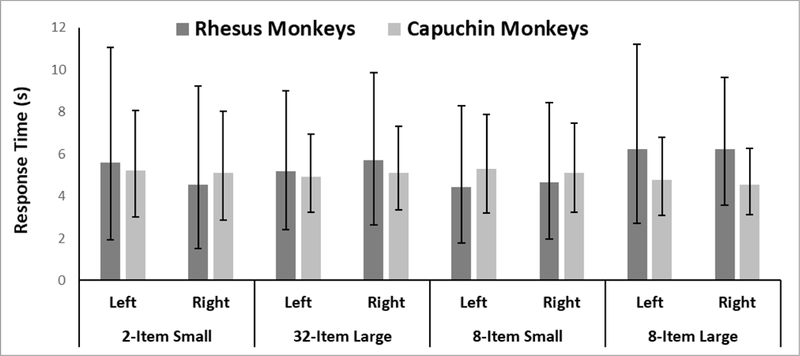
Response latencies for both species in Phase 1 and Phase 2 as a function of the number of items in the central array and the side that was chosen. Error bars indicate 95% CIs.
Table 2.
| X2 value | df | P | |
|---|---|---|---|
| Species | 3.25 | 1 | 0.07 |
| Condition | 0.43 | 3 | 0.94 |
| Selection | 0.0002 | 1 | 0.99 |
| Species x Condition | 4.85 | 3 | 0.18 |
| Species x Selection | 0.04 | 1 | 0.85 |
| Condition x Selection | 0.74 | 3 | 0.86 |
| 3-way Interaction | 0.52 | 3 | 0.92 |
Phase 3.
Table 1 presents the number of trials each monkey required to reach criterion in this phase. Although capuchin monkeys required longer on average to reach criterion (1,321 trials) compared to rhesus monkeys (278 trials), this was not a significant difference due to the high variability in both species, t(17) = 1.18, p = .26.
Phase 4.
Both species showed strong effects of the ratio of smaller to larger set size on trials in which there was a difference (Figure 4): rhesus monkeys r(15) = −.95; capuchin monkeys r(15) = −.97. This established that, with numerical differences, the monkeys readily discriminated the correct choice, and did so in a way that shows typical ratio effects.
Figure 4.
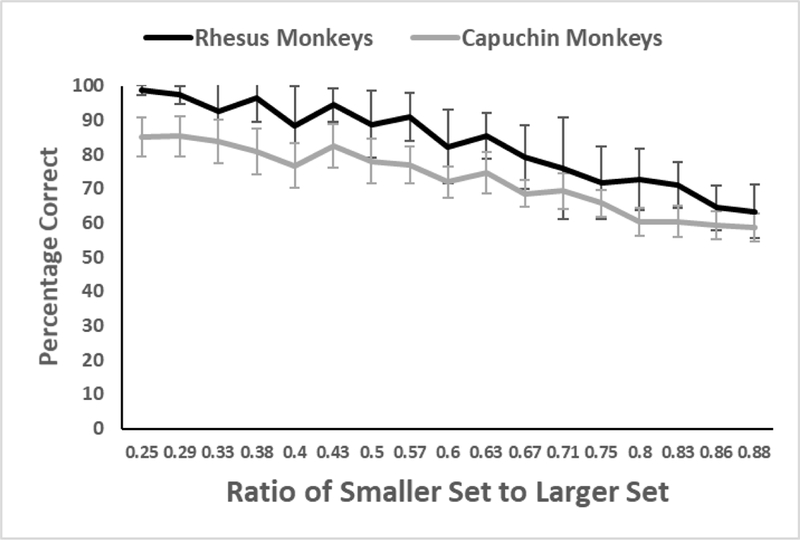
Performance of each species as a function of the ratio of smaller set to larger set on trials in Phase 4 with differences. Both species showed strong ratio effects on these trials. Error bars indicate 95% CIs.
Figure 5 presents the crucial test trials in which both sets were equal, and for each monkey the proportion of trials choosing left is shown. The SNARC effect would predict a difference in left choices as a function of quantity presented. This could be in either direction but is necessary to show a bias. The ANOVA indicated no effect of size of the dot arrays, F (1, 17) = 1.76, p = .20, ƞp2 = .09. There also was no effect of species, F (1, 17) = 0.002 p = .96, ƞp2 = 00, and no interaction of species and dot array size, F (1, 17) = 0.00, p = .99, ƞp2 = 00. The monkeys showed no differential selection of either array (left or right) as a function of the number of dots presented in these trials.
Figure 5.
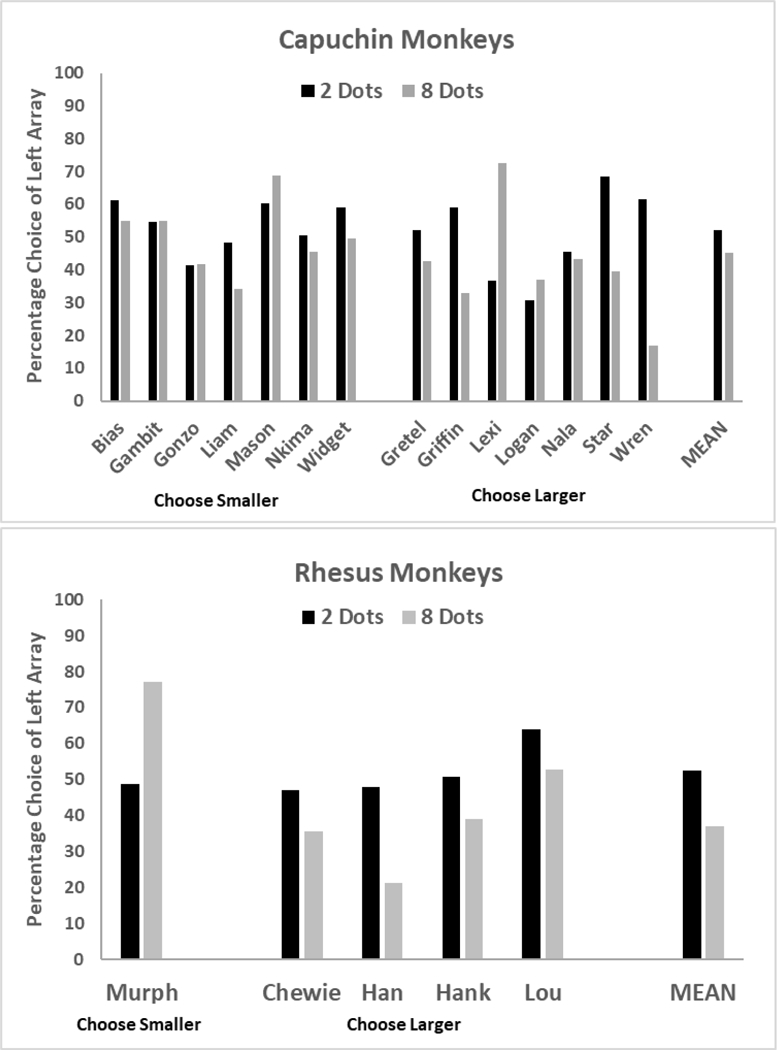
The percentage of trials each monkey selected the left array on trials in Phase 4 where both arrays contained either two or eight dots. There was no significant difference for either species as a function of array size.
After removing trials for which the response time was greater than 60 seconds (2.1% of the trials for rhesus monkeys and 0.5% of the trials for capuchin monkeys), we also examined response time analysis for trials in which both sets contained two items or eight items. There were no statistically significant effects on RT as a function of species, condition, or selection on these trials (Figure 6 and Table 3).
Figure 6.
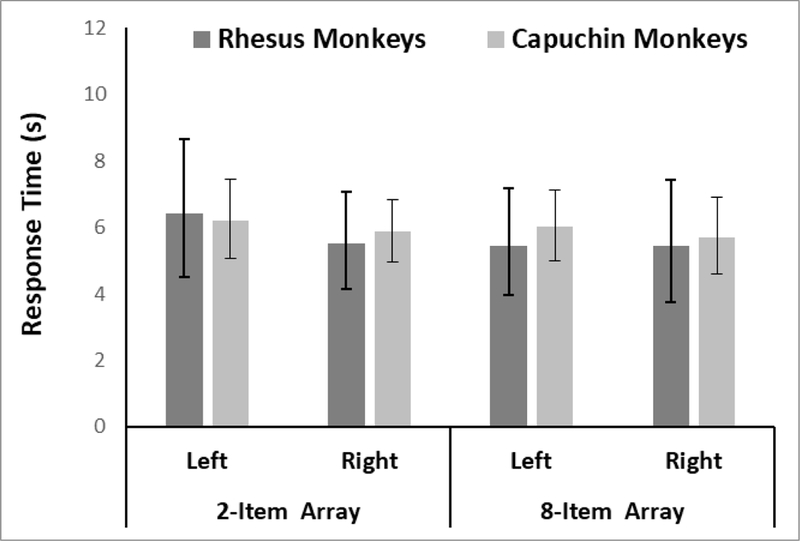
Response latencies for both species in Phase 4 as a function of the number of items in both arrays on equal trials and the side that was chosen. Error bars indicate 95% CIs.
Table 3.
Analysis of deviance table for response times in Phase 4.
| X2 value | df | p | |
|---|---|---|---|
| Species | 0.38 | 1 | 0.54 |
| Condition | 1.66 | 1 | 0.20 |
| Selection | 2.66 | 1 | 0.10 |
| Species x Condition | 0.46 | 1 | 0.50 |
| Species x Selection | 0.006 | 1 | 0.94 |
| Condition x Selection | 0.40 | 1 | 0.53 |
| 3-way Interaction | 1.06 | 1 | 0.30 |
Finally, we examined performance (the percentage of trials correct) for those trials with quantity differences. Because there was no evidence of species differences to this point, we combined all monkeys for the remaining analyses. For each monkey, for each comparison with a numerical difference (all possible combinations of two to eight items, excluding the trials with equal quantities), we calculated a difference score for pairs of quantities in which the smaller quantity was on the left compared to when it was on the right. Thus, a positive score would yield a left-to-right SNARC bias as the monkeys would have higher performance patterns when the small number was positioned on the left versus when the number was positioned on the right (e.g., 2 vs. 3 yields higher performance than 3 vs. 2). A negative score would yield a right-to-left SNARC bias as the monkeys would have performed better when the smaller number was positioned on the right versus when the number was positioned on the left (e.g., 3 vs. 2 yields higher performance than 2 vs. 3). We first took the monkeys’ mean difference scores across all comparisons (Figure 7) and assessed whether there was any group level bias toward a left-to- right mental number line or the reverse. There was not a difference, t(17) = .67,p = .51. We also assessed the same possible effect when only including adjacent comparisons (2v3, 3v4, 4v5, 5v6, 6v7, and 7v8). There was not an effect, t(17) = 1.39, p = .18. We assessed this possible effect for only comparisons between small quantities (2v3, 2v4, and 3v4). There was not an effect, t(17) = 0.23, p = .83. We assessed this possible effect for only comparisons between large quantities (6v7, 6v8, and 7v8). There was not an effect, t(17) = 1.94, p = .07. And, we assessed this possible effect for only comparisons that bridged a small quantity (2, 3, or 4) and a large quantity (6, 7, or 8). There was not an effect of training rule, t(17) = 0.46, p = .65. At the group level, this indicated no evidence of SNARC-like effects.
Figure 7.
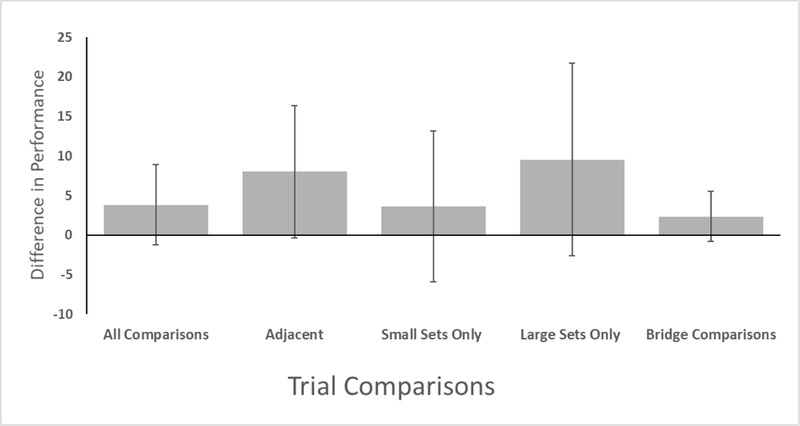
Difference scores for trials in which the two arrays had different numbers of items. These scores reflect the difference in performance on trials in which the smaller array was at left minus performance on trials in which the smaller array was at right. Four comparisons are presented. From left to right, those are all comparisons, all adjacent pairs, only comparisons of small numbers (2v3, 2v4, 3v4), only comparisons of large numbers (6v7, 6v8, 7v8), and comparisons that bridge between small (2, 3, or 4) and large (6, 7, or 8) set sizes. Error bars indicate 95% CIs.
However, the monkeys were trained on different discrimination rules (choose large or choose small). So, we compared the mean difference scores across all comparisons for each monkey to zero difference using a one-sample t-test. This allowed us to determine if specific monkeys showed any increase or decrease in performance depending on where the smaller set was located. These data are presented in Figure 8, and the t-test outcomes are presented in Table 4. Interestingly, this was the strongest evidence of the SNARC effect in these monkeys. Twelve of 19 monkeys showed a significant difference from zero for their mean difference scores. Of these 12, seven monkeys showed better performance when the smaller quantity was at left, whereas five monkeys showed better performance when the small quantity was at right.
Figure 8.
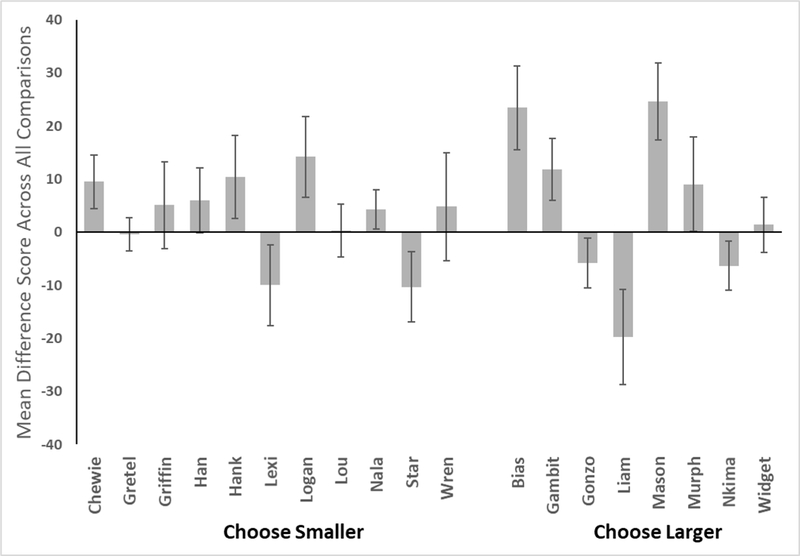
Mean difference scores across all quantity comparisons for each monkey. These scores are calculated as the percentage of trials correct when the smaller array was at left minus the percentage of trials correct when the smaller array was at right. Error bars indicate 95% CIs.
Table 4.
Outcomes of the one-sample t-tests for data from Phase 4.
| t test value | p | |
|---|---|---|
| Choose Smaller | ||
| Chewie | 3.71 | 0.001* |
| Gretel | −0.23 | 0.821 |
| Griffin | 1.22 | 0.237 |
| Han | 1.91 | 0.071 |
| Hank | 2.60 | 0.017* |
| Lexi | −2.57 | 0.018^ |
| Logan | 3.66 | 0.002* |
| Lou | 0.13 | 0.901 |
| Nala | 2.24 | 0.036* |
| Star | −3.05 | 0.006^ |
| Wren | 0.93 | 0.365 |
| Choose Larger | ||
| Bias | 5.84 | <0.001* |
| Gambit | 3.99 | 0.001* |
| Gonzo | −2.39 | 0.027^ |
| Liam | −4.31 | <0.001^ |
| Mason | 6.67 | <0.001* |
| Murph | 1.98 | 0.062 |
| Nkima | −2.68 | 0.014^ |
| Widget | 0.53 | 0.603 |
Note. The df for all of these tests was 20.
indicates that for a given monkey, performance was better when the smaller array was at left compared to right.
indicates that for a given monkey, performance was better when the smaller array was at right compared to left.
However, there did not seem to be any relation between choice rule (choose larger or choose smaller) and this split of the monkeys that showed better performance as a function of spatial arrangement (see Figure 8).
Discussion
We did not find evidence of the SNARC effect in either choice data (left-right selection of stimuli) when two arrays had identical numbers of items or response latency data on those trials for rhesus macaques or capuchin monkeys. We conceptually replicated the procedure of Rugani et al. (2015) in terms of the trial counts and the number of stimuli that the monkeys saw on the computer screen. In Phase 1 and Phase 2, monkeys first were presented with a single target quantity of dots (Phase 1 - five dots; Phase 2 – 20 dots). When subsequently presented with two identical dot arrays, monkeys’ selection of the left or right array did not differ when shown either two or eight dots on both sides (Phase 1) or either eight or 32 dots on both sides (Phase 2). A side preference for smaller numbers (relative to the single target quantity presented in the first 20 trials of each phase) and an opposite-side preference for larger numbers (relative to the single target quantity) would have reflected a SNARC effect. However, this pattern did not emerge. Nor did any pattern in the reaction time analyses that would have reflected a spatial bias in terms of response speed.
Monkeys next learned to choose either the larger or smaller array of dots when there were differences in the number of dots presented (Phase 3). When presented with numerical differences in Phase 4, both species demonstrated classic ratio effects, with performance decreasing as the ratio between sets approached one. This finding is a strong replication of similar past ratio effects in relative quantity judgments in nonhuman primates including some of these same monkeys (e.g., Beran, 2007, 2008; Beran, Evans, Leighty, Harris, & Rice, 2008), and this shows that capuchin monkeys and rhesus monkeys were proficient in discriminating differences in quantities.
In assessing performance for a possible SNARC effect, there was no differential selection of the left-side or right-side array for equal-quantity trials (2 vs. 2 and 8 vs. 8). Overall, there was no effect of response latency in Phase 4 on these trials either. The only evidence of a possible SNARC effect in these monkeys came from Phase 4 trials in which there was a difference in quantity in the two sets. For these trials, it was possible to compare the same numerical pair when the smaller array was at left versus being at right (e.g., 2 vs. 3 and 3 vs. 2). This allowed us to generate a difference score, to see if a specific spatial arrangement (smaller at left, or smaller at right) might lead monkeys to perform better than the opposite arrangement. Here, we did find such an effect at the individual level for 12 of 19 monkeys. What was interesting was that some monkeys showed better performance when smaller sets were at left, whereas others showed this for smaller sets at right. These individual differences did not match the choice rule (choose larger or choose smaller) that had been taught to the monkeys in Phase 3. These results are consistent with Gazes et al. (2017) and Johnson-Ulrich and Vonk (2018) who also found variability among apes, black bears, and humans in the direction of the difference scores, with some subjects showing what would be considered a left-to-right spatial organization of magnitude and others a right-to-left spatial organization. Thus, our results, and the results of past comparative studies suggest that there may not be a natural and consistent orientation for spatial representation of quantities, but the idiosyncratic spatial representations of numerosity do appear in monkeys. In our study, these difference scores were the only evidence we saw for possible spatial representations of magnitude in these monkeys, also suggesting that such spatial representation may not occur in all situations. But, our results (and those of these previous comparative studies) suggest that important work remains to be done to discover what might account for these individual differences, and how robustly they might appear in other kinds of tasks. Our approach is not the only way, or even the most common way, to assess mental number lines in humans, and so it will be important to adapt other designs for use with nonhuman primates. Ideally, testing the same individuals in different kinds of SNARC assessments should aid in helping us learn more about the extent of this effect from a comparative perspective.
The present results from Phase 1 and Phase 2 stand in contrast to recent comparative evidence of the SNARC effect in three-day-old domestic chicks presented with a nearly identical paradigm (Rugani et al., 2015), although one in which the chicks moved through actual space. After familiarization with a five-item array, chicks spontaneously demonstrated a preference for the smaller number (2 items) on the left side and the larger number (8 items) on the right side. This preference was not absolute; chicks then preferred the 8-item array positioned on the left when it was relatively smaller than the 20-item target quantity. Notably, the response mode differed between the present work and the Rugani et al. task in which chicks circumnavigated panels within their home enclosures by physically moving behind them to obtain food. In the present study, responses were made when the monkeys deflected a joystick-controlled cursor with their hand to the left of right sight of a computer monitor to contact one of the two dot arrays. The additional effort associated with physical movements of the body through space required of the chicks (relative to joystick deflections by the monkeys) may have had a differential impact on the results; however, SNARC-like effects have emerged in primates using touch-screen computer tasks such as that used by Gazes et al (2017) and Adachi (2014).
Other behavioral studies with nonhuman primates assessing the relationship between number and space have yielded evidence to support such a relationship between numerical processing and response behavior, as well as neural evidence for a link between space and number in the parietal cortex of both monkeys and humans (e.g., Hubbard et al., 2005). For example, Drucker and Brannon (2014) reported that rhesus macaques successfully learned to select the fourth of five vertically-oriented stimuli across a variety of presentation formats that manipulated shape, color, overall array position, and inter-stimulus distance. Of relevance to the current study, when the stimuli were presented horizontally, the monkeys continued to select the fourth stimulus but only from the left side, suggesting that stimuli were somehow ordered from left to right. In another study, rhesus macaques that were trained to sequence multiple stimuli in a vertical array were more successful in a subsequent transitive inference task (if A>B and B>C then A>C) using the same stimuli congruently positioned to the sequence task versus stimuli arranged incongruent to the sequencing task (Gazes, Lazareva, Bergene, & Hampton, 2014). Taken together with the results of Adachi (2014), Gazes et al. (2017), and Johnson-Ulrich and Vonk (2018) demonstrating the SNARC effect in various great ape species, these comparative studies suggest that a spatial relationship of magnitude may be shared across the animal kingdom and may extend beyond human-unique linguistic and cultural experiences.
But, not all recent results from nonhuman species reflect SNARC effects. The only replications to date of Rugani et al. (2015) were those of Noyek (2016) with other chicks, and a study with cleaner fish (Triki & Bshary, 2018). Noyek did not replicate the effects reported by Rugani et al., and although the fish showed good discrimination abilities when two arrays differed in quantity, they did not show any side biases in their choices for equal array options as would be predicted for a SNARC effect. Our present results from Phase 1 and Phase 2 match those of Noyek and of Triki and Bshary, and also fail to support the idea of SNARC effects in nonhuman species using equal quantity comparisons.
It is worth noting that our animals were well-trained on computer tasks and particularly on tasks using a relative quantity discrimination procedure as used here, and they almost certainly approach new tasks with the goal of maximizing reward. Equal-array trials always led to reward, and perhaps the monkeys quickly came to realize this, and therefore were not as susceptible to natural space-number biases as would be young chicks in some of their first perceptual discriminations after birth. This is also an important future avenue for research, to examine whether these biases may be more prevalent in task naïve animals or come to be “dampened” through engagement of cognitive control mechanisms that override natural response tendencies such as spatial-numerical representations. In our task, this was perhaps a likely contributor to the lack of evidence of SNARC effects, although at least Phase 1 and Phase 2 of our task allowed for a fairly unique task that was not like most that our monkeys have performed.
We cautiously conclude that the present results suggest limits to when SNARC effects might be seen in nonhuman primates, although we did see some evidence in Phase 4 of biases for certain spatial representations of quantity. Again, these biases were inconsistent across individuals with some monkeys showing a left-to-right bias whereas others showed a right-to-left bias. Continued cross-species comparisons are important in resolving the degree to which SNARC effects are broadly exhibited versus more narrowly exhibited. That our monkeys did not show a SNARC effect in this test, using these methods, does not mean that no test could show a different result. It has recently been proposed that the SNARC effect may not be a unitary phenomenon (Moro, Dell’Acqua, & Cutini, 2018), and that it may emerge as a result of different causes including spatial representation mechanisms and different processing modes.
Comparative contributions can continue to offer valuable insights for better understanding the nature of the SNARC effect, and so we encourage a broader assessment of this effect in nonhuman animals. Importantly, the tests given to animals need also to be given to humans, as in the work of Johnson-Ulrich and Vonk (2018), so that the methods developed for use with nonhuman animals can be appropriately evaluated for their ability (or inability) to generate SNARC-like effects in humans.
Acknowledgments
This research was supported by NICHD grant HD060563. The authors thank the care staff at the Language Research Center for assistance with testing and for animal care.
Contributor Information
Michael J. Beran, Department of Psychology and the Language Research Center, Georgia State University
Kristin French, Department of Psychology and the Language Research Center, Georgia State University.
Travis R. Smith, Department of Psychology, Kansas State University
Audrey E. Parrish, Department of Psychology, The Citadel
References
- Adachi I (2014). Spontaneous spatial mapping of learned sequence in chimpanzees: Evidence for a SNARC-like effect. PLoS One, 9, e90373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bächtold D, Baumüller M, & Brugger P (1998). Stimulus-response compatibility in representational space. Neuropsychologia, 36, 731–735. [DOI] [PubMed] [Google Scholar]
- Bates D, Maechler M, Bolker B, Walker S, Christensen RHB, Singmann H, ... & Bolker MB (2016). Package ‘lme4’. In R Package Version 1 1–10. [Google Scholar]
- Beran MJ (2007). Rhesus monkeys (Macaca mulatta) enumerate large and small sequentially presented sets of items using analog numerical representations. Journal of Experimental Psychology: Animal Behavior Processes, 33, 42–54. [DOI] [PubMed] [Google Scholar]
- Beran MJ (2008). Monkeys (Macaca mulatta and Cebus apella) track, enumerate, and compare multiple sets of moving items. Journal of Experimental Psychology: Animal Behavior Processes, 34, 63–74. [DOI] [PubMed] [Google Scholar]
- Beran MJ, Evans TA, Leighty K, Harris EH, & Rice D (2008). Summation and quantity judgment of simultaneously and sequentially presented sets by capuchin monkeys (Cebus apella). American Journal of Primatology, 70, 191–194. [DOI] [PubMed] [Google Scholar]
- Berch DB, Foley EJ, Hill RJ, & Ryan PM (1999). Extracting parity and magnitude from Arabic numerals: Developmental changes in number processing and mental representation. Journal of Experimental Child Psychology, 74, 286–308. [DOI] [PubMed] [Google Scholar]
- Bulf H, de Hevia MD, & Macchi Cassia V. (2016). Small on the left, large on the right: Numbers orient visual attention onto space in preverbal infants. Developmental Science, 19, 394–401. [DOI] [PubMed] [Google Scholar]
- Cantlon JF, & Brannon EM (2005). Semantic congruity affects numerical judgments similarly in monkeys and humans. Proceedings of the National Academy of Sciences, 102, 16507–16511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cantlon JF, & Brannon EM (2006). Shared system for ordering small and large numbers in Nieder, A. (2009). Prefrontal cortex and the evolution of symbolic reference. Current Opinion in Neurobiology, 19, 99–108. [DOI] [PubMed] [Google Scholar]
- Cohen Kadosh R, & Dowker A (Eds.) (2015). Oxford handbook of mathematical cognition. Oxford, UK: Oxford University Press. [Google Scholar]
- Cohen Kadosh R, Lammertyn J, & Izard V (2008). Are numbers special? An overview of chronometric, neuroimaging, developmental and comparative studies of magnitude representation. Progress in Neurobiology, 84, 132–147. [DOI] [PubMed] [Google Scholar]
- Dehaene S, Bossini S, & Giraux P (1993). The mental representation of parity and number magnitude. Journal of Experimental Psychology: General, 122, 371–396. [Google Scholar]
- Dehaene S, Piazza M, Pinel P, and Cohen L (2003). Three parietal circuits for number processing. Cognitive Neuropsychology, 20, 487–506. [DOI] [PubMed] [Google Scholar]
- de Hevia MD, Girelli L, & Macchi Cassia V. (2012). Minds without language represent number through space: Origins of the mental number line. Frontiers in Psychology, 3, 466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Hevia MD, & Spelke ES (2009). Spontaneous mapping of number and space in adults and young children. Cognition, 110, 198–207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diamond RF, Gazes RP, & Hampton RR (2015, June). Flexible spatial representation of magnitude in monkeys (Macaca mulatta). In Primate Research Supplement The 31th Congress Primate Society of Japan (pp. 73–73). Primate Society of Japan. [Google Scholar]
- Drucker CB, & Brannon EM (2014). Rhesus monkeys (Macaca mulatta) map number onto space. Cognition, 132, 57–67. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drucker CB, & Brannon EM (2015). Commentary on: “Number-space mapping in the newborn chick resembles humans’ mental number line.” Frontiers in Psychology, 6, 352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evans TA, Beran MJ, Chan B, Klein ED, & Menzel CR (2008). An efficient computerized testing method for the capuchin monkey (Cebus apella): Adaptation of the LRC-CTS to a socially housed nonhuman primate species. Behavior Research Methods, 40, 590–596. [DOI] [PubMed] [Google Scholar]
- Gazes RP, Diamond RF, Hope JM, Caillaud D, Stoinski TS, & Hampton RR (2017). Spatial representation of magnitude in gorillas and orangutans. Cognition, 168, 312–319. [DOI] [PubMed] [Google Scholar]
- Gazes RP, Lazareva OF, Bergene CN, & Hampton RR (2014). Effects of spatial training on transitive inference performance in humans and rhesus monkeys. Journal of Experimental Psychology: Animal Learning and Cognition, 40, 477–489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geary D, Berch D, & Mann Koepke K (Eds.) (2015). Evolutionary origins and early development of number processing. Amsterdam: Elsevier. [Google Scholar]
- Gelman A, & Hill J (2007). Data analysis using regression and multilevel/hierarchical models. Cambridge, MA: Cambridge University Press University Press. [Google Scholar]
- Gevers W, Reynvoet B, & Fias W (2003). The mental representation of ordinal sequences is spatially organized. Cognition, 87, B87–B95. [DOI] [PubMed] [Google Scholar]
- Gevers W, Verguts T, Reynvoet B, Caessens B, & Fias W (2006). Numbers and space: A computational model of the SNARC effect. Journal of Experimental Psychology: Human Perception and Performance, 32, 32–44. [DOI] [PubMed] [Google Scholar]
- Ginsburg V, & Gevers W (2015). Spatial coding of ordinal information in short- and longterm memory. Frontiers in Human Neuroscience, 9, 8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harshaw C (2015). Comment on “Number-space mapping in the newborn chick resembles humans” mental number line.” Science, 348, 1438b. [DOI] [PubMed] [Google Scholar]
- Harvey BM, Klein BP, Petridou N, & Dumoulin SO (2013). Topographic representation of numerosity in the human parietal cortex. Science, 341, 1123–1126. [DOI] [PubMed] [Google Scholar]
- Henik A (Ed.) (2016). Continuous issues in numerical cognition: How many or how much. San Diego: Academic Press. [Google Scholar]
- Hubbard EM, Piazza M, Pinel P, & Dehaene S (2005). Interactions between number and space in parietal cortex. Nature Reviews Neuroscience, 6, 435–448. [DOI] [PubMed] [Google Scholar]
- Hung Y, Hung DL, Tzeng OJL, & Wu DH (2008). Flexible spatial mapping of different notations of numbers in Chinese readers. Cognition, 106, 1441–1450. [DOI] [PubMed] [Google Scholar]
- Johnson-Ulrich Z, & Vonk J (2018). Spatial representation of magnitude in humans (Homo sapiens), Western lowland gorillas (Gorilla gorilla gorilla), and American black bears (Ursus americanus). Animal Cognition, 21, 531–550. [DOI] [PubMed] [Google Scholar]
- Lourenco SF (2016). How do humans represent numerical and nonnumerical magnitudes? Evidence for an integrated system of magnitude representation across development In Henik A (Ed.), Continuous issues in numerical cognition: How many or how much (pp. 375–403). London: Elsevier Academic Press. [Google Scholar]
- Lourenco SF, & Longo MR (2010). General magnitude representation in human infants. Psychological Science, 21, 873–881. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mangalam M, & Karve SM (2015). Comment on ““Number-space mapping in the newborn chick resembles humans” mental number line.” Science, 348, 1438b. [DOI] [PubMed] [Google Scholar]
- Mapelli D, Rusconi E, & Umiltà C (2003). The SNARC effect: An instance of the Simon effect? Cognition, 88, B1–B10. [DOI] [PubMed] [Google Scholar]
- Moro SB, Dell”Acqua R, & Cutini S (2018). The SNARC effect is not a unitary phenomenon. Psychonomic Bulletin & Review, 25, 688–695. [DOI] [PubMed] [Google Scholar]
- Nieder A, & Merten K (2007). A labeled-line code for small and large numerosities in the monkey prefrontal cortex. The Journal of Neuroscience, 27, 5986–5993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nieder A, & Miller EK (2003). Coding of cognitive magnitude: Compressed scaling of numerical information in the primate prefrontal cortex. Neuron, 37, 149–157. [DOI] [PubMed] [Google Scholar]
- Nieder A, & Miller EK (2004). A parieto-frontal network for visual numerical information in the monkey. Proceedings of the National Academy of Sciences, 101, 7457–7462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Noyek S (2016). The mental number line in domestic chicks. Undergraduate Honors Theses. 29 https://ir.lib.uwo.ca/psychduht/29 [Google Scholar]
- Nuerk HC, Wood G, & Willmes K (2005). The universal SNARC effect: The association between number magnitude and space is amodal. Experimental Psychology, 52, 187–194. [DOI] [PubMed] [Google Scholar]
- Nunez RE (2011). No innate number line in the human brain. Journal of Cross-Cultural Psychology, 42, 651–668. [Google Scholar]
- Patro K, & Haman M (2012). The spatial-numerical congruity effect in preschoolers. Journal of Experimental Child Psychology, 111, 534–542. [DOI] [PubMed] [Google Scholar]
- Restle F (1970). Speed of adding and comparing numbers. Journal of Experimental Psychology, 83, 274–278. [Google Scholar]
- Richardson WK, Washburn DA, Hopkins WD, Savage-Rumbaugh ES, & Rumbaugh DM (1990). The NASA/LRC computerized test system. Behavior Research Methods, Instruments, & Computers, 22, 127–131. [DOI] [PubMed] [Google Scholar]
- Rugani R, & de Hevia MD (2017). Number-space associations without language: Evidence from preverbal human infants and non-human animal species. Psychonomic Bulletin & Review, 24, 352–369. [DOI] [PubMed] [Google Scholar]
- Rugani R, Vallortigara G, Priftis K, & Regolin L (2015). Number-space mapping in the newborn chick resembles humans” mental number line. Science, 347, 534–536. [DOI] [PubMed] [Google Scholar]
- Rusconi E, Umiltà C, & Galfano G (2006). Breaking ranks: Space and number may march to the beat of a different drum. Cortex, 42, 1124–1127. [DOI] [PubMed] [Google Scholar]
- Shaki S, & Fischer MH (2008). Reading space into numbers - a cross-linguistic comparison of the SNARC effect. Cognition, 108, 590–599. [DOI] [PubMed] [Google Scholar]
- Shaki S, & Fischer MH (2015). Newborn chicks need no number tricks. Commentary: Number-space mapping in the newborn chick resembles humans” mental number line. Frontiers in Human Neuroscience, 9, 451. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shaki S, Fischer MH, & Petrusic WM (2009). Reading habits for both words and numbers contribute to the SNARC effect. Psychonomic Bulletin & Review, 16, 328–331. [DOI] [PubMed] [Google Scholar]
- Shaki S, & Gevers W (2011). Cultural characteristics dissociate magnitude and ordinal information processing. Journal of Cross-Cultural Psychology, 42, 639–650. [Google Scholar]
- Shaki S, Petrusic WM, & Leth-Steensen C (2012). SNARC effects with numerical and non- numerical symbolic comparative judgments: Instructional and cultural dependencies. Journal of Experimental Psychology: Human Perception and Performance, 38, 515–530. [DOI] [PubMed] [Google Scholar]
- Triki Z, & Bshary R (2018). Cleaner fish Labroides dimidiatus discriminate numbers but fail a mental number line test. Animal Cognition, 21, 99–107. [DOI] [PubMed] [Google Scholar]
- van Dijck JP, & Fias W (2011). A working memory account for spatial-numerical associations. Cognition, 119, 114–119. [DOI] [PubMed] [Google Scholar]
- van Dijck JP, Gevers W, & Fias W (2009). Numbers are associated with different types of spatial information depending on the task. Cognition, 113, 248–253. [DOI] [PubMed] [Google Scholar]
- van Galen MS, & Reitsma P (2008). Developing access to number magnitude: a study of the SNARC effect in 7- to 9-year-olds. Journal of Experimental Child Psychology, 101, 99–113. [DOI] [PubMed] [Google Scholar]
- Walsh V (2003). A theory of magnitude: Common cortical metrices of time, space and quantity. Trends in Cognitive Sciences, 7, 483–488. [DOI] [PubMed] [Google Scholar]
- Wood G, Nuerk HC, & Willmes K (2006). Crossed hands and the SNARC effect: A failure to replicate Dehaene, Bossini and Giraux (1993). Cortex, 42, 1069–1079. [DOI] [PubMed] [Google Scholar]
- Wood G, Willmes K, Nuerk HC, & Fischer MH (2008). On the cognitive link between space and number: A meta-analysis of the SNARC effect. Psychology Science, 50, 489–525. [Google Scholar]
- Zebian S (2005). Linkages between number concepts, spatial thinking, and directionality of writing: The SNARC effect and the reverse SNARC effect in English and Arabic monoliterates, biliterates, and illiterate Arabic speakers. Journal of Cognition and Culture, 5, 165–190. [Google Scholar]


