Magnitude‐based Inference is not Bayesian and is not a valid method of inference

When people thought the earth was flat, they were wrong. When people thought the earth was spherical, they were wrong. But if you think that thinking the earth is spherical is just as wrong as thinking the earth is flat, then your view is wronger than both of them put together. 1 Isaac Asimov

Recently, Diong2 wrote a commentary for the Scandinavian Journal of Medicine and Science in Sports critiquing a study by Pamboris et al3 for not correctly interpreting confidence intervals that contained zero. Pamboris et al4 wrote a response letter in return, seeking to rebut Diong's critique and arguing that they were appropriately implementing Magnitude‐based Inference (MBI), which they argue is “based on Bayesian inference and [the] conclusions are robust.”4 They neglect, however, that multiple statisticians5, 6, 7 including Bayesian statisticians8, 9 have strongly critiqued and even called for rejection of MBI as a method of inference. In this commentary, we hope to resolve some of that ambiguity and concisely explain why MBI is not a robust method of statistical inference.

In their response letter, Pamboris et al4 correctly note that Diong2 defined confidence intervals inaccurately. However, Diong's definitional error does not undermine her central argument, which is that the original authors have reached conclusions that are not justified by the data. Pamboris et al compared slow dynamic stretching (SDS) to fast dynamic stretching (FDS) in an 18‐person crossover design.3 They concluded that “SDS showed greater improvement than FDS in both neuromechanical and sensorimotor performance,” but the differences observed between conditions in this small sample were completely consistent with random variation due to sampling variability, as we will show. As with numerous papers in the sport and exercise literature, the use of MBI led the authors to reach overly optimistic conclusions.

Pamboris et al4 claim that their conclusions are justified because the “interpretation of our results was according to the recommended MBI procedures,” but MBI is not an established statistical method. To date, MBI has never been published in a statistical journal10, 11, 12 nor have equations with formal notation ever been provided. Instead, MBI is implemented in Microsoft Excel spreadsheets, solely available from www.sportsci.org, with no clear documentation or version control.13, 14 Pamboris et al4 also fail to cite the numerous critiques of MBI from statisticians in the academic literature5, 6, 7, 8, 9 and in the popular press.15, 16 Further, their arguments neglect that MBI has been questioned or outright banned by major sports medicine journals.17, 18 Prima facie, this evidence should make one skeptical about the legitimacy of MBI. Using the Pamboris et al paper3 as a motivating example, we will give a brief review of MBI and explain why it is not a robust method of inference.

1. WHAT IS MBI?

As a method, MBI arose from an understandable desire to put more emphasis on effect sizes and estimation. MBI classifies results into three categories of effect size: harmful (or negative), trivial, and beneficial (or positive). Pamboris et al3 defined as trivial any values between −0.2 and +0.2 in standardized effect size units, the default values recommended by MBI's creators,10, 11 and, in our experience, the values selected by the vast majority of MBI practitioners.

MBI next assigns probabilities that the true effect is either beneficial (positive), trivial, or harmful (negative). For example, Pamboris et al3 report a 74% chance that SDS improves positional error relative to FDS (their table 33). These probabilities are derived from an interpretation of confidence intervals and P‐values that we will demonstrate is incorrect. In the MBI Excel spreadsheets, MBI calculates one‐sided P‐values from standard hypothesis tests.5 The one‐sided P‐value for benefit gives the probability that the observed data (or values more extreme) would have arisen if the intervention was not beneficial (eg, true effect ≤ 0.2). For example, a P‐value of 0.10 tells us that an effect at least as large as the one in our sample had a 10% chance of arising if the intervention was not beneficial. This can be written as:

$$P-\text{value}=P\left(\text{data}|\text{true}\text{effect}\le 0.2\right)=10\%$$

Recall that the “|” symbol means “given that” or “conditioned on.” Also, note that for simplicity, we will use “data” to denote the observed value and all values more extreme. As is taught in all introductory statistics classes, the P‐value does not tell us the probability that the true effect is beneficial or not beneficial given the data:

$$P\left(\text{true}\text{effect}\le 0.2|\text{data}\right)\ne P\left(\text{data}|\text{true}\text{effect}\le 0.2\right)\ne 10\%$$

Yet, this is exactly how MBI interprets it. MBI concludes that there is a 10% chance that the intervention is not beneficial and a 90% chance that it is beneficial. Interpreting P‐values in this way is equivalent to interpreting frequentist confidence intervals as if they were Bayesian credible intervals; we will later show why this is incorrect.

Interestingly, Pamboris et al appear to be unaware of the math underlying the spreadsheets as they state in their response letter4 that their inferences “have nothing whatsoever to do with NHST [null hypothesis significance testing].” In fact, the MBI probabilities are calculated based on standard hypothesis tests. The spreadsheets used by Pamboris et al implement two one‐sided t tests with non‐zero null values.5 This was shown mathematically by Welsh & Knight.5 To confirm this, we simulated data from a randomized trial with n = 10 per group and a normally distributed outcome (with SD 1.0 and means of 0.1 and 0 in the experimental and control groups, respectively). When we analyzed these data in the MBI spreadsheet for comparing two means (xCompare2groups.xls), we got a probability of benefit of 35.603%. When we ran Welch's t test for unequal variances with H₀ = 0.2 and one‐sided (for benefit) in SAS version 9.4, we got a P‐value of 0.64397. 1‐0.64397 = 0.35603.

Magnitude‐based Inference provides the following qualitative descriptors for the probabilities: 0.5% is most unlikely; 0.5%‐5% is very unlikely; 5%‐25% is unlikely; 25%‐75% is possible; 75%‐95% is likely; 95%‐99.5% is very likely; and 99.5% is most likely.10, 11 MBI also deems effects unclear when the probabilities of harm and benefit are both elevated, typically ≥5%, which is equivalent to the 90% confidence interval overlapping both the harmful and beneficial ranges. Accordingly, in their tables, Pamboris et al3 label effects as “unlikely,” “possible,” “likely,” “very likely,” and “unclear.”

2. HOW HAVE STATISTICIANS CRITICIZED MBI?

Statisticians have noted several problems with MBI, including that it lacks a sound mathematical foundation, incorrectly interprets frequentist statistics (P‐values and confidence intervals), and gives overly optimistic inferences, increasing the risk of finding spurious effects, especially when using small samples.

Magnitude‐based Inference was first introduced in the peer‐reviewed literature in 2006.10 The method was later criticized in the same journal by the statisticians Richard Barker and Matthew Schofield, who argued that the only way to make probabilistic statements about true effects—such as: “There is a 90% chance that the intervention is beneficial”—is to adopt a fully Bayesian approach.8 They also noted that MBI draws incorrect, and overly optimistic, inferences from confidence intervals, as shown in Figure 1.

Figure 1.

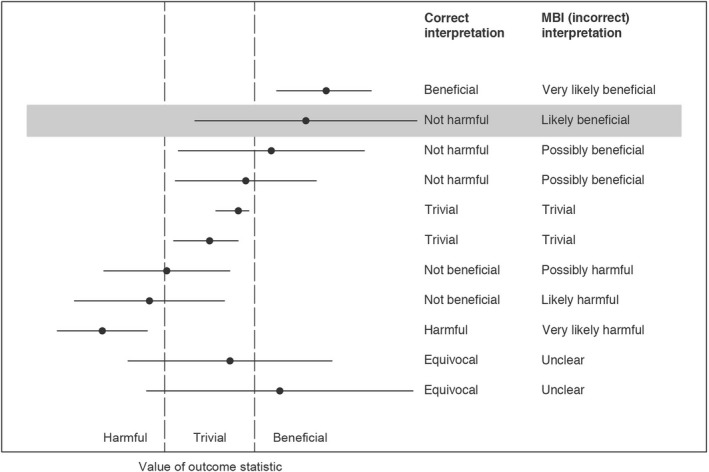
This figure shows the appropriate inferences that can be drawn from different 95% confidence intervals (or 90% for a lower level of confidence, as in the Pamboris paper3) based on how they fall relative to the harmful, trivial, and beneficial ranges and contrasts these with the incorrect inferences that MBI draws. Shaded 90% confidence interval is similar to the confidence interval, −16.9% to 96.5%, for improvement in muscle strain for SDS versus FDS in the paper by Pamboris et al3. They used this finding as well as several “possibly” beneficial findings to justify their conclusion that “SDS showed greater improvement than FDS in both neuromechanical and sensorimotor performance.” Figure is based on Barker and Schofield8

For example, in the Pamboris study,3 participants experienced an average 39.8% improvement in muscle strain in the SDS compared with the FDS condition with 90% confidence interval of −16.9% to 96.5% (Figure 1). According to MBI methodology, this gives the conclusion that SDS is “likely beneficial” compared with FDS. But the correct interpretation of this confidence interval (assuming that −16.9% is within the trivial range) is that SDS is “not harmful” relative to FDS (Figure 1). As such, concluding that “SDS showed greater improvement than FDS in both neuromechanical and sensorimotor performance” is not warranted.

In 2015, another pair of statisticians—Alan Welsh and Emma Knight—again raised the alarm about MBI.5 The mathematical formulas implemented in the MBI spreadsheets are not published anywhere, so Welsh and Knight painstakingly extracted the algorithms from the cells of the Excel spreadsheets. They showed that, among other issues, the method leads to inflated rates of Type I error. Recall that Type I errors are false‐positive errors.

In response to this critique, MBI's creators published a 2016 paper in the journal Sports Medicine claiming that MBI has better Type I and Type II error rates than standard hypothesis testing.19 This claim is dubious at face value, since Type I and Type II error necessarily trade off. Indeed, statistician Kristin Sainani (co‐author of this paper) used both math and simulation to definitively disprove their claim.6 She showed that, for typical usage, MBI yields unacceptably high Type I error rates and that MBI's sample size calculators are tuned to maximize Type I error.

The crux of Welsh and Knight's, and Sainani's arguments is that MBI inflates the risk of concluding benefit for ineffective interventions. Like statistical significance testing, MBI provides thresholds of evidence. Instead of highlighting P < 0.05 or P < 0.01, MBI practitioners highlight “possible” or “likely” effects. For example, Pamboris et al3 call out one “likely” and several “possible” differences between SDS and FDS (see their table 3)3 and use these findings to justify their conclusion that “SDS showed greater improvement than FDS in both neuromechanical and sensorimotor performance.” But MBI's evidentiary thresholds are extremely weak.20 Using math and simulation, we estimate that—for the way MBI is typically applied in the literature—the “possible” bar is comparable to using a significance threshold as high as P < 0.60, and the “likely” bar is comparable to using a significance threshold as high as P < 0.25.¹ This means that when an intervention is completely ineffective, MBI practitioners will find false‐positive “possible” effects as much as 60% of the time and false‐positive “likely” effects as much as 25% of the time. Unfortunately, MBI practitioners have not been informed that these levels of evidence are weak: Pamboris et al, for instance, insist that “our conclusions are robust.”4

In fact, the evidence that Pamboris et al3 present to support their claims is weak. Though Pamboris et al3 did not present standard P‐values for their comparisons, it is easy to calculate these from the confidence intervals provided. The P‐value gives important information about the level of evidence that the data provide regardless of whether one performs a binary significance test. For example, Pamboris et al3 found that SDS has a “likely beneficial” effect on muscle strain compared with FDS. We back‐calculated the two‐sided P‐value for this comparison (for the null hypothesis of true effect = 0) as P(T₁₇≥(39.8%/32.4%) or T₁₇≤(−39.8%/32.4%)) = 0.24. This means that if there was truly no difference between the conditions, we would have seen a difference of 39.8% or bigger in nearly a quarter of studies just by chance. Note that all other between‐condition comparisons (eg, torque) were associated with even higher P‐values, meaning they represent even weaker levels of evidence.

Claims from MBI studies are being propagated in the literature as definitive findings. In their discussion section, Pamboris et al3 cite a previous study21 that they say: “found a decrease in muscle fascicle strain combined with an increase in muscle stiffness.” This reference is to an MBI study that provided similarly weak levels of evidence for its conclusion. Yet, the findings are not qualified as being based on weak evidence, but instead are presented as conclusive. When these claims are wrong, they are false‐positive errors.

MBI's creators have argued against these various critiques not in the peer‐reviewed literature, but on their personal website, which is primarily trafficked by sports scientists, not statisticians.22 This creates the illusion of an active debate, when in fact MBI has no support from the mainstream statistical community. It is important to note, additionally, that their counterarguments have never questioned the math presented by statisticians.5, 6, 8, 9 Rather, in response to these various critiques, MBI's creators have focused on attacking classical frequentism and then shifted their description of MBI. In response to Welsh and Knight's paper,5 they wrote that “MBI is quite possibly the ideal frequentist‐Bayesian hybrid.”12 More recently, they have begun to describe MBI as purely Bayesian as a method to avoid critiques of MBI. On their website, they write:

We advise researchers to describe their inferences about magnitudes as the legitimate reference Bayes with a dispersed uniform prior when submitting manuscripts to any journal banning MBI.22

Pamboris and colleagues’ response letter adopts this tactic,4 claiming “Our inferences are Bayesian” despite never describing the methods as Bayesian in the original paper.3 In the sections that follow, we will explain what a Bayesian analysis is and why MBI is not a valid Bayesian analysis.

3. WHAT IS A BAYESIAN ANALYSIS?

As previously described, P‐values give the probability of the observed data (and all more extreme values) given a null hypothesis such as “the true effect is not beneficial” or “the true effect is 0”:

$$P-\text{value}=P\left(\text{data}|\text{true}\text{effect}\le 0.2\right)$$

The P‐value is not the probability that the true effect is or is not beneficial given the data:

$$P\left(\text{data}|\text{true}\text{effect}\le 0.2\right)\ne P\left(\text{true}\text{effect}\le 0.2|\text{data}\right)$$

The latter quantity is what we would often like to know, but we cannot infer this probability directly from the data. Rather, we have to apply Bayes’ rule, which requires additional information (in red):

$$P(\text{true}\text{effect}\le 0.2|\text{data})=\frac{P(\text{data}|\text{true}\text{effect}\le 0.2)P(\text{true}\text{effect}\le 0.2)}{P(\text{data})}$$

The additional information in the numerator is called the “prior probability” and reflects our beliefs about the true effect prior to conducting the study. Probabilities about the data are called the “likelihood” function. Combining the likelihood function and the prior probability gives the “posterior probability,” which is what we want to know. For simplicity, this is often written as:

$$\text{posterior}\propto \text{likehood}\times \text{prior}$$

Bayesian analysis of data does not calculate a single probability alone, but instead calculates a full probability distribution. Using the posterior probability distribution, Bayesians can compute “credible intervals” which give the probability that the true effect falls within a certain range. For example, a 90% Bayesian credible interval of −1.5 to 5.0 tells us “There is a 90% chance the true effect lies between −1.5 and 5.0.” Interpreting a P‐value as a Bayesian posterior probability is equivalent to interpreting a confidence interval as a Bayesian credible interval.

Finally, it is important to note that just because a posterior distribution can be calculated that does not make it necessarily valid or reliable. The prior distribution represents an assumption about the nature of reality. As with any model assumption, the prior distribution must be explained, justified, and tested.

4. WHY IS MBI NOT A BAYESIAN ANALYSIS?

The MBI spreadsheets make inferences solely based on frequentist statistics.5 They do not implement any type of Bayesian analysis. What MBI does is to interpret frequentist statistics as if they were Bayesian statistics. In this section, we will explain why this is not an acceptable approach.

A defining feature of a Bayesian analysis is the incorporation of a prior probability distribution. As previously mentioned, frequentist statistics give probabilities about data given a hypothesis (eg, “The probability of the data if the intervention were equivalent to control is 10%.”). The problem is that we would prefer to obtain the probability of a hypothesis given the data (eg, “There is a 90% chance that the intervention is beneficial.”). Bayesian statistical methods calculate these probabilities by incorporating additional information beyond what the data alone provide. This additional information is called the “prior probability distribution.” As described above, the choice of prior can greatly affect the results, particularly when dealing with small samples.

Pamboris and colleagues equate MBI to “Bayesian inference with a default prior.”4 But “default prior” is not sufficient detail for a scientific paper. For example, a common “default” choice when comparing means is the Cauchy probability distribution (which looks like a normal distribution but has more area in the tails). Even then, there is not a single Cauchy distribution—there is an infinite number determined by the distribution's scale parameter. A Bayesian employing a Cauchy prior would perform a sensitivity analysis to determine how the choice of scale parameter affects the results. MBI practitioners do not specify a prior and do not reflect on how the choice of prior might affect their results. This is because they do not actually incorporate a prior.

Magnitude‐based Inference attempts to simply bypass the prior. Rather than using the central Bayesian formula: posterior ∝ likelihood × prior, MBI instead assumes that posterior = likelihood in all cases, and thus that frequentist P‐values and confidence intervals can be given a direct Bayesian interpretation. In MBI, P‐values are interpreted as Bayesian posterior probabilities or, equivalently, confidence intervals are interpreted as Bayesian credible intervals. There are several problems with this: (1) MBI users are never required to specify or justify their prior, think about its implications, or perform sensitivity analyses to gauge the effect of the choice on their results; and (2) For simple problems, such as comparing means with a known standard deviation, confidence intervals are equivalent to credible intervals (and P‐values to posterior probabilities) when one assumes a “flat” (or “uniform”) prior.8, 23 But flat priors are unrealistic for most applications in biomedicine and sports science, as we will explain below.

Magnitude‐based Inference has been described as a Bayesian analysis with a flat prior,10 but writings on MBI fail to inform users of the implications of a flat prior. A flat prior means that literally all effect sizes are equally likely. This is an unrealistic assumption in biomedicine because it implies that almost every intervention has a substantial effect, many have impossibly large effects, and all of these effects are equally likely.23, 24, 25 A flat prior will almost always lead to overly optimistic inferences because—by starting with the assumption that the intervention almost certainly works (has a non‐trivial effect)—it stacks the deck in favor of finding a non‐trivial effect. As Zwet23 writes: “The uniform prior is not realistic at all in the context of bio‐medical research. Consequently, its use leads to overestimation of the magnitude of the regression coefficient and overconfidence about its sign.” As Greenland24 states: “…a flat prior is generally nonsensical in scientific terms and suboptimal for both frequentist and Bayesian decision and inference; at most flat priors only serve to bound results from optimized or sensible priors.”

For instance, Pamboris et al3 report that stretching increased isometric torque, a measure of muscle force, from 91 to 95 Newton meters (Nm). A flat prior implies that it is just as likely that stretching would reduce torque to zero, or conversely, create superhuman strength with post‐stretching torque being 1000 Nm. This is obviously a completely unrealistic assumption. Flat priors are particularly unrealistic for sports science as empirical data show that effect sizes in sport and exercise science are predominantly small.26, 27, 28 In fact, MBI is specifically advertised as a tool that is needed because small effects predominate in sports science.22

Greenland has demonstrated that frequentist P‐values and confidence intervals can be viewed as providing bounds on Bayesian posterior probabilities when assuming a prior symmetric around the null.25 We indeed believe that MBI probabilities provide an upper limit for a Bayesian posterior probability. In other words, when MBI returns “50% chance of beneficial” what this actually means is that 50% is the maximum chance that the intervention is beneficial. The choice of any other prior (assuming priors symmetric around the null) will lead to a lower probability. This means that using MBI as currently implemented will almost always present an overly optimistic picture of an intervention's effectiveness.

It is easy to see that interpreting all frequentist confidence intervals as Bayesian credible intervals (or, equivalently, interpreting all P‐values as Bayesian posterior probabilities) will lead to overly optimistic inferences. Just imagine if all the 95% confidence intervals in the medical literature were suddenly interpreted as Bayesian credible intervals (as MBI would allow you to do29, 30, 31!). This would imply that at least 97.5% of all significant beneficial results would represent true positives, which runs directly counter to what we know to be true based on the current reproducibility crisis in biomedicine.32, 33, 34, 35

Finally, it is important to recognize that MBI's evidentiary thresholds (eg, “likely” and “possible”) represent weak levels of evidence whether taking a frequentist or Bayesian perspective. “Likely” beneficial effects typically correspond to what Bayesians would consider “anecdotal evidence” of an effect.36

5. PRACTICAL ISSUES WITH THE USE OF MBI

In addition to the theoretical issues with MBI, we believe that its use encourages poor statistical practices. Researchers performing MBI analyses overwhelmingly use the MBI Excel spreadsheets. Unfortunately, the black box approach that these spreadsheets promote means that researchers are neither exposed to the statistical theory claimed to underpin MBI (Bayesian inference), nor the computational procedures involved in generating the test statistics, creating confusion regarding the methods used and results produced. For example, in their response letter, Pamboris et al4 make the bizarre claim:

We have used the pre‐post parallel groups trial spreadsheet, as this calculation tool compares the difference from pre‐ to post‐changes between the slow and fast dynamic stretching condition thus eliminating type I error 4 (emphasis added).

This statement is erroneous—Type I error is not eliminated by comparing pre‐ and post‐changes. Also, their reference to MBI as a “Bayesian analysis with a default prior” without any explanation of its implications suggests a lack of understanding of Bayesian statistics. Finally, their claim that their inferences “have nothing whatsoever to do with NHST”4 suggests a lack of awareness that the Excel spreadsheets implement standard hypothesis tests.

MBI encourages this lack of critical thinking, fostering instead the application of “statistical rituals.”37 Rather than exercising judgment over the validity of their statistical methods, researchers instead heedlessly transcribe results generated through the calculations of the MBI spreadsheets. MBI is not alone in operating as a black box (indeed, many programs allow users to implement statistical methods the users do not understand), but MBI critically lacks rigorous review and documentation. As we have mentioned, MBI's authors have never presented a mathematical formulation of the method and the method has never been published in a statistical journal. MBI's supporting documentation is also limited. Tracking the workflow through the various dependencies within the spreadsheets is at once confusing and time‐consuming, and subject to following the often‐verbose instructions and explanations—a “note” attached to one spreadsheet cell is over 800 words long. This can be contrasted with other statistical software, where code and documentation are reviewed, critiqued, and published in the mainstream literature (eg, the Journal of Statistical Software).

An example of this cookbook approach is in the transformation of variables. In reviewing numerous MBI papers, we have noticed that authors commonly log‐transform their data with little explanation given other than that they did so to “deal with the non‐uniformity of errors.”38, 39, 40, 41, 42, 43 This phrase is not conventional statistical language at all: a Google search reveals that it is used on www.sportsci.org and then almost exclusively in MBI papers in the sports medicine literature. In most cases, there is no indication that authors have actually examined their data distributions or checked assumptions such as normality and homogeneity of variances to warrant a log transformation. While it is sometimes appropriate to log‐transform, it should not be done indiscriminately or without justification. Log transformation can make the results difficult to interpret (eg, what would it mean to say that a certain type of warm‐up improves the log of race time by 0.8?). Use of logs can also make it harder to check simple numbers, thus making it easier for numerical errors and inconsistencies to go undetected.

Pamboris et al3 log‐transformed all but two of their variables, with no explanation for these choices. The log transformation makes their tables extremely difficult to follow and we believe has introduced inconsistencies in the inferences. For example, muscle strain changed by −38.00% in the SDS condition (see their table 1) and −13.20% in the FDS condition (see their table 2), which—presumably due to the log transformations—somehow translates to a between‐condition difference of 39.80% (see their table 3).3 This 39.80% is reported alongside a standardized effect size of 0.50, with no explanation of how the standardized effect size was calculated. Worryingly, the confidence interval for the raw data, 39.80% ± 56.70%, yields different inferences than the confidence interval for the effect size, 0.50 ± 0.89. The back‐calculated P‐value from the former is 0.24 but from the latter is 0.32, demonstrating inconsistency. Furthermore, we can use the effect size confidence interval to directly calculate the MBI beneficial probability as follows: p(T₁₇>(0.50‐0.20)/(0.89/1.75)) = 72%. But this does not match the value given in the table, which is 80%. Finally, it is unclear as to why the confidence intervals are symmetric: if confidence intervals were built on the log‐transformed data and then back‐transformed (exponentiated), one would expect the confidence intervals to be asymmetric.

Researchers that use the MBI Excel spreadsheets frequently neglect to provide adequately detailed descriptions of their methods, precluding appraisal of their validity. We note that in the Statistical Analysis section of their article, Pamboris et al3 simply state which spreadsheets they used and then cite a webpage (www.sportsci.org) that only provides instructions for how to use the spreadsheets, not the mathematical theory that underpins them, nor the computations that produce the results.13 This makes it hard to vet or replicate the results. For example, we cannot determine whether Pamboris et al3 used the correct analysis for comparing the SDS and FDS conditions. When comparing conditions in a crossover trial, one needs to account for the within‐person correlation. Pamboris et al3 say they used the “pre‐post parallel groups trial spreadsheet” for this analysis, but having downloaded and scrutinized the spreadsheet13—which appears intended only for independent groups—it is unclear whether it correctly handles correlated observations. Indeed, we suspect that the MBI approach used treats correlated observations as independent, a basic statistical error described in any introductory statistics course.

Curiously, the necessity for thorough specification of methods is conceded to some degree in a commentary appended to the spreadsheets on the www.sportsci.org website:

Data analysis through use of the spreadsheet will require careful description in the methods section of submitted manuscripts to satisfy those reviewers committed to more traditional statistical significance 44 (emphasis added).

There is a theme here: MBI should be described in whatever terms are necessary for wider acceptance. We believe it self‐evident that careful description of methods is essential for all scientific articles submitted for publication and especially so when the study authors are using unconventional and unvalidated methods. How else are we as peers to judge the validity of their approach? Suggestions that sufficient disclosure is necessary merely to appease reviewers of any particular statistical inclination stands antithetical to the drive for an open research culture45 and contributes nothing to remedying the reproducibility problems in scientific research.32, 33, 34, 35

6. CONCLUSION

Magnitude‐based Inference has admirable goals. Researchers should pay less attention to statistical significance and more attention to effect sizes and precision. The devil is in the details, however, and MBI does not solve the problems associated with statistical significance testing. For the mathematical and practical reasons listed above, MBI increases the number of false‐positive findings in the literature, does not have a reproducible implementation, and does all of these things with a pastiche of Bayesian rigor. Thus, far from being a methodological remedy, MBI actually hurts reproducibility.

Despite regular criticism, the alleged benefits of MBI have led many teams of researchers to uncritically apply MBI in their own work. MBI's creators even write on their website22:

MBI has become popular in exercise and sports science, because we have provided the tools, and the tools provide the researchers with an avenue for publishing previously unpublishable effects from small samples 22 (emphasis added).

The problem with small studies is that chance variation has a greater relative effect on findings, making it more difficult to distinguish real effects from noise. Indeed, it is easily demonstrated that we should have less faith in the results of a small study irrespective of whether the results are to reject or not reject the null hypothesis. MBI increases the risk of false positives—interpreting noise as signal—and it is doubly problematic that proponents of MBI specifically advocate this as an advantage of their method in the setting of small samples.

Statistical methods used in medical research studies are reported first in the methodologic literature and are often subject to considerable discussion, debate, and testing. For instance, see the legitimate debate about significance testing and its appropriate use in different fields of study.46, 47 In some cases, statistical methods are proposed that are later found to be invalid by other statisticians, and their use is then dropped. With MBI, a circuitous path of self‐citation suggests rigorous methods development, but deeper digging reveals this is not the case. MBI has never been published in a statistical journal where its strengths and weaknesses could be empirically tested and debated by individuals versed in methods for the evaluation of statistical methods.48 Instead, papers on MBI have only been published in sports medicine journals or on the website www.sportsci.org. This history can also be seen in how critiques of MBI5, 6 are met with counterarguments19, 49 that fail to directly address the criticisms raised or math presented20 and never result in modifications or adaptations to the method. Instead, proponents of MBI have continually shifted the goal‐posts—for example, first claiming that MBI has superior Type I and Type II errors19 and then claiming that Type I and Type II errors are irrelevant because MBI is a Bayesian method.22

We have also been struck how MBI proponents have adopted language found more typically in cultural and political battles than in science. For instance, in a blog post50 that starts “I am not a qualified statistician,” Buchheit states that “MBI changed my life” and describes critiques of MBI using phrases such as “battle of position or power,” “close minded‐attitudes,” and “like … battles of religion.” Without engaging substantively with any criticism of MBI, Buchheit says that he “trust[s] the analytical foundations of MBI” and that this “trust is based on the following: [Batterham] and [Hopkins] are amongst the most highly cited researchers in exercise and sport, their knowledge of the inference literature is clearly beyond reproach.” This is us‐and‐them talk: “they” (established statisticians) are close‐minded and using their power against “us” (MBI users), good people who can be trusted; yes, every reputable statistician who has examined MBI has concluded it to be invalid, but (with a strange sort of logic) that just shows how biased “they” are.

To their credit, the creators and proponents of MBI have a deep concern for statistical practices in sport and exercise science and have highlighted legitimate issues: over‐reliance on statistical significance, erroneous “acceptance” of the null hypothesis, persistent publication bias, and chronically under‐powered studies are all problems. However, correct identification of a problem does not provide a solution and there are plenty of means for addressing these problems while using valid statistical methods.

Regardless of the method of inference, we also need to fix more basic issues: errors in experimental design, data integrity, data cleaning and checking, basic statistical literacy, and basic logical reasoning.51 We need better statistical education so that researchers understand the strengths and limitations of valid analysis methods. We also need a healthy dose of statistical respect. Applied statistics is its own discipline with rigorous pipelines for methodological development. Researchers should not feel safe behind MBI's claim of producing a result consistent with a “default prior.”48 Flat priors represent very specific assumptions about the nature of reality, and those assumptions are (almost always) wrong for sports scientists. Furthermore, if one is to adopt a prior, it needs to be done in a Bayesian analysis with appropriate justification and sensitivity testing. MBI ignores the specification of a prior completely and is thus definitively not Bayesian.

Magnitude‐based Inference has certain superficial similarities with Bayesian statistics. But you cannot send a baseball team to England and describe them as cricket players just because they try to hit a ball with a bat. The incorrect claim that MBI is a Bayesian analysis is similarly just not cricket and does real damage. This claim has led Pamboris et al4 to assert that, “Nevertheless, readers may be assured that our analysis based on Bayesian inference methods and our conclusions are robust.” As we have shown however, conclusions drawn from “possible” or “likely” results in MBI are neither Bayesian nor robust. MBI is not a valid nor reproducible method of statistical inference and should not be used.