How smooth is a dolphin? The ridged skin of odontocetes

Abstract

Dolphin skin has long been an inspiration for research on drag reduction mechanisms due to the presence of skin ridges that could reduce fluid resistance. We gathered in vivo three-dimensional surface data on the skin from five species of odontocetes to quantitatively examine skin texture, including the presence and size of ridges. We used these data to calculate k⁺ values, which relate surface geometry to changes in boundary layer flow. Our results showed that while ridge size differs among species, odontocete skin was surprisingly smooth compared to the skin of other swimmers (average roughness = 5.3 µm). In addition, the presence of ridges was variable among individuals of the same species. We predict that odontocete skin ridges do not alter boundary layer flows at cruising swimming speeds. By combining k⁺ values and morphological data, our work provides evidence that skin ridges are unlikely to be an adaptation for drag reduction and that odontocete skin is exceptionally smooth compared to other pelagic swimmers.

1. Introduction

At Cambridge University over 80 years ago, Sir James Gray estimated the drag on swimming dolphins and declared that to overcome drag forces, dolphin muscle would need to be producing energy at a rate at least seven times faster than any known mammalian muscle [1]. This became known as Gray's Paradox and stimulated research to discover how dolphins could modify fluid flow at their skin surface to decrease drag and resolve the paradox. A number of interesting and verified examples of drag reduction achieved by manipulating surfaces resulted from this research, including drag reduction from ridged, compliant and mucus-like surfaces [2]. However, we now know that Gray's Paradox resulted from incorrect assumptions regarding muscle force generation and the swimming speed of dolphins, and that dolphins can easily generate sufficient thrust to overcome the drag produced by their bodies during swimming [3]. Despite the resolution of Gray's Paradox, research continues on a number of different drag reduction mechanisms that were inspired by dolphins, and one example is dolphin's ridged skin.

Dolphins and their relatives are reported to have ridges on their skin, especially on the front half of their bodies [4]. Previous research on ridges has focused on their role in creating visual patterns [5] and reducing drag to increase swimming performance [6]. In these studies, ridges on the body were described based on either histological sections or microscope measurement of epoxy moulds, and ridges were found to be 7–112 µm in height depending on species, with wavelengths (spatial periods) of 0.41–2.35 mm [7]. These ridges are also generally present posterior to the head, but not on fins or flukes, and the ridges are perpendicular to the body axis on the dorsal side of the animal, but are oblique to the body axis laterally [4,7]. In this paper, we use rapid moulding and high-resolution profilometry to make in vivo measurements of ridges on five species of odontocetes on five locations on both body and control surfaces (e.g. flukes, flipper and fin). We then use these morphological data in concert with fluid dynamic theory to discuss the potential for drag reduction during swimming.

2. Methods

It is crucial to measure the dimensions of odontocete skin ridges in vivo—any cutting or fixation of the skin could deform the sample because skin is under tension (skin parts away from cuts) and fixation often leads to soft tissue deformation [7,8]. We used a high-fidelity (less than 0.1 µm resolution), fast-curing (less than 4 min), silicone moulding compound (RepliSet, Struers Inc.) to make moulds of the skin surface of live individuals of five odontocete species: bottlenose dolphin (Tursiops truncatus), white-sided dolphin (Lagenorhynchus obliquidens), pilot whale (Globicephala macrorhynchus), killer whale (Orcinus orca) and beluga whale (Delphinapterus leucas). Animals were voluntarily positioned out of water onto a pad, and skin moulding occurred with animals in a relaxed posture (see electronic supplementary material). Effects of gravity are limited due to the short working time of the moulding compound (30 s) and the tautness of dolphin skin. We studied three to five individuals of each species (individual sizes: electronic supplementary material, table S2), sampled five regions on each animal (figure 1) and used gel-based profilometry [9] to image the surface topography of resin casts of each mould (electronic supplementary material, figure S5). Gel-based profilometry works by pressing a painted gel into a surface of interest and taking stereo-photographs of the surface of the gel using different lighting angles [9,10] (see also electronic supplementary material, Methods). These stereo-photographs are then reconstructed into a topographic image, ensuring accurate three-dimensional (3D) in vivo skin measurements [11].

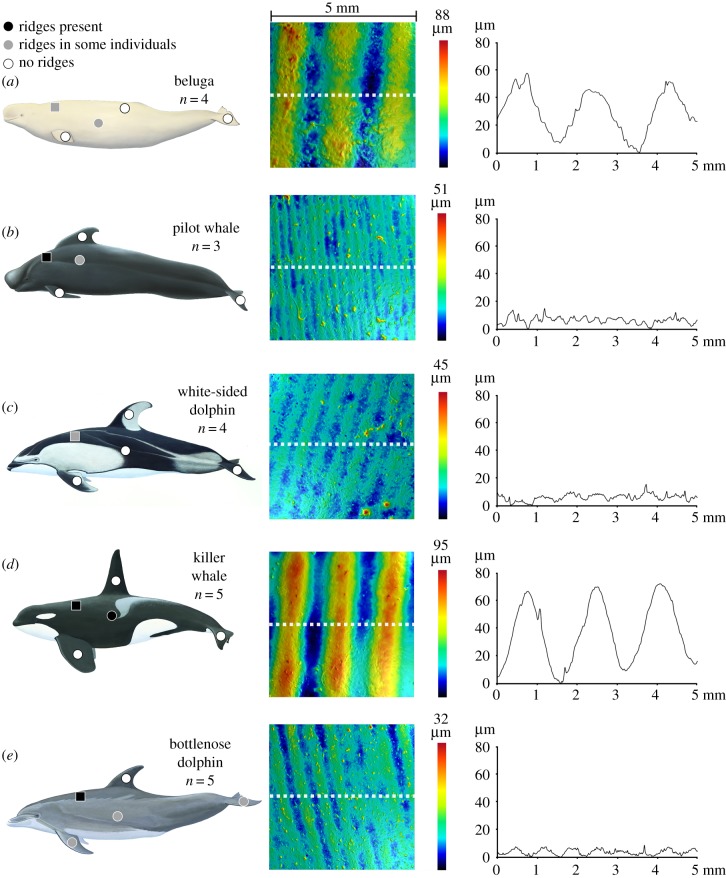
Figure 1.

Three-dimensional skin structure in odontocetes (a) beluga whale, Delphinapterus leucas, (b) pilot whale, Globicephala macrorhynchus, (c) white-sided dolphin, Lagenorhynchus obliquidens, (d) killer whale, Orcinus orca and (e) bottlenose dolphin, Tursiops truncatus. Species, sample size and sampled regions shown in the left column, with colour indicating the presence of ridges (black: ridges in all individuals, grey: ridges in some individuals, white: no ridges). The centre column shows the topographic images (anterior to left) corresponding to the boxed region in the left panel, with colour indicating surface height. The right column shows height profiles from stippled lines in centre images. Mammal illustrations courtesy of Pieter Arend Folkens.

We measured ridge height (trough-to-peak height), ridge wavelength (peak-to-peak distance between ridges), roughness (root-mean-square of height difference from average height within a sample), skew, and kurtosis from topographic images [12]. Skew (skewness) measures the unequal distributions of heights on a surface, such that positive skew indicates more positive surface features (ridges, peaks), and negative skew indicates more negative surface features (valleys, holes). Kurtosis measures the shape of the distribution of heights with values centred around three. Kurtosis values above three indicate increasingly extreme height values compared to a normal distribution, while values below three indicate a surface with less variability in height than expected (equations for skew and kurtosis are given in the electronic supplementary material).

We used our measurements of ridge height to calculate the non-dimensional fluid dynamic parameter k⁺, which relates surface feature size to potential changes in the boundary layer [13] (see also electronic supplementary material text on k⁺). The parameter k⁺ is defined as

$$k^{+}=\frac{k{u}_{\tau }}{\nu },$$

where k is a defining or characteristic roughness height (in this case the trough-to-peak height of ridges), u_τ is friction velocity, and ν is the kinematic viscosity of seawater (10⁻⁶ m² s⁻¹ at 15°C). Friction velocity was found through a relationship with wall stress (C_f) by assuming a turbulent boundary layer [3,6,14] and ignoring effects like pressure gradients, body curvature and three-dimensionality. Wall stress (C_f) is assumed to be given by a power law relationship (electronic supplementary material), so that

$$C_{\mathrm{f}}=\frac{0.0576}{R{e}_x^{0.2}}=\frac{2u_t^2}{U_{\mathrm{\infty }}^2},$$

where Re_x is the Reynolds number at the skin region we measured (800 000—4 250 000 for cruising speeds and 4 200 000—25 000 000 for sprinting, depending on species and region) and U_∞ is the swimming velocity, from published cruising and sprinting speeds for each species (electronic supplementary material, table S1) [13,15]. We calculated k⁺ for cruising and sprinting speeds at the dorsal and lateral sampling locations, where ridges were most often present across all five species (figure 1). Values of k⁺ greater than four indicate that surface roughness may be large enough to change the boundary layer, while values less than four indicate effects of surface roughness are negligible [13]. In a turbulent boundary layer, k⁺ values greater than four will generally increase the drag of a surface, although some special cases can decrease drag (riblets, denticles).

For statistical analysis, we pooled data by species and used analysis of variance (ANOVA) to determine if species were different in measured variables. In addition, we performed Tukey-HSD post hoc tests upon significant ANOVA results to determine which species were different.

3. Results

Silicone moulds and subsequent resin casts replicated the natural surface of the sampled cetacean species and created ideal, non-deformable samples for profilometry imaging (electronic supplementary material, figure S5). Ridges occurred in at least one location on the body of all species that we imaged; however, ridge height and presence at sampled locations were variable among individuals of the same species (figure 1; electronic supplementary material, table S3 and figures S6–S10). Ridges were most consistently present between the blowhole and the dorsal fin on the dorsal side of animals, and on the lateral sides. However, every species except killer whales showed variability in ridge presence at one or more of those locations. Ridges did not commonly occur on other regions we sampled. Where present, ridge heights varied from 2 to 180 µm with a median of 12.8 µm and a mean of 25.6 µm (standard error of mean = 6.3 µm). Ridges varied among species: pilot whales and bottlenose dolphins had smaller ridge heights (means: 5.1 µm and 6.1 µm) than beluga whales (mean: 66.2 µm), with killer whales and white-sided dolphins intermediate and indistinguishable (table 1 and figure 2a, ANOVA: p = 0.006, Tukey HSD: pilot–beluga p = 0.022, bottlenose–beluga p = 0.004).

Table 1.

Mean surface texture metrics pooled for each odontocete species. Standard error of the mean in parentheses.

species	roughness (µm)	skew	kurtosis	ridge height (µm)
bottlenose dolphin	2.6 (0.29)	2.6 (0.34)	28 (5.4)	6.1 (0.8)
white-sided dolphin	4.0 (0.39)	1.5 (0.25)	14 (1.5)	11.8 (3.4)
pilot whale	4.0 (0.45)	2.6 (0.32)	22 (2.9)	5.1 (1.5)
killer whale	5.2 (0.80)	0.8 (0.16)	9 (1.4)	29.8 (5.9)
beluga whale	11.1 (2.23)	0.1 (0.13)	5 (0.4)	66.2 (24.7)

Figure 2.

Surface metrology and k⁺ for odontocetes. Significant groups are marked by letters. (a) Ridge height versus species where all ridged surfaces for each species are pooled. (b) Ridge wavelength versus species where all ridged surfaces for each species are pooled. (c) Roughness versus species. (d) k⁺ at cruising speed for dorsal and lateral surfaces where ridges are present. (e) k⁺ at sprinting speed for dorsal and lateral surfaces where ridges are present. Line in (d) and (e) shows the cut-off value of four for k⁺.

We also measured ridge wavelength and found that beluga and killer whales had larger wavelength values compared to pilot whales, white-sided dolphins and bottlenose dolphins (figure 2b, ANOVA p < 0.001, Tukey HSD: other species–beluga or killer whale, p < 0.001). Beluga surfaces were rougher than other odontocete surfaces (figure 2c, ANOVA: p < 0.001, Tukey HSD: beluga–other species, p < 0.002).

Our calculation of k⁺ at cruising speed shows that no species had values high enough to alter the boundary layer (figure 2d). There was one high k⁺ value for one individual beluga that appeared to be an outlier, but we found no reason to remove this point (it was accurately measured). However, at sprinting speeds, k⁺ values for beluga and killer whales were large enough to influence the boundary layer, and values for the white-sided dolphins are close (figure 2e).

We compared skew and kurtosis values for odontocetes to other swimming animals and showed that odontocete surfaces tend to have relatively more peaks and more extreme peaks (higher skew and kurtosis), indicating a fundamental difference in surface geometry (tables 1 and 2).

Table 2.

Surface texture of swimming animals and common surfaces. Unless noted, animal skin data are from the lateral body surface.

type	surface	roughness (µm)	skew	kurtosis
non-swimmer	aluminium	0.4	−0.63	3.7
non-swimmer	chicken egg shell	4.8	−0.40	3.6
non-swimmer	back of human hand	9.8	−0.71	4.3
non-swimmer	500 grit sandpaper	15.0	−0.03	3.2
non-swimmer	80 grit sandpaper	50.5	0.24	2.9
high-performance swimmer	mako shark (Isurus oxyrhinchus)	9.0	−0.74	4.5
high-performance swimmer	white shark (Carcharodon carcharias)	9.8	0.18	3.1
high-performance swimmer	tunas (Thunnus albacares, T. thynnus, T. obesus)	10.8	0.10	3.1
high-performance swimmer	swordfish (Xiphias gladius)	11.6	0.71	4.7
high-performance swimmer	marlin (Kajikia audax)	21.3	0.05	3.5
high-performance swimmer	marlin ‘bill' (Kajikia audax)	58.5	0.40	2.9
swimmer	trout skin with mucus present (Salvelinus fontinalis)	2.3	−0.05	2.6
swimmer	bluegill skin with mucus present (Lepomis macrochirus)	33.5	−0.29	2.1
swimmer	sea snake (Pelamis platurus)	46.1	0.05	3.5
swimmer	manatee fluke (Trichechus manatus)	72.6	−0.41	2.9

4. Discussion

Our measurements of in vivo ridge height on five species of odontocetes reveal that ridges are generally small but also vary in presence and size (figures 1 and 2). Intraspecific differences in ridge presence suggest that ridges may not be as important as previously suggested to odontocete locomotion, although the dorsal region of orcas has large and consistently present ridges, and thus could be a model for future studies. Ridge height, roughness and wavelength show differences among species—generally, beluga and killer whales have larger ridges, higher roughness and larger ridge wavelength compared to pilot whales, white-sided dolphins and bottlenose dolphins (figures 1 and 2). Among the species sampled, white-sided dolphins, bottlenose dolphins and pilot whales are likely the higher performance swimmers, but our data suggest that their ridges are the least likely to confer a performance benefit as their skin surface is extremely smooth [16]. Body size did not appear to have an effect in this study.

In general, our calculated k⁺ values show that skin ridges on the dorsal and lateral regions of the five species sampled are unlikely to change the boundary layer at cruising speeds. These low k⁺ values combined with the lack of consistent ridges among individuals leads us to believe that odontocete skin ridges are unlikely to be causing drag reduction at normal cruising speeds. At sprinting speeds, k⁺ values for beluga and killer whales suggest that their surfaces may alter the boundary layer (figure 2), but the lack of consistent ridge presence in belugas challenges that idea for that species. Our measurements also demonstrate that previous experimental studies [6] using scaled-up physical models of dolphin skin are inaccurate with respect to ridge geometry because ridge wavelength is around 20 times ridge height, not equal as tested in previous work. Future experiments using accurate models of dolphin skin would be valuable in exploring function.

Comparative data show that odontocetes are smooth compared to other high-performance swimming animals, such as tuna, marlin and pelagic sharks (tables 1 and 2). Killer whales, pilot whales, white-sided dolphins and bottlenose dolphins have skin surface roughness values of 2–5 µm, while beluga whales have roughness values of about 11 µm (table 1). The considerably larger beluga roughness overlaps with the region of high-performance swimmers such as tunas, mako and white sharks, and swordfish, which occupy roughness values 9–12 µm (table 2). However, belugas are not considered high-performance swimmers and have been shown to have high drag compared to other odontocetes, so this convergence in skin roughness is unlikely to reflect a convergence in function [16]. Most odontocetes we sampled have comparatively smooth skin—in the range of the smoothest, mucus-covered fish species, such as trout (table 2). This low roughness is consistent with our calculations of k⁺ that suggest little hydrodynamic effect of odontocete skin ridges among the species sampled here—perhaps odontocetes' solution to skin friction is to make their skin smooth and taut to prevent boundary layer separation during body oscillation. Ridges may instead increase skin sensitivity to flow and touch [14], as innervated dermal papillae lie within the skin [17,18]. Future experiments that focus on higher speed flow and larger ridges that are emblematic of killer whales would be valuable in testing if ridges are situationally beneficial or even detrimental to boundary layer control.

Ethics

All work followed institutional animal use, ethical guidelines and permits through Sea World San Diego, West Chester University (WCU) and the University of California at Santa Cruz (UCSC). The research was approved by each institutional IACUC through WCU (project no. 201506) and UCSC, and was conducted under an institutional Marine Mammal Permit through the US NOAA National Marine Fisheries Service Office of Protected Species (permit no. 19590).

Data accessibility

Data for this manuscript can be found at: https://osf.io/9bf2w/ [19].

Authors' contributions

D.K.W., F.E.F., J.S.L., T.M.W. and S.I. collected data. F.E.F., G.V.L. and A.J.S. contributed fluids expertise and analysis. All authors contributed to the writing of the manuscript. All authors agree to be held accountable for the content herein and approve the final version of the manuscript.

Competing interests

We declare we have no competing interests.

Funding

This work was funded by ONR MURI Grant N000141410533 to F.E.F., G.V.L. and A.J.S. and monitored by Bob Brizzolara, and ONR N000141712737 to T.M.W.