Abstract
Experimental observations suggest that cells change the intracellular localization of key enzymes to regulate the reaction fluxes in enzymatic networks. In particular, cells appear to use sequestration and co-clustering of enzymes as spatial regulation strategies. These strategies should be equally useful to achieve rapid flux regulation in synthetic biomolecular systems. Here, we leverage a theoretical model to analyse the capacity of enzyme sequestration and co-clustering to control the reaction flux in a branch of a reaction–diffusion network. We find that in both cases, the response of the system is determined by two dimensionless parameters, the ratio of total activities of the competing enzymes and the ratio of diffusion to reaction timescales. Using these dependencies, we determine the parameter range for which sequestration and co-clustering can yield a biologically significant regulatory effect. Based on the known kinetic parameters of enzymes, we conclude that sequestration and co-clustering represent a viable regulation strategy for a large fraction of metabolic enzymes, and suggest design principles for reaction flux regulation in natural or synthetic systems.
Keywords: reaction–diffusion dynamics, metabolic flux regulation, spatial regulation strategies, purine biosynthesis pathway
1. Introduction
Cells must exert rapid and precise control over the flux of molecules in their reaction networks [1], and similar tasks are pursued in synthetic biology [2]. At a branch point in a reaction network, where an intermediate product is used in two or more competing pathways, it is often necessary to regulate the reaction flux into each branch, e.g. in response to a change in the environmental conditions. One way to regulate reaction fluxes, albeit slowly, is to adjust enzyme abundances, by controlling transcription, translation or degradation rates. More rapid flux regulation can be achieved by adjusting enzyme activities, via allosteric mechanisms or post-translational modifications [3–5]. However, an increasing amount of evidence suggests that cells complement these biochemical regulation mechanisms with mechanisms based on the spatial rearrangement of enzymes [6–8]. First synthetic systems have also been created, in which a metabolic flux is regulated by controlling the clustering of enzymes [2]. Here, we focus on the capacity of such physical mechanisms to regulate reaction fluxes at a branch point in a reaction network.
Many enzymes have been found to form intracellular aggregates [7,9,10], through diverse mechanisms that include direct binding between the enzymes or with scaffolds, adsorption to specific spots on the cellular membrane or the cytoskeleton, or liquid-droplet phase separation [9,11–16]. Importantly, assembly and disassembly of enzyme clusters is often reversible upon depletion or supply of metabolites or other environmental stimuli [7,8,17,18]. This suggests that cells use enzyme localization as a strategy to regulate biochemical reaction fluxes dynamically [9,19]. In particular, co-clustering of enzymes that operate sequentially within the same reaction pathway may upregulate the pathway flux [20], whereas the sequestration of enzymes may downregulate the pathway flux, as illustrated in figure 1.
Figure 1.
Regulation of reaction fluxes via changes in the intracellular localization of enzymes. At a branch point in a reaction network, the sequestration of one downstream enzyme (here called EP) into clusters can direct the reaction flux away from the reaction catalysed by the sequestered enzyme. By contrast, co-clustering of the upstream enzyme EI with the downstream enzyme EP can bias the flux towards the product P. We analyse the effectiveness of these spatial regulation strategies within a reaction–diffusion model. Geometrical parameters of this model are illustrated on the right-hand side. (Online version in colour.)
A well-known example for the co-clustering strategy is the purinosome, a multi-enzyme cluster comprising enzymes of the de novo purine biosynthesis pathway [17,21]. Co-clustering has also been observed for enzymes involved in glucose metabolism and de novo pyrimidine biosynthesis [22–25]. In some such assemblies, intermediate products are directly ‘channelled’ or transferred between enzymes [20]. However, theoretical analyses have shown that proximity of consecutive enzymes is sufficient to increase the efficiency of diffusive transfer, without the need for direct or guided transfer of intermediate products [26–28]. Furthermore, it has been demonstrated experimentally that the efficiency enhancement obtained by co-clustering can change the ratio of fluxes at a branch point in a reaction network [28].
The reversible sequestration of individual enzymes into filaments or clusters has been observed in the de novo CTP and purine biosynthesis pathways [7,19], and was often associated with downregulation of the corresponding pathway [29,30]. For example, FGAMS, one of the six enzymes of the de novo purine biosynthesis pathway, can be sequestered into a cluster, leading to downregulation of the pathway [30]. Thus, this pathway appears to have the capacity for two spatial regulation strategies in response to changing environmental conditions: the assembly of all pathway enzymes into the purinosome as a mechanism for pathway upregulation, and the sequestration of a single enzyme into a cluster as a mechanism for pathway downregulation [19]. While the mechanistic origin of this downregulation remains unclear, the spatial sequestration alone may suffice, without the need for reducing the catalytic activities of the enzymes.
Here, we analyse the reaction–diffusion dynamics associated with enzyme sequestration and co-clustering to assess the capacity of these mechanisms to regulate reaction fluxes. Prior theoretical work on the reaction–diffusion dynamics of spatially arranged enzymes [26–28,31] has primarily focused on the question of how the reaction flux can be maximized, or considered fixed parameter values to describe specific experimental situations. By contrast, our focus here is on the question of flux regulation. Furthermore, while the prior studies considered co-clustering, they did not analyse the sequestration of enzymes as a spatial regulation strategy. Here, we treat co-clustering and sequestration on an equal footing and explore their flux regulation capacity over the entire parameter space. Our analysis reveals that in both cases, the strength of the regulatory effect, i.e. the fold-change in the reaction flux, is determined by two quantitative characteristics, which are dimensionless combinations of the biochemical and physical parameters of the system: (i) the ratio of the total activities of the two competing enzymes and (ii) a ratio of diffusion to reaction timescales. This result leads us to an approximate criterion for whether a given enzyme with known biochemical parameters will permit significant flux regulation by co-clustering or sequestration. The criterion is general, based only on the assumption of diffusive substrate transfer, i.e. without invoking direct or guided transfer of intermediate products. To illustrate the use of this criterion, we apply it to the well-studied case of purine biosynthesis, and also to a large dataset of biochemically characterized enzymes.
2. Results and discussion
The spatial flux regulation strategies considered here rely on the fact that changes in the localization of enzymes can alter the concentration profile of intermediate products, which in turn determines the reaction fluxes produced by enzymes that further process the intermediate product. Clearly, if all enzymes using the intermediate product are saturated irrespective of their location, spatial regulation strategies can have no effect. For the purpose of our study, it is therefore important to verify that the relevant enzymes are not all saturated. Further below, we will consider this question in some detail for the example of the branch point at the end of the purine biosynthesis pathway. On a global level, the results from a recent study [32] indicate that in a substantial fraction of metabolic reactions (approx. 30%), the cellular metabolite concentration is smaller than the Michaelis constant of the enzyme (fig. 6a of [32]). This observation suggests that an analysis of spatial regulation strategies is broadly relevant, both for understanding natural biological systems and for the design of synthetic systems.
2.1. Reaction flux regulation at a branch point
In the following, we consider a branch point in a reaction network, as illustrated in figure 1, bottom. Intermediate products I, produced by an upstream enzyme EI, are processed by two downstream enzymes, EP and EQ, into two distinct products, P and Q. We assume both EP and EQ to be in the regime of low substrate saturation, such that their reaction fluxes are susceptible to spatial regulation (and approximately linear in the substrate concentration). We define the branching fraction Jp as the fraction of I that is converted into P, and similarly Jq = 1 − Jp as the fraction that is converted into Q.
Our reference scenario is that of no spatial regulation, i.e. a uniform distribution of all three enzymes, illustrated in figure 1a (‘well-mixed’ enzymes). The branching fractions for this reference scenario, and , take on the simple form
| 2.1 |
where α is defined as
| 2.2 |
with kp, kq denoting the catalytic efficiencies (kcat/KM) of the competing downstream enzymes EP and EQ, and [EP], [EQ] their concentrations. The dimensionless quantity α therefore corresponds to the ratio of the total activities of the two enzymes, i.e. it quantifies the intrinsic bias of the branched pathway at given enzyme concentrations and catalytic efficiencies.
The α-dependence of the branching fraction can be regarded as a regulation function for non-spatial control of flux branching towards the product P. This function describes regulation via changes of the enzyme concentrations [EP], [EQ] or via changes of their catalytic efficiencies kp, kq by allosteric or other means, all affecting the ratio α according to equation (2.2). As shown in figure 2, black curve, the splitting of intermediates between the two branches is symmetric about α = 1, with when the total activity of EQ is greater than that of EP (α < 1) and vice versa. However, this symmetry will be broken when the spatial arrangements of the downstream enzymes differ. The pathway flux can be biased towards P and away from Q by co-clustering EI with EP to decrease the average distance between these sequential enzymes, as illustrated in figure 1c. Conversely, the flux can be shunted away from P by sequestering only the EP enzymes into clusters, which increases the EI − EP distance (figure 1b). We now turn to the description of such effects, which amount to post-translational flux regulation by spatial localization.
Figure 2.
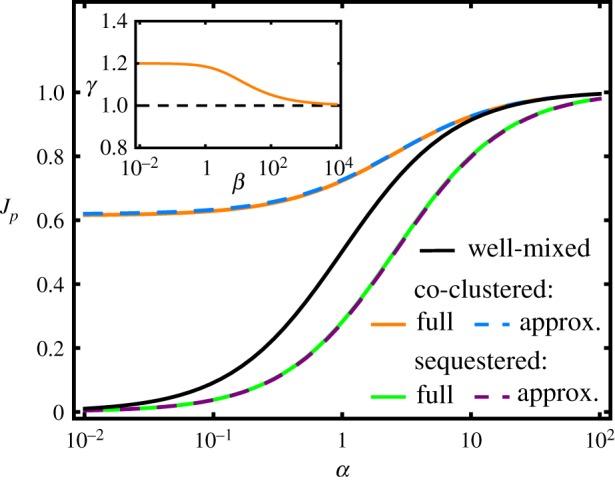
Branching fraction Jp as a function of the enzyme activity ratio α for the enzyme sequestration strategy (green solid curve), the enzyme co-clustering strategy (orange solid curve) and for a well-mixed system of uniformly distributed enzymes (black curve). The dashed lines show the corresponding approximative forms in the limit [EP]/cc,s ≪ 1, equation (2.7). The parameter values are kp = kq = 105 M−1 s−1, cc,s = 25 mM, rc = rs = 0.4 μm, and D = 100 μm2 s−1. (Inset) The behaviour of the dimensionless function γ(β), introduced in equation (2.7) and defined in equation (2.9). (Online version in colour.)
2.2. Reaction–diffusion dynamics of spatial flux regulation
To analyse the regulation capacity of both localization strategies, i.e. enzyme co-clustering and enzyme sequestration, we consider a model that describes the reaction–diffusion dynamics within a spherical domain with a single central enzyme cluster, as illustrated in figure 1. This domain represents the spatial region around a typical example of one of several such clusters within a larger cell. Since we are interested in the branching fraction (rather than the absolute magnitude) of the fluxes, we only need to consider a single, representative domain. We denote the radius of this domain by R, which corresponds to half of the typical distance between clusters. We consider the typical cluster radius, denoted by rs for EP sequestration and rc for EP − EI co-clusters, as a fixed intrinsic property of the particular enzymes and their assembly processes. The associated fixed local concentration of EP enzymes within each type of cluster is denoted by cs and cc, respectively.
As a reference for the spatial regulatory effect, we take the spatially uniform, well-mixed scenario (see previous section). Hence, we consider as the basal, unregulated level of the branching fraction, to be compared with the Jp value obtained for each localization strategy. Importantly, we always compare branching fractions obtained for the same total number of enzymes and the same catalytic efficiency, assuming that the enzymes are merely rearranged for spatial regulation. This constraint relates the domain radius R, the cluster radii rc,s and the local EP concentrations cc,s within the clusters to the concentration [EP] of the well-mixed scenario via R = rc,s(cc,s/[EP])1/3.
We assume that I molecules move by diffusion and denote their diffusion coefficient by D. The steady-state radial concentration profile of I molecules, denoted as ρ(r), must then satisfy the local diffusion–reaction balance
| 2.3 |
where the reaction term F [ρ(r), r] depends on the localization strategy. For sequestration of EP, the reaction term is
| 2.4 |
where js denotes the production flux of intermediates by EI outside the EP cluster and is the concentration of EQ outside the cluster (chosen to guarantee that the mean concentration over the whole domain is the same as in the well-mixed case). For EP − EI co-clusters, the reaction term is
| 2.5 |
where jc is the production flux of I in the cluster, while is the concentration of EQ between the clusters. Local conservation of mass requires that the radial concentration profile ρ(r) is continuous and smooth at the interface of the clusters and the bulk, i.e. at rs or rc. At the boundaries, we have reflective (no-flux) boundary conditions, such that ρ′(0) = ρ′(R) = 0. At the outer boundary, this boundary condition represents symmetric exchange of intermediates I with the adjacent domains around neighbouring clusters.
For both localization strategies, the model can be solved analytically to determine the steady-state fluxes. In particular, the branching fraction towards the product P is obtained as the ratio between the absolute flux towards P and the production flux of I,
| 2.6 |
In general, these branching fractions depend separately on the mean enzyme concentrations [EP] and [EQ] (see appendix A for the full solutions). However, in the regime of typical biological parameter values, with [EP] and [EQ] (nano- to micromolar range) much smaller than the local concentrations cc,s inside the clusters (millimolar range), the branching fractions depend on [EP] and [EQ] only via the total enzyme activity ratio α of equation (2.2), as we will see below (and in appendix A).
2.3. Effects of sequestration and co-clustering on the regulation function
Figure 2 compares the α-dependence of the branching fraction Jp for the three localization strategies (well-mixed, co-clustered and sequestered) for a representative parameter set (see caption). Across the full α-range, co-clustering of EI and EP increases Jp compared to the well-mixed system, although the enhancement becomes negligible at α > 10. By contrast, sequestration of EP generally decreases Jp (see also equation (2.10) further below). At the same α-value, these two effects correspond to spatial up- and downregulation of Jp, respectively. For instance, for α = 0.5 co-clustering increases the flux towards P about twofold, while sequestration of EP reduces the flux about twofold. The magnitude of these effects grows with the number of enzymes in each cluster, irrespective of whether the cluster size rc,s or the enzyme concentration cc,s in the cluster is increased (see appendix A). For co-clustering, the branching fraction tends to a finite value for α ≪ 1. In this parameter regime, the largest enhancement compared to a well-mixed system can be achieved.
To characterize and understand the behaviour of the branching fractions, we Taylor expand the full analytical solution of appendix A, using the ratio [EP]/cc,s as the small parameter. The leading-order expressions for the branching fractions take the simple forms
| 2.7 |
for sequestration and co-clustering, respectively, which are shown as dashed lines in figure 2. Here, the dimensionless parameters βs and βc are defined as
| 2.8 |
and correspond to the ratio of two timescales, the typical time for I molecules to diffuse through the cluster, , and the timescale for I to react with EP enzymes within the cluster, τr ∼ (kpcc,s)−1. Additionally, in equation (2.7) we have introduced the dimensionless function
| 2.9 |
which depends only weakly on β, with values varying between 1 and 1.2 (figure 2, inset).
We now turn to the biophysical interpretation of the above results. By comparing the form of the regulation functions (2.7) with the one for the well-mixed case, equation (2.1), we immediately see that co-clustering effectively shifts the regulation function to the left, according to α → α + βcγ(βc). While this does not change the shape of the regulation function, it cuts off the low α-regime of , since the total enzyme activity ratio α is necessarily positive. In the case of sequestration, we can rewrite equation (2.7) as
which by comparison with equation (2.1) shows that sequestration effectively stretches the α-axis of the regulation function according to α → α/(1 + βsγ(βs)). Furthermore, we can interpret the function γ(β) of equation (2.9) physically using a coarse-grained approximation of the full reaction–diffusion dynamics. Towards this end, we consider the cluster and the bulk region as two separate domains, in each of which the intermediates are well mixed. We describe transport between the domains with an effective permeability, D/Δ, where Δ is an effective exchange length scale. By comparing the expressions for the branching fractions obtained from this approximation (see appendix A) with equation (2.7), we find that γ corresponds to the exchange length scale rescaled by the cluster radius, γ(βc,s) = Δ/rc,s. Therefore, γ(β) is a dimensionless measure for the efficiency of the transport of I molecules between the clusters and their surroundings.
2.4. Branch point regulation factors
For both clustering strategies, the effect on the branching fraction is greatest when reactions within the cluster are faster than exchange between domains (β ≫ 1), whereas there is little effect on the branching fraction when exchange is fast compared with reactions (β ≪ 1). We quantify the regulatory effect of the two enzyme clustering strategies by the spatial regulation factor , which measures the fold-change of the branching fraction towards P for clustering relative to the well-mixed case. These regulation factors take the form
| 2.10 |
for enzyme sequestration and co-clustering, respectively (implying that ηs < 1 and ηc > 1). The strongest upregulation by enzyme co-clustering is achieved when two conditions are met: (i) the average enzymatic activity of EQ is much larger than of EP (small α) and (ii) the enzymatic activity in the cluster is large compared with the rate of diffusive exchange (large βc), see figure 3a. On the other hand, when the average enzymatic activity of EP is much larger than that of EQ () the pathway is strongly biased towards P already with uniformly distributed enzymes, and hence the enhancement from enzyme co-clustering becomes negligible.
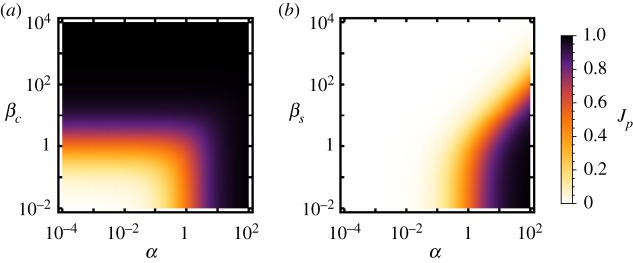
Figure 3.

Capability of the spatial strategies to regulate the flux distribution at the branch point. (a) Enhancement towards the P branch by EI − EP co-clustering. Black lines divide regimes at the enhancement threshold ηc = 2, while green lines divide regimes based on the upregulated branching fraction . (b) Downregulation of the P branch by enzyme sequestration. Black lines denote ηs = 0.5, green lines indicate where the branching fraction of the well-mixed system . (Online version in colour.)
The spatial regulation factors, equation (2.10), quantify the strength of the regulatory effects. In order to identify the biologically interesting parameter regimes of the spatial regulation strategies, we consider a twofold regulatory effect as the minimum for biological significance. Hence, we consider upregulation by co-clustering to be biologically relevant only when the regulation factor is at least ηc ≥ 2, while for downregulation via sequestration we require ηs ≤ 0.5. However, a large regulation factor alone does not guarantee that the regulatory effect is biologically useful. The biological relevance also depends on the absolute value of the branching fraction, which is shown in figure 4a,b for the co-clustered and sequestered enzyme arrangement, respectively, again as a function of α and β. In particular, it is important for each regulation scenario that the branching fraction in the higher state is not too small to be significant. For instance, strong downregulation would be of no significance, if the basal branching fraction was already small. As an exemplary threshold for biological significance we consider Jp ≥ 0.2, i.e. in the case of co-clustering we require the branching fraction in the upregulated state to be at least , and in the case of sequestration we require the basal branching fraction of uniformly distributed enzymes to be at least .
Figure 4.
Branching fractions Jp for the (a) co-clustering and (b) sequestration scenarios as a function of α and βc,s. (Online version in colour.)
Together, these constraints render the parameter region delimited by the solid lines in figure 3 as biologically relevant. For the case of co-clustering, the minimum relevant value of βc is independent of α as long as α ≲ 0.1. When βc is above this minimum threshold, the co-cluster is sufficiently large and dense, such that the required fraction of I molecules is converted to P before diffusing out of the cluster. For the case of enzyme sequestration, the strongest downregulation of Jp is achieved for large βs and α ≤ 1, which however lies outside the biologically relevant parameter regime (top left in figure 3b). Nevertheless, sequestration can suppress the production of P more than a 100-fold within the relevant regime, where .
Interestingly, for both localization strategies, and for either up- or downregulation of Jp, the criteria combine to produce a lower bound on the timescale ratio β of equation (2.8) in a similar range
Note that β depends only on the molecular properties of the enzyme P (its catalytic efficiency kp and diffusion constant D) and the physical properties of the clusters (their radius rc,s and local enzyme concentration cc,s). Hence the condition is a molecular design constraint, i.e. only enzymes with a combination of physical and biochemical parameters that satisfy this constraint will be suitable for regulation of reaction fluxes via enzyme sequestration and co-clustering. The biologically relevant parameter regime in figure 3 also constrains the total activity ratio α. However, this constraint is less limiting, since α is more easily changed to fall within the desired regime by adjusting the concentrations of the enzymes P and Q (cf. equation (2.2)).
2.5. Application of the theoretical framework
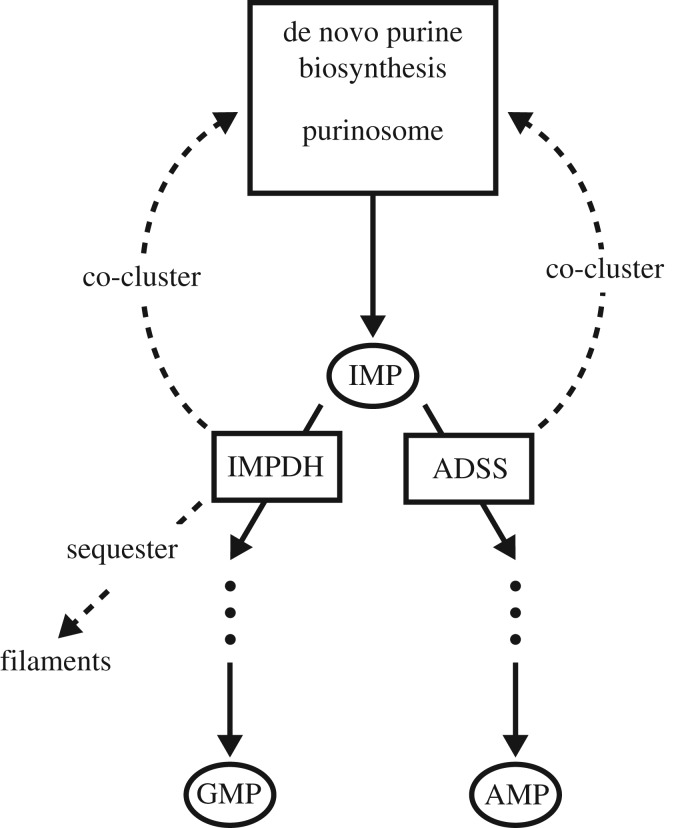
To apply the general framework presented above, we first consider the example of the branch point at the end of the de novo purine biosynthesis pathway (figure 5). The product of the purine biosynthesis pathway, inosine monophosphate (IMP), can be processed further in two competing pathways, to produce the nucleoside monophosphates GMP or AMP. The two competing enzymes at this branch point are inosine-5’-monophosphate dehydrogenase (IMPDH) and adenylosuccinate synthase (ADSS). These competing enzymes display a high degree of spatial organization. The enzyme IMPDH, in particular, has been found to either colocalize with the purinosome or form large filamentous structures under different conditions [33]. The enzyme ADSS has also been observed to colocalize with the purinosome [33]. Thus, this branch point appears to have the capacity for two spatial regulation strategies in response to changing environmental conditions: co-clustering with the purinosome as a mechanism for upregulation, and sequestration of a single enzyme into a cluster as a mechanism for downregulation.
Figure 5.
Schematic of the branch point at the end of the de novo purine biosynthesis pathway. Experimentally observed condition-dependent enzyme localizations, featuring both co-clustering and sequestration, are indicated by the dashed arrows. (Online version in colour.)
The enzyme kinetics of the branch point enzymes is relatively well characterized. The kinetic parameters of human IMPDH are kcat = 1.8 s−1 and KM = 14 μM for type I IMPDH and kcat = 1.4 s−1 and KM = 9 μM for type II IMPDH [34], which leads to a catalytic efficiency of kcat/KM ≈ 105 M−1 s−1 in both cases. For ADSS, the kinetic parameters are kcat = 5.4 s−1 and KM = 45 μM [35], leading to kcat/KM ≈ 3.5 × 105 M−1 s−1. The intracellular concentration of IMP has been determined for HeLa cells to 0.02 nmol/(million cells) under purine rich conditions and to 0.06 nmol/(million cells) under purine-depleted conditions [33]. With a typical volume ∼4 × 103 μm3 of a HeLa cell [36], this converts to 5 μM and 15 μM under purine rich and depleted conditions, respectively. Thus, the concentration of IMP in both conditions is of the order of the Michaelis constant of IMPDH and ADSS, which indicates that the enzymes are not saturated under typical conditions, such that the corresponding fluxes remain sensitive to the spatial organization of the enzymes. By contrast, the cofactor NAD+ required by IMPDH has a cellular concentration of around 0.3 mM [37], while the Michaelis constant of IMPDH for NAD+ is around KM ≈ 0.07 mM [38], such that the flux of the GMP branch of the pathway is expected to be insensitive to small variations in the concentration of this cofactor.
Taken together, the literature values on the enzyme kinetics of the branch point enzymes in the de novo purine biosynthesis pathway suggest that the key assumptions of our theoretical framework are satisfied for this system. In order to verify whether this system is also in the parameter regime where co-clustering and sequestration have a biologically significant effect, we revisit the criterion for biological significance obtained in the previous section. Assuming a local enzyme concentration within clusters of cc,s ∼ 25 nM [28], a cluster radius of rc,s ∼ 0.4 μm [30] and a diffusion coefficient D ∼ 100 μm2 s−1 for a small metabolite [39], this lower bound translates into a threshold for the catalytic efficiency of the clustered enzyme of
| 2.11 |
According to the literature values (see above), both ADSS and IMPDH satisfy the criterion (2.11). Thus, we expect that co-clustering (with the purinosome) and sequestration of these enzymes will have a significant post-transcriptional regulation effect, purely from the spatial rearrangement of the enzymes, i.e. without requiring additional allosteric interactions. Note that based on this logic, one would expect single cells to never simultaneously sequester IMPDH into filaments and co-cluster in purinosomes, since simultaneous usage of two antagonistic regulatory effects would appear to be counterproductive. By contrast, mixtures of diffuse IMPDH with sequestered filaments, or mixtures of diffuse IMPDH with co-clustered purinosomes would be useful intermediate states, enabling gradual regulation. To the best of our knowledge, the experimental data required to verify this expectation are currently not yet available.
How broadly are the spatial regulation strategies of co-clustering and sequestration applicable in cells? In other words, what fraction of enzymes with known enzyme kinetics satisfies the criterion of equation (2.11)? To address this question, we relied on a quantitative survey of enzymes [40]. These data suggest that approximately 70% of enzymes in carbohydrate metabolism and approximately 50% of other classes of metabolic enzymes satisfy the bound of equation (2.11). Given that about 30% of all metabolic reactions fulfil the additional requirement that the in vivo metabolite concentration is smaller than the KM of the enzyme (see above), our criterion suggests that both sequestration and co-clustering are viable flux regulation strategies for a large fraction of metabolic enzymes.
3. Conclusion
According to our model and analysis, the control that can be exerted on a reaction–diffusion system by clustering of catalysts can be understood in simple physical terms. As long as the clusters are well separated (such that [EP]/cc,s ≪ 1), the branching fraction of both clustering strategies (sequestration or co-clustering of catalysts) is determined by two dimensionless parameters, (i) the ratio of the total activities of the two competing enzymes and (ii) the relative timescales of diffusion through and reactions within a cluster. We have seen that both strategies can achieve significant levels of regulation for realistic parameters and for a substantial fraction of natural enzymes. Taken together, our findings help to interpret the design of biological systems and suggest design principles for synthetic systems.
The general perspective that we took here is also relevant from an evolutionary angle: in order for more specialized mechanisms such as direct channelling or guidance of intermediate products to evolve, spatial proximity must already have been established. Since we found that a functional effect of spatial proximity is expected already for generic enzymes within a broad parameter regime, this functional effect may already provide a selective force for clustering. After clustering has evolved, more specialized mechanisms that build upon spatial proximity can then be explored by evolution.
Appendix A
(a) Analytic solution for the full reaction–diffusion model
Our model is based on the assumption of a larger system, in which identical clusters are arranged with a typical spacing, such that the system can be partitioned into domains as illustrated in figure 1. Each domain contains a cluster positioned at its centre. Since in this work we are only interested in the branching fraction (rather than the absolute magnitude) of the fluxes, it suffices to consider a single, representative domain in isolation. By assuming that both the cluster and the domain are spherically symmetric, the reaction–diffusion dynamics, as described by equations (2.3)–(2.5) together with the boundary conditions, becomes analytically solvable. To determine the steady-state radial concentration profile of I molecules, ρ(r), we solve these equations inside and outside of the cluster, to obtain the general solutions ρc(r) (within the cluster) and ρb(r) (for the bulk outside of the cluster). We match these solutions by requiring that the concentration profile is continuous and differentiable at the interface, ρc(rc,s) = ρb(rc,s) and ρ′c(rc,s) = ρ′b(rc,s). Subsequently, the obtained solution for ρ(r) is inserted into equation (2.6) to determine the branching fraction.
The full analytic solution of the branching fractions for the co-clustering and sequestration strategies are given by
| A 1 |
and
| A 2 |
where, for ease of notation, we expressed all parameter dependencies in terms of the three non-dimensional parameters , , and .
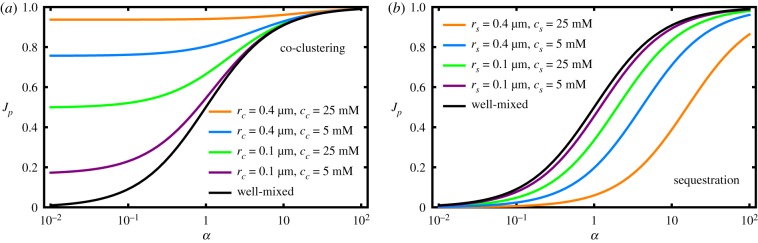
In the limit ep/cc,s ≪ 1, the expressions of the branching fraction take on the simple form of equation (2.7), which only depends on α and . Figure 6 plots the branching fractions as a function of α with different values for the cluster sizes and enzyme concentrations within the clusters, illustrating that the spatial effects generally increase with the number of enzymes in each cluster.
Figure 6.
Regulation function Jp(α) for (a) the co-clustering and (b) the sequestration strategy, with different cluster radii rc,s and concentrations cc,s. The well-mixed case is shown as a reference. These graphs illustrate that the magnitude of the spatial effects grows with the number of enzymes in each cluster, irrespective of whether the cluster size or the enzyme concentration in the cluster is increased. The other parameters were fixed to kp = kq = 106 M−1 s−1, and D = 100 μm2 s−1. (Online version in colour.)
(b) Partially well-mixed approximation of the branching fraction
Here we show that the function γ(βc,s) that appears in equation (2.7) can be interpreted as an exchange length scale rescaled by the cluster radius rc,s. Towards this end, we consider a coarse-grained description, where the cluster and the surrounding bulk are assumed to be two separate domains, in each of which the intermediates are well mixed. The transport of intermediates between these two domains occurs with an effective permeability, D/Δ, where Δ is the exchange length scale (and D is the diffusion coefficient of the full reaction–diffusion model).
For the sequestration strategy, the steady-state density of the intermediate in the cluster and bulk, ρc and ρb, can be calculated from the flux balance equations
| A 3 |
and
| A 4 |
Using the solution of the intermediate concentration inside the cluster, ρc, we then obtain the branching fraction
| A 5 |
For the strategy of EI − EP co-clustering, the flux balance equations are
| A 6 |
and
| A 7 |
leading to the branching fraction
| A 8 |
Comparing these expressions with equation (2.7), we see that the function γ(βc,s) corresponds to the ratio of the exchange length scale Δ and the cluster radius rc,s.
Data accessibility
This article has no additional data.
Authors' contributions
All authors designed the research. F.H. and F.T. performed the research. All authors analysed the results and wrote the paper.
Competing interests
The authors declare no competing interests.
Funding
This work was supported by the German Excellence Initiative via the programme ‘Nanosystems Initiative Munich’ and the German Research Foundation via SFB 1032 ‘Nanoagents for Spatiotemporal Control of Molecular and Cellular Reactions’. F.H. was supported by a DFG Fellowship through the Graduate School of Quantitative Biosciences Munich (QBM).
References
- 1.Fell D, Cornish-Bowden A. 1997. Understanding the control of metabolism, vol. 2 London, UK: Portland Press. [Google Scholar]
- 2.Zhao EM, Suek N, Wilson MZ, Dine E, Pannucci NL, Gitai Z, Avalos JL, Toettcher JE. 2019. Light-based control of metabolic flux through assembly of synthetic organelles. Nat. Chem. Biol. 15, 589–597. ( 10.1038/s41589-019-0284-8) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Krebs EG, Beavo JA. 1979. Phosphorylation–dephosphorylation of enzymes. Ann. Rev. Biochem. 48, 923–959. ( 10.1146/annurev.bi.48.070179.004423) [DOI] [PubMed] [Google Scholar]
- 4.Wang Q. et al. 2010. Acetylation of metabolic enzymes coordinates carbon source utilization and metabolic flux. Science 327, 1004–1007. ( 10.1126/science.1179687) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Gerosa L, Sauer U. 2011. Regulation and control of metabolic fluxes in microbes. Curr. Opin. Biotech. 22, 566–575. ( 10.1016/j.copbio.2011.04.016) [DOI] [PubMed] [Google Scholar]
- 6.Gaertner F. 1978. Unique catalytic properties of enzyme clusters. Trends Biochem. Sci. 3, 63–65. ( 10.1016/S0968-0004(78)94045-8) [DOI] [Google Scholar]
- 7.Liu J-L. 2016. The cytoophidium and its kind: filamentation and compartmentation of metabolic enzymes. Ann. Rev. Cell Dev. Biol. 32, 349–372. ( 10.1146/annurev-cellbio-111315-124907) [DOI] [PubMed] [Google Scholar]
- 8.Sweetlove LJ, Fernie AR. 2018. The role of dynamic enzyme assemblies and substrate channelling in metabolic regulation. Nat. Commun. 9, 2136 ( 10.1038/s41467-018-04543-8) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.O’Connell JD, Zhao A, Ellington AD, Marcotte EM. 2012. Dynamic reorganization of metabolic enzymes into intracellular bodies. Annu. Rev. Cell Dev. Biol. 28, 89–111. ( 10.1146/annurev-cellbio-101011-155841) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Wilson MZ, Gitai Z. 2013. Beyond the cytoskeleton: mesoscale assemblies and their function in spatial organization. Curr. Opin. Microbiol. 16, 177–183. ( 10.1016/j.mib.2013.03.008) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Zhang Y. et al. 2017. Protein–protein interactions and metabolite channelling in the plant tricarboxylic acid cycle. Nat. Commun. 8, 15212 ( 10.1038/ncomms15212) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Jørgensen K, Rasmussen AV, Morant M, Nielsen AH, Bjarnholt N, Zagrobelny M, Bak S, Møller BL. 2005. Metabolon formation and metabolic channeling in the biosynthesis of plant natural products. Curr. Opin. Plant Biol. 8, 280–291. ( 10.1016/j.pbi.2005.03.014) [DOI] [PubMed] [Google Scholar]
- 13.Laursen T. et al. 2016. Characterization of a dynamic metabolon producing the defense compound dhurrin in sorghum. Science 354, 890–893. ( 10.1126/science.aag2347) [DOI] [PubMed] [Google Scholar]
- 14.An S, Deng Y, Tomsho JW, Kyoung M, Benkovic SJ. 2010. Microtubule-assisted mechanism for functional metabolic macromolecular complex formation. Proc. Natl Acad. Sci. USA 107, 12 872–12 876. ( 10.1073/pnas.1008451107) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Banani SF, Lee HO, Hyman AA, Rosen MK. 2017. Biomolecular condensates: organizers of cellular biochemistry. Nat. Rev. Mol. Cell Biol. 18, 285–298. ( 10.1038/nrm.2017.7) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Hyman AA, Weber CA, Jülicher F. 2014. Liquid–liquid phase separation in biology. Annu. Rev. Cell Dev. Biol. 30, 39–58. ( 10.1146/annurev-cellbio-100913-013325) [DOI] [PubMed] [Google Scholar]
- 17.An S, Kumar R, Sheets ED, Benkovic SJ. 2008. Reversible compartmentalization of de novo purine biosynthetic complexes in living cells. Science 320, 103–106. ( 10.1126/science.1152241) [DOI] [PubMed] [Google Scholar]
- 18.Narayanaswamy R, Levy M, Tsechansky M, Stovall GM, O’Connell JD, Mirrielees J, Ellington AD, Marcotte EM. 2009. Widespread reorganization of metabolic enzymes into reversible assemblies upon nutrient starvation. Proc. Natl Acad. Sci. USA 106, 10 147–10 152 ( 10.1073/pnas.0812771106) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Schmitt DL, An S. 2017. Spatial organization of metabolic enzyme complexes in cells. Biochemistry 56, 3184–3196. ( 10.1021/acs.biochem.7b00249) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Wheeldon I, Minteer SD, Banta S, Barton SC, Atanassov P, Sigman M. 2016. Substrate channelling as an approach to cascade reactions. Nat. Chem. 8, 299–309. ( 10.1038/nchem.2459) [DOI] [PubMed] [Google Scholar]
- 21.Pedley AM, Benkovic SJ. 2016. A new view into the regulation of purine metabolism: the purinosome. Trends Biochem. Sci. 42, 141–154. ( 10.1016/j.tibs.2016.09.009) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Srere PA. 1987. Complexes of sequential metabolic enzymes. Ann. Rev. Biochem. 56, 89–124. ( 10.1146/annurev.bi.56.070187.000513) [DOI] [PubMed] [Google Scholar]
- 23.Kohnhorst CL. et al. 2017. Identification of a multienzyme complex for glucose metabolism in living cells. J. Biol. Chem. 292, 9191–9203. ( 10.1074/jbc.M117.783050) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Jin M. et al. 2017. Glycolytic enzymes coalesce in G bodies under hypoxic stress. Cell Rep. 20, 895–908. ( 10.1016/j.celrep.2017.06.082) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Chitrakar I, Kim-Holzapfel DM, Zhou W, French JB. 2017. Higher order structures in purine and pyrimidine metabolism. J. Struct. Biol. 197, 354–364. ( 10.1016/j.jsb.2017.01.003) [DOI] [PubMed] [Google Scholar]
- 26.Buchner A, Tostevin F, Gerland U. 2013. Clustering and optimal arrangement of enzymes in reaction–diffusion systems. Phys. Rev. Lett. 110, 208104 ( 10.1103/PhysRevLett.110.208104) [DOI] [PubMed] [Google Scholar]
- 27.Buchner A, Tostevin F, Hinzpeter F, Gerland U. 2013. Optimization of collective enzyme activity via spatial localization. J. Chem. Phys. 139, 135101 ( 10.1063/1.4823504) [DOI] [PubMed] [Google Scholar]
- 28.Castellana M, Wilson MZ, Xu Y, Joshi P, Cristea IM, Rabinowitz JD, Gitai Z, Wingreen NS. 2014. Enzyme clustering accelerates processing of intermediates through metabolic channeling. Nat. Biotech. 32, 1011–1018. ( 10.1038/nbt.3018) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Barry RM. et al. 2014. Large-scale filament formation inhibits the activity of CTP synthetase. eLife 3, e03638 ( 10.7554/eLife.03638.001) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Schmitt DL, Cheng Y-j, Park J, An S. 2016. Sequestration-mediated downregulation of de novo purine biosynthesis by AMPK. ACS Chem. Biol. 11, 1917–1924. ( 10.1021/acschembio.6b00039) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Hinzpeter F, Gerland U, Tostevin F. 2017. Optimal compartmentalization strategies for metabolic microcompartments. Biophys. J. 112, 767–779. ( 10.1016/j.bpj.2016.11.3194) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Park JO, Rubin SA, Xu Y-F, Amador-Noguez D, Fan J, Shlomi T, Rabinowitz JD. 2016. Metabolite concentrations, fluxes and free energies imply efficient enzyme usage. Nat. Chem. Biol. 12, 482–489. ( 10.1038/nchembio.2077) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Zhao H. et al. 2015. Quantitative analysis of purine nucleotides indicates that purinosomes increase de novo purine biosynthesis. J. Biol. Chem. 290, 6705–6713. ( 10.1074/jbc.M114.628701) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Hager PW, Collart FR, Huberman E, Mitchell BS. 1995. Recombinant human inosine monophosphate dehydrogenase type I and type II proteins. Biochem. Pharmacol. 49, 1323–1329. ( 10.1016/0006-2952(95)00026-V) [DOI] [PubMed] [Google Scholar]
- 35.Borza T, Iancu CV, Pike E, Honzatko RB, Fromm HJ. 2003. Variations in the response of mouse isozymes of adenylosuccinate synthetase to inhibitors of physiological relevance. J. Biol. Chem. 278, 6673–6679. ( 10.1074/jbc.M210838200) [DOI] [PubMed] [Google Scholar]
- 36.Puck TT, Marcus PI, Cieciura SJ. 1956. Clonal growth of mammalian cells in vitro: growth characteristics of colonies from single HeLa cells with and without a ‘feeder’ layer. J. Exp. Med. 103, 273–284. ( 10.1084/jem.103.2.273) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Yang H. et al. 2007. Nutrient-sensitive mitochondrial NAD+ levels dictate cell survival. Cell 130, 1095–1107. ( 10.1016/j.cell.2007.07.035) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Mortimer SE, Hedstrom L. 2005. Autosomal dominant retinitis pigmentosa mutations in inosine 5′-monophosphate dehydrogenase type I disrupt nucleic acid binding. Biochem. J. 390, 41–47. ( 10.1042/BJ20042051) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Milo R, Phillips R. 2015. Cell biology by the numbers. New York, NY: Garland Science. [Google Scholar]
- 40.Bar-Even A, Noor E, Savir Y, Liebermeister W, Davidi D, Tawfik DS, Milo R. 2011. The moderately efficient enzyme: evolutionary and physicochemical trends shaping enzyme parameters. Biochemistry 50, 4402–4410. ( 10.1021/bi2002289) [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
This article has no additional data.