The mechanobiology of actin cytoskeletal proteins during cell–cell fusion

Abstract

Myosin II and spectrin β display mechanosensitive accumulations in invasive protrusions during cell–cell fusion of Drosophila myoblasts. The biochemical inhibition and deactivation of these proteins results in significant fusion defects. Yet, a quantitative understanding of how the protrusion geometry and fusion process are linked to these proteins is still lacking. Here we present a quantitative model to interpret the dependence of the protrusion size and the protrusive force on the mechanical properties and microstructures of the actin cytoskeleton and plasma membrane based on a mean-field theory. We build a quantitative linkage between mechanosensitive accumulation of myosin II and fusion pore formation at the tip of the invasive protrusion through local area dilation. The mechanical feedback loop between myosin II and local deformation suggests that myosin II accumulation possibly reduces the energy barrier and the critical radius of fusion pores. We also analyse the effect of spectrin β on maintaining the proper geometry of the protrusions required for the success of cell–cell fusion.

1. Introduction

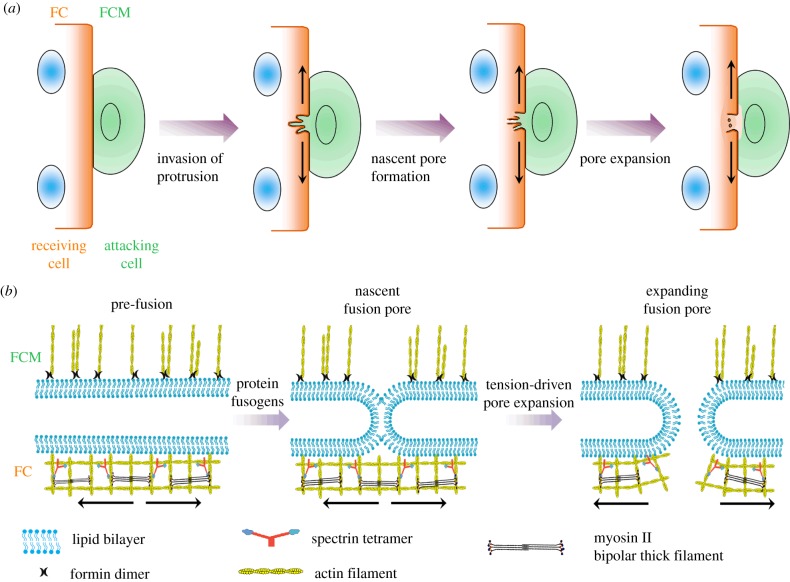
Cell–cell fusion is an important biological process for development and disease such as myogenesis, nerve repair and tumorigenesis [1–3]. Over past decades, accumulating experimental evidence has demonstrated that cell–cell fusion requires not only a set of transmembrane proteins for cell–cell recognition but also actin cytoskeletal proteins for the formation of invasive protrusions and completion of the fusion process [4–6]. Among different experimental systems, the Drosophila embryo provides a unique animal model to dissect the underlying molecular mechanism for skeletal muscle development. In Drosophila myoblasts, cell–cell fusion starts with the formation of a dense F-actin structure, also known as the actin focus (figure 1a). Subsequently, the actin focus leads to an asymmetric fusion process between two distinct cell types: a fusion-competent myoblast (FCM) and a founder cell (FC) [7–10]. The actin focus in the FCMs is mainly composed of multiple actin bundles that generate a thrust force to create multiple invasive protrusions (figure 1b). These protrusions produce invaginations in the FCs. On the other hand, the actin sheath in the FCs provides a counteracting force against the thrust force produced in the FCMs. These forces result in protrusions with diameter about 200 nm and length about 500 nm [8–11].

Figure 1.

Schematic diagram of the cell–cell fusion process. (a) The fusion process starts with the formation of multiple invasive protrusions in a fusion-competent cell, followed by the formation and expansion of fusion pores. (b) At the tip of the protrusion, the tension in the actin cytoskeleton facilitates the pore expansion during cell–cell fusion. The ‘attacking cell’ and ‘receiving cell’ refer to the FCM and FC, respectively. The arrows indicate the tension in the actin cytoskeleton underneath the plasma membrane. (Online version in colour.)

Recently, two mechanosensitive proteins, myosin II and spectrins, have been found to accumulate in the invaginations in the FCs during cell–cell fusion [8,11]. The mechanosensitive accumulations of these proteins do not require cell adhesion signals since the indentations produced by an atomic force microscope (AFM) probe can trigger these accumulations in the absence of FCMs. In addition, these accumulations occur in different regions of an inward protrusion. Specifically, myosin II mostly aggregates at the tip, whereas spectrin β is mainly localized at the base of the protrusions. It is suggested that the active spatial partitioning of these proteins is probably due to their distinct mechanosensitivity for different deformations. The bipolar thick filament assembled by myosin monomers binds two parallel actin filaments and senses the area dilation of the actin meshes (electronic supplementary material, figure S1a) [12]. On the other hand, spectrins form Y-shaped tetramers and might sense the shear deformation of the actin meshes, similar to the V-shaped filamin dimers (electronic supplementary material, figure S1b) [11]. The biochemical inhibition and deactivation of these proteins result in significant fusion defects, indicating that proper cell–cell fusion requires the normal expression and function of these proteins. Despite a large amount of xisting biological evidence at the cellular and molecular levels, a quantitative understanding of how the protrusion size and the protrusive force are linked to the microstructures and mechanical properties of the actin cytoskeleton and plasma membrane in the FCs and FCMs is still lacking. Additionally, how exactly the mechanosensitive accumulations of myosin II and spectrin β facilitate cell–cell fusion remains elusive.

In this study, we investigate the cell–cell fusion of myoblasts from the physics point of view. Firstly, we present a quantitative model to analyse the dependence of the protrusion size and the protrusive force on the mechanical properties and microstructures of the actin cytoskeleton and plasma membrane in the FCs and FCMs based on a mean-field theory. Secondly, we build a quantitative linkage between the mechanosensitive accumulation of myosin II and the fusion pore expansion at the tip of the invasive protrusions through local area dilation. Thermodynamics analysis suggests that myosin II accumulation possibly reduces the energy barrier and critical radius of the fusion pore by a mechanical feedback loop. Lastly, we discuss the biophysical functions of spectrin β regarding the geometry and microstructures of the protrusions.

2. Material and methods

2.1. The continuum theory for actin-propelled invasive membrane protrusions

During cell–cell fusion, the actin cytoskeleton in an FCM produces multiple finger-like protrusions that push into the neighbouring FC. These invasive protrusions are generated through the formation of parallel actin bundles by actin polymerization. Normally, the actin cortex and plasma membrane in cells are bridged by various anchoring proteins, such as ezrin, radixin and moesin (ERM proteins), constituting a composite-like structure [13,14]. According to the Canham–Helfrich theory, the energy of the membrane–cytoskeleton composite can be written as [15,16]

$$E=\int (2\kappa H^2+\sigma )\mathrm{d}A,$$ 2.1

where H is the mean curvature, κ is the bending modulus, σ is the tension of the composite and dA is the area element. As the cell radius (approx. 5 µm) is much larger than the protrusion radius (approx. 200 nm), the bending energy associated with the cell radius is neglected and only the part associated with the protrusions is taken into account. As a result, for an FC–FCM doublet, the change of the system energy for the invasive protrusion is [17–19]

$$\mathrm{\Delta }{E}_{\mathrm{total}}=\int 2({\kappa }_a+{\kappa }_r)H^2\mathrm{d}{A}_p+({\sigma }_a+{\sigma }_r)\mathrm{\Delta }A-\gamma A_c-fl,$$ 2.2

where dA_p is the area element for the protrusion portion, ΔA is the excess surface area induced by the protrusion, A_c is the contact area around the protrusion, γ is the specific adhesion energy, l is the length of the protrusion, and f is the net force exerting at the tip of the protrusion, the difference between the active forces (protrusive force due to actin polymerization in FCMs and contractile force associated with myosin II motor activity in FCs). The subscripts ‘a’ and ‘r’ represent the ‘attacking’ cell and ‘receiving’ cell, respectively. The attacking cell refers to the FCM where the invasive protrusions are produced. On the other hand, the receiving cell refers to the FC. For a long protrusion whose length l is much larger than its radius r, the change of the system energy is approximately given by [17]

$$\mathrm{\Delta }{E}_{\mathrm{total}}\approx 2\pi rl\left[{\displaystyle \frac{{\kappa }_a+{\kappa }_r}{2r^2}+{\sigma }_a+{\sigma }_r-\gamma }\right]-fl.$$ 2.3

Here it is assumed that ΔA ≈ A_c and the spontaneous curvature of the protrusion is close to zero. The minimization of ΔE_total with respect to r and l determines the equilibrium radius and critical force of the protrusion,

$$r_0=\sqrt{{\displaystyle \frac{{\kappa }_a+{\kappa }_r}{2({\sigma }_a+{\sigma }_r-\gamma )}}}$$ 2.4

and

$$f_0=2\pi \sqrt{2({\sigma }_a+{\sigma }_r-\gamma )({\kappa }_a+{\kappa }_r)}.$$ 2.5

It is worth pointing out that the mean-field approximation is used in the above derivation and the quantities of these physical parameters are average values.

2.2. Coarse-grained molecular mechanics model for the receiving cells (the FCs)

In general, the membrane and underlying actin cortex deform simultaneously since they are bridged together tightly by anchoring proteins. In the coarse-grained model, the membrane–cytoskeleton composite is discretized by a triangulated network where the nodes denote the crosslinking positions and the triangles resemble the meshes in the actin network. This network structure consists of the cytoskeletal proteins such as actin, actin crosslinkers (ACs) and myosin II. The system energy of the composite at the coarse-grained molecular level is [20,21]

$$E_{\mathrm{total}}=E_{\mathrm{bending}}+E_{\mathrm{in}-\mathrm{plane}}+E_{\mathrm{surface}}+E_{\mathrm{volume}}.$$ 2.6

The bending energy E_bending is mainly contributed by the plasma membrane and is calculated by

$$E_{\mathrm{bending}}={\displaystyle \frac{1}{2}\sum _{i,j}{K}_{\mathrm{bend}}(1-\cos ({\theta }_i-{\theta }_i^0)),}$$ 2.7

where K_bend is the bending modulus, θ_i,j is the angle between the surface normal to the neighbouring triangular elements i and j and ${\theta }_i^0$ is the reference value of θ_i at mechanical equilibrium. The dilation modulus of the membrane–cytoskeleton composite is mainly dominated by the contribution of the actin cortex [22,23]. Consequently, the in-plane elastic energy E_in-plane has the form

$$E_{\mathrm{in}-\mathrm{plane}}=\sum _i{V}_{\mathrm{WLC}}(d_i)+{\displaystyle \frac{1}{2}\sum _i{K}_{\mathrm{dilation}}{\left({\displaystyle \frac{A_i}{A_i^0}-1}\right)}^2.}$$ 2.8

The first term V_WLC(d_i) is the worm-like chain energy due to the intermolecular and intramolecular deformations of actin cytoskeletal proteins associated with the edge, d_i. As a result, the force based on the worm-like chain model is [24,25]

$$f_{\mathrm{WLC}}(d)=-{\displaystyle \frac{\mathrm{\partial }{V}_{\mathrm{WLC}}(d)}{\mathrm{\partial }x}=-{\displaystyle \frac{n{k}_{B}T}{p}\left({\displaystyle \frac{1}{4{(1-x)}^2}-{\displaystyle \frac{1}{4}+x}}\right),x={\displaystyle \frac{d}{d_{max}}\in (0,1),}}}$$ 2.9

where k_B is the Boltzmann constant, T is the temperature, n is the number of functional ACs between two connected nodes, d_max is the maximum length of edge d, and p is the average persistence length of the ACs. Here, the deformation of actin filaments is neglected because their persistence length (approx. 10 µm) is much larger than those of ACs and we mainly consider the deformation of the ACs. The second term in equation (2.8) is the energy due to the change of individual mesh of area A_i with initial value $A_i^0$ and a dilation modulus K_dilation. The energy associated with the conservation of the global surface area E_surface reads

$$E_{\mathrm{surface}}={\displaystyle \frac{1}{2}{K}_{\mathrm{surface}}{\left({\displaystyle \frac{A_{\mathrm{total}}}{A_{\mathrm{total}}^0}-1}\right)}^2,}$$ 2.10

where K_surface is the global area modulus, A_total is the total area of the membrane–cytoskeleton composite and $A_{\mathrm{total}}^0$ is the initial total area. Similarly, the energy associated with the conservation of global volume E_volume is determined by

$$E_{\mathrm{volume}}={\displaystyle \frac{1}{2}{K}_{\mathrm{volume}}{\left({\displaystyle \frac{V_{\mathrm{total}}}{V_{\mathrm{total}}^0}-1}\right)}^2,}$$ 2.11

where K_volume is the global volume modulus and V_total and $V_{\mathrm{total}}^0$ are the total volume of the cell and its corresponding equilibrium value, respectively. There are two terms associated with the area change: the one in equation (2.8) accounts for the short-range propagation of elastic deformation in individual meshes while the one in equation (2.10) is due to the long-range feedback of deformation of the whole actin network.

A surface mesh with 10 000 nodes and 19 996 triangles was created for a sphere with size equivalent to a cell of radius 5 µm. The average length of the edges is 70 nm. The average persistence length of ACs is of the order of 1 nm. The average number of ACs, n, is 1. The values of the remaining parameters are: K_bend = 100 k_BT, ${\theta }_i^0=0$, K_dilation = 100 k_BT, K_surface = 1000 k_BT, K_volume = 10 000 k_BT [21].

The motion of the node at position x is described by the overdamped Langevin dynamics equation where Gaussian noise with zero mean provides the perturbations and the viscosity of the cytoplasm dissipates the kinetic energy of the nodes. For Drosophila cells, we set the viscosity 1 Pa s⁻¹ and the node size is 30 nm [26].

The initial configuration was set by mapping the nodes on the surface to a sphere with an inward cylindrical protrusion whose geometry was defined by the radius r₀ and length l. After 20 s of Langevin dynamics simulation with a time step of 10⁻⁵ s at room temperature, the system reached its equilibrium state. The area and shear strains of each node were determined by averaging the deformations of the triangles with which the node of interest was associated.

2.3. Mechanics for the fusion pore formation

The formation of the fusion pores is a quite complex process at the tip of the invasive protrusions (electronic supplementary material, figure S2a) [27]. At first, the plasma membranes of the FCs and FCMs make contact when the cell–cell recognition molecules form a cell–cell adhesion complex. Secondly, thermal fluctuations trigger the formation of ‘hemifusion stalks’ between the plasma membranes. Eventually, these stalks evolve into the fusion pores, with or without an intermediate state known as a ‘hemifusion diaphragm’ depending on the local membrane tension. Despite the complexity of this dynamic process, a single energy barrier for fusion pore formation can be defined [28]. A nucleation theory is often used to estimate this energy barrier [29–32]. For a fusion pore with a radius r_p, the associated free energy change is defined by

$$\mathrm{\Delta }{E}_{\mathrm{pore}}=2\pi r_p{\lambda }_{\mathrm{eff}}-\pi r_p^2{\sigma }_{\mathrm{mem}},$$ 2.12

where σ_mem is the surface tension and λ_eff is the effective line tension of the membrane, respectively. Here the first term on the right of equation (2.12) is the energy cost for the formation of the edge of the pore and the second term represents the elastic energy of the fusion pore. The physical meaning of equation (2.12) is that the surface tension provides the driving force for the formation of the fusion pore, whereas the line tension resists this process [33]. In other words, the surface tension pulls the contour of the pore outward while the line tension pushes it inward. It was thought that λ_eff does not change with σ [30,32]. However, emerging evidence demonstrated that the effective tension of the membrane has an almost linear correlation with the membrane tension [34–37]. Hence, we assume that there is a linear dependence of λ_eff on σ,

$${\lambda }_{\mathrm{eff}}={\lambda }^0+\alpha {\sigma }_{\mathrm{mem}},$$ 2.13

where the superscript ‘0’ indicates the zero tension state [38]. The coefficient α characterizes the dependence of the line tension on the surface tension. In fact, α depends on the membrane thickness and the chemical properties of the lipids in the membrane. Interestingly, molecular dynamics simulations predict that α has a value about 2 nm for dioleoylphosphocholine, palmitoyloleoylphosphocholine (POPC) and dimyristoylphosphocholine (DMPC), whereas experimental observations showed that α is about −0.1 nm for the mixture of DMPC and dihydrocholesterol (DChol) [34,36,38]. In the high-tension regime where membrane fluctuation is suppressed, the membrane tension is determined by [39]

$${\sigma }_{\mathrm{mem}}=K_{\mathrm{mem}}{\displaystyle \frac{\mathrm{\Delta }A}{A^0},}$$ 2.14

where K_mem is the stretch modulus of the membrane and its typical value is in the range of 100–200 nN µm⁻¹ [38–41]. A⁰ is the initial area and ΔA is the change of area. Their ratio ε_mem = ΔA/A⁰ defines the area strain of the membrane. Usually, the area strain of the membrane is equal to that of the actin cortex, i.e. ε_mem = ε_cort, since the plasma membrane is tightly bridged to the actin cortex and they deform simultaneously.

The stretch modulus highly depends on the concentrations of the actin cytoskeletal proteins, especially myosin II [12,42,43]. The local enrichment of myosin II is expected to result in an increment of local stiffness and consequently reduce the local area strain of the actin cortex, which was observed experimentally in the mechanosensitive accumulation in the protrusions induced by micropipette aspiration [12,44]. Thus, equation (2.14) needs to be written as

$${\sigma }_{\mathrm{mem}}=K_{\mathrm{mem}}\left({\displaystyle \frac{\mathrm{\Delta }A}{A^0}-\mathrm{\Delta }{\epsilon }_{\mathrm{myo}}}\right),$$ 2.15

where Δε_myo is the strain reduction due to the mechanosensitive accumulation of myosin. Equation (2.15) indicates that myosin II accumulation results in a mechanosensory feedback loop that is schematically shown in electronic supplementary material, figure S4a. This type of feedback loop usually results in a biphasic dynamics of the local deformation and myosin II concentration where a phase lag between these two quantities exists (electronic supplementary material, figure S4b).

3. Results and discussions

Based on the Canham–Helfrich theory, we develop a model to investigate the quantitative dependence of the protrusion size and the protrusive force on the mechanical properties and microstructures of the actin cytoskeleton and plasma membrane in the FCs and FCMs. In this model (equation (2.2)), the mechanical work done by the actin polymerization and the cell–cell adhesion energy competes with the bending energy and elastic energy of the membrane–cytoskeleton complex. Here, the tension is mainly contributed by the cortex [45]. This model quantitatively predicts the equilibrium values of the critical radius and the force for formation of the protrusions (equations (2.4) and (2.5)). These predictions suggest that the adhesion between the two cells energetically favours the formation of large protrusions and helps to lower the force required for the generation of the protrusions. Additionally, it is suggested that the cortical tensions in both cells tend to reduce the size of the protrusions and increase the required force. Specifically, $({\sigma }_a+{\sigma }_r)\sim r_0^{-2}$ when σ_a + σ_r > γ. For a typical protrusion with σ_a = σ_r = 0.2 nN µm⁻¹ [8], r₀ = 200 nm and κ_a = κ_r = 100 k_BT [46,47], the corresponding specific adhesion energy is supposed to be γ = 0.39 nN µm⁻¹, which is close to the measured value for cadherin adhesion [48]. During myoblast fusion, Sticks-and-stones (Sns) and Dumbfounded (Duf) are the major adhesion proteins in the FCMs and FCs, respectively. The predicted adhesion energy indicates that the bond energy of Duf–Sns is probably close to that between two cadherins provided they have similar surface density.

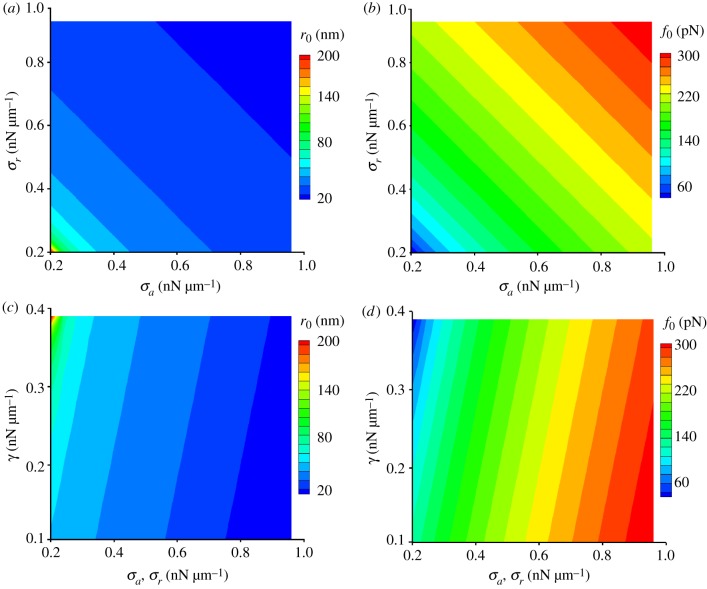
To demonstrate the predictive power of equations (2.4) and (2.5), we vary σ_a and σ_r in the range of 0.2–1.0 nN µm⁻¹ for a fixed adhesion energy γ = 0.39 nN µm⁻¹. The resulting protrusion size r₀ varies from 20 to 200 nm (figure 2a) while the net force f₀ ranges from 60 to 300 pN (figure 2b). The predicted size of the protrusions is in good agreement with the ones observed in experiments [9,10]. To evaluate the validity of the predicted net force at the tip of the protrusions, we examine the protrusive force generated by the actin polymerization occurring in a protrusion in an FCM. Assuming that the net force is equal to the force generated by actin polymerization gives the lower bound of the number of actin filaments in a protrusion, 40, provided that the force associated with the monomeric actin insertion is 1 pN [49]. This corresponds to the protrusions with the minimum radius of 30 nm since the diameter of a single actin filament in cells is about 10 nm [50], which indeed is in good agreement with the size of microvilli, which are finger-like structures filled with 50–100 bundled actin filaments [51].

Figure 2.

The protrusion size and net force depend on the cortical tensions of the FCMs and FCs, as well as the adhesion energy. (a) The protrusion size decreases with cortical tension in FCs and FCMs. (b) The net force increases with cortical tension in FCs and FCMs. (c) The protrusion size increases with adhesion energy between the FCs and FCMs. (d) The net force decreases with adhesion energy between the FCs and FCMs. The subscripts ‘a’ and ‘r’ represent the ‘attacking cell’ (the FCM) and the ‘receiving cell’ (the FC), respectively. (Online version in colour.)

As defined in equation (2.2), the adhesion energy contributes to the driving force for the formation of the protrusions. The predicted protrusion size increases with the adhesion energy (figure 2c), whereas the predicted net force decreases with the adhesion energy (figure 2d) when the values of σ_a and σ_r are fixed, suggesting that the adhesion energy favours the formation of large protrusions and lowers the force required for protrusion formation.

The Canham–Helfrich framework provides a minimal description of the interplay between the physical quantities involved in cell–cell fusion. However, this model neglects the deformation gradient along the protrusions. Additionally, the cortical tensions are also supposed to vary along the protrusion, which is supported by the experimental observation that several important cytoskeletal proteins are non-uniformly distributed in the protrusion.

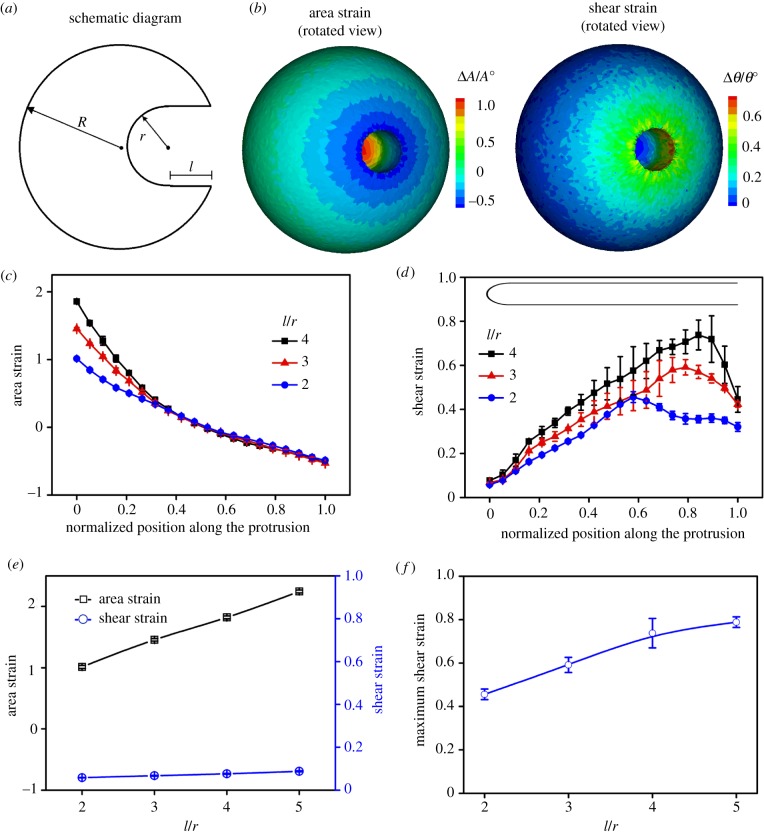
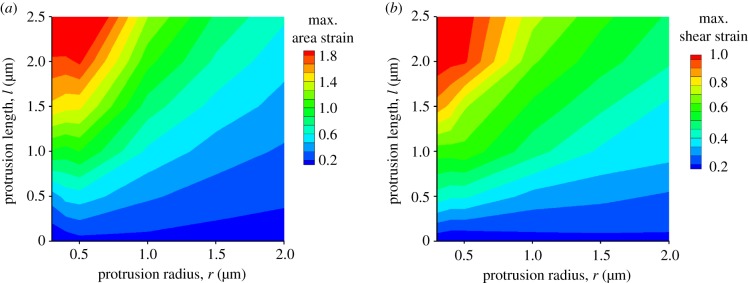
To evaluate the deformation gradients, we use the coarse-grained molecular dynamics (CGMD) simulation to calculate the local deformations in an FC [12,20,21]. For a spherical cell with radius R, the cell surface is discretized by a triangulated network where the nodes denote the crosslinking positions and the triangles resemble the actin network. We define the area strain as the ratio between the area change ΔA and the initial area A⁰. Similarly, the shear strain is the ratio between the angle change Δθ and the initial area θ⁰. We vary the aspect ratio l/r in biologically relevant ranges. The typical contour plots of these deformations on the cell surface are shown in figure 3b and electronic supplementary material, figure S3. The maximum area strain resides at the tip of the protrusion, whereas the maximum shear strain occurs near the base of the protrusion. This is also true for the protrusions with different aspect ratios (figure 3c,d). In the tip region, the shear strain remains almost the same for different protrusions (figure 3e). Although occurring in different regions, the maximum area and shear strains increase with the aspect ratio (figure 3e,f). This trend is more evident in a systematic study of the deformations of the protrusions with different length and radius, shown in figure 4.

Figure 3.

The distributions of the area and shear strains along the protrusions depend on the radius r and length l. (a) A schematic diagram of an inward protrusion with representative geometric parameters r and l in an FC. (b) The surface distribution of the area and shear strains for an FC with an inward protrusion of r = 500 nm and l = 2 µm. (c) The area strain decreases from the tip to the base along the protrusions for different l/r. (d) The shear strain peaks close to the base of the protrusions for different l/r. (e) The maximum area strain occurs at the tip of the protrusions and grows monotonically with l/r, whereas the shear strain at the tip only varies slightly at the tip. (f) The maximum shear strain at the base of the protrusions grows monotonically with l/r. For all cases, the protrusion radius r is 500 nm. (Online version in colour.)

Figure 4.

The maxima of area (a) and shear (b) strains for the protrusions with different radius r and length l. (Online version in colour.)

Notably, it is assumed that there is only one AC at each crosslinking point in the CGMD simulations, which underestimates the number of ACs compared with the actual cases. In fact, Young's modulus of the actin cortex is a power-law function of the concentration of ACs, suggesting that a small decrease in the concentration of ACs results in a great reduction of Young's modulus [43,52]. Thus, the area strains obtained by the simulation are overestimated since the number of ACs as well as the in-plane modulus in equation (2.8) are considerably underestimated. Nevertheless, the spatial distribution of the strains is expected to have similar trends regardless of the exact value of Young's modulus.

It is proposed that the deformation gradients along the protrusions determine the mechanosensitive accumulations of actin cytoskeletal proteins. Myosin II monomers assemble into bipolar thick filaments with the motor heads sticking out at the two ends of the filaments. This rod-like bipolar structure allows the myosin II thick filament to bind two parallel actin filaments and sense the distance increase between the binding sites [53]. Such a distance increase corresponds to the edge stretch of each actin mesh; equivalently, the area dilation of the actin network (electronic supplementary material, figure S1a). Large area dilation results in strong binding between myosin II monomers and actin filaments, which slows down the local disassembly rate of myosin II bipolar thick filaments [54]. Thus, myosin II monomers accumulate at the tip of the protrusions where the maximum area strain resides. On the other hand, spectrins assemble into Y-shaped tetramers, allowing them to crosslink two unparallel actin filaments with their two arms. When these two crosslinked actin filaments change their orientations during cellular deformation, the angle between the two arms of the Y-shaped tetramer will change accordingly. Consequently, the binding interfaces between the spectrins and the actins will be either strengthened or weakened. Spectrins a share similar actin binding domain with other actin crosslinking proteins such as α-actinins. Single molecule measurement showed that the binding affinity of α-actinin to F-actin increases with the load when the load is smaller than 50 pN [55]. Considering the similarity of their actin binding domains, we expect that the binding affinity of spectrin behaves similarly in response to mechanical stimuli. A typical feature of the actin mesh undergoing shear deformation is the change of the angle between two crosslinked actin filaments. Hence, we propose that local shear deformation changes the angle between two spectrin-crosslinked actin filaments and increases the binding affinity of spectrin to actin filaments (electronic supplementary material, figure S1b). Large angle change leads to strong binding between spectrins and actin filaments, reducing the local dissociation rate of spectrin tetrameters. As a result, spectrins accumulate at the base of the protrusions where the maximum shear deformation resides. In fact, a similar mechanosensitive behaviour of the filamin dimer (a Y-shaped actin crosslinked protein) is found in the sheared region of the mechanically induced protrusions [56].

Up to now, a quantitative interpretation of the spatial distribution of myosin II and spectrin β has been presented based on their molecular structures and mechanosensitive properties. However, the biological significance of their active accumulations has not been discussed. In the section below, we first analyse how myosin II accumulation affects cell–cell fusion.

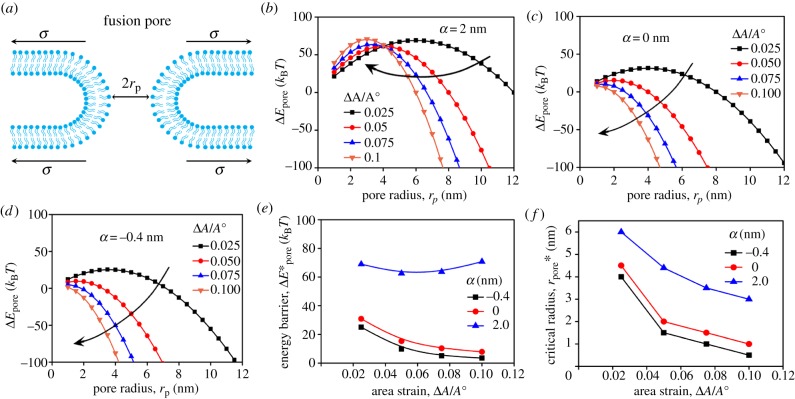
Experimental evidence showed that deactivation of myosin II motor activity in the FCs dramatically impairs the success rate of the cell–cell fusion [8]. To find the underlying mechanism, we focus on the tip region of the protrusion where both the formation of the fusion pores and the mechanosensitive accumulation of myosin II occur. Structurally, the formation of a fusion pore consists of a few intermediate states such as a hemifusion stalk and a hemifusion diaphragm (electronic supplementary material, figure S2a). Despite these dynamic configurations, we can define an effective energy barrier for the transition from the state of smooth parallel plasma membranes to the state of the fusion pore (electronic supplementary material, figure S2b) [28]. This energy barrier can be determined by equation (2.12), where the reaction path is along the radius of the fusion pore [29–32]. The physical meaning of this equation is that the surface tension of the membrane provides the driving force against the resistance force from the line tension of the pore perimeter [33]. In comparison with other models [30,32], the effective line tension λ_eff in equation (2.12) depends linearly on the membrane tension σ (equation (2.13)). Experimental and computational results showed that the coefficient α characterizing this dependence can be either positive or negative [36,38]. As the membrane is tightly bridged to the actin cortex, we assume that the area strain of the membrane is equal to that of the actin cortex. Based on the results of CGMD simulations (figure 2), it is expected that the membrane tension has its maximum in the tip region of the protrusions. Considering that the membrane tension σ is linearly proportional to the local area strain ΔA/A⁰ (equation (2.14)), the energy change ΔE_pore for the formation of a fusion pore of radius r_p can be quantified based on equations (2.12)–(2.14). Figure 5b–d shows the ΔE_pore profiles for α = 2 nm, 0 nm and −0.4 nm, respectively, at different area strains. In general, the ΔE_pore curve has a concave shape. The peak value of the ΔE_pore curve defines the energy barrier $\mathrm{\Delta }{E}_{\mathrm{pore}}^{\ast }$ for the kinetics of the pore formation and the corresponding pore radius is the critical pore radius $r_{\mathrm{pore}}^{\ast }$. During fusion pore formation, the pores start to expand automatically once the condition $r_p>r_{\mathrm{pore}}^{\ast }$ is satisfied. Commonly, the $\mathrm{\Delta }{E}_{\mathrm{pore}}^{\ast }$ increases with α for the same area strain (figure 5e). By comparison, $\mathrm{\Delta }{E}_{\mathrm{pore}}^{\ast }$ decreases monotonically with the area strain ΔA/A⁰ for a non-positive α, whereas it displays a non-monotonic change for a positive α when ΔA/A⁰ is smaller than 0.1. For large ΔA/A⁰, $\mathrm{\Delta }{E}_{\mathrm{pore}}^{\ast }$ for a positive α increases almost linearly since the value of λ_eff is mostly dominated by the contribution from the membrane tension term (electronic supplementary material, figure S6d). Nevertheless, the critical radius $r_{\mathrm{pore}}^{\ast }$ decreases with the area strain ΔA/A⁰ for all cases (figure 5f and electronic supplementary material, figure S6e). Meanwhile, the higher the α, the larger the $r_{\mathrm{pore}}^{\ast }$ becomes for the same area strain. These results indicate that the membrane tension indeed facilitates fusion pore formation through reducing the critical radius $r_{\mathrm{pore}}^{\ast }$. However, the impact of the tension on the energy barrier $\mathrm{\Delta }{E}_{\mathrm{pore}}^{\ast }$ displays different trends for α > 0 and α ≤ 0.

Figure 5.

The energy barrier for fusion pore formation depends on the local area strain as well as the local tension characterized by α. (a) Schematic diagram of a fusion pore under tension. The energy barrier changes with the pore radius at different area strains for α = 2 nm (b), 0 nm (c) and −0.4 nm (d). The energy barrier $\mathrm{\Delta }{E}_{\mathrm{pore}}^{\ast }$ and critical radius $r_{\mathrm{pore}}^{\ast }$ for the cases in (b–d) are plotted in (e) and (f), respectively. For curves in panels (b–d), λ⁰ = 10 pN and K_mem = 100 nN µm⁻¹. (Online version in colour.)

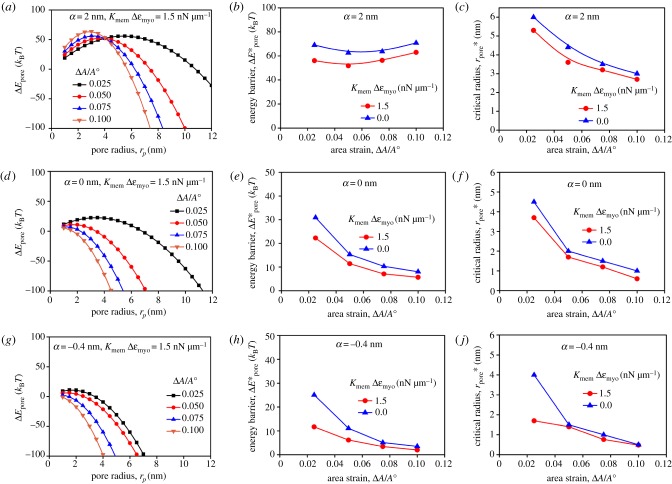
To connect the local tension to the myosin II accumulation, it is useful to point out that the stretch modulus of the actin network highly depends on the concentrations of actin cytoskeletal proteins, especially myosin II [12,42,43]. The local enrichment of myosin II is expected to lead to an increment of local stiffness and consequently reduce the local area strain of the actin cortex, which was observed experimentally from the mechanosensitive accumulation in the protrusions induced by micropipette aspiration [12,44]. This effect can be quantitatively determined based on several physical and mechanical properties of myosin II [44]. It is known that the concentration of myosin II in the assembly state is about 30% of the total cellular concentration of 0.5 µM, i.e. 0.15 µM [57,58]. Although the unloaded duty ratio of Drosophila non-muscle myosin II is about 0.1 [59], it can grow 10-fold and reach 1.0 when myosin II is under tension [54]. Assuming the thickness of the actin cortex in an FC is 0.5 µm, the in-plane tension contributed by the myosin II contractility is about 0.5 nN µm⁻¹ since one myosin II monomer has two myosin heads and each head generates a force of about 3 pN [60]. The experimentally observed mechanosensitive accumulation of myosin II at the tip of the protrusions can be three times that in the actin cortex in the absence of invasive protrusions (figure 6). This accumulation corresponds to a tension change of 1.5 nN µm⁻¹. The effect of myosin II accumulation on local stiffness (or tension) has already been reported in other studies and is described by a mechanosensory feedback loop (electronic supplementary material, figure S4) [12,44]. To include this effect, the term K_memΔε_myo is introduced such that equation (2.14) is rewritten as equation (2.15). The influence of a tension change of K_memΔε_myo = 1.5 nN µm⁻¹ on the energy change for the fusion pore with α = 2 nm is shown in figure 7a. The corresponding energy barrier and critical radius are shown in figure 7b,c, respectively. In comparison with the cases without the stiffening effect (K_memΔε_myo = 0), the cases with the stiffening effect (K_memΔε_myo > 0) have a lower energy barrier $\mathrm{\Delta }{E}_{\mathrm{pore}}^{\ast }$ as well as a reduced critical radius $r_{\mathrm{pore}}^{\ast }$. This is also true for the cases of α = 0 and −0.4 nm when the stiffening effect is considered (figure 7d–j). From a thermodynamics point of view, the reduced $\mathrm{\Delta }{E}_{\mathrm{pore}}^{\ast }$ and $r_{\mathrm{pore}}^{\ast }$ boost the fusion process. Thus, the local stiffening due to the mechanosensitive accumulation described in equation (2.15) quantitatively explains the phenotype where the success rate of cell–cell fusion of Drosophila myoblasts is greatly impaired by deactivating myosin II.

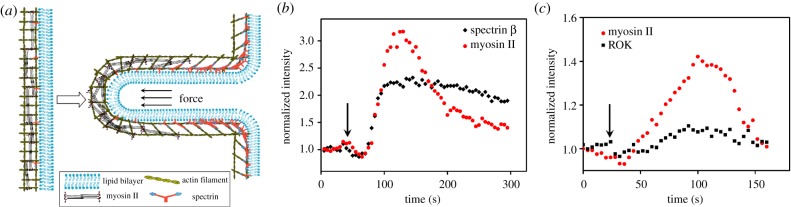
Figure 6.

The spatial partitioning of mechanosensitive myosin II and spectrin β in an FC. (a) The schematic diagram of the spatial distribution of myosin II and spectrin β along the protrusion: myosin II and spectrin β accumulate at the tip and base, respectively, when the planar membrane becomes concave. (b) The dynamics of the mechanosensitive accumulations of myosin II and ROK in the same FC. (c) The dynamics of the mechanosensitive accumulations of myosin II and spectrin β in the same FC. The data in (b) and (c) are obtained by quantifying the movies provided in [8] and [11], respectively. The black arrows indicate the time points when the indentation by AFM starts. (Online version in colour.)

Figure 7.

The local stiffening induced by myosin II accumulation reduces the energy barrier and critical radius for fusion pore formation. The energy penalty changes with the pore radius at different area strains for α = 2 nm (a), 0 nm (d), −0.4 nm (h) when the stiffening effect K_memΔε = 1.5 nN µm⁻¹ is considered. The energy barrier $\mathrm{\Delta }{E}_{\mathrm{pore}}^{\ast }$ for the cases in (a), (d) and (h) is plotted in (b), (e) and (i), respectively. The critical radius $r_{\mathrm{pore}}^{\ast }$ for the cases in (a), (d) and (h) is plotted in (c), (f) and (j), respectively. For all cases, λ⁰ = 10 pN and K_mem = 100 nN µm⁻¹. (Online version in colour.)

It is noted that the energy change defined by equation (2.12) does not work for r_p < 1 nm where the hemifusion stalk forms. In this regime, certain lipid molecules such as phosphatidylserine move from the inner leaflet to the outer leaflet of the plasma membrane at the pore [61], which leads to a discontinuity in the first-order derivative of the energy profile [38]. Hence, several data points in the r_p < 1 nm regime determined by equation (2.12) shown in figures 5 and 7 should be taken cautiously. For a non-positive α, the energy barrier decreases monotonically with the area strain ΔA/A⁰ and becomes negative when ΔA/A⁰ > 0.1, indicating that cell–cell fusion occurs spontaneously in this regime. Hence, the energy barrier is analysed only in the range of 0.0 < ΔA/A⁰ < 0.1 for the non-positive αs. On the other hand, the energy barrier does not change monotonically with ΔA/A⁰ for the positive αs. The local stiffening due to the mechanosensitive accumulation of myosin II significantly reduces the energy barrier and the critical pore radius when ΔA/A⁰ < 0.1. However, this effect is quite weak for ΔA/A⁰ > 0.1 (electronic supplementary material, figure S7). In reality, the area strain of the plasma membrane can only reach up to 0.1 before the membrane ruptures. The data plotted for 0.2 < ΔA/A⁰ < 1.0 are only for theoretical discussion. Experimental observations demonstrate that many vesicles diffuse to the fusion sites and provide additional lipid molecules for the area expansion during cell–cell fusion of Drosophila myoblasts [62], which greatly reduces the area strain of the plasma membrane near the fusion site such that membrane rupture is avoided.

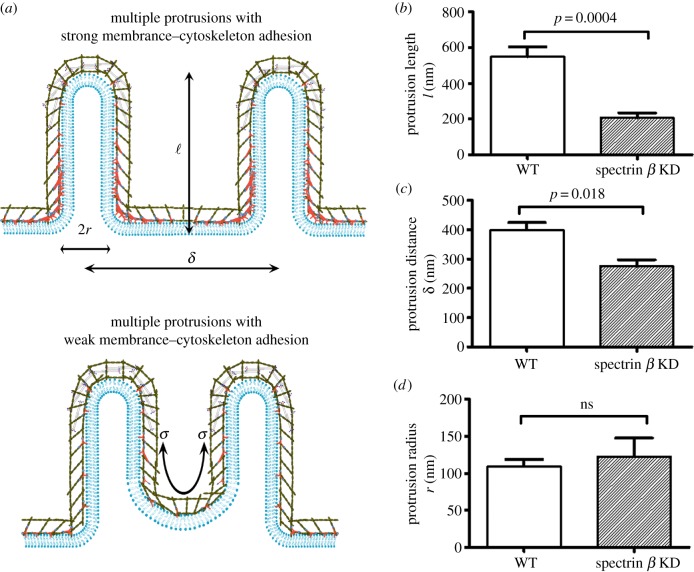
Next, we investigate the effect of mechanosensitive accumulation of spectrin β on cell–cell fusion. In addition to the actin binding domains, spectrin β has a phosphatidylinositol(4,5)bisphosphate (PIP₂) binding motif, which allows it to anchor the actin filament to the plasma membrane [63]. Moreover, spectrins are able to interact with diverse transmembrane proteins, providing an alternative way to link the actin cytoskeleton to the plasma membrane [64]. The spectrin β accumulation in response to the shear deformation is expected to greatly enhance the structural linkages between the actin cortex and the plasma membrane at the fusion site, especially at the base of the inward protrusions in the FCs. Both the knock-down of spectrin β and the disruption of the spectrin tetramerization results in severe fusion defects [11]. To quantify the structural changes associated with the fusion defects, three parameters are used to quantify the morphology of the invasive protrusions: the protrusion radius r, the protrusion length l and the distance between two neighbouring protrusions δ (top panel in figure 8a).

Figure 8.

Spectrin β enhances the adhesion between the plasma membrane and the actin cytoskeleton, stabilizing the inward protrusions in FCs. (a) Schematic diagram of the morphologies of the inward protrusions with (upper panel) and without (lower panel) local accumulation of spectrins near the base of the protrusions. (b) Spectrin β knock-down (KD) leads to the shrinkage of the protrusion length. (c) Spectrin β KD results in the reduction of the distance between neighbouring protrusions. (d) Spectrin β KD does not affect the protrusion radius. The measurements in (b–d) were performed on the electron micrographs published in [8,11]. The statistical significance (p-value) was calculated using a two-tailed non-parametric Mann–Whitney test. For wild-type (WT) cells, n = 9; for spectrin β knock-down cells, n = 5. (Online version in colour.)

We begin by examining the effect of spectrin β knock-down on the protrusion length l. The local curvature at the protrusion tip region is smaller than that at the base region, resulting in higher tension at the tip than at the base. Additionally, the contractility of the accumulated myosin II around the tip of the protrusions also elevates the local tension in the actin cortex. Hence, the cortical tension gradient from the tip to the base tends to pull the cortex away from the base (bottom panel in figure 8a). As long as the linkages between the plasma membrane and the actin cortex are strong enough, the morphology of the protrusions will not be affected. The knock-down of spectrin β and the disruption of the spectrin tetramerization weaken the linkages built by spectrins. It is expected that the impaired linkages cannot sustain the tension gradient and eventually lead to the detachment between the actin cortex and the plasma membrane at the base of the protrusions in the FCs, which alters the protrusion length l. This prediction is consistent with the experimental observation in the electron micrographs where the ruptures between the actin cortex and the membrane at the base are identified as the light grey regions indicated by the yellow arrows while the protrusions coloured in purple are indicated by black arrows (electronic supplementary material, figure S8). The statistical analysis of the geometry of the protrusions in the micrograph demonstrates that the protrusion length l of the spectrin β knock-down shrank significantly compared with that in the intact cells (figure 8b).

The spectrin β knock-down is also supposed to affect the distance between the neighbouring protrusions. It has been predicted by Derényi et al. [18] that there is an attractive potential between these protrusions, which tends to reduce the distance between the neighbouring protrusions. The attractive force is resisted by the membrane–cytoskeleton composite at the base of the protrusions. The detachment between the actin cortex and the plasma membrane at the base makes the membrane more vulnerable to the attractive force as the actin cortex retracts away from the base region due to the contractility by accumulated myosin II at the tip. Therefore, the distance between the neighbouring protrusions is expected to decrease when spectrin β knock-down results in the ruptures between the actin cortex and the plasma membrane. In fact, the distance between the protrusions δ for the spectrin β knock-down in the electron micrograph (electronic supplementary material, figure S8) was dramatically reduced compared with that in the intact cells (figure 8b), consistent with our prediction.

Our mean-field theory suggests that the protrusion radius r at equilibrium depends on the bending rigidity and the tension of the membrane–cytoskeleton composites along the protrusions in the FCs and FCMs, as well as the adhesion energy between them (equation (2.3)). Spectrin β is primarily localized at the base of the membrane and its knock-down does not significantly alter the above physical quantities that determine the size of the protrusion radius. In fact, the experimentally observed protrusion radius with spectrin β knock-down does not differ from that of the wide-type FCs (figure 8c), suggesting that the strength between the membrane and the actin cortex at the base does not affect the protrusion size.

The mean-field theory (equation (2.2)) in this study reaches similar conclusions (equations (2.4) and (2.5)) to those in other studies [17,18,65]. The major difference is that previous studies are mainly focused on the formation of the membrane tube and our work considers the formation of the membrane–cortex protrusions. Additionally, our theory explicitly considers the effect of the cell–cell adhesion energy that promotes the formation of large protrusions and lowers the force required for the generation of the protrusions. Despite its strong predictive power, the mean-field theory assumes that the effective tension is uniform along the protrusions, which is not really true since some of the cytoskeletal proteins are unevenly distributed. Additionally, this theory only predicts the equilibrium or steady-state configurations of the protrusions, whereas the bundling of actin filaments as well as the elongation of the protrusions is dynamic and the fusion process is thermodynamically out of equilibrium. To capture the dynamics of the bundling and elongation processes, a mesoscopic model based on Brownian ratchets, such as those proposed by Mogilner & Rubinstein [66], is highly desired.

In contrast to the analytical methods, the coarse-grained numerical simulations are able to reveal more details of a dynamic process. The CGMD simulations implemented in this study naturally encapsulate the elastic behaviour of cytoskeletal proteins and the viscous nature of the cytoplasm. Recently, Maître et al. [67] have constructed a similar numerical method to investigate the cell shape changes during embryo development. Their simulations successfully capture the cortical heterogeneity associated with the polarization of cytoskeletal proteins and the cellular deformations at much larger scale where one cell completely internalizes another cell. Moreover, their method is able to reproduce the dynamic configurations of cell aggregates where the cellular viscosity and tissue viscosity coexist.

Besides the cell–cell fusion of myoblasts, it was observed that the actin cytoskeleton also plays a critical role in the endocytosis and vesicle–cell fusion processes [68–70]. The fusion also occurs between contacting vesicles where there are no adhesion proteins and actin cytoskeletal proteins [28]. The energy barrier of the vesicle–vesicle fusion is comparable to that of the cell–cell fusion discussed above. However, recognition molecules such as Duf and Sns are required for myoblast fusion, indicating that the adhesion energy compensates for the energy of elastic deformations of the cytoskeletons underneath the plasma membrane in cells.

4. Conclusion

In summary, we built a quantitative model and used CGMD simulations to understand the distinct dynamics and spatial aggregation of actin, myosin II and spectrin β in the protrusions during cell–cell fusion of Drosophila myoblasts. We showed that the polymerization of actin in the front of the bundled actin filaments generates enough force to create invasive protrusions at the fusion site in the FCMs. Our theory, which is based on the mechanical feedback loop, demonstrated that the enhanced contractility due to mechanosensitive accumulation of myosin II facilitates fusion pore formation at the tip of the protrusions by reducing the energy barrier and critical radius. Our analysis argues that the mechanosensitive accumulation of spectrin β at the base of the protrusions ensures the proper geometry of the protrusions in the FCs. As Drosophila cells and mammalian cells share many common genes, our results might also apply to the cell–cell fusion of mammalian myoblasts. The distinct molecular structures of the rod-shaped myosin II and Y-shaped spectrin tetramer allow them to respond to different deformations and actively accumulate accordingly. Other crosslinking proteins with similar structures might behave similarly. These mechanosensitive mechanisms may provide guidance for the tuning of certain cellular processes by genetically editing the sequence of proteins. Additionally, the mechanosensitive behaviours of these proteins might operate in other biological processes such as neural development since spatial partitioning of different cytoskeletal proteins was also found in axons, where actin–myosin rings alternate with spectrin cables to form periodic structures [1,71].

Data accessibility

Additional data can be found in the electronic supplementary material.

Competing interests

We declare we have no competing interests.

Funding

This work was supported by the National Science Foundation of China (grant no. 11572316 to T.L., grant no. 51605091 to B.F., grant no. 51605094 to T.G.), the Fundamental Research Funds for Central Universities (grant no. WK2090050042 to T.L.), the Thousand Young Talents Program of China (to T.L.) and the Center for Micro and Nanoscale Research and Fabrication at the University of Science and Technology of China.