Independent components in stimulus-related BOLD signals and estimation of the underlying neural responses

Abstract

We measured blood oxygen level dependent (BOLD) responses to the onset of dynamic noise stimulation in defined regions of the primary retinotopic projection (V1) in visual cortex. The response waveforms showed a remarkable diversity across stimulus types, violating the basic assumption of a unitary general linear model of a uniform BOLD response function convolved with each stimulus sequence. We used independent component analysis (ICA) to analyze the component mechanisms contributing to these responses. The underlying neural responses for the components were estimated by nonlinear optimization through the Friston–Buxton hemodynamic model of the BOLD response. Our analysis suggests that one of the identified components reflected a sustained neural response to the stimulus and that another reflected an extremely slow neural response. A third component exhibited nonlinear change-specific transient responses. The first two components showed stable spatial structure in the V1 region of interest with respect to the eccentricity of the noise stimulus.

1. Introduction

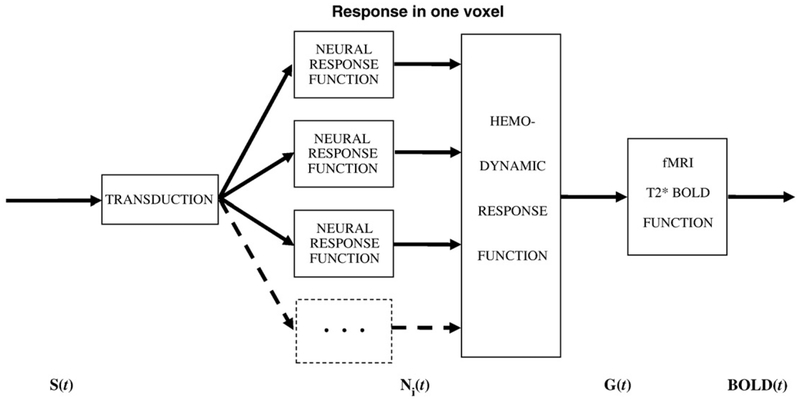
Functional magnetic-resonance imaging (fMRI) based on the blood oxygenation-level dependent (BOLD) signal is a powerful technique for studying the neural response in the cortex. Most previous work has been based on the assumption that the BOLD signal is a unitary response to a single form of stimulus S(t), usually in the form of a linear convolution of a hemodynamic response function (HRF) with the temporal waveform of the stimulus time sequence (Bandettini et al., 1993; Friston et al., 1994; Boynton et al., 1996). In most cases, it is assumed that the HRF incorporates both the cortical response to the stimulus and the hemodynamic response of the blood to the oxygen requirements of the cortical response. However, the situation may be much more complicated, with multiple components of neural response to the stimulus weighted differentially across the cortex (Zacks et al., 2001; d’Avossa et al., 2003; Bellgowan et al., 2003; Calhoun et al., 2004a; Fox et al., 2005), such that any one voxel contains contributions from more than one neural time course. If these time course variations are small relative to the BOLD temporal resolution, they may be negligible for an overall analysis of response strength, but the cited studies show non-negligible variations that require a more detailed analysis. For this reason, consistent with Friston et al. (1998, 2000), Buxton et al. (2004) and others, we restrict the term HRF to the dynamics of the blood response to the metabolic demands of the neural processing and consider the neural response to the stimulus as a separate process. This leads to the model of the BOLD mechanisms shown in Fig. 1.

Fig. 1 –

Model of the processes leading to the BOLD signal. Each stage represents an operator on the signals represented by the arrows, and is subject to processing nonlinearities (see text).

Based on the multiplicity of neurons within a given voxel, the BOLD response may consist of several components N_i(t) having different temporal properties, with each component weighted differently in each voxel. Moreover, each component may be nonlinear in its intensity response relationships and temporal integration properties (Birn, Saad and Bandettini, 2001; Bandettini and Ungerleider, 2001; see Boynton et al., 1996). The energy required to generate both the intracellular changes in potential and the axonal spikes make metabolic demands M(t) on the cellular energy mechanisms that activate the hemodynamic response of the blood H(t), both of which are also nonlinear processes (Buxton et al., 1998; Zheng et al., 2002) leading to the paramagnetic BOLD response Y(t). We therefore need an account of such multiple nonlinearities of the stimulus-evoked BOLD signal.

Below we introduce two major assumptions that constitute the foundation of our analysis. Let the response N_i(t) of a cortical neuron of a specific type (denoted by the subscript i) to a visual stimulus S(t) be

$$N_i(t)=f_i[S(t)]$$ (1)

where each f_i() is a filter function on the set of stimuli S(t).

Unlike the assumptions of the general linear model, or GLM (Friston et al., 1995; Penny and Friston, 2003), in our treatment the filter functions f_i() are allowed to be nonlinear. We then assume that the hemodynamic response is determined by the average neural activity in a voxel; this activity is thus the weighted sum of the response time courses for the neuron types present in the voxel:

$$N(t)=\sum {\alpha }_i{N}_i(t)$$ (2)

where α_i is the density of the ith type of neuron within the voxel.

Let the nonlinear coupling from the neural activity to the BOLD signal registered by fMRI be represented by the metabolic function G().

$$\text{BOLD}(t)=\text{G}(\text{N}(t))$$ (3)

We assume that for small neural signals this metabolic function G() combines the effects of the components linearly. Thus

$$\text{BOLD}(t)\approx \sum _i{\alpha }_{i}G\left(N_i(t)\right)$$ (4)

However, the linearity of Eq. 4 is intended to reflect linearity with respect to amplitude and superposition, but does not imply that the metabolic function G() is a linear convolution of a response kernel with respect to time t, because the filter functions f_i in Eq. 1 may incorporate nonlinear relationships. (This small signal linearization is justified empirically in Appendix B.)

When a stimulus has spatial structure, neurons of similar kind in different locations may be activated differently. In the experiments to be described we presented various spatial patterns of noise and blank regions, so a neuron could be in a location where noise goes on and off or a location where no noise ever appears. The neural responses for these two kinds of stimulation should be treated as independent contributing components. In one likely scenario, the slow potential in a neuron in non-stimulated location can actually be inhibited by the surrounding stimulated neurons, and its temporal profile may be the inverse of the profile of the stimulated neurons. In this case we may expect both positive and negative contribution factors (α_i) for the activity profiles to be reconstructed. In most cases our analysis produced contributory factors that had predominantly one polarity, although some cases of the opposite polarity were also evident (as in Fig. 5 below).

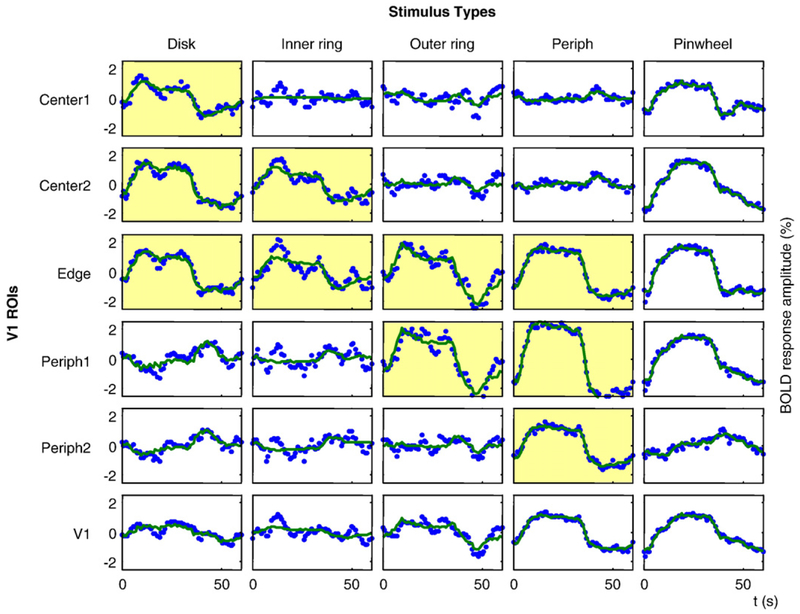
Fig. 5 –

Example of voxel-averaged data for five stimuli and six ROIs (blue dotted curves). Observer LLK, right hemisphere. The data were fit by linear combinations of the time courses for the first three ICs as shown by green curves. Yellow coloration indicates cases where the activation region was within the analysis region for the stimulus location.

Current models of the hemodynamics in human fMRI, including the balloon model (Buxton et al., 1998) and multi-compartment models (Zheng et al., 2002), describe purely local hemodynamic response to neural activity, leaving possible long-range interactions out of the picture. These models are not only local but unitary, generally making the assumption that each local region of cortex has a uniform BOLD response to whatever neural driving signal is activated by the visual stimulation. Both the unitary assumption and the localization assumption have been challenged. In particular, Thompson et al. (2005) have identified two components with different spatial ranges in the oxygen concentration signal recorded in cat cortex, with the longer-range component corresponding to the main activation signal recorded in human fMRI. Thus, the two spatial ranges identified by Thompson et al. (2005) should sum together because they both fall within the measurable range of the models applicable to the spatial resolution of the human case. The differential temporal properties, on the other hand, should be resolvable in human fMRI.

However, studies of multiple different response waveforms (Zacks et al., 2001; d’Avossa et al., 2003; Bellgowan et al., 2003; Calhoun et al., 2004a; Fox et al., 2005) have typically identified different cortical regions with differential response dynamics to the same or different stimulus conditions. The issue of multiple components within a given region of cortex is not addressed in these studies. D’Avossa et al. (2003), for example, explicitly assumed that each voxel could be categorized as exhibiting one of a variety of response waveforms. Moreover, they identified the components by means of Principal Components Analysis, which incorporates the assumption that the derived components are orthogonal (uncorrelated) functions, which is implausible in the case of neural signals. On the other hand, the classic sustained and transient types of neural signal (Leventhal and Hirsch, 1978; Henry, Mustari and Bullier, 1983; Mullikin, Jones and Palmer, 1984) are categorically distinct but are not mathematically orthogonal. The appropriate method for dissociating such signals is Independent Components Analysis (ICA; HyvÌrinen and Oja, 1997; McKeown et al., 1998; Calhoun et al., 2001; HyvÌrinen et al., 2002; Formisano et al., 2004), which identifies parametric clusters of components regardless of their degree of correlation. Although it cannot identify multiple components within a single voxel, the present application of ICA relies on the variation in the weights of multiple components across a set of voxels, to identify the relative contribution of the components to each voxel. We will thus use ICA to identify the temporal components contributing to cortical responses (see Experimental procedures).

One example of a long-range component that differs in spatial and temporal characteristics from the activation signals is demonstrated by the existence of negative BOLD signals outside the activated cortical regions. For example, Chen et al. (2005), measured impulse response functions for stimulated and adjacent unstimulated cortical areas. They found that the negative BOLD impulse response was triphasic and substantially faster than the positive response, which had a biphasic profile, and argued that these differences were most likely attributable to different neural components because there were different perceptual responses in the stimulated and un-stimulated regions of the field after the stimulus is turned off. Shmuel et al. (2002) emphasized the similarity in shape between the positive and negative BOLD (other than the difference in polarity). However, their claim should be interpreted as a first-order approximation because their own examples showed detailed shape differences that were supported by statistical analyses. Moreover, the positive/negative similarity was exaggerated by the use of long-duration stimulus epochs, masking a significant difference in the derivable impulse responses that would have been very similar to that of Chen et al. (2005), as further validated by Shmuel et al. (2006).

Shmuel et al. (2002) addressed the origin of negative BOLD response by analysis of both the BOLD and cerebral blood flow measured for identical conditions. Based on a well-validated model of cortical energy consumption and blood supply (Hoge et al., 1999), they argued for a decrease in the local rate of cortical oxygen consumption in non-activated areas compared to the rest state, which indicates reduction of neural activity. Thus, the positive and negative BOLD responses in both studies most likely represent separate neural components with different temporal characteristics rather than a unitary response governed by a linear HRF that is blind to neural variations (as implied by Shmuel et al., 2002). This analysis of the negative BOLD components is one way to reveal the influence of distinct neural components on the BOLD waveform, although the Chen et al. (2005) analysis to identify negative components per se.

1.1. Independent components analysis

In the present study we will use the ICA approach to identify multiple mechanisms contributing in the BOLD responses of both polarities. ICA is a powerful technique that extracts the statistically independent components from the signal distributions, which, as practitioners in many domains have successfully demonstrated, can accurately represent the effects of the actual contributing mechanisms (HyvÌrinen et al., 2002). The goal of the ICA decomposition is to rotate the signal components so as to minimize the mutual information between each pair of components, which is equivalent to maximizing the deviation of each component from the Gaussian distribution expected on the Central Limit Theorem.

In the fMRI domain, the application of ICA has usually been focused on extracting large effects due to causes unrelated to observer’s task, such as head movements, heartbeat, breathing, instrument drift, drift due to general alertness levels, swallowing, etc (e.g., McKeown et al., 1998; Thomas et al., 2002; Calhoun et al., 2002a,b; 2004a,b). This is a relatively straightforward analysis based on the assumption that the analyzed signals are statistically independent in time. This assumption cannot be adapted to the analysis of the separate components of neural activity, which is time-locked to the stimulus, because the synchrony in time necessitates statistical dependencies. The analysis of independent time-locked components can be addressed by applying ICA to the spatial domain, assuming that different neural mechanisms provide statistically independent activations across the voxels and stimulus types. The spatial domain approach was successfully applied in a recent study by Bartels and Zeki (2004), who attempted to resolve different visual areas in the cortex based on the differences of their neural responses to complex visual stimuli (movies). Their approach allowed them to identify different neural mechanisms in the cortex, which in many instances closely corresponded to visual areas established with localizer stimuli.

In the present study, we used spatial ICA to identify separate neural response mechanisms within a single visual area, V1, and derive their individual impulse responses. To do so, we first averaged across stimulus cycles to maximize the contribution of the stimulus-related responses to the data. For each subject, we then constructed a matrix with time points on one dimension and voxels combined with stimulus conditions along the other dimension. This matrix was subjected to PCA to reduce the dimensionality of the data sufficiently to permit the application of an ICA analysis to separate the BOLD response corresponding to different neural populations. (Without such dimensionality reduction, the analysis is computationally intractable.) The underlying neural signals were estimated for each independent component by optimizing their waveforms through a contemporary hemodynamic model (see Appendix A), based upon the contributions of Friston et al. (2000) and Buxton and Frank (1997), to obtain the best fit to the measured BOLD response. This model is formally nonlinear in its temporal integration properties, but behaves approximately linearly with respect to amplitude and linear superposition (see Appendix B). The need for such a nonlinear model was made evident by inspection of the original time series data, which often showed an increase in the BOLD signal after stimulus offset without a corresponding decrease at stimulus onset. Such an On/Off asymmetry cannot be captured by any linear model, and raises the question of whether it is compatible with current understanding of nonlinear hemodynamics or requires a non-linearity in the neural processing.

Our analysis is explicitly based on the following assumptions:

1. The component signals are similar during each stimulus presentation, varying only in their weight across stimulus types and voxels.

2. The weights of the component responses are statistically independent across the cortical space.

3. The hemodynamic model used to reconstruct the neural signals of the identified neural mechanism is approximately linear with respect to amplitude over the measured range.

The first assumption allows us to average across stimulus onset events to improve the signal/noise ratio. The second assumption states that there are neural responses with stable temporal waveform whose strength varies independently across voxels. (Response mechanisms that spatially co-vary cannot be separated.) The third assumption was made to allow for the analysis of multiple neural mechanisms from the BOLD waveforms. It permits any form of nonlinearity of the transform from the neural signal to the BOLD waveform as long as its temporal response is amplitude-invariant over the range of 0–2%. Validation for this assumption is provided in Appendix B.

2. Results

The results consist of four types of analysis of the responses to dynamic noise stimuli waveforms for the set of voxels identified as V1 in each hemisphere, as specified in Experimental procedures. The first type consisted of the derivation of a set of independent components (ICs) in the time-locked response that varied across voxels within retinotopic area V1 to account for the waveform variation across the voxels for five spatially different stimulation patterns. The second type consisted of an analysis of the consistency of the component waveforms across observers and across cortical regions. The third analysis consists of the projection of the temporal components onto the spatial array of the V1 map to illustrate the differential pattern of weightings between the stimulated and unstimulated regions of cortex. The final analysis employs the Friston–Buxton hemodynamic model to derive estimates of the underlying neural signal waveforms giving rise to each of the BOLD response components.

2.1. Independent components of the bold response in V1

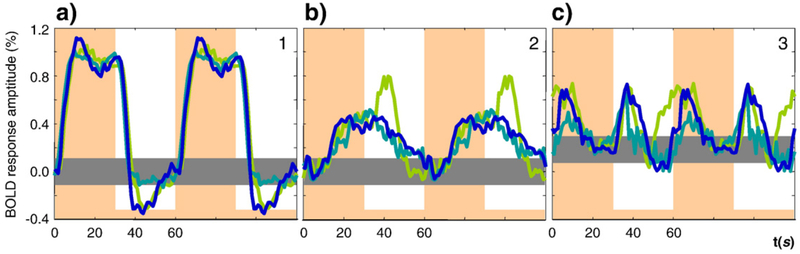
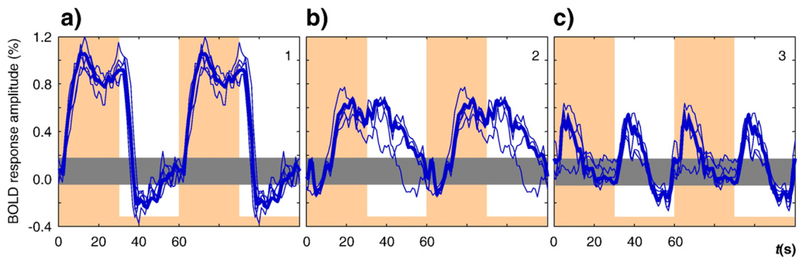
Spatial ICA analyses were conducted in retinotopically-defined V1 separately in the two hemispheres of three observers. The analysis identified three ICs that were similar for all three observers for the dynamic sensory stimulation (see Experimental procedures for details). The time courses for the same IC for the left and right V1 from the same observer differed much less than across the observers. We therefore combined the IC time courses for the left and right V1 areas together in each observer, as shown in Fig. 2. The waveforms are vertically positioned and scaled to provide the best match of the shapes among observers (scaled to those for observer ARW shown in blue).

Fig. 2 –

The time courses for first three ICs for three different brains are shown for two periods each, scaled to their relative weighting in the overall responses, with the mean peak amplitude of the first component scaled to 1. The orange vertical overlays show time periods when the test was presented. The horizontal gray bar shows the estimated range of the BOLD signal in the rest state. Signals in different colors for the three observers are overlaid in each panel.

To provide a common reference, we have depicted all components as if the test stimulus onset predominantly causes positive activation. In fact this choice is arbitrary and facilitation with a negative magnitude is, indeed, most likely to represent an inhibition (as is addressed below). The baseline shown in Fig. 2 by the gray stripe depicts the range of the signal during the rest state. Despite the long off-period of 30 s, the signal for the blank interval did not reach a horizontal asymptote for two of the observers, indicating the presence of very slow processes in the BOLD response in these cases.

The primary IC (Fig. 2a) rises with a time constant of several seconds with an overshoot and a slow rebound that peaks near stimulus offset, then falls with a similar rebound that is less structured; this IC has a double-peaked appearance on the positive deflection only. This positive/negative asymmetry reflects nonlinear behavior of either the neural or hemodynamic contributions to this component. The second IC has an early negativity followed by a slow positive rebound, which does not reach the asymptotic level even after 30 s of stimulation. This result illustrates that the early negativity may be isolated from the generic BOLD signal by means of the ICA analysis. The decline of the second IC is also slow, and there is no sign that it reached the rest state after 30 s of the blank interval. The third IC we interpret as a combined response of On and Off mechanisms responding to stimulus changes. Their combined effect doubles the frequency of the BOLD signal and contributes to the double-peaked appearance of the mean BOLD response (as in Fig. 8 below). It is worth mentioning here that this component cannot be due to temporal jitter of the first IC, because in this case it would be its first derivative and the peaks at onset and offset would have opposite signs.

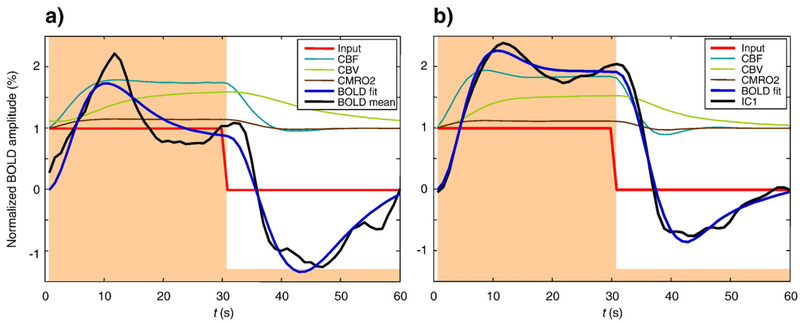
Fig. 8 –

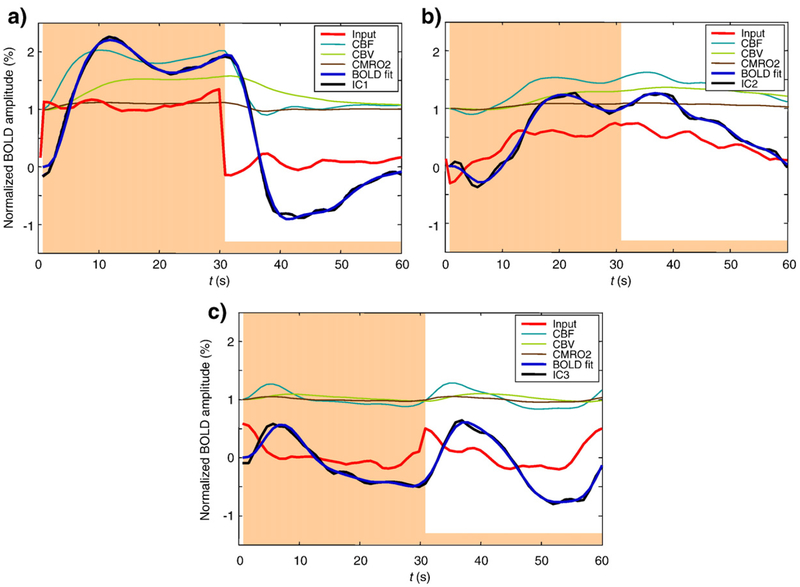
Best fits of the hemodynamic model to the mean BOLD response (left) and to the first IC (right), for observer ARW. CBF, CBV and CMRO2 are all fractional values, normalized to baseline. Smoothed data (dashed lines) and steady-state model BOLD responses (solid black lines) are expressed in percent. Model BOLD responses are shifted to zero at the origin; data are shifted to have the same mean as the model. In terms of the variables in Appendix A: CBV=v, CBF=f_in, and CMRO2=f_in E/E₀.

2.2. The structure of the response for different stimulus regions

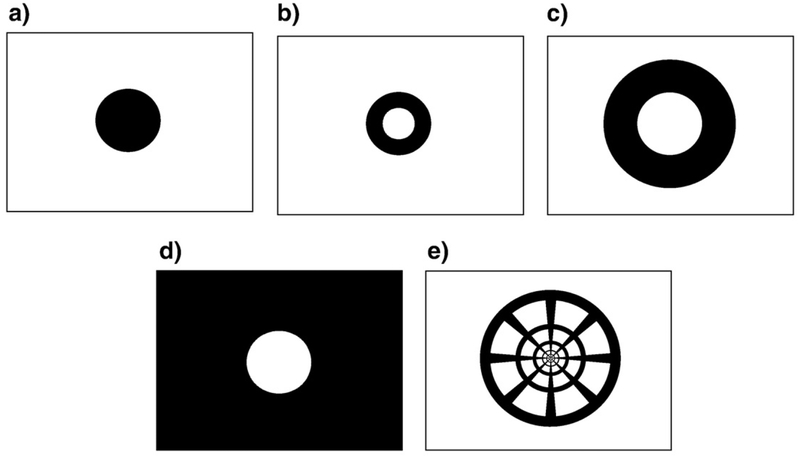
In order to probe the spatial structure of the neural response in visual cortex, we chose eccentricity-scaled stimuli that stimulated defined regions of the retinotopic projection region, V1. The stimulus areas shown by black in Fig. 3 were filled with a random noise pattern of radial checkerboard elements (see Experimental procedures for details). The retinotopic visual areas, V1, V2, etc. were already established in previous studies for each of the observers (Tyler et al., 2005; Schira et al., 2007). The present study focused only on area V1. Each V1 region was subdivided into at least three regions of interest (ROIs): the central part of V1 (to be called ‘Center’), the V1 region where activations from the central disk and peripheral field stimuli overlapped (‘Edge’), and the remaining peripheral part of V1, which was preferentially activated by the peripheral field (‘Periphery’). In larger V1 maps, each of the Center and Periphery ROIs were subdivided into two regions based on eccentricity (see Fig. 4). Each area was projected to its retinotopic representation in V1. Thus, for example, the small disk region in Fig. 4a should be activated directly by the central disk stimulus (Fig. 3a) and less strongly for the inner ring stimulus (Fig. 3b), and to be subject to lateral inhibitory effects for the outer ring and periphery stimuli (panels c and d) in Fig. 3. Corresponding effects would be expected for analysis zones b–d of Fig. 4, while all stimuli might be expected to show similar waveforms in the whole-field region (4e). Zone 4f is included to isolate any edge-specific response component in the responses.

Fig. 3 –

The stimuli were (a) central disk, (b) inner ring, (c) outer ring, (d) periphery, (e) pinwheel. The stimulus areas shown as black were filled with a random noise pattern of radial checkerboard elements scaled with eccentricity.

Fig. 4 –

The V1 analysis zones were designed as probes of the separate subregions of stimuli a–d (Fig. 3), together with a narrow zone around the edge (dashed line) that was in common between them and the whole stimulus field. These regions were the V1 projections labeled as (a) Center1, (b) Center2, (c) Periph1, (d) Periph2, (e) Whole Field, (f) Edge. Each area was projected to its retinotopic representation in V1 to form the corresponding ROI. The dashed circle indicates the edge region common among stimuli b and c (Fig. 3).

The responses for the stimuli of Fig. 3 for all the retinotopic regions corresponding to the zones of Fig. 4 are depicted for one subject in Fig. 5. The panels highlighted in yellow in Fig. 5 are those in which the projection zone contained dynamic stimulus activation, while those in the other panels did not.

2.3. Evidence that the ics are each consistent throughout V1

We expect that each region of V1 is populated by multiple neuron types, and that ICA can successfully separate these components. One concern is that the identified components might not be representative for the whole of V1, but instead may be a result of averaging over response properties that vary gradually across the cortex. Although such a spatial variation is unlikely because ICA was applied to non-spatially-averaged data, we nevertheless provide two tests that indicate that the derived ICs are present in every location of V1. First, we compute the average response to every stimulus for the five eccentricity-defined ROIs and for V1 as a whole. These aggregate responses are shown by the blue dotted curves in Fig. 5. Next, we computed the best fit to these responses by linear combinations of the three ICs identified by the ICA procedure, as shown by green curves in Fig. 5. This fit accounts for 92k of the variance in the original data. (In Experimental procedures we mentioned that the first 4 PCs accounted for only about 60% of the data variance, but that number was computed for individual voxels, which have higher noise variance than the ROI- based averages of Fig. 5.)

Table 1 provides the weights for each of the three ICs in each panel of Fig. 5, together with the standard error of the variation over the voxels in each ROI. These weights show the high consistency of the pattern of individual contributions where the waveforms for each stimulus type are similar; differences across stimulus types are considered in the Discussion.

Table 1 –

Weights of the three ICs for each panel of Fig. 5

ROI	Stimulus configuration
	Disk	Inner ring	Outer ring	Periph	Pinwheel
Centerl	0.55 ± 0.06	0.04 ± 0.04	0.02 ± 0.04	−0.10 ± 0.04	0.54 ± 0.04
	−0.30 ± 0.07	0.02 ± 0.04	−0.01 ± 0.06	0.14± 0.07	−0.19 ± 0.09
	0.11 ± 0.04	0.02 ± 0.06	0.45 ± 0.12	−0.04 ± 0.06	−0.42 ± 0.07
Center2	0.83 ± 0.08	0.60 ± 0.07	0.06 ± 0.05	−0.06 ± 0.04	0.73 ± 0.09
	−0.06 ± 0.09	−0.23± 0.05	0.23 ± 0.07	0.21 ± 0.08	0.56 ± 0.19
	−0.04 ± 0.18	0.10 ± 0.12	0.34 ± 0.52	−0.17 ± 0.10	−0.65 ± 0.18
Edge	0.75 ± 0.18	0.53 ± 0.15	0.89 ± 0.16	1.02 ± 0.25	0.95 ± 0.19
	−0.23 ± 0.53	−0.16± 0.08	0.09 ± 0.14	−0.02 ± 0.12	0.12 ± 0.24
	−0.06 ± 0.13	0.13 ± 0.15	0.63 ± 0.20	−0.12 ± 0.13	−0.44± 0.18
Periphl	−0.30 ± 0.13	−0.12± 0.05	1.06 ± 0.08	1.56 ± 0.13	0.79 ± 0.07
	0.29 ± 0.09	0.23 ± 0.04	0.14 ± 0.06	−0.12 ± 0.06	0.48 ± 0.13
	−0.20 ± 0.06	0.22 ± 0.05	0.55 ± 0.09	−0.20 ± 0.07	−0.46 ± 0.08
Periph2	−0.27 ± 0.03	−0.20± 0.03	0.02 ± 0.04	0.83 ± 0.11	−0.13 ± 0.06
	0.37 ± 0.06	0.16 ± 0.03	0.30 ± 0.04	0.02 ± 0.03	0.53 ± 0.07
	−0.06 ± 0.04	0.09 ± 0.04	0.39 ± 0.06	−0.06 ± 0.03	−0.20 ± 0.05
V1	0.25 ± 0.04	0.17 ± 0.03	0.41 ± 0.04	0.72 ± 0.06	0.56 ± 0.05
	0.10 ± 0.04	0.01 ± 0.02	0.18 ± 0.03	0.04 ± 0.03	0.41 ± 0.07
	−0.08 ± 0.06	0.12 ± 0.04	0.44 ± 0.05	−0.12 ± 0.04	−0.43 ± 0.06

Each panel specifies the weights of three ICs for the corresponding case in the example data of Fig. 5, with standard errors of the mean weights, given for all combinations of stimulation regions and ROI projection regions. The weights are scaled in percent BOLD units.

For an additional test we conducted ICA separately in each of the five eccentricity-specific ROIs employed in the previous test. Despite the smaller data sets for each ROI and noisier results, we found all three IC time courses among the four dimensions included in the analysis, with the exception of only one IC for one ROI where the IC was apparently excluded at the PCA stage. An example of these replicable ICs is shown by the thin lines in Fig. 6, overlaid with the IC waveforms computed for the whole V1 depicted by thick lines. The shape similarity in the responses across eccentricity indicates that there are indeed three statistically independent processes contributing to the BOLD response in visual area V1, and that these processes have a stable temporal waveform across eccentricities.

Fig. 6 –

Time courses for the first three independent components computed for the whole of V1 (thick blue line) and for five eccentricity-specific ROIs (thin blue lines), with the mean peak amplitude of the first component scaled to 1. These independent component time courses have similar shapes in the different locations of V1. Gray band indicates ±2σ of the initial points. Observer ARW, right hemisphere.

2.4. Distribution of ics across V1

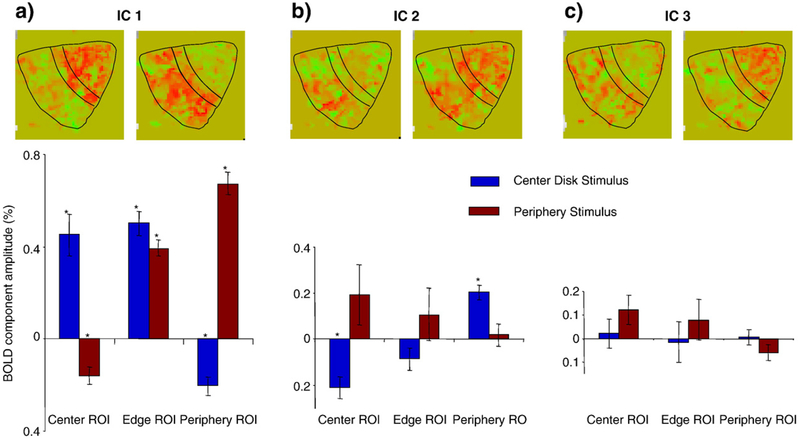
To understand the properties of the ICs that were found, note how the independent components are distributed across the cortex for central and peripheral stimuli. (The distribution of an IC can be treated as the magnitude distribution of the IC time course across voxels.) The cortical layout of individual component weights within the V1 ROI in one hemisphere is mapped in the top row of Fig. 7 for the sample data of Fig. 5. These maps suggest that all components are represented in both activation conditions shown, but with different signs and to different extents. Statistical tests for stability across hemispheres and subjects, however, support definitive statements about IC-1 and IC-2 only. The Center Disk stimulus shows predominantly positive activation for IC-1 and negative activation for IC-2 in the foveal projection of V1, and the opposite pattern of activation in the peripheral projection of V1. The Periphery stimulus shows the converse pattern of activation in both regions. IC-3 has a spatial pattern of activation that is mostly negative for the foveal projection of V1 for the periphery stimulus but had minimal activation for the Center Disk stimulus.

Fig. 7 –

The bar graphs depict the average component magnitudes of first three ICs normalized to the total activity in V1 (three panels) for three ROIs (Center, Edge, and Periphery—on the abscissa) and two stimuli (Center Disk and Periphery—blue and brown bars). The data are averaged across six V1 areas. The error bars represent the standard errors and the asterisks indicate statistically significant activations at p<0.001 (≈p<0.05, corrected for multiple applications). Each pair of magnitude maps above the bar graphs (right hemisphere, subject ARW) illustrate the spatial distributions for each of the 3 ICs for the Center Disk (left) and Periphery (right) stimuli. The black contours show Center, Edge and Periphery ROIs in V1; the foveal representation is at top–right.

The net contribution of an IC for different combinations of stimuli and ROIs was evaluated as its mean amplitude across voxels for a given ROI and stimulus. Fig. 7 depicts the mean and the standard error of these contributions estimated for six V1 areas (two hemispheres in each of the three observers in the main study). For this figure, we analyzed the responses for three ROIs and two stimuli: Center Disk and Periphery, as shown in Figs. 3a and b respectively. The Center ROI consisted of voxels activated by the Central Disk stimulus (Fig. 3a) and not activated by the Periphery stimulus (Fig. 3d), the Edge ROI consisted of voxels stimulated by both the Central Disk and the Periphery stimulus, and the Periphery ROI consisted of voxels activated by the Periphery stimulus and not activated by the Central Disk stimulus. The Edge ROI was analyzed to explore whether some of the ICs are specific to edges.

IC-1 clearly follows the overall pattern of activation, being of large positive value where the stimulus is present. In the areas that are not activated this component has a smaller negative magnitude, indicating the presence of a spreading neural suppression. IC-2, which was very slow (see Fig. 2), was positive in non-activated areas, and may thus be revealing an early facilitation component in the neural suppression process. IC-3 did not reach significance in terms of spatial stability across subjects and hemispheres; however, lack of spatial stability does not contradict the existence of IC-3 as a significant contributor to the temporal response waveform.

2.5. Model fits assuming a neural response replicating the stimulus: n(t)=s(t)

Fig. 8a shows the best fit of the Friston–Buxton model to the grand mean BOLD response for all V1 voxels of observer ARW, assuming that N₁(t)=S(t). The model behavior is somewhat reasonable, but major discrepancies remain. For the positive deflection, the data are more double-peaked than the best-fit model. For the negative deflection, the curvature of the model function appears to have the wrong sign. These observations apply to most if not all of the fitted results.

Fig. 8b shows the best fit of the model to IC-1 for observer ARW, assuming that N₁(t)=S(t). The quality of the fit is clearly better than for the mean BOLD response: the unaccounted variance for IC-1 is as small as 0.9%, whereas for the average signal it is as high as 7.2%. The F-test for this difference is highly significant [F(49, 49)=4.44; P<10⁻⁵]. This improvement is primarily because IC-1 has a less pronounced dip at the positive deflection, and the negative deflection has less curvature overall.

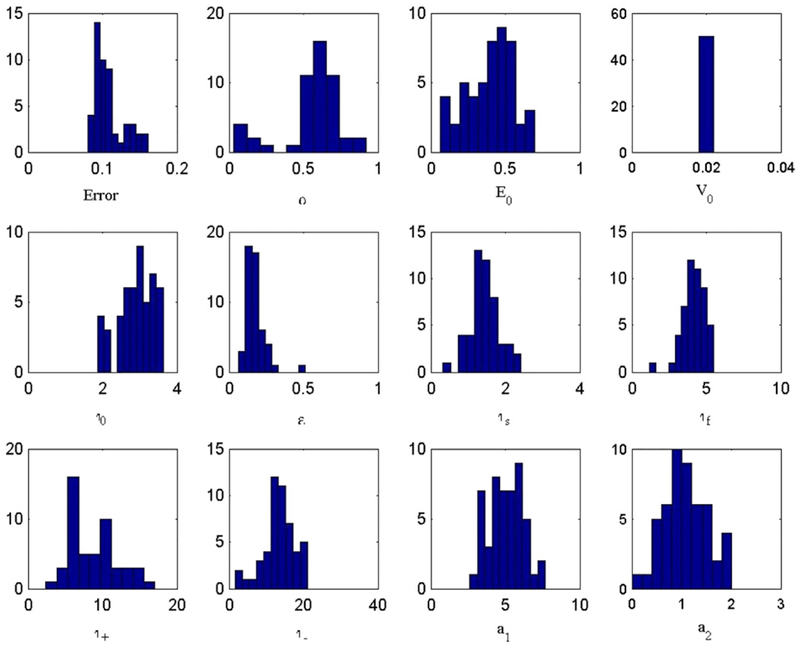
We determined the distributions of parameters and errors for the 50 trial fits to IC-1. Expressed as percent root-mean-squared values, the errors were clustered around 0.1% for IC-1 in Fig. 8b, versus 0.2% for the mean response in Fig. 8a. All of the parameters, with the exception of α and perhaps τ₊, had unimodal distributions centered near the default values (see Appendix A, Fig. 11); this unimodality is satisfying in light of the multi-dimensional nature of the parameter space. The finding that the values of τ₊ and τ₋ are very different, as shown in Table 2, suggests that the best-fit model of IC-1 is indeed nonlinear, consistent with the response asymmetry between On and Off blocks that is visible in Fig. 8b (i.e., the Off waveform is not an inverted copy of the On waveform).

Fig. 11 –

Error distributions for the eleven parameters of the fitted hemodynamic model specified in Table 2.

Table 2 –

Default and fitted parameters of the hemodynamic model

	α	E0	V0	τ0	ε	τs	τf	τ+	τ-	a1	a2
Default	0.38	0.40	0.02	2	0.5	1.54	2.46	10	10	5.73	1.15
Fit to BOLD	0.86	0.51	0.02	2.71	0.10	2.10	7.85	7.65	17.3	3.87	0.35
Fit to IC-1	0.70	0.40	0.02	3.63	0.16	2.07	5.17	5.56	12.8	4.35	0.95

Comparison of the default starting parameters and their final fitted values for the fit to the BOLD response and to the first independent component (IC-1).

We found that the Friston–Buxton model was unable to give a good fit to the mean BOLD responses in our data (see Fig. 8a). The major discrepancy was the prominence of the double peak on the positive deflection. It has previously been noted that the balloon model can exhibit such a prominent double peak, an inherently nonlinear property, when the input scale parameter ε is large enough (Calvisi et al., 2004). Still, the double peak in the mean data in Fig. 8a is not well fit by the Friston–Buxton model, even though the parameter ε was free to vary during optimization. Obata et al. (2004) showed very similar BOLD responses in the supplementary motor areas (see their Fig. 4b), which they were able to fit with the balloon model (see their Figs. 5b, c). We attribute this success to their measurement and modeling of CBF, which continues to rise for the entire duration of the On block and falls rapidly to baseline during the Off block. In contrast, the Friston et al. (2000) model of neurovascular coupling, computing CBF as a function of neural input N(t), is a second-order linear equation that is incapable of producing the desired behavior if the input function N(t) is assumed to be a square wave. Rather than attempting to derive an alternative functional form for neurovascular coupling, we took the approach of attributing discrepancies between the waveform and the best-fit model output to the input function N_i(t) and solved for N_i(t) using a multi-start simulated annealing algorithm.

The Friston–Buxton hemodynamic model involves nominally 11 parameters (see Appendix A). When fitting these, some authors (Mildner et al., 2001; Obata et al., 2004) have chosen to fix the values of some parameters (e.g., α, E₀, V₀, τ₀, a₁ and a₂) on the grounds that these parameters are known approximately from experiments. Others (Friston et al., 2000) have chosen to search on all parameters in light of experimental uncertainties and model assumptions, e.g., the widely cited value α ≈ 0.38 relates f_out and CBV only in steady-state (Grubb, 1974) and cannot be assumed to hold generally. In our searches, we allowed all the model parameters to be free, with the exception of V₀, which is redundant with a₁ and a₂. Accordingly, ε scales the input, while a₁ and a₂ scale the output. If the model were perfectly linear then ε too would be redundant, but in fact the degree of model nonlinearity depends partly upon the input scale ε (Calvisi et al., 2004). This approach of allowing the model maximum flexibility to fit the mean response (Fig. 8a) and IC-1 (Fig. 8b) allows the model to “hang itself” if no good fit were obtained. Simulations in which some or all of these parameters were fixed provided similar fits with slightly higher errors. We take the best-fit to IC-1 (Fig. 8b) to be the most plausible determination of the hemodynamic model parameters given the assumed input N₁(t)=S(t).

2.6. Estimated neural response n(t)

It is natural to relate the recorded BOLD response to the neural response driving the metabolic demands on blood oxygenation (Hyder et al., 2001; Logothetis, 2002; Kayser et al., 2004). In our case, we are interested in the distinct neural responses that could have been driving the three independent components identified by the analysis. In order to estimate the neural response waveform presumed to underlie each IC, we optimized a neural response estimate in each case while keeping the hemodynamic model parameters fixed. This is effectively a deconvolution procedure, although the nonlinearity of the balloon model precluded the use of Fourier analysis or linear correlation. Instead we treated the 60 time points of the function as unknown parameters and optimized them, while keeping the model parameters fixed. Fig. 9 shows the results of estimating the neural response N_i(t) presumed to underlie each IC in observer ARW, assuming the parameters for the best-fit model shown in Fig. 8b. The neural inputs to the Friston–Buxton model were obtained by multiparameter optimization with regularization to ensure smoothness, as described in Experimental procedures. From these results, we may infer the nature of the neural response underlying each IC (red curves in Fig. 9). Although the hemodynamic model parameters were fit to IC-1, the underlying neural component N₁(t) was also estimated. Fig. 9a shows that the global form does not deviate from the assumed boxcar, but the fine details were varied. The analysis of these inferred neural responses is left to the Discussion. Here we note that the three neural waveforms are very different in character and imply previously undiscovered nonlinearities in the population of neural responses underlying the recorded BOLD responses.

Fig. 9 –

Estimated neural responses N_i(t) and hemodynamic variables underlying each IC (see legend), assuming best-fit model parameters in Fig. 8b. Smoothing parameter λ =130

3. Discussion

The goal of this study was to apply ICA to the component space of fMRI responses from direct sensory stimulation, in order to extract multiple components of the BOLD response within a unitary cortical region, the primary visual projection area V1. We first show by means of Principal Components Analysis that the responses to the presence and absence of a dynamic texture can be faithfully accounted for by a three-dimensional signal space across the whole extent of retinotopic V1. This behavior suggests that the measured response properties are likely to result from a small number of separate processes, each adding an extra dimension of variation to the overall signal. However, knowledge of the space of response variation does not uniquely identify the underlying response waveforms. For this, we applied Independent Components Analysis to determine the basis set that generates this response space with the greatest independence between the generating components. The most prominent component is attributable to a sustained response to the dynamic noise stimulation; the second component is very slow sustained response (with an early negativity at the onset), and the third component consists of transient responses following both stimulus onset and offset. We were unable to identify further components in a consistent fashion. Importantly, we show that all three components have stable temporal waveforms across the V1 region, though their contribution varies with eccentricity.

Assuming that all response components are driven by neural activity, we reconstructed such activity based on the hemodynamic model of the BOLD response, suggesting the action of three different neural populations with different temporal responses to the stimulus. The time courses of these neural response estimates are compatible with the slow-wave time courses that underlie neural spike generation in monkey cortex (Logothetis, 2002; Logothetis and Pfeuffer, 2004). The neural response underlying IC-1 is close to the boxcar waveform of the stimulus S(t) with two notable differences: a relative increase just around the time of stimulus offset that provides the second peak on the positive deflection IC-1, and a late positive bump near t=36 s to provide the curvature during the OFF period. The simulation of Fig. 8 shows that neither of these features is present in the best-fitting BOLD waveform of the hemodynamic model, so it is reasonable to assume that both features derive from the neural signal per se.

IC-2 is a slow sustained response with a notable negative dip near t=5 s, and a corresponding peak near t=36 s following the stimulus offset. In fact, the negative dip has been a well-known as feature of fMRI BOLD analysis for many years (Ernst and Hennig, 1994; Hu et al., 1997; Yacoub et al., 1999; Duong et al., 2000; Rother et al., 2002; Calhoun et al., 2004a,b), although other groups have had difficulty identifying these features directly in the BOLD waveforms at 3 T (Ugurbil et al., 1999). The maps of Fig. 7 do not, however, support the idea that this negativity corresponds to the early oxygen drain local to the neural activation (Thompson et al., 2005), since IC-2 pre-dominates in the unstimulated regions of the cortex, while the early negativity should predominate in the stimulated cortical regions.

The neural response underlying IC-3 has two distinct bumps near t=0 and 30 s, suggesting a transient On/Off response to the stimulus. Such nonlinear transient components of the BOLD response are well-known for cognitive tasks (Courtney et al., 1997; Postle, Zarahn and D’Esposito, 2000; Konishi, Donaldson and Buckner, 2001; Posse et al., 2001; Huettel, Guzeldere, McCarthy, 2001; Shulman et al., 2001; Zacks et al., 2001; Calhoun et al., 2001, 2002a,b; d’Avossa, Shulman and Corbetta, 2003; Krasnow et al., 2003; Calhoun et al., 2004a; Cabeza et al., 2004; Chen and Desmond, 2005; Fox et al., 2005; Meegan and Honsberger, 2005; Scheibe et al., 2006; Vuilleumier et al., 2005) but we are not aware of reports of such transient responses the offset of repeated or steady-state stimulation. In either case, the rectifying nonlinearity of a positive response to both stimulus onsets and offsets goes far beyond any nonlinear properties of the hemodynamic models per se, and implies the operation of a pronounced (rectifying) nonlinearity in the underlying neural response to these stimulation conditions. The reconstructions of Fig. 9c specify the neural nonlinearity required to account for the rectifying IC identified by the present analysis.

Fig. 7 shows that the activation for the rectifying transient predominates in the unstimulated regions of the cortex in a manner similar to that for the linear component identified in unstimulated cortical regions by Chen et al. (2005). Their analysis could not have isolated the nonlinear or rectified aspect of this component, but we note that the Off-transient in IC-3 has about twice the amplitude from baseline as the On-component (Fig. 9), corresponding to the transient linear component at stimulus offset in the analysis of Chen et al. (2005). The lack of a linearity constraint in the ICA analysis allows it to reveal the additional nonlinear component from the unstimulated cortical regions.

The nonlinear deconvolution analysis provided by the hemodynamic model fits of Fig. 9 provides a significant capability for estimating the neural responses of subpopulations operating within the same region of cortex (in this case, V1). Each component response can be investigated for its behavior with respect to stimulus variables. Figs. 5 and 7 indicate that different components had different responsiveness to some of the stimulus conditions that we employed here. This is a proof of principle that the Independent Components approach can be used to track the behavior of neural subpopulations below the spatial resolution of fMRI. The temporal analysis of Fig. 9 has a resolution down to about 1 s, about 5 times faster than that of the BOLD signal itself, even for the slow stimulus paradigm of the present studies. The nonlinear deconvolution analysis can therefore provide useful enhancement of the temporal resolution of the fMRI analysis, in addition to its ability to isolate independent neural subpopulations.

3.1. Stimulus specificity

Having identified three component response shapes operating across cortical area V1, we turn to the issue of the variation of the averaged responses in different regions of V1 as expressed by variations in the weightings of the three components in relation to the region of stimulation. The predominant response in the data set of Fig. 5 is an On response with an initial overshoot in the stimulated regions, while there is only a minimal response in the non-stimulated regions. However, the narrow-barred Pinwheel stimulus (Fig. 3e) generates a much more gradual approach to the asymptotic activation level, implying that the early overshoot is a property of large-area stimulation patterns (Figs. 3a–d) that is not activated by narrow strips of pattern (Fig. 3e).

The average time course magnitudes for each of the three ICs for each stimulus type for and each cortical ROI, as provided in Table 1, show consistent differences across stimulus types. Generally, the major contribution is from IC-1, minor from IC-2 and non-significant from IC-3. The last column of Table 1 (for the Pinwheel stimulus), however, shows a consistent weighting of about −0.4 for IC-3 in every ROI, implying a negative expression of the double- peaked waveform corresponding to a transient inhibition following both the onset and offset of the Pinwheel stimulus. Such inhibition is consistent with the idea that the activation in narrow bar regions generates inhibition in the surrounding cortex, but reveals that such inhibition is evoked in a transient form at both the onset and offset of the stimulus.

The only other stimulus type that consistently expresses IC-3 is the Outer Ring stimulus, where its expression has a positive rather than negative weight in all ROIs (Table 1). This specificity is more difficult to understand in the context of the lack of an IC-3 for stimulation at any other eccentricity. It cannot derive from a foveal specialization for lateral inhibition, since the Outer Ring has the same inner border as the Peripheral stimulus. Inspection of the waveform reveals that its main support derives from the post-stimulus negativity that is unique to this stimulus, and therefore appears to represent a regional specialization for this particular activation pattern within the general picture of cortical homogeneity exhibited by all the other components.

In conclusion, the responses to activation of retinotopically separated regions of V1 reveal a surprising diversity of response waveforms, violating the linearity assumption of a GLM with a homogenous HRF for this primary visual response region. The application of stimulus-driven ICA to the waveforms of this family of BOLD responses shows that three independent component waveforms can account for more than 90% of the variance of the mean response waveforms in the analyzed ROIs. Since these different waveforms are derived from the same underlying cortical tissue for different stimulus configurations, the most plausible interpretation for the three components is that they represent three different populations of neural response types. We therefore ran an inverse optimization of the precise neural signal that would have generated each BOLD response type, under plausible constraints for the hemodynamic model of the BOLD response properties. These neural response estimates had time courses that were compatible with the slow-wave time courses that underlie neural spike generation in monkey cortex (Logothetis, 2002; Logothetis and Pfeuffer, 2004).

4. Experimental procedures

The T2* BOLD time sequences were obtained in a GE MRI Signa 3 T scanner at a flip angle of 70° with 10 inplanes at 3 mm separation with 2.5×2.5 mm in-plane resolution and TR=1 s. The inplane images were positioned in a coronal orientation to cover the primary visual areas at the posterior pole (specifically, V1). The stimuli were presented with the binocular Avotec system (Avotec, Stuart, FL) with a stimulus field of 24×18° at 800×600 resolution controlled by PowerMac G5 computer with a 850 MHz processor.

Each observer viewed a battery of dynamic noise stimuli (Fig. 3) in a block design in which each dynamic noise stimulus alternated with blank intervals every 30 s. Each complete scan consisted of 5 cycles, which took a total duration of 5 min. Scans for all stimulus types were run in a single scanning session for each observer. In order to probe the spatial structure of the neural response in visual cortex, we chose eccentricity-scaled stimuli that stimulated defined regions of the retinotopic projection region, V1. The dynamic stimulus areas shown as black in Fig. 3 were filled with a random noise pattern of radial checkerboard elements themselves scaled with eccentricity and dynamically updated every 75 ms. The element size was scaled to 6% of its eccentricity from the disk center.

The primary stimuli were a central noise disk (with radius 3.5°) and the complementary stimulus of noise in the whole screen area outside the disk, as shown in Figs. 3a, b. Next, to probe responses to fine spatial structure, the whole retinotopic projection was stimulated with a radial pinwheel of thin lines consisting of dynamic noise (Fig. 3e). Additionally, a subset of observers was shown inner and outer ring stimuli to focus the activation close to the border region of the disk (Figs. 3b, c). For each observer, all stimuli were presented within a single scanning session of 90 min duration.

In total, 5 observers were scanned (4 males and 1 female, 32–60 years old, all with normal or corrected to normal visual acuity), some of them twice or thrice. An initial study, which was performed with TR=3 s, and 15-s alternation rate in three observers, required 3 principal components to account for approximately 80% of the variance in the data. However, the results could not be interpreted unambiguously in the absence of a secure baseline. We therefore designed the main experiment with TR=1 s and 30-s alternation rate for a detailed analysis of the data for 3 further observers (visual area V1 in 6 hemispheres) with the experimental protocol described above.

Interpretation of the BOLD response profiles depends critically on the position of the baseline that corresponds to the response of the blank stimulus. Previous measurements of the BOLD impulse response function suggest that its rise time is about 5 s, recovering to baseline by about 15 s. For this reason we chose the On/Off presentation time to be 30 s in order to allow all transients to be finished and the BOLD response to reach its rest state level within the 30-s blank half of this cycle.

To minimize attentional modulation, an attentional task was presented in the center of the stimulus. The element to fixate consisted of a small square (2×2 pixels) surrounded by a frame 1 pixel wide. The colors of the central square and the frame were continuously changed every 0.5 s, with the square and frame always having different colors. The experimental task for the viewer was to respond when he or she detected the specific combination of a red square and a green frame. Because this task was attentionally demanding and the fixation target was small, it enforced stable fixation at the center of the display.

4.1. Independent components analysis

The analysis consists of the following steps. First, any linear trend over the time series was removed because our interest was in identifying different stimulus-related components. The time series for voxels and stimulus types was averaged across stimulus cycles, to maximize the signal/noise ratio. This step diminished the noise to levels acceptable for retrieval of the stimulus-locked components.

Second, PCA was applied to these cycles across voxels and conditions. This is necessary step prior to ICA for two reasons. Primarily, it makes the ICA procedure computationally tractable, and it also tends to isolate the predominant signal subspace. The use of PCA as a first step of ICA is widespread in the literature (McKeown et al., 1998; Ikeda and Toyama, 2000; Yanmei and Sahin, 2005; Rodionov et al., 2007). In fact, ICA may be viewed as an oblique rotation of the principal components from the PCA (Dien et al., 2007). Typically, four principal components accounted for approximately 60% of variance across individual voxels, while adding the fifth component increased this value by less than 4%. The 60% of accounted variance for individual voxel analysis should not be considered as a low value because most of the residual variance beyond this level was due to high-frequency noise in the BOLD signal, which we preferred not to filter out in order to preserve the temporal integrity of the BOLD signal sampling. The lessthan-4% variance added by the fifth component implies that the distribution of weights across the higher PCA components mostly represent noise rather than signal. Reduction of the signal dimensionality in this way reduces the number of local minima in the independent component search and makes ICA more robust. We found that increasing the number of principal components above four did not lead to extraction of reliable components in the ICA processing.

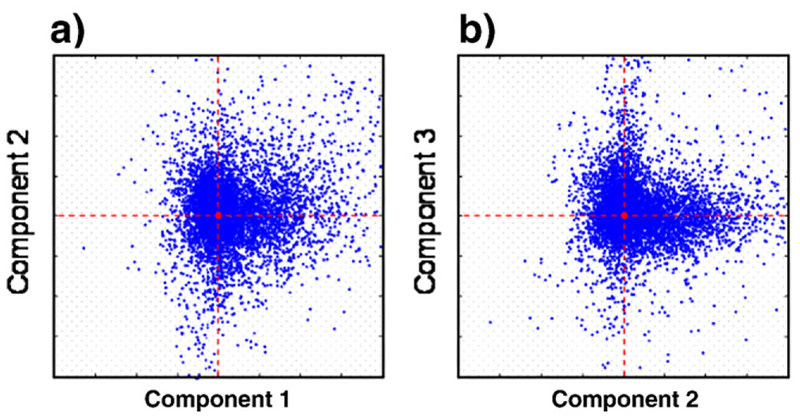
Third, ICA was applied using a public domain fastICA function (HyvÌrinen and Oja, 1997) for MATLAB™ (Mathworks, Natick, MA), which represents a widely-accepted standard in the ICA field. The concept underlying ICA is to find deviations from an elliptical Gaussian distribution of scatter plots, often in the form of spurs extending from the main distribution. The presence of these spurs means that, for a particular stimulus, the waveform in a typical voxel is dominated by only one of the three component mechanisms rather than by their combination. Note that the dominant component can differ for different stimulus types. When the principal components comprise the basis, the waveforms in the response clusters of these spurs are typically not orthogonal in the time domain; however, when IC time courses are chosen for the basis (see Fig. 10), the clusters appear to be extended along the axes. We found that symmetric decorrelation and use of the tanh nonlinearity produced consistently robust clusters identifying independent components in the scatter plots of one component versus another, whereas other options were not as successful. However, the initial guess factor still left a minimal degree of ambiguity: infrequently the ICA converged to local minima with no evident structure in the scatter plots. To ensure that the global minimum was found, we ran the ICA three or more times with different initial guesses; if the first three disagreed, we ran ten or more and took the most common minimum of the set.

Fig. 10 –

Scatter plots across voxels (for all conditions) of the weights for the second vs. the first IC and the third IC vs the second. Clustering along the coordinate axes suggests that the data are likely to be produced by different mechanisms. Observer ARW, right hemisphere.

To illustrate the results of the fastICA routine, Fig. 10 provides examples of the scatter plots of the IC weights in the component coordinates for the responses in each voxel of V1 across all stimulus types. Fig. 10a shows the weights for the second vs. the first IC; Fig. 10b has the third vs. the first IC, with the first IC coordinate as the abscissa in both panels. The clustering of the points along the coordinate axes implies that FastICA algorithm picked appropriate directions for the components.

4.2. Hemodynamic modeling

To assess the neural contribution to each ICA component, we optimized their fits to the BOLD signal for each component according to Eqs. 1–4. To determine whether our measured BOLD responses could be fit using a contemporary hemodynamic model, we used the balloon model (Buxton et al., 1998) together with a simple model of neurovascular coupling (Friston et al., 2000), as described in Appendix A. Its key features are a second-order linear relationship between neural activity and blood flow, conservation of blood volume and oxygen, an elastic venous compartment, and a dependence of the BOLD response on changes in both deoxyhemoglobin and blood volume. An important issue in modeling the BOLD response is the assumed relationship between the stimulus waveform S(t) (boxcar) and the function N(t) that represents neural activity driving the increased blood flow. Many fMRI studies implicitly assume N(t)=S(t) for the purposes of BOLD modeling. The function N(t) is discussed in Friston et al. (1998, 2000), where it was taken to be a series of Dirac delta functions occurring with the presentation of words. For our visual stimuli, presented in a block design, the presence of transient On/Off responses and sensory adaptation (Hubel and Wiesel, 1968; Maunsell and Gibson, 1992; Kapadia et al., 1999; Logothetis, 2002; Logothetis and Pfeuffer, 2004) imply that N(t) is likely to differ in shape from S(t). We therefore interpret N(t) as some measure of neural activity or its metabolic demand that drives the CBF through a second-order differential equation (see Appendix A). The resulting hemodynamic model used here has 10 free parameters. Before fitting the model, the BOLD time series were smoothed with a 3-point moving-window average, to remove fast fluctuations from the BOLD signal that were unlikely to be meaningful. We fit the 10 parameters using a multi-start simulated annealing algorithm (Masters, 1995) that moves stochastically through the parameter space to minimize the sum-squared error

$$SSE=\sum _{\text{t}=1}^{60}{[B(t)-D(t)]}^2$$ (5)

where B(t) is the model BOLD response, and D(t) is the cycle- and voxel-averaged BOLD time series.

This algorithm is reasonably robust to local minima (see Appendix A), which are characteristic of fits to real data. The stochastic nature of the search algorithm produced a different result each time, so the search for each dataset was repeated 50 times with different initial guesses drawn from a Gaussian distribution around a set of default parameters obtained from the literature (see Table 2). The best overall fits are reported here, but for a given data set all 50 fits were qualitatively similar in their ability to fit the BOLD response. There was a range of behaviors of their underlying variables, however; a problem that was noted by Obata et al. (2004). In particular, some fits involved CBF values greater than 2, which is inconsistent with the other work in this area (Buxton and Frank, 1997; Buxton et al., 1998; Buxton et al., 2004; Obata et al., 2004). To bias our search toward fits that were plausible in their CBF response, the value of SSE was multiplied by the factor [max(f_in) – 1] if max(f_in)>2. This yielded search results which fit B(t) similarly, and for which CBF, CBV and CMRO2 all exhibited plausible behavior.

Initial attempts to fit the model to the average BOLD response were reasonable but inaccurate in several details (see Fig. 8a). This deficiency could not be corrected by adjusting the simulated annealing parameters. A key assumption of the present analysis is that the hemodynamic response to a given input N(t) is the same throughout the V1 retinotopic region, so the different ICs are interpreted to reflect different neural responses N_i(t). We therefore attempted to fit the hemodynamic model to the first IC, on the grounds that the neural response N₁(t) underlying this component is expected to have the sustained character of this IC and thus be a close approximation to S(t): N₁(t)≈S(t). The resulting fits were still imperfect, but were deemed preferable because they had smaller SSE (see Fig. 8b). Assuming that the combined Friston–Buxton model is correct, and that the best-fit model parameters to IC-1 provide the best estimate of the hemodynamic response, we ascribed the remaining differences to the neural response, and solved for N_i(t) separately for each component.

To indicate the stability of the fits, the error distributions for the fitted Balloon Model are shown in Fig. 11. The main point to note is that the distributions are all unimodal within experimental error, and most have no significant skew. The coefficients of variation for these parameters are relatively tight, spanning a range from about 0.01 to 0.3.

4.3. Estimating the neural response

In order to estimate the neural response waveform N(t) presumed to underlie each IC, we fitted N(t) in each case while keeping the hemodynamic model parameters fixed. This is effectively a deconvolution procedure, although the nonlinearity of the Balloon Model precluded the use of Fourier analysis or linear correlation. Instead we treated the 60 time points of the function N(t) as unknown parameters and optimized them, while keeping the model parameters fixed. To do this we adapted the same simulated annealing algorithm to minimize the revised sum-squared error function

$$SSE=\sum _{t=1}^{60}{[B(t)-C(t)]}^2+\lambda \sum _{\tau \ne 30,60}{[N(t)-N(t+1)]}^2$$

where C(t) is any one of the independent components.

Because the BOLD response acts as a low-pass filter, initial attempts with λ=0 gave solutions for N(t) that oscillated wildly while still fitting the ICs reasonably well. The second term was therefore included to bias the search toward smoother solutions, with λ>0 playing the role of a spring constant between neighboring points. This term acts to correlate neighboring points in N(t) and effectively reduces the number of independent degrees of freedom in the fit so that the problem becomes well-posed. The value λ=1/2 assured that repeated runs of the fitting algorithm produced nearly identical results for Y(t) and N(t); smaller values of λ fit B(t) equally well but produced quite variable N(t). The points t=30, 60 s were excluded from this term because the boxcar S(t) – our best initial guess of the neural response underlying IC-1 – clearly violates smoothness at these points. The end result is a plausible estimate of the neural response waveform N(t) underlying each IC.

Appendix A. The hemodynamic model

The metabolic basis of the hemodynamic model employed here is the steady-state relationship between oxygen extraction fraction E in the capillary bed and inward flow f_in (Buxton and Frank, 1997).

$$E=1-{\left(1-E_0\right)}^{1/f\text{in}}$$

The variable E is a decreasing function of f_in, due to the shorter time in contact with the capillaries. Modeling E this way does not include a direct neural coupling that could reflect an initial dip. Rather the changes in E are considered to be due entirely to neural activity-induced changes in blood flow.

The balloon model (Buxton et al., 1998) relates fractional blood volume V, inward blood flow F_in, and deoxyhemoglobin Q in the venous compartment. Each variable is normalized to its resting state value: V₀, F₀ and Q₀, to yield the dimensionless variables: v, f_in and q. Conserving total blood volume and total deoxyhemoglobin in the venous (balloon) compartment leads to the following differential equations:

$${\tau }_0\frac{\text{d}v}{\text{d}t}=f_{\text{in}}-f_{\text{out}}$$

$${\tau }_0\frac{\text{d}q}{\text{d}t}=f_{\text{in}}\frac{E}{E_0}-f_{\text{out }}\frac{q}{v}$$

The time constant τ₀=V₀/F₀ has the interpretation of the mean transit time across the balloon. In the simplest version of the model, it sets the time scale for the rate of change of both v and q.

Outward flow is determined physically by the relative pressures between the venous compartment and the downstream vein, but that introduces new variables that are not directly accessible. The balloon model replaces this detail with a simple algebraic relationship between f_out and v. We consider two variants of this relationship. The first variant is valid at steady-state (Grubb et al., 1974):

$$f_{\text{out }}=v^{1/\alpha }$$

In this case, the expression for f_out may be inserted directly into the expression for dq/dt. The second variant accounts for the slow nature of the expansion and contraction of the venous compartment (Buxton et al., 2004), i.e., a dynamic relationship between flow and volume:

$$f_{\text{out }}=v^{1/\alpha }+{\tau }_v\frac{\text{d}v}{\text{d}t}$$

and is termed delayed compliance. In this case, the two equations involving dv/dt and f_out may be solved simultaneously to modify the mass conservation equations. The result for dv/dt is:

$$\left({\tau }_0+{\tau }_{\text{v}}\right)\frac{\text{d}v}{\text{d}t}=f_{\text{in}}-v^{1/\alpha }$$

The result for f_out is:

$$f_{\text{out }}={\left(1+\frac{{\tau }_v}{{\tau }_0}\right)}^{-1}\left[f_{\text{in }}\frac{{\tau }_v}{{\tau }_0}+v^{1/\alpha }\right]$$

which can be substituted into the expression for dq/dt. Following Buxton et al. (2004), we allow τ_v to take on different values during balloon expansion and contraction, and denote these parameters τ₊ and τ₋, respectively.

The input to the balloon model is inward flow, not neural activity. In order to related neural activity to the BOLD signal, an additional model component is needed. Following Friston et al. (2000), we model the relationship between neural activity and inward flow by a second-order differential equation

$$\frac{d^2{f}_{\text{in}}}{d{t}^2}=-\frac{f_{\text{in}}-1}{{\tau }_f}-\frac{1}{{\tau }_s}\frac{d{f}_{\text{in}}}{dt}+\epsilon N(t)$$

Fig. A1 –

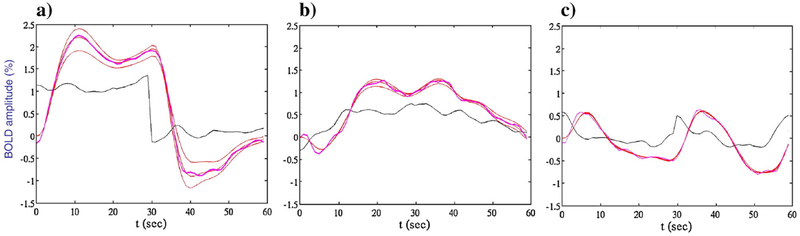
Empirical linearity test of the effect of increasing or decreasing the input signal by a factor of 2, and compensating the hemodynamic model output by the converse factor (smooth flanking curves). For perfect amplitude linearity, the flanking curves should overlie the thick smooth curve exactly. Thus, IC-1 is linear within about 10%, and IC-2 and IC-3 are almost exactly linear.

The input N(t) is flow-inducing neuronal activity, but beyond that its exact relationship to neural activity is not specified in this model. Normally it is taken to be the stimulus waveform, or a task vector of a more complicated design matrix. In the present paper, we conceptualize this as spike rate, for example. Given an input function N(t), the above system of three coupled differential equations (for q, v, f_in) may be integrated numerically. For the first cycle of the stimulus (1≤t≤60 s), the result depends upon the initial conditions, which we chose to be q=v=f_in=1. Because a 30-s OFF period is not quite sufficient for the model response to return to baseline, we often integrated for several cycles and kept the last one for comparison with data.

Following Obata et al. (2004), we model the BOLD time series a linear function of q and v:

$$B=V_0\left[a_1(1-q)-a_2(1-v)\right]$$

(Earlier papers, beginning with Buxton et al., 1998, included a nonlinear term q/v, which was subsequently corrected in Obata et al., 2004.) The parameters a₁ and a₂ have been estimated at 1.5 T (Buxton et al., 2004) and 3T (Obata et al., 2004), but with residual uncertainties. We therefore treated a₁ and a₂ as unknown parameters and included them in model optimization, starting with initial estimates computed for 3 T. Because the parameter V₀ multiplies amplitudes a₁ and a₂ in the equation for B, it is redundant; we therefore fixed V₀ at its default value of 0.02.

Appendix B. Small-signal linearity

As indicated in Eq. 4, a critical assumption of the analysis is that the estimated component waveforms sum linearly to form the output of each voxel, or group of voxels. Such linear summation may be expected to hold if the BOLD response waveforms are invariant with respect to the α_i weights in Eq. 4. We expect such linearity to hold within the typical amplitude range of BOLD responses, i.e., within an amplitude range of about ±1%. As a test of this effective amplitude linearity, we multiplied the input signal for each of the three components of Fig. 9 by factors of 0.5 and 2, and divided the output proportionately. If linearity holds, the scaled responses to halved and doubled inputs should match the original estimate exactly. The degree of mismatch indicates the extent to which the linearity assumption was violated. We emphasize that this is a test of linearity with respect to the scaling parameter, and is independent of the degree of nonlinearity of the time courses of either the neural signals or the hemodynamic model outputs with respect to their inputs.

Fig. A1 shows the results of the linearity test for each component of Fig. 9. The smooth and noisy magenta curves show the original optimization to the mean data, while the red curves show the results of the compensated scaling by factors of 0.5 and 2. For the first IC (Fig. A1(a)), linearity is violated to a small extent, between about 10 and 20% for the decrease and increase, respectively. The combined reconstruction of the full BOLD waveform should not be expected to be any more accurate than the 10% value for the 0.5 scaling. The other two waveforms (Fig. A1(b,c)), although strikingly nonlinear in their time-courses, show almost perfect amplitude linearity with respect to scaling by factors of 0.5 and 2 (since the compensated waveforms are almost indistinguishable from the unscaled original). We conclude that the computed waveforms for this example support the linearity assumption (Eq. 4) required for the component analysis.