Revisiting Trade-offs between Rubisco Kinetic Parameters

Abstract

Rubisco is the primary carboxylase of the Calvin cycle, the most abundant enzyme in the biosphere, and one of the best-characterized enzymes. On the basis of correlations between Rubisco kinetic parameters, it is widely posited that constraints embedded in the catalytic mechanism enforce trade-offs between CO₂ specificity, S_C/O, and maximum carboxylation rate, k_cat,C. However, the reasoning that established this view was based on data from ≈20 organisms. Here, we re-examine models of trade-offs in Rubisco catalysis using a data set from ≈300 organisms. Correlations between kinetic parameters are substantially attenuated in this larger data set, with the inverse relationship between k_cat,C and S_C/O being a key example. Nonetheless, measured kinetic parameters display extremely limited variation, consistent with a view of Rubisco as a highly constrained enzyme. More than 95% of k_cat,C values are between 1 and 10 s^–1, and no measured k_cat,C exceeds 15 s^–1. Similarly, S_C/O varies by only 30% among Form I Rubiscos and <10% among C₃ plant enzymes. Limited variation in S_C/O forces a strong positive correlation between the catalytic efficiencies (k_cat/K_M) for carboxylation and oxygenation, consistent with a model of Rubisco catalysis in which increasing the rate of addition of CO₂ to the enzyme–substrate complex requires an equal increase in the O₂ addition rate. Altogether, these data suggest that Rubisco evolution is tightly constrained by the physicochemical limits of CO₂/O₂ discrimination.

Ribulose-1,5-bisphosphate carboxylase/oxygenase (Rubisco) is the primary carboxylase of the Calvin–Benson–Bassham (CBB) cycle, the carbon fixation cycle that is responsible for growth throughout the green lineage and many other autotrophic taxa, and the ultimate source of nearly all carbon atoms entering the biosphere.¹ Typically, 20–30% of total soluble protein in C₃ plant leaves is Rubisco.² As Rubisco is so strongly expressed and plants are the dominant constituents of planetary biomass,³ it is often said that Rubisco is the most abundant enzyme on Earth.^1,4 Because Rubisco is ancient (>2.5 billion years old) and abundant and remains central to biology, one might expect it to be exceptionally fast, but Rubisco is not fast.⁵⁻⁸ Typical central metabolic enzymes have a turnover number (k_cat) of ≈80 s^–1.⁷ However, >95% of Rubisco carboxylation k_cat,C values are between 1 and 10 s^–1, and no measured k_cat,C values exceed 15 s^–1.

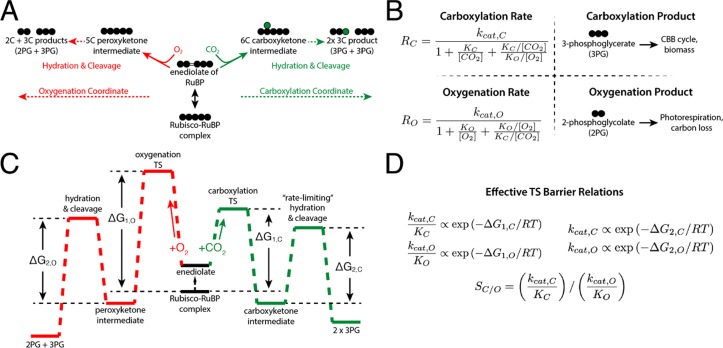
In addition to relatively low k_cat,C values, Rubisco reacts with O₂ in a process called oxygenation (Figure 1A). Although both carboxylation and oxygenation of the five-carbon substrate ribulose 1,5-bisphosphate (RuBP) are energetically favorable,⁹ carboxylation is the productive reaction for incorporating carbon from CO₂ into precursors that generate biomass (Figure 1B). While it may play a role in sulfur, nitrogen, and energy metabolism,^10,11 oxygenation is often considered counterproductive as it occupies Rubisco active sites and yields a product, 2-phosphoglycolate (2PG), that is not part of the CBB cycle and must be recycled through metabolically expensive photorespiration at a partial loss of carbon.¹² As such, oxygenation can substantially reduce the net rate of carboxylation by Rubisco, depending on CO₂ and O₂ concentrations and the kinetic parameters of the particular enzyme. There are at least four distinct Rubisco isoforms in nature,¹³ but all isoforms catalyze carboxylation and oxygenation of RuBP through the multistep mechanism described in panels A and C of Figure 1.^14,15 Even though many autotrophs depend on Rubisco carboxylation for growth, all known Rubiscos are relatively slow carboxylases and fail to exclude oxygenation.

Figure 1.

Description of the catalytic mechanism of Rubisco. The “middle-out” diagram in panel A shows the ordered mechanisms of carboxylation and oxygenation. Circles represent carbon atoms. RuBP is isomerized to an enediolate before carboxylation or oxygenation. Addition of CO₂ or O₂ to the enediolate of RuBP is considered irreversible as are the subsequent hydration and cleavage steps of the carboxylation and oxygenation arms. (B) Carboxylation displays effective Michaelis–Menten kinetics (maximum catalytic rate k_cat,C, half-maximum CO₂ concentration K_M = K_C) with competitive inhibition by O₂ (assuming half-maximum inhibitory O₂ concentration K_i = K_O). Carboxylation results in net addition of one carbon to the five-carbon RuBP, producing two 3PG molecules. 3PG is part of the CBB cycle and can therefore be used to continue the cycle and produce biomass. Oxygenation also displays effective Michaelis–Menten kinetics (k_cat,O, K_M = K_O, half-maximum inhibitory CO₂ concentration K_I = K_C). Oxygenation of RuBP produces one 3PG and one 2PG. Rates of carboxylation (R_C) and oxygenation (R_O) are calculated from kinetic parameters and the CO₂ and O₂ concentrations. The reaction coordinate diagram in panel C describes carboxylation and oxygenation as a function of two “effective” barriers.⁶ The first effective barrier includes enolization and gas addition, while the second includes hydration and cleavage. (D) Given standard assumptions (Supporting Information), catalytic efficiencies (k_cat/K_M) are related to the height of the first effective barrier while k_cats are related to the second. The first barrier to oxygenation is drawn higher than for carboxylation because oxygenation is typically slower than carboxylation. Net reactions of RuBP carboxylation and oxygenation are both quite thermodynamically favorable.⁹

The fastest-carboxylating Rubisco observed (at 25 °C) is from the cyanobacterium Synechococcus elongatus PCC 7942.¹⁶ This enzyme has a maximum per-active site carboxylation rate (k_cat,C) of 14 s^–1. However, because the present-day atmosphere contains abundant O₂ and relatively little CO₂ (≈21% O₂ and ≈0.04% CO₂), PCC 7942 Rubisco carboxylates at a rate 20-fold below maximum under ambient conditions [R_C ≈ 0.7 s^–1 per active site (rate law in Figure 1A)]. Due to its relatively low CO₂ specificity, PCC 7942 Rubisco will also oxygenate RuBP appreciably under ambient conditions (R_O ≈ 0.3 s^–1), necessitating substantial photorespiratory flux to recycle 2PG. As downstream processing of 2PG by the C₂ photorespiratory pathway leads to the loss of one carbon for every two 2PGs,^11,12 every two oxygenations “undo” a carboxylation. In ambient air, therefore, the net rate of carboxylation by PCC 7942 Rubisco would be f = R_C – R_O/2 ≈ 0.6 s^–1, or ≈4% of k_cat,C. Given the kinetics of PCC 7942 Rubisco, it is not surprising that all known cyanobacteria use a CO₂-concentrating mechanism to ensure Rubisco functions in a CO₂-rich environment. An elevated level of CO₂ ensures that oxygenation is competitively inhibited and that carboxylation proceeds at a near-maximum rate.¹⁷ Thirtyfold enrichment of CO₂ above ambient increases the carboxylation rate of PCC 7942 Rubisco to 8.9 s^–1 and suppresses the oxygenation rate to 0.14 s^–1, giving a net carboxylation rate f = 8.8 s^–1 per active site (≈60% of k_cat,C).

For comparison, the Rubisco from spinach leaves (Spinacia oleracea) is characteristic of plant Rubiscos in having a lower k_cat,C of ≈3 s^–1 and a CO₂ affinity much greater than that of the S. elongatus enzyme (spinach half-maximum CO₂ concentration K_C of ≈12 μM, PCC 7942 K_C of ≈170 μM). As a result, the spinach enzyme outperforms the cyanobacterial one in ambient air, with an R_C of ≈1.2 s^–1, an R_O of ≈0.4 s^–1, and a net carboxylation rate f ≈1 s^–1. Spinach is a C₃ plant, meaning it does not have a CO₂-concentrating mechanism, which may explain why it employs a slow-but-specific Rubisco. Still, most central metabolic enzymes catalyze far more than one reaction per second,⁷ leading many to wonder if Rubisco catalysis could be improved. Improved Rubisco carboxylation might increase C₃ crop yields,^18,19 but a substantially improved enzyme has evaded bioengineers for decades.²⁰ The repeated evolution of diverse CO₂-concentrating mechanisms, which modulate the catalytic environment rather than Rubisco itself, raises further doubts about whether Rubisco catalysis can be strictly improved.²¹

Various nomenclatures have been used to describe the kinetics of Rubisco carboxylation and oxygenation since its discovery in the 1950s.^5,6,22,23 Here we use k_cat,C and k_cat,O to denote turnover numbers (maximum rates per active site, units of inverse seconds) for carboxylation and oxygenation, respectively. K_C and K_O denote the Michaelis constants (half-saturation concentrations in micromolar) for carboxylation and oxygenation. Specificity factor S_C/O = (k_cat,C/K_C)/(k_cat,O/K_O) is a unitless measure of the relative preference for CO₂ over O₂ (Figure 1D). Because S_C/O relates only to the ratio of kinetic parameters, a higher S_C/O does not necessarily imply higher carboxylation rates. Rather, absolute carboxylation and oxygenation rates depend on CO₂ and O₂ concentrations (Figure 1B), which can vary between organisms and environments (Supporting Information).

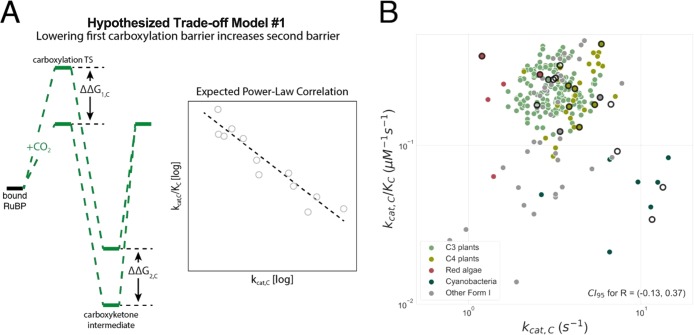
As data on bacterial, archaeal, and plant carboxylases have accumulated over the decades, many researchers have noted that fast-carboxylating Rubiscos are typically less CO₂-specific.²⁴⁻²⁶ In other words, Rubiscos with high k_cat,C values were observed to have lower S_C/O values due to either a lower CO₂ affinity (high K_C) or more efficient oxygenation (higher k_cat,O/K_O). A negative correlation between k_cat,C and S_C/O is often cited to motivate the idea that a trade-off between carboxylation rate and specificity constrains Rubisco evolution.^5,6,26,27

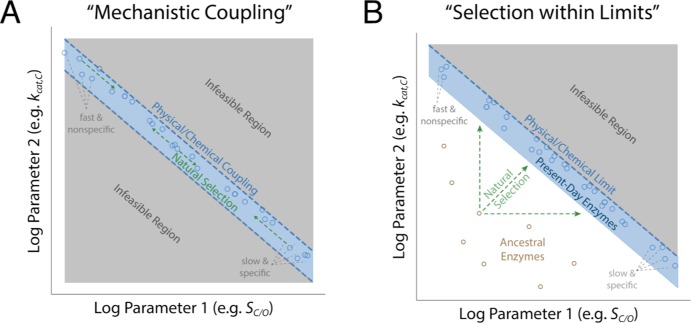
It is worth pausing to clarify the concepts of “trade-off”, “constraint”, and “correlation” (Figure 2). Correlation indicates an apparent linear (or log–log, etc.) relationship between two kinetic parameters. Correlations between enzyme kinetic parameters can result from a “trade-off” due to two distinct kinds of underlying constraints (Figure 2).⁶ In the “mechanistic coupling” scenario, the enzymatic mechanism forces a strict quantitative relationship between two kinetic parameters such that varying one forces the other to vary in a defined manner. This results in a situation in which the value of one parameter strictly determines the other and vice versa [i.e., an “equality constraint” (Figure 2A)]. This could arise for Rubisco, for example, if a single catalytic step [e.g., enolization of RuBP (Figure 1A)] determines the rates of both CO₂ and O₂ entry.

Figure 2.

Scenarios that produce strong correlations between enzyme kinetic parameters. As the logs of the kinetic parameters are linearly related to energy barriers, linear energetic trade-offs should manifest as log–log correlations between kinetic parameters (power laws). Panel A describes a situation in which two kinetic parameters are inextricably linked by the enzyme mechanism, diagrammed here as negative coupling between k_cat,C and S_C/O as an example. These couplings take the form of “equality constraints” in which one parameter determines the other within measurement error. Correlation is expected as long as diverse enzymes are measured. In panel A, selection moves enzymes along the blue curve but cannot produce enzymes off the curve (gray) because they are not feasible. Panel B diagrams an alternative scenario in which the enzyme mechanism imposes an upper limit on two parameters (an inequality constraint). In the “selection within limits” scenario, effective selection is required for correlation to emerge because suboptimal enzymes (e.g., ancestral sequences) are feasible. In the examples plotted, different environmental CO₂ and O₂ concentrations should select for different combinations of rate (k_cat,C) and affinity (S_C/O), resulting in present-day enzymes occupying distinct regions of the plots in panels A and B.

In the “selection within limits” model (Figure 2B), in contrast, the catalytic mechanism imposes an upper limit on kinetic parameters, i.e., an inequality constraint. A clear correlation between parameters will emerge only if there is sufficient selection to reach the boundary. To highlight the difference between these models, consider the kinetics of ancestral enzymes. In the “mechanistic coupling” model, kinetic parameters of ancestors should lie along the same curve as present-day enzymes because the gray regions off the curve are disallowed. Selection could act by moving enzymes along the line of mechanistic coupling, e.g., from a region of high selectivity and low rate toward higher rate and lower selectivity (Figure 2A). According to the “selection within limits” model, in contrast, ancestral enzymes can lie beneath the upper limit determined by the catalytic mechanism (Figure 2B). This second model requires selection to produce a situation in which the kinetics of present-day Rubiscos extracted from various organisms trace out a curve determined by the upper limit enforced by the mechanism.²⁸

Previous research advanced two distinct families of mechanistic models to explain correlations between Rubisco kinetic parameters.^5,6 The first model, which we term “k_cat,C–K_C coupling”, hypothesizes a trade-off between the rate and affinity of carboxylation that leads to a negative correlation between k_cat,C and S_C/O (Figure S2).⁵ A second model, which was advanced in a study in which the last author of this work participated,⁶ hypothesizes that multiple trade-offs constrain Rubisco such that kinetic parameters can vary only along a one-dimensional curve. In addition to k_cat,C–K_C coupling, this work hypothesized a trade-off between catalytic efficiencies for carboxylation and oxygenation (coupling k_cat,C/K_C and k_cat,O/K_O) wherein improving carboxylation efficiency also improves oxygenation efficiency.

These mechanistic models are substantively different. Though both models imply limitations on the concurrent improvement of k_cat,C and S_C/O, “k_cat,C–K_C coupling” relates only to carboxylation kinetics, leaving the possibility that oxygenation kinetics are unconstrained. Coupling between k_cat,C/K_C and k_cat,O/K_O, in contrast, relates to both reaction pathways. While these models appeal to physical and chemical intuition, they are based on data from only ≈20 organisms. Moreover, “mechanistic coupling” and “selection within limits” could plausibly underlie either model (Figure 2).⁶

Here we take advantage of the accumulation of new data to revisit correlations and trade-offs between Rubisco kinetic parameters. We collected and curated literature measurements of ≈300 Rubiscos. Though diverse organisms are represented, the Form I Rubiscos of C₃ plants make up the bulk of the data [>80% (Figure 3A)]. Most previously reported correlations between Rubisco kinetic parameters are substantially attenuated in this data set, with the negative correlation between k_cat,C and specificity S_C/O being a key example. Weakened k_cat,C–S_C/O and k_cat,C–K_C correlations imply that these parameters are not straightforwardly mechanistically coupled, suggesting that models of k_cat,C–K_C coupling should be revisited in future experiments. Overall, weakened correlations call into question previous claims that (i) Rubisco kinetics are constrained to evolve on a one-dimensional line and (ii) natural Rubiscos are optimized to suit environmental CO₂ and O₂ concentrations.^5,6

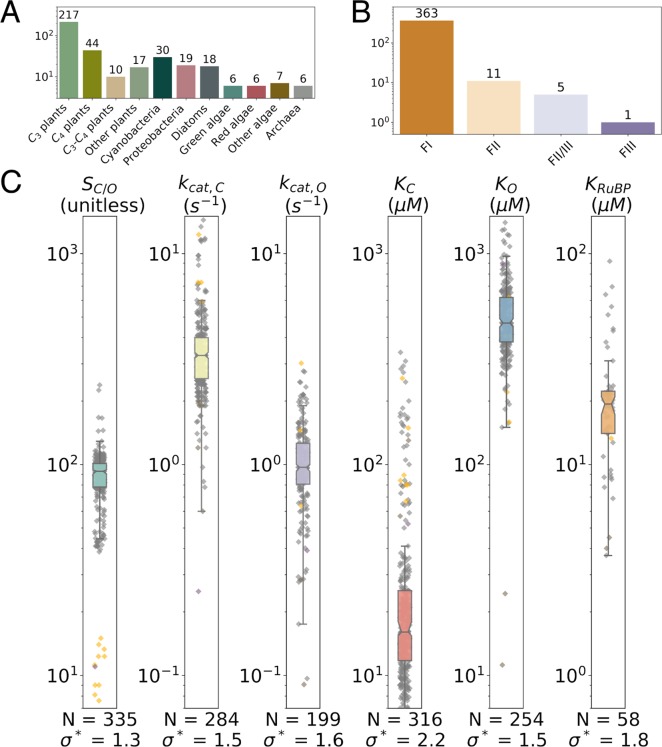
Figure 3.

Summary of the full extended data set. We collected measurements of Rubisco kinetic parameters from a variety of organisms (A) representing four classes of Rubisco isoforms (B). Form I enzymes from plants, cyanobacteria, and algae make up the bulk of the data (A and B). (C) Rubisco kinetic parameters display a narrow dynamic range. The box plot and gray points describe the distribution of Form I Rubiscos, while data for Form II Rubiscos are colored yellow. Colored boxes give the range of the central 50% of FI values, and the notch indicates the median. N is the number values, and σ* gives the geometric standard deviation of Form I data. σ* < 3 for all parameters, meaning a single standard deviation varies by <3-fold. All data are from wild-type Rubiscos measured at 25 °C and near pH 8. More detailed histograms are given in Figure S4.

Despite weakened correlations, Rubisco kinetic parameters display extremely limited variation. k_cat,C varies by only 50% among Form I Rubiscos, and S_C/O varies even less than that [≈30% (Figure 3C)]. Limited variation in S_C/O forces a strong positive power-law correlation between the catalytic efficiencies for carboxylation (k_cat,C/K_C) and oxygenation (k_cat,O/K_O).⁶ We propose a simple model of mechanistic coupling that explains how constraints on the Rubisco mechanism could restrict variation in S_C/O. In this model, variation in catalytic efficiency (k_cat,C/K_C and k_cat,O/K_O) derives solely from gating access of the substrate to the active site complex, which could help explain why Rubisco has been so recalcitrant to improvement by mutagenesis and rational engineering.

Materials and Methods

Data Collection and Curation

We reviewed the literature to find Rubisco kinetic data measured at 25 °C and near pH 8. Ultimately, 61 primary literature studies were included, yielding 335 S_C/O, 284 k_cat,C, 316 K_C, and 254 K_o values for Rubiscos from 304 distinct organisms (Data Sets S1 and S2). We also recorded 58 measurements of the Michaelis constant for RuBP (K_RuBP). The experimental error was recorded for all of these values (when reported) along with the pH, temperature, and other metadata. Data were filtered as described in the Supporting Information. k_cat,O is usually not measured directly²⁹ but is rather inferred as k_cat,O = (k_cat,C/K_C)/(S_C/O/K_O). We used 10⁴-fold bootstrapping to estimate 199 k_cat,O values and 95% confidence intervals thereof. We used an identical procedure to estimate k_cat,C/K_C and k_cat,O/K_O and confidence intervals thereof (Supporting Information). Altogether, we were able to calculate 274 k_cat,C/K_C and 199 k_cat,O/K_O values. Data Sets S1 and S2 provide all source and inferred data, respectively.

Fitting Power Laws

Certain model Rubiscos are measured frequently. For example, we found 12 independent measurements of the spinach Rubisco. In such cases, the median measured value was used to avoid bias in correlation and regression analyses. In contrast to textbook examples with one independent and one dependent variable, there is experimental error associated with both variables in all scatter plots shown here (e.g., plotting k_cat,C vs K_C in Figure 5B). As such, we used total least-squares linear regression on a log scale to fit relationships between Rubisco parameters. Because R² values of total least-squares fits do not convey the explained fraction of Y axis variance, they are challenging to interpret. We instead report the degree of correlation as Pearson R values of log-transformed values. Bootstrapping was used to determine 95% confidence intervals for the Pearson correlation coefficient, power-law exponents, and prefactors (i.e., the slopes and intercepts of linear fits on a log–log scale). In each iteration of the bootstrap, data were subsampled to 90% with replacement. Total least-squares regression was applied to each subsample, and the procedure was repeated 10⁴ times to determine 95% confidence intervals. Python source code is available at github.com/flamholz/rubisco.

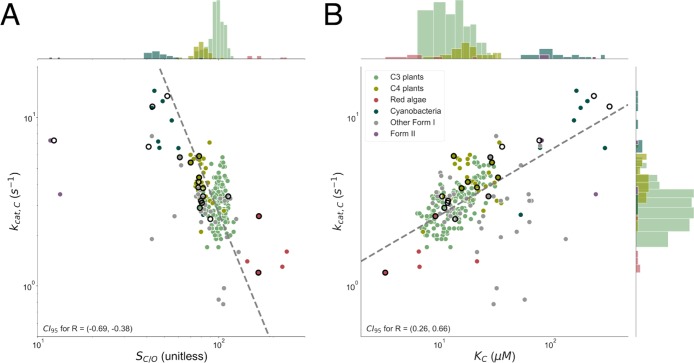
Figure 5.

Focal correlations of previous analyses are not robust to new data. Points with black outlines are from ref (6), and dashed gray lines represent the best fit to FI Rubisco data. Histograms for k_cat,C, S_C/O, and K_C are plotted on parallel axes. Panel A plots k_cat,C against S_C/O. k_cat,C and S_C/O correlate with an R of approximately −0.6 among FI Rubiscos as compared to ≈0.9 previously.^5,6 The 95% confidence intervals are (−4.0, −2.0) for the fit exponent and (3 × 10⁴, 2 × 10⁸) for the prefactor (slope and intercept on a log–log scale, respectively), indicating that the form of k_cat,C–S_C/O correlation is very uncertain. Notably, S_C/O displays very limited variation overall and especially within physiological groupings with sufficient data. Median S_C/O values are 177 for red algae (σ* = 1.2; N = 6), 98 for C₃ plants (σ* = 1.1; N = 162), 80 for C₄ plants (σ* = 1.1; N = 35), and 48 for cyanobacteria (σ* = 1.1; N = 16). Panel B plots k_cat,C against K_C. Here, the R is ≈0.5 as compared to ≈0.9 previously.⁶ This fit is more robust, with 95% confidence intervals of (0.3, 0.5) and (0.8, 1.5) for the fit exponent and prefactor, respectively.

Results

An Extended Data Set of Rubisco Kinetic Parameters

To augment existing data, we collected literature data on ≈300 Rubiscos, including representatives of clades and physiologies that had been poorly represented in earlier data sets, e.g., diatoms, ferns, CAM plants, and anaerobic bacteria (Figure 3A). We collected kinetic parameters associated with carboxylation and oxygenation (S, K_C, k_cat,C, K_O, and k_cat,O) as well as measurements of the RuBP Michaelis constant (half-maximum RuBP concentration, K_RuBP) and experimental uncertainty for all values where available. All data considered below were measured at 25 °C and near pH 8 to ensure that measured values are comparable (Supporting Information). Notably, Rubisco assays are challenging to perform, and variation in measurements across laboratories is expected. Some of the spread in the data may come from systematic differences between laboratories and assay methods. The Rubisco activation state, for example, may differ between methods and preparations.¹⁵ Though we cannot resolve this issue here, we were careful to review each study’s methods, document a small number of problematic measurements, and record experimental error when reported (Data Set S1).

The resulting data set contains Rubisco measurements from a total of 304 distinct species, including 335 S_C/O values, 284 k_cat,C values, 316 K_C values, 254 K_O values, and 199 k_cat,O values (Figure 3B). k_cat,O values are rarely measured directly (Supporting Information) and are typically inferred as k_cat,O = (k_cat,C/K_C)/(S_C/O/K_O).²⁹ The Michaelis constant for RuBP (K_RuBP) is measured infrequently, and only 58 values were extracted. We were able to estimate catalytic efficiencies for carboxylation (k_cat,C/K_C) in 274 cases and for oxygenation (k_cat,O/K_O) in 199 cases (Materials and Methods). Though the data include measurements of some Form II, III, and II/III Rubiscos, they remain highly focused on the Form I Rubiscos found in cyanobacteria, diatoms, algae, and higher plants, which make up >95% of the data set (Figure 3B). As such, we focus here on the kinetic parameters of Form I Rubiscos (abbreviated FI Rubisco).

Rubisco kinetic parameters display a very narrow dynamic range (Figure 3C). The geometric standard deviation (σ*) expresses multiplicative variability in the data set and is well below one order of magnitude (σ* ≪ 10) for all parameters. Rubisco displays a particularly low variation in k_cat,C (σ* = 1.5) as compared to other enzymes for which 20 or more k_cat measurements are available [median σ* ≈ 7 (Figure S5)]. Specificity S_C/O displays the least variation of all parameters (σ* = 1.3). This is due in part to overrepresentation of C₃ plants in the data set, which occupy a narrow S_C/O range of ≈80–120. Nonetheless, measurements of S_C/O for FI and FII enzymes are clearly distinct, with values ranging from 7 to 15 for FII measurements and from ≈50 to 200 for FI (Figure 3C).

Energetic Trade-offs Tend To Produce Power-Law Correlations

All kinetic parameters (S_C/O, k_cat,C, K_C, k_cat,O, and K_O) are mathematically related to the microscopic rate constants of the Rubisco mechanism. Given common assumptions about irreversible and rate-limiting steps, this multistep mechanism can be simplified so that logarithms of measured kinetic parameters are proportional to effective transition state barriers (Figure 1C,D and Supporting Information). As such, correlations between kinetic parameters will emerge if effective transition state barriers vary together (Figure 2). If, for example, lowering the effective transition state barrier to CO₂ addition (ΔG_1,C) requires an increase in the effective barrier to the subsequent hydration and cleavage steps of carboxylation (ΔG_2,C), then we should observe a negative linear correlation ΔG_1,C ∝ −ΔG_2,C. Because k_cat,C/K_C is related to the first effective carboxylation barrier [k_cat,C/K_C ∝ exp(−ΔG_1,C/RT)] and k_cat,C to the second [k_cat,C ∝ exp(−ΔG_2,C/RT)], a linear correlation between transition state barrier heights translates to a log scale correlation between kinetic parameters such that ln(k_cat,C/K_C) ∝ −ln(k_cat,C). These relationships are known as power laws and motivate us and others to investigate the kinetic parameters on a log–log scale.

We expect to observe strong power-law correlations between pairs of kinetic parameters in two cases. (i) The associated energy barriers co-vary because they are linked by the enzymatic mechanism [“mechanistic coupling” (Figure 2A)], or (ii) the mechanism imposes an upper bound on the sum (or difference) of two barrier heights. In case ii, strong selection favors the emergence of enzymes at or near the imposed limit [“selection within limits” (Figure 2B)]. As Rubisco is the central enzyme of photoautotrophic growth, it likely evolved under selection pressure toward maximizing the net rate of carboxylation in each host, so either of these scenarios is plausible a priori. Notably, host physiology and growth environments can affect the catalytic environment. Rubiscos from different organisms will experience different temperatures, pHs, and prevailing CO₂ and O₂ concentrations due, for example, to an anaerobic host or a CO₂ concentrating mechanism increasing the level of CO₂.⁶ Different conditions should favor different combinations of kinetic parameters (Figure 2).

Correlations between Kinetic Parameters of Form I Rubiscos

We performed a correlation analysis to investigate relationships between kinetic parameters of FI Rubiscos. Figure 4 gives log scale Pearson correlations between parameters that are measured directly: k_cat,C, K_C, K_O, S_C/O, and K_RuBP. Linear scale correlations are reported in Figure S7.

Figure 4.

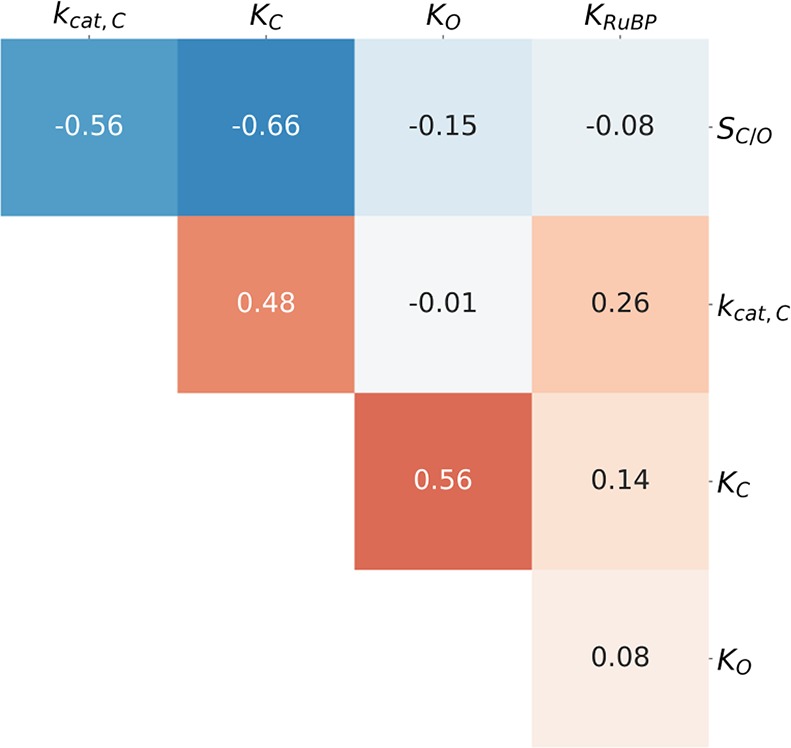
Correlations between measured kinetic parameters are attenuated by the addition of new data. This figure gives Pearson correlations (R) between pairs of log-transformed kinetic parameters of Form I Rubiscos. When multiple measurements of the same enzyme were available, the median value was used (Materials and Methods). S_C/O–K_C, S_C/O–k_cat,C, and K_C–k_cat,C correlations are of particular interest because they were highlighted in previous works, which found R values of 0.8–0.95. None of these pairs have R values exceeding 0.7 in the extended data set.

Overall, correlations are weaker in the extended data set than documented in previous studies of smaller data sets.^5,6 Nonetheless, we observed modestly strong, statistically significant correlations between k_cat,C and S_C/O (R = −0.56; p < 10^–10), k_cat,C and K_C (R = 0.48; p < 10^–10), K_C and S_C/O (R = −0.66; p < 10^–10), and K_C and K_O (R = 0.56; p < 10^–10). Because Rubisco kinetic parameters are mathematically interrelated through the microscopic mechanism as it is commonly understood, some level of correlation is expected. For example, when we derive expressions for k_cat,C and K_C from the Rubisco mechanism, they share common factors that should produce some correlation even in the absence of underlying coupling (Supporting Information). Similarly, S_C/O is defined as (k_cat,C/K_C)/(k_cat,O/K_O) and could correlate negatively with K_C for this reason. Because a modest correlation is expected irrespective of underlying trade-offs, the correlations in Figure 4 do not necessarily support any particular trade-off model.

Correlations between k_cat,C and S_C/O as well as k_cat,C and K_C were previously highlighted to support particular mechanistic trade-off models.^5,6 However, these correlations are substantially attenuated by the addition of new data (Figures 4 and 5). Plotting k_cat,C against S_C/O (Figure 5A) shows that these parameters are modestly correlated, with an R of ≈0.6 compared to an R of ≈0.9 in previous analyses.^5,6Figure 5A also highlights the extremely limited and stereotyped variation in S_C/O where Rubiscos from organisms sharing a particular physiology (e.g., C₃ plants or cyanobacteria) occupy a very narrow range of S_C/O values. Multiplicative standard deviations (σ*) of S_C/O are <1.25 in all groups. Plotting k_cat,C against K_C (Figure 5B) shows that this correlation is also weakened, with an R of ≈0.5 compared to ≈0.9 previously.⁶ We interpret weakened correlations as evidence that previously proposed trade-off models should be revisited. We therefore proceed to evaluate the correlations predicted by specific trade-off models, with an eye toward understanding the restricted variation in S_C/O shown in Figure 5A.

Re-Evaluation of Proposed Trade-off Models

Two distinct mechanistic trade-off models have been advanced.^5,6 The first model, which we term k_cat,C–K_C coupling, posits that increased specificity toward CO₂ necessitates a slower maximum carboxylation rate, k_cat,C.^5,6 It was proposed that this trade-off is due to stabilization of the first carboxylation transition state (TS).⁵ Under this model, a stable Rubisco–TS complex produces high CO₂ specificity but slows the subsequent carboxylation steps and limits k_cat,C (Figure S2). This proposal can be cast in energetic terms by relating the measured catalytic parameters to effective transition state barrier heights (Figure 1D and Supporting Information). This model can be construed in energetic terms as follows. Lowering the effective barrier to CO₂ addition (ΔG_1,C in Figure 6A) will make Rubisco more CO₂-specific even if oxygenation kinetics remain unchanged.⁶k_cat,C–K_C coupling posits a negative coupling between CO₂ addition and the subsequent carboxylation steps of hydration and bond cleavage (effective barrier height ΔG_2,C diagrammed in Figure 6A). Therefore, the energetic interpretation of this model predicts a negative correlation between ΔG_1,C and ΔG_2,C and, as a result, a negative power-law correlation between k_cat,C and k_cat,C/K_C.⁶

Figure 6.

Negative power-law correlation between k_cat,C and k_cat,C/K_C is not supported by the extended data set. In the model diagrammed in panel A, CO₂-specific Rubiscos have low barriers to enolization and CO₂ addition (first effective carboxylation barrier ΔG_1,C), but lowering the first effective barrier necessarily increases the second effective barrier (ΔG_2,C), reducing k_cat,C. In this view, stabilizing the first carboxylation TS also enhances selectivity but also slows carboxylation (Figure S2). ΔG_1,C and ΔG_2,C should be negatively correlated, which would manifest as negative power-law correlation between k_cat,C and k_cat,C/K_C under certain assumptions (Supporting Information). (B) The extended data set does not evidence the expected correlation (for Form I enzymes, R = 0.02 and p = 0.8). While previous analyses gave an R of approximately −0.9,⁶ the 95% confidence interval for R now includes 0.0. Restricting our focus to particular physiologies like C₃ plants does not result in the expected correlation.

In previous work, k_cat,C and k_cat,C/K_C were found to correlate strongly on a log–log scale.⁶ The reported correlation, however, is not strongly supported by our data set (Figure 6B). The true barrier height to CO₂ addition depends on the CO₂ concentration, which could partially explain the apparent lack of correlation. However, correlation is not improved by restricting focus to C₃ plants for which data are abundant and for which measured leaf CO₂ concentrations vary by only 20–30% due to variation in CO₂ conductance and Rubisco activity.^30,31

The absence of correlation does not necessarily imply the absence of an underlying mechanistic limitation. Rather, if the Rubisco mechanism limits the joint improvement of k_cat,C and k_cat,C/K_C, a much decreased correlation over the extended data set (R < 0.4) could result from several factors, including measurement error, undersampling of Rubiscos with high k_cat,C (e.g., from cyanobacteria), or, alternatively, insufficient selection pressure. Diminished correlation, with many points observed below the previous correlation line, suggests that the “mechanistic coupling” model is less likely than “selection within limits” in this case (Figure 2).

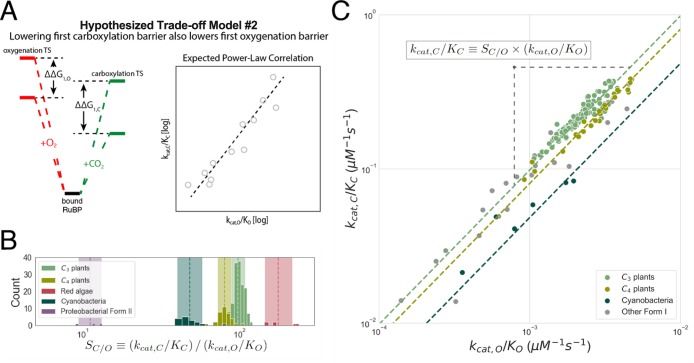
The second mechanistic model, wherein faster CO₂ addition entails faster O₂ addition,⁶ is well-supported by the extended data set (Figure 7). This model was previously supported by a power-law correlation between catalytic efficiencies for carboxylation and oxygenation [k_cat,C/K_C ∝ (k_cat,O/K_O)²]. As k_cat,C/K_C is exponentially related to the first effective carboxylation barrier [k_cat,C/K_C ∝ exp(−ΔG_1,C)] and k_cat,O/K_O to the first effective oxygenation barrier [k_cat,O/K_O ∝ exp(−ΔG_1,O)], correlation was taken to imply that lowering the barrier to CO₂ addition also lowers the barrier to O₂ addition (Figure 7A). Our data set supports a similar power law, albeit with an exponent of ≈1.0 instead of ≈2.0.

Figure 7.

Second mechanistic proposal that is remarkably well-supported by the extended data set. (A) In this proposal, mutations increasing the rate of addition of CO₂ to the Rubisco–RuBP complex also increase the rate of O₂ addition. In energetic terms, lowering the effective barrier to enolization and CO₂ addition (ΔG_1,C) lowers the first effective barrier to O₂ addition (ΔG_1,O), as well. Given this model, barrier heights should be positively correlated, which would manifest as a positive linear correlation on a log–log plot of k_cat,C/K_C against k_cat,O/K_O. (B) S_C/O displays limited variation within physiological groups such as C₃ and C₄ plants for which we have substantial data. Dashed lines give the geometric mean of S_C/O values. The multiplicative standard deviation, σ*, sets the width of the shaded region. (C) S_C/O = (k_cat,C/K_C)/(k_cat,O/K_O), so restricted S_C/O variation implies a power-law relationship (k_cat,C/K_C) = S_C/O(k_cat,O/K_O). k_cat,C/K_C is strongly correlated with k_cat,O/K_O on a log–log scale (R = 0.94; p < 10^–10). Fitting FI measurements gives k_cat,C/K_C = 119(k_cat,O/K_O)^1.04. A 95% confidence interval for the exponent is (0.94, 1.13), which includes 1.0. The geometric mean of measured S_C/O values predicts k_cat,O/K_O = (k_cat,C/K_C)/S_C/O and vice versa. This simple approach accurately predicts the k_cat,O/K_O for FI Rubiscos (prediction R² = 0.80), C₃ plants (R² = 0.84), C₄ plants (R² = 0.96), and cyanobacteria (R² = 0.79). Other groups, e.g., red algae, are omitted because of insufficient data.

Again, we found that S_C/O varies little among FI Rubiscos (Figure 3C) and even less within C₃ plants, cyanobacteria, and other physiological groupings (Figures 5A and 7B). S_C/O = (k_cat,C/K_C)/(k_cat,O/K_O) by definition, so the fact that S_C/O is approximately constant forces a positive power-law relationship of log(k_cat,C/K_C) = log(k_cat,O/K_O) + log(S_C/O). Indeed, Form I enzymes display a remarkably high-confidence power-law relationship between k_cat,C/K_C and k_cat,O/K_O (R = 0.94; p < 10^–10). Because S_C/O is the only free parameter in this equation and is nearly constant, the geometric mean of S_C/O measurements (≈90 for Form I Rubiscos) can be used to predict k_cat,O/K_O as S_C/O^–1(k_cat,C/K_C). This simple approach, which uses a power-law exponent of 1.0 and a prefactor of S_C/O^–1, predicts Form I k_cat,O/K_O values with an R² of 0.80, nearly as accurate as fitting both the prefactor and exponent as free parameters (R² = 0.81). As shown in Figure 7C, predictions of k_cat,O/K_O = S_C/O^–1(k_cat,C/K_C) generally improve when considering specific physiological groupings like C₃ and C₄ plants because S_C/O varies so little within these groups. Assuming a roughly constant S_C/O forces a 1:1 relationship ΔG_1,C = ΔG_1,O + C, meaning that decreasing CO₂ addition barrier ΔG_1,C is associated with an equal decrease in O₂ addition barrier ΔG_1,O.

Implications for the Mechanism of CO₂/O₂ Discrimination by Rubisco

A 1:1 relationship between effective barriers to CO₂ and O₂ addition suggests that a single factor controls both barriers. We offer a simple model based on the mechanism of Rubisco that can produce a 1:1 correlation between barrier heights and constant S_C/O. In this model, the RuBP-bound active site fluctuates between reactive and unreactive states (Figures 8A). The fraction of enzyme in the reactive state is denoted ϕ. In the unreactive state, neither oxygenation nor carboxylation can proceed. In the reactive state, either gas reacts at its intrinsic rate, which does not vary across Rubiscos of the same class (Figure 8B). Because RuBP must undergo enolization for carboxylation or oxygenation to occur, ϕ may be determined by the degree of enolization of RuBP (Supporting Information).

Figure 8.

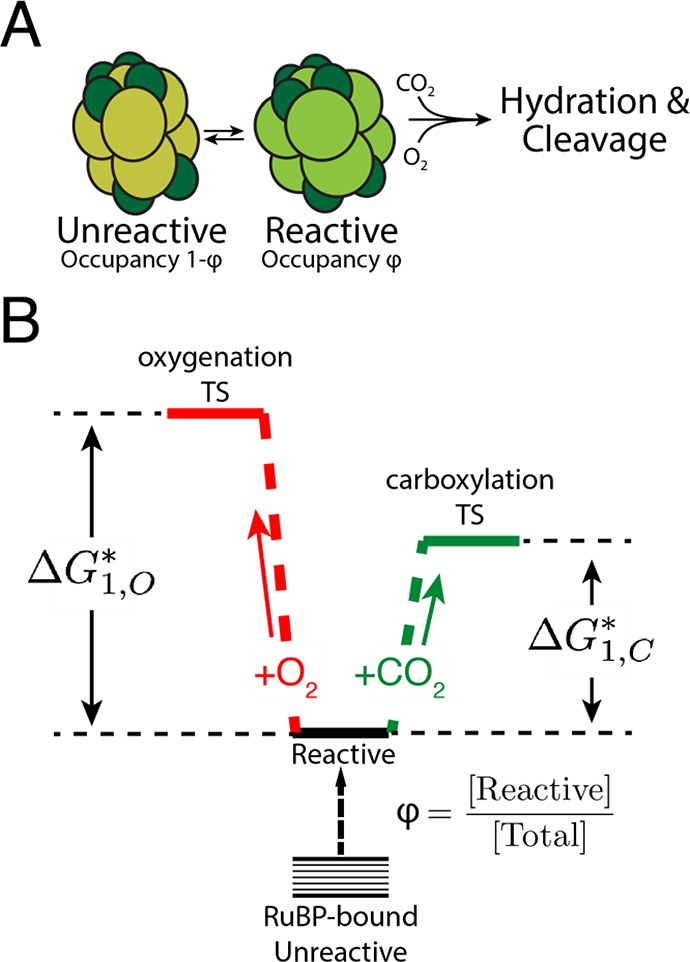
A power-law relationship between k_cat,C/K_C and k_cat,O/K_O can be explained by an active site that fluctuates between “reactive” and “unreactive” states. (A) In this model, CO₂ and O₂ react with bound RuBP only when the enzyme is in the reactive state, which has an occupancy φ. (B) φ can vary between related enzymes. In the reactive state, CO₂ and O₂ react with the bound RuBP with intrinsic reactivities ΔG*_1,C and ΔG*_1,O that do not vary between related Rubiscos. If the difference in intrinsic reactivities (ΔG*_1,O – ΔG*_1,C) is constant, we derive a power-law relationship between k_cat,C/K_C and k_cat,O/K_O with an exponent of 1.0. This relationship requires a constant S_C/O (Supporting Information).

This model can be phrased quantitatively as 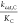∝ ϕ exp(−ΔG*_1,C/RT) and 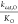∝ ϕ exp(−ΔG*_1,O/RT) where ΔG*_1,C and ΔG*_1,O are the intrinsic reactivities of the RuBP enediolate to CO₂ and O₂, respectively. Under this model, S_C/O should be roughly constant, which forces a power-law relationship between k_cat,C/K_C and k_cat,O/K_O with an exponent of 1.0 (Figure 7C). Variation in k_cat,C/K_C and k_cat,O/K_O implies that ϕ can vary between related Rubiscos, perhaps by evolutionary tuning of the equilibrium constant for RuBP enolization. S_C/O is independent of the equilibrium fraction of on-enzyme RuBP enolization, so variation in enolization should affect k_cat,C/K_C and k_cat,O/K_O without altering S_C/O. Rather, S_C/O is determined by the difference ΔG*_1,O – ΔG*_1,C, so changes to the conformation of the RuBP enediolate might explain characteristic differences between the S_C/O of C₃ plant and cyanobacterial Rubiscos.^5,8 See the Supporting Information for a derivation of this model and further discussion of its implications.

Discussion

We collected and analyzed literature measurements of ≈300 Rubiscos (Figure 3A). The literature is very phylogenetically biased, with the readily purified plant Rubiscos making up >80% of the data (Figure 3B). Despite incomplete coverage, some trends are clear. Rubisco kinetic parameters display an extremely limited dynamic range, with multiplicative standard deviations being <3-fold in all cases (Figure 3C). k_cat,C and S_C/O appear to be particularly constrained. Rubisco displays much less k_cat variability than any other enzyme for which sufficient data are available (Figure S5); 97% of k_cat,C values are between 1 and 10 s^–1, and the highest k_cat,C measured at 25 °C (14 s^–1, S. elongatus PCC 7942¹⁶) is only ≈20 times greater than the lowest reported Form I value (0.8 s^–1 from the diatom Cylindrotheca N1³²). Altogether, these data suggest that there is some limitation of the maximum rate of carboxylation by Rubisco in the presence of O₂.

Focusing on O₂, we find that measured Rubiscos oxygenate slowly. More than half of k_cat,O measurements are <1 s^–1, and k_cat,C is 4 times greater than k_cat,O on average (Figure 3C and Figure S4A). Similarly, the O₂ affinity is quite low in general. The median K_O is ≈470 μM, nearly double the Henry’s law equilibrium of water with a 21% O₂ atmosphere (≈270 μM at 25 °C).

With a multiplicative standard deviation of 1.3, S_C/O displays the least variation all Rubisco kinetic parameters (Figure 3C and Figure S4A). Figures 5A and 7B highlight the stereotyped variation in S_C/O, where C₃ plant, C₄ plant, cyanobacterial, and red algal enzymes display very limited variation around characteristic S_C/O values. All groups have multiplicative standard deviations (σ*) of <1.25. Nonetheless, FI Rubiscos are approximately 1 order of magnitude more CO₂-specific than the few characterized Form II, III, and II/III enzymes (Figure 7B and Supporting Information). This might be explained by the prevalence of FII, FIII, and FII/III enzymes in bacteria and archaea that fix CO₂ under anaerobic conditions, where it is doubtful that oxygenation affects organismal fitness. We note, however, that there is substantial variation among measurements of the model FII Rubisco from Rhodospirillum rubrum (Figure S4B). This and the paucity of data on non-Form I Rubiscos (Figure 3B) indicate that more measurements are required to evaluate FII, FII/III, and FIII enzymes. As such, we focused here on FI Rubiscos, for which data are abundant.

Rubisco kinetics were previously argued to vary in a one-dimensional landscape⁶ and hypothesized to be “nearly perfectly optimized”.⁵ Overall, FI Rubiscos appear to be less constrained than previously supposed. Figure 4 documents an overall reduction in correlation between FI Rubisco kinetic parameters, and the data set is no longer well-approximated as one-dimensional (Figure S8). Many natural Rubiscos appear to be suboptimal in plots of k_cat,C against S_C/O because other enzymes have roughly equal S_C/O values but higher k_cat,C values (Figure 5A and Figure S6). Weakened correlations could be due to measurement error and systematic biases, though we find this explanation unlikely because (i) measurements of Form I Rubiscos from similar organisms are broadly consistent (Figure S6), (ii) some correlations remain strong and statistically significant across the entire data set, (iii) systematic bias toward C₃ plants would tend to increase correlations, and (iv) standardization of Rubisco assays using stoichiometric inhibitors to quantify active sites should improve data quality over time (Supporting Information). Reduced correlations therefore lead us to reject the notion that Rubisco kinetics vary in a strictly one-dimensional landscape and to revisit previous models of mechanistic trade-off.

The mechanistic models described in Figures 6 and 7 are based on a simple chemical intuition: that the intrinsic difficulty of discriminating CO₂ and O₂ requires the enzyme to differentiate between carboxylation and oxygenation transition states. The requirement of transition state discrimination is a direct consequence of two assumptions supported by experimental evidence.²² Briefly, it is assumed that addition of either gas is irreversible and that there is no binding site for CO₂ or O₂ and, thus, no “Michaelis complex” for either gas.^5,6,22,33,34 If CO₂ bound a specific site on Rubisco before reacting, it might be possible to modulate K_C by mutation without substantially affecting the kinetics of subsequent reaction steps. In the unlikely case that gas addition is substantially reversible,^34,35 we might expect to find Rubiscos that evolved enhanced selectivity by energy-coupled kinetic proofreading. Energy coupling can enable amplification of selectivity due to differential CO₂ and O₂ off rates.³⁶ The fact that no such Rubiscos have been found suggests that gas addition is irreversible or that CO₂ and O₂ off rates are incompatible with kinetic proofreading in some other way.^6,37

As Rubisco likely does not bind CO₂ directly, it was hypothesized that high CO₂ specificity (large S_C/O) is realized by discriminating between the first carboxylation and oxygenation transition states, i.e., between the developing carboxyketone and peroxyketone (Figures S1 and S2).⁵ A late carboxylation transition state would be maximally discriminable because the developing carboxylic acid is distinguishable from the peroxyl group of the oxygenation intermediate. The extraordinarily tight binding of the carboxyketone analogue CABP to plant Rubisco provides strong support for a late carboxylation transition state.⁵ Because a late transition state resembles the carboxyketone intermediate, it was argued that CO₂-specific Rubiscos must tightly bind the intermediate, slowing the subsequent reaction steps and restricting k_cat,C (Figure S2).⁵

As k_cat,C/K_C is related to the effective barrier to enolization and CO₂ addition (ΔG_1,C) and k_cat,C is related to the effective barrier to hydration and cleavage [ΔG_2,C (Figure 1D)], an energetic framing of this model argues that decreasing ΔG_1,C (increasing k_cat,C/K_C) entails increasing ΔG_2,C [decreasing k_cat,C (Figure 6A)].⁶ Despite nuanced differences, we collectively term these models k_cat,C–K_C coupling due to the hypothesized coupling of carboxylation kinetics. Though these models are motivated by the need to discriminate between CO₂ and O₂, they invoke a trade-off between carboxylation steps only. That is, specificity requires tighter binding of the carboxylation intermediate, which slows downstream processing of that same intermediate, irrespective of O₂.

Three correlations previously supported k_cat,C–K_C coupling, correlations between k_cat,C and S_C/O, between k_cat,C and K_C, and between k_cat,C and k_cat,C/K_C. k_cat,C and S_C/O remain negatively correlated in our larger data set but more weakly than previously observed (Figure 5A). The same is true for k_cat,C and K_C (Figure 5B) and for k_cat,C–k_cat,C/K_C (Figure 6B). Rather than arguing for strong coupling of carboxylation kinetics, Figure 5 highlights the stereotyped variation in S_C/O described above. We interpret weakened correlations as implying that carboxylation kinetics are not strictly coupled. Considering residuals of the k_cat,C–K_C fit (Figure S9) shows that outliers include recent measurements of cyanobacterial³⁸ and diatom³⁹ Rubiscos, which fall well below the fit line. This is consistent with a “selection within limits” view of k_cat,C–K_C coupling (Figure 2B).

The second mechanistic trade-off model posits that faster addition of CO₂ to the Rubisco–RuBP complex necessarily allows faster O₂ addition. This model was previously supported by a positive power-law correlation between the catalytic efficiencies for carboxylation and oxygenation (k_cat,C/K_C and k_cat,O/K_O, respectively),⁶ which can be understood as a positive coupling of the effective barriers to enolization and gas addition for CO₂ and O₂ [ΔG_1,C and ΔG_1,O (Figure 7A)]. We showed that extremely limited and stereotyped variation in S_C/O = (k_cat,C/K_C)/(k_cat,O/K_O) necessitates a power-law correlation with of exponent of 1.0 between k_cat,C/K_C and k_cat,O/K_O (Figure 7B,C). An exponent of 1.0 implies that decreasing ΔG_1,C (enabling faster carboxylation) requires a roughly equal decrease in ΔG_1,O (enabling faster oxygenation, as well). Although several research groups have attempted to isolate improved Rubisco mutants, none of the mutants examined so far exceed wild-type enzymes on these axes (Figure S11).

A power-law relation with an exponent of 1.0 can be seen as resulting from an active site that fluctuates between a reactive and unreactive state (Figure 8A). This coarse-grained model is motivated by the Rubisco mechanism in two ways. Because Rubisco likely does not bind CO₂ or O₂ directly, active site concentrations are determined by solution concentrations (e.g., in the chloroplast stroma). Rubisco could close the active site to diffusion to limit O₂ entry,⁴⁰ but this would also slow carboxylation. Similarly, RuBP must enolize for oxygenation or carboxylation to proceed (Figure 1A), so modulating the degree of enolization would affect both reaction pathways equally.^14,15 In either case, the average occupancy of the reactive state mechanistically couples the rates of CO₂ and O₂ addition (Figure 2A) and throttles the subsequent steps of carboxylation and oxygenation equally (Figure 8).

In previous work, where Rubisco kinetics were thought to vary in a one-dimensional landscape, setting k_cat,C determined all other kinetic parameters.⁶ In this setting, it was argued that Rubisco kinetic parameters are determined by the prevailing CO₂ and O₂ concentrations because a unique choice of parameters on the one-dimensional curve maximizes the net rate of carboxylation.⁶ Because the data are no longer clearly one-dimensional, we cannot argue that Rubisco is “perfectly optimized” to match prevailing concentrations. Moreover, the model presented in Figure 8 sets no upper limit on k_cat,C, suggesting that selection for an increased level of carboxylation in the absence of O₂ could produce Rubisco mutants with superlative k_cat,C values (i.e., k_cat,C ≫ 15 s^–1). Such enzymes might be found in anaerobic bacteria and would be of interest in probing the limits of Rubisco catalysis.

The prospect of engineering an improved Rubisco is tantalizing, not only because it could plausibly improve crop yields¹⁸ but also because the task tests our understanding of enzymes on a very basic level. It is clear from the data presented here that there is some evolutionary constraint on Rubisco catalysis. Surely, a superlative Rubisco would have arisen if it were mutationally accessible from existing enzymes. More detailed biochemical investigation of naturally occurring Rubiscos will help delineate the evolutionary constraints imposed on Rubisco kinetics. Still, the Rubisco large subunit displays extremely limited sequence variation.⁴¹ Perhaps exploring a wider swath of sequence space via protein engineering techniques⁴²⁻⁴⁴ would enable strict improvements to Rubisco kinetics? We argue that biochemical and bioengineering techniques should be used in concert to probe the limits of Rubisco catalysis and propose several avenues of future research to evaluate the prospects of Rubisco engineering.

First, the kinetics of non-plant Rubiscos should be characterized more thoroughly. These should include the Form II, III, and II/III enzymes of bacteria and archaea as well as FI enzymes of bacteria and diverse eukaryotic autotrophs.^13,39 Ideally, these enzymes would be chosen in a manner that maximizes sequence and phylogenetic diversity⁴⁵ and characterized for their binding (e.g., of RuBP and CABP) and catalytic activity (measuring k_cat,C, K_C, k_cat,O, K_O, and S_C/O) as a function of temperature and pH.^29,46,47 A facile assay for direct measurement of oxygenation would also reduce the number of assumptions made in measuring and analyzing Rubisco kinetics.²⁹ These data would help resolve whether Rubisco isoforms display characteristic differences in catalytic potential. It is possible, for example, that non-Form I enzymes are subject to different constraints than FI Rubiscos and might serve as useful chassis for engineering.

It is also important to revisit the classic experiments undergirding our understanding of the Rubisco catalytic mechanism, especially those supporting the central assumptions that (i) there is no Michaelis complex for CO₂ or O₂ and (ii) gas addition is irreversible.^22,34,35 These assumptions substantially constrain CO₂ specificity. If we were to find Rubiscos for which these assumptions are relaxed, they might serve as a basis for engineering a fast-and-selective carboxylase. On the other hand, all Rubiscos may share the same limitations. Because these limitations are likely described as couplings between transition state barriers (as in Figures 7 and 8), measurements of barrier heights for a wide variety of Rubiscos would enable more direct testing of trade-off models. One avenue for drawing inferences about barrier heights is by measuring the binding energies of intermediate and transition state analogues.^5,48 Kinetic isotope effects for CO₂ and O₂ report indirectly on the relevant barriers⁴⁹ and can be measured by mass spectrometry.⁵⁰ Investigating the relationship between transition state barriers and kinetic parameters will help delineate which reaction steps limit carboxylation and oxygenation in different Rubisco lineages.⁵

Some disagreement about the precise ordering of carboxylation steps remains,^5,14,15 and the mechanism of oxygenation is not well understood.⁴⁸ Chemical reasoning about the mechanisms of Rubisco carboxylation and oxygenation would benefit from progress in structural biology. Intermediate and transition state analogues should be used to capture the active site at various points along the reaction trajectory.^14,40,48,51 If experiments and structural analyses confirm that the assumptions described above hold for all Rubiscos, it would greatly limit our capacity to engineer Rubisco and strongly suggest that alternative strategies for improving carbon fixation should be pursued.^19,52−54 If, however, these assumptions are invalidated, many enzyme engineering strategies would become viable. Such data and analyses will be instrumental in guiding the engineering of carbon fixation for the next decade.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.biochem.9b00237.

• Supplementary text, tables, figures, and references (PDF)

• Data set S1 (XLSX)

• Data set S2 (XLSX)

• Data set S3 (XLSX)

• Data set S4 (XLSX)

This research was supported by the U.S. National Science Foundation (NSF) (Grant MCB-1818377), the European Research Council (Project NOVCARBFIX 646827), the Israel Science Foundation (ISF) (Grant 740/16), the ISF-NRF Singapore joint research program (Grant 7662712), the Beck-Canadian Center for Alternative Energy Research, Dana and Yossie Hollander, the Ullmann Family Foundation, the Helmsley Charitable Foundation, the Larson Charitable Foundation, the Wolfson Family Charitable Trust, Charles Rothschild, and Selmo Nussenbaum. R.M. is the Charles and Louise Gartner professional chair. A.I.F. was supported by a National Science Foundation Graduate Research Fellowship. Y.M.B.-O. is an Azrieli fellow.

The authors declare no competing financial interest.