Soil‐mediated eco‐evolutionary feedbacks in the invasive plant Alliaria petiolata

Summary

1. Ecological and evolutionary processes historically have been assumed to operate on significantly different time‐scales. We know now from theory and work in experimental and model systems that these processes can feed back on each other on mutually relevant time‐scales.

2. Here, we present evidence of a soil‐mediated eco‐evolutionary feedback on the population dynamics of an invasive biennial plant, Alliaria petiolata.

3. As populations age, natural selection drives down production of A. petiolata's important antimycorrhizal allelochemical, sinigrin. This occurs due to density‐dependent selection on sinigrin, which is favoured under interspecific, but disfavoured under intraspecific, competition.

4. We show that population stochastic growth rates (λ_S) and plant densities are positively related to sinigrin concentration measured in seedling roots. This interaction is mediated by sinigrin's positive effect on seedling and summer survival, which are important drivers of λ_S.

5. Together, these illustrate how the evolution of a trait shaped by natural selection can influence the ecology of a species over a period of just years to decades, altering its trajectory of population growth and interactions with the species in the soil and plant communities it invades.

6. Our findings confirm the predictions that eco‐evolutionary feedbacks occur in natural populations. Furthermore, they improve our conceptual framework for projecting future population growth by linking the variation in plant demography to a critical competitive trait (sinigrin) whose selective advantages decrease as populations age.

Introduction

Evidence of reciprocal influences between ecological and evolutionary dynamics (i.e. eco‐evolutionary feedbacks) increasingly shapes our understanding of nature (Fussmann, Loreau & Abrams 2007; Schoener 2011). Eco‐evolutionary feedbacks occur when rapid evolutionary changes in a trait within a population alter population dynamics which then feedback to alter selection pressures on that same trait. Population sizes are not strictly determined by environmental conditions in these scenarios and can thus be affected by evolution of increased fitness in the population (Saccheri & Hanski 2006). Such feedbacks have been elegantly demonstrated in experimental and model systems (Yoshida et al. 2003; Turcotte, Reznick & Hare 2011, 2013; Travis et al. 2014), and a growing body of evidence suggests the existence of similar feedbacks in organisms under natural conditions (Hairston et al. 2005; Kinnison & Hairston 2007; Ezard, Cote & Pelletier 2009; Post & Palkovacs 2009; Shefferson & Salguero‐Gomez 2015). Given their likely role in shaping the dynamics of natural populations, eco‐evolutionary feedbacks could potentially transform how we think about population growth and regulation in species of economic or management concern.

Invasive species are ideal for investigating possible eco‐evolutionary feedbacks because the invasive populations may be far from their fitness optima in novel environments, are often in exponential phases of population growth and are frequently introduced multiple times from different source populations (Bossdorf et al. 2005), resulting in the substantial genetic variation upon which natural selection can act. Here, we marshal evidence from several linked studies along with the substantial new data to document an eco‐evolutionary feedback between population growth and genetic investment to an allelopathic secondary compound (sinigrin) in the aggressive invasive plant Alliaria petiolata (Brassicaceae, Bieb. Cavara & Grande, garlic mustard). This feedback is driven by interactions with soil microbial communities, which may act as important drivers of eco‐evolutionary feedbacks in plant systems more generally (terHorst and Zee, 2016; Van Nuland et al., 2016).

Alliaria petiolata is a widespread invader of North American forests that was introduced from multiple European populations (Durka et al. 2005). It produces several glucosinolate compounds, including sinigrin (Vaughn & Berhow 1999), which reduce populations of North American arbuscular mycorrhizal fungal (AMF) mutualists that most higher plants require for nutrient and water acquisition (Roberts & Anderson 2001; Stinson et al. 2006; Hale, Tonsor & Kalisz 2011). Sinigrin thus provides a competitive advantage to A. petiolata in interspecific competition by targeting the AMF symbionts of heterospecific plants, but this is expected to provide no benefit, or even be costly, in intraspecific competition as A. petiolata is non‐mycorrhizal (Lankau & Strauss 2007; Lankau 2008, 2012a,b).

Introduction and subsequent spread of A. petiolata has generated a continental gradient of population ages (Lankau et al. 2009). Populations across this gradient showed decreasing glucosinolate production and reduced allelopathic effects on native trees and AMF communities as populations aged (Lankau et al. 2009; Lankau 2011a). These changes could not be explained by founder effects or other stochastic evolutionary forces. Additionally, genetic variation in sinigrin was correlated with plant community composition, with heavy investment found in populations with a high frequency of heterospecific, but low frequency of conspecific, competitors (Lankau 2012a). Both soil microbial communities (including AMF) and native plant populations show signs of adapting to this invader (Lankau 2011b, 2012a).

Despite its significant impacts, A. petiolata stochastic growth rates (λ_S) vary significantly among populations from rapid growth (λ_S > 1) to decline (λ_S < 1) (Evans et al. 2012). Considering the temporal dynamics of A. petiolata's allelochemistry and its relationships with A. petiolata and native plant cover (Lankau et al. 2009; Lankau 2012a), we hypothesized that the variation in λ_S (Evans et al. 2012) was likely related to the variation in allelochemistry and thus creates a feedback between evolution (changes in allelochemistry) and ecology (population growth rates). We propose that the gradients in sinigrin result from varying selection on sinigrin that is linked to the population dynamics of the invader; specifically, that selection favours high allelopathic concentrations in newly founded populations, but reduced investment to these chemicals over time as intraspecific competition intensifies and interspecific competition weakens. We assessed this by combining the reanalysed data from ten field sites included in the previous studies of A. petiolata demography (Evans et al. 2012) with new data on quantitative genetic variation in allelochemical production to assess the relationship of population growth and vital rates with changes in secondary chemistry. Additionally, we experimentally test whether the variation in the competitive environment alters selection pressures on sinigrin under controlled conditions, in order to confirm the proposed mechanism driving the previously observed patterns in sinigrin concentrations across the invaded range.

We previously found that genetic variation in sinigrin among populations was negatively correlated with A. petiolata relative abundance and age since invasion of the population, indicating that evolution of this trait responds to ecological interactions among plant competitors (Lankau et al. 2009; Lankau 2012a). Here, we show that (i) under experimental conditions, natural selection favours increased sinigrin levels for low‐density populations facing primarily interspecific competition, but favours decreased levels for high‐density populations facing primarily intraspecific competition, (ii) genetic investment in sinigrin in a population correlates strongly with population growth rates across ten natural populations and (iii) the distribution of quantitative genetic variation in sinigrin relative to that of neutral markers across these populations suggests that this variation reflects natural selection. Together, these results demonstrate an eco‐evolutionary feedback loop in which high mean sinigrin levels allow a population to grow, increasing density to the point where selection favours reduced sinigrin levels, which then dampen population growth rates and potentially lead to stable or declining population sizes. These results highlight the need to consider eco‐evolutionary feedback loops when understanding, predicting and managing population dynamics in environmentally consequential species.

Materials and methods

Alliaria petiolata Demography

The stochastic population growth rates (λ_S) used in our analyses were recalculated from data reported in Evans et al. (2012). Readers should review that paper and its online appendices and citations for details on site selection, quantification of vital rates and matrix population model construction and interpretation. Briefly, we measured A. petiolata's vital rates in four replicate sets of quadrats within each of 12 natural field populations in southern Michigan and central to northern Illinois. All populations were sampled for three consecutive A. petiolata generations whose sampling regimes began in 2005, 2006 and 2007, respectively. We used generalized linear mixed models (GLMMs) to estimate the vital rates that were then used to parameterize a matrix population model with environmental stochasticity for each site.

There are several differences between the data and calculations in the original A. petiolata demography paper and those used in the present study. (i) For the present analysis, we excluded the Homer Lake site because seed collection for sinigrin quantification and demographic measurements were made in two different areas within the study site that had very different population densities. We also excluded the Illini Plantations site because Lankau et al. (2009) did not sample seeds there and thus could not measure sinigrin. (ii) We recalculated λ_S using just the second 2 of 3 years of demographic data from Evans et al. (2012) for two reasons. First, we wanted the demographic rates to reflect the population dynamics at the time when Lankau et al. (2009) collected seeds in the fall of 2007. Secondly, quadrat placement in demography studies can be biased towards areas with locally higher initial population densities, contributing to apparent declines in population growth rates over time (Buckley et al. 2010). We excluded the 2005 ‘cohort’ to minimize the impacts of any such bias, if present (see Appendix S1, Supportinginformation for an alternative analysis using all years of data). Using just the 2006 and 2007 vital rates, we re‐calculated stochastic lambda for each site using the popbio package in R (Stubben & Milligan 2007; R Core Team 2015). The structure of the annual population projection matrices is unchanged from Evans et al. (2012). We also calculated a composite vital rate, ‘early survival’, as the product of seedling and summer rosette survival probabilities during each site and year. Because seedling and summer survival were measured in different physical quadrats, we were not able to treat early survival as a binomial response variable (e.g. in a logistic regression context), so we restricted analyses of early survival to simple linear regressions and correlations using the mean value across years for each site. See Appendix S2.

Quantitative Genetics of Sinigrin

We estimated the genetic variation in sinigrin among populations using seeds derived from each of the 10 populations, after one generation of growth in a common greenhouse environment to reduce the variation due to maternal environment. Seeds from 10 maternal individuals were collected from each population in 2007. These seeds were cold, wet‐stratified for 90 days at 4 °C and then germinated and four individuals per maternal family were grown for 3 months in a greenhouse in Urbana, IL, and then moved to a growth chamber set at 4 °C for 6 months to simulate winter. The surviving rosettes were then brought back out to the greenhouse and allowed to bolt and flower. Flowering individuals were covered with a fine mesh to prevent pollen movement, and allowed to self‐fertilize. Alliaria petiolata is a largely selfing species in its introduced range (Durka et al. 2005), so this step was unlikely to cause the substantial inbreeding depression. We collected the seeds from all plants that successfully set seeds and stored them at 4 °C until the second stage of the experiment (c. 2 years). Greenhouse‐collected seeds were again cold, wet‐stratified for 90 days at 4 °C and then germinated at 20 °C. Due to mortality prior to flowering, failure of some flowering plants to set seed and failure of some seeds to germinate, final sample sizes of second‐generation plants were substantially reduced. We had no evidence that this mortality was biased across populations or with respect to sinigrin levels within populations. Therefore, while this loss reduces the precision of our estimates of population mean sinigrin concentrations, this should not introduce any bias that would alter our biological interpretations. In the end, we were able to grow an average of 7·3 grandmaternal families per population (i.e. on average 7·3 of the 10 field‐collected maternal families had descendants in the second‐generation experiment), with an average of 1·85 selfed maternal families per grandmaternal family, and an average of 2·39 replicate individuals per selfed maternal family, for a total of 322 individuals across the 10 populations.

Approximately 10 mg of fine root tissue was collected from each individual after 14 weeks of growth. Root material was placed immediately in 95% methanol to denature myrosinase enzyme, and stored at 4 °C until glucosinolates were extracted and quantified on an Agilent 1260 HPLC using previously described methods (see Lankau et al. 2009). We additionally sampled leaf material from each individual and stored them at −80 °C until their DNA was extracted with a commercial kit (Omega Bio‐tek, E‐Z 96 Plant DNA kit, Atlanta, GA, USA). Each sample was scored at 8 microsatellite loci using the methods from Durka, Bossdorf & Gautschi (2004). Microsatellites were scored manually by two observers in GeneMarker (Softgenetics, LLC State College, PA, USA). Sinigrin concentrations (μmol g⁻¹ fresh root tissue) were analysed using linear mixed models with the lme4 package in R (Bates et al. 2014). Population, grandmaternal family nested within population and selfed family nested within grandmaternal family were treated as random effects, with greenhouse block and linear and quadratic terms for root weight as fixed effects. Root weight refers to the mass of root tissue from which glucosinolates were extracted, and was included as a fixed covariate to account for a tendency towards lower extraction efficiencies as the amount of root tissue ground increased. Best linear unbiased predictors (BLUPs) for the mean sinigrin concentration of each population were extracted for comparison to demographic rates. Variance components for population and family terms were used to calculate Q _ST, as Variance(_population)/[Variance(_population) + Variance(_family)]. 95% confidence intervals for Q _ST were determined by parametric bootstrapping of the linear mixed model 5000 times. Variance components from each replicate were retained, corrected for any bias in the bootstrapped replicates and combined using the above formula to determine the replicate Q _ST values. Confidence intervals were taken as the 2·5% and 97·5% values of the resampled Q _ST values.

Microsatellite data were used to determine Nei's genetic distance between each population, as well as the overall degree of population differentiation using F _ST. Nei's genetic distance was calculated with the adegenet package and F _ST with the hierfstat (Goudet 2014) package in R. We used Mantel tests to determine whether the differences in either λ_S or mean sinigrin concentration among populations correlated with neutral genetic distance or geographic distance. We used partial Mantel tests to determine whether the relationship between sinigrin concentration and stochastic λ remained significant when controlling for either neutral genetic or geographic distance between the populations. Finally, we computed an overall F _ST value across the 10 populations and 8 loci, and calculated 95% confidence intervals by bootstrapping across loci using the boot (Canty & Ripley, 2015) package in R.

Experimental Test of Density‐Dependent Selection on Sinigrin

To directly test whether sinigrin concentrations would be differentially selected in populations facing competition from hetero‐ vs. conspecifics, we performed a greenhouse experiment using individuals from the same populations where demographic rates and sinigrin investment were measured (Fig. 1). This involved the 10 populations mentioned above, as well as the Homer Lake site and an additional Michigan population (Gasinski Farm) for which sinigrin, but not demographic, data were available. We grew one individual from each of the 12 populations in one of eight conditions – four competitive environments crossed with two soil environments. The four competitive conditions were (i) no competitors, (ii) three individuals of the native, mycorrhizal species Arisaema triphyllum, (iii) three A. petiolata individuals from a young population or (iv) three A. peitolata individuals from an old population. Each competition treatment was repeated in pots inoculated with live soil from a site with no history of A. petiolata (uninvaded soil community) or soil from directly underneath A. petiolata plants at a nearby site. Both sites were in central Illinois; the Vermillion River Observatory is within the introduced range of A. petiolata, but has been kept free of invasion via diligence of the site manager (S. Buck, pers. comm). This resulted in a total of 96 pots. Plants were grown in 650‐mL Deepots (Stuewe and Son, Inc. Tangent, OR, USA) with a 32‐cm² soil surface area. This resulted in a density of 0·03 plants cm⁻² for the no competition treatment and 0·125 plants cm⁻² for the competition treatments, well within the range observed at field sites (R. Lankau, pers. obs.). Plants were grown for 3 months, and the above‐ and below‐ground biomass of the target and neighbour plants in each pot were collected, dried and weighed.

Figure 1.

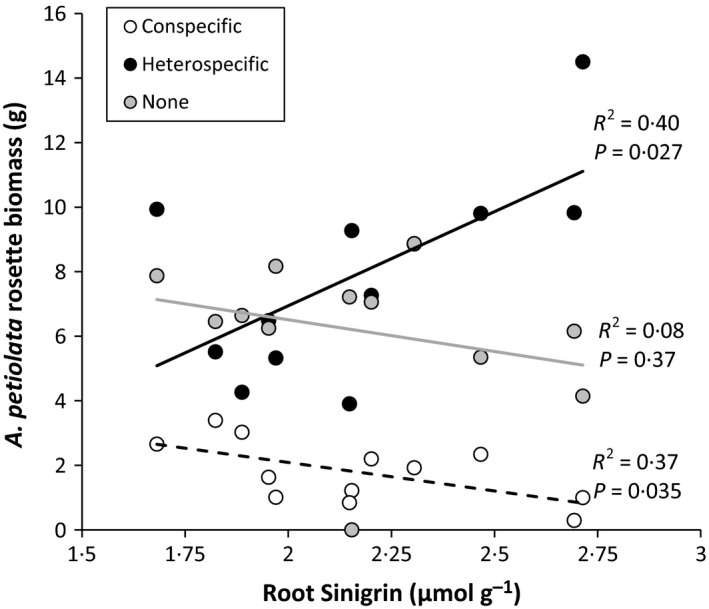
Competitive environment provides context for the relative costs and benefits of sinigrin production. Linear regressions of Alliaria petiolata rosette biomass on root sinigrin concentration in three experimental competition conditions. Solid symbols = heterospecific competitors (Arisaema triphyllum); open symbols: conspecific competitors; grey symbols: no competitors. For the heterospecific and no competition treatments, symbols are means of two replicates (one grown in invaded and one in uninvaded soil). For the conspecific treatment, symbols are the mean of four replicates (one individual per population grown with two different A. petiolata populations as neighbours in both invaded and uninvaded soils).

We used the population‐level estimate of root sinigrin concentrations taken from the quantitative genetics screen described above, as this measure controls for maternal effects and integrates across minor environmental variation in the greenhouse. Because there was very little genetic variation detected within populations, we were more confident that the population mean sinigrin concentration would be a useful predictor of genetic investment to sinigrin in our experimental plants.

To test whether the selection on root sinigrin concentrations differed between competitive conditions, we analysed total above‐ and below‐ground biomass of target A. petiolata rosettes using a linear mixed model. Competition treatment, soil treatment and sinigrin concentration and all two‐ and three‐way interactions were included as fixed effects, and population was modelled as a random effect. We used a parametric bootstrap to determine 95% confidence intervals for all model parameters. Initial analyses found no difference between A. petiolata competitors from young vs. old sites, so for simplicity we lumped these pots together into one ‘conspecific competitor’ treatment.

Statistical Analyses of Sinigrin–Demography Relationships

We conducted three sets of analyses to evaluate the relationship between A. petiolata's sinigrin production and demography. First, we used linear regressions to quantify the relationships between λ_S, seedling root sinigrin concentration and early survival (Fig. 2). Next, we used GLMMs with the lme4 package in R (Bates et al. 2014) to assess the relationships between individual, quadrat‐level, vital rates and sinigrin. We fit two models for each vital rate: one included sinigrin concentration as a covariate, and the other was a null, intercept‐only model. All models included random intercepts for quadrat and year effects to control for correlations between observations made within the same quadrat or year. Models were fitted using binomial errors for vital rates that measured survival or other binary outcomes (germination 1, germination 2 and dormant seed survival, seedling survival, summer rosette survival and winter rosette survival). Models of fecundity used Poisson errors. After fitting the sinigrin and null models for each vital rate, we ranked the two models using AICc and Akaike weights (w) to determine whether to retain the sinigrin covariate (Anderson 2008).

Figure 2.

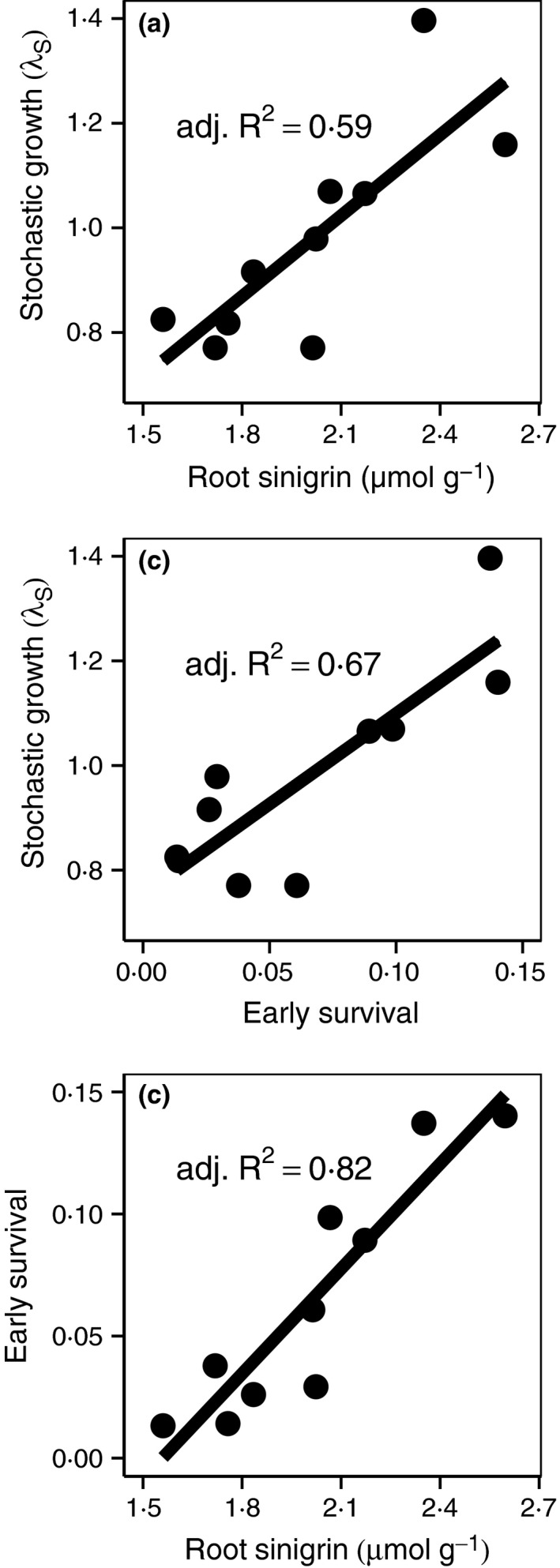
Sinigrin indirectly drives the population growth via effects on early survival. Linear regressions of (a) λ_S on sinigrin concentration of Alliaria petiolata seedling roots grown in a common environment, (b) λ_S on early survival, calculated as the mean of the product of seedling survival and summer rosette survival, and (c) early survival on seedling root sinigrin concentration. Growth rates were calculated from 2006–2007 and 2007–2008 data in Evans et al. (2012). Sinigrin concentrations represent the mean of multiple genetic families per population.

The combined effects of sinigrin concentration and plant density on seedling survival were analysed using GLMMs and model ranking similar to the previous set of analyses. We focused on seedlings because conspecific densities, and hence intraspecific competition, were greatest at this stage, and the sinigrin–survival relationship in the previous analyses was strongest for seedlings. We fit five binomial GLMMs with random quadrat and year effects and five different fixed effects structures embodying alternative competing hypotheses about the roles of sinigrin (S) and population density (D). All models included an intercept (I). These were as follows:

• mSRa) I + S + D + S*D
• mSRb) I + S + D
• mSRc) I + D
• mSRd) I + S
• mSRe) I (intercept only)

We used AICc to rank the five models (Table S1). Model mSRa had a weight of 1, indicating that there is a 100% probability that it is the best model of the data within the set being ranked. We plotted the predicted marginal mean survival rates (i.e. with no random effects) from model mSRa against population density at each site's measured sinigrin concentration (Fig. 3).

Figure 3.

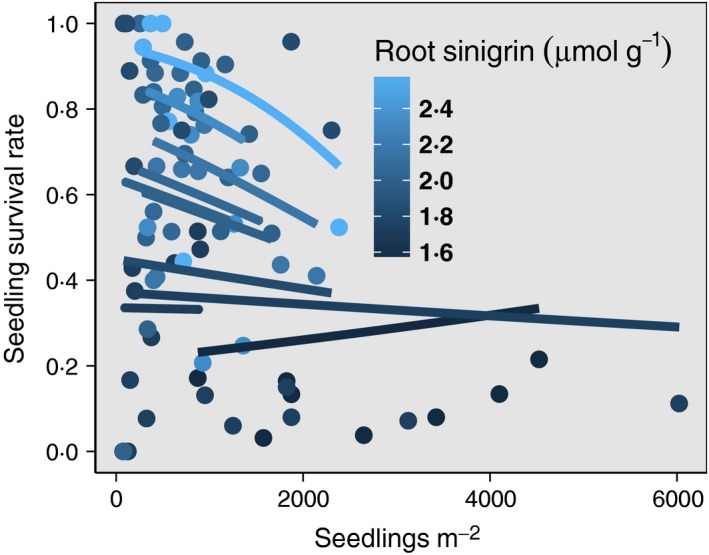
Density dependence of seedling survival decreases with sinigrin production. Interaction of density‐dependent seedling survival with sinigrin concentration of Alliaria petiolata seedling roots grown in a common environment. Mean survival is highest, and negative density dependence is strongest, in populations with the highest sinigrin concentrations. Points show observed quadrat‐level seedling survival; lines show marginal predicted seedling survival from fitted GLMM of survival vs. sinigrin, seedling density and their interaction (Tables S1 and S2; see Materials and methods).

We calculated Pearson's correlations between mean A. petiolata vital rates across years for each site and root sinigrin concentrations (Fig. 4). Figure 5 was created similarly using mean population densities which we then correlated with sinigrin concentration. Population densities were calculated as mean plants per quadrat for each site year which we then averaged across years for each site, yielding one estimate per site. Density estimates were scaled to plants m⁻² from the various quadrat sizes used in sampling. See Evans et al. (2012) for details.

Figure 4.

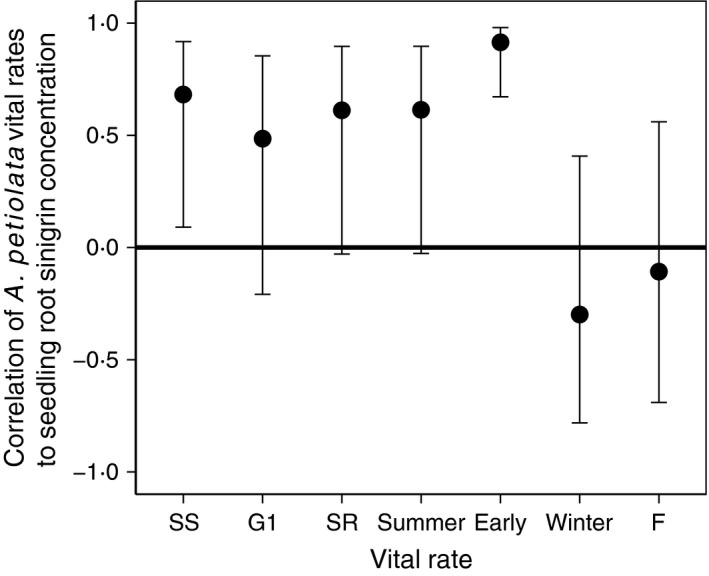
Sinigrin is positively correlated with metrics of survival early in the life cycle. Correlations of root sinigrin concentration with mean Alliaria petiolata vital rates during six successive life‐history stages. Each point in the figure represents a Pearson correlation coefficient relating variation in sinigrin concentration among populations to the variation in the vital rate. Per capita vital rates shown are SS: annual seed survival probability; G1: germination probability of seeds after one winter; SR: survival probability of seedlings to the rosette stage; Summer: survival probability of first‐year rosettes from June through October; Early: product of SR and summer survival; Winter: overwintering survival probability of rosettes from October through June the following year; F: fecundity (mean seeds produced per adult plant). The A. petiolata life cycle progresses from seed survival to reproduction in the order plotted here from left to right. N = 10 for all correlations. Error bars indicate 95% confidence intervals.

Figure 5.

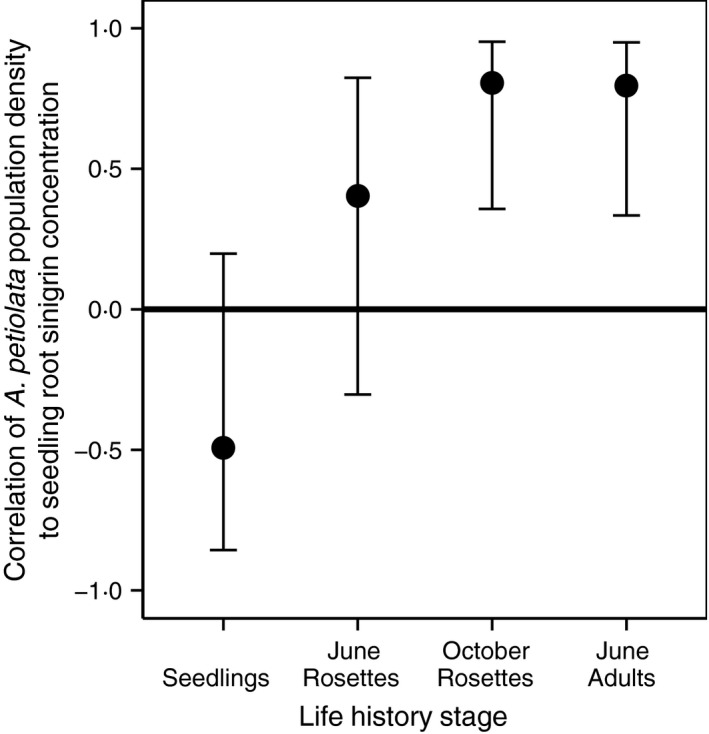
Sinigrin is positively correlated with population densities later in the life cycle. Correlations of root sinigrin concentration with mean Alliaria petiolata population density (plants m⁻²) during four successive life‐history stages. Each point represents a Pearson correlation coefficient relating the variation in sinigrin concentration among populations to the variation in conspecific plant density. N = 10 for all correlations. Error bars indicate 95% confidence intervals.

Results and discussion

Density‐Dependent Selection on Root Sinigrin Concentration

As predicted, A. petiolata biomass increased with increasing investment to root sinigrin when plants competed with interspecific competitors (Fig. 1). However, this relationship changed when A. petiolata individuals from the same populations were grown with conspecific competitors, resulting in a negative correlation between root sinigrin investment and rosette biomass (Fig. 1). In the absence of competitors, the biomass–sinigrin correlation was intermediate and not significantly different from zero (Fig. 1). A linear mixed model confirmed that the slope of the root sinigrin–rosette biomass relationship was significantly more positive in the heterospecific vs. conspecific competitor treatment (competition treatment*sinigrin interaction, estimate = 92·97, lower 95% CI = 25·31, upper 95% CI = 160·11, Table S2). These results, along with the findings of previous studies, indicate that selection on root sinigrin levels in natural populations is likely to vary based on the density of the A. petiolata population and the frequency of A. petiolata compared to other competing species in the community. This suggests the possibility of an eco‐evolutionary feedback, where at low densities/frequencies genotypes with high investment to sinigrin will have high fitness, but as densities increase, genotypes with lower investment to sinigrin will have a relative advantage.

Evolutionary Feedbacks on Population Growth Rates

Stochastic growth rates were positively related to the sinigrin concentration of A. petiolata seedling roots measured under common conditions (Fig. 2a; adj. R ² = 0·59, F _1,8 = 13·91, P < 0·01) and to mean survival rates of seedlings through the late summer (Fig. 2b; adj. R ² = 0·67, F _1,8 = 19·19, P < 0·01). These early survival rates most strongly and positively related to sinigrin concentrations (Fig. 2c; adj. R ² = 0·82, F _1,8 = 40·89, P < 0·001). Relationships between sinigrin and mean survival rates of dormant seeds, seedlings and summer rosettes were also positive (Figs 4 and S2). Germination, winter survival and fecundity were not directly related to sinigrin (see supplementary methods in Appendix S1). It is likely that sinigrin production is phenotypically plastic, and thus, the absolute levels in the field setting are likely different than those measured in our common garden. However, the tight correlation between common garden measurements and field demographic data suggests that phenotypic plasticity, while potentially important, is not so strong as to overwhelm the effect of constitutive differences in sinigrin investment among populations. This may be because phenotypic plasticity is relatively weak, or equally plausibly, plasticity is strong but does not vary much among populations, so that the relative ranking of populations in sinigrin levels is fairly consistent across environments.

Isolating selection as the culprit affecting population dynamics requires separating its effects from those of population density and other environmental factors that influence the population growth (Saccheri & Hanski 2006). Given the selection pressures acting on seedling root sinigrin levels, we predicted that (i) sinigrin should positively covary with seedling survival at low conspecific densities, as the trait should increase interspecific competitive ability, and (ii) high‐sinigrin populations should be more sensitive to negative density dependence, since these genotypes should be poorer intraspecific competitors. Indeed, seedling survival in A. petiolata was negatively density‐dependent in populations with high sinigrin production, but this effect diminished as sinigrin levels decreased (Fig. 3, Tables S1 and S3). Note that both the slopes and the intercepts of the survival–density relationship decreased with declining sinigrin. High‐sinigrin populations reach seedling survival rates up to 100% at low densities, but survival declines rapidly as conspecific density increases. In contrast, low‐sinigrin populations have uniformly low seedling survival across densities. These results have important implications for population growth and regulation; high‐sinigrin populations should grow rapidly when first colonizing a new site or patch, but their high negative density dependence will strongly regulate the population as population densities climb.

Consistent with our predictions, population genetic investment to sinigrin correlated negatively with A. petiolata population density (plants m⁻²) in early life stages (i.e. seedlings), but became successively more positively correlated in later life stages (Fig. 4). Correlations of sinigrin with mean vital rates followed an opposite pattern with positive correlations in early life‐history stages and non‐significant negative correlations later (Figs 4, S1 and S2). Intense intraspecific competition among seedlings (self‐thinning) thus appears to select for low sinigrin genotypes with a low probability of surviving to adulthood. While a population consisting of high sinigrin genotypes ultimately grows faster and at higher adult densities (Figs 2, 5 and S3), persistent selection against sinigrin at the seedling stage may act to reduce population mean sinigrin levels over time, producing the pattern observed in Lankau et al. (2009), and potentially lead to the stabilization or local decline of A. petiolata populations.

Collectively, our results suggest the following causal pathway: sinigrin enables the establishment of new populations facing high inter‐, but low intraspecific, competition by enhancing survival of young plants during the first growing season (Figs 1 and 2c), likely by reducing competition for water resources from mycorrhizal‐dependent competitors during spring and through the summer drought (Hale, Tonsor & Kalisz 2011). This yields higher plant densities by the end of the first summer which persist through seed production (Fig. 5) and drive higher λ_S (Fig. 2a), in spite of lower initial mean seedling densities in these populations (Fig. 5). Sinigrin's positive effects on survival and population density are thus restricted to the first growing season (Fig. 4). Variations in population size and mortality from winter through the following spring and summer are driven by other factors.

Genetic Basis of Sinigrin Variation

Genetic variation in sinigrin was partitioned primarily among, rather than within, populations, with c. 9% of total phenotypic variation attributable to population (Table S4) and 0% attributable to grandmaternal or selfed family. The resulting extreme estimate of Q _ST (1, 0·175–1, 95% CI) is not unexpected in a largely selfing species which likely establishes new populations from a small number of colonizing genotypes. Populations were also highly diverged in neutral markers, with an overall F _ST of 0·688 (0·556–0·772, 95% CI). Nonetheless, each population contained multiple multilocus genotypes (MLGT) (ranging from 0·63 to 2·83 multilocus genotype in offspring per field maternal family across populations), so the low within‐population quantitative genetic variation is not solely due to sampling a single selfed lineage. This finding is at odds with our previous work suggesting a rapid evolution of sinigrin concentrations, which should require high levels of intrapopulation genetic variation on which to act (Lankau et al. 2009). However, the levels of intrapopulation genetic variation are likely to vary across the introduced range. Previous work detected a positive relationship between population age and neutral genetic diversity, suggesting that over time populations accumulate genetic variation, likely via gene flow from other established populations. This suggests a scenario similar to one proposed by Kinnison & Hairston (2007) in which populations are founded by a few individuals and there is a strong selection against low sinigrin genotypes as founders. This is consistent with our finding that young populations have consistently high mean sinigrin levels and low genetic diversity (Lankau et al. 2009). As population density increases, selection may favour lower sinigrin levels due to the intense intraspecific competition among seedlings (Figs 1 and 3). However, the population can only respond to this selection if genetic variation exists for the sinigrin trait. The same gene flow that brings additional neutral genetic variation to these older populations may also bring quantitative variation in the sinigrin trait, allowing the evolution of lower mean sinigrin levels. Depending on the strength of selection and speed of the evolutionary response, this may manifest as a positive relationships between population age and quantitative genetic variation in sinigrin, or the new alleles may be swept through the population fast enough to obscure this pattern. Unfortunately, our current population sampling is not well designed to test for patterns across the invasion age gradient or provide resolved estimates of genetic variation within individual populations.

Importantly, the variation in genetic investment to sinigrin among populations was not correlated with neutral genetic distance (Mantel r = 0·055, P = 0·370). Thus, the differences in sinigrin concentration among populations cannot be attributed solely to random genetic forces or independent invasion events. Neutral genetic distance was also uncorrelated with the variation in population growth rates (Mantel r = 0·155, P = 0·216). Additionally, neither variance in sinigrin concentration, neutral genetic distance, nor population growth rates correlated with geographic distance (Mantel r = 0·237, P = 0·105, r = −0·190, P = 0·867, r = −0·006, P = 0·417, respectively). Finally, differences in mean sinigrin concentrations among populations did correlate with the differences in population growth rates (Mantel r = 0·514, P = 0·023), and this relationship remained when controlling for neutral genetic (partial Mantel r = 0·512, P = 0·018) or geographic distance (partial Mantel r = 0·530, P = 0·008). Together, these results suggest that the relationship between genetic investment to sinigrin and population dynamics is not the result of a shared correlation between geographic location and broader genetic differences among the populations as a result of historical invasion patterns.

Consequences of the Eco‐Evolutionary Feedback on A. petiolata Invasions

These and previous results from this system suggest a process in which spatial spread, local population dynamics and evolutionary change in a key trait feed back on one another to determine the temporal dynamics of the A. petiolata invasion. Specifically, our data suggest that newly founded populations at the spreading invasion front will typically have low neutral genetic diversity (Lankau et al. 2009), high mean sinigrin levels (Lankau et al. 2009), low initial densities and consequently high population growth rates driven by high survival of seedling and rosette plants (Figs 1 and 2). Over time, this high population growth will lead to an increase in seedling density and suppression of AMF and interspecific plant competitors (Lankau et al. 2014), causing selection for reduced sinigrin concentrations (Fig. 1), to which populations may respond following the introduction of genetic variation via gene flow. This evolutionary reduction in sinigrin concentration comes at the expense of per capita juvenile survival to adulthood and adult densities and consequently reduced or even negative population growth rates (Fig. 2). Ultimately, this may lead to a range‐wide pattern of continual spatial spread but stabilization, cyclical dynamics or even local extinction of established populations. The long‐term population dynamics of A. petiolata are uncertain. One possibility is that once A. petiolata densities decline enough, selection will favour increased sinigrin levels allowing the population to rebound. However, the linear decline in glucosinolate production across a c. 60‐year chronosequence provided no evidence for increasing sinigrin levels at the oldest sites (Lankau et al. 2009). While it is possible that such cyclical dynamics may occur over longer time periods, there may also be mechanisms, including low genetic variation in declining populations, to prevent this response. We urge caution against interpreting that A. petiolata populations should not be managed aggressively. Even if A. petiolata is ultimately self‐regulating, this species’ allelochemistry can cause a substantial harm to native communities if left unmanaged for decades, inducing detrimental legacies that can persist long after the invader has been removed (Lankau et al. 2014).

Many pressing challenges in applied ecology ultimately require that managers understand and accurately predict the dynamics of populations. Eco‐evolutionary feedbacks introduce additional complexity to these predictions, as these processes cause the qualities of individuals to change in addition to their numbers, and these changes in trait values directly feed back to alter the numerical dynamics of the population (Waples & Hendry 2008; Carroll 2011; Hendry et al. 2011; Carroll et al. 2014; Vander Wal et al. 2014; Cavers 2015). However, eco‐evolutionary feedbacks may also allow for underappreciated stability of populations in the face of external pressures, potentially offering managers novel opportunities to affect population dynamics via evolutionarily guided interventions.

Supporting information

Lay Summary

Fig. S1. Mean (a) seed, (b) seedling, and (c) summer rosette survival rates vs. sinigrin concentration of Alliaria petiolata seedling roots grown in a common environment.

Fig. S2. Expanded view of data used to generate Fig. 4.

Fig. S3. Expanded view of data used to generate Fig. 5.

Table S1. Information‐based model ranking of seedling survival GLMMs with binomial errors, random quadrat and year effects, and different fixed effects structures embodying alternative competing hypotheses about roles of sinigrin (S) and population density (D).

Table S2. Output of linear mixed model relating Alliaria petiolata rosette biomass to root sinigrin concentrations in a greenhouse experiment manipulating competition and soil invasion history.

Table S3. Parameter estimates from binomial GLMM mSRa (Table S2) of seedling survival as a function of seedling density, seedling root sinigrin concentration, and their interaction.

Table S4. Output of a linear mixed effects model of sinigrin concentration in root tissue of greenhouse grown Alliaria petiolata seedlings.

Appendix S1. Presentation of results with 2005 data included. Includes notes on timing of sample collection, data selection, and updated figures including 2005 data.

Appendix S2. Code and data supplement.