The spectroscopic foundation of radiative forcing of climate by carbon dioxide

Abstract

The radiative forcing (RF) of carbon dioxide (CO₂) is the leading contribution to climate change from anthropogenic activities. Calculating CO₂ RF requires detailed knowledge of spectral line parameters for thousands of infrared absorption lines. A reliable spectroscopic characterization of CO₂ forcing is critical to scientific and policy assessments of present climate and climate change. Our results show that CO₂ RF in a variety of atmospheres is remarkably insensitive to known uncertainties in the three main CO₂ spectroscopic parameters: the line shapes, line strengths, and half widths. We specifically examine uncertainty in RF due to line mixing as this process is critical in determining line shapes in the far wings of CO₂ absorption lines. RF computed with a Voigt line shape is also examined. Overall, the spectroscopic uncertainty in present‐day CO₂ RF is less than 1%, indicating a robust foundation in our understanding of how rising CO₂ warms the climate system.

Key Points

• Line mixing and line shape uncertainties contribute < 0.7% error to CO₂ radiative forcing

• Line strength and half‐width uncertainties contribute < 0.3% error to CO₂ radiative forcing

• Overall spectroscopic uncertainty in CO₂ radiative forcing is < 1%

1. Introduction

Accurate computation of radiative forcing (RF) due to increasing abundances of carbon dioxide (CO₂) forms the foundation of climate change modeling. RF is the change in net radiative flux at the tropopause for differing abundances of CO₂ and is often computed relative to preindustrial abundances. Uncertainties in RF lead to uncertainties in determination of climate sensitivity and in prediction of future climate. The uncertainty in computed RF depends on the evaluation of atmospheric transmittance in the spectral regions where CO₂ absorbs infrared radiation.

We assess the uncertainty in RF with a series of radiative transfer calculations in which key parameters involved in the computation of atmospheric transmittance are perturbed within their known uncertainties. Of particular interest is the spectral line shape function, which for CO₂ is well known to deviate from the classical Voigt function due to line mixing. Happer [2014] suggests that climate models greatly overestimate RF by CO₂ by the inappropriate use of the Voigt function, which does not account for the line mixing and the subsequent alteration of the line shapes, particularly in the far wings. We will show this suggestion to be false.

Line mixing, which is sometimes referred to as line coupling, occurs in spectral regions where numerous lines are closely spaced together and cannot be considered isolated during collisions [Hartmann et al., 2008]. This is the case for the strong infrared absorption bands of CO₂. Collisions “mix” closely spaced energy levels, resulting in additional absorption compared to isolated line Lorentz theory near the center of these lines and sub‐Lorentzian behavior in the line wings. The physics of line mixing is complex; detailed treatments of it have been developed [Niro et al., 2005] for implementation in state‐of‐the‐science radiative transfer models such as the Line‐by‐Line Radiative Transfer Model (LBLRTM [Clough et al., 2005]).

Our computational results show that CO₂ RF is remarkably insensitive to uncertainties in the line shape function, line mixing, the line strengths, and the air‐broadened half widths. The nature of these uncertainties is such that they are positively correlated and effectively cancel out in the computation of RF, which is a double difference of radiative fluxes. An error analysis confirms this result. However, under certain conditions, use of a truncated Voigt line shape yields results that agree well with the calculations that explicitly include line mixing in detail.

We review the computation of RF used in this study. We then analyze the uncertainty in RF for several standard atmospheres, detailing the correlated nature of the uncertainty in the calculation. This paper extends the work of Pinnock and Shine [1998] and Kratz [2008] by examining the uncertainty in RF in the line shape due to line mixing and in quantifying the correlated nature of the uncertainties.

2. Methodology

RF is defined as the change in net radiative flux at the tropopause due to an increase in CO₂. The net flux F _net is defined as downwelling minus upwelling, so that positive values imply an increase of energy in the climate system below the tropopause:

$$F_{\mathrm{n}\mathrm{e}\mathrm{t}}\left(z\right)=F_{-}\left(z\right)-F_{+}\left(z\right)$$ (1)

The upwelling and downwelling fluxes F₊ and F₋ are obtained by angular and spectral integration of the upwelling and downwelling monochromatic radiances I _v(μ) and I _V(−μ) over a hemisphere

$$F_{\pm }\left(z\right)=2\pi {\displaystyle {\int }_0^{\infty }{\displaystyle {\int }_0^1{I}_{\nu }\left(\pm \mu ,z\right)\mu \mathrm{d}\mu \mathrm{d}\nu }}$$ (2)

where ν is wave number and μ is the zenith direction cosine.

The radiance at ν is obtained by solving the fundamental equations of radiative transfer:

$$I_{\nu }\left(\mu ,z\right)=B_{\nu }\left({\mathrm{\Theta }}_s\right)T_{\nu }\left(z,0\right)+{\displaystyle {\int }_0^z{B}_{\nu }}\left(\mathrm{\Theta }\left(z^{\prime }\right)\right)\frac{\partial T_{\nu }\left(z,z^{\prime }\right)}{\partial z^{\prime }}\mathrm{d}{z}^{\prime }$$ (3)

$$I_{\nu }\left(-\mu ,z\right)=-{\displaystyle {\int }_z^{\infty }{B}_{\nu }}\left(\mathrm{\Theta }\left(z^{\prime }\right)\right)\frac{\partial T_{\nu }\left(z,z^{\prime }\right)}{\partial z^{\prime }}\mathrm{d}{z}^{\prime }$$ (4)

In equations (3) and (4) Θ_s and Θ are the surface and atmospheric temperatures, Bν is the Planck blackbody function, and T _ν(z, z′) is the transmittance of the atmosphere between altitudes z and z′. The transmittance function is given by

$$T_{\nu }\left(z,z^{\prime }\right)=\exp \left(-{\displaystyle {\sum }_i{S}_i}\left(\mathrm{\Theta }\right)g_i\left(\nu -{\nu }_0\right)\frac{u\left(z,z^{\prime }\right)}{\mu }\right)$$ (5)

where S _i(Θ) is the ith line strength (cm⁻¹/(molecule cm⁻²) at temperature Θ, g _i(ν − ν ₀) is the normalized line shape (cm), and u(z, z′) is the vertical optical mass (molecule/cm²) between altitudes z and z′. The line shape function is generally dependent on pressure and temperature. The RF is computed for doubled CO₂ relative to preindustrial times:

$$RF=\left(F_{-}^{560}-F_{+}^{560}\right)-\left(F_{-}^{280}-F_{+}^{280}\right)$$ (6)

The superscripts refer to the volume mixing ratios in parts per million (ppm) of CO₂, 560 ppm for doubled CO₂ and 280 ppm for preindustrial levels. Furthermore, we compute the instantaneous forcing in which atmosphere and surface temperatures are held constant. This allows us to assess the uncertainty in RF due to spectroscopy by varying only the parameters in the transmittance function.

Equations (3) and (4) are evaluated with the Line‐By‐Line Radiative Transfer Model (LBLRTM) code [Clough et al., 2005] developed and publicly available (http://rtweb.aer.com) from Atmospheric and Environmental Research (AER). Equation (2) is evaluated with three‐point Gaussian integration. We use LBLRTM version 12.2 and version 3.2 of the spectral line database also provided by AER, which is identical to the version analyzed by Alvarado et al. [2013] and is described in more detail in the supporting information. This database includes coefficients needed to implement first‐order line mixing [Rosenkranz, 1975], which is an approximation to full line mixing at atmospheric pressures [Niro et al., 2005; Hartmann et al., 2008], and accurately computes the sub‐Lorentzian behavior in the wings of the CO₂ lines. The first‐order approximation to line mixing, which is used for CO₂ lines in LBLRTM instead of the regular Voigt profile, is based on an expansion in terms of pressure of the full line mixing equation [Hartmann et al., 2008] and assumes that the first two terms of the expansion (the Voigt line shape plus an asymmetric correction term) accurately describe the effect of line mixing on the line shape. The uncertainty in the line shape may be determined by scaling all the first‐order line mixing coefficients (i.e., the coefficients of the asymmetric term) and half widths and comparing the results with calculations run with no adjustments. Finally, in LBLRTM, first‐order line mixing is applied both within 25 cm⁻¹ of line center for CO₂ lines and is used to generate the MT_CKD CO₂ continuum [Clough et al., 2005], so line mixing is accounted for throughout the line shape for CO₂ lines. When the line mixing coefficients were perturbed in this study, we also perturbed the MT_CKD CO₂ continuum appropriately, which involved perturbing it by the same factor as the widths and line mixing coefficients.

RF calculations are carried out for clear sky using five different standard atmospheres [McClatchey et al., 1972] that span a broad range of thermodynamic conditions on Earth: midlatitude summer (MLS), midlatitude winter (MLW), subarctic summer (SAS), subarctic winter (SAW), and tropical (TRO). The tropopause altitudes for these five atmospheres are 13 km, 10 km, 10 km, 9 km, and 15 km, respectively. Plots and tabulations of these are in the supporting information. The RF calculations also include absorption by water vapor, ozone, carbon monoxide, methane, and nitrous oxide, the latter three with constant mixing ratios of 0.15, 1.82, and 0.325 ppm, respectively. The abundances of these five gases are not changed in the computation of CO₂ RF nor are their spectroscopic uncertainties considered.

Figure 1 shows the instantaneous spectral RF (W/m²/cm⁻¹) computed with LBLRTM for doubled CO₂ since preindustrial times, i.e., 280 ppm to 560 ppm, for these five atmospheres. The integrated RF (480 to 2480 cm⁻¹; near‐IR CO₂ bands are not considered here) ranges from 3.62 W/m² during subarctic winter to 5.53 W/m² in the tropics. The carets at the top of each figure indicate the wave number at which the 25th, 50th, 75th, and 95th percentiles of the total RF occur, integrating from 480 cm⁻¹. The fifth caret in each figure (e.g., 98.17 for the MLS) indicates the percent of total forcing at 1100 cm⁻¹. In all cases only 2% of RF by CO₂ occurs at wave numbers larger than 1100 cm⁻¹.

Figure 1.

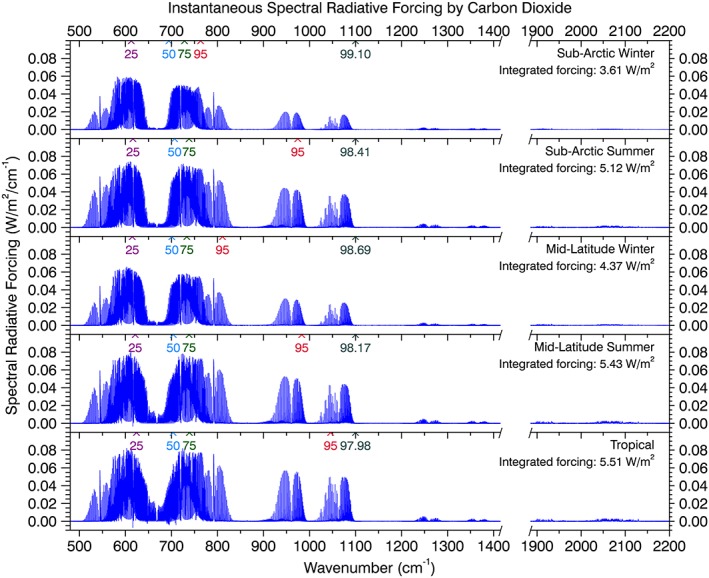
Spectra of instantaneous RF for doubled CO₂ (280 ppm to 560 ppm) for five different standard atmospheres. Percentiles of forcing integrating from 480 cm⁻¹ are indicated as a function of wave number at the top of each panel. The integrated percentile to 1100 cm⁻¹ is also indicated.

3. Uncertainty Analysis

3.1. Line Shape Function

The collision broadened half widths of CO₂ are ~ 0.07 cm⁻¹ at one atmosphere and become comparable with Doppler half widths at about 30 km altitude (10 hPa) in Earth's atmosphere. Classically, a Voigt profile is used to express the line shape for combined Doppler and collision (Lorentz) broadening. However, it has been known for 50 years that the line wings of CO₂ infrared bands are sub‐Lorentzian. Drayson's pioneering paper [1966] on line‐by‐line radiative transfer calculation noted the need to account for sub‐Lorentzian line wings in high resolution calculations of CO₂ transmittance, based on laboratory measurements of Winters et al. [1964]. Kunde and Maguire [1974] used an exponential modification of the Lorentz line shape to account for sub‐Lorentzian wings in CO₂ between 500 and 800 cm⁻¹ when modeling radiative transfer in planetary atmospheres. With respect to climate modeling, Fels and Schwarzkopf [1981] also noted the existence of sub‐Lorentzian wings and restricted the distance from line center for which they used a Voigt line shape. The advent of high spectral resolution space‐based infrared spectrometers in the late 1980's through today has necessitated detailed models of line mixing and line shapes in CO₂ infrared bands in order to accurately retrieve atmospheric temperature and composition [e.g., Strow and Reuter, 1988; Edwards and Strow, 1991; Spankuch, 1989; Funke et al., 1998; Strow et al., 2003; Alvarado et al., 2013]. The approach used in LBLRTM is based on Lamouroux et al. [2010], which, in turn, is based on the Niro et al. [2005] approach to P, Q, and R branch line mixing for CO₂. The approach developed in Niro et al. [2005] represents the current state of the science with respect to line mixing and spectral line shapes for infrared bands of CO₂.

In order to assess line shape uncertainty, we perturbed both the widths and first‐order line mixing parameters for CO₂. In general, the half widths for CO₂ are more precisely known than the line mixing coefficients. However, under the rigid rotor approximation used to calculate the line mixing coefficients, the line mixing coefficients and the half widths have to obey specific sum rules [Hartmann et al., 2008]. Thus, we have perturbed all the line widths and first‐order line mixing coefficients by the same percentage (20%), which is a reasonable estimate for the uncertainty in the line mixing coefficients but is a high estimate of the uncertainty in the half widths. Perturbing these parameters in LBLRTM perturbs the CO₂ absorption in the far wings by a similar percentage.

Figure 2 shows the results of these calculations for a 20% increase in the line mixing coefficients. Specifically, we show the difference between the unperturbed “baseline” spectral RF (Figure 1) and the spectral RF computed by perturbing the line widths and mixing parameters. Spectral differences for the MLS and SAW atmospheres are shown, and the integrated difference in RF is given in the upper right‐hand corner of each plot. There is significant but compensating spectral structure such that the integrated differences (perturbed minus baseline) are 0.015 W/m² for the MLS atmosphere and 0.022 W/m² for the SAW atmosphere, which is 0.3% and 0.6% of the baseline forcing. Calculations for the remaining three standard atmospheres yield similar spectral and integrated differences and are shown in the supporting information.

Figure 2.

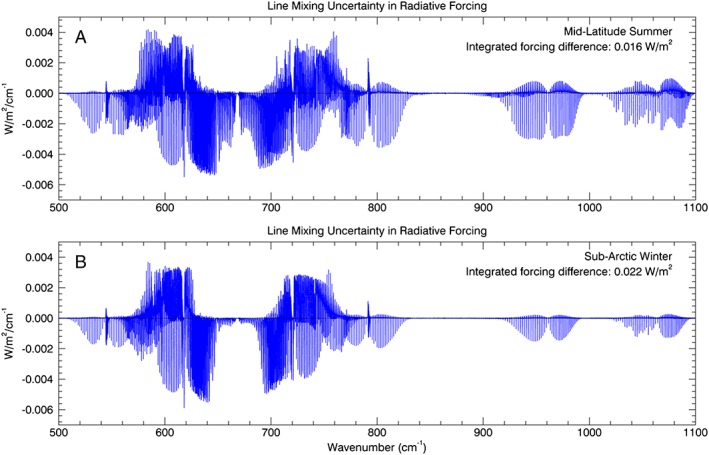
Spectra of RF differences (LBLRTM baseline minus perturbed) due to a 20% perturbation in the CO₂ line mixing coefficients for the MLS and SAW atmospheres. While substantial spectral structure is evident, the integrated forcing difference is less than 0.022 W/m² in both cases. Spectra of RF differences for the other three atmospheres are in Figure S2 in the supporting information.

The spectral differences in Figure 2 illustrate the large degree of cancelation in the terms comprising baseline and perturbed RF. Table 1 (columns 2–4) lists the baseline and perturbed RF values for each of the five atmospheres, and their difference, the latter of which is taken as the uncertainty in RF due to uncertainty in line mixing. Although the RF differences are small, the individual integrated downward and upward fluxes can be different by as much as 0.7 W/m². We have tabulated (see Table S1 in the supporting information) all four fluxes in the calculation of RF for the baseline and perturbed cases for all five atmospheres. With 20% larger line mixing coefficients, the perturbed upwelling fluxes are all smaller than the baseline fluxes, while the perturbed downwelling fluxes are all larger than the baseline values. The subsequent RF calculation, which is a double difference of the fluxes, results in a large degree of cancelation of the uncertainty, due to the correlated nature of the errors. This effect is further explored in the next section. From this analysis we conclude that a 20% uncertainty in the line mixing results in an insignificant error in CO₂ RF.

Table 1.

RF Values From LBLRTM (Baseline), With 20% Perturbation in Line Mixing, and Their Difference (Columns 2–4)^a

Atmosphere	RF LBLRTM Baseline (W/m2)	RF LBLRTM 20% Perturbation (W/m2)	Uncertainty Line Shape/Line Mixing (W/m2)	Uncertainty Line Strength (W/m2)	Uncertainty Half Width (W/m2)	RSS (W/m2)	RSS as Percent of Baseline LBLRTM Forcing
MLS	5.428	5.444	0.016	0.015	0.005	0.022	0.41
MLW	4.372	4.388	0.016	0.010	0.004	0.019	0.44
SAS	5.118	5.141	0.023	0.015	0.007	0.028	0.55
SAW	3.606	3.628	0.022	0.009	0.006	0.025	0.68
TRO	5.509	5.519	0.010	0.014	0.002	0.017	0.31

^aUncertainty in RF due to line strength and half widths (columns 5 and 6). Column 7 has the root‐sum‐square (RSS) of individual uncertainties in the three previous columns and is the spectroscopic uncertainty in CO₂ RF. Column 8 lists the RSS as a percentage of baseline forcing.

3.2. Line Strengths and Air‐Broadened (Lorentz) Half Widths

This section focuses on the RF uncertainty associated with the absorption line strengths (S _i(Θ)) and the collision broadened half width. Other spectral line parameters (line position, self‐broadened half width, temperature dependence of the half widths, and lower state energies) are not considered to be significant sources of uncertainty for the RF calculation. Radiances and fluxes are computed with the LBLRTM model.

The AER database used here provides uncertainty estimates for the line parameters. Our sensitivity studies showed that RF depends only on lines with strengths greater than 1.0 × 10⁻²⁵ cm⁻¹/(molecule cm⁻²), of which there are 16,655 lines on the AER database. Of these, the strengths of 14,311 lines have specified accuracies between 2% and 10%. To assess the uncertainty in RF due to uncertainty in line strength, we first compute RF by changing all 16,655 line strengths from −20% to +20% in steps of 1% and compute RF for each of the 41 cases. To compute the worst case, the line strengths must be perturbed by the same amount and with the same sign in the computation of the upwelling and downwelling fluxes for both preindustrial and doubled CO₂ values.

Figure 3 shows the results of this calculation for the MLS atmosphere. F _up ⁵⁶⁰ and F _up ²⁸⁰ are the upwelling fluxes at the tropopause for CO₂ mixing ratios of 560 and 280 ppm, respectively. Similarly, F _down ⁵⁶⁰ and F _down ²⁸⁰ are downwelling fluxes at the tropopause. Changing the CO₂ line strengths by ±20% changes the upwelling fluxes by as much as 2 W/m² and the downwelling fluxes by nearly 1 W/m². Based on equation (6), the net RF is essentially constant because F _i values are almost perfectly correlated and the double difference of correlated errors effectively cancels any line strength changes.

Figure 3.

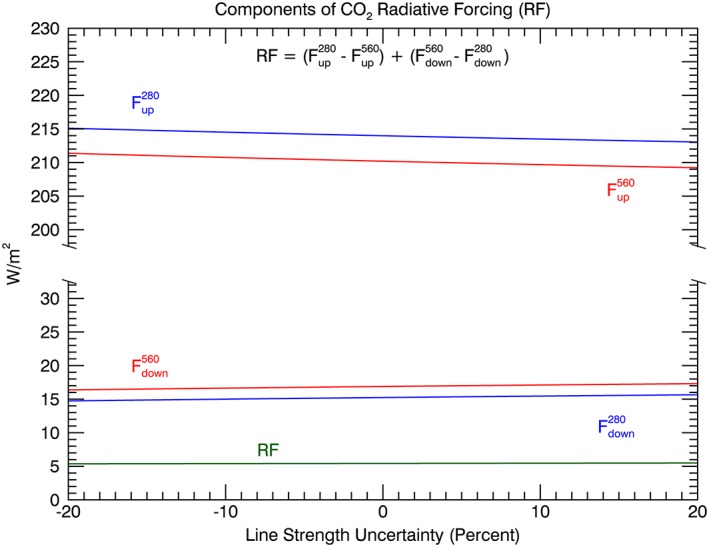
Upwelling and downwelling fluxes, and RF values obtained by varying all line strengths by ±20% in steps of 1%. The figure illustrates the correlated nature of the fluxes and hence the insensitivity of RF to uncertainty in line strengths.

We have also computed the RF uncertainty based on the actual line parameter uncertainties listed on the AER database. This is done separately for the line strength uncertainty and for the half‐width uncertainty. The approach is to read in each line and adjust either the line strength or the half width by the amount specified for that line. Again, to establish an upper bound on the resulting uncertainty, all lines are adjusted in the same direction for a given RF calculation [e.g., Pinnock and Shine, 1998]. When a range of uncertainty (e.g., 5% to 10%) is specified, we adjust by the lower level first and then do a second calculation at the higher level. We thus have a total of five RF calculations, two in which all parameters are decreased by the low and high amounts, two in which the parameters are increased by those amounts, and a baseline value with no uncertainty applied.

The uncertainty in calculated RF is then computed using the rule of propagation of uncertainty [National Institute of Standards and Technology, 1994, equation (A‐3)]. Table 1 (column 5) shows the total uncertainty in RF due to tabulated uncertainties in line strength on the AER v3.2 line list. Table 1 (column 6) gives the total uncertainty in RF due to the tabulated uncertainties in Lorentz half width. This formal uncertainty analysis confirms what is apparent in Figure 3, that the errors are strongly correlated and there is almost complete cancelation of error terms. The overall error due to either line strength uncertainty or half‐width uncertainty is a negligible fraction of the RF. These results are consistent with those of Pinnock and Shine [1998] for correlated uncertainties and confirm the validity of spectroscopic uncertainty estimates in the IPCC Fifth Assessment Report [Myhre et al., 2013] that did not include the line shape function. We further note that CO₂ air‐broadened half widths are now known to 1%–2% [Gamache and Lamouroux, 2013], as opposed to 5%–10% listed in the AER database, and thus make negligible contribution to uncertainty in RF.

Table 1 (column 7) is the root‐sum‐square (RSS) of the three prior columns and represents the total error in RF (in W/m²) due to line mixing, line strength, and air‐broadened half‐width uncertainties. The last column expresses the total uncertainty as a percentage of the baseline forcing. As is evident, the uncertainty in RF due to spectral line parameters is less than 1% of the total forcing in any of the five standard atmospheres considered.

4. Utility of the Voigt Line Shape

In this section we examine the utility of the Voigt line shape in RF calculations. We compute RF for the five standard atmospheres using the Monochromatic Radiative Transfer Algorithm (MRTA) described by Kratz et al. [1991, 2005]. MRTA is run with a Voigt line shape, with no CO₂ continuum or line mixing. For the following calculations, the Voigt line shape is truncated at distances ranging from 2 cm⁻¹ to 500 cm⁻¹ from line center, without renormalization.

Figure 4 shows the results of these calculations. The solid lines represent the RF using a Voigt profile as a function of truncation offset from line center. The RF computed with the Voigt profile is flat for offsets to 30 cm⁻¹ from line center and begins to increase substantially when the offset exceeds 100 cm⁻¹ from line center. Shown as diamonds in Figure 4 are the RF values from LBLRTM with line mixing accounted for, as in Figure 1. These are plotted for comparison with the Voigt calculations 50 cm⁻¹ offset from line center. There is an extremely close correspondence (within 0.01 W/m² for all five atmospheres) between the LBLRTM RF values with line mixing and the MRTA RF values with the Voigt profile truncated at 50 cm⁻¹ over a wide range of atmospheric conditions. Figure S3 in the supporting information shows the spectral difference in radiative forcing between MRTA with a 50 cm⁻¹ truncation and LBLRTM.

Figure 4.

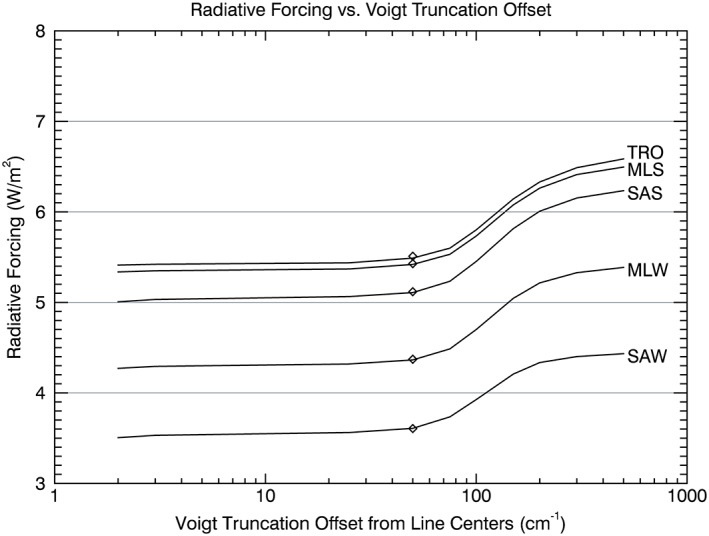
CO₂ RF computed with the MRTA code as a function of Voigt truncation offset from line center for the five atmospheres. Diamonds indicate RF values computed with LBLRTM and are shown for comparison with the Voigt calculations at 50 cm⁻¹ offset.

At 500 cm⁻¹ truncation offset, the RF is 21% to 24% larger than the forcing at 50 cm⁻¹ offset. The increased forcing results from additional absorption in the more optically thin regions at wave numbers less than 620 cm⁻¹ and greater than 720 cm⁻¹. Spectral differences in RF as a function of truncation distances are shown in Figure S4 in the supporting information. Finally, MRTA was also run with 25 cm⁻¹ truncation of the Voigt line shape including the MT_CKD CO₂ continuum beyond 25 cm⁻¹ for all CO₂ lines. The RF for each of the five standard atmospheres is within 1% of the LBLRTM values. Thus, a Voigt profile truncated at 25 cm⁻¹ and including the CO₂ continuum also provides an excellent estimate of the CO₂ RF.

The results in Figure 4 indicate that RF is overestimated only if the Voigt wings extend beyond 100 cm⁻¹ from line center, but such an overestimation is not informed by the sub‐Lorentzian nature of the CO₂ line shapes that has been known and taken into account for 50 years. Radiative transfer in climate models is often computed with a fast version of LBLRTM known as RRTMG [Mlawer et al., 1997; Iacono et al., 2000], which is built on the foundation of LBLRTM absorption coefficients and accurately reproduces LBLRTM flux and RF calculations. Therefore, RRTMG is consistent with the LBLRTM treatment of line shapes and line mixing in the CO₂ bands [Oreopoulos et al., 2012]. RRTMG is used internationally in a number of climate models (http://rtweb.aer.com/rrtm_frame.html). Radiation code intercomparisons such as Oreopoulos et al. [2012] and Pincus et al. [2015] have shown that the RF computed by most radiation codes used by general circulation models agree well with LBLRTM and RRMTG.

5. Discussion and Summary

We have computed instantaneous RF for five different standard atmospheres in order to assess the uncertainty in RF due to spectroscopic parameters. The combined uncertainty in RF due to uncertainty in line shape (including line mixing), line strength, and air‐broadened half widths is < 1% of the RF. Thus, we now have strong confidence that total spectroscopic uncertainty is a small fraction of the estimated CO₂ RF uncertainty in a cloud‐free atmosphere (i.e., much less than the estimated 2–3% out of 10% [Myhre et al., 2013]) and even a smaller fraction when cloudiness is considered. We conclude that in contrast to Happer [2014], the computation of RF is sound and that uncertainty in spectral line parameters, including the line shape function, is not a significant source of uncertainty in the evaluation of RF by CO₂.

Supporting information

Supporting Information S1

Table S1

Table S2

Table S3

Table S4

Table S5

Mlynczak, M. G. , et al. (2016), The spectroscopic foundation of radiative forcing of climate by carbon dioxide, Geophys. Res. Lett., 43, 5318–5325, doi: 10.1002/2016GL068837.