Experimental investigations on the explosivity of steam‐driven eruptions: A case study of Solfatara volcano (Campi Flegrei)

Abstract

Steam‐driven eruptions, both phreatic and hydrothermal, expel exclusively fragments of non‐juvenile rocks disintegrated by the expansion of water as liquid or gas phase. As their violence is related to the magnitude of the decompression work that can be performed by fluid expansion, these eruptions may occur with variable degrees of explosivity. In this study we investigate the influence of liquid fraction and rock petrophysical properties on the steam‐driven explosive energy. A series of fine‐grained heterogeneous tuffs from the Campi Flegrei caldera were investigated for their petrophysical properties. The rapid depressurization of various amounts of liquid water within the rock pore space can yield highly variable fragmentation and ejection behaviors for the investigated tuffs. Our results suggest that the pore liquid fraction controls the stored explosive energy with an increasing liquid fraction within the pore space increasing the explosive energy. Overall, the energy released by steam flashing can be estimated to be 1 order of magnitude higher than for simple (Argon) gas expansion and may produce a higher amount of fine material even under partially saturated conditions. The energy surplus in the presence of steam flashing leads to a faster fragmentation with respect to gas expansion and to higher ejection velocities imparted to the fragmented particles. Moreover, weak and low permeability rocks yield a maximum fine fraction. Using experiments to unravel the energetics of steam‐driven eruptions has yielded estimates for several parameters controlling their explosivity. These findings should be considered for both modeling and evaluation of the hazards associated with steam‐driven eruptions.

Key Points

• Experimental studies to unravel the steam‐driven eruption energetics

• Influence of liquid fraction and rock petrophysical properties on the explosive energy

• Steam flashing results in a faster fragmentation with respect to gas expansion and into higher ejection velocities of fragmented material

1. Introduction

Eruptions in magmatic and hydrothermal systems are violent phenomena, typically resulting in an explosive release of energy generated by the mechanical work of expanding fluids [Mastin, 1995; Zhang, 2000; Thiéry and Mercury, 2008, 2009; Thiéry et al., 2010]. The best known and studied eruptions are related to the expulsion of magma and magmatic gases through a vent at the Earth's surface [Gilbert and Sparks, 1998, Sigurdsson et al., 2015, and references therein]. Yet a large percentage of eruptions, perhaps the majority, expel no juvenile materials but rather exclusively fragments of preexisting rocks disintegrated by the expansion of flashed steam, gas, or supercritical fluids [Mastin, 1995; Browne and Lawless, 2001; Morgan et al., 2009]. Thus, the main cause of these explosive events, which we here refer to as “steam‐driven eruptions,” is the presence of water at the surface and/or shallow depths. The most common steam‐driven eruptions include both phreatic and hydrothermal eruptions. Heated ground, surface, and/or water at shallow depths is the driving fluid behind phreatic eruptions [Stearns and McDonald, 1949], while the input of mass and energy deriving from magma is thought to be the trigger [Browne and Lawless, 2001]. Hydrothermal eruptions involve specifically water close to its boiling temperature (“boiling‐point” eruption of Mastin [1995]) instead. They are generated at shallow depth and result from the rapid formation of steam following a sudden pressure decrease [Browne and Lawless, 2001; McKibbin et al., 2009]. Generally, they do not result from any input of mass or energy directly derived from magma. Moreover, these eruptions are often preceded by very short time frames of unrest which are difficult to interpret [Barberi et al., 1992; Kato et al., 2015].

The conversion of thermal energy stored in water into mechanical energy powers these eruptions. This conversion results in the fragmentation of the preexisting rocks, and acceleration and lifting of the resulting debris, as well as in the generation of seismicity and shock waves. Despite their importance, the energetics and dynamics of this type of eruptions are still not well understood. For many steam‐driven eruptions since the early 1950s [White, 1955], mechanical energy release, final temperature, and produced steam fraction have been estimated by using basic principles of thermodynamics. Several later studies have used a similar approach to estimate the energetics of specific steam‐driven eruptions [Muffler et al., 1971; Hedenquist and Henley, 1985; Nelson and Giles, 1985; Mastin, 1991]. Mastin [1995] addressed the energetic problem by considering an adiabatic and isentropic vapor expansion from initially known thermodynamic conditions. Some studies have attempted to model the dynamics of these eruptions, both theoretically [McKibbin, 1989; McKibbin et al., 2009; Fullard and Lynch, 2012a, 2012b] and experimentally [Foote et al., 2011; Haug et al., 2013; Mayer et al., 2015; Montanaro et al., 2016a]. More insight into their dynamics and energetics have been inferred from studies of the deposits of recent events at Gengissig lake in Iceland [Montanaro et al., 2016b], and at Ruapehu and Tongariro volcanoes, in New Zealand [Kilgour et al., 2010; Breard et al., 2014; Montanaro et al., 2016a].

The violence (or explosive power) of these eruptions depends largely on the different explosivity of fluids driving them (liquid or gas) and on the rate of release of mechanical energy. These are, in turn, controlled by 1) the liquid fraction and the pressure and temperature (P‐T) of a system before the explosive event [Mastin, 1995; Thiéry and Mercury, 2009; Thiéry et al., 2010; Montanaro et al., 2016a] and 2) the physical and mechanical properties (mainly connected porosity, permeability, and strength) of the host rock [Thiéry and Mercury, 2008; Thiéry et al., 2010; Haug et al., 2013; Galland et al., 2014; Montanaro et al., 2016a]. More specifically, the pressure‐temperature conditions and the porosity control the phase of the fluid and the stored explosive energy, respectively [Montanaro et al., 2016a]. The energy partitioning in terms of fragmentation and kinetic energy, in contrast, depends largely on the rock porosity, permeability, and strength [Thiéry and Mercury, 2009; Mayer et al., 2015; Montanaro et al., 2016a, 2016b]. A wide range of initial temperature, pressure and liquid fraction, and rock types characterizes the volcanic environments affected by steam‐driven eruptions [Browne and Lawless, 2001]. Consequently, this eruption type shows a wide range of eruptive styles.

To estimate the effect of these parameters on the explosion energy and its release, we investigated a likely scenario for steam‐driven eruption at the Solfatara and Pisciarelli fumarolic fields (Figure 1a). These two sites represent the main surface manifestations of the vigorous hydrothermal system within the Campi Flegrei (CF) caldera, which is thought to consist of a gas plume fed by fluids of deeper magmatic and meteoric origin [Caliro et al., 2007] (Figure 1b). Consistent with the volcanic history of CF [Orsi et al., 1996, 2004, 2009; Di Vito et al., 1999; Isaia et al., 2015], Solfatara and Pisciarelli areas have been assigned the highest probability for the opening of a future vent [Selva et al., 2012; Bevilacqua et al., 2015] and an explosive eruption. A complex fault system, related to the maar‐diatreme origin of the Solfatara crater, is believed to be driving the outgassing which in turn leads to a strong alteration of the volcanic products in both areas [Isaia et al., 2015; Piochi et al., 2015; Mayer et al., 2016]. Additionally, recent physical simulations suggest an increased fluid flux within the last two decades, which is deriving from depth and feeding the hydrothermal system [Todesco, 2009]. This may have increased the condensation of water within, and at the border, of the gas plume, and in turn influenced the heating of the rocks by the latent heat release during condensation [Chiodini et al., 2015, and reference therein]. In our scenario the presence of condensed steam migrating along the fractured zone is considered as the possible source of explosivity during a likely destabilization of the hydrothermal system [Hedenquist and Henley, 1985; Nelson and Giles, 1985]. Different types of tuffs which are inferred to reflect the rock sequence underlying the Solfatara crater have been used for the experiments.

Figure 1.

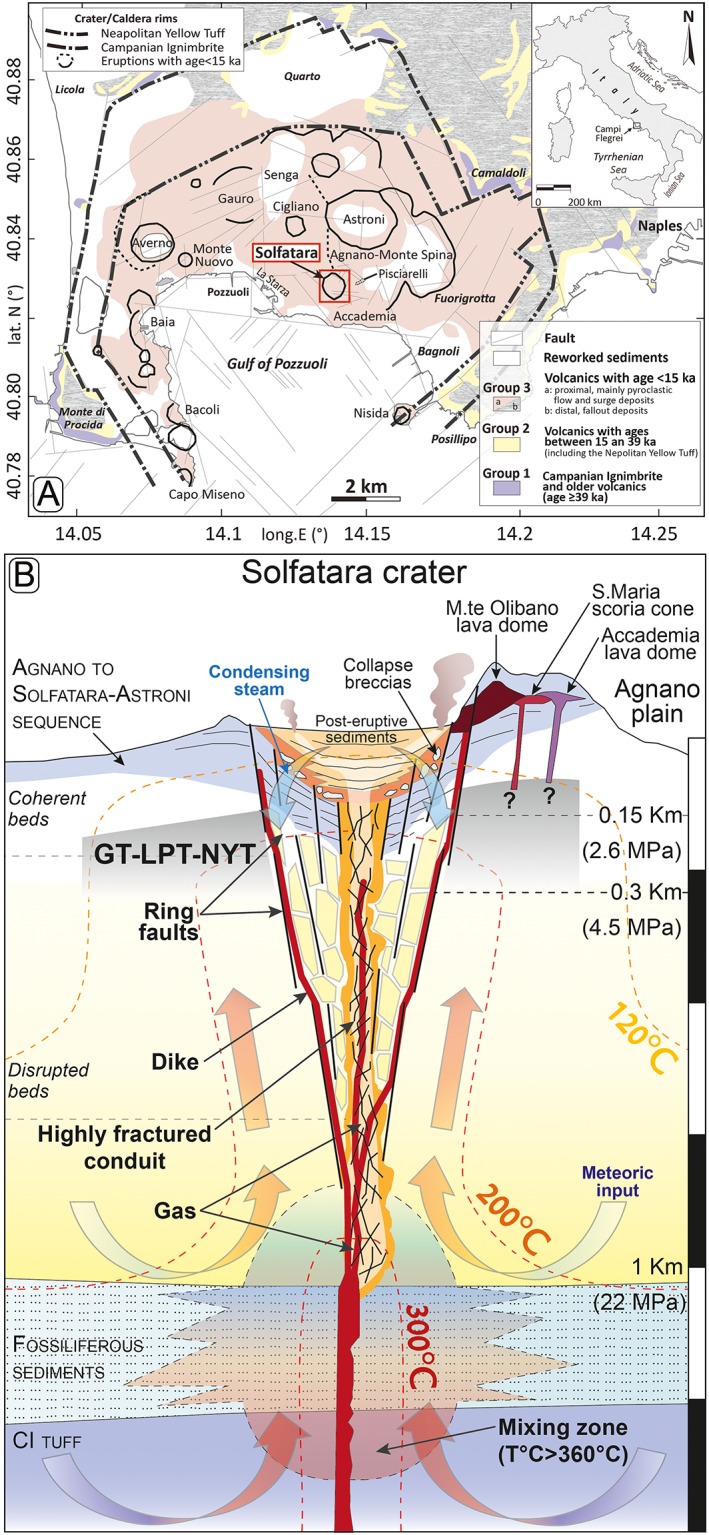
(a) Map of the central sector of Campi Flegrei from Isaia et al. [2015]. (b) Conceptual model of Solfatara crater showing the maar‐diatreme structure, containing the tuff samples used as representatives for individual areas below Solfatara. Meteoric water mix with magmatic fluid at depth, producing a gas plume arising through the fractured conduit of the Solfatara diatreme. A condensation zone is envisaged below the crater area, with condensed steam migrating downward along the fracture system. The scale bar unit on the right of the figure is 250 m. GT: Gauro Tuff, LPT: La Pietra Tuff, NYT: Neapolitan Yellow Tuff. Modified from Caliro et al. [2007] and Isaia et al. [2015].

Here we present the results of a study aimed at investigating the role of the liquid fraction (from dry through partially to fully saturated) and the rock properties (connected porosity, permeability, and strength) on the explosive power by using experimental modeling, together with thermodynamic estimates. We performed a series of rapid decompression experiments with different rock types and different degrees of sample saturation (with water), at initial elevated temperatures and pressures [Rager et al., 2014; Mayer et al., 2015]. Petrophysical properties of the used rocks were determined under static and dynamic conditions prior to the decompression experiments. Calculations based on irreversible thermodynamic approach were then performed in order to give an estimate of the involved explosive energy [Prugh, 1991; Planas‐Cuchi et al., 2004; Thiéry and Mercury, 2009].

2. Explosivity of Water in Hydrothermal Systems

An explosion is the violent response of a system to a physico‐chemical perturbation and the resulting energetic metastable state. Fast thermodynamic processes, such as the heating of water by magma, or rapid depressurization of a liquid produce highly transient metastable states, which tend to reach equilibrium in a very rapid and explosive way [Thiéry and Mercury, 2009]. Thus, rapid physical transformations of water are the causes of strong instabilities, which lead to explosive manifestations such as steam‐driven eruptions. Particularly, for hydrothermal systems, the (sudden) decompression of hot pressurized water is the main cause producing such events [Browne and Lawless, 2001]. The (rapid) release of water stored at a temperature above its atmospheric‐pressure boiling point results in instantaneous vaporization (steam flashing). Steam‐driven eruptions thus occur with different degrees of explosivity, as their violence is related to the magnitude of the decompression work that can be performed by the steam flashing [Mastin, 1995; Thiéry and Mercury, 2008, 2009; Thiéry et al., 2010].

The explosive energy released by the expansion work of the fluids (gas or liquid) in the rock pore space, from the breaking pressure in the pore up to the atmospheric pressure, is given by

$$E_{\text{Expl}}=m\times \mathrm{\Delta }U$$ (1)

where E _Expl is the available explosive energy which can be released in the expansion of the fluids (J), m is the mass of fluid already existing in the pores at the moment of the failure (g), and ΔU is the difference in internal energy of the fluid under the conditions before and immediately after the expansion (J/g). The estimated E _Expl gives the amount of energy which can be converted into fragmentation, kinetic, and all other forms of energies such as inelastic deformation and shock waves. The maximum amount of work that can be extracted from an expansion, and thus the associated explosive energy, depends upon the thermodynamic path [Mastin, 1995; Thiéry and Mercury, 2009].

By assuming a fluid expansion which is adiabatic and reversible (isentropic), the produced work must be equal to the variation in internal energy of the fluid ΔU:

$$\mathrm{\Delta }U=-P_{\mathrm{atm}}\times \mathrm{\Delta }V$$ (2)

where P _atm is the atmospheric pressure (1 bar) and ΔV is the volume increase (m³). This assumption implies that the fluid expands isentropically as an ideal gas and ignores any energy consumption through internal friction. Planas‐Cuchi et al. [2004] modified this approach by equating the internal energy change of a fluid (water) to the irreversible work performed as the expanding vapor pushes against the surrounding medium. They also assumed that immediately after the expansion, there is liquid‐vapor equilibrium at atmospheric pressure and at the corresponding saturation temperature. This assumption is much closer to the real situation and allows less conservative estimations of overpressure by taking irreversibility factors into account such as friction, heat loss, unrestrained expansion of a gas, and others. The analytical solution of equation (2) applied to a mass of liquid which vaporizes, enables calculation of the flashed steam fraction accounting for irreversibility [Planas‐Cuchi et al., 2004; Thiéry and Mercury, 2009] as

$$x=1-f=1-\left(\frac{P_{\mathrm{atm}}\times \left(v_{\text{initial}}‐v_{\mathrm{v}\mathrm{a}\mathrm{p}}\right)-U_{\mathrm{v}\mathrm{a}\mathrm{p}}+U_{\text{initial}}}{U_{\text{liquid}}-U_{\mathrm{v}\mathrm{a}\mathrm{p}}+P_{\mathrm{atm}}\times \left(v_{\mathrm{l}\mathrm{i}\mathrm{q}}‐v_{\mathrm{v}\mathrm{a}\mathrm{p}}\right)}\right)$$ (3)

where x and f represent the steam and liquid fraction, respectively; v is the molar volume; and U is the internal energy. U _initial (J/mol) and v _initial (m³/mol) are calculated at the initial condition of the system. U _liq (J/mol), v _liq (m³/mol), U _vap (J/mol), and v _vap (m³/mol) are all calculated at 100°C and 1 bar (atmospheric‐pressure boiling point). Thiéry and Mercury [2009] demonstrated that an isenthalpic hypothesis yields a good approximation of the irreversible case. However, by accounting for irreversibility more heat is consumed to produce steam resulting in a final mixture much drier than both isentropic and isenthalpic cases (see later Figure 3b and section 5.3). Under this assumption the irreversible energy of an expanding saturated liquid can be calculated as

$$E_{\text{Expl}-\mathrm{I}}=m_w\times P_{\mathrm{atm}}\times \left[x\times v_{\mathrm{v}\mathrm{a}\mathrm{p}}+\left(1-x\right)\times v_{\mathrm{l}\mathrm{i}\mathrm{q}}-v_{\text{initial}}\right]$$ (4)

where E _Expl‐I is the irreversible explosive energy released (J) and m_w is the mass of water (g) in the pore space.

Figure 3.

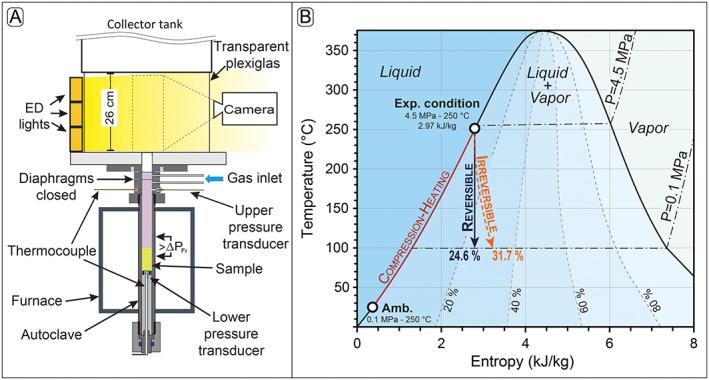
(a) Schematic drawing of the experimental setup. The bomb allows for the accurate control of temperature, gas overpressure, and decompression rate in order to best represent variable volcanic and hydrothermal conditions. The sample (l = 60 mm, d = 25 mm) is placed in the high‐pressure autoclave. Samples were pressurized up to approximately 3 MPa, then heated at 15°C /min. A final pressure of 4.5 MPa was obtained at the end. The overall pressurization, heating, and dwelling process lasted for about 40 min. A set of diaphragms allow reproducible pressurization of the sample by using argon gas or steam. The dashed box indicates the area observed with the high‐speed camera. Modified after Scheu et al. [2006] and Mayer et al. [2015]. (b) Plot of temperature versus entropy for liquid water and water vapor showing the initial temperature‐entropy state for the experimental condition used in this study (250°C, 2.79 kJ/kg). This diagram includes several types of curves: (1) the isobars (dash‐dotted lines) are calculated at 1 and 4.5 MPa; (2) the dashed lines are contours of equal mass fraction of steam in the coexisting mixture; (3) the dark red continuous line is the thermodynamic path followed during the compression‐heating phase from the ambient (0.1 MPa and ~25°C) to the final experimental condition (4.5 MPa and 250°C), and before the decompression; (4) the continuous dark blue arrow is the thermodynamic path of fluid during decompression under isentropic (reversible) condition and which result in the production of 24.6% of steam; and (5) the dashed orange arrow is the thermodynamic path of fluid during decompression under irreversible condition and which result in the production of 31.7% of steam.

3. Geological Setting of the Case Study: Solfatara and Pisciarelli

Solfatara and Pisciarelli are fumarolic areas located within the densely populated CF caldera (Figure 1a). The CF area has been affected by two large caldera forming eruptions that occurred at ~40 and ~15 ka BP, giving rise to the voluminous deposits of the Campanian Ignimbrite and Neapolitan Yellow Tuff, respectively, and generating the Campi Flegrei caldera, a nested and still resurgent structure [Acocella, 2010; Capuano et al., 2013; Orsi et al., 1996; Vitale and Isaia, 2014] (Figure 1a). Within the last 14.9 ka at least 73 phreatomagmatic eruptions, mostly clustered in three main epochs of activity and separated by intervals of at least ~1000 years, have affected the caldera [Di Vito et al., 1999; Orsi et al., 2004, 2009; Isaia et al., 2009; Smith et al., 2011; Selva et al., 2012; Bevilacqua et al., 2015]. During the last epoch most of the active vents were located in the central‐eastern sector of the caldera [Di Vito et al., 1999; Orsi et al., 2004; Vilardo et al., 2010; Selva et al., 2012]. About 15 explosive and effusive eruptions occurred at short time intervals, with a quiescence of about 100–200 years after the Agnano‐Monte Spina Plinian eruption [Isaia et al., 2009]. One of the eruptions of this epoch of activity generated the Solfatara volcano [Isaia et al., 2015]. The last epoch of activity was also followed by a long rest period before the last eruption of the caldera occurred in 1538 (Mount Nuovo tuff cone [e.g.,Guidoboni and Ciuccarelli, 2011]).

In more recent times both the crater and the eastern flanks toward Pisciarelli of the Solfatara volcanic edifice have undergone a vigorous hydrothermal and fumarolic activity [Caliro et al., 2007; Scandone et al., 2010]. During the period of 1970–1972 and 1982–1984 the crater area has been affected by the deformation accompanying the unrest in the Campi Flegrei caldera [Barberi et al., 1984; Dvorak and Gasparini, 1991]. An intense seismic activity was localized in the Solfatara crater [Orsi et al., 1999, and references therein], and new fractures were generated [Acocella, 2010; Vitale and Isaia, 2014; Isaia et al., 2015]. Since that time, Solfatara volcano and the surrounding area have been intensely monitored, and detailed geochemical and geophysical investigations have been carried out [Chiodini et al., 2001, 2015; Bruno et al., 2007; Caliro et al., 2007, 2014; Petrosino et al., 2012; Moretti et al., 2013]. Results of the geochemical analyses of fumarolic gases [Caliro et al., 2007, 2014] outline a complex hydrothermal system localized below Solfatara crater, including an upwelling of deep magmatic, CO‐rich fluids, mixed with hydrothermal liquids of meteoric origin, and forming a hydrothermal plume that feeds the fumaroles at the surface. Mixing of these fluids occurs at high temperature (>350°C) at the base of the hydrothermal system (1–1.5 km), whereas a shallow vapor‐liquid zone is imaged to be located at depth between 150 and 300 m (2.6–4.5 MPa) where temperature ranges between 190 and 250°C. [Caliro et al., 2007, 2014; Piochi et al., 2014, 2015] (Figure 1b). Recent episodes of mud emissions and formation of boiling pools of condensates at Pisciarelli [Chiodini et al., 2011], together with the presence of electrically resistive gas bodies below the fumaroles in Solfatara, overlain by conductive descending bodies of liquid condensates [Bruno et al., 2007; Byrdina et al., 2014; Isaia et al., 2015], support the occurrence of deep processes of condensation within the buried Solfatara gas plume [Chiodini et al., 2015]. Gas and liquid flows are driven by both rock permeability and fracture systems. The latter are the result of both explosive activity and collapse faulting in the crater area occurred during the maar‐diatreme eruption that generated the Solfatara crater [Isaia et al., 2015]. The interpretation of the eruptive sequence associated to this maar‐formation indicates the occurrence of an opening phreatic phase, followed by phreatomagmatic activity. The phreatic deposits contained shallow‐seated lithic fragments, including a peculiar green tuff which was also recognized in the Pozzuoli coast (La Pietra Tuff; LPT) [Rosi et al., 1983; Di Vito et al., 1999] and found in drill cores from the Agnano Plain [Piochi et al., 2014]. The presence of the tuff‐lithic component further confirms previous observations of the stratigraphy in the shallow part of the caldera and below the Solfatara area, where borehole stratigraphy indicates a widespread sequence of yellow and green tuffs [Rosi et al., 1983; Orsi et al., 1999; Piochi et al., 2014].

3.1. Material Investigated

In order to investigate the influence of rock properties on the explosivity of steam‐driven eruptions, we chose tuffs expected to be located below the Solfatara area (Figure 1b), and which are characterized by different physical and mechanical properties. In particular, rock samples from the Neapolitan Yellow Tuff (NYT), together with the La Pietra (LPT) and Gauro (GT) Tuffs, have been collected as sample material for this study (Figure 2). The NYT is considered to be one of the most abundant and widespread volcanic deposits in the CF volcanic district [Orsi et al., 2004, and reference therein]. The GT deposit is also one of most voluminous tuffs emplaced during the I epoch of the post‐NYT activity in the CF and preceded the Solfatara eruption [Di Vito et al., 1999]. The LPT, also older than the Solfatara deposits [Di Vito et al., 1999], is exposed in a nearby area, about 500 m toward the southern part of the crater. The LPT deposit is characterized by alternating pumice‐ (LPT‐1) and ash‐rich (LPT‐2) beds; therefore, both rock types were sampled and individually investigated. In terms of mineralogy, the used tuffs are trachytic in composition and contain both pyrogenic and authigenic phases [Dé Gennaro et al., 1999]. The main mineral assemblage consists of sanidine, plagioclase, clinopyroxene, and biotite phenocrysts, together with minor amounts of titaniferous magnetite and apatite within a matrix of lapilli and glass shard ash. Additionally, secondary minerals such as phillipsite, chabazite, and analcime have been recognized in previous studies [Dé Gennaro et al., 1999; Heap et al., 2012].

Figure 2.

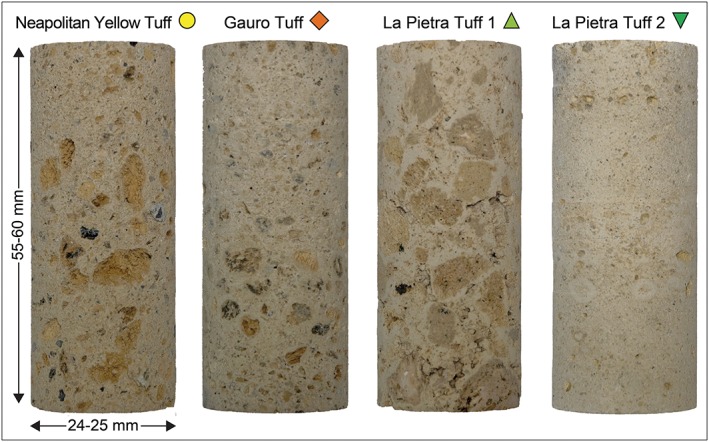
Photograph of cylindrical samples of each tuff as used in the experiments. Samples show differences in macroscopic texture, color, and particle size. The Neapolitan Yellow Tuff (NYT) and La Pietra Tuff 1 (LPT‐1) contain abundant and large pumices and lithics within a fine matrix, whereas the Gauro Tuff (GT) and the La Pietra Tuff 2 (LPT‐2) show a more ash‐dominant component.

We assume that the uppermost part of the shallow hydrothermal reservoir below Solfatara consists of similar rocks as those collected to represent the stratigraphy below the crater area [Piochi et al., 2014, and reference within]. We further assume that the properties of tuffs collected at the surface are representative of those at depth of 300 m (within the shallow hydrothermal zone). This assumption is in part supported by the fact that the mechanical properties of tuffs from drill cores at a depth of 500 m are similar in terms of porosity, permeability, density and texture (Carlino, personal communication). However, it has to be considered that the increase in temperature at depth may result in 1) an increase of rock permeability as a consequence to the formation of new thermal microcracks [Heap et al., 2014] and 2) the dissolution of thermally unstable zeolites such as phillipsite and chabazite [Dé Gennaro and Colella, 1989; Heap et al., 2012]. Additionally, alteration processes related to the active hydrothermal system, such as authigenic mineralization and argillic alteration, may further modify the rock's physical properties at the depth [Mormone et al., 2015].

4. Experimental Studies

4.1. Methods

4.1.1. Petrophysical Characterization

Petrophysical properties were determined on cylindrical samples (55–60 mm length, 24–25 mm diameter; Figure 2) of all investigated tuffs. Samples were cored perpendicular to the layering (in case of existing layers), and their end‐faces were ground flat and parallel. Bulk density, matrix density, and connected porosity of dry (oven‐dried at 65°C for 24 h), cored cylinders were measured by using a helium pycnometer (Ultrapyc 1200e®, Quantachrome). The connected porosity of the sample is calculated by using the matrix volume (Vol_meas.) derived by helium pycnometry and its geometric (bulk) volume (Vol_calc.) as

$$\text{Connected porosity}=\left[\left({\mathrm{V}\mathrm{o}\mathrm{l}}_{\text{calc}.}-{\mathrm{V}\mathrm{o}\mathrm{l}}_{\text{meas}.}\right)/\left({\mathrm{V}\mathrm{o}\mathrm{l}}_{\text{calc}.}\right)\right]\times 100$$ (5)

Gas permeability measurements of selected cylindrical dry samples were conducted under a confining pressure of 1.0 MPa by using a GasPerm (GPE‐100, Vinci Technologies). The device allows for determination of permeability to gas at steady state (constant pressure and flow through the sample). A mass flowmeter (range 5–500 cc/min) together with a relative pressure transmitter (up to 0.69 MPa) was used to sense gas flow and pressure drop across the sample. Volumetric flow rate measurements were taken under several pressure gradients. Then only the flows for which a Darcy condition were granted (depending on the sample length and the gas flow rate) were used to determine the permeability by using a Darcy's law. Ultrasonic wave velocities of dry and wet (fully saturated) samples were measured in a benchtop apparatus where the sample is placed between two vertical endcaps equipped with piezoelectric transducers (with a resonant frequency of <1 MHz) connected to a pulse generator (Agilent Technologies 33210A, 10 MHz function/waveform generator) and an oscilloscope (Agilent Technologies DSO5012A). The onset of P wave arrival at the receiver was individually picked as the first deviation from the baseline signal. Uniaxial compressive strength (UCS) tests were carried out at the Technische Universität München. Dry and wet (fully saturated) samples were compressed under a constant strain rate of 3.3 × 10⁻⁴ s⁻¹. Axial strain and stress were continuously monitored during deformation, by displacement transducers and by a load cell, until failure. Samples for UCS tests were shaped with a length‐diameter‐ratio of 2:1. Both UCS and P wave velocity were measured under dry and 100% water saturation conditions. Fragmentation threshold, which represent a dynamic response to a normal tensile stress [Spieler et al., 2004], was also determined by using a fragmentation bomb as described in the following section.

4.1.2. Decompression Experiments

We performed experiments in a decompression‐fragmentation bomb in the form of a shock‐tube apparatus [Spieler et al., 2004; Scheu et al., 2008; Alatorre‐Ibargüengoitia et al., 2010] modified by Mayer et al. [2015] (Figure 3a). In these experiments fragmentation was triggered by either 1) argon expansion (AE) or 2) steam flashing (SF) within the connected pore space of the samples. The shock‐tube apparatus is connected to a stainless steel tank (l = 3.0 m; d = 0.4 m) at ambient pressure and temperature, which is used to collect the experimentally generated pyroclasts. The sample is loaded into a high pressure‐temperature steel autoclave (Figure 3a). A series of thin copper diaphragms separate the upper low‐pressure chamber from the autoclave. Controlled rupture of the diaphragms leads to a rapid decompression of the high‐pressure autoclave producing a rarefaction wave, which propagates downward into the autoclave and through the sample. Samples are fragmented by sudden AE in a brittle, layer‐by‐layer fashion [Alidibirov and Dingwell, 2000]. In the case of SF, fracturing is less dependent on the decompression front, but rather on the orientation of pore space and possibly preexisting fractures [Rager et al., 2014]. A transparent section at the bottom of the large chamber allows monitoring of the sample ejection by a high‐speed camera (Figure 3a). The fragmented material is collected from the large chamber, and its grain size distribution analyzed by using dry sieving at half‐ϕ steps.

Our experiments were designed to mimic a decompression involving the upper part of the hydrothermal plume imaged below Solfatara and Pisciarelli areas (Figure 1). We assumed for the hydrothermal reservoir 1) a temperature of approximately 250°C and a pressure of 4.5 MPa, 2) a zonation within the plume with gas‐rich and condensed steam areas, and 3) a host rock with petrophysical properties similar to the different tuffs investigated in this study [Caliro et al., 2007; Piochi et al., 2014; Chiodini et al., 2015] (Figure 1b). Therefore, we had AE and SF as possible sources driving the fragmentation and the ejection of particles [Rager et al., 2014; Mayer et al., 2015]. The expansion ratio of argon gas is very similar to that of CO₂ (~1:25 from the experimental to ambient condition), which is the second largest contributor to the fumarolic gases in Solfatara and Pisciarelli [Caliro et al., 2007]. In order to evaluate the different behavior initiated by SF at different liquid fraction we used samples with 0% (dry), 50%, and 100% water saturation. Thereby, either a combination of AE and SF or pure SF is leading to fragmentation and ejection of the sample. The NYT, GT, and LPT (1–2) were used for these experiments in order to evaluate the effects of mechanical properties on the fragmentation and ejection behavior.

The samples used for experiments involving the SF were first mounted into a sample holder before submerging them in water and placing them under vacuum for at least 72 h; this method facilitates water to be absorbed into the connected porosity assuring maximum water saturation. For the partially saturated ones, a different approach was used. The correct amount of water required for saturating 50% of the known porosity of the sample was placed in a container together with the sample and then kept under moderate vacuum. The saturation was obtained by continuously turning the sample within the container; this method and the high imbibition capacity of the different investigated tuffs [Colella et al., 2009; Morra et al., 2010] assured a quite homogeneous distribution of water within the whole sample.

The fragmentation threshold, i.e., the initial pressure required to fragment the whole rock sample [Spieler et al., 2004; Scheu et al., 2006; Koyaguchi et al., 2008], was first determined for all the tuffs at room temperature (dry condition). Next we tested the different tuffs in dry, partially (50%), and fully water‐saturated conditions. For the experiments performed on both dry and saturated samples the system was initially pressurized to ~3 MPa. A target temperature of 250°C was reached after a heating time of 25 min. For the saturated samples the initial pressurization ensured the water to remain in the liquid state throughout the heating phase. During the last stage of the heating, the remaining pressurization, required to reach a pressure of 4.5 MPa, was applied. Holding these final conditions for a dwell time of at least 10 min ensured temperature and pressure equilibration over the entire sample before triggering the fragmentation. During the decompression of the system up to 100°C and 0.1 MPa, the boiling point is reached and a mixture of liquid water and steam is produced (Figure 3b).

Finally, for each sample the fragmentation speed is calculated by using the time delay Δt of the pressure drop over the entire sample, as recorded by the transducers above and below the sample, and the sample length [Scheu et al., 2006].

5. Results

5.1. Petrophysical Properties

Table 1 summarizes the main rock petrophysical properties of all the investigated sample, where Table 2 report only the dry properties of the tuffs used for the decompression experiments. Results are also shown in Figure 4. All tuffs show high values of connected porosity ranging between 41.3 and 50.3%. All samples contain abundant pumices and lithics within a fine matrix of zeolites (phillipsite and chabazite) forming the microporous texture of the samples [Dé Gennaro et al., 1999]. Hg‐porosimetry of the NYT performed by Colella et al. [2009] indicates a bimodal pore size distribution characterized by subordinated macro pores and primarily mesopores (30–75 µm) and micropores (0.01–1 µm). The permeability was measured only for samples later used for the decompression experiments (Table 2). Permeability ranges between 1.4 × 10⁻¹³ to 2 × 10⁻¹⁵ m², with the more permeable samples being the pumice‐rich NYT and LPT‐1 (~10⁻¹³ m²). The standard deviation for permeability values are in the range between 1.1 × 10⁻¹³ to 1.9 × 10⁻¹⁷ m² (Table 2). The relation between permeability and porosity allows us to subdivide the analyzed rocks into three main groups: 1) a highly permeable and very porous NYT and LPT‐1, 2) an intermediate permeability and low porosity GT, and 3) a very low permeability and intermediate‐to‐high porosity LPT‐2 (Figure 4a). Despite the high textural heterogeneities (Figure 2) the analyzed tuff samples showed a narrow range of the bulk and apparent density (ρ _calc. and ρ _meas. in Table 2), which varies between 1070–1330 kg/m³ and 2220–2380 kg/m³, respectively.

Table 1.

Main Petrophysical Features of All the Investigated Tuffs

		Neapolitan Yellow Tuff (NYT)	Gauro Tuff (GT)	La Pietra Tuff 1 (LPT‐1)	La Pietra Tuff 2 (LPT‐2)
Connected porosity (%)		47.8–50.3	41.3–46.6	48.3–49.2	46.4–48.5
Permeability (m2)	From	4.3 × 10−13	1.6 × 10−14	5.6 × 10−14	3.7 × 10−15
	To	1.4 × 10−13	3.3 × 10−14	2.8 × 10−13	2 × 10−15
Dry bulk sample density (kg/m3)		1070–1200	1250–1330	1180–1240	1210–1240
Dry apparent sample density (kg/m3)		2220–2320	2130–2340	2330–2380	2220–2320
Dry P wave velocity (km/s)		0.9–1.3	1.4–1.6	0.7–1.2	1.1–1.5
Wet P wave velocity (km/s)		1.9–2.2	2.1–2.2	1.6–1.8	2.1–2.7
Dry uniaxial compressive strength (MPa)		6.1–7.3	10.8–13	4.2–5.5	8.9–10.5
Wet uniaxial compressive strength (MPa)		1.2–2.3	4.3–5.1	1.3–3.1	3–5
Fragmentation threshold (MPa)		1.5–1.7	3.5–4.5	2.5–3.1	3.3–3.6

Table 2.

Dry Petrophysical Properties of the of the Tuffs Used for the Decompression Experiments

Sample (used for)	Mass (g) )	Vol.calc (cm3)	ρ calc. (g/cm3)	Vol.meas. (cm3)	ρ meas. (g/cm3)	Conn. porosity (%)		Permeability (S dev) (m2)
						Total	Effective
Argon expansion
NYT	33.4	28.6	1.2	14.3	2.3	50		2.2 × 10−13	(3.5 × 10−14)
GT	35.5	27.9	1.3	15.1	2.3	45.8		1.8 × 10−14	(3.2 × 10−16)
GT	34.8	27.1	1.3	14.6	2.3	45.9		1.6 × 10−14	(3.5 × 10−16)
LPT‐1	29.7	24.7	1.2	12.7	2.3	48.6		5.6 × 10−14	(4.5 × 10−15)
LPT‐2	35.2	28.4	1.2	15.1	2.3	46.8		3.6 × 10−15	(1.2 × 10−16)
Steam flashing (50% sat.)
NYT	33.3	28.4	1.2	14.8	2.2	47.8	23.9	2.5 × 10−13	(3.1 × 10−14)
NYT	28.5	25	1.1	12.9	2.2	48.3	24.1	4.3 × 10−13	(4.7 × 10−14)
GT	35.8	28.1	1.3	15.1	2.3	46	23	2.3 × 10−14	(7.0 × 10−16)
GT	33.8	26.7	1.3	14.4	2.3	45.9	23	2.9 × 10−14	(8.7 × 10−16)
LPT‐1	33.6	28.4	1.2	14.4	2.3	49.2	24.6	3.4 × 10−13	(1.1 × 10−13)
LPT‐2	34.8	28.8	1.2	14.8	2.3	48.5	24.3	2.0 × 10−15	(4.3 × 10−17)
Steam flashing (100% sat.)
NYT	32.9	28.3	1.2	14.3	2.3	49.6	0	1.4 × 10−13	(6.5 × 10−15)
NYT	26.7	24.6	1.1	12.2	2.2	50.3	0	3.9 × 10−13	(4.1 × 10−14)
GT	33.2	28.5	1.3	14.8	2.2	42.6	0	2.4 × 10−14	(1.9 × 10−15)
GT	34.7	27.2	1.3	14.7	2.1	46	0	1.9 × 10−14	(8.0 × 10−16)
LPT‐1	34.1	27.5	1.2	14.2	2.4	48.3	0	2.8 × 10−13	(3.4 × 10−14)
LPT‐2	35.7	29.3	1.2	15.7	2.2	46.4	0	3.7 × 10−15	(1.9 × 10−17)

Figure 4.

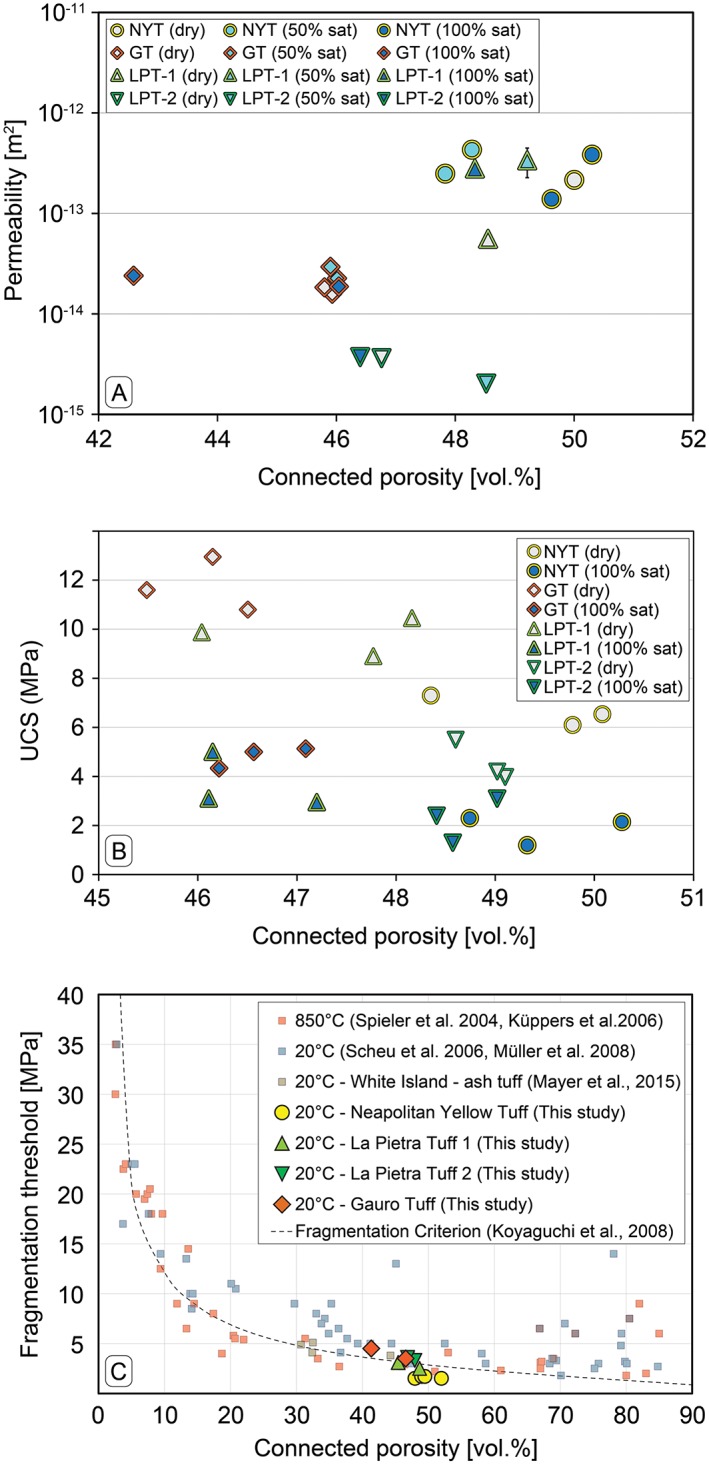
Plot of permeability against connected porosity of the tuffs used for the decompression experiments. Permeability data allow to distinguish three fields defined by 1) the highly permeable and porous NYT and LPT‐1 samples, 2) the intermediate permeability and low porosity GT samples, and 3) the very low permeability and intermediate porosity LPT‐2 samples. (b) Plot of uniaxial compressive strength (UCS) against connected porosity. The grey‐filled shapes indicate dry samples; the blue‐filled shapes indicate fully saturated samples. Results show how the more porous NYT and LPT‐1 have a lower strength under compression. (c) Fragmentation threshold of investigated samples at 20°C during rapid decompression experiments. Fragmentation threshold for several rocks obtained in other studies are also compiled. The dashed line corresponds to the fragmentation criterion proposed by Koyaguchi et al. [2008]. Samples with a higher porosity and lower strength (such as NYT and LPT‐1) fragment at a lower initial pore pressure.

For dry samples the P wave velocities of the more porous NYT and LPT‐1 (0.7 to 1.3 km/s) are lower than those for the less porous and denser LPT‐2 and GT (1.1 to 1.6 km/s). For the 100% water saturated samples P wave velocities generally increase, yet those of NYT and LPT‐1 (1.6 to 2.2 km/s) remain lower than for the GT and LPT‐2 (2.1 to 2.7 km/s).

Figure 4b shows the relation between UCS and rock connected porosity. For dry samples the UCS values of the more porous NYT and LPT‐1 (4.2 to 7.3 MPa) are lower than for the GT and LPT‐2 (8.9 and 13 MPa). For the 100% water saturated samples the UCS values are reduced in respect to the dry conditions, with the wet UCS of NYT and LPT‐1 (1.2 to 3.1 MPa) remaining lower than for the GT and LPT‐2 (3 to 5.1 MPa).

5.2. Fragmentation Threshold

Experiments determining the fragmentation threshold were repeated at least 2 times to account for sample variability. Results are reported in Table 1 and Figure 4c. The more porous NYT and LPT‐1 (~48 to 51%) required a lower initial pressures (1.5 to 3.1 MPa) for the full sample fragmentation. By contrast the low and intermediate porous GT and LPT‐2 (~41 % to 48%) fragmented at higher initial pressures (3.3 to 4.5 MPa). The results are in agreement with the fragmentation threshold defined in previous studies [Spieler et al., 2004] with NYT and LPT‐1 plotting slightly below the fragmentation criterion [Koyaguchi et al., 2008].

5.3. Explosive Energy at Experimental Conditions

The explosive energy due to the work of the expanding fluids (argon and steam) is estimated with respect to the experimental conditions. All experiments were run at 250°C and 4.5 MPa (section 4.1.2). The explosive energy varied in agreement with both connected porosity and amount of liquid fraction (Table 3 and Figure 5).

Table 3.

Experimental Results for Dry, Partially, and Fully Saturated Conditions at 250°C and 4.5 MPa

	H2O	Conn. Porosity (%)		E Expl‐R	E Expl‐I	E Unit vol.	v Frag		v Eject		Wt		Sorting
Sample	Added (g)	Total	Effective	(J)	(J)	(MJ/m3)	(±Err)	(m/s)	(±Err)	(m/s)	% > 4 ϕ	Mdϕ	σ
Argon expansion
NYT		50		76		2.7	9	(+1.5)	148	(±5)	2.9	−0.9	1.8
GT		45.8		67.8		2.4	6	(−1.8)	114	(±2.6)	1.9	−1.4	1.5
GT		45.9		66		2.4	4	(−0.4)	141	(±6.1)	2.5	−0.9	1.5
LPT‐1		48.6		64		2.6	8	(+1.3)	134	(±3.8)	1.6	−1.5	1.3
LPT‐2		46.8		70.6		2.5	6	(+1.3)	154	(±2.5)	2.3	−1.3	1.6
Steam flashing (50% sat.)
NYT	6.4	47.8	23.9	36.1	336.5	13.1	12	(+3)	208	(±21.1)	7.8	0.4	1.9
NYT	6	48.3	24.1	32.1	319.6	14.1	14	(−2.8)	222	(±6.8)	9.6	0.4	2.0
GT	6.1	46	23	34	320.3	12.6	7	(+1)	176	(±8.4)	6.6	0.3	1.6
GT	6.3	45.9	23	32.5	335.2	13.8	7	(−1.4)	177	(±8)	5.4	0.2	1.5
LPT‐1	6.9	49.2	24.6	37.1	366.7	14	13	(−2.2)	170	(±13.7)	10	0.9	1.7
LPT‐2	7	48.5	24.3	37.1	370.3	14	10	(−1.6)	198	(±22.7)	4.9	−0.5	1.5
Steam flashing (100% sat.)
NYT	12.6	49.6	0		669.4	23.7	55	(+1.2)	243	(±6.1)	5.7	0.9	1.7
NYT	11.5	50.3	0		611.3	24.8	56	(+9.8)	291	(±8.4)	9.9	0.6	1.9
GT	11	42.6	0		581.8	20.4	23	(−2.4)	137	(±12.9)	3.9	−0.8	1.5
GT	11.9	46	0		631.7	23.2	33	(−0.4)	194	(±10.6)	4.9	0.6	1.6
LPT‐1	13.6	48.3	0		722.6	26.3	54	(+5.7)	175	(±8.2)	5.6	0.9	1.6
LPT‐2	13.2	46.4	0		698.3	23.9	39	(−2.3)	196	(±11.4)	4.9	0	1

Figure 5.

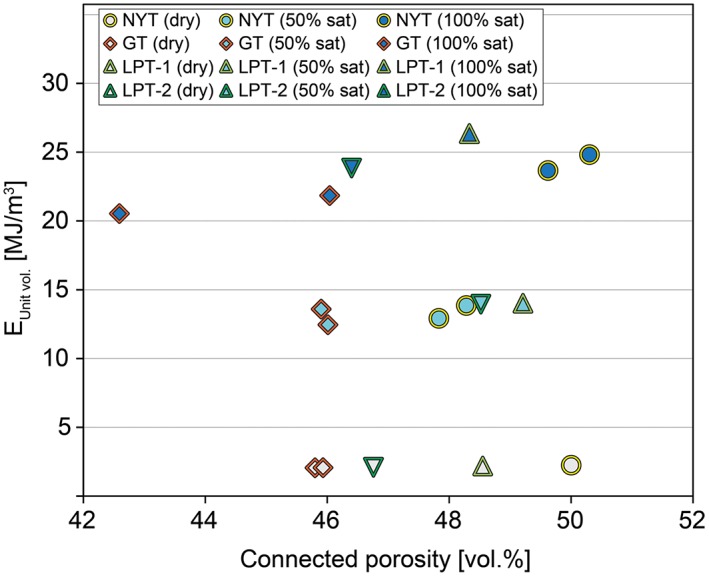
Explosive energy (E _{Unit vol.} ) as function of samples connected porosity estimated for the different experimental conditions (dry, 50% and 100% saturation). Generally, the energy increases with both porosity, and increased amount of liquid water within pore space.

For the estimation of the explosive energy under dry and partially saturated conditions we assumed that the argon behaves as an ideal gas and that the expansion is adiabatic and reversible (isentropic). By integrating equation (2) and introducing the relationship P × V^γ = constant (γ being the ratio of specific heats) the energy of expanding gas (Argon) can be calculated [Prugh, 1991] as:

$$E_{\text{Expl}‐\mathrm{R}}=\left[\frac{P\times V}{\gamma ‐1}\right]\times \left[1‐{\left(\frac{P_{\mathrm{atm}}}{P}\right)}^{\left(\frac{\gamma -1}{\gamma }\right)}\right]$$ (6)

where E _Expl‐R is the reversible explosive energy released (J), P _atm is the atmospheric pressure (bar), V is the initial volume of gas (m³), and P is the pressure (bar) in the rock pore space just before the explosive failure (Table 3). For dry experiments, equation (6) is used to estimate the reversible energy E _Expl‐R associated to the argon expansion (AE). For partially saturated conditions, the pore volume not filled by water (effective porosity; Table 2) is used to estimate the explosive energy of AE.

In presence of steam flashing (SF), the irreversible approach (section 2) was used to calculate the steam fraction, allowing for a more realistic estimation [Thiéry and Mercury, 2009]. The expansion under irreversible conditions produce final states which are much more drier mixture with respect to the isentropic expansion. The former yielded 31.7% of steam (by using equation (3), whereas the latter resulted in 24.6% of steam (as calculated from steam table; see also Figure 3b). Thus, the estimated steam fraction with equation (4) served to determine the irreversible explosive energy E _Expl‐I for the SF case (Table 3). In general, the dry conditions resulted to be the less powerful (54 to 64.4 J). In the case of partially saturated conditions the energy source is a combination of AE and SF; a lower energetic contribution is estimated for the AE (27.2 to 31.5 J) then for the SF component (319.6 to 370.3 J). The fully saturated conditions produced the most energetic explosions (581.8 to 698.3 J).

In the following, the estimated explosive energy is expressed per unit volume of fluid (E _{Unit vol.}) prior to explosive failure and is used to discuss the energies of the different samples (Table 3):

1. The NYT with a connected porosity of 50% accounted for an energy release of 2.3 MJ/m³ for the dry case. Under partially saturated condition, and for samples with an effective porosity of 23.9–24.1% that retained 6 to 6.4 g of water, an energy release of 12.9 to 13.9 MJ/m³ is calculated. The 11.5–12.6 g of water retained under fully saturated conditions equates to an energy release of 23.7 to 24.8 MJ/m³.

2. The GT with a connected porosity range of 45.8–45.9% allowed for an energy release of 2.1 MJ/m³ under dry conditions. For the partially saturated case, an effective porosity of ~23% accounted for 6.1 to 6.3 g of water, resulting in a energy release of 12.5–13.6 MJ/m³. Under fully saturated conditions the 11–11.9 g of trapped water permitted an energy release of 20.4 to 23.2 MJ/m³.

3. The LPT‐1 with its 48.3% connected pore volume allowed an energy release of 2.2 MJ/m³ in the dry case. Under a partial saturation condition, the 24.6% effective porosity together with the 6.9 g of retained water allowed an energy release of 14 MJ/m³. In case of fully saturated samples, 13.6 g of pore water accounted for an energy release of 26.3 MJ/m³.

4. The LPT‐2 with its 46.8% connected pore volume allowed for an energy release of 2.1 MJ/m³ in the dry case. For partial saturation condition, an effective porosity of 24.3% and 7 g of retained water equates to an energy release of 14 MJ/m³. Under fully saturated conditions, 13.2 g of pore water permitted for an energy release of 23.9 MJ/m³.

Figure 5 shows the relationship between the estimated energy per unit volume as function of the connected porosity which characterizes the different investigated tuffs. Although all three data sets exhibit some scattering due to the natural variability of the tuff core sample, a positive correlation between explosive energy (and therefore on the initial degree of saturation) with sample porosity can be observed. Thus, the surplus of available energy in presence of SF allows for 1) a shift of grain size toward finer size, with the production of larger amounts of very fine material (section 5.4); 2) a higher fragmentation speed (section 5.5); and 3) a higher ejection speed (section 5.6).

5.4. Grain Size Distribution

All experiments were performed at initial pressure of 4.5 MPa, which is well above the fragmentation threshold for samples (Table 1 and section 5.2). The cumulative size distributions for the different tuffs, obtained by summing the weight for each experiment in dry, partially, and fully saturated condition, are shown in Figure 6. Table 3 displays the graphic median diameter (Mdϕ), sorting (σ), and the weight percent of fines (>4ϕ) for each experiment (also shown in Figure 7). Generally for volcanic rocks the grain size distribution is shifted toward fines with increased energy for fragmentation [Spieler et al., 2003; Kueppers et al., 2006]. The following characteristics of the four sets have been observed:

1. NYT: for these highly porous samples (up to 50.3%) the coarsest grain size distribution (Md −0.9ϕ) results from dry conditions, with partial (−0.4ϕ) and fully water saturated conditions (0.6 to 0.9ϕ) showing progressively finer overall grain size. A poorly to very poorly sorted distribution (1.7 to 2σ) characterizes the produced fragments at all conditions. Fine (>4ϕ) production increased from 2.9% for the dry case to 7.8–9.6% for the partial and 5.6–9.9% for fully water saturated ones.

2. GT: for these low‐porosity samples (down to 42.6%) the AE causes a very coarse grain size distribution (Md −1.4 to −0.9ϕ), whereas partial (0.2 to 0.3ϕ) and fully water saturated conditions (0.6ϕ) generate smaller particles. A poorly sorted distribution (1.5 to 1.6σ) of the fragmented material results from all the experiments. All conditions produced few fines (>4ϕ), with 2.5 wt % resulting from the dry case, 5.4–6.6 wt % from partial and 3.9–4.9 wt % from fully water saturated case.

3. LPT‐1: as for the NYT, samples from this group are quite porous (up to 49.2%). A coarse grain size distribution, with a median diameter of −1.5ϕ, resulted from the dry experiment, but finer overall clast size is produced under partial and fully water saturated conditions (Md 0.9ϕ). A poorly sorted distribution (1.3 to 1.6σ) of the fragmented material results from all the conditions. In the case of fines (>4ϕ), dry conditions produced 2.9 wt %, while partially generated 10 wt % and fully water saturated conditions 5.6 wt %.

4. LPT‐2: these samples also produced a very coarse grain size distribution under dry conditions (Md −1.3ϕ), which progressively decreases for the partially (−0.5ϕ) and fully water saturated (0ϕ) cases. A poorly sorted distribution (1 to 1.6σ) characterize the produced fragments at all conditions. LPT‐2 produced a minor amount of fine material (>4ϕ) compared to the LPT‐1, with a weight percent of 2.3% generated by the AE, and 4.9% resulting from both partially and fully saturated conditions.

Figure 6.

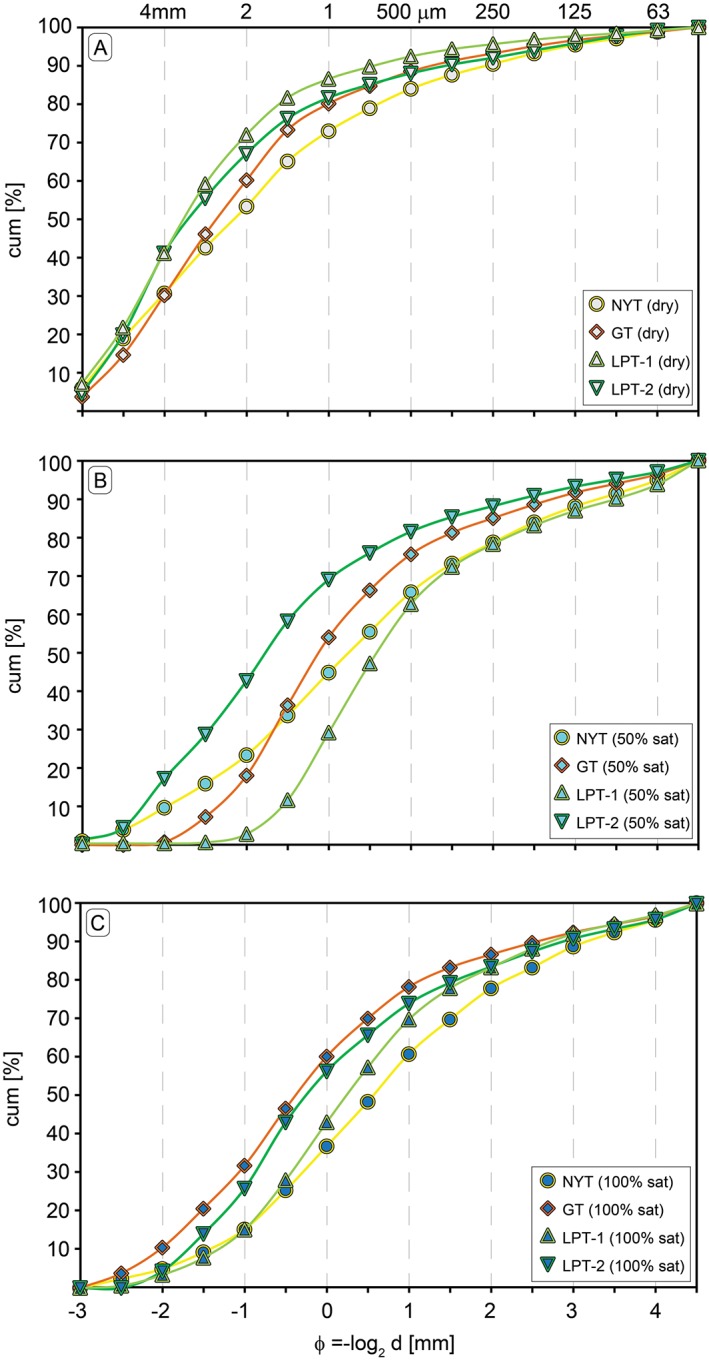
Cumulative grain size distribution plots for (a) dry, to (b) 50% and (c) 100% saturation conditions. The plots show the weight fractions of particles after rapid decompression experiments at 250°C and 4.5 MPa in half‐ϕ steps (ϕ = −log₂ d, with d = particle diameter in millimeter), and in millimeter scale. From dry to fully saturated conditions, the average particle size is decreasing in all plots.

Figure 7.

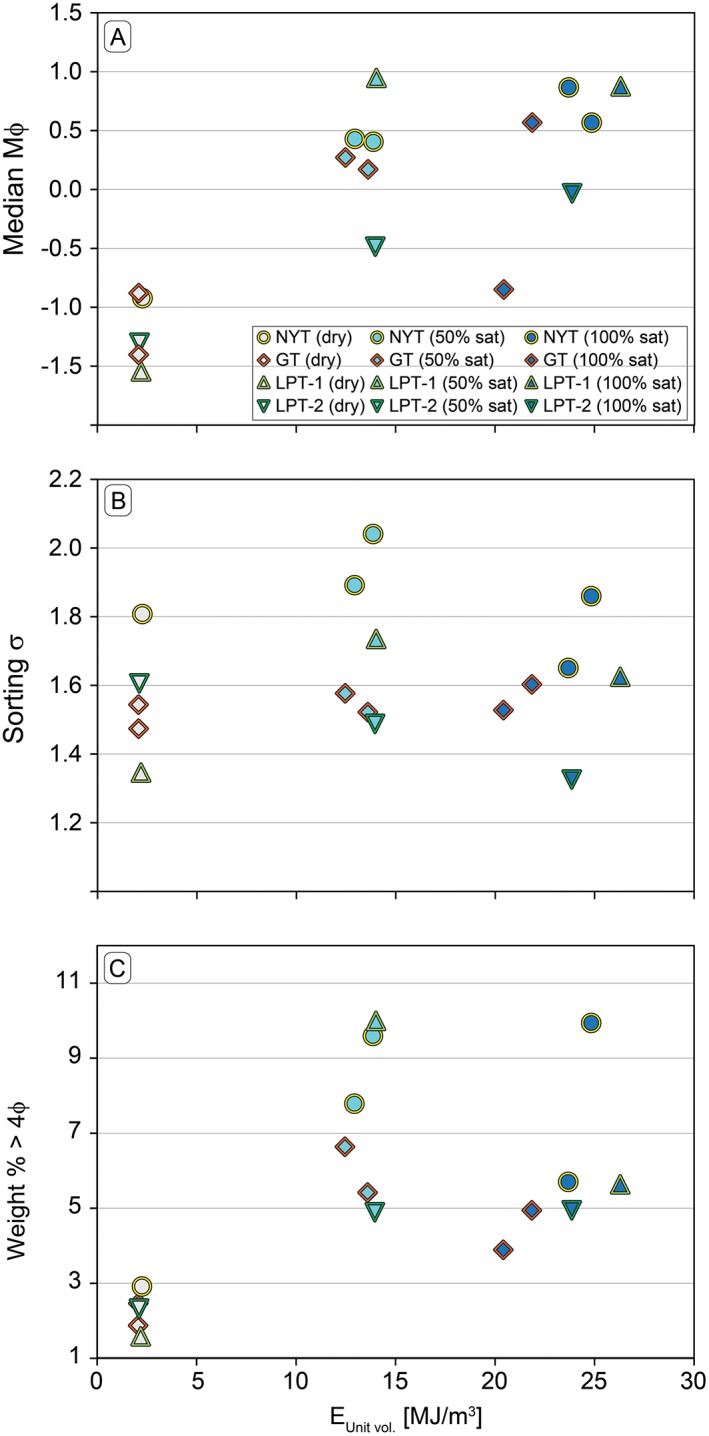
(a) Median Mdϕ, (b) particles sorting, and (c) weight % of fines >4ϕ as function of the explosive energy (E _{Unit vol.} ) for the different experimental conditions (dry, 50%, and 100% saturation). Although the plots exhibit some scattering in the explosive energy, due to the natural variability in the sample porosity, a positive correlation between this and the different parameters can be observed. In the presence of steam flashing, and for similar energetic values, the weaker NYT and LPT‐1 produce and higher amount of fine material. Noteworthy, the highest values of Mdϕ, σ, and weight of fine (>4%) are reached already for the partial saturation condition, and no further increase is observed for the full saturated samples.

5.5. Fragmentation Speed

The fragmentation speed (v _Frag) was measured for all samples and under all conditions. Mean values are reported in Table 3 and plotted as function of the explosive energy (E _{Unit vol}) in Figure 8a. Fragmentation speeds resulting from steam flashing (SF) experiments show a broad range of values depending on the initial degree of sample saturation as well as sample type. The following observations could be made for the three groups of conditions:

1. Dry conditions: fragmentation is driven purely by argon expansion (AE). The obtained speed values in this case are generally low. The NYT (9 m/s) and LPT‐1 (8 m/s) show a higher fragmentation speed with respect to GT (4 to 6 m/s) and LPT‐2 (6 m/s).

2. Partial water saturation (50%): fragmentation is driven by AE mixed with SF. In this case slightly higher fragmentation speed values, with respect to dry conditions, are obtained for NYT (12 to 14 m/s), LPT‐1 (13 m/s), LPT‐2 (10 m/s), and GT (7 m/s).

3. Full water saturation (100%): fragmentation is driven by solely SF. In this case the fragmentation speed is significantly higher than for partially water saturated and dry experiments. The NYT (55 to 56 m/s) and LPT‐1 (54 m/s) show the higher fragmentation speeds in comparison to the GT (23 to 33 m/s) and LPT‐2 (39 m/s).

Figure 8.

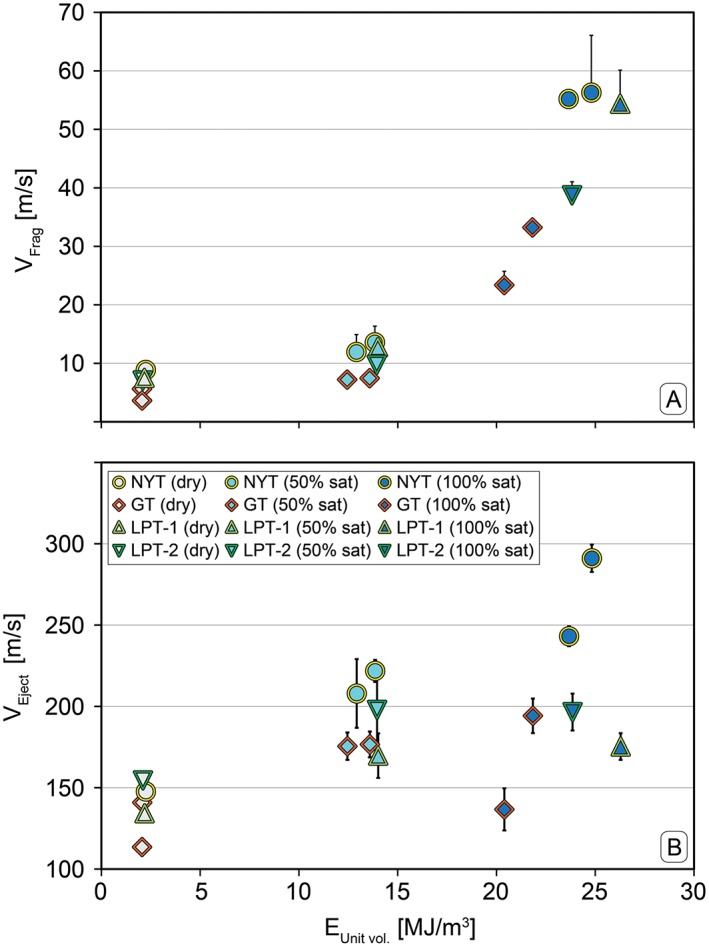
Evaluation of (a) fragmentation speed v _Frag and (b) ejection velocity v_Eject as function of the explosive energy (E _{Unit vol.} ) for the different experimental conditions (dry, 50%, and 100% saturation). An increase in fragmentation speed and ejection velocities of particles occurs from dry to fully water‐saturated conditions. The scattering in the explosive energy is mainly due to the natural variability in the tuff porosity.

The scattering of the obtained fragmentation speeds is mainly due to the natural variability of the sample's petrophysical properties. The errors for the fragmentation speed values are in the range between −2.4 to +9.8 m/s and are reported in Table 3.

5.6. Ejection Velocities

Particle ejection velocities (v _Eject in Table 3) were computed from the displacements of individual particles tracked across five successive frames of the high‐speed footage. The errors for the ejection velocities are in the range of ±22 m/s and are also reported in Table 3. An average speed of those particles at the absolute flow front was calculated by using (≥5) particle velocities [Mayer et al., 2015]. The velocities thus obtained are an approximation of the true maximum velocity, since the images are 2‐D renderings, perpendicular to the line of sight. In general, the ejection velocities show dependencies on the energy source, and therefore on the initial degree of saturation (Figure 8b and section 5.3).

In particular, the particles from the more porous NYT show the highest speed under dry (148 m/s), partially (208 to 222 m/s), full water saturation conditions (243 to 291 m/s). For the GT ejection velocities increased from dry (114 to 141 m/s), to partially (176 to 177 m/s), and full water‐saturated samples (194 m/s). A very low ejection velocity of 137 m/s was measured for one very low connected porosity sample at fully saturated conditions. Despite the relatively high explosive energy estimated for LPT‐1, quite low ejection velocities have been measured for dry (134 m/s), partially (170 m/s), and fully water‐saturated conditions (175 m/s). For the LPT‐2 instead, velocities increase from dry (145 m/s) to partial (198 m/s) and fully water saturated conditions (197 m/s).

6. Discussion

6.1. Effect of Liquid Fraction

Steam‐driven eruptions are common in many volcanic terrains as well as other areas of high heat flow, where depressurization may involve high‐temperature and liquid‐dominated hydrothermal reservoirs. For the known cases a maximal focal depth of the explosion has been estimated up to 450 m, where incipient boiling occurs at 260°C and 4.5 MPa [Browne and Lawless, 2001]. Many hydrothermal eruptions, on a wide range of size, are thought to initiate very close to the ground surface, where a flashing front generates due to local perturbations (seismic activity, pressure reduction by landslide, lake drainage, etc.) and migrates downward into the reservoir [Browne and Lawless, 2001; Montanaro et al., 2016a, 2016b]. The presence of dissolved gas in the liquid mainly controls the boiling temperature and thus the depth of initial flashing [McKibbin, 1996], not affecting the front‐migration mechanism. However, dissolved gases (e.g., CO₂) in the hydrothermal fluids could also be present, either due to normal magma degassing or related to fluid injection processes. These would drive the liquid stability field toward lower temperatures and enhance the explosivity compared to pure water [Nelson and Giles, 1985; Thiéry and Mercury, 2008; Thiéry et al., 2010; Hurwitz et al., 2016]. An experimental temperature of 250°C and a pressure of 4.5 MPa have been used in this study. For this condition water remains in the liquid state, yet very close to the boiling point. The argon gas used to pressurized the system (see section 4.1.2) is not expected to significantly dissolve in the liquid water. Notably, our experimental conditions are very close to the boiling point. Consequently, only a limited expansion of the gas within the (effective) pore space may contribute to a fragmentation process when the liquid‐vapor phase boundary is crossed. Thus for partially saturated conditions, steam flashing (SF) dominate over the argon expansion (AE).

According to our results, eruptions accompanied by an increasing amount of water flashing to steam are significantly more violent that those driven purely by gas expansion. From dry to partial and fully saturated conditions, an increase in explosive energy per unit volume from ~2 to ~14 and ~26 MJ/m³, respectively, has been estimated. Thus, compared to AE, the amount of available energy associated to SF is of 1 order of magnitude higher.

6.2. Effect of Rock Connected Porosity, Permeability, and Strength

The heterogeneous tuff samples used in this study show a range of connected porosity from 42.6 and 50.3% and a range of permeability from 2 × 10⁻¹⁵ and 4.3 × 10⁻¹³ m². The host‐rock reservoir of the hydrothermal system below Solfatara crater is thought to be built of similar tuff deposits (section 3.1). The same lithologies have also been described as lithic components within the deposits of the phreatic phase accompanying the formation of Solfatara crater itself [Isaia et al., 2015].

A decompression event (e.g., fracturing and variance in the groundwater level) may trigger explosive vaporization of water or disrupt the stress equilibrium between the pressurized gas phase and its surrounding rocks. In such a case, porosity and permeability of rocks are key factors in controlling the explosive behavior of a hydrothermal system [Mueller et al., 2011]. The former controls the amount of fluid stored and therefore the energy available for release during fragmentation for a given decompression step [Alatorre‐Ibargüengoitia et al., 2010]. The latter determines whether the expanding fluid may either fragment the surrounding rocks or escape from it via effective outgassing along an existing network of cracks and interconnected pores [Scheu et al., 2006; Mueller et al., 2008; Richard et al., 2013]. Both properties in turn affect the fragmentation behavior [Mueller et al., 2008]. Additionally, the rock strength may result in a different fragmentation process, enhancing or reducing the production of fine material [Montanaro et al., 2016a].

Under our experimental conditions, explosive energy increases with water content and connected porosity (Table 3 and Figure 5). All investigated tuffs show a permeability below the cutoff value of 10⁻¹² m² described by Mueller et al. [2008]. Accordingly, the fragmentation process should not be affected by pressure loss through fast outgassing during the decompression. This can also be seen by the fact that the tuffs with the highest permeability (NYT and LPT‐1) are those showing a higher amount of produced fines and a lower average grain size (Figures 7a and 7c and Table 3). Finally, the lower strength of some of the tuffs (NYT and LPT‐1; see also sections 5.1 and 5.2) appears to result in an increased percentage of fine material (Figure 7c).

In some way these results suggest that fine‐grained tuffs, which may have a high porosity but a low permeability, can be highly susceptible to rapid decompression events by 1) creating a barrier to overpressurized gas and 2) being capable to store a large quantity of water, and thus bearing high explosive energy. Moreover, processes like thermal weakening and hydrothermal alteration (see section 3.1) are needed to be taken into account, since these can either increase or reduce the tuffs connected porosity, permeability, and strength [Heap et al., 2014; Mormone et al., 2015; Mayer et al., 2016].

6.3. Fragmentation Behavior

The energy surplus present in the form of excess water has the ability to decrease the average grain size and enhance the production of very fine particles [Rager et al., 2014; Montanaro et al., 2016a] (Figure 7). A clear shift toward finer grain size is represented by the variation of the median diameter (Mdϕ in Figure 7a). The produced material is generally poorly to very poorly sorted (1 to 2σ), with the NYT showing a very broad distribution across all experimental conditions (Figure 7b). A significant increase in the amount of the very fine fraction (>4ϕ) is observed for samples fragmenting under partial and full water saturated conditions, in particular for the highly porous NYT and LPT‐1 samples (Figure 7c). The comparison of the sample permeability (Table 2) with both median values and weight percentage of fines (Table 3) suggests that under dry conditions there is not significant change in the fragmentation behavior. For the partially and fully saturated conditions a slight decrease in the average size, as well as an increase in the production of very fine particles, occurs at increasing sample permeability. These results may be explained as to be due to the overprint of the porosity (and then the explosive energy) effect.

In general, the highest values of median diameter, weight of fine (>4%), and (subordinately) sorting are reached for the partial saturated conditions, whereas no further increase is observed for fully saturated samples (Figure 7). This result may depend upon both our experimental conditions (section 6.1) and sample properties (section 6.2). Despite the increase in liquid fraction, the released energy may not be enough to enhance the efficiency in producing fine material [Kueppers et al., 2006].

6.4. Fragmentation Speed and Ejection Behavior

Both the fragmentation speed and ejection velocity are controlled by the initial overpressure within the pores, the connected porosity, the permeability, and the strength and brittleness of the sample [Scheu et al., 2006; Richard et al., 2013]. In this study we demonstrate that the decompression of liquid water plays a further key role [Rager et al., 2014; Mayer et al., 2015], as already discussed for hydromagmatic events which generally produce higher ejection velocities than magmatic ones [Fisher and Schmincke, 1984; Mastin, 1995].

The produced experimental decompression, from 4.5 MPa to ambient pressure, results in the flashing and expansion of superheated water (250°C). This causes approximately 24‐fold larger volume increase with respect to pure argon expansion under same conditions. Thus, the presence of steam flashing is additionally enhancing the gas expansion which powers the fragmentation processes [Mastin, 1995; Mayer et al., 2015; Montanaro et al., 2016a], accounting for an increase in energy and in turn for a faster ejection of particles [Alatorre‐Ibargüengoitia et al., 2011] (Figure 8).

In particular, and in agreement with results from previous investigations [Mayer et al., 2015], a drastic increase in fragmentation speed (up to 56 m/s) occurs from dry to fully water‐saturated samples. Whereas from dry (9 m/s) to partial water saturation (14 m/s) only a slight increase in speed is observed. The ejection velocities of the particles increase as well from dry (max 154.5 m/s) to partially (max 222 m/s) and fully saturated conditions (max 291 m/s).

The highest fragmentation speed and particle ejection velocity is yielded by the NYT under all the experimental conditions, possibly resulting from its high porosity (up to 50.3%). Their low sample strength further contributes to a lower fragmentation threshold (1.5–1.7 MPa), which implies that less energy is consumed by fragmentation; thus, more energy remains to expel the fragments [Alatorre‐Ibargüengoitia et al., 2010].

7. Conclusions

We conducted rapid decompression experiments on heterogeneous tuffs from the Campi Flegrei caldera, characterized by a range of petrophysical properties. The experiments were designed to mimic a steam‐driven explosive event by rapid depressurization of fluids within the rock pore space. We explored the influence of the liquid fraction, as well as of the rock properties, on the explosive power and in turn on the fragmentation and ejection behavior. The comparison of the experimental results with thermodynamic modeling based on an irreversible approach allowed us to estimate the explosive energy released. At initial conditions of 250°C and 4.5 MPa, rapid decompression to atmospheric pressure triggered fluid (argon and/or water‐steam) expansion, rock fragmentation, and ejection of particles. Our findings indicate the following:

1. The increasing liquid fraction within the pore space increases the explosive energy; for the fully saturated condition the energy released by steam flashing can be estimated to be 1 order of magnitude higher than for the solely argon expansion.

2. The released energy increases with sample connected porosity and is not dissipated through (rapid) outgassing during the fragmentation as all tuffs are of low permeability.

3. The energy surplus in the presence of steam flashing leads to an increased fragmentation speed and a higher ejection velocity of the fragmented particles.

4. The vaporization occurring under 50% water saturation conditions has the ability to increase the degree of fragmentation and to decrease the average ejecta size.

5. The material strength showed a secondary but observable effect on the fragmentation behavior for the investigated tuffs.

An increased liquid fraction during decompression together with the rock porosity are important fragmentation variables that should be considered for modeling of steam‐driven eruptions in hydrothermally active environments. In contrast, strength and rock texture may affect the rate of energy release and need further investigations. Overall, a potential hazard may be associated to destabilization of a hydrothermal systems under conditions including temperatures >250°C, rock porosity >40%, and small fraction of water in a liquid state, yet close to the boiling point.

Montanaro, C. , Scheu B., Mayer K., Orsi G., Moretti R., Isaia R., and Dingwell D. B. (2016), Experimental investigations on the explosivity of steam‐driven eruptions: A case study of Solfatara volcano (Campi Flegrei), J. Geophys. Res. Solid Earth, 121, 7996–8014, doi: 10.1002/2016JB013273.