Deciphering the Variability in Mg/Ca and Stable Oxygen Isotopes of Individual Foraminifera

Abstract

Foraminifera are commonly used in paleoclimate reconstructions as they occur throughout the world's oceans and are often abundantly preserved in the sediments. Traditionally, foraminifera‐based proxies like δ¹⁸O and Mg/Ca are analyzed on pooled specimens of a single species. Analysis of single specimens of foraminifera allows reconstructing climate variability on timescales related to El Niño–Southern Oscillation or seasonality. However, quantitative calibrations between the statistics of individual foraminifera analyses (IFA) and climate variability are still missing. We performed Mg/Ca and δ¹⁸O measurements on single specimens from core top sediments from different settings to better understand the signal recorded by individual foraminifera. We used three species of planktic foraminifera (Globigerinoidesruber (s.s.), T. sacculifer, and N. dutertrei) from the Indo‐Pacific Warm Pool and one species (G. ruber (pink)) from the Gulf of Mexico. Mean values for the different species of Mg/Ca versus calculated δ¹⁸O temperatures agree with published calibration equations. IFA statistics (both mean and standard deviation) of Mg/Ca and δ¹⁸O between the different sites show a strong relationship indicating that both proxies are influenced by a common factor, most likely temperature variations during calcification. This strongly supports the use of IFA to reconstruct climate variability. However, our combined IFA data for the different species only show a weak relationship to seasonal and interannual temperature changes, especially when seasonal variability increases at a location. This suggests that the season and depth habitat of the foraminifera strongly affect IFA variability, such that ecology needs to be considered when reconstructing past climate variability.

Key Points

• Variability in Mg/Ca and δ¹⁸O of individual foraminifera analyses (IFA) shows a strong relationship suggesting a common factor of influence

• Temperature is identified as the main common factor controlling both proxies supporting the use of IFA to reconstruct climate variability

• The weak relationship of the IFA data to seasonal and interannual variability suggests that ecology plays an important role

1. Introduction

Foraminifera are commonly used in paleoclimate reconstructions as they occur throughout the world's oceans and are easily preserved in the sediments. Traditionally, proxies like stable oxygen isotopes and Mg/Ca are analyzed on samples consisting of many pooled specimens of a single species. As a typical sediment sample includes the recordings of several up to hundreds or even thousands of years but a single specimen only lived and recorded several weeks, a larger number of 10–100 specimens is needed to provide a representative signal of the paleoclimatic parameter that is to be reconstructed (Katz et al., 2010; Laepple & Huybers, 2014; Lea, 2004; Nürnberg, 2000; Rosenthal et al., 2000; Schiffelbein & Hills, 1984). In the early eighties, it was already shown that the variation in stable isotope values in single specimens (individual foraminifera analysis (IFA); also known as single specimen analysis, individual specimen analysis, or single foraminifer analysis (e.g. Metcalfe et al., 2015; Thirumalai et al., 2013; Wit et al., 2010)) from the same sediment sample was much larger than expected from just long‐term temperature variations (Killingley et al., 1981; Schiffelbein & Hills, 1984). This was linked to varying water depths of calcification for different specimens and used by Schiffelbein and Hills (1984) to estimate the uncertainty of analyses commonly performed on pooled specimens. Many studies then investigated additional factors that can impact variations in single shell δ¹⁸O, including bioturbation (Billups & Spero, 1996; Stott & Tang, 1996), interspecific shell ontogeny (Spero & Williams, 1990), photosymbiont influences (Houston et al., 1999; Spero & Lea, 1993), seasonal salinity changes (Spero & Williams, 1990; Tang & Stott, 1993), discrepancies between living and recently fossilized individuals (Waelbroeck et al., 2005), or genetic differences within the same morphospecies (Morard et al., 2016; Sadekov et al., 2016). More recently, it was suggested that this variation within the same sample can be linked to shorter timescale climate variability related to El Niño–Southern Oscillation (ENSO; Khider et al., 2011; Koutavas et al., 2006; Leduc et al., 2009; Rustic et al., 2015; Sadekov et al., 2013; Scroxton et al., 2011) or the seasonal cycle (Ganssen et al., 2011; Metcalfe et al., 2015; Vetter et al., 2017; Wit et al., 2010). These studies used analyses of stable oxygen isotopes (δ¹⁸O) on individual foraminifera from the same sediment samples to determine short‐term variations. However, to what extent the IFA variations in δ¹⁸O are suitable to reconstruct past climate variability is still an open question.

Assessing different parameters of the same sample may help to identify a common driving factor of IFA variability. Mg/Ca and δ¹⁸O are analyzed on the same biotic carrier, and therefore, differences in season and habitat are avoided in the proxy signal recorded by the foraminiferal tests (Nürnberg, 2000). δ¹⁸O is already routinely measured on single specimens, but Mg/Ca in individual foraminifera has mainly been analyzed by laser ablation inductively coupled plasma‐mass spectrometry. Laser ablation has been instrumental in demonstrating that trace elements are heterogeneously distributed throughout tests related to banding during biomineralization or the deposition of primary versus secondary calcite (Eggins et al., 2004; Sadekov et al., 2008; Hathorne et al., 2009; Wit et al., 2010; Spero et al., 2015). Additionally, the effects of diagenesis can be identified by laser ablation (Groeneveld et al., 2008; Van Raden et al., 2011). Despite the advantage of laser ablation analyses for determining intratest variability, it takes many laser profiles to give a representative signal in order to be directly compared to IF analyses of δ¹⁸O (De Nooijer et al., 2014).

Flow‐through time resolved analysis and automated cleaning provides an alternative for the rigorous manual cleaning of samples for Mg/Ca (Haley & Klinkhammer, 2002). Samples are placed on a filter and then connected to an automated cleaning device, which reduces the loss of sample material during the cleaning process. This allows the analysis of trace metal/Ca in individual foraminifera (Haarmann et al., 2011), very small samples (McKay et al., 2015), or to separate diagenetic and primary calcite (Klinkhammer et al., 2009).

In this study, we analyze the Mg/Ca of individual foraminifera using flow‐through automated cleaning and analyze δ¹⁸O on individual foraminifera from the same sediment sample. This dual approach allows us to explore whether the spread between single measurements in individual foraminifera is related to environmental parameters and hence climate (e.g., seasonality) or is rather dominated by analytical and processing uncertainties. We use four species of planktic foraminifera (Globigerinoides ruber (sensu stricto (s.s.)), G. ruber (pink), Trilobatus sacculifer, and Neogloboquadrina dutertrei) from core top sediments representing a range of oceanic conditions. Core tops originate from the Indo‐Pacific Warm Pool (IPWP), both from the warm pool and from upwelling‐affected areas, and from the Gulf of Mexico (GoM), which experience seasonal variations in sea surface temperature (SST) between 1 and 7 °C (Table 1). We analyze for the first time combined individual foraminifer (IF) Mg/Ca and δ¹⁸O both on single specimens from the same samples and show that these independent parameters show similar distributions. As the sample processing and analytics are different for both proxies, this provides strong evidence for a common climatic origin of the Mg/Ca and δ¹⁸O signal. We further show that their distributions cannot be explained solely by seasonal or interannual temperature variations but are likely also related to changing habitat preferences and/or oceanographic conditions.

Table 1.

Location of the Different Core Tops Used in This Study and Which Proxies Were Performed per Species of Planktic Foraminifera for Both Pooled and Single‐Specimen Samples

Core top	Latitude	Longitude	Water depth (m)	Seasonal range SST (°C)a	Sample depth (cm)	T. sacculifer Mg/Ca‐δ18O	N. dutertrei Mg/Ca‐δ18O	G. ruber Mg/Ca‐δ18O
GeoB 10008‐4	0.95°S	98.26°E	936	1.21	1–2	x x	x x
GeoB 10058‐1	8.68°S	112.64°E	1,103	2.28	1–2	x x	x x
GeoB 10069‐4	9.60°S	120.92°E	1,249	3.64	1–2	x x	x x	xb xc
GeoB 17426‐2d	2.11°S	150.51°E	1,365	0.93	0–1	x x	x x	xb xc
2010‐GB2‐MC	26°40.19′N	55.22°W	1,776	6.85	0–0.5			x xe

^aThe seasonal range in sea surface temperature (SST) was extracted from WOA13 (Locarnini et al., 2013).

^bOnly pooled‐specimen analyses were performed for these samples due to low availability of suitable specimens.

^c G. ruber (s.s.).

^dThis sample was radiocarbon dated using T. sacculifer at the Keck Carbon Cycle Accelerator Mass Spectrometry Laboratory, University of California, Irvine (UCIAMS 142722) with fraction modern carbon (F¹⁴C; 0.9489 ± 0.002) and ¹⁴C age of 420 ± 20. Using a ΔR of 111 years (Petchey & Ulm, 2012) a calendar age of 309 results.

^e G. ruber (pink).

2. Oceanographic and Ecological Setting

Core top locations were selected based on particular oceanic conditions to include a wide range of settings (Figure 1) in terms of variability experienced. We selected one location from the Western Pacific Warm Pool (WPWP) just north of Papua New Guinea (PNG), three locations along the western coast of Indonesia (Northern Mentawai Basin (NMB), Lombok Basin, and Savu Sea), and one location from the GoM (Figure 1). The main varying characteristic between these locations is seasonality in seawater temperatures. The PNG and NMB locations are typical warm pool sites with low seasonality in temperature (seasonal range in SST ~ 1 °C; Table 1 and Figures 1 and 2), oligotrophic conditions, and a deep thermocline, although the NMB does experience significant subsurface temperature variability (Mohtadi et al., 2011). The Lombok Basin and Savu Sea are also part of the IPWP but experience stronger seasonal changes in SST (~2–4 °C; Table 1 and Figure 2) and thermocline‐depth during the austral winter when the southeast monsoon causes Ekman‐induced upwelling (Table 1; Mohtadi et al., 2011). Calcification depth of T. sacculifer is within the mixed layer varying between 40 and 95 m in the WPWP and between 20 and 50 m off Indonesia (Hollstein et al., 2017; Mohtadi et al., 2011). Although N. dutertrei occurs throughout the year, the maximum flux of specimens occurs during the upwelling season off Indonesia, and its estimated habitat depth varies between 75 and 100 m, while in the WPWP, it varies between 90 and 160 m (Hollstein et al., 2017; Mohtadi et al., 2011).

Figure 1.

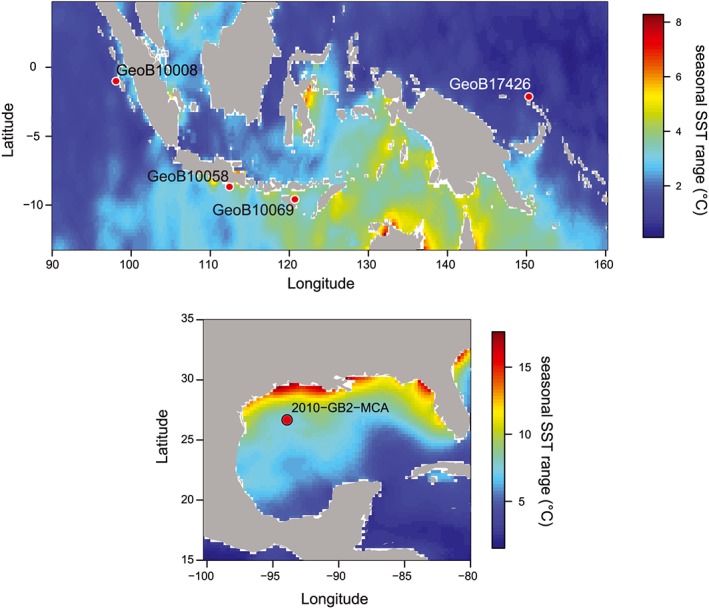
(a) Map with site locations in Indonesia (GeoB 10008‐4 (Northern Mentawai Basin); GeoB 10058‐1 (Lombok Basin); GeoB 10069‐4 (Savu Sea)) and the Western Pacific Warm Pool (GeoB 17426‐2 (Papua New Guinea)). (b) Map with the site location of 2010‐GB2‐MCA in the Gulf of Mexico. Color bar indicates the seasonal range in sea surface temperature (SST) extracted from WOA13 (Locarnini et al., 2013).

Figure 2.

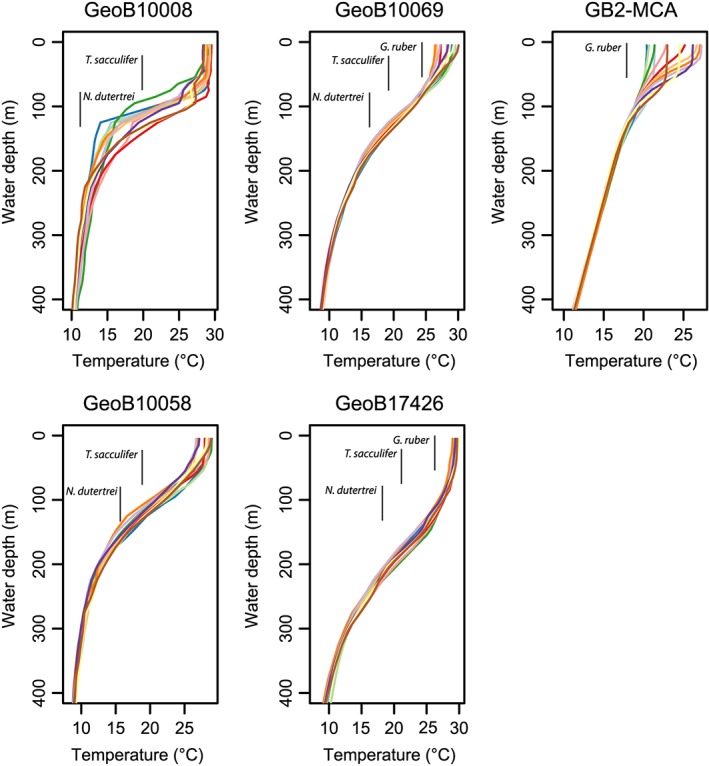
Climatological seawater temperature profiles at the site locations. The monthly water temperatures from the WOA13 database (Locarnini et al., 2013) are shown (one profile per month). Vertical lines show the assumed habitat depth ranges for G. ruber (top), T. sacculifer (middle), and N. dutertrei (bottom).

The location in the GoM was selected because of its large seasonality. Seasonal surface temperature and salinity variations of > up to 7°C (Table 1) and 0.23 salinity units, respectively, occur because the seasonal migration of the Intertropical Convergence Zone (ITCZ) moves the warm Loop Current into the GoM during boreal summer, while during boreal winter the southward migration of the ITCZ keeps the Loop Current outside of the GoM (Poore et al., 2013). G. ruber (pink) is one of the dominantly present foraminifer species in the GoM and occurs throughout the year but with highest fluxes generally during the warm season (Poore et al., 2013). The habitat depth of G. ruber is generally within the upper 50 m of the water column. In this study, we analyzed only G. ruber (pink) in the GoM as the abundance of G. ruber (s.s.) was insufficient.

3. Methods and Material

The core tops from the IPWP were collected during the R/V SONNE 228 (GeoB 17426‐2; Mohtadi et al., 2013) and R/V SONNE 184 (GeoB 10008‐4, GeoB 10058‐1, and GeoB 10069–4; Hebbeln et al., 2005) expeditions (Table 1). The core tops off Indonesia were AMS‐¹⁴C dated as modern (>1950 CE; Mohtadi et al., 2011). Core top GeoB 17426‐2 has a calibrated AMS‐¹⁴C age of 309 year BP (Table 1). Core top 2010‐GB2‐MC from the GoM was collected in Summer 2010 on the R/V Cape Hatteras and was AMS‐¹⁴C dated as modern (>1950 CE; Thirumalai et al., 2018).

The planktic foraminiferal species G. ruber (s.s.), G. ruber (pink), T. sacculifer (without sac‐like final chamber), and N. dutertrei (dextral) were picked for the analysis of stable oxygen and carbon isotopes, and Mg/Ca. All foraminifera were picked from the 315‐ to 400‐μm size fraction. For IFA of Mg/Ca, one specimen per analysis was used for T. sacculifer and N. dutertrei, and two specimens for G. ruber due to the smaller amount of calcite per specimen. Using two specimens per analysis reduces the standard deviation and expected range by $\sqrt{n}$, where n is the number of specimens used in the samples, in this case n = 2. After rescaling with this factor of ~1.4, the two‐specimen analysis can be compared with the single‐specimen analyses of T. sacculifer and N. dutertrei. For simplicity, if not stated otherwise, all values in the text, table, and figures are rescaled to represent the statistics of single‐specimen analyses and we call all the analyses (whether based on two or single specimen) single‐specimen analyses.

For pooled analyses of Mg/Ca, 25 specimens per sample were used for T. sacculifer and N. dutertrei, and 40 specimens for G. ruber. For stable oxygen isotopes, three to four specimens for N. dutertrei, four to five specimens for T. sacculifer, and five to six specimens for G. ruber were used for the pooled samples, while for IFA, one specimen per sample was used for T. sacculifer and N. dutertrei, and two specimens for G. ruber were needed to have enough material for analysis. All data presented here are stored in the Pangaea database (www.pangaea.de).

3.1. Mg/Ca

After gentle crushing, the shell fragments of the pooled samples were cleaned according to the standard cleaning protocol for foraminiferal Mg/Ca analyses (Barker et al., 2003). After dissolution, samples were centrifuged for 10 min (6,000 rpm) to exclude any remaining insoluble particles from the analyses. Samples were diluted with Seralpur water before analysis with inductively coupled plasma‐optical emission spectrometry (ICP‐OES; Agilent Technologies, 700 Series with autosampler ASX‐520 Cetac and micro‐nebulizer) at MARUM, University of Bremen. Instrumental precision of the ICP‐OES was monitored every five samples by analysis of an in‐house standard solution with a Mg/Ca of 2.93 mmol/mol (long‐term standard deviation of 0.026 mmol/mol or 0.88%). The ECRM752‐1 limestone standard, with a reported Mg/Ca of 3.75 mmol/mol, was analyzed (n = 44) to allow interlaboratory comparison (Greaves et al., 2008) with an average of 3.85 ± 0.027 mmol/mol.

A total of 451 foraminifera were gently crushed for individual shell analyses after each single foraminifer was placed on a polypropylene filter with a polytetrafluoroethylene membrane (0.45‐μm mesh; Whatman) using a pipette tip. The filters were connected to a flow‐through automated cleaning device (Haarmann et al., 2011; Klinkhammer et al., 2004). Cleaning over a filter reduces the loss of material, which occurs with traditional cleaning, allowing the analysis of single specimens. The automated cleaning involves three rinses of 10 min each with Seralpur water, 1%‐NaOH buffered H₂O₂ for oxidation, and Seralpur water. Several drops of NH₃ (suprapur) were added to the Seralpur water to increase the pH to prevent leaching during the Seralpur water rinses. For oxidation, the filters were placed in a water bath at 98 °C. After the cleaning, the filters were connected to a cleaned syringe with 1 ml of 0.075‐M QD HNO₃ to dissolve the foraminiferal fragments by placing the syringes in a rack and letting the acid slowly drop through the sample to allow enough time for dissolution. Samples were analyzed with an ICP‐OES (Agilent Technologies, 700 Series with autosampler ASX‐520 Cetac and micro‐nebulizer) at MARUM, University of Bremen. In comparison with the pooled samples the analytical method was tuned to the lower concentrations of single‐specimen samples, that is, calibration samples with lower concentrations, and a more sensitive element line for Al (167.019 nm; see below for details). Combined analytical precision for all species and locations based on three repetitions for each sample analysis for the IFA was 0.55% for Mg/Ca (n = 451).

Temperatures for the different species were calculated using the species dependent calibrations from Anand et al. (2003) Mg/Ca = B * exp (A * T), with B = species specific and A = 0.09 (assumed based on the findings of previous calibration studies (Elderfield & Ganssen, 2000)). For the main conclusions of this study, only the exponential constant of A = 0.09 is relevant as the preexponential constant B does not influence the resulting temperature spread from the IFA distribution.

We set thresholds to classify IF analyses as reliable depending on the amount of material and possible contamination. As the analysis of single foraminifera approaches the limits of the amount of material that can be measured on the ICP‐OES, we set a conservative minimum threshold of 4‐ppm Ca for an acceptable measurement (supporting information Figure S1). Potential contamination by remaining clay particles was monitored using Al/Ca. Because the absolute concentrations were close to the detection limit, the absolute values of the Al/Ca may be too high due to matrix effects. Therefore, we set a threshold of 2 mmol/mol for Al/Ca above which samples are classified as possibly contaminated and not included in further statistical analyses. After applying both thresholds, 286 samples remain. The sensitivity of the results on the Ca and Al/Ca thresholds was tested, showing that our choice is a reasonable tradeoff between minimizing the effect of potential contamination and not removing too many measurements (Figure S1). To ensure that the FT system did not get contaminated by remaining particles during the cleaning, the system was regularly rinsed with 1‐M HNO₃ (3 min) followed by buffered Seralpur water (20 min), and after the analysis of each sample was finished, the tubes were rinsed with Seralpur water (10 min). Blank samples (n = 41), which both received the same cleaning treatment as regular samples and which were taken from specific positions along the FT device (e.g., at the end of a particular tube), were regularly analyzed and had element concentrations below the detection limit for each element. The blank samples were not additionally acidified before analysis.

3.2. Stable Isotopes

Stable oxygen isotope analyses on pooled samples were performed on a Finnigan MAT 252 mass spectrometer equipped with an automated carbonate preparation device at MARUM, University of Bremen. Isotopic results were calibrated relative to the Vienna Pee Dee belemnite (VPDB) using the NBS19 standard. The standard deviation of the laboratory standard was lower than 0.07‰ for the measuring period.

Stable oxygen and carbon isotope analyses (δ¹⁸O and δ¹³C) on individual foraminifera (n = 506) were performed using a Finnigan MAT 253 mass spectrometer with the automated carbonate preparation device Kiel IV at AWI Bremerhaven. The precision of the stable oxygen isotope analyses determined on an internal laboratory standard, measured over a 1‐year period together with the samples, was better than 0.08‰. Values are reported in δ notation relative to VPDB, calibrated by using the National Institute of Standards NBS 18 and 19 standards. Samples with a sample intensity of less than 2,000 mV were excluded due to insufficient material, leading to 483 remaining samples. Although instrument specific and therefore not commonly applicable, we tested the dependency of the results on the sample intensity threshold to show that the standard deviation of the IFA variability is insensitive to this choice (Figure S2).

3.3. Statistical Methods

Despite removing samples that had a too‐low amount of sample material left for analysis or a potential threat of contamination as described above, outliers related to the presence of a higher portion of secondary crust on N. dutertrei or other unknown reasons are still possible. Therefore, we removed outliers in the Mg/Ca and δ¹⁸O data using the 1.5× interquartile range criterion, a robust method for outlier detection (Tukey, 1977). This criterion removed six (2.0%) of the single‐specimen samples for Mg/Ca and seven samples for δ¹⁸O (1.5%; Figure 3). Our main conclusions are insensitive to this outlier removal (Figures S1 and S2).

Figure 3.

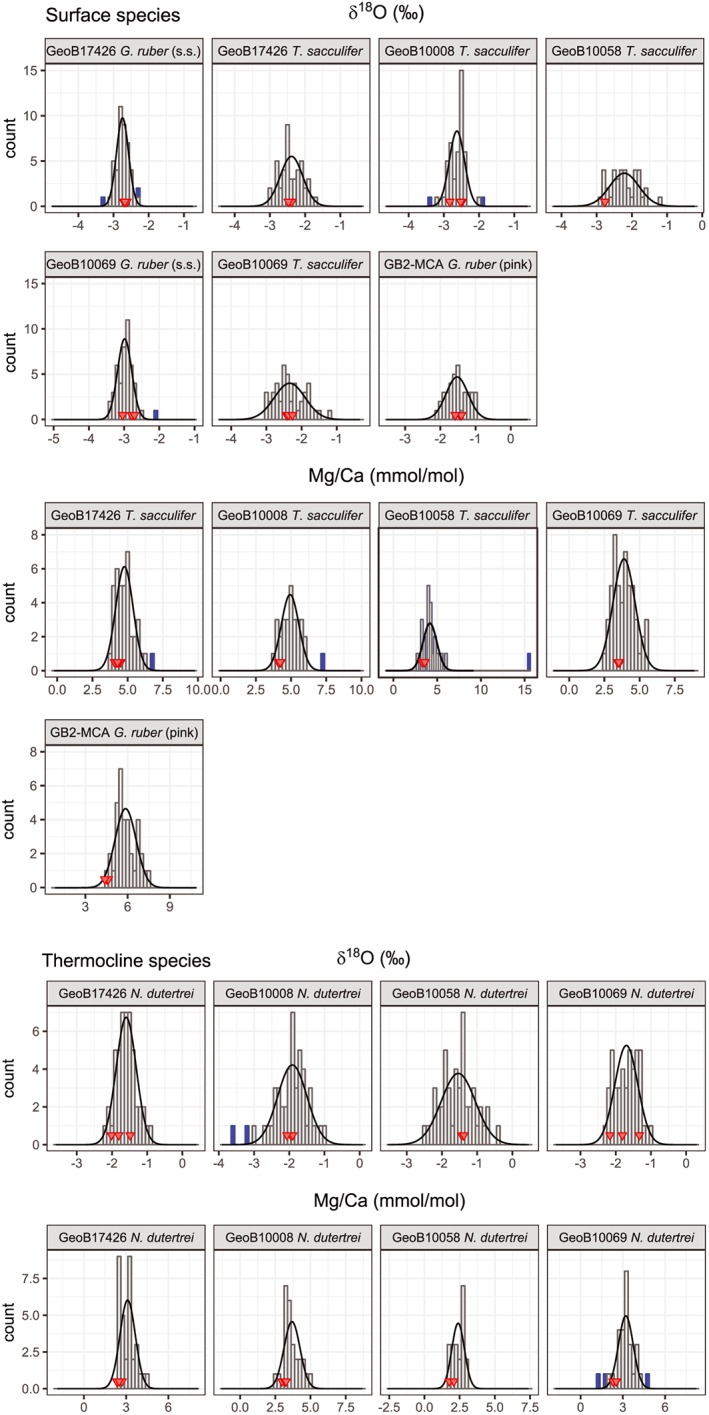
(a) Single‐specimen δ¹⁸O and Mg/Ca distribution of surface dwelling T. sacculifer and dual specimen δ¹⁸O and Mg/Ca distribution for G. ruber. (b) Single‐specimen δ¹⁸O and Mg/Ca distribution of the thermocline dwelling N. dutertrei. Red triangles indicate samples consisting of pooled specimens. Blue bars indicate IFA characterized as outliers.

To estimate the skewness of the IFA distributions, we use the Fisher‐Pearson coefficient of skewness and provide bootstrap confidence intervals as the classical confidence intervals were shown to be unreliable (Wright & Herrington, 2011). We test the IFA distributions for normality using the Shapiro‐Wilk test (Shapiro & Wilk, 1965). In only one of 20 cases (Mg/Ca GeoB17426, N. dutertrei), the null hypothesis that the data are normally distributed (p = 0.05) is rejected (Table 2). When omitting the outlier correction, four of the 20 distributions get rejected, consistent with the visually apparent outliers in these distributions (δ¹⁸O: GeoB10069 G. ruber (s.s.), GeoB10008 T. sacculifer; Mg/Ca: GeoB17426 T. sacculifer, GeoB10058 T. sacculifer). We therefore conclude that there is no evidence for a nonnormal distribution and characterize the spread of the IFA using the standard deviation and provide the analytical confidence intervals of the standard deviation based on the chi‐square distribution. We note that the normality test may be too optimistic for G. ruber as the measurements were performed on two specimens, which will reduce any higher moments of the distribution such as the skewness.

Table 2.

Summary Overview of the Individual Foraminifera Analyses per Species at Each Location After Concentration Screening and Outlier Removal per Proxy for Mg/Ca, Mg/Ca Converted to Temperature, and δ¹⁸O

Vartype	Site	Species	# Sample	# Specimen per sample	Meana	se of mean	sdb	p Value Shapiro	Skew	Skew lower	Skew upper
Mg/Ca	GeoB17426	T. sacculifer	38	1	4.77	0.10	0.62	0.58	0.42	−0.09	0.95
Mg/Ca	GeoB17426	T. sacculifer extra batch	37	1	4.85	0.10	0.59	0.27	0.43	−0.04	0.93
Mg/Ca	GeoB17426	N. dutertrei	33	1	3.11	0.10	0.55	0.02	0.64	0.17	1.30
Mg/Ca	GeoB10008	T. sacculifer	28	1	4.93	0.12	0.62	0.50	−0.25	−0.83	0.28
Mg/Ca	GeoB10008	N. dutertrei	26	1	3.69	0.11	0.57	0.49	0.41	−0.25	1.16
Mg/Ca	GeoB10058	T. sacculifer	22	1	4.17	0.17	0.79	0.88	0.37	−0.36	1.22
Mg/Ca	GeoB10058	N. dutertrei	20	1	2.39	0.10	0.45	0.21	−0.23	−0.90	0.45
Mg/Ca	GeoB10069	T. sacculifer	52	1	3.89	0.11	0.79	0.17	0.39	0.03	0.79
Mg/Ca	GeoB10069	N. dutertrei	26	1	3.21	0.10	0.52	0.68	−0.21	−0.98	0.53
Mg/Ca	GB2‐MCA	G. ruber (p)	35	2b	5.85	0.13	1.06	0.56	0.33	−0.18	0.89
T Mg/Ca	GeoB17426	T. sacculifer	38	1	29.0	0.23	1.43	0.93	0.15	−0.35	0.64
T Mg/Ca	GeoB17426	T. sacculifer extra batch	37	1	29.2	0.22	1.34	0.59	0.19	−0.28	0.70
T Mg/Ca	GeoB17426	N. dutertrei	33	1	24.3	0.33	1.90	0.04	0.37	−0.14	0.95
T Mg/Ca	GeoB10008	T. sacculifer	28	1	29.4	0.27	1.45	0.30	−0.46	−1.03	0.07
T Mg/Ca	GeoB10008	N. dutertrei	26	1	26.2	0.33	1.70	0.76	0.03	−0.68	0.79
T Mg/Ca	GeoB10058	T. sacculifer	22	1	27.4	0.45	2.10	0.98	−0.08	−0.86	0.63
T Mg/Ca	GeoB10058	N. dutertrei	20	1	21.4	0.49	2.18	0.12	−0.43	−1.22	0.25
T Mg/Ca	GeoB10069	T. sacculifer	52	1	26.6	0.31	2.24	0.58	0.03	−0.40	0.43
T Mg/Ca	GeoB10069	N. dutertrei	26	1	24.7	0.37	1.91	0.18	−0.71	−1.53	0.21
T Mg/Ca	GB2‐MCA	G. ruber (p)	35	2b	30.2	0.24	2.00	0.84	0.06	−0.53	0.65
δ18O	GeoB17426	G. ruber (s.s.)	42	2b	−2.75	0.03	0.24	0.91	0.03	−0.46	0.67
δ18O	GeoB17426	T. sacculifer	44	1	−2.39	0.05	0.32	0.69	0.11	−0.37	0.56
δ18O	GeoB17426	N. dutertrei	48	1	−1.60	0.04	0.28	0.98	0.14	−0.35	0.67
δ18O	GeoB10008	T. sacculifer	45	1	−2.63	0.03	0.22	0.07	−0.29	−1.15	0.60
δ18O	GeoB10008	N. dutertrei	44	1	−1.91	0.06	0.42	1.00	−0.14	−0.84	0.47
δ18O	GeoB10058	T. sacculifer	38	1	−2.22	0.07	0.42	0.44	0.33	−0.20	1.02
δ18O	GeoB10058	N. dutertrei	46	1	−1.54	0.07	0.49	0.92	0.09	−0.38	0.58
δ18O	GeoB10069	G. ruber (s.s.)	45	2b	−2.99	0.03	0.20	0.53	−0.27	−0.73	0.24
δ18O	GeoB10069	T. sacculifer	44	1	−2.34	0.07	0.44	0.19	0.51	0.04	1.10
δ18O	GeoB10069	N. dutertrei	43	1	−1.70	0.05	0.33	0.17	−0.06	−0.50	0.42
δ18O	GB2‐MCA	G. ruber (p)	37	2b	−1.52	0.05	0.44	0.49	0.10	−0.38	0.62

Note. The columns include the number of samples, number of specimens per sample, mean IFA values, standard error of the mean, the standard deviation across samples, p value of the Shapiro‐Wilks test for normality, skewness estimate, and lower and upper bound of the 95% confidence interval.

^aMg/Ca is in millimole per mole; T _Mg/Ca is in degrees Celsius; δ¹⁸O is in per mill.

^bFor G. ruber (s.s.) and G. ruber (pink), two specimens were used per analysis and the standard deviation was adjusted by multiplying with $\sqrt{2}$ to represent the expected spread of single‐specimen analyses.

We use a bias corrected estimator for the standard deviation that assumes a normally distributed random variable (Brugger, 1969). The bias correction is only relevant for the comparison of the pooled and IFA spread but has no discernible effect on the analysis of the IFA variability as the sample sizes are large enough (>30 individuals).

3.4. Oceanographic Data and Expected Proxy Variability

We use the monthly climatological seawater temperature and salinity from the World Ocean Atlas 2013 on a 1° × 1° grid (Locarnini et al., 2013; Zweng et al., 2013). To estimate the effect of interannual variations on the expected proxy variability, we use annual seawater temperature and salinity from the National Centers for Environmental Prediction Global Ocean Data Assimilation System (GODAS; Behringer & Xue, 2004).

We further use the global gridded data set of the oxygen isotopic composition in seawater (version 1.1; LeGrande & Schmidt, 2006) to extract the δ¹⁸O_sw at the core positions. Even though most of our core tops are dated as modern, the time period recorded by the foraminifera is likely not the same as the time period represented by the oceanographic data. However, in contrast to a warming trend in the last decades, the change in variability is expected to be minor and discrepancies in the recorded time period should thus have no discernable influence on our results.

To estimate the effect of seasonal and interannual variations on δ¹⁸O_sw, we predicted the δ¹⁸O_sw anomalies from the monthly World Ocean Atlas and annual GODAS salinity anomalies. For this step, we assumed a linear relationship between both variables with a slope of 0.257‰ per practical salinity unit for the GoM (Spero & Williams, 1990) and 0.42‰ per practical salinity unit for the remaining sites (Morimoto et al., 2002). For simplicity, we extracted the δ¹⁸O_sw and temperature at fixed species‐dependent water depth ranges (G. ruber (s.s.) and G. ruber (pink) at 0–50 m, T. sacculifer at 20–70 m, and N. dutertrei at 80–120 m), but we confirmed that our results are not sensitive to the use of site‐specific depth ranges (Regenberg et al., 2009; Mohtadi et al., 2011; Hollstein et al., 2017; not shown). As interannual and seasonal variability are largely independent, we approximate the total variability expected to influence the single specimen as ${\mathit{sd}}_{\text{total}}=\sqrt{{{\mathit{sd}}_{\text{seasonal}}}^2+{{\mathit{sd}}_{\text{interannual}}}^2}$. Testing this approximation with monthly SST data shows that deviations from the true variability at our study sites are less than 20%.

Isotopic calcification temperatures of the foraminifera were calculated, using the paleotemperature equation from Bemis et al. (1998), from measured δ¹⁸O (from the planktic foraminifera in VPDB units) and estimates of δ¹⁸O_sw (in SMOW units):

$$T=14.9-4.8*\left({\mathrm{\delta }}^{18}\mathrm{O}-\left({\mathrm{\delta }}^{18}{\mathrm{O}}_{\mathrm{sw}}-0.27\right)\right).$$

4. Results and Discussion

4.1. Variability in Single‐Specimen Mg/Ca and δ¹⁸O

Individual foraminifer Mg/Ca values for T. sacculifer varied between 2.50 and 6.24 mmol/mol with an average of 4.38 mmol/mol (Figure 3 and Table 2). Assuming that temperature calibrations based on pooled specimens can also be applied to single specimens, this translates into a range between 22.0 and 32.1 °C (average = 28.0 °C). Individual foraminifer Mg/Ca values for N. dutertrei varied between 1.64 and 4.93 mmol/mol (17.4–29.6°) with an average of 3.14 mmol/mol (24.3 °C), and for G. ruber (pink) between 4.39 and 7.50 mmol/mol (27.1–33.0 °C) with an average of 5.85 mmol/mol (30.2 °C). As two specimens per sample were used for G. ruber (pink), the range is ~1.4 times less than expected for single‐specimen analyses. The average values are all higher than the average Mg/Ca of the pooled specimen analysis for each respective species (T. sacculifer: 4.38 vs. 4.03 mmol/mol; N. dutertrei: 3.14 vs. 2.52 mmol/mol; G. ruber (pink): 5.85 vs. 4.51 mmol/mol; Table 3). The results show that the single‐specimen Mg/Ca values for all three species are close to normally distributed as the Shapiro‐Wilk test rejected the null hypothesis for only one of the distributions (Mg/Ca GeoB17426, N. dutertrei; Figure 3 and Table 2).

Table 3.

Summary Overview of the Pooled‐Specimen Analyses per Species at Each Location per Proxy for Mg/Ca, Mg/Ca Converted to Temperature, and δ¹⁸O

Vartype	Site	Species	# Sample	# Specimen per sample	Meana	se of mean
Mg/Ca	GeoB17426	G. ruber (s.s.)	3	30	5.35	0.12
Mg/Ca	GeoB17426	T. sacculifer	8	25	4.31	0.04
Mg/Ca	GeoB17426	N. dutertrei	3	24	2.51	0.11
Mg/Ca	GeoB10008	T. sacculifer	3	25	4.20	0.05
Mg/Ca	GeoB10008	N. dutertrei	3	25	3.14	0.08
Mg/Ca	GeoB10058	T. sacculifer	2	20	3.46	0.12
Mg/Ca	GeoB10058	N. dutertrei	3	25	1.98	0.11
Mg/Ca	GeoB10069	G. ruber (s.s.)	3	40	4.61	0.08
Mg/Ca	GeoB10069	T. sacculifer	3	26	3.52	0.04
Mg/Ca	GeoB10069	N. dutertrei	3	25	2.45	0.07
Mg/Ca	GB2‐MCA	G. ruber (p)	3	30	4.51	0.07
T Mg/Ca	GeoB17426	G. ruber (s.s.)	3	30	29.0	0.26
T Mg/Ca	GeoB17426	T. sacculifer	8	25	28.0	0.11
T Mg/Ca	GeoB17426	N. dutertrei	3	24	22.1	0.48
T Mg/Ca	GeoB10008	T. sacculifer	3	25	27.7	0.12
T Mg/Ca	GeoB10008	N. dutertrei	3	25	24.6	0.30
T Mg/Ca	GeoB10058	T. sacculifer	2	20	25.5	0.38
T Mg/Ca	GeoB10058	N. dutertrei	3	25	19.5	0.62
T Mg/Ca	GeoB10069	G. ruber (s.s.)	3	40	27.3	0.19
T Mg/Ca	GeoB10069	T. sacculifer	3	26	25.7	0.12
T Mg/Ca	GeoB10069	N. dutertrei	3	25	21.9	0.34
T Mg/Ca	GB2‐MCA	G. ruber (p)	3	30	27.4	0.18
δ18O	GeoB17426	G. ruber (s.s.)	3	5	−2.67	0.02
δ18O	GeoB17426	T. sacculifer	3	4	−2.41	0.03
δ18O	GeoB17426	N. dutertrei	3	3	−1.77	0.16
δ18O	GeoB10008	T. sacculifer	3	4	−2.61	0.11
δ18O	GeoB10008	N. dutertrei	3	3	−1.97	0.05
δ18O	GeoB10058	T. sacculifer	1	4	−2.77	n.a.
δ18O	GeoB10058	N. dutertrei	3	3	−1.40	0.02
δ18O	GeoB10069	G. ruber (s.s.)	3	5	−2.84	0.10
δ18O	GeoB10069	T. sacculifer	3	4	−2.35	0.05
δ18O	GeoB10069	N. dutertrei	3	3	−1.77	0.24
δ18O	GB2‐MCA	G. ruber (p)	3	5	−1.47	0.05

Note. The columns include the number of samples, number of specimens per sample, mean pooled specimen values, and the standard error of the mean.

^aMg/Ca is in millimole per mole; T _Mg/Ca is in degrees Celsius; δ¹⁸O is in per mille.

An additional, replicate batch of 59 IFA (37 samples after concentration thresholding and outlier removal) was performed using T. sacculifer specimens from GeoB 17426‐2, which included an extra, short ultrasonic bath step before the FT cleaning. Comparison between both batches shows that the mean (4.85 vs. 4.77 mmol/mol using the standard procedure), standard deviation (0.59 vs. 0.62), and skewness (0.43 vs. 0.42) are statistically indistinguishable from the sample set prepared using the standard procedure (Table 2). This suggests that the cleaning process for IFA was sufficient to extract the primary signals and underlines the robustness of the IFA statistics when conservatively removing samples with too low concentrations or signs for potential contamination.

For stable oxygen isotopes of the single specimens a total of 476 samples were included in further analyses after intensity screening and outlier removal. For T. sacculifer, δ¹⁸O varied between −1.16‰ and −3.23‰ with an average of −2.40‰ (Figure 3a and Table 2; supporting information). G. ruber (s.s.) and G. ruber (pink) δ¹⁸O varied between −2.33‰ and −3.40‰ with an average of −2.87‰ and between −0.97‰ and −2.15‰ with an average of −1.52‰, respectively (Figure 3a and Table 2). As for Mg/Ca, the range in values is ~1.4 times less than expected for single‐specimen analysis because two specimens were analyzed per sample. For the thermocline‐dwelling N. dutertrei, the spread in δ¹⁸O was between −0.44‰ and −2.97‰ with an average of −1.68‰ (Figure 3b and Table 2). Because no different preparation techniques are performed as with Mg/Ca, the average δ¹⁸O values for single specimens are similar to the average δ¹⁸O for pooled‐specimen samples for each species (Table 3). There is no indication that the δ¹⁸O values for the respective samples are not normally distributed (Table 3). The skewness of the distributions ranges from −0.29 to 0.51 but is only significantly different from 0 for the distribution in one sample (GeoB10069 T. sacculifer, skewness = 0.51).

Because stable carbon isotopes are affected by many additional factors than just temperature, we did not include them in the discussion but only show them in the supporting information (Figure S3) and the data are available via Pangaea.

4.2. Comparing Pooled Versus Single‐Specimen Analyses; Mean Values

4.2.1. Mg/Ca

Average Mg/Ca of the individual foraminifera for each species and core top is on average 0.66 mmol/mol (~1.9 °C) higher than for the pooled‐specimen samples (Figure 4 and Table 3). The smallest difference was found for T. sacculifer in GeoB 10069‐4 (0.37 mmol/mol or ~0.9 °C), and the largest difference was for G. ruber (pink) in GB2‐MCA (1.34 mmol/mol or ~2.84 °C). The relatively constant offset between both approaches points to a systematic difference possibly due to sample preparation.

Figure 4.

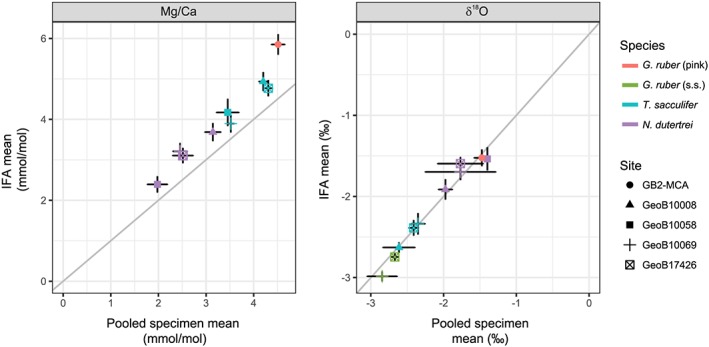
Comparison between pooled specimen mean and single‐specimen mean values for each species and core top location for Mg/Ca (a) and δ¹⁸O (b). Error bars indicate the 90% confidence intervals. IFA = individual foraminifera analysis.

As individual and pooled specimens are picked from the same samples and are indistinguishable for δ¹⁸O, the differences have to be caused by the different cleaning and measurement process. The analyses of the consistency standards, which were diluted to reflect typical IF and pooled specimen concentrations, show the same values excluding evidence for instrumental drift, that is, between IF and pooled sample, or specific bias in the Mg/Ca measurements themselves suggesting that the differences stem from the cleaning protocols. Possibilities include either a too intense cleaning of the samples with pooled specimens or remaining contamination on single foraminifera.

Previous cleaning experiments have shown that with more intense cleaning, the higher Mg parts of the tests are more affected by dissolution thus lowering Mg/Ca (Barker et al., 2003; Brown & Elderfield, 1996; Regenberg et al., 2006; Rosenthal et al., 2000); for example, adding a reduction step to the cleaning resulted in 1–2 °C lower temperatures (Barker et al., 2003; Rosenthal et al., 2004). The main reason to use an FT cleaning device in the current study was to reduce the loss of material during the cleaning process, which normally occurs during the manual cleaning, thus making the cleaning procedure less intense. Accordingly, it can be expected that when no material is lost the resulting Mg/Ca may be slightly higher than the traditionally cleaned samples of pooled specimens. This implies that an FT‐specific Mg/Ca versus temperature equation needs to be calibrated for optimum precision when Mg/Ca paleotemperature records are reconstructed using FT preparation.

The higher IFA Mg/Ca may also have been caused by a less efficient cleaning of the FT method. After cleaning, the samples were dissolved by running the dissolution acid over the samples. This may have led to the inclusion of some <0.45‐μm particles, which could have been freed by the dissolution of the calcite. However, we already removed samples with suspiciously high Al/Ca from further discussion (Figure S1). And additional evidence that the samples were clean comes from the extra batch of samples for which an extra cleaning step, that is, ultrasonic treatment, was performed and which shows the same mean and standard deviation as the first batch (Table 2).

We compare the replicate pooled specimens and single specimens variability of all species to infer the origins of the single‐specimen variability. In the case of no measurement uncertainty, the spread of the pooled‐specimen samples after adjusting for the number of tests in each sample by multiplying with √n, where n is the number of foraminifera per sample, should be similar to the spread of the single‐specimen samples. The mean spread for the different species in Mg/Ca of the single‐specimen samples is 0.7 mmol/mol, similar to the mean spread of the pooled‐specimen samples of 0.75 mmol/mol after adjusting for the number of tests in each sample. This confirms for Mg/Ca that variations in the foraminiferal Mg/Ca and not analytical uncertainties are the main driver for the replicate variability.

4.2.2. Stable Oxygen Isotopes

The mean δ¹⁸O from the pooled‐specimen samples and mean δ¹⁸O of the IFA are indistinguishable within their statistical uncertainty in spite of differences in sample size and instruments used (Figure 4). The overall mean value of δ¹⁸O of the pooled‐specimen samples of −2.13‰ differs from the overall mean values of the single‐specimen δ¹⁸O samples by less than 0.01. This reproducibility also applies when comparing the means for every species and every site specifically (Figures 3 and 4 and Table 3). As the samples for pooled‐specimen analyses consisted only of three to six specimens, the mean IFA values based on the values of ~40 separate specimens are the more reliable estimates of the true δ¹⁸O value.

As we typically measured three replicate samples of pooled specimens with three to six foraminiferal tests in each sample as well as the measurements of typically ~40 individual foraminifera, we can compare the replicate pooled specimen and IFA variability similar to the comparison for Mg/Ca. The mean spread for the different species for single‐specimen samples of 0.33‰ is similar to the adjusted mean spread of the pooled‐specimen samples of 0.27‰ providing confidence that the signal and not the measurement process dominates the δ¹⁸O variability.

4.3. Comparison of δ¹⁸O Versus Mg/Ca With Pooled Specimen Calibrations

We compare the calcification temperatures calculated from the measured δ¹⁸O with the mean Mg/Ca values calculated from the pooled specimen and the single‐specimen measurements (Figure 5). For δ¹⁸O we combine the pooled specimen and the single‐specimen measurements to one mean value, as both are indistinguishable, and the pooled‐specimen samples contain too few specimens to deliver reliable mean δ¹⁸O values.

Figure 5.

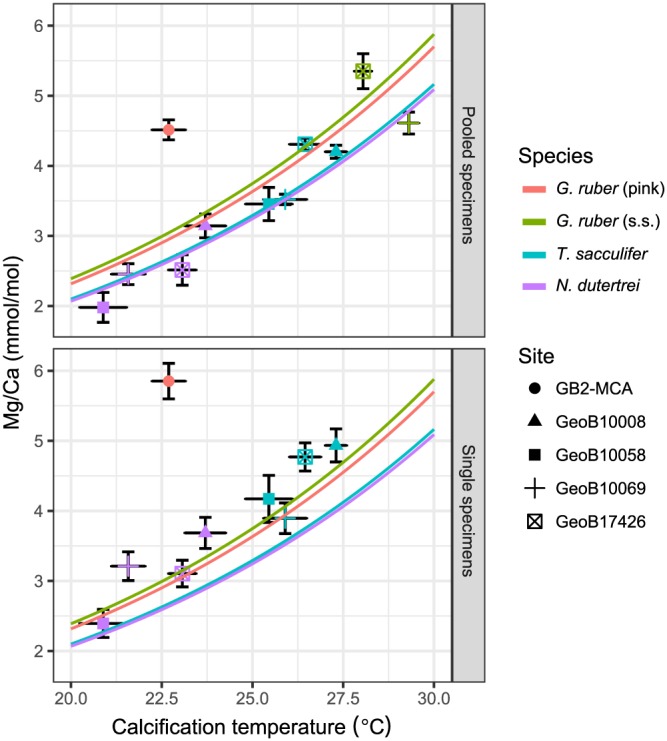
Mean Mg/Ca for each species at each core top location for pooled specimens (a) and single specimens (b) versus calcification temperature. Calcification temperatures were calculated using the paleotemperature equation of Bemis et al. (1998) using analyzed δ¹⁸O_foram and δ¹⁸O_sw from LeGrande and Schmidt (2006). Core top locations are indicated by different symbols, while foraminifer species are indicated by colors. The same color scheme is used to denote the previously published species‐specific calibration equations from Anand et al. (2003) with the same temperature dependency (0.09) and species‐specific B coefficients (G. ruber (pink) = salmon; G. ruber (s.s.) = green; T. sacculifer = blue; N. dutertrei = purple). Error bars indicate two standard errors (~95% confidence intervals).

For both IF and pooled specimens, the mean Mg/Ca to calcification temperature relationship follows existing species‐specific calibrations (Anand et al., 2003; Figure 5). In general, the pooled specimen values are consistent with the standard calibrations as expected, as this follows the commonly applied procedure. As discussed previously (section 4.2.1), the IF mean values are slightly higher than the pooled specimen mean and thus slightly above the calibration curve. For both pooled‐specimen and single‐specimen Mg/Ca, the GoM G. ruber (pink) values deviate from the expected relationship by 1.3‰ for pooled specimens and 1.7‰ for single specimens. While the gridded data set (LeGrande & Schmidt, 2006) suggests a value of 0.7‰ at the core position, observational data suggest values up to 1.9‰ for the northern GoM (Grossman & Ku, 1986; Surge & Lohmann, 2002) and could thus resolve the discrepancy from the calibration relationship.

Estimating an own calibration equation from the IFA data by excluding the GoM site results in an exponential constant of 0.096 ± 0.011 (1 se), thus statistically indistinguishable from the standard calibration slope of 0.09 (Anand et al., 2003). This result also holds when using the Shackleton (1974) equation for the δ¹⁸O to temperature relationship. However, the intercept is sensitive to the calibration equation and using the Shackleton (1974) equation leads to pooled specimen values being below the calibration lines and IFA values matching the calibration relationship (not shown).

4.4. Variability in IF Analyses

The spread in IFA is often interpreted as climate variability (Ganssen et al., 2011; Khider et al., 2011; Koutavas et al., 2006; Leduc et al., 2009; Metcalfe et al., 2015; Vetter et al., 2017). As temperature is the main driver at our sites for both Mg/Ca and δ¹⁸O, we expect that both Mg/Ca and δ¹⁸O IFA should show similar variability when accounting for their respective temperature calibrations. Indeed, using an exponential constant of 0.09 results in a mean T _Mg/Ca spread (1 sd ± 1 se) of 1.8 ± 0.2 °C and a mean δ¹⁸O spread of 0.37 ± 0.04‰, thus a ratio sd (T _Mg/Ca) to sd (δ¹⁸O) of 5.1 ± 0.8 (1 se). Similar results (ratio of 4.5–5.6) are obtained when analyzing each species separately. The similarity of this ratio with the published δ¹⁸O sensitivity on calcification temperature (e.g., 4.8 for Bemis et al., 1998) strongly supports that both signals are largely driven by variability in the calcification temperature and thus encouraging for the use of IFA as a climate proxy.

Comparing the site‐specific IF Mg/Ca and δ¹⁸O variability after converting Mg/Ca to temperature units (Figure 6, right panel) shows that the T _Mg/Ca and δ¹⁸O variability scatter around the slope of 4.8 as expected from the sensitivity of δ¹⁸O to temperature during calcification (Bemis et al., 1998; Bouvier‐Soumagnac & Duplessy, 1985; Shackleton, 1974). The variability of both proxies shows a statistically significant positive correlation (R = 0.75, p = 0.02). Interestingly, this relationship largely breaks down when comparing the Mg/Ca and δ¹⁸O variability before calibration, showing the importance of the nonlinear (exponential) Mg/Ca to temperature relationship that leads to a different scaling of T _Mg/Ca to Mg/Ca variability depending on the mean temperature. Additionally, the intercept is only slightly positive, which also suggests that the majority of Mg/Ca and δ¹⁸O variability is dominated by the same mechanism. This also shows that the effect of salinity on the variability of the δ¹⁸O signal is limited, consistent with the expected variability predicted from the oceanographic data (not shown).

Figure 6.

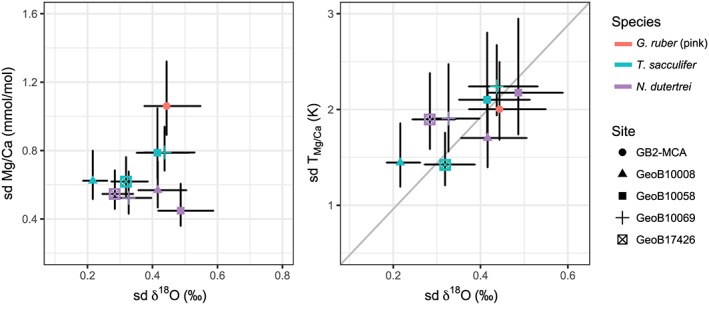
Standard deviation of single‐specimen Mg/Ca versus standard deviation of single‐specimen δ¹⁸O (left) and as calculated temperature variation (right) for surface and thermocline dwelling species. This shows that both Mg/Ca and δ¹⁸O are responding to the same climatic parameters. Error bars indicate the 90% confidence intervals.

Analyzing surface dwellers and thermocline dwellers separately supports our finding (Figure S4) but also shows that the relationship for thermocline dwellers is more sensitive to the outlier definition. Although the number of samples is too small to draw a robust conclusion, this might indicate that the analysis on single N. dutertrei specimens is more challenging (see also section 4.5), potentially also as N. dutertrei, in contrast to T. sacculifer and G. ruber, builds a secondary crust later in the life cycle. This crust is thought to form deeper in the water column recording lower temperatures. This was also shown for other deeper‐dwelling foraminifera with a distinction between higher Mg/Ca in the primary calcite and lower Mg/Ca in the crust (Groeneveld & Chiessi, 2011; Hathorne et al., 2009; Jonkers et al., 2012; Steinhardt et al., 2014). Although only specimens of N. dutertrei without an obvious crust were selected, the formation of a crust is gradual such that it cannot be avoided that some specimens contain some crust. This would skew the analyses of either one of the proxies toward “colder” values preventing a linear relationship between the averages from different locations (Figure S4). The relationship between the variability displayed by Mg/Ca and δ¹⁸O also argues against a strong influence of vital effects (De Nooijer et al., 2014) or genetic variations (Morard et al., 2016; Sadekov et al., 2016) on the variability of Mg/Ca and δ¹⁸O in single specimens. These mechanisms could only explain our findings by simultaneously influencing δ¹⁸O and Mg/Ca with the relative amount of this effect for both proxies following the temperature calibrations, which is unlikely as a vital effect is usually thought to only affect a specific component like the Mg inclusion. Nevertheless, it has been shown that temperature has an influence on the growth rate of the foraminifera that may at least partly be similar for both proxies (Lombard et al., 2011; Spero & Lea, 1993).

4.5. Relationship Between Single‐Specimen Variability and Oceanographic Conditions

One of the main motivations for IFA is to reconstruct past changes in seasonal and interannual temperature variability. Comparing our core tops to the temperature and salinity variability at the different sites allows testing the skill of the IFA method to reconstruct oceanographic variability (Figures 1 and 2).

As a first test, we compare the observed single‐specimen variability to the predicted variability derived from analyzing the seasonal and interannual SST and δ¹⁸O_sw (predicted from salinity) variations at a fixed depth level (Figure 7, top row). We choose the mean depth level of their assumed habitat range (G. ruber, 25 m; T. sacculifer, 35 m; N. dutertrei, 100 m; Figure 2) but confirmed that the results are stable when varying this assumption.

Figure 7.

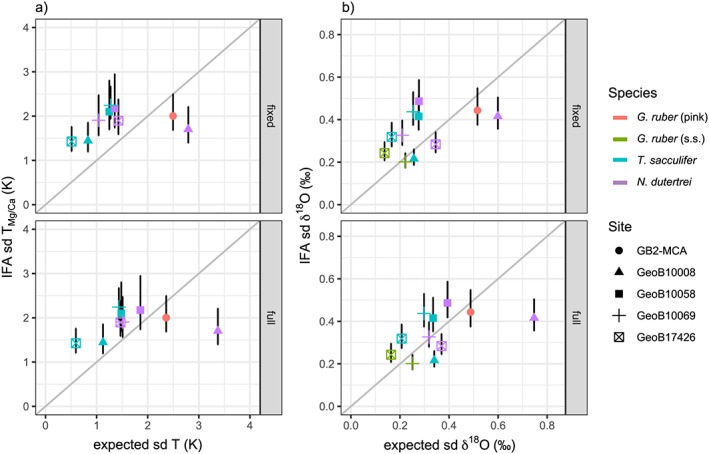
Predicted versus reconstructed variability of individual foraminifera analysis (IFA). Standard deviation based on IFA for Mg/Ca (a) and δ¹⁸O (b) shows that the proxy variation is larger than the seasonality at the locations in Indonesia and the Western Pacific Warm Pool. The variability of G. ruber (pink) in the Gulf of Mexico and N. dutertrei at GeoB 10008 is lower than the seasonal range would suggest. Error bars indicate the 90% confidence intervals.

The seasonal range in SST off Indonesia and in the WPWP is much lower than in the GoM (<4 vs. ~7 °C), but this is not always reflected in the spread in IF Mg/Ca and δ¹⁸O. For sites in the WPWP and off Indonesia with an expected variability below sd = 2 °C, the observed variability from T _Mg/Ca is above the expected variability (Figure 7). This behavior is largely mirrored for the observed IF δ¹⁸O, showing that it is not a measurement or proxy artifact. In contrast, G. ruber in the GoM (GB2‐MCA) and especially N. dutertrei at GeoB 10008‐4 in the Northern Mentawai Basin show less reconstructed than predicted variability, both for T _Mg/Ca and δ¹⁸O. The range for N. dutertrei at GeoB 10008‐4 of the reconstructed spread (around 1 °C sd T _Mg/Ca, 0.3‰ sd δ¹⁸O) is much lower than the range of the predicted spread in seasonal and interannual temperatures (around 3 °C sd T _Mg/Ca, 0.5‰ sd δ¹⁸O; Figures 1 and 7). Thermocline conditions vary significantly throughout the year at the location of GeoB 10008‐4, but a sediment trap study from off Java showed a clear seasonal flux for N. dutertrei (Mohtadi et al., 2009). This may explain why the analyzed variability in N. dutertrei is smaller than the expected variability, that is, when the flux is concentrated to a short period of the year the expected variability will be skewed toward this time period and be less than the variability for a full year. This shows that the interpretation of thermocline dwellers for IFA may be more complicated when the variability in the conditions becomes so large that the foraminifera restrict their habitat in which they live.

As there might also be variations in the depth habitat and thus the recorded water temperature from one foraminifer to the next, we also compared our reconstructed variability to the predicted variability derived from integrating the variability over the habitat range instead of a fixed average depth (G. ruber (s.s.) and G. ruber (pink) at 0–50 m, T. sacculifer at 20–70 m and N. dutertrei at 80–120 m). However, the results (Figure 7, lower panel) are largely unchanged.

Given our evidence that seawater temperature variability is the dominating factor for the single‐specimen variability, the likely explanation for our findings are site‐specific seasonal and depth habitat changes. The single‐specimen variability can be reduced compared to the seasonal variability by only integrating one specific season or enhanced compared to the variability at one single depth level by integrating across depth. In our results (Figure 7), the range of the recorded variations for Mg/Ca as well as for δ¹⁸O is smaller than the range of the expected variations from the oceanographic data suggesting that there is a preference of the species toward keeping their conditions constant (Mix, 1987) and thus to underestimate the true change in variability. The effect is likely stronger when the variability is large, such as in the thermocline of site GeoB 10008‐4 where the largest mismatch between data and proxy (N. dutertrei) is observed (Figure 7).

Indeed, it is well known that planktic foraminifera have seasonal preferences and also migrate vertically during their life cycle, recording the signal of the water depth in which they calcify throughout their habitat range (Anand et al., 2003; Elderfield & Ganssen, 2000; Fairbanks et al., 1982; Jonkers & Kučera, 2015; Mohtadi et al., 2009). Accordingly, the characteristics of different water depths and seasons control the signal that is reflected by the shell chemistry and will thus modulate the recorded spread in IF Mg/Ca and δ¹⁸O.

A previous example of how site‐specific conditions may affect IFA variability was shown in a study from the Mediterranean Sea, which is characterized by a large salinity gradient. It was concluded that the spread in laser ablation‐based Mg/Ca and δ¹⁸O on single specimens of G. ruber was similar to the seasonal cycle (Wit et al., 2010). However, the lack of a relationship between Mg/Ca and δ¹⁸O suggested that an additional impact of (seasonal) changes in salinity and the carbonate ion concentration might have affected the proxy signals and led to a differing impact of salinity on Mg/Ca and δ¹⁸O (Wit et al., 2010). Additionally, when seasonal changes in SST are high as in the Mediterranean Sea, the seasonal flux of foraminifera may become more concentrated over a shorter time period also affecting the spread in IF geochemistry (Jonkers & Kučera, 2015).

4.6. Implications for Paleoceanographic Reconstructions

We have demonstrated a strong relationship between the single‐specimen variability in Mg/Ca and δ¹⁸O. The consistency of the ratio of variability with the standard temperature calibration as well as the relationship between the variability of both proxies across individual sites demonstrates that single‐specimen variability is dominated by seawater temperatures during calcification.

However, while consistent between both temperature proxies, the observed variability cannot be fully explained by simple predictions from oceanographic temperature and salinity data alone. For example, comparing the full seasonal and interannual SST variability at our sites with the single‐specimen variability of the surface dwellers showed only a weak relationship, suggesting an effect of ecology leading to site‐specific seasonal and depth habitat changes. Where the oceanographic variability is the strongest, the IFA variability (e.g., N. dutertrei at GeoB 10008‐4) is significantly less than expected, as N. dutertrei appears to concentrate its flux to minimize varying conditions. This finding also suggests that the general relationship between IFA and variability may be less robust for sites affected by strong oceanographic/climatic variability.

This has important implications for paleostudies using the variability in IFA to reconstruct seasonality (Ganssen et al., 2011) and/or interannual variability like ENSO (Koutavas et al., 2006; Leduc et al., 2009; Rustic et al., 2015; Sadekov et al., 2013; Scroxton et al., 2011). The flux of foraminifera to the sediment can strongly depend on the species‐specific preference for certain conditions. A certain species will thrive at the time of year and water depth where it experiences ideal conditions (Jonkers & Kučera, 2017; Mix, 1987; Skinner & Elderfield, 2005). If these conditions change through time, for example, last glacial in comparison with today, the season and depth recorded by a species may be shifted and thus affect the recorded mean and variability (Fraile et al., 2009). Using the spread in IF Mg/Ca and δ¹⁸O as indicator for past changes in climate conditions may therefore be biased by the ecology reacting to changes in the structure of the water column.

Simple models parametrizing the foraminiferal flux as a function of environmental parameters (Mix, 1987; Schmidt & Mulitza, 2002; Roche et al., 2018; Dolman & Laepple, 2018) might allow first‐order estimates of these ecological effects. Further, more complex ecosystem modeling that also includes the interaction of secondary parameters such as nutrients has the potential to provide indications on how seasonality and habitat depth change in a different climatic setting (Kretschmer et al., 2018; Lombard et al., 2011). This would help in isolating the part of the signal in IFA, which represents changes in interannual variability or changes due to a shift in seasonality and depth habitat migration. However, the predictive quality of such an approach should be tested first on core top data with known oceanographic conditions, such as the data set presented here, or by directly comparing the geochemistry of foraminiferal tests from depth‐specific plankton tows with water analyses before using it to reconstruct past climate variability.

5. Conclusions

We present for the first time a combined approach of the analysis of Mg/Ca and δ¹⁸O on single specimens of foraminifera to investigate if its variability is related to climatic conditions or affected by analytical biases, intrinsic variability, or ecological changes. The mixed‐layer species G. ruber (s.s.), G. ruber (pink), and T. sacculifer and the thermocline‐dwelling N. dutertrei were selected from core tops with widely differing seasonalities from the Indo Pacific Warm Pool, seasonal upwelling off Indonesia, and the GoM where large seasonal variations occur.

Our results indicate that the variability in Mg/Ca and δ¹⁸O is mainly driven by seawater temperature and less by δ¹⁸O_sw variations during calcification, which allows the use of single‐specimen variability to infer environmental changes experienced by foraminifera. The results show that there is not always a simple relationship between the strength of the seasonal cycle and the spread in IFA; generally all species show more variability than expected, but when conditions become highly variable, like for N. dutertrei in the thermocline at GeoB 10008‐4, the variability is less than expected. It is likely that the spread is additionally modulated by variations in the habitat depth of the foraminifera and its seasonality. Accordingly, IFA may also contain information on how the foraminifera respond to changing climate conditions by adapting their season and habitat depth occurrence to optimize their living conditions thus minimizing variability when living in a highly variable setting. Our results suggest that the classic interpretation of IFA would be prone to underestimating the true extent to variability changes.

Our results call for further single‐specimen studies on modern core tops and depth‐stratified plankton tows to cover a larger range of oceanographic conditions and to estimate how variability changes in the water column. This would allow better characterizing the IFA signal, on one hand, as a direct proxy of seasonal and interannual climate variability and on the other hand, as a tool to constrain past changes in habitat depth. This may additionally be improved by performing IFA on foraminifera from depth‐stratified plankton tows that can directly be compared with the water mass characteristics at the sampled water depth. Such data sets would also provide an ideal test bed for statistical and ecosystem model‐based approaches to predict the habitat of foraminifera and thus to ultimately improve the interpretation of foraminiferal‐based paleoclimate records.

Supporting information

Supporting Information S1

Figure S1

Groeneveld, J. , Ho, S. L. , Mackensen, A. , Mohtadi, M. , & Laepple, T. (2019). Deciphering the variability in Mg/Ca and stable oxygen isotopes of individual foraminifera. Paleoceanography and Paleoclimatology, 34, 755–773. 10.1029/2018PA003533