EMIC Waves in the Outer Magnetosphere: Observations of an Off‐Equator Source Region

Abstract

Electromagnetic ion cyclotron (EMIC) waves at large L shells were observed away from the magnetic equator by the Magnetospheric MultiScale (MMS) mission nearly continuously for over four hours on 28 October 2015. During this event, the wave Poynting vector direction systematically changed from parallel to the magnetic field (toward the equator), to bidirectional, to antiparallel (away from the equator). These changes coincide with the shift in the location of the minimum in the magnetic field in the southern hemisphere from poleward to equatorward of MMS. The local plasma conditions measured with the EMIC waves also suggest that the outer magnetospheric region sampled during this event was generally unstable to EMIC wave growth. Together, these observations indicate that the bidirectionally propagating wave packets were not a result of reflection at high latitudes but that MMS passed through an off‐equator EMIC wave source region associated with the local minimum in the magnetic field.

Key Points

• Several hours of EMIC wave activity were observed off‐equator in the outer magnetosphere with plasma conditions favorable for local growth

• Changes in direction of the wave Poynting vector indicate transition of source region from poleward, to local, to equatorward of spacecraft

• Observations confirm association of EMIC wave source region with local minimum‐B of the field line, possibly related to Shabansky orbits

1. Introduction

Electromagnetic ion cyclotron (EMIC) waves are a fundamental instability in the magnetosphere that regulate ion temperature anisotropy (Anderson et al., 1996; Cornwall, 1965; Kennel & Petschek, 1966; Rauch & Roux, 1982), heat heavy ions through resonant interactions (e.g., Zhang et al., 2010, 2011), scatter energetic electrons in the inner magnetosphere resulting in radiation belt electron loss (e.g., Jordanova et al., 2008; Lyons & Thorne, 1972; Miyoshi et al., 2008; Thorne & Kennel, 1971), and lead to ion precipitation and ring current ion loss during geomagnetic storms through wave scattering (e.g., Erlandson & Ukhorskiy, 2001; Jordanova et al., 2001; Spasojevic et al., 2011; Yahnin & Yahnina, 2007). Typically, the source regions of EMIC waves in the inner magnetosphere have been thought to be confined near the equator (magnetic latitudes [MLATs] within about ±11°; Loto'aniu et al., 2005), particularly where the ring current and plasmapheric ion populations overlap in the afternoon sector (magnetic local time [MLT] of about 12–16 hr; e.g., Rauch & Roux, 1982; Tetrick et al., 2017). This inner magnetospheric source of EMIC waves has been well documented by statistical studies (Anderson et al., 1992a, 1992b; Fraser & Nguyen, 2001; Loto'aniu et al., 2005; Min et al., 2012; Usanova et al., 2013; Allen et al., 2015; Saikin et al., 2015). To better characterize the spatial extent of this source region, Loto'aniu et al. (2005) utilized the direction of the Poynting vector associated with these waves to determine the latitudinal extent of the excitation region: Within the source region, the waves can propagate bidirectionally (both parallel and antiparallel to the background magnetic field), while outside of the source region, only propagation directed away from the source region is observed. The survey conducted by Loto'aniu et al. (2005) of the inner magnetosphere, using Combined Release and Radiation Effects Satellite (CRRES), found that all of the EMIC waves observed outside of MLATs of ±11° were propagating away from the equator, while observations within ±11° were composed of both waves propagating parallel and antiparallel. These results led to the conclusion that the inner magnetospheric source region was confined to ±11° MLAT.

However, statistical surveys of EMIC waves have also shown that these waves occur frequently in the outer magnetosphere across the dayside region (Allen et al., 2015, 2016; Anderson et al., 1991; Min et al., 2012; Wang et al., 2017). Theoretical/numerical analyses have predicted that there could be high‐latitude EMIC wave generation regions for larger L shells due to the effects of drift‐shell splitting and particles executing Shabansky orbits (Shabansky, 1971) around local minimums in the magnetic field occurring off‐equator in the dayside magnetosphere (McCollough et al., 2009, 2010, 2012). Statistical studies of EMIC waves in the middle to outer magnetosphere (i.e., L shell ≳ 7) have suggested that these high‐latitude source regions may indeed exist, given the observed wave and plasma properties along with instability threshold proxies (Allen et al., 2015, 2016). While the dayside outer magnetosphere has been shown to be conducive for wave growth over a large latitudinal range, there have only been a couple of case studies of bidirectionally propagating EMIC waves at high latitudes (Allen et al., 2013; Liu et al., 2013). Similarly to the approach of Loto'aniu et al. (2005), Allen et al. (2013) observed EMIC waves with bidirectional Poynting flux during times when the background magnetic field and plasma conditions were seen to meet criteria for wave growth based on the linear theory for EMIC wave generation (Blum et al., 2009; Gary & Lee, 1994). However, because of the orbit of Cluster, neither the observations in Allen et al. (2013) nor those in Liu et al. (2013) were fully sufficient for discerning whether the bidirectional Poynting vector of the waves were actually due to local generation or were a result of reflection, due to the entire interval being observed as bidirectionally propagating. As has been theorized and shown recently in simulations, EMIC waves propagating along the magnetic field from a low‐latitude source region can be reflected back toward the equator as the waves pass through some critical frequency at high latitudes, like the bi‐ion hybrid or crossover frequency [see Kim & Johnson, 2016]. So while the data in Allen et al. (2013) and Liu et al. (2013) favored local generation as the mechanism behind the bidirectional Poynting vector, whether equatorially directed Poynting flux at high latitudes imply an off‐equator source or simply the reflection of waves at the bi‐ion hybrid frequency remains uncertain, especially at large L shells in the dayside magnetosphere.

We present observations from the Magnetospheric Multiscale (MMS) spacecraft of EMIC waves occurring for several hours in the outer magnetosphere. Sufficient plasma, magnetic field, and electric field measurements were obtained to determine the wave Poynting vector and evaluate the favorability of local instability to EMIC waves throughout the event. The event duration and radial profile of MMS allow us to track changes in local wave instability conditions and Poynting vector direction as MMS passed inbound from the outer magnetosphere where the local minimum in B was poleward of MMS, through the local minimum‐B region near MMS, to where the minimum‐B region was equatorward of MMS.

2. Observations of EMIC Waves on 28 October 2015

The four identical MMS spacecraft fly with unprecedented close interspacecraft separations in a near‐tetrahedral configuration and carry a full complement of field and particle instruments to diagnose fundamental plasma processes (Burch et al., 2016). On 28 October 2015 from 13:00 to 17:15 UT, EMIC wave activity was observed by MMS nearly continuously (Figure 1). Because of spacecraft separations on the order of 10 km for 28 October 2015 (see Fuselier et al., 2016), only data from MMS2 are shown here (the field and particle signatures of the waves were essentially identical at all four MMS spacecraft). Observations of both the background magnetic field and the wave magnetic field are from the Fluxgate Magnetometer (FGM; Russell et al., 2016). The wave electric field data are from the electric field double probes (EDP) instrument (Torbert et al., 2016), a combined product of the Spin‐plane Double Probes (Lindqvist et al., 2016) and the Axial Double Probes (Ergun et al., 2016) that gives full three‐dimensional electric field measurements. Ion composition measurements used here are from the Hot Plasma Composition Analyzer (HPCA; Young et al., 2016), which measures three‐dimensional distributions of H⁺, He⁺, He⁺⁺, and O⁺ ions from ~ 1 eV to 40 keV. The low‐energy limit of HPCA is determined by the spacecraft potential, which is usually a few volts positive and is sometimes actively controlled (Torkar et al., 2016). For the observations on 28 October 2015, the spacecraft potential was actively controlled over the majority of the interval (from 13:05 to 16:20 UT) and held around 3.5 V (after 16:20 UT, the spacecraft potential increased to ~10 V). During this time interval, MMS instruments were operated in two different modes, “fast survey” from 13:00 to 16:03:30 UT and then “slow survey” from 16:03:30 to 17:15 UT. The FGM time cadence changed from 16 vectors/s in fast survey mode to 8 vectors/s in slow survey mode. The EDP time cadence also changed from 64 vectors/s in fast survey down to 8 vectors/s in slow survey. For HPCA, the time cadence for the ion distributions and moments changed from a 10‐s cadence in fast survey to a 70‐s cadence in slow survey. To examine the EMIC wave fields and power spectral densities, the magnetic and electric fields were first band‐pass‐filtered over a frequency range of 0.1–2 Hz and then rotated into magnetic field‐aligned coordinates, where z = b = B/|B|, y = b × X _GSE, and x = y × b completes the set. Fast Fourier transforms were then done with 1,024 points for the fast survey electric and magnetic field data and then with 512 points for the slow survey data. Various cross‐spectral quantities were then evaluated from the magnetic and electric field Fourier spectra.

Figure 1.

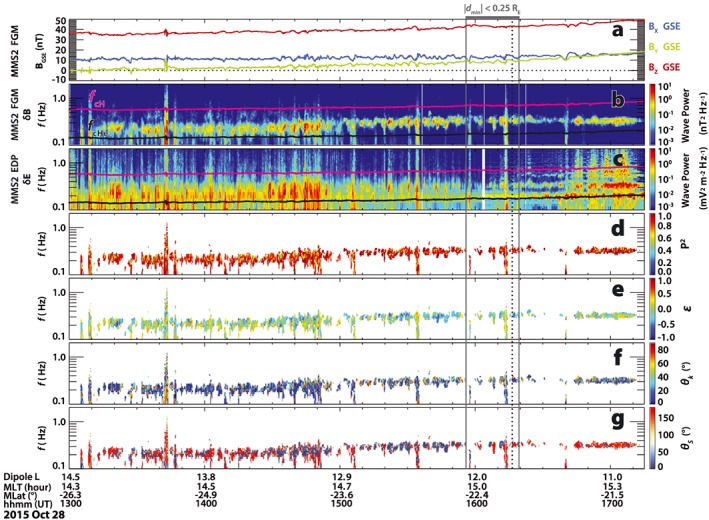
MMS2 observations of an EMIC wave train and wave properties on 28 October 2015. (a) The magnetic field components in GSE from FGM; (b) δB wave power between 0.1 and 2 Hz from FGM; (c) δE wave power between 0.1 and 2 Hz from EDP; (d) the degree of polarization of the waves, P ²; (e) wave ellipticity, ε; (f) wave normal angle, θ _k; and (g) wave Poynting angle, θ _S (wave Poynting vector direction relative to the background magnetic field). The degree of polarization, ellipticity, and wave normal angle are determined from the δB wave fields and shown where the δB power is greater than 0.05 nT²/Hz. The gray bar at the top and the gray vertical lines denote where the distance from MMS2 to the local minimum in B (B _min) in the southern hemisphere (d _min) is less than 0.25 R _E. The black dashed vertical line marks d _min = 0, indicating the orbit of MMS intersects the local B _min location.

Figure 1 shows an overview of the EMIC waves observed by MMS2 during this 4‐hr interval. The background magnetic field is generally directed northward (Figure 1a), and the wave power in both the magnetic and electric fields shows primarily a single band at a frequency of 0.2–0.4 Hz and between the local H⁺ and He⁺ gyrofrequencies (magenta and black lines, respectively, in Figures 1b and 1c). Figures 1d–1f give the EMIC wave degree of polarization (P ²), ellipticity (ε), and wave normal angle (θ _k), respectively, determined from minimum variance analysis of δB (Samson & Olson, 1980) and shown where the δB power was greater than 0.05 nT²/Hz. For the entire wave train, the degree of polarization was greater than 70%, indicating that the wave power at the frequencies of interest are coherent signals. Particularly after 15:00 UT, the EMIC waves are generally left handed to linear (Figure 1e), and the wave normal angle is generally small (<20°). This is consistent with previous observations of EMIC wave properties in the outer magnetosphere (e.g., Allen et al., 2015 ; Min et al., 2012 ; Wang et al., 2017). Finally, the Poynting vector was derived using the formulation from Loto'aniu et al. (2005, their equation 9):

$${\mathbf{S}}_{\mathit{av}}=\frac{1}{4{\mu }_0}\left(\mathrm{\delta }{\mathbf{E}}^{*}\times \mathrm{\delta }\mathbf{B}+\mathrm{\delta }\mathbf{E}\times \mathrm{\delta }{\mathbf{B}}^{*}\right)$$ (1)

where δB and δE are the three‐dimensional wave field spectra and S _av is the complex spectral Poynting vector. Figure 1g shows the angle between the Poynting vector and the background magnetic field, θ _S (referred to here as the “Poynting angle”). Because the magnetic field is predominantly in the +Z _GSE direction and MMS is in the southern hemisphere, a Poynting angle of 0° corresponds to equatorward propagation along the magnetic field (to lower |MLAT|) and an angle of 180° corresponds to poleward propagation (to higher|MLAT|). Focusing on the time interval of 15:00–17:15 UT, θ _S changes from primarily parallel to the magnetic field (θ _S ~ 0°) before 15:50 UT to antiparallel (θ _S ~ 180°) after 16:20 UT. Between 15:50 and 16:20 UT, the θ _S distribution is bidirectional (alternating between 0° and 180°), indicating that wave packets occur with S _av directed both toward and away from the magnetic equator.

At the start of this interval (13:00 UT), MMS was just past its orbit apogee (12 R _E) in the afternoon sector and was inbound toward the inner magnetosphere. From 13:00 to 17:15 UT, MMS went from MLT = 14.3 hr, MLAT = −26.3°, and dipole L shell = 14.5 to MLT = 15.3 hr, MLAT = −21.5°, and dipole L shell = 11.0 (also listed on the bottom of Figure 1). Despite being at a radial distance optimized for capturing magnetopause crossings (see Fuselier, Lewis, et al., 2016), MMS never encountered the magnetopause during this orbit, due to a prolonged period of fairly low dynamic pressure (<1 nPa) with a largely radial and slightly northward interplanetary magnetic field (IMF) prior to these observations. Figure 2 illustrates the inbound orbit of MMS in relation to the location of local magnetic field minima in each hemisphere (B _min, marked by the purple X's). The magnetic field line traces were calculated using the T01 magnetic field model (Tsyganenko, 2002a, 2002b) and upstream solar wind data from 1‐min‐averaged OMNI data (King & Papitashvili, 1994; https://omniweb.gsfc.nasa.gov) that is interpolated to the MMS spacecraft position data time cadence of 30 s. Modeled magnetic field lines in Figure 2 are shown at every 15 min from 13:00 to 17:15 UT in Figure 2 (left). The location of the northern hemisphere B _min at each time step in the interval is determined by finding the minimum along the modeled magnetic field where Z _GSM > 0. The southern B _min locations are found in the same fashion but for where Z _GSM < 0. The B _min locations are also shown at every 15 min in Figure 2.

Figure 2.

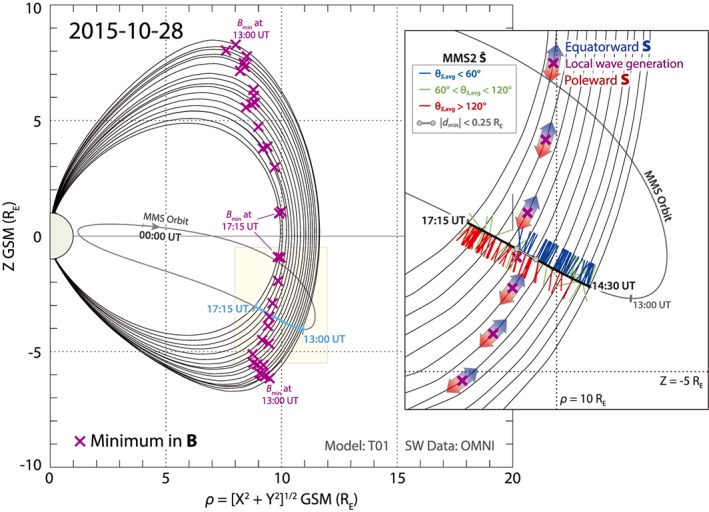
(left) MMS orbit on 28 October 2015 in the ρ‐Z GSM plane (ρ = [X ² + Y ²]^1/2), with the Sun to the right. The light blue portion of the orbit shows the time interval of the EMIC wave observations in Figure 1. The black traces show the magnetic field line corresponding to the position of MMS from the T01 magnetic field model using OMNI upstream solar wind data, plotted at every 15 min from 13:00 to 17:15 UT. The purple X's overlaid on the field lines show the location of the minimum in B of the modeled magnetic field lines for both the northern and southern hemisphere. The yellow‐shaded region highlights the region of interest (ρ = 8 to 12 R _E, Z = −0.5 to −5.5 R _E) of the EMIC wave observations from 14:30 to 17:15 UT. (right, inset) A closer view of the modeled magnetic field lines and B _min locations in the yellow‐shaded region, as well as the Poynting unit vector per wave packet projected into the ρ‐Z GSM plane from 14:30 to 17:15 UT. Each Poynting unit vector is colored by the average θ _S shown in Figure 1g for that wave packet, where blue denotes θ _S,avg < 60° (parallel to the magnetic field), green 60° < θ _S,avg < 120° (perpendicular), and red θ _S,avg > 120°(antiparallel). The light gray circles and line segment show where d _min is less than ±0.25 R _E, coinciding with the bidirectional Poynting vector observations around 15:55–16:20 UT. The large blue‐to‐red arrows centered on the B _min locations show schematically how the observed wave Poynting vector direction depends on the position of the spacecraft relative to a wave generation region, especially for an off‐equator generation region.

Figure 2 (right inset) shows a closer view of the MMS orbit and magnetic field line traces from 14:30 to 17:15 UT. Figure 2 also shows a projection of the Poynting unit vector (Ŝ) in the ρ‐Z GSM plane, where the Poynting unit vector is found for each EMIC wave packet from 14:30 to 17:15 UT. Times of broadband wave power (e.g., around 15:06 and 15:34 UT) are not shown, as the EMIC wave signatures are difficult to distinguish. The color of the Poynting unit vector in Figure 2 is determined by average of the Poynting angle for each packet from Figure 1g and denotes where the Poynting vector is predominantly parallel to the magnetic field (blue, θ _S < 60°), antiparallel to the field (red, θ _S > 120°), or in a more perpendicular direction (green, 60° < θ _S < 120°). How the Poynting vector direction relates to a local wave generation region is shown schematically in Figure 2 by the thick red‐to‐blue arrows centered on the modeled B _min locations in the southern hemisphere. For the case of MMS on 28 October 2015, if the spacecraft is at higher southern latitudes than a local generation region, the observed Poynting vector will be predominantly antiparallel. Conversely, EMIC wave observations from the spacecraft at lower southern latitudes than the generation region (e.g., from a local source region tied to an off‐equator minimum in B occurring at large L shells) will primarily show a parallel Poynting vector direction.

As the spacecraft moved to lower L shells, the local magnetic minimum on the MMS field line in the southern hemisphere moved to lower latitudes, crossing the orbit of MMS around 16:15 UT. To further examine the relative location of the local magnetic minima, the distance along the magnetic field line from the location of the southern B _min to MMS2 (d _min) was also calculated. The time interval where d _min is less than ±0.25 R _E is marked in Figures 1 and 3 by the gray bar at the top of the plots and in Figure 2 (right) by the light gray circles. The intersection of the southern B _min location and the MMS2 orbit (d _min ~ 0) is shown by the dashed black vertical line at 16:16 UT in Figures 1 and 3. As evident in Figure 1g, the time when|d _min|< 0.25 R _E, 15:55–16:20 UT, corresponds to the time when the Poynting vector direction is highly variable between equatorward, θ _S < 30°, and poleward, θ _S > 150°.

Figure 3.

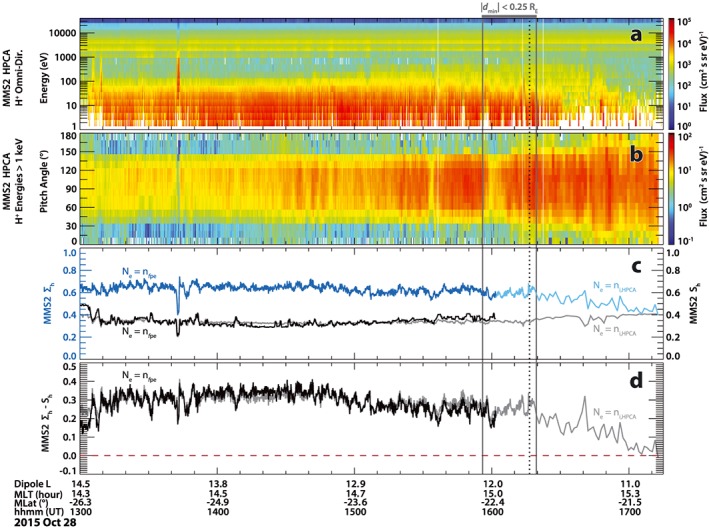
Associated plasma conditions observed with the EMIC waves from MMS2 used for calculating linear theory‐based wave growth proxies. (a) The HPCA proton omnidirectional flux from 1 eV to 40 keV; (b) pitch angle distribution of protons with energies >1 keV (“hot protons”) from HPCA; (c) observational EMIC wave growth parameter, Σ_h, shown in the dark and light blue traces, with the theoretical EMIC wave instability threshold parameter, S _h, shown in black and gray; and (d) the linear theory proxy for local generation from the difference between Σ_h and S _h. The dark blue and black lines are calculated using a total density derived from the electron plasma frequency (n_fpe), and the light blue and gray lines are calculated using the total ion density (n_i,HPCA) from all species measured by HPCA (H⁺, He⁺, He²⁺, and O⁺). The locations of |d _min| < 0.25 R _E and d _min = 0 are also marked as done in Figure 1.

The local plasma conditions and linear theory proxies for wave growth (Blum et al., 2009) for the EMIC wave interval are shown in Figure 3. Throughout the interval of EMIC wave observations on 28 October 2015, there was a substantial cold proton population (<100 eV) present in the outer magnetosphere (Figure 3a), but with an anisotropic hot proton population (energies >1 keV). While the temperature anisotropy of the hot proton population remains roughly constant from 13:00 to 17:15 UT (T_⊥/T_|| − 1 ≈ 0.8), the pitch angle distribution of the hot protons (Figure 3b) becomes increasingly trapped during the wave interval before about 16:15 UT (i.e., flux at pitch angles of ~30–150° is orders of magnitude greater than flux at pitch angles of 0–30° and 0–180°). Heavy magnetospheric ions (He⁺ and O⁺) were also observed during this time, particularly higher densities of lower‐energy He⁺ (reaching up to ~0.1 cm⁻³ for energies of a few 100 eV) than generally seen at large L shells (not shown). Narrow‐band high‐frequency (up to 100 kHz) electric field wave power in fast survey mode was used to identify the electron plasma frequency and obtain a total plasma density (N_e = n_fpe). Using the total plasma density and the density and parallel temperature of the hot protons from HPCA, the observational EMIC wave growth parameter, Σ_h (light blue and dark blue traces), and the theoretical EMIC wave instability threshold parameter derived from a fit to the linear kinetic theory dispersion relation, S _h (gray and black traces), are calculated (see Blum et al., 2009) and shown in Figure 3c. After 16:03 UT the electric field data are from slow survey mode in which high‐frequency electric field data are not obtained, and so emission at the electron plasma frequency was no longer observed. Because of this, the total ion density from HPCA (N_e = n_i,HPCA) was also used for calculating the linear theory proxies in Figures 3c and 3d. That the proxies calculated with the two different densities agree quite well when both are available indicates that nearly all of the ion distribution was observed by HPCA during this period. The difference between the observational EMIC growth parameter and the theoretical instability threshold, Σ_h − S _h, is shown in Figure 3d. The positive value of Σ_h − S _h in Figure 3d throughout the entire interval indicates that conditions were favorable for local EMIC wave growth. Interestingly, no large‐scale global magnetospheric activity or convection was seen on 28 October 2015, and there had been a prolonged interval of slow solar wind speeds with a strongly radial IMF for over 12 hr before the EMIC wave observations (not shown).

3. Discussion and Summary

A several hours‐long EMIC wave train was observed by MMS on 28 October 2015 as the spacecraft headed inbound in the afternoon sector (MLT of 14 to 15 hr). Because of the relatively slow speed of MMS at that point in the orbit (~ 2 km/s just after the orbit apogee), MMS2 was able to sample the outer magnetospheric wave activity for hours, tracking the evolution of the EMIC wave properties and local plasma conditions throughout the period.

The key notable feature of the waves during this time period is that the Poynting vector direction changed systematically over the course of the interval. Examining Figure 1g, for the first 1.5 hr from 13:00 to 14:30 UT, there is not a clear dominant directionality of the Poynting vector, suggesting that this period may be in a broad region favorable to wave generation due to the general compression of the dayside magnetopause by the solar wind (Anderson & Hamilton, 1993; Engebretson et al., 2002) or that the observations result from the superposition of waves generated in both hemispheres (i.e., antiparallel [parallel] θ _S for waves generated in the northern [southern] hemisphere). However, after 14:30 UT, the Poynting vector becomes more clearly field‐aligned, θ _S < 30° (indicating equatorward propagation), particularly for the wave packets between 14:30–14:50 UT and 15:20–15:50 UT. The Poynting angle is then seen to vary between either θ _S < 30° or θ _S > 150°, and, unlike the first hour of this interval, the adjacent wave packets are more isolated from each other and have more distinct values of θ _S that alternate between ~0° and ~180° from 15:50 to 16:20 UT. After 16:20 UT, the Poynting vector direction becomes predominantly antiparallel to the magnetic field (indicating poleward propagation) and remains that way for the rest of the interval through 17:15 UT. Because MMS is in the southern hemisphere during this part of the inbound orbit (going from −26° to −21° MLAT), the Poynting vector direction of the waves changing from parallel to the magnetic field, to bidirectional, to antiparallel indicates a wave source region that begins at a higher latitude than MMS at the start of interval to equatorward of MMS by the end of the event. The occurrence of persistent equatorward Poynting flux from 14:30 to 15:15 UT is not consistent with wave reflection but instead strongly indicates that the waves during this time were generated away from the magnetic equator, poleward of MMS.

The interval with bidirectionally propagating waves in this observation (15:50−16:20 UT) is very similar to the off‐equator EMIC waves reported by Allen et al. (2013) and Liu et al. (2013). Both Allen et al. (2013) and Liu et al. (2013) discussed that because they did not observe a leading or trailing unidirectional Poynting vector direction associated with their EMIC wave observations, they could not determine whether the bidirectional waves were a result of local propagation or reflection at a critical bi‐ion hybrid frequency. However, through the fortuitous observation of the leading and trailing unidirectionally propagating packets between 14:30–15:50 UT and after 16:20 UT, we can rule out the possibility of reflection for this interval. As in the cases highlighted in Loto'aniu et al. (2005), on either side of the bidirectionally propagating region, the waves in this interval consistently indicate propagation away from a source region. Comparing the regions of parallel, bidirectional, and antiparallel propagation after 14:30 UT to the location of the local B _min along the field line connected to MMS provides additional insight. During the times when the wave packets are observed to be propagating equatorward (poleward), the B _min region is poleward (equatorward) of MMS (see Figure 2). However, the interval of bidirectionally propagating wave packets (alternating θ _S values between about 15:50 and 16:20 UT) are all observed to be within about ±0.25 R _E of the location of the southern hemisphere B _min (Figures 1g and 2, right). This would suggest that for this interval the source region extended about 0.5 R _E in Z _GSM around MLATs near −22° for a dipole L shell of 12. MMS within the source region during this time implies that particles executing Shabansky orbits were contributing to off‐equator wave generation, as previously predicted but not confirmed (e.g., Allen et al., 2016; McCollough et al., 2009).

This interpretation for the period after 14:30 UT is supported by the plasma measurements, which indicate that the region MMS measured throughout the period of EMIC wave observation is generally favorable for local EMIC wave growth. As seen in Figure 3, the flux of 90° pitch angle particles increases as MMS approaches the B _min region (marked by the gray bar and vertical lines in Figure 3). After passing through the B _min region, the H⁺ anisotropy is seen to decrease, consistent with the confinement of 90° pitch angle particles to the local off‐equator B _min (e.g., McCollough et al., 2012). Additionally, the entire interval satisfies the linear theory and observationally derived wave growth proxy, Σ_h − S _h (Figure 3d). This linear theory proxy is largest prior to 15:00 UT, slightly lower from 15:00 to 16:20 UT, and then decreases most (but remains slightly positive) after 16:20 UT. There are limitations to this proxy, however (e.g., the proxy does not account for effects from curvature in the magnetic field (e.g., Denton, 2018), nor does it incorporate feedback based on the relative abundance of different ion species (e.g., Lee & Angelopoulos, 2014b)), so it is entirely possible that the local generation region is more spatially confined than suggested by Figure 3d. Regardless, the Σ_h − S _h proxy does indicate that up until about 16:20 UT, MMS was in a region that was unstable to EMIC waves and that the local instability was reduced after 16:20 UT. So the linear theory proxy combined with the wave observations in Figure 1 and the correlations with the B _min latitude relative to MMS and Poynting vector direction in Figure 2 suggests that the source region moved equatorward of MMS after 16:20 UT.

Interestingly, the magnetosphere was quiet during this time period, with no indications of auroral activity in geomagnetic indices (AE), enhanced convection in the global field‐aligned currents, or sudden compressions of the magnetosphere in magnetic field (Geostationary Operational Environmental Satellite [GOES], Sym‐H) or solar wind data. Yet something was maintaining the temperature anisotropy of the outer magnetosphere for an extended period of time, and more low‐energy, ionospheric‐originating plasma was present at larger radial distances than is typical for the outer magnetosphere during quiet times (see Fuselier et al., 2016; Lee & Angelopoulos, 2014a). The effects on the wave generation and characteristics from the population of lower‐energy He⁺ and O⁺ present during this interval is outside the scope of this paper, but it is a rather singular observation that the majority of the ion distribution has been energized into the range of detection for HPCA. This event is observed for L > 11, and at an average MLAT of −24°, during a prolonged quiet period. Especially in the absence of any global storm activity, being off‐equator and at high L shells would indicate another mechanism leading to EMIC wave generation such as the combination of drift‐shell splitting and Shabansky orbits off‐equator due to the compressed magnetic field on the dayside. The combination of drift‐shell splitting and Shabansky orbits as a wave generation mechanism is different from the well‐studied EMIC wave generation due to the plasmaphere‐ring current overlap in the inner magnetosphere or the plasmaspheric plume during active times (e.g., Chen et al., 2009; Rauch & Roux, 1982; Usanova et al., 2013). As plasma is supplied by convection, drift‐shell splitting would lead to a higher ion anisotropy at large L shell (Sibeck et al., 1987). The bifurcated minimums in B in the dayside outer magnetosphere (e.g., the locations of B _min in Figure 2) would then lead the near‐90° pitch angle particles to be magnetically trapped off‐equator, thereby executing Shabansky orbits (McCollough et al., 2012; Shabansky, 1971). This region of high anisotropy and lower magnetic field could then become unstable for EMIC wave excitation, as is suggested by the magnetic field tracing and wave and plasma observations from MMS for 28 October 2015. For the outer magnetosphere, which was shown to be generally marginally unstable to EMIC wave generation (Anderson et al., 1992a, 1992b), this mechanism has been suggested by the statistical surveys of Allen et al. (2015, 2016) and Min et al. (2012) and has been studied in depth by McCollough et al. (2009, 2010, 2012). Wave generation due to drift‐shell splitting and Shabansky orbits was first invoked as an explanation for very low frequency wave observations at high latitudes (Tsurutani & Smith, 1977) and for ground observations of very low frequency waves consistent with an off‐equator source region (e.g., Alford et al., 1996) but has not been observationally confirmed for EMIC wave generation.

This EMIC wave event offers an opportunity to study several different aspects of EMIC wave growth and characteristics near and within an off‐equator source region. Fortuitously, the MMS orbit is particularly well suited to probing the latitudinal structure of EMIC wave occurrence, properties, and propagation. To the best of our knowledge, this is the first definitive observation of an off‐equator source region that includes waves propagating equatorward, within the source (both poleward and equatorward propagation), and then poleward in sequence. This full observation, as well as having a multispecies low‐energy ion component fully observed throughout the interval, allows for exciting in‐depth examinations of effects on wave generation and propagation that is now enabled because of fully three‐dimensional fields and multipoint measurements.

Vines, S. K. , Allen, R. C. , Anderson, B. J. , Engebretson, M. J. , Fuselier, S. A. , Russell, C. T. , et al. (2019). EMIC waves in the outer magnetosphere: Observations of an off‐equator source region. Geophysical Research Letters, 46, 5707–5716. 10.1029/2019GL082152