Accurate estimation of SNP-heritability from biobank-scale data irrespective of genetic architecture

Abstract

SNP-heritability is a fundamental quantity in the study of complex traits. Recent works have shown that existing methods to estimate genome-wide SNP-heritability yield biases when their assumptions are violated. While various approaches have been proposed to account for frequency- and LD-dependent genetic architectures, it remains unclear which estimates reported in the literature are reliable. Here we show that genome-wide SNP-heritability can be accurately estimated from biobank-scale data irrespective of genetic architecture, without specifying a heritability model or partitioning SNPs by allele frequency and/or LD. We show analytically and through extensive simulations starting from real genotypes (UK Biobank, N = 337K) that, unlike existing methods, our closed-form estimator is robust across a wide range of architectures. We provide estimates of SNP-heritability for 22 complex traits in the UK Biobank and show that, consistent with our results in simulations, existing biobank-scale methods yield estimates up to 30% different from our theoretically-justified approach.

Editorial Summary:

The authors use theoretical justifications coupled with extensive simulations to accurately estimate SNP-heritability for 22 complex traits and diseases from the UK Biobank data irrespective of the underlying genetic architecture of the trait.

SNP-heritability, the proportion of phenotypic variance attributable to the additive effects of a given set of SNPs, is a fundamental quantity in genetics¹; it provides an upper bound on risk prediction from a linear model² and, when defined as a function of all SNPs on an array, yields insights into the “missing heritability” of complex traits^3–5. Traditionally, SNP-heritability is estimated by fitting variance components models with REML^3,6–9. With some exceptions⁸, REML-based methods are not scalable to biobanks that assay hundreds of thousands of individuals (e.g., UK Biobank¹⁰). SNP-heritability can also be estimated by assessing the deviation in marginal association statistics as a function of LD scores^11–14; such methods can scale to millions of individuals. More recently, a randomized extension of Haseman-Elston regression¹⁵ was shown to estimate a single genetic variance component from individual-level data as accurately as REML methods but in a fraction of the run-time¹⁶.

To facilitate inference, all existing methods for genome-wide SNP-heritability inference make assumptions on genetic architecture, which is typically parametrized by polygenicity (the number of variants with effects larger than some small constant δ) and MAF/LD-dependence (the coupling of effects with minor allele frequency (MAF), local linkage disequilibrium (LD), or other functional annotations)¹⁷. Since the true genetic architecture of any given trait is unknown, existing methods are susceptible to bias and often yield vastly different estimates even when applied to the same data^9,14,18. Although multi-component methods that stratify SNPs by MAF/LD ameliorate some of these robustness issues^7,18,19, fitting multiple variance components to biobank-scale data with REML is highly resource-intensive⁸ and it is unclear whether multi-component methods based on summary statistics produce accurate estimates of total SNP-heritability. Alternate methods that explicitly model MAF/LD-dependency^6,9,14 are also sensitive to model misspecification^6,9,14,18,19. In addition, genetic architecture varies across traits and populations due to, for example, variable degrees of negative selection acting on different traits in different populations^17,20–25. Methods that jointly infer SNP-heritability and parameters such as the strength of negative selection or polygenicity^14,23,26 are computationally intensive and/or sensitive to LD-dependency. Thus, it remains unclear which estimates of SNP-heritability computed from biobank-scale data are reliable.

In this work, we investigate whether genome-wide SNP-heritability can be accurately estimated under a generalized random effects (GRE) model that makes minimal assumptions on genetic architecture. Under this model, every causal effect has an arbitrary SNP-specific variance, and SNP-heritability is defined as the sum of the SNP-specific variances (Methods). To the best of our knowledge, all existing methods make additional assumptions on top of the GRE model (Table 1). For example, GREML³ (and several other methods^8,16,27) imposes an inverse relationship between MAF and allelic effect size whereas LDAK assumes that each SNP-specific variance is inversely proportional to both MAF and LD tagging^6,9. We derive a closed-form estimator for SNP-heritability as a function of marginal association statistics and in-sample LD and show that this estimator is consistent (approaches the true SNP-heritability as sample size increases) and unbiased (its expectation is equal to the true SNP-heritability) when the number of individuals exceeds the number of SNPs. Most importantly, the accuracy of this estimator is invariant to genetic architecture. While the GRE estimator is similar in form to previously proposed “fixed effect estimators,”^28,29 our approach differs from previous work in two main ways. First, SNP-heritability defined under a fixed effect model is different from the estimand of interest here (Methods). Second, previous work applied the estimator locally to identify regions contributing disproportionately to the genome-wide signal^28,29; here we define a different genome-wide estimator (Equation 1) that requires large-scale genotype data. In addition, previous work applied an SVD-based regularization to account for errors in LD estimation from reference panels²⁹ which was unnecessary in this work (Methods).

Table 1.

Existing methods to estimate SNP-heritability impose additional assumptions on top of the generalized random effects (GRE) model. Under the GRE model, the causal effects at any two SNPs are assumed to be independent ($\text{E}[{\beta }_i{\beta }_j]=0$ for all $i\ne j$) and genome-wide SNP-heritability is defined as $h_g^2\equiv {\sum }_{i=1}^M{\sigma }_i^2$, where each ${\sigma }_i^2$ can be an arbitrary nonnegative real number as long as $0\le h_g^2\le 1$ (Methods). All existing methods make assumptions on the distribution of ${\beta }_i$ and/or the form of ${\sigma }_i^2$ that can be subsumed under the GRE model. To simplify notation, we assume for each model that phenotypes are standardized in the population (i.e. $\text{Var}\left[y_n\right]=1$ for every individual $n$).

Model	Assumptions on ${\beta }_i$	Description
Generalized random effects	$\text{E}\left[{\beta }_i\right]=0$, $\text{Var}\left[{\beta }_i\right]={\sigma }_i^2$, ${\sigma }_i^2\ge 0$	Each SNP $i$ has a nonnegative SNP-specific variance ${\sigma }_i^2$. Total SNP-heritability is $h_g^2\equiv {\sum }_{i=1}^M{\sigma }_i^2$.
GREML-SC 3,8,16	${\beta }_i\sim N\left(0,h_g^2/M\right)$	Each SNP explains an equal portion of $h_g^2$. In other words, ${\sigma }_i^2=h_g^2/M$ for all $i=1,\dots ,M$.
GREML-MC 7,8,18,42,43	${\beta }_i\sim N\left(0,\hspace{0.17em}{\sum }_{c\in C}\left[{\text{SNP}}_i\in c\right]h_c^2/m_c\right)$	$h_g^2$ is partitioned by a set of disjoint SNP partitions $C$ that span all $M$ SNPs. Partition $c\in C$ contains $m_c$ SNPs that have per-SNP variances $h_c^2/m_c$. Total SNP-heritability is $h_g^2={\sum }_{c\in C}{h}_c^2$.
LDAK6,9	${\beta }_i\sim N\left(0,\hspace{0.17em}{\sigma }_i^2\right)$, ${\sigma }_i^2\propto w_i{[f_i\left(1-f_i\right)]}^{1+\alpha }$	Each SNP-specific variance is proportional to a function of $f_i$ (the MAF of SNP $i$) and to $w_i$ (a SNP-specific weight that is a function of the inverse of the LD score of SNP $i$).$\alpha$ controls the relationship between ${\sigma }_i^2$ and $f_i$. The most recent recommendation by ref.9 is to assume $\alpha =-0.25$.
LDSC11	$\text{E}[{\beta }_i]=0$, $\text{Var}\left[{\beta }_i\right]=h_g^2/M$	Each SNP explains an equal portion of $h_g^2$ (similar to the GREML-SC model when $h_g^2$ is defined with respect to the same set of $M$ SNPs).
S-LDSC12,13,30	$\text{E}[{\beta }_i]=0$, $\text{Var}[{\beta }_i]={\sum }_{a\in A}{\tau }_{a}a\left(i\right)$	Each SNP-specific variance is a linear function of a set of annotations $A$ where each $a\in A$ represents a binary or continuous-valued annotation. $a\left(i\right)$ is the value of annotation $a$ at SNP $i$. ${\tau }_a$ is the expected contribution of a one-unit increase in annotation $a$ to each SNP-specific variance.
SumHer14	$\text{E}[{\beta }_i]=0$, $\text{Var}\left[{\beta }_i\right]\propto w_i{\left[f_i\left(1-f_i\right)\right]}^{1+\alpha }$	An extension of the LDAK model to operate on summary-level data; can also efficiently partition $h_g^2$ by multiple annotations. The most recent recommendations by refs.9,14 is to set $\alpha =-0.25$.

Through extensive simulations across a range of MAF/LD-dependent architectures starting from real genotypes from the UK Biobank¹⁰ (337K individuals, 593K SNPs), we find that the GRE estimator is nearly unbiased across all architectures whereas existing methods are sensitive to model misspecification. For example, across 126 distinct architectures, the maximum bias of the GRE estimator is 2% of the simulated SNP-heritability whereas stratified LD score regression (S-LDSC)^12,13 and SumHer¹⁴ yield biases between −64% and 28%. For completeness, we also contrast the GRE estimator with several REML-based methods in simulations at lower sample sizes (due to the computational burden of most REML methods) and find that, consistent with recent reports¹⁸, all REML-based methods are biased when their model assumptions are violated, and multi-component REML methods that stratify SNPs by MAF and LD score (GREML-LDMS-I¹⁸) are more accurate than single-component REML methods. The performance of the GRE estimator is similar to that of GREML-LDMS-I, thereby confirming that SNP-heritability can be accurately estimated without stratifying SNPs or specifying a heritability model^6,9,14.

Finally, we use marginal association statistics and in-sample LD from 290K unrelated British individuals and 460K SNPs (MAF > 1%) to estimate SNP-heritability for 22 complex traits in the UK Biobank¹⁰. Consistent with simulations, estimates from S-LDSC and SumHer differ from the GRE estimates by a median of −9% and 11%, respectively, across the 18 traits with SNP-heritability estimates exceeding 0.05. For example, for height, estimates from S-LDSC (0.56) and SumHer (0.63) are approximately 7% lower and 5% higher, respectively, than our estimate of 0.60. Similarly, for hypertension, estimates from S-LDSC (0.14) and SumHer (0.18) are ±12.5% different from our estimate of 0.16. Taken together, our results demonstrate that SNP-heritability can be accurately estimated from biobank-scale data without prior knowledge of the genetic architecture the trait, motivating the development of scalable methods with fewer modeling assumptions.

Results

Overview of the approach

We investigate the utility of an estimator derived under a model that makes minimal assumptions on genetic architecture. We model the standardized phenotype of an individual as $y={\mathbf{x}}^T\mathbf{\beta }+ϵ$ where $\mathbf{x}$ is an M-vector of standardized genotypes, $\mathbf{\beta }$ is the corresponding vector of standardized effects, and $ϵ\sim N\left(0,\hspace{0.17em}{\sigma }_e^2\right)$ is environmental noise (Methods). The effect size of each SNP is assumed to have mean zero and a finite SNP-specific variance (${\sigma }_i^2$ for SNP $i$) that is allowed to be 0; the covariance between all pairs of effects is assumed to be zero. We term this model the “generalized random effects” (GRE) model as, to the best of our knowledge, all existing methods impose additional assumptions on top of this model. For example, the single-component GREML model³ assumes ${\sigma }_i^2=h_g^2/M$ for $i=1,\dots ,M$ whereas the most recent LDAK model⁹ assumes ${\sigma }_i^2\propto w_i{[f_i\left(1-f_i\right)]}^{0.75}$ (where $w_i$ is a SNP-specific LD weight and $f_i$ is MAF) (Table 1). Under the GRE model, the SNP-heritability explained by the $M$ SNPs is the sum of the SNP-specific variances: $h_g^2\equiv \text{Var}\left[{\mathbf{x}}^T\mathbf{\beta }\right]/\text{Var}\left[y\right]\hspace{0.17em}={\sum }_{i=1}^M{\sigma }_i^2$ (Methods).

Given genotype measurements across $N$ individuals at $M$ SNPs and assuming $N>M$, the estimator ${\widehat{h}}_g^2=\frac{N{\widehat{\mathbf{\beta }}}^T{\widehat{\mathbf{V}}}^{†}\widehat{\mathbf{\beta }}-q}{N-q}$, where $\widehat{\mathbf{\beta }}$ is the vector of estimated marginal effects, ${\widehat{\mathbf{V}}}^{†}$ is the pseudoinverse of the in-sample LD matrix, and $q$ is the rank of the in-sample LD, is an unbiased estimator of SNP-heritability under the GRE model. That is, $\text{E}\left[{\widehat{h}}_g^2\right]={\sum }_{i=1}^M{\sigma }_i^2=h_g^2$ (Methods). Unfortunately, even the largest biobanks currently have $N<M$ (i.e. UK Biobank has genotyped $M\approx 593\text{K}$ SNPs in $N\approx 337\text{K}$ unrelated British individuals), which limits the utility of the above estimator. We therefore extend our approach by partitioning the genome by chromosome:

$${\widehat{h}}_{\text{GRE}}^2=\sum _{k=1}^{22}\frac{N{\widehat{\mathbf{\beta }}}_k^T{\widehat{\mathbf{V}}}_k^{†}{\widehat{\mathbf{\beta }}}_k-q_k}{N-q_k}$$ #(1)

where for chromosome $k$ with $p_k$ SNPs, ${\widehat{\mathbf{\beta }}}_k$ is the $p_k-\text{vector}$ of estimated effects, ${\widehat{\mathbf{V}}}_k^{†}$ is the pseudoinverse of the in-sample LD matrix, and $q_k$ is the rank of the in-sample LD. Although this estimator introduces bias, we show through extensive simulations that the magnitude of the bias is extremely small when $N$ is sufficiently larger than $p_k$.

The GRE estimator is robust in simulations

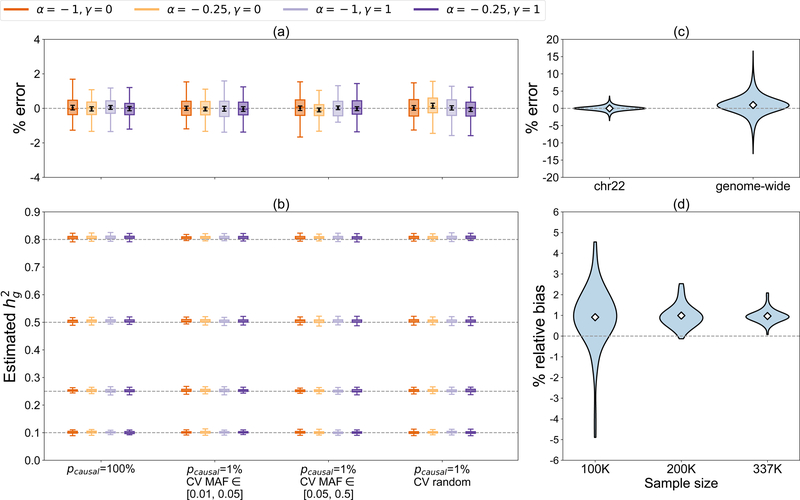
To investigate the bias and variance of ${\widehat{h}}_{\text{GRE}}^2$, we perform simulations starting from real genotypes $(N=337205$, UK Biobank¹⁰). First, we simulate 64 MAF/LD-dependent quantitative trait architectures from chromosome 22 $(M=9654$ typed SNPs) by varying the SNP-heritability $\left(h_g^2\right)$, proportion of causal variants $\left(p_{\text{causal}}\right)$, distribution of causal variant MAF (CV MAF), and strength of coupling between effect size and MAF/LD; we use “LDAK-LD-dependent” to describe causal effects that are coupled with “LDAK weights” (Methods). To compare estimates across different values of $h_g^2$, we assess bias as a percentage of the simulated value of $h_g^2$ (relative bias). Errors of individual estimates are also expressed as percentages of $h_g^2$. Consistent with analytical derivations, the GRE estimator restricted to chromosome 22 is unbiased across the 64 architectures (bias p-value < 0.05/16 is considered significant in order to correct for 16 tests (architectures) at each value of $h_g^2$; Methods) (Figure 1ac, Supplementary Table 1). The average relative bias across the 64 architectures is $0.00015\text{\%}\times h_g^2$ and the largest bias under any single architecture is $\pm 0.2\%\times h_g^2$ (Supplementary Figure 1a, Supplementary Table 1). In simulations of unascertained case-control studies (Methods), the GRE estimator is approximately unbiased across a range of disease prevalences (for $h_g^2=0.10$, relative bias range is [−0.20%, 0.30%]) and has larger variance for lower prevalences (Supplementary Figure 2a, Supplementary Table 2). For ascertained case-control studies, estimates are downward-biased but invariant to architecture (when $h_g^2=0.10$, prevalence = 0.10, and $N_{\text{case}}=N_{\text{control}}$, relative bias is approximately −4%) (Supplementary Table 3). Masking 0%, 50%, or 100% of causal SNPs from the observed summary statistics induces downward-bias when CV MAF = [0.01, 0.05] due to lower average LD between the observed SNPs and masked causal SNPs (Supplementary Figure 3). The analytical estimator of the standard error (Methods) is well-calibrated (Supplementary Figure 4a, Supplementary Table 4). As expected, partitioning chromosome 22 into disjoint, non-independent blocks induces upward bias that increases as block size decreases (Supplementary Figure 5, Supplementary Table 5).

Figure 1.

Simulations under 64 distinct MAF/LD-dependent architectures (N = 337205). For each value of $h_g^2$, phenotypes were drawn according to one of 16 genetic architectures defined by $p_{\text{causal}}$, CV MAF, $\alpha$, and $\gamma$ (Methods). (a) Distribution of errors ${\widehat{h}}_{\text{GRE}}^2\left(i\right)-h_g^2$ (as a percentage of $h_g^2$), where ${\widehat{h}}_{\text{GRE}}^2\left(i\right)$ is the estimate from the $i$-th simulation under a given genetic architecture, in simulations on chromosome 22 (M = 9654 SNPs). ${\widehat{h}}_{\text{GRE}}^2$ was computed with 1 chromosome-wide LD block. Black points and error bars represent the mean and $\pm 2$ standard errors of the mean (s.e.m.) which were used to test whether the bias under a single architecture is significant (Methods). (b) Distribution of ${\widehat{h}}_{\text{GRE}}^2$ in genome-wide simulations (M = 593300 SNPs) where ${\widehat{h}}_{\text{GRE}}^2$ was computed with 22 chromosome-wide LD blocks. In (a) and (b), each boxplot represents estimates from 100 simulations. Boxplot whiskers extend to the minimum and maximum estimates located within $1.5\times \text{IQR}$ from the first and third quartiles, respectively. (c) Distribution of errors for chromosome 22 and genome-wide simulations. Each violin plot represents the errors of 6400 estimates (64 genetic architectures × 100 simulation replicates). (d) Distribution of relative bias (as a percentage of $h_g^2$) as a function of sample size (N = 100K, 200K, or 337K) in genome-wide simulations. Each violin plot represents 64 estimates of relative bias. In (c) and (d), the white diamonds mark the mean of each distribution.

Next, we perform genome-wide simulations $(N=337K$ individuals, $M=593K$ SNPs) to assess ${\widehat{h}}_{\text{GRE}}^2$ with the 22-block approximation (Equation 1). Despite the approximation, ${\widehat{h}}_{\text{GRE}}^2$ is highly accurate and robust across all 64 MAF- and LDAK-LD-dependent quantitative trait architectures (Figure 1b, 1c). Across the 64 architectures, the bias ranges from 0.07% to $2.1\%\times h_g^2$ $\left(\text{average}\hspace{0.17em}\text{=}\hspace{0.17em}0.97\%\times h_g^2\right)$ (Supplementary Figure 1b, Supplementary Table 6). Across all 6400 simulations (64 genetic architectures × 100 simulation replicates), the largest error of any single estimate is approximately $17\%\times h_g^2$ (Figure 1c). As $N/M$ increases, the variance of ${\widehat{h}}_{\text{GRE}}^2$ decreases while the relative bias appears to be approximately fixed, ranging between 0.91% $\left(N=100K\right)$ and 0.99% $\left(N=200K\right)$ (Figure 1d). These trends hold for a range of $p_{\text{causal}}$ (Supplementary Figure 6, Supplementary Table 6), for unascertained case-control studies (Supplementary Figure 2b, Supplementary Table 7), and in a smaller set of simulations with $N=7685$ individuals of South Asian ancestry and $M=1642$ SNPs (Supplementary Table 8; Methods). Most importantly, the accuracy of the GRE estimator is invariant to the underlying architecture (Figure 1b). The analytical estimator for the standard error is downward-biased (and invariant to genetic architecture) with respect to the empirical standard deviation of ${\widehat{h}}_{\text{GRE}}^2$ estimates (Supplementary Figure 4b, Supplementary Table 9). For example, across 16 architectures where $h_g^2=0.25$, the empirical standard deviation of 100 independent estimates ranges from 0.0049 to 0.0064, whereas our estimated standard errors are approximately 0.0036 across all architectures (Supplementary Figure 4b, Supplementary Table 9).

We investigate the effects of unmodeled substructure and/or cryptic relatedness by filtering individuals at different kinship coefficient thresholds (Methods) and find that using stricter relatedness thresholds increases the variance of the estimates (due to smaller sample size) while reducing bias, albeit not significantly (Supplementary Figure 7, Supplementary Table 10). To assess the impact of population stratification, we simulated an effect of the first genetic principal component (PC) on phenotype and computed OLS association statistics both with and without adjusting for the first PC (Methods). As expected, OLS without PC adjustment yields inflated estimates while OLS with PC adjustment yields approximately unbiased estimates (Supplementary Figure 8, Supplementary Table 11). However, even when a relatively large proportion of phenotypic variance is explained by the first PC (e.g., $h_g^2=0.25$, ${\sigma }_s^2=0.05$), the maximum bias we observe using unadjusted association statistics is $5\%\times h_g^2$ ($\text{bias p-value}=2.7\times {10}^{-9}$). Together, these results indicate that the GRE estimator is robust to modest amounts of unmodeled substructure and/or stratification. In all subsequent analyses, we compute ${\widehat{h}}_{\text{GRE}}^2$ with the 22-block approximation as this provides sufficiently accurate estimates and a fair comparison to other methods.

Comparison of methods to estimate SNP-heritability

We compare ${\widehat{h}}_{\text{GRE}}^2$ with existing state-of-the-art methods that are easily scalable to the full UK Biobank data $\left(N=337K\right)$: LD score regression (LDSC), which assumes $\alpha =-1$ and no coupling of effects with LD¹¹; stratified LD score regression (S-LDSC), which partitions $h_g^2$ by a set of annotations of interest^12,13; and SumHer, a scalable extension of LDAK which explicitly models MAF/LD-dependency through a specific form of the SNP-specific variances¹⁴ (Table 1). To ensure a fair comparison, LD scores for all methods are computed using in-sample LD among the M SNPs, and in all simulations we aim to estimate the SNP-heritability explained by the same M SNPs (Methods).

As expected, ${\widehat{h}}_{\text{GRE}}^2$ is robust across all architectures while LDSC, S-LDSC, and SumHer are sensitive to model misspecification. For example, when $h_g^2=0.25$ (Figure 2), LDSC is approximately unbiased under the “single-component GREML model” ($\text{relative bias}=0.04\%$, $p=0.86$) but is sensitive to CV MAF and the degree of coupling between effect size and MAF/LD (e.g., when $p_{\text{causal}}=1\%$, relative bias ranges from −44% to 50%) (Supplementary Table 12). Similarly, SumHer is accurate under the “LDAK model” ($\text{relative bias}=5.3\%$)but highly sensitive to other architectures (when $p_{\text{causal}}=1\%$, relative bias ranges from −19% to 22%) (Figure 2, Supplementary Table 13). S-LDSC (MAF), which partitions $h_g^2$ by 10 MAF bins (Supplementary Table 14; Methods), is less biased than LDSC when effects are coupled with only MAF, but is significantly downward-biased when effects are also coupled with LDAK weights (for $h_g^2=0.25$, relative bias range is [1.9%, 7.0%] when $\gamma =0$ and [−58%, −37%] when $\gamma =1$) (Figure 2, Supplementary Table 15). S-LDSC with 10 MAF bins and an additional “level of LD” annotation, denoted S-LDSC (MAF+LLD) (Methods), produces similar results (for $h_g^2=0.25$, relative bias range is [1.8%, 6.5%] when $\gamma =0$ and [−80%, −33%] when $\gamma =1$) (Supplementary Table 16). In contrast, the relative bias of ${\widehat{h}}_{\text{GRE}}^2$ ranges from 0.45% to 1.3% across the same 16 architectures where $h_g^2=0.25$ and $p_{\text{causal}}=1\%$ (Figure 2, Supplementary Table 6). These trends hold for a range of $h_g^2$ and $p_{\text{causal}}$: across 112 LDAK-LD- and/or MAF-dependent architectures, the average and range of the relative bias of each method are 0.96% [−0.06%, 2.1%] (GRE), −2.2% [−71%, 70%] (LDSC), −22% [−62%, 8.7%] (S-LDSC (MAF)), −29% [−89%, 9.0%] (S-LDSC (MAF+LLD)), and 2.8% [−27%, 28%] (SumHer) (Figure 1b, Figure 2, Supplementary Figures 9–12, Supplementary Tables 6,12,13,15,16). Across 14 alternative LD-dependent architectures where SNP-specific variances are coupled with inverse LD scores instead of LDAK weights (“LD-score-dependent” architectures; Methods, Supplementary Figure 13), ${\widehat{h}}_{\text{GRE}}^2$ remains nearly unbiased (relative bias range [0.52%, 1.3%]) whereas S-LDSC (MAF), S-LDSC (MAF+LLD), and SumHer are generally downward-biased (Supplementary Figure 14, Supplementary Table 17).

Figure 2.

Comparison of ${\widehat{h}}_{\text{GRE}}^2$ with LDSC, S-LDSC (MAF), and SumHer in genome-wide simulations (N = 337205, M = 593300, $h_g^2=0.25$). Left: Phenotypes were drawn under one of 16 MAF- and/or LDAK-LD-dependent architectures by varying $p_{\text{causal}}$, $\alpha$, $\gamma$, and CV MAF (Methods). Each boxplot contains estimates of $h_g^2$ from 100 simulations. Right: Relative bias of each method (as a percentage of $h_g^2$) across 112 distinct MAF- and LDAK-LD-dependent architectures (Methods). Each boxplot contains 112 points; each point is the relative bias estimated from 100 simulations under a single genetic architecture. The white diamonds mark the average of each distribution. Boxplot whiskers extend to the minimum and maximum estimates located within $1.5\times \text{IQR}$ from the first and third quartiles, respectively.

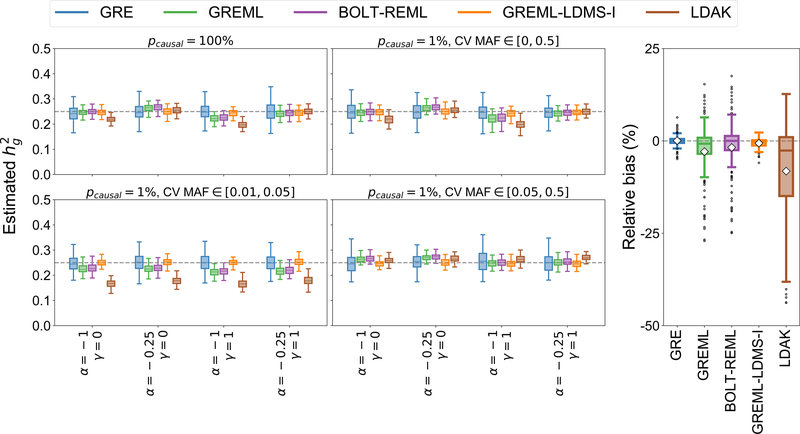
For completeness, we compare to four widely used REML-based methods: GREML, which assumes $\alpha =-1$ and no coupling of effects with LD³; GREML-LDMS-I, a multi-component extension of GREML that partitions SNPs by MAF and LD score¹⁸; BOLT-REML, a computationally efficient variance components estimation method with assumptions similar to those of GREML⁸; and LDAK, which assumes a specific form of the SNP-specific LD weights and recommends setting $\alpha =-0.25$ ^6,9 (Table 1). Because it is computationally intractable to apply the REML-based methods to thousands of genome-wide simulations with 337K individuals, we perform simulations using a reduced number of individuals $\left(N=8430\right)$ and SNPs $\left(M=14821\right)$ (Methods). As expected, the single-component methods (GREML, BOLT-REML, and LDAK) are sensitive to MAF/LD-dependency whereas the GRE estimator is robust across all architectures. For example, when $h_g^2=0.25$ (Figure 3), GREML and BOLT-REML are accurate under the GREML model (GREML: $\text{relative bias}=-1.4\%$, $p=6.0\times {10}^{-3}$, Supplementary Table 18; BOLT-REML: $\text{relative bias}=-0.16\%$, $p=0.75$, Supplementary Table 19) and LDAK is approximately unbiased under the LDAK model ($\text{relative bias}=0.16\%$, $p=0.77$, Supplementary Table 20), but all three are sensitive to CV MAF, $\alpha$ and $\gamma$. Across 12 architectures where $p_{\text{causal}}=1\%$ (Figure 3), the relative biases are within [−15%, 7.9%] (GREML), [−14%, 9.1%] (BOLT-REML), and [−34%, 8.2%] (LDAK) (Supplementary Tables 18–20). In contrast, for the same 12 architectures, ${\widehat{h}}_{\text{GRE}}^2$ yields relative biases in the range [−2.1%, 1.7%], which is comparable to the relative bias of GREML-LDMS-I (range [−2.9%, 1.5%]) using 8 GRMs (4 LD quartiles × 2 MAF bins) that align with CV MAF (Figure 3, Supplementary Tables 21, 22). These trends hold over a range of $h_g^2$ and $p_{\text{causal}}$: across 112 LDAK-LD- and/or MAF-dependent architectures (Supplementary Figures 15–19), the average and range of the relative bias are 0.09% [−4.9%, 6.4%] (GRE), −0.6% [−5.9%, 2.3%] (GREML-LDMS-I), −2.9% [−27%, 15%] (GREML), −1.8% [−25%, 18%] (BOLT-REML), and −8.2% [−44%, 13%] (LDAK) (Supplementary Tables 18–22). Similar trends are observed for LD-score-dependent architectures (Supplementary Figure 20, Supplementary Table 23). In an extreme example where CV MAF is tightly concentrated near 1%, GREML-LDMS-I with the same 8 GRMs as before is downward-biased whereas the GRE estimator remains robust (Supplementary Figure 21, Supplementary Tables 18–22). While the variance of our estimator is larger than the variances of the REML-based methods (Figure 3), our approach is designed for sample sizes several orders of magnitude larger than what we used in these simulations. In summary, our results confirm that it is possible to accurately estimate $h_g^2$ under the GRE model.

Figure 3.

Comparison of ${\widehat{h}}_{\text{GRE}}^2$ with GREML, BOLT-REML, GREML-LDMS-I, and LDAK in small-scale simulations (N = 8430, M = 14821 SNPs). Left: Phenotypes were drawn under one of 16 MAF- and/or LDAK-LD-dependent architectures by varying $p_{\text{causal}}$, $\alpha$, $\gamma$, and CV MAF (Methods). Each boxplot contains estimates of $h_g^2$ from 100 simulations. Right: Relative bias of each method (as a percentage of the true $h_g^2$) across 112 distinct MAF- and LDAK-LD-dependent architectures (Methods). Each boxplot represents the distribution of 112 points; each point is the relative bias estimated from 100 simulations under a single genetic architecture. The white diamonds mark the average of each distribution. Boxplot whiskers extend to the minimum and maximum estimates located within $1.5\times \text{IQR}$ from the first and third quartiles, respectively.

SNP-heritability of 22 complex traits in the UK Biobank

Finally, we compute ${\widehat{h}}_{\text{GRE}}^2$ for 22 complex traits in the UK Biobank (290K unrelated British individuals, 460K SNPs; Methods)¹⁰. For comparison, we also provide estimates from LDSC, S-LDSC (controlling for the baseline-LD model^13,30), and SumHer. Of the 22 traits analyzed (6 quantitative, 16 binary), we focus on 18 traits for which ${\widehat{h}}_{\text{GRE}}^2>0.05$ (Table 2). For the 6 quantitative traits, ${\widehat{h}}_{\text{GRE}}^2$ ranges from 0.12 (smoking status) to 0.60 (height). Across the 12 binary traits, ${\widehat{h}}_{\text{GRE}}^2$ ranges from 0.064 (autoimmune disorders) to 0.16 (hypertension) (Table 2). These estimates are robust to filtering of individuals based on relatedness (Supplementary Table 24). We also computed ${\widehat{h}}_{\text{GRE}}^2$ from two additional sets of SNPs (MAF > 0.1% and MAF > 0.01%) and found that the estimates increase slightly for lower MAF thresholds (Supplementary Table 25), which is expected due to the increased number of SNPs. To enable a direct comparison between ${\widehat{h}}_{\text{GRE}}^2$ and the quantities estimated by LDSC, S-LDSC, and SumHer, we run the summary-statistics-based methods with LD scores and regression weights computed from in-sample LD and estimate $h_g^2$ defined as a function of the same set of SNPs (Methods). Across the 18 traits, S-LDSC (baseline-LD/in-sample) and SumHer (in-sample) differ from ${\widehat{h}}_{\text{GRE}}^2$ by a median of −9% and 11%, respectively (expressed as a percentage of ${\widehat{h}}_{\text{GRE}}^2$) (Figure 4, Table 2). As expected¹¹, LDSC (in-sample) yields inflated estimates.

Table 2.

Estimates of $h_g^2$ from the GRE approach, LDSC (in-sample), S-LDSC (baseline-LD/in-sample), and SumHer (in-sample) for 22 complex traits and diseases in the UK Biobank (N = 290K unrelated British individuals, M = 460K typed SNPs).

Trait	GRE	S.E.	LDSC	S.E.	S-LDSC	S.E.	SumHer	S.E.
Smoking Status	0.122	3.90E-03	0.178	7.70E-03	0.110	8.50E-03	0.132	4.30E-03
Height	0.602	4.70E-03	0.730	2.70E-02	0.555	3.10E-02	0.634	2.70E-02
BMI	0.285	4.20E-03	0.436	1.20E-02	0.289	1.70E-02	0.315	9.00E-03
WHR	0.173	4.00E-03	0.256	1.20E-02	0.184	1.60E-02	0.198	9.40E-03
Systolic Blood Pressure	0.159	4.20E-03	0.243	9.00E-03	0.134	9.70E-03	0.177	5.70E-03
Diastolic Blood Pressure	0.154	4.20E-03	0.233	8.60E-03	0.130	9.70E-03	0.170	6.40E-03
Eczema	0.116	4.20E-03	0.165	1.10E-02	0.107	1.20E-02	0.130	8.80E-03
Asthma	0.116	4.90E-03	0.163	1.20E-02	0.116	1.70E-02	0.131	1.20E-02
Hypertension	0.162	4.00E-03	0.244	9.40E-03	0.142	1.10E-02	0.180	6.10E-03
High Cholesterol	0.082	5.10E-03	0.127	1.30E-02	0.138	5.80E-02	0.088	8.30E-03
Diabetes (Any)	0.070	3.70E-03	0.093	5.90E-03	0.062	8.70E-03	0.074	5.00E-03
Type 2 Diabetes	0.071	3.80E-03	0.090	6.10E-03	0.057	8.80E-03	0.071	4.00E-03
Hypothyroidism	0.088	5.20E-03	0.142	1.30E-02	0.078	1.20E-02	0.110	1.70E-02
Thyroid Disorders	0.084	5.20E-03	0.141	1.30E-02	0.080	1.20E-02	0.110	2.00E-02
Endocrinopathies	0.069	5.10E-03	0.084	7.00E-03	0.058	9.90E-03	0.068	5.00E-03
Cardiovascular Diseases	0.143	5.30E-03	0.228	1.10E-02	0.140	1.40E-02	0.164	6.00E-03
Respiratory and ENT Diseases	0.086	5.20E-03	0.120	1.20E-02	0.079	1.40E-02	0.090	9.50E-03
Psoriasis	0.019	5.00E-03	0.071	3.10E-02	0.035	1.20E-02	0.059	4.20E-02
Dermatologic Disorders	0.023	5.00E-03	0.049	1.40E-02	0.034	9.90E-03	0.031	1.10E-02
Rheumatoid Arthritis	0.008	5.00E-03	0.041	2.10E-02	0.010	7.90E-03	0.021	1.20E-02
Autoimmune Disorders (Broad)	0.063	5.10E-03	0.105	1.20E-02	0.050	9.50E-03	0.079	1.70E-02
Autoimmune Disorders (Certain)	0.015	5.00E-03	0.052	2.60E-02	0.005	7.60E-03	0.047	3.40E-02

Figure 4.

Percent difference of $h_g^2$ estimates from LDSC (in-sample), S-LDSC (baseline-LD/in-sample), and SumHer (in-sample) with respect to ${\widehat{h}}_{\text{GRE}}^2$ for 18 complex traits and diseases in the UK Biobank for which ${\widehat{h}}_{\text{GRE}}^2>0.05$ (N = 290K unrelated British individuals, M = 460K typed SNPs; Methods). Each bar represents the difference between the estimated $h_g^2$ from one of the methods (LDSC, S-LDSC, or SumHer) and ${\widehat{h}}_{\text{GRE}}^2$ as a percentage of ${\widehat{h}}_{\text{GRE}}^2$. Black bars mark $\pm 2$ standard errors.

To compare ${\widehat{h}}_{\text{GRE}}^2$ to estimates reported in the literature, we also run the summary-statistics methods with their recommended parameter settings^11,12,14,30 and with LD scores and regression weights computed from the 1000 Genomes Phase 3 reference panel (489 Europeans)³¹ – we note that when running these methods as recommended, their estimands are not equivalent to our definition of $h_g^2$ (see Methods and refs.^11,12,14,19 for details). Across the 18 traits for which ${\widehat{h}}_{\text{GRE}}^2>0.05$, the median differences with respect to ${\widehat{h}}_{\text{GRE}}^2$ are −11% for LDSC (1KG), −14% for S-LDSC (baseline-LD/1KG), and 38% for SumHer (1KG) (Supplementary Figure 22, Supplementary Table 26). For 9 of these traits, a previous study reported single-component BOLT-REML estimates (computed from a similar UK Biobank cohort²⁷) that differ from our estimates by a median of 8% (Supplementary Table 26).

Runtime and memory requirement

We report the runtime and memory requirements for computing ${\widehat{h}}_{\text{GRE}}^2$ with the 22-block approximation from 337K individuals and 593K SNPs. First, computing chromosome-wide LD has complexity $O\left(N{p}_k^2\right)$ for chromosome $k$ with $p_k$ SNPs. In practice, this step does not impose a computational bottleneck because the computations can be parallelized over SNPs. Second, the pseudoinverse of each LD matrix is computed via truncated SVD, which has complexity $O\left(p_k^3\right)$ for chromosome $k$. For 50K typed SNPs this takes about 3 hours and 60GB of memory. Lastly, given the pseudoinverse LD matrices and OLS association statistics, computing ${\widehat{h}}_{\text{GRE}}^2$ has complexity $O\left(p_1^2+\cdots +p_{22}^2\right)$ For any of the traits analyzed in this work, this takes less than 1 hour and requires 24GB of memory; most of this time is spent loading the data into memory. For comparison, running LDSC, S-LDSC, or SumHer consists of precomputing LD scores and SNP-specific weights and performing linear regression to estimate the variance parameters. Precomputing LD scores and SNP-specific weights can be parallelized over blocks of SNPs. The second step (least squares regression) is $O\left(C^{2}M\right)$ for M SNPs in the regression and C variance parameters.

Discussion

In this work, we show that SNP-heritability can be accurately estimated under minimal assumptions on genetic architecture. Our proposed estimator allows the SNP-specific variances to capture arbitrary relationships between effect size and MAF/LD, and we demonstrate through simulations that its accuracy is invariant to genetic architecture. We show that all existing methods impose additional assumptions on the GRE model, and we confirm through simulations that these methods can be sensitive to model misspecification. One practical advantage of our approach over summary-statistics methods is that the estimand of our approach is always the same for a given genotype matrix, whereas the definitions and interpretations of the estimands of LDSC, S-LDSC, and SumHer depend on which SNPs are used in each step of inference (e.g., the SNPs used to compute LD scores need not be the same SNPs defining the estimand)^11,12,19. Overall, our results show that while existing methods can yield biases, for the purpose of estimating total SNP-heritability, most methods are relatively robust.

We conclude with several caveats and future directions. First, the utility of ${\widehat{h}}_{\text{GRE}}^2$ critically depends on the ratio between the number of SNPs (M) and the number of individuals (N) – as $M/N$ increases, the eigenstructure of the in-sample LD matrix becomes increasingly distorted (larger eigenvalues are overestimated; smaller eigenvalues are underestimated)³². We mitigate this by assuming that chromosomes are approximately independent; as long as N exceeds the number of array SNPs per chromosome, ${\widehat{h}}_{\text{GRE}}^2$ provides meaningful estimates of SNP-heritability. While the utility of our approach is limited by the availability of individual-level biobank-scale data, this concern will abate as more biobanks are established^33–35. A major limitation remains with respect to imputed/sequencing data as M will continue to be orders of magnitude larger than N for the foreseeable future. We defer an investigation of regularized estimation of LD in high-dimensional settings $\left(M>N\right)$ to future work.

Second, the theoretical guarantees of ${\widehat{h}}_{\text{GRE}}^2$ rely on the assumption that OLS association statistics and LD are estimated from the same genotypes. While summary statistics have been made publicly available for hundreds of large-scale GWAS, in-sample LD is usually unavailable for these studies since most are meta-analyses³⁶. In addition, summary statistics are often computed using linear mixed models to control for confounding, and previous works have noted that the LD computation must be adjusted to accommodate mixed model association statistics^36,37. Thus, the sensitivity of ${\widehat{h}}_{\text{GRE}}^2$ to reference panel LD (with or without regularized LD estimation) and/or mixed model association statistics remains unclear^29,38. Furthermore, we simulate phenotypes from typed SNPs because imputed genotypes have highly irregular LD patterns^9,18. Although it would be more realistic to simulate from sequencing data¹⁸, our simulation design required individual-level genotype measurements in biobank-scale sample sizes.

Third, ${\widehat{h}}_{\text{GRE}}^2$ does not correct for population structure/stratification. In real data, we mitigate this by considering only unrelated individuals (> 3rd degree relatives) and including age, sex, and the top 20 PCs as covariates when computing association statistics. While recent work has found evidence of assortative mating for some traits in the UK Biobank (e.g., height)³⁹, our estimates are robust to different relatedness thresholds, suggesting that adjusting for the top 20 PCs sufficiently controls for population stratification. Still, it remains unclear how to quantify the bias of our genome-wide estimator due to structure or assortative mating in real data. Future work is needed to extend the GRE approach to control for ascertainment bias^15,16,40,41.

Finally, while previous works applied similar estimators (defined under fixed effects models) to estimate local SNP-heritability within small regions^28,29, additional work is needed to extend our approach to perform partitioning of SNP-heritability by functional annotations. Existing methods for partitioning SNP-heritability make various assumptions on genetic architecture^8,12–14,30, motivating the development of new methods in this area.

Methods

The generalized random effects model

We model the phenotype for an individual n randomly sampled from the population as $y_n={\mathbf{x}}_{\mathbf{n}}^{\text{T}}\mathbf{\beta }+{ϵ}_n$, where ${\mathbf{x}}_{\mathbf{n}}={\left(x_{n1}\dots x_{nM}\right)}^T$ is a vector of standardized genotypes measured at M SNPs for individual n, $\mathbf{\beta }={\left({\beta }_1,\hspace{0.17em}\dots ,\hspace{0.17em}{\beta }_M\right)}^T$ is an M-vector of the corresponding standardized SNP effects, and ${ϵ}_n\sim N\left(0,\hspace{0.17em}{\sigma }_e^2\right)$ is environmental noise. We assume $\text{Var}\left[y_n\right]=1$ and that the genotype at each SNP $i$ is centered and scaled in the population such that $\text{E}\left[x_{ni}\right]=0$ and $\text{Var}\left[x_{ni}\right]=1$; i.e. $x_{ni}=\left(g_{ni}-2f_i\right)/\sqrt{2f_i\left(1-f_i\right)}$, where $g_{ni}\in \left\{0,1,2\right\}$ is the number of copies of the effect allele at SNP $i$ for individual $n$, and $f_i$ is the population frequency of the effect allele at SNP $i$. We define the population LD between two SNPs $i$ and $j$ to be $v_{ij}\equiv \text{E}\left[x_{ni}{x}_{nj}\right]$ for all $i\ne j$. The population LD matrix among the $M$ SNPs is therefore $\mathbf{V}\equiv \text{Cov}\left[{\mathbf{x}}_n^{\text{T}}\right]$. For simplicity, we use “SNP effects” in lieu of “standardized SNP effects” to refer to $\mathbf{\beta }$. We assume that ${\mathbf{x}}_{\mathbf{n}}$ and $\mathbf{\beta }$ are independent given allele frequencies $\left(f_1,\hspace{0.17em}\dots ,\hspace{0.17em}{f}_M\right)$ and $\mathbf{V}$.

Under the generalized random effects (GRE) model, the first two moments of ${\beta }_i$ are $\text{E}\left[{\beta }_i\right]=0$ and $\text{Var}\left[{\beta }_i\right]={\sigma }_i^2$, where ${\sigma }_i^2$ can be any arbitrary nonnegative finite number. We assume the covariance between the effects of different SNPs is 0 (i.e. $\text{Cov}\left[{\beta }_i,\hspace{0.17em}{\beta }_j\right]=\text{E}\left[{\beta }_i{\beta }_j\right]=0$ for all $\text{i}\ne \text{j}$). Because the SNP-specific variances can capture any degree of polygenicity and any relationship between genomic features (e.g., MAF and LD) and effect size, the GRE model encompasses most realistic genetic architectures (Table 1).

We define total SNP-heritability $\left(h_g^2\right)$ to be the proportion of phenotypic variance attributable to the additive effects of a set of M SNPs whose genotypes are directly measured:

$$\begin{gathered} h_g^2\equiv \frac{\text{Var}\left[{\mathbf{x}}_n^T\mathbf{\beta }\right]}{\text{Var}\left[y_n\right]} \\ \hspace{1em}=\text{E}\left[\text{Var}\left[{\mathbf{x}}_n^T\mathbf{\beta }|\mathbf{\beta }]\right]+\text{Var}\right[\text{E}\left[{\mathbf{x}}_n^T\mathbf{\beta }|\mathbf{\beta }\right]] \\ \hspace{1em}=\text{E}\left[{\mathbf{\beta }}^T\text{Var}\left[{\mathbf{x}}_n^T\right]\mathbf{\beta }\right]+\text{Var}\left[\text{E}\left[{\mathbf{x}}_n^T\right]\mathbf{\beta }\right] \\ \hspace{1em}=\text{E}\left[{\mathbf{\beta }}^T\mathbf{V}\mathbf{\beta }\right]+0 \\ \hspace{1em}=\text{E}\left[\text{tr}\left(\mathbf{V}\mathbf{\beta }{\mathbf{\beta }}^T\right)\right] \\ \hspace{1em}=\text{tr}\left(\mathbf{V}\text{E}\left[\mathbf{\beta }{\mathbf{\beta }}^T\right]\right) \\ {h}_g^2=\sum _{i=1}^M{\sigma }_i^2 \end{gathered}$$ #(2)

Thus, $h_g^2$ is defined with respect to a given population and a given set of SNPs. By definition, $0\le h_g^2\le 1$ Similarly, we define regional SNP-heritability $\left(h_k^2\right)$ to be the proportion of phenotypic variance due to the additive effects of the genotyped SNPs in region $k$ We assume that the set of SNPs that defines $h_k^2$ is a subset of the $M$ SNPs that define $h_g^2$ (thus, $0\le h_k^2\le h_g^2$). If region $k$ is the whole genome, $h_k^2=h_g^2$.

Estimating SNP-heritability under the GRE model

We are interested in estimating $h_g^2$ under the GRE model (Equation 2). In a GWAS with $N$ individuals genotyped at $M$ SNPs, let $\mathbf{X}={\left({\mathbf{x}}_1^T,\dots ,{\mathbf{x}}_N^T\right)}^T$ be the $N\times M$ matrix of standardized genotypes (each column of $\text{X}$ has been standardized to have mean 0 and variance 1), $\mathbf{y}={\left(y_1,\dots ,y_N\right)}^T$ be the $N$-vector of standardized phenotypes, and $\widehat{\mathbf{V}}=\left(1/N\right){\mathbf{X}}^T\mathbf{X}$ be the $M\times M$ in-sample LD matrix (an estimate of population LD, $\text{V}$) with rank $q$, where $1\le q\le M$. Let $\mathbf{X}=\left({\mathbf{X}}_1,\dots ,\hspace{0.17em}{\mathbf{X}}_K\right)$ be the genotype matrices for $K$ independent regions spanning all $M$ SNPs (e.g., chromosomes). For region $k$ containing $p_k$ SNPs, ${\mathbf{X}}_k$ is the $N\times p_k$ standardized genotype matrix and ${\widehat{\mathbf{V}}}_k$ is the corresponding $p_k\times p_k$ in-sample LD matrix with rank $q_k$ $\left(1\le q_k\le p_k\right)$. We propose the following estimator for genome-wide SNP-heritability:

$${\widehat{h}}_{\text{GRE}}^2=\sum _{k=1}^K\frac{N{\widehat{\mathbf{\beta }}}_k^T{\widehat{\mathbf{V}}}_k^{†}{\widehat{\mathbf{\beta }}}_k-q_k}{N-q_k}$$

where ${\widehat{\mathbf{\beta }}}_k=\left(1/N\right){\mathbf{X}}_k^T\mathbf{y}$ is the $p_k$-vector of marginal SNP effects estimated by ordinary least squares (OLS) for region $k$ and ${\widehat{\mathbf{V}}}_k^{†}$ is the pseudoinverse of ${\widehat{\mathbf{V}}}_k$. Detailed derivations for ${\widehat{h}}_{\text{GRE}}^2$ can be found in the Supplementary Note.

Analytical variance of ${\widehat{h}}_{\text{GRE}}^2$

Following quadratic form theory^29,44, the variance of ${\widehat{h}}_{\text{GRE}}^2$ in the single-block case is

$$\text{Var}\left[{\widehat{h}}_{\text{GRE}}^2\right]={\left(\frac{N}{N-q}\right)}^2\left(2q\left(\frac{1-h_g^2}{N}\right)+4h_g^2\right)\left(\frac{1-h_g^2}{N}\right)$$ #(3)

When using the K-block approximation, which assumes that the blocks are independent, we approximate Equation 3 as the sum of the variances of the local SNP-heritabilities:

$$\text{Var}\left[{\widehat{h}}_{\text{GRE}}^2\right]=\sum _{\text{k}=1}^{\text{K}}{\left(\frac{N}{N-q_k}\right)}^2\left(2q_k\left(\frac{1-h_k^2}{N}\right)+4h_k^2\right)\left(\frac{1-h_k^2}{N}\right)$$ #(4)

Equation 3 is estimated by plugging in ${\widehat{h}}_{\text{GRE}}^2$ and Equation 4 is estimated by plugging in $\left({\widehat{h}}_1^2,\dots ,{\widehat{h}}_K^2\right)$, the estimates of the regional SNP-heritabilities.

Simulation Framework

We simulated quantitative phenotypes from real genotype array data (UK Biobank¹⁰) under a range of genetic architectures. We obtained a set of $N=337205$ unrelated British individuals by extracting individuals with self-reported British ancestry who are > 3rd degree relatives (pairs of individuals with kinship coefficient $<1/2^{\left(9/2\right)})$¹⁰ and excluding individuals with putative sex chromosome aneuploidy. In all simulations, we standardize the genotypes before drawing phenotypes. That is, for each SNP $i$ and individual $n$, we compute $x_{ni}=\left(g_{ni}-2f_i\right)/\sqrt{2f_i\left(1-f_i\right)}$ where $g_{ni}\in \left\{0,1,2\right\}$ is the number of minor alleles and $f_i$ is the in-sample minor allele frequency (MAF).

Simulations of quantitative traits with no population stratification

Given $\mathbf{\text{X}}$ and a fixed value of $h_g^2$, phenotypes are drawn according to the following model. The proportion of causal variants, $p_{\text{causal}}$, is set to 1, 0.01, or 0.001. Let $c_i\in \left\{0,1\right\}$ be the causal status of SNP $i$. If $p_{\text{causal}}=1$, $c_i=1$ for $i=1,\dots ,\hspace{0.17em}M$. If $0\le p_{\text{causal}}<1$, we draw $p_{\text{causal}}\times M$ SNPs from the set of SNPs with MAF in one of three ranges: (0, 0.5], (0.01, 0.05], or (0.05, 0.5]. We use “CV MAF” to refer to the MAF range from which the causal variants are drawn. Standardized effects and phenotypes are then drawn according to the model

$${\sigma }_i^2\propto c_i\cdot w_i^{\gamma }{\left[2f_i\left(1-f_i\right)\right]}^{1+\alpha }$$ #(5)

$${\left({\beta }_1,\dots ,\hspace{0.17em}{\beta }_k\right)}^T\sim N\left(0,\hspace{0.17em}\text{diag}\left({\sigma }_1^2,\dots ,\hspace{0.17em}{\sigma }_M^2\right)\right)$$ #(6)

$${\left(y_1,\dots ,\hspace{0.17em}{y}_N\right)}^T|\mathbf{\beta }\sim N\left(\mathbf{X}\mathbf{\beta },\hspace{0.17em}\left(1-h_g^2\right){\mathbf{I}}_N\right)$$ #(7)

where $\alpha$ controls the coupling of MAF and effect size, $w_i$ is a SNP-specific LD weight, and $\gamma \in \left\{0,1\right\}$ specifies whether effects are coupled with the LD weights. We simulate two types of LD-dependent architectures by defining $w_1,\dots ,w_M$ to be either (1) the default “LDAK weights” computed by the LDAK software⁶, or (2) the inverse unpartitioned “LD score” of each SNP computed within a 2-Mb window ($w_i^{-1}={\sum }_j{v}_{ij}^2$ where $j$ indexes the set of SNPs within a 2-Mb window centered on SNP $i$)¹¹. When $\gamma =1$ both the LDAK weights and inverse LD score weights cause SNPs in regions of higher LD to have smaller effects than do SNPs in regions of lower LD. We set $\alpha$ to one of two values: $\alpha =-1$ (a relatively strong inverse relationship between MAF and effect size) or $\alpha =-0.25$ (a weaker inverse relationship between MAF and effect size). Each per-SNP variance is multiplied by a scaling factor so that ${\sum }_{i=1}^M{\sigma }_i^2=h_g^2$. Note that ${\sigma }_i^2=0$ if $c_i=0$.

Finally, given phenotypes $y={\left(y_1,\dots ,y_N\right)}^T$ and genotypes $\mathbf{X}={\left({\mathbf{x}}_1^T,\dots ,\hspace{0.17em}{\mathbf{x}}_N^T\right)}^T$, we compute marginal association statistics through ordinary least squares (OLS): $\widehat{\mathbf{\beta }}=\left(1/N\right){\mathbf{X}}^T\mathbf{y}$.

Simulations of case-control phenotypes with no population stratification

To simulate case-control studies, we first draw each individual’s continuous liability ($l_n$ for individual n) according to Equation 7. For a given population prevalence $\left(0\le d_{pop}\le 1\right)$ we compute the corresponding liability threshold $L={\mathrm{\Phi }}^{-1}\left(1-d_{pop}\right)$, where $\Phi$ is the CDF of the standard normal distribution. Each $l_n$ is then converted into a case-control status: $y_n=1$ if $l_n\ge L$ or $y_n=0$ if $l_n<L$. For unascertained case-control studies, we assume that the proportion of cases in the study is equal to the population prevalence $\left(d_{GWAS}=d_{pop}\right)$. For ascertained case-control studies $\left(d_{GWAS}>d_{pop}\right)$, we set $d_{GWAS}=0.5$ and select a random set of controls to satisfy $N_{case}=N_{control}$.

We compute association statistics by regressing the binary case-control statuses on genotypes. The GRE estimator produces an estimate of SNP-heritability on the observed scale $\left({\widehat{h}}_{obs}^2\right)$. Assuming we know the population prevalence, we convert ${\widehat{h}}_{obs}^2$ to the liability scale with the transformation ${\widehat{h}}_{liab}^2={\widehat{h}}_{obs}^2{d}_{pop}^2{\left(1-d_{pop}\right)}^2/\left({\left[f\left(L\right)\right]}^2{d}_{GWAS}\left(1-d_{GWAS}\right)\right)$, where $f$ is the standard normal probability density function⁴⁵.

Simulations with population stratification

To simulate GWAS with population stratification, we draw phenotypes from a model where a covariate that is correlated to genotypes has a nonzero effect on phenotype. To this end, we simulate an effect of the first genetic principal component $\left(\mathbf{P}{\mathbf{C}}_1\right)$. Letting ${\sigma }_s^2$ be the proportion of total phenotypic variance explained by $\mathbf{P}{\mathbf{C}}_1$, phenotypes are drawn from the model

$${\left(y_1,\dots ,\hspace{0.17em}{y}_N\right)}^T|\mathbf{\beta }\sim N\left(\mathbf{X}\mathbf{\beta }+\mathbf{P}{\mathbf{C}}_1{\mathbf{\beta }}_s,\hspace{0.17em}\left(1-h_g^2-{\sigma }_s^2\right){\mathbf{I}}_N\right)$$

where $\text{Var}\left[\mathbf{P}{\mathbf{C}}_1{\mathbf{\beta }}_s\right]/\text{Var}\left[\mathbf{y}\right]={\mathbf{\beta }}_s^2\text{Var}\left[\mathbf{P}{\mathbf{C}}_1\right]={\sigma }_s^2$. We compute association statistics from one of two models: $\mathbf{y}={\mathbf{X}}^T\mathbf{\beta }+\mathbf{ϵ}$, which ignores population stratification and other sources of confounding, or $\mathbf{y}={\mathbf{X}}^T\mathbf{\beta }+\mathbf{P}{\mathbf{C}}_1{\mathbf{\beta }}_s+\mathbf{ϵ}$, which controls for the effect of $\mathbf{P}{\mathbf{C}}_1$.

Comparison of methods in simulations

Unless otherwise specified, in all genome-wide simulations, we use real genotypes of N = 337205 unrelated British individuals measured at M = 593300 array SNPs to draw causal effects for all M SNPs and phenotypes for all N individuals. OLS summary statistics are computed for all M SNPs using the simulated phenotypes and real genotypes of all N individuals. We compare to three methods that operate on summary statistics and are computationally tractable for these simulations: LD score regression (LDSC)¹¹, stratified LD score regression (S-LDSC)^12,13, and SumHer¹⁴.

For LDSC and S-LDSC, we compute the unpartitioned LD score of each SNP as a function of its LD to all other SNPs in a 2-Mb window centered on the SNP. For each annotation included in S-LDSC, the partitioned LD score of each SNP is a function of its LD to all SNPs within a 2-Mb window that are in the annotation. For both LDSC and S-LDSC, LD scores are computed with the LDSC software (https://github.com/bulik/ldsc/) from a random sample of 40K individuals to reduce the amount of memory required by the LDSC software. We run the regression with an unconstrained intercept, using all M SNPs as observations in the response variable. Each SNP is weighted to account for heteroscedasticity and correlations between association statistics¹¹. For both methods, $h_g^2$ is estimated as a function of all M SNP-specific variances by using the flags --not-M-5–50 and --chisq-max 99999 (the latter option prevents the LDSC software from dropping high-effect SNPs).

We run S-LDSC in two ways to account for MAF/LD-dependent architectures. S-LDSC (MAF) refers to S-LDSC with 10 binary MAF bin annotations (each bin contains exactly 10% of the typed SNPs), which is intended to mirror the 10 MAF annotations in the “baseline-LD model”¹³ (see Supplementary Table 14 for precise MAF bin ranges for the UK Biobank Axiom Array). S-LDSC (MAF+LLD) refers to S-LDSC with the same 10 MAF bins and an additional continuous “level of LD” (LLD) annotation computed by quantile-normalizing the unpartitioned LD scores within each MAF bin to a standard normal distribution¹³. While our definition of LLD is intended to mirror the LLD annotation in the baseline-LD model, we do not set the LLD of variants with MAF < 0.05 to 0 because our estimand of interest includes the effects of SNPs with MAF < 0.05¹³.

To run SumHer, we use the LDAK software (https://dougspeed.com/ldak/) to compute the default “LDAK weights” using in-sample LD^6,9,14. We then compute “LD tagging” (i.e. LD scores) using 1-Mb windows centered on each SNP and setting $\alpha =-0.25$ as recommended¹⁴. The LDAK software is memory-efficient, allowing us to use all 337K individuals to compute LDAK weights and LD tagging. Unless otherwise specified, all default parameter settings are used to run SumHer in simulations.

We also perform simulations with N = 8430 unrelated individuals at M = 14821 array SNPs. These individuals and SNPs are a subset of the data used in the genome-wide simulations, chosen by selecting approximately 2.5% of individuals and the first 2.5% of SNPs from the beginning of each chromosome in order to preserve the LD structure among the SNPs. We run single-component GREML^3,46 (GCTA software: https://cnsgenomics.com/software/gcta/) and single-component BOLT-REML⁸ (https://data.broadinstitute.org/alkesgroup/BOLT-LMM/) with default parameters. We run GREML-LDMS-I^18,46 using 8 GRMs created from 2 MAF bins ($\text{MAF}\le 0.05$ and MAF > 0.05) and 4 LD score quartiles; LD scores were computed using the GCTA software with the default window size of 200-kb. We run LDAK using the default LDAK weights, setting $\alpha =-0.25$ as recommended^6,9.

A third set of simulations was performed using 7,685 individuals of South Asian ancestry in the UK Biobank. This group was composed of individuals of Indian (n = 5,716), Pakistani (n = 1,748), and Bangladeshi (n = 221) ancestry. Due to the small sample size, we used a reduced set of 803 SNPs from chromosome 21 and 839 SNPs from chromosome 22 (1,642 SNPs in total) which were chosen so that $N/p_k$ for each chromosome k was similar to $N/p_k$ in the “white British” cohort.

For a given genetic architecture, we generate 100 simulation replicates and obtain 100 estimates of $h_g^2$ from each method. We estimate the bias of an estimator ${\widehat{h}}_g^2$ under a given architecture as bias $[{\widehat{h}}_g^2]=\text{E}[{\widehat{h}}_g^2]-h_g^2\approx \left(1/100\right){\sum }_{i=1}^{100}{\widehat{h}}_g^2\left(i\right)-h_g^2$ where ${\widehat{h}}_g^2\left(i\right)$ is the estimate from the i-th simulation. To test whether the bias is statistically significant (null hypothesis: bias $[{\widehat{h}}_g^2]=0$), we assess the z-score of the bias $(z_{\text{bias}}=\text{bias}[{\widehat{h}}_g^2]/\text{SEM}[{\widehat{h}}_g^2]$, where $\text{SEM}[{\widehat{h}}_g^2]$ is the standard error of the mean of the 100 estimates) which follows a $N(0,1)$ distribution under the null hypothesis. The p-value of the bias is computed with a two-tailed test. To enable a comparison of estimators across different values of $h_g^2$, we assess the relative bias of an estimator under a single architecture $(\text{bias}[{\widehat{h}}_g^2]/h_g^2)$ as a percentage of $h_g^2$. In Figure 1a and 1c, we compute the error of a single estimate as $({\widehat{h}}_g^2\left(i\right)-h_g^2)/h_g^2$; errors are also reported as percentages of $h_g^2$.

Analysis of UK Biobank phenotypes

We estimate SNP-heritability for 22 complex traits (6 quantitative, 16 binary) in the UK Biobank¹⁰. We use PLINK⁴⁷ (https://www.cog-genomics.org/plink2) to exclude SNPs with MAF < 0.01 and genotype missingness > 0.01 as well as SNPs that fail the Hardy-Weinberg test at significance threshold ${10}^{-7}$. We keep only the individuals with self-reported British white ancestry and no kinship (i.e. > 3rd degree relatives, defined as pairs of individuals with kinship coefficient $<1/2^{\left(9/2\right)}$)¹⁰. After removing individuals who are outliers for genotype heterozygosity and/or missingness, we obtain a set of N = 290,641 individuals to use in the real data analyses. For all traits, marginal association statistics are computed through OLS in PLINK, using age, sex, and the top 20 genetic principal components (PCs) as covariates in the regression; these 20 PCs were precomputed by UK Biobank from a superset of 488,295 individuals. Additional covariates were used for waist-to-hip ratio (adjusted for BMI) and diastolic/systolic blood pressure (adjusted for cholesterol-lowering medication, blood pressure medication, insulin, hormone replacement therapy, and oral contraceptives). We compute ${\widehat{h}}_{\text{GRE}}^2$ for each trait using in-sample LD estimated from all N individuals.

When using LDSC, S-LDSC, or SumHer to estimate SNP-heritability, it is necessary to define and distinguish between the following sets of SNPs: the set of SNPs containing all possible causal SNPs of interest (used to compute LD scores and LDAK weights), the set of SNPs used as observations in the regression, and the set of SNPs that defines the SNP-heritability estimand of interest. We run two versions of LDSC, S-LDSC (controlling for the most recent baseline-LD model^12,13,30), and SumHer¹⁴. First, to enable a direct comparison between ${\widehat{h}}_{\text{GRE}}^2$ and the estimands of LDSC, S-LDSC, and SumHer, we run an “in-sample LD” version of each method where the M typed SNPs are used to compute LD scores and LDAK weights, perform the regression, and define the SNP-heritability estimand of interest. We refer to these as LDSC (in-sample), S-LDSC (baseline-LD/in-sample), and SumHer (in-sample). To run LDSC (in-sample) and S-LDSC (baseline-LD/in-sample), we use the LDSC software to compute LD scores and regression weights within 2-Mb windows centered on each SNP, using a random sample of 40K individuals to reduce the memory requirement. To run SumHer (in-sample), we use the LDAK software to compute LD tagging from the genotypes of all N individuals, using 1-Mb windows centered on each SNP and setting $\alpha =-0.25$ as recommended^9,14. Unless otherwise specified, all other parameters were set to the default settings.

To enable comparisons between ${\widehat{h}}_{\text{GRE}}^2$ and estimates reported in the literature, we also run each method with its recommended parameter settings and LD estimated from reference panel sequencing data. We refer to these methods as LDSC (1KG), S-LDSC (baseline-LD/1KG), and SumHer (1KG) to indicate that LD is estimated from 489 Europeans in the 1000 Genomes Phase 3 reference panel³¹. We run LDSC (1KG) and S-LDSC (baseline-LD/1KG) with LD scores and regression weights (1-cM windows) from 9,997,231 SNPs with minor allele count greater than 5 in the reference panel, and we define the SNP-heritability estimand to be a function of the array SNPs with MAF > 0.05^11,12. We run SumHer (1KG) using 8,569,062 SNPs with MAF > 0.01 in the reference panel to compute LDAK weights and LD tagging (1-cM windows) and to define the SNP-heritability estimand; we control for a multiplicative inflation of test statistics as recommended¹⁴. See refs.^11,12,14,19 for details about the definitions and interpretations of the estimands of LDSC, S-LDSC, and SumHer.

Life Sciences Reporting Summary

Additional information on experimental design can be found in the Life Sciences Reporting Summary.