Abstract
Fillet yield (FY) and harvest weight (HW) are economically important traits in Nile tilapia production. Genetic improvement of these traits, especially for FY, are lacking, due to the absence of efficient methods to measure the traits without sacrificing fish and the use of information from relatives to selection. However, genomic information could be used by genomic selection to improve traits that are difficult to measure directly in selection candidates, as in the case of FY. The objectives of this study were: (i) to perform genome-wide association studies (GWAS) to dissect the genetic architecture of FY and HW, (ii) to evaluate the accuracy of genotype imputation and (iii) to assess the accuracy of genomic selection using true and imputed low-density (LD) single nucleotide polymorphism (SNP) panels to determine a cost-effective strategy for practical implementation of genomic information in tilapia breeding programs. The data set consisted of 5,866 phenotyped animals and 1,238 genotyped animals (108 parents and 1,130 offspring) using a 50K SNP panel. The GWAS were performed using all genotyped and phenotyped animals. The genotyped imputation was performed from LD panels (LD0.5K, LD1K and LD3K) to high-density panel (HD), using information from parents and 20% of offspring in the reference set and the remaining 80% in the validation set. In addition, we tested the accuracy of genomic selection using true and imputed genotypes comparing the accuracy obtained from pedigree-based best linear unbiased prediction (PBLUP) and genomic predictions. The results from GWAS supports evidence of the polygenic nature of FY and HW. The accuracy of imputation ranged from 0.90 to 0.98 for LD0.5K and LD3K, respectively. The accuracy of genomic prediction outperformed the estimated breeding value from PBLUP. The use of imputation for genomic selection resulted in an increased relative accuracy independent of the trait and LD panel analyzed. The present results suggest that genotype imputation could be a cost-effective strategy for genomic selection in Nile tilapia breeding programs.
Keywords: complex traits, cost-efficient, genomic prediction, GWAS, genotype imputation, low-density panel, Oreochromis niloticus, GenPred, Shared Data Resources
Investment in selective breeding programs generates economic return because genetic selection is aimed at improving productivity of important economic traits that result in permanent, cumulative and sustainable changes in a farm’s population over generations of selection (Gjedrem 2012). In a simulation study, Ponzoni et al. (2007) estimated that the benefit/cost ratio reached a maximum of 60/1 with the implementation of family based breeding programs in Nile tilapia. The improvement in the benefit/cost ratio by using genomic information has never been reported in the literature for aquaculture species. However, Sonesson et al. (2009) suggested that the extra cost of genotyping can be partly recovered by higher genetic gains due to the increased accuracy by genomic prediction compared to breeding values estimated using conventional pedigree-based best linear unbiased prediction (BLUP). Therefore, selective breeding is an important tool to increase aquaculture production and profitability, satisfying the increasing demand for animal protein (Gjedrem 2012).
The first Nile tilapia breeding program was established in 1988 and since then high levels of genetic gains have been achieved for economically important traits, e.g., genetic gains for body weight ranged from 7 to 20% per generation (Bentsen et al., 2017; Eknath et al., 1998; Gjedrem et al., 2012 and Khaw et al., 2008). However, until now the Nile tilapia breeding programs have been based only on pedigree and phenotype information for genetic evaluations. The incorporation of genomic information for genetic analysis has not been evaluated or implemented in tilapia breeding programs. This is mainly due to the fact that dense SNP panels were not available until recently (Joshi et al. 2018; Yáñez et al. 2019). The use of genomic information for the implementation of genomic selection has already been assessed in various aquaculture species, e.g., Atlantic salmon, rainbow trout, salmon coho, common carp, channel catfish and Pacific oyster (Barria et al., 2018; Garcia et al., 2018; Gutierrez et al., 2018; Palaiokostas et al., 2018; Vallejo et al., 2018; Yoshida et al., 2018a; Bangera et al., 2017; Correa et al., 2017; Meuwissen et al., 2014; Ødegård et al., 2014; Tsai et al., 2016). As it has been demonstrated in these studies, an increase in selection accuracy when including genomic information from dense SNP panels, especially for traits which are difficult to measure in selection candidates (Yañez and Martinez 2010; Yáñez et al. 2014). Carcass quality traits (e.g., fillet yield) are considered key traits in the breeding goal for Nile tilapia genetic improvement (Nguyen et al. 2010; Ponzoni et al. 2011) and these traits could be more efficiently improved through the inclusion of genomic information in genetic evaluations.
The use of genomic information from dense SNP panels provides the opportunity to increase the rate of genetic progress in breeding programs (Meuwissen et al. 2001). However, the cost of genotyping is high and alternative methods are necessary for cost-efficient genomic applications (VanRaden, et al. 2011; Carvalheiro et al. 2014). Strategies such as selective genotyping (Sen et al. 2009; Jiménez-Montero et al. 2012; Ødegård and Meuwissen 2014), genotyping animals using low-density panels (Tsai et al. 2016; Bangera et al. 2017; Correa et al. 2017; Yoshida et al. 2018a) and genotype imputation (Cleveland and Hickey 2014; Sargolzaei et al. 2014; Chen et al. 2014) have been tested as alternative strategies for reducing costs for the practical implementation of genomic information in breeding programs.
Imputation of genotypes reduces the cost of genomic selection by genotyping a small proportion of animals (e.g., parents or influential animals) using a dense SNP panel and selection candidates using a LD SNP panel, and then imputing (predicting) missing genotypes from the lower to the HD SNP panel (Sargolzaei et al. 2009). In aquaculture species, these cost-effective strategies have been assessed and reported to generate genomic prediction accuracies similar to those obtained when all selection candidates are genotyped with HD SNP panels (Dufflocq et al., 2019; Tsai et al., 2017; Yoshida et al., 2018b).
The objectives of this study were: (i) to perform a genome-wide association study to dissect the genetic architecture and identify molecular markers for growth and fillet yield; (ii) to evaluate the accuracy of genotype imputation as a cost-effective strategy for genotyping, and (iii) to assess the accuracy of genomic selection for growth and fillet yield using true and imputed SNP genotypes in farmed Nile tilapia. To our knowledge, this is the first study evaluating the incorporation of true and imputed dense genotypes for the implementation of genomic predictions in farmed Nile tilapia.
Material And Methods
Phenotypes
The Nile tilapia population used in the current study belong to a breeding nucleus established by Aquacorporación Internacional group (GACI) in Costa Rica. The origin of the population is described in detail by Yoshida et al. (2019a). This population consisted of eight generations selected for growth rate. Here, we used phenotype information for fillet yield and harvest weight from four generations. In addition, for all analysis (GWAs, genotype imputation and genomic predictions) we used the pedigree information of all animals from the eight generations (65,570 animals). To generate the families from each year-class, briefly, the eggs of each full-sib family were incubated and reared in separate hapas until tagging. A mating design of two dams per sire was used to produce full and half-families, which varied from 74 to 89 families across the year-classes (Table 1). For each year-class an average number of 18 fish/family (ranging from 5 to 49) were tagged at an average weight and age of 13 g (SD = 8 g) and 104 days (SD = 18 days), respectively. After, the fish were reared until an average of 13 months old, where the traits fillet yield (FY (%) = (fillet weight/harvest weight*100) and harvest weight (HW in grams) were recorded for each individual fish and the fillet weight was measured for both fillet.
Table 1. Summary statistics for phenotyped animals by year-class.
| Year-class | Number of Families | Animals genotyped | Age | Fillet Yield | Harvest Weight | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | SD2 | Number | Mean (%) | SD2 | Number | Mean (g) | SD2 | |||
| 2011 | 89 | — | 376.25 | 24.24 | 1,004 | 36.34 | 1.85 | 1,027 | 919.15 | 257.61 |
| 2012 | 82 | — | 343.48 | 16.33 | 0760 | 34.47 | 2.05 | 0767 | 730.79 | 235.62 |
| 2013 | 80 | — | 514.22 | 14.49 | 2,628 | 34.07 | 2.45 | 2,636 | 907.91 | 268.04 |
| 2017 | 74 | 1,130* | 370.54 | 20.04 | 1,474 | 31.74 | 2.16 | 1,479 | 953.57 | 252.86 |
Number of genotyped animals after quality control. Additionally 108 parents of year-class 2017 were genotyped using 50K SNPs panel to perform genotype imputation.
Genotypes
Genomic DNA was extracted from fin clip samples from 108 parents (45 sires and 63 dams) and 1,364 offspring from year-class 2017. Samples were then genotyped using a 50K SNP Illumina BeadChip, which is described in detail by Yáñez et al. (2019). Genomic DNA was purified from all the samples using the DNeasy Blood & Tissue Kit (QIAGEN) according to the manufacturer’s protocol. Before the genome-wide association study (GWAS) and imputation analysis, genotypes and samples were filtered according to the following exclusion criteria: Hardy-Weinberg Disequilibrium (HWE, p-value < 1×10−6), Minor Allele Frequency (MAF < 0.05) and genotyping call-rate for SNP and samples < 0.95.
Genome-wide association analysis
We performed the GWAS to dissect the genetic architecture and to identify regions of the Nile tilapia genome containing SNPs with important effects on FY and HW. We used the weighted single step genomic best linear unbiased prediction (wssGBLUP) method (Wang et al. 2012) implemented in postGSf90 module from BLUPf90 family programs (Misztal et al. 2016). The following model was used:
| (1) |
where is a vector of phenotypes (FY or HW), is a vector of contemporary group as fixed effects that comprise the year-class:sex:tank, and harvest weight or age for FY and HW as covariate, respectively; a is a vector of random additive direct genetic effects; c is a vector of common environmental effect and e is a vector of residual effect. , and W are incidence matrices for , a and c effects, respectively.
The wssGBLUP is similar to the pedigree-based BLUP (PBLUP) method except for the use of a combined genomic and pedigree relationship. The kinship matrix A−1 is replaced by matrix H−1 (Aguilar et al. 2010), which combines genotype and pedigree relationship coefficients:
where, is the inverse of a pedigree-based relationship matrix for genotyped animals; and is the inverse genomic relationship matrix. The SNPs were assumed with an initial value of one corresponding to the single-step genomic BLUP (ssGBLUP) method (Misztal et al. 2009). In the wssGBLUP the marker variances were estimated from allele frequencies and used as weights, which were updated on each iteration (Wang et al. 2014). We tested three iterations of weights, and used the second iteration to manhattans plots, as suggested by Wang et al. (2012) and Zhang et al. (2016), who proposed that two iterations were sufficient to correctly identify major SNPs in wssGBLUP. The wssGBLUP included all HD genotyped animals (parents and offspring) which passed quality control (n = 1,238) and all the phenotyped fish present in Table 1.
To evaluate the presence of putative genes associated with the traits under study, we reported all genes between the first and last SNP position of each 20-SNP window, searched using BLAST (Basic Local Alignment Search Tool) of the SNP probes against the last version of the Oreochromis niloticus reference genome (Conte et al. 2019), publicly available at NCBI (GenBank assembly accession GCA_001858045.3).
Genotype imputation
Three in silico LD panels were constructed with SNP densities of 500 (LD0.5K), 1,000 (LD1K) and 3,000 (LD3K). The SNPs from the LD panels were selected using the option–indep-pairwise of Plink v1.9 software (Purcell et al. 2007), with a window size of 180,432 kb, a step of 1 SNPs and a variable r2 according to chromosome. This command produced a subset of markers that are proportional for chromosome size, are approximately evenly spaced and in low linkage disequilibrium with each other as recommended by Cleveland and Hickey (2014).
The imputations were run using genotype information from 108 parents and 20% of the offspring (n = 225) as a reference set (HD panel) and 80% of offspring (n = 904) were used as the validation set (LD panel). The assignment of the offspring to the reference and validation sets was random, and five replicates were used each time. In addition, we used pedigree information available for all individuals for imputation (65,770 animals), consisting of eight generations of selection. Imputation of genotypes was performed using the FImpute v2.2 software (Sargolzaei et al., 2014) and the accuracy of imputation was calculated as the correlation between true and imputed genotypes for the validation set.
Genomic prediction
We used two scenarios to assess prediction accuracies using a fivefold cross validation. The first scenario used the true genotyped LD panels (LD0.5K, LD1K and LD3K) and represented the same in silico LD panel constructed for genotype imputation. The second scenario used the imputed genotypes from LD0.5K, LD1K and LD3K to 32K panel. In addition, accuracy of breeding values was also estimated using pedigree-based information (PBLUP method) and the true 32K SNPs (true markers that passed in quality control). Briefly, all genotyped animals (n = 904) with phenotypes were randomly divided into five exclusive training sets (80% of the dataset; n = 721 and SD = 5 animals) which were used to estimate the SNP effects; the remaining animals were used as validation sets (20% of the dataset; mean = 193 and SD = 5 animals), for which their phenotypes were masked and their performance was predicted based on the marker effects. This fivefold cross validation was replicated five times for each SNP panel density and the results are presented as a mean for all replications.
We used the BLUPF90 family of programs (Misztal et al. 2016) to perform the genetic evaluations using pedigree-based information and the ssGBLUP method which uses both pedigree and genomic information, and additional information of the animals with only phenotypes (Table 1) in the validation set. The statistical model fitted was the same of the equation 1, except for PBLUP method, for which the kinship matrix used was A−1 instead of H−1 in ssGBLUP.
Prediction accuracies were calculated in the validation sets using the following equation:
| (2) |
where is the correlation between the estimated breeding value (EBV) or genomic estimated breeding values (GEBV) of a given model (predicted for the validation set using information from the training set) and the true phenotypic record, while is the square root of the pedigree-based estimate of heritability.
Genetic parameters and heritability
The total additive genetic variance ( was estimated using the kinship matrix A and H for PBLUP and ssGBLUP, respectively. For all traits studied, the heritabilities were computed using the following equation:
| (3) |
where, is the common environmental and residual variance, respectively.
Cost evaluation
We evaluated the direct savings when genotyping a proportion of animals using a LD panel and performing genotyping imputation. Costs were calculated on the basis of one discrete generation, for seven different sizes of a Nile tilapia breeding populations, ranging from a total of 4,150 to 10,150 fishes, with half of the animals were used as reference population (RP) and the other half as selection candidates (SC). All animals descend from a fixed number of parents (P; 100 females and 50 males) (Table S2). We evaluated four different scenarios: scenario A: all animals (P, RP and SC) were genotyped using a HD panel; and, scenario B, C and D, in which all parents and 20% of RP were genotyped using a HD SNP panel and the remaining animals were genotyped using a 3K, 1K or 0.5K LD panel, respectively. The genotyping cost was calculated assuming prices of U$50, $25, $20 and $10 per sample for HD (50K), 3K, 1K, and 0.5K, respectively. In addition, for scenario A, we assumed a price reduction of 10% in each increase of 1,000 animals genotyped using a HD panel, which resulted in prices ranging from $50 to $26.60 per sample for genotyping 4,150 and 10,150 animals, respectively. The results of the genotyping cost evaluation (Table S3) are presented as terms of cost reduction (%) comparing scenario A to other scenarios.
Data availability
All raw phenotypic and genotypic data used in the current study can be found at Figshare public repository (https://figshare.com/s/9b265a22b7e138c5a839). Furthermore, Supplementary Figures (Figure S1-S4) and Supplementary Tables (Table S1-S3) are available at Figshare: https://figshare.com/s/9b265a22b7e138c5a839.
Results
Basic statistics and genotype quality control
The total number of individuals phenotyped ranged from 5,866 to 5,909 for FY and HW, respectively, and varied per year-class with the maximum number of animals phenotyped in 2013. On average, the recorded fish were 401 days old at harvest weight. The average FY was 34.2% (SD = 2.13% g) and the average HW was 878 g (SD = 254 g) for phenotyped fish (Table 1).
Out of the initial 1,364 individuals and 43,272 SNPs which were effectively genotyped, a total of 1,130 animals and 32,306 SNPs (32K) passed in the quality control. The MAF < 0.05 parameter excluded the highest number of SNPs (4,779), whereas HWE and genotyped call-rate excluded 1,982 and 4,205 SNPs, respectively.
Genetic parameters and heritability
For both FY and HW the additive genetic variance and heritability were slightly higher when using genomic information compared to the pedigree-based method. For instance, heritability values using ssGBLUP were 0.21 and 0.36 for FY and HW, respectively. For PBLUP heritability for FY and HW was estimated to be 0.21 to 0.31, respectively (Table 2). Additionally, a reduction in error of heritability estimates was shown for ssGBLUP when compared with PBLUP.
Table 2. Estimates of variance components and heritability for fillet yield and harvest weight in Nile tilapia.
| Traits | PBLUP | ssGBLUP* | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | h24 | SE5 | 1 | 2 | 3 | h24 | SE5 | |
| Fillet yield | 0.972 | 0.174 | 3.498 | 0.209 | 0.053 | 0.972 | 0.168 | 3.491 | 0.210 | 0.038 |
| Harvest weight | 19,312 | 4,296 | 39,522 | 0.306 | 0.073 | 23,161 | 3,823 | 37,345 | 0.360 | 0.047 |
Estimated for true 32K genotype panel.
Additive genetic variance;
Common environment variance;
Residual variance;
Heritability;
Standard error.
Genome-wide association analysis
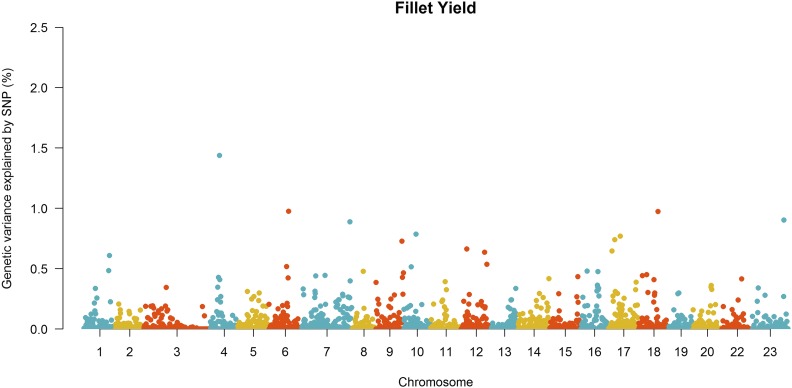
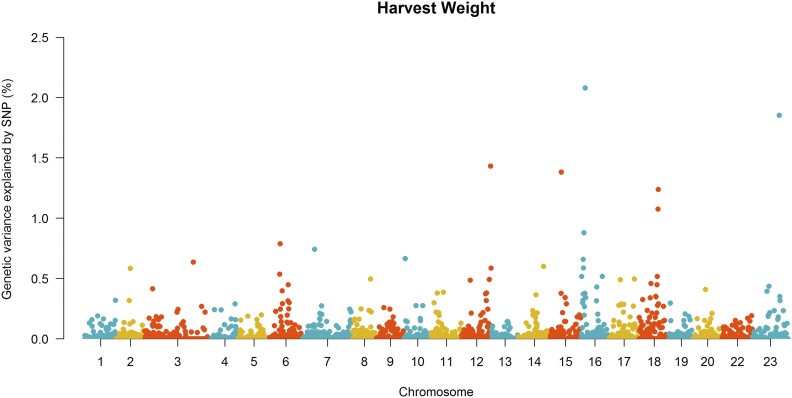
Manhattan plots for the proportion of genetic variance explained by each 20-SNP window for FY and HW are shown in Figures 1 and 2. A total of 1,624 20-SNP windows with average length of 530 kb (range from 10 to 6,690 kb) were obtained. After the second iteration of wssGBLUP, the top five windows cumulatively explained 5.2 and 8.0% of the total genetic variance for FY and HW, respectively (Table 3).
Figure 1.
Manhattan plot of genetic variance explained by 20-SNP windows for fillet yield in the 2nd iteration of wssGBLUP.
Figure 2.
Manhattan plot of genetic variance explained by 20-SNP windows for harvest weight in the 2nd iteration of wssGBLUP.
Table 3. Top five ranked 20-SNP windows that explain the largest proportion of genetic variance for fillet yield and harvest weight in Nile tilapia.
| CHR1 | Position | Pvar2 (%) | Window length (bp) | Genes3 | |
|---|---|---|---|---|---|
| Initial | Final | ||||
| Fillet Yield | |||||
| LG04 | 11,812,441 | 12,225,401 | 1.439 | 412,960 | cacng3, clcn7, dctn5 |
| LG06 | 25,191,450 | 25,573,340 | 0.981 | 381,890 | adap2, rab11, utp6 |
| LG18* | 24,563,797 | 24,886,884 | 0.969 | 323,087 | ankrd12, mtcl1, rab31 |
| LG23 | 40,389,783 | 41,076,465 | 0.907 | 686,682 | armh1, atp5f1d, fstl3 |
| LG07 | 61,517,871 | 61,850,135 | 0.889 | 332,264 | — |
| Harvest Weight | |||||
| LG16 | 05,380,219 | 05,989,612 | 2.082 | 609,393 | calcrl, gulp1 |
| LG22 | 34,016,287 | 34,585,708 | 1.852 | 569,421 | dnai2, ints3, npr1 |
| LG12 | 37,027,113 | 37,559,043 | 1.434 | 531,930 | endog, entr1, med27 |
| LG15 | 14,423,480 | 14,846,999 | 1.383 | 423,519 | cpsf2, extl3, fut8 |
| LG18* | 24,563,797 | 24,886,884 | 1.238 | 323,087 | — |
Coincident window for both traits.
Chromosome;
Percentage of genetic variance explained by each 20-SNP window;
Oreochromis niloticus used as reference species (full list of genes are available in Table S1).
The full list of genes located within the top five 20-SNPs windows associated with FW and HW is shown in Table S1. Some candidate genes found within the top five most important windows have been suggested to be involved with growth-related traits in previous studies. For FY we identified genes U3 small nucleolar RNA-associated protein 6 homolog (UTP6), Ras-related protein (Rab31) and Follistatin-related protein (FLRG or FSTL3), located in chromosome 06, 18 and 23, respectively. For HW we identified the genes Natriuretic Peptide Receptor 1 (NPR1) and Exostosin Like Glycosyltransferase 3 (EXTL3) located in chromosome 22 and 15, respectively.
Accuracy of genotype imputation
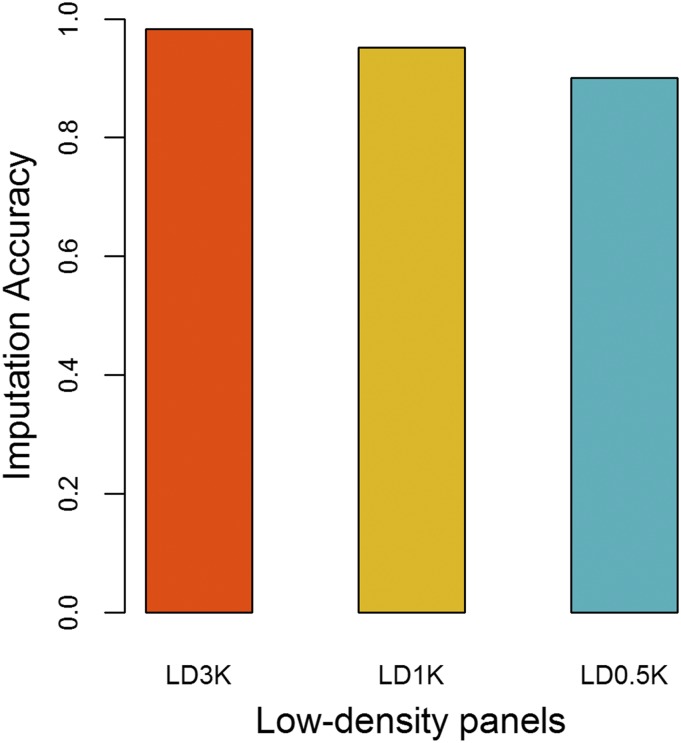
We observed that imputation accuracy decreased with reduced marker density going from LD3K to LD0.5K SNP panels with values ranging from 0.98 to 0.90, respectively (Figure 3). The largest increase in imputation accuracy occurred when increasing SNP density from 0.5K to 1K, with an increase in imputation accuracy of about 6%.
Figure 3.
Imputation accuracy from low-density (LD3K, LD1K and LD0.5K) to high-density (HD) panel in Nile tilapia using parents (n = 108) and 20% of offspring (n = 226) genotyped with the HD panel as the reference set and 80% of offspring (n = 904) as the validation set.
Figures S1, S2 and S3 show the correlation between observed and imputed genotypes for each SNP in all chromosomes using the LD3K, LD1K and LD0.5 panels, respectively. Imputation accuracy was not consistent across chromosomes, especially for LD0.5K. Inconsistencies may happen because of the physical position of imputed SNP and the location of the SNP on the LD panel. The imputation accuracy decreased greatly at telomeres, and increased considerably with increased SNP density.
Accuracy of PBLUP and ssGBLUP
Based on the fivefold cross validation, the prediction accuracy for GEBV from genomic methods outperformed the accuracy for EBV from PBLUP. In addition, the accuracy of genomic selection using imputed genotypes from LD to HD SNP panels outperformed both PBLUP and ssGBLUP using true LD genotypes (Table 4).
Table 4. Mean accuracy of EBV and GEBV for fillet yield and harvest weight in Nile tilapia using pedigree-based information, true and imputed genotypes.
| Traits | Pedigree-based BLUP | True genotypes1 | Imputed genotypes2 | |||||
|---|---|---|---|---|---|---|---|---|
| 32K | 3K | 1K | 0.5K | 3K | 1K | 0.5K | ||
| Fillet yield | 0.539 | 0.621 | 0.612 | 0.574 | 0.560 | 0.621 | 0.620 | 0.585 |
| Harvest weight | 0.479 | 0.601 | 0.539 | 0.537 | 0.500 | 0.607 | 0.600 | 0.586 |
High-density (32K) and different true in silico low-density panel.
Imputed genotypes from different low-density panel (3K, 1K or 0.5K) to high-density panel (32K).
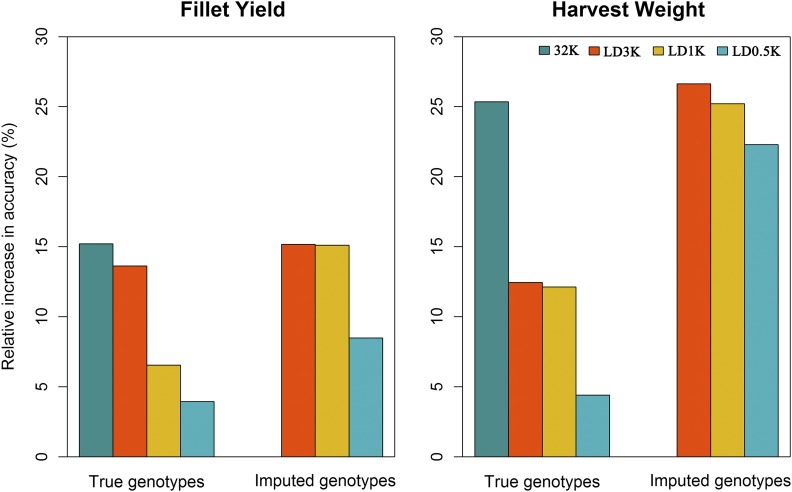
The relative increase in accuracy of predicted GEBV compared with EBV from PBLUP varied moderately between the LD panels and traits (Figure 4). Thus, the relative increase in accuracy for FY when comparing ssGBLUP to PBLUP ranged from 4 to 15% for true 0.5 and 32K genotypes, respectively and from 8 to 15% for imputed genotypes using the 0.5 and 3K LD SNP panels respectively. For HW the relative increase in accuracy when comparing ssGBLUP to PBLUP ranged from 4 to 25% for true 0.5 and 32K genotypes, respectively and from 22 to 27% for imputed genotypes using the 0.5 and 3K LD SNP panels respectively. In general, the relative increase in accuracy of predicted GEBV from all true LD SNP panels and imputed genotypes were always better than EBV from PBLUP even at the lowest marker density of 0.5 K for all traits. The relative increase in accuracies when comparing ssGBLUP to PBLUP were almost always higher for HW than for FY, except for the use of true 3K genotypes for prediction of FY (14%) which was slightly higher than for HW (13%) using the same 3K genotypes.
Figure 4.
Relative increase in accuracy of different genomic selection methods for fillet yield, harvest weight and waste weight compared to PBLUP in Nile tilapia using true and imputed genotypes.
The genomic prediction accuracy using imputed genotypes, was identical or very similar between the LD panels compared to the 32K SNP genotypes, especially for FY (Figure 4). When comparing the use of true and imputed genotypes for genomic selection it was evident that genotype imputation resulted in a higher increase in relative accuracy independently of trait and LD SNP panel. As expected, the lowest genomic prediction accuracy when using imputed genotypes was always observed for the SNP panel with lowest imputation accuracy (LD0.5K), which resulted in an accuracy slightly lower than the 32K SNP panel, but higher than PBLUP.
Cost evaluation
The costs using different LD genotyping panels and different sizes of Nile tilapia breeding populations, ranged from an increase of 4.74% to a reduction of 69.40%, when compared to scenario A, where all animals were genotyped using a HD panel. As expected, scenario D, resulted in the most substantial cost reduction, ranging from 69 to 45%, depending on the size of the breeding population and scenario B resulted in the worst cost reduction (Figure S4). Interestingly, due to value adjustment when increasing the number of samples to genotype, for scenario B and a number of RP + SC equal to 10,150, it is more cost efficient to genotype all animals using a HD panel than genotyping a proportion of animals using LD panel.
Discussion
Heritability
We found moderate heritability values for FY and HW which agrees with previous estimates calculated using pedigree-based methods (Gjerde et al., 2012; Nguyen et al., 2010; and Rutten et al., 2005). HW and FY heritability values in tilapia, estimated using genomic information, are reported for the first time in this study. We found slightly higher estimates of heritability when using genomic information compared to PBLUP, especially for HW, which is in accordance with what has been reported in other fish species for fillet yield and growth traits (Tsai et al. 2015; Gonzalez-Pena et al. 2016).
Genome-wide association analysis
In the present study, we found no evidence of major quantitative trait loci for both fillet yield and harvest weight in Nile tilapia. The small effect of these loci reinforces evidence of the polygenic nature of these traits. Our results support previous findings which have shown the polygenic nature of fillet yield and growth-related traits in different aquaculture species, with no evidence of major effect genes or genomic regions assessed by GWAS (Gutierrez et al. 2015; Tsai et al. 2015; Gonzalez-Pena et al. 2016; Yoshida et al. 2017; Garcia et al. 2018; Reis Neto et al. 2019). Furthermore, within the five 20-SNP windows that explained the higher proportion of genetic variance, we found several genes that could potentially be involved in growth and fillet yield.
Although, it is out of the scope of the present study to discuss in detail the putative genes involved in FY and HW, we found it worthy to mention some of the most biologically relevant candidates that may be worthy of functional validation. For instance, the UTP6 gene is suggested to enhance cellular growth through an increase in the number of ribosomes in Chinese hamster ovary cells (Courtes et al. 2013). For both FY and HW, between position 24,563,797 and 24,886,884 bp, we identified the RAB31 gene, which has a role in trafficking the epidermal growth factor receptor (EGFR) gene (Chua and Tang 2014), an important receptor of tyrosine kinase in animals that functions in development, growth and tissue regeneration (Wang et al. 2018). In addition, FSTL3, present in one of the top 5 SNP windows explaining a high proportion of the genetic variance for FY, is a member of follistatin family, which has been suggested to be an inhibitory binding protein of myostatin activity (Hill et al. 2002, 2003). Rebhan and Funkenstein (2008) reported experimental evidence that myostatin activity can be inhibited by follistatin. Chu et al. (2016) observed an increase in the number of muscle fibers, satellite cell activation and decreased expression of myostatin in animals treated with FSTL3; suggesting that the gene might be involved to muscle development in the Chinese Perch (Siniperca chuatsi).
In plants NPR1 is an essential regulator of systemic acquired resistance, conferred immunity to broad-spectrum of pathogens (Cao et al. 1997; Mou et al. 2003). However, Vanacker et al. (2001) reported a novel function for NPR1, which is associated with growth control, cell division and suppressing endoreduplication during leaf development in Arabidopsis. In humans, a mutation affected the EXTL3 gene causing skeletal dysplasia, immune deficiency and development delay. In zebrafish abnormalities of cartilage development and defective formation in fin and branchial arch were reported (Norton et al. 2005). Other genes located in a 20-SNP window flanking the top five windows are presented in Table S1.
Accuracy of genotype imputation
The imputation accuracy, on average, was above 90%, independent of the LD SNP panel used but decreased from LD3K to LD0.5K, which is in accordance with the same pattern seen by Habier et al. (2009), Hickey et al. (2012) and Yoshida et al. (2018b). The imputation errors could be higher in LD panels because they could be less efficient in capturing the linkage and linkage disequilibrium between the markers. Like previous studies we found accuracies of genotype imputation to be very similar using panels of 3K SNPs or denser (Druet et al. 2010; Zhang and Druet 2010; Duarte et al. 2013; Carvalheiro et al. 2014; Cleveland and Hickey 2014; Kijas et al. 2016; Tsai et al. 2017). However, it is likely that 3K or denser SNP panels will be considerably more expensive than 0.5K or 1K SNP panels, thus cost-effectiveness must be carefully evaluated in further studies.
Some imputation studies tested the size of the reference population (Zhang and Druet 2010; Cleveland and Hickey 2014; Tsai et al. 2017; Yoshida et al. 2018b), and have shown that the number of animals used in this study should be sufficient to not influence the imputation accuracy. Therefore, we did not include the effect of different genotyping strategies in the final results; however, in preliminary tests we found imputation accuracies lower than 90% using a small proportion of offspring (less than 10%) in the reference set when imputing genotypes from the 0.5K SNP panel (results not show). This is probably because of the small number of animals per family in the reference population, which can influence imputation accuracy (Hickey et al. 2012). In this case we had approximately 18 sibs genotyped/family and we used as reference set 20% of offspring in addition to the parents genotyped with the 32K SNP panel to achieve similar accuracy values to those reported by Yoshida et al. (2018b) for Salmo salar, where 31 sibs/family and just 10% of offspring were needed to surpass an imputation accuracy of 90%.
Figures S1, S2 and S3 indicate regions of the genome containing markers with high imputation errors, especially at the beginning and end of the chromosomes. This is could be an effect of recombination rates, that are known to be higher around the telomeres (Chowdhury et al. 2009; Tortereau et al. 2012). The physical location of the SNP is another factor that has been shown to be affect the imputation accuracy and to reduce the errors in these regions, some previous studies suggested increasing the coverage of SNP chromosomal extremes (Badke et al. 2012; Boichard et al. 2012; Dassonneville et al. 2012). In addition, high imputation errors far from chromosome extremes can be the result of erratic patterns of linkage disequilibrium, which suggests potential issues related to physical maps and reference genome assembly (Druet et al. 2010; Carvalheiro et al. 2014; Yoshida et al. 2018b).
Another important factor that may affect the imputation accuracy is the linkage disequilibrium between markers (Hickey et al. 2012; Carvalheiro et al. 2014). A previous study, showed a more rapid decrease of linkage disequilibrium with inter-marker distance for this Nile tilapia population (Yoshida et al. 2019a) when compared to other populations of different aquaculture species (Gutierrez et al. 2015; Kijas et al. 2016; Vallejo et al. 2018; Barría et al. 2019). Nevertheless, our imputation accuracies are close to the imputation values reported in the literature for salmonids (Kijas et al. 2016; Tsai et al. 2017; Yoshida et al. 2018b) and terrestrial species (Badke et al. 2012; Hayes et al. 2012; Duarte et al. 2013; Hozé et al. 2013; Carvalheiro et al. 2014), suggesting that the family-based imputation approach is less sensitive to linkage disequilibrium patterns by efficiently exploiting information of highly related animals.
The imputation methods can be classified in family-based and population-based methods. The first exploits linkage information from close related animals and the second uses linkage disequilibrium information of the population (Sargolzaei et al. 2014). Previous studies tested the use of different imputation methods as well as different imputation software (Hayes et al. 2012; Carvalheiro et al. 2014; Sargolzaei et al. 2014). Here, we used the FImpute software (Sargolzaei et al., 2014) that consider both family and population-based approaches, or only population-based when the pedigree information is not available. The imputation proceeds using overlapping sliding windows, starting with long haplotypes and moving to short haplotypes (Sargolzaei et al., 2014). This method results in high imputation accuracy when close relatives of targeted individuals are present in the reference group (Carvalheiro et al. 2014; Sargolzaei et al. 2014; Larmer et al. 2014). Furthermore, the computing requirements are considerably lower than other software used for imputation (Sargolzaei et al., 2014).
Accuracy of genomic prediction
Our results showed that the use of genomic information for estimating breeding values achieved higher accuracies compared to using only pedigree information for FY and HW, independent of the LD SNP panel used, with or without imputation of genotypes (Figure 4). The relative increase in GEBV accuracies compared to PBLUP has been previously reported for growth (Garcia et al., 2018; Tsai et al., 2015) and for different disease resistance traits in farmed aquaculture species (Tsai et al. 2016; Vallejo et al. 2017; Bangera et al. 2017; Correa et al. 2017; Barria et al. 2018; Yoshida et al. 2018a, 2018b).
The accuracy of GEBV depends on some factors such as the number of genotyped and phenotyped individuals in the training population, the heritability and the number of loci affecting the trait (Daetwyler et al. 2008; Goddard 2009). Furthermore, the accuracy of genomic prediction is highly dependent on the genotype density used, which means that increasing marker densities tends to generate higher GEBV accuracies (Tsai et al. 2016; Bangera et al. 2017; Correa et al. 2017; Yoshida et al. 2018a). In addition, the use of different methods to estimate the GEBV can directly affect the accuracy of genomic prediction. In general, the genomic methods differ in distributional assumptions of marker effects and the calculation of the genetic relationship matrix. Here, we used the ssGBLUP method (Misztal et al. 2009), which assumed a normal distribution of marker effects and has some of practical advantages, given that it uses information from genotyped and nongenotyped animals (Lourenco et al. 2014), and it has also been demonstrated to provide higher accuracy than the PBLUP method and other genomic methods (Chen et al. 2011; Christensen et al. 2012; Vallejo et al. 2017; Yoshida et al. 2018a).
To test the impact of genotype imputation errors in genomic predictions we estimated the accuracy of genomic predictions for FY and HW using imputed genotypic data and compared the data to true 32K and LD SNP genotypes (LD3K, LD1K and LD0.5K). Our results indicate that genomic prediction accuracies using imputed genotypes were always higher than those obtained using true LD genotypes and equal or slightly lower than using true 32K genotypes (Figure 4). For HW the accuracy of GEBV was substantially higher using the imputed LD0.5K than true LD0.5K, LD1K and even LD3K, whereas for FY the accuracy using imputed LD0.5K did not surpass the true LD3K panel. Our results are in accordance with previous studies in aquaculture (Dufflocq et al., 2019; Tsai et al., 2017; Yoshida et al., 2018b) and livestock species (Berry and Kearney 2011; Erbe et al. 2012); indicating that the use of genotype imputation can decrease the cost of genotyping by means of using less expensive LD SNP panels without compromising prediction accuracies. In addition, the influence of imputation error on genomic prediction accuracy depends on the genetic architecture underlying the studied traits. For traits that are influenced by few QTL with large effect, accuracy of genomic prediction could be more sensitive to imputation errors than polygenic traits, such FY and HW (Chen et al. 2014).
Implications
The extra costs to genotyping animals represents a key limiting factor for the practical implementation of genomic selection in freshwater fish species. One of the main objectives of this study was to test genotyping imputation as an alternative to reduce the costs of genotyping for genomic selection in Nile tilapia breeding programs. The cost to genotype depends on the density of the SNP panel, genotyping technology used and number of samples. In general, the price ranges from USD $5 to USD $75 for low- (0.5K) and high-density panels (50K), respectively. We did a cost evaluation, that resulted in a reduction of cost ranging from 45 to 69% (Figure S4), assuming different sizes of a breeding population and a strategy aimed to genotyping a proportion of animals using a HD panel and the remaining animals using a 0.5K panel. These values represent the direct savings on genotyping fewer animals using a HD panel and support the results suggested by Dufflocq et al. (2019) and Tsai et al. (2017) for aquaculture species. The previous authors suggested that the use of imputation strategies can reduce the cost of genotyping by at least 60% compared to genotyping all animals with a HD panel. Therefore, the strategies used in the present study to genotype both parents using a HD panel and a proportion of offspring using a HD and LD panel resulted in accuracies of genomic prediction similar to when all animals were genotyped with the HD panel. These results suggest that genotype imputation can decrease the costs for the practical implementation of genomic prediction in Nile tilapia breeding programs.
Conclusions
The GWAS indicated a polygenic architecture for fillet yield and harvest weight, with some markers explaining a small proportion of genetic variance; indicating that the implementation of marker assisted selection could not be successfully applied for these traits in the present Nile tilapia population. In contrast, the use of genomic selection could increase the response to selection and improve genetic progress. The use of genotype imputation can reduce genotyping costs and allow the implementation of genomic selection in Nile tilapia breeding programs.
Acknowledgments
This work has been funded by Corfo (project number 14EIAT-28667). The authors are grateful to Acuacorporación Internacional for providing the Nile tilapia dataset and fin samples.
Footnotes
Supplemental material available at Figshare: https://figshare.com/s/9b265a22b7e138c5a839.
Communicating editor: R. Houston
Literature Cited
- Aguilar I., Misztal I., Johnson D. L., Legarra A., Tsuruta S. et al. , 2010. Hot topic: A unified approach to utilize phenotypic, full pedigree, and genomic information for genetic evaluation of Holstein final score. J. Dairy Sci. 93: 743–752. 10.3168/jds.2009-2730 [DOI] [PubMed] [Google Scholar]
- Badke Y. M., Bates R. O., Ernst C. W., Schwab C., and Steibel J. P., 2012. Estimation of linkage disequilibrium in four US pig breeds. BMC Genomics 13: 24 10.1186/1471-2164-13-24 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bangera R., Correa K., Lhorente J. P., Figueroa R., and Yáñez J. M., 2017. Genomic predictions can accelerate selection for resistance against Piscirickettsia salmonis in Atlantic salmon (Salmo salar). BMC Genomics 18: 121 10.1186/s12864-017-3487-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barria A., Christensen K. A., Yoshida G. M., Correa K., Jedlicki A. et al. , 2018. Genomic predictions and genome-wide association study of resistance against Piscirickettsia salmonis in coho salmon (Oncorhynchus kisutch) using ddRAD sequencing. G3 Genes, Genomes. Genet. 8: 1183–1194. 10.1534/g3.118.200053 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barría A., Christensen K. A., Yoshida G., Jedlicki A., Leong J. S. et al. , 2019. Whole genome linkage disequilibrium and effective population size in a coho salmon (Oncorhynchus kisutch) breeding population using a high density SNP array. Front. Genet. 10: 498 10.3389/fgene.2019.00498 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bentsen H. B., Gjerde B., Eknath A. E., de Vera M. S. P., Velasco R. R. et al. , 2017. Genetic improvement of farmed tilapias: Response to five generations of selection for increased body weight at harvest in Oreochromis niloticus and the further impact of the project. Aquaculture 468: 206–217. 10.1016/j.aquaculture.2016.10.018 [DOI] [Google Scholar]
- Berry D. P., and Kearney J. F., 2011. Imputation of genotypes from low- to high-density genotyping platforms and implications for genomic selection. Animal 5: 1162–1169. 10.1017/S1751731111000309 [DOI] [PubMed] [Google Scholar]
- Boichard D., Chung H., Dassonneville R., David X., Eggen A. et al. , 2012. Design of a Bovine Low-Density SNP Array Optimized for Imputation. PLoS One 7: e34130 10.1371/journal.pone.0034130 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cao H., Glazebrook J., Clarke J. D., Volko S., and Dong X., 1997. The Arabidopsis NPR1 Gene That Controls Systemic Acquired Resistance Encodes a Novel Protein Containing Ankyrin Repeats. Cell 88: 57–63. 10.1016/S0092-8674(00)81858-9 [DOI] [PubMed] [Google Scholar]
- Carvalheiro R., Boison S. A., Neves H. H. R., Sargolzaei M., Schenkel F. S. et al. , 2014. Accuracy of genotype imputation in Nelore cattle. Genet. Sel. Evol. 46: 1–11. 10.1186/s12711-014-0069-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen L., Li C., Sargolzaei M., and Schenkel F., 2014. Impact of Genotype Imputation on the Performance of GBLUP and Bayesian Methods for Genomic Prediction. PLoS One 9: e101544 10.1371/journal.pone.0101544 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen C. Y., Misztal I., Aguilar I., Tsuruta S., Meuwissen T. H. E. et al. , 2011. Genome-wide marker-assisted selection combining all pedigree phenotypic information with genotypic data in one step: An example using broiler chickens. J. Anim. Sci. 89: 23–28. 10.2527/jas.2010-3071 [DOI] [PubMed] [Google Scholar]
- Chowdhury R., Bois P. R. J., Feingold E., Sherman S. L., Cheung V. G. et al. , 2009. Genetic Analysis of Variation in Human Meiotic Recombination. PLoS Genet. 5: e1000648 10.1371/journal.pgen.1000648 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Christensen O. F., Madsen P., Nielsen B., Ostersen T., and Su G., 2012. Single-step methods for genomic evaluation in pigs. Animal 6: 1565–1571. 10.1017/S1751731112000742 [DOI] [PubMed] [Google Scholar]
- Chu W., Cheng J., Zhu X., Wu P., Chen L. et al. , 2016. Identification and Characterization of Follistatin-Related Protein-1 Involved in the Regulation of Chinese Perch Skeletal Muscle Hyperplasia. Curr. Mol. Med. 16: 596–604. 10.2174/1566524016666160607122105 [DOI] [PubMed] [Google Scholar]
- Chua C. E. L., and Tang B. L., 2014. Engagement of the small GTPase Rab31 protein and its effector, early endosome antigen 1, is important for trafficking of the ligand-bound epidermal growth factor receptor from the early to the late endosome. J. Biol. Chem. 289: 12375–12389. 10.1074/jbc.M114.548321 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cleveland M. A., and Hickey J. M., 2014. Practical implementation of cost-effective genomic selection in commercial pig breeding using imputation 1. 3583–3592. 10.2527/jas.2013-6270 [DOI] [PubMed]
- Conte M. A., Joshi R., Moore E. C., Nandamuri S. P., Gammerdinger W. J. et al. , 2019. Chromosome-scale assemblies reveal the structural evolution of African cichlid genomes. Gigascience 8: giz030 10.1093/gigascience/giz030 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Correa K., Bangera R., Figueroa R., Lhorente J. P., and Yáñez J. M., 2017. The use of genomic information increases the accuracy of breeding value predictions for sea louse (Caligus rogercresseyi) resistance in Atlantic salmon (Salmo salar). Genet. Sel. Evol. 49: 15 10.1186/s12711-017-0291-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Courtes F. C., Lin J., Lim H. L., Ng S. W., Wong N. S. C. et al. , 2013. Translatome analysis of CHO cells to identify key growth genes. J. Biotechnol. 167: 215–224. 10.1016/j.jbiotec.2013.07.010 [DOI] [PubMed] [Google Scholar]
- Daetwyler H. D., Villanueva B., Woolliams J. A., Schaeffer L., and Crawford A., 2008. Accuracy of Predicting the Genetic Risk of Disease Using a Genome-Wide Approach. PLoS One 3: e3395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dassonneville R., Fritz S., Ducrocq V., Boichard D., Berry D. P. et al. , 2012. Short communication: Imputation performances of 3 low-density marker panels in beef and dairy cattle. J. Dairy Sci. 95: 4136–4140. 10.3168/jds.2011-5133 [DOI] [PubMed] [Google Scholar]
- Druet T., Schrooten C., and de Roos A. P. W., 2010. Imputation of genotypes from different single nucleotide polymorphism panels in dairy cattle. J. Dairy Sci. 93: 5443–5454. 10.3168/jds.2010-3255 [DOI] [PubMed] [Google Scholar]
- Duarte J. L. G., Bates R. O., Ernst C. W., Raney N. E., Cantet R. J. C. et al. , 2013. Genotype imputation accuracy in a F2 pig population using high density and low density SNP panels. BMC Genet. 14: 38 10.1186/1471-2156-14-38 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dufflocq P., Pérez-Enciso M., Lhorente J. P., and Yáñez J. M., 2019. Accuracy of genomic predictions using different imputation error rates in aquaculture breeding programs: A simulation study. Aquaculture 503: 225–230. 10.1016/j.aquaculture.2018.12.061 [DOI] [Google Scholar]
- Eknath A. E., Acosta B. O., Eknath A. E., and Acosta B. O., 1998. Genetic Improvement of Farmed Tilapias (GIFT) Project: final report, March 1988 to December 1997.
- Erbe M., Hayes B. J., Matukumalli L. K., Goswami S., Bowman P. J. et al. , 2012. Improving accuracy of genomic predictions within and between dairy cattle breeds with imputed high-density single nucleotide polymorphism panels. J. Dairy Sci. 95: 4114–4129. 10.3168/jds.2011-5019 [DOI] [PubMed] [Google Scholar]
- Garcia A. L. S., Bosworth B., Waldbieser G., Misztal I., Tsuruta S. et al. , 2018. Development of genomic predictions for harvest and carcass weight in channel catfish. Genet. Sel. Evol. 50: 66 10.1186/s12711-018-0435-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gjedrem, T., 2012 Genetic improvement for the development of efficient global aquaculture: A personal opinion review. Aquaculture 344–349: 12–22. 10.1016/j.aquaculture.2012.03.003 [DOI]
- Gjedrem T., Robinson N., and Rye M., 2012. The importance of selective breeding in aquaculture to meet future demands for animal protein. Rev. Aquacult. 350–353: 117–129. 10.1016/j.aquaculture.2012.04.008 [DOI] [Google Scholar]
- Gjerde B., Mengistu S. B., Ødegård J., Johansen H., and Altamirano D. S., 2012. Quantitative genetics of body weight, fillet weight and fillet yield in Nile tilapia (Oreochromis niloticus). Aquaculture 342–343: 117–124. 10.1016/j.aquaculture.2012.02.015 [DOI] [Google Scholar]
- Goddard M., 2009. Genomic selection: prediction of accuracy and maximisation of long term response. Genetica 136: 245–257. 10.1007/s10709-008-9308-0 [DOI] [PubMed] [Google Scholar]
- Gonzalez-Pena D., Gao G., Baranski M., Moen T., Cleveland B. M. et al. , 2016. Genome-Wide Association Study for Identifying Loci that Affect Fillet Yield, Carcass, and Body Weight Traits in Rainbow Trout (Oncorhynchus mykiss). Front. Genet. 7: 203 10.3389/fgene.2016.00203 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gutierrez A. P., Matika O., Bean T. P., and Houston R. D., 2018. Genomic Selection for Growth Traits in Pacific Oyster (Crassostrea gigas): Potential of Low-Density Marker Panels for Breeding Value Prediction. Front. Genet. 9: 391 10.3389/fgene.2018.00391 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gutierrez A. P., Yáñez J. M., Fukui S., Swift B., and Davidson W. S., 2015. Genome-Wide Association Study (GWAS) for Growth Rate and Age at Sexual Maturation in Atlantic Salmon (Salmo salar). PLoS One 10: e0119730 10.1371/journal.pone.0119730 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Habier D., Fernando R., and Dekkers J., 2009. Genomic selection using low-density marker panels. Genetics 182: 343–353. 10.1534/genetics.108.100289 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hayes B. J., Bowman P. J., Daetwyler H. D., Kijas J. W., and van der Werf J. H. J., 2012. Accuracy of genotype imputation in sheep breeds. Anim. Genet. 43: 72–80. 10.1111/j.1365-2052.2011.02208.x [DOI] [PubMed] [Google Scholar]
- Hickey J. M., Crossa J., Babu R., and de los Campos G., 2012. Factors Affecting the Accuracy of Genotype Imputation in Populations from Several Maize Breeding Programs. Crop Sci. 52: 654 10.2135/cropsci2011.07.0358 [DOI] [Google Scholar]
- Hill J. J., Davies M. V., Pearson A. A., Wang J. H., Hewick R. M. et al. , 2002. The myostatin propeptide and the follistatin-related gene are inhibitory binding proteins of myostatin in normal serum. J. Biol. Chem. 277: 40735–40741. 10.1074/jbc.M206379200 [DOI] [PubMed] [Google Scholar]
- Hill J. J., Qiu Y., Hewick R. M., and Wolfman N. M., 2003. Regulation of Myostatin in Vivo by Growth and Differentiation Factor-Associated Serum Protein-1: A Novel Protein with Protease Inhibitor and Follistatin Domains. Mol. Endocrinol. 17: 1144–1154. 10.1210/me.2002-0366 [DOI] [PubMed] [Google Scholar]
- Hozé C., Fouilloux M.-N., Venot E., Guillaume F., Dassonneville R. et al. , 2013. High-density marker imputation accuracy in sixteen French cattle breeds. Genet. Sel. Evol. 45: 33 10.1186/1297-9686-45-33 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiménez-Montero, J. A., O. González-Recio, and R. Alenda, 2012 Genotyping strategies for genomic selection in small dairy cattle populations. Animal 6: 1216–1224. 10.1017/S1751731112000341 [DOI] [PubMed]
- Joshi R., Árnyasi M., Lien S., Gjøen H. M., Alvarez A. T. et al. , 2018. Development and Validation of 58K SNP-Array and High-Density Linkage Map in Nile Tilapia (O. niloticus). Front. Genet. 9: 472 10.3389/fgene.2018.00472 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khaw H. L., Ponzoni R. W., and Danting M. J. C., 2008. Estimation of genetic change in the GIFT strain of Nile tilapia (Oreochromis niloticus) by comparing contemporary progeny produced by males born in 1991 or in 2003. Aquaculture 275: 64–69. 10.1016/j.aquaculture.2008.01.022 [DOI] [Google Scholar]
- Kijas J., Elliot N., Kube P., Evans B., Botwright N. et al. , 2016. Diversity and linkage disequilibrium in farmed Tasmanian Atlantic salmon. Anim. Genet. 48: 237–241. 10.1111/age.12513 [DOI] [PubMed] [Google Scholar]
- Larmer S. G., Sargolzaei M., and Schenkel F. S., 2014. Extent of linkage disequilibrium, consistency of gametic phase, and imputation accuracy within and across Canadian dairy breeds. J. Dairy Sci. 97: 3128–3141. 10.3168/jds.2013-6826 [DOI] [PubMed] [Google Scholar]
- Lourenco D. A. L., Misztal I., Tsuruta S., Aguilar I., Ezra E. et al. , 2014. Methods for genomic evaluation of a relatively small genotyped dairy population and effect of genotyped cow information in multiparity analyses. J. Dairy Sci. 97: 1742–1752. 10.3168/jds.2013-6916 [DOI] [PubMed] [Google Scholar]
- Meuwissen T. H. E., Hayes B. J., and Goddard M. E., 2001. Prediction of Total Genetic Value Using Genome-Wide Dense Marker Maps. Genetics 157: 1819–1829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meuwissen, T. H. E., R. Vallejo, and U. States, 2014 Genomic prediction in an admixed population of Atlantic salmon (Salmo salar). 5: 1–8. [DOI] [PMC free article] [PubMed]
- Misztal I., Legarra A., and Aguilar I., 2009. Computing procedures for genetic evaluation including phenotypic, full pedigree, and genomic information. J. Dairy Sci. 92: 4648–4655. 10.3168/jds.2009-2064 [DOI] [PubMed] [Google Scholar]
- Misztal I., Tsuruta S., Lourenco D., Masuda Y., Aguilar I. et al. , 2016. Manual for BLUPF90 family of programs.
- Mou Z., Fan W., and Dong X., 2003. Inducers of Plant Systemic Acquired Resistance Regulate NPR1 Function through Redox Changes. Cell 113: 935–944. 10.1016/S0092-8674(03)00429-X [DOI] [PubMed] [Google Scholar]
- Nguyen N. H., Ponzoni R. W., Abu-Bakar K. R., Hamzah A., Khaw H. L. et al. , 2010. Correlated response in fillet weight and yield to selection for increased harvest weight in genetically improved farmed tilapia (GIFT strain), Oreochromis niloticus. Aquaculture 305: 1–5. 10.1016/j.aquaculture.2010.04.007 [DOI] [Google Scholar]
- Norton W. H. J., Ledin J., Grandel H., and Neumann C. J., 2005. HSPG synthesis by zebrafish Ext2 and Extl3 is required for Fgf10 signalling during limb development. Development 132: 4963–4973. 10.1242/dev.02084 [DOI] [PubMed] [Google Scholar]
- Ødegård J., and Meuwissen T. H., 2014. Identity-by-descent genomic selection using selective and sparse genotyping. Genet. Sel. Evol. 46: 3 10.1186/1297-9686-46-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ødegård J., Moen T., Santi N., Korsvoll S. A., Kjøglum S. et al. , 2014. Genomic prediction in an admixed population of Atlantic salmon (Salmo salar). Front. Genet. 5: 1–8. 10.3389/fgene.2014.00402 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palaiokostas C., Kocour M., Prchal M., and Houston R. D., 2018. Accuracy of Genomic Evaluations of Juvenile Growth Rate in Common Carp (Cyprinus carpio) Using Genotyping by Sequencing. Front. Genet. 9: 82 10.3389/fgene.2018.00082 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ponzoni R. W., Nguyen N. H., and Khaw H. L., 2007. Investment appraisal of genetic improvement programs in Nile tilapia (Oreochromis niloticus). Aquaculture 269: 187–199. 10.1016/j.aquaculture.2007.04.054 [DOI] [Google Scholar]
- Ponzoni R. W., Nguyen N. H., Khaw H. L., Hamzah A., Bakar K. R. A. et al. , 2011. Genetic improvement of Nile tilapia (Oreochromis niloticus) with special reference to the work conducted by the WorldFish Center with the GIFT strain. Rev. Aquacult. 3: 27–41. 10.1111/j.1753-5131.2010.01041.x [DOI] [Google Scholar]
- Purcell S., Neale B., Todd-Brown K., Thomas L., Ferreira M. A. R. et al. , 2007. PLINK: A Tool Set for Whole-Genome Association and Population-Based Linkage Analyses. Am. J. Hum. Genet. 81: 559–575. 10.1086/519795 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rebhan Y., and Funkenstein B., 2008. Inhibition of fish myostatin activity by recombinant fish follistatin and myostatin prodomain: Potential implications for enhancing muscle growth in farmed fish. Aquaculture 284: 231–238. 10.1016/j.aquaculture.2008.07.007 [DOI] [Google Scholar]
- Reis Neto R. V., Yoshida G. M., Lhorente J. P., and Yáñez J. M., 2019. Genome-wide association analysis for body weight identifies candidate genes related to development and metabolism in rainbow trout (Oncorhynchus mykiss). Mol. Genet. Genomics 294: 563–571. 10.1007/s00438-018-1518-2 [DOI] [PubMed] [Google Scholar]
- Rutten M. J. M., Bovenhuis H., and Komen H., 2005. Genetic parameters for fillet traits and body measurements in Nile tilapia (Oreochromis niloticus L.). Aquaculture 246: 125–132. 10.1016/j.aquaculture.2005.01.006 [DOI] [Google Scholar]
- Sargolzaei M., Chesnais J. P., and Schenkel F. S., 2014. A new approach for efficient genotype imputation using information from relatives. BMC Genomics 15: 478 10.1186/1471-2164-15-478 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sargolzaei, M., J. P. Chesnais, and F. S. Schenkel, 2009 Accuracy of a family-based genotype imputation algorithm. GEB Open Ind. Sess. 1–4.
- Sen Ś., Johannes F., and Broman K. W., 2009. Selective Genotyping and Phenotyping Strategies in a Complex Trait Context. Genetics 181: 1613–1626. 10.1534/genetics.108.094607 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sonesson A. K., Meuwissen T. H., Figueroa R., Lhorente J. P., Yáñez J. M. et al. , 2009. Testing strategies for genomic selection in aquaculture breeding programs. Genet. Sel. Evol. 41: 37 10.1186/1297-9686-41-37 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tortereau F., Servin B., Frantz L., Megens H.-J., Milan D. et al. , 2012. A high density recombination map of the pig reveals a correlation between sex-specific recombination and GC content. BMC Genomics 13: 586 10.1186/1471-2164-13-586 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsai H.-Y., Hamilton A., Tinch A. E., Guy D. R., Bron J. E. et al. , 2016. Genomic prediction of host resistance to sea lice in farmed Atlantic salmon populations. Genet. Sel. Evol. 48: 47 10.1186/s12711-016-0226-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsai H. Y., Hamilton A., Tinch A. E., Guy D. R., Gharbi K. et al. , 2015. Genome wide association and genomic prediction for growth traits in juvenile farmed Atlantic salmon using a high density SNP array. BMC Genomics 16: 969 10.1186/s12864-015-2117-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsai H.-Y., Matika O., Edwards S. M., Antolín–Sánchez R., Hamilton A. et al. , 2017. Genotype Imputation To Improve the Cost-Efficiency of Genomic Selection in Farmed Atlantic Salmon. G3 Genes, Genomes. Genet. 7: 1377–1383. 10.1534/g3.117.040717 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vallejo R. L., Leeds T. D., Gao G., Parsons J. E., Martin K. E. et al. , 2017. Genomic selection models double the accuracy of predicted breeding values for bacterial cold water disease resistance compared to a traditional pedigree-based model in rainbow trout aquaculture. Genet. Sel. Evol. 49: 17 10.1186/s12711-017-0293-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vallejo R. L., Silva R. M. O., Evenhuis J. P., Gao G., Sixin L. et al. , 2018. Accurate genomic predictions for BCWD resistance in rainbow trout are achieved using low-density SNP panels : evidence that long-range LD is a major contributing factor. J. Anim. Breed. Genet. 135: 263–274. 10.1111/jbg.12335 [DOI] [PubMed] [Google Scholar]
- Vanacker H., Lu H., Rate D. N., and Greenberg J. T., 2001. A role for salicylic acid and NPR1 in regulating cell growth in Arabidopsis. Plant J. 28: 209–216. 10.1046/j.1365-313X.2001.01158.x [DOI] [PubMed] [Google Scholar]
- VanRaden P. M., O’Connell J. R., Wiggans G. R., and Weigel K. A., 2011. Genomic evaluations with many more genotypes. Genet. Sel. Evol. 43: 10 10.1186/1297-9686-43-10 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Q., Hao R., Zhao X., Huang R., Zheng Z. et al. , 2018. Identification of EGFR in pearl oyster (Pinctada fucata martensii) and correlation analysis of its expression and growth traits. Biosci. Biotechnol. Biochem. 82: 1073–1080. 10.1080/09168451.2018.1459174 [DOI] [PubMed] [Google Scholar]
- Wang H., Misztal I., Aguilar I., Legarra A., Fernando R. L. et al. , 2014. Genome-wide association mapping including phenotypes from relatives without genotypes in a single-step (ssGWAS) for 6-week body weight in broiler chickens. Front. Genet. 5: 1–10. 10.3389/fgene.2014.00134 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang H., Misztal I., Aguilar I., Legarra A., and Muir W. M., 2012. Genome-wide association mapping including phenotypes from relatives without genotypes. Genet. Res. 94: 73–83. 10.1017/S0016672312000274 [DOI] [PubMed] [Google Scholar]
- Yáñez J. M., Houston R. D., and Newman S., 2014. Genetics and genomics of disease resistance in salmonid species. Front. Genet. 5: 1–13. 10.3389/fgene.2014.00415 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yañez J. M., and Martinez V., 2010. Genetic factors involved in resistance to infectious diseases in salmonids and their application in breeding programmes. Arch. Med. Vet. 42: 1–13. [Google Scholar]
- Yáñez J. M., Yoshida G., Barria A., Palma-Véjares R., Travisany D. et al. , 2019. High-throughput single nucleotide polymorphism (SNP) discovery and validation through whole-genome resequencing of hundreds of individuals in Nile tilapia (Oreochromis niloticus). bioRxiv. 1–24. [DOI] [PubMed] [Google Scholar]
- Yoshida G. M., Bangera R., Carvalheiro R., Correa K., Figueroa R. et al. , 2018a Genomic prediction accuracy for resistance against Piscirickettsia salmonis in farmed rainbow trout. G3 Genes, Genomes. Genet. 8: 719–726. 10.1534/g3.117.300499 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yoshida G., Barria A., Caceres G., Correa K., Jedlicki A. et al. , 2019a Genome-wide patterns of population structure and linkage disequilibrium in farmed Nile tilapia (Oreochromis niloticus). bioRxiv. 1–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yoshida G. M., Carvalheiro R., Lhorente J. P., Correa K., Figueroa R. et al. , 2018b Accuracy of genotype imputation and genomic predictions in a two-generation farmed Atlantic salmon population using high-density and low-density SNP panels. Aquaculture 491: 147–154. 10.1016/j.aquaculture.2018.03.004 [DOI] [Google Scholar]
- Yoshida G. M., Carvalheiro R., Rodríguez F. H., Lhorente J. P., and Yáñez J. M., 2019b Single-step genomic evaluation improves accuracy of breeding value predictions for resistance to infectious pancreatic necrosis virus in rainbow trout. Genomics 111: 127–132. 10.1016/j.ygeno.2018.01.008 [DOI] [PubMed] [Google Scholar]
- Yoshida G. M., Lhorente J. P., Carvalheiro R., and Yáñez J. M., 2017. Bayesian genome-wide association analysis for body weight in farmed Atlantic salmon (Salmo salar L.). Anim. Genet. 48: 698–703. 10.1111/age.12621 [DOI] [PubMed] [Google Scholar]
- Zhang Z., and Druet T., 2010. Marker imputation with low-density marker panels in Dutch Holstein cattle. J. Dairy Sci. 93: 5487–5494. 10.3168/jds.2010-3501 [DOI] [PubMed] [Google Scholar]
- Zhang X., Lourenco D., Aguilar I., Legarra A., and Misztal I., 2016. Weighting Strategies for Single-Step Genomic BLUP: An Iterative Approach for Accurate Calculation of GEBV and GWAS. Front. Genet. 7: 151 10.3389/fgene.2016.00151 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
All raw phenotypic and genotypic data used in the current study can be found at Figshare public repository (https://figshare.com/s/9b265a22b7e138c5a839). Furthermore, Supplementary Figures (Figure S1-S4) and Supplementary Tables (Table S1-S3) are available at Figshare: https://figshare.com/s/9b265a22b7e138c5a839.