Parameters controlling the strength of stochastic fibrous materials

Abstract

Many materials of everyday use are fibrous and their strength is important in most applications. In this work we study the dependence of the strength of random fiber networks on structural parameters such as the network density, cross-link density, fiber tortuosity, and the strength of the inter-fiber cross-links. Athermal networks of cellular and fibrous type are considered. We conclude that the network strength scales linearly with the cross-link number density and with the cross-link strength for a broad range of network parameters, and for both types of networks considered. Network strength is independent of fiber material properties and of fiber tortuosity. This information can be used to design fiber networks for specified strength and, generally, to understand the mechanical behavior of fibrous materials.

1. Introduction

Many biological and engineering materials are fibrous. Biological connective tissue, the extracellular matrix, the cellular cytoskeleton, fiber composites, non-wovens, paper and various textiles are just few examples from a broad range of materials in which fibers are the key structural element. Biological fibrous materials are fiber networks embedded in a viscoelastic fluid and their mechanical performance is controlled by the network behavior subjected to the condition of incompressibility mandated by the embedding matrix (no-drainage case). Some engineering fibrous materials do not have an embedding matrix. These can be random, as in non-wovens, or periodic, as in woven textiles. While all these types of fibrous materials are of high practical importance, we restrict the discussion here to random networks without embedding matrix.

From a design point of view, it is important to establish the relationship between structure and macroscopic material behavior. The best understood such relation refers to the network stiffness. The stiffness of random networks depends on network architecture (Head et al., 2003a; Huisman et al., 2007; Islam and Picu, 2018), network density, ρ (Head et al., 2003b; Shahsavari and Picu, 2013a; Wilhelm and Frey, 2003), density of cross-links, ρ_b (Alava et al., 2006; Shahsavari and Picu, 2013b), fiber and cross-link properties (Ban et al., 2016a; Borodulina et al., 2016; Deogekar and Picu, 2017). Specifically, random networks with no embedding matrix exhibit two types of mechanical behavior: at high ρ, ρ_b and/or when the fiber bending mode is stiff, the deformation is approximately affine. In this limit it is generally observed that the stiffness (Young’s and shear moduli) is proportional to the network density (Alava and Niskanen, 2006; Head et al., 2003b). Networks of low ρ and ρ_b, and/or networks constructed from thin fibers which are soft in bending, deform non-affinely. In this case the network modulus scales as a power function of the density, with the exponent depending on the network architecture and embedding space dimensionality (Gibson and Ashby, 1999; Kroy and Frey, 1996; Licup et al., 2016; Shahsavari and Picu, 2013b).

The mechanical response of random networks is generally strongly non-linear in all loading modes (tension, compression, shear) (Islam and Picu, 2018; Onck et al., 2005; Picu et al., 2018; Stein et al., 2011). The non-linearity is primarily geometric and is associated with the reorientation of fibers during loading. In dense networks such as paper - the non-linearity may also originate from the fiber and cross-link behavior (Borodulina et al., 2012; Seth and Page, 1981). The evolution of the network structure during deformation leads to the large variation of the material volume (Bancelin et al., 2015; Mauri et al., 2015; Pieu et al., 2018), which is possible due to the large free volume typically present in non-molecular network materials in the undeformed state. The constitutive behavior of fibers may be linear or non-linear, but this aspect is of secondary importance in most networks which are not of very large density, since in such structures the global strains are typically much larger than the fiber-level strains (Eppell et al., 2006; Svensson et al., 2010) and hence, in these cases, the effect of fiber constitutive non-linearity on the overall material behavior is weak. In cases in which the cross-links are compliant, their constitutive behavior may reflect in the network behavior (Fallqvist et al., 2014; Kasza et al., 2010). It is generally observed that networks strain stiffen at large deformations. Biological tissue strain stiffens exponentially (Bancelin et al., 2015; Lake and Barocas, 2011; Mauri et al., 2015), but in other networks the functional form of the Cauchy stress-stretch relation can be either exponential or power, depending on the network architecture (Islam and Picu, 2018).

Failure of random networks is either brittle, i.e. occurs by the propagation of a major crack, or gradual, emerging from the accumulation of diffuse damage which eventually localizes into a rupture band. High density networks tend to behave more brittle than low ρ and/or low ρ_b networks. The process is intrinsically complex since random networks are, by definition, highly heterogeneous structures that may deform to large strains before the onset of damage. In addition, damage accumulation is a loading path-dependent process, which renders the analysis of the strength and failure mode of such structures quite complex. Nevertheless, progress along the lines of identifying the structural features that control the strength has been made. Both experimental (Alava and Niskanen, 2006; Chen et al., 2016) and modeling (Heyden and Gustafsson, 1998) works indicate that strength, σ_c, scales linearly with the network density. The exact dependence of strength on ρ and ρ_b has not been established to date, but it is observed in cellulose networks (paper) that an increase of the number of inter-fiber contacts per fiber, due to the increase of fiber flexibility (Askling et al., 1998; Clark, 1985; Forsstrom et al., 2005) or due to treatment with polyamines (Marais et al., 2014), leads to increased strength. A linear scaling of the tensile strength with the number of inter-fiber cross-links was also observed in biological tissues (Akins et al., 2011). Models in both 2D and 3D support the increase of σ_c with ρ (Heyden, 2000). In (Deogekar and Picu, 2018) it is shown that this relation holds both when peak stress is reached at small strains, i.e. when the network preserves its initial geometry up to the peak load, and when peak stress is reached at large strains, after substantial fiber re-orientation.

Structural heterogeneity has a strong effect on the failure mode of materials. This issue was studied in detail in the context of stochastic composites in which it is known that material stochasticity promotes intermittency and diffuse damage formation during failure, which contributes to increased toughness (Bonamy, 2009; Hägglund and Isaksson, 2006; Herrmann et al., 1989). Crack pinning and crack deflection are also discussed as toughening mechanisms in the context of the propagation of a major crack through a heterogeneous body (Daguier et al., 1997; Faber and Evans, 1983; Rosti et al., 2001; Roux et al., 2003). Networks being examples of materials with stochastic microstructure, inherit all these characteristics. It was shown that non-wovens exhibit notch insensitivity, i.e. the failure stress of a panel with two opposing notches (or with a central crack) is independent of the distance between the crack tips (or the distance between -crack tips and the boundary of the sample) (Ridruejo et al., 2015; Stachewicz et al., 2011). This is due to the strong fiber alignment that takes place in front of the crack, leading to crack blunting and to the elimination of the stress concentration. In the absence of a pre-existing major crack, networks develop either localized or diffuse damage. As discussed in (Deogekar and Picu, 2018), affinely-deforming networks of high fiber and cross-link density exhibit brittle failure dominated by localized damage (as seen, in general, in paper (Hägglund and Isaksson, 2006)), while non-affinely-deforming networks, which therefore exhibit more heterogeneous mechanical fields, fail by a more gradual damage accumulation process. Both types of behavior are observed experimentally (Chen et al., 2016; Isaksson et al., 2012).

Network failure usually takes place by the failure of cross-links, while failure of fibers happens in exceptional situations (Chen et al., 2016; Chen and Silberstein, 2018; Farukh et al., 2014; Ridruejo et al., 2011). It is established that increasing the cross-link strength leads to a proportional increase of the network strength. This conclusion is supported by experimental (Forsstrom et al., 2005; Marais et al., 2014) and modeling (Deogekar and Picu, 2018; Heyden, 2000) results. In many practical situations, the strength of cross-links formed between individual fibers is a stochastic variable. In this case one may wonder whether the strength depends exclusively on the mean of the cross-link strength distribution, or also on its variance. Numerical studies (Deogekar and Picu, 2018; Malakhovsky and Michels, 2007) established that increasing the variance of the distribution, while maintaining the mean constant, leads to a gradual reduction of the network strength. This points to the importance of gaining control on the process of cross-link formation such to minimize the cross-link strength variability.

In this work we extend our previous study reported in (Deogekar and Picu, 2018) by analyzing the importance of controllable structural parameters in defining the network strength. First, we intend to clarify the relative importance of network density, ρ, and of cross-link density, ρ_b. It was observed in (Shahsavari and Picu, 2013b) that both parameters define the/small strain stiffness of random networks. The experimental results available in the literature do not seem to clearly delineate the relative importance of these two parameters in defining the strength. Second, we investigate the effect of fiber tortuosity on strength. This is an important structural parameter since most biological and engineering networks are made from fibers which are not perfectly straight. It is known that increasing tortuosity reduces the stiffness of the network (Ban et al., 2016b). Studies that isolate the effect of this parameter on strength do not seem to be available. Further, we investigate the extent to which fiber properties influence the strength of the network. It is known that network stiffness, E, is proportional either to the fiber axial rigidity, E_fA (where E_f is the fiber material Young’s modulus and A is the fiber cross-sectional area), or to the bending rigidity, E_fI (where I is the fiber cross-section moment of inertia). Specifically, E~E_fA if network deformation is affine and the axial deformation mode of fibers prevails, and E~E_fI when fibers deform primarily in their bending mode and the overall network deformation is non-affine. We reconsider previous reports that σ_c~EfA and show that this result pertains to a particular case, while in general, the strength is independent of fiber material properties.

2. Model and simulation set-up

We address the questions stated above using numerical models of fibrous networks similar to those used in previous studies (Deogekar and Picu, 2018; Islam and Picu, 2018). In order to account for the influence of network architecture, we consider two types of networks: cellular and fibrous. The cellular structures are of Voronoi type, while the fibrous networks are the 3D equivalent of the 2D Mikado networks (Islam and Picu, 2018; Shahsavari and Picu, 2013b). Voronoi networks represent open cell foams, while most biological (collagen, fibrin) and some man-made networks (non-wovens, paper, fiberglass insulation) are of fibrous type. By considering both types of structures in the present study we extend the validity of the present results to a broad range of network materials of high practical interest. In the following we present the details of the network structure and generation procedure, cross-link definition and simulation parameters.

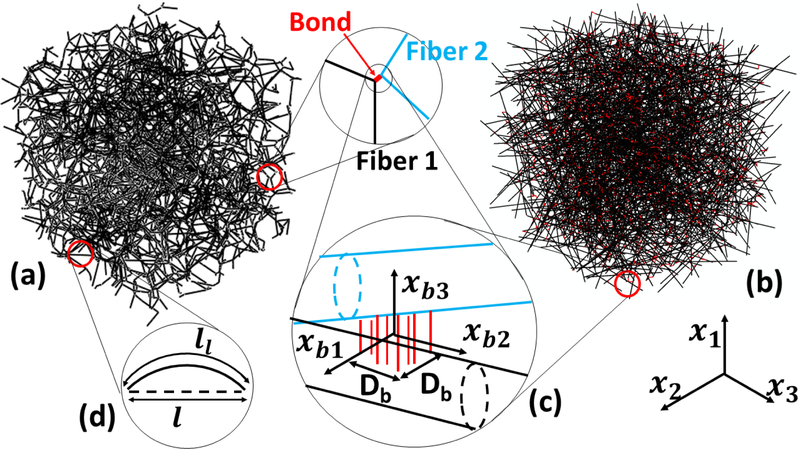
Cellular networks (Fig. 1a) are generated using a Voronoi tessellation of the 3D problem domain (a cube of edge length L). Random seeds are used to generate a Voronoi tessellation and the network results by placing fibers along all edges of the resulting polyhedra. Each fiber has two cross-links at the two ends. The network density is controlled by the number of seed points. As in (Deogekar and Picu, 2018), the Voronoi network is decomposed into paths that traverse the problem domain. These paths are connected to each other randomly at network cross-links. The paths are divided in segments of nominal length L₀. To this end, each path is traversed and cuts are introduced such to produce segments of length as close as possible to the imposed L₀. The resulting segments are denoted as ‘fibers’ and the fiber span between two successive cross-links is a ‘fiber segment’.

Figure 1:

Realization of a (a) 3D cellular network and (b) 3D fibrous network. In both these networks, an inter-fiber cross-link is composed from a number of fibrils uniformly distributed over the contact area of size D_b × D_b, as shown in (c). The global coordinate system is x₁, x₂ and x₃, while the cross-link deformation is measured in a local coordinate system associated with the cross-link, x_b1, x_b2 and x_b3. Fiber tortuosity is introduced in cellular networks as shown in (d), where straight fiber segments are modified to half-sine curves. The segment contour length, l_l and its end-to-end length, l, are shown in (d).

Fibrous networks (Fig. 1b) are generated using the method described in (Islam and Picu, 2018). The random sequential adsorption (RSA) technique is used to generate sparse assemblies of fibers, each of length L₀. Further, dynamic finite element simulations are performed to reduce the volume of the simulation cell and bring the fibers within crosslink-able distance. Surface-based contact constraints between fiber-to-fiber surfaces are introduced in these compaction simulations in order to avoid inter-penetration. The compacted fiber assembly is then transformed into a network structure by introducing inter-fiber cross-links at all sites where the inter-fiber distance is smaller than twice the fiber diameter. These cross-links divide the fibers into segments. The segment length is Poisson distributed. After the cross-linking process, isolated fibers may remain unconnected to the main network. These, as well as the dangling ends of fibers, are removed. In both cellular and fibrous cases, the fibers are distributed in space with random orientation and positions of their centers of mass.

In order to test the effect of fiber stiffness on network strength, we consider in separate models cylindrical fibers of identical diameter, D, and fibers with generalized cross-section for which the axial and bending stiffnesses can be varied independently (are not related to the fiber diameter). The generalized cross-section cases represent networks of filaments which cannot be modeled as continuum beams, e.g. molecular filaments such as tropocollagen. The excluded volume interactions between fibers, i.e. the formation of contacts at sites other than the cross-links, are not considered in these models. In the fibrous case, the fiber length, L₀, is sufficiently smaller than the model size (L₀ = 0.25L) to avoid strong size effects.

The important network parameters are: (i) the network density, ρ, defined as the total length of fiber per unit network volume. This parameter is related to the volume fraction occupied by the network, ϕ, as ϕ = Aρ. (ii) The cross-link number density, ρ_b, defined as the number of crosslinks per unit network volume, (iii) The connectivity number, z. This represents the number of fiber segments emerging from each cross-link. Voronoi and fibrous networks have nominally z = 4. The trimming of dangling ends leads to an average z slightly smaller than 4. (iv) The fiber material is considered linear elastic of Young’s modulus E_f. This parameter is considered here the unit of stress, (v) The fiber diameter, D, is also an important parameter in models in which fibers are considered cylindrical beams.

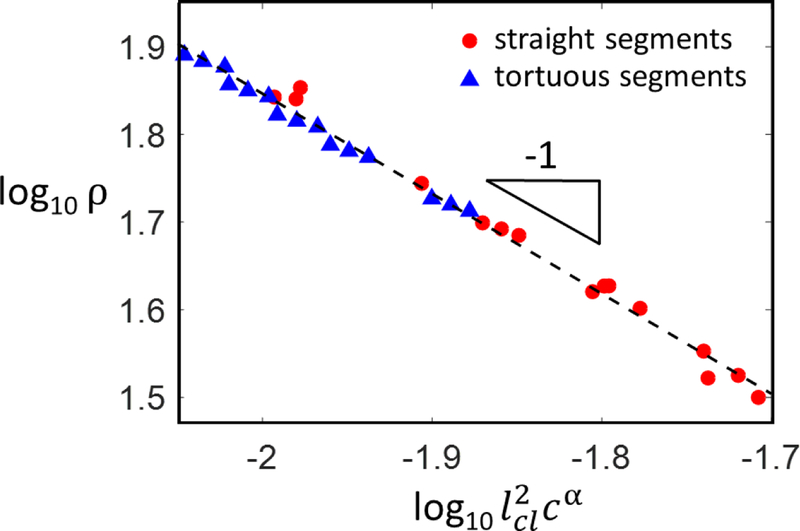
If all fiber segments are straight, the mean segment length, l_c, is related to the network density, ρ, as $\rho l_c^2=q$, with q being a proportionality constant. Figure 2 shows the variation of ρ with l_c for cellular networks with straight fiber segments.

Figure 2:

Variation of network density, ρ, with the mean contour length of fiber segments, l_cl and fiber tortuosity, c. The red circles represent networks with no tortuosity, case in which l_cl ≡ l_c and α = 1. The blue triangles represent cases in which 45% of the fiber segments are tortuous with various values of the tortuosity parameter, c. The exponent leading to data collapse in this particular case is α = 2.3. This value is derived in Appendix A.

In models in which fiber tortuosity is considered, parameter c = l/l_l, i.e, the ratio of the end-to-end length to the contour length of the fiber segment (Fig. 1d), is used to quantify the tortuosity. In these cases, we denote by l_c the mean end-to-end length of a fiber segment, and by l_cl the mean contour length of a segment. If all fibers have the same tortuosity, l_c = cl_cl and ρ(c) = ρ(l)/c, where ρ(1) is the density computed based on the end-to-end lengths, i.e. with c = 1. It results that the relation between the density in networks with tortuous fibers, ρ(c), and l_cl, is

$$\rho (c)l_{cl}^2=q/c^3.$$ (1)

In some networks, not all fiber segments are tortuous since short segments tend to remain straight. The relation between network density and l_cl for such situations is derived in Appendix A and can be approximated by an equation similar to eq. (1):

$$\rho (c)l_{cl}^2\approx q/c^{\alpha }$$ (2)

where α depends on the fraction of fibers that remain straight. When this fraction vanishes, α = 3, while α < 3 in all other cases. We include in Fig. 2 data for cellular networks with 45% of fiber segments being tortuous. The data collapse on the line of slope −1 provided parameter α used ire the group on the horizontal axis is taken 1 for the red circles representing networks with no tortuosity (in this case l_cl = l_c), and 2.3 for the blue triangles which represent networks with a fraction (45%) of tortuous fiber segments. The value α = 2.3 valid for this set of parameters is derived in Appendix A.

The inter-fiber cross-links are represented as connectors that transmit both forces and moments, therefore providing unconditional stability to the network. Physically, one may consider the situation in Fig. 1(c), where a cross-link is composed from fibrils that fail in tension at a prescribed force, while the contact between fibers resists compression. This imparts resistance to separation, shear add rolling of one fiber relative to the other. The fibrils are not represented explicitly in the model, rather their net effect is accounted for using a connector element with specified stiffness and strength. The axial and bending stiffness of the connector are taken to be approximately two orders of magnitude larger than the axial and bending stiffness of a fiber segment of length equal to the mean segment length, l_c. It was determined that this ensures that the maximum cross-link deformation remains below 6 × 10⁻³D such that cross-link deformation does not contribute to the overall network kinematics.

The cross-link failure criterion is identical to that used in (Deogekar and Picu, 2018). To summarize, the force and moments associated with the deformation of the cross-link are defined in the coordinate system of the cross-link, {x_b1,x_b2,x_b3}, shown in Fig. 1(c), as F_bi = K_bFu_bi and M_bi = K_bMθ_bi, where, u_bi and θ_bi are the i^th components of the relative displacement and relative rotation of the two fibers in contact, respectively, and K_bF and K_bM are the effective cross-link stiffnesses in the opening and peeling modes. The cross-link failure criterion has the form:

$$F_{eq}=\sqrt{F_{b1}^2+F_{b2}^2+{\langle F_{b3}-\frac{6}{D_b}\sqrt{M_{b1}^2+M_{b2}^2}\rangle }^2}=f_c$$ (3)

Here, F_b1, F_b2, F_b3 are the forces transmitted by the cross-link in the direction of the three local coordinate axes (Fig. 1c), and M_b1 and M_b2 are the moments transmitted about the local axes x_b1 and x_b2. D_b represents the characteristic size of the cross-link (D_b < D). < > indicates Macaulay bracket, which vanishes if the quantity in the bracket is negative and is equal to the respective quantity when it is positive. f_c represents the critical equivalent force which causes cross-link failure and is considered a material parameter. The term within the Macaulay bracket accounts for the combined effect of relative fiber rolling and separation in the direction of the cross-link normal, while the first two terms under the square root represent the contribution of relative shear.

Using a force-based failure criterion for the cross-links is justified in part by the observation that, in general, random networks deform in the lowest energy mode available to the fibers. Specifically, as discussed at the end of section 1, if the bending mode of fibers is soft (large l_c and/or small E_fI/E_fA), the overall constitutive behavior of the network bears the signature of bending, while in the opposite situation, it reflects the axial deformation of fibers. Likewise, if cross-links undergo large deformations without rupture, their constitutive behavior reflects in the response of the network. Hence, the structure behaves as if the bending, axial and cross-link deformation modes are connected in series, with the softer mode dominating the overall network behavior; considering such serial effective arrangement, using a failure criterion based on equivalent force seems natural. The effectiveness of a force-based failure criterion was also emphasized in (Chen and Silberstein, 2018), where cohesive zone elements were used to represent cross-links. An energy-based criterion is suggested as being appropriate for cases in which the cross-link compliance is large in (Borodulina et al., 2012).

The models are discretized using multiple Timoshenko beam elements per fiber segment (Shahsavari and Picu, 2012). A sensitivity analysis to the level of discretization was performed to ensure mesh-insensitive results while retaining computational efficiency. Models are loaded in uniaxial tension by applying displacements on two opposing faces of the cubic model in the direction of loading. The lateral faces of the model are kept planar but are free to move in the direction perpendicular to the loading axis such to insure zero average tractions in the respective directions.

Cross-links are modeled in Abaqus using the connector element CONN3D2 and the connector section BUSHING. This allows independent control of the translational and rotational cross-link stiffnesses. To model cross-link failure, a connector potential equal to F_eq (in eqn. 3) is defined, and the cross-link is ruptured when the connector potential reaches a user-defined critical value (i.e. when F_eq = F_c). The cross-link translational and rotational stiffnesses remain constant prior to the cross-link rupture.

The solution is obtained with the 6.13–1 version of the finite element solver Abaqus/Explicit. Inertial effects occur due to the dynamic scheme used. We use a numerical damping scheme (bulk viscosity) to minimize the contribution of inertial forces. The kinetic energy of the model is kept lower than 1% of the total energy prior to the onset of cross-link failure, and lower than 5% of the total energy up to a strain larger than that corresponding to the peak stress. The algorithmic damping is adjusted to ensure that this condition is fulfilled in each simulation. In the stress-strain curves reported here, the regime in which this condition is fulfilled is represented with continuous line, while dashed line is used for larger strains. To further limit the effect of the kinetic component on the reported results, we compute the second Piola-Kirchoff stress by taking the derivative of the strain energy density relative to the Green-Lagrange strain, and then compute the Cauchy stress, which is used in all calculations reported here. The justification for this procedure can be found in Appendix A of (Deogekar and Picu, 2018).

3. Results

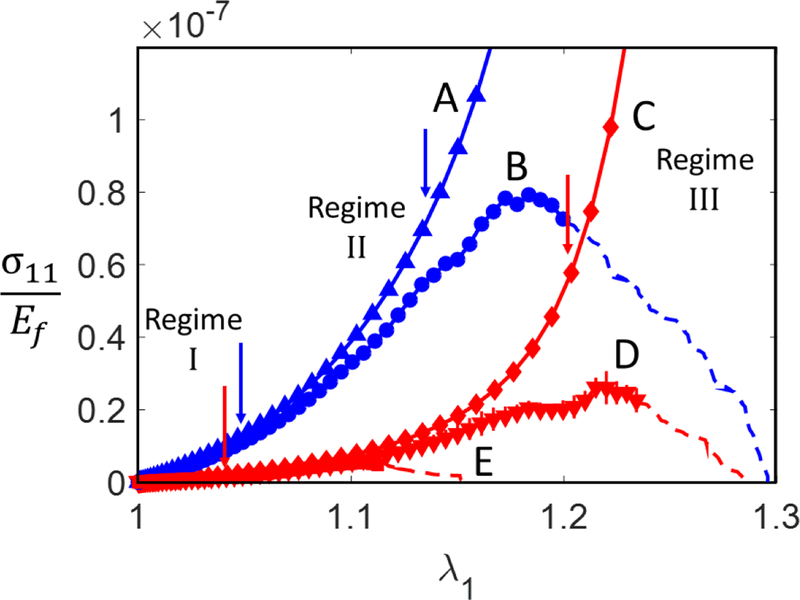
To demonstrate the general tensile behavior of networks in presence of cross-link failure, Fig. 3 shows three Cauchy stress vs. stretch curves for several cellular networks. Two of the curves correspond to models of same cross-link strength, but different values ofρD², while two other curves correspond to the same ρD² and different cross-link strengths. Both the small strain modulus and the peak stress decrease with decreasing ρD², while the stretch at peak stress increases as the network becomes more compliant. Curves A and C represent the stress-stretch curves of the same networks without failure (infinite cross-link strength). Note that the curves with and without failure overlap up to close to the peak stress. This is due to the fact that a relatively small number of cross-links fail before peak stress. Both models (Abhilash et al., 2012; Borodulina et al., 2016) and experiments (Chen et al., 2016) agree in predicting that a small fraction of the cross-links fail before peak stress. In exceptional situations, when additional heterogeneity is introduced, for example, by rendering the cross-link strength stochastic, the fraction may increase (Borodulina et al., 2016; Deogekar and Picu, 2018). When the cross-link strength is reduced, the stress-stretch curve follows the virgin material curve and develops a peak at a lower value of stress.

Figure 3.

Cauchy stress vs. stretch ratio for networks with ρD² = 1.12 × 10⁻³ (curves A and B) and ρD² = 5.28 × 10⁻⁴ (curves C, D and E) with and without failure. Curves A and C represent network behavior in absence of failure, curves B, D and E depict network behavior with failure. The cross-link strength corresponding to case D is 6 times larger than that corresponding to case E. The bars represent standard deviation over 3 realizations. The arrows indicate the transition between the three regimes of deformation discussed in the text. The continuous curves and symbols correspond to loading conditions in which the kinetic energy is smaller than 5% of the total energy of the model, while the dashed lirais correspond to the situations when this condition is not fulfilled.

As discussed elsewhere (Broedersz and Mackintosh, 2014; Licup et al., 2015), the characteristic curves exhibit three distinct regimes: a linear elastic regime at small strains (regime I), followed by a stiffening regime (regime II), after which a linear third regime (regime III) develops. The transition between these regimes is indicated with arrows in Fig. 3. Stiffening in regime II is either exponential or power law, function of the network architecture (Islam and Picu, 2018) and is due to the orientation of fibers in the loading direction (geometric non-linearity). Regime III corresponds to the development of load paths across the model, along which most of the load is transmitted. The response is linear since these paths are loaded primarily in tension and hence fibers are loaded axially Modifying the cross-link strength, f_c, one may shift the peak stress from one regime to another. The results discussed here are obtained with a broad range of crosslink strength values and hence are relevant for all regimes.

In the following, we address the questions posed in the Introduction referring to the specific dependence of σ_c on network parameters, and discuss the results in the context of the previous findings reported in the literature.

3.1. Strength is independent of fiber tortuosity

Physical networks generally contain fibers with some degree of tortuosity, c. It is therefore of interest to inquire to what extent this parameter influences σ_c. To address this question, we consider cellular networks and vary the tortuosity in the range 0.6 < c ≤ 1, by allowing fibers to be non-straight in the initial, undeformed and stress free configuration. As the fiber contour length increases, the effective network density, ρ, increases (eq. (2)). In addition, as the free volume of the network decreases, the probability of non-bonded, excluded volume interactions between fibers increases. We neglect here this effect which is expected to be weak as long as the volume fraction of the network ϕ = ρA remains below ~10%. To this end, contacts between fibers are not accounted for. Previous work (Islam and Picu, 2018) indicated that these interactions do not contribute to the stress and stiffness measured in tension for any realistic volume fractions.

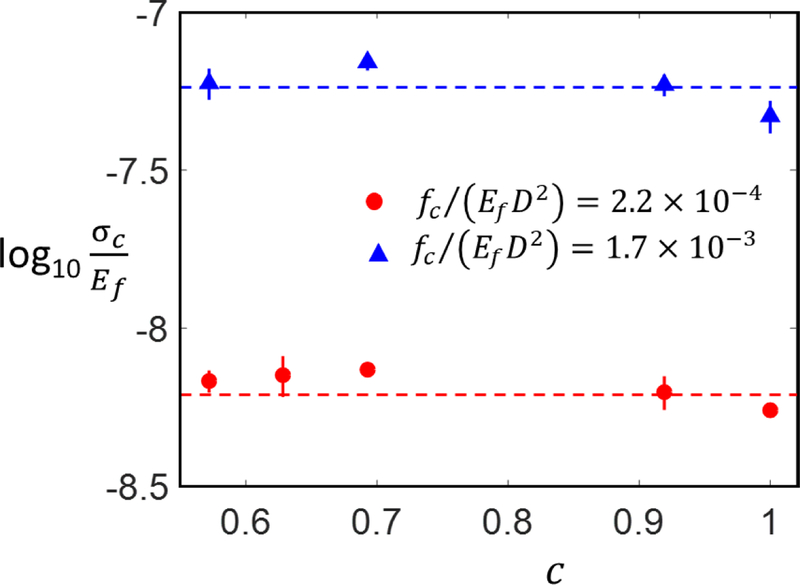
Figure 4 shows the variation of the cellular network strength with parameter c for networks of fixed ϕ and two values of the bond strength. Fibrous networks cannot be used to study the effect of tortuosity since fibrous models with c < 1 loose their geometric characteristics. Two situations are considered: one of low f_c, f_c/(E_fD²) = 4.3 × 10⁻⁴, in which the peak stress is reached in regime I of network deformation, and another of f_c, f_c/(E_fD²) = 1.7 × 10⁻³, for which peak stress is shifted to the strain stiffening regime II. In both cases we observe no dependence of the network strength on fiber tortuosity. Previous numerical studies on networks with transient bonding/debonding properties also indicated that the strength was independent of fiber tortuosity (Kulachenko and Uesaka, 2012). Note that the procedure used here allows varying c without modifying the cross-link number density, ρ_b.

Figure 4:

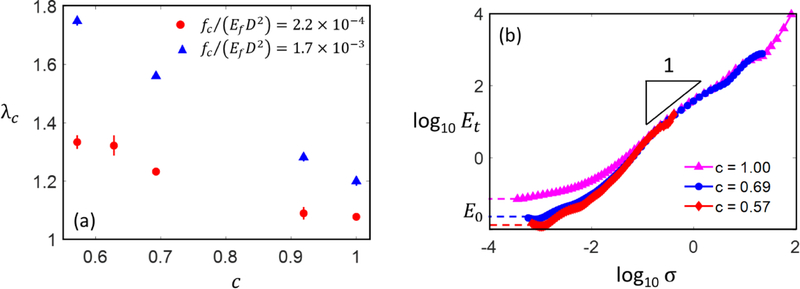
Variation of the normalized network strength, σ_c, with mean fiber tortuosity, c, at different values of cross-link strength and for networks of same ρ_b,,D. The bars represent the standard deviation of 3 realizations and, where not visible, are smaller than the size of the symbol.

Fiber tortuosity increases significantly the stretch at peak stress, λ_c, since such networks are more compliant than the equivalent ones with c = 1. Figure 5a shows the variation of the stretch at peak stress for the networks whose strength is shown in Fig. 4. The rapid increases of λ_c(c) with decreasing c (increasing tortuosity) correlates with the strong sensitivity of E₀ to parameter c. Figure 5b shows the tangent modulus, E_t = ∂σ₁₁/δ(lnλ₁), versus stress curves for several networks considered in Fig. 4, with various values of c, in which cross-link rupture is inhibited. The data shows that increasing c leads to a rapid decrease of the small strain modulus E₀ (the plateau at small σ), while the curves corresponding to the different c values overlap in the strain stiffening regime. This indicates that the functional form of the stress-stretch relation is independent of tortuosity. This effect as well as the variation of E₀ with c are discussed in detail in (Ban et al., 2016b).

Figure 5:

(a) Stretch corresponding to peak stress, λ_c, versus segment tortuosity parameter c, for two different values of cross-link strength, f_c. This increase in λ_c is due to a reduction in the small strain modulus E₀ with increasing fiber tortuosity, as seen in (b). The plateaus at small stress values indicate E₀ for the respective curves.

3.2. Strength scales with the inter-fiber cross-link number density

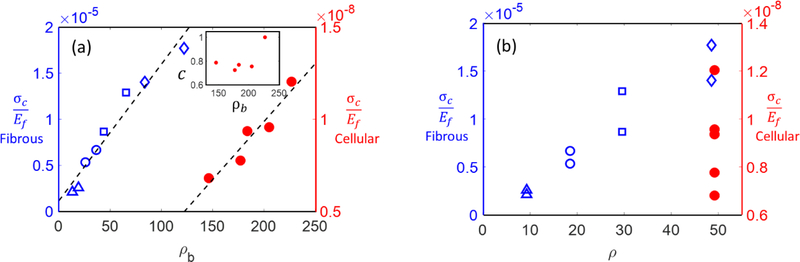
A number of experimental data (Akins et al., 2011; Chen et al., 2016) as well as numerical results (Borodulina et al., 2016; Heyden and Gustafsson, 1998) indicate that a_c scales linearly with network density. However, in most situations, the network density, ρ, and cross-link number density, ρ_b, are proportional. Therefore, it is necessary to clarify the relative importance of ρ and ρ_b in defining σ_c. We address this issue in two ways. First, fibrous networks are considered and ρ_b is varied at constant ρ by gradually removing some of the cross-links along fibers while retaining the cross-links closest to the fiber ends along each fiber of the network. Therefore, removing cross-links does not disconnect the network and does not introduce additional dangling segments, but decreases ρ_b. Second, we consider cellular structures and take advantage of the way fibers are defined on the initial Voronoi network. A fiber of length L₀ contains multiple segments, each of average length l_c and each cross-linked to other fibers at both ends (the nodes of the Voronoi tessellation). Therefore, it is possible to remove (disconnect) some of the cross-links while preserving the overall ρ, the continuity of each fiber and the overall geometry of the structure.

Figure 6a shows the variation of the network strength with ρ_b for cellular and fibrous cases. Fibers remain straight in the fibrous case as ρ_b decreases. In the cellular case, the method used to vary ρ_b at constant ρ introduces fiber tortuosity. The inset to Fig. 6a shows the values of the average tortuosity parameter, c, for all cellular networks considered in the main figure. As expected based on geometric considerations, c reaches a plateau as ρ_b decreases. This has no effect on the strength since, as discussed in section 3.1, introducing tortuosity does not modify the strength.

Figure 6:

(a) Variation of network strength, σ_c, with the cross-link number density, ρ_b, for fibrous (blue, open symbols) and cellular (red, filled circles) networks. For the fibrous networks, symbols of same type indicate networks of same density. For the cellular networks, the network density is kept constant for all cases shown here. The inset shows the mean tortuosity introduced in cellular networks as ρ_b varies at constant ρ. In all these models, fibers are cylindrical, of same D and L₀. The data in (a) is replotted in (b) versus the network density, ρ.

In both cases, the data indicates that strength is proportional to the cross-link number density,

$${\sigma }_c~{\rho }_b.$$ (4)

Figure 6b shows the same data plotted against network density, ρ. Since in the fibrous case ρ is proportional to ρ_b, the data align. However, in the cellular case, σ_c of networks with same ρ has different values for realizations with different ρ_b.

3.3. Collected results and discussion

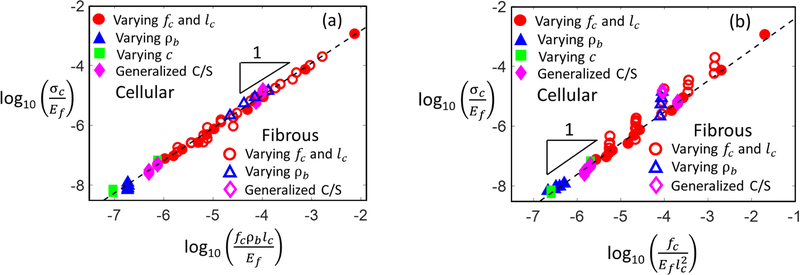
Considering the results discussed in sections 3.1 and 3.2, indicating that σ_c~ρ_b and that σ_c is independent of c, we aim now to determine whether any other structural parameter influences σ_c. To this end, a large number of models of both cellular and fibrous type and with a broad range of parameters is considered. The parameters are allowed to vary in ranges shown in Table 1. Guided by eq. (4) and by the observation that σ_c ~ f_c, which was substantiated previously both numerically (Deogekar and Picu, 2018; Heyden, 2000) and experimentally (Forsstrom et al., 2005; Marais et al., 2014), we plot in Fig. 7a the normalized strength, σ_c/E_f, versus the non-dimensional group ρ_bf_cl_c/E_f, where E_f is introduced as the unit of stress, for non-dimensionalization purposes. The results for cellular networks include cases in which parameters c,D,ρ,f_c and ρ_b are varied independently and are shown with different symbols. Cases in which the fiber bending and axial rigidities are varied independently using the generalized cross-section formulation are also included. Similar data is presented for fibrous models, with the exception that in these models c = 1 in all cases. Excellent collapse is observed for both network types. This indicates that σ_c is proportional to the cross-link density and the cross-link strength and is independent of fiber properties (axial and bending rigidities, and modulus).

Table 1:

Network parameters for cellular and fibrous networks considered. The parameters are reported in non-dimensional form.

Parameters	Cellular networks	Fibrous networks
Network density, $\rho L_0^2$	8.2 – 16.8	2.3 – 12.2
Mean segment length, lc/L0	0.20 – 0.35	0.22 – 0.56
Fiber diameter, D/Lo	0.002 – 0.2	0.02 – 0.4
Cross-link strength, $f_c/E_f{L}_0^2$	1.11 × 10−7 – 1.11 × 10−3	1.60 × 10−6 – 3.87 × 10−4
Cross-link density, ${\rho }_b{L}_0^3$	16.2 – 46.1	1.6 – 15.3
Fiber tortuosity, c	0.57 – 1.00	NA

Figure 7.

(a) Variation of network strength, σ_c, with the non-dimensional group ρ_bf_cl_c/E_f for cellular and fibrous networks with a broad range of network parameters: f_C, ρ_b, l_C, c, and properties of the fiber cross-section (Talble 1). Generalized C/S stands for the generalized cross-section model of fibers. Filled symbols represent cellular networks, while open symbols represent fibrous networks. The data is replotted in (b) versus the non-dimensional group $f_c/E_f{l}_c^2$.

This result can be understood based on the following argument. Consider the cellular case and the observation that σ_c/E_f is proportional to ρ_b and f_c. One can write the right hand side of this equation in non-dimensional form as:

$$\frac{{\sigma }_c}{E_f}~\frac{1}{E_f}{\rho }_b{f}_c{L}^{*},$$ (5)

where L* is a length parameter which is left unspecified. Consider further the geometric relationship between the network density, ρ, and the cross-link number density, ρ_b:

$$\rho (c)={\rho }_b\frac{\overline{z}}{2}{l}_{cl}$$ (6)

where $\overline{z}$ is the mean connectivity number of the network and ρ(c) does not include segments which are not fully connected to the network, such as dangling segments and unconnected fibers. With eq. (1), one may eliminate ρ and ρ_b from eq. (4), which becomes

$$\frac{{\sigma }_c}{E_f}~\frac{2q}{\overline{z}}\frac{1}{E_f}\frac{f_c}{l_c^2}\frac{L^{*}}{l_c}$$ (7)

The collapse seen in Fig. 7a indicates that L* = l_c and the strength can be written as

$${\sigma }_C=\xi \frac{f_c}{l_c^2},$$ (8)

which holds for cellular networks with and without tortuosity. Note that although eq. (6) depends on tortuosity, c is not present in eq. (8), which supports the conclusions of section 3.1. Specifically, l_c represents the mean end-to-end length of segments or the shortest distance between cross-links, as defined above. Figure 7b shows the data in Fig. 7a replotted versus $f_c/l_c^2$, as suggested by eq. (8). It is observed that the data remain aligned, as expected, although the collapse is slightly perturbed in the case of the fibrous networks for which eq. (1) applies only approximately.

Equation (8) has an attractive geometric interpretation: consider a regular network with crosslinks distributed in a square lattice. In this case, the straight line distance (fiber end-to-end length) between cross-links is l_c, and $f_c/l_c^2$ becomes the natural reference value for strength. It is the nominal strength of a lattice network in which only the cross-links matter (separated by l_c) but not the total length of fiber between them. Therefore, the emergence of this group in eq. (7) is not surprising.

The coefficient of proportionality, ξ, which is smaller than 1, is independent of network parameters other than $\overline{z}$ (note that $\overline{z}$ is identical in the two types of networks Considered here). We expect that, in general, ξ is a function of network architecture. However, Fig. 7a indicates that ξ has the same value for cellular and fibrous networks. The value of ξ can be determined only numerically at present and the factors controlling it are a subject of future work.

It should be emphasized that, since network strength depends on the cross-link number density and their spatial distribution, fibers not connected to the network or dangling fibers connected at only one point to the backbone network contribute to ρ, but do not contribute to σ_c. This situation might change to some extent when the network volume fraction, ϕ, increases significantly. This may lead to a situation in which the excluded volume interactions of fibers contribute to stress and hence to strength. This is not expected to be a strong effect. However, if in addition to the excluded volume interactions, surface forces such as inter-fiber adhesion (Picu and Sengab, 2018), are also present, the mechanics is drastically modified and the strength is expected to depend strongly on the magnitude of these interactions.

It is well-known that rupture in a material with stochastic microstructure exhibits strong size effects (Alava et al., 2009, 2008; Curtin, 1998). Typically, the weakest link theory applies and this was shown to be the case for fibrous networks as well (Deogekar and Picu, 2018). The size effect is defined by a power function dependence of σ_c on the model size, with the exponent being related to the Weibull modulus (Deogekar and Picu, 2018; Weibull, 1939). Therefore, parameter ξ is expected to depend on the model size, L, and account for the size effect of strength.

It is also useful to discuss the present conclusion against the results reported in (Deogekar and Picu, 2018), where the strength of cellular networks with no tortuosity was reported to scale as σ_c~ρu_cD². u_c represents the critical equivalent (relative displacement of the surfaces of the two fibers forming the contact, Fig 1c) at which the cross-link fails. The present results are a generalization of this scaling relationship which appears as a particular case of eqns. (5) and (8). Equation (6) becomes $\rho =(\overline{z}/2){\rho }_b{l}_c$ in this case. Furthermore, in the respective study, cross-link failure was described in terms of the critical deformation of the cross-link, u_c, while in the present case the cross-link strength is defined in terms of an effective applied force, f_c; converting from one formulation to the other requires specifying the cross-link stiffness. In cases considered in (Deogekar and Picu, 2018), the cross-link stiffness was made proportional to D². Therefore, σ_c~ρu_cD² becomes equivalent to ${\sigma }_c~{\rho }_b{f}_c{l}_c~f_c/l_c^2$, as defined here for a much more general range of parameters and network architectures.

4. Conclusions

The dependence of the strength of stochastic fiber networks on network parameters is studied in this work. Two 3D network architectures are considered, of cellular and fibrous type. It is concluded that the network strength is independent of fiber tortuosity and of fiber properties, including the fiber modulus. It scales linearly with the cross-link strength and with the cross-link number density. Network strength does not depend on the density (total fiber length per unit volume), although a linear scaling with density may be observed in situations in which the crosslink number density scales linearly with the network density. It is concluded that network strength is defined by the mean distance between cross-links and by the cross-link strength, being proportional to the stress-like parameter $f_c/l_c^2$, where l_c is the average end-to-end length of fiber segments. The coefficient of proportionality is much smaller than 1 and has the same value in the cellular and fibrous networks considered. However, we expect that, in general, this coefficient depends on network architecture and on the model size. These results hold for networks that fail in the linear regime I as well as in the strain stiffening regime II of network deformation.

Appendix A

In this Appendix we develop the relationship between network density, ρ, the mean contour length of segments, l_cl, and the tortuosity parameter, c, for cases in which a fraction of segments are crimped, while the others remain straight.

Consider a network with straight segments of mean segment length l_c. The segment length distribution if Poisson: p(l) = (l/l_c) exp(− l/l_c). Consider that fibers shorter than l_t remain straight, while all others are rendered tortuous with parameter c. The fraction of straight segments is ${\mu }_1={\int }_0^{l_t}p(l)dl=1-\text{exp}\left(-l_t/l_c\right)$. The mean length of straight segments is $l_{c1}={\int }_0^{l_t}lp(l)dl=l_c-\left(l_c+l_t\right)\text{exp}\left(-l_t/l_c\right)$, while the mean end-to-end length of tortuous segments is $l_{c2}={\int }_{l_t}^{\infty }lp(l)dl=\left(l_c+l_t\right)\text{exp}\left(-l_t/l_c\right)$.

The mean contour length of the population is

$$l_{cl}={\mu }_1{l}_{c1}+\left(1-{\mu }_1\right)l_{c2}/c,$$ (A1)

while the tortuosity-dependent density can be written as:

$$\rho (c)=\left[{\mu }_1{l}_{c1}+\left(1-{\mu }_1\right)l_{c2}/c\right]\rho (1)/l_c$$ (A2)

Using the relation $\rho (1)l_c^2=q$ (eq. (1) with c = 1) which is valid for networks of straight segments (Fig. 2), the product $\rho (c)l_{cl}^2$ can be written as:

$$\rho (c)l_{cl}^2=q{\left[\left(1-e^{-\beta }\right)\left(1-(1+\beta )e^{-\beta }\right)+e^{-2\beta }(1+\beta )/c\right]}^3,$$ (A3)

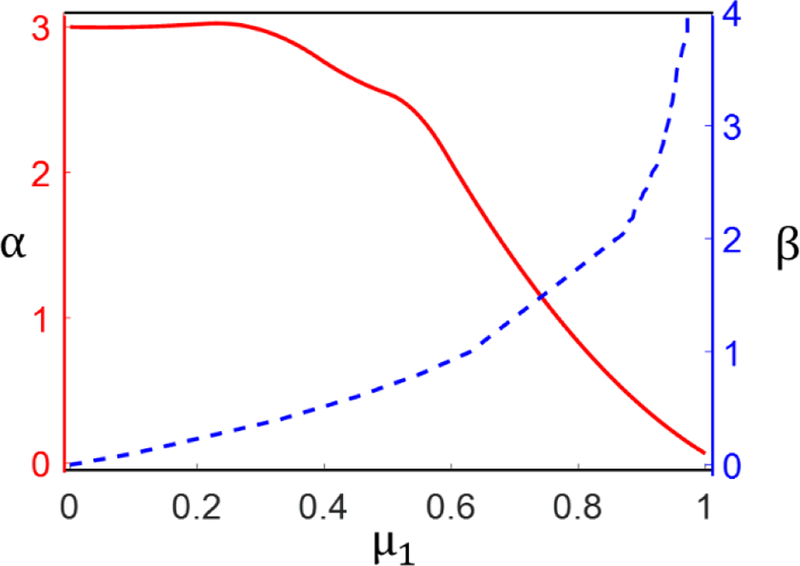
where β = l_t/l_c. Equation (A3) can be approximated with good accuracy, for 0.2 < c < 1, with eq. (2):$\rho (c)l_{cl}^2\approx q/c^{\alpha }$, where α is a function of β and hence of the fraction of straight segments μ₁. This function is shown in Fig. A1.

Figure A1:

Variation of exponent α, and parameter β, with the fraction of straight segments, μ₁.