Abstract
In 2009, the Interstellar Boundary Explorer (IBEX) discovered the existence of a narrow “ribbon” of intense energetic neutral atom (ENA) emission projecting approximately a circle in the sky. It is believed that the ribbon originates from outside of the heliopause in radial directions (r) perpendicular to the local interstellar magnetic field (ISMF), B, i.e., B∙r = 0. Swaczyna et al. (2016a) estimated the distance to the IBEX ribbon via the parallax method comparing the ribbon position observed from the opposite sides of the Sun. They found a parallax angle of 0.41° ± 0.15°, yielding a distance of au to a portion of the ribbon at high ecliptic latitudes. In this study, we demonstrate how the apparent shift of the ribbon in the sky, and thus the apparent distance to the ribbon’s source found via the parallax, depends on the transport effects of energetic ions outside the heliopause. We find that the apparent shift of the ribbon based on the “spatial retention” model with ion enhancement near B∙r = 0, as proposed by Schwadron & McComas (2013), agrees with the parallax of the source region. Parallax is also accurate for a homogeneously-distributed emission source. However, if there is weak pitch angle scattering and ions propagate freely along the ISMF, the apparent shift is significantly smaller than the expected parallax because of the highly anisotropic source. In light of the results from Swaczyna et al. (2016a), our results indicate that the IBEX ribbon source is spatially confined.
1. Introduction
NASA’s Interstellar Boundary Explorer (IBEX; McComas et al. 2009a) has been detecting hydrogen energetic neutral atoms (ENAs) since shortly after launch in October 2008. Its initial observations revealed a narrow, intense “ribbon” of ENAs encircling the sky (McComas et al. 2009b), with average width ~20° (Fuselier et al. 2009) and radius ~75° projected in the sky (Funsten et al. 2009b). While the ribbon was not expected or predicted by any prior models, it was realized that the ribbon fluxes were likely originating from look directions perpendicular to the local interstellar magnetic field (ISMF) draped around our heliosphere (Schwadron et al. 2009).
Since the ribbon’s discovery, many theories have been suggested to explain its origin (McComas et al. 2009b, and see reviews in McComas et al. 2010, 2014b), such as forming at the termination shock (Kucharek et al. 2013), in the inner heliosheath (IHS; Siewert et al. 2013; Fichtner et al. 2014; Sylla & Fichtner 2015), in the outer heliosheath (OHS) outside the heliopause (e.g., McComas et al. 2009b; Heerikhuisen et al. 2010; Chalov et al. 2010; Möbius et al. 2013; Schwadron & McComas 2013; Isenberg 2014, 2015; Giacalone & Jokipii 2015; Gamayunov et al. 2010, 2017; Zirnstein et al. 2018), or in the distant local interstellar medium (LISM; Grzedzielski et al. 2010). One of the most studied theories, the “secondary ENA” mechanism, has qualitatively and quantitatively reproduced many aspects of the ribbon (e.g., Zirnstein et al. 2015a), and is currently believed to be its source based on the latest IBEX observations (McComas et al. 2017; Schwadron et al. 2018).
In the secondary ENA scenario, cold and slow interstellar neutral atoms propagate into the heliosphere and charge-exchange with fast-moving solar wind (SW) protons, creating neutralized solar wind (NSW) atoms that propagate radially away from the Sun. Most of these neutral atoms will propagate outside the heliosphere into the OHS since their mean free path is much larger than the heliosphere, creating a non-thermal population of “pickup ions from neutral SW,” or PINS, outside the heliopause. After a few years (depending on the energy of the ion and the local interstellar neutral hydrogen density), some of these PINS will create secondary ENAs that propagate back into the heliosphere and can be detected by IBEX.
A model-independent method for determining the origin of the ribbon is based on utilizing the parallax method. Swaczyna et al. (2016a) provided the first determination of the distance to the source of the IBEX ribbon using parallax by utilizing the motion of the Earth (and thus IBEX) around the Sun every year, and IBEX’s rotation about its Sun-pointing axis (McComas et al. 2009a). Swaczyna et al. (2016a) analyzed the apparent motion of a section of the ribbon fluxes in the sky at high ecliptic latitudes and determined the distance to that source to be au, consistent with models that predict a source near the heliopause, such as the secondary ENA mechanism, but also consistent with a source inside the IHS. While the secondary ENA mechanism can explain many aspects of the ribbon (e.g., Zirnstein et al. 2015a), it has not yet been determined how the parent PINS behave in the OHS before they charge-exchange. Thus, the consistency of the result from Swaczyna et al. (2016a) with the secondary ENA mechanism motivates us to better understand how the parallax method may be affected by the dynamics of PINS outside the heliopause.
The first model of the ribbon from the secondary ENA mechanism assumed that PINS are immediately scattered onto a partial shell distribution, with an angular spread in velocity space that depends on the initial PINS pitch angle. This process would create a higher concentration of PINS and secondary ENAs in radial look directions (r) perpendicular to the local interstellar magnetic field (B), such that B∙r = 0 (Heerikhuisen et al. 2010). This is similar to models that assume negligible pitch-angle scattering close to B∙r = 0 (Chalov et al. 2010; Möbius et al. 2013; Zirnstein et al. 2018). Alternatively, Schwadron & McComas (2013) suggested that, rather than assume the PINS must retain their initial pitch angle for a few years before they charge-exchange, they quickly scatter to nearly-isotropic shell distributions that are spatially-retained around where B∙r = 0 and produce an enhancement in PINS there. Isenberg (2014) constructed a similar model but produced a more homogeneous source distribution in the retention region that produces fewer ribbon ENAs. Under these various mechanisms for the behavior of PINS in the OHS, the ribbon observed at 1 au may appear different (i.e., different intensity and structure; Zirnstein et al. 2019). Further, its angular shift every 6 months may be different, which is why it is important for studies to focus on how PINS behave in the OHS (see also, e.g., Florinski et al. 2010, 2016; Summerlin et al. 2014; Niemiec et al. 2016).
In this study, we demonstrate the sensitivity of applying the parallax method to the ribbon due to the dynamics of PINS outside of the heliopause. In Section 2, we describe several ribbon models used in the analysis, including modeling the ribbon under strong and weak pitch angle scattering. In Section 3, we present our results by computing the apparent motion of the ribbon under the different models, and in Section 4, discuss their implications for the ribbon’s source.
2. Methodology
2.1. Simulation of the Heliosphere and Neutral SW Source
We use the results from a three-dimensional MHD-plasma and kinetic-neutral simulation of the SW-VLISM interaction in order to simulate the ribbon fluxes at 1 au. The MHD/kinetic simulation couples a single-fluid plasma (solving ideal magnetohydrodynamic equations) to neutral hydrogen atoms (solving the Boltzmann transport equation) by energy-dependent, charge-exchange and photo-ionization source terms (e.g., Pogorelov et al. 2008; Heerikhuisen et al. 2009). The VLISM boundary conditions for the MHD simulation, imposed at 1000 au from the Sun, are: ISMF strength of 2.93 μG and direction (227.28°, 34.62°) in ecliptic J2000 (Zirnstein et al. 2016), interstellar plasma/neutral temperature 7500 K and flow speed 25.4 km s−1 from inflow direction (255.7°, 5.1°) in ecliptic J2000 coordinates (McComas et al. 2015), interstellar plasma density of 0.09 cm−3, and neutral hydrogen density of 0.154 cm-3. The ISMF reproduces the position of the IBEX ribbon (Zirnstein et al. 2016) and is consistent with the interstellar neutral hydrogen deflection plane (Lallement et al. 2010). The interstellar densities are chosen such that the simulation reproduces (1) the distance to the heliopause observed by Voyager 1 (Stone et al. 2013; Gurnett et al. 2013) and Voyager 21, and (2) an interstellar neutral hydrogen density of ~0.1 cm−3 at the termination shock in the nose-ward direction of the heliosphere (Bzowski et al. 2009).
The SW boundary conditions at 1 au are the same as those applied in Zirnstein et al. (2016): plasma density of 5.74 cm−3, plasma temperature of 51,100 K, flow speed of 450 km s−1, and magnetic field radial component of 37.5 μG. These values are then advected to a distance of 10 au (the inner boundary of the simulation) using adiabatic expansion. The neutral hydrogen source terms from our kinetic-neutral module are computed using statistics from individual charge-exchange events, accumulated on a Cartesian grid. To better simulate the very narrow width of the neutralized SW distribution outside the heliopause (see, e.g., Florinski & Heerikhuisen 2017), in this study we create an analytic representation of the neutralized SW distribution following Swaczyna et al. (2016b) who demonstrated the dependence of the ribbon’s position in the sky with the energy-dependent, latitudinal structure of the SW. This distribution is used as the source term for creating the ribbon in our post-processing model of the ribbon (see Sections 2.2-2.4).
It is essential for this study that we generate as accurate as possible a neutralized SW distribution in order to model the apparent motion of the ribbon. This motion (on the order of 0.1°) is much smaller than the angular grid resolution of kinetic neutral particles produced by the heliosphere simulation (6°; e.g., Heerikhuisen et al. 2016). In order to simulate small angular shifts in the ribbon’s position as well as the small but finite thermal spread in the neutral SW distribution (see Section 2.4), we artificially generated a neutral SW distribution following Swaczyna et al. (2016b) and Zirnstein et al. (2019), as described below.
We utilize results from a model of the SW speed and density derived from interplanetary scintillation (IPS) observations as a function of heliographic latitude (Sokól et al. 2015) to produce a neutral SW source for the ribbon population. We use SW speed and density at 1 au (uSW,0 and nSW,0, respectively) from 2000 through 2009, which accounts for the predicted ~4 to 9 yr delay between SW observations at 1 au and IBEX ribbon observations at 1 au (Zirnstein et al. 2015b) and allows us to compare to IBEX data time-averaged from 2009 through 2013 (McComas et al. 2014a). The neutralized SW differential flux, INSW, at the radial distance of the termination shock, rTS = 100 au, is given by (e.g., Swaczyna et al. 2016b)
| (1) |
where v is the neutral SW speed, θ is the heliographic latitude, i is the Carrington rotation number averaged over 1958 through 2091 (total M = 134) to years 2000 to 2009, r0 = 1 au, nH = 0.09 cm−3 is the interstellar neutral hydrogen density in the supersonic SW (e.g., Bzowski et al. 2009), σex is the energy-dependent, charge-exchange cross section (Lindsay & Stebbings 2005), r is the radial distance from the Sun, mp is the proton mass, and N is a Gaussian speed distribution with mean speed uSW,i(r) and speed variation δv = 100 km s−1 which smooths the SW speed. The factor (r0/rTS)2 is derived from a combination of the expansion of the SW density at r0 to distance r, (r0/r)2, and the expansion of the neutral SW flux from distance r to rTS, (r/rTS)2. For more details on Equation (1), see Swaczyna et al. (2016b) and Zirnstein et al. (2019).
Finally, the neutral SW flux outside the heliopause at radial distance r from the Sun is given by
| (2) |
where we take into account the r−2 expansion of the neutral SW flux and the loss of neutral SW atoms by charge-exchange with interstellar protons outside the heliopause, whose distance rHP is derived from the MHD/kinetic simulation. Equation (2) is used as the source distribution for PINS outside the heliopause when simulating the ribbon flux (see Sections 2.2-2.4).
2.2. Ribbon Model: Spatial Retention with Enhanced PINS
In this study, we simulate three different secondary ENA models for the ribbon. The first ribbon model we test is the spatial retention model developed by Schwadron & McComas (2013). In this model, PINS are spatially retained via strong pitch angle scattering in a region of space close to B∙r = 0, producing an enhancement in PINS density close to the heliopause. In our recent paper, we implemented this model in a 3D simulation of the heliosphere (Zirnstein et al. 2019). Zirnstein et al. (2019) showed that this model not only produces an enhancement in ENA flux compared to the case where PINS just scatter isotropically and more homogenously in the retention region, but also that the model introduces an asymmetry in the flux profile perpendicular to the ribbon, i.e., the cross-ribbon profile is non-Gaussian. Swaczyna et al. (2016a) assumed that the ribbon profiles are Gaussian. Consequently, this effect is important to consider because it may affect analyses of the ribbon’s position using the parallax method.
The source PINS distribution, f0, inside the retention region is given by (Schwadron & McComas 2013)
| (3) |
where v║ is the PINS initial speed parallel to the local ISMF, vA is the local Alfvén speed, SNSW is the neutral SW source rate (in units of s2 cm−6), 1/τx = nH(r) σex(v)v is the charge-exchange rate, nH is the interstellar neutral hydrogen density, derived here from the MHD-kinetic simulation, and σex is the energy-dependent, charge-exchange cross section (Lindsay & Stebbings 2005). The second term (f) describes the balance between the supply and loss of particles moving into and out of the retention region, where z defines the distance along the local ISMF line away from the center of the retention region (center located at B∙r = 0).
The source PINS distribution outside the retention region is
| (4) |
where describes the pitch angle scattering rate (1/τs) and the charge-exchange rate (1/τx). If 1/τs >> 1/τx, then PINS will quickly scatter isotropically before becoming secondary ENAs, forming a low-level background of ENA fluxes in all directions of the sky away from the ribbon. If 1/τs << 1/τx, then PINS will charge-exchange before experiencing any significant pitch angle scattering and cannot produce ENAs observable at Earth viewed from directions away from the ribbon. In this study, we present results for 1/τs << 1/τx and note that this assumption does not affect the main results of this paper. For more details of the model and implementation in our 3D MHD/kinetic simulation of the heliosphere, see Schwadron & McComas (2013) and Zirnstein et al. (2019).
The neutral SW source rate, SNSW, is given by (Zirnstein et al. 2019)
| (5) |
where the neutral SW differential flux INSW is from Equation (2).
2.3. Ribbon Model: Spatial Retention with Isotropic Scattering
The second model that we test is the isotropic scattering model from Zirnstein et al. (2019). This model is similar to the spatial retention model, except that we assume all PINS scatter isotropically in the retention region, without any enhancement in PINS density close to B∙r = 0, such that a more homogenous distribution is produced in the retention region. As shown by Zirnstein et al. (2019), this model produces a factor of ~3 less flux than the spatial retention model (see similar fluxes from Heerikhuisen et al. 2014; Isenberg 2014), and a slightly different asymmetry in the flux profile perpendicular to the ribbon.
The source PINS distribution inside the retention region is given by
| (6) |
and the distribution outside the retention region is
| (7) |
For more details of this model, see Zirnstein et al. (2019). This model is similar to the spatial retention model where 1/τs << 1/τx, with the same source term (Equation 5), except that there is no enhancement of PINS in the retention region, and there is no flux visible at Earth produced outside the retention region.
2.4. Ribbon Model: Weak Scattering Velocity Retention
The final ribbon model assumes there is negligible pitch angle scattering of PINS outside the heliopause (Chalov et al. 2010; Zirnstein et al. 2018). Under this scenario, PINS may stream along the local ISMF, advect with the bulk plasma flow with a drift component perpendicular to the ISMF, experience the magnetic mirror force as PINS traverse over spatial gradients in the ISMF magnitude, or experience betatron acceleration as they are advected towards increasing ISMF magnitudes close to the heliopause. As demonstrated by Zirnstein et al. (2018), the parallel streaming and magnetic mirroring of PINS are the most significant processes that control the ribbon fluxes observed at 1 au. The motion of PINS before they become secondary ENAs may be significant enough to affect the parallax motion of the IBEX ribbon. Zirnstein et al. (2018) also demonstrated that the advection of PINS with the interstellar flow and resulting betatron acceleration are not important, so we ignore those effects in this study.
The source PINS distribution for this model is given by (Zirnstein et al. 2018)
| (8) |
| (9) |
where we integrate over a weighting function W(t) (where we set tmax = 3×τex) to account for the source of particles propagating along the ISMF that can contribute to creating secondary ENAs at position r (see Zirnstein et al. 2018 for more details). Since, in this model, we follow the guiding center motion of the PINS distribution and its evolving pitch angle, at each time step we integrate over the neutral SW source that could produce the PINS with that pitch angle, i.e., integrating over the gyro-phase Ω.
In (Equation 8), we also assume that PINS experience a small but finite amount of pitch angle scattering (Δφ) around the nominal pitch angle (φ) of the guiding center motion of the PINS. Florinski et al. (2016) simulated the stability of the PINS distribution in the OHS and found that the PINS distribution may be stable for a long period of time if the temperature of the background VLISM plasma is within a certain range (see their Figure 1; see also Summerlin et al. 2014). If true, this demonstrates that the PINS ring beam will not significantly scatter in pitch angle as previously assumed, but may slightly widen in pitch angle (e.g., Florinski et al. 2010). Thus, we take this scenario for our “weak scattering” model of the ribbon and allow the PINS distribution to slightly widen within a small range in pitch angle about φ. In Equation (8), we perform a box-car integration in pitch angle around the nominal pitch angle of the PINS guiding center, i.e., φ ± Δφ/2. Here we set Δφ = 5°. Note that the results of this study do not significantly depend on this small scattering angle.
Figure 1.

Model all-sky maps of ENA fluxes for the spatial retention (top), isotropic scattering (middle) and weak scattering (bottom) ribbon models. We show results for IBEX-Hi ESA bins 3 (left) and 5 (right), which have central energies of 1.11 and 2.73 keV, respectively. Note that we scaled the isotropic model fluxes by a factor of 3. The red dashed lines at 45° latitude represent the pixels we use to calculate the distance to the ribbon’s source using parallax.
The neutral SW source function for this model is similar to Equation (5) except that, instead of assuming the entire neutral SW distribution at speed v can contribute to the PINS distribution, we choose from the neutral SW distribution at a specific pitch angle, such that
| (10) |
| (11) |
| (12) |
where INSW(r,v) is the same as Equation (2), and vp = vp(Ω,φ) is the desired PINS velocity vector (with magnitude v). Since we are integrating over a narrow ring beam in the neutral SW distribution, we introduce a realistic temperature (transverse to the radial direction) to the neutral SW distribution (at the termination shock, Ttr,TS = 5000 K; Florinski & Heerikhuisen 2017). We use the Heaviside step function, H, to ensure that PINS are created in the correct hemisphere.
We note that the results presented in this study for the weak scattering ribbon model, which utilize an analytic neutral SW distribution described in Section 2.1, are similar to the results from Zirnstein et al. (2018) which used a neutral hydrogen distribution generated directly from charge-exchange source terms in the MHD/kinetic simulation. In this study, we choose not to use the MHD/kinetic simulation source terms due to the computational limitations in generating a distribution from counting statistics with sufficient resolution in phase space (typically ~5°). The methods described in Section 2.1 are preferred for the purposes of calculating the angular motion of the ribbon with accuracy much better than the expected angular shift on the order of ~0.1°.
2.5. Modeling the Ribbon in IBEX “Ram” and “Anti-ram” Frames
IBEX “ram” maps are constructed when the IBEX spacecraft is moving with some velocity component towards the direction in which the instrument aperture is viewing, whereas “anti-ram” maps are constructed when IBEX is moving away from its viewing direction. This is possible due to (1) the motion of the Earth around the Sun each year, (2) IBEX spinning about its Sun-pointing axis, and (3) the detector boresight pointing perpendicular to the spin axis (McComas et al. 2009a). ENA fluxes detected from the upwind hemisphere of the heliosphere are measured during the roughly first 6 months of each year in IBEX’s ram frame, followed by the downwind hemisphere during the last 6 months (anti-ram maps are constructed first in the backward then forward hemispheres). While IBEX ram and anti-ram maps are observed in the spacecraft (or Earth) frame and must be corrected for the Compton-Getting effect if analyzing in the solar inertial frame, we simulate the ribbon directly in the solar inertial frame (for details see Zirnstein et al. 2013) but simulate IBEX’s position and look direction in each frame. Moreover, to emulate the IBEX-Hi instrument, we (1) integrate over the IBEX-Hi energy response function and (2) smooth the simulated fluxes in the sky using a triangular function with full-width at half-maximum of 7° to mimic the instrument’s angular response (Funsten et al. 2009a).
The ENA differential flux equation, integrated from the heliopause to the simulation’s outer boundary, rOB (taken to be 700 au), is
| (13) |
where f0 is the source PINS distribution from Equations (3), (4), (6-8), P(rLOS, v) is the survival probability of ENAs from their point of creation to the termination shock, and ψ is the line-of-sight direction in the sky. We note that P only accounts for the losses of ENAs from their point of creation to the termination shock since this makes our simulation results directly comparable to the survival probability-corrected IBEX data, as recommended by McComas et al. (2017). Note also that the position vector rLOS in Equation (13) is not a radial position vector originating from the Sun, but rather IBEX’s line-of-sight vector.
In Figure 1 we show model all-sky maps of each ribbon model from Section 2 at ENA energies of 1.1 and 2.7 keV, simulated using IBEX’s position around the Sun and lines-of-sight in the ram frame (note that the anti-ram frame results would appear identical at this scale). All model results emulate the IBEX angular response, and the spatial retention and isotropic scattering models also emulate the IBEX energy response. Due to computational limitations, the weak scattering model simulates the ribbon at exactly 1.11 keV and 2.73 keV. We note that the integration over IBEX’s energy response function does not significantly change the results of this study (≤1% difference compared to simulation at exactly 1.11 or 2.73 keV).
It is clear in Figure 1 that the intensities for each model are significantly different, where the spatial retention model is ~3 times higher than the isotropic model, and the weak scattering model is ~2 times higher than the spatial retention model. While the weak scattering model fluxes compare better to IBEX fluxes (e.g., Schwadron et al. 2014), in Section 3 we demonstrate how the apparent angular shift from the ram to anti-ram of each model provides another way to differentiate them with IBEX data.
3. Apparent Motion of the Ribbon
3.1. Parallax Method
The distance to the ribbon source may be determined using the parallax technique, which is illustrated in Figure 2. For a distance R = 1 au between the detector (IBEX) and the Sun, one can determine the half angle (γ) at which the emission source moves across the sky as the detector moves around the Sun. The distance to the emission source D is related to γ by
| (14) |
Figure 2.
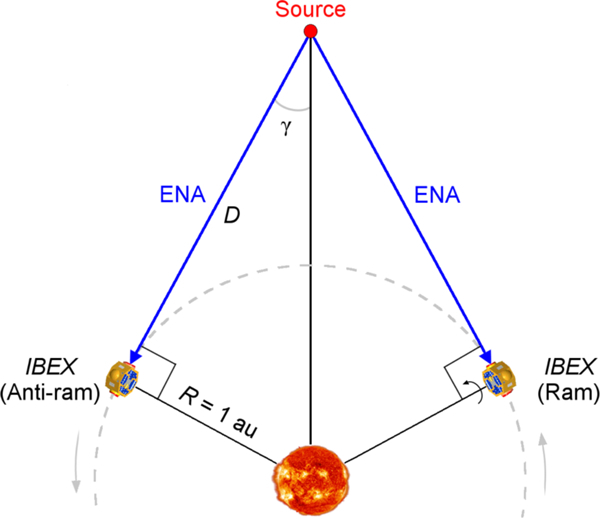
Simplified illustration (not to scale) of the parallax technique used to determine the distance to the IBEX ribbon’s source. As Earth orbits the Sun (gray dashed line), IBEX’s rotation about its Sun-pointing axis (black line) allows it to observe the same emission source while on either side of the Sun every 6 months.
The parallax method is normally used for point-like, isotropic emission sources, whose source position does not change with time. The ribbon’s source, however, is an extended region in space that is largely ordered by the draping of the ISMF around the heliopause (e.g., Pogorelov et al. 2011; Zirnstein et al. 2015a, 2016). Moreover, the behavior of PINS outside the heliopause determine whether the ribbon’s source distribution is created via “spatial retention” (e.g., Schwadron & McComas 2013) or “velocity retention” (e.g., Heerikhuisen et al. 2010). Thus, it is not immediately clear how well the parallax method performs for the ribbon’s source. In fact, in Section 3.2 we show that the behavior of the PINS distribution significantly affects the ability to compute an accurate distance to the ribbon’s source from parallax.
Analyzing parallax from the ribbon is further complicated by the fact that the distance to the ribbon’s source changes with angle from the peak flux (e.g., Heerikhuisen & Pogorelov 2011; Zirnstein et al. 2019). For example, in Figure 3 we show the distance to the ribbon’s source for each all-sky map shown in Figure 1. It is clear that fluxes from the ribbon’s inner edge (closer towards the nose direction of the heliosphere) originate closer to the observer than fluxes from the ribbon’s outer edge. This is due to the draping of the ISMF around the heliosphere (Zirnstein et al. 2019) and occurs for any secondary ENA ribbon source originating outside the heliopause.
Figure 3.
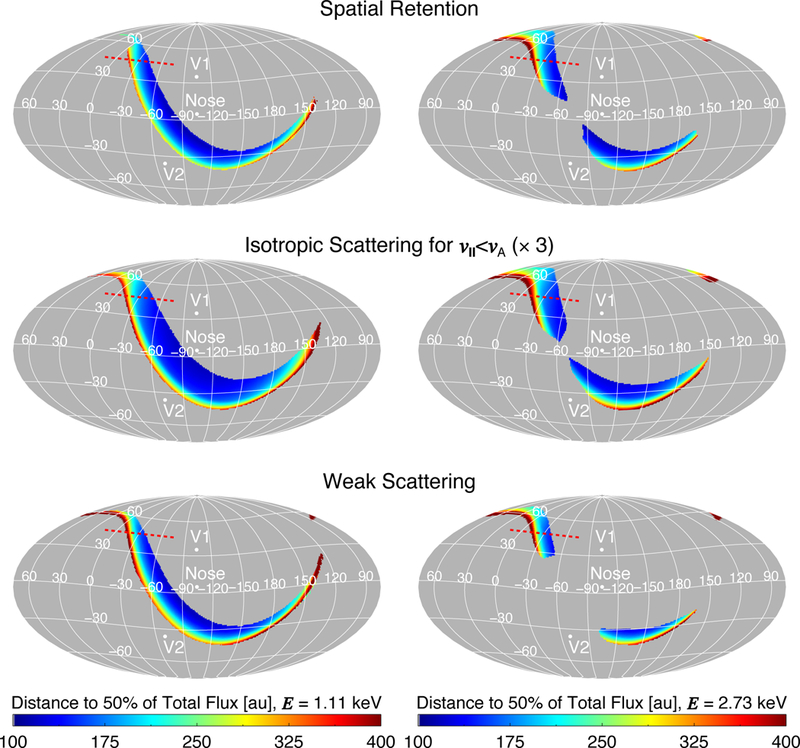
Similar to Figure 1, except we show the three models’ distance (50% of the total integrated flux) to the ribbon’s source. Gray pixels represent directions where the flux is <10% of the maximum flux in the sky.
Next, we calculate the apparent angular shift of the simulated ribbon in the ram vs. anti-ram frames for the flux profiles shown in Figure 4, derived from pixels at ecliptic latitude +45° from Figure 1 (dashed red lines). We choose this latitude since the ribbon fluxes at both 1.1 and 2.7 keV are reasonably large at the same location (note that we have tested the robustness of our results at different latitudes and found no significant change). The angular shift of the ribbon from ram to anti-ram frames is calculated by finding the mean location of the flux distribution as a function of ecliptic longitude and differencing the ram and anti-ram frame locations. Rather than assume a shape of the flux profile (e.g., skew Normal distribution) and fit the shape to the fluxes to derive a mean location of the shape, we instead integrate the area under the curve to find its mean location.
Figure 4.
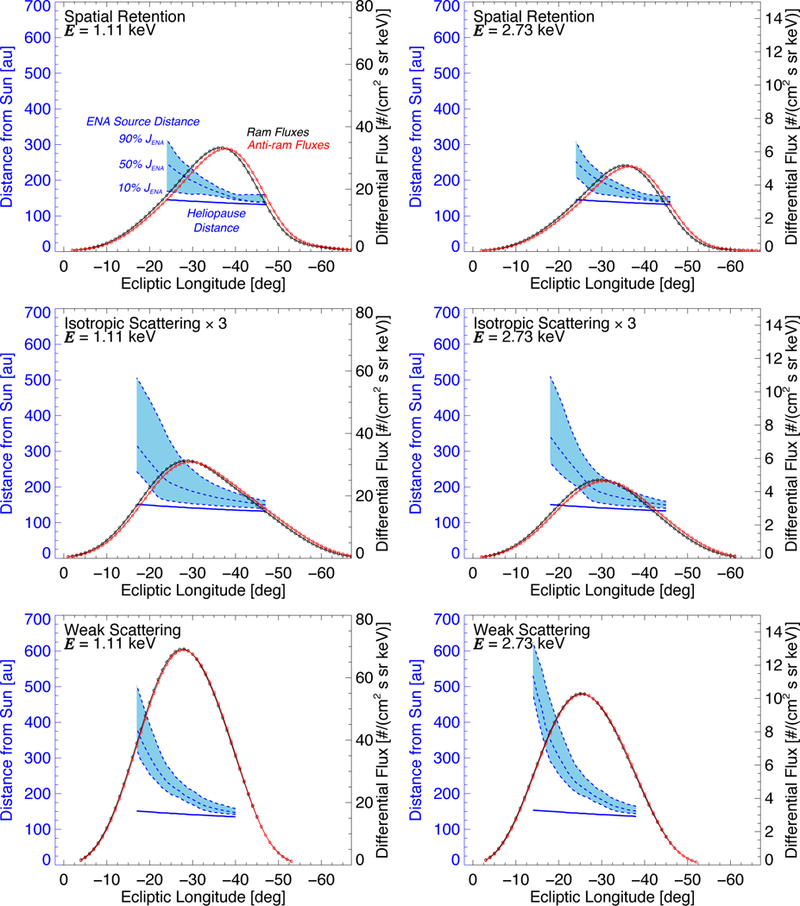
Simulated ribbon flux profiles as a function of ecliptic longitude for spatial retention (top), isotropic scattering (middle) and weak scattering (bottom) models, at ENA central energies of 1.1 (left) and 2.7 keV (right). The ribbon fluxes (right y-axis) are simulated in the IBEX spacecraft ram (black circles) and anti-ram (red circles) frames. We also show the distances from the Sun (left y-axis) to the heliopause (blue curve) and distance to the ribbon source at the 10%, 50% and 90% integration levels (dashed blue curves), for pixels with fluxes >50% of the peak ribbon flux.
The longitude ranges of the fluxes in the integrals are chosen such that the fluxes of the left and right-most edges are small and approximately the same values (~1% level of peak flux in each panel). Then, we perform a high-order Gauss-Kronrod quadrature integration to compute the area under the curve. We perform cubic spline interpolation between the simulation grid points to calculate fluxes during the integration. The mean location of the distribution, λmean, is determined by the following:
| (15) |
where JENA(λmin) and JENA(λmax) are small. These procedures are repeated for both ram and anti-ram frames, for each panel in Figure 4.
We difference the mean longitudes of the ram and anti-ram frame results (λR and λA, respectively) to estimate the apparent shift of the ribbon, similar to that used in parallax analyses, given by (e.g., Swaczyna et al. 2016a)
| (16) |
where β = 45° is the ecliptic latitude. This process is repeated for each ribbon model at ENA energies 1.1 and 2.7 keV. The results are shown in Table 1 along with the apparent distance to the ribbon source based on the angular shift γ (Equation 14). We also show the actual distances to the ribbon source derived from the simulation, which are defined by the distance at which 50% of the ribbon flux is line-of-sight integrated starting from the heliopause. The results are also visualized in Figure 5.
Table 1.
Model results for the apparent distance to the ribbon’s source using its apparent angular shift.
|
Model |
ENA Energy (keV) |
Apparent Angle Shift, γ (°) |
Distance from the Apparent Shift, D (au) |
Distance to Heliopause a (au) |
Distance to Ribbon Source b (au) |
|
|---|---|---|---|---|---|---|
|
Pixels > 50% of ribbon peak |
Ribbon peak |
Pixels > 50% of ribbon peak |
||||
| Spatial Retention |
1.1 | 0.311 | 184c | 130–145 | 170 | 140–250 |
| 2.7 | 0.309 | 185c | 130–145 | 175 | 140–250 | |
| Isotropic Scattering |
1.1 | 0.290 | 198c | 130–150 | 180 | 150–320 |
| 2.7 | 0.286 | 200c | 130–150 | 180 | 150–340 | |
| Weak Scattering |
1.1 | 0.051 | 1122c | 135–150 | 200 | 145–385 |
| 2.7 | 0.057 | 1005c | 135–155 | 210 | 150–530 | |
Derived from pixels whose ribbon fluxes are >50% of the peak ribbon flux in Figure 4. We use directions from the simulated antiram map results as examples. The results are rounded to the nearest 5 au.
Distance at which 50% of the total ribbon flux is integrated starting from the heliopause. We show the distance in the direction of the peak antiram ribbon flux, as well as the range of pixels with fluxes >50% of the peak antiram ribbon flux, both derived from pixels in Figure 4. Note the distances to the simulated ram and antiram ribbon fluxes give similar results. The results are rounded to the nearest 5 au.
Numerical uncertainties in D are estimated by changing the position of IBEX (R), recomputing D, and calculating the percent relative difference (PRD). Here we set R = 5 au. For the spatial retention model, the PRD is ≤1% for both 1.1 and 2.7 keV. For the isotropic scattering model, the PRD is ≤3% for both 1.1 and 2.7 keV. For the weak scattering model, the PRD is ≤5% for both 1.1 and 2.7 keV. Note also that we tested the dependence of D on λmin and λmax in Equation (15). By setting λmin and λmax to various percentages of the peak flux (1%, 2%, 5% and 10%), we find that the uncertainty in D is less than 2% for every ribbon model and ENA energy as long as λmin and λmax are <2% of the peak flux.
Figure 5.
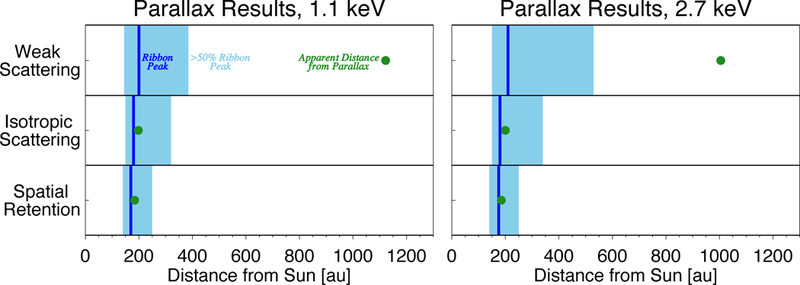
Model results for the apparent distance to the ribbon’s source from parallax (green) compared to the actual simulated distance (blue). The dark blue bar is the distance to the ribbon peak, and the light blue bar shows the range of distances to pixels from Figure 4 with flux >50% of the ribbon peak.
3.2. Results
The results shown in Table 1 and Figure 5 present an interesting difference in the apparent source distance of the ribbon from the apparent shift of the ribbon position, depending on the physical behavior of the parent PINS outside the heliopause. For the spatial retention model, the apparent distance to the ribbon source, D ~ 185 au, is close to the actual simulated distance to the peak ribbon (~175 au). Note, however, that the ribbon is made up of line-of-sight integrated ENA sources at varying distances from the Sun, with a closer average source on its inner edge (right side of plots in Figure 4) than its outer edge (ranging from ~130 to >300 au, depending on ENA energy). The apparent distance to the ribbon derived from our parallax analysis produces a distance slightly farther from the distance to the source of the peak of the ribbon, likely due to this asymmetry.
Similar to the spatial retention model, the apparent source distance D for the isotropic scattering model also predicts a realistic distance to the ribbon’s source, yielding a distance slightly farther than the actual simulated distance to the peak of the simulated ribbon. The parallax method is normally applied to sources that have angular extensions much smaller than the parallax angle. However, as we demonstrated so far in this study, the parallax method can also be used for the case of the IBEX ribbon, which has a large, extended source (see Figure 6).
Figure 6.
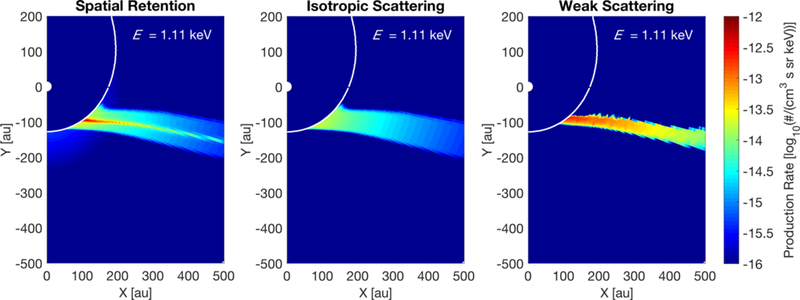
Conical cross section of the ribbon ENA production rate from the spatial retention (left), isotropic scattering (middle), and weak scattering (right) models at 1.1 keV. The cross section is extracted from a conical surface with apex located at the Sun and surface which passes through ecliptic latitude +45°, projected to the ecliptic (x-y) plane.
Moreover, this supports the results presented by Swaczyna et al. (2016a), who found a distance to the IBEX ribbon close to that expected for the secondary ENA source of the ribbon.
Finally, the apparent source distance D to the weak scattering ribbon (~1000 au) is much farther than the actual simulated distance (~200 au). However, the PINS are not spatially retained in this model, but rather their distribution as viewed from Earth depends on the observer’s line-of-sight.
This is demonstrated in Figure 7, which shows that a PINS source will appear farther away if PINS are capable of streaming along the ISMF before experiencing charge-exchange.
Figure 7.
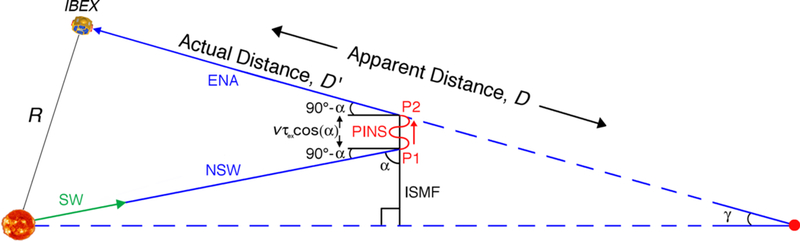
Simplified illustration of the effect of the weak scattering ribbon model on the parallax method (not to scale). The SW and neutralized SW (NSW) propagate radially away from the Sun, creating PINS outside the heliopause (P1) with pitch angle α. The PINS propagate along the ISMF until charge-exchange occurs (P2), creating ENAs that are detected at 1 au by IBEX. In this model, the streaming of PINS along the ISMF makes it appear that their source derived from parallax (red dot) with angular shift γ is farther away than the actual simulated distance (P2). Under the assumptions in this illustration, α = 90°-γ.
For example, suppose we observe an angular shift of the 1.1 keV ribbon to be γ = 0.051°, similar to our simulation result for the simulated shift of the ribbon shown in Table 1. This would yield, from Equation (14), an apparent distance to the source of D = 1122 au, which is represented in Figure 7 as the apparent distance D from IBEX to the apparent source location (red dot). However, in reality, for any finite distance that PINS travel before experiencing charge-exchange in the OHS, depending on their pitch angle and the observer’s look direction, the observed angular shift γ will overestimate the actual distance to the source.
The reason for this is illustrated in Figure 7, with a few assumptions. First, we reasonably assume for this example that the ISMF line over which the PINS travels before charge-exchange is planar, and it is perpendicular to the radial line from the Sun to the apparent source location (red dot). Second, assuming that the PINS does not change pitch angle before charge-exchange (i.e., “weak scattering”), its initial pitch angle α must equal its final pitch angle. Under these assumptions, the pitch angle of the PINS α must equal 90°-γ, where γ is the apparent angular shift from parallax.
In the illustration presented in Figure 7, the actual simulated distance to the source, D’, is given by
| (17) |
For this example, vτex = 1/(nHσex) ~ 266 au, where we assume nH = 0.15 cm−3 in the OHS (this value is calculated by averaging the neutral H density extracted along a line-of-sight through our MHD/kinetic simulation in the middle of the ribbon source region, i.e., 140–250 au from the Sun). This reduces the apparent source distance to D’ = 428 au. At 2.7 keV, the energy-dependent charge-exchange cross section is approximately ~20% smaller (Lindsay & Stebbings 2005), and 2.7 keV PINS move faster and travel farther before charge-exchange, reducing the apparent distance at 2.7 keV from D = 1005 au to D’ = 332 au. We note that, while Equation (17) does reduce the apparent source distances calculated in this study, D’ still overestimates the actual simulated source distance to the ribbon peak. Unsurprisingly, this suggests that the simulated ribbon source is not as simple as that illustrated in Figure 7, likely due to the draping of the ISMF around the heliosphere and three-dimensionality of the SW-VLISM interaction.
4. Discussion and Conclusions
In this study we have presented three different models of the ribbon to offer insight into how the dynamics of PINS outside the heliopause affect the observed angular shift of the IBEX ribbon every 6 months, which may be used to estimate the distance to the ribbon’s source. The spatial retention model assumes that PINS rapidly scatter in pitch angle before becoming ENAs, producing enhanced ion densities in a retention region close to B∙r = 0 near the heliopause. The isotropic scattering model neglects the enhancement in PINS density and produces a more homogeneous distribution in the retention region. The weak scattering ribbon model assumes that PINS do not experience significant pitch angle scattering and may freely propagate along the ISMF before becoming ENAs.
We have shown that the ribbon simulated at 1 au under these three ribbon mechanisms produce significantly different source distances when estimated with the parallax method. Our analysis concludes that the parallax method, which is nominally applied to point-like sources, produces a realistic result for the spatial retention and isotropic scattering ribbon sources, but not for the weak scattering case. This is because the spatial retention and isotropic scattering models produce an isotropically-emitting, spatially-confined source region whose location is independent of the observer’s look direction, and thus remains stationary in space. In general, if an isotropically-emitting source is stationary in space, regardless of its spatial structure or asymmetry, then the apparent shift of the observed emission can be used with the parallax method to derive the distance to the source.
Under the scenario of weak pitch angle scattering, where PINS can freely propagate along the ISMF, the apparent source distance from parallax is overestimated. In this case, the PINS that are observed as ENAs by IBEX depend on the pitch angle of the particles, and their motion along the ISMF. Any motion of the ribbon’s source and any dependence on the detector’s look direction will negate the accuracy of the parallax method applied to ribbon observations.
We note that we estimated the numerical accuracy of the results presented in Table 1. For the spatial retention and isotropic scattering models, regardless of the distance R at which IBEX is located from the Sun, the distance to the source should be the same (for R << D). Thus, to test the numerical accuracy of the results, we simulated the apparent motion of the ribbon for the scenario when R = 5 au. This resulted in an insignificant change in D for both models. The weak scattering case is more difficult to test, since changing the position of IBEX will result in a change in the pitch angle of particles preferential to be observed as ENAs by IBEX. Nevertheless, when testing the variation in D for R = 5 au for this model, the results still did not significantly change. Moreover, we tested different spreads in pitch angle of the PINS distribution. This also does not significantly affect the results.
The results of this study strongly suggest that care needs to be taken when utilizing the parallax method to derive the distance to the source of the IBEX ribbon data. Depending on the physical mechanisms controlling PINS outside the heliopause, parallax analysis may not be trustworthy. However, our analysis also shows that a ribbon mechanism that spatially confines PINS in space, e.g., via strong pitch angle scattering, can produce a realistic distance to the source using the parallax method. This suggests that the results presented by Swaczyna et al. (2016a), who reported a distance of au to the IBEX ribbon, may in fact be evidence for a spatially-retained ribbon source like that provided by Schwadron & McComas (2013). This could also be reproduced by a source retained in space by magnetic mirroring, as suggested by Giacalone & Jokipii (2015). Future analyses of ribbon observations by the upcoming Interstellar Mapping and Acceleration Probe (IMAP; McComas et al. 2018) mission, which will have better angular resolution and higher statistics than IBEX, will provide more accurate measurements of the ribbon’s position and its source.
Acknowledgements.
This work was funded by the IBEX mission as part of the NASA Explorer Program (80NSSC18K0237), and the IMAP mission as part of NASA’s Solar Terrestrial Probes (STP) mission line (80GSFC19C0027). E.Z. and J.H. acknowledge support from NASA grant 80NSSC17K0597. The work reported in this paper was partly performed at the TIGRESS high performance computer center at Princeton University, which is jointly supported by the Princeton Institute for Computational Science and Engineering and the Princeton University Office of Information Technology’s Research Computing department.
Footnotes
References
- Bzowski M, Möbius E, Tarnopolski S, Izmodenov V, & Gloeckler G 2009, SSRv, 143, 177 [Google Scholar]
- Chalov SV, Alexashov DB, McComas D, et al. 2010, ApJL, 716, L99 [Google Scholar]
- Fichtner H, Scherer K, Effenberger F, et al. 2014, A&A, 561, A74 [Google Scholar]
- Florinski V, & Heerikhuisen J 2017, ApJ, 838, 50 [Google Scholar]
- Florinski V, Heerikhuisen J, Niemiec J, & Ernst A 2016, ApJ, 826, 197 [Google Scholar]
- Florinski V, Zank GP, Heerikhuisen J, Hu Q, & Khazanov I 2010, ApJ, 719, 1097 [Google Scholar]
- Funsten HO, Allegrini F, Bochsler P, et al. 2009a, SSRv, 146, 75 [Google Scholar]
- Funsten HO, Allegrini F, Crew GB, et al. 2009b, Sci, 326, 964. [DOI] [PubMed] [Google Scholar]
- Fuselier SA, Allegrini F, Funsten HO, et al. 2009, Sci, 326, 962. [DOI] [PubMed] [Google Scholar]
- Gamayunov KV, Heerikhuisen J, & Rassoul H 2017, ApJ, 845, 63 [Google Scholar]
- Gamayunov K, Zhang M, & Rassoul H 2010, ApJ, 725, 2251 [Google Scholar]
- Giacalone J, & Jokipii JR 2015, ApJL, 812, L9 [Google Scholar]
- Grzedzielski S, Bzowski M, Czechowski A, et al. 2010, ApJL, 715, L84 [Google Scholar]
- Gurnett DA, Kurth WS, Burlaga LF, & Ness NF 2013, Sci, 341, 1489. [DOI] [PubMed] [Google Scholar]
- Heerikhuisen J, Gamayunov KV, Zirnstein EJ, & Pogorelov NV 2016, ApJ, 831, 137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heerikhuisen J, Pogorelov NV, Florinski V, Zank GP, & Kharchenko V 2009, in ASP Conf. Ser. 406, Numerical Modeling of Space Plasma Flows, ed. Pogorelov NV, Audit E, Colella P, & Zank GP (San Francisco, CA: ASP; ), 189 [Google Scholar]
- Heerikhuisen J, Pogorelov NV, Zank GP, et al. 2010, ApJL, 708, L126 [Google Scholar]
- Heerikhuisen J, Zirnstein EJ, Funsten HO, Pogorelov NV, & Zank GP 2014, ApJ, 784, 73 [Google Scholar]
- Isenberg PA 2014, ApJ, 787, 76 [Google Scholar]
- Isenberg PA 2015, JPCS, 577, 012014 [Google Scholar]
- Kucharek H, Fuselier SA, Wurz P, et al. 2013, ApJ, 776, 109 [Google Scholar]
- Lallement R, Quémerais E, Koutroumpa D, et al. 2010, in AIP Conf. Proc. 1216, Twelfth International Solar Wind Conference, ed. Maksimovic M, Issautier K, Meyer-Vernet N, Moncuquet M, & Pantellini F (Melville, NY: AIP; ), 555 [Google Scholar]
- Lindsay BG, & Stebbings RF 2005, JGR, 110, A12213 [Google Scholar]
- Markwardt CB 2009, in ASP Conf. Ser. 411, Astronomical Data Analysis Software and Systems XVIII, eds. Bohlender DA, Durand D, & Dowler P(San Francisco, CA: ASP; ), 251 [Google Scholar]
- McComas DJ, Allegrini F, Bochsler P, et al. 2009a, SSRv, 146, 11 [Google Scholar]
- McComas DJ, Allegrini F, Bochsler P, et al. 2009b, Sci, 326, 959 [Google Scholar]
- McComas DJ, Allegrini F, Bzowski M, et al. 2014a, ApJS, 213, 20 [Google Scholar]
- McComas DJ, Bzowski M, Frisch P, et al. 2010, JGR, 115, A09113 [Google Scholar]
- McComas DJ, Bzowski M, Fuselier SA, et al. 2015, ApJS, 220, 22 [Google Scholar]
- McComas DJ, Christian ER, Schwadron NA, et al. 2018, SSRv, 214, 116 [Google Scholar]
- McComas DJ, Lewis WS, & Schwadron NA 2014b, RvGeo, 52, 118 [Google Scholar]
- McComas DJ, Zirnstein EJ, Bzowski M, et al. 2017, ApJS, 229, 41 [Google Scholar]
- Möbius E, Liu K, Funsten H, Gary SP, & Winske D 2013, ApJ, 766, 129 [Google Scholar]
- Niemiec J, Florinski V, Heerikhuisen J, & Nishikawa K-I 2016, ApJ, 826, 198 [Google Scholar]
- Pogorelov NV, Heerikhuisen J, Zank GP, et al. 2011, ApJ, 742, 104 [Google Scholar]
- Pogorelov NV, Zank GP, Borovikov SN, et al. 2008, in ASP Conf. Ser. 385, Numerical Modeling of Space Plasma Flows, ed. Pogorelov NV, Audit E, & Zank GP (San Francisco, CA: ASP; ), 180 [Google Scholar]
- Schwadron NA, Allegrini F, Bzowski M, et al. 2018, ApJS, 239, 1 [Google Scholar]
- Schwadron NA, Bzowski M, Crew GB, et al. 2009, Sci, 326, 966. [DOI] [PubMed] [Google Scholar]
- Schwadron NA, & McComas DJ 2013, ApJ, 764, 92 [Google Scholar]
- Schwadron NA, Moebius E, Fuselier SA, et al. 2014, ApJS, 215, 13 [Google Scholar]
- Siewert M, Fahr H-J, McComas DJ, & Schwadron NA 2013, A&A, 551, A58 [Google Scholar]
- Sokół JM, Swaczyna P, Bzowski M, & Tokumaru M 2015, SoPh, 290, 2589 [Google Scholar]
- Stone EC, Cummings AC, McDonald FB, et al. 2013, Sci, 341, 150. [DOI] [PubMed] [Google Scholar]
- Summerlin EJ, Viñas AF, Moore TE, Christian ER, & Cooper JF 2014, ApJ, 793, 93 [Google Scholar]
- Swaczyna P, Bzowski M, Christian ER, et al. 2016a, ApJ, 823, 119 [Google Scholar]
- Swaczyna P, Bzowski M, & Sokół JM 2016b, ApJ, 827, 71 [Google Scholar]
- Sylla A, & Fichtner H 2015, ApJ, 811, 150 [Google Scholar]
- Zirnstein EJ, Heerikhuisen J, & Dayeh MA 2018, ApJ, 855, 30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zirnstein EJ, Heerikhuisen J, Funsten HO, et al. 2016, ApJL, 818, L18 [Google Scholar]
- Zirnstein EJ, Heerikhuisen J, & McComas DJ 2015a, ApJL, 804, L22 [Google Scholar]
- Zirnstein EJ, Heerikhuisen J, McComas DJ, & Schwadron NA 2013, ApJ, 778, 112 [Google Scholar]
- Zirnstein EJ, Heerikhuisen J, Pogorelov NV, McComas DJ, & Dayeh MA 2015b, 804, 5 [Google Scholar]
- Zirnstein EJ, McComas DJ, Schwadron NA, et al. 2019, ApJ, 876, 92. [DOI] [PMC free article] [PubMed] [Google Scholar]


