Subcortical substrates of explore-exploit decisions in primates

Summary

The explore-exploit dilemma refers to the challenge of deciding when to forego immediate rewards and explore new opportunities that could lead to greater rewards in the future. While motivational neural circuits facilitate reinforcement learning based on past choices and outcomes, it is unclear if they also support computations relevant for deciding when to explore. We recorded neural activity in the amygdala and ventral striatum of rhesus macaques, as they solved a task that required them to balance novelty driven exploration with exploitation of what they had already learned. Using a partially-bserved Markov decision process model to quantify explore-exploit trade-offs, we identified that the ventral striatum and amygdala differ in how they represent the immediate value of exploitative choices and the future value of exploratory choices. These findings show that subcortical motivational circuits are important in guiding exploratory decisions.

eTOC Blurb

How do we decide when to explore a new opportunity or stick with what we know? Costa et al. reveal that neurons in amygdala and ventral striatum, motivational centers of the brain, help to solve this complex reinforcement learning problem.

Exploration allows humans and animals to learn if novel actions are more valuable than past actions. Deciding when to forego immediate rewards and explore is known as the explore-exploit dilemma (Sutton and Barto, 1998). It is a classic problem in reinforcement learning (RL) and while theoretical solutions exist (Averbeck, 2015; Gittins, 1979; Wilson et al., 2014a), their neural implementation has received limited attention (Cohen et al., 2007; Daw et al., 2006; Frank et al., 2009). Previous studies have focused on the roles of cortical circuits (Beharelle et al., 2015; Blanchard and Gershman, 2018; Daw et al., 2006; Ebitz et al., 2018; Pearson et al., 2009; Sugrue et al., 2004; Zajkowski et al., 2017) and catecholamines (Aston-Jones and Cohen, 2005; Costa et al., 2014; Frank et al., 2009; Warren et al., 2017) in switching between modes of exploration and exploitation. Cortical areas are typically more active in humans and monkeys when they deviate from specified RL policies to explore alternative options. However, without explicit task constraints it is difficult to tell if policy deviations reflect exploration, decision noise, or poor learning (Averbeck, 2015).

Exploration can be made explicit by replacing familiar choice options with novel options. Moreover, novelty seeking is an evolved solution to the explore-exploit dilemma that varies with development and is observed across species (Kidd and Hayden, 2015). Increasing extracellular dopamine levels heightens novelty-driven exploration (Costa et al., 2014) and dopamine neuron responses to novelty decrease with learning (Lak et al., 2016). These results support the hypothesis that dopamine regulates explore-exploit tendencies (Kakade and Dayan, 2002) and suggests that brain regions receiving dopaminergic input, such as the ventral striatum and amygdala mediate novelty-driven exploration. For example, in humans ventral striatum activation tracks novelty related enhancement of reward prediction errors RPEs; (Wittmann et al., 2008) and monkeys with amygdala lesions more readily approach novel stimuli (Burns et al., 1996; Kluver and Bucy, 1939; Mason et al., 2006). Yet motivational circuits are mainly assumed to contribute to exploitative choices (Daw et al., 2006; Frank et al., 2009), given their involvement in associative learning (Averbeck and Costa, 2017) and value-based decision making (Floresco, 2015; Haber and Knutson, 2010).

To determine the computational roles of the amygdala and ventral striatum in explore-exploit decisions, we recorded neural activity from monkeys as they performed a task where explore-exploit trade-offs were induced by introducing novel choices. We used a partially-observed Markov decision process (POMDP) model to derive the optimal policy, quantify the value of exploration and exploitation, and relate these values to the activity of individual neurons. The POMDP formalism is complex, however, the model generates value estimates using a straightforward one-layer neural network of radial basis functions, that has been used extensively to model neural computations (Poggio, 1990; Pouget and Sejnowski, 2001). We found that neuronal activity in the amygdala and ventral striatum not only reflects the immediate value of exploiting what the monkeys had already learned, but also the potential future gains and losses associated with exploration.

Results

Three rhesus monkeys learned to play a multi-arm bandit task (Fig. 1). On each trial, the monkey viewed three choice options assigned different reward values. The monkeys had to learn the stimulus-outcome relationships by sampling each option. However, the number of opportunities they had to learn about the value of each option was limited, as every so often one of the three options was randomly replaced with a novel option. Whenever a novel option was introduced uncertainty about its value was high, because the monkey could not predict its assigned reward probability. In order to reduce uncertainty and learn the value of the novel option, the monkey had to explore it. But in doing so, he gave up the opportunity to exploit what he had learned about the two remaining options.

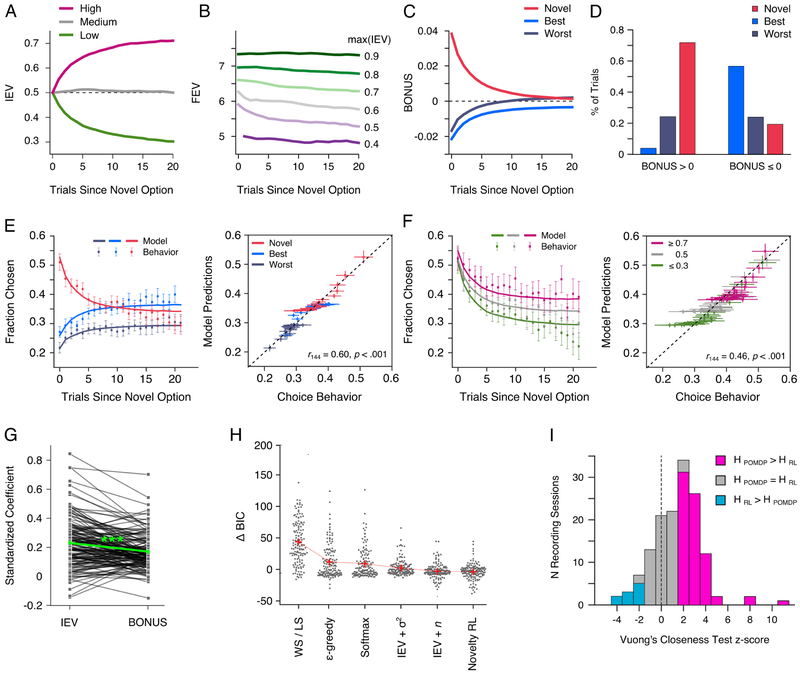
Figure 1. Monkeys managed explore-exploit trade-offs.

(A) Structure of an individual trial in the bandit task. (B) Each block of n trials, up to 650 trials, began with the presentation of 3 novel images. This set, s₁, of visual choice options was repeatedly presented to the monkey for j trials. After a minimum of 10 and up to a maximum of 30 trials, one of the existing options was randomly replaced with a novel image. This formed a new of set options, s₂, that were presented for j trials. The novel option in this set was randomly assigned its own reward probability from a symmetric distribution, {0.2, 0.5, 0.8}. This process of introducing a novel option was repeated up to 32 times within a block. (C) MRI guided reconstruction of recording locations in the amygdala (red) and ventral striatum (blue) projected onto views from a macaque brain atlas (Saleem and Logothetis, 2007). (D) Fraction of times the monkeys chose each option type in terms of the number of trials since the introduction of a novel option (E) The fraction of times the monkeys chose novel options based on their assigned value. (F) The fraction of times, across all trials, the monkeys chose each option type as a function of the empirical reward value of the best alternative option. (G) Choice RTs based on which option was chosen and the number of trials elapsed since a novel option was introduced.

Choice behavior

The monkeys showed a novelty preference (Fig. 1D; Option Type, F(2,138) = 499.35, p<.0001), however, they did transition to choosing the best alternative option (Option Type × Trial, F(2,138) = 145.87, p<.0001). This was a sensible strategy, as the novel option had, on average, a lower expected value (0.5) than the best alternative option (M = 0.64, SD = 0.16). Since every option was novel at one point and was assigned its own reward probability, we also assessed if the monkeys were efficient in exploiting what they learned about each option (Fig. 1E). Despite their novelty preference, the monkeys learned to discriminate between high, medium, and low value options (Reward Value, F(2,126) = 28.88, p<.001; Reward Value × Trial, F(2,126) = 10.27, p<.001).

Across all trials, novelty-driven exploration scaled with opportunity costs (Fig. 1F). As the empirical value of the best alternative option increased, selection of the novel option decreased (β = −0.66, t(144) = −3.8, p<.001). Although, the monkeys were still biased to select the novel option when the best alternative option was rewarded at a high rate (> 0.8; t(131) = 3.06, p=003). Selection of the best alternative mirrored this trend (β = 0.86, t(144) = 3.83, p<.001), whereas selection of the worst alternative was unrelated to the value of the best alternative option (β = −.13, t(144) = −0.32, p=749). Monkeys are known to trade-off information and reward (Blanchard et al., 2015; Bromberg-Martin and Hikosaka, 2009), however, in these previous studies opportunity costs due to information seeking did not affect what the monkeys experienced on future trials.

Analysis of choice reaction times (RTs) indicated that RTs were related to identifying the location of a pre-selected option, rather than value guided deliberation (Fig. S1). Therefore, changes in encoding before or after choice onset should not be interpreted as a pre- or post-decision signal. One exception is when a novel option was introduced, since the monkeys could not anticipate these events. When a novel option was introduced, choice RTs were longer when the monkeys chose the novel option (M = 160.24 ms, SE = 1.84), versus the best (M = 155.87 ms, SE = 2.17) or worst alternative option (M = 154.02 ms, SE = 2.17; F(2,332) = 10.66, p<.001; Fig. 1G). This effect was also seen on the next trial (F(2,332) = 7.76, p<.001), but not on subsequent trials.

Computational modeling of explore-exploit decisions

Optimal policies for managing explore-exploit trade-offs can be modeled using a POMDP. POMDP models are based on estimates of state and action values (see STAR methods). State value is defined as the value of the option with the highest action value among the three available options. The action value, Q (s,a) of each option in the current state is defined in terms of the sum of its IEV and future expected value (FEV). The IEV estimates the likelihood that the current choice will be rewarded based on past outcomes. For example, the initial IEV was the same for novel options assigned a high, medium or low value, and then diverged as the monkeys learned the assigned reward probabilities (Fig. 2A). The FEV is the discounted sum of the number of rewards that can be earned in the future and reflects the richness of the reward environment. For example, the FEV is higher if in the current state the best available option has a high IEV compared to when it has a medium or low IEV (Fig. 2B). This occurs because there is a greater opportunity to earn rewards in the future when the best option has a high IEV (see Fig. S2 for specific examples of how the FEV changes based on the IEV of the available options).

Figure 2. Computational modeling of explore-exploit decisions using a POMDP.

(A) Mean trial by trial changes in the IEV of novel options assigned different reward values (B) Mean trial by trial changes in the FEV, averaged across all three options, as a function of the maximum available IEV. (C) Mean trial by trial changes in the exploration BONUS for each option type (see Fig. S2 for detailed examples) (D) How often the monkeys chose each option type when the exploration BONUS was positive or negative in value. (E and F) The correlation between POMDP model predictions and actual choices based on the option type chosen, E, and the a priori reward probability assigned to each option, F. (G) Parameter estimates used to weight the IEV and exploration BONUS value of chosen and unchosen options in the fitted POMDP model (Table S1). (H) The difference in BIC between alternative choice models and the POMDP model (see STAR Methods and Table S1). (G) Histogram of the number of sessions in which the POMDP model (H_POMDP) better predicted monkeys’ choices than the RL model that incorporated a fixed novelty bonus (H_RL).

The FEV of each option differs based on how many times the monkey has sampled it. On each trial, the difference in the FEV of individual options relative to the average FEV of all three options, quantifies the gain or loss in future rewards associated with choosing each option. We refer to this quantity as the exploration BONUS (e.g. BONUS_novel = EEV_novel − (∑_{j = novel,best,worst} FEV_j)/3. When an option is sampled the monkey becomes more certain about its actual value and the exploration BONUS decreases. Vice versa, foregoing an option increases uncertainty about its value and causes an increase in the exploration BONUS. This dissociation between sampling and habituation is important because over trials it dissociates the exploration BONUS from perceptual novelty. An option must be chosen and not simply seen for its exploration BONUS to decrease. On average, the exploration BONUS was highest when novel options were introduced and decreased over trials as the monkey explored and ascertained the value of the novel option (Fig. 2C; see Fig. S2 for specific examples). In parallel, the exploration BONUS for the alternative options was, on average, negative when a novel option was introduced because the monkeys had already sampled each option and were more certain about their value (Fig. 2C). Thus, choices with a positive BONUS value mostly corresponded to the selection of the novel option, whereas choices with a negative BONUS value mostly corresponded to the selection of the best alternative option (Fig. 2D).

To determine whether the value estimates derived from the POMDP predicted choices, we computed the IEV and BONUS of each choice option, on each trial. Across sessions, there was a negative correlation between the IEV and BONUS value of the chosen options (r = −0.19, t(144) = −18.6, p<0001; Fig. S3). We then passed these value estimates through a softmax function, specifying two free parameters to predict choices (Fig. 2D and F). The IEV and exploration BONUS parameters were both positive and their magnitude differed (Fig. 2G; t(144) = 5.13, p<001; Table S1).

We evaluated the ability of the POMDP model to predict choices against six different exploration heuristics (Fig. 2H). We confirmed that the POMDP model outperformed each alternative model in predicting choice behavior (all p<031; Table S1). The model with the smallest change in its Bayesian information criterion (BIC), relative to the POMDP model, was the RL model that incorporated a fixed novelty bonus (Costa et al., 2014; Djamshidian et al., 2011; Wittmann et al., 2008). Although, there was not a significant difference between the change in the BIC for this model and the model that weighed choices by their IEV and the number of times they had been sampled (t(144) = 0.346, p=731). BIC can be an inconsistent model selection criterion when comparing non-nested models. Thus, for each session, we computed Vuong’s closeness test to ascertain if the POMDP model was preferred to the novelty bonus RL model, under the null hypothesis that both models equally predicted choices. Choices were better fit by the POMDP model in 51% of the recording sessions, whereas the RL model was preferred in only 6.89% of the recording sessions (Fig. 2I; χ² = 58.79, p<0001).

Neurophysiological recordings

We recorded the activity of 329 neurons in the amygdala (195 in monkey H, 59 in monkey F, and 55 in monkey N) and 281 neurons in the ventral striatum (149 in monkey H, 55 in monkey F, and 77 in monkey N; Fig. 1C). We used a sliding window ANOVA to assess the effects of 13 task factors on the activity of individual neurons (see STAR Methods) and found that 83.28% (n = 274) of amygdala neurons and 81.85% (230) of ventral striatum neurons encoded at least one task factor (Table S2). Subsequent percentages are reported as a fraction of these task responsive neurons. Reported effects were consistent across animals, therefore the data were pooled.

Baseline firing rates were higher for amygdala compared to ventral striatum neurons (F(3,603) = 4.41, p= 006), and spike width durations were shorter for ventral striatum compared to amygdala neurons (F(3,606) = 96.7, p<.001). These features are sometimes used to define cell types in the amygdala (Likhtik et al., 2006) and striatum (Apicella, 2017), however, we were unable to detect distinct cell clusters in either region (Fig. S4).

Neural encoding of exploitation and exploration value

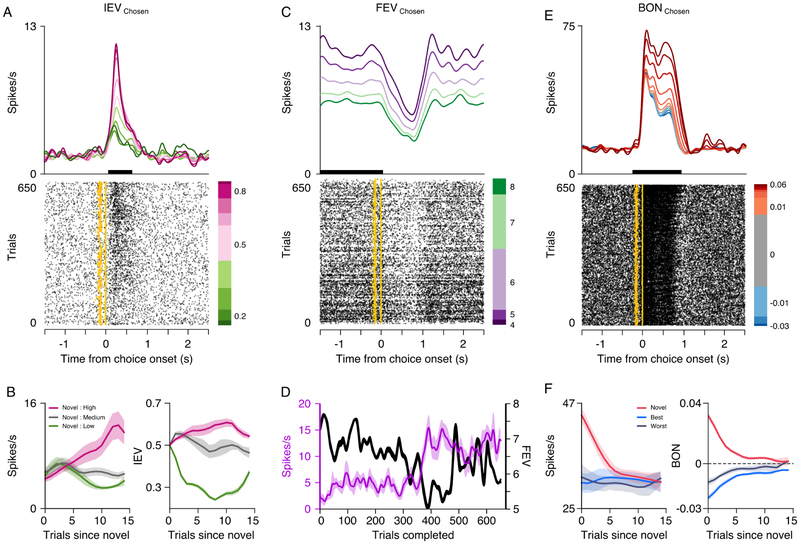
The activity of individual neurons in the amygdala and striatum encoded the POMDP derived value signals. For example, the activity of a neuron we recorded in the ventral striatum was positively correlated with the IEV of the chosen option (Fig. 3A). To illustrate learning related changes in the activity of this neuron, we plotted its mean activity as the monkey learned the value of novel options that were assigned different reward probabilities (Fig. 3B). When a novel option was introduced the activity of the cell did not discriminate between novel options assigned different reward values. As learning progressed, the firing rate of the neuron increased when the monkey chose a high value novel option and decreased when he chose a low value option. This trial-by-trial divergence in the activity of the neuron reflected POMDP derived changes in the IEV for each option (Fig. 3B).

Figure 3. Single cell examples of POMDP derived value encoding.

(A) Spike density function and raster plot depicting the activity of a neuron in ventral striatum encoding the IEV of the chosen option. The amber line indicates choice onset and the amber dots indicate visual onset of the cues. (B) The left panel shows the mean activity of the neuron when the monkey chose novel options assigned different values. Mean responses were averaged over the epoch when the neuron showed significant IEV encoding (black bar in A) and based on a moving average of 3 trials. The right panel shows the corresponding mean IEV of each option derived from the POMDP model. (C) Spike density function and raster plot depicting the activity of a neuron in the amygdala encoding the FEV of the chosen option. (D) Trial to trial changes in the mean activity of the neuron during the baseline epoch when the neuron showed significant FEV encoding (black bar in C) and based on a moving average of three trials. The secondary axis shows the corresponding FEV of the chosen option. (E and F) Same as A and B, for a neuron in the amygdala that encoded the exploration BONUS for the chosen option.

The activity of single neurons in the amygdala and ventral striatum also tracked the FEV of choices. The firing rate of an amygdala neuron we recorded increased when the monkey was limited to choosing a low value option and decreased when they had the opportunity to choose a high value option (Fig. 3C). The observation that FEV was encoded by an overall shift in the baseline firing rate of the neuron is consistent with the FEV changing slowly over trials to track the richness of the reward environment. This was clearly seen when we plotted trial-by-trial changes in the baseline activity of the neuron and the FEV of the chosen option (Fig. 3D).

Individual neurons in the amygdala and ventral striatum also encoded the exploration BONUS. For example, the firing rate of an amygdala neuron we recorded was positively correlated with the exploration BONUS of the chosen option. Its firing rate increased when the monkey explored options associated with future gains (Fig. 3E). When we plotted the activity of the neuron based on which option the monkey chose, it was clear that the firing rate of the neuron was higher when the monkey chose to explore novel choice options, compared to when the monkey chose to exploit the value of alternative options (Fig. 3F, left panel). This pattern of activity reflected the mean model derived changes in the BONUS value of each option type (Fig. 3F, right panel). It is worth noting, this neuron also encoded the number of trials since a novel option was introduced, as well as the number of times an option was chosen. We can differentiate these individual effects, because on a trial-by-trial basis these variables are not strongly correlated (Table S3). Therefore, for this example neuron and all of the neurons we recorded, we can statistically determine if encoding of the exploration BONUS occurs independent of perceptual novelty and other measures of uncertainty.

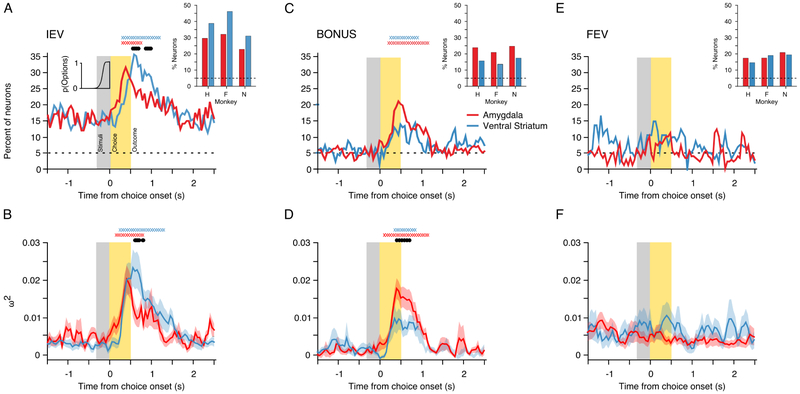
IEV.

Approximately 15-20% of neurons recorded in the amygdala or ventral striatum showed a sustained representation of the IEV during the baseline ITI (Fig. 4A). This is indicative of learning across trials. Once the three choice options were displayed and the monkey chose an option, both populations of neurons exhibited a phasic increase in IEV encoding. In the population of amygdala neurons, IEV encoding peaked just prior to the outcome of the choice (31.8%), whereas among ventral striatum neurons IEV encoding peaked after the trial outcome (35.65%). Thus, a larger percentage of the ventral striatum population encoded the IEV of the chosen option, up to 500 ms after the trial outcome. Whereas the fraction of neurons that significantly encode a variable only indicates whether a neuron encodes that variable relative to a statistical threshold, the strength of encoding is captured by the effect size (ω²; see STAR Methods). The mean effect size was larger in the population of ventral striatum compared to amygdala neurons (Fig. 4B), and based on effect size estimates, phasic increases in IEV encoding occurred earlier in the amygdala (160 ms post-choice) than in the ventral striatum (340 ms).

Figure 4. Population encoding of POMDP derived value signals.

(A) Percentage of task responsive neurons in each region that encoded the IEV of the chosen option. The inset histogram indicates the cumulative RT distribution, averaged across sessions. The inset bar plot indicates the percentage of neurons in each monkey that encoded the IEV of the chosen option, ± 250 ms from the trial outcome. (B) Mean effect size (ω²) in neurons that encoded the IEV of the chosen option in each region. (C and D) Same as A and B for encoding of the exploration BONUS for the chosen option. (E and D) Same as A and B for encoding of the FEV of the chosen option. If present, the X symbols at the top of each panel indicate for each region the time bins where encoding exceeded baseline, while the black symbols indicate a significant difference between the amygdala and ventral striatum (both FWE cluster corrected at p<.05).

BONUS.

In both populations, we observed a phasic increase in encoding of the exploration BONUS that started post-choice and peaked around the trial outcome (Fig. 4C). A larger percentage of neurons in the amygdala (21.17%) encoded the exploration BONUS than in the ventral striatum (14.8%), although this did not reach significance (χ² = 1.91, p=055). Yet, at the time of the trial outcome the mean effect size among these neurons was larger in the amygdala than in the ventral striatum (Fig. 4D). Based on effect size estimates, we also found earlier encoding of the BONUS in the amygdala (150 ms) than in the ventral striatum (260 ms).

We did not observe sustained encoding of the exploration BONUS during the baseline ITI. However, the exploration bonus could already be encoded during the ITI, once a novel option has been introduced for the first time, as we found for IEV encoding. Therefore, we reran our regression analyses excluding trials on which a novel option was introduced. We found that the proportion of each population that encoded the exploration BONUS did not differ based on whether we included or excluded these trials (amygdala: χ² = 0.41, p=819; ventral striatum: χ² = 0.33, p=741).

FEV.

Unlike phasic encoding of the IEV and BONUS of choices, the percentage of neurons in the amygdala and ventral striatum encoding the FEV was constant throughout the trial (Fig. 4E). This is likely because the FEV represents the richness of the reward environment and changes slowly over time. Approximately 10% of the neurons in each population encoded the FEV of the chosen option, with equivalent effect sizes (Fig. 4F). These results are consistent with prior studies indicating that the amygdala encodes changes in the reward environment (Bermudez et al., 2012; Bermudez and Schultz, 2010; Grabenhorst et al., 2016; Saez et al., 2015).

Neural encoding of states and state transitions

Valuing choices in terms of their IEV and relative FEV helps to manage explore-exploit trade-offs, however, derivation of these values would require the monkeys to keep track of the state space and state transitions. In our task, the state and state transitions were defined on each trial by the stimulus identity and IEV of the chosen and unchosen options, and the trial outcome. By maintaining an estimate of how frequently specific stimuli were chosen and rewarded, the monkeys would have the necessary information to calculate both the IEV and exploration BONUS for any given choice. To determine if neurons in the amygdala and ventral striatum encoded information relevant for tracking states and state transitions, we next examined encoding of the stimulus identity and choice outcomes.

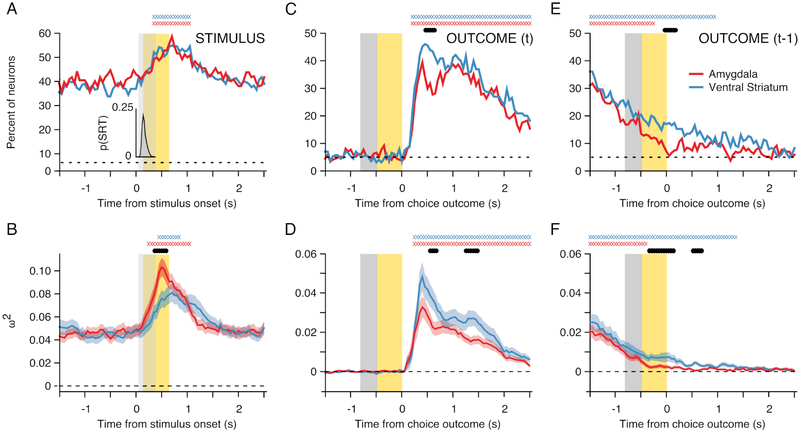
Choice identity.

When we aligned neural activity to the visual onset of the three choice options, the majority of amygdala and ventral striatum neurons encoded the identity of the chosen stimulus (Fig. 5A). The percentage of neurons in each population that encoded choice identity was equivalent. In both the amygdala and ventral striatum, there was sustained encoding of the option that the monkey chose on the current trial during the baseline ITI, before visual onset of the current choice options. As we saw for IEV encoding, this is indicative of learning. There was a phasic increase in choice identity encoding following the visual onset of the choice options, which peaked just after the trial outcome. During this epoch, the effect size among the population of neurons that encoded choice identity in the amygdala was larger than in the ventral striatum (Fig. 5B).

Figure 5. Population encoding of stimulus identity and choice outcomes.

(A) Percentage of task responsive neurons in each region that encoded the stimulus identity of the chosen option. Data were aligned to stimulus onset before analysis. The inset histogram indicates the choice RT distribution following stimulus presentation, averaged across sessions. (B) Mean effect size (ω²) for neurons that encoded the stimulus identity of the chosen option. (C and D) Same as A and B for encoding of the choice outcome on the current trial, except that the data were aligned to the trial outcome before analysis. (E and F) Same as C and D for encoding of the choice outcome that occurred on the previous trial. If present, the X symbols at the top of each panel indicate for each region the time bins where encoding exceeded baseline, while the filled black symbols indicate a significant difference between the amygdala and ventral striatum (both FWE cluster corrected at p<.05).

Current trial and previous trial outcomes.

Neurons in the amygdala and ventral striatum also encoded choice outcomes. The horizontal distance of ventral striatum neurons from the midline predicted the likelihood that they encoded choice outcomes (β = −0.365, χ² = 14.31, p<.001; Fig. S5). Outcome encoding was not spatially organized in the amygdala.

In each region, encoding of the current trial outcome peaked 500 to 750 ms after it occurred. Ventral striatum neurons (46.96%) were more likely to encode the current trial outcome than amygdala neurons (29.2%; χ² = 4.08, p<.001), from 450 to 700 ms after it occurred. At the same time the mean effect size among neurons that encoded the trial outcome, was larger in ventral striatum than in the amygdala (Fig. 5D; t(313) = 2.5, p=0129). The mean effect size was also larger in the ventral striatum versus the amygdala, approximately 1500 ms after the current trial outcome (t(313) = 2.85, p=.0047). This corresponded to when the monkeys re-acquired central fixation in preparation for the next trial.

We also examined how the choice outcomes on the previous trial were encoded during the current trial (Fig. 5E and F). There was persistent encoding of the previous trial outcome during the baseline ITI, in both the amygdala (31.02%) and ventral striatum (36.09%). As the current trial progressed, there was a decrease in encoding of the previous trial outcome in each region. However, when the monkeys received feedback on the current trial, the previous trial outcome was represented more prominently in the ventral striatum (16.27%) than in the amygdala (6.93%; χ² = 4.4, p<.001). While population encoding of the previous trial outcome in the amygdala fell below chance 250 ms prior to the current trial outcome, population coding of the previous trial outcome in ventral striatum neurons persisted into the subsequent ITI. We obtained similar results using effect sizes (Fig. 5F).

Exclusive and overlapped encoding of choice identity, value and outcomes.

While It is clear that neurons in the amygdala and ventral striatum encode state space features, it is not clear if they do so uniquely or in combination. To examine overlapped encoding of choice identity, IEV, and outcome we computed, for each region, the percentage of neurons that exclusively encoded each factor or specific combinations of each factor (Fig. 6). In each region, a sizeable percentage of the neurons exclusively encoded the identity of the chosen option or the trial outcome, but not the IEV of the chosen option (Fig. 6A and B). Rather, neurons that encoded the IEV, usually also encoded the stimulus identity of the chosen option. Combined encoding of choice identity and outcome was also prominent (Fig. 6C and D).

Figure 6. Exclusive and overlapped encoding of choice identity, value, and outcome.

(A and B) The percentage of task responsive neurons in the amygdala, A, and ventral striatum, B, that exclusively encoded the stimulus identity, IEV, or outcome of choices. (C and D) The percentage of task responsive neurons in each region that exhibited complete or partially overlapped encoding of the stimulus identity, IEV, and outcome of choices. The color of each line corresponds to the sets in the inset Venn diagrams.

Neural encoding of alternative task factors.

The location of the chosen option on the screen was unimportant in estimating its value. Nevertheless, neurons in the amygdala (15.1%) and ventral striatum (7%) encoded the screen location of the chosen option (Fig. S6A and B). A greater percentage of amygdala neurons encoded the screen location of the chosen option than in the ventral striatum (χ² = 3.23, p=0013). We also determined that amygdala and ventral striatum neurons similarly encoded the number of trials that had elapsed since the introduction of a novel stimulus (i.e. perceptual novelty; Fig. S6C and D), as well as the number of times the option had been chosen (Fig. S6E and F). Population encoding of the outcome variance (i.e. the variance of the binomial distribution associated with the chosen option, up to the current trial) did not exceed chance.

Decoding of explore-exploit decisions from neural activity in amygdala and striatum

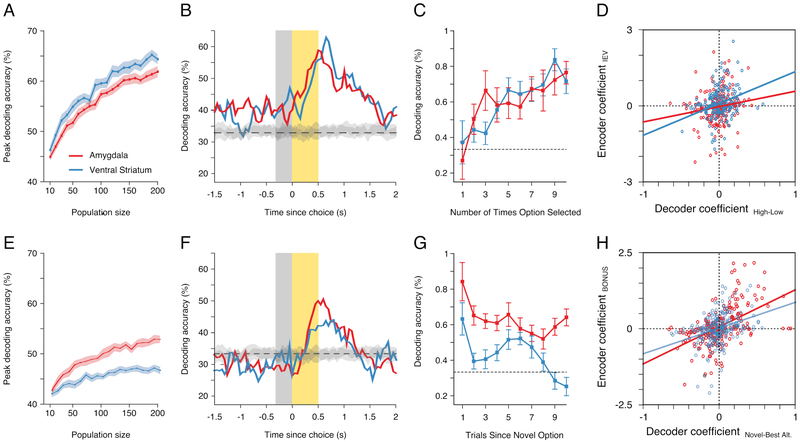
We could predict whether the monkey had chosen a low, medium, or high value option based on the activity of pseudo-populations of amygdala or ventral striatum neurons. Decoding accuracy generally increased with ensemble size, but performance was always higher in the ventral striatum versus the amygdala populations (Fig. 7A). In both regions, decoding accuracy peaked at the trial outcome. In addition, decoding accuracy exceeded chance levels during both the baseline and subsequent ITI, indicative of learning (Fig. 7B). We also found that our ability to decode the a priori reward value of the monkeys’ choices at the time of the trial outcome varied with experience. In both the amygdala and ventral striatum, decoding accuracy was at chance the first time the monkeys sampled an option, but then increased as they continued to sample it and learned its assigned reward value (Fig. 7C).

Figure 7. Decoding of exploitative and exploratory choices.

(A) Decoder accuracy in predicting the a priori assigned reward value of choices as function of pseudo-population size for each region. (B) For each region, the time course of mean decoding accuracy using a pseudo-population of 200 neurons. (C) Mean decoder performance (± 250 ms from the trial outcome) in predicting the a priori assigned reward value of choices, as a function of the number of times an option was selected. (D) For each region, the correlation between the decoder coefficients that discriminated selection of high versus low value options and the encoding coefficients that described learning related changes in IEV of the chosen option. (E and F) Same as A and B, when decoding whether the monkey had chosen the novel, best, or worst alternative option. (G) Mean decoder performance (± 250 ms from the trial outcome) in predicting the which option was chosen, as a function of the number of trials since a novel option was introduced. (H) For each region, the correlation between the decoder coefficients that discriminated selection of novel versus the best alternative options and the coefficient that described encoding of the exploration BONUS. In D and H, each point represents the coefficients for individual neurons.

To confirm that decoding performance was due to learning related changes in neural activity, we examined how the decoder coefficients discriminating the selection of high versus low value options related to the coefficients from our encoding analysis. Specifically, we extracted coefficients that described the relative difference between the current IEV of the chosen option and its a priori assigned reward probability. The decoder coefficients were positively correlated with these IEV coefficients (Fig. 7D; amygdala: r = .15, t(197) = 2.18, p=.039; ventral striatum: r = .26, t(186) = 3.61, p<.001). Among neurons that showed significant IEV encoding, the decoder coefficient distributions did not differ by region (t(178) = 1.1, p=.2723) or deviate from a normal distribution (amygdala: M = −0.03, 95% CI [−0.091, 0.031]; ventral striatum: M = 0.031, 95% CI [−0.002, 0.063]). This implies that neurons were equally likely to code changes in IEV via increases or decreases in firing rates.

We could also predict whether the monkey had chosen the novel, best alternative, or worst alternative option from the activity of separate amygdala and ventral striatum pseudo-populations. Again, decoding accuracy generally increased with ensemble size, but performance was always higher in the amygdala versus the ventral striatum populations (Fig. 7E). In both regions, accuracy peaked shortly after the trial outcome (Fig. 7F) and was highest when a novel option was introduced and declined over subsequent trials (Fig. 7G). This pattern was evident both in the amygdala and ventral striatum.

Next, we determined if our ability to decode which option the monkey chose was due to neural encoding of the exploration BONUS. For each region, we correlated the decoder coefficients that discriminated the selection of the novel versus the best alternative option with BONUS coefficients from our encoding analysis. In each region the two sets of coefficients were positively correlated (Fig. 7H; amygdala: r = .51, t(229) = 9.04, p<.001; ventral striatum: r = .33, t(199) = 4.88, p<.001). However, among neurons that showed significant BONUS encoding, the distribution of decoder coefficients in the amygdala (M = 0.073, 95% CI [−0.003, 0.16]) was positively skewed compared to the distribution of decoder coefficients in the ventral striatum, which were normally distributed (M = −0.017, 95% CI [−0.077, 0.067]; t(208) = 2.56, p=.011). This implies that, on average, amygdala neurons increased their firing rate when the monkey chose a novel option.

Discussion

Cortical encoding of choices is linked to the initiation of specific actions, which suggests that top-down cortical control is necessary for switching between exploratory and exploitative states (Daw et al., 2006; Ebitz et al., 2018; Sugrue et al., 2004; Zajkowski et al., 2017). Our results question that assumption and highlight how exploration can unfold as a continuous process. Parallel valuation of exploratory and exploitative choices is likely also observed in specific cortical areas. The current task explicitly induced explore-exploit trade-offs by introducing novel options, whereas prior studies implicitly induced exploration by drifting option values in restless bandit tasks (Daw et al., 2006; Ebitz et al., 2018; Pearson et al., 2009). Formally, both tasks make exploration valuable by increasing uncertainty. The POMDP model used here can be extended to characterize the immediate and future expected value of choices in restless bandit tasks (Averbeck, 2015). This might help clarify which regions contribute to directed (Beharelle et al., 2015; Zajkowski et al., 2017) versus random exploration (Daw et al., 2006; Ebitz et al., 2018) and establish how cortical and subcortical motivational circuits interact to bias exploration in clinically relevant directions (Addicott et al., 2017; Averbeck et al., 2013a; Morris et al., 2016; Sethi et al., 2018).

Rather than simply treating novel options as intrinsically rewarding (Costa et al., 2014; Djamshidian et al., 2011; Kakade and Dayan, 2002; Wittmann et al., 2008), the monkeys appeared to value options in terms of their immediate and future expected value, in a manner consistent with the POMDP model. The POMDP model characterizes the valuations of an optimal agent that has perfect knowledge of the underlying task statistics. While It is unlikely that the monkeys had a perfect knowledge of the task statistics, they were overtrained on the task which could have led to them developing sophisticated model-based strategies (Costa et al., 2015; Jang et al., 2015; Saez et al., 2015; Seo et al., 2014). To be clear, we do not think the monkeys are implementing forward computations of all possible future outcomes prior to choosing an option. The exponential expansion of the state space in the current task renders direct policy learning intractable. Therefore, the animals likely rely on function approximation to learn efficiently. Neural implementations of basis function networks that support explore-exploit computations may have developed on evolutionary time-scales to allow for learning in dynamic environments. For example, infants have preferences for novelty (Slater et al., 1985) and human abilities to use information about exploration bonuses improves with development (Somerville et al., 2017).

The POMDP model also allows for principled comparisons of how different circuits and regions contribute to explore-exploit decision making in different contexts (Averbeck, 2015). Exploration is sometimes equated to foraging (Addicott et al., 2017; Daw et al., 2006). A fundamental difference between foraging and bandit tasks is that exploration in bandit tasks is driven by uncertainty about future outcomes, whereas exploration in foraging tasks is driven by direct comparisons of the discounted IEV of patches, whose reward distributions are already known (Stephens and Krebs, 1986). Therefore, while discounted MDPs with tractable state spaces can be used to solve foraging tasks, optimal policies for exploration in bandit tasks should be derived using POMDPs. Put another way exploration in bandit tasks requires learning from unobserved events and foraging tasks do not. While the amygdala appears to regulate foraging in aversive environments (Amir et al., 2015; Choi and Kim, 2010) and the ventral striatum contributes to value-based decision making (Floresco, 2015; Haber and Knutson, 2010), these structures might support different computations during foraging tasks than those we have identified here during novelty-driven exploration.

Effective management of explore-exploit trade-offs relies on valuing choice options in terms of their IEV and FEV. This requires that agents keep track of the state space and state transitions, in order to derive these values (Averbeck, 2015). While the orbitofrontal cortex is thought to have a specific role in tracking state spaces (Schuck et al., 2016; Wilson et al., 2014b), population coding in the amygdala also tracks state space variables that describe contextual value encoding (Saez et al., 2015). We also found that population coding in the amygdala and ventral striatum represents the state space of our task. Thus, there is increasing support for the idea that state space representations are not the exclusive purview of cortical regions. This has relevance for studying mechanisms of RL in other animals. Also, despite the prevalent view that the amygdala and ventral striatum compute general value signals, we found little evidence of pure value encoding in either region. This result fits with increasing evidence that value coding in both structures is multidimensional and heterogenous (Cai et al., 2011; Gore et al., 2015; Kyriazi et al., 2018), similar to coding schemes in cortical areas (Rigotti et al., 2013).

There has been considerable focus on the striatum and dopamine system in RL (Costa et al., 2015; O'Doherty et al., 2004; Parker et al., 2016; Schultz, 2015). However, we have recently shown that when visual stimulus-outcome associations underlie choices, that the amygdala plays a fundamental role in RL, comparable to that ascribed to the ventral striatum and dopamine (Averbeck and Costa, 2017; Costa et al., 2016; Rothenhoefer et al., 2017; Taswell et al., 2018). Although it is established that the amygdala (Averbeck and Costa, 2017; Belova et al., 2008; Morrison and Salzman, 2010; Paton et al., 2006) and ventral striatum (Cai et al., 2011; Shidara et al., 1998; Simmons et al., 2007; Strait et al., 2015) represent value, their relative contributions to more complex forms of RL is not well understood. Using a POMDP model to quantify explore-exploit trade-offs, we have identified that ventral striatum and amygdala neurons respectively differ in the strength with which they represent the immediate value of exploitative choices and the future value of exploratory choices.

When the monkeys learned the outcome of their choices, there was a stronger representation of immediate reward value in the ventral striatum compared to the amygdala. Parallel encoding of choice value and outcomes in the ventral striatum establishes a basis for computing RPEs. However, we found that only a small fraction of ventral striatum neurons jointly encoded the IEV of a choice and its outcome. Exclusive encoding of outcomes, or overlapped encoding with specific stimulus features was much more common. These results fit with evidence that ventral striatum inputs onto dopamine neurons exhibit mixed coding of reward and value, rather than direct signaling of RPEs (Tian et al., 2016). It is also worth noting that at the time the monkeys learned about the outcome of their current choice, the outcome of their previous choice was still represented in the ventral striatum. This coding scheme is particularly advantageous when making sequential decisions in a noisy environment (Averbeck, 2017) and suggests that the ventral striatum might play a role in stabilizing value representations during probabilistic RL. For example, the ventral striatum is critical for learning probabilistic stimulus-outcome mappings, but is not necessary for learning deterministic stimulus-outcome mappings (Costa et al., 2016; Taswell et al., 2018).

Population encoding of exploration bonuses was stronger in the amygdala compared to the ventral striatum, and exploratory choices were more readily decoded from the activity of amygdala neurons. This is consistent with the known role of the amygdala in responding to novel or unpredictable events (Bradley et al., 2015; Burns et al., 1996; Camalier et al., 2019; Herry et al., 2007; Hsu et al., 2005; Mason et al., 2006). The exploration bonus derived from the POMDP model quantifies relative uncertainty about the future value of exploring novel options. Integrated encoding in the amygdala of the future value of exploration and the immediate value of exploitation, suggests it plays a key role in deciding when to explore, consistent with its contributions to attentional orienting and salience detection (Bradley, 2009). However, explore-exploit decisions likely rely on multiple neural circuits, rather than specific brain regions or neuromodulators. Amygdala projections to the ventral striatum are known to invigorate reward seeking, support positive reinforcement, and affect dopamine release (Jones et al., 2010; Namburi et al., 2015; Stuber et al., 2011). Future studies should examine if specific circuit interactions between the amygdala and ventral striatum regulate exploratory decision making.

STAR Methods

Contact for Reagent and Resource Sharing

Further information and requests for resources should be directed to and will be fulfilled by the Lead Contact, Vincent Costa (costav@ohsu.edu).

Experimental Model and Subject Details

Three experimentally naive adult male rhesus macaques (Macca mulatta), monkeys H, F, and N served as subjects. Their ages and weights at the start of training ranged between 6-8 years and 7.2-9.3 kg. Animals were pair housed when possible, had access to food 24 hours a day, were kept on a 12-h light-dark cycle, and tested during the light portion of the day. On testing days, the monkeys earned their fluid through performance on the task, whereas on non-testing days the animals were given free access to water. All procedures were reviewed and approved by the NIMH Animal Care and Use Committee.

Method Details

Experimental Setup

Monkeys were trained to perform a saccade-based bandit task for juice rewards. Stimuli were presented on a 19-inch LCD monitor situated 40 cm from the monkey’s eyes. During training and testing monkeys sat in a primate chair with their heads restrained. Stimulus presentation and behavioral monitoring were controlled by a PC computer running Monkeylogic (Asaad and Eskandar, 2008), a MATLAB-based behavioral control program. Eye movements were monitored using an Arrington Viewpoint eye tracker (Arrington Research, Scottsdale, AZ) and sampled at 1kHz. On rewarded trials a fixed amount of undiluted apple juice (0.08-0.17 mL depending on each monkey’s level of thirst) was delivered through a pressurized plastic tube gated by a computer controlled solenoid valve (Mitz, 2005).

Task Design and Stimuli

The monkeys were trained to completed up to 6 blocks per session of a three-arm bandit choice task (Fig. 1). The task design was based on a multi-arm bandit task previously used in humans and monkeys to study explore-exploit trade-offs (Costa et al., 2014; Djamshidian et al., 2011; Wittmann et al., 2008). Each block consisted of 650 trials, in which the monkey had to choose among three images that were probabilistically associated with juice reward. On each trial, the monkey had to first acquire and hold central fixation for a variable length of time (250-750 ms). After holding fixation, three peripheral choice targets were presented at the vertices of a triangle. The main vertex of the triangle either pointed up or down on each trial and the locations of the three stimuli were randomized from trial-to-trial. The animals were required to saccade to and maintain fixation on one of the peripheral choice targets for 500 ms. We excluded trials on which the monkey attempted to saccade to more than one choice target (<1% of all trials). After this response, a juice reward was delivered probabilistically. Within a single block of 650 trials, 32 novel stimuli were introduced. When a novel stimulus was introduced it randomly replaced one of the existing choice options, under the criterion that no single choice option could be available for more than 160 consecutive trials. The trial interval between the introduction of two novel stimuli followed a discrete uniform distribution, t ∈ [10,30].

At the start of a block, the three initial choice options were randomly assigned a reward probability of 0.2, 0.5 or 0.8. Novel choice options were randomly assigned one of these reward probabilities when they were introduced. The assigned reward probabilities were fixed for each stimulus. The only constraint was that no more than two of the three options could be assigned the same reward probability. This allowed for rare instances when the IEV of the two remaining alternative options was equivalent, and as a result the value of the novel choice option could be inferred without exploration. These scenarios were infrequent (M = 6.2% of trials per session) and the monkeys’ novelty seeking behavior did not reflect such an inference (Fig. S7). Thus, we proceeded under the assumption that uncertainty about option values motivated the monkeys to explore novel choice options.

The stimuli were naturalistic scenes downloaded from the website Flickr (www.flickr.com). The images were screened for image quality, discriminability, uniqueness, size, and color to obtain a final daily set of 210 images (35 images per block and up to 6 blocks). Images were never repeated across sessions. To avoid choices driven by perceptual pop out, choice options were spatial frequency and luminance normalized using functions adapted from the SHINE toolbox for MATLAB (Willenbockel et al., 2010).

Neurophysiological Recordings

Before data acquisition, monkeys were implanted with titanium headposts for head restraint. In a separate procedure, monkeys were fit with custom 28 × 36 mm chambers oriented to allow bilateral vertical grid access to the amygdala and ventral striatum. Chamber placements were planned and verified through MR T1 scans of grid coverage with respect to the amygdala and ventral striatum.

In all three animals, we recorded simultaneously from each structure using single tungsten microelectrodes (FHC, Inc. or Alpha Omega; 0.8-1.5 MΩ at 1 kHz). Up to four electrodes were lowered into each structure. The electrodes were advanced to their target location by an 8-channel micromanipulator (NAN Instruments, Nazareth, Israel) that was attached to the recording chamber. Additional MR T1 scans with lowered electrodes were performed to verify recording trajectories (Fig. 1C). Multichannel spike and local field potential recordings were acquired with a 16-channel data acquisition system (Tucker Davis Technologies, Alachua, FL). Spike signals were amplified, filtered (0.3-8kHz), and digitized at 24.4 kHz. Spikes were initially sorted online on all-channels using real-time window discrimination. Digitized spike waveforms and timestamps of stimulus events were saved for sorting offline. Offline sorting was based on principal-components analysis, visually differentiated waveforms, and inter-spike interval histograms. All units were graded according to isolation quality and multiunit recordings were discarded. Neurons were isolated while the monkeys viewed a nature film and before they engaged in the bandit task. Other than isolation quality, there were no selection criteria for deciding whether to record a neuron.

Amygdala recordings primarily targeted the basolateral and central nuclei, based on MR guided reconstruction of each recording site (Fig. 1C). All amygdala recordings were between 18 and 22 mm anterior to the interaural plane. Ventral striatum recordings targeted the vicinity of striatum below the internal capsule. All ventral striatum recordings were anterior to the appearance of the anterior commissure and between 23 and 28 mm anterior to interaural plane.

Quantification and Statistical Analysis

Partially Observable Markov Decision Process Model

We modeled the task using a finite horizon, discrete time, discounted, partially observable Markov decision process (POMDP), details of which were published previously (Averbeck, 2015). The utility, u, of a state, s, at time t is

$$u_t(s_t)=ma{x}_{a\in A_{s_t}}\{r(s_t,a)+\gamma {\sum }_{j\in S}p(j\mid s_t,a)u_{t+1}(j)\}$$ (1)

where A_st is the set of available actions in state s at time t, r(s_t, a) is the reward that will be obtained in state s at time t if action a is taken. The summation on j is taken over the set of possible subsequent states, S at time t+1. It is the expected future utility, taken across the transition probability distribution p(j∣S_t, a). The transition probability is the probability of transitioning into each state j from the current state, s_t if one takes action a. The γ term represents a discount factor, set to 0.9 for the current analyses. The terms inside the curly brackets are the action value, Q(s_t, a) = r(s_t, a) + γ∑_j∈s p(j∣s_t, a)u_t+1 (j), for each available action. We define three acronyms that we use throughout the manuscript to refer to specific terms in this equation. The immediate expected value (IEV) is the first term in the utility function IEV = r(s_t, a). The future expected value (FEV) is the second term, FEV = γ∑_j∈s p(j∣s_t, a)u_t+1 (j) and the exploration bonus is the FEV of a given choice, a, relative to the average FEV: BONUS(a) = FEV(a)−(∑_j=1:3 FEV(j))/3.

The utilities were fit using the value iteration algorithm (Puterman, 1994). This algorithm proceeds as follows. First, the vector of utilities across states, v⁰, was initialized to random values. We set the iteration index, n = 0. Then computed:

$$v^{n+1}=ma{x}_{a\in A_{s_t}}\{r(s,a)+\gamma {\sum }_{j\in S}p(j\mid s_t,a)v^n(j)\}.$$ (2)

After each iteration we calculated the change in the value estimate, Δv = vⁿ⁺¹ − vⁿ, and examined either ∥Δv∥ <∈ or span(Δv) < ∈. The span is defined as span(v) = max_s∈S v(s) − min_s∈S v(s). We also used approximation methods for the value function as the state space was intractable over relevant time horizons. For this we used a b-spline basis functions (Hastie et al., 2001), and approximated the utility with

$$\widehat{v}(s)={\sum }_{i=1}^M{a}_i{\varphi }_i(s).$$ (3)

We used fixed basis functions so we could calculate the basis coefficients, a_i, using least squares techniques. We assembled a matrix Φ_i,j = ϕ_i(s_j), which contained the values of the basis functions for specific states, s_j. We then calculated a projection matrix

$$H=\Phi ({\Phi }^{\prime }\Phi {)}^{-1}{\Phi }^{\prime }$$ (4)

and calculated the approximation

$$\widehat{v}=H\mathit{v}.$$ (5)

The bold indicates a vector over states, or the sampled states at which we computed the approximation. When using the approximation in the value iteration algorithm, we first compute the approximation, $\widehat{v}$ . We then plug the approximation into the right hand side of equation 2, $v^{n+1}={\mathit{max}}_{a\in A_{s_t}}\{r(s,a)+\gamma {\sum }_{j\in s}p(j\mid s_t,a){\widehat{v}}^n(j)\}$. We then calculate approximations to the new values ${\widehat{\mathit{v}}}^{\mathit{n}+1}=H{\mathit{v}}^{\mathit{n}+1}$. This is repeated until convergence.

The novelty task is a three-armed bandit task. The options are rewarded with different probabilities, but the amount of reward is always 1. The reward probabilities for each bandit are stationary while that option is available. On each trial there is a 5% chance that one of the bandit options will be replaced with a new option. We have previously modeled this task with a truncated time horizon (Averbeck et al., 2013a). However, the exploration bonus increases with increasing time horizon. Therefore, we developed an approach that allowed us to examine longer time horizons. The underlying model is a discrete MDP. The state space is the number of times each option has been chosen, and the number of times it has been rewarded, s_t = R₁, C₁, R₂, C₂, R₃, C₃. Note that one could model the task assuming that the animal was trying to infer whether the underlying reward associated with each option was 0.2, 0.5 or 0.8, instead of a binomial probability. However, there would be no exploration bonus in this case if there was a 0.8 option in the array. As animals do explore in this case, the binomial assumption is more appropriate.

This state space was approximated using a continuous approximation sampled discretely. The immediate reward estimate is given by the maximum a-posteriori estimate, $r(s_t,a=i)=\frac{r_i+1}{c_i+2}$. The set of possible next states, s_t+1, is given by the chosen target, whether or not it is rewarded, and whether one of the options is replaced with a novel option (Averbeck et al., 2013b). Thus, each state leads to 21 unique subsequent states. We define q_i = r_t(s_t, a = i), and p_switch = 0.05, as the probability of a novel substitution. The transition to a subsequent state without a novel choice substitution and no reward is given by:

$$p_t(...,C_i+1,R_i,\dots \mid s_t=[...,C_i,R_i,...],a=\mathit{choose}i)=(1-q_i)(1-p_{\mathit{switch}})$$

and for reward by

$$p_t(...,C_i+1,R_i+1,...\mid s_t=[...,C_i,R_i,...],a=\mathit{choose}i)=q_i(1-p_{\mathit{switch}}).$$

When a novel option was introduced, it could replace the chosen stimulus, or one of the other two stimuli. In this case if the chosen target, i, was not rewarded and a different target, j, was replaced, we have

$$p_t(...,C_i+1,R_i,C_j=0,R_j=0\mid s_t=[...,C_i,R_i,...],a=\mathit{choose}i)=(1-q_i)p_{\mathit{switch}}∕3$$

and if the chosen target was not rewarded and was replaced

$$p_t(...,C_i=0,R_i=0,...\mid s_t=[...,C_i,R_i,...],a=\mathit{choose}i)=(1-q_i)p_{\mathit{switch}}∕3.$$

And correspondingly, following a reward and replacement of a different target, j, we have

$$p_t(...,C_i+1,R_i+1,C_j=0,R_j=0\mid s_t=[...,C_i,R_i,...],a=\mathit{choose}i)=q_i{p}_{\mathit{switch}}∕3$$

and

$$p_t(...,C_i=0,R_i=0,...\mid s_t=[...,C_i,R_i,...],a=\mathit{choose}i)=q_i{p}_{\mathit{switch}}∕3.$$

Note that when a novel option is substituted for the chosen stimulus, the same subsequent state is reached with or without a reward.

Data analysis

Choice behavior.

We quantified choice behavior during the explore-exploit task in two ways. We first computed the fraction of times the monkey chose either the novel choice option, best alternative option, or worst alternative option up to 20 trials after a novel option was introduced. The best alternative option was defined as the remaining option with the highest IEV. In cases in which the remaining alternative options had equivalent IEVs, the best alternative was defined as the option with the higher action value as estimated by the POMDP model. We also computed the fraction of times the monkeys chose novel options based on their a priori assigned reward probabilities, up to 20 trials after they were introduced. Choice estimates were computed for each recording session, arcsine transformed, and entered into mixed effects ANOVAs that specified trials, monkey identity, and either option type or reward probability as fixed effects. The testing session was hierarchically nested under monkey identity and specified as a random effect.

We also constructed models to predict, trial-by-trial, the monkeys’ choices using the POMDP value estimates. The POMDP choice model predicted the monkeys’ choice with two parameters:

$$p_{{}_{\mathit{MDP}}}(a_i)=\frac{\text{exp}(b_1{\mathit{IEV}}_i+b_2{\mathit{BONUS}}_i)}{{\sum }_{j=1}^3\text{exp}(b_1{\mathit{IEV}}_j+b_2{\mathit{BONUS}}_j)}$$ (6)

The performance of the POMDP model was compared to several alternative heuristics (Kakade and Dayan, 2002; Kuleshov, 2000; Steyvers, 2009).

Win-stay/lose-shift.

Under this heuristic the monkeys randomly choose an option on the first trial, then on subsequent trials choose the same option if their previous choice was rewarded, or randomly switch to choosing a different option if their previous choice was not rewarded. This model has the likelihood function:

$$p_{{}_{\mathit{WSLS}}}(a_i)=\left\{\begin{array}{cc}\hfill \lambda \hfill & \hfill a_{t-1}=i\text{and}{R}_{t-1}=1\hfill \\ \hfill (1-\lambda )∕(N-1)\hfill & \hfill a_{t-1}\ne i\text{and}{R}_{t-1}=1\hfill \\ \hfill 1-\lambda \hfill & \hfill a_{t-1}=i\text{and}{R}_{t-1}=0\hfill \\ \hfill \lambda ∕(N-1)\hfill & \hfill a_{t-1}\ne i\text{and}{R}_{t-1}=1\hfill \end{array}\right\}$$ (7)

ε-greedy.

This choice rule (Sutton & Barto, 1998) exploits the arm with the maximum expectancy with probability 1 - ε, and with probability ε chooses randomly from the remaining two options. This model has the likelihood function:

$$p_{\epsilon -\mathit{greedy}}(a_i)=\left\{\begin{array}{cc}\hfill 1-\mathrm{\epsilon }\hfill & \hfill if{\mathit{IEV}}_i(t)>{\mathit{IEV}}_k(t),\forall i\ne k\hfill \\ \hfill \mathrm{\epsilon }∕2\hfill & \hfill otherwise\hfill \end{array}\right\}$$ (8)

Fixed softmax.

This choice rule (Luce, 1959; Sutton & Barto, 1998) picks each option proportional to its IEV. Arms with a greater expected value are chosen with a higher probability. The randomness of choice is controlled by the inverse temperature parameter, β In this case β can take values along the entire real line, with values greater than or equal to 1 indicating consistent selection of the most valuable option and values less than 1 indicating increasingly random choices. This model has the likelihood function:

$$p_{\mathit{softmax}}(a_i)=\frac{\text{exp}(\beta {\mathit{IEV}}_i(t))}{{\sum }_{i=1}^3\text{exp}(\beta {\mathit{IEV}}_i(t))}$$ (9)

Combined weighting of IEV and outcome uncertainty for individual options (IEV + σ²).

Under this heuristic we constructed a model to predict, trial-by-trial, the monkeys’ choices based on the IEV and reward variance for each of the three options. The reward variance was modeled as a binomial distribution, np_i(1-p_i) wherep_i is the IEV for option i, and n is the number of times an i has been sampled. For novel options we assumed a Beta(1,1) prior. The model predicted the monkeys’ choice with two parameters (b₁, b₂):

$$p_{\text{IEV}+{\sigma }^2}(a_i)=\frac{\text{exp}(b_1{\mathit{IEV}}_i+b_2{{\sigma }^2}_i)}{{\sum }_{i=1}^3\text{exp}(b_1{\mathit{IEV}}_i+b_2{{\sigma }^2}_i)}$$ (10)

Combined weighting of IEV and the number of times an option was sampled (IEV + n).

Under this heuristic we constructed a model to predict, trial-by-trial, the monkeys’ choices based on the IEV of each option, i, and the number of times, n, it was sampled up to the current trial, t. The model predicted the monkeys’ choice with two parameters (b₁, b₂):

$$p_{\text{IEV}+n}(a_i)=\frac{\text{exp}(b_1{\mathit{IEV}}_i+b_2{n}_i)}{{\sum }_{i=1}^3\text{exp}(b_1{\mathit{IEV}}_i+b_2{n}_i)}$$ (11)

Reinforcement learning model with a novelty bonus.

In this model values were updated trial-by-trial according to:

$$v_i(t+1)=v_i(t)+\alpha (R-v_i(t))$$ (12)

These value estimates were then passed through a soft-max function to generate choice probabilities:

$$p_{\mathrm{Novelty}\mathrm{RL}}(a_i)=\frac{\text{exp}(\beta v_i(k))}{{\sum }_{j=1}^3\text{exp}(\beta v_j(k))}$$ (13)

The parameter α is a learning rate parameter, and β is an inverse temperature, or choice consistency parameter. In addition, when a novel option was introduced, its value was set to a fixed constant, which was also floated as a free parameter, v_novel. The predictions of the two models, p_MDP (a_i) and P_h−RW (a_i) were optimized using the fminsearch function in MATLAB. The fits were then compared by computing the BIC for each model (Hastie et al., 2001) and Vuong’s closeness test (Vuong, 1989). The POMDP model had two free parameters whereas the RL model that incorporated the novelty bonus had three free parameters (α, β, v_novel.

Neural data.

To identify task-related neurons, all trials on which monkeys chose one of the three stimuli were analyzed. Trials in which the monkey broke fixation, failed to make a choice, or attempted to saccade to more than one option were excluded (<1% of all trials). On valid trials, the firing rate of each cell was computed in 200 ms bins, advanced in 50 ms increments, time locked to the monkey’s initiation of a saccade to the chosen option. We fit a sliding window fixed-effects ANOVA model to these windowed spike counts. The ANOVA included factors for the IEV, BONUS, FEV, and stimulus identity of the chosen option, the outcome of the current trial, the outcome of the previous trial, the number of trials since a novel option was introduced, the number of times the chosen option was sampled, the outcome variance of the chosen option, the screen location of the chosen option, the display orientation of the three options, and residuals from our task-based analysis of choice reaction times. The IEV of choices was modeled as two factors: the a priori reward value of the option, modeled as a nominal variable (i.e. high, medium, and low), and the difference between the current empirical IEV of the chosen option and its assigned reward probability, modeled as a continuous factor. The latter factor served to model value updating. All plotted effects of IEV were significant for one or both factors. Stimulus identity was nested under the nominal IEV factor. This allowed us to model separate effects of reward value and stimulus identity on neural activity. FEV, BONUS, trial effects, and residual choice RTs were modeled as continuous factors. All other factors were modeled as nominal variables.

In order to correct for multiple comparisons, we controlled the familywise error rate using permutation tests. ANOVA models were fit for each neuron 100 times per factor. In each permutation, trial labels or values for the factor of interest were randomly shuffled and the ANOVA results recomputed. The temporal order of the neural data was maintained and with nearby bins assumed to be dependent. The value of the largest number of consecutive bins that were significant for the factor of interest (p<05) was retained and used to generate a null distribution to determine the critical cluster size for each factor (95^th percentile). For individual factors this ranged between 5 and 10 consecutive bins.

Decoding analyses.

The decoding analyses were carried out on pseudo-populations of neurons that were, mostly, non-simultaneously recorded. We used a linear Gaussian classifier for all analyses. Because the analyses were based on pseudo-populations of non-simultaneously recorded neurons, we used a diagonal covariance matrix. The neural activity encoded multiple task factors that were not all orthogonal to the factors we wanted to decode. Therefore, we first reran ANOVAs for individual neurons, dropping the variable we wanted to decode. Thus, when we decoded reward value, we dropped the two IEV factors from the ANOVA model, reran the ANOVA with the remaining variables, and computed the residual. We then carried out the decoding analysis on these residuals. Similarly, when we decoded option type, we dropped BONUS from the ANOVA model, and recalculated the residual. We then assembled pseudo-populations of cells recorded across sessions and decoded either the a priori reward value of choices (i.e. high, medium or low reward probability), or the chosen option type (i.e. novel, best alternative or worst alternative option). Therefore, for both analyses chance performance was 33%. For each cell we used at least 200 trials, across all three conditions. Analyses were carried out using leave-one trial out cross validation. The model was fit with the remaining trials and tested on the trial that was held out of the analysis. This analysis was carried out on 100 pseudo populations of each size, assembled by sampling, without replacement, from the larger population.

Data and Software Availability

Analysis-specific code and data are available by request to the Lead Contact.

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Experimental Models: Organisms/Strains
Rhesus macaques (Macaca mulatta)	NIMH/NIH	N/A
Software and Algorithms
Monkeylogic	Asaad, W.F., Eskandar, E.N. (2008). A flexible software tool for temporally-precise behavioral control in Matlab. J Neurosci Methods. 174, 245–258. doi: 10.1016/j.jneumeth.2008.07.014.	https://www.brown.edu/Research/monkeylogic/
MATLAB	Mathwords	https://www.mathworks.com/products/matlab.html
SHINE	Willenbockel, V., Sadr, J., Fiset, D., Horne, G.O., Gosselin, F., and Tanaka, J.W. (2010).      Controlling low-level image properties: the SHINE toolbox. Behavior research methods 42, 671-684. doi: 10.3758/BRM.42.3.671	http://www.mapageweb.umontreal.ca/gosselif/SHINE/

Highlights.

Monkeys use sophisticated choice strategies to manage explore-exploit tradeoffs

Amygdala and ventral striatum neurons code both exploratory and exploitive choices

Task states and state transitions are encoded in the amygdala and ventral striatum